A bioinspired snap-through metastructure for manipulating micro-objects

Abstract

Micro-objects stick tenaciously to each other—a well-known show-stopper in microtechnology and in handling micro-objects. Inspired by the trigger plant, we explore a mechanical metastructure for overcoming adhesion involving a snap-action mechanism. We analyze the nonlinear mechanical response of curved beam architectures clamped by a tunable spring, incorporating mono- and bistable states. As a result, reversible miniaturized snap-through devices are successfully realized by micron-scale direct printing, and successful pick-and-place handling of a micro-object is demonstrated. The technique is applicable to universal scenarios, including dry and wet environment, or smooth and rough counter surfaces. With an unprecedented switching ratio (between high and low adhesion) exceeding 10⁴, this concept proposes an efficient paradigm for handling and placing superlight objects.

Nature teaches us how to design reliable grippers for moving and placing super-small objects that tend to stick to everywhere.

INTRODUCTION

Nature has evolved enviable materials architectures with programmable response to ensure survival (1). A prominent example is the so-called snap-through elastic instability, which allows, for example, the Venus flytrap to catch prey by closing its leaves (2), the hummingbird to elastically snap the beak to catch insects (3), or the Australian triggerplant Stylidium to immobilize and pollinate insects when touched (Fig. 1A) (4). Inspired by such powerful actuation mechanisms, applications include inflatable soft jumpers (5), bistable valves for autonomous control (6), bifurcation-based embodied logic (7), wave transition with bidirectionality (8), stable memory with reprograming ability (9), multistable inflatable origami (10), and devices to absorb energy under dynamic impact (11) or to tailor the mechanical behavior (12). To trigger the snap-through, stimuli such as swelling (7), hydraulic or pneumatic control (5, 6, 13), dielectric (14, 15), and temperature (16, 17) have been reported. Here, we present a bioinspired design that derives heuristically from the phenomenon that the triggerplant Stylidium uses for pollination by snap-through action and for solving a crucial problem in microrobotic handling: the release and placement of superlight objects that, for dimensional reasons, tend to stick tenaciously to other surfaces.

Fig. 1. Concept of the bioinspired two-way switchable adhesive based on a curved beam with tunable boundary condition.

(A) Release of elastic energy for dynamic pollination of the triggerplant (Stylidium). (B) Schematic demonstrating the switching principle derived. At small compressive preloads, the object is picked up and then moved to a new position. For release, higher loading induces the snap-through bistability. Upon release, the system relaxes back to its original shape. Insets represent the force analyses that include the weight of the object, F_g and the adhesive force, F_ad. (C) Schematic of the curved beam model with a fully (left) and partially (right) clamped end. The horizontal displacement of the right end is constraint by a spring with stiffness, k. When the applied normal displacement, d, is exerted at the center of the beam, the length of the beam changes from L₀ to L. (D) The two limiting boundary conditions lead to either monostable (k = 0) or bistable (k = ∞) response. (E) Normalized force-displacement and (F) elastic strain energy-displacement curves of a curved beam with the shape parameters L₀ = 24 mm, h/L₀ = 0.2, h/t = 4.8, and b = 6 mm. The normalized stiffness of the spring $\overline{k}=k{L}_0^3/EI$ was 200 (yellow), 700 (green), and 20,000 (purple). Solid lines represent the analytical solutions, and the dot-dashed lines represent the results of the finite element analysis (FEA). (G) Design map for monostable (yellow and green) and bistable (purple) response in terms of the normalized stiffness $k{L}_0^3/EI\in [10^2,10^5]$ and the shape parameter h/L₀ ∈ [0.03,0.33]. Blue circles correspond to the individual curves shown in (D) and (E).

A prerequisite for the occurrence of a snap-through instability is the existence of bi- or metastable states. Two common designs that have been well studied are the curved beam (18–23) and the curved shell (5, 24, 25). By using beam and shell theories, the mechanical responses including force-displacement and pressure-volume relationships have frequently been investigated. However, an open question is the impact of varying boundary conditions on the snap-through bistability and the formulation of explicit conditions for the transition from mono- to bistable states. The application of such a transition between two different mechanical responses could constitute a switching strategy, e.g., for innovative adhesive grippers that are actuated by robotic systems (26).

Switchable adhesives are programmable systems exhibiting an “on” state—for adhering to the target object—and an “off” state—for the release on demand (27). Existing concepts rely on electric and electromagnetic (28–31), chemical (32–34), thermal (35, 36), and mechanical inputs (37–42). Most of them, however, are based on specific responsive materials or function only in combination with subsidiary devices, both of which enhance the complexity of the adhesive system and are difficult to integrate into microsystems. An exception is the purely mechanical release that can be integrated into the trajectory of a robotic system without further equipment. Examples include compression-induced detachment via buckling (37–42) and the shear actuation of unidirectional adhesives (43–47). Intriguingly, we learn that the fast movement of the column of the triggerplant is evoked by external mechanical stimuli, i.e., the touching by the nectar-gathering insects (Fig. 1A). The pollen is then released from the column, which inspires us to release the micro-objects in a similar way without requiring additional means like heat, chemical, electric/magnetic-field generators, etc.

In this work, we use a metastructure concept to create a snap-through instability for gripping and releasing microscopic objects. The approach is based on the tuning of boundary conditions for the snap-through instability, which allows a reversible transition from mono- to bistability. The metastructure design consists of three parts: a rigid frame, a laminated spring, and a curved beam (U-shaped) unit (Fig. 1B). During the pick-and-place process, as shown in the schematic in Fig. 1B, the rigid frame tunes the boundary condition of the curved beam unit from “compliant” to “stiff” in conjunction with the compression load. Thus, because of the triggering of the snap-through of the curved beam, the contact area between the curved beam and the target object separates, resulting in the releasing action. Thereafter, the compressed laminated spring pushes the curved beam out of the rigid frame for cyclic operation of the metastructure. First, we theoretically analyze a curved beam model with tunable boundary conditions (Fig. 1C), i.e., a fully and a partially clamped end, where the latter is confined by a spring with a given stiffness. We systematically investigate and optimize the evolution of the force-displacement response of the curved beam and validate our theoretical model with numerical simulations and experiments. Then, we design a two-way switchable adhesive as a general platform for reversibly switching between mono- and bistability. Last, a two-photon direct writing is used to downscale the design for handling superlight objects with smooth and rough surfaces and under versatile circumstances including dry and underwater conditions.

RESULTS

Snap-through of a curved beam with tunable boundary conditions

To analyze the snap-through instability, we introduce a model involving a stress-free beam with a curved profile described by the following equation (black dashed curve in Fig. 1C)

$$w_0=-\frac{h}{2}\cos \frac{2\mathrm{\pi }x}{L_0}+\frac{h}{2}$$ (1)

where L₀ is the segment length of the curved beam, and h is the maximum lateral deflection. By t and b, we denote the beam in-plane and out-of-plane thicknesses. The in-plane thickness of the beam geometry is obtained by offsetting the deflection profile w₀ with the distance t along the normal direction of the beam profile. The left end of the beam is fully clamped, while the right end is constrained by a spring with stiffness k, which enables one lateral degree of freedom. An external vertical force f is applied at the center of the beam and creates a displacement of that position denoted as d. The spring attached to the beam can induce opposite scenarios for d = 2h at an external force f set to 0: (i) For k = 0, the curved beam bounces back to the original geometry, whereas (ii) for k = ∞, it stays in the second stable position (Fig. 1D).

Both scenarios were proven by experimental demonstrations and mechanical tests displayed in fig. S1. For this purpose, a curved beam, which was connected to a trilateral U-shaped frame, was fabricated from a polyurethane (PU) elastomer with a modulus of 20 MPa (see methods in the Supplementary Materials). This configuration will be referred to as the curved beam unit (fig. S1A). Figure S1A depicts that the side walls of the frame expanded outward (white arrows) during downward compression of the beam center point, representing the boundary condition of a soft spring with a small stiffness k. After removing the imposed force, the curved beam returned to its initial geometry, which corresponds to a monostable behavior. In contrast, when confining the curved beam unit within a mechanically stiffer frame, the deformed beam remained in a new stable position, which corresponds to a bistable behavior (fig. S1B). The rigid frame drastically enhanced the spring stiffness in comparison to the first scenario. Recorded force-displacement curves experimentally supported the transition from the monostable to the bistable case (fig. S1, C and D, and movies S1 and S2).

To quantitatively understand the impact of the spring stiffness on the mechanical and snap-through behavior of the curved beam, we developed an analytical model based on a variational principle. During deflection by the external force f(L) = f, the segment length of the beam changes from L₀ to L. The deflection of the deformed curved beam is expressed as

$${w(x)\mid }_{F=f}=h\cdot \sum _{i=1}^{\mathrm{\infty }}{B}_i\cdot w_i(x)$$ (2)

where F is the external force and B_i is the amplitude of the ith buckling mode. w_i(x) is a complete set of basis functions in the form of the buckling mode shapes of a straight beam (eq. S9), which naturally fulfills the boundary conditions and permits the variational solution to readily capture the bifurcation, i.e., the snap-through response. We carefully consider the influence of lateral changes L₀ to L during deformation on the variational solutions (eqs. S14 to S22), and the overall force-displacement relationship is solved (fig. S2 and section S1 in the Supplementary Text).

In Fig. 1 (E and F, solid lines), the theoretically predicted force-displacement curves and the corresponding elastic strain energy u_b + u_s are plotted for three curved beam units characterized by L₀ = 24 mm, h/L₀ = 0.2, $\frac{h}{t}=4.8$, and $k{L}_0^3/EI$ = 200, 700, and 20,000 where E is the Young’s modulus of the beam material, and I is the second moment of area of the beam cross-section. With increasing normalized spring stiffness $\overline{k}=k{L}_0^3/EI$, three characteristic shapes of force-displacement curves were identified (Fig. 1E):

1) No snap-through, monostable ($\overline{k}=200$): The slope of the force-displacement curve is always positive.

2) Snap-through, monostable ($\overline{k}=700$): Part of the curve has negative slope, while the force is always larger than zero.

3) Snap-through, bistable ($\overline{k}=20,000$): Part of the curve has negative slope, and the minimum of the force F_min is below zero.

The evolution of the elastic strain energy (Fig. 1F) also indicated that a second energy minimum exists only for the snap-through (i.e., the bistable) case, whereas the energies increased monotonically for the other two cases.

We conducted finite element analyses (FEA) using the commercial package ABAQUS 2016/Standard (48) to validate the analytical model (methods are in the Supplementary Materials). The numerical results (dashed curves in Fig. 1, E and F) are in good agreement with the theoretical data and confirm the three mechanical regimes predicted analytically. We further analyzed the curved beam model based on Euler-Bernoulli beam analysis (fig. S3 and section S1 in the Supplementary Text). The solution (eq. S3) is in fairly good agreement with solutions obtained from the variational principle and FEA for low spring stiffnesses, i.e., $\overline{k}$ of 200 and 700 (fig. S4). However, the solution of the Euler-Bernoulli differential equation does not capture the snap-through instability induced by a higher spring stiffness ($\overline{k}=20,000$) (fig. S4). Note that the Euler-Bernoulli solution reflects a possible deformation of the beam when the spring with the highest stiffness is present, but after the snap-through instability is reached, the solution is no longer unique but bifurcates into several branches at different bifurcation points, and the solution procedure fails to find the lowest energy mode of deformation. As a consequence, the Euler-Bernoulli solution procedure fails to find the correct load-deflection behavior for snap-through. Presumably, this could be improved by use of a better solution procedure that can search among the nonunique possibilities. However, the setting of snap-through favors the usage of the solution obtained from the variational method as it contains a complete set of buckling mode shapes of a straight beam, which permits the variational solution to readily capture the snap-through response.

In Fig. 1G, we depict a design map for a constant segment length L₀ = 24 mm and a systematic variation of h/L₀ $ϵ$ [0.03,0.33] and of the normalized stiffness $\overline{k}ϵ[10^2,10^5]$. We found that the responses of the beams were always monostable for h/L₀ ≤ 0.05 and any choice of $\overline{k}ϵ[10^2,10^5]$, while the snap-through appeared at larger stiffness. Differently, the snap-through behavior always happened for h/L₀ ≥ 0.295 and any $\overline{k}ϵ[10^2,10^5]$, but the responses of the curved beams changed from the monostable to the bistable state as the spring stiffness increases. The stiffness needed for the mono- to bistable transition was smaller for larger h/L₀. In the following sections, we refer to the monostable state as state I and the bistable state as state II, which we also used for describing the state of the curved beam unit in Fig. 1B.

Structural changes to improve the snap-through

Consider the case that the center of the curved beam is compressed in a displacement-controlled mode (and no tensile force can be exerted). The mechanical response will then follow the solid force-displacement curves until position “d₁” marked in Fig. 2A, where it triggers the snap-through to the second stable state. In Fig. 2B, the critical displacement d₁ as a function of the normalized stiffness $k{L}_0^3/EI$ is depicted for several h/L₀ values from 0.15 to 0.33. The results indicate that d₁ is insensitive to h/L₀ for a given fixed $k{L}_0^3/EI$. Furthermore, d₁ decreases with increasing stiffness and seems to saturate at ~1.33 for high stiffness. Consequently, the curved beam unit will fail to undergo the transition to state II when pressed against a flat target substrate, as is shown in Fig. 2C and movie S3. Here, the frame touches the substrate and therefore limits the maximum displacement d/h ≈ 1 < d₁. In addition, we noticed that an asymmetric deformation was extremely likely to appear during compression (Fig. 2D). The bold yellow curve in Fig. 2A represents such a possible trajectory of the mechanical response when the asymmetric deformation was triggered during the loading process (see section S1 in the Supplementary Text). The snap-through threshold in this case (marked as d₂ in Fig. 2A) indicates that the asymmetric deformation postponed or even suppressed the snap-through instability to some extent. The architectures in Fig. 2 (C and D) therefore do not lead to a reliable snap-through.

Fig. 2. Improved snap-through characteristic by a curved beam with designed thickness variation.

(A) Normalized force-displacement responses of the curved beam with k = ∞ with symmetric (solid line) and asymmetric (dot-dashed line) deformation. Position d₁ represents the critical snap-through threshold leading to the new position d₂. The yellow marked path represents a possible transition from symmetric to asymmetric deformation that can suppress the snap-through. (B) Critical snap-through position d₁ as functions of the normalized stiffness $\overline{k}=k{L}_0^3/EI$ for various shape parameter h/L₀. (C and D) Snapshots of the symmetrically deformed curved beam with k = ∞ without snap-through (C) and the asymmetrically deformed curved beam with k = ∞, which also hinders the snap-through (D). (E) Schematic of the curved beam with variable thickness. The ratio of the thickest to the thinnest beam thickness is β. (F) Variation of the buckling eigenvalues in terms of β for the symmetric (left) and asymmetric (right) buckling modes. (G) Numerically obtained force-displacement responses for β = 1.0, 1.4, and 2.0. The inset demonstrates the shift of the snap-through to smaller displacements, i.e., d₁ decreases. (H) Experimental snapshots of the symmetrically compressed curved beam unit with β = 1.4 confined in the rigid frame. Note the clearly visible snap-through instability.

To reduce the critical distance for switching into state II and to suppress asymmetrical deformation, we introduce a curved beam with a variable thickness along the beam as illustrated in Fig. 2E. The shape of such a beam is described as follows

$$t(x)=t_{\mathrm{a}}[1-\frac{\mathrm{\beta }-1}{\mathrm{\beta }+1}\cos 4\mathrm{\pi }\frac{x}{L_0}]$$ (3)

where t_a is the averaged thickness and β is the ratio of the largest thickness to the smallest thickness, t_max/t_min, along the curved beam. The image in Fig. 2H is a fabricated sample of the curved beam with β = 1.4.

We conducted two sets of simulations to assess the advantages of the variable thickness beam over the constant thickness beam:

1) The mechanical force-displacement responses of the variable thickness curved beam was investigated by selecting β = 1.0, 1.4, and 2.0 (Fig. 2G).

2) The second and third buckling modes of the counterparts of the variable thickness beam were found (Fig. 2F and fig. S5).

Figure 2G shows that the maximum compressive force decreased with increasing β, but the minimum force increased. Simultaneously, the critical distance d₁ decreased, indicating that the snap-through transition would occur earlier.

Furthermore, we establish a connection between the eigenvalues of the buckling modes with the snap-through response. Figure S6 shows the evolution of the values of B₂ and B₃ with displacement (B₂ and B₃ are parameters in Eq. 2) used to describe the deflection and the change of the compressive force in the spring p at the boundary condition with displacement. Comparing Fig. 2A and fig. S6A, the values of B₂ and B₃ become nonzero only when the peak force is reached in Fig. 2A. Meanwhile, by considering Fig. 2A and fig. S6B, the forces in spring p remain nonzero and constant when the incremental force is negative and B₂ or B₃ is nonzero. The constant values p are exactly the respective second- and third-order buckling forces for the straight beam. The second- and third-order buckling forces control the peak force and the appearance of the negative stiffness; a reasonable deduction is that the closer the second and third buckling forces are (Δ in Fig. 2F), the better the asymmetrical deformation is suppressed. The result in Fig. 2F implies that the asymmetric deformation can be suppressed by larger β. This allows for some tuning of the snap-through mechanism, although the sensitivity of d₁ to changes in β is not very high. The sequential snapshots (Fig. 2H) demonstrate that the snap-through is more easily achieved by purely uniaxial compression using the curved beam with β = 1.4. It should be pointed that regardless of the critical displacement d₁ of the curved beam with β > 1.0, the snap-through succeeds (movie S4); this could be due to a kinetic effect or a mixed displacement/force-loading mode due to compression by hand in movie S4 instead of a purely displacement-controlled loading.

Realization of a two-way switchable adhesive

Taking the proposed design discussed in the previous section, we built a one-way switchable adhesive by pasting an adhesive tape at the center of the curved beam unit and confined the system by a rigid frame. Figure S7 depicts that, following attachment at small compressive preloads, the object was successfully released by the compression-induced snap-through mechanism (movie S5). This mechanism demonstrates the one-way switch, as the beam must be manually returned before a second handling cycle can be conducted.

We further present a two-way switchable adhesive by adding a laminated spring located between the curved beam unit and the rigid frame to the previous demonstrator (Fig. 3A). The spring consists of two identical curved beams placed face-to-face in series with the boundary condition k = 0 (see inset in Fig. 3B). Figure 3B displays the force-displacement response of the spring, which is almost linear with a small hysteresis. During loading of the beam, the spring induces a translational relative movement between the curved beam unit and the rigid frame and changes the boundary condition, i.e., stiffness k of the curved beam unit. To be specific, in the initial relaxed state (denoted as “open” in right top image in Fig. 3C), the curved beam unit is outside the rigid frame, leading to a small stiffness. In contrast, the stiffness is high when the curved beam unit is confined inside the rigid frame (denoted as “closed” in right bottom image in Fig. 3C). Last, the spring was designed such that the maximum travel distance corresponds to the height distance between the top end of the rigid frame and the position of the curved shaped beam (i.e., distance L_d in Fig. 3C). The colored curve in Fig. 3D illustrated an approximate mechanical response when the boundary condition switches between small k and high k during the compressive loading/unloading.

Fig. 3. Demonstration of a handling process using the two-way switchable adhesive.

(A) A spring made from two curved beams is added between the curved beam unit and the stiff frame. (B) Experimental force-displacement response of the laminated spring. The insets highlight the undeformed and elastically deformed spring representing the open and closed state, respectively. (C and D) Schematic of the switching mechanism and schematic force-displacement curve, demonstrating the transition from a monostable system, where the spring is in the open state in the unloaded case with a small-stiffness k boundary condition, to a bistable system where the spring converges to the closed state as k increases with ongoing compression. (E) Evolution of maximum principal strains in the entire metastructure in FE simulation. The inset indicates localization of the maximum strain to extremely small regions at the ends of the curved beam.

A complete pick-and-place cycle process based on the evolved design schematically shown in Fig. 1B, which was integrated into the trajectory of a robotic system without any further equipment, was demonstrated with a macroscopic demonstrator (see fig. S8 and movie S6 for more macroscopic demonstrations). First, the object is brought into contact with the adhesive by a small compressive preload (state I). Then, the entire system is moved to the target position, where the object is released. The release is triggered by the snap-through instability of the curved beam under the high-k boundary condition (i.e., state II). Upon withdrawing the entire system, the elastic strain energy stored in the spring releases the curved beam unit out of the frame. Thus, the system returns into the small-k boundary condition, and the beam snaps back into its initial shape, i.e., state I.

The FE simulation of the entire metastructure was conducted to investigate the overall snap-through process (Fig. 3E and movie S7). The curved beam at initial compression expands horizontally, exceeding the inner lateral dimension of the rigid frame. Afterward, the rigid frame squeezes the straightened beam into the rigid frame, which would be bent inward relative to the rigid frame to coordinate the deformation. Quickly, the bent beam snaps through and stays at the second stable state within the confinement of the rigid frame. At that moment, the adhesion area is fully detached from the target object. The maximum strain of ~14% is only localized to tiny regions at both ends of the curved beam after buckling, while other regions are slightly deformed with a strain below ~5% (Fig. 3E and fig. S9).

Miniaturized two-way switchable adhesive device by direct printing

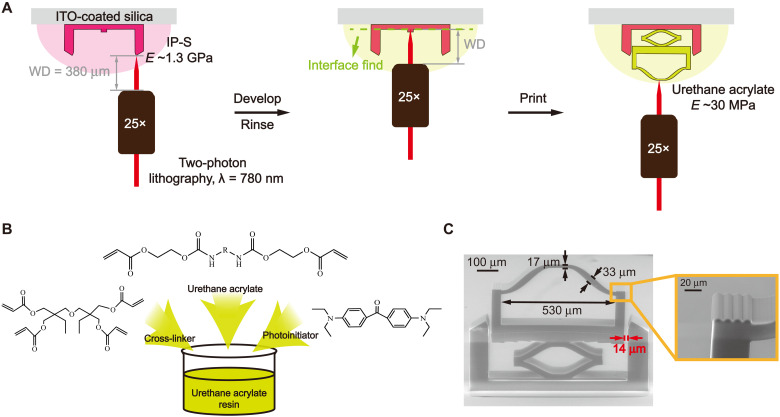
Because the analysis above does not contain explicit size effects, the proposed design can be scaled down to micrometer dimensions and thus be potentially useful for handling micro-objects. A miniaturized version of the snap-through device was realized in submillimeter dimensions using two-photon lithography (Fig. 4A). Two materials of differing stiffness were used to realize the deformable and nondeformable parts of the design. The soft polymer is cross-linked from a customized resin consisting of a urethane acrylic oligomer, a cross-linker, di(trimethylolpropane) tetraacrylate (DTMPTA), and a photoinitiator, 4,4′-bis(diethylamino) benzophenone (EMK) (Fig. 4B and see methods in the Supplementary Materials for more details). The curved beams with variable thickness distributions β = 1.4 and 1.9 were precisely printed with the smallest feature sizes in the curved beam of only 22 and 17 μm (Fig. 4C and fig. S10). For pickup, the intrinsic adhesion force F_ad must be larger than the weight of the object F_g (illustration in Fig. 1B). The adhesion force and pull-off strength of the curved beam due to van der Waals force for dry adhesion were about 0.75 mN and 64 kPa (measured directly against the object’s surface used for demonstration in fig. S11). This adhesion was easily sufficient to lift an object with a mass of 1.4 mg.

Fig. 4. Miniaturized device of submillimeter dimensions by direct printing.

(A) Multistep two-photon lithography process for fabricating the two-material device (pink: IP-S; yellow: urethane acrylate resin; WD, working distance; ITO, indium tin oxide). (B) Urethane acrylate oligomer, cross-linker, and photoinitiator are mixed to form a urethane acrylic resin compatible with high-precision printing. (C) The complete device is composed of the stiff frame and the deformable curved beam and spring. Inset shows the wavy surface of the curved beam end to reduce its adhesion. ITO, indium tin oxide.

To ensure detachment from the object during release, the ends of the curved beam unit were modified by adding low adhesive wavy surfaces (insets in Fig. 4C) or rounded edges as shown in fig. S12. Furthermore, the snap-through mechanism did not introduce lateral forces and hence allowed for high-precision placement in contrast to other mechanisms. The entire cycle of a successful handling process is displayed in fig. S11 (see also movies S8 and S9). Moreover, a cyclic test with at most 1000 cycles was conducted on the printed metastructure, and fig. S13 shows no obvious change in shapes before and after 1000 cycles, demonstrating long-time reliability.

Because the entire metastructure is directly printed, a gap between the U-shaped frame and the rigid frame is unavoidable. The gap width controls the occurrence of snap-through (fig. S14), and a larger gap cannot trigger the snap-through and thus fails to release the picked object (movie S10). Therefore, the width of the U-shaped frame should be smaller than, but as close as possible in size to, the inner width of the rigid frame; besides, the height of the U-shaped frame should be sufficient for accommodating the deformed curved beam without presenting an obstacle. The thickness of the laminated spring should be comparable to the average thickness of the curved beam. A spring that is too compliant would delay the full recovery of the curved beam due to the adhesion between the soft material surfaces in the metastructure as well as the friction between the curved beam and the U-shaped frame (section S3 in Supplementary Text and figs. S15 to S17).

Notably, the manipulated objects must be larger than the lateral dimension of the U-shaped frame for the mechanism to function. A sufficiently high withdrawal speed must be used to avoid reattaching to the object, as the curved beam can snap back quickly. The curved beam can alternatively be made of a material with significant viscoelasticity, and then more time would elapse before snapback of the curved beam and the withdrawal speed could be slowed down.

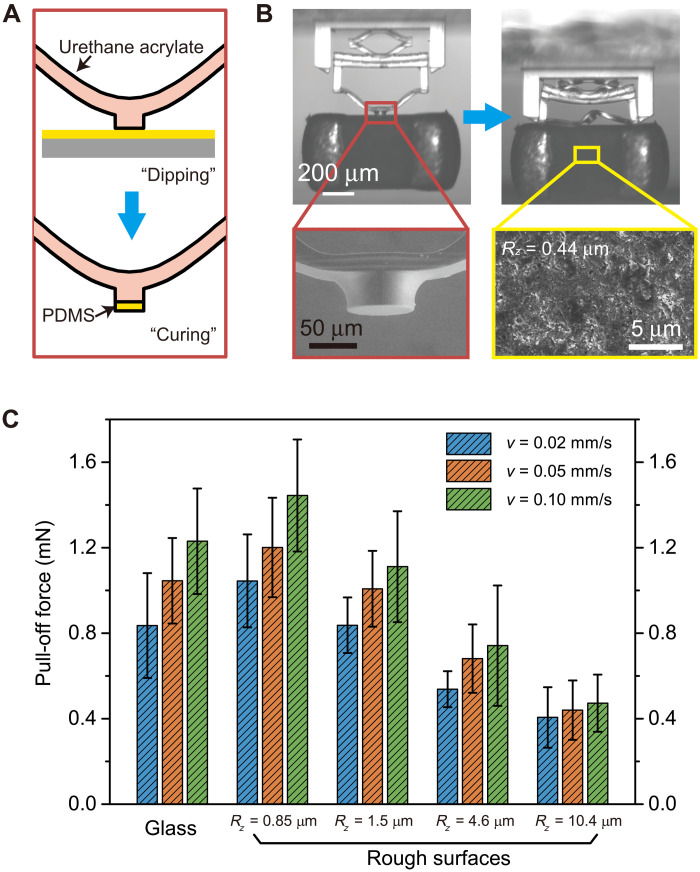
Last, the snap-through concept was extended to underwater or manipulation of rough objects. A cupped fibril design (Fig. 5A), which was previously demonstrated to exhibit high adhesion due to pressure differences under water (49) was directly printed in the center of the curved beam. With a cup diameter of ~20 μm, an adhesion force of ~1 mN under water was obtained (Fig. 5B). A complete underwater pick-and-place process was demonstrated with a fragile silicon chip with a mass of 6 μg and complex microstructure, while displacement and force were monitored (Fig. 5, C and D, and movie S11). To be noticed, after the snap-through occurrence, only two soft ends but not the rigid ends touched the object (snapshot ④ in Fig. 5D), and, in this case, the maximum stress (the maximum force of ~12 mN is divided by the contact area) is only ~0.92 MPa, which is not strong to destroy the stiff object. However, because compression is a necessity for releasing objects, the counter surface of the object must be able to withstand this stress. In addition, a dipping-in method was adopted to coat the basic switchable adhesive with a soft polydimethylsiloxane (PDMS) film, successfully demonstrating a precise pick-and-place operation on a microcapacitor with a rough surface R_z = 0.44 μm (Fig. 6, A and B, and movie S12). Additional adhesion force tested on different rough surfaces (Fig. 6C) proves a broad realization of manipulating micro-objects with different surface roughness (fig. S18).

Fig. 5. Demonstration of underwater pick-and-place with the miniaturized device.

(A) Scanning electron microscopy (SEM) image of the cupped fibril design. (B) Adhesion test of the miniaturized device with the cupped fibril against the glass substrate showing a strong adhesion of ~1 mN. (C and D) Experimental evolution of displacement and force with time, along with snapshots of the underwater pick-and-place process of a silicon chip. The two round balls are air bubbles introduced when immersing the whole system in water.

Fig. 6. Application of the miniaturized device adapting to rough surface objects.

(A) Scheme of the dipping-in method for adding a soft thin PDMS terminal film on the basic structure. (B) Demonstration of picking up a microcapacitor with rough surface and placing due to snap-through instability. Insets show SEM images of the film-terminating central part and rough surface of the capacitor. (C) Adhesion force of the miniaturized device on various rough surfaces.

DISCUSSION

An important figure of merit for evaluating switchable adhesive mechanism is the switching ratio, i.e., the adhesion force ratio between the on and the off states. Most demonstrated values so far typically ranged from 2 to 10 for mechanically triggered detachments (27, 39). For calculating the switching ratio of our design, the gravitation of the lightest object of 6 μg in our demonstrations can be considered as the smallest adhesion due to its successful release. Last, a high switching ratio of 10⁴ is derived (see section S2 in the Supplementary Text). Such a high value exceeds those for most switchable adhesives reported in the literature (50, 51) and, especially, is much higher than those associated with devices with mechanical triggers (typically ~2 to 10) (27, 39).

In the present work, we introduce a novel strategy for a release mechanism based on a reversible snap-through mechanism inspired by biological examples. A curved beam model was proposed as a two-way switchable device. The mechanics was examined in analytical detail and validated by numerical simulations and experiments. The following conclusions can be drawn:

1) The proposed beam model led to the successful realization of a bistable mechanism. The response of the curved beam could be programmed by the boundary conditions. If one end of the curved beam was constrained by a spring, then the deformation was (i) monostable for low stiffness and (ii) bistable for high stiffness.

2) A novel design map predicts the relationship between the beam parameters and the switching behavior. It allows for rational design of the desired functionality. In an improved design, with variable thickness along the beam, the instability was triggered at a smaller displacement, and higher buckling modes were suppressed. This can result in more precise and reliable handling performance.

3) Miniaturization was demonstrated by high-resolution direct printing from two resins of different moduli using two-photon lithography. Handling and release of micro-objects under dry and wet conditions on smooth and rough surfaces were successfully demonstrated. After the object was released, the elastic restoring force returned the system to its initial state. Pick-and-place of a 6-μg silicon chip (the lightest among all tested samples) was demonstrated, with an unprecedented switching ratio of more than 10⁴, which is three orders of magnitude larger than by a typical buckling-induced release using micropillars (39, 40).

The proposed snap-through concept has the potential to create an efficient paradigm for handling and placing superlight objects such as, e.g., microlight-emitting diodes, microlenses, or components for microelectrical-mechanical systems.

MATERIALS AND METHODS

Fabrication and assembly of the components for the macroscopic demonstrator

The switchable adhesive system consisted of four parts: the curved beam unit equipped with an adhesive patch, the rigid frame, and the laminated spring between the frame and the curved beam unit. Three-dimensional (3D) models of all parts (except the adhesive patch) were generated using the software Inventor (Autodesk, San Rafael, CA, USA) and subsequently 3D printed using the stereolithography system Asiga PICO 2 (Sydney, Australia). The laser wavelength was 385 nm. For all parts, the resin Optiprint Splint 385 (Dentona, Dortmund, Germany) was used. The curved beam unit and the spring were then replicated into elastomeric PU by molding. The mold was made from PDMS (Sylgard 184, Dow Corning, Midland, MI, USA). The mixture was poured into the 3D-printed master templates and thermally cured in an oven at 95°C for 3 hours. Upon demolding, the PDMS negative molds were filled with PU (PMC-780, KauPo Plankenhorn eK, Spaichingen, Germany). To remove entrapped air, the prepolymer was degassed at 1 mbar for 1 hour before curing in an oven at 65°C for 12 hours. For the adhesive patch, we used a 3 mm–by–3 mm double-sided pressure-sensitive tape (Scotch, 3M, MN, USA). The tape was added at the center of the curved beam unit. For the final assembly of all parts, a glue (Pattex, Henkel, Düsseldorf, Germany) was used.

Direct printing of the miniaturized device

The entire device was printed using the two-photon lithography system GT+ (Nanoscribe, Karlsruhe, Germany). The stiff frame was printed using the IP-S resin (Nanoscribe, Germany) with a Young’s modulus of about 1.3 GPa. The laser power and scan speed were 45 mW and 100,000 μm/s. The printed structure was developed in propylene glycol methyl ether acetate (PGMEA) for 20 min and rinsed with isopropanol. Note that the vertical dimensions of the stiff frame should be lower than the working distance of the 25× objective to avoid a collision during the second print step, where the curved beam unit and the laminated spring were printed using a custom-made urethane(meth)acrylate resin with a laser power of 40 mW and a scan speed of 100,000 μm/s. The resin contained aliphatic urethane acrylate oligomers (CN9002, Sartomer, USA), tetra-acrylate cross-linker (DTMPTA; Sigma-Aldrich, USA), and a photoinitiator (EMK; Rahn AG, Switzerland) and exhibited a Young’s modulus of about 30 MPa. The structure was developed in PGMEA for 40 min and rinsed with isopropanol. To align the deformable parts to the stiff frame, a squared marker was used. Last, the developed device was postcured by exposure to ultraviolet light for 10 min in a nitrogen atmosphere. To reduce friction between the deformable curved beam unit and the stiff frame, a gap of 14 μm was introduced into the design. In case of a larger gap, the snap-through instability was suppressed as shown in fig. S11 (see also movie S7), which is in line with our design criteria presented in Fig. 2C, as the stiffness reduces with increasing gap size.

Mechanical tests

The mechanical response of the curved beam unit with and without the rigid frame was tested using a tensile tester equipped with a 10-N load cell (Inspekt table BLUE, Hegewald & Peschke, Nossen, Germany). For the test without the frame, a flat cylindrical indenter with a diameter of 3 mm compressed the center of the beam at a rate of 2 mm/min. For the test with the frame, a flat cylindrical indenter with a diameter of 14 mm and a rate of 100 mm/min was used to avoid the occurrence of asymmetric deformation.

Numerical simulations

The numerical simulations were conducted using the software ABAQUS (Dassault Systèmes Simulia Corporation, RI, USA). The curved beam was modeled as an incompressible elastic solid with a Young’s modulus of 20 MPa and a Poisson’s ratio of 0.49 in accordance with the PU used in the experiments. For the calculations, curved beam models were parametrically established using Python codes. For the calculation of the actual deformation by uniaxial loading, the step dynamic, implicit was used. For the buckling modes, the analysis step linear perturbation, buckling was used. One end of the beam was fully fixed, and the other end was constrained using the spring settings in the interaction module. The element type C3D8 was used to avoid the occurrence of the hourglass mode. The entire model (fig. S9A) was simulated using the step dynamic, explicit, and the kinetic energy during the deformation process was monitored to lie always below 0.01% of the elastic energy, such that the simulation could be considered as a quasi-static loading.

Supplementary Materials

This PDF file includes:

Supplementary Text

Sections S1 to S3

Figs. S1 to S18

Other Supplementary Material for this : manuscript includes the following:

Movies S1 to S12