The construction of cross-population polygenic risk scores using transfer learning

Summary

As most existing genome-wide association studies (GWASs) were conducted in European-ancestry cohorts, and as the existing polygenic risk score (PRS) models have limited transferability across ancestry groups, PRS research on non-European-ancestry groups needs to make efficient use of available data until we attain large sample sizes across all ancestry groups. Here we propose a PRS method using transfer learning techniques. Our approach, TL-PRS, uses gradient descent to fine-tune the baseline PRS model from an ancestry group with large sample GWASs to the dataset of target ancestry. In our application of constructing PRS for seven quantitative and two dichotomous traits for 10,285 individuals of South Asian ancestry and 8,168 individuals of African ancestry in UK Biobank, TL-PRS using PRS-CS as a baseline method obtained 25% average relative improvement for South Asian samples and 29% for African samples compared to the standard PRS-CS method in terms of predicted R². Our approach increases the transferability of PRSs across ancestries and thereby helps reduce existing inequities in genetics research.

Existing polygenic risk score (PRS) models have limited transferability across ancestry groups. We propose a PRS method, TL-PRS, using transfer learning techniques to fine-tune the baseline PRS model to the target ancestry. The simulation and application results show that our approach increases the transferability of PRSs across ancestries.

Introduction

Genetic risk prediction is one of the widely investigated topics in genetic epidemiology, as it can help us better understand the genetic architecture of complex traits and potentially aid clinical decision-making.^1,2,3 Many polygenic risk score (PRS) construction methods have been developed, including pruning and thresholding (PT),⁴ Lassosum (Lsum),⁵ polygenic prediction via continuous shrinkage priors (PRS-CS),⁶ and LDpred.⁴ Overall, these methods perform well and help to identify high-risk individuals within the same ancestry group.^2,4,7,8 However, due to insufficient GWAS data from non-European-ancestry groups such as South Asian and African ancestry, PRSs for these cross-population groups often show only limited prediction performance.^5,6 In addition, due to genetic differences across ancestry groups, the direct use of PRS models trained with European data to non-European individuals was shown to lead to reduced prediction accuracy.^4,8

To address this issue, Márquez-Luna et al. proposed a cross-population PRS model by linearly combining two PRSs, each trained from different-ancestry GWAS summary statistics.⁹ They attained more than 70% relative improvement in prediction accuracy for type 2 diabetes in both Latino and South Asian cohorts compared to prediction models from a single-ancestry GWAS. PRS-CSx¹⁰ implemented the same linear-combination approach using two PRSs trained with PRS-CS. However, this linear-combination approach implicitly assumes that the optimal effect sizes (or beta coefficients) weighting for prediction are a linear combination of the effect sizes of two PRSs, which may not hold in all situations. In addition, this method cannot be used when GWAS summary statistics are available for only one ancestry.

Here we propose a cross-population PRS using transfer learning techniques,¹¹ borrowed from machine learning literature. Transfer learning is a widely used tool that applies a pre-trained model to a different but related problem. The usual procedure of transfer learning is a gradient-based optimization when modeling the second task.^12,13 From the practical viewpoint, the reuse or transfer of information from previously learned tasks for the learning of new tasks has the potential to significantly improve the prediction performance compared to the baseline methods as well as reduce the required sample size of training data.¹¹

Our approach, transfer learning PRS (TL-PRS), fine-tunes the baseline model pre-trained with GWAS summary statistics from an ancestry group of larger sample size to a smaller target ancestry group. TL-PRS can use PRSs from any existing PRS methods (such as Lsum and PRS-CS) as a baseline model. Using the effect sizes of the baseline model as initial values, TL-PRS iterates the gradient descent algorithm to adapt the effect sizes for the target ancestry group. In the presence of multiple GWAS summary statistics from different ancestries, TL-PRS fine-tuned linearly combined PRS. Since TL-PRS uses a simple gradient descent, it is scalable for large datasets.

In our simulations, TL-PRS outperformed existing PRS methods in a wide range of genetic architectures and cross-ancestry genetic correlations. In a real-world example with individual-level data from the UK Biobank (UKBB), we use a European-ancestry GWAS from UKBB and an East-Asian-ancestry GWAS from BioBank Japan (BBJ) as pre-training data to predict nine traits in 10,285 samples of South Asian (SAS) and 8,168 samples of African ancestry (AFR). Compared to the baseline methods, TL-PRS substantially improved the prediction accuracy for most traits. For example, TL-PRS using PRS-CS as the baseline method obtained 25% average relative improvement for SAS samples and 29% for AFR samples comparing directly using PRS-CS in terms of predicted R². By improving the polygenic risk prediction in non-European-ancestry individuals, our approach helps reduce the prevailing inequities in genetic and health research until we attain comparable sample sizes across all ancestry groups.

Material and methods

Polygenic risk score construction using single-ancestry GWAS summary statistics

With GWAS summary statistics (i.e., the effect-size estimate and standard error), a PRS is constructed as the summation of the estimated effects across all genetic variants on a given phenotype. For individual $i$, PRS can be defined as

$$PR{S}_i=\sum _{j=1}^M{\hat{\beta }}_j{G}_{ij},$$

where M is the number of variants, $G_{ij}$ is the genotype of the genetic variant j, and ${\hat{\beta }}_j$ is the effect size. There are several well-known methods that estimate the effect sizes ${\hat{\beta }}_j$ using GWAS summary and linkage disequilibrium (LD) information, such as PT, Lsum, and PRS-CS. PT computes the PRS on a subset of genetic variants based on LD-pruning and p value thresholding. Lsum re-estimates the effect sizes using elastic net on GWAS summary statistics. The hyperparameters include the coefficients of L1 and L2 penalties. PRS-CS is a Bayesian polygenic prediction approach that uses a continuous shrinkage prior to deriving posterior effect sizes. Overall, PT and Lsum are computationally fast, whereas PRS-CS requires more computational time. In terms of prediction accuracy, Lsum and PRS-CS generally outperform PT.^5,6

Transfer learning (TL-PRS) using single-ancestry GWAS summary statistics

Supposing that we have pre-trained a PRS model using GWAS summary statistics from a source ancestry, this model could be considered as prior knowledge to predict the genetic effects in the target ancestry. However, due to different LD patterns and possible effect-size heterogeneity across ancestries, effect-size estimation from the source ancestry can result in biased estimators of effect sizes in the target ancestry. To adapt the model to the target population and achieve better prediction performance, we borrow the idea of transfer learning and attempt to combine information from the baseline model and the target sample data.

Specifically, for the target ancestry group, we have the following model:

$$Y=\sum _{j=1}^M{G}_j{\beta }_j+C\gamma +\epsilon =\sum _{j=1}^M{G}_j({\beta }_j^{pre}+{\tau }_j)+C\gamma +\epsilon ,$$

where ${\beta }_j$ is the true effect size of the target ancestry group, assumed to be unknown; ${\beta }_j^{pre}$ is given by the pre-trained model; ${\tau }_j$ is the difference between ${\beta }_j^{pre}$ and ${\beta }_j$; $C$ is the covariate matrix including the intercept; and $\gamma$ is a vector of covariate coefficients. Our goal is to minimize the following loss function:

$$Loss={(Y-\sum _{j=1}^M{G}_j{\beta }_j-C\gamma )}^2.$$

The first and second derivative of loss function with respect to ${\beta }_j$ is

$$\frac{\partial Loss}{\partial {\beta }_j}=-2G_j^T\left(Y-G\beta -C\gamma \right),\frac{{\partial }^{2}Loss}{\partial {\beta }_j^2}=2G_j^T{G}_j^{}>0.$$

Since the second derivative is constantly larger than 0, we can perform a gradient descent algorithm on ${\beta }_j$ with the initial value ${\beta }_j^{pre}$. Given the current estimate ${{\beta }_j}^{\left(r\right)}$ in the r-th iteration, the next value, i.e., ${{\beta }_j}^{(r+1)}$ is

$${{\beta }_j}^{\left(r+1\right)}={{\beta }_j}^{\left(r\right)}-{\alpha }^{\prime }\frac{\partial Loss}{\partial {\beta }_j}={{\beta }_j}^{\left(r\right)}+2{\alpha }^{\prime }{G}_j^T\left(Y-G{\beta }^{\left(r\right)}-C\gamma \right),$$ (Equation 1)

and we define the learning rate $\alpha =2{\alpha }^{\prime }$. Like many existing methods, such as Lsum, LD blocks were used when updating ${\beta }_j$. LD blocks were defined by Berisa and Pickrell in 2016 to partition the whole region.¹⁴ In addition, early stopping of iteration is required to avoid overfitting.

Both the learning rate $\alpha$ and the number of iterations $t_{stop}$ can be selected based on the validation dataset in terms of the best prediction accuracy. In order to reduce computation cost, we suggest choosing $\alpha$ from a small grid of values $min\left(\frac{\mathrm{1,10,100,1000}}{m},1\right)$, where $m$ is the number of variants with non-zero effect sizes from the pre-trained model.

TL-PRS in Equation 1 requires individual-level data for both model fitting and hyper-parameter tuning, and we refer to it as TL-PRS(ind) specifically. When the individual-level data from the training sample are not accessible, TL-PRS can still be applied if GWAS summary statistics of the target ancestry are available. In the step of model fitting, $G^{T}Y$ can be estimated by the summary statistics of the target ancestry,⁵ and $G^{T}G$ can be estimated by the target ancestry using a public reference dataset, such as the 1000 Genomes Project. In the step of hyper-parameter tuning, the approach of using individual-level data is applied in default. The model requirements of TL-PRS and TL-PRS(ind) can be found in Table S1.

Combining multiple GWAS summary statistics from different ancestries

Supposing two PRSs, $PR{S}_1$ and $PR{S}_2$, are constructed from two different GWAS summary statistics, then the cross-population PRS can be built as

$$PRS=\pi PR{S}_1+\left(1-\pi \right)PR{S}_2,$$

where $\pi$ is a tuning parameter with range [0,1] and can be decided using the cross-validation method.⁹ Specifically, $\pi$ is selected from a vector of 0, 0.05, 0.1, …, 0.95, and 1. This idea was proposed by Márquez-Luna et al. in 2017 using PT to construct a single-ancestry PRS, which was referred as PT-multi, and also used with PRS-CS (PRS-CSx¹⁰). This can be also used with Lsum, and we refer to it as Lsum-multi.

Similarly, the linear combination can also be applied to TL-PRS models. For example, with TL-PRS-Lsum models from two ancestries, we can linearly combine them first as the initial value and then implement transfer learning (referred as MTL-PRS-Lsum). MTL-PRS-CS can also be constructed in the same way.

Beyond the combination of two ancestries, we can further extend this idea to three or more different ancestries. Supposing that we have PRSs from three different ancestries, $PR{S}_1$, $PR{S}_2$, and $PR{S}_3$, then the cross-population PRS can be built as

$PRS={\pi }_{1}PR{S}_1+{\pi }_{2}PR{S}_2+\left(1-{\pi }_1-{\pi }_2\right)PR{S}_3,$ where ${\pi }_1,{\pi }_2\ge 0$ and ${\pi }_1+{\pi }_2\le 1$, and then MTL-PRS can be constructed using linearly combined PRS as initial inputs.

Simulations using SAS samples in the UK Biobank

We simulated quantitative phenotypes using real data from 10,285 SAS sample genotypes in UKBB. The proportion of causal markers was fixed at 0.1% and 1%, and the SNP heritability ${h_g}^2$ was fixed at 0.5. The normalized effect sizes $b_i$ were generated from a normal distribution with mean 0 and variance equal to ${h_g}^2$ divided by the number of causal markers. The per-allele effect size is ${\beta }_i=\frac{b_i}{\sqrt{2p_i(1-p_i)}}$, where $p_i$ is the minor allele frequency of the i-th SNP. We simulated phenotypes as $Y_j=\sum _{i=1}^M{\beta }_i{g}_{ij}+{\epsilon }_j,$ where ${\epsilon }_j\sim N(\mathrm{0,1}-{h_g}^2)$ and $M$ is the number of SNPs, and only HapMap3 variants¹⁵ were included in the simulation.

The GWAS summary statistics, based on 10,000 individuals of South Asian and 100,000 individuals of European ancestry, were generated based on the formula ${\hat{\beta }}_i\sim N(\hat{R}{\beta }_i,\hat{R}/n)$, where n is the sample size and $\hat{R}$ is the estimated correlation matrix of the LD block region. We assumed that causal variants could be shared across all ancestries (European and South Asian ancestries), but varying effect sizes were allowed and sampled from a multivariate normal distribution with a genetic correlation of 0.4, 0.7, or 1.0. Two sources (South Asian and European ancestry) of GWAS summary statistics were further generated, and the sample sizes were 10,000 and 100,000, respectively. The simulation of the phenotype was repeated 20 times.

We randomly split the 10,285 simulated samples into training, validation, and testing datasets (Table S2). Ten PRS methods were included in our comparison, including single-source prediction methods (PT, Lsum, TL-PRS-Lsum, PRS-CS, and TL-PRS-CS) and multi-source prediction methods (PT-multi, Lsum-multi, MTL-PRS-Lsum, PRS-CSx, and MTL-PRS-CS). Their predictive performances were measured by $R^2$ between the simulated and predicted phenotypes in the testing dataset.

Although TL-PRS doesn’t require individual-level data of the training dataset, individual-level validation data are recommended. For a fair comparison, we applied the PRS baseline models (PT, Lsum, PRS-CS) using the combination of training and validation datasets for validation. Among them, PT and Lsum require individual-level data, whereas PRS-CS does not. PT-multi, Lsum-multi, and PRS-CSx were then implemented by linearly combining PT, Lsum, and PRS-CS models, respectively. We note that when selecting the tuning parameter $\pi$, PRS-CSx also requires individual-level data. For the TL-PRS methods, baseline models (Lsum, Lsum-multi, PRS-CS, and PRS-CSx) were first pre-trained using a 1000 Genomes Project reference panel, and Scalable and Accurate Implementation of GEneralized mixed model (SAIGE)^16,17,18 was used on the training dataset to calculate GWAS summary statistics. Based on the pre-trained models and calculated summary statistics of the target population, TL-PRS can further be fine-tuned given the individual-level data of the validation dataset. We note that TL-PRS doesn’t require individual-level data for training. The implementation details of all methods can be found in Table S3.

Analysis of SAS and AFR samples in the UK Biobank

We constructed PRSs for the following target samples in UK Biobank: individuals of South Asian ancestry (SAS) and individuals of African ancestry (AFR). UK Biobank protocols were approved by the National Research Ethics Service Committee, and participants signed written informed consent agreements. In each target sample, we used the software Kinship-based INference for Genome-wide association studies (KING)¹⁹ to exclude one individual in each related pair up to second-degree relatives. We then built the polygenic prediction models on the following nine traits: high-density lipoprotein (HDL), low-density lipoprotein (LDL), body mass index (BMI), triglycerides (TGs), systolic blood pressure (SBP), diastolic blood pressure (DBP), height (HGT), coronary artery disease (CAD), and type 2 diabetes (T2D). The first seven traits were quantitative, and the last two traits were dichotomous.

Summary statistics of GWAS analyses on White British individuals in UK Biobank (UKBB) and Japanese individuals in BioBank Japan (BBJ) were downloaded from UKBB (https://pheweb.org/UKB-Neale/) and BBJ PheWeb (http://jenger.riken.jp/en/result). We restricted our analysis to common variants (MAF ≥ 0.01) presented in summary data and target genotype files after removing A/T and C/G SNPs to eliminate potential strand ambiguity.⁹

For each ancestry, the target samples were randomly split into a training dataset, a validation dataset, and a testing dataset (Table S2). We followed the same strategy of training models as the simulation (Table S3). We applied single-source prediction methods (PT, Lsum, TL-PRS-Lsum, PRS-CS, TL-PRS-CS) to UKBB and BBJ summary statistics and used multi-source prediction methods (PT-multi, Lsum-multi, MTL-PRS-Lsum, PRS-CSx, MTL-PRS-CS) to combine UKBB and BBJ GWAS results. The prediction accuracy was assessed in the testing dataset of each target ancestry separately, adjusting for age, sex, and the top four principal components (PCs). We used ${\mathrm{R}}^2$ as the prediction accuracy metric for quantitative traits and Nagelkerke ${\mathrm{R}}^2$ for dichotomous traits. A bootstrap method was implemented to estimate 95% bootstrap confidence intervals for all prediction metrics. Specifically, we resampled the testing data with replacements 1,000 times to calculate prediction metrics, and the 2.5% and 97.5% percentiles were used to estimate bootstrap confidence intervals.

Results

Overview of TL-PRS

We first built PRS models using existing methods, and these models provided effect-size estimates of genetic variants, which were used as initial values for TL-PRS. In this paper, we used models pre-trained using Lsum⁵ and PRS-CS⁶ as the baseline methods, which are referred to as TL-PRS-Lsum and TL-PRS-CS, respectively. The TL-PRS method can also be applied to any other pre-trained models, such as MegaPRS²⁰ and LDpred.⁴ When more than one summary source is available, we can linearly combine the baseline models first as the initial value and then implement transfer learning (referred to as MTL-PRS).

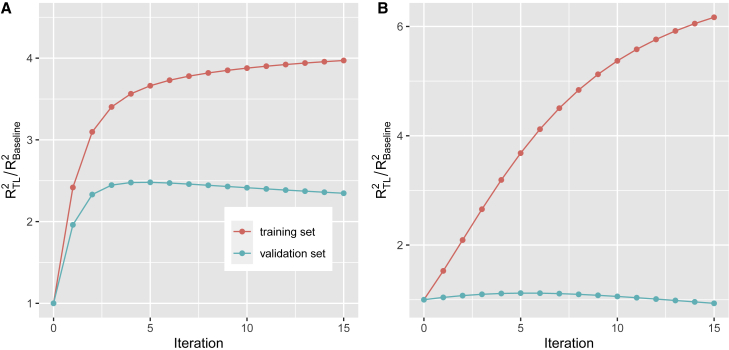
The hyperparameters in TL-PRS include the learning rate and the number of iterations. Given TL-PRS models from different GWAS summary sources, we can integrate them by learning an optimal linear combination and then use it as the initial value to implement TL-PRS (Figure 1). Figure 2 shows the relative accuracy ($R_{TL}^2/R_{Baseline}^2$) of TL-PRS as a function of iterations. The relative accuracy in the training dataset continues to increase as the number of iterations increases, which caused the overfitting. However, the fifth iteration reached the maximum relative accuracy in the validation sets of both simulation and real-data analysis, which suggested that the fifth iteration was the optimal point to stop in these two examples. A similar strategy can be applied to choose the learning rate.

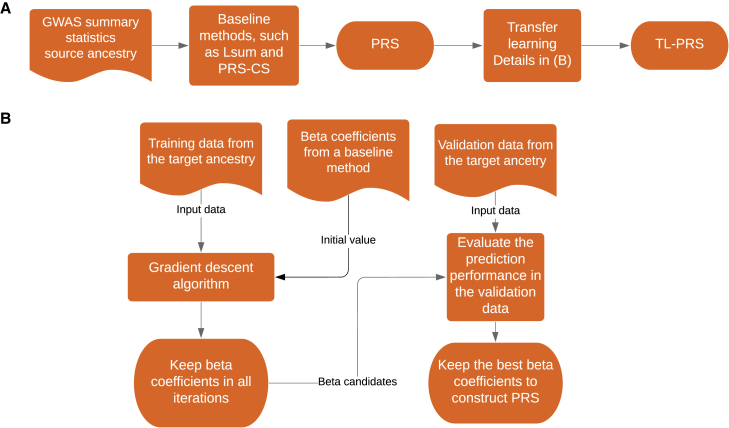
Figure 1.

Overview of TL-PRS methods

(A) The general procedure to construct TL-PRS.

(B) The detailed procedure of TL-PRS. The training data from the target population do not require individual-level data. Validation data are recommended to be at the individual level to achieve the best prediction performance.

Figure 2.

Relative accuracy of transfer learning method by the number of iterations

(A) The simulation result, where the proportion of causal markers was 0.1%, genetic correlation was 0.4, and European summary statistics were used.

(B) The real data analysis of HDL in a South Asian cohort from UK Biobank, where UKBB summary statistics were used.

Simulations using SAS samples in the UK Biobank

In the simulation, different scenarios were considered by randomly selecting 0.1% or 1% variants across the genome as causal variants, which explained 50% of the phenotypic variance in total. Additionally, causal variants were assumed to be the same across ancestry groups, but different effect sizes were simulated from a multivariate normal distribution using the cross-ancestry genetic correlation 0.4, 0.7, and 1.¹⁰ We generated 20 datasets in each scenario to evaluate the predictive performance of different PRS construction methods. We evaluated single-source prediction methods (PT, Lsum, TL-PRS-Lsum, PRS-CS, and TL-PRS-CS) that use a single-ancestry-group GWAS to build prediction models and multi-source prediction methods (PT-multi, Lsum-multi, MTL-PRS-Lsum, PRS-CSx, and MTL-PRS-CS) that utilize multiple-ancestry-group GWASs. The implementation details can be found in Table S3.

Results of single-source polygenic prediction methods in simulation

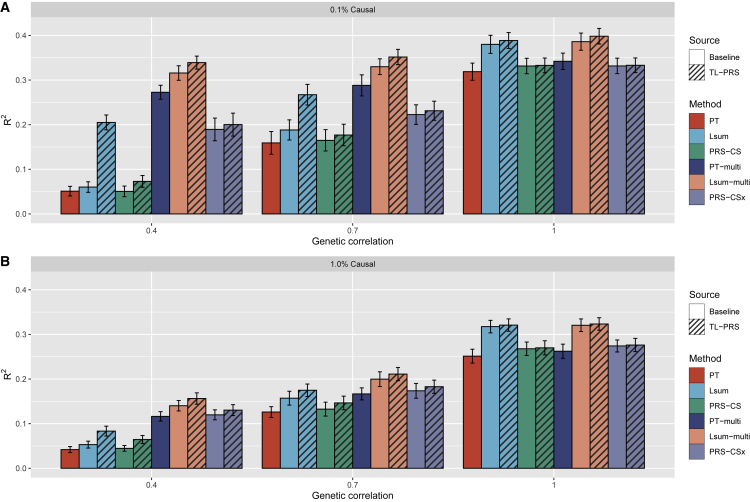
The prediction accuracy of single-source and multi-source polygenic prediction methods in the simulations can be found in Figure 3. For a fixed heritability of 0.5, the predictive performance of all ten PRS methods decreased when the genetic architecture became more polygenic (0.1% vs 1% causal). Although the causal variants were identical across the ancestries, all ten PRS methods showed decreased prediction accuracy when the genetic effects were less correlated among ancestries. This is also the situation where TL-PRS could further improve the prediction accuracy. For example, when genetic correlation was 0.4, TL-PRS-Lsum improved the average prediction accuracy by 241% and 57.1% compared to Lsum when the proportion of causal variants was 0.1% and 1%, respectively (Figure 4). The relative improvement of TL-PRS-CS over PRS-CS was 44.4% and 44.8% on average. However, when genetic correlation was 1.0, Lsum and PRS-CS are sufficient for prediction in target ancestry because the training and testing data shared same true effect sizes. TL-PRS-Lsum and TL-PRS-CS could attain limited relative improvement of the prediction accuracy in this situation. In general, TL-PRS performed better when the genetic correlation was smaller and when the causal variants were sparser.

Figure 3.

Prediction accuracy of single-source and multi-source polygenic prediction methods in simulations

(A and B) The proportion of causal variants in (A) is 0.1% and the proportion of causal variants in (B) is 1.0%. In each setting, three different cross-population genetic correlations (0.4, 0.7 and 1.0) were considered. Heritability was fixed at 50%. Prediction accuracy was measured by the squared correlation (R²) between the simulated and predicted phenotypes in the testing dataset, averaged across 20 simulation replicates. Error bar indicates the standard deviation of R² across simulation replicates.

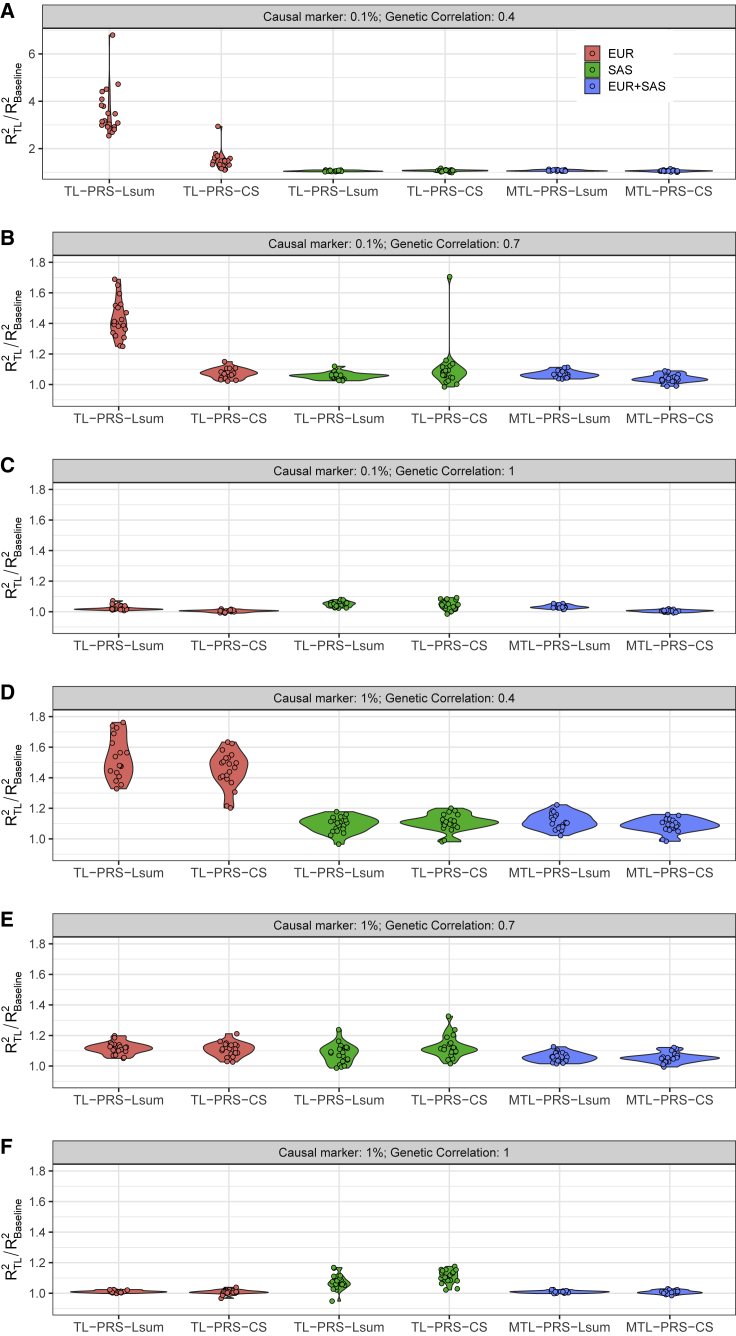
Figure 4.

Relative prediction accuracy of single-source and multi-source TL-PRS, with respect to the baseline models across 20 replicates in the simulation

Note the maximum value of y axis is 7 for (A) and 1.8 for all other plots.

Table S4 shows the selected learning rates and iterations across different simulation scenarios. When the genetic correlation was low (0.4), the selected learning rate was large. Conversely, when the genetic correlation was high, the learning rate was relatively small. However, we did not observe the same trend for the number of iterations, as the number of iterations highly depends on the choice of learning rate. In terms of different proportions of causal markers, there was no difference in selected learning rate and iterations.

Results of multi-source polygenic prediction methods in simulation

We further assessed whether multi-source prediction methods (PT-multi, Lsum-multi, MTL-PRS-Lsum, PRS-CSx, MTL-PRS-CS) could improve cross-ancestry polygenic prediction. Specifically, we combined PRS models from European-ancestry summary statistics (N = 100K) and SAS summary statistics (N = 10K). When the genetic correlation was 1, the multi-source prediction methods cannot improve prediction accuracy in comparison with the single-source prediction methods using European-ancestry summary statistics, because European ancestry shared the same true effect sizes as SAS and had ten times the sample size. In the scenario where the genetic correlation was less than 1, multi-source prediction methods improved prediction accuracy over single-source prediction methods, reflecting the increase in source sample size. Overall, while Lsum-multi outperformed PT-multi and PRS-CSx in most cases, MTL-PRS-Lsum further improved cross-ancestry prediction accuracy comparing Lsum-multi across all simulation settings (Figures 3 and 4). For example, when genetic correlation was 0.4, MTL-PRS-Lsum improved the average prediction accuracy by 7.38% and 11.6% compared to Lsum-multi when the proportion of causal variants was 0.1% and 1%.

In the training step, TL-PRS does not require individual-level data, as the gradients can be calculated with summary statistics. To evaluate whether using summary statistics can reduce the performance of TL-PRS, we compared it with a TL-PRS implemented with individual-level data, TL-PRS(ind). Table S1 compares the model requirements of TL-PRS and TL-PRS(ind). Figure S1 further showed that TL-PRS had similar predicted R² compared to TL-PRS(ind), which shows that summary statistics are sufficient for TL-PRS training.

Overall, our simulation shows that TL-PRS-Lsum and TL-PRS-CS robustly improve cross-ancestry prediction over PT, Lsum, and PRS-CS across varying genetic architectures and genetic correlations. The relative improvement of TL-PRS compared to the baseline method is over 40% when genetic correlation is 0.4.

Prediction performance for SAS and AFR samples in the UK Biobank

After excluding related individuals, the target sample sizes of SAS and AFR were 10,285 and 8,168, respectively. We randomly split them into training dataset (for model fitting), validation dataset (for hyper-parameter tuning), and testing dataset (for the evaluation of predictive performance) (Table S2). We applied single-source prediction methods to the UKBB or BBJ GWAS summary results and used multi-source prediction methods to combine the UKBB and BBJ GWAS results.

Table 1 shows the prediction accuracy of different PRS construction methods in analyses of LDL in the AFR cohort of UK Biobank. We selected LDL because it showed the largest improvement compared to all other traits. When using UKBB GWAS results, the predicted R² of TL-PRS-Lsum (0.058) was significantly higher than Lsum (0.033). In addition, when using BBJ GWAS results, the predicted R² of TL-PRS-Lsum (0.068) was significantly higher than Lsum (0.048), demonstrating higher prediction accuracy in TL-PRS models. In addition, TL-PRS-CS also performed better than PRS-CS using single-source data. When combining UKBB and BBJ GWAS results, both Lsum-multi (0.052) and PRS-CSx (0.037) outperformed PT-multi (0.030), as expected. At the same time, MTL-PRS-Lsum (0.068) and MTL-PRS-CS (0.044) reached the best prediction accuracy. The consistent conclusions were reached when using the criteria of beta coefficients of normalized PRS or the mean difference between top 10% and bottom 10% PRS. The detailed results of other traits in the SAS and AFR samples can be found in Tables S5 and S6, respectively.

Table 1.

Prediction accuracy of 15 different approaches to construct PRS in the analyses of LDL in the African cohort of UK Biobank

Model	Predicted R2of PRS	Mean difference between top 10% and bottom 10% PRS
Single-source PRS methods
PT (UKBB)	0.012 (0.004, 0.023)	0.388 (0.199, 0.564)
Lsum (UKBB)	0.033 (0.019, 0.048)	0.625 (0.423, 0.779)
TL-PRS-Lsum (UKBB)	0.058 (0.040, 0.079)	0.779 (0.602, 0.943)
PRS-CS (UKBB)	0.022 (0.012, 0.037)	0.552 (0.369, 0.714)
TL-PRS-CS (UKBB)	0.028 (0.015, 0.044)	0.506 (0.343, 0.721)
PT (BBJ)	0.028 (0.018, 0.045)	0.474 (0.326, 0.639)
Lsum (BBJ)	0.048 (0.032, 0.067)	0.595 (0.456, 0.770)
TL-PRS-Lsum (BBJ)	0.068 (0.048, 0.090)	0.795 (0.625, 0.967)
PRS-CS (BBJ)	0.023 (0.012, 0.036)	0.421 (0.274, 0.602)
TL-PRS-CS (BBJ)	0.028 (0.016, 0.044)	0.565 (0.389, 0.733)
Multi-source PRS methods
PT-multi	0.030 (0.019, 0.046)	0.531 (0.405, 0.715)
Lsum-multi	0.052 (0.036, 0.073)	0.727 (0.581, 0.895)
MTL-PRS-Lsum	0.068 (0.047, 0.088)	0.926 (0.727, 1.073)
PRSCSx	0.037 (0.022, 0.054)	0.662 (0.483, 0.823)
MTL-PRS-CS	0.044 (0.028, 0.062)	0.721 (0.569, 0.908)

The bootstrap confidence interval is shown in the parentheses. For single-source PRS methods, the training GWAS summary source is shown in the parentheses. The approach with highest predicted R² is highlighted using italics. UKBB, UK Biobank; BBJ, BioBank Japan.

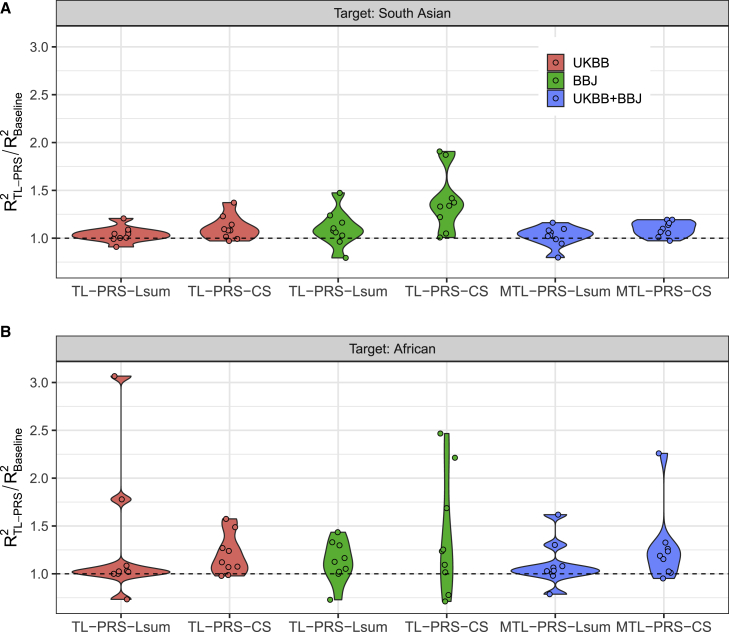
Consistent with the simulation results, TL-PRS-Lsum and TL-PRS-CS outperformed Lsum and PRS-CS in most traits from SAS and AFR samples (Figure 5). For SAS, TL-PRS-Lsum attained 10% and 4% average relative improvement in prediction accuracy using BBJ and UKBB GWAS results compared to Lsum; the relative improvement of TL-PRS-CS over PRS-CS was on average 39% and 11%, respectively. For AFR samples, TL-PRS-Lsum attained 13% and 30% relative improvement of prediction accuracy in BBJ and UKBB GWAS results compared to Lsum; TL-PRS-CS improved prediction accuracy by 38% and 20% compared to PRS-CS. When combining BBJ and UKBB GWAS results, MTL-PRS-Lsum and MTL-PRS-CS had higher prediction performance than Lsum-multi and PRS-CSx (Figure 5).

Figure 5.

Relative prediction accuracy of single-source and multi-source TL-PRS, with respect to the baseline models across nine traits in South Asian and African populations

(A and B) South Asian populations are shown in (A) and African populations in (B). In both panels, every point shows the relative predicted R² of a trait.

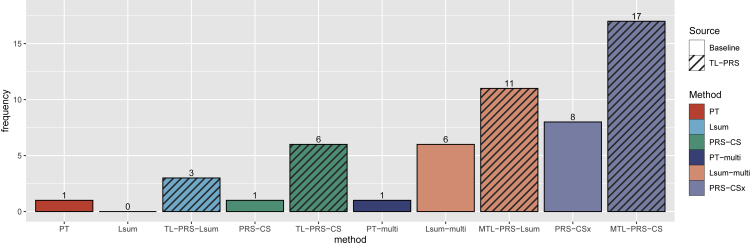
Figure 6 further compares all ten PRS methods among all nine traits in the SAS and AFR samples. This bar plot summarizes the number of times each PRS method ranked in the top 3 methods in terms of predicted R² for 18 traits and ancestry combinations (9 traits × 2 ancestries). (The detailed comparison can be found in Table S7.) Compared to the baseline methods, TL-PRS appeared more times in the top 3 than the baseline methods, demonstrating the ability of TL-PRS to improve prediction accuracy. In addition, MTL-PRS generally performed better than TL-PRS because MTL-PRS incorporated two different ancestries. Overall, MTL-PRS-CS shows the most robust performance across all situations since it ranks in the top 3 in almost all situations (17/18).

Figure 6.

The method comparison across all nine traits in the individuals of South Asian and African ancestry

The y axis represents the number of times that each PRS method ranked in the top 3 in terms of predicted R² for 18 traits and ancestry combinations (9 traits × 2 ancestries). Single-source prediction methods (PT, Lsum, TL-PRS-Lsum, PRS-CS, TL-PRS-CS) based on UKBB and BBJ GWAS results and multi-source PRS methods (PT-multi, Lsum-multi, MTL-PRS-Lsum, PRS-CSx, MTL-PRS-CS) were included in the comparison.

Figure S2 shows the cumulative event plot using the samples in the top 10% PRS across two ancestries. Across all situations, TL-PRS methods were found to have a similar or higher cumulative event curve than the baseline method. For example, in the analysis of CAD in the AFR cohort, when the age was up to 70, the cumulative prevalence of the samples with the top 10% PRS constructed by TL-PRS-Lsum(UKBB) was 0.16, while the prevalence in the samples with the top 10% PRS using Lsum(UKBB) was 0.12, suggesting that the TL method can improve the prediction of individualized disease risk and trajectories.

In general, TL-PRS using PRS-CS as baseline method obtained 25% average relative improvement for SAS samples and 29% for AFR samples comparing directly using PRS-CS; TL-PRS using Lsum as baseline method obtained 7% average relative improvement for SAS samples and 22% for AFR samples comparing directly using Lsum. Among all ten PRS methods, MTL-PRS-CS is recommended due to its robust performance across all possible situations.

Discussion

We have presented the TL-PRS method, which can adapt the PRS model from other ancestries to the target ancestry. We have shown, through simulation studies, that TL-PRS-Lsum and TL-PRS-CS robustly improved cross-ancestry prediction over Lsum and PRS-CS across traits with varying genetic architectures and genetic correlations between source and target ancestries. Using both quantitative and dichotomous traits from SAS and AFR samples in UK Biobank, we have demonstrated that TL-PRS can leverage large-scale European and East Asian GWASs to boost the accuracy of polygenic prediction, for which ancestry-matched GWAS results may be orders of magnitude smaller in sample size. In addition, MTL-PRS, which combined two sources, robustly improved cross-ancestry prediction over the linear-combination methods, such as PT-multi, Lsum-multi, and PRS-CSx, across different circumstances.

Overall, the performance of TL-PRS depends on many factors, such as target ancestries and trait types. When genetic correlations between source and target ancestries are large, the baseline methods are sufficient for prediction, and TL-PRS might not further improve the prediction performance. When genetic correlations are small, TL-PRS helps to adapt the effect sizes of the existing model to the target data. The performance of TL-PRS also depends on the baseline methods we choose. When changing the European GWAS sample size from 100,000 to 50,000 in the simulation, TL-PRS performed worse (Table S8) because the baseline method wasn’t trained well with fewer samples. Because TL-PRS can be applied to a variety of PRS methods, we expect that its predictive power will improve with the development of better PRS baseline methods. For example, Zhang et al. developed a software, MegaPRS,²⁰ which reportedly outperformed other methods by allowing the specification of more realistic heritability models.

In addition, when GWAS summary data from more than one source ancestry are available, MTL-PRS, especially MTL-PRS-CS, is recommended in general due to its robust performance in real-data analysis. For most traits and diseases, European GWAS results are already available, and East Asian GWAS results are also available for many common traits and diseases. Consequently, these two sources allow the implementation of MTL-PRS. As larger and more diverse biobanks, such as the pan-African biobank, are being developed, we believe that there will be future opportunities to combine three or more ancestries. Moreover, TL-PRS could be further extended to admixed populations with simple modifications. Future work is needed to better evaluate the performance in admixed populations.

TL-PRS can use GWAS summary results of the target samples to calculate gradients for transfer learning. In our simulation and real-data analysis, we used only GWAS summary results for TL-PRS training. However, TL-PRS still requires individual-level data for validation and test datasets. When the individual-level validation data are unavailable, pseudo-validation⁵ could be applied for the hyper-parameter selection, but the performance would be unstable.²¹ Alternatively, recent studies^20,22 showed that summary statistics can be divided into pseudo-summary statistics, i.e., two independent sub-datasets for training and validation, and by doing so circumvent the requirement of individual-level data, e.g., when only summary statistics of the target population are available.

Despite these advantages, our work is subject to limitations and leaves several questions open for future exploration. First, although we have demonstrated large relative improvements in prediction accuracy, absolute prediction accuracies are not sufficiently high to achieve clinical utility for most traits;^23,24 our simulations suggest that cross-population PRS will continue to produce improvements when more diverse GWAS results are available and the sample sizes are larger. Second, when combing two summary sources, the improvement of our MTL-PRS over the existing best PRS methods (PT-multi, Lsum-multi, and PRS-CSx) is limited. More research work is needed to combine more than one summary source. For example, the heritability of the traits, which may differ across ancestries due to environmental factors, such as health behaviors and socioeconomic factors, can also be used to tune the model. Additionally, we did not incorporate data from the X chromosome, which is likely to harbor additional heritability that could improve prediction in some traits.²⁵ Finally, we restricted our analyses to common variants, but we may wish to incorporate the effects of rare variants in future work.

While extending the present research to acquire more diverse ancestry genomes with sample sizes equivalent to European ancestry samples is the ideal, in the meantime, all existing available information should be efficiently used to improve prediction across ancestries. We believe that TL-PRS can increase the usefulness of PRS in multiple ancestry groups and reduce potential health inequities.

Data and code availability

The codes generated during this study are available at https://github.com/ZhangchenZhao/TLPRS. The example data and scripts can be found at https://www.dropbox.com/sh/40vewd1kuxcbeev/AAD7Dj3H-sBTWv2ObUIDEHFya?dl=0.

Published: October 13, 2022

Web resources

• 1000 Genomes Project, https://www.internationalgenome.org/

• BBJ summary statistics, http://jenger.riken.jp/en/result

• KING software, https://www.kingrelatedness.com/manual.shtml

• Lassosum, https://github.com/tshmak/lassosum

• PRS-CS, https://github.com/getian107/PRScs

• PRS-CSx, https://github.com/getian107/PRScsx

• TL-PRS, https://github.com/ZhangchenZhao/TLPRS

• UK Biobank, https://www.ukbiobank.ac.uk/