FastRNA: An efficient solution for PCA of single-cell RNA-sequencing data based on a batch-accounting count model

Summary

Almost always, the analysis of single-cell RNA-sequencing (scRNA-seq) data begins with the generation of the low dimensional embedding of the data by principal-component analysis (PCA). Because scRNA-seq data are count data, log transformation is routinely applied to correct skewness prior to PCA, which is often argued to have added bias to data. Alternatively, studies have proposed methods that directly assume a count model and use approximately normally distributed count residuals for PCA. Despite their theoretical advantage of directly modeling count data, these methods are extremely slow for large datasets. In fact, when the data size grows, even the standard log normalization becomes inefficient. Here, we present FastRNA, a highly efficient solution for PCA of scRNA-seq data based on a count model accounting for both batches and cell size factors. Although we assume the same general count model as previous methods, our method uses two orders of magnitude less time and memory than the other count-based methods and an order of magnitude less time and memory than the standard log normalization. This achievement results from our unique algebraic optimization that completely avoids the formation of the large dense residual matrix in memory. In addition, our method enjoys a benefit that the batch effects are eliminated from data prior to PCA. Generating a batch-accounted PC of an atlas-scale dataset with 2 million cells takes less than a minute and 1 GB memory with our method.

FastRNA is an efficient data analysis framework for single-cell RNA-seq. With unique algebraic techniques, it reduced time and memory requirement by orders of magnitude. When applied to an atlas-scale dataset with 2 million cells, it takes 1 min and 1 GB of memory to complete feature selection and dimension reduction.

Introduction

The analysis of single-cell RNA-sequencing (scRNA-seq) data almost always begins with the generation of the low dimensional embedding of the data by principal-component analysis (PCA). PCA results are needed both for visualization after 2D transformation (tSNE, t-distributed stochastic neighbor embedding, or UMAP, uniform manifold approximation and projection) and for clustering of the cells with unsupervised clustering algorithm and are thus considered essential for the analysis of scRNA-seq data, for which we do not know which cells are which types a priori. Because PCA explains the variance existent in the data in a linear space, it is highly preferred for the data to be normally distributed than to be skewed. However, scRNA-seq data are count data by nature. For this reason, researchers have traditionally applied a log-normal transformation to the data so that the resulting data look normal.¹ However, studies often argued that the use of log normalization can induce artificial bias and exaggerate the effects of small counts.^2,3,4

To address this potential bias, recent studies have developed methods that directly assume a count model.^5,6 In these methods, instead of applying a log transformation, a Poisson or negative binomial distribution is assumed for the observed count. Then, residuals of the counts are calculated after accounting for the effects of cell size factors and occasionally for batches. As residuals approximate a normal distribution, they can be subsequently used for PCA. The most popular methods are GLM-PCA,² scTransform,⁵ and the analytic Pearson residual.⁶ Count-based models have the theoretical advantage of directly modeling the count nature of data and the flexibility of accounting for batches prior to PCA. The authors of these papers showed that count-based normalization performed better than log normalization across a variety of tasks in scRNA-seq analysis. Nevertheless, a large-scale benchmarking study showed that GLM-PCA performs poorly on some datasets.⁷ Therefore, further exploration and experimentation will be needed to assess the actual performance of count-based methods over a wide range of datasets. Methods applying PCA to Pearson residuals have been called correspondence analysis (CoA) as pointed out by Hsu et al. and are recently gaining attention.⁸

As scRNA-seq data grow in size, the most important challenge becomes the time and memory usage in analysis. This challenge is critical for count-based methods, but it also affects standard log normalization. Count-based methods are memory intensive and slow for large datasets because they generate large dense residual matrices. scRNA-seq data are sparse by nature, but once the data have been transformed to count residuals, the data matrix is no longer sparse. Although not as severely as with count-based methods, the efficiency of log normalization is also affected by the data size. This is because a dense matrix of the selected features still must be formed in the memory for the mean centering and variance standardization.

Here, we present FastRNA, an efficient solution for PCA of scRNA-seq data based on a full count model accounting for both categorical batches and cell size factors. We assume the same general count model as a previous method (scTransform), but we obtain the solution by using two orders of magnitude less time and three orders of magnitude less memory than other count-based methods. Even compared to the standard log normalization, our method is an order of magnitude faster and an order of magnitude more memory efficient. This achievement results from our unique algebraic strategy that exploits a number of key observations, such as (1) that the PCA of the count residual matrix can be obtained from the covariance of that matrix, which is often of a much smaller size; (2) that the latter covariance matrix can be decomposed into a sum of elements, each of which can be computed by sparse algebra; and (3) that the batch-wise count summation can serve as a sufficient statistic for calculation of batch-corrected residuals. These unique algebraic ideas work together seamlessly as a combination to completely eliminate the need for expanding the actual residual matrix in memory for both feature selection and dimension reduction tasks. Because the data does not need to be stored in memory, our method achieves extreme efficiency, faster than standard log normalization, while still having the benefits of count-based methods: the count data are directly modeled and that batches can be corrected prior to dimension reduction. Generating a batch-accounted PC of an atlas-scale dataset with 2 million cells takes less than 1 min and 1 GB memory with our method.

Material and methods

Notations

We first explain the symbols and notations that describe the dimension of the data. $n_B$ is the number of batches and is indexed by $b=1,\dots ,n_B$. Cells are indexed by c. Note that each cell c comes from a particular batch b, which we write as $c\in {\text{Φ}}_b$. For a cell $c\in {\text{Φ}}_b$, c ranges from 1 to $n_b$ where $n_b$ is the number of cells in batch b. The total number of cells is $n_C={\sum }_{b=1}^{n_B}{n}_b$. Finally, genes (or transcripts) are indexed by $g=1,\dots ,n_G$ in which $n_G$ is the number of genes. scRNA-seq data are stored in a matrix, which we write as $\mathbf{Y}\in {\mathbb{R}}^{n_C\times n_G}$. Y is a stacked matrix, i.e.,

$$\begin{array}{l}\mathbf{Y}={\left[\begin{array}{lllll}{\mathbf{Y}}_1^T\hfill & \cdots \hfill & {\mathbf{Y}}_b^T\hfill & \cdots \hfill & {\mathbf{Y}}_{n_B}^T\hfill \end{array}\right]}^T\hfill \end{array},$$ (Equation 1)

where ${\mathbf{Y}}_b\in {\mathbb{R}}^{n_b\times n_G}$ is a submatrix of Y that stores the data of cells in batch b. We write the elements of ${\mathbf{Y}}_b$ as $Y_{bcg}$. This is the entry at row c and column g of matrix ${\mathbf{Y}}_b$.

Log normalization

There are several forms of log normalization, but most if not all, methods share the following transformation:

$${\tilde{Y}}_{bcg}=\text{log}\left(1+f\cdot \frac{Y_{bcg}}{{\sum }_g{Y}_{bcg}}\right).$$ (Equation 2)

There are several choices for the scaling factor f. A default choice found in Seurat is f=10,000.⁹ Some authors use $f={\text{median}}_{c\in {\text{Φ}}_b}\left(m_{bc}\right)$, where m_bc is the total gene count of cell c in batch b.¹⁰ In this paper, we benchmarked the first choice. Note that if $Y_{bcg}$ is zero, ${\tilde{Y}}_{bcg}$ is also zero. Hence, $\tilde{\mathbf{Y}}$ is sparse if Y is sparse.

Feature selection is then performed with the transformed count $\tilde{\mathbf{Y}}$. Several methods including non-parametric regression such as loess are employed during this process.⁹ After feature selection, $\tilde{Y}$ is mean centered and divided by its standard deviation.

$$R_{\text{Log,}bcg}=\frac{{\stackrel{\sim }{Y}}_{bcg}-{\mathbb{E}}_{c\in {\text{Φ}}_b}\left[{\stackrel{\sim }{Y}}_{bcg}\right]}{\sqrt{{\text{Var}}_{c\in {\text{Φ}}_b}\left({\stackrel{\sim }{Y}}_{bcg}\right)}},$$ (Equation 3)

where ${\mathbb{E}}_{c\in {\text{Φ}}_b}$ and ${\text{Var}}_{c\in {\text{Φ}}_b}$ are sample mean and variance over cells c in batch b. $R_{\text{Log,}bcg}$ is generally non-zero, so the resulting scaled matrix ${\mathbf{R}}_{\text{Log}}$ is not sparse. Nevertheless, this process is only applied to the selected features, so it does not require as much memory as applying it to the whole data.

Previous count-based normalization methods

We briefly describe two normalization methods: scTransform⁵ and analytic Pearson residual.⁶

scTransform fits a negative binomial model with the following specification. We modified the notation of the original paper to conform to the notations described in the previous subsection.

$$·Y_{bcg}\sim \text{NB}\left({\mu }_{bcg}\text{,}{\theta }_g\right)$$

$$·\text{ log}\left({\mu }_{bcg}\right)={\beta }_{0g}+{\beta }_{1g}{\text{log}}_{10}\left(m_{bc}\right)+{\sum }_{b=2}^{n_B}{\beta }_{bg}{X}_{bc}$$

Note that the summation ${\sum }_{b=2}^{n_B}$ starts from $b=2$ because $b=1$ is used as a reference. $X_{bc}$ ($b=2,\dots ,n_B$) is the batch indicator that is 1 if $c\in {\text{Φ}}_b$ and 0 otherwise. ${\theta }_g$ is the gene-dependent dispersion parameter and $m_{bc}=\sum _g{Y}_{bcg}$ is the total gene count of cell $c\in {\text{Φ}}_b$ often called the cell size factor. scTransform fits ${\beta }_{•}$ (abbreviation for all ${\beta }_{bg}$: $b=1,\dots ,n_B$ and $g=1,\dots ,n_G$) and ${\theta }_g$ with negative binomial regression that is implemented in glmGamPoi.¹¹ After fitting the parameters, it produces a matrix of residuals ${\mathbf{R}}_{\text{SCT}}$, which is defined as

$$R_{\text{SCT},bcg}=\frac{Y_{bcg}-{\mu }_{bcg}}{\sqrt{{\mu }_{bcg}+{\mu }_{bcg}^2/{\theta }_g}},$$ (Equation 4)

where $R_{\text{SCT},bcg}$ is the c-th row, g-th column of ${\mathbf{R}}_{\text{SCT},b}$, which is defined to be the submatrix of ${\mathbf{R}}_{\text{SCT}}$ identical to Y and ${\mathbf{Y}}_b$.

Analytic Pearson residual is based on a more parsimonious model.

$$\cdot Y_{bcg}\sim \text{Poisson}\left({\mu }_{bcg}\right)$$

$$\cdot \text{ log}\left({\mu }_{bcg}\right)={\beta }_{0g}+\text{log}\left(m_{bc}\right)$$

The fitted values in this case can be obtained analytically as follows:

$${\hat{\mu }}_{bcg}=\frac{{\sum }_g{Y}_{bcg}\cdot {\sum }_c{Y}_{bcg}}{{\sum }_{c,g}{Y}_{bcg}}.$$ (Equation 5)

This fitted mean is used to compute the residual matrix ${\mathbf{R}}_{\text{APR}}$.

$$R_{\text{APR},bcg}=\frac{Y_{bcg}-{\hat{\mu }}_{bcg}}{\sqrt{{\hat{\mu }}_{bcg}}},$$ (Equation 6)

where $R_{\text{APR},bcg}$ is the c-th row, g-th column of ${\mathbf{R}}_{\text{APR},b}$, which is defined similarly to scTransform. They also suggest a negative binomial approach by setting a fixed dispersion parameter φ for all genes and replacing the denominator with the negative binomial variance.

$$R_{\text{APR},bcg}=\frac{Y_{bcg}-{\hat{\mu }}_{bcg}}{\sqrt{{\hat{\mu }}_{bcg}+{\hat{\mu }}_{bcg}^2/\phi }}$$ (Equation 7)

For both methods (scTransform and analytic Pearson residual), the calculated residual matrices are used to calculate the variance for each gene (which is used for feature selection) and singular value decomposition (SVD) for dimension reduction.

SVD and spectral decomposition

Let $M\in {\mathbb{R}}^{p\times q}$ be a p-by-q matrix and $r=\text{min}\left\{p\text{,}q\right\}$. The SVD widely used in scRNA-seq is the reduced SVD.

$$M=U\cdot \text{diag}\left(S\right)\cdot V^T\text{ where }U\in {\mathbb{R}}^{p\times r},S\in {\mathbb{R}}^r,V\in {\mathbb{R}}^{q\times r}$$ (Equation 8)

U and V have orthonormal columns (the norm of the columns are 1 and the columns are orthogonal to each other). Conventionally, the principal component of scRNA-seq data refers to $U\cdot \text{diag}\left(S\right)$. What naturally follows is that multiplying V to both sides of Equation 8 gives

$$MV=U\cdot \text{diag}\left(S\right)\cdot V^T\cdot V=U\cdot \text{diag}\left(S\right).$$ (Equation 9)

For a square matrix $L\in {\mathbb{R}}^{p\times p}$, spectral decomposition calculates the eigenvalues and eigenvectors of L. An important connection between SVD and spectral decomposition is that the SVD output V of M has eigenvectors of $M^{T}M$ as its columns. To see this,

$$\begin{array}{cc}{M}^{T}MV& =V\cdot \text{diag}\left(S\right)U^{T}U\cdot \text{diag}\left(S\right)\cdot V^{T}V\\ & =V\cdot \text{diag}{\left(S\right)}^2{V}^{T}V\\ & =V\cdot \text{diag}{\left(S\right)}^2\end{array}.$$ (Equation 10)

Therefore, to obtain the principal components, one can use Equation 10 instead of Equation 8. This should be a preferred approach when M is prohibitively large but $M^{T}M$ is small and can be directly computed without obtaining M, which is the strategy we take in this paper.

Conditional likelihood approach

In this section, we describe the probabilistic model of FastRNA. Similar to scTransform but with slightly different parameterization, we assume the following model.

$$\cdot Y_{bcg}\sim \text{Poisson}\left({\mu }_{bcg}\right)$$

$$\cdot \text{log}\left({\mu }_{bcg}\right)={\text{Γ}}_{bg}+\text{log}\left(m_{bc}\right)\text{for}c\in {\text{Φ}}_b$$

Note that ${\text{Γ}}_{bg}={\beta }_{0g}+{\sum }_{b=2}^{n_B}{\beta }_{bg}{X}_{bc}$ (for $X_{bc}$ defined in the second equation in “previous count-based normalization methods”), so our proposed model is identical to scTransform, and the only difference is in the distribution, where we used Poisson instead of negative binomial, and it is more general than analytic Pearson residual. Identical to the previous methods, $m_{bc}$ is the cell size factor.

At the heart of count-based normalization methods, residuals measure the departure of the data from the null distribution. In this case, null means that only the technical variation and no biological variation drives the observation. Hence, measuring the departure by residuals can measure the biological variability that is not described in the null model.

This is done by subtracting the conditional mean ${\mu }_{bcg}=\mathbb{E}\left[Y_{bcg}|{\beta }_{•g},m_{bc},X_{•c}\right]$ (note that ${\beta }_{•g}$ is an abbreviation for all ${\beta }_{0g},{\beta }_{1g},\dots ,{\beta }_{n_{B}g}$ and $X_{•c}$ is an abbreviation for all $X_{2c},\dots ,X_{n_{B}c}$) from the observed count $Y_{bcg}$ and dividing it with the square root of the conditional variance $\text{Var}\left[Y_{bcg}|{\beta }_{•g},m_{bc},X_{•c}\right]$. This is essentially the approach scTransform is taking—estimating the mean and variance conditioned on the covariates (batch) and size factors. However, this requires estimating $n_B$ parameters, which grows together with the number of cells. Hence, it is computationally demanding for large scale data with many batches.

To overcome this difficulty, we suggest conditioning additionally on $\sum _{c\in {\text{Φ}}_b}{Y}_{bcg}$ as well as ${\beta }_{•g},m_{b•}$ (where $m_{b•}$ is an abbreviation of $m_{b1},\dots ,m_{b{n}_b}$) and $X_{•}$ (where $X_{•}$ is an abbreviation of $X_{bc}$ for all combinations of $b=1,\dots ,n_b$ and $c\in {\text{Φ}}_b$). The major advantage of our approach is that it can eliminate the need for estimating ${\beta }_{•g}$ for all $g=1,\dots ,n_G$. To show this, we consider the likelihood conditioned on these variables including $\sum _{c\in {\text{Φ}}_b}{Y}_{bcg}$.

$$P\left({\left\{Y_{bcg}\right\}}_{c\in {\text{Φ}}_b}|\sum _{c\in {\text{Φ}}_b}{Y}_{bcg},{\beta }_{•g},m_{b•},X_{•}\right)=\frac{P\left(Y_{b1g}\text{,}\dots \text{,}{Y}_{b{n}_{b}g}|{\beta }_{•g},m_{b•},X_{•}\right)}{P\left({\sum }_{c\in {\text{Φ}}_b}{Y}_{bcg}|{\beta }_{•g},m_{b•},X_{•}\right)}=\frac{{\prod }_{c\in {\text{Φ}}_b}P\left(Y_{bcg}|{\beta }_{•g},m_{bc},X_{•c}\right)}{P\left({\sum }_{c\in {\text{Φ}}_b}{Y}_{bcg}|{\beta }_{•g},m_{b•},X_{•}\right)}=\frac{{\prod }_{c\in {\text{Φ}}_b}\frac{{\mu }_{bcg}^{Y_{bcg}}{e}^{-{\mu }_{bcg}}}{Y_{bcg}!}}{\frac{{\left({\sum }_{c\in {\text{Φ}}_b}{\mu }_{bcg}\right)}^{{\sum }_{c\in {\text{Φ}}_b}{Y}_{bcg}}{e}^{-{\sum }_{c\in {\text{Φ}}_b}{\mu }_{bcg}}}{\left({\sum }_{c\in {\text{Φ}}_b}{Y}_{bcg}\right)!}}=\frac{\left({\sum }_{c\in {\text{Φ}}_b}{Y}_{bcg}\right)!}{{\prod }_{c\in {\text{Φ}}_b}{Y}_{bcg}!}\cdot \prod _{c\in {\text{Φ}}_b}{\left(\frac{{\mu }_{bcg}}{{\sum }_{c^{\text{′}}\in {\text{Φ}}_b}{\mu }_{b{c}^{\text{′}}g}}\right)}^{Y_{bcg}}=\frac{\left({\sum }_{c\in {\text{Φ}}_b}{Y}_{bcg}\right)!}{{\prod }_{c\in {\text{Φ}}_b}{Y}_{bcg}!}\cdot \prod _{c\in {\text{Φ}}_b}{\left(\frac{m_{bc}{e}^{{\text{Γ}}_{bg}}}{{\sum }_{c^{\text{′}}\in {\text{Φ}}_b}{m}_{b{c}^{\text{′}}}{e}^{{\text{Γ}}_{bg}}}\right)}^{Y_{bcg}}=\frac{\left({\sum }_{c\in {\text{Φ}}_b}{Y}_{bcg}\right)!}{{\prod }_{c\in {\text{Φ}}_b}{Y}_{bcg}!}\cdot \prod _{c\in {\text{Φ}}_b}{\left(\frac{m_{bc}}{{\sum }_{c^{\text{′}}\in {\text{Φ}}_b}{m}_{b{c}^{\text{′}}}}\right)}^{Y_{bcg}}$$ (Equation 11)

Therefore, the conditional likelihood is independent of the batch parameter ${\beta }_{•g}$, which means

$$P\left(Y_{b1g}\text{,}\dots \text{,}{Y}_{b{n}_{b}g}|\sum _{c\in {\text{Φ}}_b}{Y}_{bcg},{\beta }_{•g},m_{b•},X_{•}\right)=P\left(Y_{b1g}\text{,}\dots \text{,}{Y}_{b{n}_{b}g}|\sum _{c\in {\text{Φ}}_b}{Y}_{bcg},m_{b•}\right).$$ (Equation 12)

A nearly identical calculation has been used to derive a computationally efficient algorithm to fit high dimensional regression models.¹² Equation 12 shows that $\sum _{c\in {\text{Φ}}_b}{Y}_{bcg}\left(b=1,\dots ,n_B\right)$ is a sufficient statistics for ${\beta }_{•g}$, i.e., the distribution of $Y_{bcg}$ is independent of ${\beta }_{•g}$ when conditional on $\sum _{c\in {\text{Φ}}_b}{Y}_{bcg}$.

With Equation 12, we can calculate the residual to measure the departure of observed data from the null distribution of $Y_{bcg}$ conditioned on $\sum _{c\in {\text{Φ}}_b}{Y}_{bcg}$ and $m_{b•}$. Equation 11 shows that this distribution is a multinomial distribution with the following parameters.

$$\begin{array}{c}\left(Y_{b1g}\text{,}\dots \text{,}{Y}_{bcg}\text{,}\dots \text{,}{Y}_{b{n}_{b}g}\right)|\sum _{c\in {\text{Φ}}_b}{Y}_{bcg},m_{b•}\sim \text{Mult}\left(\sum _{c\in {\text{Φ}}_b}\text{,}{Y}_{bcg}\text{,}{\left\{{\mathrm{\pi }}_{bcg}\right\}}_{c\in {\text{Φ}}_b}\right)\\ \text{where }{\mathrm{\pi }}_{bcg}=\frac{{\mu }_{bcg}}{{\sum }_{c\in {\text{Φ}}_b}{\mu }_{bcg}}=\frac{m_{bc}}{{\sum }_{c^{\text{′}}\in {\text{Φ}}_b}{m}_{b{c}^{\text{′}}}}\end{array}$$ (Equation 13)

Therefore, we can easily calculate the conditional mean and the variance that are required to calculate the residuals with the formula of the multinomial distribution as follows.

$$\begin{array}{l}\mathbb{E}\left[Y_{bcg}|\sum _{c\in {\text{Φ}}_b}{Y}_{bcg},m_{bc}\right]=\left[\sum _{c\in {\text{Φ}}_b}{Y}_{bcg}\right]\cdot {\mathrm{\pi }}_{bcg}\\ \text{Var}\left[Y_{bcg}|\sum _{c\in {\text{Φ}}_b}{Y}_{bcg},m_{bc}\right]=\left[\sum _{c\in {\text{Φ}}_b}{Y}_{bcg}\right]\cdot {\mathrm{\pi }}_{bcg}\cdot \left(1-{\mathrm{\pi }}_{bcg}\right)\end{array}$$ (Equation 14)

Equation 14 is then used to calculate the residual matrix ${\mathbf{R}}_{\text{FastRNA}}$.

$$R_{\text{FastRNA},bcg}=\frac{Y_{bcg}-\mathbb{E}\left[Y_{bcg}|{\sum }_{c\in {\text{Φ}}_b}{Y}_{bcg},m_{bc}\right]}{\sqrt{\text{Var}\left[Y_{bcg}|{\sum }_{c\in {\text{Φ}}_b}{Y}_{bcg},m_{bc}\right]}},$$ (Equation 15)

where $R_{\text{FastRNA},bcg}$ is the element of ${\mathbf{R}}_{\text{FastRNA}}$ as before.

After the residuals are obtained, one can perform feature selection and dimension reduction by calculating the variance gene-wise and applying SVD, respectively. However, as in scTransform and analytic Pearson residual, the residual matrix ${\mathbf{R}}_{\text{FastRNA}}$ is dense and can be prohibitively large for large scale data. In the following sections, we propose alternative algorithms that can perform feature selection and dimension reduction rapidly without forming large dense matrices.

FastRNA algorithm

We describe the algebra underlying FastRNA, our novel algorithm for high-speed feature selection and dimension reduction in scRNA-seq analysis. First, we introduce additional notations regarding matrix algebra. Let $M\in {\mathbb{R}}^{n\times m},N\in {\mathbb{R}}^{m\times l}$ be matrices and let $M_{ij}$, $N_{jk}$ be the elements of M and N, respectively. The subscripts denote the row and column indices, respectively. Then the element at the i-th row and k-th column of the product of two matrices is

$${\left(MN\right)}_{ik}=\sum _l{M}_{il}{N}_{lk},$$ (Equation 16)

so to show that a matrix is a product of two matrices, one can demonstrate by proving the above expression. This technique will be used throughout our derivation. Additionally, we write R and $R_{bcg}$, omitting the subscript FastRNA because the residual appearing in the following description will only refer to our method. Also, for notational simplicity, we define

$${\mu }_{bcg}=\mathbb{E}\left[Y_{bcg}|\sum _{c\in {\text{Φ}}_b}{Y}_{bcg},m_{bc}\right]=\left[\sum _{c\in {\text{Φ}}_b}{Y}_{bcg}\right]\cdot {\mathrm{\pi }}_{bcg}$$ (Equation 17)

and

$${\sigma }_{bcg}=\sqrt{\text{Var}\left[Y_{bcg}|\sum _{c\in {\text{Φ}}_b}{Y}_{bcg},m_{bc}\right]}=\sqrt{\left[\sum _{c\in {\text{Φ}}_b}{Y}_{bcg}\right]\cdot {\mathrm{\pi }}_{bcg}\cdot \left(1-{\mathrm{\pi }}_{bcg}\right)}.$$ (Equation 18)

Feature selection

As in scTransform and analytic Pearson residual, we calculate the variance of the residual for each gene under the null distribution. Hence, we must calculate the following

$$V_g=\frac{1}{{\sum }_b{n}_b}\sum _b\sum _{c\in {\text{Φ}}_b}{R}_{bcg}^2$$ (Equation 19)

because $\text{Var}\left(X\right)=\mathbb{E}\left(X^2\right)-\mathbb{E}{\left(X\right)}^2$ and $\mathbb{E}\left(R_{bcg}\right)=0$ by construction.

Previous methods have calculated $V_g$ from $R_{bcg}$. However, this requires calculating $R_{bcg}$ and storing it in memory. As we have described earlier, the time and memory requirement for forming this matrix can be highly demanding for large datasets. We show that $V_g$ can be calculated directly from raw data Y through manipulating only non-zero elements. Because scRNA-seq data are sparse by nature, if we can only selectively utilize non-zero elements in the calculation (sparse matrix algebra), we can dramatically reduce time and memory cost. Note that Y is a sparse matrix, but R is not sparse in general.

First, we expand $R_{bcg}^2$ to obtain

$$R_{bcg}^2=\frac{Y_{bcg}^2}{{\sigma }_{bcg}^2}-2\cdot \frac{Y_{bcg}{\mu }_{bcg}}{{\sigma }_{bcg}^2}+\frac{{\mu }_{bcg}^2}{{\sigma }_{bcg}^2}.$$ (Equation 20)

We show that each of these three terms in the right-hand side can be calculated in a sparse manner. We can sum over the first term only with non-zero elements because the numerator is mostly zero in scRNA-seq data. By substituting Equation 14, we can simplify the second and the third term.

$$\begin{array}{l}\frac{Y_{bcg}{\mu }_{bcg}}{{\sigma }_{bcg}^2}=\frac{Y_{bcg}}{1-{\mathrm{\pi }}_{bcg}}\\ \frac{{\mu }_{bcg}^2}{{\sigma }_{bcg}^2}=\left[\sum _{c^{\text{′}}\in {\text{Φ}}_b}{Y}_{b{c}^{\text{′}}g}\right]\cdot \frac{{\mathrm{\pi }}_{bcg}}{1-{\mathrm{\pi }}_{bcg}}\end{array}$$ (Equation 21)

This shows that the second term is mostly zero so it can be calculated like the first term with only non-zero elements.

What deserves attention is the third term, which incurs summation over the cells and therefore is mostly non-zero. Substituting Equation 21 into Equation 20 shows that

$$\sum _b\sum _{c\in {\text{Φ}}_b}\left[\sum _{c^{\text{′}}\in {\text{Φ}}_b}{Y}_{b{c}^{\text{′}}g}\right]\cdot \frac{{\mathrm{\pi }}_{bcg}}{1-{\mathrm{\pi }}_{bcg}}=\sum _b\left[\sum _{c^{\text{′}}\in {\text{Φ}}_b}{Y}_{b{c}^{\text{′}}g}\right]\cdot \sum _{c\in {\text{Φ}}_b}\frac{{\mathrm{\pi }}_{bcg}}{1-{\mathrm{\pi }}_{bcg}}.$$ (Equation 22)

The first term of the product, $\sum _{c^{\text{′}}\in {\text{Φ}}_b}{Y}_{b{c}^{\text{′}}g}$, can be calculated for each batch in a sparse manner. ${\mathrm{\pi }}_{bcg}$ in the second term of the product is a precalculated constant per cell, which is independent of gene g in our conditional Poisson model (Equation 13). Hence, there is no need to form $R_{bcg}$, which is generally a very large dense matrix.

Dimension reduction

We have described two approaches (SVD and spectral decomposition) to obtain principal components of cells in the previous section. We adapt the second strategy because after feature selection, the number of genes usually ranges from 500 to 5,000, which is much smaller than the number of cells that can go up to millions. Even without feature selection, the number of cells $n_C$ will go beyond the number of genes $n_G$ (∼50,000) when the data are large.

We first obtain the eigenvectors V of R by applying spectral decomposition on ${\mathbf{R}}^T\mathbf{R}$. To do this, we developed an algorithm that computes ${\mathbf{R}}^T\mathbf{R}$ directly from raw data Y through sparse algebra.

$${\mathbf{R}}^T\mathbf{R}=\left[\begin{array}{lll}{\mathbf{R}}_1^T\hfill & \cdots \hfill & {\mathbf{R}}_{n_B}^T\hfill \end{array}\right]\cdot \left[\begin{array}{l}{\mathbf{R}}_1\hfill \\ ⋮\hfill \\ {\mathbf{R}}_{n_B}\hfill \end{array}\right]=\sum _{b=1}^{n_B}{\mathbf{R}}_b^T{\mathbf{R}}_b$$ (Equation 23)

Thus, we now have to expand ${\mathbf{R}}_b^T{\mathbf{R}}_b$ for each b.

We define matrices A and B in terms of their entries.

$$\begin{array}{l}{\mathbf{A}}_{bcg}=\frac{Y_{bcg}}{{\sigma }_{bcg}}\\ {\mathbf{B}}_{bcg}=\frac{{\mu }_{bcg}}{{\sigma }_{bcg}}\end{array}$$ (Equation 24)

A is sparse because the numerators are mostly zero. However, B is generally a dense matrix. Now we expand ${\mathbf{R}}_b^T{\mathbf{R}}_b$.

$${\mathbf{R}}_b^T{\mathbf{R}}_b={\mathbf{A}}_b^T{\mathbf{A}}_b-2{\mathbf{A}}_b^T{\mathbf{B}}_b+{\mathbf{B}}_b^T{\mathbf{B}}_b$$ (Equation 25)

Examining Equation 25, it is clear that the first term ${\mathbf{A}}_b^T{\mathbf{A}}_b$ is a multiplication of two sparse matrices. Therefore, the difficult parts are the latter two. To proceed, we introduce new notations.

$$·m_{bc}=\sum _g{Y}_{bcg},m_{bg}=\sum _{c\in {\text{Φ}}_b}{Y}_{bcg},m_b=\sum _{g,c\in {\text{Φ}}_b}{Y}_{bcg}$$

• $p_{bc}=m_{bc}/m_b$ ($={\mathrm{\pi }}_{bcg}$ in Equation 13)

Expand ${\mathbf{A}}_b^T{\mathbf{B}}_b$ by substituting Equation 14.

$${\left({\mathbf{A}}_b^T{\mathbf{B}}_b\right)}_{g{g}^{\text{′}}}=\sum _{c\in {\text{Φ}}_b}{\mathbf{A}}_{bcg}{\mathbf{B}}_{bc{g}^{\text{′}}}=\sum _{c\in {\text{Φ}}_b}{\mathbf{A}}_{bcg}\sqrt{m_{b{g}^{\text{′}}}\frac{p_{bc}}{1-p_{bc}}}=\sqrt{m_{b{g}^{\text{′}}}}\cdot \sum _{c\in {\text{Φ}}_b}{\mathbf{A}}_{bcg}\sqrt{\frac{p_{bc}}{1-p_{bc}}}$$ (Equation 26)

In the light of Equation 16, $\sum _{c\in {\text{Φ}}_b}{\mathbf{A}}_{bcg}\sqrt{\frac{p_{bc}}{1-p_{bc}}}$ is a multiple of ${\mathbf{A}}_b$ (a sparse matrix) and vector (which is also a one-dimensional matrix) ${\left[\frac{p_{bc}}{1-p_{bc}}\right]}_{c\in {\text{Φ}}_b}$. Since ${\left[\sqrt{m_{b{g}^{\text{′}}}}\right]}_{g=1,\dots ,n_G}$ is also a vector, Equation 26 is an outer product of two vectors. Hence, only non-zero elements are involved and manipulations or large dense matrices are not required.

Next, expand ${\mathbf{B}}_b^T{\mathbf{B}}_b$ by substituting Equation 14.

$${\left({\mathbf{B}}_b^T{\mathbf{B}}_b\right)}_{g{g}^{\text{′}}}=\sum _{c\in {\text{Φ}}_b}{\mathbf{B}}_{bcg}{\mathbf{B}}_{bc{g}^{\text{′}}}=\sum _{c\in {\text{Φ}}_b}\sqrt{\frac{m_{bg}{p}_{bc}}{1-p_{bc}}}\cdot \sqrt{\frac{m_{b{g}^{\text{′}}}{p}_{bc}}{1-p_{bc}}}=\sqrt{m_{bg}{m}_{b{g}^{\text{′}}}}\sum _{c\in {\text{Φ}}_b}\frac{p_{bc}}{1-p_{bc}}$$ (Equation 27)

Similar to Equation 26, we can view Equation 27 in the light of Equation 16 to realize that this is simply a self outer product (multiplying the vector by itself) of vector ${\left[m_{bg}\right]}_{g=1,\dots ,n_G}$. The last part $\sum _{c\in {\text{Φ}}_b}\frac{p_{bc}}{1-p_{bc}}$ is simply a scalar, which is again a summation over a vector.

Finally, the principal component of cells $U\cdot \text{diag}\left(S\right)$ can be obtained after calculating the eigenvectors of ${\mathbf{R}}^T\mathbf{R}$, which we write as V.

$${\left({\mathbf{R}}_{b}V\right)}_{ck}={\left({\mathbf{A}}_{b}V\right)}_{ck}-{\left({\mathbf{B}}_{b}V\right)}_{ck}={\left({\mathbf{A}}_{b}V\right)}_{ck}-\sum _g{\mathbf{B}}_{bcg}{V}_{gk}={\left({\mathbf{A}}_{b}V\right)}_{ck}-\sum _g\sqrt{\frac{m_{bg}{p}_{bc}}{1-p_{bc}}}{V}_{gk}={\left({\mathbf{A}}_{b}V\right)}_{ck}-\sqrt{\frac{p_{bc}}{1-p_{bc}}}\sum _g\sqrt{m_{bg}}{V}_{gk}$$ (Equation 28)

$\sum _g\sqrt{m_{bg}}{V}_{gk}$ is a matrix-vector multiplication where the matrix is a $n_G\times n_P$ matrix ($n_P$ is the number of principal components), which is dense but small. This results in a vector, so Equation 28 is an outer product of two vectors ${\left[\sqrt{\frac{p_{bc}}{1-p_{bc}}}\right]}_{c\in {\text{Φ}}_b}$ and ${\left[\sum _g\sqrt{m_{bg}}{V}_{gk}\right]}_{k=1,\dots ,n_P}$ at the final stage. For ${\mathbf{A}}_{b}V$, it is a multiple of a large sparse matrix and a small dense matrix, which can be readily calculated with standard sparse linear algebra routines (e.g., mkl_sprase_?_mm of Intel MKL).

In sum, our calculation of the principal components only involves (1) sparse matrix algebra when a matrix is used in a multiplication; (2) vector-vector product, which is very fast and memory efficient in general; and (3) (exceptional) dense matrix multiplication only when the matrix size is small. By completely avoiding algebraic calculations involving large dense matrices, we remove the need for computing and storing the residual matrix in the memory, therefore improving time and memory efficiency dramatically.

Software implementation

The program was written with C++ and Cython. Intel Math Kernal Library (Intel MKL) routines were directly called with Cython interface to perform the described algorithm.

Potential numerical issues

There might be concerns on potential numerical issues such as underflows due to the small values (e.g., $p_{bc}$) in the algorithm. Specifically, $p_{bc}$ might be small resulting in underflow. Our method is built upon float32 and this datatype ranges approximately from ${10}^{-38}$ to ${10}^{38}$. By definition of $p_{bc}$, it is approximately at the range near $1/n_b$ $\left(b=1,\dots ,n_B\right)$, which is the reciprocal of the number of cells in batch b. Hence, for this value to underflow, $n_b$ should be large as ${10}^{38}$, which is larger than the number of cells in any living organism (e.g., approximately ${10}^{13}$ for human). Therefore, we conclude that there is no need for protection against underflow while running our algorithm.

Input/output formats

Our implementation takes CSC (compressed sparse column) format sparse matrix as an input. After taking the input, however, the internal functions only consider the triple (data, indices, indptr) and ignore the input CSC format. This is because our implementation directly calls the low-level sparse BLAS/LAPACK routines from Intel MKL, which takes the triple as an input rather than high-level sparse matrix layouts such as scipy.sparse. The advantage of directly manipulating the triple is that one can move between CSR (compressed sparse row) and CSC formats without additional overhead. For example, mkl_sparse_syrk only takes CSR inputs to calculate $\mathbf{A}{\mathbf{A}}^T$ (or ${\mathbf{A}}^T\mathbf{A}$ if a transpose option is set to True) for an input matrix A. A simple trick to apply this function to a CSC matrix B is to create a CSR matrix with the triple that constitutes B. This creates ${\mathbf{B}}^T$ in a CSR format by definition. Then we supply ${\mathbf{B}}^T$ to mkl_sparse_syrk with the transpose option, which computes ${\left({\mathbf{B}}^T\right)}^T{\mathbf{B}}^T=\mathbf{B}{\mathbf{B}}^T$.

Benchmark environment

Silhouette score and k-NN classification: Silhouette score and k-NN classification algorithm from scikit-learn version 1.0.1 were used for benchmark. For cell-type Silhouette score, the raw value ranging from −1 to 1 was obtained from the metrics.silhouette_samples function. For batch Silhouette score, we applied the absolute function to the raw Silhouette score obtained from the same function.

GLM-PCA and scry: We used the scry version 1.8 downloaded from Bioconductor. The accompanying version of GLM-PCA in scry was used. In benchmarks, scry feature selection and GLM-PCA were paired.

Scanpy and Analytic Pearson residual: We used the implementation in Scanpy version 1.9.

Seurat and scTransform: Seruat version 4.1.3 was downloaded from the CRAN. scTransform was provided within Seurat.

Splatter: Splatter 1.2.0 was downloaded through Bioconductor. A total of 1,500 genes and 4,000 cells were created. Five cell types were simulated in equal size from two batches. Six DEG thresholds were set: $\left\{1.2\text{,}1.5\text{,}2\text{,}2.5\text{,}3\text{,}4\right\}$.

t-SNE visualization: We used the openTSNE 0.6.2 implementation within Python 3.9.

Benchmarking hardware: We used the Intel(R) Xeon(R) Gold 6136 CPU @ 3.00 GHz processor for all the analysis. The system memory was 251 GB and 4 cores were used.

Runtime and memory measurement: Runtime was measured with the %timeit header in jupyter notebook. Memory was measured with the htop command in linux.

Datasets

Zhengmix8eq:¹³ This is a widely used mixture dataset comprising eight different FACS-labeled cell types. The dataset was downloaded with the DuoClustering2018. We used 3,000 top highly variable genes (HVGs) for each method and supplied 20 PCs for visualization (t-SNE exaggeration = 2 and perplexity = 30) and LISI benchmark.

PBMC from three 10X experiments:¹⁴ The data was downloaded from Broad single cell portal. We used 2,000 top HVGs for each method and supplied 50 PCs for visualization (t-SNE exaggeration = 2 and perplexity = 30). The dataset provides curated author-provided labels for the cells.

Mouse organogenesis atlas:¹⁵ The dataset was downloaded from GEO database accession number GEO: GSE119945. We selected 2,000 HVGs for the benchmark. Batch was controlled by “batch” variable in the metadata provided by the authors. Batch was controlled by “id” variable in the metadata provided by the authors. Top 50 principal components were supplied to t-SNE with exaggeration = 4 and perplexity = 30. Gene removal process to remove batch artifacts was done by the following procedure as described by Lause et al.⁶ For each batch and gene, the number of cells that expressed $>10$ unique molecular identifiers (UMIs) were counted. Next, they compared the fold-change in the numbers of such cells across batches. Genes that had $>100$-fold difference in the batch with the largest and the third largest number of such cells were excluded from analysis. This way, genes that enriched in two or less embryos were removed.

Results

Benchmarking of time and memory requirement

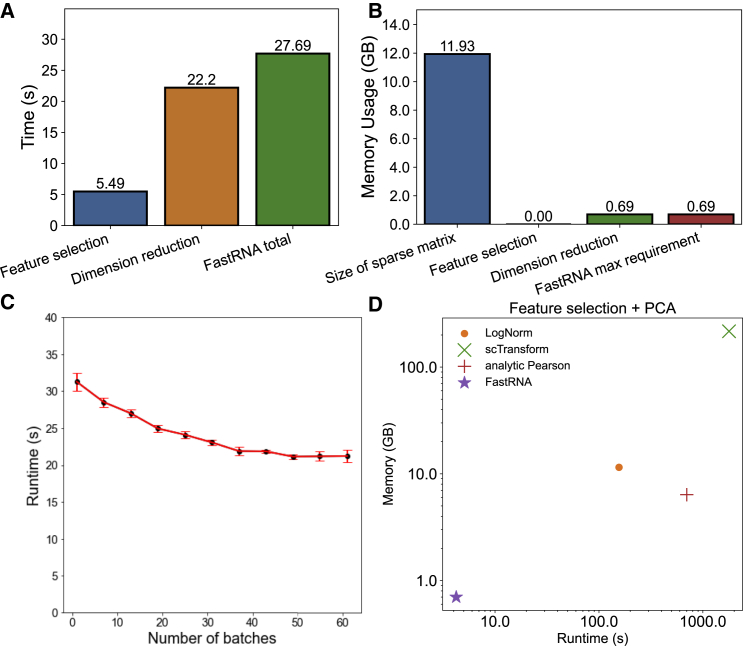
To benchmark the time and memory efficiency of FastRNA, we performed dimension reduction (PCA) of an atlas-scale mouse dataset with 2 million cells.¹⁵ This organogenesis dataset included 62 batches. The runtime and memory usage measured in our benchmarking environment shows that our method takes 27.7 seconds and 690 MB of memory to complete dimension reduction of the whole dataset (Figure 1A and 1B). This is a dramatic improvement because it has been reported that $\ge$100 GB memory and several hours of time are required to perform dimension reduction in such data via various PCA implementations (all based on log normalization).¹⁶ Using our method, several GB of memory in an ordinary laptop can be enough to run the analysis for large population-scale datasets.

Figure 1.

Time and memory efficiency of FastRNA

(A) Runtime of feature selection and dimension reduction of FastRNA.

(B) Memory use of FastRNA. Both memory usage and runtime were measured with respect to the time of execution of the program. The static memory allocation of the sparse matrix (12 GB) was not included.

(C) Runtime of FastRNA pipeline with respect to the number of batches. The error bars represent the interquartile ranges (IQRs) of 10 trials.

(D) Runtime (s) and memory usage (GB) of four methods in the downsampled ($n=\mathrm{200,000}$) mouse organogenesis data during feature selection and dimension reduction.

To measure the impact of the number of batches on the efficiency, we ignored the true batch labels of this dataset and assigned random batches, while gradually increasing the number of batches from 1 to 62. Unlike other previous methods whose performance is sensitive to the number of batches, the efficiency of our method was not affected by the number of batches (Figure 1C). This was expected because our conditional Poisson model accounts for the batch effects prior to the dimension reduction. In fact, when the number of batches increased, the efficiency slightly increased; we are investigating on why this is the case.

Next, we compared the efficiency of FastRNA to log normalization and previously proposed count-based methods: GLM-PCA, scTransform, and analytic Pearson residuals. For this atlas-scale mouse dataset, a direct comparison to competing methods was not possible because FastRNA was the only method that successfully ran on the full dataset in our benchmarking environment. To make the comparison feasible, we downsampled the dataset to 200,000 cells. The runtime and memory requirements of FastRNA on the downsampled dataset were considerably smaller than scTransform and analytic Pearson residuals as well as log normalization (Figure 1D). To process 200,000 cells, FastRNA only required 30 MB memory and took 4 s. By contrast, scTransform required 216 GB memory and took 6,424 s, and the analytic Pearson residual required 6.76 GB memory and took 700 s. GLM-PCA did not finish in 3 days for this subsampled dataset and was omitted. Thus, both the time and memory requirements of FastRNA were two orders of magnitude smaller than the second best count-based method. Log normalization took 11.47 GB memory and took 156 s. Thus, FastRNA required $\ge$300 times less memory and $\ge$30 times less time than log normalization.

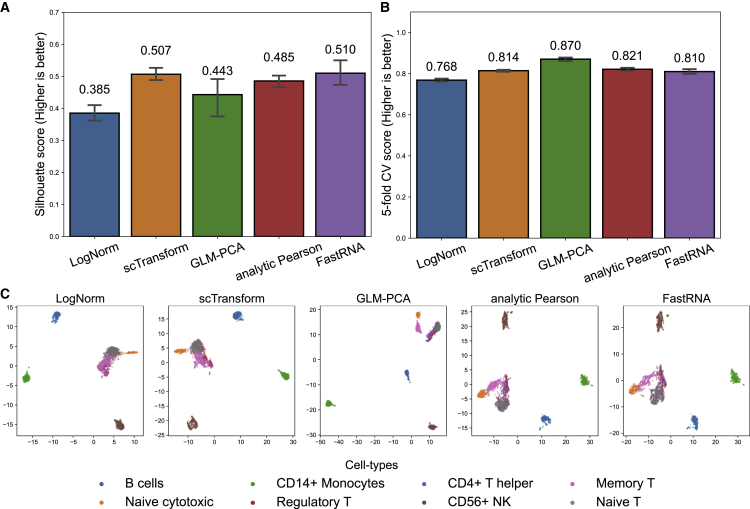
Benchmarking of the quality of dimension reduction using real data

Whereas the speed and the memory requirement of methods can be objectively measured, evaluating the quality of the resulting PC can be more challenging. What we can do is to look at whether the cells of the same cell type are clustered together in the PC space. For this purpose, we used the Zhengmix8eq dataset, a fluorescent-activated cell sorting (FACS)-labeled dataset widely used for benchmarking. This is an artificial mix of the cells for which we know the true types by FACS, and it can therefore be used to indirectly suggest the quality of the PC. Note that the following results are meant as a guide at best, as the benchmarking is based on a single artificial dataset.

We compared FastRNA to three other count-based methods, scTransform, GLM-PCA, and analytic Pearson residual. For completeness, we added the standard non-count-based log normalization (LogNorm) to this comparison. We measured Silhouette score, which measures how well the PC coordinates reflect the known labels. In addition, we measured 5-nearest-neighbor (NN) cell-type classification accuracy by 5-fold cross-validation (CV), which measures how well the five nearest neighbors of a point can predict the label of a point, when the point is in the test set (20%) and the neighbors are from the train set (80%). Note that 5-NN accuracy only measures the local structure and tends to not much penalize the situation that a true cluster is split into two or three chunks in the PC space.

Figure 2 shows that all count-based models had similar performance, while LogNorm stands behind the four methods. For the Silhouette score (Figure 2A), the four methods were similar (FastRNA 0.510, scTransform 0.507, GLM-PCA 0.443, and analytic Pearson 0.485), while LogNorm was lower (0.385). For 5-NN accuracy (Figure 2B), FastRNA (0.810) was slightly lower than scTransform (0.814), GLM-PCA (0.870), and analytic Pearson (0.821) but higher than LogNorm (0.768). GLM-PCA performed the 2nd worst in terms of Silhouette score (0.443) but performed the best in the 5-NN benchmark (0.870). Figure 2C shows the 2D embedding of the PC by tSNE, for which an objective assessment of the quality by human eyes is difficult.

Figure 2.

Benchmark of common normalization methods in the Zhengmix8eq dataset

(A) Cell-type Silhouette score of log normalization + RPCA, scTransform, GLM-PCA, analytic Pearson residual, and FastRNA. The error bars represent the 95% confidence intervals of the median silhouette score.

(B) 5-fold cross-validation 5-NN accuracy of the five methods. The error bars represent the interquartile range (IQR) of 5 trials of cross-validation.

(C) t-SNE visualization of the five methods colored by cell type.

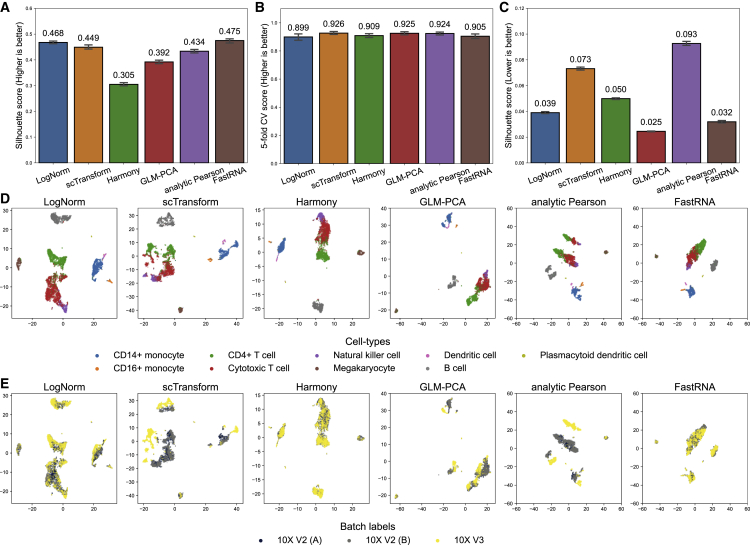
FastRNA excels in multi-batch benchmarking

We considered an additional benchmarking experiment assuming multiple batches exist in one dataset. To this end, we used a peripheral blood mononuclear cell (PBMC) dataset generated from three 10X experiments.¹⁴ Although the cell types are not FACS labeled, the author-provided labels can be used for benchmarking. Importantly, the dataset was a mixture of data generated by three different versions of technology (10X V2A, 10X V2B, and 10X V3). Because every technology can have its own bias, we can consider the generating technology as a batch with a batch effect.

In this experiment, we compared six methods. In addition to FastRNA and three count-based methods (GLM-PCA, scTransform, analytic Pearson residual), we tried LogNorm with batch correction by RPCA⁹ and Harmony.¹⁷ Harmony is an integration method of scRNA results and thus can be applied to correct for batches.

Like the previous experiment, the overall performance of three count-based methods were similar. For the Silhouette score (Figure 3A), FastRNA (0.475) was higher than scTransform (0.449), GLM-PCA (0.392), and analytic Pearson (0.434). Log normalization with batch correction (via RPCA) performed better than scTransform and analytic Pearson residual (0.468). Harmony (0.305) performed worse than the other methods. For the 5-NN accuracy (Figure 3B), all six methods were similar. FastRNA (0.905) was slightly lower than others (scTransform 0.926, Harmony 0.909, GLM-PCA 0.925, analytic Pearson residual 0.924) and better than log normalization with batch correction (0.899) (Figure 3C). The 2D embedding shows that while log normalization (with RPCA), Harmony, GLM-PCA, and FastRNA properly corrected batch effects, scTransform and analytic Pearson residuals split CD4⁺ T cells (and cytotoxic T cells) into two subclusters according to batch membership (Figure 3D and 3E). This partially explains why FastRNA had a slightly higher Silhouette score and slightly lower 5-NN accuracy: because the Silhouette score penalizes the split of a true cluster, while 5-NN accuracy (almost) does not.

Figure 3.

Benchmark of common normalization methods in a PBMC dataset from three 10X experiments

(A) Cell-type Silhouette score of log normalization + RPCA, scTransform, Harmony, GLM-PCA, analytic Pearson residual, and FastRNA. The error bars represent the 95% confidence interval of the median silhouette score.

(B) 5-fold cross-validation 5-NN accuracy of the six methods. The error bars represent the interquartile range (IQR) of 5 trials of cross-validation.

(C) Batch-wise Silhouette score of the six methods. The error bars represent the 95% confidence interval of the median silhouette score.

(D) t-SNE visualization of the six methods colored by cell type.

(E) Same as (D) but colored by batch label.

Nevertheless, when considering the batches of this data, FastRNA exceled. We calculated the Silhouette score with respect to batches (batch Silhouette score). A lower score is better because we do not want the cells clustered by batches. FastRNA showed much better (lower) score than the other methods. The score of FastRNA (0.032) was smaller than all methods except for GLM-PCA (0.025). Log normalization (with RPCA) and Harmony showed slightly worse performance. As expected from the 2D t-SNE embedding, scTransform and analytic Pearson residual could not correct batch effects well and thus showed worse scores.

To see whether the batch information was important for both logNorm and count-based methods, we additionally applied log normalization and GLM-PCA both without batch correction. Silhouette score was smaller than the batch-corrected counterparts (log normalization 0.201 versus 0.468 and GLM-PCA 0.274 versus 0.392) (Figure S1), showing that the batch information was crucial. 5-NN accuracy was slightly higher than the batch-corrected counterparts, which comes from the fact that 5-NN does not penalize split by batches. These findings are reconfirmed in the 2D t-SNE embeddings in Figure S2. As was observed for scTransform and analytic Pearson residual, log normalization and GLM-PCA showed splitting the same cell type into distinct clusters according to batch labels when the batch information was not given.

We measured the computation time of the methods for completing analysis in this dataset (Figure S3). This dataset was small with 9,806 cells, and thus all methods finished in 30 min. Nevertheless, we can expect that the relative efficiency of the methods will be similarly scaled as the size of the data grows. Again, FastRNA was the fastest among all methods (2.1 seconds). When we excluded the three methods that failed to correct for batches in this dataset (log normalization without batch correction, scTransform, and analytic Pearson residual) from our consideration, the second fastest method was Harmony, which took 37.1 s. Thus, FastRNA was an order of magnitude faster.

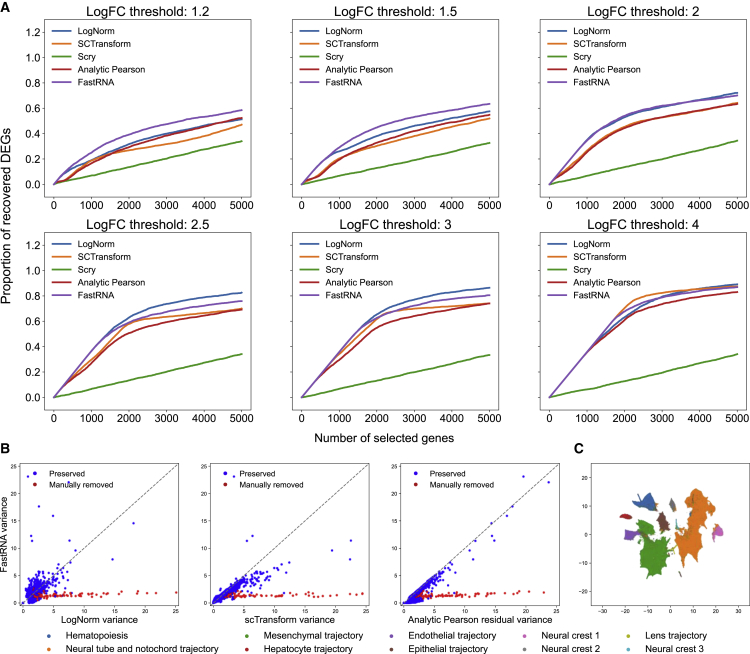
Batch correction of FastRNA helps feature selection

In the conditional Poisson framework of FastRNA, the effects of batches are eliminated prior to feature selection and dimension reduction. This preclusion of batch effects can help feature selection because it prevents artificial features from being selected only as a result of batch effects.

We simulated data by using Splatter.¹⁸ We generated five cell types from two batches (see material and methods). As true differentially expressed genes (DEGs) are known in a simulation setting, we measured the proportion of recovered true DEGs under various DEG thresholds (Figure 4A). We compared FastRNA with feature selections by log normalization, scTransform, analytic Pearson residual, and Scry.¹⁹ FastRNA performed better than the other methods when DEG thresholds were low. As the DEG threshold increased (larger log fold change), the other methods’ performance became comparable to FastRNA.

Figure 4.

Comparison of feature selection methods

(A) Proportion of recovered DEGs versus number of selected genes of log normalization, scTransform, scry, analytic Pearson residual, and FastRNA. The data was simulated with Splatter.

(B) Feature variances computed by FastRNA versus log normalization, scTransform, and analytic Pearson residual.

(C) t-SNE plot of the mouse organogenesis dataset with FastRNA dimension reduction.

For real data analysis, we applied these methods to the atlas-scale mouse organogenesis dataset that we used for speed benchmarking.¹⁵ This dataset comprises a large number (62) of batches. Because of the size of the dataset (2 million cells), it is impossible to run scTransform that can account for batches. A previous study instead applied analytic Pearson residual for the analysis of this dataset, as analytic Pearson was faster and feasible. But because analytic Pearson residual cannot account for batches, a manual curation process was required.⁶ The authors evaluated the final tSNE plot and found many single-batch clusters. To remove these clusters, they designed an additional quality control (QC) procedure for feature selection so that the artificial clusters can be cleaned out. Specifically, they selected genes that are exclusively high in less than two embryos and removed them (see material and methods).

We compared the variance of features calculated by FastRNA with log normalization, scTransform, and analytic Pearson residual in Figure 4B. As scTransform did not run for the full dataset, we subsampled 200,000 cells and used them for comparing the variance of features. Scry was excluded because it failed to run on the subsampled dataset. Figure 4B shows that as FastRNA precludes the batch effects from data, no additional manual curation is required for feature selection. The red dots denote the features that the previous study was able to manually detect and remove. For these artificial features, the variance calculated by FastRNA is already low, and therefore they are not selected as important features at the first stage. As a result, the t-SNE visualization using FastRNA coordinates was concordant with developmental trajectories and does not require further manual curation (Figure 4C).

Discussion

We proposed FastRNA, an extremely efficient and scalable method for dimension reduction and feature selection of scRNA-seq data. Our method accommodates flexible model parameters such as batch- and gene-dependent covariates while improving speed and memory efficiency through sparse matrix algebra. Our method enables population-scale scRNA-seq analysis inside a personal computer within minutes without sacrificing model complexity or accuracy. The experimental results show that our method can process small to moderate sized datasets within a second and millions of cells within a minute. It would even be possible to process billions of cells within a day according to our extrapolation.

The key features of FastRNA can be divided into two parts. The first is the conditional likelihood approach that is used to define batch-corrected residuals. The second is the alternative PCA algorithm using spectral decomposition of ${\mathit{R}}^T\mathit{R}$ (where R is the residual matrix) instead of SVD applied to R directly. Because R is large and dense, many SVD methods employ approximate strategies such as subsampling to obtain eigenvectors. FastRNA, on the other hand, using its spectral decomposition-based strategy, computes the eigenvectors without such approximation. The computed eigenvectors are algebraically equivalent to the eigenvector obtained by applying the full non-approximate SVD to R.

FastRNA enjoys many favorable theoretical properties. Our theory suggests that the efficiency is invariant under gene- and batch-dependent covariates and robust to the number of batches, which we confirmed in our benchmarking. This is because our conditional model eliminates the need to estimate these factors. One unique property of our method is that it completely removes the need to calculate or store the dense matrix of residuals, R. Although the derivations for dimension reduction and feature selection are based on R, the final equations only require sparse algebra.

Recently, out-of-core implementations of PCA have been suggested.^16,20 They are also called on-disk methods. These methods read only a block of the data from the disk when needed. The major drawback is that it requires many disk-accesses, which is much slower than accessing data from memory. PCAone, a recently proposed on-disk PCA method, also mentions this shortcoming and recommends the use of on-memory mode when the computing system has enough memory to store the whole data.²⁰ After loading the block of data from the disk, out-of-core methods convert the data into a dense matrix to make further calculations (e.g., log normalization). By contrast, FastRNA loads the whole data into memory prior to analysis, but it never converts the data into a dense form and always keeps it sparse to avoid excessive memory use.

There are concerns on the use of Poisson distribution rather than the more general negative-binomial distribution. Another concern is the dropout issue where more zeros are observed than expected. As FastRNA depends on the Poisson assumption, the method might not be adequate for data showing large over-dispersion or dropouts. Models such as ZIFA and ZINB-WaVE include zero-inflated components in the likelihood to overcome this issue.^21,22 However, such models can be prohibitively slow and, hence, may not be applied to large data like FastRNA. Furthermore, these methods do not have their own feature selection scheme that FastRNA has.

The scale of single-cell omics data is increasing rapidly, which calls for an urgent need for efficient methods that can handle large data. Sparsity of single-cell data is one of the most important key features for performance optimization, and FastRNA proposes one way to achieve extreme scalability by exploiting this feature, which is likely to motivate future method developments. Because FastRNA relies on the Poisson count model, future developments may incorporate extensions such as the negative-binomial model. Also, the model only supports categorical covariates so future developments for more flexible covariates is warranted.

The automation of the analysis is of utmost interest in both academia and industry as scRNA-seq technology becomes popular. Our approach automates a large portion of a typical scRNA-seq analysis pipeline from preprocessing (such as normalization) to dimension reduction (PCA) and batch correction. The speed, convenience, and performance of our method all stem from a single theory, which opens a door for future extensions of the framework. We expect that our method will directly serve as a practical tool in the era of population-level scRNA-seq analysis.

Published: October 6, 2022

Data and code availability

The source code of FastRNA is available at https://github.com/hanbin973/FastRNA. We also provide reproducible codes at https://github.com/hanbin973/FastRNA_paper. A use example can be found at https://fastrna.readthedocs.io/en/latest/.