Distribution of cholesterol in asymmetric membranes driven by composition and differential stress

Abstract

Many lipid membranes of eukaryotic cells are asymmetric, which means the two leaflets differ in at least one physical property, such as lipid composition or lateral stress. Maintaining this asymmetry is helped by the fact that ordinary phospholipids rarely transition between leaflets, but cholesterol is an exception: its flip-flop times are in the microsecond range, so that its distribution between leaflets is determined by a chemical equilibrium. In particular, preferential partitioning can draw cholesterol into a more saturated leaflet, and phospholipid number asymmetry can force it out of a compressed leaflet. Combining highly coarse-grained membrane simulations with theoretical modeling, we investigate how these two driving forces play against each other until cholesterol’s chemical potential is equilibrated. The theory includes two coupled elastic sheets and a Flory-Huggins mixing free energy with a $\chi$ parameter. We obtain a relationship between $\chi$ and the interaction strength between cholesterol and lipids in either of the two leaflets, and we find that it depends, albeit weakly, on lipid number asymmetry. The differential stress measurements under various asymmetry conditions agree with our theoretical predictions. Using the two kinds of asymmetries in combination, we find that it is possible to counteract the phospholipid number bias, and the resultant stress in the membrane, via the control of cholesterol mixing in the leaflets.

Significance

While we do not yet know the reason or purpose for biomembrane asymmetry, the fact that it is conserved across a broad spectrum of organisms implies that it is of fundamental importance. Additionally, interactions between cholesterol and phospholipids have been recognized as important components of membrane structure and cholesterol homeostasis. It remains unclear how asymmetry influences cholesterol-phospholipid interactions and, ultimately, partitioning of cholesterol in lipid bilayers. We investigate how cholesterol reacts to the presence of several forms of lipid membrane asymmetries using a combination of coarse-grained simulations and theoretical modeling. We anticipate that our simple model can shed light on the long-standing puzzle of how cholesterol distributes in plasma membranes and whether the resulting equilibrium puts them under differential stress.

Introduction

Biological membranes realize one of the key spatial organizing principles in living organisms. At their core, they are built on the structural motif of a self-assembled lipid bilayer, comprising hundreds of different lipid types, with a wide variety of additional proteins or larger-scale cellular assemblies adsorbed to or embedded into it (1,2). Many of these biomembranes, in particular the plasma membranes of eukaryotic cells, are asymmetric: their two constitutive leaflets differ in at least one physical property. This has been well known since work in the early 1970s (3, 4, 5, 6) and was recently shown to be widely conserved across all eukarya (7), suggesting that asymmetry plays a vital functional role—even though we have only started to unravel what this might be (8).

With the advent of techniques for preparing artificial asymmetric membranes—such as the phase-transfer protocol (9, 10, 11, 12, 13), the lipid-exchange protocol (14, 15, 16, 17, 18), and the hemifusion protocol (19)—it has become possible to disentangle the physical principles of lipid bilayer asymmetry from a host of confounding factors present in living biological systems. Working with such idealized model systems, scientists have discovered a number of unexpected phenomena that appear to rest entirely on asymmetry. For instance, several experimental studies have demonstrated that asymmetric membranes can be more rigid than their cognate symmetric counterparts: increases of the curvature modulus between 50% (13,20) and even 150% (12) have been reported. The fluid-gel transition in large unilamellar vesicles may happen separately in the two leaflets and over a much larger temperature range than is typically observed, depending on which lipids reside in the outer or inner leaflet (21). At the same time, molecular dynamics simulations of asymmetric bilayers have also observed elastic stiffening (22,23) and the stabilization of new types of phases (23,24) while discovering effects that so far remain incompletely understood, such as the existence of a residual tension in simulations of area balanced membranes (25, 26, 27).

Asymmetry is fundamentally a non-equilibrium phenomenon since it can decay by lipids “flip flopping” between leaflets. Cells must therefore maintain it by a variety of mechanisms that actively transport lipids against gradients in chemical potential (28,29), which requires the pertinent cellular machinery to outpace relaxation rates. This is easy for regular phospholipids, whose flip-flop timescales range from hours to days (30,31) but essentially impossible for cholesterol, where these timescales are believed to be in the microsecond range (32, 33, 34, 35). How cholesterol partitions between the two lipid leaflets is hence determined by thermal equilibrium conditions, which are set by the phase states in each leaflet. Notice that this view is legitimate even if the phospholipid content is in a non-equilibrium steady state because we can view it as an externally imposed boundary condition—much like a capacitor that is kept charged with the help of a battery or a fridge that is kept cold via a heat pump.

Cholesterol affects many properties of lipid membranes—ranging from their elastic response (22,36, 37, 38) to the emergence of rafts in multi-component mixtures (39, 40, 41, 42). It is therefore distressing that we know so little about how cholesterol is shared between the two leaflets: for mammalian plasma membranes, claims that the cholesterol content in the outer leaflet exceeds that of the inner one by more than an order of magnitude (43) coexist with claims that 60%–70% (44) or even 80% (45) of the total cholesterol content resides in the inner leaflet.

The conceptual challenge is that there are multiple thermodynamic driving forces that affect the distribution of cholesterol. Most obvious is an entropic preference for dispersing evenly between the two leaflets, all else being equal. However, in asymmetric membranes all else is not equal, and this creates at least two more drivers. First, the chemical composition of the lipid environment affects cholesterol’s free energy of partitioning because it prefers to solvate in saturated phases (34,40). Second, if the two leaflet tensions differ, cholesterol can lower the elastic energy associated with this differential stress (22) by translocating from the compressed into the tense leaflet, as has recently been shown in simulations (26). In reality, all three effects operate together, codetermining cholesterol’s thermodynamic potential and thus its transbilayer equilibrium. But while we have precise techniques to analyze the chemical composition of individual leaflets (7), currently no experimental method exists for measuring the differential stress—either directly or at least semi-quantitatively via some proxy observable. This incomplete understanding of driving forces makes it difficult to rationalize what cholesterol distribution to even expect.

In this work, we use a combination of coarse-grained simulations and theoretical modeling to examine how cholesterol responds to the presence of various types of lipid membrane asymmetries—individually or in combination. Our simulations employ a recent revision (46) of the coarse-grained Cooke model (47, 48, 49) designed to suppress the unphysically high lipid flip-flop rate inherent to many low-resolution lipid models. Our theory balances elastic, entropic, and mixing contributions and refines an earlier version proposed in ref. (22) by accounting for specific lipid area differences and a more explicit representation of lipid mixing via a mean-field lattice-gas model. We find that the interplay between these elastic and thermodynamic drivers explains all main trends in our simulations, often quantitatively. While several routes toward refinement exist (e.g., including inter-leaflet coupling, stresses due to curvature-elastic torques, and going beyond simple area additivity), our model offers a predictive framework for reasoning about the physics of asymmetric membrane states. It thereby constrains properties that are currently hard to measure directly, such as the magnitude of differential stress and the distribution of cholesterol.

methods

Theory

We begin by proposing a theoretical model for describing the distribution of cholesterol between the leaflets of an asymmetric membrane. It will be simplified in nature, accounting only for what we believe to be the two dominant effects—lipid number asymmetry and preferential partitioning. Moreover, we will make several idealized assumptions (for instance, specific lipid areas add and mixing can be described in a mean-field fashion). This leaves room for substantial quantitative improvements, but our present goal is rather to arrive at a first understanding of how the main players interact and how well this captures observations in (similarly idealized) model simulations.

Despite these simplifications, our modeling efforts admittedly unleash a startling amount of algebra that not every reader might want to brave. We hence assure those who prefer to eschew the details that they will be able to understand all our main conclusions, as long as they take note of 1) the key observables that emerge along the way (a glossary at the end of the paper will assist in the process) and 2) the main physical ideas that propel the argument. We will supplement our main result with many special cases and illustrations that afford a qualitative understanding of all major effects.

Consider, therefore, a bilayer that contains $L_{\pm }$ lipids of type $\pm$ and specific areas $a_{\pm }$ in its $\oplus$ or $\ominus$ leaflet, to which we add $C$ cholesterol molecules of specific area $a$, of which $C_{\pm }$ are in the $\oplus$ or $\ominus$ leaflet. To proceed, it will be useful to define the following variables:

$${\mathcal{A}}_{\pm }=L_{\pm }{a}_{\pm }+C_{\pm }a,$$ (1a)

$${\varphi }_{\text{a}}=\frac{Ca}{L_{+}{a}_{+}+L_{-}{a}_{-}+Ca},$$ (1b)

$$\Delta A_0=L_{+}{a}_{+}-L_{-}{a}_{-},$$ (1c)

$$\delta c=\frac{C_{+}-C_{-}}{C_{+}+C_{-}}.$$ (1d)

Their physical interpretation is as follows: ${\mathcal{A}}_{+}$ and ${\mathcal{A}}_{-}$ are the areas each leaflet individually would assume if they were under no tension; ${\varphi }_{\text{a}}$ is the area-weighted cholesterol fraction in the system; $\Delta A_0$ is the leaflet area difference in the absence of cholesterol; and $\delta c$ measures the cholesterol imbalance, i.e., how much the fraction of cholesterol differs from a 50:50 distribution. Recall that we make the strong assumption that specific lipid areas simply add.

Since generally ${\mathcal{A}}_{+}\ne {\mathcal{A}}_{-}$, the bilayer must compromise to a common area between these two values and hence will be differentially stressed even at zero net tension. This may prompt cholesterol to flip from the overfilled leaflet to the underfilled one. In addition, the difference in cholesterol’s free energy of solvation into either leaflet creates an independent partitioning bias. The equilibrium distribution then arises from a competition between those two drivers.

Number asymmetry

We will assume that a flat bilayer of individual stress-free leaflet areas ${\mathcal{A}}_{\pm }$ that compromises on a shared area $A$ has an elastic energy of

$$G_{\text{el}}\left(A\right)=\frac{1}{2}{K}_{A,\text{m}+}\frac{{\left(A-{\mathcal{A}}_{+}\right)}^2}{{\mathcal{A}}_{+}}+\frac{1}{2}{K}_{A,\text{m}-}\frac{{\left(A-{\mathcal{A}}_{-}\right)}^2}{{\mathcal{A}}_{-}},$$ (2)

where $K_{A,\text{m}\pm }$ are the area expansion moduli of the two leaflets. The net bilayer tension is $\Sigma =(\partial G_{\text{el}}/\partial A)$, a relation we can invert for the equilibrium area as a function of tension:

$$\frac{1}{A_{\text{eq}}\left(\Sigma \right)}=\frac{{\alpha }_{+}}{{\mathcal{A}}_{+}}+\frac{{\alpha }_{-}}{{\mathcal{A}}_{-}}\text{with}{\alpha }_{\pm }=\frac{K_{A,\text{m}\pm }}{K_A+\Sigma },$$ (3)

where $K_A=K_{A,\text{m}+}+K_{A,\text{m}-}$ is the bilayer stretching modulus. Inserting this back into Eq. 2 gives the tension-dependent energy

$$G_{\text{el}}\left(\Sigma \right)=\frac{1}{2}\frac{{({\mathcal{A}}_{+}-{\mathcal{A}}_{-})}^2}{\frac{{\mathcal{A}}_{+}}{K_{A,\text{m}+}}+\frac{{\mathcal{A}}_{-}}{K_{A,\text{m}-}}}+\frac{1}{2}\frac{{\Sigma }^2}{\frac{K_{A,\text{m}+}}{{\mathcal{A}}_{+}}+\frac{K_{A,\text{m}-}}{{\mathcal{A}}_{-}}}.$$ (4)

This expression takes its minimum at $\Sigma =0$, i.e., when the applied bilayer tension vanishes. We will from now on restrict to this important special case. If we further assume that $K_{A,\text{m}+}=K_{A,\text{m}-}$, which is typically true to very good approximation even if the leaflets consist of different lipids, we arrive at a very succinct expression for the elastic energy a bilayer has stored in its differential stress,

$$G_{\text{el}}\left(\Sigma =0\right)=\frac{1}{4}{K}_A\frac{{({\mathcal{A}}_{+}-{\mathcal{A}}_{-})}^2}{{\mathcal{A}}_{+}+{\mathcal{A}}_{-}},$$ (5)

which is the expression we will use to derive the rest of our theory.

Even if the net membrane tension $\Sigma$ vanishes, the individual leaflet tensions do not. Instead, they are given by the derivative of the $\pm$ contribution to the free energy with respect to area, evaluated at $A_{\text{eq, 0}}$:

$${\Sigma }_{\pm ,0}={\left(\frac{\partial G_{\text{el},\pm }\left(A\right)}{\partial A}\right)}_{\begin{array}{l}A=A_{\text{eq}}\hfill \\ \Sigma =0\hfill \end{array}}=\mp K_{A,\text{m}\pm }\frac{{\mathcal{A}}_{+}-{\mathcal{A}}_{-}}{{\mathcal{A}}_{+}+{\mathcal{A}}_{-}}.$$ (6)

Using the definitions from (1a), (1b), (1c), (1d), we can rewrite this as

$${\Sigma }_{\pm ,0}=\mp K_{A,\text{m}\pm }{\varphi }_{\text{a}}\left(\frac{\Delta A_0}{Ca}+\delta c\right),$$ (7)

which leads to a differential stress $\Delta {\Sigma }_0$ (at $\Sigma =0$) of

$$\Delta {\Sigma }_0:={\Sigma }_{+,0}-{\Sigma }_{-,0}=-K_A{\varphi }_{\text{a}}\left(\frac{\Delta A_0}{Ca}+\delta c\right).$$ (8)

Observe the two effects that contribute to it: the total stress-free phospholipid leaflet areas may differ $(\Delta A_0\ne 0)$ or cholesterol distributes unevenly between the leaflets $(\delta c\ne 0)$. Unless these two effects compensate, $\Delta {\Sigma }_0\ne 0$.

Partitioning asymmetry

In our previous work (22), we have modeled cholesterol’s preferential solvation by an empirical specific free-energy difference $\Delta g$ between the two leaflets, amended by the entropy of distributing among them. Here, we put this ansatz on a slightly more microscopic foundation by using a classical mean-field model for the free energy of solutions.

Consider a two-dimensional binary mixture with $N_i$ particles of type $i\in \left\{\mathrm{1,2}\right\}$ and molecular areas $a_i$. Defining $\overline{A}=N_1{a}_1+N_2{a}_2$, the area fractions are ${\varphi }_i=N_i{a}_i/\overline{A}$. We now write the mixing free energy as

$$\beta G_{\text{sol}}=N_1\log {\varphi }_1+N_2\log {\varphi }_2+\chi N_1{N}_2\frac{\sqrt{a_1{a}_2}}{\overline{A}},$$ (9)

where $\beta =1/k_{\text{B}}T$ is the inverse thermal energy. This equation mirrors Flory-Huggins theory (50,51), except that molecular areas take the place of the degrees of polymerization. The first two terms describe the ideal entropy of mixing, and the last term captures the mixing energy, which we write as a geometric average between interaction terms of the type $N_1{\varphi }_2$ and $N_2{\varphi }_1$ in order to symmetrize the definition of the mixing parameter $\chi$ (i.e., what lipid area it refers to). Such a system phase separates for

$$\chi >{\chi }_{\text{c}}=\frac{1}{2}{\left[{\left(\frac{a_1}{a_2}\right)}^{1/4}+{\left(\frac{a_2}{a_1}\right)}^{1/4}\right]}^2\ge 2,$$ (10)

a situation we wish to stay away from. This restricts us to mixing parameters smaller than ${\chi }_{\text{c}}$.

We now construct the free energy of an asymmetric bilayer from two parts: first, an expression of the form of Eq. 9 for each leaflet, with the two particle types being $+$ phospholipids and cholesterol in the $\oplus$ leaflet and $-$ phospholipids and cholesterol in the $\ominus$ leaflet, and second, the elastic energy from Eq. 5, which accounts for the stresses created by an inter-leaflet area mismatch.

Chemical equilibrium

Over the timescales we wish to describe, the phospholipids stay within their respective leaflets, while cholesterol can flip between them. This means that the numbers $C_{\pm }$ will adjust such as to minimize the free energy. This is equivalent to the statement that cholesterol’s chemical potential ${\mu }_{\pm }$ is the same in the two leaflets, as can be seen by the identity

$$0=\frac{\partial G}{\partial C_{+}}=\frac{\partial (G_{+}+G_{-})}{\partial C_{+}}=\frac{\partial G_{+}}{\partial C_{+}}-\frac{\partial G_{-}}{\partial C_{-}}={\mu }_{+}-{\mu }_{-}.$$ (11)

After a little bit of algebra, this equilibrium condition takes the form

$$0={\tilde{K}}_A{\varphi }_{\text{a}}\left[\frac{\Delta A_0}{Ca}+\delta c\right]+\log \frac{c_{a+}}{c_{a-}}+c_{a+}^2{\mathcal{X}}_a\left({\chi }_{+},b_{+},\frac{L_{+}}{C_{+}}\right)-c_{a-}^2{\mathcal{X}}_a\left({\chi }_{-},b_{-},\frac{L_{-}}{C_{-}}\right),$$ (12)

where we defined

$${\tilde{K}}_A:=\beta K_{A}a,$$ (13a)

$$c_{a\pm }:=\frac{C_{\pm }a}{L_{\pm }{a}_{\pm }+C_{\pm }a},$$ (13b)

$$b_{\pm }:=\frac{a_{\pm }}{a},$$ (13c)

and

$${\mathcal{X}}_a(\chi ,b,\zeta ):={\zeta }^2\left[(b-1)(b+{\zeta }^{-1})+b^{3/2}\chi \right].$$ (13d)

Here, ${\tilde{K}}_A$ is a scaled area expansion modulus, $c_{a\pm }$ is the area fraction of cholesterol in the $\oplus$ or $\ominus$ leaflet, and $b_{\pm }$ is a scaled area that approaches 1 if the respective phospholipid and cholesterol areas become the same.

The equilibrium condition Eq. 12 is quite complicated. To gain a bit more intuition for what it says, it is instructive to look at a few special cases:

• 1.Ignoring the solvation part of cholesterol’s free energy, only the term proportional to ${\tilde{K}}_A$ remains in Eq. 12. Comparing it with Eq. 8 shows that the differential stress $\Delta {\Sigma }_0$ vanishes in equilibrium. Cholesterol is pushed from the over- into the underfilled leaflet to exactly cancel the stress difference between them.
• 2.However, taking $G_{\text{sol}}\equiv 0$ is not the same as merely assuming no preferential partitioning, ${\chi }_{\pm }=0$. There are two reasons for this: first, the function ${\mathcal{X}}_a$ generally does not vanish in that case because different specific lipid areas slightly affect the intra-leaflet phospholipid-cholesterol mixing entropy. Second, even if the areas are the same, so that ${\mathcal{X}}_a$ vanishes when ${\chi }_{\pm }=0$, the inter-leaflet distribution entropy $\log (c_{a+}/c_{a-})$ still remains. These two entropy contributions will oppose a full stress relaxation, or in other words, stress-induced reshuffling of cholesterol is entropically unfavorable.
• 3.If there are no elastic contributions to the free energy, equilibrium is determined by the ${\tilde{K}}_A$-independent terms in Eq. 12. At this point, it is difficult to see what this implies, but the physics is very transparent in the limit where all specific lipid areas are identical—as we will discuss below. For now, it is important to realize, though, that ${\tilde{K}}_A=0$ is not the same as merely assuming an initially balanced phospholipid distribution, $\Delta A_0=0$, because of the remaining $\delta c$ term. Hence, a partitioning-induced redistribution of cholesterol is also limited by the resulting elastic stresses. In addition, if we add cholesterol to a bilayer that starts out as perfectly area balanced, preferential solvation will create a differential stress where there was none before.

Predicting the cholesterol distribution

To find the equilibrium cholesterol distribution, we need to solve Eq. 12 for $\delta c$. Combining Eq. 1d with Eq. 13b yields

$$c_{a\pm }:=\frac{\frac{1}{2}Ca(1\pm \delta c)}{L_{\pm }{a}_{\pm }+\frac{1}{2}Ca(1\pm \delta c)}=\frac{1\pm \delta c}{{\overline{c}}_{a\pm }^{-1}\pm \delta c},$$ (14)

where we defined

$${\overline{c}}_{a\pm }=c_{a\pm }(\delta c=0)=\frac{Ca}{2L_{\pm }{a}_{\pm }+Ca},$$ (15)

which is cholesterol’s area fraction in the two leaflets at 50:50 distribution. Inserting Eq. 14 into Eq. 12 reveals that solving for $\delta c$ analytically is not an option. But as long as $\delta c$ is not too large, i.e., for weakly asymmetric situations, we can make progress by expanding Eq. 12 around $\delta c=0$. This can be done in closed form since the expansion of the ${\mathcal{X}}_a$ terms reproduce similar ${\mathcal{X}}_a$ terms:

$$c_{a\pm }^2{\mathcal{X}}_a\left({\chi }_{\pm },b_{\pm },\frac{L_{\pm }}{C_{\pm }}\right)={\sum }_{n=0}^{\infty }{\left(-{\overline{c}}_{a\pm }\delta c\right)}^n{X}_{a\pm }^{(n+1)},$$ (16)

where

$$X_{a\pm }^{\left(n\right)}={\overline{c}}_{a\pm }^2{\mathcal{X}}_a\left(n{\chi }_{\pm },b_{\pm },\frac{2L_{\pm }}{C}\right).$$ (17)

At linear order in $\delta c$, and after a bit more algebra, we obtain the cholesterol asymmetry

$$\delta c=\frac{X_{a+}^{\left(1\right)}-X_{a-}^{\left(1\right)}+\log \frac{{\overline{c}}_{a+}}{{\overline{c}}_{a-}}+{\tilde{K}}_A{\varphi }_{\text{a}}\frac{\Delta A_0}{Ca}}{{\overline{c}}_{a+}(X_{a+}^{\left(2\right)}+1)+{\overline{c}}_{a-}(X_{a-}^{\left(2\right)}+1)-2-{\tilde{K}}_A{\varphi }_{\text{a}}}.$$ (18)

Unpacking a few key points

We will later on use Eqs. 17 and 18 to describe our simulations. Unfortunately, their implications are not easy to discern, largely because the conditions of unequal specific lipid areas clutter up the algebra. To gain a better intuition for the basic physics, let us more closely examine the special case of equal specific lipid areas, $a_{+}=a_{-}=a$, which we will flag using the label “e.a.” in equations that only hold in that case. While this is a reasonably good assumption for phospholipids, it evidently works poorly for cholesterol, which is much smaller, and hence the simplified e.a. formulas should not be used for real systems. They do work quite well for our simplified simulations, though, in which a “cholesterol” lipid mostly looks like a normal lipid, except it can flip flop. The main benefit of this simplification is that most predictions of Eq. 18 are qualitatively robust, and the added clarity is worth the loss of quantitative accuracy.

If all specific lipid areas are equal, it is more convenient to measure lipid content in numbers and mole fractions. Let us thus define the new variables

$$\varphi :=\frac{C}{L_{+}+L_{-}+C},$$ (19a)

$$\delta \ell :=\frac{L_{+}-L_{-}}{L_{+}+L_{-}},$$ (19b)

$${\overline{c}}_{\pm }:=\frac{C}{2L_{\pm }+C},$$ (19c)

which are, respectively, the mole fraction of cholesterol in the system, the relative phospholipid asymmetry across the leaflets, and the mole fraction of cholesterol in each leaflet under a hypothetical 50:50 distribution. The latter replaces the area fraction ${\overline{c}}_{a\pm }$ from Eq. 13b, and it relates to the former two via

$$\frac{1}{{\overline{c}}_{\pm }}=\left(\frac{1}{\varphi }-1\right)\left(1\pm \delta \ell \right)+1.$$ (20)

If we now go to the equal specific lipid area (e.a.) scenario outlined above, our prediction for the cholesterol distribution strongly simplifies:

$$\delta c\stackrel{\text{e.a.}}{=}\frac{X_{+}-X_{-}+\log \frac{{\overline{c}}_{+}}{{\overline{c}}_{-}}+{\tilde{K}}_A(1-\varphi )\delta \ell }{{\overline{c}}_{+}(2X_{+}+1)+{\overline{c}}_{-}(2X_{-}+1)-2-{\tilde{K}}_A\varphi },$$ (21)

where

$$X_{\pm }:={\overline{c}}_{\pm }^2{\mathcal{X}}_a\left({\chi }_{\pm },1,\frac{2L_{\pm }}{C}\right)={(1-{\overline{c}}_{\pm })}^2{\chi }_{\pm },$$ (22)

which is now proportional to the $\chi$ parameter of the $\oplus$ or $\ominus$ leaflet and, in the limit of low cholesterol concentration, becomes identical to it.

At this point, it makes sense to compare with our previous model from ref. (22), which, from the start, assumed equal specific lipid areas for the mixing terms but not for the elastic term. Equalizing areas also for the latter, our older model predicts

$$\delta c\stackrel{\text{e.a.}}{=}\frac{-\beta \Delta g+{\tilde{K}}_A(1-\varphi )\delta \ell }{-2-{\tilde{K}}_A\varphi }\left(\text{old model}\right).$$ (23)

In the dilute limit, ${\overline{c}}_{\pm }\to 0$, Eq. 21 almost converges towards this when we identify $-\beta \Delta g={\chi }_{+}-{\chi }_{-}$, except for the remaining term $\log ({\overline{c}}_{+}/{\overline{c}}_{-})$ in the numerator. That term is important, though, to make this interpretation consistent. To see this, imagine the stress drops out of the chemical equilibrium (i.e., just set ${\tilde{K}}_A=0$). Eq. 11 then states that

$$0\stackrel{\text{e.a.}}{=}\log \frac{c_{+}}{c_{-}}+{\chi }_{+}{(1-c_{+})}^2-{\chi }_{-}{(1-c_{-})}^2.$$ (24)

In the dilute limit this yields $c_{+}/c_{-}={\text{e}}^{-({\chi }_{+}-{\chi }_{-})}={\text{e}}^{\beta \Delta g}$, as we would expect for a partitioning equilibrium driven by a difference in solvation free energy alone.

Let us now examine the interplay between stress and solvation in two important examples. First, consider a bilayer with a given cholesterol mole fraction $\varphi$. We can bias the cholesterol distribution either by imposing a phospholipid asymmetry $\delta \ell$ or by some non-zero mixing parameters ${\chi }_{\pm }$. Since the dominant influence will turn out to be the difference between ${\chi }_{+}$ and ${\chi }_{-}$, let us also introduce the symmetrized variables

$$\begin{array}{ll}\delta \chi ={\chi }_{+}-{\chi }_{-}\hfill & \hfill \\ 2\overline{\chi }={\chi }_{+}+{\chi }_{-}\hfill & \hfill \end{array}\leftrightarrow {\chi }_{\pm }=\overline{\chi }\pm \frac{1}{2}\delta \chi .$$ (25)

Specifically, let us pick a symmetric situation in which $\overline{\chi }=0$. Observe that with increasing $\delta \chi$ or with increasing $\delta \ell$, cholesterol is pushed out of the $\oplus$ leaflet and drawn into the $\ominus$ leaflet, thereby decreasing $\delta c$. An important part of the subsequent investigations will be to quantify how these two effects combine.

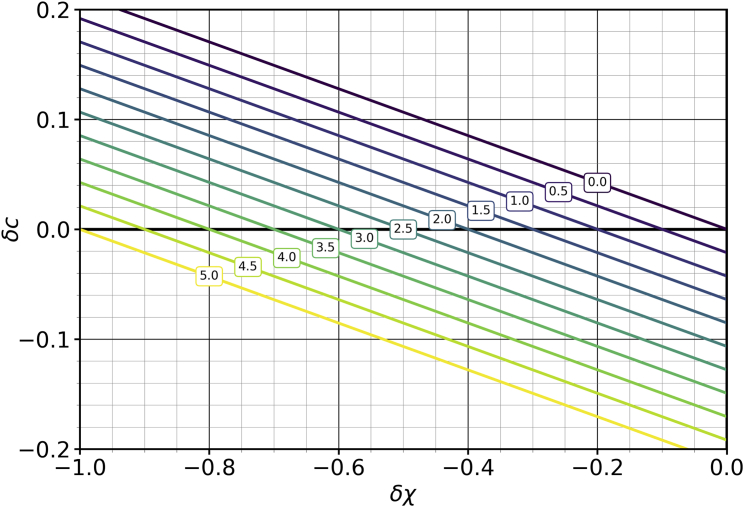
Fig. 1 illustrates this scenario for a set of $\delta c\left(\delta \chi \right)$ curves, parametrized by $\delta \ell$ values. Even though the curves’ decrease with $\delta \chi$ and $\delta \ell$ both appear linear, this is not strictly so. Nevertheless, this almost linearity suggests to expand $\delta c(\delta \chi ,\delta \ell )$ to first order in both arguments, which yields

$$2\delta c(\delta \chi ,\delta \ell )\stackrel{\text{e.a.}}{\approx }-\frac{{(1-\varphi )}^2\delta \chi +({\tilde{K}}_A-2)(1-\varphi )\delta \ell }{1+\frac{1}{2}({\tilde{K}}_A-2)\varphi }.$$ (26)

Figure 1.

Cholesterol asymmetry $\delta c$ as a function of the mixing parameter difference $\delta \chi$ (assuming also that $\overline{\chi }=0$). The individual curves correspond to lipid asymmetries $\delta \ell$ between 0% and 5%, as indicated in the boxed labels. For this figure, the cholesterol mole fraction is $\varphi =10\%$, and the scaled stretching modulus is ${\tilde{K}}_A=20$. To see this figure in color, go online.

For the case of Fig. 1, this linearization would be indistinguishable from the full curves (the absolute difference is around $5\times {10}^{-5}$). Moreover, had we distributed push/pull asymmetrically by defining $\overline{\chi }=\frac{1}{2}\epsilon \delta \chi$ (such that for $\epsilon =1$, the entire effect rests on ${\chi }_{+}$ while ${\chi }_{-}=0$, and for $\epsilon =-1$, it is the other way around), we would have found that the term in Eq. 26 proportional to $\delta \chi$ acquires a correction, which in the limit of large ${\tilde{K}}_A$ (the typical situation) is smaller than the base term by a factor of $2\epsilon \delta \ell$. The $\epsilon$ correction is hence proportional to both smallness parameters, $\delta \chi$ and $\delta \ell$, and so it is effectively quadratic. Stated differently, the effect of the average mixing parameter $\overline{\chi }$ on the cholesterol distribution is subdominant.

Eq. 26 makes a simple prediction for the iso-asymmetric dependence of the mixing parameter on the lipid number asymmetry—meaning, what change in $\delta \chi$ is needed to compensate for a change in number asymmetry $\delta \ell$:

$$\delta c=\text{const.}\leftrightarrow {\left(\frac{\partial \delta \chi }{\partial \delta \ell }\right)}_{\delta c,\varphi }\stackrel{\text{e.a.}}{\approx }-\frac{{\tilde{K}}_A-2}{1-\varphi }.$$ (27)

A phospholipid number bias can be undone by a proportional solvation bias, and the constant of proportionality—the right-hand side of Eq. 27—consists entirely of experimentally measurable observables. For instance, in the case of Fig. 1, each percentage point increase in $\delta \ell$ requires decreasing $\delta \chi$ by 0.2 to keep the cholesterol asymmetry constant. The effect is essentially proportional to the expansion modulus ${\tilde{K}}_A$ because a larger value makes it more expensive to counteract an imposed lipid number asymmetry. The extra “$-2$” shift originates from the term $\log ({\overline{c}}_{+}/{\overline{c}}_{-})$ in Eq. 21, which once again shows that entropy helps (a little bit) to even out the cholesterol distribution. The term $1-\varphi$ in the denominator implies that at a larger cholesterol mole fraction, we also need a larger shift in the mixing parameter. This happens because more cholesterol also means fewer phospholipids, and only the latter impose the solvation bias.

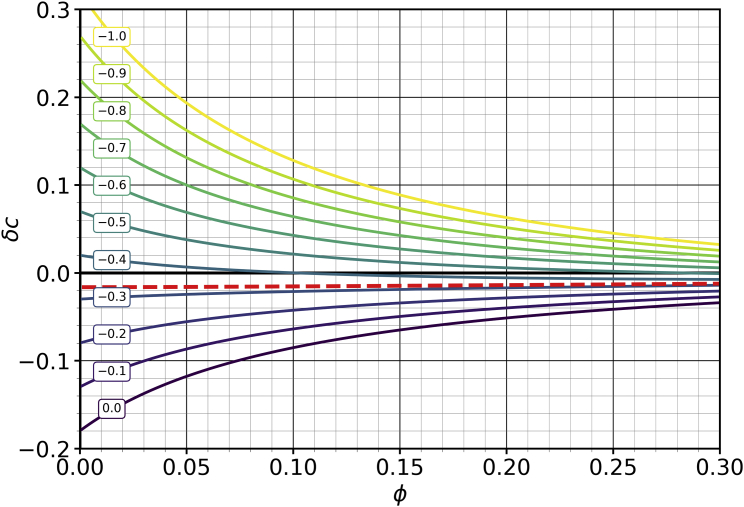
As a second example, consider the dependence of cholesterol asymmetry $\delta c$ on cholesterol mole fraction $\varphi$, as indicated in Fig. 2 for $\delta \ell =2\%$ and again ${\tilde{K}}_A=20$. The individual curves once more correspond to mixing parameter differences $\delta \chi$ that vary between $-1$ and 0 in steps of 0.1, as indicated in the small, boxed labels. For $\delta \chi =0$, cholesterol has no solvation preference for either leaflet but is pushed out of the $\oplus$ leaflet due to overcrowding, leading to $\delta c<0$. Tuning $\delta \chi$ negative renders the $\oplus$ leaflet more attractive for cholesterol, while the $\ominus$ leaflet becomes less so. This acts against the stress-based redistribution and increases $\delta c$ at all values of $\varphi$. For a sufficiently negative $\delta \chi$ value, the imbalance reverses: even if the upper leaflet is overcrowded, cholesterol nevertheless prefers to go there, since the free-energy gain due to preferential solvation overcomes the elastic energy cost.

Figure 2.

Cholesterol asymmetry $\delta c$ as a function of cholesterol mole fraction $\varphi$ for different values of leaflet mixing parameter differences $\delta \chi \in \{-1,-0.9,\dots ,0\}$ as indicated in the boxed labels (while $\overline{\chi }=0$). The red dashed curve for $\delta \chi \approx -0.327$ is not exactly horizontal ($\delta c$ varies approximately between $-0.016$ and $-0.012$), but this small $\varphi$ dependence is invisible at this scale. For this figure, the asymmetry $\delta \ell =2\%$, and the scaled stretching modulus is again ${\tilde{K}}_A=20$. To see this figure in color, go online.

Observe that the redistribution of cholesterol is typically more pronounced for lower cholesterol mole fractions, except near a special value $\delta \tilde{\chi }$ (red dashed curve), where $\delta c\left(\varphi \right)$ appears to be (but is not exactly) flat. We can find this curve by setting $\delta c^{\prime }(\varphi =0)=0$. To linear order in $\delta \ell$, this yields

$$\delta \tilde{\chi }\stackrel{\text{e.a.}}{\approx }-\frac{{\tilde{K}}_A-2}{{\tilde{K}}_A+2}{\tilde{K}}_A\delta \ell \stackrel{{\tilde{K}}_A\gg 1}{\to }-{\tilde{K}}_A\delta \ell ,$$ (28a)

$$\delta \tilde{c}\stackrel{\text{e.a.}}{\approx }-\frac{{\tilde{K}}_A-2}{{\tilde{K}}_A+2}\delta \ell \stackrel{{\tilde{K}}_A\gg 1}{\to }-\delta \ell$$ (28b)

for that special value $\delta \tilde{\chi }$ and its associated asymmetry $\delta \tilde{c}$. A comparison with Eq. 26 shows that $\delta \tilde{\chi }$ is close to, but not identical to, the $\delta \chi$-value at which the asymmetry vanishes.

Eq. 26 expresses the cholesterol asymmetry using $\delta \ell$ as a measure for the bilayer’s overall phospholipid asymmetry. We can alternatively write the latter in terms of the differential stress $\Delta {\Sigma }_0$. Combining Eq. 26 with Eqs. 1b, 1c, and 8, we readily find the rather concise relation

$$2\delta c(\delta \chi ,\Delta {\tilde{\Sigma }}_0)\stackrel{\text{e.a.}}{\approx }({\tilde{K}}_A-2)\text{Δ}{\tilde{\Sigma }}_0-{(1-\varphi )}^2\delta \chi ,$$ (29)

where we also defined the dimensionless differential stress $\Delta {\tilde{\Sigma }}_0:=\Delta {\Sigma }_0/K_A$. Remarkably, in the special case of zero preferential partitioning, $\delta \chi =0$, the cholesterol asymmetry becomes independent of the overall cholesterol fraction $\varphi$ and is just proportional to differential stress. This level of universality does not hold if asymmetry is instead characterized by $\delta \ell$. Furthermore, the equivalent iso-asymmetric dependence of the mixing parameter on the differential stress is given by

$$\delta c=\text{const.}\leftrightarrow {\left(\frac{\partial \delta \chi }{\partial \Delta {\tilde{\Sigma }}_0}\right)}_{\delta c,\varphi }\stackrel{\text{e.a.}}{\approx }\frac{{\tilde{K}}_A-2}{{(1-\varphi )}^2},$$ (30)

showing how partitioning bias needs to counter differential stress without changing the cholesterol asymmetry.

Simulations

Molecular dynamics simulations were performed using the highly coarse-grained (CG) implicit solvent lipid model by Cooke et al. (47,48) in a modified version by Foley and Deserno (46). We adjusted it to include a flip-competent lipid species (cholesterol), as detailed below. The simulations were carried out using the ESPResSo package (52).

We recall that ref. (22) compared a simplified earlier version of our present theory for cholesterol partitioning against simulations using the MARTINI model, which is slightly less CG and hence represents real lipids and their mixtures better (53). However, the wide parameter scans conducted in this work would have been very costly at this level, and they are not needed to test most of the predictions of the current theory.

Cooke model

The Cooke model is a versatile lipid model used to simulate bilayer membranes (47, 48, 49). Each lipid is represented by a string of three consecutive beads, with one bead representing the hydrophilic head and two comprising the hydrophobic tail region. The latter attract via a pair potential of range $w_{\text{c}}$, which drives self-assembly in the absence of an explicit solvent. When simulating asymmetric membranes, there is much insight to be gained from even a highly CG model such as this, since most aspects of asymmetry that are relevant to our discussion only depend on low-resolution features such as density differences and lipid interactions. However, while the simplicity of CG aids efficiency, we run into an entirely separate problem: to simulate long-lived metastable asymmetric systems, we need the lipid number asymmetry $\delta \ell$ to stay constant over the timescales of interest. But CG lipid models tend to have much higher flip-flop rates compared to real systems, which quickly eradicates any phospholipid number asymmetry set up at the beginning of the simulation.

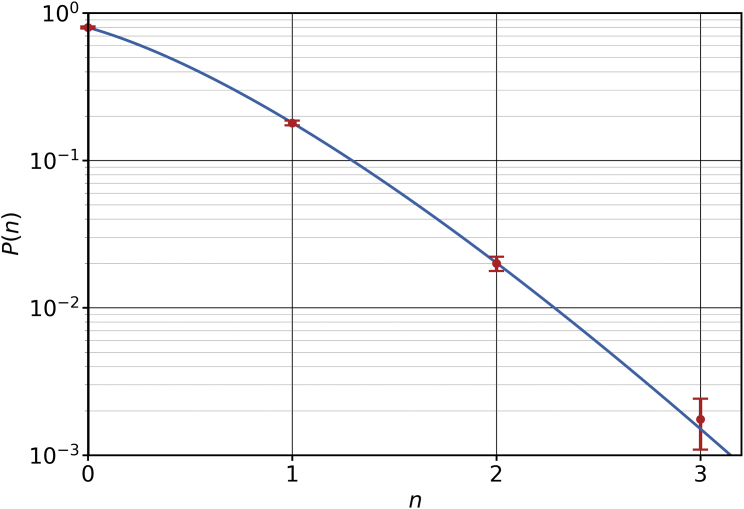
The four-bead, “flip-fixed” Cooke model (46) overcomes this drawback and succeeds in maintaining imposed $\delta \ell$ values of up to 11%. It achieves this by assigning a leaflet identity to each lipid at the start of the simulation and rendering interactions between lipids of different leaflet identity energetically unfavorable. Modeling the lipids with four beads instead of three—one “head” bead, two “middle” beads, and one “tail” bead—creates more pair interactions and enables higher overall cross-identity penalties without too strongly affecting the interactions between same-identity lipids (and hence bilayer structure and thermodynamics). In our case, the $\pm$-type lipids, native to the $\oplus$ and $\ominus$ leaflets, respectively, are flip suppressed and are expected to stay in their native leaflets throughout the simulation—with the exception of a few rare and temporary excursions. More precisely, if a single lipid experiences an energetic penalty ${\epsilon }^{\ast }$ for trespassing into the wrong leaflet, and if individual excursions happen independently, then the probability $P\left(n\right)$ of finding a small number $n$ of lipids on the wrong side is easily seen to be

$$P\left(n\right)=\left(\begin{array}{c}N\\ n\end{array}\right)\frac{{\text{e}}^{-\beta {\epsilon }^{\ast }n}}{{(1+{\text{e}}^{-\beta {\epsilon }^{\ast }})}^N},$$ (31)

where $N$ is the number of lipids in the leaflet from which the $n$ lipids escaped. Fig. 3 illustrates that this is an excellent description of trespass occurrences; in fact, it permits us to estimate a flipping penalty of ${\epsilon }^{\ast }\approx 7k_{\text{B}}T$.

Figure 3.

Probability $P\left(n\right)$ of $n$$\oplus$-type lipids venturing into the $\ominus$ leaflet, for a symmetric membrane containing 512 lipids in total (but no additional cholesterol). The solid curve is a fit to Eq. 31, giving ${\epsilon }^{\ast }\approx 7k_{\text{B}}T$. Error bars show the error of the mean. To see this figure in color, go online.

Modifications

To investigate how a rapidly flip-flopping species affects membrane asymmetry, we introduce another type of lipid for which the leaflet-identity-based penalization is simply turned off. Since the flip-flop rate of our highly CG lipids is large in the absence of special interventions, this species will fairly quickly equilibrate between the leaflets. It resembles cholesterol in its ability to do so, but of course lacks many of cholesterol’s other idiosyncratic effects on membranes—an obvious limitation of our approach, which focuses on the basic physics of a constrained partitioning equilibrium.

It is important to note that our mechanism of maintaining phospholipid number asymmetry becomes more challenging in the presence of a flip-competent species. Recall that we penalize certain interactions between, say, a trespassing $+$-type lipid and its surrounding $-$-type neighbors. Cholesterol dilutes the occurrence of these contacts to an extent roughly proportional to its mole fraction $\varphi$, and beyond a certain concentration, the remaining penalty is too weak to maintain asymmetry. We tested our model over a range of cholesterol concentrations and found that asymmetry can no longer be maintained reliably for $\varphi \underset{˜}{>}25\%$. We therefore will restrict ourselves to $\varphi \le 20\%$. To be clear, this does not imply that real asymmetric membranes would lose their asymmetry at a cholesterol content beyond 25%; for now, this is merely a limitation of the way our model is set up.

Besides phospholipid number asymmetry, and the ensuing elastic stresses, we investigate the preferential interaction of cholesterol with the host lipids of a given leaflet as a second factor regulating its distribution. This was realized by setting the Cooke model interaction strength $w_{\text{c}}$ acting between cholesterol and $\pm$-type lipids to a value $w_{\text{c,}\pm }$ different from the standard value $w_{\text{c,0}}=1.6\sigma$, our baseline for interaction strength. This only applies to interactions between the two middle beads of lipids.

While flip suppression assures that the $\pm$ lipids do not flip away from their native leaflets, it does not assume anything about the identities of these lipids. The physical nature of these lipids is decided on the basis of how they interact with other lipids in the system. We simulate cases where the $\pm$ lipids are physically identical for all intents and purposes, and we also look at cases where there is a clear physical distinction between the two in how each lipid type interacts with cholesterol. To be more specific: if $w_{\text{c,}+}=w_{\text{c,0}}=w_{\text{c,}-}$, cholesterol interacts in exactly the same manner with the $+$- and $-$-type lipids, and there is no physical difference between the two. In contrast, if $w_{\text{c,}+}>w_{\text{c,0}}$ while $w_{\text{c,}-}=w_{\text{c,0}}$, or if $w_{\text{c,}+}=w_{\text{c,0}}$ but $w_{\text{c,}-}<w_{\text{c,0}}$, we have $w_{\text{c,}+}>w_{\text{c,}-}$, and cholesterol prefers the $+$ over the $-$ lipids, even though by a slightly different mechanism: in the first case, cholesterol is pulled into the $\oplus$ leaflet via a preferred interaction, while in the second case, it is pushed out of the $\ominus$ leaflet via a disfavored interaction. Observe that the $+$- and $-$-type lipids acquire different identities by virtue of cholesterol’s preference for one over the other, even if the interaction among themselves is identical. This way, we can model cholesterol’s well-known affinity toward saturated lipids over unsaturated ones, without creating the additional non-trivial complication that the two leaflets would differ in lipid type and might hence produce a residual tension by virtue of a spontaneous curvature difference (22,27).

At $k_{\text{B}}T=1.4\epsilon$ and $w_{\text{c,0}}=1.6\sigma$, where $\epsilon$ and $\sigma$ are the CG units of energy and length, respectively, the system is above the gel transition while simultaneously allowing the use of large values of $\delta \ell$ (46). We hence chose this state point for our simulations.

Using the modified four-bead, flip-fixed Cooke model, we measured a flip-flop rate $r_{\text{f}}$ for a cholesterol-like species on the order of ${10}^5\tau$, where $\tau$ is the CG unit of time, with no direct dependence on number of lipids in the simulated membrane. We obtained values for the specific areas (in CG units) $a_{\pm }/{\sigma }^2=1.1632\pm 0.0002$ and $a/{\sigma }^2=1.2436\pm 0.0003$, which are important parameters in the theoretical framework we use to measure the extent of cholesterol mixing in the leaflets, as discussed above. The statistical uncertainties were obtained via a blocking analysis (54). In all simulations discussed below, we take the bilayer area modulus to be $K_A=41.6\epsilon /{\sigma }^2$, consistent with the measurements in ref. (46).

In all our simulations, we fix the total number of lipids (i.e., phospholipids and cholesterol) to $\mathcal{L}=512$ and then potentially 1) impose a number symmetry $\delta \ell$ and 2) adjust the cholesterol mole fraction $\varphi$ by changing some portion $C$ of all lipids to be of cholesterol type, such that

$$L_{\pm }=\frac{1\pm \delta \ell }{2}(\mathcal{L}-C)\text{and}\varphi =\frac{C}{\mathcal{L}}.$$ (32)

Measuring differential stress

The lateral stress profile of flat membranes spanning the $xy$ plane is measured using the Irving-Kirkwood formalism (55), as described in detail by Hardy (56) for implementation in molecular dynamics simulations. Using mechanical stability and symmetry arguments, the box-aligned stress tensor is seen to be diagonal; in particular, the in-plane components depend only on the $z$ coordinate, and the $z$ component is constant, equal to the bulk pressure (57) (which vanishes in our implicit-solvent case). The lateral stress is then defined as

$$\sigma \left(z\right)=\langle \frac{1}{2}\left({\sigma }_{xx}\left(z\right)+{\sigma }_{yy}\left(z\right)\right)-{\sigma }_{zz}\left(z\right)\rangle ,$$ (33)

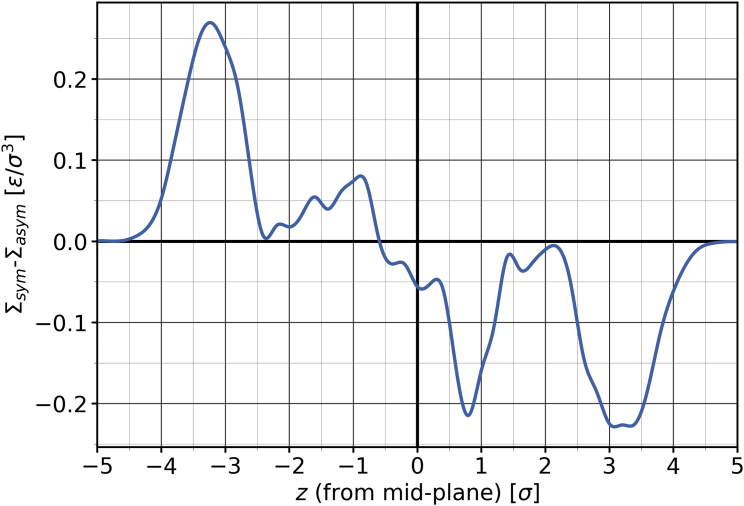
where ${\sigma }_{ii}\left(z\right)$ is the diagonal component of the local stress tensor in a slice of the membrane centered at position $z$. The lateral stress is evaluated at 51 evenly spaced $z$ values, and the uncertainty of these values is obtained through blocking. Fig. 4 demonstrates how the stress in a membrane with lipid number asymmetry varies from its symmetric counterpart as a function of the distance from the mid-plane. We calculate the tension in the individual leaflets as the following integral, with the $z$ values ranging from the bilayer mid-plane to an outer boundary at $Z^{\pm }$ that is chosen sufficiently far away from the membrane:

$${\Sigma }_{\pm }={\int }_0^{Z^{\pm }}\text{d}z\sigma (\pm z).$$ (34)

Here, $z=0$ marks the mid-plane of the membrane, which we determine by separately averaging the $z$ coordinates of the final tail bead of the lipids in each monolayer and then picking the mid-point between the two average values. This two-step process is necessary because defining the mid-plane position simply via the center of mass would skew its position in the case of asymmetric membranes.

Figure 4.

Difference between the lateral stress profiles of a completely symmetric membrane and an asymmetric membrane with $\delta \ell =2\%$, as a function of the distance from the mid-plane. Neither membrane contains any cholesterol. To see this figure in color, go online.

Results and discussion

Effects of number asymmetry

To gauge the extent to which a simple lipid number mismatch between the two leaflets affects the cholesterol distribution, we studied asymmetric bilayers in which the phospholipids were identical but the $\oplus$ leaflet was overfilled by $\delta \ell =2\%$, while a total fraction $\varphi$ of cholesterol-like lipids was initially distributed evenly between the leaflets.

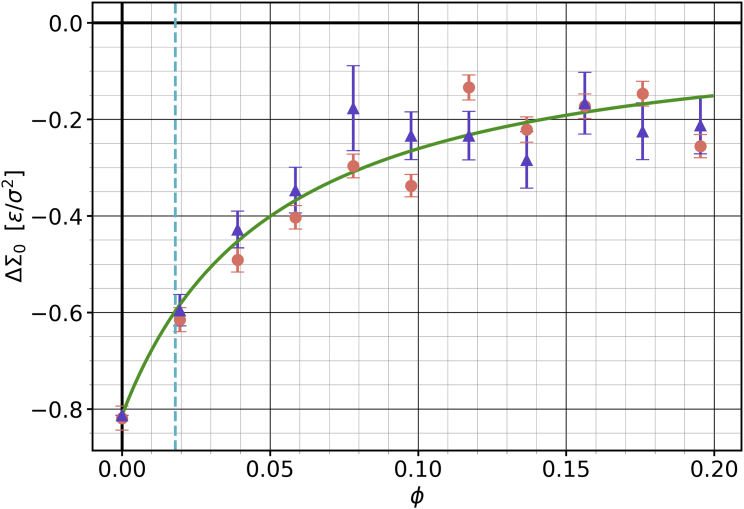
We measured the resulting differential stress $\Delta {\Sigma }_{\text{0}}$ as a function of the cholesterol fraction $\varphi$ and compared it with predictions using our theory, specifically Eqs. 8 and 18. The result is shown in Fig. 5. While the membrane was maintained at zero net tension, the individual leaflet tensions do not vanish, since the $\oplus$ leaflet is overfilled and the $\ominus$ leaflet is underfilled. This leads to a net negative differential stress $\Delta {\Sigma }_{\text{0}}$, whose value in the absence of cholesterol agrees excellently with our prediction. Upon increasing the cholesterol fraction $\varphi$, the magnitude of the differential stress decreases, but the membrane never relaxes completely to a state where $\Delta {\Sigma }_{\text{0}}=0$, in contrast to previous claims by Miettinen and Lipowsky (26).

Figure 5.

Differential stress $\Delta {\Sigma }_{\text{0}}$ as a function of cholesterol fraction $\varphi$ for an asymmetric membrane at $\delta \ell =2\%$. The orange points are directly measured from the stress profile. The purple triangles are inferred from the measured cholesterol asymmetry $\delta c$ via Eq. 8, while the green curve instead predicts $\delta c$ via Eq. 18, where ${\chi }_{+}$ is the only free parameter. The blue vertical dashed line represents the critical $\varphi$ value past which $\Delta {\Sigma }_{\text{0}}=0$ if the cholesterol distribution were exclusively determined by differential stress reduction—see Eq. 35b. Error bars show the error of the mean. To see this figure in color, go online.

As recently emphasized by Hossein et al. (22), the thermodynamic condition that determines the cholesterol distribution between the leaflets is the equality of cholesterol’s chemical potential (58). If stress equilibration were the only factor in this balance, we would expect the differential stress to vanish once enough cholesterol is available to “plug the holes” left in the underfilled $\ominus$ leaflet after redistributing into it.

This critical concentration would be reached once

$$L_{+}{a}_{+}=L_{-}{a}_{-}+C_{\text{crit}}a,$$ (35a)

which implies the critical cholesterol mole fraction

$${\varphi }_{\text{crit}}=\frac{(1+\delta \ell )a_{+}-(1-\delta \ell )a_{-}}{(1+\delta \ell )a_{+}-(1-\delta \ell )a_{-}+2a}\stackrel{\text{e.a.}}{=}\frac{\delta \ell }{\delta \ell +1}.$$ (35b)

This gives ${\varphi }_{\text{crit}}\approx 2\%$, a value indicated by the dashed blue line in Fig. 5. Evidently, the differential stress does not vanish at this point. Even for an order of magnitude more cholesterol, $\varphi =20\%$, the differential stress is still quite sizable. Leaflet area matching alone does not dictate the fate of cholesterol, and even in the absence of any partitioning preference, entropy can become a significant source of differential stress.

We wish to point out an interesting experimental consequence of Fig. 5: consider an area-imbalanced vesicle whose differential stress is buffered by cholesterol and expose it to (unloaded) $\beta$-cyclodextrin, thereby extracting cholesterol. Due to rapid flip flop, we will deplete both leaflets but not evenly so, for otherwise the differential stress would remain unchanged rather than increase in magnitude. If the vesicle was stable before $\beta$-cyclodextrin exposure, this suggests that the bending torque due to differential stress (approximately $z_0\Delta {\Sigma }_0$, where $z_0$ is the neutral surface distance from the bilayer midplane) was balanced, for instance by a spontaneous curvature torque (approximately $\kappa K_{0\text{b}}$, where $K_{0\text{b}}$ is the bilayer’s spontaneous materials curvature) (22). Upsetting this balance by a $\beta$-cyclodextrin-driven increase of $\left|\Delta {\Sigma }_0\right|$ may hence induce tubulation or other bilayer-destabilizing processes.

Effects of partitioning asymmetry

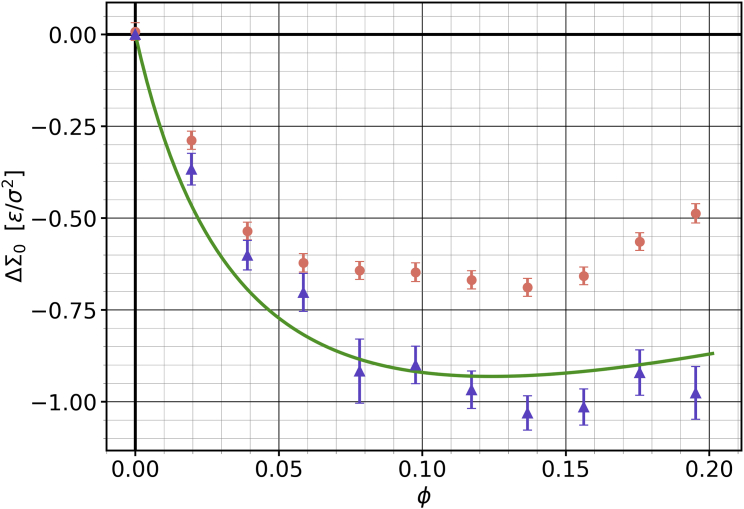
Cholesterol has different affinities for different lipid types. For instance, it prefers saturated over unsaturated tails or sphingomyelin over phosphatidylethanolamine headgroups (59, 60, 61, 62). How does such a bias affect the differential stress in a compositionally asymmetric membrane? To find out, we created an evenly packed membrane $(\delta \ell =0)$ but adjusted the phospholipid-cholesterol interaction parameters $w_{\text{c,}\pm }$ to induce a partitioning bias, specifically one in which cholesterol favors the $\oplus$ leaflet. We start the simulation with cholesterol evenly distributed between the leaflets, $\delta c=0$, a state that should have no differential stress. But since cholesterol prefers to solvate in the $\oplus$ leaflet, it preferentially redisributes into it and induces a (negative) differential stress where there was none before. This behavior once again illustrates the fact that cholesterol flip flop is not merely driven by stress cancellation.

Fig. 6 illustrates how the differential stress in the bilayer changes as a function of cholesterol content $\varphi$, for $w_{\text{c,}-}=w_{\text{c,0}}<w_{\text{c,}+}$, such that cholesterol gets pulled into the $\oplus$ leaflet. Taking a closer look at Eq. 8, and recalling that $\Delta A_0=0$ when $\delta \ell =0$, we see two main factors that contribute to a non-zero $\Delta {\Sigma }_{\text{0}}$: the measure of cholesterol imbalance $\delta c$ and the area-weighted cholesterol fraction ${\varphi }_{\text{a}}$. Cholesterol’s tendency to favor the $\oplus$ leaflet initially places the leaflet under an increased elastic stress, driving $\Delta {\Sigma }_{\text{0}}$ further away from 0 with an increase in $\delta c$. But this is soon counteracted by an increase in ${\varphi }_{\text{a}}$ and a subsequent decrease in $\delta c$, a trend that is visible not only in the predictions from our theory but also in the results from our measurements. Intuitively, the stress decay past a certain amount of cholesterol in the system results because more and more of the bias-inducing phospholipids make way for cholesterol.

Figure 6.

Differential stress $\Delta {\Sigma }_{\text{0}}$ as a function of cholesterol concentration $\varphi$, under conditions of a partitioning bias—cholesterol prefers to be in the $\oplus$ leaflet—while the number asymmetry $\delta \ell =0$. The orange points are directly measured from the stress profile. The purple triangles are inferred from the measured cholesterol asymmetry $\delta c$ via Eq. 8, while the green curve instead predicts $\delta c$ via Eq. 18, where ${\chi }_{+}$ is the only free parameter. Error bars show the error of the mean. To see this figure in color, go online.

If we were to expose asymmetric membranes of this type to $\beta$-cyclodextrin, the differential stress would again change, but observe that the direction of the effect now tends to be opposite to the one we discussed in the previous section. Whether $\beta$-cyclodextrine increases or decreases the magnitude of differential stress depends on why this stress exists in the first place: in phospholipid-number asymmetric vesicles, cholesterol can buffer differential stress, so depleting cholesterol will increase that stress. Conversely, in partitioning asymmetric vesicles, cholesterol creates the differential stress, and so lowering its concentration will also lower the stress. Either way, a change in stress would again upset a pre-existing torque balance, which could trigger tubulation.

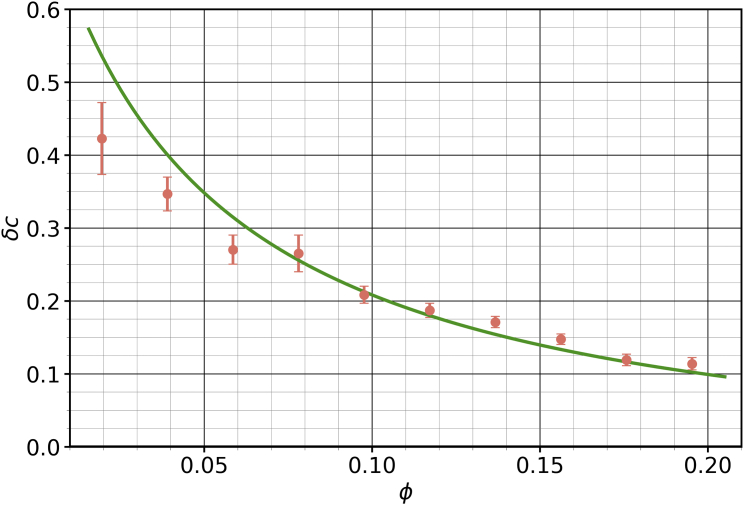
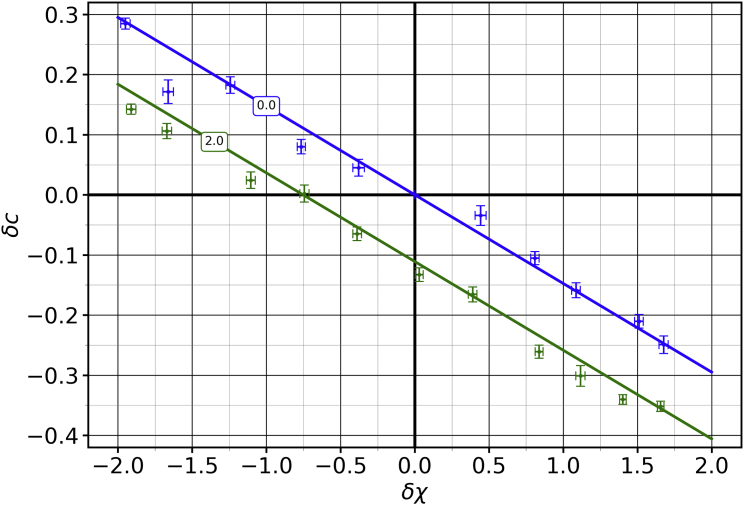
Fig. 7 shows the cholesterol asymmetry $\delta c$ as a function of cholesterol mole fraction $\varphi$ for the membrane described above (compare this with Fig. 2). The green curve is a fit performed using Eq. 18, with ${\chi }_{-}=0$ and ${\chi }_{+}$ as the free parameter. This plot suggests the following question: since the interaction between cholesterol and the $\pm$-type lipids and any resultant partitioning asymmetry affects the mixing in either leaflets, what is the relationship between ${\chi }_{+}$ and $w_{\text{c,}+}$? Having this information, even if only empirically, would let us control the degree of mixing in each leaflet, which is a physical property of the membrane, simply by tuning the interaction strength $w_{\text{c,}+}$, a model parameter that we have control over while performing the simulations. In order to obtain this relationship, we measured ${\chi }_{+}$ for a range of $w_{\text{c,}+}$ values at $\delta \ell =0\%$ using the formalism detailed in Fig. 7. The uncertainties in ${\chi }_{+}$ were obtained by bootstrapping (63) the fit in Fig. 7.

Figure 7.

Plotting cholesterol asymmetry $\delta c$ against $\varphi$ for fixed values of $w_{\text{c,}\pm }$ and $\delta \ell$ lets us obtain a fit (in green) for the mixing parameter $\chi$ using Eq. 18. This is analogous to the theoretical plots in Fig. 2. This particular plot is for $w_{\text{c,}-}=w_{\text{c,0}}$, $w_{\text{c,}+}=1.675\sigma$, and $\delta \ell =0$, and it leads to ${\chi }_{+}(\delta \ell =0)=-1.24$. Error bars show the error of the mean. To see this figure in color, go online.

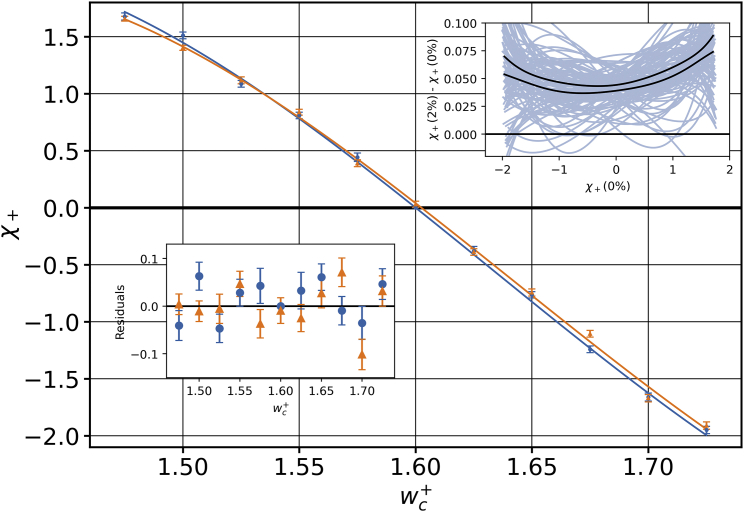
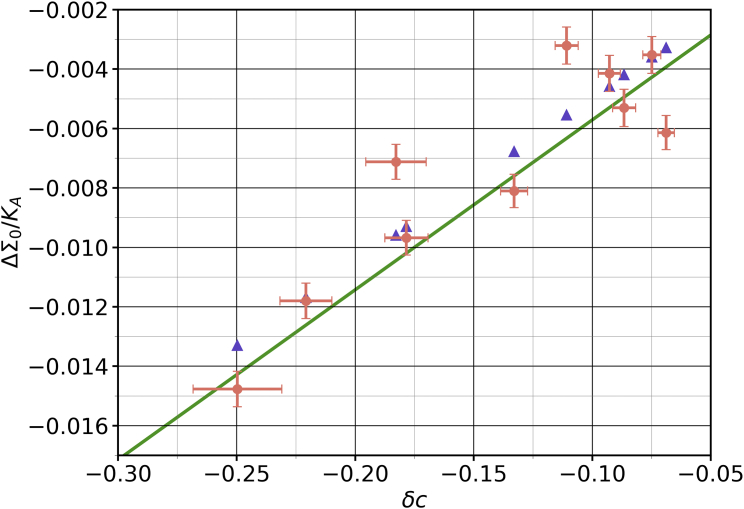
The overall trend, shown in Fig. 8, suggests an approximately linear dependence of ${\chi }_{+}$ on $w_{\text{c}}-w_{\text{c,0}}$, signifying that cholesterol’s miscibility in the $\oplus$ leaflet improves as $w_{\text{c}}$ becomes bigger than $w_{\text{c,0}}$ and worsens otherwise. The data points are precise enough to rule out a straight line fit, though. Judging by the shape of the curve, we performed an empirical cubic fit (constrained by ${\chi }_{+}(w_{\text{c}}=w_{\text{c,0}})=0$ for $\delta \ell =0$, which is enforced by symmetry). Interestingly, a conceivably expected point symmetry ${\chi }_{+}(w_{\text{c}}-w_{\text{c,0}})=-{\chi }_{+}(w_{\text{c,0}}-w_{\text{c}})$ is ruled out by the data (the term ${(w_{\text{c}}-w_{\text{c,0}})}^2$ has a coefficient significantly different from zero), which indicates that “pushing” cholesterol out of the $\ominus$ leaflet versus “pulling” it into the $\oplus$ leaflet is not entirely equivalent.

Figure 8.

${\chi }_{+}$ values for a range of interaction strengths $w_{\text{c,}+}$, at $\delta \ell =0\%$ (blue dots) and $\delta \ell =2\%$ (orange triangles). The data points and the corresponding fits are shown in the same color for clarity. The residuals for the cubic polynomial fit (bottom left inset) indicate that there is no other underlying trend. The parametric plot (top right inset) tells us that there is a relatively constant positive offset for $\delta \ell =2\%$. Error bars show the error of the mean. To see this figure in color, go online.

Having calibrated the ${\chi }_{+}\left(w_{\text{c}}\right)$ relationship for $\delta \ell =0$, we initially hoped that this enables predictions of cholesterol distributions even in number asymmetric membranes because $\delta \ell$ and mixing are different aspects of the physical situation. Remarkably, this turned out not to be so. For instance, the measured value of ${\chi }_{+}$ in a membrane for a fixed cholesterol mole fraction $\varphi$ and an asymmetry of $\delta \ell =2\%$ was off by about 15% when compared with the prediction from the relation inferred at $\delta \ell =0\%$. We therefore remeasured the calibration curve ${\chi }_{+}\left(w_{\text{c,}+}\right)$ for $\delta \ell =2\%$, shown in Fig. 8 as the orange curve. Even though the two curves are very close, their predictions noticeably differ because the cholesterol asymmetry $\delta c$ depends rather sensitively on the mixing parameters. Observe also that for $\delta \ell \ne 0$, we lose the symmetry argument that enforces ${\chi }_{+}(w_{\text{c}}=w_{\text{c,0}})=0$, leading to a small but statistically significant offset of about 0.035 (Fig. 8, top right inset).

Joint effects of number asymmetry and partitioning asymmetry

Let us now look at the interplay between the major drivers of cholesterol redistribution in our asymmetric membrane: number asymmetry and partitioning asymmetry. Consider a membrane with $\delta \ell =2\%$ and $w_{\text{c,}+}>w_{\text{c,0}}=w_{\text{c,}-}$ for a given cholesterol mole fraction $\varphi \approx 10\%$. As we have seen in the previous discussion, the overcrowding of the $\oplus$ leaflet pushes cholesterol out of it for elastic reasons while setting $w_{\text{c,}+}>w_{\text{c,}-}$ biases cholesterol toward the $\oplus$ leaflet for partitioning reasons. Simultaneously, entropy prefers an equal distribution of cholesterol among the leaflets and hence disfavors reshuffling driven by either stress or preferential interactions.

The combined effect of these two types of asymmetries is illustrated in Fig. 9 as the green curve. The points are measurements of $\delta c$ from simulations at a fixed cholesterol concentration $\varphi$, shown as a function of the difference in the leaflet’s mixing parameters (that were measured as detailed in Fig. 2). The solid line is the prediction—not a fit—from our theory, using Eq. 26. The blue set of points in Fig. 9 represent the cholesterol asymmetry in the absence of a phospholipid number asymmetry, i.e., at $\delta \ell =0$, for the same fixed cholesterol content $\varphi \approx 10\%$. Comparing the two, it is clear that the cholesterol distribution $\delta c$ arises as an (almost linear) interplay between number and partitioning asymmetry. A higher phospholipid number asymmetry $\delta \ell$ drives more cholesterol into the $\ominus$ leaflet, causing a decrease in the cholesterol asymmetry $\delta c$, but it is possible to counteract this by tuning the solvation bias via the mixing preference $\delta \chi$.

Figure 9.

Cholesterol asymmetry $\delta c$ as a function of $\delta \chi$, for phospholipid asymmetry $\delta \ell =0\%$ (blue) and $2\%$ (green). The prediction from our theory is shown as a solid line against the simulated data points. These plots mirror the ones in Fig. 1. Error bars show the error of the mean. To see this figure in color, go online.

An alternative way of looking at the combined effects of number and partitioning asymmetry is to determine how the differential stress $\Delta {\Sigma }_{\text{0}}$ varies as a function of cholesterol asymmetry $\delta c$. Fig. 10 tells us that these two variables are closely related, as indicated by measurements from our simulations as well as predictions from our theory, using Eq. 29. The cholesterol distribution has long been understood to play a significant role in regulating membrane functions, and differential stress is now seen to be strongly entangled with it. Since both aspects of a membrane’s thermodynamic state are very challenging to measure directly in experiment, the appearance of differential stress as a second “hidden variable” appears to exacerbate the challenge of pinning down this state. However, our investigations suggest that cholesterol partitioning and differential stress form two complementary parts of the same puzzle, and learning something about either one will teach us about the other.

Figure 10.

Differential stress $\Delta {\Sigma }_{\text{0}}$ versus cholesterol asymmetry $\delta c$, for a system in which all lipids interact identically $(w_{\text{c,}\pm }=w_{\text{c,0}})$ but there is a number asymmetry $\delta \ell =2\%$. Measurements are shown in orange with horizontal and vertical uncertainties calculated from blocking and bootstrapping, respectively. Purple triangles are predictions from our theory using Eq. 29, while the green line is a prediction that ignores the small contribution from a residual mixing parameter $\delta \chi$. To see this figure in color, go online.

Example: The human red blood cell membrane

Let us apply our theoretical analysis to a specific biological membrane whose lipidome is known in exquisite detail: the human red blood cell (RBC). Both the composition of phospholipids in its two leaflets (7) and their overall abundance have been measured, with preliminary findings indicating that the cytosolic (inner) leaflet contains $1.7\dots 2$ times as many phospholipids as the exoplasmic (outer) one (64,65). This phospholipid asymmetry (in our notation: $\delta \ell =-0.26\dots -0.33$) is much larger than what we have considered so far, so our predictions should be viewed more cautiously. It seems clear, though, that a sizable fraction of the RBC’s cholesterol content of 40 mol % (7) will translocate to the exoplasmic side to compensate for the large phospholipid area mismatch. Our goal is to estimate the extent of this effect.

To make numerical predictions, we need to estimate several material parameters. The most straightforward one is the bilayer expansion modulus $K_A$, which for a wide range of lipids is about 240 mN/m (66). We will take the phospholipid area in the highly unsaturated cytosolic leaflet to be $a_{\text{cyto}}=0.7{\text{nm}}^2$ and use $a_{\text{exo}}=0.65{\text{nm}}^2$ for the more ordered exoplasmic leaflet. A thorny issue is cholesterol since our assumption of area additivity cannot account for condensation effects. In view of its effective area in cholesterol-DPPC mixtures (67), we will for now compromise on $a=0.35{\text{nm}}^2$. To estimate the partitioning preference, we recall that $\delta \chi \approx -\beta \Delta g$ (see our discussion near Eq. 23). Data by Tsamaloukas et al. (62) suggest that transferring cholesterol from a pure POPC membrane into a membrane in which 50% of lipids have been replaced by sphingomyelin lowers its chemical potential somewhere between 1 and 3 k_BT, depending on the overall cholesterol concentration. We hence consider a partitioning bias into the exoplasmic leaflet of $\delta \chi \approx -1\dots -2$ likely. But since neither $\delta \ell$ nor in fact $\delta \chi$ are known well, let us present predictions for a range of both variables, which also clarifies how much the answer depends on them.

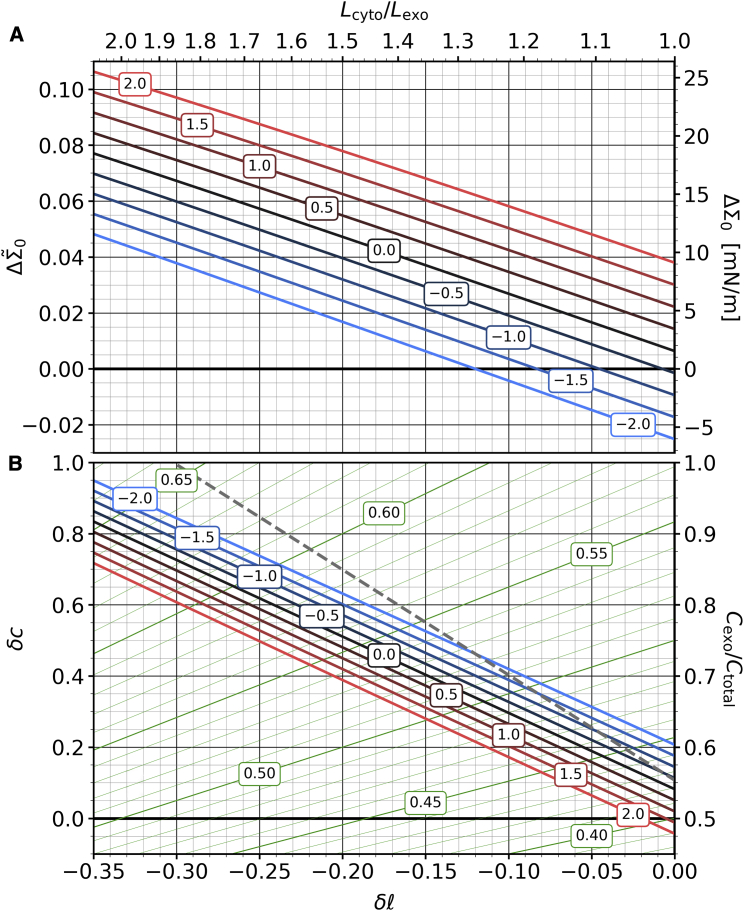
The joint Fig. 11 illustrates the differential stress (Fig. 11 A) and the cholesterol asymmetry (Fig. 11 B) as a function of phospholipid imbalance. Even for $\delta \ell =0$ and $\delta \chi =0$, cholesterol slightly prefers the exoplasmic leaflet, whose lipids have a smaller area. Increasing the abundance of cytosolic lipids shifts cholesterol to the exoplasmic side. If only area balance mattered (effectively, if $K_A\to \infty$), this would give an asymmetry (dashed gray line) of

$$\delta c_{\infty }=-\frac{1-\varphi }{\varphi }\frac{(1+\delta \ell )a_{\text{exo}}-(1-\delta \ell )a_{\text{cyto}}}{2a},$$ (36)

at which also the differential stress vanishes. Since $\left|\delta c\right|\le 1$ must hold, perfect compensation ceases to be possible for sufficiently large phospholipid imbalances—here, $\delta \ell \approx -0.309$ or $L_{\text{cyto}}/L_{\text{exo}}\approx 1.89$. In reality, entropy counteracts perfect area balance, which lowers the cholesterol asymmetry but comes at the expense of very sizable differential stress. For instance, at the lower end of the experimentally claimed cytosolic abundance, $L_{\text{cyto}}/L_{\text{exo}}=1.7$, we find $\Delta {\Sigma }_0\approx 14\mathrm{m}\mathrm{N}/\mathrm{m}$ for evenly partitioning cholesterol (i.e., $\delta \chi =0$). This is enormous, but it decreases if we allow realistic $\delta \chi$ values: for $\delta \chi =-1.5$, we get $\Delta {\Sigma }_0\approx 9\mathrm{m}\mathrm{N}/\mathrm{m}$, and for $\delta \chi =-2$, the differential stress drops to 7 mN/m, half the unbiased value. The fraction of cholesterol residing in the exoplasmic leaflet is large—between 86% and 88%—but in the range of what has been experimentally claimed (43). Furthermore, it is physically permissible, since the overall cholesterol mole fraction in the exoplasmic leaflet (between 61% and 62%) remains below the solubility limit (which is about 66% in bilayers whose lipids have phosphatidylcholine headgroups (68)—as indeed holds for the exoplasmic leaflet (7)).

Figure 11.

Differential stress and cholesterol asymmetry as a function of phospholipid asymmetry. (A) The latter given as $\delta \ell$ (lower common axis) or $L_{\text{cyto}}/L_{\text{exo}}$ (upper common axis). Stress is either measured in dimensionless form (${\tilde{K}}_A$, left axis) or in units of mN/m (right axis), while cholesterol asymmetry is given as $\delta c$ (left axis) or as a fraction on the exoplasmic side, $C_{\text{exo}}/C_{\text{total}}$ (right axis). The blue-to-red lines correspond to a set of non-ideal mixing parameters $\delta \chi \in \{-2,-1.5,\dots ,+2\}$ as indicated in the boxed labels. The green iso-lines in (B) indicate the exoplasmic cholesterol mol fraction $C_{\text{exo}}/(C_{\text{exo}}+L_{\text{exo}})$, with values given in the boxed labels. The dashed gray line in (B) is the cholesterol asymmetry $\delta c_{\infty }$ for the hypothetical case in which only area-matching matters; see also Eq. 36. To see this figure in color, go online.

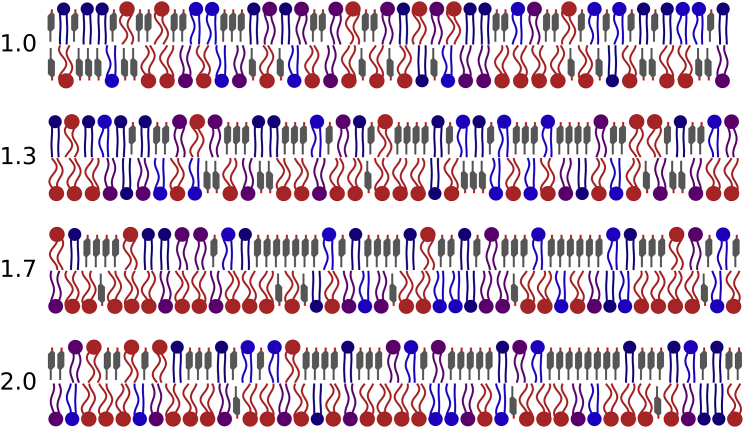
Fig. 12 schematically illustrates RBC membranes over a range of phospholipid imbalances and the associated cholesterol asymmetry as predicted by our model, picking a mid-range solubility bias of $\delta \chi =-1.5$. If the phospholipid imbalance is indeed as large as found in refs. (64,65), the exoplasmic leaflet differs substantially from a more conventional textbook view, given its very large cholesterol content, with numerous consequences for protein insertion and solvation, solute permeation, and (presumably) mechanical properties. It seems particularly unsettling that 60 mol % cholesterol is far above the value for which ternary mixtures of low-melting lipids, high-melting lipids, and cholesterol are known to show a liquid-ordered-liquid-disordered phase coexistence (69,70), which subverts a widely embraced biophysical model for lipid rafts (71, 72, 73). While this may well require us to carefully reassess this model, we should also recall that human RBCs are quite special in aspects directly connected to their plasma membrane physiology: they lack an endomembrane system, have fewer reasons for hosting sophisticated signaling platforms, and must withstand extensive mechanical deformations and stresses during circulation. Even though rafts—in the original notion of “detergent-resistant membranes”—were in fact first described in human RBCs, rafts according to the 2006 Keystone Symposium consensus (74) appear to be a far more subtle issue—see ref. (75) for a fascinating historical perspective.

Figure 12.

Schematic illustrations of asymmetric red blood cell bilayers with a phospholipid imbalance $L_{\text{cyto}}/L_{\text{exo}}$ as indicated next to each image. Lipid types represent different degrees of saturation, as measured by the number of double bonds: 0 (dark blue), 1 (blue), 2 (purple), and $\ge 2$ (red). Cholesterol is indicated as shorter gray sticks. The relative abundances of phospholipids in each leaflet approximately reflect those given in Fig. 1 b of ref. (7), while the cholesterol distribution is calculated from our model, using $\delta \chi =-1.5$. To see this figure in color, go online.

Conclusions

Cholesterol influences many properties and coregulates many functions of biological membranes. As a rapidly flip-flopping species, it is also uniquely sensitive to numerous manifestations of lipid bilayer asymmetry—a property of many biomembranes (most notably the plasma membrane) that seems to be evolutionarily conserved across all of eukarya (7). By combining theoretical modeling and CG simulations, our goal was to propose a path forward for disentangling the resulting dependencies, most prominently the interplay between differential stress and partitioning bias.

Our theory, which refines an earlier version (22) by accounting for lipid mixing using a mean-field lattice-gas approach, derives a number of predictions for—and relations between—cholesterol leaflet asymmetry $\delta c$ and the membrane’s state of differential stress $\Delta {\Sigma }_{\text{0}}$ as a function of several other control parameters (such as lipid asymmetry in terms of number and type or cholesterol’s overall mole fraction). Our CG simulations confirm all major predictions but also point to some routes for improvement. Let us list a few of the major takeaways:

• 1.A differential stress due to a phospholipid packing asymmetry is not automatically canceled by cholesterol backfilling the tense leaflet. This is obvious in the presence of a competing partitioning bias, but even in its absence, perfect stress cancellation is strongly entropically disfavored.
• 2.If cholesterol has a preference for one leaflet over the other, the resulting redistribution can create differential stress even if the membrane’s phospholipid complement is well balanced.
• 3.Both phospholipid number imbalance and cholesterol partitioning bias drive cholesterol asymmetry in an almost linear fashion. In particular, one can compensate for the other, and their relative “strength” depends only on measurable quantities (such as the membrane’s area expansion modulus and the cholesterol concentration).
• 4.In this balance, differential stress can replace number asymmetry, leading again to a linear compensation—this time between partitioning and differential stress.
• 5.As a consequence, cholesterol asymmetry and differential stress are highly correlated. While both are exceedingly difficult to measure, they are two sides of the same coin: inferences about one immediately constrain the other.
• 6.In our CG simulations, we tuned partitioning preferences via inter-molecular potentials. Calibrating this relation proved unexpectedly sensitive to the imposed lipid number asymmetry.
• 7.Applying our theory to the human RBC membrane, using the most recent data on composition and relative lipid abundance, suggests that close to 90% of all cholesterol resides in the exoplasmic leaflet, with a large remaining differential stress of $\mathcal{O}\left(10\right)\mathrm{m}\mathrm{N}/\mathrm{m}$. All predicted numbers are biophysically permissible but are often at the extreme ends of previously estimated ranges, suggesting that—if true—plasma membrane structure differs considerably from older, more moderate textbook views.

We have extensively compared our theoretical model against CG simulations, and even though agreement is typically high, some discrepancies remain, for instance in the stress predictions in Fig. 6. Let us hence indicate a few avenues for improvement.

An important limitation of our approach is the assumption that lipid areas simply add. This premise is especially questionable for cholesterol, which strongly affects the conformational ensemble of its surrounding lipids (76). For instance, ordering the embedding lipid phase can condense the bilayer, giving cholesterol a negative differential area (67). In our highly CG simulations, in which the flippable cholesterol species does not actually differ structurally from the other lipids, area additivity likely holds fairly well, but this approximation would be less reliable for atomistic models or, in fact, real systems. A possible way to go beyond this is to amend the elastic portion of our model by more realistic equations of state.

A second simplification is that our treatment ignores leaflet spontaneous curvature. This might seem innocuous given that we restrict ourselves to flat bilayers, but there are at least two reasons why curvature elasticity still matters. First, bending energy does not merely arise when a membrane ceases to be flat. Instead, what is penalized is the squared difference between each leaflet’s actual and its spontaneous curvature. Since the latter depends on cholesterol content, there is a bending energy contribution to cholesterol partitioning that we have not yet accounted for—but which has been discussed in great detail by Allender et al. (58), who find it to be quite important. And second, a spontaneous curvature difference between the leaflets creates a bending torque. In a membrane forced flat via periodic boundary conditions, this torque can induce additional stress differences even if the individual leaflets are perfectly area balanced—as recently confirmed in simulations (25,26) and rationalized using two slightly different theoretical arguments (22,27). While all lipids have the same shape in our simulations, as judged by their repulsive interactions, unequal $w_{\text{c,}\pm }$ values will pull lipid tails together with a leaflet specific strength, creating a spontaneous curvature difference that adds differential stress on top of any packing-induced stress. Indeed, the discrepancy between measured and predicted stress in Fig. 6 arises in such a system, while the much better agreement in Fig. 5 occurs for membranes in which all lipids interact with the same strength.

While plasma membranes typically contain about 40 mol % cholesterol (7), we have restricted our simulations to $\varphi \le 20\%$ for two technical reasons. First, our current mechanism for suppressing flip flop of the ordinary phospholipid species fails in the presence of too many flippable lipids; this includes situations where extreme preferential interaction strengths $w_{\text{c,}\pm }$ strongly enhance the cholesterol concentrations in one leaflet. And second, our theoretical analysis relied on an expansion of Eq. 12 for small values of the cholesterol asymmetry $\delta c$. To pursue the influence of various thermodynamic driving forces on cholesterol’s inter-leaflet partitioning, this restriction is of little consequence; but when we applied our model to human RBCs, we found that the actual asymmetries might be fairly large (say, $\delta c\sim 0.7$), rendering our small $\delta c$ expansions quantitatively less reliable.

Our predictions for RBCs depend on the recent preliminary claims of their huge phospholipid imbalance (64,65), and they call into question the notion of rafts being exoplasmic domains or fluctuations connected to a liquid-ordered-liquid-disordered phase coexistence. However, further corroboration of this imbalance is needed; and even if confirmed, it is not obvious that it would also exist in non-RBC plasma membranes. We hence wish to briefly point out that our theory also has implications for the more conventional exoplasmic raft picture. These are more difficult to predict, but the following two qualitative effects are easy to understand: first, liquid-ordered and liquid-disordered regions differ in both their lipid area and their lateral compressibility, rendering their relative stability sensitive to (outer leaflet) tension. And second, since differential stress can rebalance the cholesterol content between leaflets, this entangles the compositional aspect of phase behavior and coexistence in a raft-containing exoplasmic leaflet with mechanics, including the state of stress in the cytoplasmic leaflet.

Should this view hold up, then examining raft-like domains in symmetric model membranes under vanishing lateral tension might be insufficient; we should also inquire how they behave in a single leaflet whose lateral tension may reach several mN/m and conceivably even vary over time. Indeed, recent experiments have shown that (for certain cells, under certain conditions) local changes in plasma membrane tension only relax via surprisingly slow diffusive processes (77,78). If so, local membrane tension—and hence also differential stress—might conceivably coregulate complex dynamical signaling mechanisms. However, investigating these exciting possibilities quantitatively would require us to measure the underlying new degrees of freedom, and this is currently still very difficult—both for the cholesterol asymmetry and especially for the differential stress. We hope that the theoretical framework we have started to develop here will help in this process, for instance by embedding the relevant observables into a consistent framework and identifying correlations between them that may assist in constraining their measurements.

Glossary

For the convenience of the reader, Table 1 gives a non-exhaustive list of the most common mathematical symbols and notations we use.

Table 1.

Glossary

Symbol	Description
$\pm$	subscript distinguishing lipid properties belonging to the $\oplus$ (upper) and $\ominus$ (lower) leaflet
${\mathcal{A}}_{\pm }$	equilibrium area of an individual leaflet, Eq. 1a
$\Delta A_0$	leaflet area difference with no cholesterol, Eq. 1c
$a_{\pm }$	phospholipid specific lipid area
$a$	cholesterol specific lipid area
$C_{\pm }$	number of cholesterol molecules in each leaflet
$C$	total number of cholesterols, $=C_{+}+C_{-}$
$\delta c$	cholesterol number asymmetry, Eq. 1d
$K_A$	bilayer area expansion modulus
${\tilde{K}}_A$	scaled bilayer area expansion modulus, Eq. 13a
$L_{\pm }$	number of native phospholipids in each leaflet
$\delta \ell$	phospholipid number asymmetry, Eq. 19b
$w_{\text{c,}\pm }$	the interaction strength between phospholipids and cholesterol in the Cooke model (47)
${\Sigma }_{\pm }$	individual leaflet tension, Eqs. 6 and 34
$\Sigma$	net bilayer tension, $={\Sigma }_{+}+{\Sigma }_{-}$
$\Delta {\Sigma }_{\text{0}}$	differential stress at $\Sigma =0$, Eq. 8
${\varphi }_{\text{a}}$	area-weighted cholesterol fraction, Eq. 1b
$\varphi$	cholesterol mole fraction, Eq. 19a
${\chi }_{\pm }$	mixing parameter in each leaflet, Eq. 9
$\delta \chi$	mixing parameter leaflet difference, $={\chi }_{+}-{\chi }_{-}$

Author contributions

M.D. suggested the subject, acquired funding for it, and, with input from M.V., developed the theory. M.V. expanded the flip-fixed Cooke model to include cholesterol-like molecules, carried out all simulations, and analyzed all data. M.V. and M.D. jointly wrote the manuscript.

Editor: Heiko Heerklotz.