Effect of water activity on the mechanical glass transition and dynamical transition of bacteria

Abstract

The purpose of this study was to clarify the glass-transition behavior of bacteria (Cronobacter sakazakii) as a function of water activity (a_w). From the water sorption isotherm (298 K) for C. sakazakii, monolayer water content and monolayer a_w were determined to be 0.0724 g/g-dry matter and 0.252, respectively. Mechanical relaxation was investigated at 298 K. In a higher a_w range of over 0.529, the degree of mechanical relaxation increased with an increase in a_w. From the effect of a_w on the degree of mechanical relaxation, the mechanical a_wc (a_w at which mechanical glass transition occurs at 298 K) was determined to be 0.667. Mean-square displacement of atoms in the bacteria was investigated by incoherent elastic neutron scattering. The mean-square displacement increased gradually with an increase in temperature depending on the a_w of samples. From the linear fitting, two or three dynamical transition temperatures (low, middle, and high T_ds) were determined at each a_w. The low-T_d values (142–158 K) were almost independent from a_w. There was a minor effect of a_w on the middle T_d (214–234 K) except for the anhydrous sample (261 K). The high T_d (252–322 K) largely increased with the decrease in a_w. From the a_w dependence of the high T_d, the dynamical a_wc was determined to be 0.675, which was almost equivalent to the mechanical a_wc. The high T_d was assumed to be the glass-transition temperature (T_g), and anhydrous T_g was estimated to be 409 K. In addition, molecular relaxation time (τ) of the bacteria was calculated as a function of a_w. From the result, it is suggested that the progress of metabolism in the bacterial system requires a lower τ than approximately 6 × 10⁻⁵ s.

Graphical abstract

Significance

There is a phenomenological similarity between glass to rubber transition (glass transition) of polymers and bacterial inactive (no growing) to active (growing) transition. To understand the bacterial inactive-active transition based on the polymer-bacteria analogy, the isothermal mechanical relaxation and mean-squared displacement of bacteria (Cronobacter sakazakii) were investigated. The mechanical glass transition could correspond to dynamical transition with pronounced a_w dependence. From the results, molecular relaxation time (τ) of the bacteria was calculated as a function of a_w. The results suggest that the progress of metabolism in the bacterial system requires a lower τ than approximately 6 × 10⁻⁵ s.

Introduction

Water activity (a_w) is defined as the water vapor pressure in a system relative to the vapor pressure of pure water at a given temperature (1). It is known that various types of degradation rates can be described as a function of a_w independent from the system. For example, the growth rate of bacteria becomes negligible at an a_w lower than approximately 0.85 (2). The bacterial activity, however, recovers at least partially when the a_w increases. From a physical viewpoint, bacterial inactive-active transition is somewhat similar to glass-rubber transition (in short, glass transition). Glass transition is a physical phenomenon observed in amorphous materials. Amorphous materials turn into a glassy state at a lower temperature than the glass-transition temperature (T_g). Since the molecular mobility of a glassy material is sufficiently low, it is impossible to diffuse despite its liquid nature. When a glassy material is warmed at a higher temperature than the T_g, the amorphous material regains its molecular mobility for diffusion and behaves as a rubbery material. In the case of a hydrophilic amorphous material, glass transition occurs by dehydration and rehydration even at a constant temperature because the T_g increases and decreases with the decrease and increase in a_w, respectively, due to the water plasticizing effect. The water content and a_w at which the T_g becomes 298 K (typical room temperature) are described as the critical water content (w_c) and critical a_w (a_wc), respectively (3).

The T_g of amorphous materials is commonly determined using differential scanning calorimetry. Complex systems such as food products (4, 5, 6) and bacteria (7), however, show unclear glass transition behavior. In such cases, thermomechanical approaches such as thermal rheological analysis (TRA) are expected to be effective tools. In TRA measurement, the sample is initially compressed with a certain force at a temperature below the expected T_g, and then heat scanned. The T_g of the sample can be detected as a force drop (softening) induced by glass transition. The T_g determined by a thermomechanical approach is described as the mechanical T_g.

Bacterial control based on glass transition is a challenging concept for food preservation. In our previous studies, the glass-transition behavior of Salmonella enterica (8) and Cronobacter sakazakii (C. sakazakii) (9) was investigated using TRA, and the effect of a_w on the mechanical T_g was reported. As an experimental issue for TRA studies, the effect of artifacts on the mechanical glass-transition behavior was pointed out. The force drop detected in the study showed great curvature and thus provided a degree of uncertainty with respect to the mechanical T_g.

To solve this problem and to clarify the glass-transition behavior of bacteria in more detail, two experimental approaches were undertaken in this study. One is isothermal mechanical relaxation measurement. This approach has been employed to validate the a_wc of complex systems such as carbohydrate mixtures (10,11), plant roots (12), food (6), and yeast (13). The samples with varying a_w are compressed at 298 K and held for a given period. The force drop between the initial force and the force after the period (ΔF) is evaluated as the degree of isothermal mechanical relaxation under a given condition. A glassy sample shows a low constant ΔF independent of the a_w, but a rubbery sample shows a larger ΔF depending on the a_w. Thus, a_wc will be determined from the crossover point between the a_w dependence of ΔF for glassy samples and that for rubbery samples.

The other approach is incoherent elastic neutron scattering. Incoherent elastic neutron scattering can detect molecular dynamics of atoms (mainly hydrogen) on a picosecond to nanosecond timescale and sub nano-meter spatial scale. Q (scattering vector) dependence of the incoherent elastic incoherent neutron scattering gives the atomic mean-square displacement (MSD) based on the Gaussian approximation (14,15). Because the incoherent scattering cross section of hydrogen is quite large compared with that of other atoms, the advantage of incoherent elastic neutron scattering is the selective observation of dynamics in biological systems in combination with selective deuteration. From the temperature dependence of the MSD of atoms, harmonic-anharmonic transition can be evaluated as “dynamical transition” (14). The dynamical transition temperature (T_d) does not agree with T_g, but they are interrelated physical phenomena (16,17). In previous studies, the molecular dynamics of various biomaterials such as proteins (15,18, 19, 20, 21, 22), DNA (23), RNA (24), polysaccharides (25), and phospholipids (26) have been investigated using neutron scattering. In addition, water dynamics for bacteria such as Shewanella oneidensis (27) and Escherichia coli (28) have also been investigated using neutron scattering. However, there are no reports on the effect of a_w on the T_d of bacteria.

The purpose of this study was to understand the effect of a_w on the isothermal mechanical glass-transition behavior and dynamical transition behavior of bacteria. As the bacterial sample, C. sakazakii, which is an opportunistic Gram-negative rod, was employed. It is known that C. sakazakii is resistant to desiccation and heating (29,30) and is a causative microorganism of neonatal infections (31).

Materials and methods

Sample preparation

A strain of C. sakazakii (JCM 1233^T) was purchased from RIKEN BioResource Center (Ibaraki, Japan). The strain was preserved in 10% glycerol solution containing tryptic soy broth (TSB; Merck, Darmstadt, Germany). The preserved strain was incubated on tryptic soy ager (TSA; Merck) plates at 310 K for 24 h. Colonies were transferred into 5 mL TSB and then incubated for 24 h at 310 K. The cultured suspension was added into 400 mL TSB and incubated for 48 h at 310 K. The suspension was centrifuged (3,000 × g for 10 min), and the supernatant was removed. The precipitate was homogenized with 5 mL distilled water, then centrifuged, and the excess water was removed. This process was repeated twice in order to wash the precipitate of C. sakazakii. The sample was frozen at 193 K for 12 h in a freezer and freeze dried at 193 K for 24 h (FDU-2200; Tokyo Rikakikai, Tokyo, Japan). The freeze-dried sample was powdered manually and then hermetically sealed in a sterile tube.

Adjustment of a_w and water sorption isotherm

The freeze-dried sample was vacuum dried at 310 K (stage temperature) for 6 h in order to remove as much residual moisture as possible. The fully dehydrated was equilibrated at 298 K in a desiccator at a range of relative humidity (RH) conditions for 7 days. The RH was adjusted using saturated salts: LiCl (RH = 11.3%), MgCl₂ (RH = 32.8%), Mg(NO₃)₂ (RH = 52.9%), KI (RH = 68.9%), NaCl (RH = 75.3%), KCl (RH = 84.3%), and NH₄H₂PO₄ (RH = 92.5%) (32). It was previously reported that the viable cells of freeze-dried samples decreased by three orders at RH = 43% and seven orders at RH = 87% during storage at 298 K for 7 days (9). The a_w of the sample was assumed from the equilibrium RH (a_w = RH/100).

For the incoherent elastic neutron scattering experiment, the sample was equilibrated using saturated salts in D₂O to observe the dynamics of C. sakazakii. To promote H-D exchange, the dehydration-rehydration process was repeated two times as follows: the fully dehydrated sample was semi-equilibrated for 3 days, re-dehydrated, and equilibrated for 7 days.

The equilibrium water content (g/g-DM, dry matter) was measured gravimetrically by oven drying at 378 K for 16 h. The measurements were performed in triplicate, and the results were averaged.

The effect of a_w on the water content was analyzed using the Guggenheim-Anderson-de Boer (GAB) model (Equation 1),

$$W=\frac{W_{m}CK{a}_w}{\left(1-K{a}_w\right)\left(1+\left(C-1\right)K{a}_w\right)},$$ (1)

where W is the water content (g/g-DM), W_m is the monolayer water content (g/g-DM), C is a factor correcting the sorption properties of the monolayer with respect to the bulk liquid, and K is a factor correcting the sorption properties of the multilayer with respect to the bulk liquid.

Isothermal mechanical relaxation measurement

Isothermal mechanical relaxation measurement was carried out using a rheometer (CR-150; Sun Scientific, Tokyo, Japan) according to a previous study (13). The sample (approximately 50 mg) was placed in a stainless-steel sample holder (diameter = 7 mm), and transferred to the cup of the heat sink attached to the texture meter. The temperature of the cup was kept at 298 K using a water bath circulator (LTB-125; As One, Osaka, Japan). The sample was compressed using a plunger (diameter = 5 mm) at 80 N (approximately 2.1 MPa) and held for 3 min. The ΔF (the difference between the initial force and the force after 3 min) was evaluated as the degree of isothermal mechanical relaxation (6,10, 11, 12, 13). The measurements were carried out in triplicate, and the results were averaged.

Incoherent elastic neutron scattering experiment

The sample (approximately 150 mg) equilibrated in saturated salts prepared by D₂O was wrapped with aluminum foil approximately 40 mm in height and hermetically sealed in a cylindrical aluminum sample holder (14 mm inner diameter, 0.25 mm thick) using indium wire. In order to prevent water sorption/desorption during preparation, this procedure was carried out under an RH-adjusted atmosphere in a glove box using saturated salt solutions as described above.

The neutron scattering experiment was carried out using the Biomolecular Dynamics Spectrometer (BL02-DNA) in the Material and Life Science Experimental Facility at Japan Proton Accelerator Research Complex, Tokai, Ibaraki (33). The energy resolution was 3.5 μeV using an Si (111) analyzer and pulse shaping chopper at 225 Hz operation, and the the covered Q range was from 0.1 to 1.86 Å⁻¹. The measurement can detect molecular dynamics of atoms (mainly hydrogen) on approximately 190 psec. The fixed window scan was performed at the temperature range of 100–350 K at cooling and heating rates of 1 K/min and 2 K/min, respectively. The measurement was carried out once.

Under the assumption of harmonic oscillator approximation, the elastic intensity (I) at a given scattering vector (Q) and absolute temperature (T) is as follows:

$$I=A\text{exp}\left(\frac{-u^2{Q}^2}{3}\right),$$ (2)

where A is a constant and u² is the MSD at T (K). The observed scattering intensity (including elastic scattering) in the system, C. sakazakii hydrated using D₂O, was treated as incoherent scattering from hydrogen atoms in C. sakazakii due to the large incoherent scattering cross section of hydrogen. Thus, the molecular mobility in C. sakazakii at T was evaluated by the MSD obtained from the Q dependence of I (15). The data was analyzed using Igor Pro 9 (WaveMetrics, Lake Oswego, OR, USA).

Results and discussion

Water sorption isotherm

The water sorption isotherm (water content versus a_w) for C. sakazakii is shown in Fig. 1. The water content of the sample sigmoidally increased with the increase of a_w. A solid line was obtained by fitting the experimental data to the GAB equation. The GAB parameters W_m, C, and K were determined to be 0.0724 g/g-DM, 13.1, and 0.859, respectively. In addition, the W_m can be converted to monolayer a_w through the water sorption isotherm. The monolayer a_w for C. sakazakii, which can be converted from W_m and the GAB equation, was determined to be 0.252.

Figure 1.

Water sorption isotherm for C. sakazakii at 298 K. The values are expressed as mean ± SD (n = 3). The solid line was obtained by fitting to the GAB equation (Eq. 1).

Among the GAB parameters, W_m and/or monolayer a_w are important parameters because the monolayer water molecules affect the storage stability of biomaterials (34). It is known that lipid oxidation shows a minimum rate at around the W_m (2). As a result, the biological activity of dry yeast decreases gradually during storage at a lower a_w than the monolayer a_w (13). The W_m values for bacteria (Streptococcus thermophilus strains) reported in a previous study (35) were in the range of 0.044–0.070 g/g-DM. In addition, the monolayer a_w values were estimated to be 0.307–0.382 from the data. The values were relatively near to those of C. sakazakii. The major component of dehydrated bacteria is protein. It is known that 42%–60% protein (proteome) exists in the system, depending on the growth stage (36). Thus, W_m and monolayer a_w are primarily corresponded to those of hydrated protein. The effect of monolayer a_w on the mechanical properties and molecular dynamics of bacteria is discussed below.

Isothermal mechanical glass-transition behavior of C. sakazakii

Typical results of the isothermal mechanical relaxation behavior of C. sakazakii are shown in Fig. 2 a. The sample having a_w = 0.328 showed a small mechanical relaxation, indicating high elasticity (low molecular mobility). The sample having a_w = 0.843, on the other hand, exhibited a large mechanical relaxation, indicating low elasticity (high molecular mobility). From the isothermal mechanical relaxation behavior, ΔF between the initial force and the force after 3 min was evaluated as a typical parameter for isothermal mechanical relaxation.

Figure 2.

(a and b) Typical isothermal mechanical relaxation behavior for C. sakazakii samples at 298 K (a) and the effect of a_w on ΔF for C. sakazakii samples at 298 K (b). The values are expressed as mean ± SD (n = 3).

The effect of a_w on ΔF of C. sakazakii at 298 K is shown in Fig. 2 b. The ΔF value slightly increased but was almost constant in the low a_w region (a_w ≤ 0.529). In the higher a_w range, the ΔF value increased gradually with an increase in a_w. This suggests that the glass transition occurred at the turning point. The a_w dependence of ΔF was described by two linear functions, and the crossover point was determined to be 0.667. The w_c corresponding to a_w was 0.160 g/g-DM through the GAB equation (Eq. 1). The water content and a_w are described as “mechanical w_c” and “mechanical a_wc,” respectively, hereafter.

In the many previous studies, w_c is evaluated as an interpolated value from the effect of water content on the calorimetric T_g (3,37, 38, 39) or mechanical T_g (5,40). In addition, a_wc is converted from w_c through the GAB equation. To the best of our knowledge, the approach of a_wc determination employed in this study is a first. In order to valid the mechanical a_wc, the a_wc values determined previously from the effect of water content on the calorimetric or mechanical T_g (6,10, 11, 12,41) were compared with the mechanical a_wc determined by the approach suggested in this study. There was good agreement among the values (R² = 0.856), as seen in Fig. S1.

As mentioned above, the major component of dehydrated bacteria is protein (proteome). Thus, the origin of the mechanical glass-transition behavior for bacteria will be primarily discussed based on that of hydrated proteins. The w_c for a globular protein (bovine serum albumin [BSA]) was estimated to be approximately 0.2 g/g-DM from the effect of water content on T_g (42,43). The reason C. sakazakii showed a much lower w_c (0.16 g/g-DM) than BSA is that bacteria contain water-insoluble materials (e.g., phospholipids and cell wall components) in the system. The water-insoluble materials are not involved in glass transition but are included in the weight of the dry matter. Thus, T_g at each water content (g/g-DM) becomes lower through the existence of water-insoluble materials. That is, the w_c decreases “apparently” with the increase in water-insoluble materials (11). Since a_w is affected not by water-insoluble materials but by water-soluble materials, similar to T_g, a_wc is more suitable as a reference parameter. The a_wc for BSA can be estimated to be 0.71–0.75 from w_c and the effect of a_w on the water content (44,45). The a_wc for C. sakazakii (0.667) was slightly lower than that for BSA. This suggests that proteome is plasticized by other hydrophilic amorphous small molecules in the cell. The effect of a_w on the T_g of C. sakazakii is further discussed in the context of the following incoherent elastic neutron scattering study.

Temperature dependence of MSD for C. sakazakii

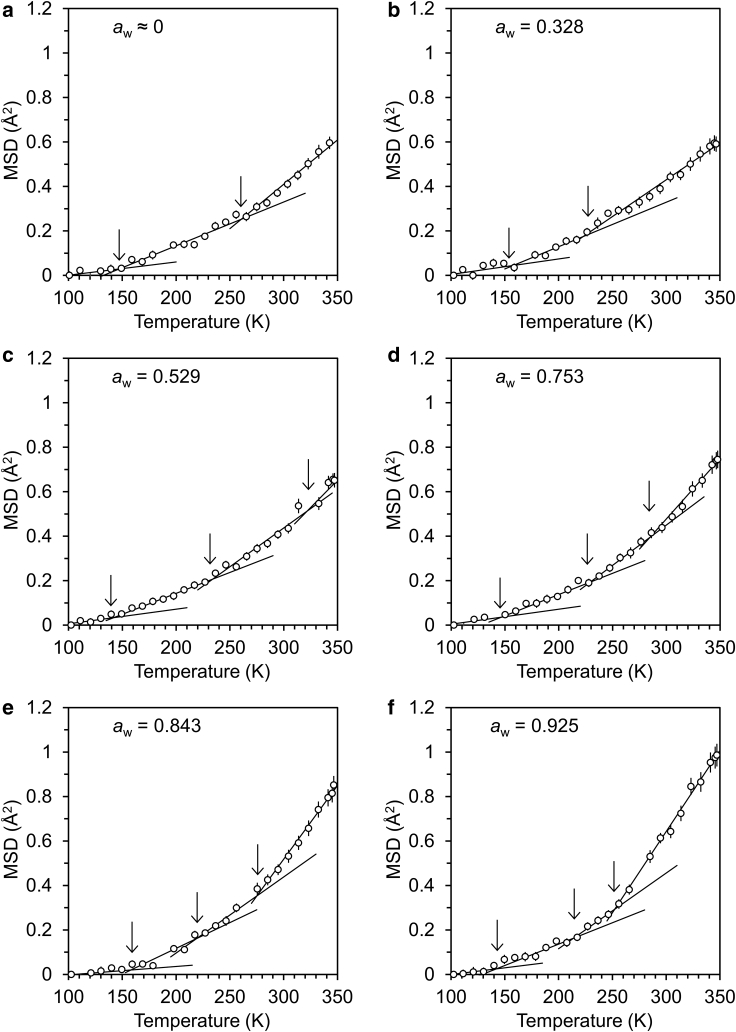
The effect of temperature on the MSD of C. sakazakii (heating measurement) at varying a_w conditions is shown in Fig. 3 a–f. Strictly speaking, a_w is a function of temperature, and thus a_w decreases slightly with a decrease in temperature (32). For simplification, the a_w provided at 298 K was treated as a typical a_w value. The MSD can be mainly attributed to the molecular dynamics of C. sakazakii because there is a negligible contribution of D₂O to the neutron scattering data due to the large incoherent scattering cross section of hydrogen (46). The MSD increased gradually with an increase in temperature depending on the a_w of samples. For hydrated biomaterials such as proteins (15,18,21,22), saccharides and polysaccharides (25,47, 48, 49), and DNA (23), the MSD increases linearly with the increase in temperature, and the slope of the linear function becomes greater at a certain temperature. This means that the MSD of atoms changes in nature from harmonic (solid-like) motion to anharmonic (liquid-like) motion at that temperature. The turning point has been determined to be T_d. In the case of C. sakazakii, there was unclear turning point in the temperature dependence of the MSD. This suggests that various motions activate continuously with the increase in temperature. The results were described by three (a_w = 0 and 0.328) and four (a_w = 0.529–0.925) linear functions, and T_d values were determined from the crossover points. For the high a_w samples (0.843 and 0.925), there is a possibility that hydration water crystalizes during the measurement (13). When water crystalized during the cooling, MSD drastically increases at the melting point of ice. It is noted that there was no experimental evidence indicating crystallization of water in Fig. 3.

Figure 3.

Temperature-dependence of MSD for C. sakazakii (heating measurement) at each a_w. Arrows indicate T_ds.

The effect of a_w on the T_d values for C. sakazakii is shown in Fig. 4. The vertical dashed and dotted lines are monolayer a_w and mechanical a_wc, respectively. As mentioned above, the major component of bacteria is protein (proteome), and thus it will be effective to discuss the dynamical transition behavior of bacteria based on protein dynamics. However, the interpretation of protein dynamics is somewhat controversial (20,21,50,51). In addition, bacteria system is heterogeneous due to the presence of other components (e.g., cell membrane, DNA, and lipopolysaccharide), and the effects of the components should be taken into account.

Figure 4.

Effect of a_w on the T_ds for C. sakazakii. The vertical dashed and dotted lines are monolayer a_w and mechanical a_wc, respectively. The horizontal dashed line is a reference temperature (298 K).

The T_d observed at a low temperature (142–158 K) was denoted as low T_d. It is noted that the low-T_d values were almost independent from a_w. It is reported that the first onset of anharmonic molecular dynamics appears at around 100 K regardless of hydration level in protein (lysozyme) system (51). This is thought to be originated from methyl group rotation. In the case of bacteria, phospholipid in cell membrane will also contribute to the methyl group rotation. The low T_d of C. sakazakii was higher than the temperature of which methyl group rotation of hydrated protein activates. As mentioned above, it is suggested that various motions in the cell activate continuously with the increase in temperature because of its heterogeneous natures. In this case, the individually different motions in the cell interlock with each other; low-T_d dynamics will shift to a higher temperature.

The T_d observed at a middle temperature (214–261 K) was denoted as middle T_d. The dynamical transition is reported at a similar temperature range (220–240 K) in the hydrated protein in the hydration range of 0.3–0.62 g/g-protein (14,22,52,53). Golub et al. (20) suggested that vibrational anharmonicity of protein is observed above 160 K and that softening of the protein matrix occurs at approximately 240 K. In addition, the T_d value strongly depends on the solvent (21,54). Demmel et al. (55) suggested that glass transition of solvent is transmitted to polar side chains on the protein surface and to the main chain. On the other hand, the T_g values of 187–226 K for 0.12–0.43 g/g-protein (42), 188–216 K for 0.23–0.96 g/g-protein (56), and 148–248 K for 0.08–0.84 g/g-protein (57) were reported by adiabatic calorimetry. The origin of the T_g for hydrated proteins is suggested to be the local motion originated from the polar side chains of amino acids coupled with hydration water. Translational motion for polymeric main chain (polypeptide) will be freezing at this stage, as long-chain polymers commonly have a high T_g (16).

The middle T_d slightly increased with a decrease in a_w because the hydration water played the role of plasticizer for the bacteria (57). The middle T_d for anhydrous C. sakazakii was slightly higher than that expected through linear regression of the middle T_d for hydrated C. sakazakii (a_w = 0.328–0.925). It is thought that the polar side chains are hydrated sufficiently at a higher a_w than the monolayer a_w (0.252) because they are mainly located in the surface of bacteria. A lack of hydration water (plasticizer) will cause greater elevation of the middle T_d.

The T_d observed at the highest temperature (high T_d) was more sensitive to a_w in the whole range. The high T_d increased from 252 to 322 K with a decrease in a_w (Fig. 4). According to the knowledge on the glass-transition behavior of hydrated proteins (16,42), it is thought that the high T_d corresponds to the rearrangement of the polymeric main chain composed of amino acids (polypeptide). Other polymeric materials will also contribute to the motion in the temperature region. For example, it is known that DNA (polynucleotide) has slightly higher T_g than protein (58). In addition, Gram-negative bacteria have a large number of hydrophilic short chains (lipopolysaccharide) on the surface of cell (59). T_g of polysaccharide increases with an increase in molar mass (60).

The macroscopic molecular motion can directly correspond to mechanical relaxation behavior. From the linear regression in the measured range, the a_w at which high T_d becomes 298 K (dynamical a_wc) was estimated to be 0.675. The dynamical a_wc was almost equivalent to the mechanical a_wc (0.667). To evaluate the MSD of C. sakazakii, the hydrated sample was prepared not by H₂O but by D₂O. Since D₂O is slightly slower mobility than H₂O, the dynamical a_wc may have been evaluated as a slightly higher value than mechanical a_wc.

Predicted anhydrous T_g and molecular relaxation time of C. sakazakii

It is known that T_g is the temperature at which the viscosity (η) and molecular relaxation time (τ) become 10¹² Pa s and 10² s, respectively (61). As discussed above, the high T_d can be identified with the T_g because they are thought to be intrinsically same physical origin (rearrangement of polymeric main chain). As is well known, the effect of water content on the T_g can be analyzed by the Gordon-Taylor equation (Eq. 3),

$$T_g=\frac{W_1{T}_{g1}+k{W}_2{T}_{g2}}{W_1+k{W}_2},$$ (3)

where W₁ and W₂ are the mass fraction of the bacteria and water, respectively, T_g1 and T_g2 are T_g for anhydrous bacteria and water, respectively, and k is a constant. The T_g2 was set as 136 K from the literature (62,63). The T_g values were replaced by the determined high-T_d values at each water content, and then T_g1 and k were determined as fitting parameters. The fitting result is shown as a solid line in Fig. 5 a.

Figure 5.

Effect of a_w on the T_g for C. sakazakii predicted by the Gordon-Taylor and GAB equations (a). The high T_d was identified with the T_g. The vertical and horizontal dashed lines indicate dynamical a_wc and a reference temperature (298 K), respectively. The effect of a_w on the τ for C. sakazakii predicted by the Williams-Landel-Ferry equation (b). The vertical dashed and dotted lines indicate dynamical a_wc and the typical a_w (0.85) for inactive-active transition for bacteria, respectively.

The anhydrous T_g (T_g1) and k for C. sakazakii were estimated to be 409 K and 4.17, respectively. The anhydrous T_g for C. sakazakii was slightly lower than that (approximately 420 K) for globular proteins (42). As stated above, this suggests that proteome is plasticized by other hydrophilic amorphous small molecules in the cell. It is confirmed that the glass-transition behavior of C. sakazakii can be assumed to be a typical amorphous biopolymer.

As suggested above, bacteria have similar glass-transition behavior as biopolymers. The effect of temperature on the η of polymers can be characterized as a function of T_g using the Williams-Landel-Ferry equation (Eq. 4),

$$\log \left(\frac{{\eta }_T}{{\eta }_{T_g}}\right)=\frac{-C_1\left(T-T_g\right)}{C_2+T-T_g},$$ (4)

where η_T and η_Tg are the viscosities at T and T_g, respectively. The C₁ and C₂ are set as 17.4 and 51.6, respectively, as universal constants (64). As stated above, T_g corresponds to the temperature at which η and τ become approximately 10¹² Pa s and 10² s, respectively (61). In addition, η and τ at an infinite temperature can be set to 10⁻⁵ Pa s and 10⁻¹⁴ s, respectively. It is known that the η is an interconversion to τ. According to the linear proportion between log η and log τ, η can be converted to τ as follows:

$$\log \tau =0.9412\log \eta -9.2941.$$ (5)

The effect of a_w on the expected log τ at T = 298 K for C. sakazakii is shown in Fig. 5 b. The vertical dashed and dotted lines are the mechanical a_wc and the typical a_w (0.85) required for the growth of bacteria, respectively. As mentioned above, bacterial inactive-active transition generally occurs at around a_w = 0.85 (2). The a_w is slightly higher than the mechanical a_wc point, and thus bacteria are suggested to be in a rubbery state at the given condition. As a matter of course, the bacterial inactive-reactive transition requires molecular mobility at least for the progress of metabolism in the system. From Fig. 5 b, the τ for C. sakazakii was estimated to be 6 × 10⁻⁵ s at a_w = 0.85. It is known that this time narrowly allows for DNA synthesis (helix-coli transition) and chemical reactions such as hydrolysis (65).

Conclusion

This study demonstrated that the mechanical a_wc value of C. sakazakii could be evaluated from isothermal mechanical relaxation behavior. In addition, neutron scattering was applied to clarify the temperature dependence of the MSD for C. sakazakii, and three different dynamical transition processes were established. Furthermore, a_w dependences of T_g and τ were estimated from the results obtained via analytical models established in polymer science. This is fundamental knowledge regarding amorphous polymers but represents novel data regarding bacteria. Given the fact that metabolism is a result of multiple and continuous chemical reactions, it is thought that the inactive-active transition of bacteria will be affected by the molecular dynamics in bacteria. The glass-transition behavior of other bacteria (e.g., a_w sensitive or resistant) is an interesting topic for future research.

Author contributions

Conceptualization, T.S., H.N., T.Y., S.K., and K.K.; formal analysis, T.S., H.N., and T.Y.; investigation, T.S., H.N., S.K., and K.K.; writing – original draft preparation, T.S.; project administration, H.N., T.Y., S.K., and K.K.; investigation, T.Y. and S.K.; funding acquisition, S.K.; supervision, K.K.; writing – review & editing, K.K.

Editor: Frank Gabel.