T cell microvilli simulations show operation near packing limit and impact on antigen recognition

Abstract

T cells are immune cells that continuously scan for foreign-derived antigens on the surfaces of nearly all cells, termed antigen-presenting cells (APCs). They do this by dynamically extending numerous protrusions called microvilli (MVs) that contain T cell receptors toward the APC surface in order to scan for antigens. The number, size, and dynamics of these MVs, and the complex multiscale topography that results, play a yet unknown role in antigen recognition. We develop an anatomically informed model that confines antigen recognition to small areas representing MVs that can dynamically form and dissolve and use the model to study how MV dynamics impact antigen sensitivity and discrimination. We find that MV surveillance reduces antigen sensitivity compared with a completely flat interface, unless MV are stabilized in an antigen-dependent manner, and observe that MVs have only a modest impact on antigen discrimination. The model highlights that MV contacts optimize the competing demands of fast scanning speeds of the APC surface with antigen sensitivity. Our model predicts an interface packing fraction that corresponds closely to those observed experimentally, indicating that T cells operate their MVs near the limits imposed by anatomical and geometric constraints. Finally, we find that observed MV contact lifetimes can be largely influenced by conditions in the T cell/APC interface, with these lifetimes often being longer than the simulation or experimental observation period. This work highlights the role of MVs in antigen recognition.

Significance

T cells search for foreign-derived antigens on the surface of antigen-presenting cells (APC) by dynamically extending tubular protrusions called microvilli (MVs), which form membrane close contacts. Although known for decades, their role in antigen recognition remains unclear. Guided by recent experiments, we built an anatomically informed stochastic model of MV scanning and compared it with a topologically flat interface. We find that MV scanning modestly impacts antigen discrimination, yet it enables T cells to balance the competing effects of maintaining sensitivity while conducting rapid APC surveillance. The model can reconcile discrepancies in observed MV lifetimes and demonstrates that observed area coverage fractions correspond to geometric packing limits. Our work suggests that MVs promote positive signaling outcomes despite anatomical constraints to close contact formation.

Introduction

T cells are immune cells that continuously search for the molecular signatures (antigens) of pathogens and, upon antigen recognition, can initiate adaptive immune response. T cells recognize antigen through binding of their T cell receptor (TCR) to antigens presented by antigen-presenting cells (APCs). In addition, T cells search for antigen on APCs via small tubular membrane protrusions, termed microvilli (MVs). The existence of MVs has been known for decades, yet the function of these structures is largely unknown.

MVs are generally described to be $\approx$50–400 nm wide with micrometer-long structures (1). They first became apparent when imaging T cells by electron microscopy (2, 3, 4). Due to their small size, conventional light microscopy cannot resolve them. However, recent developments have allowed imaging of MVs on cells (5,6), greatly increasing our understanding of their dynamics in homeostasis or during antigen recognition. While they only cover about 40% of the interface at a given time, through their dynamic movements, they are able to scan 98% of the interface with an APC within physiological dwell times of T cell/APC contacts in vivo (5,7, 8, 9). The lifetime of an individual MV is short when it does not recognize antigen ($\approx$8 s) but can increase upon antigen recognition, with reported lifetimes ranging from 9 s to 18 min (5,6). Super-resolution microscopy has revealed that MV tips are enriched in TCR and adhesion molecules (4,10), consistent with their role in forming the small close contacts required for TCR/antigen binding (11). One hypothesis is that MVs are a necessity of the biophysical constraints of the T cell/APC interface (1). Both the surfaces of APCs and T cells are covered with glycoproteins, such as the abundant CD45 on T cells, generating a thick glycocalyx that causes steric and electrostatic repulsion (12, 13, 14). As both TCRs and antigen are much shorter in comparison, the penetration of this matrix is required for the formation of close membrane contacts and binding to occur (6,14).

The potential role of MVs in antigen recognition is unclear. The process of antigen recognition is marked by rapid recognition speeds with single-molecule sensitivity to agonist ligands. For example, CD4⁺ T cells can exhibit ${\text{Ca}}^{2+}$ signaling, a precursor of T cell activation, when stimulated with a single molecule of foreign antigen (15). Similarly, CD8⁺ T cells have been shown to recognize as few as three molecules of a foreign antigen (16). This single-digit molecule sensitivity is particularly remarkable given how short lived TCR/antigen interactions are. TCRs bind foreign antigen with typical bond lifetimes in the range of 1–10 s (17). Moreover, this level of sensitivity is achieved with a high speed, since T cells have been shown to exhibit ${\text{Ca}}^{2+}$ signaling in as little as 7 s upon antigen binding (18). Intuitively, MVs would be expected to decrease the sensitivity when compared with a flat interface, as they only contact 40% of the surface at a given time.

Lastly, T cells are able to amplify small differences in antigen affinity into large differences in their responses (19). Furthermore, T cells can ignore APCs that express a high abundance of self-derived antigen while retaining sensitivity to only a few foreign antigen, even in cases where they may be chemically similar (20). We have previously speculated that small contacts, such as the ones formed by MVs, could improve the antigen discrimination (21). In this theory, creating small domains improves signal/noise, effectively implementing kinetic proofreading on a topological level. Furthermore, antigen discrimination was shown to be improved by a biophysical phenomenon that can increase the lifetime of foreign antigens (catch bond), while decreasing the lifetime of self-antigens (slip bond) (22, 23, 24, 25). In this model, MVs may act as the source of the bond stress (1).

In the present work, we develop a new computational model that combines stochastic topography induced by MV surveillance of the APC surface together with TCR/antigen interactions. We investigate the effect of MVs on sensitivity, speed, and antigen discrimination when compared with a hypothetical flat interface. We find that the sensitivity and speed are decreased with MVs, while the discrimination is largely unchanged. However, when introducing signaling-dependent MV stabilization, sensitivity and speed are markedly improved. Lastly, we show that MV scanning operates near the packing limit of MVs in the contact interface and that discrepancies in the experimentally measured MV lifetimes are likely a result of censored data collection. Together, these results support the hypothesis that MVs have evolved out of biophysical constraints rather than to improve antigen recognition or discrimination.

Materials and methods

Our model of T cell activation is compartmentalized between a spatial search component describing APC surface exploration and a kinetic proofreading (KP) component describing TCR/antigen interactions. See Fig. 1 for a detailed schematic.

Figure 1.

Model overview. (Left) Illustrations of the three layers involved in the stochastic MV scanning model. TCR/antigen interactions are facilitated by circular close contacts formed on the tips of MVs. All interactions take place in a circular T cell/APC interface (IS) of radius r_IS = 50 μm with $N_{\text{a}}$ antigen green dots). (Right) Illustrative description of the simulated dynamics of the T cell/APC interface. Close contacts by MV (small disks radius $r_{\text{MV}}$) are formed at rate $k_{\text{a}}$ and are removed with rate $k_{\text{d}}$, given that the contact has not been stabilized. TCRs and antigens interact within the close contact zones according to the displayed kinetic proofreading mechanism. MV contacts that contain an activated TCR within the contact boundary stabilize with rate $k_{\text{s}}$. Stabilized MV contacts cannot be removed, i.e., $k_{\text{d}}=0$. Instead, these contacts can only be destabilized with rate $k_{\text{u}}$, given that there are no activated TCRs within the MV contact boundary. To see this figure in color, go online.

MV dynamics and packing limits of the immunological synapse (IS)

Close contacts between circular MV tips (radius $r_{\text{MV}}$) and the circular T cell/APC interface (radius $r_{\text{IS}}$) are subject to addition (rate $k_{\text{a}}$) and removal (rate $k_{\text{d}}$). Steric clashes between MVs are prevented by placement of new contacts only into open spaces of the IS.

To ascertain the availability of free space for new contacts to be placed, we use a separate simulation to predetermine the packing limit of the IS for a given MV tip radius $r_{\text{MV}}$. This is accomplished by repeated random placement attempts (T) in the T cell/APC interface. After placement attempts exceed a threshold ($T>T_{\text{Max}}$), the final number of MV contacts ($N_{\text{max}}$) is recorded, with the results being averaged over 100 realizations. In Fig. 4 B, the results of packing simulations for different MV radii ($r_{\text{MV}}$) are shown. The vertical axis ($1/T$) approximates the probability of placing an additional MV contact into an open space in the T cell/APC interface as the number of contacts ($N_{\text{MV}}$) increases.

Figure 4.

Stochastic simulations of MV placement and dynamics in model with stabilization. (A) Contour plot of average MV lifetimes ($t_{\text{MV}}$) over antigen population ($N_{\text{a}}$) and TCR/antigen disassociation rates ($k_{\text{off}}$). (B) Likelihood of successful MV tip placement into open space of the T cell/APC interface against MV coverage fraction. (C) Instantaneous (solid line) and cumulative (dashed line) scanning area fractions in the absence of agonist antigen for several MV tip radii. (D) Similar to (C), but curves represent different numbers ($N_{\text{a}}$) of agonist antigen present. To see this figure in color, go online.

TCR/antigen interaction

We assume that MV tips are densely packed in TCRs so that whenever an MV contact houses one or more antigens, interactions occur through a KP mechanism (26). KP posits that a productive immune signal can arise from TCR/antigen interactions only after a sequence of intermediate binding steps have occurred. Each intermediate step is irreversible, such that upon TCR/antigen dissociation (rate $k_{\text{off}}$), the TCR reverts to its original unphosphorylated state before a new antigen binds. KP predicts that T cell activation is linked to the lifetime ($1/k_{\text{off}}$) of the TCR/antigen complex (26). An outcome of this mechanism is that a time delay is induced between an initial binding event and eventual signaling, such that only long-lived TCR/antigen complexes progress into a signaling state. With multiple steps, KP can discriminate with high accuracy between antigens of different TCR/antigen dissociation rates ($k_{\text{off}}$).

Our model consists of $N_{\text{kp}}$ intermediary states $\left\{B_1\text{,}\dots \text{,}{B}_{N_{\text{kp}}}\right\}$ with transition rate $k_{\text{t}}$. The rate at which signal accumulates from individual activated TCRs, as well as the threshold of total signal required for T cell activation, is chosen so that antigen discrimination is possible within experimentally observed dissociation times. As reported by Iezzi et al. and Huppa et al., TCR/antigen complexes can experience lifetimes as short as 0.1 to 10 s (27, 28, 29). The accumulated signal $X\left(t\right)$ to the T cell is modeled by dynamics

$$\frac{dX}{dt}=S\left(t\right)k_{\text{act}}\left(1-X\right),t>0;X\left(0\right)=0,$$ (1)

where $k_{\text{act}}$ is the signaling rate and $S\left(t\right)$ is the number of TCR/antigen pairs in a signaling state at time t (in the stochastic model, this is a discrete valued function). We assume signal accumulation occurs globally, meaning that regardless of the spatial location of activated TCR/antigen pairs in the IS, they contribute equally to the total accumulated signal. Similar behavior has been observed in experiments utilizing photoactivation of micro-scale regions of the IS, where it was found that localized signals propagate away from stimulated regions, indicating that signals from upstream events act cooperatively to elicit a generalized calcium response (18). To obtain a digital response, we define the threshold $X_{\text{act}}=0.9$ and a T cell to be activated when $X>X_{\text{act}}$, with associated activation time $t_{\text{act}}={\text{min}}_{t>0}\left\{X\left(t\right)=X_{\text{act}}\right\}$. The dynamics of this function resemble experimental observations of signal accumulation in T cells (30,31). The probability of activation for a single T cell/APC interaction follows a Bernoulli distribution whose mean we determine from an average over $N_{\text{sim}}=100$ simulations (statistical model error is discussed in section 3 of the supporting material).

MV scanning and stabilization

We extend the KP model to incorporate MV dynamics, with the assumption that TCR/antigen interactions only occur when the MV provides a close contact. MV contacts are represented by nonoverlapping circular regions of fixed radii, $r_{\text{MV}}$, and are placed randomly in the IS with rate $k_{\text{a}}$. When a contact is added to the interface, its position is fixed until the MV is removed. If the MV contact encompasses one or more antigens, then TCR/antigen interactions can occur (Fig. 1). Each MV contact is capable of having multiple simultaneously activated TCRs, up to the number of antigens covered. If the MV contact does not cover any antigen, then the contact can only be removed.

In the presence of foreign antigen, extended lifetimes of MV contacts have been observed (5,32). We reproduce this behavior by extending the dynamics to include a stabilized MV state (rate $k_{\text{s}}$) in which contacts must first become destabilized (rate $k_{\text{u}}$) before being subject to removal. In the MV scanning model without stabilization ($k_{\text{s}}=0$), contacts may be removed regardless of the state of any resident TCRs. When $k_{\text{s}}>0$, MV lifetimes can be significantly extended when a TCR becomes activated.

Flat interface model

Our idealized flat topology model is a stochastic implementation of KP (26). There are no structures such as MV, and all antigens within the IS are accessible to TCRs. This nonspatial model assumes that the T cell surface is densely packed with TCRs and implies that when the contact is formed, every antigen present in the contact area is close enough to bind to one or more TCRs. Utilizing this assumption, we consider only the discrete population of antigen in binding interactions rather than concentrations of both species (Fig. 1). This idealized model serves as an upper bound of antigen accessibility to TCRs and is utilized due to its likeness to the deterministic mass action model.

Discrimination power

To assess discrimination across model and parameter regimes, we utilize a discrimination power (γ) to quantify the amplification of T cell response from variations in dissociation rates ($k_{\text{off}}$). The factor γ is determined as the slope of a linear fit of $P_{15}$ (antigen population necessary to elicit a 15% chance of T cell activation) with $k_{\text{off}}$ (19). Larger values of γ imply better discrimination (Fig. 2 A and B).

Figure 2.

MV scanning and discrimination power over antigen populations $N_{\text{a}}={10}^0-{10}^4$. (A) Proportion of activated T cells across antigen numbers. The quantity $P_{15}$ is the antigen number required to produce at least a 15% chance of activation. (B) Determination of the discrimination power γ. (C–H) Comparisons of the measured discrimination powers among several models. Results shown are of models with either $N_{\text{kp}}=3$ or $N_{\text{kp}}=10$ kinetic proofreading steps. Times shown at the bottom of each graph indicate the simulated duration of the T cell/APC contact. (C and D) Discrimination powers for 3- (C) and 10-step (D) kinetic proofreading steps, simulated for 1 min of T cell/APC contact time. (E and F) Discrimination powers for 3- (E) and 10-step (F) kinetic proofreading steps, simulated for 5 min of T cell/APC contact time. (G and H) Discrimination powers between MV models for different T cell/APC interface times with 3- (G) and 10-step (H) kinetic proofreading. To see this figure in color, go online.

Parameter selection

Experimental observations are used whenever possible to identify parameter ranges for both the scanning compartment and the signaling compartment of the model. A summary is given in Table 1.

Table 1.

A summary of parameters used and values

Parameter	Meaning	(Unit)	Flat interface	MV scanning	MV stabilization	Source
$k_{\text{a}}$	MV placement	(s−1)	N/A	$\frac{2}{3}$	$\frac{2}{3}$	(5)
$k_{\text{d}}$	MV removal	(s−1)	N/A	$\frac{1}{7}$	$\frac{1}{7}$	(5)
$k_{\text{s}}$	MV stabilization	(s−1)	N/A	0	$(\mathrm{0,100}]$	(5)
$k_{\text{u}}$	MV destabilization	(s−1)	N/A	N/A	0.03	(5)
$k_{\text{on}}$	TCR/pMHC binding	(s−1)	100	100	100	(34,36)
$k_{\text{off}}$	TCR/pMHC disassociation	(s−1)	$\left[{10}^{-1}\text{,}{10}^{1.5}\right]$	$\left[{10}^{-1}\text{,}{10}^{1.5}\right]$	$\left[0.01\text{,}10\right]$	(27, 28, 29)
$k_{\text{act}}$	TCR/pMHC signaling	(s−1)	0.2	0.2	0.2	(30,31)
$k_{\text{t}}$	proofreading rate	(s−1)	1.0	1.0	1.0	(19)
$N_{\text{kp}}$	# of proofreading steps	–	3	3	3	(19)
$N_{\text{a}}$	# of antigens in T cell/APC interface	–	$\left[{10}^0\text{,}{10}^4\right]$	$\left[{10}^0\text{,}{10}^4\right]$	$\left[{10}^0\text{,}{10}^4\right]$
$N_{\text{MV}}$	# of engaged MVs	-	–	N/A	N/A	Eq. 2
$N_{\text{max}}$	maximum # of MVs in the IS	–	N/A	N/A	N/A
$r_{\text{MV}}$	MV tip radius	(nm)	–	267.5	267.5	(3,4,6)
$r_{\text{IS}}$	T cell/APC interface radius	(μm)	5.0	5.0	5.0	(5)
$t_{\text{sim}}$	simulation period	(s)	$(\mathrm{0,300}]$	$(\mathrm{0,300}]$	$(\mathrm{0,300}]$	(5,6)

Following recent experimental work (19), the number of KP steps was set to $N_{\text{kp}}=3$ (unless stated otherwise) and the KP transition rate set to k_t = 1.0 s⁻¹. An assumption in our model is that antigen discrimination is primarily influenced by the dissociation rate $k_{\text{off}}$ and that its value is varied according to those reported in the literature (27, 28, 29). The rate $k_{\text{on}}$ is assumed to be the product of the bimolecular on rate and the two-dimensional radial density of TCRs (k_on = 100 s⁻¹) and is taken to be relatively fast compared with other model parameters. The TCR concentration is assumed to be relatively high, i.e., the flat interface and MV tips are densely packed with TCRs. If the model relies on multiple rebinding steps (TCR + antigen $\to B_1$) before a TCR can become activated, then on rates can greatly influence antigen sensitivity, as observed experimentally (33, 34, 35). In such a case, antigen with fast on rates led to T cell activation, while those with slower binding rates did not. Other evidence for fast TCR/antigen binding was seen in Cai et al. (5), who observed that TCR recognition occurred at the same time as surface deformations (MVs) contacted the APC. Other studies have suggested that describing TCR/antigen binding with an on rate may be inappropriate (36), with their results indicating that binding may occur after a minimal encounter duration ($t_{\text{on}}<1$ ms). In the signal accumulation equation (1), the parameter values k_act = 0.2 s⁻¹ and $X_{\text{act}}=0.9$ were chosen such that T cell activation is unlikely to occur with a single visit to a signaling state by a weak agonist while also ensuring that discrimination occurs within the varied interval of $k_{\text{off}}$.

We choose the average lifetime of stabilized MV contacts to exceed the 11.1 s observed by Cai et al. (5) due to their finding that 25% of stabilized contacts were stable for the entire observation period $t_{\text{sim}}$. We surmise that stabilization is a rapid process induced when a TCR enters an activated state and reflect this in the parameter selection k_s = 100 s⁻¹. This effectively stabilizes MV after a short period of TCR/antigen binding. In Fig. 2, we vary $k_{\text{s}}\in \left[0\text{,}100\right]$ and find that there is limiting behavior as $k_{\text{s}}\gg k_{\text{d}}$. The most significant effects of contact stabilization are seen when $k_{\text{s}}$ approaches this limit (Fig. 2 G). Hence, we utilize a maximum stabilization rate of $100s^{-1}=k_{\text{s}}\gg k_{\text{d}}=1/7s^{-1}$. For MV destabilization, we choose k_u = 0.03 s⁻¹ to replicate experimental observations of long MV lifetimes in the presence of agonists (5).

The instantaneous fraction of T cell surface area covered by MVs was reported to be $f\approx 40\text{\%}\pm 5\text{\%}$ (5). This area fraction range was observed in both the IS and isolated regions of the T cell, with and without agnostic antigen. For a given fraction f and individual MV radius $r_{\text{MV}}$, the average number of MV contacts ($N_{\text{MV}}$) in the T cell/APC interface are related by

$$N_{\text{MV}}{r}_{\text{MV}}^2=f{r}_{\text{IS}}^2.$$ (2)

For example, when $r_{\text{MV}}\approx 267.5nm$ (3,4,6), the average number of MV contacts in the T cell/APC interface is $N_{\text{MV}}\approx 140$. The rates of MV contact placement $k_{\text{a}}$ and MV contact removal $k_{\text{d}}$ are related at equilibrium by

$$k_{\text{a}}\left(N_{\text{max}}-N_{\text{MV}}\right)=k_{\text{d}}{N}_{\text{MV}}.$$ (3)

The term $N_{\text{max}}$ represents the packing limit or maximum number of nonoverlapping circular contacts with fixed radius $r_{\text{MV}}$ that can simultaneously occupy the IS.

Implementation details

The numerical solution of our model comprises a large scale stochastic algorithm based on the next-reaction Gillespie method (37). The code is written in Python and parallelized to allow for exploration of large parameter spaces and can be found at https://github.com/jmorga15/mv_code. To validate the code, we derived an explicit formula for the equilibrium configuration and verified convergence to these states over a wide range of parameters (see section 4 of the supporting material).

Results and discussion

MV scanning modestly affects antigen discrimination

We measured discrimination power (γ) over three models (flat topology, MV scanning with both strong stabilization and no stabilization) and across parameter regimes (N_kp = 3 and 10 proofreading steps and simulated T cell/APC contact times t_sim = 1, 5, and 10 min). Across these scenarios, we found that γ did not vary over biologically significant ranges, suggesting that MV scanning neither significantly hampers nor greatly improves antigen discrimination (Fig. 2). This is despite MV scanning only facilitating instantaneous contact between 40% of the opposing surfaces, therefore generally reducing the probability of T cell activation at a given TCR/antigen dissociation rate when compared with a flat topology.

The most significant modulation in discrimination power was observed in the case of short lived T cell/APC contacts ($t_{\text{sim}}=1$ min) with strong MV stabilization (k_s = 100 s⁻¹) (Fig. 2 G and H). Clearly, stabilization can partially negate some constraints imposed by MV scanning by extending MV lifetimes, thus allowing sufficient time for productive TCR/antigen interactions to occur. To explore the relevance of short contact times and to better understand model predictions of antigen discrimination, we derived potency curves ($P_{15}$) from a mean-field approximation of the stochastic model. We found that in small populations of antigen, or for short T cell/APC contact times ($t_{\text{sim}}$), stochastic effects can play an outsize role such that stabilization of MV contacts results in significant improvement to sensitivity (see section 5 of supporting material).

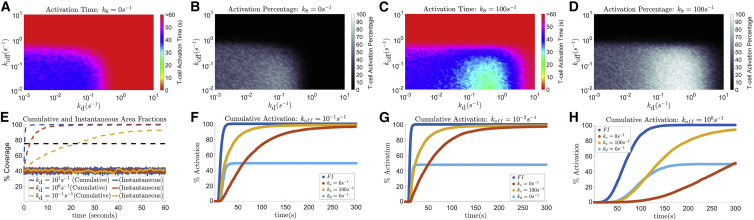
MV stabilization optimizes scanning speed and agonist sensitivity

In addition to exploring the discrimination powers of MV and flat interface models, we further sought to investigate the role of MV contact stabilization on T cell activation time and antigen sensitivity. In the structure of our model, larger values of $k_{\text{d}}$ correspond to faster surveillance of the APC surface (see materials and methods) which results in a more rapid cumulative survey of the interface (Fig. 3 E). However, rapid scanning by MV further constrains antigen recognition by increasing the probability that a contact is removed before a TCR can become activated. To explore this trade off, we simulate the T cell/APC interface with a single antigen and display, in Fig. 3 A–D, the average T cell activation times and the percentage of activated T cells in a population over a varying $k_{\text{d}}$ and $k_{\text{off}}$. In the absence of MV contact stabilization, we observe that T cell activation times are approximately homogeneous in regions where T cell activation is likely (Fig. 3 A). In such regions, the probability of T cell activation is also similar (Fig. 3 B). For example, changing $k_{\text{d}}$ from $k_{\text{d}}={10}^{-3}$ to $k_{\text{d}}={10}^{-1}$ yields little variation in T cell activation times and probabilities, given a strong agonist ($k_{\text{off}}={10}^{-2}$). Without MV stabilization, increasing $k_{\text{d}}$ increases MV scanning speeds but also decreases the probability of T cell activation. The same is not always true for models with MV contact stabilization. For a model with contact stabilization, there are cases where increasing $k_{\text{d}}$ increases both MV scanning speed and the probability of T cell activation (Fig. 3 C and D). This is due to MV stabilization reducing the probability of contact removal following TCR activation, i.e., reducing the probability of having to search for an agonist again, once an agonist is found. Additionally, the fastest T cell activation times and the highest probability of activation occur in this region of higher scanning speeds. This region of optimal $k_{\text{d}}$ is nearly completely absent in models without contact stabilization.

Figure 3.

Results for $N_{\text{kp}}=3$ kinetic proofreading steps and a T cell/APC interface time of t_sim = 60 s. (A) Average T cell activation time with $N_{\text{a}}=1$ agonist in the interface over a varying $k_{\text{d}}$ and $k_{\text{off}}$ without stabilization (k_s = 0 s⁻¹). Simulations that did not activate were weighted in the average by the total simulation time, t_sim = 60 s. (B) Percentage of T cells that are activated under the same conditions as (A). (C and D) Similar to (A) and (B) with strong stabilization k_s = 100 s⁻¹. (E) A single realization of cumulative (dashed) and instantaneous (solid) area fractions from MV scanning with and without stabilization, over a varying $k_{\text{d}}$ (3). (F–H) Cumulative activation percentage in a population of T cells given an increasing TCR/antigen dissociation rate. Simulations performed for $N_{\text{a}}=1$ and simulated T cell/APC interface time of t_sim = 300 s. To see this figure in color, go online.

In Fig. 3 A–D, the instantaneous area fraction is maintained at 40% for all $k_{\text{d}}$, which is accomplished by setting $k_{\text{a}}=\left(14/3\right)k_{\text{d}}$ (see materials and methods). Such a fraction has been observed experimentally when imaging MVs (5). In Fig. 3 E, we show how this relationship is maintained in individual simulations. The instantaneous scanning fraction remains approximately within the bounds of 40% ± 5%, while the cumulative scanning speed can increase or decrease drastically given an increase or decrease in $k_{\text{d}}$, respectively. The extreme case $k_{\text{d}}\to 0{\text{s}}^{-1}$, which implies $k_{\text{a}}\to 0{\text{s}}^{-1}$ by our definition of $k_{\text{a}}$, reflects a variant of the flat interface model where 40% of the T cell surface is covered in TCR clusters (leftmost regions of Fig. 3 A–D).

We further explore the intricacies of T cell activation in our model by observing the cumulative T cell activation in a population over a period of time, $t_{\text{sim}}$. We simulate four separate models corresponding to a flat interface, MV scanning, MV scanning and contact stabilization, and an additional model in which k_d = 0 s⁻¹ and $k_{\text{a}}$ is constant. The additional model here is representative of a flat interface in which only certain regions are densely packed with TCRs, i.e., a model with TCR clusters. In Fig. 3 F–G, we show the results of such simulations for models with $N_{\text{kp}}=3$ KP steps simulated for t_sim = 300 s and a single agonist in the interface with a TCR/antigen dissociation rate of k_off = 10⁻² s⁻¹ (Fig. 3 F), k_off = 10⁻¹ s⁻¹ (Fig. 3 G), and k_off = 10⁰ s⁻¹ (Fig. 3 H). As would be expected, the flat interface model (dark blue), where the entire surface is assumed to be densely packed with TCRs, achieves the highest percentage of activation in the shortest amount of time. This is due to the absence of a search process for agonists, as well as every agonist being accessible to TCRs in the T cell/APC interface. Additionally, we observe that the flat interface model with localized TCR clusters (light blue) is just a scaled cumulative activation profile of the densely packed flat interface model. Hence, we can expect that any flat interface model with differing distributions of TCR clusters will be a scaled variant of the densely packed flat interface model, in which the magnitude of the scaling is approximately the fraction of surface area covered by said clusters. However, it is important to note that this is a model dependent phenomenon and does not take into account the role of antigen diffusion. In the MV scanning models, we observe faster T cell activation in a population when MV contacts can be stabilized (gold) versus MV scanning without contact stabilization (red). This is unsurprising given the results shown in Fig. 3 A–D, as we found that T cells with stabilized MV contacts, opposed to those without, activated the fastest when there was only a single agonist in the interface. Since faster scanning speeds serve little to no purpose in large antigen populations, this optimal scanning speed is present in only smaller populations of antigen.

Model explains observed discrepancies in MV contact lifetimes

Observed MV lifetimes ($t_{\text{MV}}$) in experiments have varied significantly. For example, Cai et al. observed MV lifetimes of $t_{\text{MV}}\approx 7.7\text{s}$ in the absence of agonists and $t_{\text{MV}}\approx 8.9\text{s}$ in the presence of agonists (5). In contrast, another group studying membrane protrusions on T cells observed much longer MV lifetimes, on the range $t_{\text{MV}}\approx 60\text{s}$ when agonists were not present and $t_{\text{MV}}\approx 18$ min when agonists were present (6). To understand the plausibility of such a discrepancy, we use our model with MV stabilization to explore lifetimes over a range of varying dissociation rates and antigen populations. We find that MV lifetimes can easily surpass our simulation time (Fig. 6 in supporting material) when large numbers of agonists with low TCR/antigen off rates are used (Fig. 4 A). This is expected, given that the probability of finding a TCR/antigen complex in a state where the stabilized MV is capable of being destabilized is $t_{\text{kp}}/\left(t_{\text{kp}}+t_{\text{S}}\right)$ and is the steady state probability that the TCR is not in an activated state. Here, $t_{\text{kp}}$ is the average time it takes a TCR/antigen pair to bind and undergo all $N_{\text{kp}}$ KP modifications (see section 1 in the supporting material), including all dissociation events, before becoming activated, and $t_{\text{S}}=1/k_{\text{off}}$ is the average time a TCR stays activated once it reaches the final, signaling-competent stage. As $k_{\text{off}}$ decreases, $t_{\text{kp}}$ decreases and $t_{\text{S}}$ increases for a given antigen capable of binding TCRs. Hence, the probability of finding the antigen not bound to an activated TCR decreases. When there are $N_{\text{a}}$ antigens covered by an individual stabilized MV contact, this probability becomes ${\left(t_{\text{kp}}/\left(t_{\text{kp}}+t_{\text{S}}\right)\right)}^{N_{\text{a}}}$ and tends toward zero as $N_{\text{a}}$ grows large. The small probability of finding all antigens not bound to an activated TCR also indicates that the MV contacts spend very little time in a state capable of being destabilized. Conversely, if there are very few antigens, or the antigens are weak agonists, MV stabilization may be a rare event. In these conditions, the average MV lifetime would be approximately $t_{\text{MV}}=1/k_{\text{d}}$, which is 7 s in our parameterization. This suggests that MV lifetimes are not constant and are determined by the conditions in the T cell/APC interface.

Observations of MV dynamics indicate operation near theoretical packing limits

We explored the dynamics of other MV radii (50, 155, and 268 nm) in our model, which span the range of widths reported from light and electron microscopy measurements (3,4,6). When we ran MV packing simulations (see section 6 in the supporting material), where MVs cannot be removed and locations for additional MVs are randomly chosen, but overlap between MV is forbidden, we found that the maximum packing fraction converged to approximately 50% coverage (Fig. 4 B). While the exact packing fraction may depend on the MV radius, the practical packing fraction (i.e., what can be achieved by random placement and without replacing MVs) did not vary strongly. This indicates that the 40% ± 5% instantaneous area coverage observed when imaging T cells interacting with APCs (5) may be a result of a practical packing limit of MVs. Furthermore, we show that our stochastic model of MV scanning can achieve similar cumulative scanning fractions to that of observations by Cai et al. (5), as well as maintain the instantaneous area fraction at approximately 40% ± 5% (Fig. 4 C). We note that varying the MV radius had little effect on the cumulative scanning fractions, with only a slight increase in scanning speed resulting from a smaller MV radii. In addition, previous studies reported a decreased scanning speed of MVs when foreign antigens were present on an APC surface (5,6). Consistent with this, our MV stabilization model can reproduce this observation, where foreign antigen slow cumulative scanning and increasing numbers of agonists slows scanning speed further (Fig. 4 D). When there are very large populations of strong agonists in the T cell/APC interface, the instantaneous scanning fraction approaches the maximum packing fraction, and the cumulative scanning of MV halts. This is the result of MV contacts being fixed in place by stabilization for the entirety of a simulation.

Conclusion

MVs on T cells have been described for decades, yet their function remains enigmatic. We developed a new stochastic model of T cell/APC engagement that reveals that MV scanning and the stabilization of MV contacts work jointly to maximize the probability and speed of T cell activation by optimizing both sensitivity to agonists and MV scanning speeds of the opposing APC surface. In particular, MV scanning with stabilization can significantly improve the sensitivity of T cells to small populations of agonists.

We sought to identify how antigen discrimination might be modulated given recent observations that only 40% of the T cell/APC interface is in physical contact. Over a wide range of modeling scenarios and parameter regimes, we found that antigen discrimination was neither diminished nor significantly improved by the action of MVs. It is therefore possible that MV-based scanning mode has not evolved to improve discrimination but rather due to the biophysical constrains preventing formation of large flat interfaces. Specifically, the glycocalyces of T cells and APCs are expected to prevent large contact zones due to steric, electrostatic, and entropic effects (1). Hydrodynamic effects have been suggested as limits on the speed of contact formation—an effect that becomes more significant with increasing contact size (38). Overall, the duration and strength of immune signaling likely depends on a combination of geometrical, biophysical, and biochemical factors at the T cell/APC interface (39).

Our model yields a wide range of MV lifetimes (5,6) and suggests that MV lifetimes may be highly dynamic in nature. The average MV lifetime can be highly dependent on the conditions in the T cell/APC interface. It is not unusual to have MV lifetimes that can far exceed the T cell/APC interface time when there are medium to large populations of agonists present. When MV lifetimes exceed the T cell/APC interface time, or recording period, the average of these MV lifetimes also becomes dependent on the length of time over which the data are collected. Finally, we point out that the 40% ± 5% instantaneous area coverage by MVs may be close to a packing limit of MV contacts in the T cell/APC interface. Our results show that as more contacts become stabilized by TCR interactions with agonists, MV scanning slows significantly, and the instantaneous area coverage will approach this limit. Further research may reveal if they have primarily evolved to improve discrimination or due to the biophysical constrains preventing a flat interface.

Author contributions

A.E.L. and O.D. designed research, and J.M. and J.P. performed research. All authors contributed to writing the manuscript.

Editor: Alexander Fletcher.