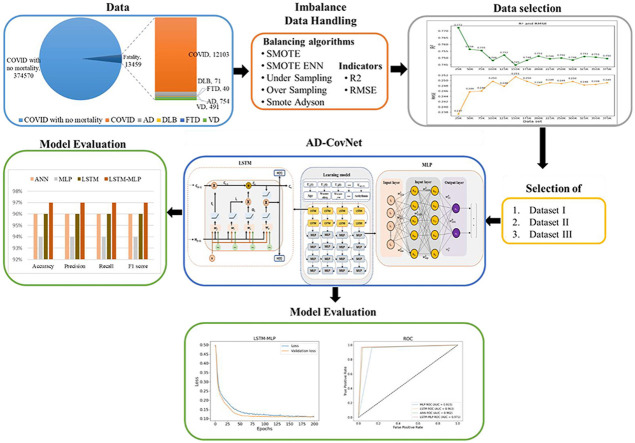
Abstract
Alzheimer's disease (AD) is the leading cause of dementia globally, with a growing morbidity burden that may exceed diagnosis and management capabilities. The situation worsens when AD patient fatalities are exposed to COVID-19. Because of differences in clinical features and patient condition, a patient's recovery from COVID-19 with or without AD varies greatly. Thus, this situation stimulates a spectrum of imbalanced data. The inclusion of different features in the class imbalance offers substantial problems for developing of a classification framework. This study proposes a framework to handle class imbalance and select the most suitable and representative datasets for the hybrid model. Under this framework, various state-of-the-art resample techniques were utilized to balance the datasets, and three sets of data were finally selected. We developed a novel hybrid deep learning model AD-CovNet using Long Short-Term Memory (LSTM) and Multi-layer Perceptron (MLP) algorithms that delineate three unique datasets of COVID-19 and AD-COVID-19 patient fatality predictions. This proposed model achieved 97% accuracy, 97% precision, 97% recall, and 97% F1-score for Dataset I; 97% accuracy, 97% precision, 96% recall, and 96% F1-score for Dataset II; and 86% accuracy, 88% precision, 88% recall, and 86% F1-score for Dataset III. In addition, AdaBoost, XGBoost, and Random Forest models were utilized to evaluate the risk factors associated with AD-COVID-19 patients, and the outcome outperformed diagnostic performance. The risk factors predicted by the models showed significant clinical importance and relevance to mortality. Furthermore, the proposed hybrid model's performance was evaluated using a statistical significance test and compared to previously published works. Overall, the uniqueness of the large dataset, the effectiveness of the deep learning architecture, and the accuracy and performance of the hybrid model showcase the first cohesive work that can formulate better predictions and help in clinical decision-making.
Keywords: COVID-19, AD-CovNet, Alzheimer's disease, Deep learning, Mortality, Fatality, MLP, LSTM, Risk factors
Graphical abstract
Exploratory analysis of COVID-19 patient with Alzheimer's disease using AD-CovNet.
1. Introduction
Alzheimer's disease (AD) is a neurodegenerative disorder that mainly prevalent among the elderly population aged 60 or older at higher risk. Evidence suggests that two histopathological findings (deposition of Amyloid beta-protein and Tau-protein, increased calcium ion concentration) are principally responsible for the abnormal changes in the brain of AD patients [1]. The global prevalence of all cases of dementia has been projected to reach almost 65.7 million by 2030 and 115.4 million by 2050, doubling every 20 years with a tremendous financial burden [2]. Alone in the U.S., the number of cases of Alzheimer's dementia is expected to reach a benchmark of 13.8 million accompanying people aged 65 and older [1]. However, the early emergence of the infectious severe acute respiratory syndrome coronavirus 2 (SARS-CoV-2) in late December 2019, has altered this estimation to a significant degree. According to the Centers for Disease Control and Prevention (CDC), the number of deaths in the US due to AD and other dementias escalated by approximately 16% during the pandemic, compared with the average of the past five years (2015–2019) [3]. It is a matter of great concern because this substantial increase in AD in the older population will not only affect the individual's personal life but also may result in different socioeconomic burdens [1].
However, the direct association of the fatality rate of AD patients with COVID-19 (AD-COVID-19) has been studied on a small scale. In one study, 31 AD patients (80.36 ± 8.77 years old) were diagnosed with COVID-19, and 13 among them (41.9%) died due to respiratory complications [4]. Another study estimated the proportion of death to be 19% among 260 patients with COVID-19 and AD [5]. Many studies have identified associated risk factors based on demographic characteristics of different cohorts separately responsible for AD and COVID-19. For example, the equivalent risk factors include older age (>60 years), dementia, cardiovascular disease (CVD), hypertension, obesity, genetic factors (SNPs) [6], diabetes, and smoking [7,8]. Understanding the complexity of AD patients with COVID-19 distress, it is pivotal to specifically recognize the risk factors which are common in both diseases. A substantial magnitude of positive associations between AD patients with COVID-19 deaths came from a comparative study that analyzed 17,456,515 individual records in a cohort [9].
Scientists have speculated several neurobiochemical cross-talks between COVID-19 and AD. Transsynaptic transfer via olfactory nerve or expression of angiotensin-converting enzyme 2 (ACE2) receptor in the vascular endothelium of the blood-brain-barrier (BBB) could be the route of viral entry into the brain [10]. Several pathophysiological changes induced by SARS-CoV-2 can aggravate neurodegeneration in AD patients, increasing the risk of having high viral load and fatality risk [11]. However, theoretical postulations are drawn from empirical data seldom resonate with the complexity of natural biological systems. Thus, it is essential to harness the heterogeneity of biological data to produce qualitative and quantitative predictions.
State-of-the-art supervised learning models such as ANN, random forest, AdaBoost, XGBoost, MLP, unsupervised learning models LSTM, and RNN are utilized to understand the disease pattern and prognosis. However, all these models exhibit individual limitations. For example, ANN unexplained functioning of the network, hence ANN reduces trust in the network. Random Forest is less interpretable than a single decision tree. A trained forest may require significant memory for storage, due to the need for retaining the information from several hundred individual trees. Adaboost has the potential to overfit the training set because its objective is to minimize errors on the training set. XGBoost does not perform well on sparse and unstructured data. In this essence, researchers have explored Deep learning (DL) algorithms to make an advancement for predicting more complex biological relationships. It has revolutionized this experience by substituting the need for human intervention [12] and offering the flexibility of customizing different algorithms. DL overcomes a lot of problems faced in the arena of medical science such as its overwhelming classical statistical models (i.e., t-test, ANOVA, Chi-square test) and traditional software (i.e., SPSS, Stata) which are frequently used by health professionals to carry out their primary data analysis. Moreover, if the number of input variables expands with increasing data and sample size, the inference becomes more inaccurate [13]. DL also alleviates the need for ‘clinical chart review’ commonly practiced by physicians who oversee previous medical records to make assumptions about a disease or a health condition, classify risk factors and recommend treatments or medications [14]. In addition, as often labeled data are scarce and expensive in the field of healthcare, DL can harness the potential of rapidly accumulating, inexpensive unlabeled data to improve the generalized performance [15]. In healthcare systems, data repositories are dynamic. This multi-layered strategy enables DL models to complete classification tasks such as identifying subtle abnormalities in kidney images, grouping patients with risk-based cohorts, or highlighting relationships between symptoms and outcomes within massive amounts of unstructured data.
In recent years, deep learning architectures and algorithms have evolved based on their application in different fields; speech recognition, image processing, and solving biological questions [16,17]. In biological conditions, their risk association may rely upon other independent causal factors which deeply correlate with the disease. But diverse and imbalanced datasets often restrict model performance [18]. The key reasons are two folds: (1) the optimum results for the unbalanced class are difficult to achieve because the model/algorithm can't get the chance to look at the underlying class and (2) DL poses an issue when creating a validation or test sample because it is difficult to have representation across classes when the number of observations for a few classes is extremely low. The nature of medical big data and rationalizing the time dependency in collecting patient records have posed severe concerns among medical practitioners, researchers, and health professionals. Thus, we have chosen to develop a hybrid model using AD-CovNet. We exerted two different neural networks, combined them, and proposed a novel hybrid AD-CovNet algorithm for classification and risk factor identification. It is hypothesized that the hybrid AD-CovNet model will perform significantly better than its counterparts to represent the complex interdependence of fatality of AD patients in COVID-19. Thus, three research questions (RQs) are formulated to measure the effectiveness of the proposed approach for state-of-the-art approaches:
RQ1: How imbalanced data can be handled efficiently and ready for the DL models or find the suitable approaches to balance the dataset prepared for DL models processing?
RQ2: How efficient hybrid model AD-CovNet is capable of classifying AD-COVID-19 fatality?
RQ3: What are potential risk factors associated with AD-COVID-19 fatality?
2. Related works
Earlier studies regarding AD risk factor prediction were conducted based on standard machine learning models. A study by Casanova et al. used regularized logistic regression (RLR) as a classifier and proposed a new risk scoring method called AD Pattern Similarity (AD-PS) scores to geometrically represent a disease probability map (hypercube) [19]. The position of these metrics inside the hypercube depicts the risk of developing AD. Another study by Mahyoub et al. performed a study on ADNI dataset applying four different ML models, namely, Random Forest (RF), Support Vector Machines, Neural Networks, and Multi-Layer Perceptron (MLP). Lifestyle and behavior patterns and APOE4 gene were classified as critical risk factors for developing AD [20]. But it did not discuss the accuracy of the machine learning models. The number of studies exerting deep learning algorithms on AD datasets is relatively low.
Qiu et al. used the concept of a disease probability map to diagnose the status of AD. They collected four different datasets and individually applied a fully convolutional network (FCN) with six convolutional layers for classification and model training from patches of neuroimaging data [21]. Model performance increased when non-imaging features such as gender, age, and Mini-Mental State Examination (MMSE) scores, were incorporated alongside the probability map. Usually, CNNs are more prevalent in the field of harnessing neuroimaging data. Thus, a comparison between the traditional CNN and FCN-MLP model revealed the latter had more efficiency. On the other hand, Wang et al. used clinical documentation of patient-level data obtained from electronic health records (EHRs) [22]. It focused on RNN's accuracy for text classification to rank essential topics which could be held accountable for the risk of death for patients with Alzheimer disease-related dementias. The recorded AUC scores were 0.978, 0.956, and 0.943 for 6-month, 1-year, and 2-year fatality prediction models, respectively.
Like studies regarding AD, the identification of fatality-related risk factors for COVID-19 patients has also been addressed through different ML approaches. Dabbah et al. included a cohort of 11,245 COVID-19 positive cases and implemented Random Forest (RF) and Cox Proportional Hazard (CPH) ML algorithm. RF model had better accuracy and stability based on the AUC (0.90) and F-β statistic score [23]. Mahdavi et al. [24], Bertsimas et al. [25], and Kar et al. [26] conducted their analysis based on the clinical information collected from hospital records. Mahdavi et al. separately measured the accuracy of the SVM model to predict the COVID-19 fatality risk based on invasive, non-invasive, and combined features. Non-invasive features like oxygen saturation (SpO2), age, and cardiovascular diseases together with increased levels of blood urea nitrogen (BUN), lactate dehydrogenase (LDH), and partial thromboplastin time (PTT) had a higher predominance towards fatality. The authors showed that the non-invasive model had better performance despite having fewer features because individual weights of those features were more elevated in terms of fatality prediction.
By contrast, Bertsimas et al. and Kar et al. used the Extreme Gradient Boosting (XGB) algorithm on overall selected features without dividing them according to their invasiveness. These studies showed XGB model demonstrated better performance in terms of AUC, accuracy, and specificity scores, for training and testing datasets. Liang et al. displayed a deep learning Cox proportional hazard (CPH) model in a COVID-19 positive cohort [27]. They extracted ten critical risk factors and evaluated their performance according to the model. Among these features, age (>49 years), dyspnea, cancer history, and Chronic Obstructive Pulmonary Disease (COPD) had the highest magnitude of risk. Naseem et al. introduced a new framework to add new features (Neo-V) based on existing features within a predefined dataset. A coalition of this framework with a deep neural network (Deep-Neo-V) had the highest accuracy, precision, AUC-ROC score, compared to 5 conventional ML models [28]. Zhang et al. and Wang et al. harnessed the features of radiologic (CT-scan) images for COVID-19 diagnosis by two different approaches. Zhang et al. used a five-layer deep convolutional neural network (DCNN) with stochastic pooling [29]. Conversely, Wang et al. applied wavelet Renyi entropy (WRE) for feature extraction and combined feedforward neural network (FNN) with a three-segment biogeography-based optimization (3SBBO) to train the classifier [30].
All the previous works were separately carried out among AD and COVID-19 patients. To identify the risk factors of AD, most of the works were based on neuroimaging data and heavily emphasized the abnormal structural changes in the brain. On the contrary, fatality related risk factors for COVID-19 were identified based on the demographic and medical records for COVID-19 survivors and non-survivors. Nevertheless, all these studies were amenable to several limitations. Most of the previous works lack to tackle the following few key challenges. Extant studies primarily focus on traditional ML models and small population sizes. In standard ML, well-defined features influence performance results. However, the greater the complexity of the data, the more difficult is to select optimal features. A limited number of articles have been highlighted or discussed regarding the dataset imbalance. It is important to note that if the data is imbalanced, the chance of misdiagnosis increases and sensitivity decreases. In a few instances, only SMOTE was utilized to establish the balance of the data. Till today, no studies have been reported which depict the complex interrelationship among comorbidities between AD and COVID-19 patients.
The followings are the key contributions of the study:
-
•
The study explored state-of-the-art resampling techniques and utilized evaluation metrics (R2 and RMSE) to balance large imbalanced datasets. This dataset is large compared to the existing literature and unbalanced. The data balancing approach considered can be trusted by domain experts.
-
•
The study developed a novel hybrid DL model AD-CovNet using LSTM-MLP for the classification of COVID-19 and AD patients based on a real dataset. The models are optimized by utilizing sweeping hyperparameters throughout the experiment.
-
•
The study presented a robust approach to detect risk factors from coexisting heterogeneous feature sets associated with COVID-19 and AD patients without removing feature subsets.
-
•
The study demonstrated a possibility of implementing DL models in clinical practice by producing superior performance and accuracy, and risk factors for COVID- 19 and AD patients with clear medical significance.
The following sections are mentioned as follows: Section 3 describes the dataset and Section 4 highlights the research methods. Data balancing approaches are indicated in Section 5. Section 6 explains the model and model performance evaluation are shown in Section 7. Risks are analyzed in Section 8. Finally, Sections 9, 10 highlight the discussion and conclusion.
3. Dataset description
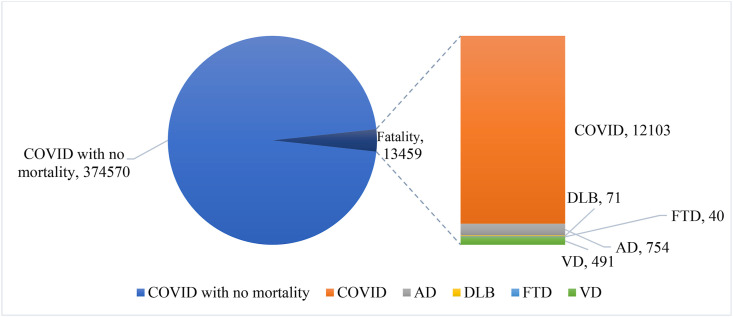
The dataset utilized in this study was retrieved from TriNetX. It is a health research database that contains de-identified medical records from over 50 million people and the majority of them are from the United States. The data was taken on April 14, 2021, although information up to February 17, 2021, was utilized [31]. Pre-major COVID-19 variant dissemination and vaccination caused the huge infection [14]. There were no imputations for missing data. The dataset includes adult patients aged 18 and above, with the median age of the AD patient population being 50. Initially, we received a dataset of 388,029 COVID-19 patients. However, 188 individuals with undetermined gender were excluded. To limit selection bias, we did not apply any further exclusion criteria. We identified 387,841 patients with COVID-19, among them 4174 had AD, 2765 had vascular dementia, 375 had DLB, and 235 had FTD. As depicted in Fig. 1 , the entire data set is a practical example of imbalance class.
Fig. 1.
Distribution of data.
4. Research methodology
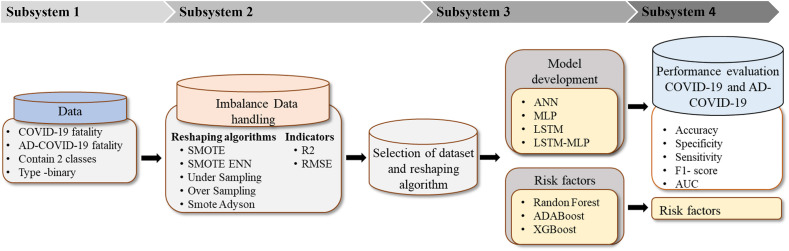
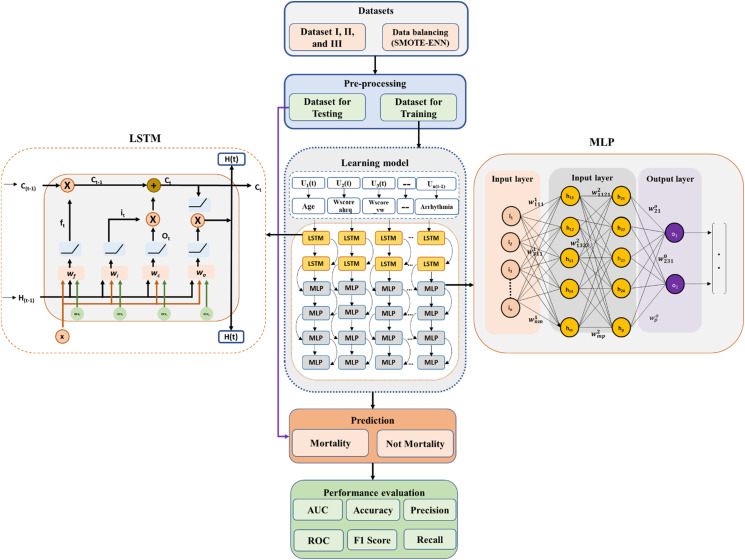
The proposed classification framework comprises four subsystems (Fig. 2 ). The first subsystem explains data characterization and categorization. This subsystem describes how data is arranged between AD fatalities and AD-COVID-19 fatalities. The second subsystem addresses the approach of imbalanced data handling. Various balancing algorithms have been utilized to identify the best possible representation of the data using statistical indicators (R2 and RMSE). The balancing subsystem is used to oversample the minority class samples of the unbalanced dataset. Subsequently, these approaches support selecting datasets that will identify the best balancing algorithm and can represent the suitable dataset for classification. The third subsystem highlights the model development of DL algorithms using LSTM and MLP. The risk factors specified in Table 1 are identified, and their clinical significance is evaluated. In addition, risk factors associated with COVID-19 along with AD data are identified based on the three-feature selection algorithm (AdaBoost, Random Forest, and XGBoost). Finally, the fourth subsystem reflects the performance matrices (Accuracy, Precision sensitivity, F1-score, and AUC curve) among the four models.
Fig. 2.
Proposed research methodology.
Table 1.
Dataset description.
| Attribute | Type | Description |
|---|---|---|
| Chf | Binary | Congestive heart failure |
| carit | Binary | Cardiac arrhythmias |
| valv | Binary | Valvular disease |
| pcd | Binary | Pulmonary circulation disorders |
| pvd | Binary | Peripheral vascular disorders |
| hypunc | Binary | Hypertension, uncomplicated |
| hypc | Binary | Peripheral vascular disorders |
| para | Binary | Paralysis |
| ond | Binary | Other neurological disorders |
| cpd | Binary | Chronic pulmonary disease |
| diabunc | Binary | Diabetes, uncomplicated |
| diabc | Binary | Diabetes, complicated |
| hypothy | Binary | Hypothyroidism |
| rf | Binary | Renal failure |
| ld | Binary | Liver disease |
| pud | Binary | Peptic ulcer disease, excluding bleeding |
| aids | Binary | AIDS/HIV |
| lymph | Binary | Lymphoma |
| metacanc | Binary | Metastatic cancer |
| solidtum | Binary | Solid tumor, without metastasis |
| rheumd | Binary | Rheumatoid arthritis/collagen vascular disease |
| coag | Binary | Coagulopathy |
| obes | Binary | Obesity |
| wloss | Binary | Weight loss |
| fed | Binary | Fluid and electrolyte disorders |
| blane | Binary | Blood loss anemia |
| dane | Binary | Deficiency anemia |
| alcohol | Binary | Alcohol abuse |
| drug | Binary | Drug abuse |
| psycho | Binary | Psychoses |
| depre | Binary | Depression |
| score | Numeric | A non-weighted version of the Elixhauser score |
| index | Binary | A non-weighted version of the grouped Elixhauser index |
| wscore_ahrq | Numeric | A weighted version of the Elixhauser score using the AHRQ algorithm |
| wscore_vw | Numeric | A weighted version of the Elixhauser score using the algorithm in van Walraven |
| windex_ahrq | Binary | A weighted version of the grouped Elixhauser index using the AHRQ algorithm |
| windex_vw | Binary | A weighted version of the grouped Elixhauser index using the algorithm in van Walraven |
| Age | Numeric | Age |
| Gender | Nominal | 0: Male, 1: Female, 2: Third gender |
| Ethnicity | Nominal | Ethnicity |
| Fatality | Binary | Fatality |
| Race | Nominal | Race |
| ad | Binary | Alzheimer's disease |
5. Data preprocessing
5.1. Data imbalance handling
If the class attribute categories are not equally represented, the classification performance will be skewed. In such instances, the size of the abundant class is either lowered (undersampling) or expanded (oversampling). The primary goal of class balancing is to increase the frequency of the minority class while decreasing the frequency of the dominant class. Balancing has been done to ensure that each class has roughly the same number of instances. The literature also demonstrates a mix of under and over-sampling. Table 2 summarizes the most frequent rebalancing strategies used, as well as their benefits and drawbacks. To stratify the imbalanced data, we employed six resampling techniques – Random oversampling, Undersampling, SMOTE, STOME-ADASYN, STOME-TOMEK, and SMOTE-ENN. Considering all these techniques is to establish and identify the best resampling techniques to identify the best representative sets. In this essence, two key performance indicators R2 and RMSE are used.
Table 2.
Definition and characterization of resampling techniques.
| Sl. No. | Resample technique | Key features | Pros and cons |
|---|---|---|---|
| 1 | Random Over-Sampling |
|
|
| 2 | Random undersampling |
|
|
| 3 | SMOTE |
|
|
| 4 | SMOTE-ADASYN |
|
|
| 5 | SMOTE-Tomek |
|
|
| 6 | SMOTE- ENN |
|
|
5.2. Evaluation metrics
5.2.1. R2
R Square is a measure of not only Goodness-of-Fit but also how well the model explains the behavior (or variance) of the unbalanced data and dependent variables. The formula of is as follows:
| (1) |
5.2.2. RMSE
The Root Mean Square Error represents the square root of the average of the square of the differences between predicted values and observed values. It can assess the reliability of model predictions. The RMSE calculation formula is as follows:
| (2) |
5.3. Baseline approach
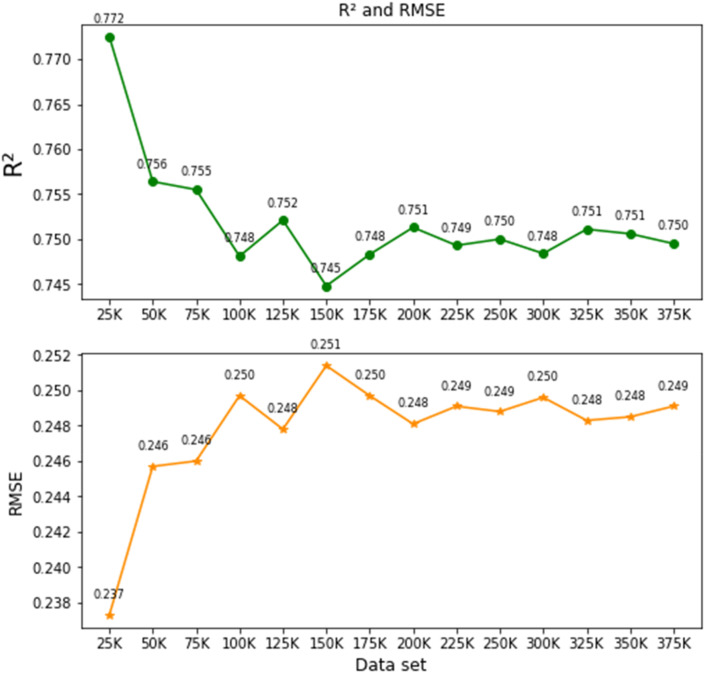
The dataset has been divided into 14 groups as a multiple of 25K (i.e., 25K, 50K, 75K, …., 375K). The next step is to select different resampling algorithms to assess the best evaluation metric possible. In order to show the impact of the imbalance problem on regression more explicitly, we performed simple experiments using AdaBoost and XGBoost on the 14 datasets utilizing each resampling technique. In the beginning, we analyzed the raw data and found an average R2 value of 0.166 (range 0.144–0.223) and RMSE value of 0.168 (range 0.166–0.169). This represents highly imbalanced data. Subsequently, we performed all the resampling techniques (Table 2) used to calculate R2 and RMSE values. Table 3 depicts R2 and RMSE values of a different set of data. SMOTE-ENN showed the best performance among all resampling techniques having an average R2 and RMSE values of 0.755 and 0.240 respectively. Hence, we selected SMOTE-ENN as the best resample technique to balance the dataset for preprocessing to implement the DL models. Table 3 depicts the result of the R2 and RMSE values against each group of datasets using XGBoost algorithm.
Table 3.
R2 and RMSE values of different sets of data using resampling algorithms.
| Resampling Algorithms | Indicators |
|||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| R2 |
RMSE |
|||||||||
| 25K | 50K | 100K | 200K | 300K | 25K | 50K | 100K | 200K | 300K | |
| Raw data | 0.223 | 0.164 | 0.156 | 0.143 | 0.144 | 0.166 | 0.169 | 0.169 | 0.169 | 0.169 |
| Random Over-Sampling | 0.577 | 0.509 | 0.498 | 0.487 | 0.492 | 0.324 | 0.35 | 0.354 | 0.357 | 0.356 |
| Under sampling | 0.649 | 0.546 | 0.514 | 0.488 | 0.497 | 0.295 | 0.336 | 0.348 | 0.357 | 0.354 |
| SMOTE | 0.681 | 0.639 | 0.624 | 0.603 | 0.605 | 0.282 | 0.3 | 0.306 | 0.314 | 0.313 |
| SMOTE- ADASYN | 0.677 | 0.62 | 0.608 | 0.588 | 0.589 | 0.287 | 0.3 | 0.312 | 0.32 | 0.320 |
| SMOTE-Tomek | 0.686 | 0.638 | 0.624 | 0.606 | 0.606 | 0.28 | 0.3 | 0.306 | 0.313 | 0.313 |
| SMOTE-ENN | 0.772 | 0.756 | 0.748 | 0.751 | 0.748 | 0.221 | 0.231 | 0.243 | 0.251 | 0.258 |
5.4. Dataset balancing using SMOTE-ENN
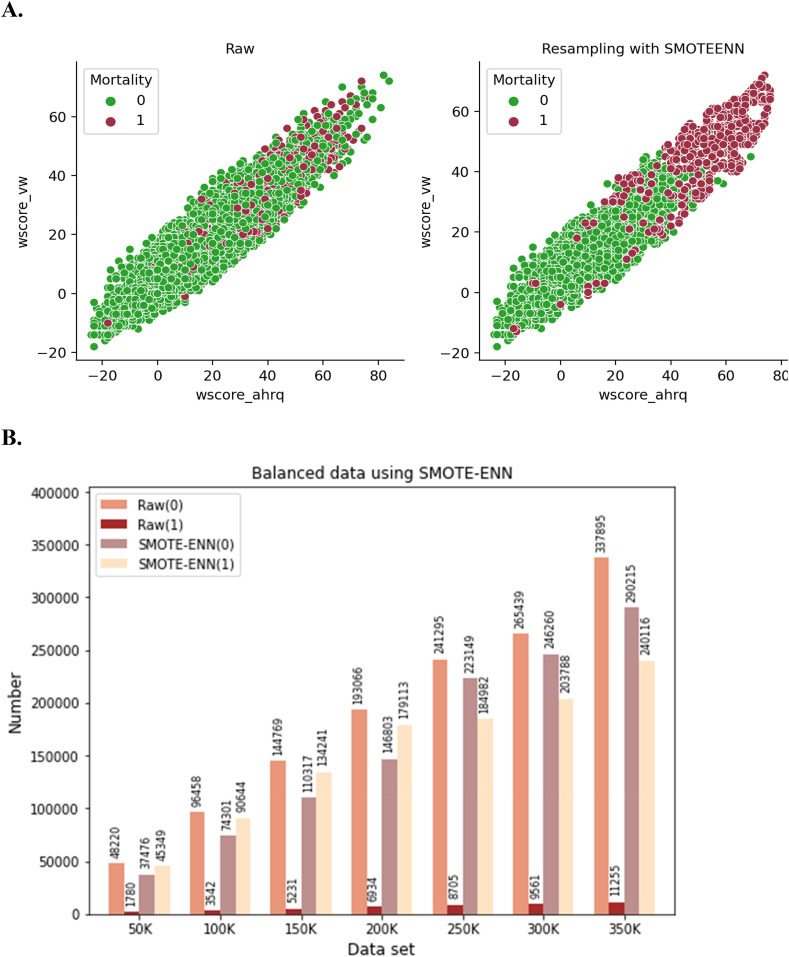
SMOTE–ENN algorithm works by combining the two data balancing techniques: SMOTE and ENN. SMOTE is an oversampling technique and edited nearest-neighbor (ENN) functions as an undersampling approach [32]. SMOTE calculates the distance between the random data and its k-nearest neighbors, selected from the minority class. ENN finds the k-nearest neighbor of the observed class and returns the majority class. Subsequently, unmatched classes are removed. This iterative process continues until the desired proportion of classes is achieved. To illustrate the SMOTE–ENN process, Fig. 4 A depicts how SMOTE–ENN is generated in the synthetic sample (red color) with respect to two features, i.e., wscore_vw and wscore_ahrq to reach a certain proportion against the raw dataset. Fig. 4B depicts the raw data augmentation using SMOTE–ENN on the various dataset. For example, in the case of 100k data raw data, without and with mortality class, there are 96,458 and 3542 respectively, that have been resampled to 74,301 and 90,644 respectively. The previous ratio (96:3) was converted to 48:45. In addition, it is observed that almost similar ratios were maintained constantly for the respective groups of data using SMOTE-ENN.
Fig. 4.
Data resampling using SMOTE-ENN (A and B).
5.5. Selection of dataset
As mentioned earlier, the evaluation metric R2 and RMSE values were identified by XGBoost. It is observed that the R2 value ranges from 0.772 to 0.750 (±0.032) and the RMSE value ranges from 0.137 to 0.1249 (±) derived from 14 sets of data groups. Hence, we have selected 50K (R2 = 0.756 and RMSE = 0.146) and 200K (R2 = 0.743 and RMSE = 0.251) to classify the COVID-19 patient mortality with or without AD. Hence, three datasets have been selected for the analysis and are shown in Table 4 . The reasons are two folds: (1) to represent the scale of 3.88 K, and (2) two different sets will give us efficient and comparable outcomes for performance evaluation of the DL models. In addition, the AD patient mortality due to COVID-19 (754 data) will be the third dataset in the study.
Table 4.
Selected three datasets.
| Data | Number of instances | Features | R2 and RMSE |
|---|---|---|---|
| Dataset I | 50,000 | COVID-19 mortality | 0.756 and 0.246 |
| Dataset II | 200,000 | COVID-19 mortality | 0.751 and .248 |
| Dataset III | 754 | AD-COVID-19 mortality | – |
6. AD-CovNet description and execution process
6.1. AD-CovNet description
In the hybrid DL model development, we considered two key aspects. Firstly, finding the essential characteristics of heterogeneous data; secondly, constructing a good performance classifier model to accurately differentiate and classify the fatality data. AD-CovNet is the organic integration of LSTM and MLP. LSTM is mainly used so that data can be arranged in a sequence by utilizing its memory concept and MLPs are suitable for classification prediction problems where inputs are assigned a class or label. They are also suitable for regression prediction problems where a real-valued quantity is predicted given a set of inputs This hybrid model extracts the essence of binary code data, reduces the complexity of the model, and improves classification accuracy.
The LSTM architecture comprises of self-connecting memory cells that can Recall values from the previous stages in the network. For example, LSTM possesses special multiplicative units called gates for controlling the flow of information (Fig. 5 ). An input gate, an output gate, and a forget gate are the basic components of each memory cell. The input gate controls the flow of input activations, while the output gate controls the flow of cell activations into the remaining network. Moreover, the forget gate scales the internal state of the cell, which is then returned to the cell as input through a self-recurrent connection. LSTM has three gates: 1. Input Gate(it), 2. Forget Gate (f t), 3. Output Gate (ot). The gate equations are as follows:
Fig. 5.
The operational outline of the proposed AD-CovNet model.
Input Gates,
| (3) |
| (4) |
here, t = timestep, = input gate at t, = weight matrix of sigmoid operator between input gate and output gate, = Bias vector at t, the value generated by ReLU. = weight matrix of ReLU operator between cell state information and network output, = Bias vector at = . Forget gate operation.
Forget Gates,
| (4.1a) |
here, = forget gate at t, = input, = previous hidden state, weight matrix between forget gate and input gate. = connection bias at t. Cell state operation,
| (4.1b) |
here, = cell state information, = forget gate at t, = input gate at t. = previous timesteps, = value generated by ReLU. Output gate operation.
Output
| (4.2) |
| (4.3) |
here, = Output gate at t, = Weight matrix of output gate, = bias vector at and = LSTM output.
MLP is built from the connections of artificial neurons, which are conceptually inferred from biological neurons, and these neurons are organized into layers. The input layer provides an ordered set (a vector) of predictor variables, and each neuron transmits its value to all the neurons organized in the middle layer. The middle neuron receives the product of the values that are supplied from the input neuron and the connection weight through the connections. Each neuron localized in the middle layer implements a logistic function on the sum of the weighted inputs. Lastly, the output neuron applies the logistic function to the weighted sum of its inputs, and the outcome of this function subsequently becomes the final output. An MLP consists of three layers: input, hidden, and output. The general equation of MLP is:
| (5) |
f denotes activation function, w T and b are weights and bias respectively.
6.2. Model execution process
The proposed AD-CovNet model consists of two hierarchy levels. The upper hierarchy LSTM level learns the relations amongst the features extracted from the dataset. The lower hierarchy MLP uses to learn the features for classification. LSTM is relatively more complex than MLPs which is flexible and numerous layers can be added. But both can be implemented as a fully connected network with multiple layers. As a result, increasing depth avoids overfitting in models since the network's inputs must pass through multiple nonlinear functions. While the memory feature of LSTM supports handling the same number of inputs, outputs, and hidden nodes, MLP utilizes a supervised learning technique called backpropagation for training. Hence, AD-CovNet can be applied to complex non-linear problems and works well with extensive input data. Fig. 5 shows an outline of the proposed neural network model; a pipeline of the input data preparation process, including preprocessing.
The first stage was the amplification of the dataset using SMOTE-ENN software, then divided into training (80%) and testing (20%). We have defined and adjusted the model parameter values. The second stage was the pre-training phase in which the input layer receives the feature sets, which are used to train LSTM for reaching the optimal local parameters. The first layer is the LSTM layer which uses 256 length vectors to represent each data. The next layer is the LSTM layer with dropout. Finally, we used an output layer of Dense neurons with 65 neurons and a ReLU activation function (Eq. (6)) to make 0 or 1 predictions for the two classes; Mortality and No Mortality in the study. LSTM standardizes the ReLU activation function and rectifies the values of the inputs less than zero to zero to eliminate the observable vanishing gradient problem Eq. (6)). Then this output is taken as the input layer of Batch normalization for MLP (Eq. (7)) We have implemented four MLP layers taking a batch of training data and performing forward propagation to compute the loss. Then the model back propagates (Eq. (8)) the loss to get the gradient of the loss to each weight. Adding Batch Normalization (BN) layers leads to faster and better convergence (higher accuracy). Finally, the gradients were used to update the weights of the network.
The ReLU function is described below:
| (6) |
where xi is an input to a neuron.
| (7) |
γ-hyperparameter, β that normalizes the batch {xi}, μB, the mean and variance
| (8) |
here, L is the loss for output y and target value z, and z is the target output for a training sample.
y is the actual output of the output neuron, w is weight, learning rate, and derivative of error in terms of weight.
The second stage is the fine-tuning the Back Propagation algorithm which was used to fine-tune the whole network parameters to reach the global optimal parameters using kernel initializer to initialize the weights to train the MLP with labeled data. In the learning process of recognizing weights, a collection of labels is applied to the hidden layers to determine the network's category boundaries. The third stage was the classification (test) where the trained model with optimal weights with biases was obtained, so data could be classified into the proper class. Alternately, various dropout has been applied to the input and recurrent connections of the memory units with the LSTM and MLP precisely.
Enhanced overall computation speed is the main advantage of using the ReLU which allows faster computation since it does not compute exponentials and divisions [34]. The whole process is called hyper-parameter tune which was done explicitly to analyze such a big dataset with the proposed hybrid model. For all models, the number of epochs is 200, and the learning rate is 0.001. We have estimated Accuracy, Recall, F1-score, Precision, validation loss for test data, the loss for train data, and plotted AUC-ROC curve of three models that includes one hybrid model. We applied python programming to perform all computation, visualization, and processing. All analyses were executed on Google Collaboration. This hybrid model extracts the essence of binary code data, reduces the complexity of the model, and improves classification accuracy. Table 5 depicts all the hyperparameters used to execute the hybrid and other models in this study.
Table 5.
Model hyperparameters.
| Models | Activation function | Optimizer/Tuning | Loss calculation | Learning rate | Batch size | Dropout |
|---|---|---|---|---|---|---|
| ANN | ReLU | Adam | Mean Squared Error | 0.01 | 175 | 0.5 |
| LSTM | ReLU | Adam | Mean Squared Error | 0.001 | 256 | 0.1 |
| MLP | ReLU | Adam | Mean Squared Error | 0.01 | 256 | 0.5 |
| AD-CovNet | ReLU | Adam | Mean Squared Error | 0.001 | 256 | 0.7 |
7. Result and analysis
7.1. Model performance
The study has evaluated the performance of implemented DL models by calculating Accuracy, Recall, F1-score, Precision, validation loss for test data, and the loss for train data. We have also plotted the AUC-ROC curve for each model. Typically, a confusion matrix is made up of 2 × 2 matrices with four attributes. These are 1) predicted COVID-19 fatality (TP), predicted no fatality of COVID-19 (TN), Wrongly detected COVID-19 fatality (FP) and wrongly predicted no fatality of COVID-19 (FN) (Table 6 ).
Table 6.
Confusion matrix.
| Predicted: 0 (No mortality) | Predicted: 1 (Mortality) | |
|---|---|---|
| Actual: 0 (No mortality) | No fatality of COVID-19 (TN) | Wrongly predicted COVID-19 fatality (FP) |
| Actual: 1 (Mortality) | wrongly predicted no COVID-19 fatality (FN) | COVID-19 fatality (TP) |
The most utilized forecast performance parameter is accuracy. It is expressed as a percentage and represents the worth of categorized instances events (percent). The higher the accuracy, the better the classification results (close to 100% is considered very good results), as defined in Eq. (9).
| (9) |
Precision evaluates and determines positive classes representing TP (fatality), as defined in Eq. (10).
| (10) |
Recall computes predicted positive classes in the total positive occurrences in the dataset, as defined in Eq. (11).
| (11) |
The F1-score calculates the accuracy of the testing process. The average is calculated using precisions and Recall sets Eq. (12). The formula is as follows:
| (12) |
FPR denotes negative occurrences categorized as positive Eq. (13).
| (13) |
True Positive Rate (TPR) is the ratio that describes the positive classes accurately identified as positive to the combined positive instances (actual). It is represented in Eq. (14).
| (14) |
FNR entails the miss classified rate of a model calculating positive classes categorized as negative.
It is calculated from the equation below:
| (15) |
And it is expected to be as close to zero.
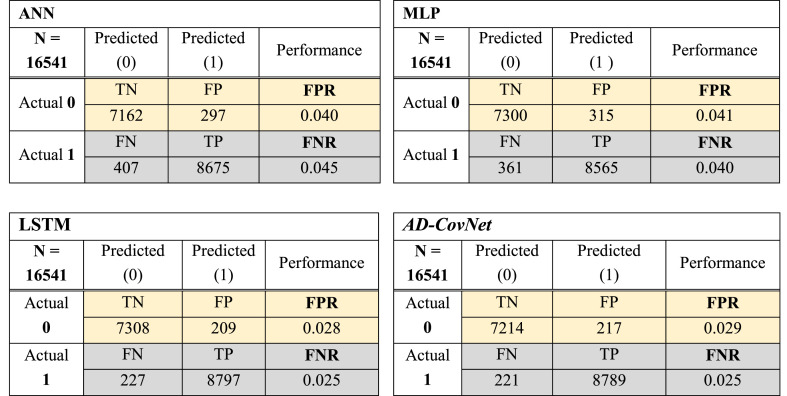
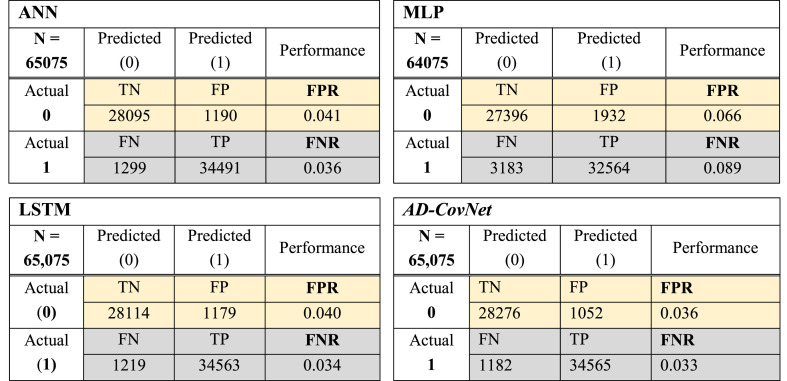
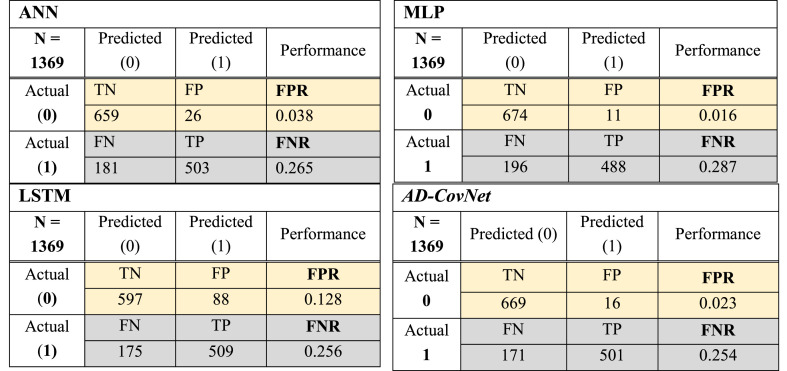
The best performance is evaluated by a minimal value of FNR and FPR (close to zero). Fig. 6, Fig. 7, Fig. 8 showed the confusion matrix of Dataset I, II, and III respectively, considering all the attributes with respect to four DL algorithms. This matrix shows TP, TN, FP, and FN together with FNR and FPR of models for three datasets. The hybrid model: AD-CovNet generated the lowest FNR and FPR for Dataset I, II, and III (FPR; 0.029, 0.036, 0.023, and FNR; 0.025, 0.033, 0.254). LSTM provided the low FNR (0.025 and 0.256) for Dataset I and III compared to other models. MLP showed the highest FNR; 0.089 and 0.287 respectively for Dataset II and III, but the lowest FPR (0.016) in detecting the Fatality of COVID-19 patients having AD (Dataset III). In addition, ANN showed low FPR values for Dataset III. The hybrid model performed best in terms of FNR and FPR.
Fig. 6.
Confusion matrix of four DL models (Dataset I).
Fig. 7.
Confusion matrix of four DL models (Dataset II).
Fig. 8.
Confusion matrix of four DL models (Dataset III).
7.2. Accuracy, recall, F1-Score, precision
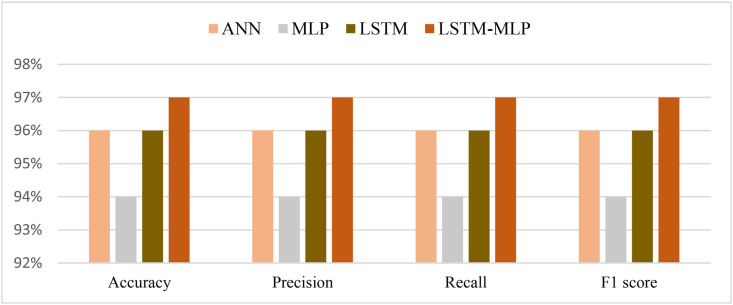
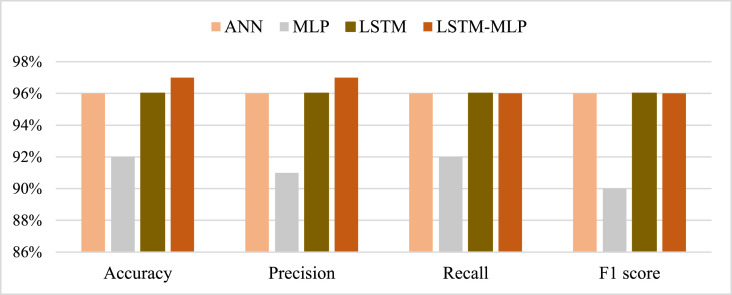
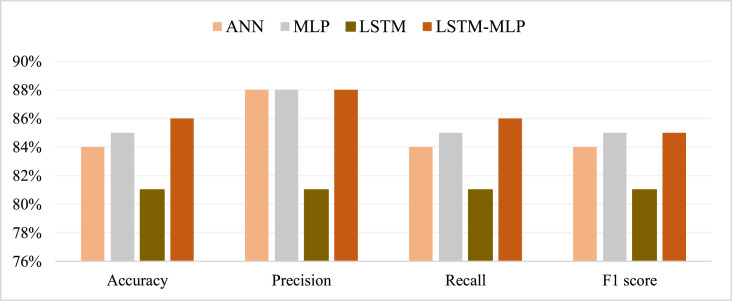
From the prediction analysis with DL hybrid and generic models, it has been found that the AD-CovNet model performed superior with higher Accuracy, Precision, Recall, and F1-score compared to the other three models. Table 7, Table 8, Table 9 and Fig. 9, Fig. 10, Fig. 11 present the accuracy, precision, recall, and F1-score for the proposed hybrid model along with generic models considering Dataset I, II, and III, respectively. AD-CovNet delivered the maximum performance regarding all performance measurements. The values are the same for Dataset I. For Dataset II, these measures are as follows; Accuracy 97%, Precision 97%, Recall 96%, and F1-score 96%. We evaluated Dataset III with implemented DL algorithms and found that the performance measurements were than Dataset I and II. For example, with Dataset III, LSTM-MLP predicted the fatality of all AD-COVID-19 patients with the highest accuracy together with other performance measurements. This hybrid model showed 86% accuracy,86% recall score, 88%precision, and 85% F1 score. In the case of other generic models: MLP provided low performance compared to the hybrid model in terms of all measurements. (Description for Dataset III must be included).
Table 7.
Performance of DL models for Dataset I.
| Models | Accuracy | Recall | F1-score | Precision | Loss | Validation Loss |
|---|---|---|---|---|---|---|
| ANN | 96% | 96% | 96% | 96% | 0.0361 | 0.033 |
| MLP | 94% | 94% | 94% | 94% | 0.059 | 0.061 |
| LSTM | 96% | 96% | 96% | 96% | 0.0572 | 0.036 |
| AD-CovNet | 97% | 97% | 97% | 97% | 0.0292 | 0.022 |
Table 8.
Performance of DL models for Dataset II.
| Models | Accuracy | Recall | F1-score | Precision | Loss | Validation Loss |
|---|---|---|---|---|---|---|
| ANN | 96% | 96% | 96% | 96% | 0.032 | 0.028 |
| MLP | 92% | 91% | 92% | 93% | 0.144 | 0.079 |
| LSTM | 96% | 96% | 96% | 96% | 0.031 | 0.027 |
| AD-CovNet | 97% | 96% | 96% | 97% | 0.032 | 0.027 |
Table 9.
Performance of DL models for Dataset III.
| Models | Accuracy | Recall | F1-score | Precision | Loss | Validation Loss |
|---|---|---|---|---|---|---|
| ANN | 84% | 84% | 84% | 88% | 0.119 | 0.848 |
| MLP | 85% | 85% | 85% | 88% | 0.120 | 0.119 |
| LSTM | 81% | 81% | 81% | 81% | 0.134 | 0.136 |
| AD-CovNet | 86% | 86% | 85% | 88% | 0.108 | 0.110 |
Fig. 9.
Graphical representation of performance metrics- Dataset I.
Fig. 10.
Graphical representation of performance metrics- Dataset II.
Fig. 11.
Graphical representation of performance metrics- Dataset III.
7.3. Loss and validation loss
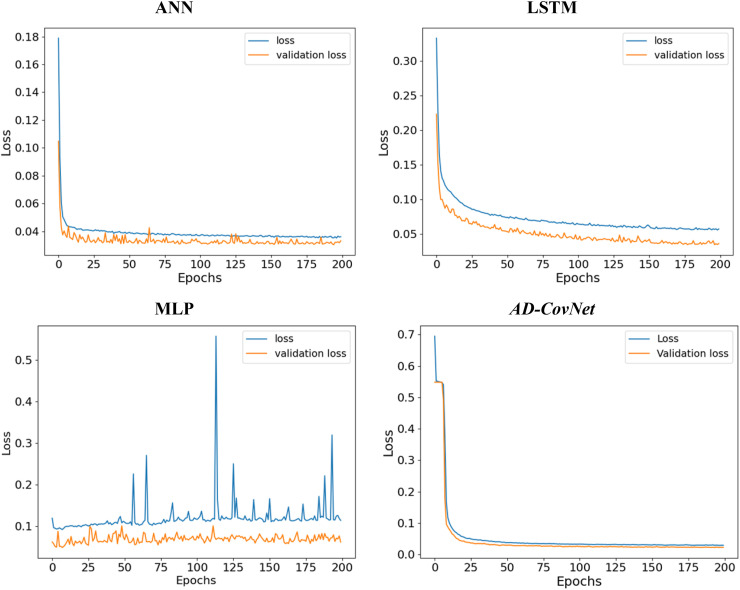
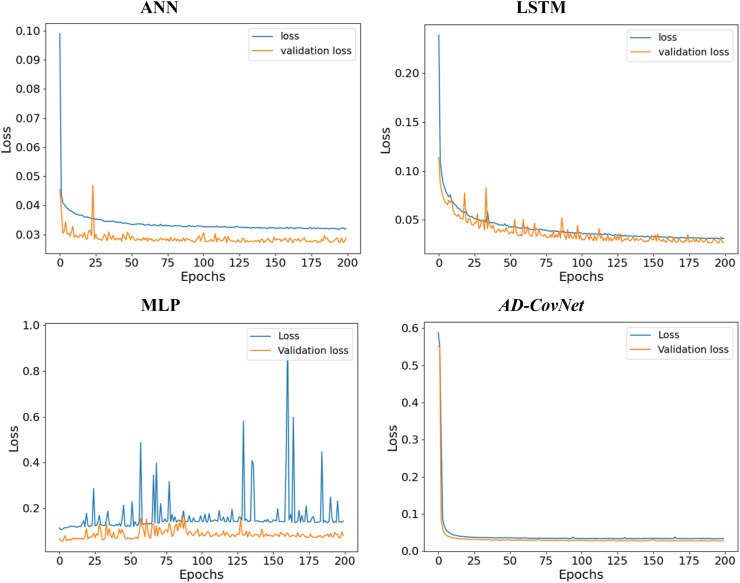
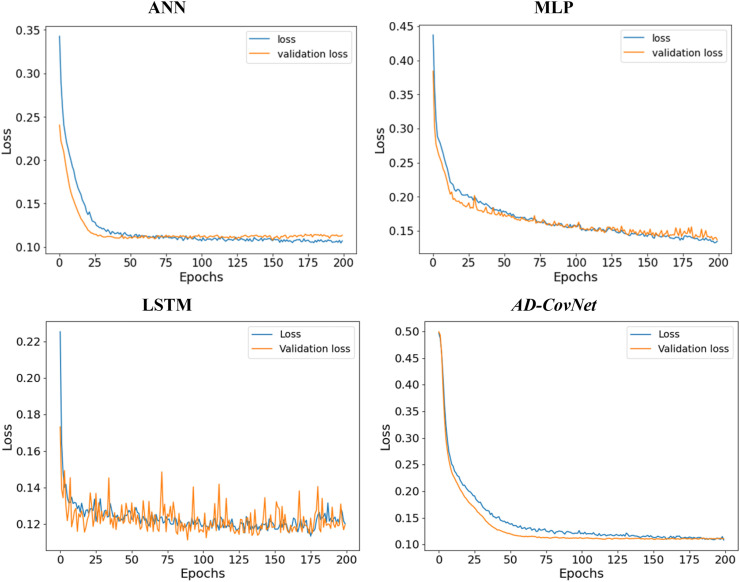
We calculated loss (error for training data) and validation loss (error for testing data) in each epoch. Fig. 12, Fig. 13, Fig. 14 represent the loss and validation loss of the proposed DL models presenting Dataset I, II, and III, respectively. For all the models, a similar pattern was observed in both loss and validation loss during the analysis using all algorithms. The pattern and very minute difference in loss and validation loss indicate the perfect fitting of the model. For example, AD-CovNet, showed the lowest loss (0.029, 0.032, and 0.108) and validation loss, (0.022, 0.027, and 0.1107)for Dataset I, II, and Dataset III respectively. MLP provided higher loss (0.059, 0.144, and 0.l20) and validation loss (0.061, 0.079, and 0.119) while analyzing three datasets. However, LSTM showed high loss and validation loss (0.134 and 0.136) and ANN provided the largest validation loss (0.848) while predicting fatality in Dataset III. These findings are presented in Table 7, Table 8, Table 9. Therefore, the hybrid model provided the lowest error in all data categories compared to other models.
Fig. 12.
Loss-validation curve (Dataset I).
Fig. 13.
Loss-validation curve (Dataset II).
Fig. 14.
Loss-validation curve (Dataset III).
7.4. AUC-ROC: Area Under Curve (AUC) and Receiver Operating Characteristic (ROC)
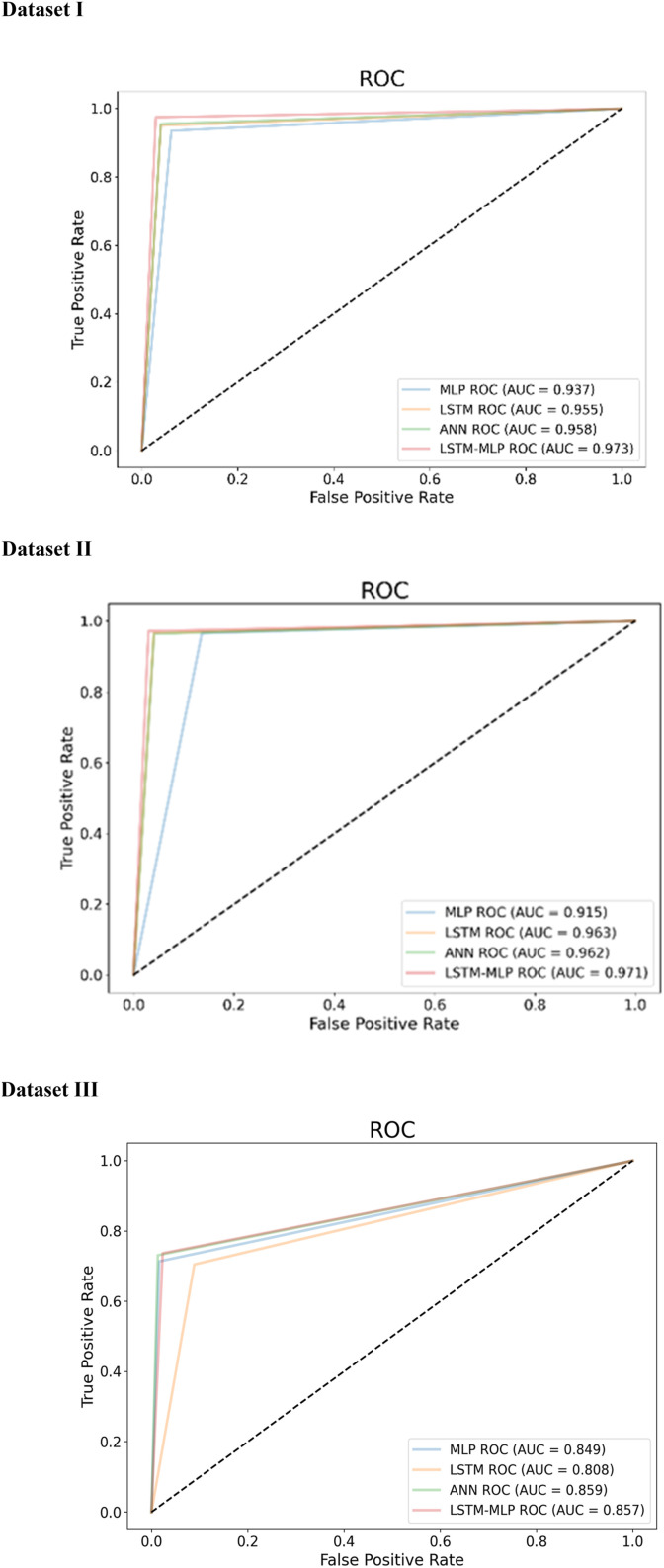
AUC-ROC curve is another essential criterion to assess the performance of the models. While ROC defines the probability curve (correctly classified over wrongly classified) of performance, AUC measures the capacity of a model to differentiate among classes. The higher ROC and AUC, the higher the performance meaning that the better the model is at separating patients with the disease and no disease. In this study, we have plotted AUC-ROC curve for three datasets (Fig. 15 ). It depicts the AUC curve, with the x and y axes representing the FPR and TPR, respectively. Higher AUC (near to 1) indicates better performance in determining whether the patient has a disease or not. Here, AD-CovNet demonstrated the highest AUC (0.973, 0.97, and 0.857) for detecting AD-COVID-19 mortality with Dataset I, II, and III, respectively. MLP showed relatively low AUC scores (0.93 and 0.91) compared to other models while analyzing Dataset I and II. In addition, LSTM provided the lowest AUC score (0.808) in Dataset III.
Fig. 15.
AUC curves of Dataset I, II, and III.
7.5. Statistical significance test
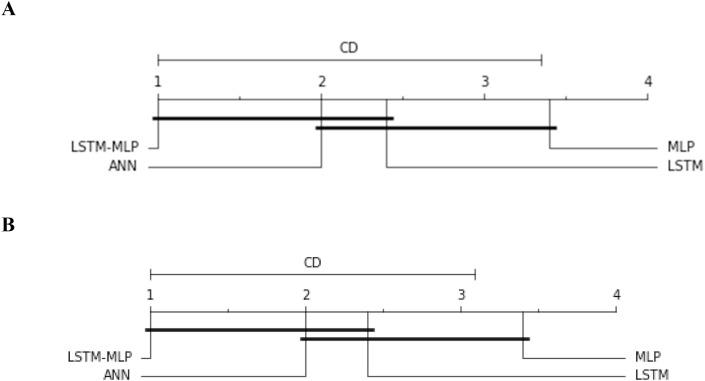
To compare the performance among the DL models in terms of accuracy, we have executed one nonparametric test named Friedman test [33] and Quade test [34]. Later on, we performed Nemenyi post hoc test to compare the pairwise differences [35]. The former two tests calculate the p-value of the overall comparison that indicates whether the algorithms perform differently or not. Our comparison of DL models with these tests provides a p-value of (0.05 and 0.1) and proves that the models acted differently. Then we proceed with Nemenyi post hoc test. The nemenyi Test functions to calculate the critical difference (CD) as well as all pairwise differences. It is built on the absolute difference between the classifiers' average ranks. The test establishes the CD for a significance level (alpha); if the distinction between the average ranking of two models is more than CD, the null hypothesis is rejected stating that the algorithms perform differently. In this study, the average ranking of the models is follows; ANN-2.0, MLP-3.4, LSTM-2.4, and AD-CovNet-1.0. Thus, it is observed that AD-CovNet performed better than MLP and LSTM with a significance level of alpha = 0.05 and 0.1 (the difference between Avg ranking of MLP and AD-CovNet is 2.4 which is higher than CD; 2.34). The significance level and the difference in avg rankings are represented in Fig. 16 .
Fig. 16.
Nemenyi test for pairwise comparisons. A. Nemenyi test for pairwise comparisons (alpha = 0.05 and CD = 2.34), B. Nemenyi test for pairwise comparisons (alpha = 0.1 and CD = 3.14).
8. Risk factor
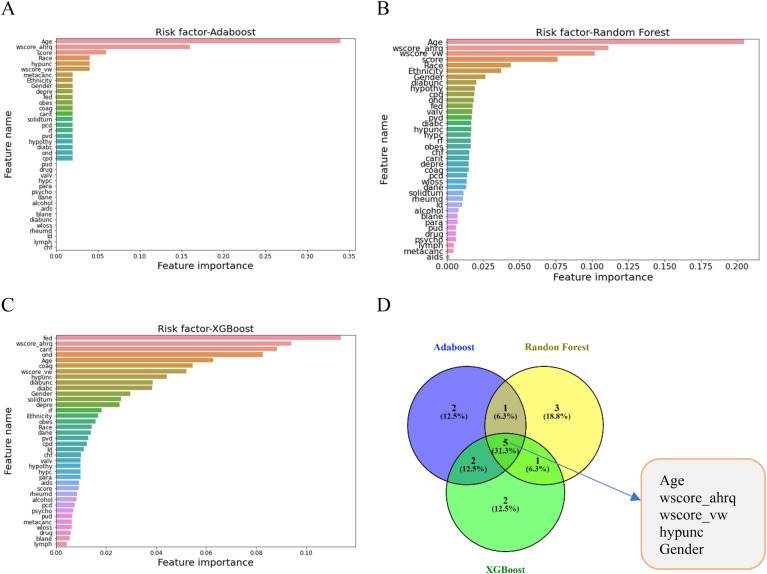
We evaluated the risk factors of COVID-19 patients' and AD patients' data by implementing Random Forest, AdaBoost, XGBoost classifier models. Fig. 17 presents the risk factors of COVID-19 fatality utilizing the DL models. After preprocessing and normalizing, models were fitted to the data. The relevance of each feature in predicting the class was assigned as a rank and defined as a risk factor. All these three models evaluated the risk factors considering all the features in the data set. XGBoost evaluated the top 10 features as follows: ‘Age’, ‘wscore_ahrq’, ‘score’, ‘hypunc’, ‘wscore_vw’, ‘metacanc’, ‘Ethnicity’, ‘Gender’, ‘depre’, ‘fed’. AdaBoost ranked top 10 features as follows: ‘Age’, ‘wscore_ahrq’, ‘wscore_vw’,‘score’, ‘hypunc’,‘Ethnicity’, ‘Gender’, ‘diabunc’, ‘hypothy’, ‘cpd’. Random Forest classifier model placed 10 important features which are as follows: ‘fed’, ‘wscore_ahrq’, ‘carit’, ‘ond’, ‘Age’, ‘wscore_vw’, ‘hypunc’,‘diabunc’ ‘diabc’, ‘Gender’. All these features have a great medical significance. While assessing these ranked features for these models, it has been observed that 5 features; ‘Age’, ‘wscore_ahrq’, ‘wscore_vw’,‘hypunc’, ‘Gender’ are common which are presented in Fig. 17D. The significance of these 5 risk factors towards the fatality of COVID-19 patients having neuro diseases have been validated in the medical science and health sectors together with ‘carit’, ‘fed’, and ‘depre’.
Fig. 17.
Risk factors of AD-COVID-19 fatality.
9. Discussion
The COVID-19 fatality rate increases with underlying conditions such as heart diseases, diabetes, high blood pressure, and neurodegenerative diseases like AD, VD, or others. A spectrum of imbalanced data generated from varying clinical features and conditions of AD patients with COVID-19 leads to misinterpretation of the fatality rate of AD patients with COVID-19. Hence, the study aims to develop a novel hybrid deep learning model using Multi-layer Perceptron (MLP) and Long Short-Term Memory (LSTM) algorithms for effective utilization of imbalanced data and predict the fatality rate of AD patients with COVID-19. Six balancing algorithms have been tested to ensure that each class has roughly the same number of instances by increasing the frequency of the minority class while decreasing the frequency of the dominant class. Based on R2 and RMSE values, the SMOTE-ENN hybrid algorithm was found to have the best performance to balance and classifying the imbalance dataset for preprocessing to execute the DL models. To reach a certain proportion against the raw dataset, SMOTE–ENN generates synthetic samples in the raw dataset with respect to two features, i.e., wscore_vw and wscore_ahrq. The synthetic samples generated by SMOTE–ENN constantly maintain the ratio of mortality class (without and with) in the raw data, which is a prerequisite for appropriate fatality rate prediction. The proposed LSTM-MLP (AD-CovNet) hybrid deep learning model utilized the datasets (I, II, and III) balanced by the SMOTE–ENN to predict the fatality rate. The proposed AD-CovNet showed the highest optimum (overall 97%) performance according to accuracy, precision, recall, and F1-score, and hence, was considered the best performing hybrid DL model with three different datasets. Besides, the model exhibited the lowest error in terms of loss and validation loss scores, suggesting the proposed model is more accurate and efficient in classifying COVID-19 or AD patients with COVID-19 and predicting mortality rate. Furthermore, age (>65), gender, cardiac arrhythmias, and depression were identified as prominent critical risk factors for AD onset and AD-COVID-19 fatality. The overall discussion and major contributions to the biomedical informatics field are explained through the three RQs:
RQ1: In recent years, there has been growing attention to the issue of imbalance. Imbalanced datasets can be found in a variety of real-world settings. Several solutions have been demonstrated in this study to the class-imbalance problem. We categorically grouped the data and experimented with all the resampling techniques. Based on the assessment metrics R2 and RMSE values (Fig. 3), we chose the best combination. The study demonstrated all the combinations obtained the best predictive metrics with different resampling techniques. The dataset is quite large, and the risk of overfitting while utilizing resample technology is significant which might lead to inaccurate conclusions. Also, it is imperative to overcome this challenge for larger datasets, since the minority class plays the determinant role. Here in this study, overfitting was avoided during optimization by adjusting the parameters used to determine the error between testing and training datasets. While selecting the dataset set (Dataset I, II, and III), the higher value of R2 (0.76) showed the relative measure of fit. In contrast, lower values of RMSE indicated the absolute measure of fit and subsequently accelerated AD-CovNet model performance by indicating a better fit. In this dataset, the ratio of the majority class to the minority class was 96:3 affected the classification performance catastrophically and prediction results could not be obtained correctly. Though DL models can handle very large datasets well to solve the classification problems, due to the huge imbalance issue, DL models performed very severely with all performance metrics. Thus, we attempted to balance the dataset in terms of class and balanced the dataset using all available resampling techniques (Table 3), and identified a well-performed technique named SMOTE-ENN, providing the best R2 and RMSE values with the augmented dataset while considering the selected three datasets.
RQ2: The overall performance of AD-CovNet based on accuracy, precision, recall, and F1-score, AUC-ROC, loss, and validation loss score were evaluated with three different datasets, and results were compared. Overall, AD-CovNet (97%), LSTM (96%), and MLP (91%–94%) demonstrated high accuracy in the analysis of predicting fatality of COVID-19 patients with all neuro diseases (Dataset I and II). In addition, AD-CovNet accomplished the highest accuracy in predicting fatalities in comparison to other deep learning models while analyzing these three datasets (Fig. 9, Fig. 10, Fig. 11). However, for dataset III (4176 samples)), the models did not achieve results as good as the large dataset (81–85% accuracy). In both cases, AD-CovNet showed the best performance in analyzing and predicting the classes.
Fig. 3.
R2 and RMSE values of different sets of data using SMOTE- ENN only.
All models provided a minimal error of roughly 0.1–0.15 for both the training and testing data (loss and validation loss). Both types of errors were reduced with higher time and epochs. The results show that the data was correctly fitted to the implemented DL generic and hybrid models. When compared with other models, AD-CovNet provided the error as loss (0.0292 and 0.0271) and validation loss (0.0326, 0.0227), which was considered the lowest for this study and Dataset I, and II, respectively. For Dataset III, AD-CovNet also provided the lowest loss and validation loss values compared to other models, while ANN provided a maximum error of 0.8488. As a result, AD-CovNet is the best fit for three types of data. Furthermore, AD-CovNet is more accurate and efficient than the other three models in classifying COVID-19 or AD patients with COVID-19 illnesses. Moreover, when considering the four DL models, the variation between loss and validation loss was extremely tiny, implying that the data was perfectly fitted to all algorithms and models. Therefore, it can be concluded that the models did not overfit the training data.
Due to the availability of diverse neural network topologies in recent eras, selecting the appropriate blend of hyperparameters that decreases or raises the fitness function is one of the most challenging components of any deep learning project. Given a large number of benchmarks, building a constant search process may be problematic. Therefore, the objective of this study was to create a fitness function and a search method including the tuning of hyperparameters as an optimizer, activation function, network layer depth, learning rate, and batch size. As a result, we were able to determine the best hyperparameter design for rapid, efficient, urgent, and adaptive deep learning analysis.
RQ3: Further, the study detected the risk factors of COVID-19 and AD fatality. AdaBoost, Random Forest, and XGBoost classifier models were used. Age is a very critical factor in AD which was described in annual reports of the Alzheimer's association in 2021; aged 65 and older, 6.2 million Americans had AD, and the number is expected to rise from 6.2 million to 13.8 million by the end of 2060 [36] in the USA. Age is also a prominent critical factor in COVID-19 fatality that has shown for the last two years in the whole world. Gender is another factor in AD and described in the previous reports as 2/3 of American women suffer from AD. wscore_ahrq’, ‘wscore_vw’ are two comorbidities' scores. The weighted Elixhauser score known as the comorbidity score (wscore_ahrq and wscore_vw) is calculated using both the AHRQ and the van Walraven algorithms. This score indicates the possible fatality of critically ill patients. The higher the score, the higher the probability of a patient's fatality. Carit is another risk that was identified by the models in this study. ‘carit’ (Cardiac arrhythmias) can be justified by different medical diagnosis reports. If the heart is not functioning properly, any individual is at risk of becoming seriously ill if infected with any pathogenic agent. Thus, the mortality incidence is higher in the AD-COVID-19 patients with heart problems. Depression (depre) is a critical factor for AD onset. Depression creates pressure on brain memory cells and combined with AD makes the condition worse.
9.1. Limitations in this work
The study has flaws as well. The overall data had 43 features with pathologies information, very imbalanced classes (mortality vs. no mortality), and 400,000 samples that caused the predictive performance to be very challenging. We used a binary dataset for the classification, considering the split of raw data into different datasets. The three representative datasets were chosen to analyze as the analysis with DL models for the whole data set did not work out well in terms of computational efficiency and performance. The reason behind this problem was the huge, augmented dataset of around 1 million. However, multi-view learning algorithms [38] may be studied for an improved prediction results by combining heterogeneous feature sets consisting of multiple clinical factors such as examinations, medications, and lab tests of different data types (e.g., categorical and continuous).
9.2. Future work
Future work may be directed toward exploring analysis by incorporating various experimental approaches and data processing. It would be interesting to use the AD-CovNet technique to forecast the variation in time of COVID-19 fatalities in AD patients by a certain experimental threshold [9]. Another highly intriguing and appealing study may be expanding AD-CovNet to a multiclass classification of neuro disorders.
9.3. Comparative study
The results of the AD-CovNet model are compared with relevant studies and illustrated in Table 10 . These findings demonstrated that the AD-CovNet model demonstrated competitive performance compared to the other models. However, we did not find any binary datasets of COVID-19 patients having AD with clinical information to compare. Hence, we showed the comparison of the model performance of AD-CovNet with that of the other studies using X-ray images where they used RNN, LSTM, and MLP. Overall, AD-CovNet showed better performance, with an accuracy of 97.0%.
Table 10.
Comparative study.
| Description | Type of dataset | Implemented algorithm | Prediction accuracy | Reference |
|---|---|---|---|---|
| COVID-19 prediction | X-ray image | LSTM | 96% | [37] |
| RNN | 93% | |||
| COVID-19 prediction | X-ray image | LSTM-RNN | 86% | [38] |
| COVID-19 prediction | X-ray image | LSTM-GRU | 87% (for Confirmed case) | [39] |
| 67.8% (for Negative cases) | ||||
| 62% (for Deceased cases) | ||||
| 40.5% (for Released case) | ||||
| COVID-19 prediction | X-ray image | LSTM | 90% | [40] |
| COVID-19 prediction | X-ray image | MTU-COVNet | 97.7% | [41] |
| COVID-19 prediction | X-ray image | Res-CovNet | 96.2% | [42] |
| AD-COVID-19 Mortality | Binary dataset | AD-CovNet | 97.0% | Present study |
10. Conclusion
We began the investigation by describing the complexities of dealing with a large and diverse dataset. This condition is typical of a real-world general practice scenario in which class samples are substantially imbalanced. We categorically selected the dataset for classification once the balanced approach was initiated. Following that, we suggested four DL models together with a hybrid AD-CovNet model for predicting AD-COVID-19 fatalities and evaluating risk factors on various characteristics in an actual dataset. We demonstrated that the AD-CovNet technique could predict and categorize AD-COVID-19 fatalities with high accuracy and precision. Because of its effective but complicated architecture for capturing large amounts of data, the AD-CovNet model was generally capable of gaining relevant information. Adding statistical significance (Fig. 16) established the reliability of the outcome. Risk factors identified through three ML models categorized the risk factors with medical relevancy. The AD-CovNet model, which also has a high level of interpretability (i.e., it can cope with heterogeneous data and large datasets), maybe the best candidate in common practice to be integrated into a decision support system for disease fatality screening purposes. This framework provides a generalizable approach for linking deep learning to pathophysiological processes in human disease. Based on the research, we believe that AD-CovNet i.e., deep learning approaches, could be effectively used to translate large amounts of clinical and biochemical data into improved human health.
Acknowledgment
We sincerely acknowledge the support provided to the authors by Dr. Qianga Zhang, and Prof. Nandakumar Narayanan of the Department of Neurology, University of Iowa, Iowa City, IA, USA. The authors also acknowledge the support provided by Mumtahina Ahmed and Mahdita Ahmed.
References
- 1.2020 Alzheimer's disease facts and figures. Alzheimers. Dement. 2020 doi: 10.1002/alz.12068. Mar. [DOI] [PubMed] [Google Scholar]
- 2.Brodaty H., et al. The world of dementia beyond 2020. J. Am. Geriatr. Soc. May 2011;59(5):923–927. doi: 10.1111/j.1532-5415.2011.03365.x. [DOI] [PubMed] [Google Scholar]
- 3.2021 Alzheimer's disease facts and figures. Alzheimers. Dement. 2021;17(3):327–406. doi: 10.1002/alz.12328. Mar. [DOI] [PubMed] [Google Scholar]
- 4.Matias-Guiu J.A., Pytel V., Matías-Guiu J. Death rate due to COVID-19 in Alzheimer's disease and frontotemporal dementia. J. Alzheim. Dis. : JAD. 2020;78(2):537–541. doi: 10.3233/JAD-200940. Netherlands. [DOI] [PubMed] [Google Scholar]
- 5.Wang Q., Davis P.B., Gurney M.E., Xu R. COVID-19 and dementia: analyses of risk, disparity, and outcomes from electronic health records in the US. Alzheimers. Dement. 2021;17(8):1297–1306. doi: 10.1002/alz.12296. Aug. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Akter S., Roy A.S., Tonmoy M.I.Q., Islam M.S. Deleterious single nucleotide polymorphisms (SNPs) of human IFNAR2 gene facilitate COVID-19 severity in patients: a comprehensive in silico approach. J. Biomol. Struct. Dyn. 2021:1–17. doi: 10.1080/07391102.2021.1957714. [DOI] [PubMed] [Google Scholar]
- 7.Knopman D.S., et al. Alzheimer disease. Nat. Rev. Dis. Prim. May 2021;7(1):33. doi: 10.1038/s41572-021-00269-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Dessie Z.G., Zewotir T. Mortality-related risk factors of COVID-19: a systematic review and meta-analysis of 42 studies and 423,117 patients. BMC Infect. Dis. 2021;21(1):855. doi: 10.1186/s12879-021-06536-3. Aug. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Bhaskaran K., et al. Factors associated with deaths due to COVID-19 versus other causes: population-based cohort analysis of UK primary care data and linked national death registrations within the OpenSAFELY platform. Lancet Reg. Heal. Eur. 2021;6 doi: 10.1016/j.lanepe.2021.100109. Jul. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Mok V.C.T., et al. Tackling challenges in care of Alzheimer's disease and other dementias amid the COVID-19 pandemic, now and in the future. Alzheimers. Dement. 2020;16(11):1571–1581. doi: 10.1002/alz.12143. Nov. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Wang H., et al. Alzheimer's disease in elderly COVID-19 patients: potential mechanisms and preventive measures. Neurol. Sci. Dec. 2021;42(12):4913–4920. doi: 10.1007/s10072-021-05616-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Min S., Lee B., Yoon S. Deep learning in bioinformatics. Brief. Bioinform. 2016;18(5):851–869. doi: 10.1093/bib/bbw068. [DOI] [PubMed] [Google Scholar]
- 13.Bzdok D., Altman N., Krzywinski M. Statistics versus machine learning. Nat. Methods. 2018;15(4):233–234. doi: 10.1038/nmeth.4642. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Vassar M., Holzmann M. The retrospective chart review: important methodological considerations. J. Educ. Eval. Health Prof. 2013;10:12. doi: 10.3352/jeehp.2013.10.12. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Bernardini M., Romeo L., Frontoni E., Amini M.-R. A semi-supervised multi-task learning approach for predicting short-term kidney disease evolution. IEEE J Biomed Heal Info. 2021;25(10):3983–3994. doi: 10.1109/JBHI.2021.3074206. [DOI] [PubMed] [Google Scholar]
- 16.Akter S., Shamrat F.M., Chakraborty S., Karim A., Azam S. COVID-19 detection using deep learning algorithm on chest X-ray images. Biology. 2021;10(11):1174. doi: 10.3390/biology10111174. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Akter S., et al. IEEE Access; 2021. Comprehensive Performance Assessment of Deep Learning Models in Early Prediction and Risk Identification of Chronic Kidney Disease. [Google Scholar]
- 18.Lusa L., Blagus R. vol. 2. 2012. The class-imbalance problem for high-dimensional class prediction; pp. 123–126. (2012 11th International Conference on Machine Learning and Applications). [DOI] [Google Scholar]
- 19.Casanova R., et al. Alzheimer's disease risk assessment using large-scale machine learning methods. PLoS One. 2013;8(11):1–13. doi: 10.1371/journal.pone.0077949. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Mahyoub M., Randles M., Baker T., Yang P. 2018 11th International Conference on Developments in eSystems Engineering. DeSE); 2018. Comparison analysis of machine learning algorithms to rank Alzheimer's disease risk factors by importance; pp. 1–11. [DOI] [Google Scholar]
- 21.Qiu S., et al. Development and validation of an interpretable deep learning framework for Alzheimer's disease classification. Brain. 2020;143(6):1920–1933. doi: 10.1093/brain/awaa137. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Wang L., et al. Development and validation of a deep learning algorithm for mortality prediction in selecting patients with dementia for earlier palliative care interventions. JAMA Netw. Open. 2019;2(7) doi: 10.1001/jamanetworkopen.2019.6972. e196972–e196972. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Dabbah M.A., et al. Machine learning approach to dynamic risk modeling of mortality in COVID-19: a UK Biobank study. Sci. Rep. 2021;11(1) doi: 10.1038/s41598-021-95136-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Mahdavi M., et al. A machine learning based exploration of COVID-19 mortality risk. PLoS One. 2021;16(7):1–20. doi: 10.1371/journal.pone.0252384. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Bertsimas D., et al. COVID-19 mortality risk assessment: an international multi-center study. PLoS One. 2020;15(12) doi: 10.1371/journal.pone.0243262. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Kar S., et al. Multivariable mortality risk prediction using machine learning for COVID-19 patients at admission (AICOVID) Sci. Rep. 2021;11(1) doi: 10.1038/s41598-021-92146-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Liang W., et al. Early triage of critically ill COVID-19 patients using deep learning. Nat. Commun. 2020;11(1):3543. doi: 10.1038/s41467-020-17280-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Naseem M., Arshad H., Hashmi S.A., Irfan F., Ahmed F.S. Predicting mortality in SARS-COV-2 (COVID-19) positive patients in the inpatient setting using a novel deep neural network. Int. J. Med. Inf. 2021;154 doi: 10.1016/j.ijmedinf.2021.104556. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Zhang Y.-D., Satapathy S.C., Liu S., Li G.-R. A five-layer deep convolutional neural network with stochastic pooling for chest CT-based COVID-19 diagnosis. Mach. Vis. Appl. 2020;32(1):14. doi: 10.1007/s00138-020-01128-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Wang S.-H., Wu X., Zhang Y.-D., Tang C., Zhang X. Diagnosis of COVID-19 by wavelet Renyi entropy and three-segment biogeography-based optimization. Int. J. Comput. Intell. Syst. 2020;13(1):1332–1344. doi: 10.2991/ijcis.d.200828.001. [DOI] [Google Scholar]
- 31.Zhang Q., et al. COVID-19 case fatality and Alzheimer's disease. J. Alzheim. Dis. 2021;84(4):1447–1452. doi: 10.3233/JAD-215161. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Batista G.E., Prati R.C., Monard M.C. International Symposium on Intelligent Data Analysis. 2005. Balancing strategies and class overlapping; pp. 24–35. [Google Scholar]
- 33.Friedman M. The use of ranks to avoid the assumption of normality implicit in the analysis of variance. J. Am. Stat. Assoc. 1937;32(200):675–701. [Google Scholar]
- 34.García S., Fernández A., Luengo J., Herrera F. Advanced nonparametric tests for multiple comparisons in the design of experiments in computational intelligence and data mining: experimental analysis of power. Inf. Sci. 2010;180(10):2044–2064. [Google Scholar]
- 35.Demšar J. Statistical comparisons of classifiers over multiple data sets. J. Mach. Learn. Res. 2006;7:1–30. [Google Scholar]
- 36.Association A. 2021. Alzheimer's and Dementia(Facts and Figures) [Google Scholar]
- 37.Alassafi M.O., Jarrah M., Alotaibi R. Time series predicting of COVID-19 based on deep learning. Neurocomputing. 2022;468:335–344. doi: 10.1016/j.neucom.2021.10.035. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Alorini G., Rawat D.B., Alorini D. ICC 2021 - IEEE Int. Conf. Commun. 2021. LSTM-RNN based sentiment analysis to monitor COVID-19 opinions using social media data; pp. 1–6. [DOI] [Google Scholar]
- 39.Dutta S., Bandyopadhyay S.K. Machine learning approach for confirmation of COVID-19 cases: positive, negative, death and release. Iberoam. J. Med. 2020;2(3):172–177. doi: 10.53986/ibjm.2020.0031. [DOI] [Google Scholar]
- 40.Tomar A., Gupta N. Elsevier Connect , the company ’ s public news and information; 2020. Since January 2020 Elsevier Has Created a COVID-19 Resource Centre with Free Information in English and Mandarin on the Novel Coronavirus COVID- 19 . The COVID-19 Resource Centre Is Hosted on. January. [Google Scholar]
- 41.Kavuran G., In E., Geçkil A.A., Şahin M., Berber N.K. MTU-COVNet: a hybrid methodology for diagnosing the COVID-19 pneumonia with optimized features from multi-net. Clin. Imag. 2022;81:1–8. doi: 10.1016/j.clinimag.2021.09.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Madhavan M.V., Khamparia A., Gupta D., Pande S., Tiwari P., Hossain M.S. Res-CovNet: an internet of medical health things driven COVID-19 framework using transfer learning. Neural Comput. Appl. 2021:1–14. doi: 10.1007/s00521-021-06171-8. [DOI] [PMC free article] [PubMed] [Google Scholar]