Abstract
The performance of an inertial measurement unit (IMU) system for directly measuring thoracolumbar trunk motion was compared to that of the Lumbar Motion Monitor (LMM). Thirty-six male participants completed a simulated material handling task with both systems deployed simultaneously. Estimates of thoracolumbar trunk motion obtained with the IMU system were processed using five common methods for estimating trunk motion characteristics. Results of measurements obtained from IMUs secured to the sternum and pelvis had smaller root-mean-square differences and mean bias estimates in comparison to results obtained with the LMM than results of measurements obtained solely from a sternum mounted IMU. Fusion of IMU accelerometer measurements with IMU gyroscope and/or magnetometer measurements was observed to increase comparability to the LMM. Results suggest investigators should consider computing thoracolumbar trunk motion as a function of estimates from multiple IMUs using fusion algorithms rather than using a single accelerometer secured to the sternum in field-based studies.
Keywords: musculoskeletal disorders, manual handling, inertial measurement
1. Introduction
Low back pain (LBP) is a common work-related musculoskeletal disorder (MSD) with an estimated 1-month prevalence of 23.2% and lifetime prevalence ranging as high as 84% (Hoy et al., 2012; Walker, 2000). Occupational exposure to non-neutral trunk postures and manual material handling (MMH) activities may be associated with LBP (Coenen et al., 2013; da Costa and Vieira, 2010; Manchikanti, 2000; Hoogendoorn et al., 2000; Vieira and Kumar, 2004; van Oostrom et al., 2012). Evidence of these associations, however, is inconsistent (Roffey et al., 2010; Wai et al., 2010a, 2010b). In part, characterization of associations between non-neutral trunk postures and LBP has been limited by use of easily administered but imprecise and potentially biased self-report or observation-based exposure assessment methods (Burdorf and van der Beek, 1999; David, 2005; Li and Buckle, 1999; Vieira and Kumar, 2004).
Common approaches for directly measuring thoracolumbar trunk motion in a field setting include electrogoniometry and body mounted electromechanical sensors. The Lumbar Motion Monitor (LMM) is a field-capable, triaxial electrogoniometer used to directly measure kinematics of the thoracolumbar spine (Marras et al., 1992, 1995; Gill and Callaghan, 1996). The LMM is secured to the trunk of a worker using chest and pelvic harnesses and measures thoracolumbar angular displacement of the trunk relative to the pelvis in the three primary motion planes. With software, numerical differentiation of the angular displacement measurements is then used to obtain estimates of trunk angular velocities and angular accelerations in the three motion planes. Although the LMM has been used in numerous studies (e.g., Ferguson et al., 2002; Gallagher et al., 2002; Marras et al., 2004; Marras et al., 1999), its bulky size and limited range (i.e., through direct cable connection to a computer or through telemetry) make it impractical for prolonged field-based exposure assessments recommended to obtain stable and representative estimates of trunk motion during non-routinized work activities (e.g., construction and agriculture) (Trask et al., 2007).
Accelerometers (or inclinometers) have been used frequently in field-based research to obtain direct measurements of trunk motion over extended time periods (e.g., Fethke et al., 2011; Koehoorn, 2010; Paquet et al., 2001; Teschke et al., 2009; Van Driel et al. 2013; Wong et al., 2009). Trunk motion estimates have been reported using a variety of sensor configurations (e.g., dual axis or triaxial) and sensor placement strategies (e.g., one sensor placed on the anterior torso as in Fethke et al. [2011] vs. one sensor on the posterior torso as in Wong et al. [2009] vs. one sensor on the anterior torso combined with one sensor on the posterior pelvis as in Koehoorn [2010]). Axial rotations about the transverse plane, however, cannot be assessed through the use of an accelerometer alone, and the accuracy of accelerometer-based estimates in the flexion/extension (sagittal) and lateral bending (coronal) planes depends on the characteristics of the motion (static, quasi-static, or complex dynamic) (Amasay et al., 2009; Brodie et al., 2008; Godwin et al., 2009; Hansson et al., 2001).
Inertial measurement units (IMUs) have recently emerged as a potential alternative to accelerometers for measurement of human trunk motion in occupational settings. An IMU is a small and portable device that permits estimation of the spatial orientation of an object by combining the outputs of multiple electromechanical sensors (accelerometers, gyroscopes, and/or magnetometers) through recursive sensor fusion algorithms such as a Kalman filter or complementary weighting algorithm (Bachmann et al., 2000; Gallagher et al., 2004; Higgins, 1975; Kalman, 1960; Luinge and Veltink, 2005; Sabatini, 2006; Wagenaar et al., 2011; Yun and Bachmann, 2006). Theoretically, using sensor fusion algorithms for motion measurement can help overcome the limitations of each individual sensor component. For example, gyroscope measurements can be used to compensate for limitations of the accelerometer to more accurately measure motion in the flexion/extension and lateral bending planes under dynamic conditions, and magnetometers can provide orientation information necessary to make estimates of trunk motion in the axial rotation plane. Raw data streams from the individual sensor components may also be extracted for singular analysis.
Despite their unique capabilities and promise, few studies have used IMUs to directly measure thoracolumbar trunk motion in the field. One potential explanation for their limited use may be a lack of comparison to more widely known methods such as accelerometers or electrogoniometer systems such as the LMM. While many studies have examined the accuracy of IMU systems in comparison to optoelectric motion capture systems (Cuesta-Vargas et al., 2010) and/or have evaluated corrective factors for accelerometers (e.g., Van Driel et al., 2013), the potential benefit of using IMUs to estimate thoracolumbar motion in comparison to other field-capable systems remains unclear. For example, estimates of trunk motion can be made using information obtained from an IMU’s accelerometer alone, from an IMU’s accelerometer and gyroscope, or from the full complement of IMU sensors (i.e., accelerometers, gyroscopes, and magnetometers). Exploration of the different sensor configurations and processing methods possible with an IMU system will provide information about the potential advantages of IMU use in comparison to simpler options.
The objectives of this study were, therefore, to (i) compare estimates of thoracolumbar trunk motion obtained with a commercially available IMU system with estimates of thoracolumbar trunk motion obtained with a field-capable reference system, the LMM, and to (ii) explore the effect of alternative sensor configurations and processing methods on the agreement between LMM and IMU-based estimates of trunk motion during a simulated MMH task with both systems deployed simultaneously.
2. Methods
2.1. Participants
A convenience sample of 36 healthy, male participants (mean age = 24.9 years, SD= 4.5) was recruited from the University of Iowa community. Potential participants were excluded for any self-reported 1) physician-diagnosed MSDs of the back in the past six or fewer months, 2) orthopedic surgery of the back, 3) back pain in the past two weeks, or 4) chronic neurodegenerative disease (e.g., Parkinson’s disease). All study procedures were approved by the University of Iowa Institutional Review Board and written informed consent was obtained prior to participation.
2.2. Experimental Design
Participants completed a simulated MMH task in a laboratory setting. The MMH task required participants to manually move 4.5 kg plastic crates (42 × 35 × 27 cm) from a waist-high material feeder (Point A in Figure 1, as depicted from above) to one of six potential unloading areas (Point B in Figure 1). Two handholds were molded into each crate and used by workers for manual grasping. The six potential unloading areas varied across two factors: the unloading height (adjusted to each participant to be approximately waist height or knee height) and the total magnitude of axial rotation (twisting) needed to move a crate from the material feeder to the unloading area (90°, 135°, or 180°). The pace of the task was set to either 6 lifts/min or 3 lifts/min. Block randomization was used to assign each participant to one of the 12 task conditions (2 unloading heights × 3 axial rotation magnitudes × 2 work paces; 3 participants per condition). The modest crate weight and work pace levels were selected to ensure that the recommended weight limit of the NIOSH Lifting Equation was not exceeded when considering all combinations of the unloading height, amount of axial rotation, and work pace parameters (Waters et al., 1993).
Figure 1.
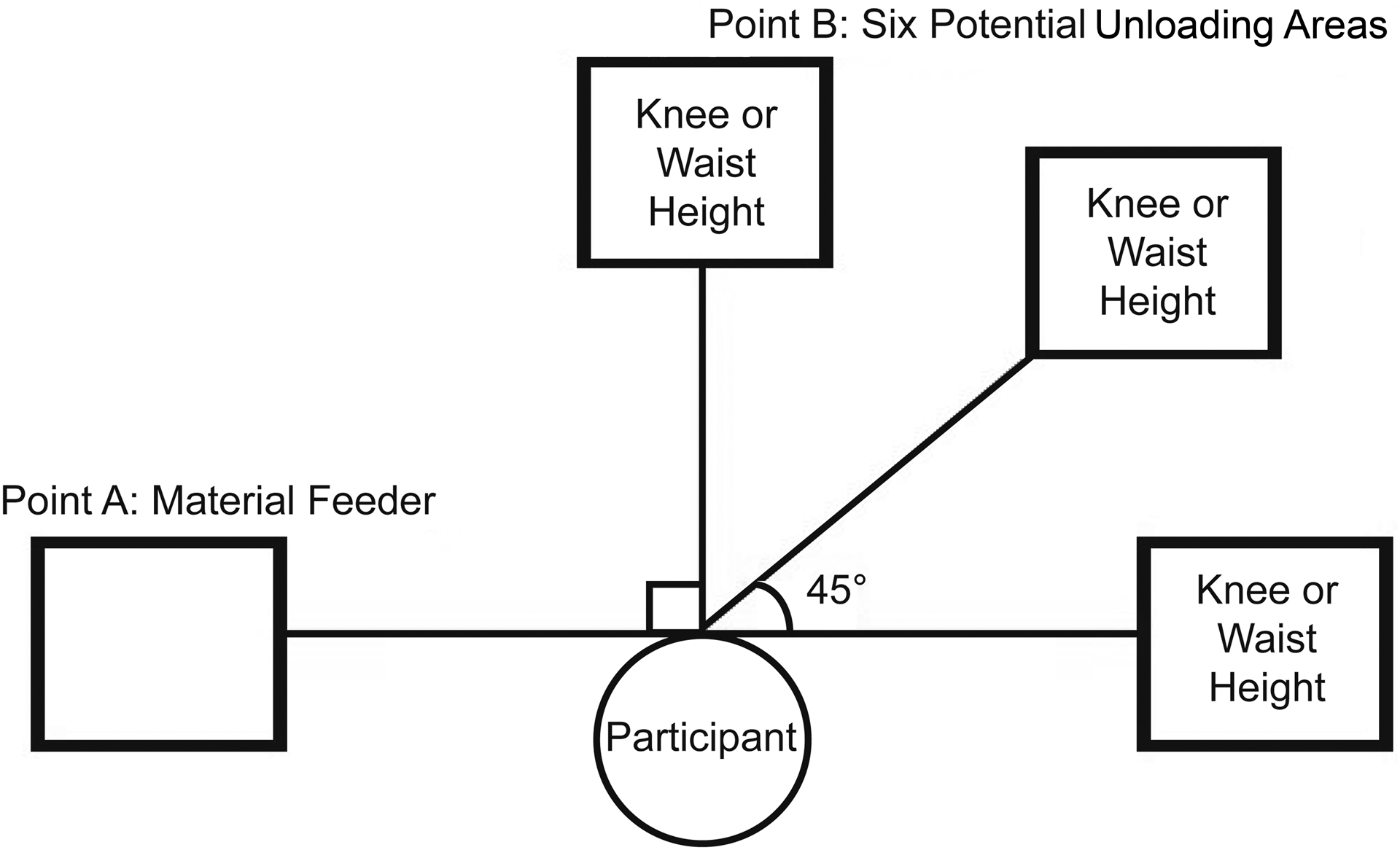
Simulated manual material handling task positions.
2.3. Instrumentation and Data Processing
Angular displacements of the thoracolumbar region of the trunk in the flexion/extension, lateral bending, and axial rotation planes were estimated using two commercially-available instrumentation systems: the ACUPATH™ Industrial Lumbar Motion Monitor™ (Biomec Inc., Cleveland, OH) and the I2M Motion Tracking System (series SXT IMUs, Nexgen Ergonomics, Inc., Pointe Claire, Quebec). For each participant, one IMU sensor was secured to the anterior torso at the sternal notch and a second IMU sensor was secured to the posterior pelvis at the L5/S1 vertebrae. Standard procedures were used to outfit participants with the LMM as in previous studies (e.g., Marras et al., 1995). The LMM was calibrated prior to fitting by using procedures described in the LMM manual. Data streams obtained from the LMM included angular displacement (in degrees) of the trunk in the flexion/extension, lateral bending, and axial rotation planes. The LMM was connected to a computer using a communications cable and the data streams were sampled at 60 Hz using manufacturer-supplied software (Ballet 2.01, Biomec Inc., Cleveland, OH).
The small size of the IMU sensors (48.5 × 36 × 12 mm) allowed them to be worn simultaneously with the LMM. The IMU sensors were calibrated after the LMM was fit using an ‘I-pose’ calibration posture in which each participant stood in a neutral trunk position with hands relaxed to the sides and the feet hip-width apart as if forming an ‘I’. Calibration quality was visually inspected before beginning the MMH task. Data streams obtained from each IMU sensor included acceleration (triaxial, +/− 6 g), angular velocity (triaxial, +/− 2000° s−1), magnetic field strength (triaxial, +/− 6 Gauss), and local sensor spatial orientation in the form of quaternions derived from a manufacturer-provided Kalman filter. The IMU data streams were sampled wirelessly at 128 Hz using manufacturer-supplied software (HM Analyzer, Nexgen Ergonomics, Pointe Claire, Quebec). An event mark was used during data collection to facilitate synchronization of the LMM and IMU data during post-processing. A custom LabVIEW program (version 2012, National Instruments, Austin TX) down sampled the IMU estimates of trunk motion from 128 Hz to 60 Hz using linear interpolation and exported the data for later analysis.
Five IMU processing methods were used to obtain estimates of thoracolumbar angular displacement in the flexion/extension and lateral bending motion planes. The five methods were: (i) a low passed (zero-phase, 2nd order Butterworth; 3 Hz cutoff frequency) accelerometer-based estimate from the IMU secured to the sternum only (Accel-1); (ii) a complementary weighting algorithm-based estimate incorporating accelerometer and gyroscope measurements from the IMU secured to the sternum only (Comp-1); (iii) a low passed (zero-phase, 2nd order Butterworth; 3 Hz cutoff frequency) accelerometer-based estimate calculated as the difference of the estimates provided from the IMUs secured to the sternum and L5/S1 body segments (Accel-2); (iv) a complementary weighting algorithm-based estimate calculated as the difference of complementary-based estimates from the IMUs secured to the sternum and L5/S1 body segments (Comp-2); and (v) a manufacturer provided Kalman-based estimate which incorporated raw acceleration, angular velocity, and magnetic field strength information from the IMUs located on the sternum and L5/S1 body segments (HM Analyzer). The manufacturer provided Kalman-based estimate (HM Analyzer) was also used to provide estimates of angular displacement in the axial rotation motion plane.
Accelerometer-based angular displacement estimates reflected accelerometer inclination angle with respect to the gravity vector and were calculated as the arctangent of the acceleration reading pointing away from the sternum (i.e., the z-axis of the SXT IMU) and the acceleration reading corresponding to the gravity vector (i.e., the x-axis of the SXT IMU and not the norm of gravity). For example, the accelerometer-based inclination angle estimates from the IMU secured to the sternum only (Accel-1) were calculated as tan−1(Az/Ax). Accelerometer-based angular displacement estimates were calculated in this manner so that they could be paired with gyroscope measurements in the corresponding axis of rotation.
The custom complementary weighting algorithm was developed in MATLAB (r2013b, The MathWorks, Inc., Natick, MA) and used the raw data streams of acceleration and angular velocity to estimate the trunk motion angles from the orientation of the IMU’s accelerometer with respect to the gravitational vector and angular velocity information from the IMU’s gyroscope. The complementary weighting algorithm adjusted the accelerometer-based inclination angle estimate at each sample using angular velocity information from the IMU’s gyroscope according to Equation (1):
| (Equation 1) |
where θn is the complementary inclination angle estimate at the current sample, θn−1 is the complementary inclination angle estimate at the previous sample, ωn is the angular velocity at the current sample, αn is the inclination angle at the current sample based solely on the orientation of the accelerometer with respect to gravity, and dt is the time between samples. The relative influence of the angular velocity and the accelerometer-based inclination angle at each sample on the resulting complementary inclination angle estimate was set using the algorithm’s weighting coefficient (K). While we are aware of no widely accepted guidelines for selecting the weighting coefficient, a value of 0.01 was determined to provide a sufficient acceleration reference to compensate for the drift that occurs when a raw gyroscope signal is integrated (Luinge and Veltnik, 2005), and has been used in a previous study (Schall et al., 2014).
The complementary weighting algorithm had a time constant of 0.77 sec, based on the weighting coefficient, the sampling rate (128 Hz), and the IMU gyroscope drift rate (approximately 1° s−1). The inclination angle (αn) was low pass filtered (zero-phase, 2nd order Butterworth; 3 Hz cutoff frequency) and the angular velocity (ωn) signals were high pass filtered (zero-phase, 2nd order Butterworth; 0.5 Hz cutoff frequency) prior to computation of complementary inclination angle estimates.
2.4. Experimental Procedure
A custom LabVIEW program was used to control the simulated MMH task. Specifically, the program produced an auditory tone at the assigned work pace to signal the participant when to move each crate. Data collection began with the participant standing in a neutral upright stance and the arms hanging relaxed and the feet hip-width apart. At each auditory tone, the participant would, (i) rotate left to the material feeder location and grasp the crate’s handles using two hands, (ii) rotate right and set the crate on the assigned unloading location, and then (iii) return to the neutral standing position to wait for the next auditory tone. Participants were instructed to keep their feet stationary while performing the lifts and to use the crate handholds. The material feeder and unloading locations were set close to the body (within arm’s reach) for all participants. No other instructions were given. The task was performed for 10 minutes, resulting in 30 or 60 lifting cycles, depending on the assigned work pace.
2.5. Statistical Analysis
Using the angular displacement waveform obtained from the LMM for each participant, a custom MATLAB program was used to identify the peak (maximum) point of flexion for the flexion/extension plane, lateral bending to the right for the lateral bending plane, or axially rotating to the left for the axial rotation plane of each lifting cycle and the corresponding four seconds before and after each peak. This eight second window encompassed all phases of each lift cycle for all participants (e.g., start of lift, peak flexion, and end of lift). The arithmetic mean of each respective sample estimate from the 30 or 60 cycles comprising the entire 10 minute MMH task was then calculated to form an ensemble average of a lifting cycle lasting eight seconds in duration (ensemble averages were generated for each participant separately).
Ensembles averages of the angular displacement waveforms were differentiated to obtain an ensemble average waveform estimate of velocity. The velocity waveform was rectified to represent the absolute value of velocity (indicating either increasing or decreasing speed). The rectified ensemble average waveform of velocity was differentiated to obtain an ensemble average waveform of acceleration (Marras et al., 1995). The minimum, maximum, mean, 10th percentile, 90th percentile, and 99th percentile were then calculated for each ensemble average waveform. In addition, we calculated a sample-to-sample root-mean-square difference (RMSD) of the ensemble average waveforms obtained with each IMU processing method in comparison to the ensemble average waveforms obtained with the LMM. The RMSD for each participant was calculated using Equation (2), where θ is the estimate from an IMU processing method, θ′ is the estimate from the LMM, n is the number of samples included in the ensemble waveform, and i is the specific sample of interest.
| (Equation 2) |
Pearson correlation analyses were used to quantify the strength of the linear relationships between the estimates of mean angular displacement and angular displacement variation (defined as the difference between the estimates of the 90th and 10th percentile) from the LMM and each measurement method in the flexion/extension, lateral bending, and axial rotation motion planes. Bland and Altman (1986, 1995, 1999, 2010) bias calculations and 95% “limits of agreement” (LoA) were used to assess agreement between estimates of mean angular displacement for the flexion/extension, lateral bending, and axial rotation motion planes obtained with the LMM and each applicable IMU measurement method.
3. Results
The LMM and each of the IMU measurement methods produced waveforms of trunk angular displacement with similar characteristics (Figure 2). In general and consistent with our expectations, estimates of mean angular displacement in the flexion/extension motion plane were lower for participants assigned to the waist high unloading areas in comparison to participants assigned to the knee high unloading areas. Moreover, the greatest estimates of mean angular displacement in the flexion/extension motion plane were observed for participants assigned to the knee high unloading areas and the faster work pace.
Figure 2.
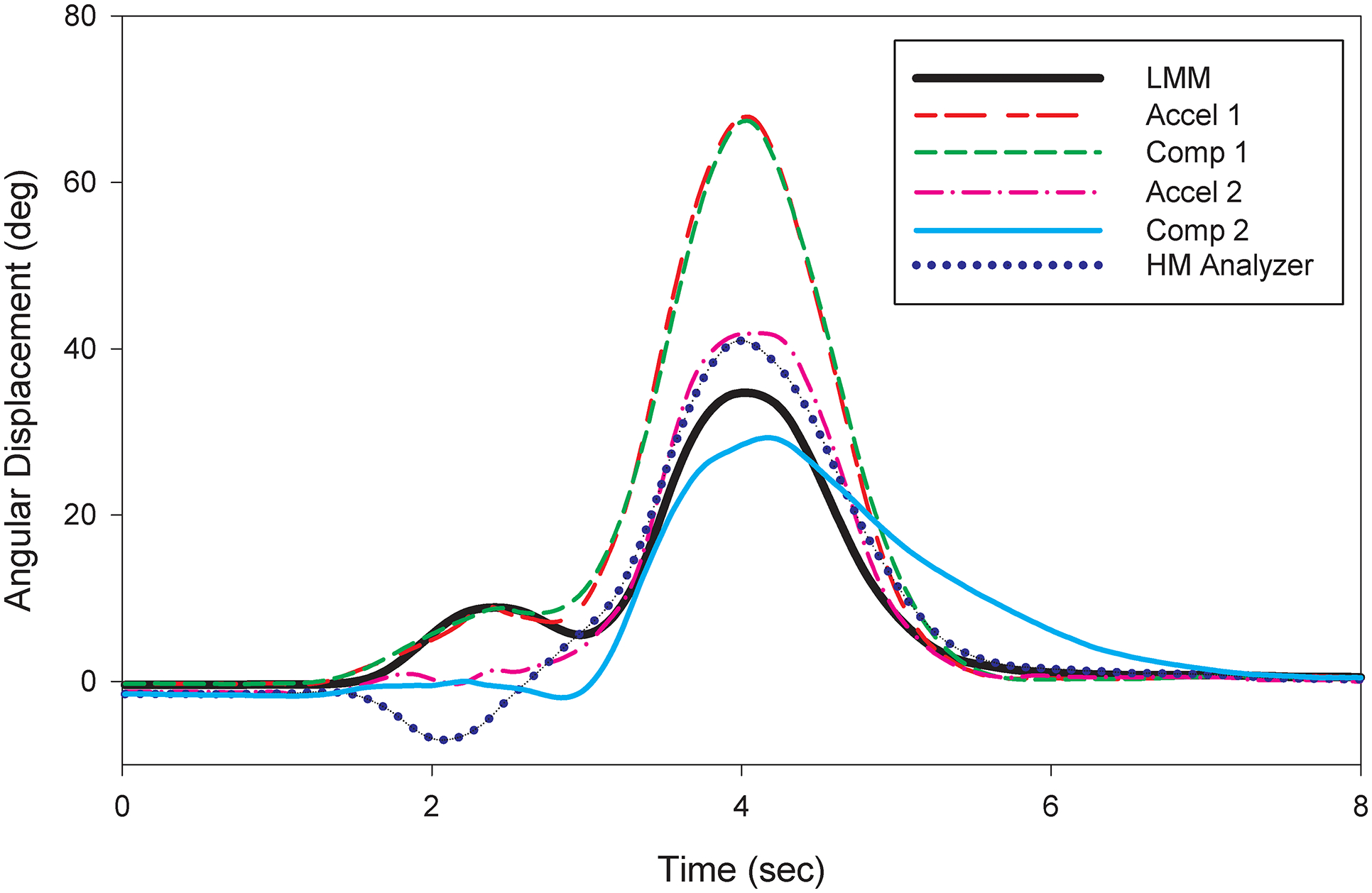
Ensemble averages of the angular displacement waveforms for the LMM and the five IMU measurement methods in the flexion/extension motion plane for one participant.
Distributions of summary measures of trunk angular displacement, velocity, acceleration, and estimates of the RMSD between the LMM and the IMU measurement methods for the flexion/extension, lateral bending, and axial rotation motion planes are provided in Tables 1, 2, and 3, respectively. RMSD estimates were similar across methods obtained using only the IMU secured to the sternum and across methods obtained using both the IMUs secured to the sternum and L5/S1 body segment. In general, the methods that used the IMUs secured to the sternum and L5/S1 body segment were observed to be more comparable to the LMM than methods obtained with IMUs secured to the sternum only. Summary measure estimates such as the mean, 10th percentile, 90th percentile, and 99th percentile angular displacement were the most comparable with the LMM for the complementary weighting algorithm-based method that calculated the estimate of thoracolumbar angular displacement as the difference of complementary-based estimates provided from the IMUs secured to the sternum and L5/S1 body segments (Comp-2). Similarly, estimates of mean, 10th percentile, 90th percentile, and 99th percentile velocity and acceleration obtained with the complementary weighting algorithm-based method that calculated the estimate of thoracolumbar angular displacement as the difference of complementary-based estimates provided from the IMUs secured to the sternum and L5/S1 body segments (Comp-2) were the most comparable to the LMM.
Table 1.
Mean (SD) of trunk motion estimates in the flexion/extension plane by measurement method for ensemble averages.
| Summary measure | LMM | Accel-1 | Comp-1 | Accel-2 | Comp-2 | HM Analyzer |
|---|---|---|---|---|---|---|
| Angular Displacement | ||||||
| Maximum Extension (°) | −1.0 (0.6) | −1.2 (0.8) | −1.2 (0.8) | −2.1 (1.8) | −2.0 (1.7) | −2.4 (2.0) |
| Mean (°) | 3.7 (2.5) | 7.6 (5.7) | 7.7 (5.7) | 5.5 (5.0) | 4.9 (4.8) | 5.3 (5.2) |
| Maximum Flexion (°) | 17.2 (9.8) | 34.9 (27.7) | 34.5 (27.0) | 26.3 (22.3) | 20.3 (17.6) | 26.9 (23.6) |
| 10th Percentile (°) | −0.8 (0.5) | −1.0 (0.7) | −0.9 (0.7) | −1.5 (1.5) | −1.6 (2.2) | −1.5 (1.4) |
| 90th Percentile (°) | 14.6 (9.4) | 30.3 (24.5) | 30.2 (23.5) | 23.2 (20.4) | 17.8 (15.8) | 22.8 (21.0) |
| 99th Percentile (°) | 17.2 (9.8) | 34.8 (27.7) | 34.4 (27.0) | 26.3 (22.3) | 20.3 (17.5) | 26.9 (23.6) |
| Sample-to-Sample RMSD (°) | -- Ref -- | 8.8 (6.5) | 8.9 (6.2) | 6.4 (5.2) | 6.6 (4.8) | 6.7 (5.1) |
| Absolute Value of Velocity | ||||||
| Mean (°/sec) | 5.1 (2.7) | 9.5 (7.0) | 9.0 (6.8) | 7.7 (5.8) | 5.8 (4.7) | 7.6 (6.0) |
| Maximum (°/sec) | 24.5 (12.7) | 44.1 (33.6) | 37.1 (30.1) | 38.5 (30.0) | 22.6 (17.4) | 33.1 (26.4) |
| 10th Percentile (°/sec) | 0.1 (0.1) | 0.2 (0.1) | 0.1 (0.1) | 0.2 (0.1) | 0.3 (0.4) | 0.1 (0.1) |
| 90th Percentile (°/sec) | 17.8 (9.8) | 32.6 (27.0) | 30.0 (25.7) | 26.2 (21.8) | 14.3 (11.4) | 24.8 (21.3) |
| 99th Percentile (°/sec) | 24.4 (12.7) | 44.0 (33.7) | 36.8 (30.1) | 38.3 (30.0) | 22.1 (17.2) | 32.8 (26.5) |
| Sample-to-Sample RMSD (°/sec) | -- Ref -- | 10.9 (7.5) | 10.1 (6.8) | 9.0 (6.1) | 7.3 (4.3) | 8.7 (6.0) |
| Acceleration | ||||||
| Maximum Deceleration (°/sec2) | −72.8 (31.4) | −138.2 (69.8) | −133.2 (92.1) | −146.7 (74.3) | −120.9 (93.3) | −153.5 (104.1) |
| Maximum Acceleration (°/sec2) | 83.7 (46.0) | 141.4 (80.2) | 140.8 (95.9) | 166.9 (113.0) | 125.9 (82.4) | 147.1 (88.7) |
| 10th Percentile (°/sec2) | −29.1 (14.5) | −54.0 (36.1) | −43.1 (30.8) | −52.2 (27.5) | −30.8 (17.7) | −42.3 (25.7) |
| 90th Percentile (°/sec2) | 30.5 (15.5) | 57.1 (38.2) | 46.2 (33.6) | 52.4 (27.1) | 33.5 (20.1) | 44.3 (28.5) |
| 99th Percentile (°/sec2) | 75.8 (43.2) | 123.3 (74.8) | 107.1 (73.6) | 133.7 (79.8) | 87.9 (54.4) | 103.0 (63.3) |
| Sample-to-Sample RMSD (°/sec2) | -- Ref -- | 46.4 (23.7) | 41.0 (21.7) | 47.4 (21.3) | 39.6 (18.2) | 42.3 (20.3) |
LMM = Lumbar Motion Monitor; Accel-1= Low passed (zero-phase, 2nd order Butterworth, 3 Hz cutoff) accelerometer based estimate from the IMU secured to the sternum only; Comp-1 = Complementary weighting algorithm-based estimate using accelerometer and gyroscope measurements from the IMU secured to the sternum only; Accel-2 = Low passed (zero-phase, 2nd order Butterworth, 3 Hz cutoff) accelerometer-based estimate calculated as the difference of the estimates provided from the IMU secured to the sternum and L5/S1 body segments; Comp-2 = Complementary weighting algorithm-based estimate calculated as the difference of complementary-based estimates provided from the IMUs secured to the sternum and L5/S1 body segments; HM Analyzer = Manufacturer provided Kalman-based estimate (HM Analyzer) which incorporated raw acceleration, angular velocity, and magnetic field strength information from the IMU located on the sternum and L5/S1 body segments.
Table 2.
Mean (SD) of trunk motion estimates in the lateral bending plane by measurement method for ensemble averages.*
| Summary measure | LMM | Accel-1 | Comp-1 | Accel-2 | Comp-2 | HM Analyzer |
|---|---|---|---|---|---|---|
| Angular Displacement | ||||||
| Maximum to the Left (°) | −2.2 (1.6) | −3.8 (2.6) | −7.9 (4.8) | −4.9 (2.6) | −3.9 (2.0) | −8.5 (5.9) |
| Mean (°) | 0.5 (0.9) | 0.1 (0.8) | 0.0 (1.1) | 0.1 (0.9) | 0.1 (0.7) | 0.0 (2.2) |
| Maximum to the Right (°) | 4.8 (4.1) | 3.8 (2.9) | 8.8 (7.3) | 4.8 (3.6) | 3.4 (2.3) | 8.1 (10.7) |
| 10th Percentile (°) | −1.7 (1.3) | −2.3 (1.7) | −5.4 (3.6) | −2.9 (1.9) | −2.3 (1.5) | −6.4 (4.7) |
| 90th Percentile (°) | 3.7 (3.7) | 2.6 (2.5) | 6.5 (5.6) | 3.3 (2.9) | 2.4 (2.0) | 6.6 (9.7) |
| 99th Percentile (°) | 4.7 (4.1) | 3.8 (2.9) | 8.7 (7.3) | 4.7 (3.5) | 3.4 (2.3) | 8.1 (10.7) |
| Sample-to-Sample RMSD (°) | -- Ref -- | 2.1 (1.3) | 4.4 (2.5) | 2.1 (1.4) | 2.2 (1.3) | 4.2 (3.5) |
| Absolute Value of Velocity | ||||||
| Mean (°/sec) | 1.9 (1.2) | 3.0 (1.7) | 5.3 (3.5) | 4.0 (1.9) | 2.8 (1.3) | 4.5 (3.6) |
| Maximum (°/sec) | 7.4 (4.7) | 12.8 (7.0) | 19.5 (11.5) | 18.2 (8.4) | 11.5 (5.9) | 19.9 (15.4) |
| 10th Percentile (°/sec) | 0.1 (0.0) | 0.2 (0.1) | 0.3 (0.2) | 0.3 (0.2) | 0.2 (0.1) | 0.2 (0.1) |
| 90th Percentile (°/sec) | 5.2 (3.7) | 7.6 (4.4) | 13.9 (9.2) | 10.3 (5.3) | 7.3 (3.8) | 13.2 (11.6) |
| 99th Percentile (°/sec) | 7.3 (4.7) | 12.3 (7.0) | 19.2 (11.6) | 17.5 (8.4) | 11.2 (5.9) | 19.6 (15.5) |
| Sample-to-Sample RMSD (°/sec) | -- Ref -- | 3.2 (1.7) | 6.4 (4.4) | 4.3 (2.1) | 3.3 (1.6) | 5.5 (4.9) |
| Acceleration | ||||||
| Maximum Deceleration (°/sec2) | −38.7 (10.3) | −94.3 (44.3) | −86.8 (35.9) | −150.3 (74.4) | −77.4 (47.3) | −100.6 (72.2) |
| Maximum Acceleration (°/sec2) | 33.6 (14.8) | 95.2 (46.6) | 94.1 (37.3) | 171.8 (99.5) | 88.4 (57.1) | 126.2 (135.3) |
| 10th Percentile (°/sec2) | −10.8 (4.2) | −32.4 (13.5) | −29.2 (13.4) | −50.1 (19.0) | −23.7 (8.9) | −30.7 (16.1) |
| 90th Percentile (°/sec2) | 11.0 (5.0) | 33.3 (15.1) | 29.6 (13.4) | 49.2 (18.8) | 22.9 (8.1) | 30.6 (17.1) |
| 99th Percentile (°/sec2) | 26.3 (13.3) | 73.3 (35.0) | 69.0 (28.6) | 113.0 (47.2) | 56.9 (32.5) | 75.4 (45.6) |
| Sample-to-Sample RMSD (°/sec2) | -- Ref -- | 28.8 (11.3) | 28.1 (9.8) | 43.2 (15.8) | 23.5 (8.3) | 28.0 (13.4) |
Column headers are defined in text and Table 1.
Table 3.
Mean (SD) of trunk motion estimates in the axial rotation plane by (applicable) measurement method for ensemble averages.*
| Summary measure | LMM | HM Analyzer |
|---|---|---|
| Angular Displacement | ||
| Maximum to the Left (°) | −13.0 (6.3) | −22.6 (8.1) |
| Mean (°) | −1.5 (1.1) | −1.3 (2.5) |
| Maximum to the Right (°) | 3.5 (5.2) | 11.8 (10.3) |
| 10th Percentile (°) | −10.9 (5.5) | −16.3 (6.6) |
| 90th Percentile (°) | 3.2 (4.9) | 10.1 (9.0) |
| 99th Percentile (°) | 3.4 (5.2) | 11.8 (10.2) |
| Sample-to-Sample RMSD (°) | -- Ref -- | 6.2 (2.6) |
| Absolute Value of Velocity | ||
| Mean (°/sec) | 4.2 (2.6) | 8.8 (3.8) |
| Maximum (°/sec) | 29.8 (18.0) | 38.1 (15.8) |
| 10th Percentile (°/sec) | 0.0 (0.0) | 0.1 (0.1) |
| 90th Percentile (°/sec) | 0.8 (0.7) | 3.9 (3.1) |
| 99th Percentile (°/sec) | 29.8 (17.9) | 37.9 (15.9) |
| Sample-to-Sample RMSD (°/sec) | -- Ref -- | 9.7 (4.0) |
| Acceleration | ||
| Maximum Deceleration (°/sec2) | −83.0 (49.2) | −156.3 (98.3) |
| Maximum Acceleration (°/sec2) | 164.8 (109.4) | 158.4 (72.9) |
| 10th Percentile (°/sec2) | −27.5 (15.8) | −45.2 (16.8) |
| 90th Percentile (°/sec2) | 20.2 (16.3) | 46.7 (18.3) |
| 99th Percentile (°/sec2) | 141.8 (95.9) | 113.7 (47.8) |
| Sample-to-Sample RMSD (°/sec2) | -- Ref -- | 45.4 (19.4) |
Column headers are defined in text and Table 1.
Pearson correlation coefficients and Bland and Altman evaluations used to assess agreement between the estimates of mean angular displacement and angular displacement variation between the LMM and each measurement method in the flexion/extension and lateral bending motion planes further suggest that the complementary-based estimates provided from the IMUs secured to the sternum and L5/S1 body segments (Comp-2) generally had the greatest agreement with LMM measures than the other measurement methods (Table 4). Overall, stronger correlation coefficients were observed for estimates of mean angular displacement in the flexion/extension plane than estimates of mean angular displacement in the lateral bending plane.
Table 4.
Pearson correlation coefficients (r)a of mean angular displacement and angular displacement variation (90th – 10th percentile) and Bland Altman bias and limits of agreement of mean angular displacement for the flexion/extension, lateral bending, and axial rotation motion planes.*
| Summary Measure | Accel-1 | Comp-1 | Accel-2 | Comp-2 | HM Analyzer |
|---|---|---|---|---|---|
| Flexion/Extension | |||||
| Mean Angular Displacement (r) | 0.87 | 0.87 | 0.84 | 0.83 | 0.80 |
| 90th – 10th Percentile (r) | 0.87 | 0.86 | 0.87 | 0.85 | 0.82 |
| Mean Bias (°) | 3.91 | 3.99 | 1.82 | 1.23 | 1.60 |
| Lower Limit of Agreement (°) | −3.40 | −3.27 | −4.50 | −4.72 | −5.37 |
| Upper Limit of Agreement (°) | 11.22 | 11.26 | 8.14 | 7.17 | 8.56 |
| Upper – Lower (°) | 14.62 | 14.53 | 12.64 | 11.89 | 13.93 |
| Lateral bending | |||||
| Mean Angular Displacement (r) | 0.23b | 0.08c | 0.37 | 0.38 | 0.42 |
| 90th – 10th Percentile (r) | 0.60 | 0.12d | 0.85 | 0.78 | 0.35 |
| Mean Bias (°) | −0.42 | −0.52 | −0.41 | −0.42 | −0.53 |
| Lower Limit of Agreement (°) | −2.56 | −3.19 | −2.44 | −2.27 | −4.39 |
| Upper Limit of Agreement (°) | 1.72 | 2.16 | 1.61 | 1.44 | 3.33 |
| Upper – Lower (°) | 4.28 | 5.35 | 4.05 | 3.71 | 7.72 |
| Axial Rotation | |||||
| Mean Angular Displacement (r) | --- | --- | --- | --- | 0.15e |
| 90th – 10th Percentile (r) | --- | --- | --- | --- | 0.73 |
| Mean Bias (°) | --- | --- | --- | --- | 0.18 |
| Lower Limit of Agreement (°) | --- | --- | --- | --- | −4.95 |
| Upper Limit of Agreement (°) | --- | --- | --- | --- | 5.31 |
| Upper – Lower (°) | --- | --- | --- | --- | 10.26 |
Column headers are defined in text and Table 1.
All Pearson correlation coefficients (r) were statistically significant (p<0.05) unless otherwise noted.
p = 0.18;
p = 0.67;
p = 0.48;
p = 0.38
4. Discussion
Relatively small mean angular displacement RMSD estimates in the flexion/extension, lateral bending, and axial rotation motion planes were observed between the IMU system and the LMM. Strong correlation coefficients in the flexion/extension plane and small Bland and Altman bias estimates in the flexion/extension, lateral bending, and axial rotation planes were observed across a range of experimental conditions that included a variety of movements and work speeds. Although not directly comparable, RMSD estimates from this study were reasonably similar to those reported in studies comparing trunk motion measurements obtained with IMU-based instrumentation systems and other novel monitoring devices (e.g., anthropometry-corrected accelerometers) to optoelectric motion capture systems (Goodvin et al., 2006; Kim and Nussbaum, 2013; O’Sullivan et al., 2012; Plamondon et al., 2007; Van Driel et al., 2013; Wong and Wong, 2008). Overall, the results suggest the IMU system examined in this study may serve as a comparable alternative to other existing instruments for directly measuring thoracolumbar trunk motion in field-based studies.
Errors in thoracolumbar trunk motion measures obtained during field-based assessments may vary based on the applications of interest (e.g., different work activities), characteristics of the individual direct measurement technology components (e.g., noise parameters of sensors), and methods used to estimate and/or summarize motion. One possible limitation of one sensor accelerometer or IMU methods is that trunk inclination with respect to gravity may not fully capture relevant trunk motion information. While some research has been conducted investigating the accuracy of two accelerometer systems (mounted over the sternum and sacrum) to assess trunk flexion (Koehoorn, 2010; Van Driel et al., 2009), it is unclear if methods using two accelerometer or IMU sensors may be a more appropriate for estimating “risk” of adverse health outcomes in comparison to trunk motion estimates from one sensor.
In this study, processing methods that computed thoracolumbar trunk motion as a function of measurements obtained from IMUs secured to both the sternum and L5/S1 body segments were more comparable to the LMM than processing methods that computed thoracolumbar trunk motion as a function of measurements obtained solely from the sternum mounted IMU. For example, the mean 90th percentile angular displacement value estimated by the complementary weighting algorithm-based method (Comp-1) was nearly 15° greater than the estimate obtained with the LMM in the flexion/extension motion plane whereas the two sensor complementary weighting algorithm-based method (Comp-2) was within about 3° of the LMM. When considering that the 90th percentile of angular displacement in the flexion/extension plane is commonly used as an estimate of the ‘peak’ amount of trunk flexion in field studies aimed at estimating exposure to non-neutral working postures associated with musculoskeletal outcomes (e.g., Fethke et al., 2011; Kazmierczak et al., 2005), the results of this study suggest investigators should strongly consider computing thoracolumbar trunk motion as a function of estimates from multiple IMUs rather than using a single accelerometer secured to the sternum. However, future research examining the association between exposures to non-neutral working postures as measured with both one and two sensor methods and adverse health effects such a MSDs is necessary.
Another main finding of this study was that summary measures estimated with fusion algorithms such as the complementary weighting algorithm that combined gyroscope measurements with accelerometer measurements obtained from the IMUs agreed more strongly with summary measure estimates from the LMM than summary measures based solely on measurements from accelerometers. For example, the mean 90th percentile estimates from the two IMU complementary weighting algorithm-based method (Comp-2) consistently agreed more strongly with the LMM than the two accelerometer method (Accel-2) for angular displacement, velocity, and acceleration in both the flexion/extension and lateral bending motion planes. The implication of this result is that use of IMU sensors and fusion algorithms may be an effective method for increasing the accuracy of accelerometer-based motion measurements that are known to be negatively affected by dynamic work processes (Amasay et al., 2009; Brodie et al., 2008; Godwin et al., 2009; Hansson et al., 2001).
Several limitations of this study should be acknowledged. First, although widely used in field studies, the LMM is not considered the “gold-standard” of trunk motion measurement. However, the objective of this study was not to compare IMU estimates of thoracolumbar trunk motion to a “gold-standard” system (i.e., optical motion capture). Rather, we compared two systems used in field-based studies where the IMU is less intrusive than the LMM. Mean angular displacement RMSD estimates may, therefore, be reduced or increased in comparison to an optical motion capture system. Regardless, the conclusions regarding the use of two sensor IMU systems versus one sensor systems and the utility of the fusion algorithms hold. Strengths of this study include data collection across of a range of experimental conditions which allowed comparison of the IMU methods to the LMM across a variety of MMH task conditions. Additionally, the large number of participants (N=36) in comparison to previous, similar studies enhances generalizability and statistical stability.
The manufacturer provided Kalman-based estimate (HM Analyzer) was the only processing method that used the magnetometer measurements obtained with the IMUs in this study, and was therefore the only measurement method used to provide estimates of axial rotation (see Table 3). Performance of the HM Analyzer method may have been affected by ferromagnetic disturbances in the laboratory environment or as a result of the proximity of the IMUs to the LMM during the experimental procedures. However, we visually inspected the calibration quality of the Kalman-based estimate after fitting both sensor systems and monitored signal quality during the MMH task using the HM Analyzer software and observed no evidence that such disturbances transpired. Thus, substantial performance degradation was not believed to have occurred.
While correlation coefficients assessing the linear relationship between the LMM and all of the IMU methods for mean angular displacement and angular displacement variation in the flexion/extension motion plane were strong, correlation coefficients in the lateral bending and axial rotation motion planes were generally weak to only moderately strong. The relatively poor performance of the IMU methods in the lateral bending and axial rotation motion planes are likely the result of a lack of variation between participants in the amount of lateral bending and axial rotation required by the MMH task. Much of the axial rotation movement completed by participants to reach the box may be explained by reaching of the arms and rotation of the pelvis and trunk together.
5. Conclusions
The IMU system evaluated in this study produced estimates of trunk angular displacement that agreed reasonably well with analogous estimates from the LMM and thus is a promising alternative to the LMM for field-based studies. Several features of the IMU system, such as small size, wireless sensors, and data logging capability, are attractive from the perspective of obtaining high quality measurements of trunk motion in field settings. Measurements obtained from IMUs secured to the sternum and pelvis had smaller root-mean-square differences and mean bias estimates in comparison to results obtained with the LMM than results of measurements obtained solely from a sternum mounted IMU. Additionally, fusion of IMU accelerometer measurements with IMU gyroscope measurements was observed to increase comparability to the LMM. Investigators should strongly consider computing thoracolumbar trunk motion as a function of estimates from multiple IMUs using fusion algorithms rather than using a single accelerometer secured to the sternum in field-based studies. Further exploration of fusion algorithms may improve the accuracy of IMU measurements for more complex joints such as the shoulder and/or wrist and documented field use of the IMU system under dynamic working conditions are needed.
Highlights.
Inertial measurement unit estimates agreed with Lumbar Motion Monitor estimates
Use of two inertial measurement units increased comparability
Fusion of accelerometer and gyroscope measurements increased comparability
Acknowledgments
This work was supported by two extramural research grants of the Centers for Disease Control and Prevention / National Institute for Occupational Safety and Health (NIOSH) including the Great Plains Center for Agricultural Health and Safety (Grant no: 5U54OH007548-13A) and a pilot project research training grant from the Heartland Occupational Safety and Health Research Center (Grant no: 5T42OH008491-08).
References
- Amasay T, Zodrow K, Kincl L, Hess J, & Karduna A (2009). Validation of tri-axial accelerometer for the calculation of elevation angles. International Journal of Industrial Ergonomics, 39(5), 783–789. doi: 10.1016/j.ergon.2009.03.005 [DOI] [Google Scholar]
- Bachmann ER Inertial and magnetic tracking of limb segment orientation for inserting humans into synthetic environments, Ph.D. dissertation, Naval Postgraduate School, Monterey, CA, 2000. [Google Scholar]
- Bland JM, & Altman DG (1995). Comparing methods of measurement: why plotting difference against standard method is misleading. The lancet, 346(8982), 1085–1087. [DOI] [PubMed] [Google Scholar]
- Bland JM, & Altman DG (1999). Measuring agreement in method comparison studies. Statistical methods in medical research, 8(2), 135–160. [DOI] [PubMed] [Google Scholar]
- Bland JM, & Altman DG (2010). Statistical methods for assessing agreement between two methods of clinical measurement. International Journal of Nursing Studies, 47(8), 931–936. [Google Scholar]
- Bland M, & Altman D (1986). Statistical methods for assessing agreement between two methods of clinical measurement. The lancet, 327(8476), 307–310. [PubMed] [Google Scholar]
- Brodie MA, Walmsley A, & Page W (2008). Dynamic accuracy of inertial measurement units during simple pendulum motion. Comput Methods Biomech Biomed Engin, 11(3), 235–242. doi: 10.1080/10255840802125526 [DOI] [PubMed] [Google Scholar]
- Burdorf A, & Van Der Beek A (1999). Exposure assessment strategies for work-related risk factors for musculoskeletal disorders. Scandinavian Journal of Work, Environment & Health, 25(suppl 4), 25–30. [PubMed] [Google Scholar]
- Coenen P, Kingma I, Boot CR, Twisk JW, Bongers PM, & van Dieën JH (2013). Cumulative low back load at work as a risk factor of low back pain: A prospective cohort study. Journal of Occupational Rehabilitation, 23(1), 11–18. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cuesta-Vargas AI, Galan-Mercant A, & Williams JM (2010). The use of inertial sensors system for human motion analysis. Phys Ther Rev, 15(6), 462–473. doi: 10.1179/1743288X11Y.0000000006 [DOI] [PMC free article] [PubMed] [Google Scholar]
- da Costa BR, & Vieira ER (2010). Risk factors for work-related musculoskeletal disorders: A systematic review of recent longitudinal studies. Am J Ind Med, 53(3), 285–323. doi: 10.1002/ajim.20750 [DOI] [PubMed] [Google Scholar]
- David GC (2005). Ergonomic methods for assessing exposure to risk factors for work-related musculoskeletal disorders. Occup Med (Lond), 55(3), 190–199. doi: 10.1093/occmed/kqi082 [DOI] [PubMed] [Google Scholar]
- Ferguson S, Gaudes-MacLaren L, Marras W, Waters T, & Davis K (2002). Spinal loading when lifting from industrial storage bins. Ergonomics, 45(6), 399–414. [DOI] [PubMed] [Google Scholar]
- Fethke NB, Gant LC, & Gerr F (2011). Comparison of biomechanical loading during use of conventional stud welding equipment and an alternate system. Appl Ergon, 42(5), 725–734. doi: 10.1016/j.apergo.2010.11.007 [DOI] [PubMed] [Google Scholar]
- Gallagher S, Marras WS, Davis KG, & Kovacs K (2002). Effects of posture on dynamic back loading during a cable lifting task. Ergonomics, 45(5), 380–398. [DOI] [PubMed] [Google Scholar]
- Gallagher A, Matsuoka Y, & Ang WT (2004). An efficient real-time human posture tracking algorithm using low-cost inertial and magnetic sensors, in Proc. IEEE Int. Conf. Robot. Autom., Sendai, Japan, Sep. 28-Oct. 2, 2004, pp. 2967–2972. [Google Scholar]
- Gill K, & Callaghan M (1996). Intratester and intertester reproducibility of the lumbar motion monitor as a measure of range, velocity and acceleration of the thoracolumbar spine. Clinical Biomechanics, 11(7), 418–421. [DOI] [PubMed] [Google Scholar]
- Goodvin C, Park EJ, Huang K, & Sakaki K (2006). Development of a real-time three-dimensional spinal motion measurement system for clinical practice. Medical and Biological Engineering and Computing, 44(12), 1061–1075. [DOI] [PubMed] [Google Scholar]
- Hansson G-Å, Balogh I, Byström J, Ohlsson K, Nordander C, Asterland P, … Skerfving S (2001). Questionnaire versus direct technical measurements in assessing postures and movements of the head, upper back, arms and hands. Scandinavian Journal of Work, Environment & Health, 27(1), 30–40. doi: 10.5271/sjweh.584 [DOI] [PubMed] [Google Scholar]
- Higgins WT (1975). A comparison of complementary and Kalman filtering. IEEE Transactions on Aerospace and Electronic Systems, 11(3), 321–325. [Google Scholar]
- Hoogendoorn WE, Bongers PM, de Vet HC, Douwes M, Koes BW, Miedema MC, Arien GA, Bouter LM (2000). Flexion and rotation of the trunk and lifting at work are risk factors for low back pain: results of a prospective cohort study. Spine, 25(23), 3087–3092. [DOI] [PubMed] [Google Scholar]
- Hoy D, Bain C, Williams G, March L, Brooks P, Blyth F, … & Buchbinder R (2012). A systematic review of the global prevalence of low back pain. Arthritis & Rheumatism, 64(6), 2028–2037. [DOI] [PubMed] [Google Scholar]
- Kalman RE (1960). A new approach to linear filtering and prediction problems. Journal of basic Engineering, 82(1), 35–45. [Google Scholar]
- Kazmierczak K, Mathiassen SE, Forsman M, & Winkel J (2005). An integrated analysis of ergonomics and time consumption in Swedish ‘craft-type’ car disassembly. Appl Ergon, 36(3), 263–273. doi: 10.1016/j.apergo.2005.01.010 [DOI] [PubMed] [Google Scholar]
- Kim S, & Nussbaum MA (2013). Performance evaluation of a wearable inertial motion capture system for capturing physical exposures during manual material handling tasks. Ergonomics, 56(2), 314–326. [DOI] [PubMed] [Google Scholar]
- Koehoorn M (2010). Evaluating Methods to Use the Virtual Corset™ Inclinometer for Trunk Posture and Spinal Compression Measurements. Final Report to WorkSafeBC. [Google Scholar]
- Li G, & Buckle P (1999). Current techniques for assessing physical exposure to work-related musculoskeletal risks, with emphasis on posture-based methods. Ergonomics, 42(5), 674–695. doi: 10.1080/001401399185388 [DOI] [PubMed] [Google Scholar]
- Luinge HJ, & Veltink PH (2005). Measuring orientation of human body segments using miniature gyroscopes and accelerometers. Medical and Biological Engineering and Computing, 43(2), 273–282. [DOI] [PubMed] [Google Scholar]
- Manchikanti L (2000). Epidemiology of low back pain. Pain physician, 3(2), 167–192. [PubMed] [Google Scholar]
- Marras W, Fathallah F, Miller R, Davis S, & Mirka G (1992). Accuracy of a three-dimensional lumbar motion monitor for recording dynamic trunk motion characteristics. International Journal of Industrial Ergonomics, 9(1), 75–87. [Google Scholar]
- Marras W, & Granata K (1995). A biomechanical assessment and model of axial twisting in the thoracolumbar spine. Spine, 20(13), 1440–1451. [DOI] [PubMed] [Google Scholar]
- Marras WS, Ferguson SA, Burr D, Davis KG, & Gupta P (2004). Spine loading in patients with low back pain during asymmetric lifting exertions. The Spine Journal, 4(1), 64–75. [DOI] [PubMed] [Google Scholar]
- Marras WS, Ferguson SA, Gupta P, Bose S, Parnianpour M, Kim J-Y, & Crowell RR (1999). The quantification of low back disorder using motion measures: Methodology and validation. Spine, 24(20), 2091. [DOI] [PubMed] [Google Scholar]
- O’Sullivan K, O’Sullivan L, Campbell A, O’Sullivan P, & Dankaerts W (2012). Towards monitoring lumbo-pelvic posture in real-life situations: Concurrent validity of a novel posture monitor and a traditional laboratory-based motion analysis system. Man Ther, 17(1), 77–83. [DOI] [PubMed] [Google Scholar]
- Paquet VL, Punnett L, & Buchholz B (2001). Validity of fixed-interval observations for postural assessment in construction work. Appl Ergon, 32(3), 215–224. [DOI] [PubMed] [Google Scholar]
- Plamondon A, Delisle A, Larue C, Brouillette D, McFadden D, Desjardins P, & Larivière C (2007). Evaluation of a hybrid system for three-dimensional measurement of trunk posture in motion. Appl Ergon, 38(6), 697–712. [DOI] [PubMed] [Google Scholar]
- Roffey DM, Wai EK, Bishop P, Kwon BK, & Dagenais S (2010). Causal assessment of awkward occupational postures and low back pain: results of a systematic review. Spine J, 10(1), 89–99. doi: 10.1016/j.spinee.2009.09.003 [DOI] [PubMed] [Google Scholar]
- Sabatini AM (2006). Quaternion-based extended Kalman filter for determining orientation by inertial and magnetic sensing. Biomedical Engineering, IEEE Transactions on, 53(7), 1346–1356. [DOI] [PubMed] [Google Scholar]
- Schall MC Jr, Fethke NB, Chen H, & Kitzmann AS (2014). A Comparison of Examination Equipment Used During Common Clinical Ophthalmologic Tasks. IIE Transactions on Occupational Ergonomics and Human Factors, 2(2), 105–117. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Teschke K, Trask C, Johnson P, Chow Y, Village J, & Koehoorn M (2009). Measuring posture for epidemiology: comparing inclinometry, observations and self-reports. Ergonomics, 52(9), 1067–1078. doi: 10.1080/00140130902912811 [DOI] [PubMed] [Google Scholar]
- Trask C, Teschke K, Village J, Chow Y, Johnson P, Luong N, and Koehoorn M (2007). Measuring low back injury risk factors in challenging work environments: an evaluation of cost and feasibility. American journal of industrial medicine, 50(9), 687–696. [DOI] [PubMed] [Google Scholar]
- VanDriel R, Teschke K, Callaghan JP, Trask C, Koehoorn M, and Johnson PW (2009). A Comparison of Trunk Posture Movements: A Motion Capture System and a New Data-Logging Inclinometer. Presented at IEA 2009, 17thWorld Conference on Ergonomics. Beijing, China. [Google Scholar]
- Van Driel R, Trask C, Johnson PW, Callaghan JP, Koehoorn M, & Teschke K (2013). Anthropometry-corrected exposure modeling as a method to improve trunk posture assessment with a single inclinometer. J Occup Environ Hyg, 10(3), 143–154. doi: 10.1080/15459624.2012.757479 [DOI] [PubMed] [Google Scholar]
- van Oostrom SH, Verschuren M, de Vet HC, Boshuizen HC, & Picavet HSJ (2012). Longitudinal associations between physical load and chronic low back pain in the general population: The doetinchem cohort study. Spine, 37(9), 788–796. [DOI] [PubMed] [Google Scholar]
- Vieira ER, & Kumar S (2004). Working postures: a literature review. Journal of Occupational Rehabilitation, 14(2), 143–159. [DOI] [PubMed] [Google Scholar]
- Wagenaar RC, Sapir I, Zhang Y, Markovic S, Vaina LM, & Little TD (2011). Continuous monitoring of functional activities using wearable, wireless gyroscope and accelerometer technology. Paper presented at the Engineering in Medicine and Biology Society, EMBC, 2011 Annual International Conference of the IEEE. [DOI] [PubMed] [Google Scholar]
- Wai EK, Roffey DM, Bishop P, Kwon BK, & Dagenais S (2010). Causal assessment of occupational bending or twisting and low back pain: results of a systematic review. The Spine Journal, 10(1), 76–88. [DOI] [PubMed] [Google Scholar]
- Wai EK, Roffey DM, Bishop P, Kwon BK, & Dagenais S (2010). Causal assessment of occupational lifting and low back pain: results of a systematic review. The Spine Journal, 10(6), 554–566. [DOI] [PubMed] [Google Scholar]
- Walker BF (2000). The prevalence of low back pain: a systematic review of the literature from 1966 to 1998. Journal of Spinal Disorders & Techniques, 13(3), 205–217. [DOI] [PubMed] [Google Scholar]
- Waters TR, Putz-Anderson V, Garg A, & Fine LJ (1993). Revised NIOSH equation for the design and evaluation of manual lifting tasks. Ergonomics, 36(7), 749–776. [DOI] [PubMed] [Google Scholar]
- Wong KC, Lee RY, & Yeung SS (2009). The association between back pain and trunk posture of workers in a special school for the severe handicaps. BMC Musculoskelet Disord, 10(1), 43. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wong WY, & Wong MS (2008). Trunk posture monitoring with inertial sensors. European Spine Journal, 17(5), 743–753. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yun X, & Bachmann ER (2006). Design, implementation, and experimental results of a quaternion-based Kalman filter for human body motion tracking. Robotics, IEEE Transactions on, 22(6), 1216–1227. [Google Scholar]


