How can infectious medical waste be forecasted and transported during the COVID-19 pandemic? A hybrid two-stage method

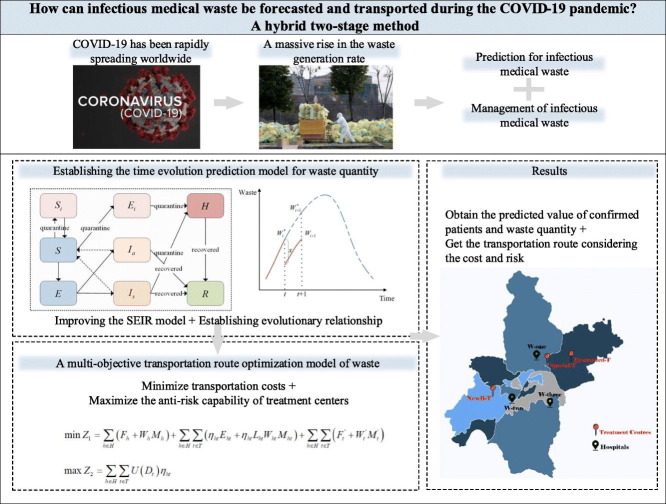
Abstract

The COVID-19 pandemic has caused an unforeseen collapse of infectious medical waste (IMW) and an abrupt smite of the conveying chain. Hospitals and related treatment centers face great challenges during the pandemic because mismanagement may lead to more severe life threats and enlarge environmental pollution. Opportune forecasting and transportation route optimization, therefore, are crucial to coping with social stress meritoriously. All related hospitals and medical waste treatment centers (MWTCs) should make decisions in perspective to reduce the economic pressure and infection risk immensely. This study proposes a hybrid dynamic method, as follows: first to forecast confirmed cases via infectious disease modeling and analyze the association between IMW outflows and cases; next to construct a model through time-varying factors and the lagging factor to predict the waste quantity; and then to optimize the transportation network route from hospitals to MWTCs. For demonstration intentions, the established methodology is employed to an illustrative example. Based on the obtained results, in finding the process of decision making, cost becomes the common concern of decision-makers. Actually, the infection risk among publics has to be considered simultaneously. Therefore, realizing early warning and safe waste management has an immensely positive effect on epidemic stabilization and lifetime health.

Graphical abstract

1. Introduction

Due to the infectious characteristic of the COVID-19 pandemic, social deaths from the virus have been higher than in past years (Jacobson and Jokela, 2021). In addition to the high death toll, the ongoing COVID-19 pandemic has, since its global concern in late 2019, led to social disorders, changes in lifestyle habits and environmental pollution (Wenham et al., 2021). A high-risk infectious rate, a large number of patients and large-scale spread paths have always been typical features of COVID-19. The coronavirus propagates easily via respiratory droplets, close contact and aerosols. Meanwhile, the explosive demand for medical materials and related services has caused a massive rise in the waste generation rate (Kargar et al., 2020). Virus-contaminated infectious medical waste (IMW), such as masks, protective clothing, pharmaceutical packaging and domestic waste, is generated in the process of prevention, control, treatment and recovery, with various potential risks to humans (Hantoko et al., 2021). The peak daily IMW produced in Wuhan City, the epicenter of China, reached 247 tons by 1 March 2020, which is a 5- to 6-fold increase from between 40 and 50 tons (You et al., 2020). Accurate forecasting and reasonable waste transportation will help reduce infectious risk and build an environmental-friendly atmosphere.

All of these special considerations, sudden breakouts, rare occurrences and global scopes, place limitations on the practicality of forecasting waste quantity during the COVID-19 outbreak as urgent social issues. Many previous papers in the waste forecasting field have focused on other types of waste, such as household waste, electronic waste, construction and demolition waste (Song et al., 2017; Althaf et al., 2019; Sunayana et al., 2021; Wang et al., 2021; Johnson et al., 2017). The methods involved in these studies may be listed into several categories: grey model (GM), support vector regression (SVR), logistics forecasting models, nonlinear autoregressive (NAR) models, variational mode decomposition (VMD), exponential smoothing model (ESM) and gradient boosting models. There was one respect, however, in which these modeling methodologies rely on sufficient existing data and have their own disadvantages.

Due to the particularity of infectious medical waste during the epidemic, which is different from general waste, the main difficulty of the existing method is that it cannot be proven correct for its application in the epidemic. Some researchers proposed that the quantity of healthcare hazards is proportional to the confirmed cases, and further, there is informative information about the association between IMW outflows and diagnosed cases as well as a special lagged relationship (Richter et al., 2021). Some authors offered constructive insights to predict COVID-19 trends and patients, which may support more directional and targeted approaches to be provided, so as to forecast the number of IMW in other perspectives. A multi-logistic model method (Devezas and Miranda, 2021) is applied to predict the trend of the COVID-19 pandemic. Furthermore, infectious disease models are used extensively for real-time epidemic forecasting, particularly in the case of COVID-19. Rezapour et al. (Rezapour et al., 2020) modified the susceptible–exposed-infected–recovered (SEIR) model for the transmission of COVID-19 by the Caputo fractional derivative. Pokharel et al. (Pokharel et al., 2021) provided a novel agent based simulation (ABS) model using the SEIR framework to evaluate the effectiveness of manual contact tracing compared to bulletin board contact tracing under COVID-19. Shou et al. (Shou et al., 2021) combined a SEIR epidemic model with non-pharmaceutical interventions to analyze the number of infected patients under different conditions. Annas et al. (Annas et al., 2020) considered isolation and vaccination factors and obtained the basic reproduction numbers of the SEIR model via the generation matrix method. Considering the abundant literature on the SEIR model and the correlation between IMW outflows and diagnosed cases for some time yet, the contributions of the proposed prediction method may be extremely meaningful for the medical and cleaning industry.

Aside from this, appropriate waste management is also crucial to health and safety at all times, let along during the COVID-19 pandemic (Richter et al., 2021). Multi-criteria decision making (MCDM) methods are broadly applied to the process of medical waste management, especially in seeking results regarding management techniques, disposal methods and processing sites aspects (Xiao, 2018; Aung et al., 2019; Dursun et al., 2011; Liu et al., 2013; Narayanamoorthy et al., 2020; Manupati et al., 2021). Although Analytic Hierarchy Process (AHP), Technique for Order Preference by Similarity to Ideal Solution (TOPSIS), VIKOR, fuzzy set theory, grey theory and other decision-making methods are involved in the above researches, the decision-makers are generally considered to be absolutely rational when facing risk. This study singles out the details, which have been neglected in existing relevant studies, and enriches the theories and methods by exploring the bounded rationality from IMW management during COVID-19.

Along with the works listed above, optimization has been actively employed for medical waste collection (Vu et al., 2019; Mantzaras and Voudrias, 2017) and treatment to lessen environmental influences and socioeconomic pressure. Yao et al. (Yao et al., 2019) provided a soft-path solution to meet the medical waste disposal demand in optimal medical waste disposal center sites. And Taslimi et al. (Taslimi et al., 2020) presented a Periodic Load-dependent Capacitated Vehicle Routing Problem (PLCVRP) for the plan of a weekly inventory routing arrangement to carry medical waste to treatment locations. All of the above considered social cost and management risk in the route optimization, which allow us to solve IMW transportation challenges and select medical waste treatment centers (MWTCs) better during COVID-19.

There are growing policy recommendations to cope with severe stress that have arisen with the epidemiological trend. Large quantities of IMW require desperate forecasting and transportation, and both are important to environmental safety and socioeconomics, which are useful to reduce the pressure on hospitals and MWTCs. In response to the ongoing COVID-19 crisis, the United Nations Industrial Development Organization supports medical waste management efforts around the world.

This paper proposes a hybrid two-stage method to achieve accurate prediction and transportation route optimization based on the contributions and deficiencies of existing articles. The remainder of the paper is structured as follows: Section 2 presents a brief introduction to preliminaries. Section 3 proposes the hybrid two-stage method. Section 4 gives a case study to demonstrate the practicability of the presented methodology. Finally, the conclusions are made in Section 5.

2. Preliminaries

This section briefly introduces some basic concepts regarding triangular fuzzy numbers (TFNs), linguistic term sets, and cumulative prospect theory (CPT), which provides a basis for this article.

2.1. Triangular fuzzy numbers and linguistic term sets

TFNs are proposed to solve the problem in an uncertain environment and have an excellent ability to guarantee the completeness of decision information. In this section, we introduce TFNs to describe the language information of experts.

Definition 1. The fuzzy number $\tilde{u}$ is a TFN, and its membership function is expressed as follows by the mathematical method:

$${\mathbb{U}}_{\stackrel{\sim }{u}}\left(x\right)=\left\{\begin{array}{l}0\mathit{if}x<\overline{u}\\ \left(x-\overline{u}\right)/\left(u-\overline{u}\right)\mathit{if}\overline{u}\le x\le u\\ \left(\underset{¯}{u}-x\right)/\left(\underset{¯}{u}-u\right)\mathit{if}u\le x\le \underset{¯}{u}\\ 0\mathit{if}x\ge \underset{¯}{u}\end{array}\right)$$ (1)

where $\overline{u}$ and $\underset{¯}{u}$ are the lower and upper limits of the fuzzy number, and u is the most likely value, then the TFN is expressed as $\tilde{u}=\left(\underset{¯}{u},u,\overline{u}\right)$.

Definition 2. Let $\tilde{u}=\left(\underset{¯}{u},u,\overline{u}\right)$ be a TFN, and the defuzzification value is as follows (Chang, 1996):

$$D\left(\tilde{u}\right)=\left(\underset{¯}{u}+4u+\overline{u}\right)/6$$ (2)

Definition 3. The Euclidean distance can be used to describe the difference value between ${\tilde{u}}_1=\left({\underset{¯}{u}}_1,u_1,{\overline{u}}_1\right)$ and ${\tilde{u}}_2=\left({\underset{¯}{u}}_2,u_2,{\overline{u}}_2\right)$:

$$d\left({\tilde{u}}_1,{\tilde{u}}_2\right)={\left[\left({\left({\underset{¯}{u}}_1-{\underset{¯}{u}}_2\right)}^2+{\left(u_1-u_2\right)}^2+{\left({\overline{u}}_1-{\overline{u}}_2\right)}^2\right)/3\right]}^{1/2}$$ (3)

To realize the transformation between linguistic terms and TFNs, it is necessary to determine the relationship mapping. Let S = {S ₀,  S ₁, ⋯,  S _T} be a fully ordered linguistic item set with an odd number of bases, where S _t is the t+1th language term and T+1 is the base of S. It proposed a method to represent the multi-granularity linguistic information by fuzzy numbers (Jiang et al., 2008).

$$\tilde{u}=\left(\underset{¯}{u},u,\overline{u}\right)=\left(max\left(\left(t-1\right)/T,0\right),\frac{t}{T},min\left(\left(t+1\right)/T,1\right)\right),t=0,1,\cdots ,T$$ (4)

2.2. Cumulative prospect theory

Tversky and Kahneman (Tversky and Kahneman, 1992) proposed CPT, which was developed by prospect theory and expected utility theory. It includes q experts {E ₁,  E ₂, ⋯,  E _k, ⋯,  E _q} and n alternatives {A ₁,  A ₂, …,  A _i, …,  A _n} as well as m criteria {C ₁,  C ₂, …,  C _j, …,  C _m}. As one of the influential behavior decision theories, CPT considers both the psychology and the behavior of decision-makers under risk. It has been increasingly used in abundant and extensive decision-making fields.

It proposed a value function to represent the risk preference, which is described by Eq. (5).

$$\left\{\begin{array}{l}{v}_{\mathit{ij}}^{+}={\left(x\right)}^{\alpha }\mathit{if}x\ge 0\\ v_{\mathit{ij}}^{-}=-\lambda {\left(-x\right)}^{\beta }\mathit{if}x<0\end{array}\right)$$ (5)

where λ is the coefficient of risk aversion, which indicates that decision-makers are more sensitive to losses than to gains, λ > 1; and x < 0 represents the losses, x ≥ 0 represents the gains; α and β are two index parameters that are relevant to gains and losses, respectively, 0 ≤ α ≤ β ≤ 1. According to the previous experiments (Tversky and Kahneman, 1992), we suppose the values of these parameters are α = β = 0.88 and λ = 2.25.

As shown in Eq. (6), the weight function was described. The value function shows that decision-makers are inclined to overrate small probability events while underestimating high and medium possibility events.

$$\left\{\begin{array}{l}{\pi }^{+}\left({\omega }_j\right)={\left({\omega }_j\right)}^{\chi }/\left({\left({\left({\omega }_j\right)}^{\chi }+{\left(1-{\omega }_j\right)}^{\chi }\right)}^{1/\chi }\right)\\ {\pi }^{-}\left({\omega }_j\right)={\left({\omega }_j\right)}^{\delta }/\left({\left({\left({\omega }_j\right)}^{\delta }+{\left(1-{\omega }_j\right)}^{\delta }\right)}^{1/\delta }\right)\end{array}\right)$$ (6)

where χ and δ indicate the attitude of decision-makers toward gains and losses, respectively, χ = 0.61, δ = 0.69; π ⁺(ω _j) and π ⁻(ω _j) are the weight functions.

The cumulative prospect value V _i can be obtained as follows:

$$V_i=\sum _{j=1}^m{v}_{\mathit{ij}}^{+}{\pi }^{+}\left({\omega }_j\right)+\sum _{j=1}^m{v}_{\mathit{ij}}^{-}{\pi }^{-}\left({\omega }_j\right)$$ (7)

3. Problem description

This section gives a detailed description of the proposed hybrid two-stage model and a resolution framework. Moreover, the notations are defined to describe the variables and sets.

3.1. Problem description and resolution framework

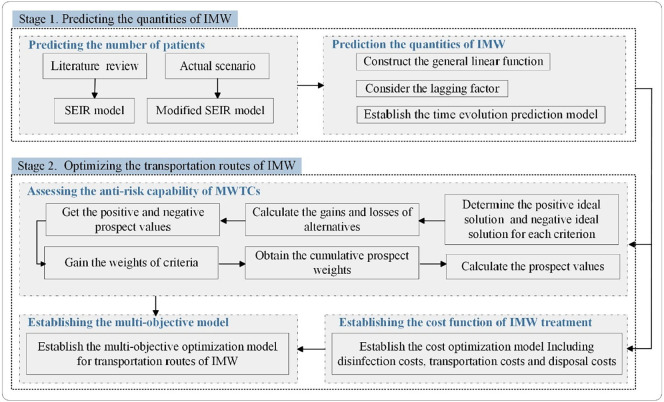
During the epidemic outbreak, there was a surplus of infectious medical waste, which may have resulted in a higher virus risk of individual exposure. Therefore, hospitals first have to collect and transport medical waste to MWTCs. Additionally, MWTCs are supposed to dispose of medical waste quickly. If we can develop a new approach to better predict the amount of medical waste, hospitals and MWTCs may better handle the epidemic. First, the two-stage method proposes a time evolution prediction model to predict the daily waste quantity. Second, with the goal of reducing the total social cost and the infection risk, this paper builds the multi-objective model to realize the optimization of transportation routes and select the appropriate MWTCs for hospitals. Put together, the resolution framework is drawn in Fig. 1 .

Fig. 1.

Resolution framework.

3.2. Notations

The mathematical symbols used in the model are explained as follows:

h is the subscript of the point of hospitals, h = 1, 2, ⋯, H;

t is the subscript of the point of MWTCs, t = 1, 2, …, T;

W_h is the amount of waste generated by the hospital h that is equivalent to the volume initially disinfection by the hospital h;

F_h is the fixed cost of disinfection in the hospital h;

M_h is the unit disinfection cost in the hospital h;

E_ht is the fixed cost of transporting IMW from the hospital h to the treatment center t;

M_ht is the unit cost of transporting IMW from the hospital h to the treatment center t;

L_ht is the distance from the hospital h to the treatment center t;

F_t^' is the fixed disposal cost of IMW in the waste treatment center t;

M_t^' is the unit disposal cost of IMW in the treatment center t.

4. The hybrid two-stage method

4.1. Stage 1: predicting the quantity of infectious medical waste

Predicting the waste quantity involves two major steps: (1) In addition to considering quarantine measures and asymptomatic infected individuals, this paper introduces the effect of exposed individuals on susceptible people and thus establishes an improved SEIR model. This includes selecting an appropriate infectious disease model and then improving it according to the actual situation; (2) Establishing a time evolution prediction model. This step proposes a new function to predict the daily waste quantity accurately based on the confirmed cases and the lagged relationship.

4.1.1. Determining the modified SEIR model

This paper revises the existing dynamic models of epidemic transmission (Tang et al., 2020). Because exposed individuals can transmit risk and asymptomatic infected individuals are infectious but not easily identifiable, we describe the compartments and redefine the interaction relationship between different populations. It covers susceptible(S), exposed(E), infectious(I)and recovered(R)populations in the classic SEIR model. Considering the actual scenario of COVID-19, infectious people fall into two categories: symptomatic(I _s)and asymptomatic(I _a)infected individuals. Considering quarantine measures against infectious diseases, the compartments are further refined as isolated susceptible(S _i), isolated exposed(E _i)and isolated infectious(I _i). Given the circumstances, I _i will be immediately sent to designated hospitals for isolation and treatment, so they are all transformed into hospitalized patients(H). Therefore, S, E, I _s and I _a refer to susceptible, exposed, symptomatic and asymptomatic persons missed in isolation, respectively. The transformation relationship is shown in Fig. 2 . The model assumes that all people can be infected. Quarantined susceptible individuals are transferred back to susceptible people after being released from quarantine. Both infectious and exposed populations have different degrees of ability to infect susceptible people and then turn them into exposed individuals.

Fig. 2.

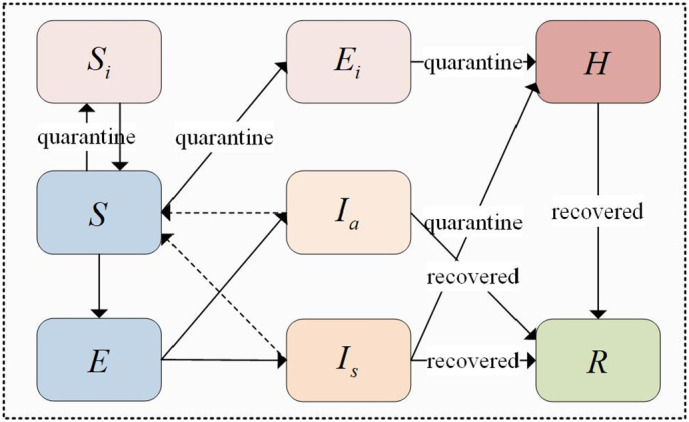
Diagram of the modified SEIR model considering isolation.

The differential equations in Eq. (8) can describe the modified SEIR model.

$$\begin{array}{l}\mathit{dS}/\mathit{dt}=-\left[\mathit{\rho ci}\left(1-{\beta }^{\text{'}}\right)+\mathit{\rho ci}{\beta }^{\text{'}}+\mathit{\rho c}\left(1-i\right){\beta }^{\text{'}}\right]S\left(I_s+{\tau }_{1}E+{\tau }_2{I}_a\right)+{\mathit{rS}}_i\\ \mathit{dE}/\mathit{dt}=\left[\mathit{\rho c}\left(1-i\right){\beta }^{\text{'}}\right]S\left(I_s+{\tau }_{1}E+{\tau }_2{I}_a\right)-{\alpha }^{\text{'}}E\\ {\mathit{dI}}_s/\mathit{dt}={\alpha }^{\text{'}}\mathit{bE}-\left({\mu }_I+d+{\omega }_s\right)I_s\\ {\mathit{dI}}_a/\mathit{dt}={\alpha }^{\text{'}}\left(1-b\right)E-{\omega }_a{I}_a\\ {\mathit{dS}}_i/\mathit{dt}=\left[\mathit{\rho c}\left(1-{\beta }^{\text{'}}\right)i\right]S\left(I_s+{\tau }_{1}E+{\tau }_2{I}_a\right)-{\mathit{rS}}_i\\ {\mathit{dE}}_i/\mathit{dt}=\mathit{\rho ci}{\beta }^{\text{'}}S\left(I_s+{\tau }_{1}E+{\tau }_2{I}_a\right)-{\mu }_i{E}_i\\ \mathit{dH}/\mathit{dt}={\mu }_I{I}_s+{\mu }_i{E}_i-\left(d+{\omega }_h\right)H\\ \mathit{dR}/\mathit{dt}=I_a{\omega }_a+I_s{\omega }_s+H{\omega }_h\end{array}$$ (8)

where i is the isolation ratio; β ^' is the transmission probability; c is the contact rate; ρ is the effective contact coefficient; α ^' is the conversion ratio of exposed people to infectious people. Because the average latency period of the early hypothesis is seven days, the value of α ^' is 1/7; r is the rate of isolation release. So r is equal to 1/14, considering that the average isolation period is 14 days; b is the proportion of individuals with symptoms; μ _I is the rate at which infectious people with symptoms turn into isolated infectious people; μ _i is the rate at which isolated exposed people turn into isolated infectious people; ω _a is the rate at which asymptomatic infected people convert to recovered people; ω _h is the rate at which inpatients convert to recovered people; d is the death rate; τ ₁ is the infection intensity in the exposed people compared to symptomatic infected people; τ ₂ is the infection intensity in the asymptomatic infected people compared to symptomatic infected people. Consider i, β, c, b, μ _I, μ _i, ω _a, ω _h, d > 0, and τ ₁ = τ ₂ = 1.

4.1.2. Establishing the time evolution prediction model

The next step is to establish the prediction function of IMW quantity based on the SEIR model. Predicting waste quantity has been studied in various methods, such as machine learning, neural networks, support vector machines, etc., but all of these need to be built on massive historical data. Although some researchers advised predicting IMW quantity based on the SEIR model, but it did not give a specific modeling method.

To compensate for these deficiencies, this paper proposes the following linear time-varying function between the waste quantity and the SEIR model at time t:

$$W_t=\mathit{\pi \epsilon H}\left(t\right)$$ (9)

where W _t refers to the waste quantity at time t, and ε is the ratio coefficient, which corresponds to the volume of IMW per infected person per day; π is the waste volume correction factor and H(t) is the number of existing confirmed patients at time t. As much waste as there is demand. Liu and Xiao (Liu and Xiao, 2015) described the relationship between healthcare demand and the number of people infected, and we further transform and improve the relationship. Considering the short supply in the early stage of the epidemic, the waste quantity is less than the demand. The supply and demand are matched in the middle and late stages, and then the waste quantity and demand reach an equilibrium state, so the early stage π < 1 and the later stage π = 1.

Nevertheless, the influence of early medical supplies on material demand in later stages should be considered in the linear relationship. For example, if the amount of medical waste at cycle t is W _t ^∗, the number at cycle t+1 would have been W _t+1 ^∗ according to Eq. (9). However, the medical materials in decision cycle t will have a positive impact on t+1, which will change the waste quantity of cycle t+1 to W _t+1 ^∗−x, and x is the lagging effect. Hence, the expected volume at cycle t+1 should be W _t+1 instead of W _t+1 ^∗. The lagging factor is introduced to describe the lagging effect:

$${\chi }_t=\left(W_{t+1}^{\ast }-W_t^{\ast }\right)/W_t^{\ast }$$ (10)

Hereon, the lagging factor χ _t can be either increasing volume or decreasing volume and may change with medical materials at cycle t. For an infected person, there are only two states of transition: recovery or death. No matter which one they become, they no longer have the possibility to infect others. In other words, the virus is effectively blocked in this case. We denote the blocking rate as θ and the cure cycle as σ, which is an integer multiple of the decision-making cycle, then the blocking rate of each cycle can be described as θ/σ. Such a hypothesis would reasonable because the decision-making cycle is small enough (one day). Therefore, we get the recurrence Eq. (11).

W₁ = πεH(1) is the initial waste volume, and H(1) is the initial number of confirmed cases. Eq. (11) is the defined time evolution prediction model for the quantity of IMW.

$$\begin{array}{l}t=1:W_1=\mathit{\pi \epsilon H}\left(1\right)\\ t=2:W_2=\left(1+{\chi }_1\right)\left(1-\frac{\theta }{\sigma }\right)W_1\\ t=3:W_2=\left(1+{\chi }_2\right)\left(1-\frac{\theta }{\sigma }\right)W_2\\ =\left(1+{\chi }_1\right)\left(1+{\chi }_2\right){\left(1-\frac{\theta }{\sigma }\right)}^2{W}_1\\ \cdots \\ t=n:W_n=\prod _{i=1}^{n-1}\left(1+{\chi }_i\right){\left(1-\frac{\theta }{\sigma }\right)}^{n-1}{W}_1\end{array}$$ (11)

4.2. Stage 2: a multi-objective optimization model for the transportation route of infectious medical waste

The discharge of IMW will surge in a short period of time, and the limited area within hospitals cannot meet the preservation demand, so it needs to be transferred to MWTCs as soon as possible. It is important to assess the anti-risk capability of MWTCs to help hospitals choose the right one for waste disposal and thus reduce the infection risk. Meanwhile, reducing the total cost can relieve socioeconomic stress. The transportation network route of IMW involves three major steps: (1) Adopting the CPT to assess the anti-risk capability of MWTCs. (2) Establishing a cost optimization function to relive socioeconomic stress. (3) Based on the cost function and anti-risk capability evaluation results, the multi-objective optimization model is established, and the appropriate MWTC is selected to realize the optimization of the transportation route.

4.2.1. Assessing the anti-risk capability of treatment centers

Step 1 Determine the positive and negative reference points

Choosing the right reference point is vital when we employ CPT. Generally speaking, reference points should be selected from some representative points, such as zero value, average value, peak value and least value. Referring to the idea of the TOPSIS method, we choose the positive ideal solution (PIS) and the negative ideal solution (NIS) as the reference points to reflect the decision maker's risk attitude, which is expressed as R _g ^j and R _l ^j, respectively (Li et al., 2017; Li and Chen, 2018). If the reference point is R _g ^j, decision-makers are often risk seekers because they face losses, otherwise, investors tend to be risk averters. Eq. (2) is employed to deblur TFNs in the decision matrix. Sorting the defuzzification values under each alternative, where the largest value is defined as R _g ^j and the smallest value is defined as R _l ^j.

Step 2 Calculate gains and losses

Let G _ij be the gains, and L _ij be the losses. The distance between each alternative and R _g ^j/R _l ^j is calculated using Eq. (3), which is the L _ij/G _ij.

Step 3 Compute the positive and negative prospect value matrixes of gains and losses

Computing the positive and negative prospect value matrixes V _ij ⁺ and V _ij ⁻ via Eq. (5).

Step 4 Determine the cumulative prospect weights

Eq. (6) is used to determine the cumulative prospect weights.

Step 5 Gain the cumulative prospect values

Calculating the cumulative prospect value V _i for each alternative via Eq. (7).

4.2.2. Establishing the cost optimization function

Because infectious medical materials are different from the other types, hospitals should first perform preliminary sterilizing work to reduce the infection risk during the transport and disposal process. There are various costs involved in the whole process, such as transportation cost, sterilizing cost, disposal cost, etc. We have to consider how to optimize the waste transportation route to minimize the costs of the whole process.

According to the actual situation, the following assumptions are made:

• (i)Hospitals have enough space to store the clinical waste generated each day and can establish primary sites for health-infection;
• (ii)The roads between hospitals and treatment centers are interconnected, and the waste can be successfully transported to the centers;
• (iii)Each treatment center can handle all kinds of IMW, such as discarded protective clothing, masks, contaminated instruments, etc.

The cost optimization model based on the transportation network of hospitals and MWTCs is established as follows:

$$min{Z}_1=\sum _{h\in H}\left(F_h+W_h{M}_h\right)+\sum _{h\in H}\sum _{t\in T}\left({\eta }_{\mathit{ht}}{E}_{\mathit{ht}}+{\eta }_{\mathit{ht}}{L}_{\mathit{ht}}{W}_{\mathit{ht}}{M}_{\mathit{ht}}\right)+\sum _{h\in H}\sum _{t\in T}\left(F_t^{\text{'}}+W_t^{\text{'}}{M}_t^{\text{'}}\right)$$ (12)

Eq. (12) is the optimization model for minimizing costs, including the disinfection, transportation and disposal costs. W _ht is the volume of waste transported from hospital h to treatment center t. η _ht is the binary variable that decides if there is IMW transported from hospital h to treatment center t,η _ht ∈ {0, 1}. $\sum _{h\in H}\left(F_h+W_h{M}_h\right)$ represents the fixed and unit disinfection costs in hospitals. $\sum _{h\in H}\sum _{t\in T}\left({\eta }_{\mathit{ht}}{E}_{\mathit{ht}}+{\eta }_{\mathit{ht}}{L}_{\mathit{ht}}{W}_{\mathit{ht}}{M}_{\mathit{ht}}\right)$ denotes the fixed and unit transportation costs from hospitals to MWTCs. $\sum _{h\in H}\sum _{t\in T}\left(F_t^{\text{'}}+W_t^{\text{'}}{M}_t^{\text{'}}\right)$ shows the fixed and unit disposal costs.

4.3. Building and solving the multi-objective optimization model

It is assumed that the cumulative prospect value of treatment center t is U(D _t), so we can establish the multi-objective optimization model as follows:

$$min{Z}_1=\sum _{h\in H}\left(F_h+W_h{M}_h\right)+\sum _{h\in H}\sum _{t\in T}\left({\eta }_{\mathit{ht}}{E}_{\mathit{ht}}+{\eta }_{\mathit{ht}}{L}_{\mathit{ht}}{W}_{\mathit{ht}}{M}_{\mathit{ht}}\right)+\sum _{h\in H}\sum _{t\in T}\left(F_t^{\text{'}}+W_t^{\text{'}}{M}_t^{\text{'}}\right)$$ (13)

$$max{Z}_2=\sum _{h\in H}\sum _{t\in T}U\left(D_t\right){\eta }_{\mathit{ht}}$$ (14)

Constraints:

$$\sum _{h\in H}{W}_h=\sum _{t\in T}{W}_t^{\text{'}}$$ (15)

$$W_h=\sum _{t\in T}{W}_{\mathit{ht}},\forall h\in H$$ (16)

$$W_t^{\text{'}}=\sum _{h\in H}{W}_{\mathit{ht}},\forall t\in T$$ (17)

$$W_t^{\text{'}}\le {\mathit{CapW}}_t^{\text{'}},\forall t\in T$$ (18)

$$W_t^{\text{'}}\ge 0,\forall t\in T$$ (19)

$$W_{\mathit{ht}}\ge 0,\forall h\in H,\forall t\in T$$ (20)

$${\eta }_{\mathit{ht}}\in \left\{01\right\},\forall h\in H,\forall t\in T$$ (21)

Eq. (13) means to minimize transportation cost. Eq. (14) represents the maximum anti-risk capability; Eq. (15)-Eq. (17) are the flow conservation constraints. Eq. (18) is the capacity constraint of MWTCs. Eq. (19) and Eq. (20) denote non-negative constraints. Eq. (21) gives the domain of variables.

To transform them into a single objective optimization model, the multi-objective problem is resolved by the weighting method (Chen et al., 2008). Assuming that the maximum and minimum values of function Z ₁ are Z ₁ ^max and Z ₁ ^min, respectively, and similarly, the maximum and minimum values of function Z ₂ are Z ₂ ^max and Z ₂ ^min. Then, the membership functions of Eq. (13) and Eq. (14) can be expressed as follows:

$$\varphi \left(Z_1\right)=\left(Z_1^{\max }-Z_1\right)/\left(Z_1^{\max }-Z_1^{\min }\right)$$ (22)

$$\varphi \left(Z_2\right)=\left(Z_2^{\max }-Z_2\right)/\left(Z_2^{\max }-Z_2^{\min }\right)$$ (23)

Assuming that the weight coefficients of functions ϕ(Z ₁) and ϕ(Z ₂) are κ ₁ and κ ₂, respectively, and thus the multi-objective optimization model can be transformed into a single-objective model via the linear weighting method, which can be expressed as follows:

$$max{Z}_3={\kappa }_1\varphi \left(Z_1\right)+{\kappa }_2\varphi \left(Z_2\right)$$ (24)

Finally, Eq. (24) can be solved by intelligent optimization algorithms or optimizing software packages.

5. Illustrative example

5.1. Background

COVID-19 has been rapidly spreading worldwide since December 2019, with a massive surge of infections in a short period, followed by a large amount of medical waste. The waste quantity is closely related to the number of confirmed cases, and the SEIR model-based methods for predicting epidemic diseases have been relatively mature. This paper assumed that COVID-19 was spreading in W city, and the infectious medical waste during the outbreak period was predicted and treated. There are not many centers dedicated to IMW, and the existing MWTCs are unable to meet the treatment needs. In this case, it is necessary to transform general waste treatment centers or to build specialized MWTCs in a short time. IMW is mainly disposed of by three typical MWTCs. Special-T Environmental Engineering Co., Ltd. is the only medical waste treatment company. Forced by the grim situation, with the Ministry of Ecology and Environment's support, the Environmental Protection Bureau transformed W‘s most significant industrial waste treatment plant, Reconstructed-T Environmental Protection Technology Co., Ltd., to help dispose of some medical waste. Meanwhile, W city builds the NewB-T Medical Waste Disposal Center, an emergency MWTC with a daily capacity of 30 tons, within half a month. As many as 40 treatment institutions are receiving COVID-19 patients, which can accommodate 13,605 patients. W-one Hospital, W-two Hospital and W-three Hospital are the most representative hospitals that can treat 1000, 1500, 720 patients, respectively. According to the total amount of waste predicted, the daily waste quantity of each hospital can be calculated.

5.2. Data generation

Based on existing literature (Tang et al., 2020) and the empirical situation, the parameters' values of the improved SEIR model are shown in Table 1 .

Table 1.

Parameters' values of the improved SEIR model.

Parameter	Definitions	Value
i	Isolation ratio	1.8887 × 10−7
β'	Transmission probability	2.1011 × 10−8
c	Contact rate	2
ρ	Effective contact coefficient	0.8
α'	The proportion conversion ratio of exposed people to infectious people	1/7
r	The rate of isolation release	1/14
b	The proportion of people with symptoms	0.86834
μI	The rate at which infectious people with symptoms turn into isolated infectious people	0.13266
μi	The rate at which isolated exposed people turn into isolated infectious people	0.1259
ωa	The rate at which asymptomatic infected people convert to recovered people	0.13978
ωs	The rate at which symptomatic infected people convert to recovered people	0.33029
ωh	The rate at which inpatients convert to recovered people	0.46634
d	Death rate	1.7826 × 10−5
τ1	The infection intensity in the exposed people compared to symptomatic infected people	1
τ2	The infection intensity in the asymptomatic infected people compared to symptomatic infected people	1

Initial values	Definitions	Value
S(0)	Initially unisolated susceptible individuals	11,081,000
E(0)	Initially unisolated exposed individuals	105.1
Ia(0)	Initially asymptomatic infected individuals	53.839
Is(0)	Initially symptomatic infected individuals	27.679
R(0)	Initially recovered individuals	2
Si(0)	Initially isolated susceptible individuals	739
Ei(0)	Initially isolated exposed individuals	1.1642
H(0)	Initially hospitalized patients	1

Infectious diseases require more medical resources, such as masks, goggles, protective suits, disinfectants, etc., than common diseases, so each person produces more medical waste every day. We assumed that each COVID-19 patient produced 4.8 kg of medical waste per day. Additionally, we assume that the patients' medical needs can be met, namely π = 1. Because the transmission of the disease is blocked, whether the patient is cured or dies, the interruption rate of a single decision cycle is 1, θ = 1. It is assumed that patients have a mean cure cycle of 20, so the effective blocking rate of a single cycle is 1/20.

According to previous studies (Zhao et al., 2016) and the actual situation, we determined the cost-related parameters, as shown in Table 2 .

Table 2.

Cost-related parameters.

Treatment centers	Fixed operating cost (￥)	Unit treatment cost (￥/kg)
Special-T	390,000	0.900
Reconstructed-T	380,000	1.000
NewB-T	400,000	0.800

Treatment centers	Fixed transport cost (￥)	Unit transport cost (￥/kg/km)	Capacity (kg/day)
Special-T	1500	0.035	20,000
Reconstructed-T	2000	0.040	30,000
NewB-T	1750	0.050	50,000

Hospitals	Fixed cost (￥)	Unit “health infected” cost (￥/kg)
W-one	3000	0.065
W-two	2000	0.060
W-three	2000	0.060

Distance	W-one	W-two	W-three
Special-T	7.7 km	40 km	50 km
Reconstructed-T	28 km	84 km	19 km
NewB-T	31 km	41 km	41 km

5.3. Results

Based on Eq. (8)-Eq. (11) and the obtained data, the results are calculated.

Data for the criteria of five experts are gathered and concentrated by the weighted average operator. Then, the decision matrix ${\left[\overline{u_{\mathit{ij}}}\right]}_{\mathit{mn}}$expressed by TFNs can be received, as given in Table 3 .

Table 3.

The decision matrix represented by TFNs.

Experts	Criteria	Treatment centers			Expert	Treatment centers
		Special-T	Reconstructed-T	NewB-T		Special-T	Reconstructed-T	NewB-T
Expert 1	Experience and qualification(C1)	(0.75,1,1)	(0.5,0.75,1)	(0.25,0.5,0.75)	Expert 4	(0.5,0.75,1)	(0.5,0.75,1)	(0.75,1,1)
	Equipment and technology(C2)	(0.5,0.75,1)	(0.25,0.5,0.75)	(0.75,1,1)		(0.5,0.75,1)	(0.25,0.5,0.75)	(0.75,1,1)
	Waste disposal site exposure to public(C3)	(0,0.25,0.5)	(0,0,0.25)	(0.25,0.5,0.75)		(0,0,0.25)	(0,0,0.25)	(0,0.25,0.5)
	Area covered by HCW disposed(C4)	(0.25,0.5,0.75)	(0,0.25,0.5)	(0.75,1,1)		(0.25,0.5,0.75)	(0,0.25,0.5)	(0.75,1,1)
	Release with health effects(C5)	(0,0.25,0.5)	(0,0,0.25)	(0.25,0.5,0.75)		(0,0,0.25)	(0,0,0.25)	(0,0.25,0.5)
	Instance from urban area(C6)	(0.25,0.5,0.75)	(0.5,0.75,1)	(0.75,1,1)		(0,0,0.25)	(0,0.25,0.5)	(0.25,0.5,0.75)
	Probability of infection(C7)	(0,0.25,0.5)	(0,0,0.25)	(0.25,0.5,0.75)		(0.25,0.5,0.75)	(0,0.25,0.5)	(0.25,0.5,0.75)
Expert 2	Experience and qualification(C1)	(0.75,1,1)	(0.5,0.75,1)	(0.5,0.75,1)	Expert 5	(0.5,0.75,1)	(0.25,0.5,0.75)	(0.5,0.75,1)
	Equipment and technology(C2)	(0.75,1,1)	(0.5,0.75,1)	(0.75,1,1)		(0.75,1,1)	(0.5,0.75,1)	(0.75,1,1)
	Waste disposal site exposure to public(C3)	(0,0.25,0.5)	(0,0,0.25)	(0.25,0.5,0.75)		(0,0,0.25)	(0,0,0.25)	(0,0.25,0.5)
	Area covered by HCW disposed(C4)	(0.25,0.5,0.75)	(0,0.25,0.5)	(0.5,0.75,1)		(0.25,0.5,0.75)	(0,0.25,0.5)	(0.75,1,1)
	Release with health effects(C5)	(0.25,0.5,0.75)	(0,0.25,0.5)	(0.25,0.5,0.75)		(0.25,0.5,0.75)	(0,0.25,0.5)	(0.25,0.5,0.75)
	Instance from urban area(C6)	(0.25,0.5,0.75)	(0.5,0.75,1)	(0.75,1,1)		(0,0.25,0.5)	(0.25,0.5,0.75)	(0.5,0.75,1)
	Probability of infection(C7)	(0.25,0.5,0.75)	(0,0.25,0.5)	(0.25,0.5,0.75)		(0,0.25,0.5)	(0,0,0.25)	(0,0.25,0.5)
Expert 3	Experience and qualification(C1)	(0.75,1,1)	(0.75,1,1)	(0.5,0.75,1)	Aggregation information	(0.65,0.90,1.00)	(0.50,0.75,0.95)	(0.50,0.75,0.95)
	Equipment and technology(C2)	(0.5,0.75,1)	(0.5,0.75,1)	(0.75,1,1)		(0.60,0.85,1.00)	(0.40,0.65,0.90)	(0.75,1.00,1.00)
	Waste disposal site exposure to public(C3)	(0,0.25,0.5)	(0,0,0.25)	(0,0.25,0.5)		(0.00,0.15,0.40)	(0.00,0.00,0.25)	(0.10,0.35,0.60)
	Area covered by HCW disposed(C4)	(0.25,0.5,0.75)	(0,0.25,0.5)	(0.5,0.75,1)		(0.25,0.50,0.75)	(0.15,0.40,0.60)	(0.50,0.75,0.90)
	Release with health effects(C5)	(0,0.25,0.5)	(0,0,0.25)	(0,0.25,0.5)		(0.10,0.30,0.55)	(0.00,0.10,0.35)	(0.15,0.40,0.65)
	Instance from urban area(C6)	(0,0.25,0.5)	(0.25,0.5,0.75)	(0.5,0.75,1)		(0.10,0.30,0.55)	(0.30,0.55,0.80)	(0.55,0.80,0.95)
	Probability of infection(C7)	(0.25,0.5,0.75)	(0,0.25,0.5)	(0.25,0.5,0.75)		(0.15,0.40,0.65)	(0.00,0.15,0.40)	(0.20,0.45,0.70)

The defuzzification values are calculated according to the decision matrix ${\left[\overline{u_{\mathit{ij}}}\right]}_{\mathit{mn}}$and Eq. (2). After that, the reference points of every MWTC under each criterion are described as follows:

$$\begin{array}{l}{R}_g^j=\left\{R_g^1,R_g^2,\cdots ,R_g^m\right\}\\ =\left\{\underset{1\le i\le n}{max}\left({\tilde{u}}_{i1}\right),\underset{1\le i\le n}{max}\left({\tilde{u}}_{i1}\right),\cdots ,\underset{1\le i\le n}{max}\left({\tilde{u}}_{\mathit{im}}\right)\right\}\\ =\left\{\left(\mathrm{0.650.901.00}\right),\left(\mathrm{0.751.001.00}\right),\left(\mathrm{0.100.350.60}\right),\left(\mathrm{0.500.750.90}\right),\right)\\ \left(\left(\mathrm{0.150.400.65}\right),\left(\mathrm{0.550.800.95}\right),(0.20,0.45,0.70)\right\}\end{array}$$

$$\begin{array}{l}{R}_L^j=\left\{R_L^1,R_L^2,\cdots ,R_L^m\right\}\\ =\left\{\underset{1\le i\le n}{min}\left({\tilde{u}}_{i1}\right),\underset{1\le i\le n}{min}\left({\tilde{u}}_{i1}\right),\cdots ,\underset{1\le i\le n}{min}\left({\tilde{u}}_{\mathit{im}}\right)\right\}\\ =\left\{\left(\mathrm{0.500.750.95}\right),\left(\mathrm{0.400.650.90}\right),\left(\mathrm{0.000.000.25}\right),\left(\mathrm{0.150.400.60}\right)\right),\\ \left(\mathrm{0.000.100.35}\right),\left(\mathrm{0.100.300.55}\right),\left(\left(\mathrm{0.000.150.40}\right)\right\}\end{array}$$

The gains or losses values can be obtained by Eq. (3). The calculation results are as follows:

$$G_{\mathit{ij}}=\left[\begin{array}{l}d\left(A_1,R_g^j\right)\\ d\left(A_2,R_g^j\right)\\ d\left(A_3,R_g^j\right)\end{array}\right]=\left[\begin{array}{l}0.00000.12250.17320.22170.08660.45180.0500\\ 0.12580.29150.29150.33420.25980.22170.2708\\ 0.12580.00000.00000.00000.00000.00000.0000\end{array}\right]$$

$$L_{\mathit{ij}}=-\left[\begin{array}{l}d\left(A_1,R_L^j\right)\\ d\left(A_2,R_L^j\right)\\ d\left(A_3,R_L^j\right)\end{array}\right]=-\left[\begin{array}{l}0.12580.17320.12250.11900.17320.00000.2217\\ 0.00000.00000.00000.00000.00000.23450.0000\\ 0.00000.29150.29150.33420.25980.45180.2708\end{array}\right]$$

After obtaining the gain and loss values, we can determine the prospect values V _ij ⁺ and V _ij ⁻ by Eq. (5).

$$V_{\mathit{ij}}^{+}=\left[\begin{array}{l}0.16820.22140.16430.16030.22140.00000.2738\\ 0.00000.00000.00000.00000.00000.28730.0000\\ 0.00000.34650.34650.38960.31380.50500.3251\end{array}\right]$$

$$V_{\mathit{ij}}^{-}=-\left[\begin{array}{l}0.00000.37300.50260.62150.27691.14640.1726\\ 0.38180.78650.78650.88440.71220.62150.7381\\ 0.38180.00000.00000.00000.00000.00000.0000\end{array}\right]$$

Based on judgments about expert consensus, the weights of criteria are obtained,ω _j = {0.1, 0.1, 0.15, 0.05, 0.25, 0.05, 0.3}. The cumulative prospect weights can be determined by Eq. (6) and expressed as follows:

$${\pi }^{+}\left({\omega }_j\right)=\left[0.18630.18630.22690.13160.29070.13160.3184\right]$$

$${\pi }^{-}\left({\omega }_j\right)=\left[0.17010.17010.21670.11140.29350.11140.3276\right]$$

Finally, Eq. (7) is used to obtain the comprehensive prospect value of each MWTC.

$$V_1=-0.2127,V_2=-0.9166,V_3=0.3831$$

MWTCs sorted in descending order at infectious risk is represented as follows: A ₃ > A ₁ > A ₂. This means that NewB-T is the optimal MWTC, followed by Special-T and Reconstructed-T. For decision-makers, NewB-T is the best solution if only the minimum risk is considered. However, both risk and cost are critical factors in practice, and decision-makers should consider all aspects and then make the final decision.

Eq. (24) is solved using the software package Lingo 18.0, and the multi-objective transportation route optimization result is obtained. The optimal transport route of IMW between three designated hospitals and three MWTCs, when cost and risk are targeted, is obtained. The results indicate that W-one and W-two should transport IMW to Reconstructed-T and W-three should select Special-T.

5.4. Discussion

To reflect the effects of α,β and λ on the anti-risk capability of MWTCs in CPT, Table 4 presents the corresponding results based on different α,β and λ values. From Table 4, we know that parameter values have no influence on the sorting results and have a slight effect on the cumulative prospect values. Therefore, we determine the values of these parameters as α = β = 0.88, λ = 2.25, which is feasible both in theory and in practice.

Table 4.

Anti-risk capability based on different parameter values.

α	β	λ	Vi	Sorting results
0.88	0.88	2.25	V1 = − 0.2127, V2 = − 0.9166, V3 = 0.3831	NewB-T≻Special-T≻Reconstructed-T
0.86	0.86	2.26	V1 = − 0.2225, V2 = − 0.9457, V3 = 0.3910	NewB-T≻Special-T≻Reconstructed-T
0.84	0.84	2.27	V1 = − 0.2328, V2 = − 0.9757, V3 = 0.3989	NewB-T≻Special-T≻Reconstructed-T
0.82	0.82	2.28	V1 = − 0.2328, V2 = − 1.0066, V3 = 0.4070	NewB-T≻Special-T≻Reconstructed-T
0.80	0.80	2.29	V1 = − 0.2551, V2 = − 1.0386, V3 = 0.4153	NewB-T≻Special-T≻Reconstructed-T
0.78	0.78	2.30	V1 = − 0.2671, V2 = − 1.0715, V3 = 0.4236	NewB-T≻Special-T≻Reconstructed-T
0.76	0.76	2.31	V1 = − 0.2799, V2 = − 1.1055, V3 = 0.4321	NewB-T≻Special-T≻Reconstructed-T
0.74	0.74	2.32	V1 = − 0.2933, V2 = − 1.1406, V3 = 0.4408	NewB-T≻Special-T≻Reconstructed-T
0.72	0.72	2.33	V1 = − 0.3074, V2 = − 1.1767, V3 = 0.4495	NewB-T≻Special-T≻Reconstructed-T
0.70	0.70	2.34	V1 = − 0.3224, V2 = − 1.2141, V3 = 0.4584	NewB-T≻Special-T≻Reconstructed-T
0.68	0.68	2.35	V1 = − 0.3382, V2 = − 1.2526, V3 = 0.4674	NewB-T≻Special-T≻Reconstructed-T

Prevention and control measures during an epidemic can affect the transmission probability β, and the development of new drugs and treatments can increase the cure rate ω _h. To reflect the effects of β and ω _h on waste quantity and confirmed patients, Table 5 presents the corresponding results based on different β and ω _h values.

Table 5.

Waste quantity and confirmed patients based on different parameter values.

β	ωh	Maximum waste volume	MaximumH	β	ωh	Maximum waste volume	MaximumH
2.1111−8	0.45634	60,540 kg	38,220	2.1011−8	0.46634	58,680 kg	37,180
2.1211−8	0.44634	62,460 kg	39,300	2.0911−8	0.47634	56,880 kg	36,180
2.1311−8	0.43634	64,450 kg	40,410	2.0811−8	0.48634	55,140 kg	35,210
2.1411−8	0.42634	66,510 kg	41,580	2.0711−8	0.49634	53,450 kg	34,280
2.1511−8	0.41634	68,680 kg	42,820	2.0611−8	0.50634	51,800 kg	33,380
2.1611−8	0.40634	71,000 kg	44,120	2.0511−8	0.51634	50,320 kg	32,530
2.1711−8	0.39634	73,390 kg	45,470	2.0411−8	0.52634	48,850 kg	31,710
2.1811−8	0.38634	75,890 kg	46,880	2.0311−8	0.53634	47,420 kg	30,920
2.1911−8	0.37634	78,490 kg	48,360	2.0211−8	0.54634	46,020 kg	30,140
2.2011−8	0.36634	81,200 kg	49,900	2.0111−8	0.55634	44,660 kg	29,390
2.2111−8	0.35634	84,020 kg	51,520	2.0011−8	0.56634	43,330 kg	28,660

When β = 2.1011⁻⁸, ω _h = 0.46634, we can obtain the predicted results as shown by the bolded data in Table 5 and the dynamic evolution curve of diagnosed patients. As shown in Fig. 3 , the solid line is the trajectory of predictive values, and the dashed line is the real values of Wuhan city, Hubei Province, China during the epidemic. The two curves basically fit in quantity and trend, which can prove the rationality of selected parameters. If the epidemic changes dynamically, we can adjust the parameters to achieve the purpose of prediction.

Fig. 3.

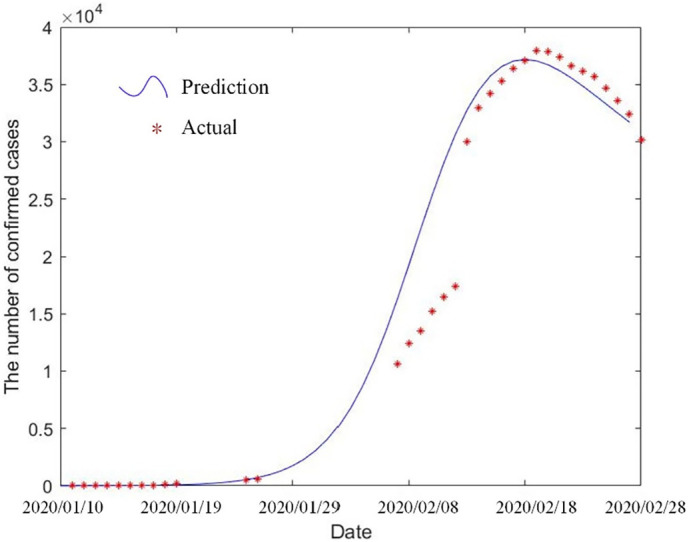
Curve comparison of predicted values and actual values in Wuhan.

6. Conclusions

Due to the specificity, recurrence and universality of COVID-19, this paper correlates waste quantity closely with confirmed cases. Then, based on the relationship, this paper proposes a hybrid two-stage method, which includes a time evolution model for IMW prediction and a multi-objective route optimization model considering risk and cost factors. Several main conclusions are drawn.

First, infectious disease models can be applied to solve many problems, but the model details are heterogeneous by different scenarios and influencing factors. The modified SEIR model considers the isolation measure and asymptomatic infected individuals to modify original approaches, which can further seek the quantitative relationship between waste and confirmed cases to establish the novel forecasting method.

Second, choosing suitable MWTCs and transportation routes may make waste management effectiveness more prominent. The waste route optimization model that takes into consideration infection risk and socioeconomic stress is provided. The model is built and solved based on the predicted values from the previous stage to achieve a dynamic linkage between the two stages.

Third, an illustrative example is given to show the effectiveness of the hybrid two-stage method. Sensitivity analysis is then performed on some of the important parameters, and the predicted values are fitted to the actual values for comparison.

This research has presented evidence that shows that massive infections triggered by the COVID-19 pandemic led to an increase in IMW quantity and to transportation pressures. These problems have been reflected in this paper. The results indicate that infectious medical waste disposal during the pandemic may have been influenced by contagious characteristics, and may cause momentous impacts on transportation routes. Detailed knowledge of waste forecasting and management during emergency events may drastically help to improve management effectiveness. The prediction and management of infectious medical waste widely exist in pandemic challenges around the world. Therefore, there are still many fields for future researches. For example, monetizing the infection risk during the COVID-19 pandemic is an important reference for quantitatively measuring the level of waste risk management. Of course, based on different types of patients with mild, common and severe disease, researchers can also refine the prediction model more precisely.

Biographies

Xin Li is a Ph.D. student at the school of Economics and Management, XiDian University, China. She researches in the areas of Management science and Engineering. And her recent research interests include medical service operation and medical decision-making method.

Xi Chen is a professor at Xidian University, China. She has been engaged in the research and teaching of operation management and management decision making for 12 years. She has presided over and participated in more than 20 scientific research projects and published more than 40 papers in international high-level journals indexed by SCI/SSCI and important journals recognized by the Management Science Department of The National Natural Science Foundation of China. Among them, the Management Science Department of The National Natural Science Foundation of China selected more than 20 papers in important journals, nearly 10 papers in SSCI/SCI journals, and 2 papers won the Best Paper Award at the 7th and 10th BIFE International Academic Conference.

Mujgan Sagir holds her BS and MS degrees from the Anadolu University and the PhD degree from the Eskisehir Osmangazi University in Industrial Engineering and Operations Research program. Her research interest lies in timetabling, cutting stock and assortment problems, and quantitative and qualitative decision making. She has worked as a visiting researcher at the University of Michigan, Ann Arbor (1996–1997), and also the University of Nottingham, UK (May–August 2008). Dr. Sagir is one of the eleven members of the Scientific Research Committee of Eskisehir Osmangazi University, and has been Vice Dean of the Engineering and Architecture Faculty of the same university from 2009 till 2012. She is the coordinator of the Quality Assurance Department of the same university. She also serves as an institutional evaluator of the Turkish Higher Education Quality Council.

Wenbo Zhang is a Ph.D. student at the school of Economics and Management, XiDian University, China. He researches in the areas of Management science and Engineering. And his recent research interests include machine learning and data-driven medical decision making.

Data availability

Data will be made available on request.