Abstract
The active stabilizer bar is used to improve the vehicle's safety when steering at high speeds. In this paper, the spatial dynamics model and nonlinear double-track dynamics model are used to simulate vehicle oscillations. Besides, the nonlinear tire model is also used. This is a completely novel and complex model. Besides, the fuzzy control algorithm is used to control the active stabilizer bar. This algorithm uses two input signals, which are obtained from the simulation. The membership function and fuzzy rules are designed optimally based on the results of many previous simulations and calculations. The simulation process is performed by MATLAB-Simulink software with three specific cases. The results of the paper show that the roll angle of the vehicle body and the change in vertical force at the wheel are significantly reduced when the vehicle uses the active stabilizer bar controlled by the fuzzy algorithm. The rollover phenomenon has been significantly improved in all the investigated cases, corresponding to three specific speeds. The stability and responsiveness of the controller are very high. The fuzzy algorithm can be combined with some other algorithms to improve system efficiency.
Keywords: Active stabilizer bar, Fuzzy control, Rollover, Vehicle dynamics
Graphical abstract
Active stabilizer bar; Fuzzy control; Rollover; Vehicle dynamics.
1. Introduction
When the vehicle moves on the road, the rollover phenomenon may occur. This is a very dangerous problem. The vehicle was determined to roll over when the wheels were lifted off the road (Anh, 2020). At this point, the vertical force at the wheels will approach zero (Anh and Binh, 2020). This phenomenon can negatively affect passengers and cargo on the vehicle. Rollover accidents often have particularly serious consequences. It can even be life-threatening.
There are many causes of the rollover phenomenon. According to Kazemian, this phenomenon occurs when the wheel is exposed to a bump on the road (Kazemian et al., 2017). However, this risk is not high because the size of the bump is usually not too large. In addition, adverse weather conditions can also make the vehicle more prone to rollover (Tian et al., 2021). The above two factors are only external influences. In fact, rollover accidents often happen because the driver makes a sudden turn (Ikhsan et al., 2021). When the vehicle enters a corner or avoids an obstacle, the driver will have to steer. Under the action of centrifugal force, the vehicle body will be tilted. At the same time, a difference in the vertical force of the wheels will also appear (Tuan and Thang, 2020). According to Li and Bei, the centrifugal force is proportional to the square of the speed, so this value will increase very quickly if the vehicle is steering at a high speed (Li and Bei, 2019). Besides, the values of steering angle and steering acceleration also greatly affect the lateral acceleration, which causes the inertia force for the vehicle (Tian et al., 2018). Several solutions have been devised to limit the phenomenon of vehicle rollover. In (Nguyen et al., 2021), Nguyen, et al. analyzed the influence of vehicle size on rollover. The larger the vehicle's height, or the smaller the trackwidth, the more likely it is to roll over. This is true for bulky vehicles. Therefore, it is necessary to optimize the dimensions when designing the vehicle. The second solution is to monitor the vehicle's speed more closely. For today's modern electric vehicles, this is possible (Dong et al., 2021). In addition, the equipping of modern mechatronic systems such as active suspension systems (Nguyen, 2021a; Nguyen et al., 2022a), integrated electronic stability systems (Yim et al., 2012), etc. It also helps to improve the rollover phenomenon. In particular, the solution using a stabilizer bar can be considered the best solution (Parczewski and Wnek, 2017).
Stabilizer bars are commonly used on most vehicles today. There are three types of stabilizer bars, including the mechanical stabilizer bar (passive), the hydraulic stabilizer bar (active), and the electronic stabilizer bar (active) (Nguyen and Hoang, 2021). The passive stabilizer bar has a simple structure, compact size, and reasonable price. However, its stabilizing efficiency is not high (Anh et al., 2020). In (Nguyen, 2021d; Nguyen et al., 2022b), Nguyen presented a new method for determining the impact force generated by the passive stabilizer bar. This method is established based on the displacement of the unsprung mass. There is another simpler method used to calculate the impact force value once the stiffness of the stabilizer bar is known in advance. This method was used by Gosselin-Brisson et al. (Gosselin-Brisson et al., 2009). The active stabilizer bar has a more complex construction. Therefore, its cost is also higher. However, the performance it brings will also be better than the passive stabilizer bar (Tuan and Thang, 2019).
ccording to Nguyen, the hydraulic stabilizer bar consists of a hydraulic motor and two arms (Nguyen, 2021b). This hydraulic motor operates based on the displacement of the servo-valve (Park et al., 2018). The pressure of the liquid inside the system is generated by the axial piston pump (Hilaire et al., 2006). In (Dawei et al., 2018), Dawei, et al. used the PID algorithm to control the operation of the stabilizer bar. The voltage signal generated by the controller will control the process of opening and closing valves on the hydraulic motor. In (Kim et al., 2012), Kim, et al. developed a logic control algorithm for systems with complex hydraulic pumps. The LQR control algorithm to minimize the cost function is also used for the active stabilizer bar (Pourasad et al., 2016). Fuzzy control methods have also been used for the stabilizer bar model by Muniandy et al. (Muniandy et al., 2015; Muniandy et al., 2017). Similarly, Khalil, et al. also introduced a tuning method for the controller of the active stabilizer bar with the Fuzzy-PID algorithm (Khalil et al., 2019). However, these studies rarely address the influence of actuators. The influence of hydraulic actuators is further indicated by Varga et al. with the model of the half-dynamics (Varga et al., 2013) and Nguyen with the model of the spatial dynamics (Nguyen, 2021c, 2021e). In addition, several studies on electronic stabilizer bars have also been published (Kong et al., 2016; Buma et al., 2010; Zhang et al., 2018; Zhen-Xing et al., 2016). The electronic stabilizer bar has a more compact structure than the hydraulic stabilizer bar. However, its cost is higher. The electronic stabilizer bar has lower hysteresis than the hydraulic stabilizer bar. In contrast, the anti-roll moment generated by this bar is more minor. Therefore, it is often used in some modern passenger cars. Overall, the effect of the active stabilizer bar is very positive.
This paper focuses on simulating the vehicle's rollover dynamics. In this research, the model of spatial dynamics is combined with the nonlinear double-track dynamics model. Besides, the nonlinear tire model is also used. This is a very complex dynamic model. A fuzzy control algorithm with two inputs is used for this model. In the first section, some concepts and research are introduced. In the next section, the dynamic model and control algorithm are established. The simulation process and results are analyzed and evaluated in the third section. In the last section, some conclusions are pointed out.
2. Material and method
There are many types of dynamics models used to simulate vehicle oscillation. The authors of (Chu et al., 2015; Richier et al., 2013) used a half-dynamics model in conjunction with a linear single-track dynamics model. This model is quite simple. However, many factors are overlooked. So, its accuracy is not high. In this paper, the author has proposed using the model of spatial dynamics, which considers all influencing factors. Besides, the nonlinear double-track dynamics model is also combined with the model of spatial dynamics. The spatial dynamics model with 7 degrees of freedom is shown in Figure 1.
Figure 1.
Spatial dynamics model with 7 DOF.
Using the object separation method, Eqs. (1), (2), (3), (4), (5), (6), (7), and (8) describing the oscillations of the vehicle are given as follows:
| (1) |
| (2) |
| (3) |
| (4) |
Where:
| (5) |
| (6) |
| (7) |
| (8) |
The lateral acceleration of the vehicle is determined by a nonlinear double-track dynamics model (Figure 2). This model has three degrees of freedom, corresponding to the three directions of vehicle motion. So, we can establish three corresponding equations, including Eqs. (9), (10), and (11).
| (9) |
| (10) |
| (11) |
Figure 2.
Nonlinear double-track dynamics model with 3 DOF.
In this model, the nonlinear deformation of the tire is considered. There are several tire models used to calculate wheel forces, such as the linear tire model (Kissai et al., 2017), the Ammon tire model (Tung, 2021), the Burckhardt tire model (Burckhardt, 1993), the Pacejka tire model (Nguyen, 2020), etc. In particular, the Pacejka tire model has more outstanding advantages. This tire model uses many experimental parameters. The longitudinal force Fx (equation 12), the lateral force Fy (equation 13), and the moment Mz (equation 14) are nonlinear functions, they depend on the value of the vertical force Fz, the slip angle α, the slip ratio sx, vehicle speed v, etc.
| (12) |
| (13) |
| (14) |
The hydraulic actuator operates on the voltage signal provided by the controller. When voltage is applied to the actuator, the internal valves will move. The voltage used for the actuator is usually not more than 24 (V). The process of opening and closing the valves will cause a difference in fluid pressure inside the motor. Therefore, the active stabilizer bar can generate torque on the two arms. Its principle is shown by the following Eqs. (15), (16), and (17):
| (15) |
| (16) |
| (17) |
The schematic diagram of the system is shown in Figure 3.
Figure 3.
Schematic of the system.
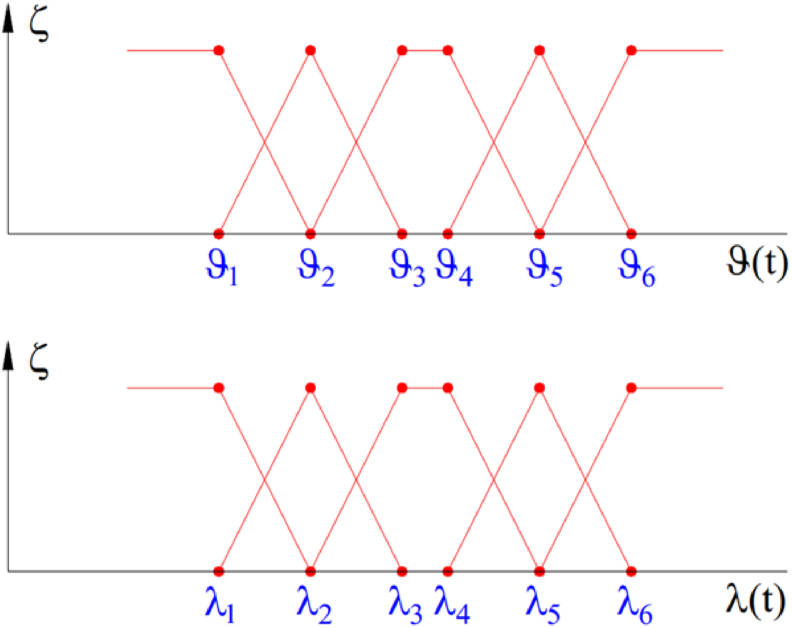
The operation of the hydraulic actuator depends on the control law for which it is designed. In this paper, the fuzzy control law is used. According to fuzzy theory, an intermediate state can exist. The state of the signal can be changed continuously. The membership function of the fuzzy algorithm is proposed by the author in Figure 4. This function has two inputs and one output. The defuzzification process is determined by functions (21) and (22). The defuzzification rule and the membership functions are optimally designed through many previous simulation calculations. In the small oscillation state, no voltage signal will be provided. If the input signals are larger, the voltage signal will change according to the input signal. However, the controller's output signal shall not exceed the acceptability of the actuator.
Figure 4.
Membership function.
Some ideas on modern defuzzification methods can be found in (Pan et al., 2021; Pan et al., 2022). The efficiency of these methods is very high.
The computational process of the fuzzy algorithm is performed based on the TSK model. The output signal of the fuzzy system can be calculated according to the WTAVER formula with equations from (18) to (22):
Where:
| (18) |
| (19) |
| (20) |
| (21) |
| (22) |
The dependence between the output signal and the two input signals is shown in Figure 5. This relationship is determined based on the fuzzy rule, which is shown in Table 1. According to this result, the value of the output signal is maximum when the value of the input signal is maximum. Conversely, if the value of the first input is small and the value of the second input is considerable, the value of the output will be neutral.
Figure 5.
Rule surface.
Table 1.
Fuzzy rule.
| BN | SN | ZE | SP | BP | |
|---|---|---|---|---|---|
| BN | VBN | BN | SN | VSN | ZE |
| SN | BN | SN | VSN | ZE | VSP |
| ZE | SN | VSN | ZE | VSP | SP |
| SP | VSN | ZE | VSP | SP | BP |
| BP | ZE | VSP | SP | BP | VBP |
3. Results and discussions
3.1. Simulation condition
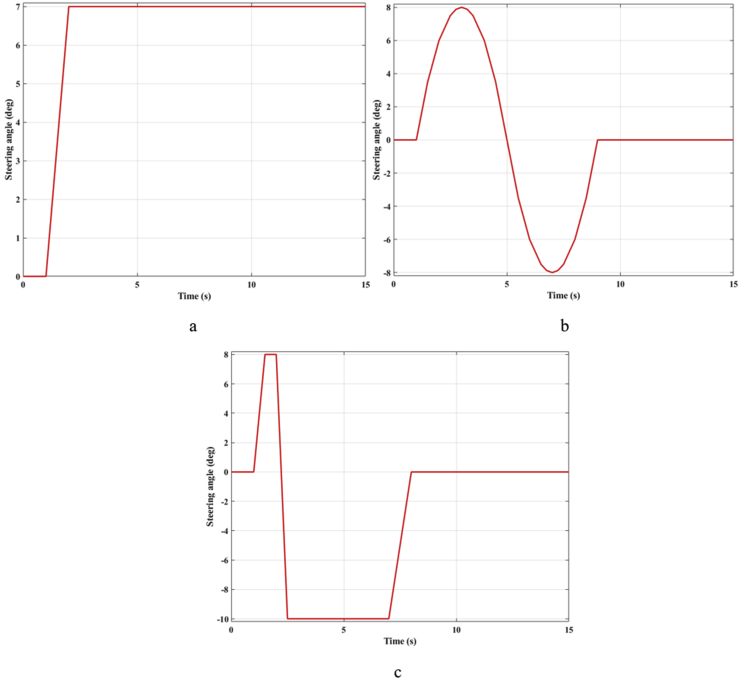
Simulation is performed in the MATLAB environment with specific cases. There are three cases, corresponding to the three steering angles of the vehicle (Figure 6). In each case, the vehicle's speed is increased by three levels: v1 = 60 (km/h), v2 = 80 (km/h), and v3 = 90 (km/h). There are three situations to be considered, including the vehicle using an active stabilizer bar, the vehicle using a passive stabilizer bar, and the vehicle not using a stabilizer bar. With the input parameters of the simulation problem such as speed, steering angle, etc., the output values considered are the roll angle of the vehicle body, vertical force at the wheel, etc. The parameters used for the simulation are given in Table 2.
Figure 6.
Steering angle (a – Case 1; b – Case 2; c – Case 3).
Table 2.
Specification parameters.
| Symbol | Description | Value | Unit |
|---|---|---|---|
| ms | Sprung mass | 1810 | kg |
| muij | Unsprung mass | 52 | kg |
| hφ | Distance from center of gravity to roll axis | 550 | mm |
| hθ | Distance from center of gravity to pitch axis | 550 | mm |
| twi | Half of the track width front/rear axle | 735/730 | mm |
| bi | Distance from center of gravity to front/rear axle | 1250/1670 | mm |
| Jx | Moment of inertia of the x-axis | 690 | kgm2 |
| Jy | Moment of inertia of the y-axis | 2820 | kgm2 |
| Jz | Moment of inertia of the z-axis | 2745 | kgm2 |
| τ | Time constant | 0.005 | s |
| Kv | Servo valve gain | 0.03 | m/A |
| Kqi | Valve flow gain coefficient | 0.02 | m2/s |
| Kce | Total flow pressure coefficient | 4 × 10−11 | m5/Ns |
| Vt | Total volume of trapped oil | 1 × 10−3 | m3 |
| βe | Effective bulk modulus of the oil | 6×106 | N/m2 |
| Dm | Flow per revolution | 1.6 × 10−5 | m3/rad |
| Bm | Viscous friction coefficient | 10 | Nms/rad |
| Jm | Moment of inertia of the hydraulic motor | 3.5 | kgm2 |
3.2. Simulation results
3.2.1. Case 1
In the first case, a "J-turn" steering angle is suggested. This type of steering is usually used when the vehicle enters a corner. The value of the steering angle will increase from zero to the maximum value in a very short time. That is, the steering acceleration is very large. This value will then be preserved.
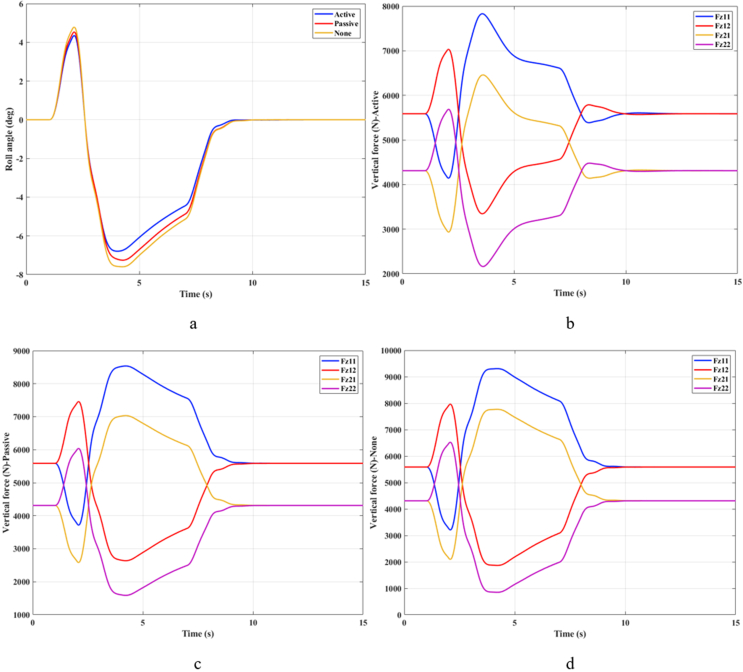
The variation of the roll angle and vertical force at the wheel with time is shown in Figure 7. This result is simulated with an average speed of v1 = 60 (km/h). Because the speed of the vehicle is not great, the change in the values is also not large. The maximum roll angle of the vehicle achieved in three situations is 5.04°, 5.45°, and 5.73°, respectively. After reaching the maximum value, the roll angle tends to decrease over time. Although the speed and steering angle remains constant, these values still decrease gradually. The cause of this phenomenon is the nonlinear deformation of the wheel. The slip angle at the wheel will gradually decrease, which causes its turning radius to increase. Therefore, the roll angle of the vehicle will also decrease over time.
Figure 7.
Results – Case 1 – v1 (a – Roll angle; b – Active; c – Passive; d – None).
As the vehicle's roll angle changes, a difference in vertical forces at the wheels will appear. The vertical force of the inner wheel will decrease. Concurrently, this value for the outer wheel will increase. If the vehicle uses an active stabilizer bar controlled by the fuzzy algorithm, the difference in vertical force is not large. However, if the vehicle is not equipped with a stabilizer bar, this difference is very large.
If the vehicle's speed increases, the change in the above values will also be greater. At v2 = 80 (km/h), the vehicle's roll angle can reach 6.78°, 7.33°, and 7.69°, corresponding to the three situations used (Figure 8). The tendency of these values to change over time is similar to that of the interest rate with velocity v1.
Figure 8.
Results – Case 1 – v2 (a – Roll angle; b – Active; c – Passive; d – None).
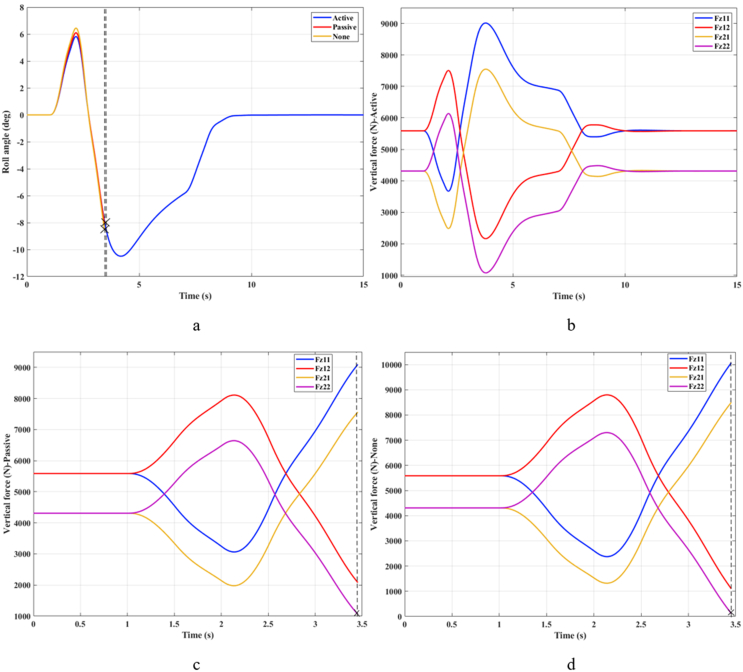
A dangerous situation can occur once the vehicle is moving at a very high speed, v3 = 90 (km/h. According to the results shown in Figure 9, the roll angle of the vehicle can reach 7.54°, 8.14°, and 8.54°. If the vehicle uses an active stabilizer bar, the vehicle's roll angle can be reduced by up to 1o compared to the situation without the stabilizer bar. This difference is quite large.
Figure 9.
Results – Case 1 – v3 (a – Roll angle; b – Active; c – Passive; d – None).
As shown above, the change in vertical force at the wheel characterizes the stability of the vehicle. If this value approaches zero, the wheel will be lifted off the road. At that time, a rollover may occur. This is very dangerous. Based on the results of the simulation, the minimum value of the vertical force corresponding to the three situations is 2254.6 (N), 1256.3 (N), and 419.1 (N), respectively. The vertical force in the third situation is very small. If the speed continues to increase, the rollover will occur. Meanwhile, the stability of the vehicle is still guaranteed if the vehicle is equipped with a stabilizer bar.
3.2.2. Case 2
In the second case, the "Lane Change" steering angle is used (Figure 6b). Compared to the first case, the amplitude of the steering angle, in this case, is larger. However, the steering acceleration is smaller. The difference in values is not too great. This case is used to check the stability of the control system for the stabilizer bar when the steering angle is returned to the original position.
The results of the simulation for the speed v1 are shown in Figure 10. Because the steering angle varies cyclically with time, the values obtained from the simulation also show a cyclical change. However, the value in the second phase will be less than the value in the first phase. The cause of this phenomenon is the nonlinear elastic deformation of the tire, which was explained above. When the steering angle returns to the original position, the value of the vehicle's body roll angle also returns to zero. Therefore, the difference in vertical force at the wheels also needs to be suppressed. A fuzzy control algorithm for the active stabilizer bar can meet this requirement well. This response is ensured by the design of the membership function as well as the fuzzy rule of the controller.
Figure 10.
Results – Case 2 – v1 (a – Roll angle; b – Active; c – Passive; d – None).
At a speed of v2 = 80 (km/h), the value of the roll angle has increased rapidly (Figure 11). This value reached 7.32°, 7.89°, and 8.29° respectively, corresponding to the three situations examined. Besides, the vertical force at the inner wheel is also quickly reduced. This is reduced to 2332.5 (N), 1347.4 (N), and 530.6 (N). This value will decrease more strongly as the velocity increases. This means that the vehicle could roll over at higher speeds without the stabilizer bar.
Figure 11.
Results – Case 2 – v2 (a – Roll angle; b – Active; c – Passive; d – None).
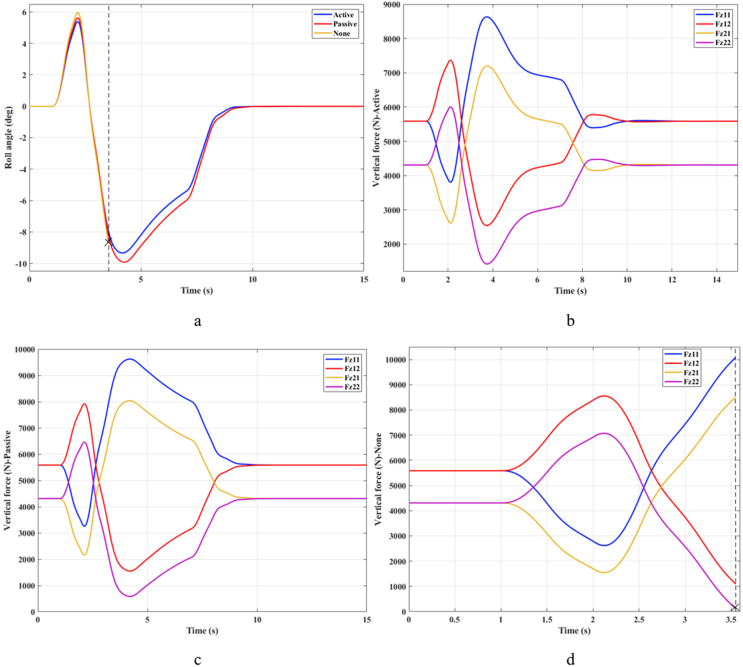
To prove the above point, the simulation process is continued at a very high speed, v3 = 90 (km/h). According to Figure 12, the vehicle would have rolled over at time t = 3.31(s) if the vehicle had not used the stabilizer bar. The vehicle's limited roll angle can reach 9.08°, corresponding to the third situation. The vehicle's limited roll angle can depend on many factors. The stability of the vehicle is still guaranteed in the first two situations: when the vehicle uses an active stabilizer bar and when the vehicle uses a passive stabilizer bar. The maximum roll angle and minimum vertical force values are 8.12° and 8.74°, 2120.5 (N), and 1026.7 (N), respectively.
Figure 12.
Results – Case 2 – v3 (a – Roll angle; b – Active; c – Passive; d – None).
3.2.3. Case 3
To demonstrate the effectiveness of the active stabilizer bar with the fuzzy algorithm, the third case is performed. In this case, a "Double Fishhook" steering angle is applied (Figure 6c). Both the amplitude and acceleration of the steering angle are significantly increased compared to the two cases above.
When the vehicle moves at an average speed, v1 = 60 (km/h), the values of the roll angle and the vertical force at the wheel change greatly (Figure 13). These values correspond to the three situations: 6.79°, 7.26°, and 7.60°, respectively; 2162.6 (N), 1587.0 (N), and 852.1 (N). These values are obtained in the second phase of the oscillation. If the velocities continue to increase, the change will be greater.
Figure 13.
Results – Case 3 – v1 (a – Roll angle; b – Active; c – Passive; d – None).
Once the vehicle was traveling at a high speed, v2 = 80 (km/h), a rollover phenomenon occurred in the third situation (Figure 14). At time t = 3.55 (s), the limited roll angle of the vehicle when it is not equipped with a stabilizer bar is 8.74°. At this time, the vertical force of the rear wheel has reached zero. If the vehicle is equipped with a mechanical stabilizer bar, the maximum roll angle can be up to 9.92°. Besides, the vertical force at the rear wheel has been drastically reduced, to only 584.2 (N). Meanwhile, the values of the first situation remain stable, reaching 9.34° and 1420.9 (N).
Figure 14.
Results – Case 3 – v2 (a – Roll angle; b – Active; c – Passive; d – None).
If the vehicle speed continues to rise to a very high level, the vehicle may roll over completely, even though it is equipped with a passive stabilizer bar (Figure 15). In this case, only the active stabilizer bar controlled by the fuzzy algorithm can keep the vehicle moving safely. The minimum value of the vertical force at the wheel is only about 1074.6 (N), which corresponds to a roll angle of 10.49°. The roll angle of the vehicle in this situation is even greater than the limited roll angle of the second and third situations. Thanks to the active stabilizer bar, the vehicle's stability has been significantly improved.
Figure 15.
Results – Case 3 – v3 (a – Roll angle; b – Active; c – Passive; d – None).
The results of the simulation process are summarized in Table 3.
Table 3.
Simulation results.
| Active | Passive | None | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Case 1 | |||||||||
| v (km/h) | 60 | 80 | 90 | 60 | 80 | 90 | 60 | 80 | 90 |
| φ (deg) | 5.04 | 6.78 | 7.54 | 5.45 | 7.33 | 8.14 | 5.73 | 7.69 | 8.54 |
| Fzmin (N) | 2920.2 | 2448.4 | 2254.6 | 2265.7 | 1560.8 | 1256.3 | 1699.5 | 806.7 | 419.1 |
| Case 2 | |||||||||
| v (km/h) | 60 | 80 | 90 | 60 | 80 | 90 | 60 | 80 | 90 |
| φ (deg) | 5.48 | 7.32 | 8.12 | 5.90 | 7.89 | 8.74 | 6.21 | 8.29 | Rollover |
| Fzmin (N) | 2817.6 | 2332.5 | 2120.5 | 2092.2 | 1347.4 | 1026.7 | 1478.2 | 530.6 | Rollover |
| Case 3 | |||||||||
| v (km/h) | 60 | 80 | 90 | 60 | 80 | 90 | 60 | 80 | 90 |
| φ (deg) | 6.79 | 9.34 | 10.49 | 7.26 | 9.92 | Rollover | 7.60 | Rollover | Rollover |
| Fzmin (N) | 2162.6 | 1420.9 | 1074.6 | 1587.0 | 584.2 | Rollover | 852.1 | Rollover | Rollover |
4. Conclusions
Rollover is a very dangerous phenomenon. This phenomenon occurs when the wheel is completely separated from the road surface. In other words, the vertical force at the wheel will approach zero, i.e., the roll angle of the vehicle will reach its limit value. The consequences of this phenomenon are often very serious. Even the lives of passengers may be at risk. To prevent this, an active stabilizer bar is proposed.
This paper focuses on evaluating the performance of the active stabilizer bar controlled by the fuzzy algorithm. The spatial dynamics model with 7 degrees of freedom is combined with the model of the nonlinear double-track dynamics with 3 degrees of freedom. The nonlinear elastic deformation of the wheel is also considered. A fuzzy algorithm is designed based on the two signals' inputs with an optimal membership function, which is designed based on the designer's point of view and experience. Simulating specific situations and cases are done. The simulation results have shown the superiority of the active stabilizer bar with the intelligent control algorithm used. The values for the roll angle and vertical force at the wheel are significantly reduced when the vehicle is equipped with a hydraulic stabilizer bar. In the investigation cases, the stability and safety of the vehicle are always guaranteed. The phenomenon of rollover has improved significantly.
The dynamics model and control algorithm used in this research is quite complex. However, its effectiveness is very high. In the future, some complex algorithms, such as ANFIS, ANN, etc., can be used to improve the system's performance. Besides, the experimental process is necessary to be able to accurately evaluate the efficiency of the system.
Declarations
Author contribution statement
Duc Ngoc Nguyen: Performed the experiments; Contributed reagents, materials, analysis tools or data; Wrote the paper.
Tuan Anh Nguyen: Conceived and designed the experiments; Performed the experiments; Analyzed and interpreted the data; Contributed reagents, materials, analysis tools or data; Wrote the paper.
Ngoc Duyen Dang: Analyzed and interpreted the data; Wrote the paper.
Funding statement
This research did not receive any specific grant from funding agencies in the public, commercial, or not-for-profit sectors.
Data availability statement
Data will be made available on request.
Declaration of interests statement
The authors declare no conflict of interest.
Additional information
No additional information is available for this paper.
References
- Anh N.T. Predict the rollover phenomenon of the vehicle when steering. Int. J. Mech. Mechatron. Eng. 2020;20(5):31–40. [Google Scholar]
- Anh N.T., Binh H.T. Determining the vertical force when steering. Advances in system science and application. Adv. Syst. Sci. Appl. 2020;20(4):27–35. [Google Scholar]
- Anh N.T., et al. Optimization of the stabilizer bar by using total scores method. Adv. Sci. Technol. Eng. Syst. J. 2020;5(1):431–435. [Google Scholar]
- Buma S., et al. Design and evaluation of a hierarchical control algorithm for an electric active stabilizer bar system. J. Syst. Design Dyn. 2010;4(1):61–76. [Google Scholar]
- Burckhardt M. Vogel Verlag; Würzburg: 1993. Fahrwerktechnik: Radschlupf-Regelsysteme. [Google Scholar]
- Chu D., et al. Mathematical Problems in Engineering 2015. 2015. Smooth sliding mode control for vehicle rollover prevention using active antiroll suspension. [Google Scholar]
- Dawei P., et al. Proceedings of the Institution of Mechanical Engineers, Part D: Journal of Automobile Engineering. Vol. 233. 2018. Design and experimental validation of control algorithm for vehicle hydraulic active stabilizer bar system; pp. 1280–1295. (5) [Google Scholar]
- Dong M., et al. Research on electric vehicle rollover prevention system based on motor speed control. World Elec. Veh. J. 2021;12 [Google Scholar]
- Gosselin-Brisson S., et al. Design of an ative anti-roll bar for off-road vehicles. Shock Vib. 2009;16:155–174. [Google Scholar]
- Hilaire A.S., et al. Pump controlled active roll stabilizer. Int. J. Fluid Power. 2006;7(1):27–40. [Google Scholar]
- Ikhsan N., et al. The effect of vehicle and road conditions on rollover of commercial heavy vehicles during cornering: a simulation approach. Sustainability. 2021;13 [Google Scholar]
- Kazemian A.H., et al. Rollover index for the diagnosis of tripped and untripped rollovers. Lat. Am. J. Solid. Struct. 2017;14:1979–1999. [Google Scholar]
- Khalil M., et al. Improving vehicle rollover resistance using fuzzy PID controller of active anti-roll bar system. SAE Int. J. Passen. Cars-Mech. Syst. 2019;12(1):35–50. [Google Scholar]
- Kim S., et al. Development of control logic for hydraulic active roll control system. Int. J. Automot. Technol. 2012;13(1):87–95. [Google Scholar]
- Kissai M., et al. 2017 2nd IEEE International Conference on Intelligent Transportation Engineering. 2017. A new linear tire model with varying parameters; pp. 108–115. [Google Scholar]
- Kong Z., et al. Design and evaluation of a hierarchical control algorithm for an electric active stabilizer bar system. J. Mech. Eng. 2016;62(10):565–576. [Google Scholar]
- Li B., Bei S. Research method of vehicle rollover mechanism under critical instability condition. Adv. Mech. Eng. 2019;11(1) [Google Scholar]
- Muniandy V., et al. Application of a self-tuning fuzzy PI-PD controller in an active anti-roll bar system for a passenger car. Veh. Syst. Dyn. 2015;53(11):1641–1666. [Google Scholar]
- Muniandy V., et al. Double anti-roll bar hardware-in-loop experiment for active anti-roll control system. J. Vibroeng. 2017;19(4):2886–2909. [Google Scholar]
- Nguyen D.N., et al. Establishing the method to predict the limited roll angle of the vehicle based on the basic dimensions. Math. Model. Eng. Probl. 2021;8(5):775–779. [Google Scholar]
- Nguyen D.N., et al. A novel sliding mode control algorithm for an active suspension system considering with the hydraulic actuator. Lat. Am. J. Solid. Struct. 2022;19(1) [Google Scholar]
- Nguyen D.N., et al. Effect of the passive stabilizer bar on the vehicle’s stability. Model. Simulat. Eng. 2022 2022. [Google Scholar]
- Nguyen T.A. Establishing the dynamics model of the vehicle using the 4-wheels steering systems. Math. Model. Eng. Probl. 2020;4(3):436–440. [Google Scholar]
- Nguyen T.A. Advance the efficiency of an active suspension system by the sliding mode control algorithm with five state variables. IEEE Access. 2021;9:164368–164378. [Google Scholar]
- Nguyen T.A. Control the hydraulic stabilizer bar to improve the stability of the vehicle when steering. Math. Model. Eng. Probl. 2021;8(2):199–206. [Google Scholar]
- Nguyen T.A. Improving the stability of the passenger vehicle by using an active stabilizer bar controlled by the fuzzy method. Complexity. 2021;2021 [Google Scholar]
- Nguyen T.A. New methods for calculating the impact force of the mechanical stabilizer bar on a vehicle. Int. J. Eng. Appl. 2021;9(5):251–257. [Google Scholar]
- Nguyen T.A. Preventing the rollover phenomenon of the vehicle by using the hydraulic stabilizer bar controlled by a two-input fuzzy controller. IEEE Access. 2021;9:129168–129177. [Google Scholar]
- Nguyen T.A., Hoang T.B. Review on the stabilizer bar equipped with the vehicle. J. Mech. Eng. Res. Develop. 2021;44(6):156–161. [Google Scholar]
- Pan Y., et al. A novel mixed control approach for fuzzy systems via membership functions online learning policy. IEEE Trans. Fuzzy Syst. 2021;30(9):3812–3822. [Google Scholar]
- Pan Y., et al. Security-based fuzzy control for nonlinear networked control systems with DoS attacks via a resilient event-triggered scheme. IEEE Trans. Fuzzy Syst. 2022;30(10):4359–4368. [Google Scholar]
- Parczewski K., Wnek H. The influence of vehicle body roll angle on the motion stability and maneuverability of the vehicle. Combust. Engines. 2017;168(1):133–139. [Google Scholar]
- Park H.G., et al. Electro hydrostatic actuator system based on active stabilizer system for vehicular suspension systems. Int. J. Precis. Eng. Manuf. 2018;19(7):993–1001. [Google Scholar]
- Pourasad Y., et al. Design of an optimal active stabilizer mechanism for enhancing vehicle rolling resistance. J. Cent. S. Univ. 2016;23(5):1142–1151. [Google Scholar]
- Richier M., et al. 2013 IEEE Jordan Conference on Applied Electrical Engineering and Computing Technologies. 2013. Rollover prevention of All-Terrain Vehicle during aggressive driving using multi-model observer. Application to ATVs in off-road context; pp. 1–6. [Google Scholar]
- Tian L., et al. A simulation based large bus side slip and rollover threshold study in slope-curve section under adverse weathers. PLoS One. 2021;16(8) doi: 10.1371/journal.pone.0256354. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tian S., et al. An earlier predictive rollover index designed for bus rollover detection and prevention. J. Adv. Transport. 2018 2018. [Google Scholar]
- Tuan A.N., Thang B.H. Research on dynamic vehicle model equipped active stabilizer bar. Adv. Sci. Technol. Eng. Syst. J. 2019;4(4):271–275. [Google Scholar]
- Tuan A.N., Thang B.H. Research on determining the limited roll angle of vehicle. Lecture Notes in Networks and Systems. 2020;104:613–619. [Google Scholar]
- Tung N.T. Setting up the braking force measurement system of the tractor semi-trailer. Eng. Solid Mech. 2021;9:415–424. [Google Scholar]
- Varga B., et al. 14th IEEE International Symposium on Computational Intelligence and Informatics. 2013. Control Design of Anti-roll Bar Actuator Based on Constrained LQ Method. Budapest, Hungary. [Google Scholar]
- Yim S., et al. An investigation into vehicle rollover prevention by coordinated control of active anti-roll bar and electronic stability program. Int. J. Control Autom. Syst. 2012;10(2):275–287. [Google Scholar]
- Zhang Y., et al. SAE Technical Paper; 2018. Sliding Mode Control of Electrical Active Roll Stabilizer Using Switched Reluctance Motor. [Google Scholar]
- Zhen-Xing K., et al. 2016 Chinese Control and Decision Conference. 2016. Design and Simulation of Hierarchical Control Algorithm for Electric Active Stabilizer Bar System; pp. 6069–6074. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
Data will be made available on request.