Upper limit of the transition temperature of superconducting materials

Summary

Why are the transition temperatures (T_c) of superconducting materials so different? The answer to this question is not only of great significance in revealing the mechanism of high-T_c superconductivity but also can be used as a guide for the design of new superconductors. However, so far, it is still challenging to identify the governing factors affecting the T_c. In this work, with the aid of machine learning and first-principles calculations, we found a close relevance between the upper limit of the T_c and the energy-level distribution of valence electrons. It implies that some additional inter-orbital electron-electron interaction should be considered in the interpretation of high-T_c superconductivity.

Graphical abstract

Highlights

• •A materials informatics study on the electronic nature of superconductivity
• •A necessary but not sufficient condition of high-T_c superconductivity
• •A convenient guidance for the exploration of high-T_c superconductors
• •A new clue to the pairing mechanism of high-T_c superconductivity

The bigger picture

For years, physicists were looking for experimental evidence to clarify the microscopic mechanism of high-temperature superconductivity. A core issue here is how the electrons are bound into Cooper pairs. Clues can be found in the patterns of how the transition temperature (T_c) varies. In this work, enlightened by the results of machine learning, we found a close correlation between the superconductivity and electron orbital hybridization. It implies that the electrons at the bottom of the valence band may play a crucial role in the high-T_c superconductivity and perhaps also in the strong correlation behaviors of the exotic metal phase at normal state. We further demonstrate that high-T_c superconductivity needs not only one but two pairing glues. By doing so, many conflicts and confusions in interpreting high-T_c superconductivity may be avoided.

The variation of transition temperature (T_c) in diverse superconducting materials can provide key clues for the understanding of superconductivity. However, it has long been challenging to find hidden key factors affecting T_c. In this work, with the help of machine learning and first-principles calculations, a parameter governing the T_c upper limit of each kind of superconducting materials was discovered. It implies a close relevance between superconductivity and energy-level distribution of valence electrons.

Introduction

Predicting the critical temperature (T_c) of superconductors has long been a great challenge.^1,2,3 Although a number of correlations between T_c and various parameters have already been discovered,^{4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24} it is still a tough job to find new superconductors with higher T_c.

Recently, the utilization of machine learning (ML) techniques inspired high hopes.^25,26,27 ML models using different algorithms were trained to predict the existence of superconductivity and the T_c of superconductors.^{28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54} Progress has been made in several areas, such as how T_c varies with doping,^{28,29,30,31,32,33,34,35} the descriptors indicating superconducting mechanism,^36,37,38,39 structural factors affecting T_c,^43,44 and candidates of new high-T_c superconductors.^46,51 So far, ML models predicting T_c have yielded good predictive scores.^{28,43,44,45,46} The feature variables in those models also indicated some governing factors for high T_c, such as “flat band,” “atomic mass,” and “number of d valence electrons,” which are in good agreement with the human experience.^43,44

However, it is too early to be optimistic because the ML studies have not yet given any successful (experimentally verified) prediction on new high-T_c superconductors, as well as any theoretical inductions beyond human expertise. Even more, the state-of-the-art models by far gave inconsistent results when proposing candidates of high-T_c superconductors. In general, ML is a powerful tool for exploring patterns in the variation of T_c, but ML models need better generalization ability and interpretability to get trustable and useful results.

In this work, we were looking for an approach to reveal key factors affecting the T_c of superconductors. ML and first-principles calculations were exploited to investigate the connection between the T_c and band structure of electrons.

Considering the practical need in materials science, we took the T_c maximum (T_c^max) of each kind of superconducting materials, instead of the T_c of each chemical composition, as the target variable in the ML. The feature variables in the ML are all derived from the electronic orbital characteristics with explicit physical meaning, which is essential for the interpretability of ML model.

Enlightened by the ML results, we found that high-T_c superconductivity has a close connection with the energy-level distribution of valence electrons. Then, based on high-throughput calculations of band structure, a correlation between T_c^max and a band structure parameter in diverse materials was discovered. It can provide convenient guidance for the design of new superconducting materials and a clue to the pairing mechanism of high-T_c superconductivity.

Results

Goal and target variable in machine learning

First of all, the target variable in our ML study is the T_c^max of each type of superconducting materials instead of the T_c of each chemical composition. Here is a domain knowledge that for each type of superconducting materials, there is a maximum of T_c, no matter how the T_c varies with doping, pressure, or gate voltage.

In practice, the T_c^max is often called “T_c” for convenience. But, in fact, the T_c and the T_c^max are of distinct physical meanings and practical application scenes. The key factors affecting T_c and the key factors affecting T_c^max are also quite different (see more details in Table S1).

T_c is the transition temperature of superconductivity for a specimen at a particular chemical composition. It is a physical parameter. Each value of T_c is obtained through one single measurement operation. Particularly, for unconventional superconductors, the variation of T_c with doping or pressure is known as the “phase diagram” of cuprate, iron-based superconductors, or heavy-Fermion superconductors. Physicists are keen to investigate the phase diagrams so as to get a deeper insight into the mechanism of high-T_c superconductivity.

On the other hand, T_c^max is the T_c maximum of each type of superconducting materials. It is a value of material performance. Each type of superconducting material has one T_c^max value. Particularly, in a phase diagram of an unconventional superconductor, the optimal T_c is the T_c^max. Driven by the desire to find room temperature superconductors, materials scientists are more interested in the variation of T_c^max.

In fact, for the issue of T_c, there are two different but equally important questions: (1) how to understand the phase diagram of unconventional superconductors. Or, in other words, for one type of materials, how the T_c varies with doping, pressure, gate voltage, or other conditions. (2) How the T_c^max varies in different types of materials. During the past decades, there have been plenty of experimental and theoretical achievements on the first question^3,55 but much less on the second one. In this work, we focus on question two, searching for unknown patterns in the data of T_c^max. Accordingly, the T_c^max is taken as the target variable in our ML investigation.

Dataset and data distribution in machine learning

The dataset of T_c^max is a subset of the dataset of T_c, which was derived from the SuperCon database of NIMS.⁵⁶ For the dataset-T_c, the entries with doubtful T_c values, obvious typing errors in the chemical formula, and T_c = 0 K were all removed. A few well-known or newfound superconductors^57,58 were added, but the superconductors at ultrahigh pressure (e.g., H₃S, LaH₁₀) are not included. Thus, dataset-T_c has 12,196 entries.

To get the dataset-T_c^max, superconductors in dataset-T_c were categorized into 1,000+ groups, according to the chemical composition (please see more details experimental procedures). In each group, the superconductor having the highest T_c (regarded as the T_c^max of a type of materials) was picked out. The dataset-T_c^max has 1,008 entries.

Twenty-four most-concerned superconductors (see Table S2) were chosen as the test data (unseen during model training) to assess the models’ generalization ability. The close neighbors of those 24 superconductors were taken out from the dataset-T_c^max. Here, “close neighbor” means a small Manhattan distance (<1.5) in the chemical composition (elemental contents) space. At last, a subset of T_c^max was used to train the models. The subset-T_c^max has 957 entries.

It should be stressed that the data distribution is vital for the model’s performance. For the ML models predicting superconductors, their generalization ability is often in suspense because of imbalanced data distribution, including data bias, dataset shift, and clustered data distribution. Both the data bias and dataset shift are due to the fact that the explored superconductors are only a small proportion of all explored materials. Specifically, there are about 200,000 entries in ICSD,⁵⁹ belonging to 70,000+ materials, while a typical dataset of T_c derived from SuperCon⁵⁶ usually has 10,000+ entries after data washing, belonging to about 3,000 materials. For the dataset-T_c, some elements (e.g., Cu, O, Fe, As, Se, H) dominate in high-T_c superconductors, leading to a significant data bias. Meanwhile, when predicting new materials, the chemical composition of each candidate (data to be predicted) would be quite different from those of explored superconductors (train and test data), which is a significant dataset shift. Meanwhile, in the dataset-T_c, many data are of the same material with different doping contents. The chemical composition of those data are close, resulting in a clustered data distribution. Imbalanced data distribution often causes overfitting. There is a good chance to get a model having a high predictive score on the test data, but the model may be no longer good when predicting new materials. It is hard to get a reliable and trustable ML model until the data distribution is improved.

In this work, the data distribution of the dataset-T_c and the subset-T_c^max are quite different. It can be seen in Figure 1 that the unconventional superconductors (only three materials families, i.e., cuprates, iron-based, and heavy-Fermion superconductors) account for nearly 52% of the total, and the high-T_c superconductors are only a small part of the total. It is an obvious data bias. It can be seen in Figure 2 that the data distribution of the dataset-T_c is highly clustered. A majority of data have at least one close neighbor (Manhattan distance <1 in chemical composition space). Whereas, in subset-T_c^max, the Manhattan distance of any neighbors is larger than 1.5, which means the data distribution is quite dispersed. Models trained with subset-T_c^max are supposed to be more trustable because of better data distribution, and the predictive score on the test data (24 most-concerned superconductors) is a good measure of the generalization ability due to the long extrapolation distances (in other words, dispersed data distribution).

Figure 1.

Data distribution of dataset-T_c and dataset-T_c^max

(A) Number of entries for different materials families.

(B) Number of entries in different range of T_c. Yellow: dataset-T_c; green: dataset-T_c^max.

Figure 2.

Data distribution of different datasets and extrapolation distances of different test sets

(A) Data distribution of dataset-T_c (for each data in dataset-T_c, find its nearest neighbor in dataset-T_c).

(B) Data distribution of dataset-T_c^max (for each data in dataset-T_c^max, find its nearest neighbor in dataset-T_c^max).

(C) Extrapolation distances from train set to test set (randomly 15%) for the dataset-T_c (for each data in the test set, find its nearest neighbor in the train set).

(D) Extrapolation distances from subset-T_c^max to the test set (24 most concerned) (for each data in the test set, find its nearest neighbor in subset-T_c^max).

“Rounded nearest distance” means the nearest distance values are rounded to one decimal place. For each data, the nearest distance (d_n) means the Manhattan distance in chemical composition space (elemental contents as the axes) between it and its closest neighbor within the dataset. The d_n >10 part is not shown for clarity.

Feature design and feature selection in machine learning

For the feature set, all features are denoted as “[orbital attribute].[shells selection].[math operator 1].[math operator 2]”, where [orbital attribute] means what attribute of the orbitals is considered, and [shell selection] means which electron shells are considered. As shown in Figure 3, three [orbital attribute], nine [shells selection], and seven [math operator] were defined by a few simple rules. Discarding the features containing empty values and the features having zero variance, we got 441 usable features, each of which has explicit physical meanings.

Figure 3.

An example of features extraction

“E.s.min.wavg” represents the weighted average value of the E_s^min for each element in a chemical formula, where E_s^min means the minimum value of the energy level of valence s shell(s) in an element.

After feature selection, a feature subset consisting of 4 features was selected to train the final model. More details of feature design and feature selection can be found in the experimental procedures and Tables S3–S6.

Results of machine learning model

Figure 4 shows the result of the final model. The coefficient of determination (R²) on the test data (24 most-concerned superconductors) is 0.84. This value is not as high as those in previous ML studies (R² is often better than 0.9), but please note that the extrapolating distance of our test data (Manhattan distance >1.5) is much larger than usual. In this case, our R² can be considered a reliable indicator of the generalization ability, especially for the prediction of new materials.

Figure 4.

Results of the ML model predicting T_c^max

(A) Plot of predicted T_c^max versus measured T_c^max.

(B–E) Plots of T_c^max versus selected features.

Colored circles: train data (subset-T_c^max, 957 superconductors), red: cuprates, orange: iron-based, blue: heavy Fermion, and green: others. White dots: test data (24 most-concerned superconductors).

According to the features in the final model, we can learn useful information. It can be seen in Figures 4B and 4C that for the feature “Nu.all.wavg.wavg” as well as “Nu.outer.min.wavg,” all cuprates have similar values. “Nu.all.wavg” means the weighted value of the unfilled number of all the valence electron shells in each element, while “Nu.outer.min” means the minimum of the unfilled number of the outer valence electron shells (s and p shells) in each element.

As most high-T_c superconductors are cuprates, those two features are of much importance because they indicate some unique characteristics of cuprates. Unfortunately, we cannot know whether they are associated with the origin of high T_c because the cuprates have many unique characteristics, but not every of those characteristics is associated with high T_c.

Meanwhile, for the other two features, “E.all.range.range” and “E.s.sum.range” (Figures 4D and 4E), there is a monotonic trend in the T_c^max-feature plot, respectively. The T_c^max only can reach high values when the values of those two features are large. It is a necessary but not sufficient condition of high T_c^max. In other words, it defines an upper ceiling of the T_c^max.

The latter two features are of importance in physics. For each element, “E.all.range” means the span of the energy level of all valence electron shells, and “E.all.range.range” for a crystal is comparable to the width of the valence band in crystal. “E.s.sum” for a crystal means the summary value of the energy level of valence s shells, and “E.s.sum.range” for a crystal is basicaflly determined by the energy level of the deepest valence s shell in the whole crystal, which is usually at the bottom of the valence band.

As those two features are both derived from the energy-level distribution of valence electrons, and they can be traced to particular electron shells, further discussion would better be made based on the band structure of crystals.

Correlation between T_c^max and a band structure parameter

First-principles calculations were performed to see the energy-level distribution in the energy band of various superconductors (more details can be found in data and code availability). After checking tens of well-known superconductors, we found a band characteristic parameter corresponding to the selected features in the final ML model.

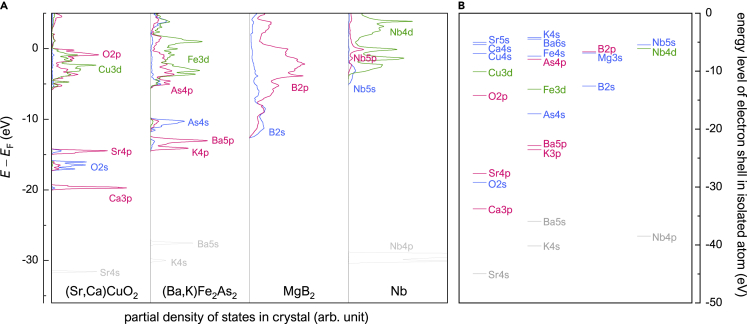
Figure 5 shows the orbital distribution characteristics of four representative superconductors. It can be seen that for a typical high-T_c superconductor, (Sr,Ca)CuO₂, there is an orbital coupling at the bottom of the valence band, between O 2s and Sr 4p (Ca 3p). Particularly, for all cuprates, the O 2s shell has a deep energy level, leading to a large value of “E.s.sum.range.” Meanwhile, the energy level interval between O 2s and O 2p shells is large, hence the value of “E.all.range.range” is large.

Figure 5.

Band structure characteristics of four typical superconductors: (Sr,Ca)CuO₂ (T_c^max = 110 K), (Ba,K)Fe₂As₂ (T_c^max = 38 K), MgB₂ (T_c^max = 40 K), and Nb (T_c^max = 9.3 K)

(A) Partial density of electron states in crystals. E is the energy level of electrons, and E_F is the Fermi-level.

(B) Energy-level distribution of electron shells in isolated atoms. Zero energy is of the state of complete free electrons. Colored lines: valence shells (blue: s shells, red: p shells, green: d shells). Gray lines: core shells.

It is also can be seen from Figure 5B that the energy levels of those involved orbitals can be roughly estimated according to their corresponding energy levels in isolated atoms,⁶⁰ which are used as the input data in the feature design of ML. Thus, the results of ML and band structure simulation are mutually verified. They both indicate a materials-dependent law about the variation of T_c^max.

As shown in Figure 6, there is a monotonous trend of T_c^max for various superconductors. It can be expressed as high T_c^max asks for larger ΔE. This trend is universal because each data shown in Figure 6 represents not only itself but also a series of similar materials (e.g. “Y-123” is not only YBa₂Cu₃O₇; it also represents all LnBa₂Cu₃O₇, Ln = rare-earth elements). So, Figure 6 actually covers hundreds of superconducting materials, including all superior superconductors (T_c^max > 15 K) as far as we know.⁵⁷

Figure 6.

Dependence of T_c^max on a characteristic parameter of the energy-level distribution of valence electrons (ΔE)

ΔE represents the energy-level interval between the lowest unsaturated orbitals and the highest saturated orbitals (or the coupled orbitals at the bottom of valence band). “HP” means high pressure. The green dashed line is an upper ceiling of T_c^max. Inset: a schematic illustration of the band characteristics, ΔE, for different superconductors. The red dash lines are a guide to the eye.

Like many well-known T_c laws (see Table S7), the T_c^max-ΔE trend in Figure 6 is informative. Here, ΔE represents the energy level interval between the hybridized valence orbitals, usually the lowest unsaturated shell (LUS) and the highest saturated shell (HSS). ΔE is related to the magnitude of orbital hybridization, orbital coupling, and orbital interactions.

For instance, among all known superconductors at ambient pressure, the cuprates have the deepest valence band. Particularly, the superconductors T_c^max >100 K are all Ca-containing cuprates (e.g., Hg-1223, Bi-2223), in which the calcium ions are sandwiched between Cu-O planes. The energy level of the HSS of Ca (i.e., Ca 3p; see Figure 5A) is deeper than that of most other elements. It is often overlooked that the Ca 3p and O 2s orbitals are also valence orbitals. Although their energy levels are as deep as about 15–20 eV below the Fermi level, they still can participate in orbital hybridization and coupling.

Furthermore, after checking the crystalline structures of those superconductors, we found that in addition to the energy level of the involved electron orbitals, the atomic distance of the two involved ions also matters. For instance, as shown in Table 1, a parameter λ is defined as “λ = d – r₁ – r₂” to compare the bond length in different crystals. Smaller λ means a compacted lattice and usually stronger orbital coupling. It can be seen that the λ of Ca–O bond in Ca-containing cuprates is much smaller than that in other Ca-containing superconductors. It also can be seen in Table 2 that for some compounds having similar crystalline structures (La-214), smaller λ (more compacted lattice) leads to higher T_c^max.

Table 1.

A comparison of several Ca-containing materials

Material	X	Involved orbitals	Eorb (eV)60	dCa-X (pm)59	rX (pm)a	λ (pm)	Tcmax (K)
CaO	O	Ca 3p – O 2s	−29.17	239	140	0	N/A
Ca (ambient pressure)	Ca	Ca 3p – Ca 3p	−33.77	395	99	197	N/A
CaLi256	Ca	Ca 3p – Ca 3p	−33.77	383	99	185	13
Ca (216 GPa)b	Ca	Ca 3p – Ca 3p	−33.77	231c	99	33	29
Bi2Sr2Ca2Cu3O10-xd	O	Ca 3p – O 2s	−29.17	252	140	13	110
HgBa2Ca2Cu3O9-x57	O	Ca 3p – O 2s	−29.17	236	140	−3	134

“X” represents the neighboring atom of Ca. E_orb is the energy level of the involved orbital in X. d_Ca-X is the bond length. r_Ca and r_X are ionic radii of Ca and X, respectively. λ = d − r_Ca − r_X is a characteristic parameter for the Ca–X bond.

^aPauling ionic radii.

^bHamlin.⁶¹

^cDFT simulated value.

^dChu, et al.⁶²

Table 2.

A comparison of several O-containing materials

Parent compound	M	Involved orbitals	Eorb (eV)60	dO-M (pm)59	rM (pm)b	λ (pm)	Tcmax (K)
La2CuO4a	La	O 2s – La 5p	−26.36	255	115	0	35
Sr2RuO457	Sr	O 2s – Sr 4p	−27.69	270	113	17	1.5
Sr2IrO4	Sr	O 2s – Sr 4p	−27.69	277	113	24	N/A

“M” represents the neighboring atom of O. E_orb is the energy level of the involved orbital in M. d_O-M is the bond length. r_O and r_M are ionic radii of O and M, respectively (r_O = 140 pm). λ = d − r_O – r_M is a characteristic parameter for the O–M bond.

^aChu et al.⁶²

^bPauling ionic radii.

It should be noted that the green dashed line in Figure 6 is not a fitting line but an upper ceiling of T_c^max. Actually, for the superconductors shown in Figure 6, their λ are relatively small. It is not shown in Figure 6, but is partially in Figure S1, that there are also many superconductors, far below the ceiling line of T_c^max, each of which has a large λ.

Discussion

Guidance for exploring superior superconductors

Figure 6 and Tables 1 and 2 lead to a useful criterion for screening candidates of high-T_c superconductor. It suggests two necessary conditions for high T_c^max: (1) having a deep-energy-level orbital coupling and (2) small bond lengths between the ions providing those deep-energy-level orbitals.

Although it cannot tell which materials are superconductors, it does can tell which superconductors can have higher T_c^max and which ones do not stand a chance at all. It suggests that high T_c^max can be supported only by some particular elements.

For example, calcium-containing superconductors should have relatively high T_c^max because the energy level of Ca 3p is rather deep (−33.77 eV). In fact, the T_c^max of many calcium-containing cuprates are over 100 K, higher than all other superconductors at ambient pressure. It is somehow unexpected because for years, it has been the Cu-O planes that have been regarded as the origin of high T_c^max in cuprates, whereas the ions nearby the Cu-O planes are thought to have a minor influence. However, our results indicate that the role of Ca cations may be much more important than we used to think. Moreover, most earlier studies on cuprates have focused on the band structure and electron interactions around the Fermi level, which is mostly derived from Cu 3d and O 2p orbitals. Now, according to this work, the orbital coupling between Ca 3p and O 2s should also be dragged into the spotlight.

The distribution of electron orbitals could be dramatically altered at ultrahigh pressure. First-principles calculations have shown that either LaH₁₀ or H₃S has a wide valence band at ultrahigh pressure.^63,64,65 There is a strong orbital hybridization between La 5p (or S 3p) and H 1s. The bottom of their valence band is deeper than −20 eV, respectively. As a comparison, the bottom of the valence band of the cuprates is slightly less than −20 eV. Besides, the lattice of LaH₁₀ and H₃S is greatly compacted at ultrahigh pressure. Although the compressed hydrides are usually thought to be BCS superconductors, which rest upon the electron-phonon interaction, our results show that their high T_c could have another explanation. In compressed hydrides, the elements other than H are not arbitrary. They should have deep-energy-level valence electrons.

Therefore, to design a high-T_c superconductor, the elements having deep-energy-level valence orbitals are preferred. Only some of the elements (alkali, alkaline, rare earth, as well as O, S, Se, As, F, Cl, …) can provide deep-energy-level valence orbitals (see also Figures S2 and S3). However, those elements are liable to form ionic crystals, which are usually insulators. To get itinerant carriers, a third element is needed to provide covalent bonds, making the crystal metallic. In general, a high-T_c superconductor is supposed to consist of more than two elements, including at least one transition element and at least one element having deep-energy-level valence orbitals.

It should be emphasized that it is still unfeasible so far to make confident predictions on new high-T_c superconductors. To the best of our knowledge, superconductivity is affected by many factors, and high-T_c superconductivity has multiple necessary conditions, some of which may yet be unknown. High T_c would not exist unless those necessary conditions are met altogether in a superconductor. Sometimes, a material meets all the conditions of high T_c, but it is just not a superconductor but rather an insulator or a magnet.

ML models often mistake insulators or magnets for high-T_c superconductors, due to the lack of relevant information in the input data. In the absence of that essential information, the ML models were only able to give a candidate list of “materials that could be high-T_c superconductors, but not necessarily superconductor.”

To get a full guidance, we need to collect all the indispensable information, including but not limited to “energy level distribution of valence electrons,” “bond lengths,” “energy dispersion near the Fermi level,” “strength of spin fluctuation,” and “strength of magnetism order.” Unfortunately, the latter three are usually not easy to obtain. That is why it is so hard to find another material family of high-T_c superconductors.

Nevertheless, more superior superconductors may be found in two-dimensional (2D) materials, although their bulk materials are insulators. Gate voltage or lattice strain may produce adequate carriers in such materials.

In brief, the existence of deep-energy-level valence shells can be seen as a necessary, but not sufficient, condition of the high T_c. Although it could not directly point out which materials must have high T_c, at least it gives a criterion that greatly narrows the search for high-T_c superconductors.

A clue to the pairing mechanism

What is the pairing glue in high-T_c superconductors? It is a core issue in the mechanism study on superconductivity. The pairing glue (strictly speaking, the electron interaction causing the attractive potential between the two pairing electrons) is supposed to be derived from some kind of quasi-particle, elementary excitation, or fluctuation, in the lattice. For instance, in cuprates, spin fluctuation is a promising candidate for pairing glue.^8,9 In compressed hydrogen-rich materials,⁶⁶ it is the lattice vibration. However, neither spin fluctuation nor lattice vibration can explain the T_c^max-ΔE trend in this work. The T_c^max-ΔE trend shows that the excitation and fluctuation of the deep-energy-level valence electrons can also serve as a pairing glue in high-T_c superconductivity. Please note that we did not rule out spin fluctuation or lattice vibration. Our results imply a physical picture of the pairing mechanism:

The unconventional high-T_c superconductors may need two pairing glues (q_k and q_s). One (q_s) gives rise to the angular momentum conservation of the Cooper pair, and the other (q_k) causes the momentum conservation of the Cooper pair. In cuprates and iron-based superconductors, the spin fluctuation can function as q_s, while the fluctuation of deep-energy-level valence electrons can function as q_k.

q_k is always indispensable to any superconductor, whereas the necessity of q_s depends on the coherent length. When the coherent length is long, it is easy for an electron to find its mate (the electron having opposite spin and momentum) within the range of coherent length (usually dozens of nanometers). The condition of angular momentum conservation (having opposite spin) is naturally met. In that case, only q_k is necessary, and it can be contributed from the electron-phonon interaction. When the coherent length is short (the case of most high-T_c superconductors), the pairing electrons need to find their mates, respectively, within several nanometers. However, in the range of several nanometers, there are only a few electrons available. The condition of angular momentum conservation is no longer naturally met. In that case, q_s is indispensable, too.

Thus, a fresh understanding of the pairing mechanism of high-T_c superconductivity is obtained. The pairing mechanism of all known superconductors can be put into a unified framework. Briefly, the pairing of two electrons needs two necessary conditions: momentum conservation and angular momentum conservation. The momentum conservation always needs a pairing glue of charge fluctuation, and the angular momentum conservation needs a pairing glue of spin fluctuation if the coherent length is too small.

Conclusion and prospects

In summary, ML models were used to predict the upper limit of T_c (T_c^max) of superconducting materials. Enlightened by the ML results, we found a correlation between T_c^max and a band structure parameter. It suggests that the energy-level distribution of valence electrons is crucial for high-T_c superconductivity. It should be noted that the T_c^max trend is in fact based on the band structure simulation results. Here, the role of ML is just to give a hint. Thanks to the explicit meaning of the features in the ML model, theoretical induction based on our ML results is effective and efficient. It implies a physical picture of electron pairing in high-T_c superconductors. It also reveals a necessary condition of the high T_c, which provides convenient guidance for designing superior superconductors.

Although artificial intelligence nowadays can give useful clues and guidance, they are still not good enough to predict new high-T_c superconductors with confidence. Improvements may beachieved by means of graph neural network algorithms, which are good at dealing with structural information, including both the crystalline structures and the electron band structures.

Experimental procedures

Resource availability

Lead contact

The lead contact is Haiyou Huang (huanghy@mater.ustb.edu.cn).

Materials availability

This study did not generate new unique reagents.

Machine learning

Dataset

Dataset-T_c^max is a subset of dataset-T_c. According to the chemical composition, superconductors in the dataset-T_c were categorized into 1,000+ groups, according to the component number and the content of each element in the chemical formulas. Each group can be labeled as “n-E-c,” where n is the component number (the compound consisting of how many elements), E is the element, and c is the content of the element. Before the categorization, all the values of c are rounded to integers. A superconductor can appear in multiple groups. For example, YBa₂Cu₃O_6.85 appears in four groups: 4-Y-1, 4-Ba-2, 4-Cu-3, and 4-O-7; Mg_0.81Al_0.19B₂ appears in two groups: 3-Mg-1 and 3-B-2; and FeSe_0.5Te_0.5 appears in three groups: 3-Fe-1, 3-Se-1, and 3-Te-1. In each group, we picked the entry having the highest T_c value and considered it the T_c^max. Sometimes, several groups give the same picked entry of T_c^max. After merging the duplicate entries, dataset-T_c^max has 1,008 entries.

Twenty-four well-known or most-studied superconductors in the dataset-T_c were picked out and retained as the test set to assess the generalization ability of the final model. In pursuit of long extrapolation distances when testing models, the train set should not include those 24 superconductors, as well as their neighboring data.

In those 24 superconductors, 10 entries are in dataset-T_c^max (1,008), and 42 entries in dataset-T_c^max (1,008) are found to be the neighbors of those 24 superconductors. Here, the word neighbor means a small Manhattan distance in the composition space (<1.5). So, those entries (10 + 42 = 52) were removed from the dataset-T_c^max, resulting in a subset of dataset-T_c^max. The subset-T_c^max has (1,008 − 52 = 957) entries.

During the feature selection, the subset-T_c^max was used to train the ML models in genetic algorithm (GA). For each model, the subset-T_c^max was randomly split into a train set (85%) and a test set (15%). The predictive accuracy of the models on the test set was used as the criterion to select better features.

For the final model after feature selection, all 957 entries of the subset-T_c^max were used as the train data, and the test data are the retained 24 superconductors.

Feature design

For the feature set, all features were designed based on the orbital attributes of valence electrons. The orbital attributes include the energy level and the occupancy of valence orbitals of isolated atoms.⁶⁰

The feature extraction imitates the way of MAGPIE.⁶⁷ Each feature is denoted as: [orbital attribute].[shells selection].[math operator 1].[math operator 2], where orbital attribute means what property of the orbitals is considered, while shell selection means which electron shells are considered.

We defined three [orbital attribute], nine [shells selection], and seven [math operator]. That’s 3 × 9 × 7 × 7 = 1,323 features in total. Discarding the features containing empty values and the features having zero variance, we got 441 usable features.

It should be noted that valence electrons here stands for the electrons participating in the orbital hybridization and coupling. The valence electrons usually come from the outmost saturated orbital and the unsaturated orbital(s). Here, we took an energy cutoff of −36 eV, and the electrons in the energy levels range [0, −36] (eV) are deemed valence electrons.

More details and two examples of feature extraction can be found in Tables S3–S5.

Feature selection

As shown in Figure 7, the feature selection consists of two steps: (1) the 441 features were filtered by their Pearson correlation coefficient (P),⁶⁸ and (2) feature subsets were filtered by GA, according to their performance in ML models.

Figure 7.

Flowchart of feature selection

In step 1, the 441 features were eliminated one by one. At first, we found the two features having the highest Pearson correlation coefficient in all features. Between those two features, we eliminated the one having the lower coefficient of variance (relative standard deviation). We repeated the procedure above until the highest P was less than 0.9. After this step, we got 124 features.

In step 2, GA was used to find the “best” subset of the 124 features. Random forest regression (RFR) models were trained to give the coefficient of determination (R²)⁶⁹ to measure the fitness of the feature subsets. For each RFR model, the dataset (subset-T_c^max, 957 entries) was randomly split into a train set (85%) and a test set (15%).

We ran the GA codes 500 times. Each GA run had 15 generations, and the population in each generation consisted of 100 feature subsets. Each feature subset had 4 features at most, which were randomly picked from the 124 features. Each GA run recommended a feature subset that had the highest R² score on the test data.

Within the feature subsets recommended by the 500 GA runs, some features appeared more often than others. Statistical analysis was made to find the best feature subset. We counted the number of appearing times of each feature (n_fea). For each feature subset, ∑n_fea was considered a score of performance. In general, a larger n_fea meant that the feature was better, and a larger ∑n_fea meant that the feature subset was better. At last, the feature subset having the highest ∑n_fea was selected to train the final model. It can be seen in Figure 8 that the model trained with the selected feature subset had a good performance in predicting the 24 most-concerned superconductors, implying a credible generalization ability.

Figure 8.

Performance of feature subsets

Each data point is corresponding to a feature subset, which is selected out by each GA run. R²_GA,15% is the R² score on the test data (randomly 15% of the subset-T_c^max) for each GA run. R²_957,24 is the R² score given by a RFR model that trained with subset-T_c^max, and test data are the 24 most-concerned superconductors. The red “X” in the plot represents the feature subset in the final model.

First-principles calculations

DFT simulations were performed using CASTEP.⁷⁰ In this work, we do not need to see the fine structure of the energy band around the Fermi level. What we care about is the holistic characteristics of the band. Therefore, the DFT method is competent, even for the strong-correlated superconductors. The primitive cell is set to an antiferromagnetic supercell for each of the cuprates, iron-based superconductors, and heavy-Fermion superconductors. The lattice parameters were optimized when necessary. The values of ΔE (in Figure 6) are not sensitive to the approximation functionals chosen in the calculation. Please note that when choosing the pseudopotentials, all the deep-energy-level valence orbitals should be taken into account.

Published: October 24, 2022; corrected online: August 17, 2023

Data and code availability

The source code and input data of ML, and the results of density functional theory (DFT) calculations, are available Data S1.