Evaluation of single-cell RNA-seq clustering algorithms on cancer tumor datasets

Graphical abstract

Abstract

Tumors are complex biological entities that comprise cell types of different origins, with different mutational profiles and different patterns of transcriptional dysregulation. The exploration of data related to cancer biology requires careful analytical methods to reflect the heterogeneity of cell populations in cancer samples. Single-cell techniques are now able to capture the transcriptional profiles of individual cells. However, the complexity of RNA-seq data, especially in cancer samples, makes it challenging to cluster single-cell profiles into groups that reflect the underlying cell types. We have developed a framework for a systematic examination of single-cell RNA-seq clustering algorithms for cancer data, which uses a range of well-established metrics to generate a unified quality score and algorithm ranking. To demonstrate this framework, we examined clustering performance of 15 different single-cell RNA-seq clustering algorithms on eight different cancer datasets. Our results suggest that the single-cell RNA-seq clustering algorithms fall into distinct groups by performance, with the highest clustering quality on non-malignant cells achieved by three algorithms: Seurat, bigSCale and Cell Ranger. However, for malignant cells, two additional algorithms often reach a better performance, namely Monocle and SC3. Their ability to detect known rare cell types was also among the best, along with Seurat. Our approach and results can be used by a broad audience of practitioners who analyze single-cell transcriptomic data in cancer research.

1. Introduction

Tumors are composed of complex subpopulations of varying cell types, including but not limited to neoplastic cells, stromal fibroblasts, endothelial and immune cells [1], [2], [3], [4]. This can be the result of a number of factors, including cancer stem cell differentiation, accumulation of mutations over time, selective pressures from the cancer microenvironment and more. A primary concern with such high heterogeneity of the tumor and its microenvironment is that it may drive metastasis and drug resistance, leading to progression of disease [2], [5]. Therefore, identifying the composite cell subpopulations of a tumor becomes critical in making diagnostic and treatment decisions. Single-cell RNA sequencing (scRNA-seq) captures the gene expression profiles of individual cells, allowing multiple cell populations within a sample to be characterized and identified based on transcriptomics. This makes clustering of scRNA-seq a powerful tool for determining tumor composition and furthering our understanding of cancer development.

Various clustering approaches have been applied to scRNA-seq data to identify multiple cell populations. Tools such as Ascend [6] and CIDR [7] use hierarchical clustering in which objects, or cells, are sequentially grouped into larger clusters based on similarity. Hierarchical clustering is reliable but can be slower or less efficient than other approaches, such as K-means clustering [8]. K-means clustering, used in tools including RaceID [9] and SC3 [10], assigns cells to the nearest cluster and then recomputes cluster centers in an iterative manner. Some of its drawbacks, however, are that the number of clusters must be set in advance, and cluster sizes are assumed to be comparable, which may result in a loss of rare cell subpopulations [8], [11]. In contrast, density-based clustering does not make assumptions regarding cluster sizing. Density-based approaches require a large sample volume to accurately estimate cell clusters and are thus well-suited to large datasets used in scRNA-seq studies [8]. Yet similarly to K-means clustering, they assume comparable density across all clusters. Density-based methods are also the basis of graph-based clustering approaches, with which complex clusters of varying sizes, shapes and densities can be identified. This, however, relies on scRNA-seq data transformation into a graph-based representation, which includes assumptions about cell population size [8], [11].

Selecting the best clustering model for a given study can be challenging, especially when applied to cancer data analysis. In high dimensional spaces typically used in the analysis of mammalian cell samples, differentiating between cell populations is a difficult task to begin with [8], and the heterogeneity associated with the cancer microenvironment increases the complexity of this task. Reliable approaches to dimensionality reduction and differential expression must therefore be taken, yet many scRNA-seq tools rely on relatively simple statistical methods to accomplish this [12]. Furthermore, many scRNA-seq clustering algorithms are developed in the context of specific studies, or are designed with specific cell types in mind: for example, RaceID was developed with the goal of identifying rare enteroendocrine cells in murine intestinal samples [9]. Although these tools can be used with any other sample type, the context in which they were created may affect how well they handle the complexities of the tumor microenvironment.

Here we present a framework for a systematic evaluation of scRNA-seq clustering algorithms. We then apply it to 15 different tools to determine which of them are best suited for identifying cell subpopulations within cancer samples in eight diverse datasets. To our knowledge, this is the largest cancer-related test set used to date for evaluating scRNA-seq clustering methods. Our results highlight the challenges associated with the clustering of cancer scRNA-seq data, and our approach to their evaluation demonstrates how currently available methods may be comprehensively scored and ranked. This, in turn, will help guide researchers and clinicians in selecting the appropriate tools to gain the most valuable information from their data.

2. Methods

2.1. Clustering algorithms

The 15 tools we selected represent a variety of clustering approaches, including but not limited to graph-based, hierarchical and K-means clustering (Table 1).

Table 1.

Algorithms included. Summary of all algorithms applied in this analysis, with three main clustering types indicated where applicable (G = graph-based, H = hierarchical, K = K-means, O = other). The Normalization used for each algorithm is also provided, where TPM = transcripts per million, RPKM = reads per kilobase per million.

Algorithm name (source)	Software	Brief description	Normalization	Type
AltAnalyze [13]	Python source code	AltAnalyze uses a guide gene selection strategy that iteratively clusters cells with the hierarchical-ordered partitioning and collapsing hybrid (HOPACH) [30] algorithm, and removes genes and clusters with low intra-correlations. The top intra-correlated genes are selected as guide genes, and the final clustering results are obtained by running HOPACH on all the guide genes.	Raw counts	H
Ascend [6]	R package	Clustering by Optimal Resolution (CORE) [31] method: Euclidean distance is first calculated based on the first 20 principal components (PCs) from the principal component analysis (PCA) reduced count matrix. Hierarchical clustering is then applied on the distance matrix to obtain the initial clustering. Outlier cells from this first round of clustering are identified and removed. A re-clustering is then performed by a top down split and clusters are merged over multiple iterations. During this process, adjusted Rand index (ARI) is used to compare different clusters and identify the most stable number of clusters.	Raw counts	H
bigSCale [14]	MATLAB source code	bigSCale first computes a pairwise cell distance matrix based on the genes with a high degree of variance. Then, Ward's linkage is used on the distance matrix to assign cells into different groups.	Raw counts. Scatter normalization is part of the pipeline	H
Cell Ranger [15]	Python/R	Cell Ranger constructs a sparse k-nearest neighbors (kNN) graph where cells are linked if they are among the k nearest Euclidean neighbors. The Louvain modularity optimization algorithm is used to find highly connected modules in the graph. Then, hierarchical clustering of cluster medoids in the PCA space is done and cluster siblings are merged if there are no differentially expressed genes between them.	TPM	G, H
CIDR [7]	R package	CIDR first imputes gene expression levels for dropout genes. Then, a dissimilarity matrix is obtained by computing the Euclidean distance between every pair of cells. Finally, PCA is used on the dissimilarity matrix, and a hierarchical clustering is applied to the first few principal components for clustering.	Raw counts	H
Monocle [16]	R package	tSNE is first performed to reduce the dimensionality of the dataset. A kNN network is then constructed with k = 20. The Louvain algorithm is used on the kNN network for clustering.	Raw counts	G
pcaReduce [17]	R package	PCA is first used on the dataset to reduce its dimensions to q. Then k-means clustering is applied on the q-dimensional matrix and divides cells into (q + 1) clusters. After that, the probability of each pair of clusters being merged is calculated, and the two clusters with the highest probability are merged. This process is repeated until one cluster remains.	Log2 normalization	H, K
PhenoGraph [18]	Python source code	A weighted kNN network is first constructed with the weights being the number of shared common nearest neighbors between two connected cells. Then, the Louvain algorithm is used to divide cells in the network into different clusters.	Raw counts	G
RaceID [9]	R/C++	A cell similarity matrix is first constructed by computing the Pearson’s correlation coefficients between all pairs of cells. Then, a distance matrix is obtained by subtracting the similarity matrix from 1. Finally, k-means clustering is used on the distance matrix to group cells into different clusters.	Raw counts. RaceID does an internal normalization based on median transcript across all cells.	K
RCA [19]	R package	A projection vector is calculated for each cell based on the Pearson correlation coefficients between the dataset and the two reference bulk transcriptomes. Average-linkage hierarchical clustering is then used on the projection vectors for clustering.	RPKM	H
SC3 [10]	R package	SC3 first runs k-means clustering on the dataset with different parameters simultaneously. Then, a consensus matrix is computed by summarizing how often each pair of cells is located in the same cluster. Finally, the result is determined by complete-linkage hierarchical clustering of the consensus matrix.	Raw counts, scatter normalization is part of the pipeline	H, K
Scran [20]	R package	Hierarchical clustering is applied on PCs. Normalization is done by deconvolving size factors from cell pools.	Raw counts	H
Seurat [21]	R package	Seurat's default pipeline first finds variable features from the dataset, then applies PCA to get the top 50 PCs. Finally, the Louvain algorithm is used on the 50 PCs for clustering.	Raw counts. Log normalization is part of the Seurat pipeline	G
SINCERA [22]	R package	Expression data are first transformed to z-scores. Hierarchical clustering is then used to divide cells into different groups.	z-score scaling is part of the pipeline	H
TSCAN [23]	R package	TSCAN first divides genes into different clusters using hierarchical clustering, which reduces the number of features to the number of gene clusters. PCA is then applied to further reduce the dataset dimensionality. Finally, a mixture of multivariate normal distributions is fitted to the data, and cells are assigned to clusters based on their probability of belonging to each cluster.	Raw counts	H, O

2.2. Datasets

Cancer microenvironments vary widely between individual cancer types, thus to accurately assess tool performance, we used eight different datasets encompassing tumors of the brain, breast, lung, colorectal and pancreatic tissues, leukemia, melanoma and metastatic melanoma (Table 2). The datasets were obtained from either Gene Expression Omnibus (GEO), ArrayExpress (AE) or Genome Sequence Archive (GSA) and are further summarized below. We have also made these datasets available previously through our R package called TMExplorer [32] and our recently developed web portal, CReSCENT (https://crescent.cloud).

Table 2.

Summary of datasets used. Summary of the datasets used to evaluate scRNA-seq clustering algorithms. Cancer type, the number of cells, genes and tumors, sequencing technology used, cell type and gene signature availability, and dataset accession numbers are provided. GEO: Gene Expression Omnibus; AE: ArrayExpress, GSA: Genome Sequence Archive.

Dataset	Cancer type	Cells	Malignant Cells	Non-malignant Cells	Genes	Tumors	Sequencing technology	Cell type available?	Gene signature available?	Accession number
AML [24]	Acute myeloid leukemia	38,410	33,733	4,677	27,899	40	Seq-well	No	No	GEO: GSE116256
Breast [25]	Primary breast cancer	515	317	198	57,915	11	Fluidigm C1	Yes	Yes	GEO: GSE75688
Colorectal [19]	Colorectal cancer	376	271	105	57,241	11	Fluidigm C1	Yes	Yes	GEO: GSE81861
Glioblastoma [26]	Primary glioblastoma	3,589	1,091	2,498	23,368	4	SMART-seq2	No	No	GEO: GSE84465
Lung [28]	Non-small cell lung carcinoma	51,775	7,424	44,351	22,533	5	10x Genomics	Yes	Yes	AE: E-MTAB-6149, E-MTAB-6653
Melanoma [27]	Melanoma	6,879	2,018	4861	23,686	33	SMART-seq2	Yes	Yes	GEO: GSE115978
Metastatic melanoma [4]	Metastatic melanoma	4,645	1,783	2,862	23,686	19	SMART-seq2	Yes	Yes	GEO: GSE72056
Pancreatic [29]	Pancreatic ductal adenocarcinoma	57,530	11,315	46,215	24,005	24 tumors 11 controls	10x Genomics	Yes	Yes	GSA: CRA001160

Acute myeloid leukemia (AML). 40 bone marrow aspirates were isolated from 16 AML patients and five healthy donors for this dataset [24]. The dataset comprises several malignant and normal hematopoietic cell types.

Breast cancer. Single cells from 11 human primary breast cancer tumors of four different subtypes comprise this dataset, including cancer cells, stromal cells, and immune cells from the tumor microenvironment [25].

Colorectal cancer. This dataset represents single cells isolated from 11 human primary colorectal cancer tumors at varying stages [19]. Cell types include T cells, B cells, macrophages, fibroblasts, mast cells, epithelial cells, and malignant cells from the tumor microenvironment.

Glioblastoma. This dataset details the single cell expression profile of cells isolated from four primary glioblastoma patients [26]. It consists of cells from the tumor core and peritumoral space of each patient, and samples are composed of tumor cells, vascular cells, immune cells, neuronal cells, and glial cells.

Melanoma. This dataset contains gene expression profiles for single cells isolated from 33 human melanoma tumors, 15 of which were newly collected from patients, and 16 of which were from previously reported tumors [27]. Cell types include malignant cells, stromal cells, and immune cells that compose the melanoma tumor microenvironment.

Metastatic melanoma. This dataset consists of single-cell expression profiles for cells isolated from 19 human melanoma tumors [4]. It includes malignant, immune and stromal cells taken from ten metastases to lymphoid tissues, five metastases to subcutaneous or intramuscular tissue, three metastases to the gastrointestinal tract, and one primary acral melanoma.

Lung cancer. For this dataset, single-cell expression profiles were generated for cells isolated from five patients with untreated, non-metastatic lung squamous carcinoma or lung adenocarcinoma [28]. Cells were isolated from both tumor and normal lung tissue, and cell types present include cancer cells, immune cells, fibroblasts, endothelial cells, alveolar cells, and epithelial cells.

Pancreatic cancer. This dataset consists of pancreatic cells isolated from 24 primary pancreatic ductal adenocarcinoma tumors and 11 control pancreases. It comprises various subgroups of malignant and stromal cell-types [29].

2.3. Data preprocessing

The specifics of data preprocessing are unique to each platform and the original research study providing the data. In this work, we used the publicly available raw counts matrix as a starting point for all of our analysis. However, the authors of each original study had applied the appropriate preprocessing steps based on the platform used. More specifically, each paper had their own criteria for excluding cells and genes from the analysis. Here we provide a brief description of the preprocessing steps for each dataset.

The breast dataset was obtained using the Fluidigm C1 platform. Cells with low quality sequencing values were removed using 4 different criteria including: (1) number of total reads; (2) mapping rate; (3) number of detected genes; and (4) portion of intergenic region. To filter out genes with low expression values, the expression data was first normalized using log₂(TPM). Genes present in less than 10 % of tumor samples were filtered out. The metastatic melanoma and melanoma datasets were obtained using the SMART-Seq2 protocol and has similar preprocessing steps. The authors quantified the number of cells with at least one mapped read and calculated the average expression level of a set of housekeeping genes. Cells and genes were filtered out if they were below a threshold value. The colorectal dataset was obtained using Fluidigm C1 platform. The authors used the following criteria to determine which cells to exclude from the analysis: (1) the ratio between exonic reads and raw reads in the BAM file; (2) total number of genes with FPKM >1; and (3) exonic reads. The glioblastoma dataset was obtained using the SMART-Seq2 protocol. First, hierarchical clustering on all cells was performed using a set of predefined housekeeping genes and then cells that have uniformly low expressions values were removed. The AML dataset was generated using Seq-well. The authors excluded cells that did not meet a minimum unique molecular identifier (UMI) count and also looked at the percent genes and ribosomal RNA. The lung and pancreatic datasets were sequenced using 10x genomics technology. They used a threshold UMI, number of expressed genes and percent of genes from the mitochondrial genome to remove low quality cells from the analysis.

While the specifics of data preprocessing are unique to each method, we performed the following steps prior to the running of each clustering algorithm: (i) collection of raw counts data; (ii) normalization of counts unique to each algorithm (Table 1). Each dataset was preprocessed by log transforming normalized values. The log₁₀(TPM + 1) values were calculated for the gene × cell matrices of every dataset. Some methods likewise required the filtering out of genes with particularly low expression levels. More specifically, AltAnalyze, Ascend, bigSCale, CIDR, RaceID, RCA, SC3, Scran, SINCERA, TSCAN require filtering out of low expressed genes. We used the default parameters of each algorithm for the gene filtering. For bigSCale, CIDR, RCA, SC3, Scran, only genes with an average raw count above 1 across all cells are kept for the analysis. For Ascend, only genes with an average raw count above 5 were kept. AltAnalyze requires the gene variance to be above a threshold. For RaceID only genes with a minimum transcript count of 1 in at least 5 cells are kept for the analysis. For TSCAN we set a threshold that only genes with a minimum expression value of 1 in at least 1 % of cells are retained. These requirements are based on each algorithm’s technical documentation.

For all clustering algorithms, default parameters were used whenever possible. This was done to reduce variability across analyses, as any parameter changes that improve algorithm performance with one dataset may not have equivalent improvements with other datasets. Furthermore, when consulting with authors of the various algorithms, use of default parameters for the purpose of performance evaluations and comparisons was the recommended approach.

2.4. Clustering measures

Each of the clustering partitions generated by the algorithms was compared to an appropriate benchmark grouping of cells, to determine either how closely the detected clusters match the original cell types, or how homogeneous the clusters are in terms of the cell types present therein.

To evaluate the performance of each clustering algorithm on each of the eight datasets, we used six different measures of similarity between clustering partitions (Table 3). These six metrics represent a broad selection of well-established approaches to measuring similarity between different clustering partitions of the same dataset.

Table 3.

Measures of clustering quality. The measures are assigned into three different groups based on principal component analysis (see Results section).

Measure	Brief description	Range	Group
Adjusted mutual information (AMI)	A variation of mutual information between two clustering partitions, adjusted for the effect of chance agreements between partitions	0 to 1	1
Adjusted Rand index (ARI)	A variation of Rand index as a measure of the percentage of correct matches, adjusted for the effect of chance agreements between partitions	0 to 1	1
F-measure	A measure of accuracy that balances both the precision and recall	0 to 1	1
Variation of information (VI)	An information-based measure that behaves like a true distance, with zero representing equality of the two partitions	0 to infinity	1
Homogeneity	Entropy-based measure that quantifies whether only those data points that are members of the same class are assigned to the same cluster.	0 to 1	2
Majority	Proportion of the data in the largest cluster	0 to 1	2
Silhouette	Clustering fitness that measures whether each data point belongs unambiguously to the cluster to which it has been assigned	−1 to 1	3

Adjusted mutual information (AMI) is an entropy-based measure that quantifies if the two partitions are independent of each other, or if knowing one of them (e.g. Seurat clusters) reduces the uncertainly about the other (e.g. the true cell subtypes). All possible intersections of the clusters from the two partition are considered, and the entropy-based measure is improved if each cluster of the first partition overlaps to a large extent with only one or few clusters of the second partition. Conversely, poor overlap between the two partitions creates a larger number of smaller intersections, thus reducing the mutual information measure. It is then adjusted so that a random cluster assignment has a baseline of 0, whereas a perfect match has a value 1.

Adjusted Rand index (ARI) is a measure of similarity between two clustering partitions. Rand index is defined as the proportion of cell pairs that either appear together in the same cluster in both clustering partitions, or appear in separate clusters in both partitions. The value is then adjusted so that a random cluster assignment has a baseline of 0, whereas a perfect match has a value 1.

F-measure, also known as F1 score, quantifies the identification of cell type as a classification problem. For a given cell type from the benchmark, we first labeled all cells across the dataset as either belonging or not belonging to that cell type, thereby forming the positive and negative class labels, respectively. Each cluster thus contained a mixture of binary class labels, from which we identified the majority label and assigned it to all cells in that cluster. This “predicted” classification was then quantified using precision (proportion of true positives among all cells labeled as positive) and recall (proportion the desired cell type that was correctly identified as such). The F-measure for a given cell type was defined as the harmonic mean of its precision and recall. The overall F-measure was computed as the average value across all cell types, weighted by their sizes.

Variation of information (VI) in an information-based measure that is similar to the mutual information measure. It is based on examining the entropy of a joined partition made of all possible intersections of the two clustering partitions being compared. Unlike the similarity measures, the VI behaves as a distance metric so that identical partitions result in the lowest possible VI value of 0, and higher VI values represent divergence between the two partitions.

The previous four measures are designed to quantify the overall similarity between two clustering partitions. We also used two measures that reflect the cell-type distributions, as follows.

Homogeneity is an information-based measure of the distribution of cell types within clusters, which uses conditional entropy of the true cell types given the clustering partition. Homogeneity takes its maximal value of 1 when each cluster contains only members of a single cell type (resulting in the lowest entropy). Conversely, homogeneity is zero when the cell-type distribution within each cluster matches the overall cell-type distribution and so the clustering provides no additional information.

Majority is defined as the proportion of the majority cell type in each cluster, where the cell types are defined in the benchmark partition. For example, if a cluster has 70% B cells, 20% T cells and 10% endothelial cells, we report a majority of 0.7 for that cluster. The overall majority was computed as the average value across all clusters, weighted by their sizes.

In addition, we also applied a well-known silhouette measure to quantify the fitness of each clustering result. For each cell, its silhouette value compares two distance values: the average distance to cells in its own cluster, and the average distance to the closest cluster other than its own. A positive silhouette value indicates that the cell is a much better fit in its own cluster than in the next-best one. A negative silhouette indicates that there is a better cluster to which the cell should be assigned. The overall silhouette for a clustering partition is computed as the average value across all cells. Unlike with the previous six measures, silhouette reflects the quality of a clustering partition without comparing it to a benchmark partition.

We used bootstrapping of each of the six performance measures to determine the significance of differences between algorithm performances for each dataset. To do this, we evaluated N measure values for each algorithm’s performance with a given dataset, where N is the number of cells in the dataset. We then sampled with replacement from N, using a sample size equal to that of N, and calculated a mean measure from this sampling. This was done 10,000 times. Using the 2.5th and 97.5th percentiles of these averages, we determined the 95% confidence interval for the performance measures.

The confidence intervals were then used to generate independent distributions of the quality measures, which were used to compute a robust ranking of the clustering algorithms. For each metric, we ran N = 10,000 random simulations by adding a different random jitter to each performance measure. The amount of jitter was determined by the confidence interval computed for that measure, dataset and algorithm. This approach allowed us to simulate randomized distributions independently for each measure, in order to reduce the effect of interdependencies between the measures and thus generate a wider coverage of their joint distribution. Each of the N = 10,000 sets of performance values was then used to compute algorithm ranks, allowing us to make robust estimates of the resulting rank distribution.

The proportion of malignant and non-malignant cells varied significantly across these data; furthermore, malignant cells may have highly aberrant gene expression with a large degree of heterogeneity, whereas non-malignant cell types typically represent stable transcriptional profiles. Therefore, we separated the cell populations into malignant and non-malignant components for benchmarking purposes. We used the cell types reported in the original publications as the truth sets to which the non-malignant cell clustering was compared. Although cell types do not necessarily correspond to all possible cell groups within the data, they nevertheless represent biologically relevant partitions of the data into major categories that should be reflected in transcriptional patterns. As such, a clustering algorithm should be able to detect such categories and perhaps to refine them further into subgroups.

For malignant cells, their grouping into cell subtypes was unavailable in all datasets except the AML. Therefore, for benchmarking purposes we derived the malignant-cell groups based on shared patterns of copy-number variation (CNV) detected by the InferCNV method of the Trinity CTAT Project (https://github.com/broadinstitute/inferCNV). We also grouped malignant cells by patient identity as an alternative benchmark, given that the transcriptional profiles in malignant cells are known to reflect individual differences.

2.5. Systematic scoring framework

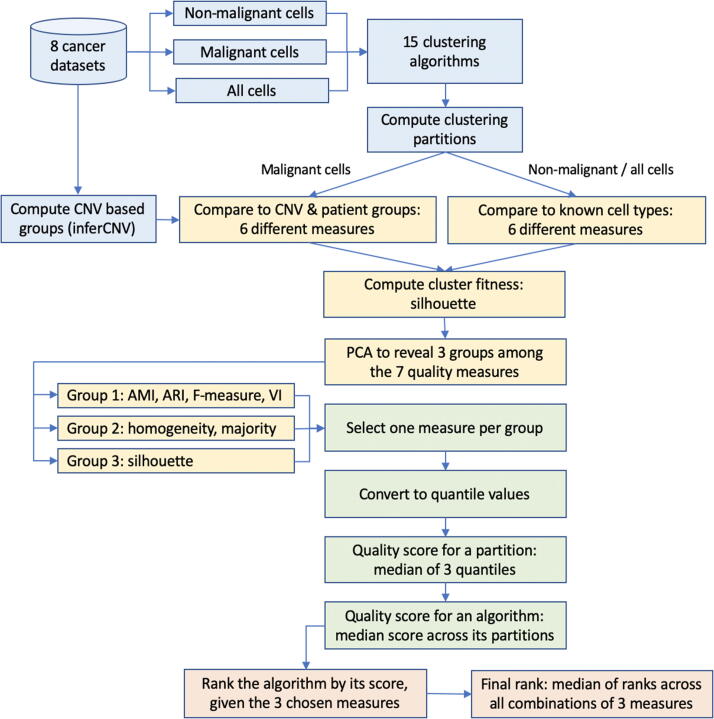
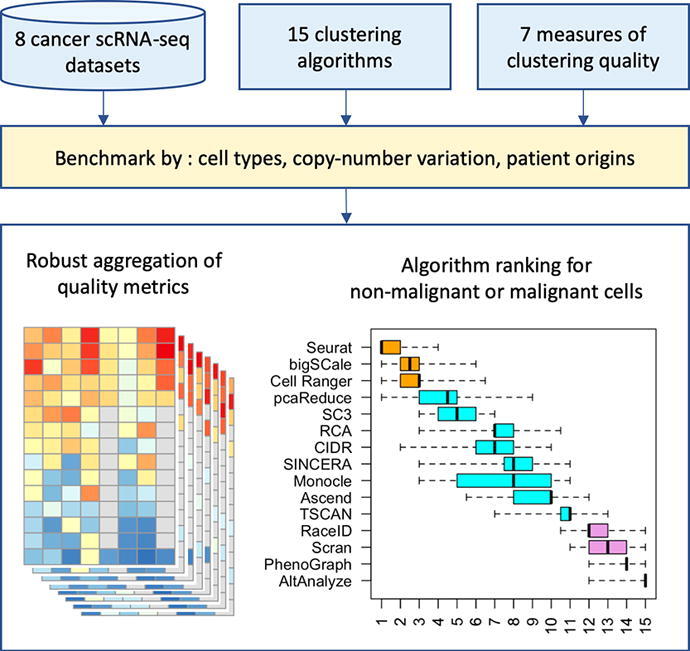
The main analysis workflow focused on combining different clustering-quality measures into a systematic ranking of algorithms (Fig. 1). We applied 15 different clustering algorithms (Table 1) to each of the eight scRNA-seq datasets (Table 2). Each such algorithm-dataset pair generated a clustering partition, which was then systematically assessed using seven different measures of clustering quality. The results were normalized to the same range from 0 (lowest) to 1 (highest) using the quantiles of the distribution of each of the seven measures used. Quality measures themselves were examined to identify redundancies between them. Thereafter groups of non-redundant measures were formed. For each group, values were aggregated using medians first among the measures, then further across all eight datasets. This robust quality score was used for the ranking of the algorithm. Finally, for each algorithm its rankings across all groups of non-redundant measures were examined to arrive at a final rank.

Fig. 1.

The main analysis workflow consisted of four stages. First, the clustering algorithms were applied to the eight cancer datasets to generate clustering partitions (blue). Then seven different metrics of clustering quality were examined and grouped into three distinct groups by similarity (yellow). By combining three representative measures, one per group, we generated quality scores first for each clustering partition and then for each algorithm (green). Finally, we ranked the algorithms by quality scores for each choice of measures, and then combined these ranks into a final ranking (pink). (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)

3. Results

We applied our evaluation framework for the scRNA-seq clustering, first by applying the 15 clustering algorithms to various versions of the eight datasets. This process generated a large collection of initial clustering partitions, which were evaluated using a range of metrics. We demonstrate how a systematic aggregation of the results eventually leads to the final algorithm ranking for either non-malignant or malignant cell types.

3.1. Data partitions

Overall, we were able to obtain 102 clustering partitions of non-malignant cells and 112 partitions of malignant cells, where each partition represented an algorithm-dataset pair (Supplementary Figure S1). Some of the algorithms were unable to scale up to the larger datasets such as the Lung and Pancreatic datasets, which contain tens of thousands of cells. For two of the datasets (Colorectal and Glioblastoma) there was no patient information in the original publication, therefore only 82 comparisons of malignant-cell clusters to patient-based groups were possible.

Most of the clustering algorithms were not scalable beyond 10 K cells and failed to cluster the full AML, Pancreatic and Lung datasets. For many of the clustering algorithms including RaceID, Ascend, CIDR, and TSCAN, the biggest memory consumer was the distance matrix calculation. For large datasets, SC3 uses a support vector machine (SVM) model and can scale up to 10 K cells but fails for the larger datasets in our analysis. Scran is a consensus clustering method that tries multiple values of K and builds a consensus. In the CIDR pipeline, imputing the expression value of dropout genes takes the longest time.

3.2. Clustering quality in non-malignant cells

We first examined the clustering quality in non-malignant cells and established the baseline distributions of the quality measures. Using non-malignant cells for this purpose had two advantages: the original studies provided the non-malignant cell type annotations and their transcriptional profiles were expected to be relatively homogeneous within each subtype (unlike those of the malignant cells). This scenario also reflected the typical usage of scRNA-seq clustering in non-cancer data.

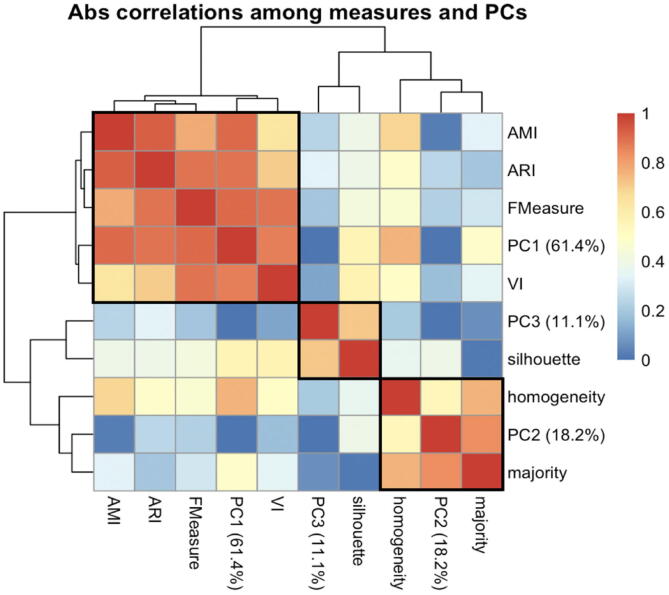
To examine the redundancies among the seven measures of clustering quality, we first applied principal component (PC) analysis to the set of 102 clustering results in the 7-dimensional space defined by the quality measures, and then computed the correlations among all measures and all PCs. This analysis revealed that the measures generally fall into three distinct groups (Fig. 2). Group 1, represented by the principal component PC1, contains AMI, ARI, F-measure and VI; these four highly correlated measures are optimized when two clustering partitions are identical. Group 2, represented by PC2, contains homogeneity and majority, two highly correlated measures that are optimized whenever clusters contain cells of only one type. Group 3 contains the silhouette, which quantifies whether each cell in the data is closer on average to the cluster into which it was assigned than to any other cluster; hence it is a measure of cluster fitness rather than similarity between partitions.

Fig. 2.

Clustering quality was assessed using seven different measures for each pair of algorithm and dataset: AMI, ARI, F-measure, homogeneity, majority, silhouette and VI distance. Principal component (PC) analysis with feature scaling was then performed on the collection of 102 clustering partitions in the space defined by the quality measures. The heatmap shows absolute Pearson correlation among the seven different measures, as well as the top three principal components (PCs). The latter collectively explain over 90% of the variance in the measurement data, as indicated in their labels. A group of four different measures: AMI, ARI, F-measure and VI are best correlated with PC1, which captures 61% of the variation. Two other measures, the homogeneity and majority, are also highly correlated and are best reflected by PC2. The remaining silhouette measure is represented by PC3.

3.3. Summary score

Next, we selected a representative measure from each of the three groups, for which there are eight possible triplets (e.g. AMI, homogeneity and the silhouette triplet). The measures may have different ranges and distributions; thus, we converted their original values into the quantiles of the respective distributions. This normalization step made the three quantiles in each triplet numerically comparable to each other in the range from 0 to 1 while reflecting different aspects of the clustering quality. We then aggregated them further into a single summary score by taking the median of the three quantile values. As a result, each of the 102 clustering partitions was represented with a single quality score derived from the three quantile values.

3.4. Algorithm ranking

For each algorithm we computed the median of its quality scores across all of the available datasets. This allowed us to generate the ranking for the 15 algorithms for each of the eight possible triplets of representative measures (Fig. 3). The heatmaps show that the quality of clustering varies across different datasets. Some datasets, such as Breast and Glioblastoma, had consistently higher clustering scores generated by each algorithm; whereas other datasets, such as Lung and Melanoma, presented difficulties to most algorithms.

Fig. 3.

Example of the ranking of the 15 clustering algorithms based on eight different combinations of the three metrics used in the generation of the summary quality score. For each dataset-algorithm pair, the three representative measures (e.g. AMI, homogeneity and silhouette) were converted into quantile values based on the three respective data distributions. Thereafter for each dataset-algorithm pair, a median of the three quantile-normalized measures was generated, and is shown in the heatmap using the color-coded scale. The heatmap rows are then ranked by their median-per-row values, with the best performing algorithms shown at the top of the heatmap. The heatmap also shows that the datasets differ significantly in terms of the clustering quality: for example, most algorithms have better performance achieved on the Glioblastoma dataset but the poorer performance on the Melanoma dataset.

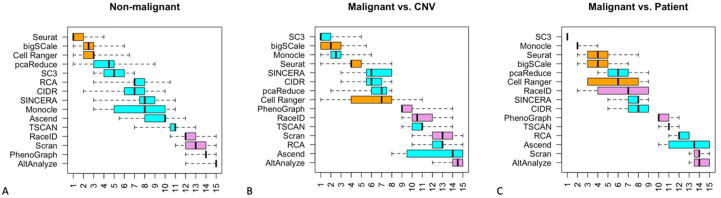
The procedure was repeated in 10,000 randomized iterations in which the performance-measure values were resampled with random jitter within their respective distributions estimated using bootstrap (see Methods). Finally, we examined the eight triplet-based rankings across all iterations and computed the distribution of ranks for each algorithm (Fig. 4A). Given the very large number of randomized iterations, the differences between the algorithm ranking distributions are robust. These results revealed a group of the top three best performing algorithms: Seurat (mean rank 1.56), bigSCale (mean rank 2.35), and Cell Ranger (mean rank 2.71). These algorithms consistently appeared at the top of the ranking, for all combinations of quality measures. They achieve the top rank of one (or tie for it) in, respectively, 61.6%, 22.3% and 12.7% of all randomized iterations. On the other hand, a group of algorithms with consistently poor performance included RaceID, Scran, PhenoGraph and AltAnalyze, which consistently appeared at the bottom of the ranking. The other nine clustering algorithms had a wider distribution of ranks in the middle of the range, neither reaching the top spots nor falling to the bottom spots.

Fig. 4.

Distribution of ranks for each of the 15 algorithms, based on eight different combinations of the three metrics used in the generation of the summary quality score, repeated in 10,000 randomized iterations. Each box in the boxplot thus represents 80,000 values of rank. The algorithms are sorted by the median rank. They fell into three categories (indicated with orange, blue, purple) based on their performance on the non-malignant cells. The top three algorithms are Seurat, bigSCale, and Cell Ranger. Fractional ranks represent ties. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)

The same analysis was then performed on the set of malignant cells. An original classification of malignant cell subtypes was unavailable for all but one of the datasets. Therefore, we instead compared malignant cell clustering to either the CNV-based or patient-based groupings, which reflected the different origins and evolutionary patterns of malignant cells in a biologically relevant way (Fig. 4B-C). Interestingly, two clustering algorithms which previously achieved only a medium-ranked performance ranking on non-malignant cells, exhibited a substantially better ranking on the malignant cells: SC3 was the top ranked algorithm in both comparisons and Monocle improved to be the top second or third. For the CNV-based comparison the best performers SC3, bigSCale and Monocle achieved the top rank (or tied for it) in 62.7%, 29.0% and 11.2% of all randomized iterations, respectively. For the patient-based comparison, SC3 was the only algorithm to reach the top rank in all 100% of randomized iterations. SC3 uses k-means, hierarchical and consensus clustering approaches, and Monocle uses graph-based clustering (see Methods). Two algorithms that were top-ranked for non-malignant cell clustering, Seurat and bigSCale, remained in the top four for the malignant cells, whereas the third one, Cell Ranger, dropped to the middle of the range. Meanwhile two algorithms that performed poorly on non-malignant cells, RaceID and PhenoGraph, improved their ranking somewhat, while the medium-ranked Ascend and RCA fell to near the bottom of the ranks. Otherwise, the remaining patterns of ranks were generally similar to those for non-malignant cells.

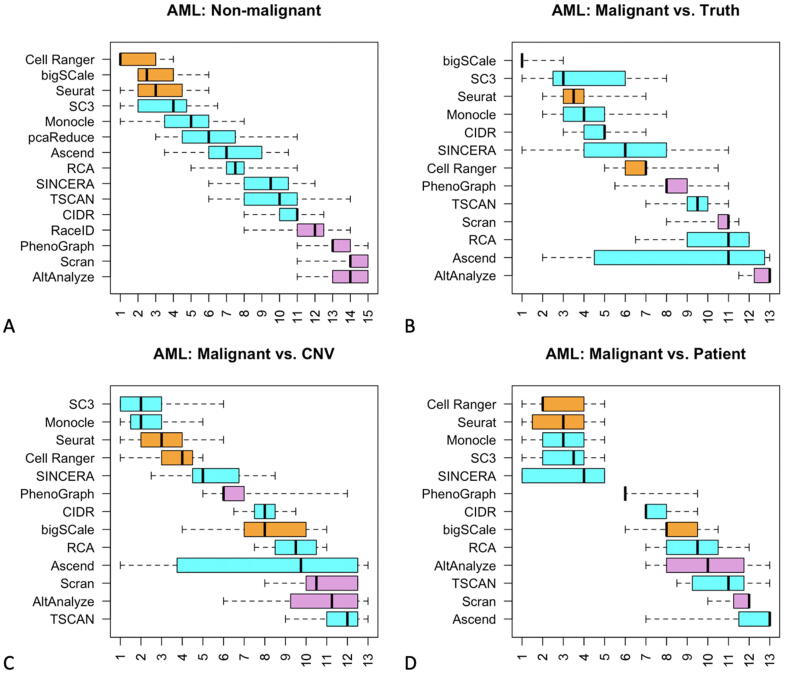
3.5. Example: AML dataset

We demonstrate our approach to algorithm evaluation on the AML dataset, which was the only dataset on our list with a sub-grouping of the malignant cells. The original publication for the AML dataset included the annotations for five known subtypes of malignant cells based on the cell origins. We examined the results of the 15 clustering algorithms on the AML data and compared them to the known cell subtypes (both malignant and non-malignant) as well as to the patient-based and CNV-based groups. The clustering of the non-malignant AML cells was roughly similar to the corresponding ranking over all eight datasets as shown before, the top three still being Cell Range, bigSCale and Seurat (although in a different order than before) and with the SC3 and Monocle being the next two highest-ranked algorithms. The clustering achieved by SC3 and Monocle on the malignant cells were ranked in the top four in all comparisons (Fig. 5).

Fig. 5.

Distribution of ranks for each of the 15 algorithms applied to the AML dataset only, based on eight different combinations of metrics used in the generation of the summary quality score, repeated in 10,000 randomized iterations. Each box in the boxplot thus represents 80,000 values of rank. Algorithms fall into three categories (indicated with orange, blue, purple) based on their performance on the non-malignant cells. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)

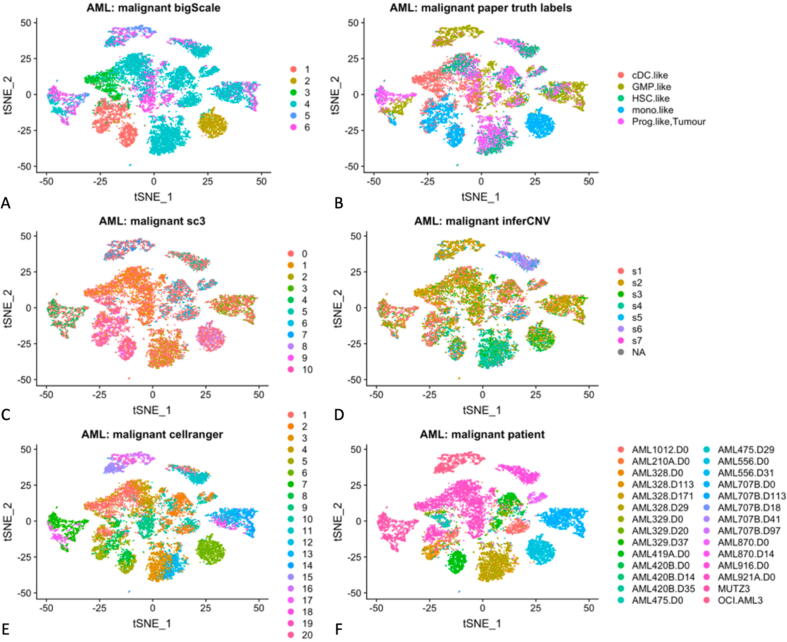
The clustering results of bigSCale, SC3 and Cell Ranger were the best matches for true malignant cell subtypes, CNV-based groups and patient-based groups, respectively (Fig. 5 B-D). We visualized these six groupings side-by-side, via the color-coding on the same t-distributed stochastic neighbor embedding (tSNE) plot (Fig. 6). Visualization of the malignant cells of the AML dataset using tSNE revealed a number of distinct groups in the data. Most of the tSNE groups comprised heterogeneous mixtures of the five “true” malignant cell subtypes (Fig. 6B), and also did not correspond well with the CNV groups (Fig. 6D). However, patient-based groups matched the tSNE groups much better (Fig. 6F). We point out that patient groups for the AML data were based on both the patient ID and the day of observation for each patient.

Fig. 6.

A visual representation of the malignant component of the AML dataset is shown using tSNE, with individual malignant cells represented with colored dots. The colors represent either the clusters detected by either the top ranked algorithms (bigSCale, SC3, Cell Ranger; left side panels); or the cell groups used as benchmarks, representing true malignant cell types, inferCNV groups or patient ID groups (right side panels).

We also observed that the clustering algorithms differed widely in their granularity, with bigSCale detecting only six clusters and Cell Ranger as many as 20 clusters within the AML dataset (Fig. 6 A, E). Of the top-ranked algorithms examined, the bigSCale clustering captured some of the tSNE groups relatively well but created heterogeneous mixtures in other tSNE groups. The three algorithms corresponded well with each other, while containing the number of clusters comparable to their respective benchmarks (Fig. 6 B, D, F).

3.6. Partition size and cell categories

Our framework for systematic algorithm evaluation is based on using established metrics of partition quality, which reflect the differences in the partition sizes. In addition, we directly examined the partition sizes and granularity of the results, and also each algorithm’s ability to detect underrepresented cell types.

Generally, the algorithms often estimated more clusters than there were cell types in the original dataset annotation (Supplementary Figure S2), some of which may reflect underlying biological subcategories of cells (such as multiple cell populations within the tumor type), while other differences may be a genuine discrepancy. Higher granularity also created opportunities to capture underrepresented cell types and smaller clusters.

We explored the ability of each clustering algorithm to detect underrepresented cell types. We defined a cell type to be underrepresented if the number of cells is less than 500 and is less than 20 % of the dataset, or the number of cells is less than 5 % of the dataset. These two different criteria were required because some datasets had more granular labels and therefore more rare cell types. Detailed cell type annotations were available only for non-malignant cells in all datasets except AML, whereas we were also interested in the malignant cells. Therefore, we applied the 15 clustering algorithms to the full datasets in order to capture the combined influence of all cell types present in the tumor microenvironment on the results.

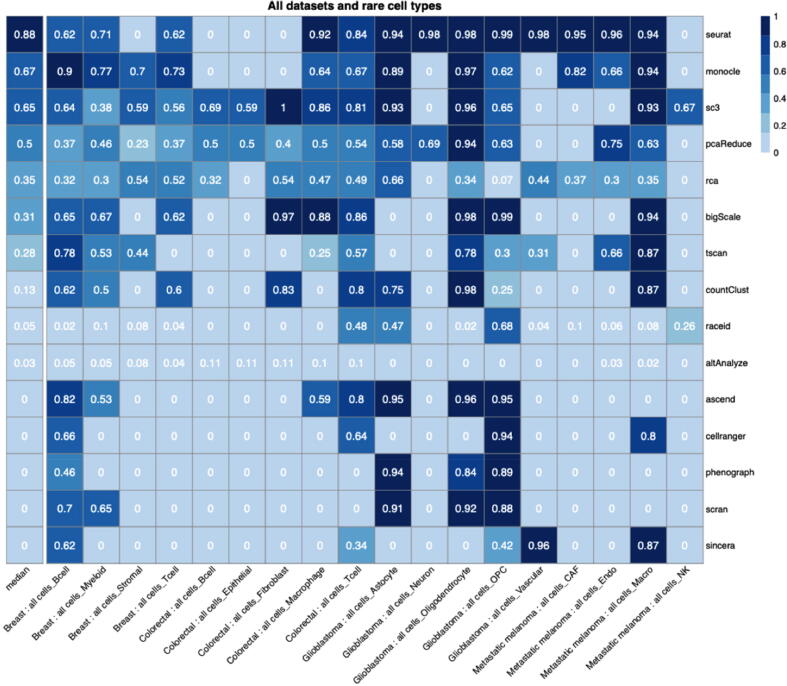
Each dataset is composed of several different cell types, some of which are common to all datasets, such as B cells and T cells, while others are unique to specific datasets, e.g. stromal cells in the Breast dataset. The number of clusters varied by algorithm, and most clusters were heterogeneous with respect to the cell categories they comprised: for example, a cluster may contain 90 % immune cells and 10 % fibroblasts. The most abundant category was assigned to the whole cluster: in the example above, the cluster would be assigned an “Immune” category. An F-measure was then computed for each cluster, comparing the predicted category to the true cell-type labels treated as binary (e.g. immune or non-immune cells). The F-measure values were averaged across all clusters for a given algorithm and cell type (Fig. 7).

Fig. 7.

The heatmap represents the F-measure of detecting each cell type (rows) in each dataset, either by clustering all cells or only non-malignant cells (columns). The left-most column represents the median values across all dataset versions.

The results show that the ability of the algorithms to detect underrepresented cell types varied substantially across the datasets, even among the same cell types: e.g. B cells were generally detected more accurately by clustering the Breast data, but less so in the Colorectal data. Nevertheless, previously top-ranked algorithms such as Seurat, Monocle and SC3 achieved the highest median F-measures overall for detecting underrepresented cell types.

3.7. Other algorithm characteristics

In addition to clustering quality, we also examined other characteristics of the algorithms in our final ranking (Table 4). In terms of software implementation, the top three best algorithms on non-malignant cells - Seurat, bigSCale and Cell Ranger - are single cell analysis pipelines that include a clustering step. Seurat and bigSCale are available as R packages, while the Cell Ranger pipeline provides command line interfaces for running the clustering step. Cell Ranger requires a hd5f file as input to the clustering step, while the other algorithms can work with a counts file or a SingleCellExperiment object.

Table 4.

Comparison of top five algorithms using all cells. The table presents a comparison of algorithm characteristics other than the clustering quality, such as the required resources or the usability of the software.

Algorithm	Average run time (all cells)	Space RAM Requirement	Software Usability
bigSCale	9 min	Scalable to more than 50 K cells	Available as an R package. Harder to tune parameters
Cell Ranger	20 min	Scalable to more than 50 K cells	Cell Ranger is comprised of single cell analysis pipelines that include a clustering step. Cell Ranger required a hd5f file as input to the clustering step while the other algorithms can work with a counts file or SingleCellExperiment object
Seurat	2 min	Scalable to more than 50 K cells	The Seurat pipeline is available as an R package and has extensive documentation and an active GitHub page
SC3	10 min	Scalable to more than 10 K cells, but does not scale to 50 K cells	SC3 is available as an R package
Monocle	5 min	Scalable to more than 50 K cells	The Monocle pipeline is available as an R package

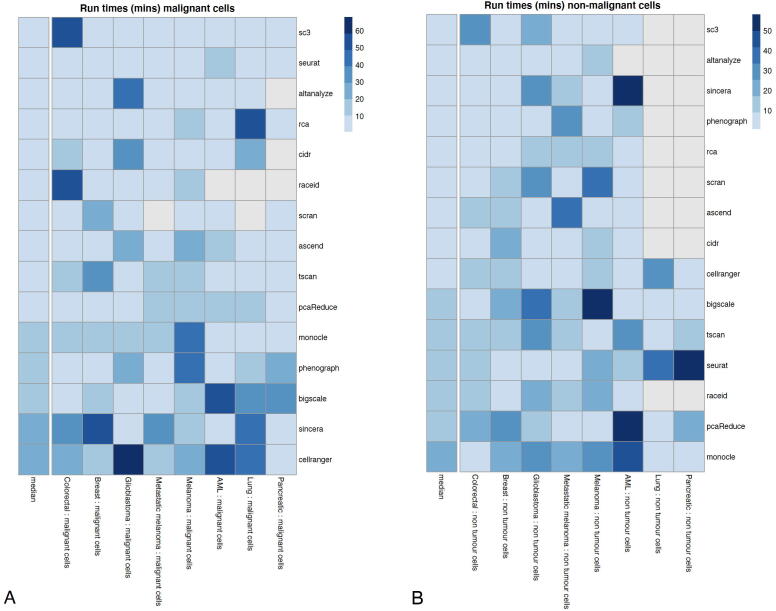
Some of the algorithms that have to compute large distance matrices did not scale to run on the large datasets. Seurat has the shortest average run time of 2 min and the lowest variability in run times ranging from 1 min to less than 2 min. Scran had the highest average run time of 12 min and the highest variability in run times ranging from 9 min to 45 min.

4. Discussion

The complexity of transcriptional dysregulation in cancer samples requires careful examination of the underlying cell populations. Many automated methods are now being developed to handle large-scale scRNA-seq datasets, and their performance characteristics vary rather widely. However, our results suggest that there are common patterns related to the quality of scRNA-seq clustering that should be taken into consideration.

While different quality measures may be applied to evaluate the clustering algorithms, we have demonstrated that there is a substantial degree of redundancy among some measures and that they generally fall into several categories. Our data-driven analysis revealed three such categories: measures that are optimized when clustering partitions are identical, measures of class homogeneity within clusters, and unsupervised measures of cluster fitness that do not compare partitions directly, such as the silhouette.

Furthermore, our framework provides a way to combine these diverse measures systematically into unified quality scores by taking a representative from each group and aggregating the results in several stages into the final algorithm ranking. We used a robust median-based approach at each step to improve the reproducibility of the results. Our analysis reveals a group of clustering algorithms whose quality is consistently high for different datasets and evaluation scenarios. Interestingly, while the commonly used Seurat pipeline appears among the top performers for non-malignant cells, other tools such as Monocle or SC3 may be preferable for malignant cell data.

We also observed that despite conceptual differences across the algorithms and quality metrics, some scRNA-seq datasets are consistently harder to cluster properly, such as the Lung and Melanoma dataset for which the unified clustering-quality scores are generally lower; whereas other datasets present much less difficulty, such as the Breast and Glioblastoma data for which such scores are consistently higher (Fig. 3).

The algorithms varied in terms of their performance (Table 4, Fig. 8). All the algorithms were running on high performance clusters with the default of one CPU core of 2.30 GHz, 60–120 GB of memory and virtual memory depending on the size of the datasets. The large datasets (Lung, Pancreatic, AML with greater than 30,000 cells) required 120 GB of memory while the smaller datasets (Breast, Colorectal with less than 10,000 cells) could successfully run with 60 GB or less. The same amount of RAM was used for all algorithms when running them on the same dataset, making the comparisons consistent across algorithms.

Fig. 8.

The heatmap represents the timing in minutes for each algorithm (rows) in each dataset (columns), by clustering malignant cells (left) and non-tumor cells (right). The left-most column in each heatmap represents the median values across all dataset versions.

There are several limitations in our study that can be improved upon. First, we could not obtain clustering partitions for some of the larger datasets due to poor algorithm scalability. Obtaining these metrics may potentially affect our final rankings. We also combined the three categories of measures on an equal basis, whereas one can devise a weighting scheme to express preferences. We also attempted to use several types of clustering ensembles but observed little if any improvement from using them. This did not justify the substantial increase in the complexity of the analysis, and therefore we did not pursue this direction further. However, a more systematic approach to ensemble clustering may be needed to make definitive conclusions about using ensembles as opposed to single top-performing algorithms for clustering.

Overall, we hope that this study demonstrates a robust and transparent approach to the ranking of scRNA-seq clustering methods, and as such will be useful to a wide range of practitioners.

5. Data availability

The data underling this article have been made available in a consistent format in our TMExplorer single-cell RNA-seq database and search tool [32]. The accession numbers (i.e., Gene Expression Omnibus (GEO), ArrayExpress (AE) or Genome Sequence Archive (GSA)) of all datasets are provided in the Table 2. The source codes of the analyses performed in this study are available in GitHub at https://github.com/shooshtarilab/Clustering/tree/master.

6. Funding information

This work was supported by Lawson Health Research Institute [Grant No R-20-303 to PS]; Natural Sciences and Engineering Research Council of Canada (NSERC) Discovery Grant [grant number DGECR-2021-00298 to PS]; and Genome Canada and Ontario Genomics [grant number OGI-167 to TP and MB]. PS is supported by the Children’s Health Research Institute and an Early Investigator Award from the Ontario Institute for Cancer Research. TP holds the Canada Research Chair in Translational Genomics and is supported by a Senior Investigator Award from the Ontario Institute for Cancer Research and the Gattuso-Slaight Personalized Cancer Medicine Fund at the Princess Margaret Cancer Centre.

CRediT authorship contribution statement

Alaina Mahalanabis: Methodology, Software, Validation, Formal analysis, Data curation, Visualization, Writing – original draft. Andrei Turinsky: Conceptualization, Methodology, Software, Validation, Formal analysis, Visualization, Writing – original draft. Mia Husic: Writing – original draft. Erik Christensen: Data curation, Visualization, Writing – review & editing. Ping Luo: Data curation. Alaine Naidas: Data curation. Michael Brudno: Funding acquisition, Writing – review & editing. Trevor Pugh: Funding acquisition, Writing – review & editing. Arun Ramani: Conceptualization, Supervision, Resources, Writing – original draft. Parisa Shooshtari: Conceptualization, Methodology, Supervision, Resources, Validation, Funding acquisition, Writing – original draft.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Appendix A. Supplementary data

The following are the Supplementary data to this article: