Abstract
The recent biotechnological progress has allowed life scientists and physicians to access an unprecedented, massive amount of data at all levels (molecular, supramolecular, cellular and so on) of biological complexity. So far, mostly classical computational efforts have been dedicated to the simulation, prediction or de novo design of biomolecules, in order to improve the understanding of their function or to develop novel therapeutics. At a higher level of complexity, the progress of omics disciplines (genomics, transcriptomics, proteomics and metabolomics) has prompted researchers to develop informatics means to describe and annotate new biomolecules identified with a resolution down to the single cell, but also with a high-throughput speed. Machine learning approaches have been implemented to both the modelling studies and the handling of biomedical data. Quantum computing (QC) approaches hold the promise to resolve, speed up or refine the analysis of a wide range of these computational problems. Here, we review and comment on recently developed QC algorithms for biocomputing, with a particular focus on multi-scale modelling and genomic analyses. Indeed, differently from other computational approaches such as protein structure prediction, these problems have been shown to be adequately mapped onto quantum architectures, the main limit for their immediate use being the number of qubits and decoherence effects in the available quantum machines. Possible advantages over the classical counterparts are highlighted, along with a description of some hybrid classical/quantum approaches, which could be the closest to be realistically applied in biocomputation.
Keywords: quantum algorithms, biomolecules, molecular modelling, genomics, quantum machine learning
Computational approaches in life science: from classical to quantum algorithms
The structure–function relationship of biomolecules
Biomolecules are the molecules governing the fate of living cells and organisms. The main classes of biomolecules are nucleic acids, proteins, carbohydrates and lipids (Figure 1). All of them are synthesized in the cells by the covalent polymerization of small monomeric units ultimately forming carbon-based macromolecules characterized by peculiar nanoscale three-dimensional conformations. For nucleic acids, four main nucleotides ensure the formation of linear polymers called DNA and RNA that respectively store the genetic information and regulate its expression, i.e. decide which gene asset is going to be translated into proteins in a certain cell type and at a certain moment of cell life [1]. In each diploid human cell, there are 46 paired DNA macromolecules named chromosomes that have a length spanning from 50 × 106 to 130 × 106 nucleotides; these macromolecules are formed by double-stranded DNA filaments and overall constitute the human cell genome [2]. On the other hand, RNA molecules are variable in length but smaller than DNA ones, and typically comprise single-stranded molecules spanning from a small-mid size of 20–400 nucleotides [3] for regulatory RNAs to 1–100 × 103 nucleotides for long non-coding RNAs and gene transcripts or messenger RNAs (mRNAs) [4].
Figure 1.
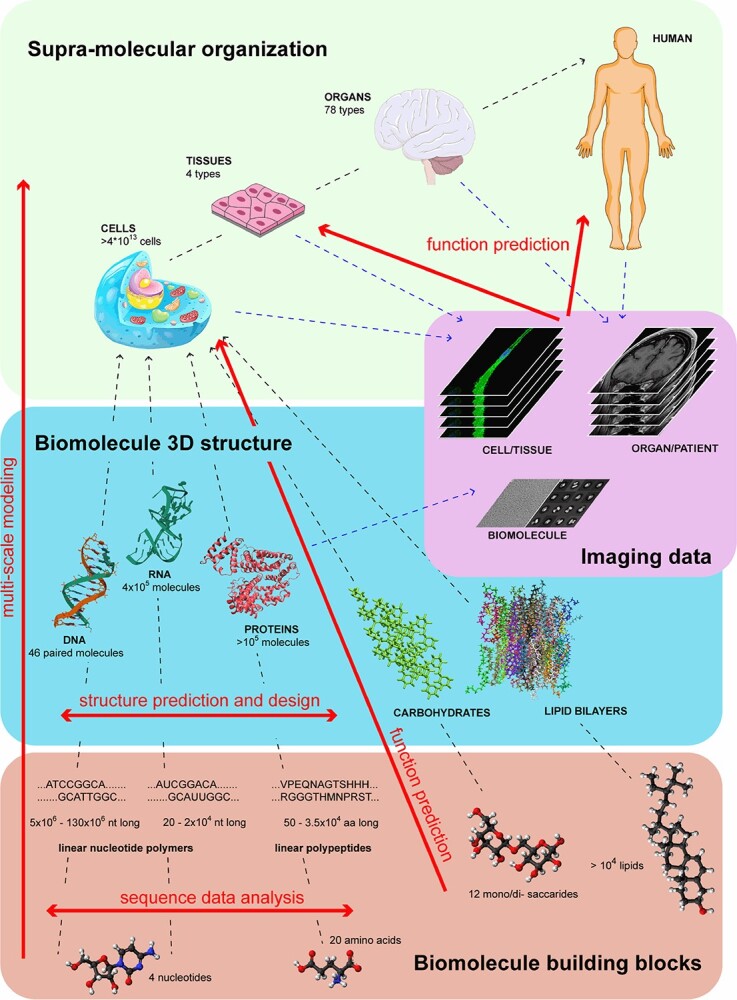
The biomolecule landscape: organization, numbers and possible computational approaches for investigation. The hierarchical organization of biomolecules is represented by dashed black arrows linking three different levels of biological complexity. Starting from the bottom (pink box), four small units named nucleotides, amino acids, mono/di- saccharides and lipids constitute the building blocks of biomolecules. For nucleic acids and proteins only, the first-synthesized linear polymers are represented on top of nucleotides and amino acids, respectively. The middle box (cyan box) includes the 3D structures of biomolecules. For all biomolecules, an exemplifying 3D spatial organization is reported (PBD structures 1BNA, 6C65 and 4L9K are used as DNA, RNA and protein structure, respectively; for carbohydrates, dextran is reported; finally, a lipid bilayer structure of lipids obtained by molecular dynamics simulation is reported). On top (green box), an exemplifying cell, tissue and human organism, representing the progressive supramolecular organization, are reported. The dashed blue arrows link different biomolecule sources to imaging data sets (purple box), which include a heterogeneous group of big data that can be analysed for biomolecule investigation. Superimposed on the landscape, the red arrows represent the computational approaches dealt with in this review, for which proof-of-concept quantum algorithms have been recently reported. The numbers reported are referred to the human cell and organism.
Genomes contain the information necessary for the cell to produce proteins; the higher the genome complexity, the larger the number of proteins that can be codified [5]. Proteins derive from the linear polymerization of mainly 20 amino acids into molecules called polypeptides. These can have a length shorter than 50 amino acids (in this case they are called peptides), but most typically comprise some hundreds of amino acids, with few outliers reaching up to >30 × 103 amino acids in humans [6–8]. Each amino acid has a common backbone structure, but importantly contains a unique side chain attached to the backbone. The side chain provides distinctive structural (size, shape) and physico-chemical properties (polarity, charge and hydrophobicity) to each amino acid, which can adopt a variety of different orientations (rotamers) in the space [9]. Once synthesized, the polypeptides then fold, i.e. assume a three-dimensional conformational structure held together mostly by non-covalent interactions [10]. Upon reaching the proper folding, proteins perform most of the structural and functional roles in a cell, such as building up the cell skeleton, serving as transporters of nutrients in and out of cells as well as acting as enzyme catalysing chemical reactions. Proteins constitute the antibodies produced by immune cells, as well as secreted hormones and growth factors.
In a similar way to nucleotides for nucleic acids and to amino acids for proteins, nine main types of monosaccharides and three main disaccharide units build up carbohydrates [11], ubiquitous biomolecules that are present within all cell types of microorganisms, plants and humans [12] and also in biological fluids [13]. Carbohydrates are constituted by long polymer chains whose structure is highly variable, being composed of few dozens to thousands repeating units that can elongate in both linear and branched configurations [12, 14]. In addition to the well-known role in metabolism and energy production, carbohydrates are crucial molecules in cellular signalling due to their ability to modify proteins substituting sugar chains to one or multiple sites of individual proteins, a process called glycosylation [15]. Glycoproteins expressed on the cell surface are involved in the fine-tuning of cell signalling in response to various extrinsic factors. Modes of glycosylation and the mechanisms of glycosylation involvement in the regulation of cell signalling are intriguing arguments in the glycobiology field [16].
The last major biomolecules listed here are lipids. These are fundamental building blocks of our cells; it is estimated that mammalian cells express tens of thousands of different lipids whose hydrocarbon chain length is variable from few to few tens of carbon atoms [17]. Lipids act either alone or undergo a regulated process of self-assembly to create structural elements of up to microscale dimensions comprising hundreds of different lipids such as the cell membranes. Cellular membranes isolate cells from their environment and compartmentalize the cell interior into organelles in higher organisms [18]. Besides the structural roles in forming both cell walls and membranes, lipids play a key role as direct energy source/storage and take part in cell physiology regulation. This is at least in part achieved via direct modulation or modification of protein structures [19].
Overall, biomolecules play a plethora of different biological functions in each cell of the human organism, and this is guaranteed by a wide range of sizes and structures reached by an ordered, hierarchical synthesis route (Figure 1). The understanding of the structure–function relationship of biomolecules is an evergreen hot topic in bio-oriented disciplines. Accordingly, in the last decades numerous computational approaches have been integrated to experimental methods to the fulfilment of this important task. The readers may find more details on computational approaches committed to the study of glycobiology and lipid biology elsewhere (see, e.g. [20–26]). Here, we will focus on computational approaches committed to the study of nucleic acids and proteins, for which quantum computing (QC) algorithms have recently started to be developed.
Molecular logic of life: biological complexity and generation of big data
A hierarchical organization is maintained also at higher levels of biological complexity. The synthesized biomolecules undergo an ordered process of assembly, by which first cells and then tissues and organs are formed, and up to 78 organs in humans build up the entire organism (Figure 1). The awareness of the number of biomolecules involved in the regulation of the human organism dates back to no more than 20 years ago, when the human genome was sequenced for the first time [27]. From that moment on, ground-breaking technological and computational advances allowed the development of high-throughput approaches to precisely describe the whole content of nucleic acids, proteins, other biomolecules and metabolites, in biological samples [28, 29]. It is now accepted that the total length of our genome, i.e. the sum of the linear length of our 46 chromosomes is of 6 × 109 paired nucleotides [30], and that the average number of RNA and protein molecules therein is respectively of 4 × 105 and >105 molecules. These data have corroborated the idea that DNA, RNA and proteins crucially undergo both interdependent and independent regulation in the cell environment [31]. Overall, these technologies are referred to as omics disciplines (http://omics.org/) and comprise e.g. genomics, transcriptomics, proteomics and metabolomics, whereby the addition of ‘omics’ to a biomolecule name implies a comprehensive, or global, assessment of this type of biomolecule in a cell, tissue or organism of interest [32].
Another type of big data in biology and health-care related applications is constituted by biomedical imaging data. These include all data stemming from the acquisition, processing and data analysis that tries to gain information from a digitized image series [33]. The imaged samples can be extremely variable (Figure 1). They can be derived from the optical or electron microscopy imaging of biological samples (purified biomolecules, isolated cell cultures, tissue or organ slices). In this context, the possibility to selectively and quantitatively investigate markers derived from molecular biology or biochemical analysis is increasingly being employed [34]. Also, this category includes all the huge amount of medical image data obtained from X-rays, CT-scan, MRI, etc., which can be used for predictive analysis in order to help diagnosis and improve prognosis in pathological anatomy and clinics [35]. Importantly, some types of image analysis involve the use of data packets in the order of terabytes. For example, a volume rendering analysis of rat spinal cord performed by synchrotron X-ray computer micro-tomography required circa 2400 projections over 360° rotation to obtain a spatial resolution of 2 μm voxel size and a total volume analysed of 4–6 mm per 0.25 cm spinal cord fragment; the analysis of the whole thoracic tract required at least four different scans [36]. For a standard biomedical approach, it is also necessary to handle the control samples in parallel with the treated/altered/pathological ones, so that the amount of data becomes significantly bigger. Furthermore, besides the memory required for data storage, additional computational cost is needed for the processing of the images in order to obtain a volume rendering, virtual slices or image segmentation. Thus, for this type of analyses a standard computer needs to access and process an impressive amount of data at the same time.
Computational approaches for biomolecule investigation
As outlined above, the space of investigation of biomolecules structure and function spans over increasing degrees of complexity (Figure 1). Several computational approaches have been developed to help navigate this space. As summarized in Figure 1, they can be roughly categorized into four different groups:
(1) Sequence analysis algorithms, i.e. algorithms supporting the analysis of DNA, RNA or protein sequences stemming from omics data [37]. These algorithms are mainly intended to (i) detect the presence and mapping the sequence of genes, transcripts and proteins in a particular biological sample and (ii) find interaction relationships among them in the same biological sample or across biological samples of different sources.
(2) Structure and function prediction algorithms, a highly heterogeneous group of computational methods. These include algorithms developed to predict the three-dimensional protein [38] or RNA [39] structures from the relative amino acid or nucleotide sequence. Additionally, other algorithms are aimed to predict gene or protein functions [40] using sequences or other features, e.g. those annotated in paradigms like Gene Ontology (GO) [41] or MIPS Functional Catalog (FunCat) [42]. Also, this category includes the algorithms developed to complement, improve and standardize the analysis of biomedical image data sets.
(3) Design algorithms, i.e. the group of algorithms aimed at designing in silico protein structures or other biomolecules with specific desired three-dimensional structure for biotechnology and therapeutic applications [43].
(4) Multi-scale modelling algorithms, i.e. algorithms used to model and simulate molecular systems at a certain time and length scale [44]. At the finest resolution, relatively small systems (up to few tens of atoms) are treated quantum mechanically. Larger systems can then be modelled relying on an approximate and simplified description of the interactions among the atoms—the so-called molecular mechanics (MM)—derived, at least conceptually, from the underlying quantum mechanical (QM) description. Less detailed, coarse-grained models can be employed at larger scales [45]. Within this category, the QM methods are, by far, the most computationally intensive.
Interestingly, in recent years the possibility of using quantum instead of or in combination with classical computing to solve biocomputing problems has emerged [46, 47]. In this review, we aim to describe the potential of QC for biocomputation, and then to focus on selected quantum algorithms which could revolutionize the computational analysis of biomedical data sets. Our intent is also to expand the communication channels of QC, reaching the interest of life scientists interested in the fields of bioinformatics and computational biology.
A primer in QC
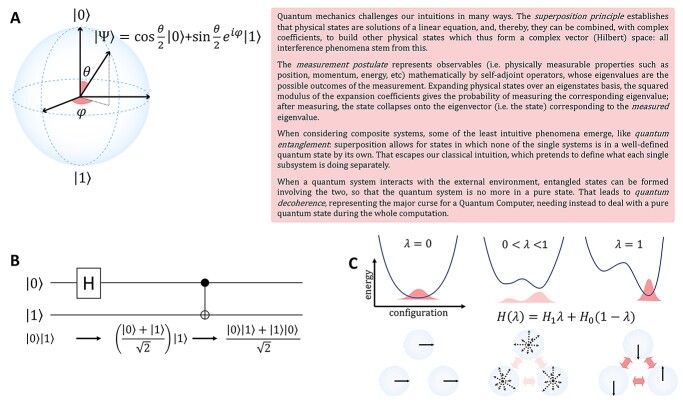
There are various differences between classical and quantum hardware. A classical computer manipulates the information stored in binary elementary memory units, bits, according to algorithms built on arithmetic and logical operations. A quantum computer manipulates the quantum state of a system composed of n qubits. Quantum mechanics describes the state of a single qubit as the normalized linear superposition, with complex coefficients, of two basis states, 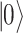 and
and 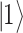 (Figure 2A). That already means more information than a bit; however, the complexity grows exponentially when considering n qubits as a whole. Their state is the superposition of all possible basis states
(Figure 2A). That already means more information than a bit; however, the complexity grows exponentially when considering n qubits as a whole. Their state is the superposition of all possible basis states 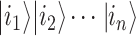 , where
, where 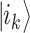 is one of the
is one of the 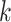 th qubit basis state i.e. either
th qubit basis state i.e. either 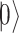 or
or 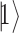 . Because of quantum entanglement, the information is far more than assigning the state of each qubit separately, and corresponds to a normalized complex vector in
. Because of quantum entanglement, the information is far more than assigning the state of each qubit separately, and corresponds to a normalized complex vector in 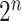 dimensions. If we add a qubit, the dimension of the Hilbert space doubles. A quantum algorithm moves the system across the state space by applying a series of unitary operators (representable classically by unitary
dimensions. If we add a qubit, the dimension of the Hilbert space doubles. A quantum algorithm moves the system across the state space by applying a series of unitary operators (representable classically by unitary 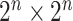 complex matrices): after that, some measurement is taken, which typically makes the state unusable for further processing. In a few words, the strengths of QC are complexity (the amount of processable information) and linearity (the possibility of performing the computation in parallel on an arbitrary superposition of states) (Figure 2).
complex matrices): after that, some measurement is taken, which typically makes the state unusable for further processing. In a few words, the strengths of QC are complexity (the amount of processable information) and linearity (the possibility of performing the computation in parallel on an arbitrary superposition of states) (Figure 2).
Figure 2.
Principles of quantum computing. (A) Graphical representation of a qubit. The two basis state 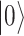 and
and 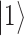 can be physically realized as, for example, two electronic states of a trapped ion, or two quantum states of a superconducting circuit. In contrast to the classical bit, the qubit can exist in a superposition
can be physically realized as, for example, two electronic states of a trapped ion, or two quantum states of a superconducting circuit. In contrast to the classical bit, the qubit can exist in a superposition 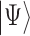 of these two states, described by the linear combination of
of these two states, described by the linear combination of 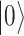 and
and 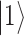 with complex coefficients. Probability conservation implies that physical states need to be properly normalized: a global phase and normalization factor are irrelevant; this is why a qubit is fixed by only two independent real parameters (
with complex coefficients. Probability conservation implies that physical states need to be properly normalized: a global phase and normalization factor are irrelevant; this is why a qubit is fixed by only two independent real parameters (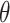 and
and 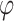 ), defining the so-called Bloch sphere. For the same reason, operators defining the evolution of physical states must be unitary, in order to preserve normalization. The pink box on the right contains a short summary of the quantum mechanical principles relevant to QC. (B) Schematic representation of an elementary quantum circuit leading to an entangled two-qubit state. The system is initially in a physical state for which the state of each single qubit is well defined, i.e.
), defining the so-called Bloch sphere. For the same reason, operators defining the evolution of physical states must be unitary, in order to preserve normalization. The pink box on the right contains a short summary of the quantum mechanical principles relevant to QC. (B) Schematic representation of an elementary quantum circuit leading to an entangled two-qubit state. The system is initially in a physical state for which the state of each single qubit is well defined, i.e. 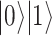 meaning that the first qubit is in
meaning that the first qubit is in 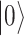 and the second in
and the second in 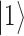 . The application of the Hadamard (H) gate followed by the CNOT gate (realized by sequential physical operations on the qubit system) leads to an entangled state,
. The application of the Hadamard (H) gate followed by the CNOT gate (realized by sequential physical operations on the qubit system) leads to an entangled state, 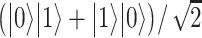 , which is well defined only globally, i.e. neither single system is in a well-defined quantum state by its own. For a composite system, the great majority of physical states are entangled, and thus escape our classical intuition. (C) In the quantum annealing process, the qubits are physically evolved from a situation governed by a Hamiltonian
, which is well defined only globally, i.e. neither single system is in a well-defined quantum state by its own. For a composite system, the great majority of physical states are entangled, and thus escape our classical intuition. (C) In the quantum annealing process, the qubits are physically evolved from a situation governed by a Hamiltonian 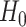 , for which the ground state is known, to a situation governed by
, for which the ground state is known, to a situation governed by 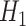 , whose unknown ground state encodes the solution of the problem. The curved lines show an idealized energy profile evolving according to the parameter
, whose unknown ground state encodes the solution of the problem. The curved lines show an idealized energy profile evolving according to the parameter 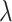 , for the two extreme cases (
, for the two extreme cases (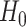 at
at 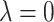 and
and 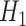 at
at 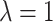 ) and for an intermediate value of
) and for an intermediate value of 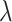 . The state of the system (pink shaded areas) evolves accordingly, and the adiabatic theorem ensures that, if the evolution is slow enough, the final state is the ground state of
. The state of the system (pink shaded areas) evolves accordingly, and the adiabatic theorem ensures that, if the evolution is slow enough, the final state is the ground state of 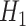 . On the bottom, the process is depicted for a three-qubit system. The evolution is realized through the controlled variation of interaction terms (pink arrows). At the end, the system is in a state where each single qubit has a defined state (
. On the bottom, the process is depicted for a three-qubit system. The evolution is realized through the controlled variation of interaction terms (pink arrows). At the end, the system is in a state where each single qubit has a defined state (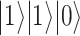 in the example), and which represents the solution to the problem. Note that the Bloch sphere representation can be used only for the initial and final states, while it would be incomplete for the intermediate entangled states.
in the example), and which represents the solution to the problem. Note that the Bloch sphere representation can be used only for the initial and final states, while it would be incomplete for the intermediate entangled states.
There are two main realizations of quantum hardware: analog or digital. In the first case, one builds a controlled quantum system, which resembles a particular case of interest and evolves according to its own physical laws, thus furnishing some information about the original problem. In the second case, the state is evolved through a programmable series of quantum gates (typically involving 1-qubit and 2-qubit gates each time, Figure 2B), by which any unitary operation can be reconstructed: different systems should be mappable onto such machine, up to digital precision, so this represents the ‘general purpose’ version of QC, which is experiencing a rapid evolution. Quantum annealers (Figure 2C), like D-Wave machines, represent a particular type of analog quantum computer, suited to optimization problems: the system is prepared in the ground (minimal energy) state of a starting Hamiltonian, which is then evolved into a programmable Hamiltonian of interest, exploiting the fact that, if the evolution is slow enough, the system keeps staying in the ground state (adiabatic theorem).
Is QC feasible? The ideal machine should contain a scalably large number of qubits with external interactions only through perfect quantum gates, keeping them in a pure quantum state (i.e. not entangled with the rest of the world) during the algorithm execution: this is far from being realizable. Present technologies for building qubits are based on superconductors, cold atoms, trapped ions and Rydberg atoms (see Refs [48–51] for recent reviews) and presently scale up to O(102) qubits (O(103) for annealers). An additional problem is that the number of quantum gates (the so-called circuit size) after which decoherence and other faults ruin the computation is presently limited to O(102), making various quantum algorithms non-implementable.
Such problems can be solved only in a long-term perspective: fault-tolerant qubits could be based on the entangled state of many standard qubits [52], but that would largely increase the required qubits, and one should also consider the increased time requested for each elementary operation [53, 54]. The near term perspective is Noisy Intermediate-Scale Quantum (NISQ) computing [55]: the quantum hardware is used only to run short depth circuits as part of more complex algorithms involving also classical hardware, i.e. the quantum computer is used as an accelerator.
QC in the life sciences
Noteworthy, QC approaches have been proposed so far for many of the computational problems listed above. An example we would like to mention is machine learning, for which the possibility to implement QC algorithms has been recently explored. Machine learning and deep learning techniques have been developed to extract features from data sets, detect patterns in the extracted data and use this information to classify the data sets [56]. These tasks can be performed on most of the biological data sets, and indeed machine learning has been demonstrated to improve the performance of most of the above-mentioned computational tasks [57]. In particular, machine learning holds great potential for the analysis of complex data sets such as biomedical imaging data (Figure 1), for which the classification and comparative analysis of different experimental classes of samples are necessary to determine all the possible sites of alteration that may be missed by the operator investigation and to make analysis as objective as possible. Of course, the final interpretation or evaluation of the biological meaning of a difference/variation observed remains the operator role, but in this condition, the difference is detected by the machine autonomously, automatically and objectively. As concerns quantum approaches, they have been proposed to improve the classification process [58, 59], either by development of quantum neural networks [60–62] or, more recently, by development of a quantum support vector machine [63]. Several approaches have been proposed to train a network using QC technology in a more accurate, robust and quick way. Most of them are reviewed elsewhere in detail [46, 47]. However, we underline here that given the current state of quantum machines and the limited number of available qubits, hybrid strategies have been recently proposed, which could possibly achieve practical and usable solutions with the existing technology. Amongst such strategies, one of the most interesting ones for biological classification is the hybrid transfer learning approach [64]. Transfer learning is a classic deep learning technique in which the knowledge that a neural network learnt for a given domain is applied to another domain to cope with training time and the lack of training examples. In the context of QC, the idea is to exploit classic deep learning networks on a standard computer [65–67] to extract features from biological images and then apply variational quantum circuits [68] to classify the extracted features. The main advantage of such an approach is that the quantum machine does not need to handle images, which may require many qubits, and the classification achieves high accuracy. Even though this reasonable hybrid strategy was demonstrated on Rigetti and IBM machines with success [64], the applicability to more complex problems is still an issue due to the limited number of features that the quantum circuit can handle as input. Nevertheless, this is one of the most promising efforts that goes beyond very simplistic toy examples.
Another computational problem for which quantum approaches have been proposed is the prediction of a protein structure starting from the linear polypeptide sequence. Protein folding is a stepwise process in which the polypeptide chain explores the configurational space and adopts a variety of structures, until the structure leading to minimal free energy is reached. One can roughly estimate that a protein of N amino acids can adopt up at least 3N possible 3D structures [69]. The understanding of this process has puzzled biochemists for decades and prompted the development of a truly interdisciplinary field comprising also experimental and theoretical biophysicists, structural biologists and computational biologists [43, 70]. Quantum annealing has been applied to the protein folding problem [71, 72], using simplified lattice models for the polypeptide chain. Each site in the lattice is mapped into a qubit and the Hamiltonian contains terms dictating the connectivity of the peptide and describing the intra-peptide interactions. The solution to the folding problem is thereby reformulated in terms of finding the minimum-energy configuration on this lattice by quantum annealing. Robert et al. [73] report a quantum gate-based approach to protein folding on a lattice, using a modified version of the VQE algorithm (discussed in the next section) and requiring a number of qubits that scales quadratically with the number of amino acids. These approaches are aimed at studying protein folding from a statistical mechanics perspective rather than at providing biomolecular structures for practical applications. Indeed in the context of protein structure prediction, physical-based methods are hardly expected to compete with artificial intelligence software such as Alphafold 2 [74] and RoseTTAFold [75]. An impact of QC on the protein structure prediction problem is more likely (if at all) to happen via the development of quantum machine learning algorithms (see comment in [74]). Other attempts to address biopolymer structural properties with quantum annealing algorithms have considered realistic all-atom models, focusing on finding most probable transition paths between different conformations [76].
Quantum annealing is also suitable to the problem of protein design [43, 77, 78], i.e. finding the amino acid sequence that minimizes the energy of a chosen main-chain configuration. The design computational problem resembles the protein folding one, in that the configurational space is explored until the sequence leading to minimal free energy is identified; however, the protein design space is even bigger than the protein folding one, as 20N configurations are possible when designing a protein of N amino acids [78]. For each position in the sequence, a chosen selection of rotamers is mapped into an equal number of qubits. The total energy can be separated into pairwise interactions that are pre-calculated (classically) for each possible choice of rotamers. The Hamiltonian contains these pairwise interactions together with terms that ensure that only one rotamer per position is feasible, by assigning high energy to situations where a single position is occupied by more than one rotamer. A proof-of-principle application led to the design of a 32-amino-acid long peptide on a D-Wave 2000Q system [79].
Gate-based quantum algorithms are also being proposed to address biopolymer conformations, including a hybrid approach combining quantum Monte Carlo and machine learning for protein structure prediction [80], another quantum Monte Carlo approach to antibody loop modelling [54] and protein design exploiting Grover’s algorithm [81].
Finally, promising quantum approaches have been also proposed in the multi-scale modelling of biomolecules and in the analysis of omics, and in particular genomics, data sets. These will be deepened in the next two paragraphs, respectively.
Quantum algorithms for the molecular modelling of biomolecules
Introduction to the computational problems
There might seem to be a wide gap between the complexity of biological macromolecules on one side and, on the other, a fully reductionist approach treating these systems as a set of atomic nuclei and electrons obeying the Schrödinger equation. Molecular simulations of proteins and nucleic acids generally adopt much simplified models [82], where the interactions among atoms in the system are described classically (as opposed to quantum mechanically) by empirical MM force fields. These methods are mostly used to address the dynamics of biomolecules, their folding and conformational transitions, and the interactions among the various components. QM methods are, however, of fundamental importance to biomolecular simulations. On the one hand, some processes (biochemical reactions, light harvesting in photosynthesis, the process of vision) can be accurately described only taking into account the electronic structure of a subsystem. Different descriptions can be combined within the same simulation. For example, in hybrid QM/MM simulations, a portion of the system is described by a QM method and the rest of the system is instead treated using a MM force field. This is a way to model enzymatic reactions, photophysical/photochemical processes or excitation and emission of photoactive proteins, which are usually confined to the active site [43, 77, 78]. On the other hand, QM methods can be considered the cornerstone of MM models, by providing benchmarks for comparison and an understanding of emerging molecular forces.
The set of theoretical and computational QM methods addressing the properties of atomic and molecular systems starting from their quantum mechanical wave function and its evolution, as determined by the Schrödinger equation, is referred to as quantum chemistry. The focus in quantum chemistry is to solve the electronic structure problem; indeed, the nuclei are mostly treated as classical particles. Much emphasis is placed on finding the ground-state energy of the electronic wavefunction at different molecular configurations. For example, the gradient of the ground-state energy with respect to the molecular coordinates can be used to find the geometry of minimum energy and of transition states, the Hessian is related to the vibrational spectrum, the electronic density gives the molecular electrostatic potential and so on. Quantum chemistry methods have been implemented in classical computation schemes, achieving, for many molecular systems, an accuracy and an efficiency that allow them to be routinely used for predicting the behaviour of molecular systems and interpreting experimental results [83]. However, as we will discuss below, some systems cannot be accurately addressed with current QM classical computation schemes and hardware. In principle, quantum algorithms could provide an exponential speed up to the ‘exact’ solution of the electronic structure problem [84]. Thereby, a considerable research effort has been recently focused on the design of quantum algorithms for quantum chemistry [85, 86], on the possible implementation of such algorithms in near term and long-term quantum hardware [87, 88], and on the identification of practical problems for which quantum advantage may be feasible in the future [89, 90]. Indeed, the electronic structure problem is considered to be among the first practical applications of QC [91]. Why is the electronic structure problem amenable to quantum algorithms? We wish to provide the readership with a basic answer to this question, with no attempt at being exhaustive. Detailed accounts of quantum chemistry in the context of quantum computation may also be found in other recent reports [86, 89, 92].
In quantum chemistry, wavefunctions are expanded in finite basis sets to make their computation tractable. Most commonly one starts from a certain molecular configuration (i.e. position of the nuclei in the molecule), which gives rise to a set of spin orbitals 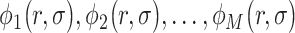 describing the value of the single-electron states as a function of the position vector
describing the value of the single-electron states as a function of the position vector 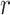 and of the spin
and of the spin 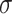 . These are at least as many as needed to accommodate the
. These are at least as many as needed to accommodate the 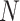 electrons in the system, but usually many more, as larger basis sets improve the accuracy of the calculation. The simplest approximated wavefunction for the ground state is the suitably anti symmetrized product (the Slater determinant) of the
electrons in the system, but usually many more, as larger basis sets improve the accuracy of the calculation. The simplest approximated wavefunction for the ground state is the suitably anti symmetrized product (the Slater determinant) of the 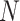 lowest-energy spin orbitals
lowest-energy spin orbitals
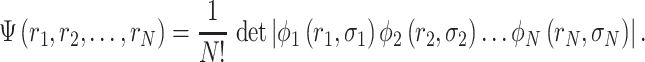 |
(1) |
Here, 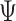 is the multi-electron wavefunction,
is the multi-electron wavefunction, 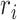 and
and 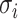 is the spatial and spin coordinate of the
is the spatial and spin coordinate of the 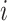 th electron. This state can be written as a
th electron. This state can be written as a 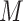 -long string of 1s and 0s, where 1 (0) indicates a (un)occupied spin orbital, i.e.
-long string of 1s and 0s, where 1 (0) indicates a (un)occupied spin orbital, i.e. 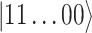 . States that are accurately described by such a single product, or single configuration, or single reference, are relatively easy to simulate. However, there are cases in which this approach fails to even qualitatively capture the behaviour of the system: covalent bond formation and breaking in chemical reactions, electronically excited states, systems containing transition metals and so on require more than one reference for their accurate simulation. In principle, the solution for these strongly correlated systems can be found by expanding the wavefunction in the basis set of all possible (anti-symmetrized) products of spin orbitals with occupation numbers compatible with
. States that are accurately described by such a single product, or single configuration, or single reference, are relatively easy to simulate. However, there are cases in which this approach fails to even qualitatively capture the behaviour of the system: covalent bond formation and breaking in chemical reactions, electronically excited states, systems containing transition metals and so on require more than one reference for their accurate simulation. In principle, the solution for these strongly correlated systems can be found by expanding the wavefunction in the basis set of all possible (anti-symmetrized) products of spin orbitals with occupation numbers compatible with 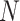 , the total number of electrons. This is the so called ‘full configuration interaction’ (FCI) approach [93], which gives the most accurate wavefunctions within the chosen basis set of single-electron states. If
, the total number of electrons. This is the so called ‘full configuration interaction’ (FCI) approach [93], which gives the most accurate wavefunctions within the chosen basis set of single-electron states. If 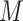 spin orbitals are used, there are
spin orbitals are used, there are 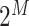 possible products (the Fock space), of which
possible products (the Fock space), of which 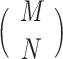 have the right occupation in terms of the total number of electrons. Even using only two spin orbitals per electron, the number of terms in these expansions, and hence the required computational resources, grow exponentially with the size of the system. This is the reason why current FCI calculations are limited to very small systems of only a few atoms, and are mostly used as benchmarks for comparison with other approximate methods.
have the right occupation in terms of the total number of electrons. Even using only two spin orbitals per electron, the number of terms in these expansions, and hence the required computational resources, grow exponentially with the size of the system. This is the reason why current FCI calculations are limited to very small systems of only a few atoms, and are mostly used as benchmarks for comparison with other approximate methods.
More commonly, in dealing with multireference states, the configuration interaction expansion is restricted to a set of chosen molecular orbitals, called the active space, contiguous in energy to the frontier orbitals (the HOMO, or highest occupied molecular orbital, and the LUMO, or lowest unoccupied molecular orbital). In the CASSCF (complete active space self-consistent field) approach [93], an FCI expansion of the subspace of 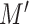 active-space spin orbitals and the
active-space spin orbitals and the 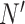 active-space electrons is coupled to orbital optimization (the SCF part). Notwithstanding this restriction, the terms needed in the CASSCF FCI expansion easily reach the limits of manageability by classical computational resources, the current record being at 22 electrons in 22 molecular orbitals, leading to 5 × 1011 terms [94].
active-space electrons is coupled to orbital optimization (the SCF part). Notwithstanding this restriction, the terms needed in the CASSCF FCI expansion easily reach the limits of manageability by classical computational resources, the current record being at 22 electrons in 22 molecular orbitals, leading to 5 × 1011 terms [94].
The interest in developing quantum algorithms for solving the electron structure problem of biomolecules is that quantum computers are naturally suitable to manipulate deeply entangled quantum states such as the multi-reference wavefunctions of correlated systems. Indeed, quantum algorithms that fit these purposes, such as the Hamiltonian simulation or Hamiltonian averaging, are expected to scale polynomially rather than exponentially with the system size [84, 95]. This different scaling makes all the difference because it would avoid the blow-up of computational requirements that FCI and other methods for correlated systems inevitably meet at increasing size of the molecular system. In the proposed schemes, the quantum computer acts as an accelerator of the subroutines for which the classical computation scaling is worse, such as the FCI part in the CASSCF method. However, the demonstration of real quantum advantage will need to compete with the impressive development of classical algorithms for tackling the FCI problem, such as, among others, FCI Monte Carlo and Density Matrix Renormalization Group (see, e.g. [96] for a recent perspective).
Promising quantum algorithms
In a quantum computer, a general quantum state in the Fock space of 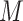 spin orbitals can be encoded in a superposition of
spin orbitals can be encoded in a superposition of 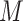 qubits. This is to be contrasted with the
qubits. This is to be contrasted with the 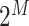 amplitudes needed to identify such a state in a classical computation scheme. The simplest mapping (known as the Jordan–Wigner mapping [97]) identifies the
amplitudes needed to identify such a state in a classical computation scheme. The simplest mapping (known as the Jordan–Wigner mapping [97]) identifies the 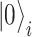 and
and 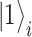 states of the
states of the 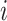 -th qubit with the unoccupied and occupied
-th qubit with the unoccupied and occupied  -th spin orbital. For example, a four-electron state in a six spin-orbital Fock space such as
-th spin orbital. For example, a four-electron state in a six spin-orbital Fock space such as 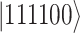 would be encoded in a register of six qubits simply as
would be encoded in a register of six qubits simply as 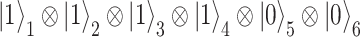 , where the subscript identifies the qubit. One complication arises from the need to take into account the symmetry under electron exchange, because electrons, in contrast to the qubits, are indistinguishable. In the case of the Jordan–Wigner mapping this means that the number of gates needed to realize the basic creation and annihilation operators increases linearly with the number of electrons in the system. Other encodings, such as the one devised by Bravyi–Kitaev [98], lead instead to a more convenient logarithmic scaling. The choice of the encoding determines how the various quantum operators, most importantly, the Hamiltonian of the system, are written in terms of products of single-qubit Pauli operators, i.e. single-qubit gates. The properties of the simulated system (e.g. the ground-state energy) can then be computed as expectation values of operators on the qubit superposition. With respect to the classical computational approach where all amplitudes of a wavefunction are easily accessed, the amplitudes of a wavefunction stored in qubits are not readily available. This is the reason why carefully designed quantum algorithms need to be employed to realize efficient quantum simulations.
, where the subscript identifies the qubit. One complication arises from the need to take into account the symmetry under electron exchange, because electrons, in contrast to the qubits, are indistinguishable. In the case of the Jordan–Wigner mapping this means that the number of gates needed to realize the basic creation and annihilation operators increases linearly with the number of electrons in the system. Other encodings, such as the one devised by Bravyi–Kitaev [98], lead instead to a more convenient logarithmic scaling. The choice of the encoding determines how the various quantum operators, most importantly, the Hamiltonian of the system, are written in terms of products of single-qubit Pauli operators, i.e. single-qubit gates. The properties of the simulated system (e.g. the ground-state energy) can then be computed as expectation values of operators on the qubit superposition. With respect to the classical computational approach where all amplitudes of a wavefunction are easily accessed, the amplitudes of a wavefunction stored in qubits are not readily available. This is the reason why carefully designed quantum algorithms need to be employed to realize efficient quantum simulations.
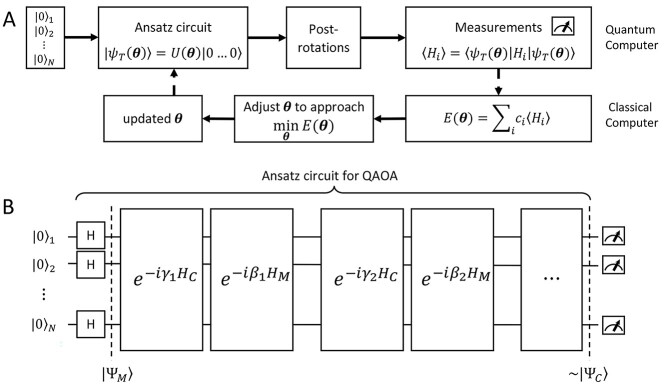
Broadly speaking, the ‘digital’ quantum computation approaches for the electronic structure problem focus on two families of algorithms: the variational quantum eigensolver (VQE) and quantum phase estimation (QPE). VQE [99] (Figure 3A) adopts a hybrid approach combining quantum and classical computation. It is based on the Ritz-Rayleigh variational principle, stating that the expectation value of the Hamiltonian (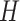 ) of a normalized trial quantum state of a system
) of a normalized trial quantum state of a system 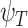 is always larger than the ground-state energy eigenvalue (
is always larger than the ground-state energy eigenvalue (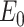 )
)
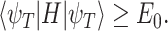 |
(2) |
Figure 3.
(A) Scheme of VQE. Starting from the initialized state where all the qubits are set to  (
(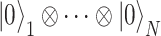 ), a trial state (commonly called with the German word ansatz) is prepared using a quantum circuit (the ansatz circuit) whose operations are parametrized by a set of variational parameters
), a trial state (commonly called with the German word ansatz) is prepared using a quantum circuit (the ansatz circuit) whose operations are parametrized by a set of variational parameters 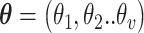 (e.g. single-qubit rotations, each parameterized by some angle
(e.g. single-qubit rotations, each parameterized by some angle 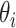 ). The choice of the ansatz circuit determines which subspace of the general Hilbert space can be spanned by the variational procedure. The electronic structure Hamiltonian can be written as a sum of appropriately weighted products of single-qubit operations, i.e.
). The choice of the ansatz circuit determines which subspace of the general Hilbert space can be spanned by the variational procedure. The electronic structure Hamiltonian can be written as a sum of appropriately weighted products of single-qubit operations, i.e. 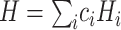 , where
, where 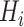 is, for example,
is, for example, 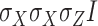 , implying
, implying 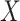 rotation on the first and second qubits,
rotation on the first and second qubits, 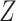 rotation on the third, identity on the fourth, in a four-qubit register. Each
rotation on the third, identity on the fourth, in a four-qubit register. Each 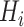 term is evaluated separately, and post-rotations can be needed to rotate the single qubits to the measurement basis (in the example, the first two qubits need to be rotated in order to measure
term is evaluated separately, and post-rotations can be needed to rotate the single qubits to the measurement basis (in the example, the first two qubits need to be rotated in order to measure 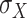 ). Thanks to these operations, the expectation value of each product in the Hamiltonian can be written in terms of the probabilities of each possible outcome, implying that, for each global cycle, a sufficiently large number of state preparation and measurement cycles needs to be performed (Hamiltonian averaging). The measurements (i.e. the probabilities of each possible outcome) are passed to the training/optimization subroutine on the classical computer, whose task is to calculate
). Thanks to these operations, the expectation value of each product in the Hamiltonian can be written in terms of the probabilities of each possible outcome, implying that, for each global cycle, a sufficiently large number of state preparation and measurement cycles needs to be performed (Hamiltonian averaging). The measurements (i.e. the probabilities of each possible outcome) are passed to the training/optimization subroutine on the classical computer, whose task is to calculate 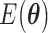 and provide a new set of
and provide a new set of 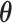 based on the previous history of
based on the previous history of  values. The cycle is repeated until convergence. (B) The ansatz circuit for the Quantum Approximate Optimization Algorithm (QAOA) used in the QuASer (see main text). The QUBO problem of finding the optimal solution of a quadratic Hamiltonian is recast into a quantum annealing form
values. The cycle is repeated until convergence. (B) The ansatz circuit for the Quantum Approximate Optimization Algorithm (QAOA) used in the QuASer (see main text). The QUBO problem of finding the optimal solution of a quadratic Hamiltonian is recast into a quantum annealing form 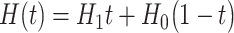 , where
, where 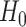 is the ‘simple’ mixing Hamiltonian
is the ‘simple’ mixing Hamiltonian 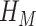 whose ground state is the equal superposition of all basis states
whose ground state is the equal superposition of all basis states 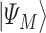 and is obtained after the application of Hadamard gates to all the qubits.
and is obtained after the application of Hadamard gates to all the qubits. 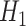 is the cost Hamiltonian
is the cost Hamiltonian 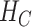 and is defined in such a way that its ground state
and is defined in such a way that its ground state 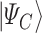 corresponds to the QUBO solution. The adiabatic evolution that would lead from
corresponds to the QUBO solution. The adiabatic evolution that would lead from 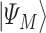 to
to 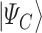 is approximated by the sequential application of
is approximated by the sequential application of 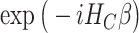 and
and 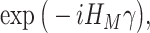 where the
where the 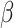 s and
s and 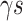 , the ‘time steps’ of the evolution, are the variational parameters (i.e. the
, the ‘time steps’ of the evolution, are the variational parameters (i.e. the 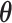 set) to be optimized by the classical subroutine.
set) to be optimized by the classical subroutine.
The quantum state is described by a set of parameters that are iteratively updated by the classical part, after receiving the results of the measurements (i.e. the expectation value, 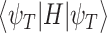 ) which are delegated to the quantum subroutine, via Hamiltonian averaging (Figure 3A). The number of cycles in Hamiltonian averaging scales as the square inverse of the precision
) which are delegated to the quantum subroutine, via Hamiltonian averaging (Figure 3A). The number of cycles in Hamiltonian averaging scales as the square inverse of the precision 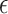 in the energy estimation, i.e. it is
in the energy estimation, i.e. it is 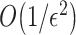 . Each step of the scheme in Figure 3A hides many possible choices which are the topics of intensive current research (see [100–102] for recent accounts). These regard for example how to group and/or approximate the various terms in the Hamiltonian in order to optimally reduce the number of subcycles for Hamiltonian averaging, and how to strike a good balance between hardware efficiency and chemical intuition in the choice of the ansatz. Indeed, the success of the algorithm largely depends on this choice which determines the general form of the state, as it can be demonstrated that the gradient of the expectation value decays exponentially as a function of the number of qubits if the trial state is chosen randomly [103] (a vanishing gradient is problematic for the classical optimization subroutine). One commonly explored route to obtain a generally valid ansatz is by the unitary coupled cluster method [104]. The attractive feature of VQE is that it requires relatively short circuits, i.e. rather short qubit coherence, and, thanks to its variational nature, gate errors may be partially compensated for, allowing its implementation in short-term NISQ. So far, VQE experiments have been performed for some small and simple molecules, such as H2, LiH, H2O, up to H12 and diazene on 2–12 qubits [90]. These molecules are very well within the reach of accurate classical algorithms, so these applications should be considered as first realizations of quantum chemistry calculations with quantum computers. Interestingly, a VQE-based method has been proposed for the accurate calculation of ligand–protein interaction energies [105]. The method is applied to lysine-specific demethylase 5A (KDM5A) using a classical computer simulation of a 16-qubit quantum computation.
. Each step of the scheme in Figure 3A hides many possible choices which are the topics of intensive current research (see [100–102] for recent accounts). These regard for example how to group and/or approximate the various terms in the Hamiltonian in order to optimally reduce the number of subcycles for Hamiltonian averaging, and how to strike a good balance between hardware efficiency and chemical intuition in the choice of the ansatz. Indeed, the success of the algorithm largely depends on this choice which determines the general form of the state, as it can be demonstrated that the gradient of the expectation value decays exponentially as a function of the number of qubits if the trial state is chosen randomly [103] (a vanishing gradient is problematic for the classical optimization subroutine). One commonly explored route to obtain a generally valid ansatz is by the unitary coupled cluster method [104]. The attractive feature of VQE is that it requires relatively short circuits, i.e. rather short qubit coherence, and, thanks to its variational nature, gate errors may be partially compensated for, allowing its implementation in short-term NISQ. So far, VQE experiments have been performed for some small and simple molecules, such as H2, LiH, H2O, up to H12 and diazene on 2–12 qubits [90]. These molecules are very well within the reach of accurate classical algorithms, so these applications should be considered as first realizations of quantum chemistry calculations with quantum computers. Interestingly, a VQE-based method has been proposed for the accurate calculation of ligand–protein interaction energies [105]. The method is applied to lysine-specific demethylase 5A (KDM5A) using a classical computer simulation of a 16-qubit quantum computation.
A critical assessment of the potentiality of VQE algorithms in the long run needs to take into account that they are heuristic methods, because, rather than providing the exact result, they give an upper bound to the energy. As such, they are not guaranteed to yield better approximations with respect to classical methods. Moreover, as the molecule size increases, VQE requires a larger number of sub cycles for Hamiltonian averaging (because of more terms in the Hamiltonian), projecting to unfeasibly long runtime for systems of practical importance [90, 102, 106, 107]. In addition, the training/optimization of the ansatz parameters (the 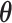 in Figure 3) has already been proven to be nondetermistic polynomial-time hard (NP-hard) [108]. The issues of trainability, accuracy and efficiency of VQE are also discussed in ref. [109]. Very recent works explore routes to alleviate some of these problems [110–112].
in Figure 3) has already been proven to be nondetermistic polynomial-time hard (NP-hard) [108]. The issues of trainability, accuracy and efficiency of VQE are also discussed in ref. [109]. Very recent works explore routes to alleviate some of these problems [110–112].
QPE is a central subroutine of many quantum algorithms [84, 113] and can be applied to the electronic structure problem rather straightforwardly. The QPE outcome is an estimation of the phase 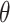 resulting from the application of a unitary operator
resulting from the application of a unitary operator 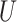 applied to a certain eigenstate
applied to a certain eigenstate 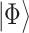 of
of 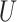
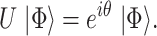 |
(3) |
Any eigenvalue of a unitary operator is a complex number of module 1 and can be thus written as the exponential in Eq. [3], where 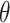 is a real number. A natural choice for
is a real number. A natural choice for 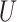 in the case of the electronic structure problem is the evolution operator, i.e. the exponential of the Hamiltonian
in the case of the electronic structure problem is the evolution operator, i.e. the exponential of the Hamiltonian 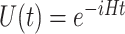 (since
(since 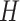 is an Hermitian operator, this exponential is guaranteed to be unitary). If
is an Hermitian operator, this exponential is guaranteed to be unitary). If 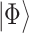 is an eigenstate of
is an eigenstate of 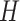
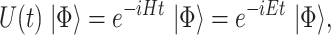 |
(4) |
where 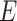 is the Hamiltonian eigenvalue, i.e. the energy, of
is the Hamiltonian eigenvalue, i.e. the energy, of 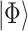 . Since, of course, the eigenstates of a general molecular
. Since, of course, the eigenstates of a general molecular 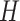 are unknown, the idea is to apply QPE to a trial state
are unknown, the idea is to apply QPE to a trial state 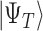 which will necessary be a superposition of eigenstates, i.e.
which will necessary be a superposition of eigenstates, i.e. 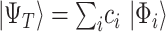 . The application of the QPE algorithm will yield the same superposition, with the energies of each eigenstates stored in appropriate registers (the ancilla qubits); then the energy of a certain eigenstate
. The application of the QPE algorithm will yield the same superposition, with the energies of each eigenstates stored in appropriate registers (the ancilla qubits); then the energy of a certain eigenstate 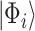 can be measured with probability
can be measured with probability 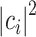 . If the target is the ground state,
. If the target is the ground state, 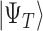 needs to be prepared with non-negligible overlap to the ground state, i.e.
needs to be prepared with non-negligible overlap to the ground state, i.e. 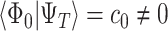 , and the number of QPE cycles needed will scale as
, and the number of QPE cycles needed will scale as 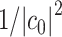 .
.
In addition to the 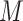 qubits required to encode the multi-electron wavefunction (
qubits required to encode the multi-electron wavefunction (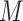 being the spin orbitals of the one-electron state basis set), QPE needs a register of
being the spin orbitals of the one-electron state basis set), QPE needs a register of 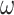 ancilla qubits, the measurement of which provides a string of 0s and 1s, encoding a binary representation of
ancilla qubits, the measurement of which provides a string of 0s and 1s, encoding a binary representation of 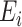 , implying that
, implying that 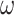 is one of the factors determining the precision to which
is one of the factors determining the precision to which 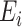 is obtained. A given precision
is obtained. A given precision 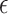 also requires a runtime scaling as
also requires a runtime scaling as 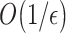 . This better scaling with respect to VQE and the guarantee to obtain exact energy eigenvalues (as opposed to variational ones) makes QPE a promising route to realize the full potential of future quantum computers. However, the long coherence times needed to realize the Hamiltonian simulation (i.e. the approximation of the time evolution operator
. This better scaling with respect to VQE and the guarantee to obtain exact energy eigenvalues (as opposed to variational ones) makes QPE a promising route to realize the full potential of future quantum computers. However, the long coherence times needed to realize the Hamiltonian simulation (i.e. the approximation of the time evolution operator 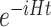 ) in QPE necessarily require fault-tolerant quantum computers. Due to this requirement, it is currently estimated that quantum advantage, i.e. runtimes faster than those of classical computations for specific problems (such as the ones described below), will be achieved by quantum computers with around 106–107 physical qubits [71, 72], clearly a long-term goal. As a proof of principle, the QPE method has been recently applied to the electronic states of H2O on a four-qubit quantum simulator [114].
) in QPE necessarily require fault-tolerant quantum computers. Due to this requirement, it is currently estimated that quantum advantage, i.e. runtimes faster than those of classical computations for specific problems (such as the ones described below), will be achieved by quantum computers with around 106–107 physical qubits [71, 72], clearly a long-term goal. As a proof of principle, the QPE method has been recently applied to the electronic states of H2O on a four-qubit quantum simulator [114].
There is a certain consensus that quantum advantage will be realized only on a subset of electronic structure problems [86, 89, 90]. These are strongly correlated/multireference systems that are not—and are not projected to be—at reach for classical algorithms, which are currently able to treat up to 50–70 single-particle states depending on the approach and on the features of the system [89]. One exemplary problem that has received much attention in this context is the structure–function relationship of nitrogenase enzymes, a family of metalloenzymes that catalyse the reduction of dinitrogen (N2) to ammonia (NH3) in the global nitrogen cycle [115]. Nitrogenases activity depends on a cofactor made of an unusual cluster of sulphur, oxygen and transition metals (Fe, Mo), and its very complex electronic structure prevents a detailed understanding of this important enzymatic reaction. A sufficiently accurate treatment of this system would require an active space of at least 54 electrons in 108 spin orbitals [116] and possibly more, well beyond the current capabilities of classical computation methods. Other biomolecular systems have been proposed as possible beneficiaries of future QC developments, because their complex electronic structure is only partially addressable using classical computation schemes [117]. These include carotenoids and chlorophyll in the light harvesting complex [118], the retinal in the vision process [119] as well as infrared fluorescent proteins [120]. In these systems, the electronic ground state may be accurately described by classical-computation methods, but to address the interaction with light one needs to simulate also excited states, which are characterized by multireference wavefunctions [121].
Proton-coupled electron transfer [122] and photoisomerization [123] are often involved in enzymatic and light-induced reactions. The simulation of these processes is further complicated by the need to take into account the quantum dynamics of the nuclei, as the Born–Oppenheimer approximation ceases to be valid. Although less discussed, particularly in the context of near-future applications, QC methods formulated using real-space 3D grids [124] or plane waves [125] as single-particle basis sets are able to simulate the total molecular wavefunction (including both the electronic and nuclear degrees of freedom) and its time evolution.
The complex biomolecular structures around these subsystems tune the energy of stationary states (i.e. minimum-energy and transition states), so that their mutual interaction needs to be taken into account. It is possible in these cases to adopt a hybrid approach, in which a subsystem is treated using a high accuracy method, and the rest is described by less computationally demanding methods. Early proposals for these embedding schemes in the context of VQE have been reviewed in ref. [126, 127].
Genome assembly and pattern matching
Introduction to the computational problems
Next-generation sequencing (NGS) is the state-of-the-art technique to sequence DNA and RNA. The advent of NGS techniques opened unprecedented possibilities for dissecting the molecular basis of complex biological processes [128]. NGS is nowadays the main tool for characterizing genomes, exomes, transcriptomes, metagenomes, nucleic acid–protein interactions, epigenomic profiles and chromatin conformational states. Its applications include, among others, fundamental science, precision medicine, environmental surveillance and rational genetic improvement of agricultural species. Genomics is probably the most mature of the omics fields. It has definitely revolutionized medical research, for the possibility of identifying genetic variants associated with a disease with unprecedented speed [129]. In addition, several genomics associated technologies have been developed, e.g. genome-wide association studies (GWAS), that can be used to identify new genetic variants associated with complex diseases in multiple human populations. In GWAS studies, thousands of individuals are genotyped for hundreds of thousands to millions of genetic variants across the genome, and statistically significant differences in minor allele frequencies between cases and controls are considered evidence of association with the disease [130]. Overall, this bulk of information can be used for several purposes, among which understanding the causes of disease susceptibility, especially in those cases in which the aetiology is multifactorial, of individual responses to drugs and possibly predicting the individual prognosis during a therapeutic treatment [29].
Basically, NGS techniques implement the highly parallelized sequencing of randomly sheared fragments (‘reads’) of DNA or RNA. Computational methods are then adopted to reconstruct the sequence of large fragments, prompting the fast, costless and high-throughput determination of whole genomes or large targeted regions [131]. A single experiment on the most modern platforms can generate up to 40 billion short reads (~ 300 nucleotides long). Such an amount of data poses significant computational challenges, in particular when considering that NGS throughput exponentially increases over the years, and the reduction of sequencing costs per genome outweighs that of the costs of computational power, as described by the Moore’s law [132]. Recently, new techniques have been developed that generate long multikilobase (i.e. thousands of nucleotides) reads [133].
The primary computational analysis aims at reconstructing larger sequences starting from short reads and differs depending on whether a reference genome for the species under investigation is available or not. In the first scenario, referred to as ‘resequencing’, the problem is to find the best match between each short read and the reference sequence (e.g. the 3 billion bases of the human genome), allowing for different types of variations, including single nucleotide mismatches, short insertions or deletions and large rearrangements. The reference genome guides the positioning of the short reads and, therefore, the reconstruction of the specific sequence under investigation. Several procedures have been introduced to perform the approximate matching between reads and reference sequence. The most efficient computational algorithms to date exploit the Ferragina–Manzini string index based on the Burrows–Wheeler transform (see [134] for a detailed survey of all short mapping read methods). When a reference genome is not available, a much more difficult problem must be tackled. The de novo (i.e. reference free) assembly aims at building long sequences, called contigs, only by exploiting the overlaps among short reads. Two basic classical approaches have been developed, both based on graph representation: the overlap-layout consensus (OLC) and the de Brujin graph approach [135].
The OLC method relies on the construction of a graph where nodes represent the reads and edges represent overlaps. The weight on the edge represents the length of the overlap. In abstract, the solution of the assembly problem is given by the maximum weight Hamiltonian path (i.e. the path that passes through all nodes of the graph exactly once and maximizes the sum of edge weights). However, the Hamiltonian problem is notoriously computationally complex (NP-hard), so different heuristics are adopted to simplify the graph and reach a reasonable solution. OLC is a method of choice for datasets consisting of a limited number of long reads. However, when the number of reads increases, the pairwise comparison of all reads to search for overlaps remains a computational bottleneck.
A more efficient solution is represented by de Brujin graphs. All words of k characters (k-mers) contained in the set of reads are extracted and mapped onto a directed graph where nodes represent all possible (k-1)-mers built from the nucleotide alphabet (A, C, G, T) and edges represent the k-mers extracted from reads: the node associated to (k-1)-mer prefix is connected with the node representing the (k-1)-mer suffix. Multiple edges between two nodes are added, one for each occurrence of the corresponding k-mer in the read set. In this framework and in the ideal case, the reconstructed sequence is retrieved by computing the Eulerian path of the graph (i.e. the path passing through all edges exactly the number of times given by the multiplicity). However, experimental data always contain sequencing errors and coverage unevenness that make the real graph non-Eulerian, and heuristics must be applied to efficiently solve the problem.
Promising quantum algorithms
In last years, a few proof-of-principle solutions based on QC have been proposed to improve the computational efficiency of algorithms for NGS problems.
In the case of resequencing, quantum algorithms aim at finding approximate pattern matching and two solutions have been proposed so far. Early work has shown the applicability of the Grover’s search algorithm to the problem of biological sequence alignment and has proposed a modified algorithm able to tackle the problem of repeated sequences and non-exact matches [136]. The application of the quantum algorithm leads to the O(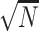 ) speedup on the classical O(
) speedup on the classical O(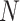 ) requirements, where
) requirements, where 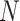 is the dimension of the search database (e.g. the length of the human genome). Different algorithms have been introduced through years to improve the solution of the string matching problem [137–139]. Although all of them can be in principle applied to the problem of resequencing, only one algorithm has been explicitly developed to this goal. This approach, called QiBAM, has been proposed by Sarkar et al. [140]. It basically extends Grover’s search algorithm to allow for errors in the alignment between reads and the reference sequence stored in a quantum memory (QRAM). The qubit complexity is equal to O(
is the dimension of the search database (e.g. the length of the human genome). Different algorithms have been introduced through years to improve the solution of the string matching problem [137–139]. Although all of them can be in principle applied to the problem of resequencing, only one algorithm has been explicitly developed to this goal. This approach, called QiBAM, has been proposed by Sarkar et al. [140]. It basically extends Grover’s search algorithm to allow for errors in the alignment between reads and the reference sequence stored in a quantum memory (QRAM). The qubit complexity is equal to O(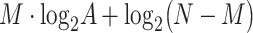 ), where
), where 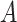 is the size of the alphabet, and
is the size of the alphabet, and 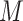 and
and 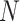 are the lengths of the string to be searched and of the database, respectively. Therefore, the number of fully connected logical qubits required for solving a real problem is about 133, for sequences of 50 base pairs to be searched in the human genome (3 × 109 base pairs). A second approach for detecting local alignments between reads and reference sequence, or a slice of it, has been described by Prousalis and Kofonaus [141]. It is based on dot matrix, a simple structure for comparing two sequences point by point. The sequences are represented in the two dimensions of the matrix and a dot is put in cells where characters correspond. Longest diagonals patterns in the matrix, possibly not perfectly shaped owing to mismatches and short insertions/deletions, highlight the regions of highest similarity and can be detected with a quantum pattern recognition scheme based on quantum Fourier transform, following the algorithm presented by Schützhold [142]. The overall time complexity of the method is O(
are the lengths of the string to be searched and of the database, respectively. Therefore, the number of fully connected logical qubits required for solving a real problem is about 133, for sequences of 50 base pairs to be searched in the human genome (3 × 109 base pairs). A second approach for detecting local alignments between reads and reference sequence, or a slice of it, has been described by Prousalis and Kofonaus [141]. It is based on dot matrix, a simple structure for comparing two sequences point by point. The sequences are represented in the two dimensions of the matrix and a dot is put in cells where characters correspond. Longest diagonals patterns in the matrix, possibly not perfectly shaped owing to mismatches and short insertions/deletions, highlight the regions of highest similarity and can be detected with a quantum pattern recognition scheme based on quantum Fourier transform, following the algorithm presented by Schützhold [142]. The overall time complexity of the method is O(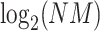 ) while current aligners show complexities at least linear in
) while current aligners show complexities at least linear in 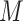 and/or
and/or 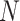 .
.
To date, both methods have been tested only on reduced problems using simulators showing good performance in both producing the correct alignment and calling the variations. However, the complexity of real problems, in terms of amount of data, length of the reference sequence and noise introduced by sequencing techniques, largely overcomes the current limits of quantum technologies.
Quantum solutions for the de novo assembly problems are based on strategies for efficiently solving the Hamiltonian path in OLC graphs (see previous section). To date and to our knowledge, no quantum version has been proposed for the de novo assembly based on the De Brujin graphs. In two approaches proposed by Boev et al. [143] and Nałęcz-Charkiewicz and Nowak [144], OLC graph is obtained with classical computations and mapped into a Quadratic Unconstrained Binary Optimization (QUBO) problem. Briefly, given a set of 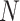 nodes in the graph, a set of
nodes in the graph, a set of  logical variables
logical variables 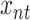 (spins) is assigned, each representing whether the Hamiltonian path passes through the node
(spins) is assigned, each representing whether the Hamiltonian path passes through the node 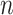 at the step
at the step 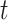 . The optimal solution comes from the minimization of a quadratic Hamiltonian function suited to cast the constraints: nodes visited at step
. The optimal solution comes from the minimization of a quadratic Hamiltonian function suited to cast the constraints: nodes visited at step 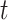 and
and 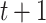 must be connected in the OLC graph, each node must be visited once, and exactly one node must be visited at each step. In this form, the problem can be embedded in a quantum annealing architecture, such as D-Wave. The number of required qubits scales as the square of the number of reads and this strongly limits its applicability to large use cases, even when procedures to efficiently decompose the problem into subtasks are applied [144].
must be connected in the OLC graph, each node must be visited once, and exactly one node must be visited at each step. In this form, the problem can be embedded in a quantum annealing architecture, such as D-Wave. The number of required qubits scales as the square of the number of reads and this strongly limits its applicability to large use cases, even when procedures to efficiently decompose the problem into subtasks are applied [144].
A similar, QUBO-based approach is described in QuASer [145], and proved correct on a D-Wave 2000Q annealer. Although the theoretical definition of the solution requires 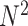 qubits, the embedding on the physical hardware considerably increases the number of required qubits, limiting to 9 the actual number of reads that could successfully be assembled. In this work, another solution is proposed based on the Quantum Approximate Optimization Algorithm (QAOA, [146]), which is an instance of the VQE algorithm (discussed in the previous section and in Figure 3B) with the following prescription for the ansatz circuit. Briefly, the QUBO, or cost, Hamiltonian, representing the cost function to be optimized, is written in terms of Pauli matrices so that the derived unitary time evolution operator (
qubits, the embedding on the physical hardware considerably increases the number of required qubits, limiting to 9 the actual number of reads that could successfully be assembled. In this work, another solution is proposed based on the Quantum Approximate Optimization Algorithm (QAOA, [146]), which is an instance of the VQE algorithm (discussed in the previous section and in Figure 3B) with the following prescription for the ansatz circuit. Briefly, the QUBO, or cost, Hamiltonian, representing the cost function to be optimized, is written in terms of Pauli matrices so that the derived unitary time evolution operator (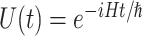 ) can be implemented as the product of rotation quantum gates. An initial state, corresponding to the ground state of a simple Hamiltonian (called mixing Hamiltonian), is prepared as a uniform superimposition of all the possible basis states. The iterative application of the time evolution operators relative to the cost and mixing Hamiltonian approximates the adiabatic transition between the ground state of the mixing Hamiltonian (initial state) and the ground state of the cost Hamiltonian that represents the optimal solution. The application of each operator depends on a parameter (the ‘time’ of application) that needs to be optimized. To this aim, classical algorithms can be adopted, so the full algorithm consists of cycles of evolution and parameter optimization, carried out on quantum and classical computer, respectively. Simulations performed on the QX Simulator provided only partially satisfactory solutions and computations on real quantum hardware have not been performed yet, to the best of our knowledge.
) can be implemented as the product of rotation quantum gates. An initial state, corresponding to the ground state of a simple Hamiltonian (called mixing Hamiltonian), is prepared as a uniform superimposition of all the possible basis states. The iterative application of the time evolution operators relative to the cost and mixing Hamiltonian approximates the adiabatic transition between the ground state of the mixing Hamiltonian (initial state) and the ground state of the cost Hamiltonian that represents the optimal solution. The application of each operator depends on a parameter (the ‘time’ of application) that needs to be optimized. To this aim, classical algorithms can be adopted, so the full algorithm consists of cycles of evolution and parameter optimization, carried out on quantum and classical computer, respectively. Simulations performed on the QX Simulator provided only partially satisfactory solutions and computations on real quantum hardware have not been performed yet, to the best of our knowledge.
As in the case of quantum algorithms for resequencing, computations conducted on quantum annealers and/or simulators proved the effectiveness of the procedures on small tests generated with artificial data. Current limitations of quantum computers still prevent the application to real problems. However, these studies pave the way to future interesting developments, even if it is still unclear whether it will be possible to devise procedures able to efficiently tackle the complexity of real cases, including experimental noise, genetic heterogeneity and repetitive sequences.
We also underline that similar QC approaches have been adopted for tackling other problems related to the comparison and overlap of sequences, such as multiple sequence alignments. These perform the alignment of three or more protein or nucleic acid sequences of similar length, in order to infer their homology and evolutionary relationships finally allowing to build-up phylogenetic trees, or to predict the structure/function of new protein sequences. Significant examples of the QC approaches proposed for these tasks are described elsewhere [95, 147–149].
Conclusions and future directions
Despite the huge progress in computational biology and bioinformatics in the last 30 years, to date many challenges remain: there is a lag between the ability to generate and that to analyse big data; furthermore, the simulation of the many parameters that recapitulate complex biomolecules or assemblies is limited by computational cost. QC is still an emerging technology at the early stages of development but unavoidably raises interest on whether and how it could overcome these limitations. As suggested by R. Feynman, QC matches the complexity of many real quantum systems; hence, it could solve various computational problems, not presently tractable by classical means, by adopting the same computational paradigm used by nature itself. Surely, more development in terms of hardware capacity and better strategies to model complex biomolecular systems will be required, before QC can be used to solve real-world problems. Also, a possibility is that QC could be useful to solve problems distinct from those tackled by classical algorithms [150], and that new classical algorithms will be inspired by the debate with the quantum community. At the moment, we have identified here some hybrid classical-quantum approaches in machine learning, multi-scale modelling and genomic data analysis, which look promising and may soon approach to real applications.
Key Points
Quantum computing (QC) holds the promise to resolve, speed up or refine the analysis of a wide range of computational biology problems.
Recently developed QC algorithms for biocomputing are reviewed with a particular focus on multi-scale modelling and genomic analyses.
Before QC can be used to solve real-world problems, further development in terms of hardware capacity and better strategies to model complex biomolecular systems will be required.
Hybrid classical-quantum approaches may be the closest to real applications in machine learning, quantum chemistry and genomic data analysis.
Data availability
All required links or identifiers for the presented data are in the manuscript or in the cited References.
Acknowledgements
We wish to thank Prof. Paolo Ferragina (Dept. Computer Science, University of Pisa) and Filippo Lipparini (Department of Chemistry, University of Pisa) for stimulating discussions and useful suggestions.
Author Biographies
Laura Marchetti is a senior researcher at the Department Pharmacy, University of Pisa and is an experimental molecular biologist who makes use of computational approaches to tailor the engineering of biomolecules and to analyse big data sets.
Riccardo Nifosì is a researcher at the NEST laboratory of the CNR-NANO institute. He is a computational physicist working on the molecular modelling of proteins and other biomolecular systems, using multi-scale approaches including molecular dynamics simulations and hybrid quantum mechanical/molecular mechanics methods.
Pier Luigi Martelli expertise includes the structural and functional characterization of biological macromolecules and their variants with computational methods, including machine and deep learning.
Eleonora Da Pozzo is an experimental biochemist who makes use of computational approaches to perform virtual screening of molecules and potential drugs and binding proteins, using pharmacophore models.
Valentina Cappello is an electron microscopist who works in the field of biomedical characterization and using computational approaches for the comparison of big imaging data sets.
Francesco Banterle is a researcher at the ISTI-CNR (Pisa, Italy), where he works on deep learning; i.e. convolutional neural networks applied to imaging, computer graphics and computer vision.
Maria Letizia Trincavelli is a biochemist who works in the signalling pathways used by the cells during survival/death decisions, differentiation processes and response to drugs.
Claudia Martini is a full professor of biochemistry with a very strong expertise in molecular mechanisms, signalling transduction systems, modulation of gene expression and cell differentiation in neurodegeneration.
Massimo D’Elia is a theoretical physicist who works primarily on the study of quantum field theories and fundamental interactions by means of computational methods.
Contributor Information
Laura Marchetti, University of Pisa, Department of Pharmacy, via Bonanno 6, 56126 Pisa Italy.
Riccardo Nifosì, NEST, Istituto Nanoscienze-CNR and Scuola Normale Superiore, P.zza San Silvestro 12, 56127 Pisa Italy.
Pier Luigi Martelli, University of Bologna, Department of Pharmacy and Biotechnology, via San Giacomo 9/2, 40126 Bologna Italy.
Eleonora Da Pozzo, University of Pisa, Department of Pharmacy, via Bonanno 6, 56126 Pisa Italy.
Valentina Cappello, Italian Institute of Technology, Center for Materials Interfaces, Viale Rinaldo Piaggio 34, 56025 Pontedera (PI), Italy.
Francesco Banterle, National Research Council, ISTI-CNR, via Moruzzi 1, 56126 Pisa Italy.
Maria Letizia Trincavelli, University of Pisa, Department of Pharmacy, via Bonanno 6, 56126 Pisa Italy.
Claudia Martini, University of Pisa, Department of Pharmacy, via Bonanno 6, 56126 Pisa Italy.
Massimo D’Elia, University of Pisa, Department of Physics, Largo Bruno Pontecorvo 3, 56127, Pisa Italy; INFN, Sezione di Pisa, Largo Bruno Pontecorvo 3, I-56127 Pisa, Italy.
Funding
University of Pisa under the ‘PRA - Progetti di Ricerca di Ateneo’ (Institutional Research Grants) - Project No. PRA 2020-2021 92 ‘Quantum Computing, Technologies and Applications’.
References
- 1. Kukurba KR, Montgomery SB. RNA sequencing and analysis. Cold Spring Harb Protoc 2015;2015:pdb.top084970. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2. Misteli T. The self-organizing genome: principles of genome architecture and function. Cell 2020;183:28–45. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3. Boivin V, Faucher-Giguère L, Scott M, et al. The cellular landscape of mid-size noncoding RNA. WIREs RNA 2019;10:e1530. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4. Lopes I, Altab G, Raina P, et al. Gene size matters: an analysis of gene length in the human genome. Front Genet 2021;12:559998. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5. Kozlowski LP. Proteome-pI: proteome isoelectric point database. Nucleic Acids Res 2017;45:D1112–6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6. de Godoy LMF, Olsen JV, Cox J, et al. Comprehensive mass-spectrometry-based proteome quantification of haploid versus diploid yeast. Nature 2008;455:1251–4. [DOI] [PubMed] [Google Scholar]
- 7. Geiger T, Wehner A, Schaab C, et al. Comparative proteomic analysis of eleven common cell lines reveals ubiquitous but varying expression of most proteins. Mol Cell Proteomics 2012;11:M111.014050. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8. Karapetyan A, Buiting C, Kuiper R, et al. Regulatory roles for long ncRNA and mRNA. Cancer 2013;5:462–90. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9. Dunbrack RL. Rotamer libraries in the 21st century. Curr Opin Struct Biol 2002;12:431–40. [DOI] [PubMed] [Google Scholar]
- 10. Stollar EJ, Smith DP. Uncovering protein structure. Essays Biochem 2020;64:649–80. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11. Seeberg PH. Monosaccharide diversity. In: Varki A, Cummings RD, Esko JD et al. (eds). Essentials of Glycobiology [Internet]. Cold Spring Harbor (NJ): Cold Spring Harbor Laboratory Press, 2015–7. [Google Scholar]
- 12. Mohammed ASA, Naveed M, Jost N. Polysaccharides; classification, chemical properties, and future perspective applications in fields of pharmacology and biological medicine (a review of current applications and upcoming potentialities). J Polym Environ 2021;29:2359–71. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13. Hanau S, Almugadam SH, Sapienza E, et al. Schematic overview of oligosaccharides, with survey on their major physiological effects and a focus on milk ones. Carbohydr Polym Technol Appl 2020;1:100013. [Google Scholar]
- 14. Nagae M, Yamaguchi Y. Three-dimensional structural aspects of protein–polysaccharide interactions. Int J Mol Sci 2014;15:3768–83. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15. Furukawa K, Ohkawa Y, Yamauchi Y, et al. Fine tuning of cell signals by glycosylation. J Biochem 2012;151:573–8. [DOI] [PubMed] [Google Scholar]
- 16. Spiro RG. Protein glycosylation: nature, distribution, enzymatic formation, and disease implications of glycopeptide bonds. Glycobiology 2002;12:43R–56R. [DOI] [PubMed] [Google Scholar]
- 17. Fahy E, Cotter D, Sud M, et al. Lipid classification, structures and tools. Biochim. Biophys. Acta BBA - Mol. Cell Biol. Lipids 2011;1811:637–47. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18. Jackson CL, Walch L, Verbavatz J-M. Lipids and their trafficking: an integral part of cellular organization. Dev Cell 2016;39:139–53. [DOI] [PubMed] [Google Scholar]
- 19. Jiang H, Zhang X, Chen X, et al. Protein Lipidation: occurrence, mechanisms, biological functions, and enabling technologies. Chem Rev 2018;118:919–88. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20. Yıldız SY. Systems glycobiology: past, present, and future. In: Behzadi P, Bernabò N (eds). Computational Biology and Chemistry [Internet]. London: IntechOpen, 2020. [Google Scholar]
- 21. Li X, Xu Z, Hong X, et al. Databases and bioinformatic tools for glycobiology and glycoproteomics. Int J Mol Sci 2020;21:6727. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22. Aoki-Kinoshita KF. Glycome informatics: using systems biology to gain mechanistic insights into glycan biosynthesis. Curr Opin Chem Eng 2021;32:100683. [Google Scholar]
- 23. Marx V. Tools to cut the sweet layer-cake that is glycoproteomics. Nat Methods 2021;18:991–5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24. Alves MA, Lamichhane S, Dickens A, et al. Systems biology approaches to study lipidomes in health and disease. Biochim Biophys Acta BBA - Mol Cell Biol Lipids 2021;1866(2):158857. [DOI] [PubMed] [Google Scholar]
- 25. Han X. Lipidomics for studying metabolism. Nat Rev Endocrinol 2016;12:668–79. [DOI] [PubMed] [Google Scholar]
- 26. Züllig T, Trötzmüller M, Köfeler HC. Lipidomics from sample preparation to data analysis: a primer. Anal Bioanal Chem 2020;412:2191–209. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27. International Human Genome Sequencing Consortium, Whitehead Institute for Biomedical Research, Center for Genome Research, Lander ES, et al. Initial sequencing and analysis of the human genome. Nature 2001;409:860–921. [DOI] [PubMed] [Google Scholar]
- 28. Buermans HPJ, den Dunnen JT. Next generation sequencing technology: advances and applications. Biochim Biophys Acta BBA - Mol Basis Dis 2014;1842:1932–41. [DOI] [PubMed] [Google Scholar]
- 29. Hasin Y, Seldin M, Lusis A. Multi-omics approaches to disease. Genome Biol 2017;18:83. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30. Piovesan A, Pelleri MC, Antonaros F, et al. On the length, weight and GC content of the human genome. BMC Res Notes 2019;12:106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31. Manzoni C, Kia DA, Vandrovcova J, et al. Genome, transcriptome and proteome: the rise of omics data and their integration in biomedical sciences. Brief Bioinform 2018;19:286–302. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32. Conesa A, Beck S. Making multi-omics data accessible to researchers. Sci Data 2019;6:251. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33. Bhargava R, Madabhushi A. Emerging themes in image informatics and molecular analysis for digital pathology. Annu Rev Biomed Eng 2016;18:387–412. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34. Marchetti L, Bonsignore F, Gobbo F, et al. Fast-diffusing p75 NTR monomers support apoptosis and growth cone collapse by neurotrophin ligands. Proc Natl Acad Sci USA 2019;116:21563–72. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35. Zhang Z, Sejdić E. Radiological images and machine learning: trends, perspectives, and prospects. Comput Biol Med 2019;108:354–70. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36. Parlanti P, Cappello V, Brun F, et al. Size and specimen-dependent strategy for x-ray micro-ct and tem correlative analysis of nervous system samples. Sci Rep 2017;7:2858. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37. Pereira R, Oliveira J, Sousa M. Bioinformatics and computational tools for next-generation sequencing analysis in clinical genetics. J Clin Med 2020;9:132. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38. Deng H, Jia Y, Zhang Y. Protein structure prediction. Int J Mod Phys B 2018;32:1840009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39. Magnus M, Kappel K, Das R, et al. RNA 3D structure prediction guided by independent folding of homologous sequences. BMC Bioinformatics 2019;20:512. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40. Gligorijević V, Renfrew PD, Kosciolek T, et al. Structure-based protein function prediction using graph convolutional networks. Nat Commun 2021;12:3168. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41. Ashburner M, Ball CA, Blake JA, et al. Gene ontology: tool for the unification of biology. Nat Genet 2000;25:25–9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42. Ruepp A. The FunCat, a functional annotation scheme for systematic classification of proteins from whole genomes. Nucleic Acids Res 2004;32:5539–45. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43. Kuhlman B, Bradley P. Advances in protein structure prediction and design. Nat Rev Mol Cell Biol 2019;20:681–97. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44. Jagger BR, Kochanek SE, Haldar S, et al. Multiscale simulation approaches to modeling drug–protein binding. Curr Opin Struct Biol 2020;61:213–21. [DOI] [PubMed] [Google Scholar]
- 45. Noid WG. Perspective: coarse-grained models for biomolecular systems. J Chem Phys 2013;139:090901. [DOI] [PubMed] [Google Scholar]
- 46. Emani PS, Warrell J, Anticevic A, et al. Quantum computing at the frontiers of biological sciences. Nat Methods 2021;18:701–9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47. Outeiral C, Strahm M, Shi J, et al. The prospects of quantum computing in computational molecular biology. WIREs Comput. Mol. Sci. 2021;11:e1481. [Google Scholar]
- 48. Polini M, Giazotto F, Fong KC, et al. Materials and devices for fundamental quantum science and quantum technologies. arXiv preprint arXiv:2201.09260. 2022. [Google Scholar]
- 49. Schäfer F, Fukuhara T, Sugawa S, et al. Tools for quantum simulation with ultracold atoms in optical lattices. Nat. Rev. Phys. 2020;2:411–25. [Google Scholar]
- 50. Monroe C, Campbell WC, Duan L-M, et al. Programmable quantum simulations of spin systems with trapped ions. Rev Mod Phys 2021;93:025001. [Google Scholar]
- 51. Adams CS, Pritchard JD, Shaffer JP. Rydberg atom quantum technologies. J Phys B At Mol Opt Phys 2020;53:012002. [Google Scholar]
- 52. Gottesman D. An introduction to quantum error correction and fault-tolerant quantum computation. Arxiv preprint arXiv:0904.2557. 2009. [Google Scholar]
- 53. Babbush R, McClean J, Newman M, et al. Focus beyond quadratic speedups for error-corrected quantum advantage. arXiv:201104149 2020. [Google Scholar]
- 54. Allcock J, Vangone A, Meyder A, et al. The prospects of Monte Carlo antibody loop modelling on a fault-tolerant quantum computer. Front Drug Discov 2022;2:908870. [Google Scholar]
- 55. Preskill J. Quantum computing in the NISQ era and beyond. Quantum 2018;2:79. [Google Scholar]
- 56. LeCun Y, Bengio Y, Hinton G. Deep learning. Nature 2015;521:436–44. [DOI] [PubMed] [Google Scholar]
- 57. Greener JG, Kandathil SM, Moffat L, et al. A guide to machine learning for biologists. Nat Rev Mol Cell Biol 2022;23:40–55. [DOI] [PubMed] [Google Scholar]
- 58. Nath RK, Thapliyal H, Humble TS. A review of machine learning classification using quantum annealing for real-world applications. SN Comput Sci 2021;2:365. [Google Scholar]
- 59. Li RY, Di Felice R, Rohs R, et al. Quantum annealing versus classical machine learning applied to a simplified computational biology problem. Npj Quantum Inf. 2018;4:14. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60. Kerenidis I, Landman J, Prakash A. Quantum algorithms for deep convolutional neural networks. Arxiv preprint arXiv:1911.01117. 2019. [Google Scholar]
- 61. Cong I, Choi S, Lukin MD. Quantum convolutional neural networks. Nat Phys 2019;15:1273–8. [Google Scholar]
- 62. Heidari N, Olgiati S, Meloni D, et al. A quantum-enhanced precision medicine application to support data-driven clinical decisions for the personalized treatment of advanced knee osteoarthritis: development and preliminary validation of precisionKNEE_QNN. MedRXiv preprint MedRXiv2021.12.13.21267704. 2022. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63. Krunic Z, Flother F, Seegan G, et al. Quantum kernels for real-world predictions based on electronic health records. IEEE Trans Quantum Eng 2022;3:1–11. [Google Scholar]
- 64. Mari A, Bromley TR, Izaac J, et al. Transfer learning in hybrid classical-quantum neural networks. Quantum 2020;4:340. [Google Scholar]
- 65. Krizhevsky A, Sutskever I, Hinton G. ImageNet classification with deep convolutional neural networks. NIPS12 Proceedings of the 25th International Conference on Neural Information Processing Systems. Curran Associates Inc., 2012; 1:1097–1105 [Google Scholar]
- 66. Simonyan K, Zisserman A. Very deep convolutional networks for large-scale image recognition. arXiv preprint arXiv:1409.1556. 2014. [Google Scholar]
- 67. He K, Zhang X, Ren S, et al. Deep residual learning for image recognition. In: 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR). IEEE (institute of electrical and electronics engineers), 2016, 770–8.
- 68. Farhi E, Neven H. Classification with quantum neural networks on near term processors. arXiv preprint arXiv:1411.4028. 2018. [Google Scholar]
- 69. Englander SW, Mayne L. The nature of protein folding pathways. Proc Natl Acad Sci USA 2014;111:15873–80. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 70. Chruszcz M, Wlodawer A, Minor W. Determination of protein structures—a series of fortunate events. Biophys J 2008;95:1–9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 71. Perdomo-Ortiz A, Dickson N, Drew-Brook M, et al. Finding low-energy conformations of lattice protein models by quantum annealing. Sci Rep 2012;2:571. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 72. Micheletti C, Hauke P, Faccioli P. Polymer physics by quantum computing. Phys Rev Lett 2021;127:080501. [DOI] [PubMed] [Google Scholar]
- 73. Robert A, Barkoutsos PK, Woerner S, et al. Resource-efficient quantum algorithm for protein folding. Npj Quantum Inf. 2021;7(38). [Google Scholar]
- 74. Jumper J, Evans R, Pritzel A, et al. Highly accurate protein structure prediction with AlphaFold. Nature 2021;596:583–9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 75. Baek M, DiMaio F, Anishchenko I, et al. Accurate prediction of protein structures and interactions using a three-track neural network. Science 2021;373:871–6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 76. Hauke P, Mattiotti G, Faccioli P. Dominant reaction pathways by quantum computing. Phys Rev Lett 2021;126:028104. [DOI] [PubMed] [Google Scholar]
- 77. Huang P-S, Boyken SE, Baker D. The coming of age of de novo protein design. Nature 2016;537:320–7. [DOI] [PubMed] [Google Scholar]
- 78. Setiawan D, Brender J, Zhang Y. Recent advances in automated protein design and its future challenges. Expert Opin Drug Discov 2018;13:587–604. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 79. Mulligan VK, Melo H, Merritt HI, et al. Designing peptides on a quantum computer. bioRxiv preprint, bioRxiv 2019;752485. [Google Scholar]
- 80. Casares PAM, Campos R, Martin-Delgado MA. QFold: quantum walks and deep learning to solve protein folding. Quantum Sci Technol 2022;7:025013. [Google Scholar]
- 81. Khatami MH, Mendes UC, Wiebe N, et al. Gate-based quantum computing for protein design. arXiv preprint arXiv:2201.12459. 2022. [DOI] [PMC free article] [PubMed]
- 82. Huggins DJ, Biggin PC, Dämgen MA, et al. Biomolecular simulations: from dynamics and mechanisms to computational assays of biological activity. WIREs Comput Mol Sci 2019;9:e1393. [Google Scholar]
- 83. Helgaker T, Klopper W, Tew DP. Quantitative quantum chemistry. Mol Phys 2008;106:2107–43. [Google Scholar]
- 84. Abrams DS, Lloyd S. Quantum algorithm providing exponential speed increase for finding eigenvalues and eigenvectors. Phys Rev Lett 1999;83:5162–5. [Google Scholar]
- 85. Kassal I, Whitfield JD, Perdomo-Ortiz A, et al. Simulating chemistry using quantum computers. Annu Rev Phys Chem 2011;62:185–207. [DOI] [PubMed] [Google Scholar]
- 86. Bauer B, Bravyi S, Motta M, et al. Quantum algorithms for quantum chemistry and quantum materials science. Chem Rev 2020;120:12685–717. [DOI] [PubMed] [Google Scholar]
- 87. Wecker D, Bauer B, Clark BK, et al. Gate-count estimates for performing quantum chemistry on small quantum computers. Phys Rev A 2014;90:022305. [Google Scholar]
- 88. Webber M, Elfving V, Weidt S, et al. The impact of hardware specifications on reaching quantum advantage in the fault tolerant regime. AVS Quantum Sci 2022;4:013801. [Google Scholar]
- 89. McArdle S, Endo S, Aspuru-Guzik A, et al. Quantum computational chemistry. Rev Mod Phys 2020;92:015003. [Google Scholar]
- 90. Elfving VE, Broer BW, Webber M, et al. How will quantum computers provide an industrially relevant computational advantage in quantum chemistry. arXiv preprint arXiv:2009.12472. 2020. [Google Scholar]
- 91. Aspuru-Guzik A, Dutoi AD, Love PJ, et al. Simulated quantum computation of molecular energies. Science 2005;309:1704–7. [DOI] [PubMed] [Google Scholar]
- 92. Cao Y, Romero J, Olson JP, et al. Quantum chemistry in the age of quantum computing. Chem Rev 2019;119:10856–915. [DOI] [PubMed] [Google Scholar]
- 93. Helgaker T, Jørgensen P, Olsen J. Molecular Electronic-Structure Theory. New York: Wiley, 2000. [Google Scholar]
- 94. Vogiatzis KD, Ma D, Olsen J, et al. Pushing configuration-interaction to the limit: towards massively parallel MCSCF calculations. J Chem Phys 2017;147:184111. [DOI] [PubMed] [Google Scholar]
- 95. Cordier BA, NPD S, Guerreschi GG, et al. Biology and medicine in the landscape of quantum advantages. arXiv preprint arXiv:2112.00760. 2021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 96. Eriksen JJ. The shape of full configuration interaction to come. J Phys Chem Lett 2021;12:418–32. [DOI] [PubMed] [Google Scholar]
- 97. Jordan P, Wigner E. Über das Paulische Äquivalenzverbot. Z Für Phys 1928;47:631–51. [Google Scholar]
- 98. Bravyi SB, AYU K. Fermionic quantum computation. Ann Phys 2002;298:210–26. [Google Scholar]
- 99. Peruzzo A, McClean J, Shadbolt P, et al. A variational eigenvalue solver on a photonic quantum processor. Nat Commun 2014;5:4213. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 100. Bharti K, Cervera-Lierta A, Kyaw TH, et al. Noisy intermediate-scale quantum algorithms. Rev Mod Phys 2022;94:015004. [Google Scholar]
- 101. Fedorov DA, Peng B, Govind N, et al. VQE method: a short survey and recent developments. Mater Theory 2022;6:2. [Google Scholar]
- 102. Tilly J, Chen H, Cao S, et al. The Variational quantum Eigensolver: a review of methods and best practices. arXiv preprint arXiv:2111.05176. 2021. [Google Scholar]
- 103. McClean JR, Boixo S, Smelyanskiy VN, et al. Barren plateaus in quantum neural network training landscapes. Nat Commun 2018;9:4812. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 104. Anand A, Schleich P, Alperin-Lea S, et al. A quantum computing view on unitary coupled cluster theory. Chem Soc Rev 2022;51:1659–84. [DOI] [PubMed] [Google Scholar]
- 105. Malone FD, Parrish RM, Welden AR, et al. Towards the simulation of large scale protein–ligand interactions on NISQ-era quantum computers. Chem Sci 2022;13:3094–108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 106. Liu H, Low GH, Steiger DS, et al. Prospects of quantum computing for molecular sciences. Mater Theory 2022;6:11. [Google Scholar]
- 107. Gonthier JF, Radin MD, Buda C, et al. Measurements as a roadblock to near-term practical quantum advantage in chemistry: resource analysis. Phys. Rev. Research 2022;4:033154. [Google Scholar]
- 108. Bittel L, Kliesch M. Training variational quantum algorithms is NP-hard. Phys Rev Lett 2021;127:120502. [DOI] [PubMed] [Google Scholar]
- 109. Cerezo M, Arrasmith A, Babbush R, et al. Variational quantum algorithms. Nat Rev Phys 2021;3:625–44. [Google Scholar]
- 110. Huggins WJ, McClean JR, Rubin NC, et al. Efficient and noise resilient measurements for quantum chemistry on near-term quantum computers. Npj Quantum Inf 2021;7:23. [Google Scholar]
- 111. Wang G, Koh DE, Johnson PD, et al. Minimizing estimation runtime on noisy quantum computers. PRX Quantum 2021;2:010346. [Google Scholar]
- 112. Kübler JM, Arrasmith A, Cincio L, et al. An adaptive optimizer for measurement-frugal variational algorithms. Quantum 2020;4:263. [Google Scholar]
- 113. AYU K. Quantum measurements and the abelian stabilizer problem. arXiv:quant-ph/9511026 1995. [Google Scholar]
- 114. Li Z, Liu X, Wang H, et al. Quantum simulation of resonant transitions for solving the eigenproblem of an effective water Hamiltonian. Phys Rev Lett 2019;122:090504. [DOI] [PubMed] [Google Scholar]
- 115. Wiig JA, Rebelein JG, Hu Y. Nitrogenase Complex. eLS, John Wiley & Sons, Ltd, 2014. [Google Scholar]
- 116. Reiher M, Wiebe N, Svore KM, et al. Elucidating reaction mechanisms on quantum computers. Proc Natl Acad Sci USA 2017;114:7555–60. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 117. Fedorov AK, Gelfand MS. Towards practical applications in quantum computational biology. Nat Comput Sci 2021;1:114–9. [DOI] [PubMed] [Google Scholar]
- 118. Segatta F, Cupellini L, Garavelli M, et al. Quantum chemical modeling of the photoinduced activity of multichromophoric biosystems: focus review. Chem Rev 2019;119:9361–80. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 119. Hahn S, Stock G. Quantum-mechanical modeling of the femtosecond isomerization in rhodopsin. J Phys Chem B 2000;104:1146–9. [Google Scholar]
- 120. Karasev MM, Stepanenko OV, Rumyantsev KA, et al. Near-infrared fluorescent proteins and their applications. Biochemistry 2019;84:32–50. [DOI] [PubMed] [Google Scholar]
- 121. Bauman NP, Liu H, Bylaska EJ, et al. Toward quantum computing for high-energy excited states in molecular systems: quantum phase estimations of core-level states. J Chem Theory Comput 2021;17:201–10. [DOI] [PubMed] [Google Scholar]
- 122. Weinberg DR, Gagliardi CJ, Hull JF, et al. Proton-coupled electron transfer. Chem Rev 2012;112:4016–93. [DOI] [PubMed] [Google Scholar]
- 123. Gozem S, Luk HL, Schapiro I, et al. Theory and simulation of the ultrafast double-bond isomerization of biological chromophores. Chem Rev 2017;117:13502–65. [DOI] [PubMed] [Google Scholar]
- 124. Kassal I, Jordan SP, Love PJ, et al. Polynomial-time quantum algorithm for the simulation of chemical dynamics. Proc Natl Acad Sci USA 2008;105:18681–6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 125. Su Y, Berry DW, Wiebe N, et al. Fault-tolerant quantum simulations of chemistry in first quantization. PRX Quantum 2021;2:040332. [Google Scholar]
- 126. Tilly J, Sriluckshmy PV, Patel A, et al. Reduced density matrix sampling: self-consistent embedding and multiscale electronic structure on current generation quantum computers. Phys Rev Res 2021;3:033230. [Google Scholar]
- 127. Cheng H-P, Deumens E, Freericks JK, et al. Application of quantum computing to biochemical systems: a look to the future. Front Chem 2020;8:587143. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 128. Levy SE, Boone BE. Next-generation sequencing strategies. Cold Spring Harb Perspect Med 2019;9:a025791. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 129. Alioto TS, Buchhalter I, Derdak S, et al. A comprehensive assessment of somatic mutation detection in cancer using whole-genome sequencing. Nat Commun 2015;6:10001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 130. Tam V, Patel N, Turcotte M, et al. Benefits and limitations of genome-wide association studies. Nat Rev Genet 2019;20:467–84. [DOI] [PubMed] [Google Scholar]
- 131. Kumar KR, Cowley MJ, Davis RL. Next-generation sequencing and emerging technologies. Semin Thromb Hemost 2019;45:661–73. [DOI] [PubMed] [Google Scholar]
- 132. Lightbody G, Haberland V, Browne F, et al. Review of applications of high-throughput sequencing in personalized medicine: barriers and facilitators of future progress in research and clinical application. Brief Bioinform 2019;20:1795–811. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 133. McCombie WR, McPherson JD, Mardis ER. Next-generation sequencing technologies. Cold Spring Harb Perspect Med 2019;9:a036798. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 134. Canzar S, Salzberg SL. Short read mapping: an algorithmic tour. Proc IEEE Inst Electr Electron Eng 2017;105:436–58. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 135. Sohn J-I, Nam J-W. The present and future of de novo whole-genome assembly. Brief Bioinform 2018;19:23–40. [DOI] [PubMed] [Google Scholar]
- 136. Hollenberg LCL. Fast quantum search algorithms in protein sequence comparisons: quantum bioinformatics. Phys Rev E 2000;62:7532–5. [DOI] [PubMed] [Google Scholar]
- 137. Ramesh H, Vinay V. String matching in O(n+m) quantum time. J Discrete Algorithms 2003;1:103–10. [Google Scholar]
- 138. Montanaro A. Quantum pattern matching fast on average. Algorithmica 2017;77:16–39. [Google Scholar]
- 139. Niroula P, Nam Y. A quantum algorithm for string matching. Npj Quantum Inf 2021;7:37. [Google Scholar]
- 140. Sarkar A, Al-Ars Z, Almudever CG, et al. QiBAM: approximate sub-string index search on quantum accelerators applied to DNA read alignment. Electronics 2021;10:2433. [Google Scholar]
- 141. Prousalis K, Konofaos N. Α quantum pattern recognition method for improving pairwise sequence alignment. Sci Rep 2019;9:7226. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 142. Schützhold R. Pattern recognition on a quantum computer. Phys Rev A 2003;67:062311. [Google Scholar]
- 143. Boev AS, Rakitko AS, Usmanov SR, et al. Genome assembly using quantum and quantum-inspired annealing. Sci Rep 2021;11:13183. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 144. Nałęcz-Charkiewicz K, Nowak RM. Algorithm for DNA sequence assembly by quantum annealing. BMC Bioinformatics 2022;23:122. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 145. Sarkar A, Al-Ars Z, Bertels K. QuASeR: quantum accelerated de novo DNA sequence reconstruction. PloS One 2021;16:e0249850. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 146. Farhi E, Goldstone J, Gutmann S. A quantum approximate optimization algorithm. arXiv preprint arXiv:1411.4028 2014. [Google Scholar]
- 147. Ali S, Abbadeni N, Batouche M. EdsMultidisciplinary computational intelligence techniques: applications in business, engineering, and medicine. IGI Global 2012. [Google Scholar]
- 148. Layeb A, Meshoul S, Batouche M. Multiple sequence alignment by quantum genetic algorithm. Proceedings 20th IEEE International Parallel and Distributed Processing Symposium. IEEE Computer Society, 2006; 8. [Google Scholar]
- 149. Huo H, Xie Q, Shen X, et al. A probabilistic coding based quantum genetic algorithm for multiple sequence alignment. Comput Syst Bioinforma 2008;15–26. [PubMed] [Google Scholar]
- 150. Sahoo S, Kumar Mandal A, Kanti Samanta P, et al. A critical overview on quantum computing. J Quantum Comput 2020;2:181–92. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
All required links or identifiers for the presented data are in the manuscript or in the cited References.