Abstract
A growing literature reports significant socio-economic gaps in investments in the human capital of young children. Because the returns to these investments may be huge, parenting programs attempt to improve children’s environments by increasing parental expectations about the importance of investments for their children’s human capital formation. We contribute to this literature by investigating the relevance of maternal subjective expectations (MSE) about the technology of skill formation in predicting investments in the human capital of children. We develop and implement a framework to elicit and analyze MSE data. We launch a longitudinal study with 822 participants, all of whom were women in the second trimester of their first pregnancy at the date of enrollment. In the first wave of the study, during pregnancy, we elicited the woman’s MSE. In the second wave, approximately one year later, we measured maternal investments using the Home Observation for the Measurement of the Environment (HOME) Inventory. The vast majority of study participants believe that the Cobb-Douglas technology of skill formation describes the process of child development accurately. We observed substantial heterogeneity in MSE about the impact of human capital at birth and investments in child development at age two. Family income explains part of this heterogeneity in MSE. The higher the family income, the higher the MSE about the impact of investment in child development. We find that a one-standard-deviation of MSE measured at pregnancy is associated with 11% of a standard deviation in investments measured when the child is approximately nine months old.
1. Introduction
In a pioneering study, Hart and Risley (1995) documented variations in the language environment of children from 9 months to 3 years old. These authors measured, among other variables, the number of words spoken to the child during an hour. The results indicate that children who live in poverty heard approximately 50% fewer words per hour compared with children of parents in professional occupations. Hart and Risley also showed that a better early language environment at home predicted more robust language development, higher IQ, and superior school performance in the children.
Rowe (2008) built on Hart and Risley’s (1995) work to understand the factors associated with the quality of the early language environment. Rowe videotaped parent-child dyads as they engaged in conversation and confirmed that child-directed parent speech correlated with the parent’s income and education. In addition, Rowe showed that parental knowledge about the role of child-directed speech in promoting language development is a mediator of this correlation. In the context of this paper, Rowe’s finding suggests that low-income mothers have low maternal subjective expectations (MSE) about the technology of skill formation. In particular, this finding implies that low-income mothers have low expectations about the impact of adult-child language interaction on the evolution of a child’s language skills.
For decades, developmental psychologists have conjectured that low MSE causes low investments in children (Hunt, 1961; Vygostky, 1978). It is only recently, however, that research in economics has considered this relationship. Our research is related to, but different from, developmental psychology’s vast body of literature focused on measuring maternal and paternal knowledge about child development. These studies show that the lower the parents’ socioeconomic status (SES), the lower their expectations about the impact of the environment on cognitive development (Epstein, 1980; Mansbach and Greenbaum, 1999; Ninio, 1988; Ninio and Rinott, 1988). Our approach blends the research on parental knowledge in developmental psychology with the literature on the elicitation and use of subjective expectations in economics (e.g., Attanasio and Kaufmann, 2014; Delavande, 2008; Manski, 2004; Wiswall and Zafar, 2015).
Another branch in the economics literature provides evidence that public information campaigns can change prenatal investment because such campaigns affect parental knowledge. Aizer and Stroud (2010), for example, tracked the smoking habits of educated and uneducated pregnant women before and after the release of the 1964 Surgeon General’s Report on Smoking and Health. Before the release of the report, college and non-college pregnant women smoked at roughly the same rates. After the report, the smoking habits of educated women decreased immediately, creating a ten-percentage-point gap in pregnancy smoking rates between educated and uneducated women. These results suggest that information campaigns with differential effectiveness across socioeconomic groups can influence MSE.
In addition to public information campaigns, public policy aims to improve the early environment of disadvantaged children through parenting programs, especially those that involve home visitation. Evidence on the effectiveness of home visitation programs is consistent with the theory that these programs work by increasing MSE. One of the most extensive programs in the United States is the Nurse-Family Partnership (NFP; Olds, 2002). In this program, nurses visit the homes of disadvantaged first-time young mothers periodically. The visits start in the second trimester of pregnancy and continue until the child reaches age two. Heckman et al. (2017) find that the program simultaneously improves the quality of the home environment and children’s cognitive development. These authors also document improvement in parenting attitudes, which suggests increases in MSE.
Researchers have designed large-scale home visitation programs suitable for the context of developing countries. Gertler et al. (2014) provide compelling evidence of the long-term benefits of the Jamaica home visitation program. Thus, it is not surprising that research teams around the world have been implementing and evaluating—after appropriate cultural adaptations—the Jamaica curriculum in many other settings (e.g., Attanasio et al., 2014).
Motivated by this research, we build on our previous joint work and implement two elicitation forms to measure MSE within a longitudinal study. Briefly, these elicitation instruments present study participants with hypothetical scenarios of “high” and “low” levels of investments with varying levels of a child’s human capital at birth. For each scenario of investment and human capital at birth, we ask study participants to estimate the expected child developmental outcomes at age two.
We implement this survey instrument in a longitudinal study with first-time mothers. In the first round of the study, when the participants are in the second trimester of their first pregnancy, we use the survey instrument to elicit MSE. In the second round of the study, we visit participants and collect information on investments in human capital when the children were approximately nine months old (roughly one year after the elicitation of MSE).
We develop an econometric framework to analyze the data. The econometric approach is robust to heaping and measurement error in responses. We use our MSE model and assumptions about measurement error to derive testable restrictions across identifying moments. We map these restrictions to transparent factor analysis. We use these restrictions to derive predictions about the number of factors in factor analysis.
We find substantial heterogeneity in MSE. We show that household income partly explains this heterogeneity. The higher the family income, the higher the MSE about the impact of investment on the human capital of children. We show that the association between MSE and family income is robust to many different analytical assumptions. We confirm that the belief data satisfy crucial cross-moment relationships imposed by the model.
Further, we show that MSE predicts investments in the human capital of children. A one-standard-deviation shift in the MSE about the investment elasticity of child development is associated with 11% of a standard deviation change in investments. We estimate LASSO regressions to determine whether MSE provides relevant information, above and beyond SES variables, to predict investments in the human capital of children. The LASSO regressions include MSE in the final prediction models but drop some of the SES variables.
This paper extends the analysis of Cunha et al. (2013) in two significant ways. First, we link our methodological framework to factor analysis and derive predictions about the number of factors. We show that maternal answers satisfy the predictions of the models about the number of factors. Second, our longitudinal data allow us to investigate the validity of MSE. We show that MSE measured in the second trimester of the first pregnancy predict investments in the human capital of children when the children were 9 to 12 months old, thus about one year apart.
The paper is closely related to the work of Attanasio et al. (2019). The papers are similar in that they both elicit beliefs and show that beliefs predict investments. The main difference is that, in the current paper, we have two different elicitation forms, and, thus, we can compare how they fare against each other in terms of predictability. We also can investigate the validity of assumptions about measurement error processes. Attanasio et al. (2019), in contrast, explore longitudinal data that are part of a parenting intervention that had exogenous variation in its deployment. Thus, in their paper, they develop a framework to compare maternal perceptions about the technology of skill formation (i.e., maternal beliefs) with objective estimates of the same technology. They find that mothers underestimate the importance of investments for the development of the human capital of children. The evidence from this work is, thus, complementary. Together, these papers reinforce the necessity for programs that aim to improve children’s environments by increasing parental MSE about the technology of skill formation.
Our work also relates to research by Boneva and Rauh (2018). In their work, they elicited maternal returns about early and late investments from a sample of mothers in the United Kingdom. They found that mothers have low expectations about returns for early investments in children (see also Biroli et al., 2018; Boneva and Rauh, 2019; Bhalotra et al., 2020).
We organize the paper as follows. In Section 2, we formally define MSE, describe the elicitation forms, and present the econometric methodology that we use to analyze the data. In Section 3, we describe the two rounds of the longitudinal study. Section 4 presents the results. Finally, we discuss the findings and suggest directions for future research.
2. MSE about the Technology of Skill Formation
2.1. The technology of Skill Formation
In this section, we first describe the parameterization of the technology of skill formation that we assume in this paper.1 Let qi,0 and qi,1 denote, respectively, the stocks of the human capital of child i at birth and 24 months. Let xi denote maternal investments in the human capital of child i during the first two years of the child’s life. Let vi denote shocks to the development process. We assume that the technology of skill formation assumes the following parametric specification:
| (1) |
The translog parameterization in equation (1) is particularly convenient to make progress on the elicitation of MSE about the technology of skill formation. To see why, let denote the mother’s information set. According to the technology function denoted in (1), it follows that:
| (2) |
where . In a fully specified economic model, equation (1) describes the constraint on child development, and equation (2) describes the constraint as perceived by the mother. For example, if ψ3 = 0, then the parameters ψ1 and ψ2 are elasticity parameters as estimated with objective data. For example, if ψ2 = 0.4, the interpretation of this parameter is that a 100% increase in investments leads to a 40% increase in child development at age 24 months. Similarly, if μi,ψ,3 = 0, then the parameters μi,ψ,1 and μi,ψ,2 capture maternal subjective expectations about the parameters ψ1 and ψ2, and, thus, have a similar elasticity interpretation. For example, if μi,ψ,2 = 0.2, this indicates that mother i believes that a 100% increase in investment leads to a 20% increase in child development at age 24 months. In this case, mother i underestimates the impact of investments because μi,ψ,2 < ψ2.
The parameter ψ3 captures the interaction of human capital at birth and investments. If ψ3 = 0, then the technology of skill formation (1) takes the Cobb-Douglas form. Otherwise, if ψ3 < 0, then it states that the elasticity of child development with respect to investment decreases as human capita at birth increases. The opposite is true if ψ3 > 0. The parameter μi,ψ,3 has a similar interpretation but from mother i’s point of view. A situation in which μi,ψ,3 = 0 indicates that mother i believes that the Cobb-Douglas parameterization describes the child development process. If μi,ψ,3 < 0, then mother i believes that the elasticity of child development with respect to investment decreases as human capita at birth increases.
In summary, ψ = (ψ1, ψ2, ψ3) describes the child development process as researchers estimate from objective data on human capital and investments. The vector μi,ψ = (μi,ψ,1, μi,ψ,2, μi,ψ,3) describes maternal subjective expectations about the parameters. The vector μi,ψ may or may not be equal to ψ. In this paper, we estimate the vector μi,ψ = (μi,ψ,1, μi,ψ,2, μi,ψ,3). Moreover, we investigate whether the elements of the vector predict parental investments in the human capital of children.
2.2. Motor Social Development Scale
The Motor Social Development Scale (MSD) plays an essential role in our analysis; thus, we briefly explain it in this section. Nationally representative studies, such as the National Health and Nutrition Examination Study 1988 (NHANES), have used the MSD because it is easy for mothers to understand. In the MSD, mothers answer 15 out of 48 items regarding the motor, language, and numeracy development. The instrument divides 48 items into eight components (Parts A through H), with each as containing 15 items, that a mother completes, contingent on the child’s age. Part A is appropriate for infants aged 0 through 3 months, and the most advanced section, Part H, is designed for children between the ages of 22 and 47 months. All items are dichotomous (“no” is equal to 0, and “yes” is equal to 1), and a child’s development score is the summation of the affirmative responses in the age-appropriate section. Because the age at which children learn how to do given tasks varies considerably across children, one MSD item may be present in many parts of the instrument. For example, the MSD item, “speak a partial sentence of three words or more,” is asked about children who are between 13 and 47 months. Thus, this particular item is present in parts E, F, G, and H of the MSD.
The MSD has properties that make it appealing to our goal. The instrument contains tasks that capture essential dimensions of child development and describes them in language easily understood by mothers. The MSD also has a severe drawback, however, for application in our elicitation study. The score produced with the summation across items is problematic for our goals due to participant burden. For reasons that will become clearer below, our elicitation method presents participants with four scenarios with different levels of human capital at birth and investments. Thus, we would have to ask these 15 MSD questions for each one of the four scenarios. This inconvenient feature of the MSD becomes even more significant because we have not one but two different forms of elicitation. Therefore, to reduce the number of items that we ask our participants, we estimate an item response theory (IRT) model, which we describe next.
Let the variable ai denote child i’s age at the time of the measurement of skills in the NHANES dataset. Let θi denote child i’s development relative to other children in the same age group. For example, θi = 0 if child i’s development is typical for his or her age; θi > 0 if child i is advanced for his or her age; and θi < 0 if child i has developmental delays relative to children in his or her age group. We use the IRT model to estimate the distribution of the latent factor θi. For each child i and MSD item j, we define the latent variable according to the following specification:
| (3) |
We do not observe the variable in equation (3). We observe, however, that the binary variable di,j is equal to 1 whenever and equal to 0 otherwise. In the IRT model of (3), the parameters bj,0 are smaller for the more difficult items. The parameter bj,1 describes how fast performance in task j improves as age increases. The parameter bj,2 denotes the informational content of item j with respect to child development. The higher the value of bj,2, the more information item j contains about child development θi.
Let Φ denote the cumulative distribution function (CDF) of a normal random variable with mean 0 and variance 1. If we assume that ηi,j~N(0,1), it follows that the probability that child i can perform MSD task j is equal to:
| (4) |
We need to make two normalizations in the IRT model: one for the location and the other for the scale of θi. Thus, we restrict the mean of θi to be equal to 0, and we set b2,j = 1 for one of the MSD items. In our empirical analysis, we assume that the distribution of the factor θi is equal to a mixture of two normal CDFs.
Suppose that we know the values of the parameters bj,0, bj,1, and bj,2.2 We can use equation (4) to translate answers from the MSE elicitation instrument. This information allows us to recover the vector μi,ψ and then investigate which elements of μi,ψ, if any, predict early investments in the human capital of children. We describe the methodology next.
2.3. Instruments to Elicit MSE
In this section, we provide details about how we adapt the MSD to elicit MSE. As we now explain, the items in the original and adapted MSD instruments differ in two critical details. In the original MSD, interviewers ask mothers with a 2-year-old child whether their child has learned how to do a particular group of 15 tasks. We adapt several questions from the MSD to ask study participants to speculate the degree to which a child is likely to reach those same developmental milestones by age two for each scenario of human capital at birth and level of investment. For example, in the original MSD used in NHANES, interviewers ask mothers of 2-year-old children to respond “yes” or “no” to a statement such as, “Does your child speak a partial sentence of three words or more?” In contrast, our interviewers ask study participants the following types of questions:
“How likely is it that a baby will learn how to say a partial sentence with three words or more by age two if human capital at birth is [low/high] and investment is [low/high]?”
“What do you think are the youngest age and the oldest age that a baby learns to speak a partial sentence of three words or more if human capital at birth is [low/high] and investment is [low/high]?”
In the first type of question, the respondent uses a sliding scale to indicate the likelihood (e.g., 40%) by age two that the child will learn how to say a partial sentence for each one of the four scenarios of human capital at birth and investment. The sliding scale allows respondents to pick any integer between 0 and 100.3 This type of question is more closely related to how the literature in economics elicits subjective expectations (Manski, 2004), so it is straightforward to use maternal answers in our analysis. Throughout this paper, we refer to this elicitation instrument as the subjective probability form.
In the second type of question, the respondent uses a sliding range scale to indicate, for each one of the four scenarios of human capital at birth and investment, the youngest and oldest ages (e.g., 18 and 30 months) that a child will learn how to speak a partial sentence of three words or more. The sliding range scale allows respondents to pick any integer between 0 and 48 months, with the constraint that the oldest age must be higher than the youngest age.4 The second question is more in line with how the literature in child development measures parental knowledge (Epstein, 1980). This type of question requires additional assumptions and steps to be able to transform answers into probabilities that are on the left-hand side of equation (4). In this paper, we refer to this elicitation instrument as the age-range form.
We chose to use sliding scales for two reasons. First, for the subjective probability form, they allow us to combine verbal and numerical representations of probabilistic statements. For the age range form, they we can combine age in months with age in years (“two and half”). Evidence in cognitive psychology shows that subjects best communicate their beliefs when they are given access to verbal expressions of probabilistic statements (Wallsten et al., 1986). The labels representing probabilities in Appendix Figure A1 (e.g., “Toss-up”) were chosen according to the findings described in Hamm (1991). Second, Delavande et al. (2011a) show that individuals report probabilities more accurately when their beliefs are represented with visual instruments.
Figure 1 presents the survey instruments in detail. Panel A reproduces the elicitation items we use in the subjective probability form. Panel B shows the exact elicitation items in the age ranges form. Panel C presents the four scenarios of human capital at birth and investments. For the study participants, we showed a five-minute video that described the scenarios before answering any questions. In the video, “high” human capital at birth means that the child’s gestation lasted nine months, the child weighed eight pounds at birth, and the child was 20 inches long at birth. These birth outcomes are typical among children who experience usual term births. In contrast, the “low” human capital at birth corresponds to a child whose gestation was seven months and weighed five pounds and was 18 inches long at birth. These birth outcomes are observed among children who are born preterm. We chose these descriptions according to data from the Children of the National Longitudinal Study (see Section A.2 in Appendix A for additional details).
Figure 1:
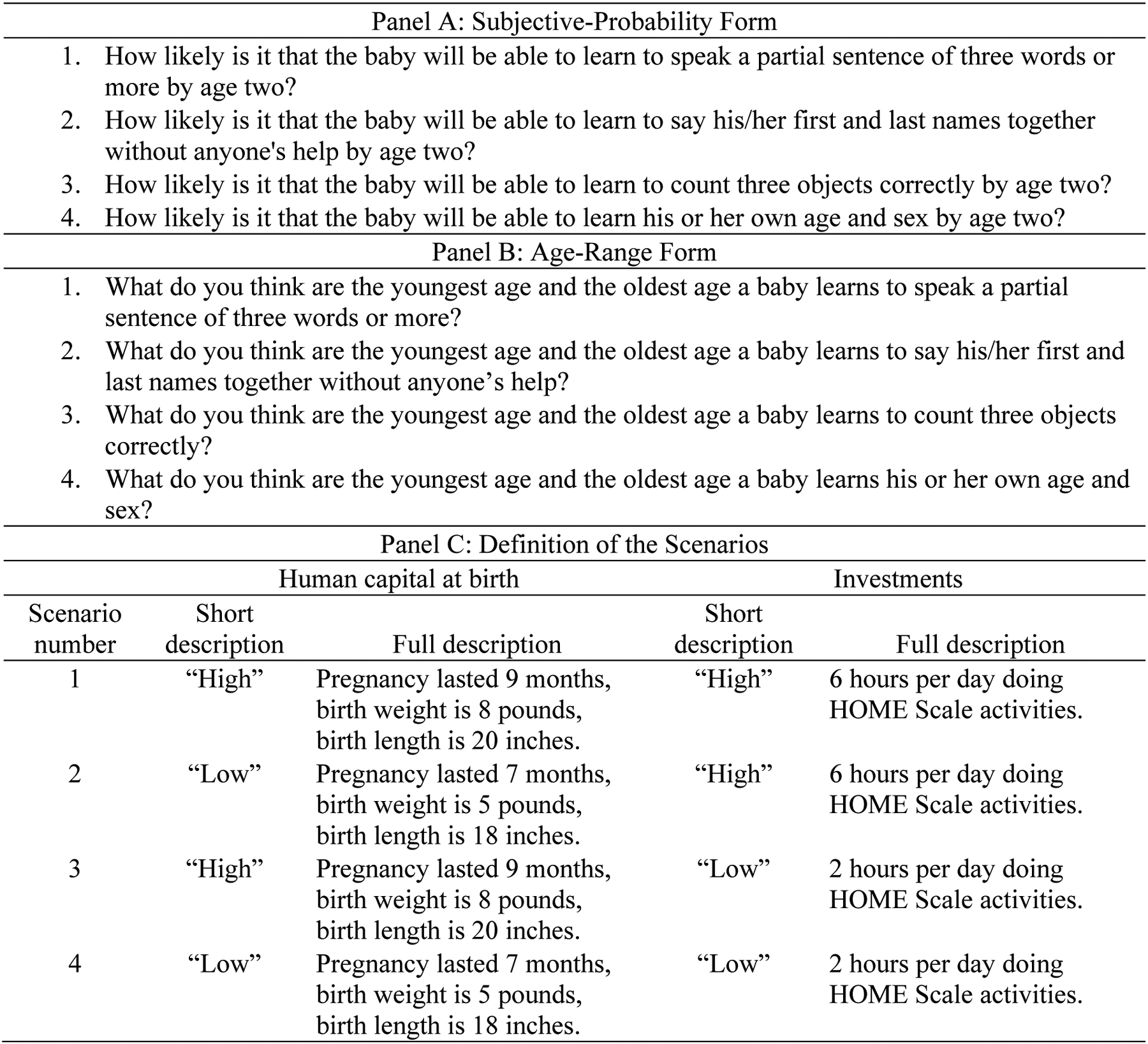
This figure provides detailed information about both forms of the elicitation instrument. Panel A reproduces the elicitation items in the subjective probability form. Panel B displays the elicitation items in the age range form. Panel C describes the scenarios of human capital at birth and investments. The study participants watched a short video describing these scenarios.
The video also showed examples of activities that mothers do with their children. Except for breastfeeding, all activities depicted are part of the Home Observation for the Measurement of Environment-Short Form (HOME-SF) (Bradley and Caldwell, 1980). The activities are the same for the “high” and “low” level of investments. The difference is in the amount of time. In the “high” level , the mothers spend six hours a day doing these types of activities, while, in the “low” level they spend only two hours a day.
We order the scenarios in the following way. In the first scenario (k = 1), the child’s human capital at birth is “high,” and the mother has a “high” level of investment . In the second scenario (k = 2), the level of investment is “high,” but the child’s human capital at birth is “low.” In the third scenario (k = 3), the baby’s human capital at birth is “high,” but the level of investment is “low.” Finally, in the fourth scenario (k = 4), both the child’s human capital at birth and investments are low.
Our elicitation method requires four scenarios because we need to estimate MSE about three parameters of the technology of skill formation. Strictly speaking, our elicitation strategy does not require questions for multiple items of MSD or the development of two distinct forms. We used multiple MSD tasks and two alternative forms due to our prior concern that maternal reports about the MSE would suffer from measurement error.
As Attanasio et al. (2019) make clear, the choice of location and scale of the scenarios of investment and human capital at birth need to be consistent with the goals of the analysis. If the objective is to compare MSE with objective estimates of the parameters of the technology of skill formation, then it is crucial that the location and scale of investment and human capital at birth used in the elicitation of μi,ψ match the location and scale of these same variables in the data used in the estimation of ψ. Otherwise, the comparison may be misleading. If, as it applies to the current analysis, the goal is to investigate whether MSE predicts investments, then the choice of location and scale of investments and human capital at birth becomes less important.
2.4. Estimation of Expectation of Child Development
In this section, we explain how we combine the IRT analysis of the MSD, as well as participant answers to the survey elicitation instrument, to estimate MSE about the technology of skill formation.
2.4.1. Estimation of Expectation of Child Development Using the Subjective Probability Form
We now discuss how we transform the answers to the questions into error-ridden measurements of the MSE of child development at age 24 months. This expectation is conditional on three objects: the maternal information set , level of human capital at birth, and investment associated with each scenario k (see equation 2).
Let denote the likelihood reported by respondent i that a child will learn MSD item j by age 24 months if human capital at birth and investments are at the levels determined in scenario k. We explore the IRT model to derive an error-ridden measure of maternal expectation of the natural log of development at age 24 months, ln , from the reported probability . To do so, we invert equation (4) and solve for :
| (5) |
We explain the algorithm described above graphically. The thick solid curve in Figure 2 shows the prediction from the IRT model for the MSD item, “speak a partial sentence of three words or more.” The horizontal axis in Figure 2 shows the natural logarithm of the child’s age (in months), while the vertical axis shows the maternal subjective probability that a child will “speak a partial sentence of three words or more.” We use the IRT model to transform the subjective probability that the mother reports into the corresponding natural log of age—the scale that we use for human capital at age two. Building on the example shown in Figure 2, suppose that the mother believes that there is a 75% chance that the child will learn how to speak a partial sentence by age two when the investment is “high.” According to the IRT model, this statement means that the mother believes that, at age 24 months, ln . In Figure 2, we depict this relationship with the thin solid line that starts at probability .75 in the vertical axis.
Figure 2:
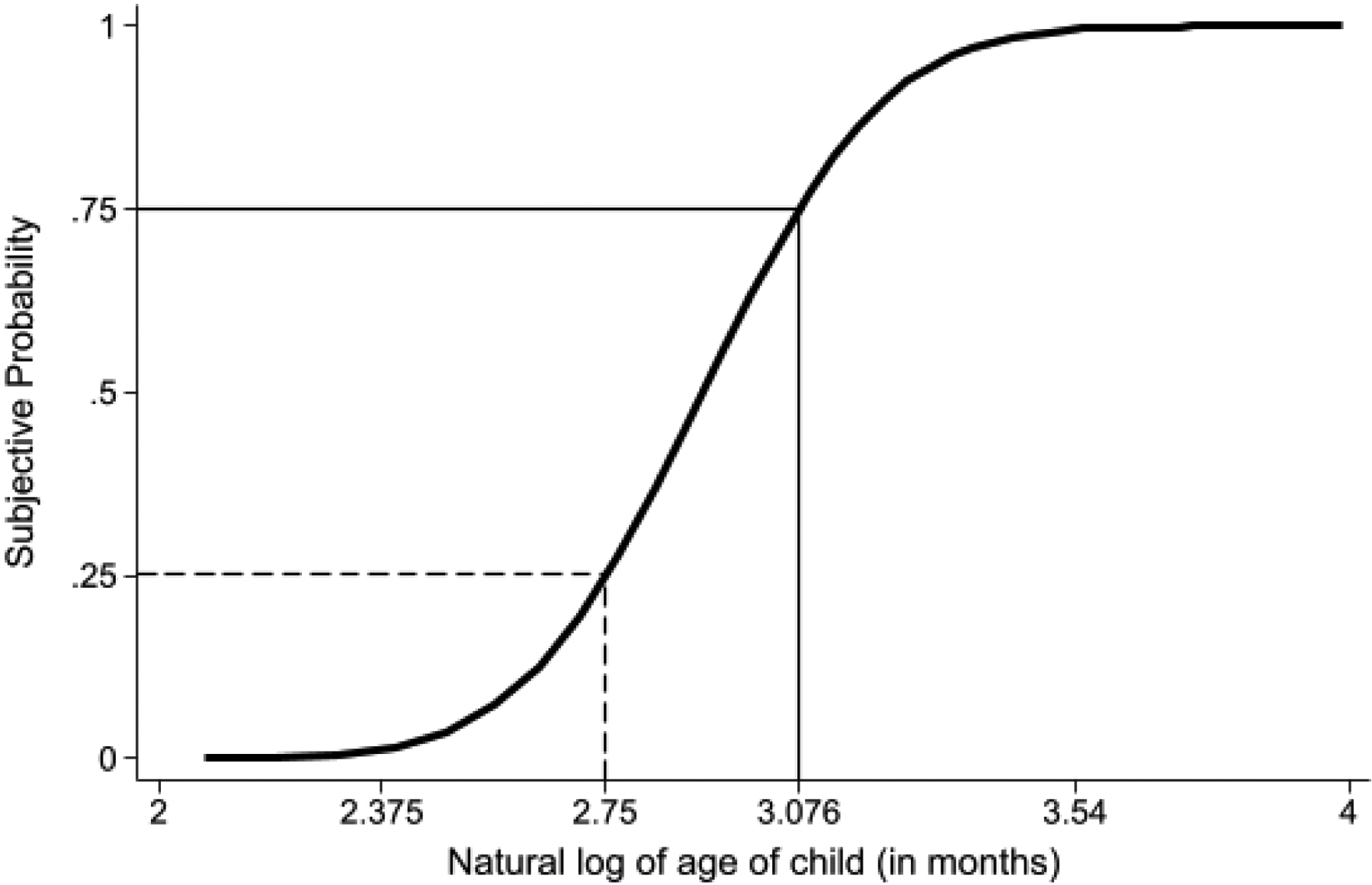
This figure shows how we use the IRT model to relocate and rescale maternal subjective probability reports (shown in the vertical axis) to error-ridden measures of the expectation of the natural log of human capital at age two years (shown in the horizontal axis) for two scenarios of investments (“high” vs. “low”) when human capital at birth is “high.” When the investment is “low,” the mother reports that there is a 25% chance that the child will learn how to speak a partial sentence with three words or more by age 24 months. When the investment is “high,” the mother reports that the probability is 75% by age 24 months. These probabilities correspond to 2.75 = ln 16 and 3.076 = ln 22, respectively. According to the IRT model, 25% of the 16-month-old children and 75% of the 22-month-old children speak a partial sentence with three words or more.
Importantly, the lower the subjective probability that the mother reports for a given item j, the lower the corresponding expectation about the natural log of child development at age 24 months. Again, we refer to Figure 2 for a visual explanation of the mechanics of the algorithm. Suppose that, for the “low” investment scenario, the mother believes that there is a 25% chance that the child will learn how to speak a partial sentence with three words or more by age 24 months. As shown in Figure 2, this statement means that the mother believes that, at age 24 months, the natural log of child development is such that ln . We display this transformation with the thin dashed line that starts at probability .25 in the vertical axis in Figure 2.
2.4.2. Estimation of Expectation of Child Development, using Age-Range Questions
For MSD item j and scenario k, suppose that the survey respondent i states that the youngest and oldest ages at which a child will learn how to speak partial sentences of three words or more are and months, respectively. To infer the respondent’s subjective probability that the child will learn how to speak partial sentences by age 24 months, we need to construct how the probability varies with age. In the analysis of the age-range data, we use the mother’s answer to estimate a mother-scenario specific IRT model along with the parameterization used in equation (3). Indeed, let denote the latent variable that is determined according to:
| (6) |
where the shock is normally distributed with mean zero and variance one. Similar to the model described in Section 2.2, let denote the binary variable that takes the value one if and zero otherwise. Note the parallelism between the IRT model described by equation (6) and its counterpart represented in equation (3). The parameters and in (6) have the same interpretations as do the parameters bj,0 and bj,1 in (3). There are, however, two important differences between the models in (3) and (6). First, the IRT model in equation (6) describes maternal beliefs about typical development if investment and human capital at birth are defined according to scenario k. Because it reflects typically from the point of view of the mother, the factor θi in equation (3) is set to 0 in (6). In addition, because the IRT model is specific for scenario k, the parameters in (6) are also indexed by k.
Second, we fit the model represented in equation (3), using actual developmental data from the NHANES study. In contrast, we estimate the model in equation (6) with respondent i’s age-range data collected with the elicitation instrument.
Our interpretation of the answer is that the respondent believes that the probability that the child will be able to speak a partial sentence of three words or more (that is, the probability that ) when is Δ0, the probability when is Δ1, and Δ0 < Δ1. Therefore, if we combine the model in equation (6) with age ranges provided by the respondent, we conclude that, according to respondent i, the probability that the child will learn how to do MSD task j in scenario k when is:
| (7) |
Analogously, the probability that the child will learn how to do MSD task j in scenario k when is
| (8) |
If we manipulate the system in equations (7) and (8), we conclude that, for arbitrary j and k, the following equalities hold:
| (9) |
and
| (10) |
Given and , the next step in the algorithm is to estimate the probability that the child will learn how to say a partial sentence with three words or more by age 24 months. The individual-specific IRT model states that this probability is:
| (11) |
We use equation (11), together with the IRT probability in equation (4), to derive an error-ridden measure of maternal expectation of the natural log of development at age 24 months, ln , from the implied probability . To do so, we invert (4) and solve for ln :
| (12) |
The parameters Δ0 and Δ1 play an essential role in transforming the age ranges to probabilities. Ideally, we would observe these parameters, and we would allow them to vary across respondents in our study. In practice, it is cumbersome to elicit participants’ beliefs about these parameters, so in our empirical analysis, we assume that Δ0 = 10% and Δ1 = 90%. These choices for the parameters are in line with evidence from the elicitation of subjective probability in developing countries (see summary in Delavande et al., 2011). In our empirical analysis, we investigate the robustness of our findings by varying parameters and interpolating functions.
We illustrate the algorithm with Figure 3. The left panel in Figure 3 captures the first step of the process, which is described by equations (9), (10), and (11). To construct this example, we assume that the study participant states that the age ranges are 21 and 25 for the scenario in which both human capital and investment are “high.” We combine the maternal reports with Δ0 and Δ1, and (9) and (10), to compute the parameters and . Once we know these two parameters, we use equation (11) to produce the solid curve for the scenario when both human capital at birth and investments are “high.” The maternal reports of age ranges, combined with the information in (9), (10), and (11), lead us to estimate that, according to the mother, there is a 75% chance that the child will learn how to speak a partial sentence with three words or more at age 24 months. We capture this transformation with a thin solid line that starts at 3.18 ≈ ln(24) in the horizontal axis and crosses the solid IRT line at .75 in the vertical axis.
Figure 3:
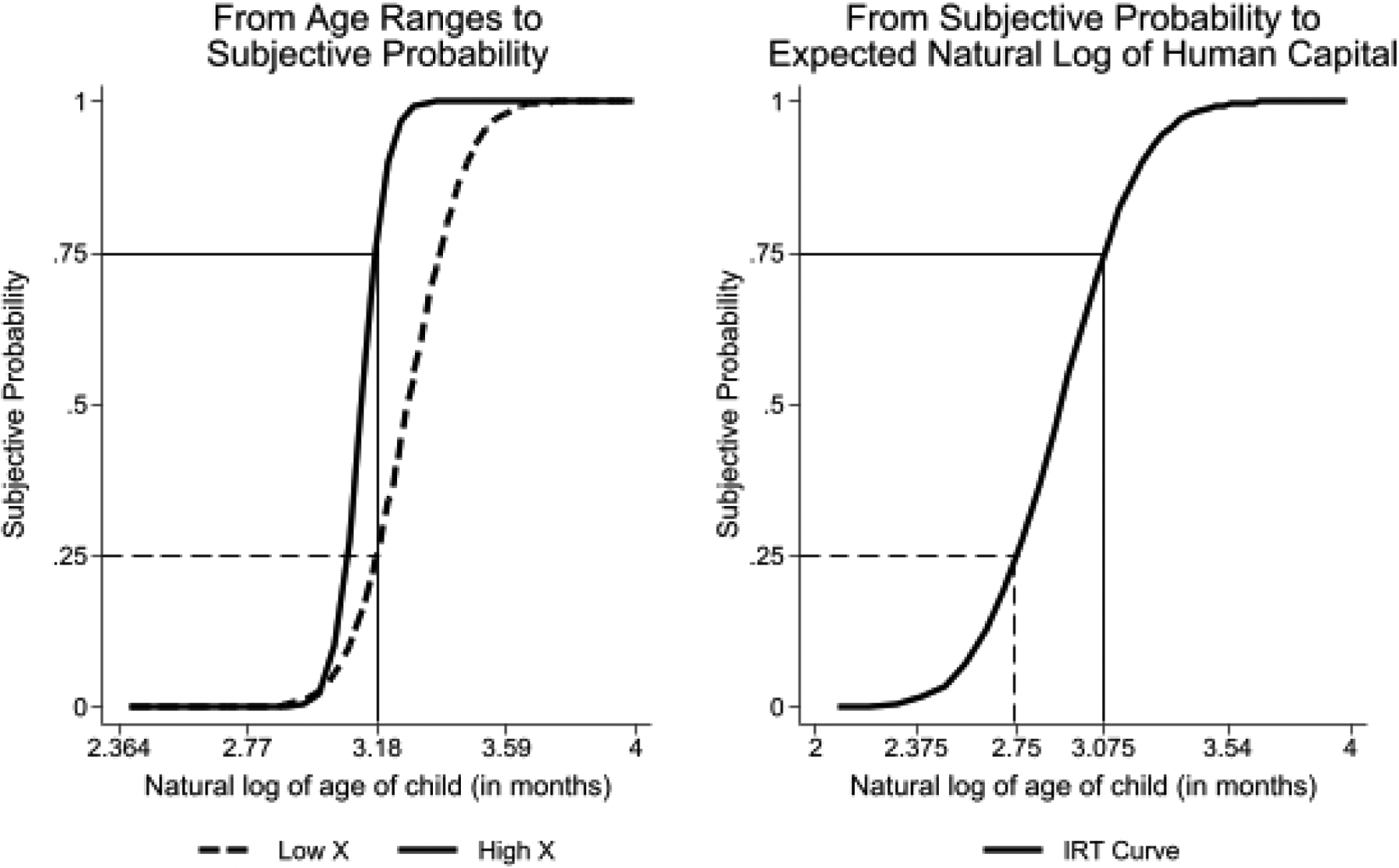
This figure shows the two steps involved in transforming age ranges to error-ridden measures of expectation of the natural log of human capital at age 24 months. In the first step, which we show in the left panel, we use maternal reports of the age ranges and assumptions about the interpolating function and the parameters Δ0 and Δ1. For this figure, we assume that the interpolating function is the normal CDF, Δ0 = 10% and Δ1 = 90%. We show the transformation from age ranges to subjective probability for two scenarios of investments (“high” vs. “low”) when human capital at birth is “high.” When the investment is “low,” the mother reports age ranges equal to 22 and 32 months. As a result, the probability that the child will learn how to “speak a partial sentence with three words or more” by age 24 months is 25%. When the investment is “high,” the age ranges are 21 and 25 months, which corresponds to a probability of 75%. The right panel shows the transformation from subjective probability to error-ridden measures of the expectation of the natural log of human capital at age 24 months. This step is identical to the transformation from subjective probability to error-ridden measures of child development in the subjective probability form (see Figure 2).
In contrast, the same participant reports that the age ranges are 22 and 32 months when the human capital at birth is “high,” and the investment is “low.” We repeat the very same steps to produce the dashed curve for this scenario. By following the algorithm, we estimate that the mother assigns a subjective probability of 25% that the child will learn how to speak a partial sentence with three words or more at age 24 months. We trace this relationship with a dashed line that starts at ln(24) in the horizontal axis and crosses the dashed IRT curve at .25 in the vertical axis.
Finally, we use equation (12) to transform the participant’s probabilities into a measure of the expected level of development according to the age range questions, ln . We reproduce this last step in the right panel of Figure 3, which is identical to Figure 2.
2.4.3. Summary
We briefly summarize the commonalities and differences between the two elicitation forms. Both elicitation forms generate data about the subjective probability that children will be able to execute specific developmental tasks at age two years for given scenarios of human capital at birth and investments. Both elicitation methods invert the IRT model (3) to relocate and rescale subjective probabilities to expected measures of child development at age two years.
The difference between the two methods is in the production of the subjective probability data. In the subjective probability elicitation form, we obtain this information directly from study participants. In the age range form, we make assumptions about interpolation forms (6) and parameters Δ0 and Δ1 to transform age ranges into subjective probabilities. Therefore, the age range elicitation form requires additional assumptions to produce the subjective probability data indirectly. For this reason, we investigate the robustness of our findings as we consider different assumptions about the transformation from age ranges to subjective probability.
2.5. Identification
Next, we shed light on the source of identification for MSE. In essence, the identifying information comes from three different types of moments from the raw data. First, to identify μi,ψ,3 in equation (2), the coefficient on the interaction between human capital at birth and investments, we rely on the following differences-in-differences:
| (13) |
where , and
The first difference in the RHS of equation (13) is the gap between two levels of the expected log of human capital at age two: one when the investment is “high” and another when the investment is “low,” both conditional on the human capital at birth to be “high.” The second difference, in contrast, is conditional on human capital at birth to be “low.” If the study participants’ answers were error-free, then we would directly observe all of these expectations. We would identify the first difference from the discrepancy between answers in Scenarios 1 and 3. Similarly, we would identify the second difference from the gap between Scenarios 2 and 4.
We can use the following moment to identify μi,ψ,2 in equation (2):
| (14) |
Note that equation (14) is just a “weighted” difference-in-difference moment in which the weights are the scenarios for human capital at birth. Finally, we can derive a moment that identifies μi,ψ,1 in equation (2):
| (15) |
Moment (15) is distinct from Moment (14) in two ways: the weights and the expectations involved in the differences.
Although these moments provide a clear indication of the source of identification, they are in practice not helpful because they assume that the data are measured without error, which is an extreme assumption. In the next section, we derive an estimation algorithm that allows for general measurement error models. Later, we will impose more restrictive assumptions about the measurement error processes and use the moments we derived in this section to derive a factor model approach for the analysis of MSE data.
2.6. Estimation of MSE
Note that ln defined in equation (5) and ln defined in equation (12) are two error-ridden measures of maternal expectations about the natural log of child development. Let denote the measurement error in form f, scenario k, MSD item j, and participant i. We define . We define in a similar fashion the vectors , ln qi and Zi, where Zi,j,k =(ln q0,i,j,k, ln x0,i,j,k, ln q0,i,j,k, ln xi,j,k). Finally, let μψ,i = (μψ,i,1, μψ,i,2, μψ,i,3). Therefore:
| (16) |
Equation (16) is the random coefficient model (RCM) described in Swamy (1970). The first equality in (16) reflects our premise that ln qi is an error-ridden measure of . The second equality follows from (2).
Next, we define the deviation ui as follows: μψ,i = μψ + μi where E(ui|Zi) = 0 and . Let ωi = Ziui + ϵi. The error term ωi contains the participant’s MSE deviation from the mean MSE as well as the measurement error. We now introduce the assumptions we use to identify these two components separately.
Assumption 1: The disturbance ωi satisfies (A) E(ωi|Zi) = 0 and (B) .
The mean independence Assumption (1A) is respected in the current setup because scenarios of human capital at birth and investments, which are the variables in Zi, are fixed across agents and exogenously determined by the elicitation procedure. Assumption (1A) does not impose that study participants are, on average, correct about the parameter vector ψ = (ψ1, ψ2, ψ3) because it allows for μψ ≠ ψ.
Assumption (1B) allows for a non-diagonal variance-covariance matrix and allows for the variance of the measurement error to be person-specific. However, it does not allow for correlation in measurement error ϵi, which is usual in measurement error models (see Schennach, 2016). In the next section, we relax this restriction and consider an estimation procedure that allows for measurement error to be correlated across scenarios within each elicitation form and MSD item.
Assumption (1) does not impose parametric assumptions about the distributions of μψ,i, or ϵi.
Appendix B provides a step-by-step implementation of the RCM estimator. In this section, we briefly verbally describe the procedure. The RCM estimator aggregates the data in two stages. First, the estimator aggregates individual-level responses to estimate the cross-sectional mean of the MSE vector.
Second, the RCM estimator computes the discrepancy between individual responses from the predicted mean. It estimates individual-level MSE as a combination of the overall mean of MSE plus the weighted sum of the discrepancies. The weights are a decreasing function of the variance of measurement error. Thus, the efficiency of the RCM estimator arises because it gives a low weight to observations with much noise. In our empirical application, we show how averaging responses across forms and MSD items play an essential role in our analysis.
In our empirical application, we also use the estimator and its variance to test hypotheses, such as whether the study participants believe that the technology of skill formation takes on a Cobb-Douglas specification.
Let T and L denote the number of observations per study participant and the dimension of the vector μψ,i, respectively. The RCM estimator requires T > L. In our practical implementation below, we have T = 32 because we obtain answers for each one of the four scenarios, for each one of the four MSD items, for each one of the two different elicitation forms. In our model, L = 3.
Note that it would be feasible to estimate our model using only one item of the MSD, only one survey instrument form, and four hypothetical scenarios (so that T = 4). Because we have multiple MSD items, however, we can investigate how the respondents’ answers vary across MSD items for a fixed scenario of human capital at birth and investments. If the respondents understand the survey instrument, we would expect them to assign a lower probability, or higher age ranges, to more difficult items, holding constant the scenario for human capital at birth and investments.
If the respondents report similar probabilities or age ranges for the same scenario across items that differ in difficulty for the child to learn, we should worry about the possibility that respondents do not understand the instrument very well or are not devoting the necessary effort to give meaningful answers. In that case, the amount of measurement error in responses will be significant, and, if not addressed, the measurement will bias the predictive relationship between beliefs and investment choices. In addition, the availability of multiple reports allows us to mitigate the effect of heaping by aggregating participants’ answers across forms and items.
Although the number of scenarios by itself is sufficient to estimate the individual MSE parameters, it is not enough, without additional restrictions, to estimate maternal subjective uncertainty (MSU) about the parameters of the technology of skill formation (1). Let , and note that, given parameterization (1),
| (17) |
in our particular application, the right-hand side of equation (17) contains seven unknowns: six parameters in the matrix Σi plus the variance term . Therefore, to estimate MSU with respect to the technology of skill formation, we would need to elicit dependence across different scenarios or impose restrictions to identify a simpler model.
2.7. A Factor Model Approach
Next, we propose a model for measurement error, which, in combination with our parameterization (2), guides the formulation of the problem in terms of factor models. In this section, we expand on the identification analysis based on the method of moments in Section 2.5. We start by introducing two assumptions for measurement error:
Assumption 2: .
Assumption 3: is uncorrelated with for f ≠ f′ or j ≠ j′.
The literature that studies measurement error in the context of repeated measures invokes some form of uncorrelatedness assumption usually (see a summary of this vast body of literature in Schennach, 2016) — thus, Assumption (3). We weaken the assumption, however, by allowing for correlation across scenarios conditional on an elicitation form and MSD item. We view this decomposition as natural because each elicitation form presents one MSD item at a time. We display, however, all of the scenarios—for a given MSD item and form—simultaneously (see Appendix Figures A1 and A2). Naturally, the answer to scenario k influences the answer to scenario k′ (and vice-versa). As a result, if there is measurement error in answer to one scenario, it is natural to assume that there is measurement error in answer to another scenario and that these errors are correlated—thus, Assumption (2).
A significant challenge in implementing the moments in Section 2.5 is that as equation (16) states clearly, we observe error-ridden measures of . Indeed, as we defined in equation (16), ln is an error-ridden measure of maternal expectations about child human capital at age two when we use elicitation form f, MSD item j, and scenario k. The variable is the measurement error, which we assume satisfies Assumptions 2 and 3. Then, the combination of parameterization (2) with Assumptions 1, 2, and 3 produces the following latent MSE model:
| (18) |
where
Note that, for each latent MSE variable, we have eight moments. They arise from the product of four different MSD items and two different elicitation forms. Not all measures, however, are equally informative. For example, note that the covariance between any of two variables in the RHS of moments in equation (18) satisfies:
| (19) |
If we fix the elicitation form f and MSD item j, then the correlation across the three moments reflect not only the correlation across the latent MSE variables μi,ψ,j but also the correlation across the difference of differences of measurement errors, captured by . The parameter depends not only on the αk’s in Assumption (2) but also on the values for the scenarios of human capital at birth and investments.
In factor analysis, researchers usually (but not always) decompose the data in orthogonal factors. If we assume that all of the factors are orthogonal, then the covariance matrix described by (19) predicts, for each elicitation form, exactly seven factors: one factor for each MSE latent variable and one MSD item-specific measurement error factor.
However, the latent MSE variables need not be orthogonal. Further, if the factors are highly correlated, the three latent MSE variables may be summarized by fewer than three factors. To illustrate the issue, we return to the ideal moments (13), (14), and (15). Some trivial algebra leads us to the following equations:
| (20) |
As we discussed in Section 2.5, the moment Mi,1 and Mi,3 contain identifying information for the latent variables μi,ψ1 and μi,ψ,3, respectively. Equations (20) indicate that crucial identifying moments may be correlated. The amount of correlation depends, in part, on study participants’ responses. For example, the term captures the change in expected human capital at age two when we increase human capital at birth from “low” to “high” while keeping constant investments at the “high” level. The interpretation of the term is similar, except that we hold investments at the “low” level. If all study participants believe that and , the moments Mi,1 and Mi,3 will be highly correlated. For this reason, both μi,ψ1 and μi,ψ,3 will also be highly correlated. In this case, we may need only one factor to summarize the identifying information for μi,ψ1 and μi,ψ,3.
These conclusions also are valid for the relationship between μi,ψ,2 and μi,ψ,3. Indeed, if we condition on scenarios for human capital at birth, then we can derive a parallel set of cross-moment relationships:
| (21) |
Finally, if the right-hand side of both cross-moment relationships in (20) and (21) are small, then the three moments Mi,1, Mi,2, and Mi,3 will be highly correlated, and the identifying information for the three latent variables μi,ψ,1, μi,ψ,2, and μi,ψ,3 will be summarized by a single factor.
To summarize, the discussion of these moment relationships helps us to understand that the three latent MSE variables μi,ψ,1, μi,ψ,2, and μi,ψ,3 need not be orthogonal. If we perform a factor analysis of the data from each elicitation form separately, our model predicts any number between five to seven factors. One to three latent factors will capture identifying information about μi,ψ,1, μi,ψ,2, and μi,ψ,3. Additionally, four factors capture MSD item-specific measurement error variables in Assumption (A2). In our empirical analysis, we investigate the restrictions on the number of factors predicted by our model. Throughout our empirical analysis sections, we refer to these restrictions on the number of factors as “testable restrictions.”
3. Data
The data come from a longitudinal study in Philadelphia. The Philadelphia Human Development (PHD) study enrolled 822 first-time pregnant women from clinics during their second trimester of pregnancy. During the first wave of the PHD study, we collected data on socio-demographic characteristics (e.g., age, education, marital status, household income) and answers from the two different forms developed to elicit MSE. Thus, all 822 participants provided valid answers to both forms of elicitation of MSE. We interviewed participants at a separate office in the prenatal clinic. All of the interviews were face-to-face and followed the same protocol. The structure of the survey was as follows. First, the respondent watched a short video that described the scenarios for human capital at birth and investments. Second, they answered the subjective probability elicitation instrument form. Third, they provided information about their health status and household income. Fourth, they completed the age range elicitation instrument form. Fifth, they reported their demographic information.
When their children were approximately nine months old, we conducted the second wave of interviews. We interviewed 687 participants. We visited their homes, and we measured family investments in children, using the full version of the Home Observation for the Measurement of the Environment (HOME) Scale. The full HOME Scale contains 45 dichotomous items to which the caretaker responds during an unstructured interview that lasts between 60 and 90 minutes. The HOME Scale measures the quality and quantity of stimulation available to the child in the environment. Researchers have used it in national studies as well as in numerous home visitation programs nationally and internationally (Totskika and Sylva, 2004).
The HOME Scale divides the 45 items into six subscales. The Responsivity subscale measures the degree to which the caregiver and the environment are responsive in an emotional, physical, or communicative sense to the infant. The subscale intends to identify an environment that the child understands to be trustworthy. The Acceptance subscale quantifies the amount of restriction and punishment the child experiences daily. The subscale’s purpose is to pinpoint environments in which the child can learn through trial and error. The Organization subscale records the amount of structure that the caregiver provides to the infant’s life. Its objective is to determine whether the environment offers the child a positive and predictable structure. The Learning Materials subscale provides a count of the props that allow the infant to develop competence for enjoyment and exploration. In other words, the subscale measures the number of opportunities for the child to learn through play. The Variety subscale measures the degree to which the child has contacts with other family members. The subscale aims to quantify whether the child has a complete and balanced portfolio of experiences. Finally, the Involvement subscale allows parents to demonstrate how they do things with their children spontaneously. The purpose is to assess whether the child benefits from having a learning facilitator in his or her environment.
4. Results
4.1. Sample Characteristics from the PHD Study
Table 1 presents the demographic characteristics of the PHD study sample. The participants are relatively young: 63.25% of the mothers enrolled in the study were born between 1988 and 1997. The majority of these mothers are Non-Hispanic Black (around 54%). At the time of recruitment into the study, 60% of the participants were single, 30% were married, and 10% were cohabiting.5 The participants tended to have lower educational attainment than do national representative samples: 42% were high-school dropouts; 42% had a high school degree or some post-secondary schooling, but only 16% had a four-year college degree or more education.
Table 1.
Demographic Characteristics of PHD Study Participants
| Characteristic | Percentage |
|---|---|
| Year of Birth | |
| Mother born between 1968 and 1977 | 3.54% |
| Mother born between 1978 and 1987 | 33.21% |
| Mother born between 1988 and 1987 | 63.25% |
| Race and Ethnicity | |
| Mother is Hispanic | 13.02% |
| Mother is Non-Hispanic Black | 53.77% |
| Mother is Non-Hispanic White | 26.64% |
| Other | 6.57% |
| Educational Attainment | |
| Less than high school diploma | 42.09% |
| High school or some college | 41.36% |
| Four-year college diploma or higher | 16.55% |
| Marital Status | |
| Singlea | 60.71% |
| Cohabiting | 9.49% |
| Married | 29.81% |
| Center for Epidemiological Studies Depression Scale | |
| The score is greater than or equal to 16 | 29.32% |
| Household Income Per Year (y) | |
| y < $25,000 | 44.77% |
| $25,000 ≤ y < $55,0000 | 20.56% |
| $55,000 ≤ y < $105,0000 | 16.06% |
| y ≥ $105,000 | 18.61% |
| Sample Size | |
| First waveb | 822 |
| Second wavec | 687 |
Notes:
In the single category, we include one participant who reported being separated and two participants who reported being divorced at the time of enrollment in the study. The remaining individuals in this category (496 out of 499) reported being single and never married at the time of enrollment into the study.
We conducted the first wave when the mothers were in the second trimester of their first pregnancy.
We conducted the second wave when the children were 9–12 months old.
We used the Center for Epidemiologic Studies Depression (CESD) scale to screen participants for depression. According to the scale’s manuals, any individual with a score above 16 is at risk for clinical depression. In the PHD study, almost 30% of the sample scores were above this cutoff. Finally, household income is low, as almost half of the sample had a household income of less than $25,000 per year, which is approximately the 25th percentile in the U.S. distribution of household income.6
4.2. Analysis of the Elicitation Data
In this section, we present the raw features of responses. We start our analysis with the data we elicited with the subjective probability elicitation form. Then, we proceed with the inspection of the data we obtained with the age ranges elicitation form. In the main text, we focus our discussion on the MSD item “speak a partial sentence,” so we can conserve space. Appendix C reproduces the tables and figures for all MSD items.
4.2.1. Subjective Probability
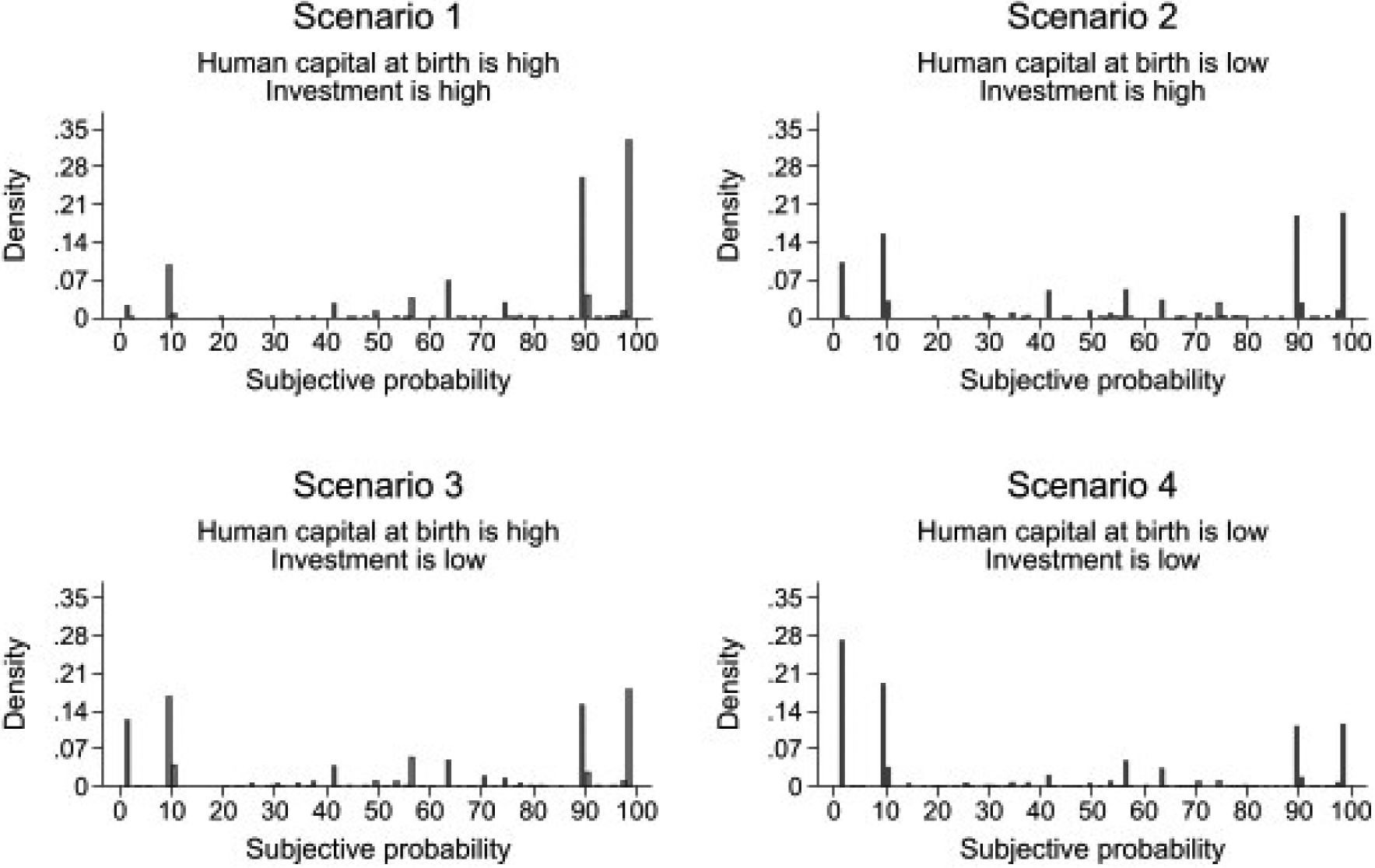
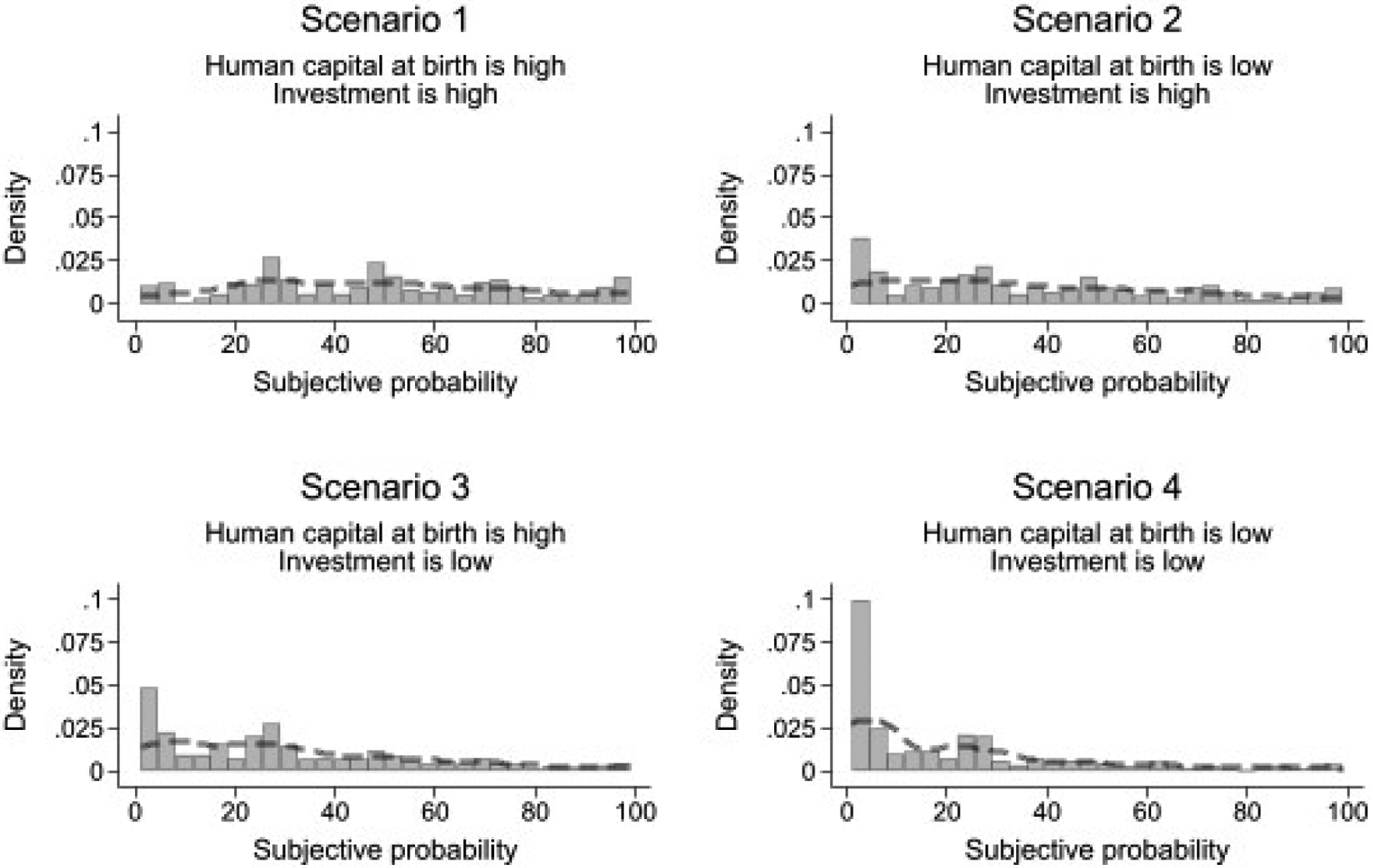
In this section, we present the features of the subjective probability data, as reported by study participants. Figure 4 presents the histograms of answers to that form. In the paper, we focus our attention on the first MSD item in both forms (“speaks a partial sentence with three words or more”). The most noticeable pattern in responses is heaping on round numbers. Although respondents could choose any integer between 0 and 100, the raw data show that respondents overwhelmingly chose multiples of 10. The heaping that we observe for “speaking a partial sentence with three words or more” is also present for the other three MSD items we use in this study.7
Figure 4:
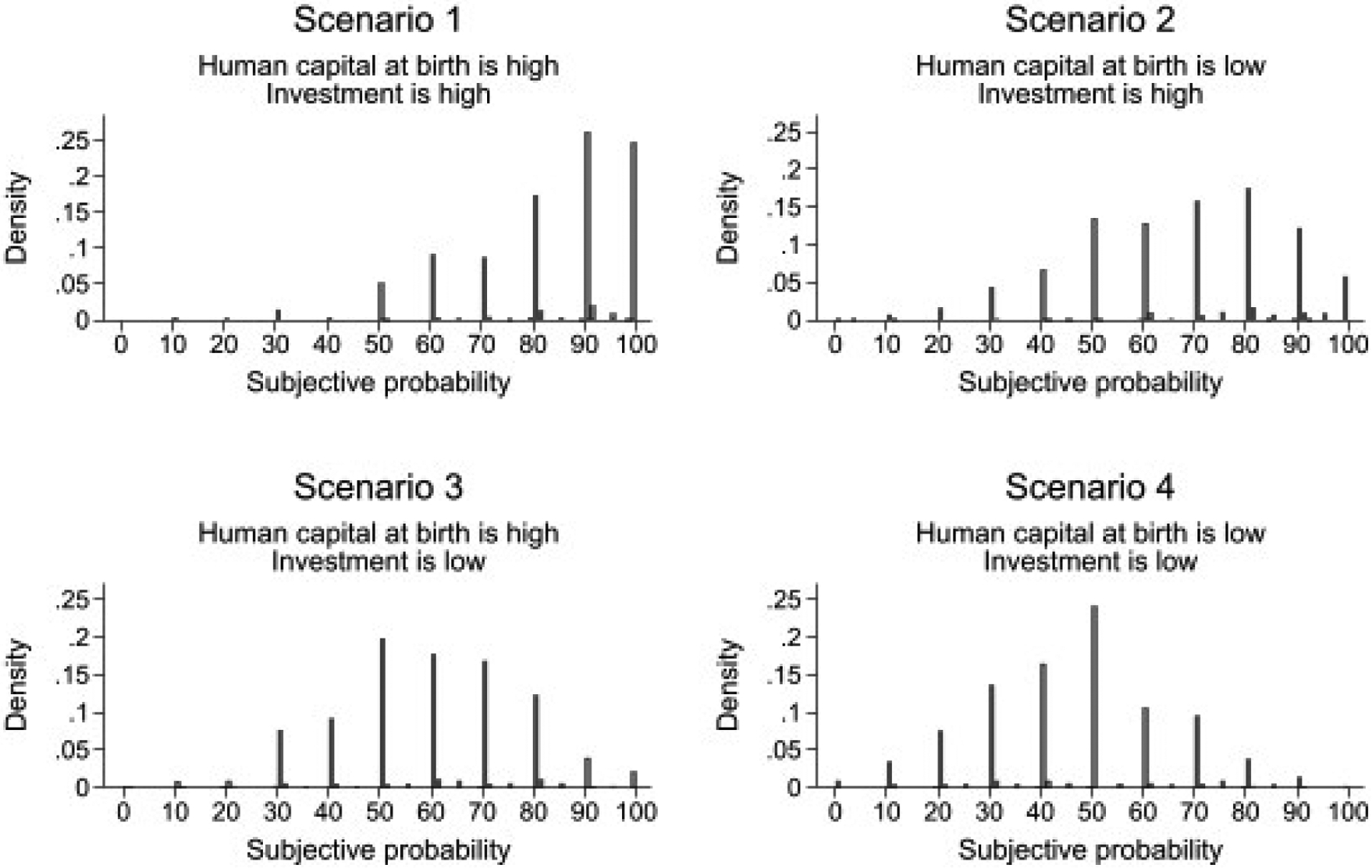
This figure shows the histograms of maternal reports of subjective probability for the MSD item “child speaks a partial sentence with three words or more” for all scenarios of human capital at birth and investments. The figure shows a pattern of answers that indicates that the higher human capital at birth or investment, the higher the likelihood that the child will be able to accomplish this task by age 24 months.
The pattern of answers also indicates that the higher the level of inputs, the higher the likelihood that the child will learn how to speak a partial sentence with three words or more by age two. For investments, we can conclude so by comparing maternal reports in Scenario 1 with the answers in Scenario 3. Alternatively, we can contrast answers to Scenarios 2 and 4. The difference calculated by the first comparison is an estimate of the average MSE about the impact of investment when human capital is “high.” The gap estimated by the second comparison is an estimate of the average MSE about the impact of investments when human capital is “low.” In either case, the difference in subjective probability is a median increase of 10 percentage points when investments move from “low” to “high.” A similar estimation for the impact of human capital at birth on the subjective probability of learning how to “speak a partial sentence” is 20 percentage points. Therefore, raw answers indicate that the higher the levels of inputs, the greater the chances of learning tasks by age two.
Table 2 presents the expectations of child developmental outcomes according to the subjective probability form (see Section 2.4.1). We present these probabilities for the four MSD items and the four different scenarios in which human capital at birth and investments are varied. Several remarkable results are evident in this table. First, the probabilities reported by respondents vary in ways that are consistent with underlying assumptions of the technology of skill formation. Ceteris paribus, the higher the stock of human capital at birth, or the level of investment, the higher the probability that a baby will learn the MSD tasks used in the subjective probability elicitation exercise.
Table 2.
Summary Statistics of Answers to the Subjective Probability-Elicitation Form
| Brief description of the MSD item | Panel A | |||||
|---|---|---|---|---|---|---|
| Scenario 1 | Scenario 2 | |||||
| Human capital at birth is “high” Investment is “high” | Human capital at birth is “low” Investment is “high” | |||||
| Mean | Median | SD | Mean | Median | SD | |
| Speaks partial sentence | 82.27 (0.59) | 90.00 (0.84) | 16.97 (4.30) | 67.28 (0.71) | 70.00 (1.68) | 20.31 (4.37) |
| Counts three objects correctly | 79.27 (0.68) | 80.00 (0.84) | 19.58 (4.74) | 65.63 (0.74) | 70.00 (0.84) | 21.32 (4.48) |
| Knows own age and sex | 83.89 (0.59) | 90.00 (0.84) | 16.81 (4.39) | 69.80 (0.70) | 70.00 (0.84) | 20.04 (4.24) |
| Says first and last names together | 82.23 (0.67) | 90.00 (0.84) | 19.30 (5.15) | 69.19 (0.75) | 70.00 (1.60) | 21.37 (4.73) |
| Brief description of the MSD item | Panel B | |||||
| Scenario 3 | Scenario 4 | |||||
| Human capital at birth is “high” Investment is “low” | Human capital at birth is “low” Investment is “low” | |||||
| Mean | Median | SD | Mean | Median | SD | |
| Speaks partial sentence | 59.18 (0.64) | 60.00 (0.92) | 18.43 (3.99) | 46.23 (0.65) | 50.00 (0.84) | 18.76 (4.02) |
| Counts three objects correctly | 56.63 (0.71) | 60.00 (0.84) | 20.25 (4.34) | 44.69 (0.68) | 41.00 (0.84) | 19.55 (4.20) |
| Knows own age and sex | 59.84 (0.66) | 60.00 (0.84) | 18.82 (4.15) | 47.15 (0.67) | 50.00 (0.84) | 19.13 (4.13) |
| Says first and last names together | 59.68 (0.70) | 60.00 (1.68) | 20.11 (4.33) | 47.15 (0.72) | 50.00 (0.84) | 20.75 (4.41) |
Note: This table shows the mean, median, and standard deviation (SD) of maternal reports of subjective probability for each MSD item and scenario. See Figure 1 for a full description of the MSD items and scenarios. We order MSD items according to their difficulty, from easiest (“speaks partial sentence”) to hardest (“says first and last name together”). The table shows that the maternal subjective probabilities increase with human capital at birth and investments. However, they do not vary with item difficulty. We show the standard errors in parentheses.
The probabilities derived from answers to the subjective probability form do not vary with the difficulty of the MSD item. The median likelihood reported by mothers for any given MSD item is around 90% for Scenario 1, 70% for Scenario 2, 60% for Scenario 3, and 50% for Scenario 4.
We further elaborate on this finding by focusing on two MSD items. The first is, “Child speaks a partial sentence with three words or more,” and the second is, “Child says first and last names without someone’s help.” According to the NHANES dataset, by age 24 months, 72% of children already will have spoken a partial sentence with three words or more, but only 26% will have already said their first and last names. This difference indicates that “say the first and the last names” is more difficult for a 2-year-old child than is “speak a partial sentence.” When we use the subjective probability form, the participants’ answers for a given scenario are about the same for both items. For example, the median mother states that, for both items, the probability is around 90% and 50% in Scenarios 1 and 4, respectively. This evidence suggests that mothers believe that these two items have about the same difficulty level, which contradicts the evidence from the NHANES dataset.
In Section 2.6, we discussed our concerns about heaping and measurement error. Now, we have presented evidence that the data suffer from heaping (Figure 4) and, possibly, measurement error (Table 2). Next, we show how the availability of multiple items within a form can help to mitigate the effects of heaping. Figure 5 presents the histograms when we aggregate maternal subjective probability reports across MSD items for the subjective probability form. For Scenario 1, we still have some heaping at high probability values, but heaping has been reduced for other scenarios because maternal reports across MSD items for a given scenario are correlated but far from perfect.8 This property of high, but imperfect, correlation is an essential result for addressing heaping and measurement error. If answers were uncorrelated, we would not be able to identify the latent MSE variables. If the correlation were perfect, we would not be able to separate latent MSE variables from measurement error.
Figure 5:
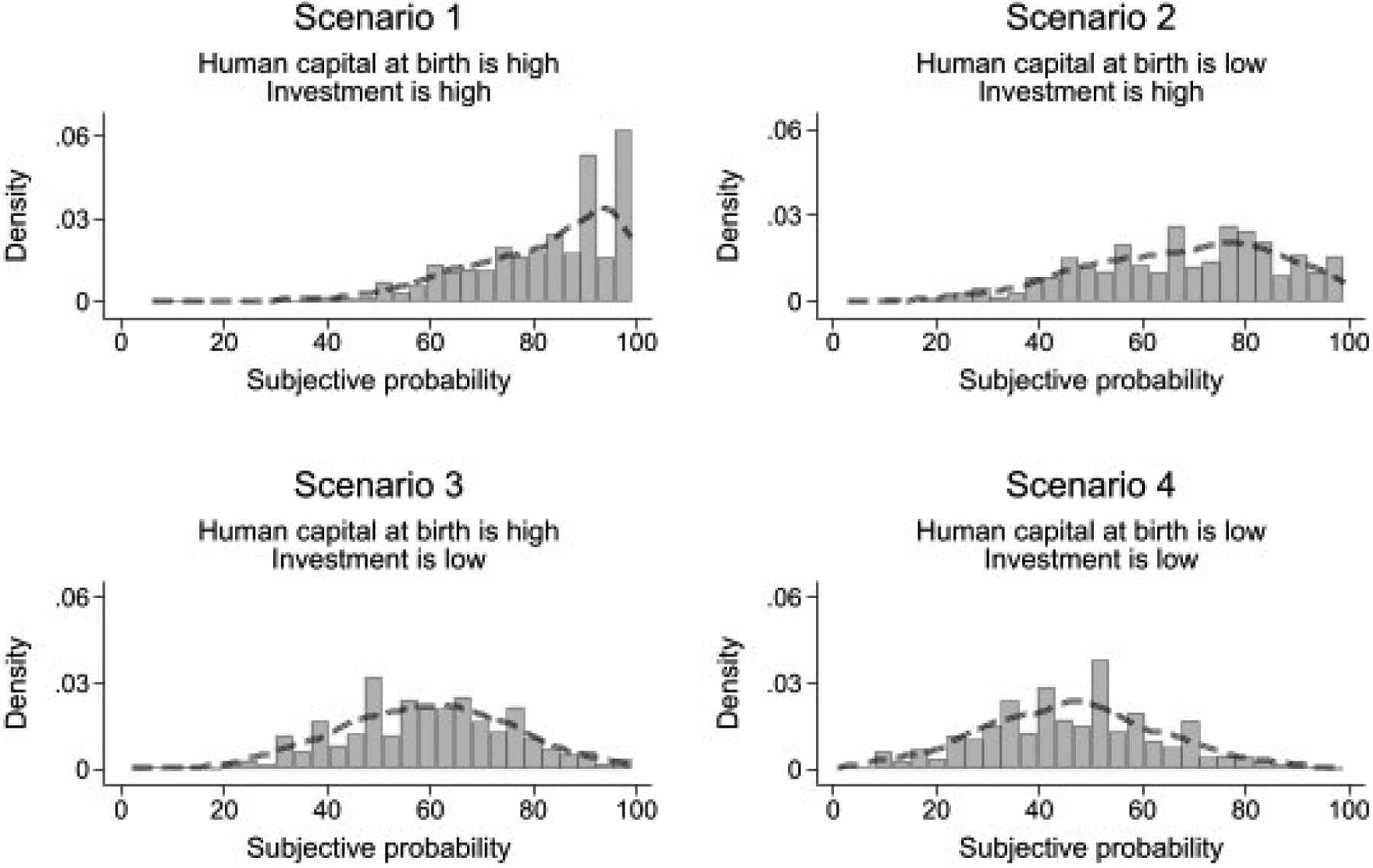
This figure shows the histograms of subjective probability after we average maternal reports across the MSD items for each scenario of human capital at birth and investment. The result is that subjective probabilities are far less likely to exhibit heaping that we observed in Figure 4.
Figure 6 presents histograms of the expected log of human capital at age two. To obtain these estimates, we proceed in two steps. In the first step, we invert the IRT equation (5). The input in equation (5) is the subjective probability for each scenario and MSD item. The output of equation (5) is an error-ridden measure of the expected log of human capital for each scenario and MSD item.
Figure 6:
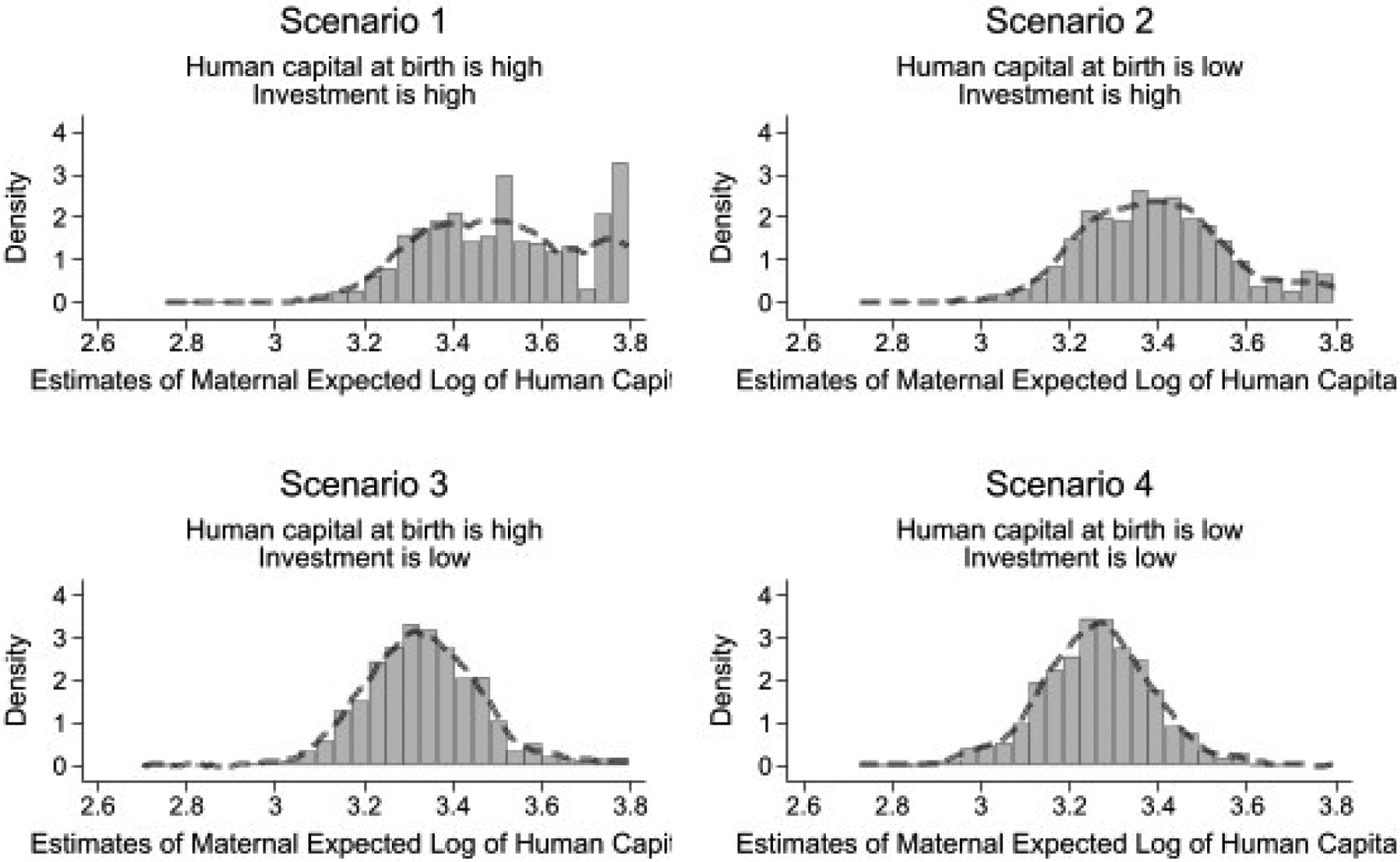
This figure displays the histograms of error-ridden measures of the expectation of the natural log of human capital at age two years for each scenario of human capital at birth and investments. To produce these measures, we proceed in two steps. In the first step, we transform, for each MSD item and scenario, the subjective probability data to an error-ridden, MSD-item specific, measure of the expectation of the natural log of human capital. In the second step, we average the measures across MSD items for each scenario. We then plot the histograms of the averaged measures.
In the second step, we average across all MSD items for a given scenario. In this section, we use uniform weighting, but the RCM estimator weighs according to the precision of each measure, thus producing an efficient estimator of the latent MSE. Figure 4 shows that the cross-sectional distribution of the expected log of human capital is not subject to heaping once we average across MSD items. Moreover, the higher the level of the input (human capital at birth or investments), the higher the output.
4.2.2. Age Ranges
In this section, we present features based on the raw answers from the age-range form. Figure 7 presents the histograms of study participants’ reports of the youngest and the oldest ages that children would learn how to “speak a partial sentence.” We show the youngest age in solid gray bars, and the oldest age in white bars delimited with black lines. As in the subjective probability form, we observe heaping, particularly at multiples of 6 months.
Figure 7:
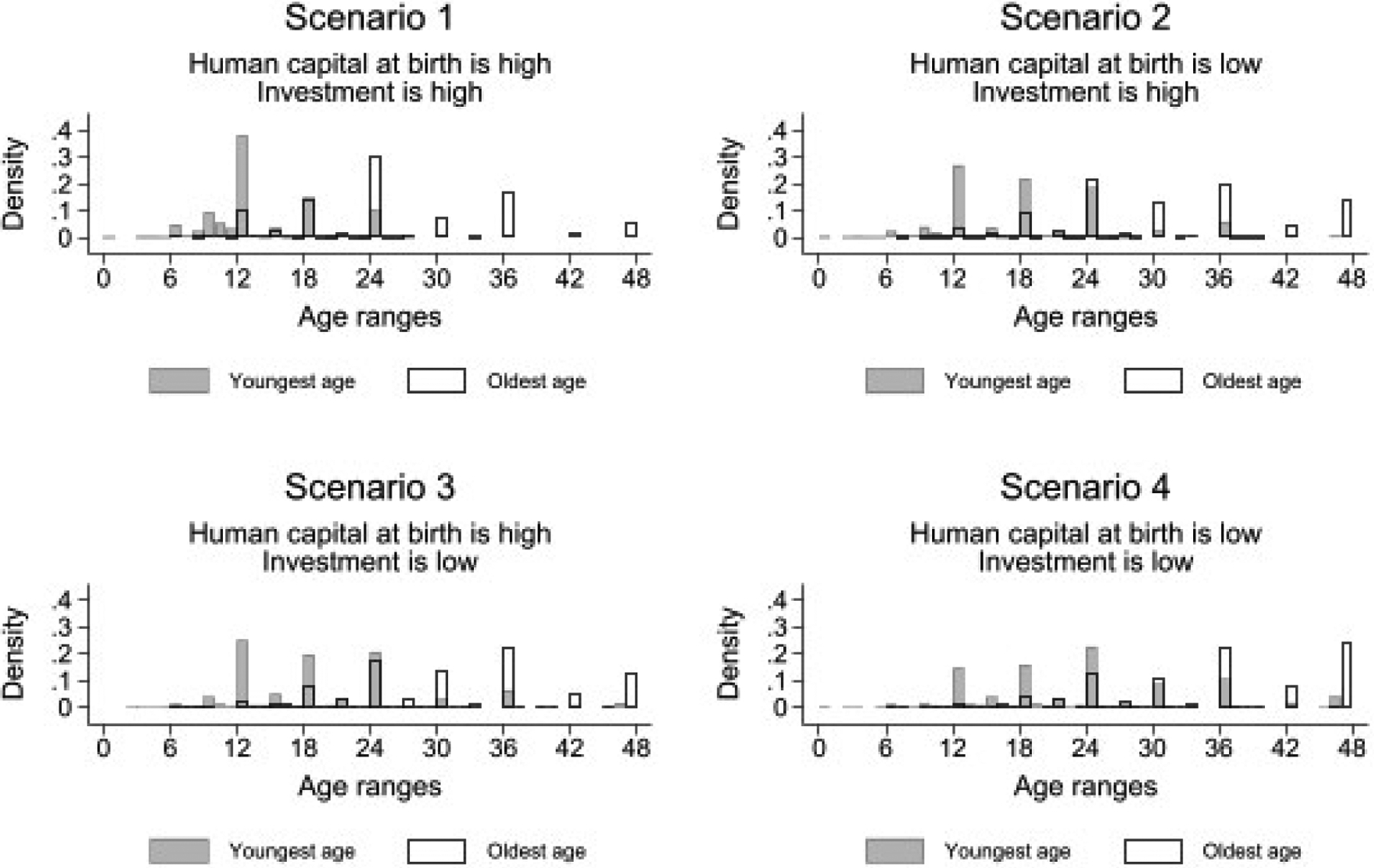
This figure plots the histograms of maternal reports of age ranges for the MSD item “speak a partial sentence with three words or more.” The solid gray bars show the youngest ages children will learn this MSD task for each scenario of human capital at birth and investments. The solid white bars show the oldest ages. This figure shows heaping around multiples of six months. This heaping pattern is similar to the one observed for the subjective probability data that we show in Figure 4.
Second, the reported youngest and oldest age vary in predictable patterns with the levels of the inputs. The higher the level of one input, ceteris paribus, the earlier the youngest and the oldest ages children will learn how to “speak a partial sentence.” We analyze this property of answers more thoroughly, as presented in Table 3. In this table, we display the mean, median, and standard error of youngest and oldest ages for each MSD item and scenario of human capital and investments. As in the subjective probability form, we see that mean and median tend to move in predictable patterns with the inputs.
Table 3.
Summary Statistics of Answers to the Age-Range Elicitation Form
| Brief description of the MSD item | Panel A | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Scenario 1 | Scenario 2 | |||||||||||
| Human capital at birth is “high” Investment is “high” | Human capital at birth is “low” Investment is “high” | |||||||||||
| Youngest age | Oldest age | Youngest age | Oldest age | |||||||||
| Mean | Median | SD | Mean | Median | SD | Mean | Median | SD | Mean | Median | SD | |
| Speaks partial sentence | 13.96 (0.20) | 12.00 (0.00) | 5.72 (1.49) | 25.37 (0.34) | 24.00 (0.00) | 9.78 (2.10) | 17.98 (0.28) | 18.00 (0.42) | 7.96 (1.97) | 30.03 (0.37) | 30.00 (0.76) | 10.49 (2.04) |
| Counts three objects correctly | 23.10 (0.32) | 24.00 (0.25) | 9.18 (1.96) | 34.14 (0.35) | 36.00 (0.50) | 9.97 (1.88) | 25.85 (0.35) | 24.00 (0.25) | 10.10 (2.07) | 36.35 (0.34) | 36.00 (0.25) | 9.77 (1.89) |
| Knows own age and sex | 19.99 (0.29) | 18.00 (0.50) | 8.19 (1.80) | 31.07 (0.34) | 30.00 (1.01) | 9.62 (1.87) | 23.28 (0.32) | 24.00 (0.50) | 9.20 (1.94) | 34.02 (0.34) | 36.00 (0.50) | 9.66 (1.85) |
| Says first and last names together | 23.62 (0.32 | 24.00 (0.00) | 9.21 (1.94) | 34.33 (0.33) | 36.00 (0.50) | 9.41 (1.85) | 26.26 (0.34) | 24.00 (0.50) | 9.75 (2.01) | 36.51 (0.32) | 36.00 (0.25) | 9.12 (1.83) |
| Brief description of the MSD item | Panel B | |||||||||||
| Scenario 3 | Scenario 4 | |||||||||||
| Human capital at birth is “high” Investment is “low” | Human capital at birth is “low” Investment is “low” | |||||||||||
| Youngest age | Oldest age | Youngest age | Oldest age | |||||||||
| Mean | Median | SD | Mean | Median | SD | Mean | Median | SD | Mean | Median | SD | |
| Speaks partial sentence | 19.07 (0.29) | 18.00 (0.25) | 8.33 (2.07) | 30.79 (0.35) | 30.00 (0.76) | 10.14 (2.00) | 22.78 (0.34) | 24.00 (0.50) | 9.65 (2.15) | 34.32 (0.36) | 36.00 (0.50) | 10.41 (1.97) |
| Counts three objects correctly | 27.55 (0.36) | 24.00 (0.50) | 10.24 (2.04) | 37.73 (0.31) | 36.00 (0.50) | 8.89 (1.78) | 30.44 (0.38) | 30.00 (0.92) | 10.83 (2.13) | 40.24 (0.30) | 42.00 (1.01) | 8.64 (1.94) |
| Knows own age and sex | 25.35 (0.33) | 24.00 (0.00) | 9.42 (1.97) | 36.17 (0.31) | 36.00 (0.00) | 8.98 (1.79) | 28.84 (0.35) | 30.00 (0.50) | 10.17 (2.03) | 39.06 (0.31) | 42.00 (0.50) | 8.91 (1.89) |
| Says first and last names together | 28.01 (0.34) | 27.00 (0.50) | 9.87 (1.95) | 38.32 (0.30) | 36.00 (0.50) | 8.61 (1.83) | 30.81 (0.36) | 30.00 (0.50) | 10.24 (2.08) | 40.72 (0.29) | 42.00 (0.67) | 8.33 (1.96) |
Note: This table shows the youngest and oldest age for each MSD item and scenario. See Figure 1 for a full description of the MSD items and scenarios. We order MSD items according to their difficulty, from easiest (“speaks partial sentence”) to hardest (“says first and last name together”). Reported ages decrease with human capital at birth and investments. Standard errors in parentheses.
We also see a minor difference between age range and subjective probability forms. The respondents report lower mean and median youngest and oldest ages for “speak a partial sentence” relative to the other three MSD items. This pattern indicates that respondents identify “speaking a partial sentence” as easier than “counting three objects,” “knowing own age and sex,” or “saying first and last names.” The respondents, however, judge the last three items to be at the same level of difficulty. As we described above, the objective data suggest that they are not.
The third pattern in Figure 7 indicates that a large percentage of study participants report the oldest ages before 24 months or the youngest ages after 24 months. For these participants, the choice of Δ0 and Δ1 significantly influence the estimated subjective probability. As we explain in Section 2.4.2, we state that the probability of developing an MSD task is Δ0 at the youngest age and Δ1 at the oldest age. We use these parameters and a parametric assumption to interpolate between the youngest and oldest ages reported by the mother. Because we are interested in estimating the probability at age 24 months, the choice of Δ0 and Δ1 influence those situations in which both youngest and oldest ages are to the left (or right) of 24 months.
For example, if the youngest age is above 24 months, the probability we estimate cannot be higher than Δ0. If the oldest age is below 24 months, this probability cannot be smaller than Δ1. These “bounds” are valid for whatever interpolation form we use, and their influence will be more significant the smaller the value of Δ0 or the higher the value of Δ1. For now, we adopt Δ0 = 10% and Δ1 = 90%. Later, we investigate the robustness of our results as we vary these parameters as well as the interpolation functions.
Table 4 provides additional evidence of the influence of Δ0 and Δ1 on our data. For each MSD item and each scenario, we estimate the share of the answers in which the youngest age is above 24 months, and we assess the fraction of answers in which the oldest age is below 24 months. Again, we find three predictable patterns. First, holding constant the MSD item, the lower the level of the inputs, the higher the fraction of the youngest ages above 24 months and the lowest the share of the oldest ages below 24 months. Second, the more difficult the MSD item, holding constant the scenario, the higher the fraction of responses with the youngest age above 24 months, and the smaller the share in which the oldest age is smaller than 24.
Table 4.
The fraction of Youngest Age above 24 months or Oldest Age below 24 months
| Brief description of the MSD item | Panel A | |||
|---|---|---|---|---|
| Scenario 1 | Scenario 2 | |||
| Human capital at birth is “high” Investment is “high” | Human capital at birth is “low” Investment is “high” | |||
| Youngest age | Oldest age | Youngest age | Oldest age | |
| Fraction above 24 months | Fraction below 24 months | Fraction above 24 months | Fraction below 24 months | |
| Speaks partial sentence | 0.129 (0.335) | 0.657 (0.475) | 0.290 (0.454) | .0437 (0.496) |
| Counts three objects correctly | 0.573 (0.495) | 0.280 (0.449) | 0.642 (0.480) | 0.186 (0.389) |
| Knows own age and sex | 0.422 (0.494) | 0.403 (0.491) | 0.540 (0.499) | 0.264 (0.441) |
| Says first and last names together | 0.620 (0.486) | 0.236 (0.425) | 0.698 (0.459) | 0.155 (0.362) |
| Brief description of the MSD item | Panel B | |||
| Scenario 3 | Scenario 4 | |||
| Human capital at birth is “high” Investment is “low” | Human capital at birth is “low” Investment is “low” | |||
| Youngest age | Oldest age | Youngest age | Oldest age | |
| Fraction above 24 months | Fraction below 24 months | Fraction above 24 months | Fraction below 24 months | |
| Speaks partial sentence | 0.335 (0.472) | 0.378 (0.485) | 0.505 (0.500) | 0.263 (0.440) |
| Counts three objects correctly | 0.706 (0.456) | 0.125 (0.331) | 0.792 (0.406) | 0.078 (0.268) |
| Knows own age and sex | 0.635 (0.482) | 0.161 (0.367) | 0.740 (0.439) | 0.105 (0.306) |
| Says first and last names together | 0.740 (0.439) | 0.111 (0.314) | 0.811 (0.391) | 0.072 (0.258) |
Note: This table shows the fraction of reported youngest (oldest) age above (below) 24 months for each MSD item and scenario. The fraction of youngest (oldest) age increases (decreases) with item difficulty and increase (decrease) with scenarios of human capital at birth and investments. Standard error in parentheses.
Third, although the youngest and the oldest ages indeed move in opposite directions, the share of responses that have one of the two problems is more or less constant across scenarios or MSD items. They fluctuate around 80%. In other words, when we use the age-range form, about 80% of the answers either report the youngest age above 24 months or the oldest age below 24 months. Therefore, it is only for about one out of five answers that the interpolation between the youngest and oldest age determines the probability at age 24 months. For the other four out of five answers, the probability is less affected by the interpolation scheme and more affected by the choice of Δ0 and Δ1. This pattern of answers reinforces the importance of investigating the robustness of our conclusions when we vary Δ0 and Δ1.
The next step in our analysis is to derive estimates of the subjective probabilities from the age range responses from study participants. As we explain in Section 2.4.2, these transformations require that we use Δ0, Δ1, and an interpolation function. Figure 8 provides the histograms of the estimates of the subjective probability based on age ranges. The histograms show not only heaping but also that respondents concentrate answers at low or high values of the probability range. When human capital at birth and investments are both “high,” the heaping is pronounced at high probabilities. When both are “low,” we observe the opposite. When one is “low” and the other is “high,” then the heaping is more or less equal at both extremes of the probability range.
Figure 8:
This figure shows the subjective probability data after transformation from age ranges. In this figure, we show the data for the MSD item “speak a partial sentence with three words or more.” To transform the data from age ranges to subjective probability, we follow the steps described in Section 2.4.2. We assume that the interpolating function is the normal CDF and that the parameters Δ0 = 10% and Δ1 = 90%. We note that the subjective probability data suffers from heaping, but unlike the one in Figure 4, the heaping in this data occurs at the extremes.
Similar to the subjective probability reports, we can mitigate the heaping and the relevance of Δ0 and Δ1 parameters by averaging answers across MSD items. Figure 9 shows the histograms of the averaged (or aggregated) probabilities. For all of the scenarios, we can eliminate heaping at high levels of probabilities when we average across MSD items. For Scenarios 3 and 4, there still is some heaping at low levels of probabilities.
Figure 9:
This figure shows the histograms of the subjective probability average across MSD items for each scenario. In this figure, we use only the data from the age ranges elicitation form. We follow two steps to produce this figure. In the first step, we transform the age ranges data to subjective probability for each MSD item. To do so, we assume that the interpolating function is a normal CDF and the parameters Δ0 = 10% and Δ1 = 90%. In the second step, we average subjective probabilities across MSD items for each scenario. The histograms show that the averaged data do not feature as much heaping.
Similar to the results presented in Section 4.2.1, we find that the youngest ages across MSD items and scenarios are positively but imperfectly correlated. The same is true for the pattern of answers for the oldest ages. Appendix Tables C2 and C3 show that the correlation tends to be lower than the correlation of reports of subjective probability.
Next, we use the algorithm in Section 2.4.2 to transform the data from estimates of subjective probability into estimates of the expected log of human capital at age two. Figure 10 shows the results. It is interesting to contrast Figure 10 with the corresponding one from the elicitation of subjective probability (Figure 6). In Figure 6, the distribution of answers for Scenario 1 is left-skewed. In Figure 6, the answers are more dispersed and do not exhibit much of a skew pattern. The situation is the opposite of the answers in Scenarios 2, 3, and 4. In these scenarios, the distribution of answers is symmetrically distributed around the mean in Figure 6 but right-skewed in Figure 10.
Figure 10:
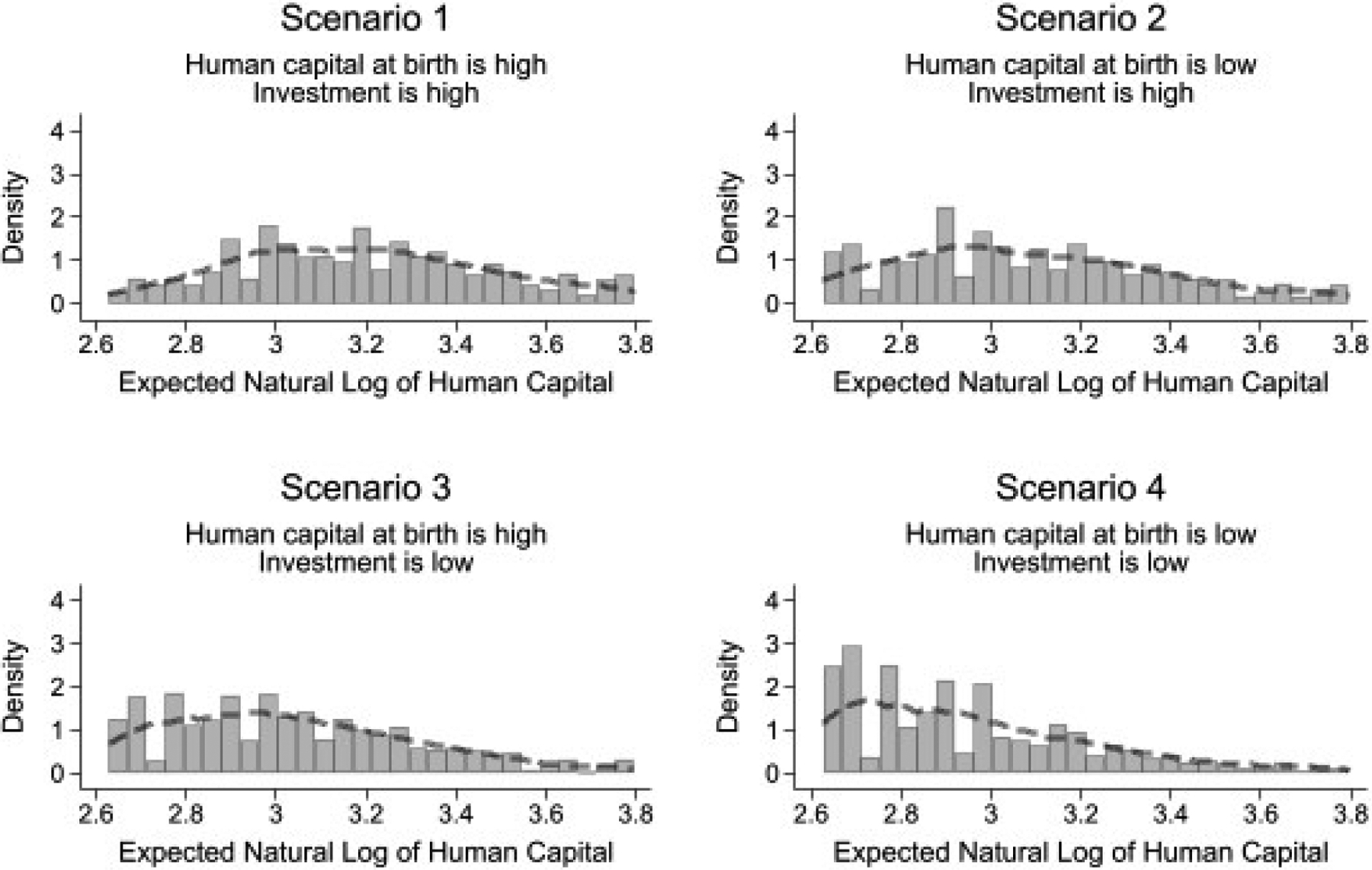
This figure shows the histograms of the averaged error-ridden measures of the expectation of the natural log of human capital for each scenario when we average across MSD items for the age ranges elicitation form. To produce this figure, we follow three steps. In the first step, we use the normal CDF as the interpolating function (with parameters Δ0 = 10% and Δ1 = 90%), to transform the age ranges data to subjective probability data. We do so for each MSD item and each scenario separately. Then, we use the IRT model (3), for each MSD item and scenario, to relocate and rescale the subjective probability data to the expectation of the natural log of human capital at age two years. In the last step, we average across MSD items for each scenario.
4.3. Measurement Error and Testable Restrictions
We emphasize three features of the raw data that both elicitation forms share. First, we identify predictable patterns: The greater the level of the inputs, the higher the probability that the child will learn a given MSD task. Second, we document heaping. With these commonalities in mind, we aggregate answers within scenarios across MSD items and elicitation forms. Figure 11 presents the histograms and kernel density estimates of the expected log of human capital at age two for each scenario after we aggregate across MSD items and elicitation forms.9 These “super-aggregate” measures still produce the same predictable patterns, but now heaping is no longer a significant feature of the data. It is the variation across scenarios in Figure 11 that the RCM estimator will explore to estimate the individual-level MSE parameters.
Figure 11:
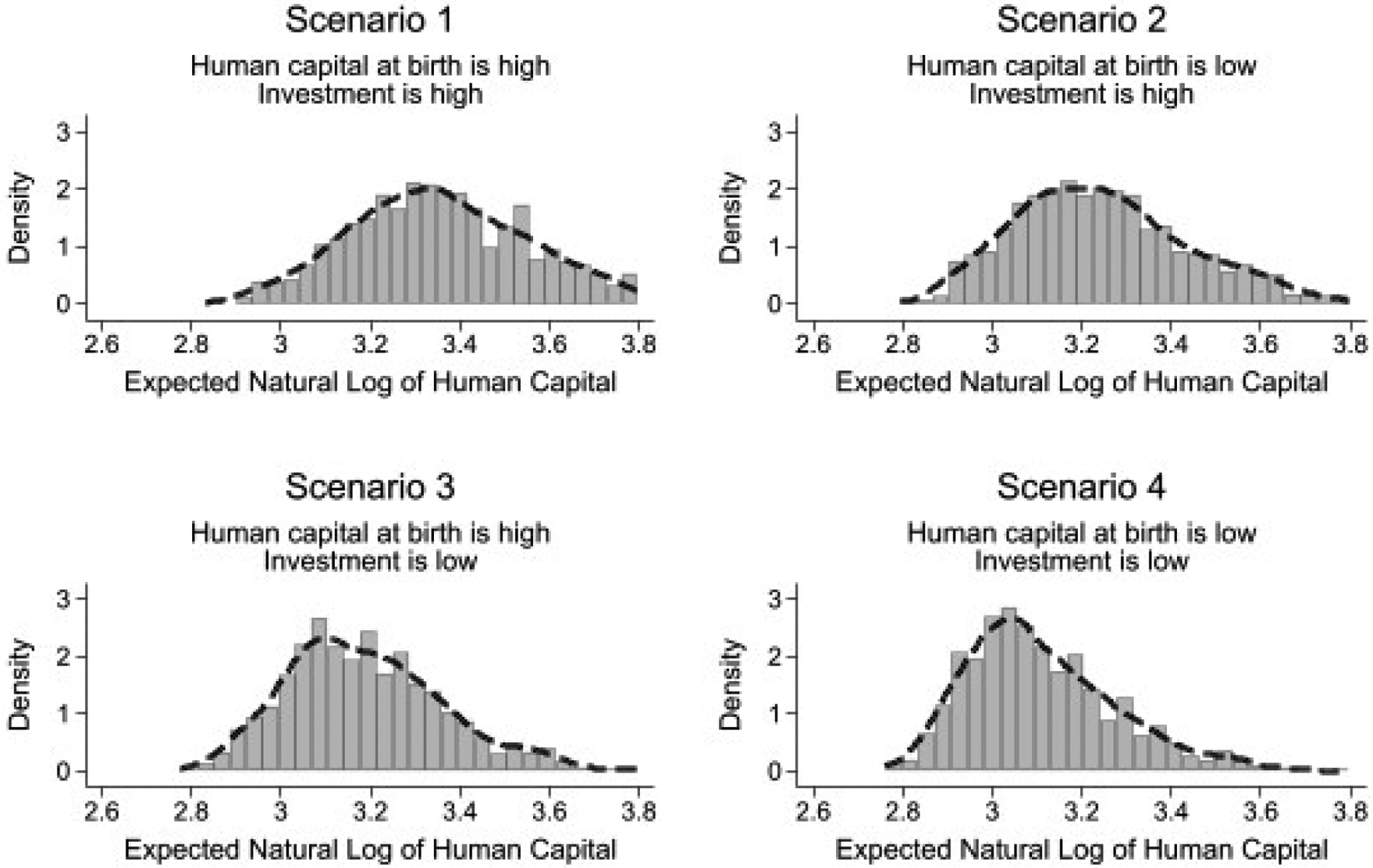
This figure shows the histograms of the averaged error-ridden measures of the expectation of the natural log of human capital for each scenario when we average both across MSD items and elicitation forms. We remark that Figure 6 and Figure 10 present the histograms when we average across MSD items but not across elicitation forms. Once we average across both MSD items and elicitation forms, as shown in this figure, we have eliminated all forms of heaping. The estimator of the MSE also averages the data across MSD items and elicitation forms but does so in an efficient manner.
Third, we provide indirect evidence of measurement error by showing that answers are invariant mainly to MSD item difficulty. When answering the survey, we would like the study participants to be able to make two-dimensional comparisons. In the first dimension, they should compare how the levels of inputs affect the child’s chances of learning a given MSD task. The evidence indicates that participants make such comparisons.
In the second dimension, we would like respondents to pay attention to the fact that different MSD items have distinct levels of difficulty. The participants seem not to be able to do so. Because of this failure, it is essential to provide some other form of validation for data on subjective expectations about the parameters of the technology of skill formation. Next, we investigate the validity of the data. First, we study whether the data satisfy the testable restrictions we derived in Section 2.7. Later, we study the validity of the belief data in terms of predicting investment choices.
Next, we perform a factor analysis of our error-ridden measures ln . We do so for each form f at a time. First, we consider the data from the subjective probability form. Specifically, we use the responses from each MSD item to construct the three moments in the system (18). Then, we conduct a factor analysis of the 12 measures. We rotate factors obliquely because the latent MSE variables need not be orthogonal. Table 5 shows the results of our analysis. For the subjective probability elicitation form, we find that six factors summarize the informational content of the data. The six factors have patterns precisely as predicted by the model presented in Section 2.7. Factors 2–5 capture information due to the term .
Table 5.
Factor Loadings of the Measurements of Expectation of Human Capital at Age 2 Subjective Probability-Elicitation Form
| Equation Number | Latent Variable | MSD Item | Factor Variances | |||||
|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | |||
| 2.951 | 2.608 | 2.538 | 2.362 | 2.320 | 0.733 | |||
| Factor Loadings | ||||||||
| 1 | 2 | 3 | 4 | 5 | 6 | |||
| 1 | μψ,3 | 1 | 0.008 | −0.034 | −0.041 | −0.886 | −0.044 | 0.170 |
| 2 | μψ,3 | 2 | −0.043 | −0.053 | −0.842 | −0.062 | −0.048 | 0.257 |
| 3 | μψ,3 | 3 | −0.048 | −0.070 | −0.033 | −0.031 | −0.861 | 0.277 |
| 4 | μψ,3 | 4 | −0.056 | −0.831 | −0.081 | −0.030 | −0.056 | 0.249 |
| 5 | μψ,2 | 1 | 0.693 | −0.047 | −0.040 | 0.489 | −0.100 | −0.033 |
| 6 | μψ,2 | 2 | 0.777 | −0.054 | 0.369 | −0.061 | −0.047 | 0.008 |
| 7 | μψ,2 | 3 | 0.827 | −0.059 | −0.068 | −0.057 | 0.381 | −0.002 |
| 8 | μψ,2 | 4 | 0.767 | 0.401 | −0.043 | −0.051 | −0.073 | 0.015 |
| 9 | μψ,1 | 1 | −0.024 | 0.054 | 0.045 | 0.841 | 0.056 | 0.300 |
| 10 | μψ,1 | 2 | 0.029 | 0.076 | 0.826 | 0.036 | 0.035 | 0.341 |
| 11 | μψ,1 | 3 | 0.008 | 0.056 | 0.046 | 0.045 | 0.841 | 0.347 |
| 12 | μψ,1 | 4 | 0.011 | 0.801 | 0.052 | 0.068 | 0.103 | 0.336 |
Notes: This table displays the factor loadings when we estimate the latent variable model (18) in Section 2.7. The data come from the subjective elicitation form. The MSD Item 1 is “Speaks partial sentence”; MSD Item 2 is “Counts three objects correctly”; MSD Item 3 is “Knows own age and sex”; and MSD Item 4 is “Says first and last names together.” See Figure 1 for a full description of the MSD items and scenarios. We order MSD items according to their difficulty, from easiest (“speaks partial sentence”) to hardest (“says first and last name together”). The bolded factor loadings highlight the equations which factor loads. Factor 1 loads in equations 5–9 in the latent variable model (18). These equations contain identifying information for the MSE parameter μψ,2. Factors 2 and 5 load on MSD item-specific equations, reflecting measurement error that correlates across scenarios within MSD items. Factor 6 loads in the equations that contain identifying information for the MSE parameters μψ,1 and μψ,3, thus indicating that these parameters are potentially highly correlated.
The first factor loads on measures that relate to the latent maternal belief μi,ψ,2. The sixth factor, in contrast, captures information that relates to the latent maternal belief μi,ψ,1 as well as μi,ψ,3.
In our analysis, we refer to Factors 2, 3, 4, and 5 as “(subjective probability form) measurement error” factors and Factors 1 and 6 as “(subjective probability form) structural” factors.10
We perform a similar factor analysis for the 12 measures from the age-range form. The results in Table 6 show that the factor analysis of the age-range form generates a factor structure that satisfies the predictions of our model. As expected, the analysis generates four factors (Factors 1–4) that summarize the correlation within MSD item measures. In our model, this correlation is consistent with the error we defined in Assumption (A2) in Section 2.7. We refer to these factors as “(age ranges) measurement error” factors.
Table 6.
Factor Loadings of the Measurements of Expectation of Human Capital at Age 2 Age-Range Elicitation Form
| Equation Number | Latent Variable | MSD Item | Factor Variances | |||||
|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | |||
| 2.951 | 2.608 | 2.538 | 2.362 | 2.320 | 0.733 | |||
| Factor Loadings | ||||||||
| 1 | 2 | 3 | 4 | 5 | 6 | |||
| 1 | μψ,3 | 1 | −0.930 | −0.020 | −0.026 | −0.024 | 0.046 | 0.056 |
| 2 | μψ,3 | 2 | 0.024 | −0.004 | −0.896 | −0.001 | 0.021 | 0.129 |
| 3 | μψ,3 | 3 | −0.001 | −0.908 | −0.026 | −0.027 | −0.014 | 0.147 |
| 4 | μψ,3 | 4 | −0.001 | −0.025 | 0.011 | −0.888 | 0.003 | 0.180 |
| 5 | μψ,2 | 1 | 0.755 | −0.010 | −0.019 | −0.020 | 0.188 | −0.054 |
| 6 | μψ,2 | 2 | 0.010 | −0.013 | 0.638 | 0.004 | 0.411 | −0.024 |
| 7 | μψ,2 | 3 | 0.016 | 0.605 | −0.051 | −0.049 | 0.447 | 0.005 |
| 8 | μψ,2 | 4 | −0.026 | −0.005 | −0.026 | 0.617 | 0.422 | 0.020 |
| 9 | μψ,1 | 1 | 0.858 | 0.007 | −0.014 | 0.002 | −0.023 | 0.203 |
| 10 | μψ,1 | 2 | 0.017 | 0.036 | 0.886 | −0.002 | 0.011 | 0.183 |
| 11 | μψ,1 | 3 | 0.019 | 0.865 | 0.034 | 0.021 | 0.010 | 0.188 |
| 12 | μψ,1 | 4 | 0.032 | 0.001 | 0.027 | 0.863 | −0.003 | 0.164 |
Notes: This table displays the factor loadings when we estimate the latent variable model (18) in Section 2.7 for the data from the age ranges form. The MSD Item 1 is “Speaks partial sentence”; MSD Item 2 is “Counts three objects correctly”; MSD Item 3 is “Knows own age and sex”; and MSD Item 4 is “Says first and last names together.” See Figure 1 for a full description of the MSD items and scenarios. We order MSD items according to their difficulty, from easiest (“speaks partial sentence”) to hardest (“says first and last name together”). The bolded factor loadings highlight the equations which factor loads. Factors 1 and 4 load on MSD item-specific equations, reflecting measurement error that correlates across scenarios within MSD items. Factor 5 loads in equations 5–12 in the latent variable model (18). Factor 6 loads in the equations that contain identifying information for the MSE parameter μψ,1 and μψ,3, thus indicating that these parameters are potentially highly correlated.
The fifth factor captures the information concerning the latent maternal belief μi,ψ,2. This result is similar to the one in Table 5 but with one significant difference. The variance of Factor 5 in Table 6 is only a third of the variance of Factor 1 in Table 5. The sixth factor loads on moments for μi,ψ,1 and μi,ψ,3. We refer to Factors 5 and 6 as “(age ranges) structural” factors.
The subjective probability and age-range forms produce slightly different factors because the underlying correlation matrices of the data generated by the two forms are slightly different. As we show in Appendix Table C4, the subjective probability form creates a correlation matrix that is very close to the prediction of the model. We can identify blocks that relate to each latent MSE variable μi,ψ,j. In contrast, the age-range method delivers a correlation matrix that features a weaker correlation within blocks; thus, they do not provide as much identifying information to each latent variable of interest μi,ψ,j.
We also factor analyze the data after we combine information from both forms, all MSD items, and all scenarios. After we rotate the factors obliquely, we obtain 13 factors, six of which reflect the findings in Table 5, and six of which reproduce the findings from Table 6 (see Appendix Table C5).11 The nonorthogonality of the factors capture, among other things, the correlation in responses across forms. Interestingly, the “subjective probability structural” factors are correlated with their “age range structural” factors counterpart. However, the correlation is small. This result indicates that the forms may not identify the same latent MSE variables. This result highlights the relevance of validating beliefs data by studying their power in predicting choices.
Overall, our analysis identifies important commonalities between both elicitation forms. The data generate predictable patterns (higher inputs lead to higher expectations about developmental outcomes). The answers exhibit considerable heaping around round numbers. We confirm not only the existence of measurement error, but we also identify its pattern. Our econometric methodology that averages across MSD items and forms plays an essential role in mitigating heaping and measurement error.
In the next subsection, we use the error-ridden measures of the expected log of human capital at age two to identify the mean belief parameters in the technology of skill formation (2).
4.4. Estimates of MSE about the Technology of Skill Formation
Table 7 displays the estimates of mean MSE, , as well as their standard errors.12 We use to estimate individual-specific MSE, , as well as their standard errors. Finally, we employ and its variance to test the null hypothesis that μi,ψ,j = 0 against the alternative hypothesis that μi,ψ,j ≠ 0. We conduct this test for each PHD study participant separately. Among other things, Table 7 presents the percentage of respondents for whom we can reject the null hypothesis.
Table 7.
Means of Maternal Beliefs about the Technology of Skill Formation
| Both Forms | Subjective-Probability Form | Age-Range Form | |
|---|---|---|---|
| 0.182 (0.008) | 0.238 (0.010) | 0.216 (0.011) | |
| 0.293 (0.009) | 0.396 (0.011) | 0.330 (0.012) | |
| 0.028 (0.006) | 0.050 (0.009) | 0.029 (0.009) | |
| Test of Parameter Constancy | |||
| H0: μi,ψ,j = μψ,j ∀i, j | Reject H0 | Reject H0 | Reject H0 |
| H1: μi,ψ,j = μψ,j for at least one i, j | |||
| Hypotheses Tests (% Reject H0) | |||
| H0: μi,ψ,1 = 0; H0: μi,ψ,1 ≠ 0 | 68.0% | 92.0% | 44.3% |
| H0: μi,ψ,2 = 0; H0: μi,ψ,2 ≠ 0 | 88.2% | 98.7% | 71.3% |
| H0: μi,ψ,3 = 0; H0: μi,ψ,3 ≠ 0 | 5.7% | 14.5% | 2.6% |
Note: Generalized least squares standard error in parentheses.
We present the discussion of Table 7 from bottom to top. First, we cannot reject the null hypothesis that the technology of skill formation is Cobb-Douglas for the majority of respondents in the PHD study. When we combine data from both forms, we can reject Cobb-Douglas for 5.7% of the sample. When we utilize the data from subjective probability form, the percentage goes up to 14.5%. The percentage is much lower (2.63%) when we use data only from the age-range form. In contrast, rejection of the null hypothesis μi,ψ,1 = 0 or μi,ψ,2 = 0 is far more common. Moreover, the rejection rates are particularly high when we use the data from the subjective probability form and much lower when we use the age-range form. This finding reinforces the difference in the pattern of answers between the two methods. As we saw in Section 4.3, the maternal answers from the subjective probability form fit more closely the structure of correlation that the model predicts.
RCM also develops a chi-square test in which the null hypothesis is that all of the mothers have the same MSE (test of parameter constancy). Below, we describe the heterogeneity in MSE, but here we note that we can formally reject that all mothers have the same MSE parameters. Given that we cannot reject Cobb-Douglas for the majority of mothers in the PHD study, the substantial heterogeneity in expectations about ψ1 and ψ2 drives the rejection of parameter constancy across individuals. We return to this issue below.
The parameter μψ,1 represents maternal beliefs about the coefficient of human capital at birth. Ignoring the interaction term, the typical mother believes that a one-standard-deviation change in the natural log of human capital at birth increases human capital at age two by approximately 18% of a standard deviation. When we use only the subjective probability form or only the age-range form, the mean estimates are slightly larger (23.8% and 21.6%, respectively).
The parameter μψ,2 captures maternal beliefs about the coefficient on investments. We find that the typical mother believes that the mean of μψ,2 ranges from 29.3% (when we combine answers from both forms) to 39.6%. Ignoring the interaction term, the interpretation of these estimates means that the typical mother believes that a one-standard-deviation change in investments increases human capital at age two by 29.3% of a standard deviation.13
Figure 12 displays the marginal densities of MSE about ψ1 for j = 1,2,3. We fix the horizontal axis so that they take common values across all j. It is, therefore, easy to see that the heterogeneity in MSE about ψ3 is of little importance, regardless of whether we combine data from different forms or use data from each one of the forms separately. Figure 12 also shows that the marginal distributions of MSE implied by the age-range form have lower means and higher variances for both ψ1 and ψ2.
Figure 12:
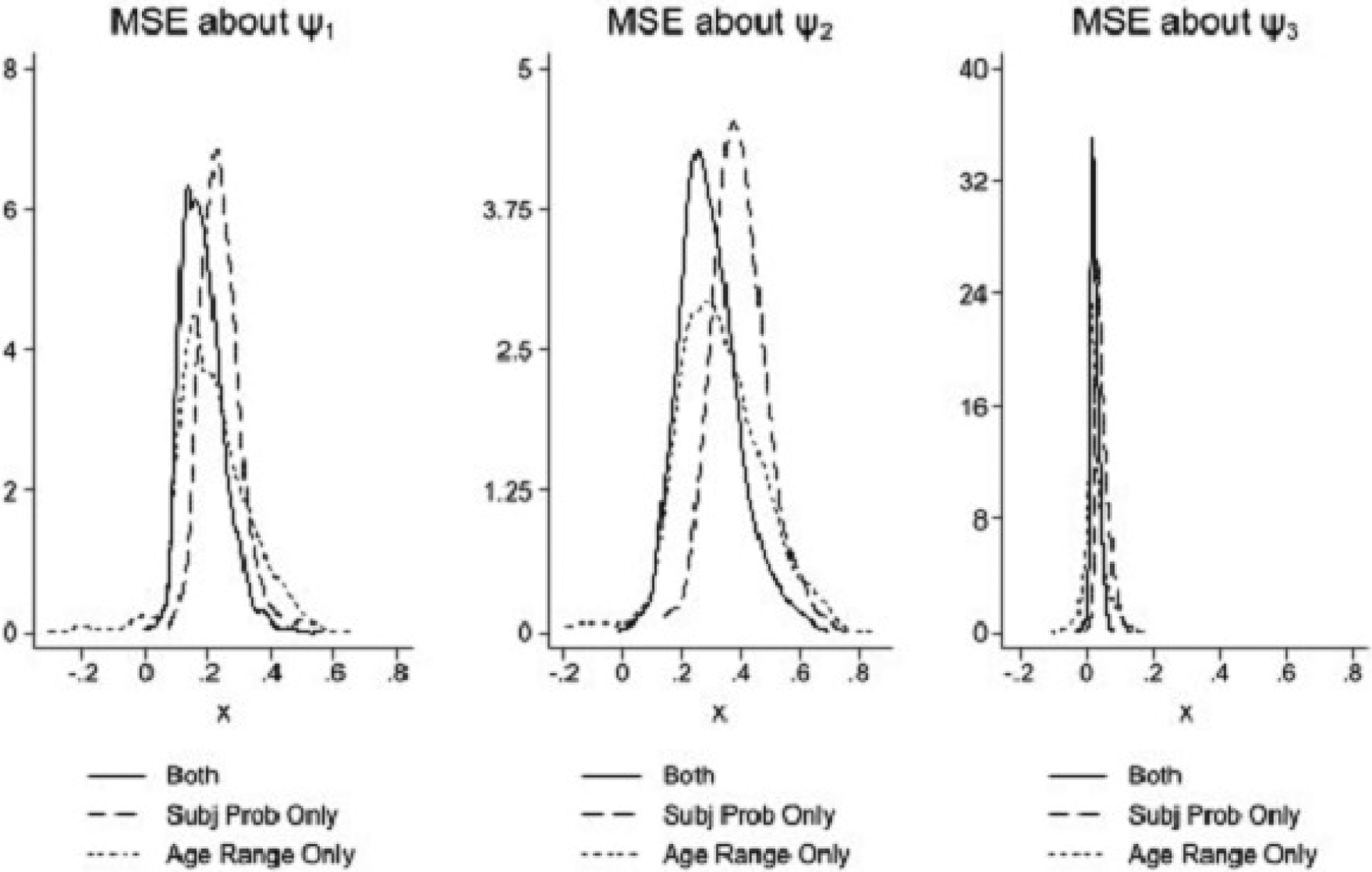
This figure shows the kernel density estimates of the individual-level MSE parameters for each elicitation form separately and jointly. We fix the horizontal axis to be able to compare the densities for the different parameters. We find that the distribution of μi,ψ,3, which capture maternal beliefs about the parameter of the interaction term between human capital at birth and investments, is concentrated in small values close to zero. This finding suggests that a Cobb-Douglas specification is a reasonable approximation for maternal beliefs. This finding is true when we consider the data from each elicitation form separately or together. We see that the variation in μi,ψ,1 is larger and distributed around 0.2. The MSE μi,ψ,2 has the largest variation in our data, and it is distributed – somewhat symmetrically – around 0.3. For both μi,ψ,1 and μi,ψ,2, the subjective elicitation probability form data has a higher mean than the distribution generated by the data from the age ranges form.
Next, we investigate the extent to which observable characteristics of the mothers explain the heterogeneity in MSE. Our analysis proceeds in the following way. First, we standardize the MSE parameters so that each has a mean equal to 0 and a variance equal to 1. Then, we regress the standardized μi,ψ,j on the demographic variables listed in Table 1. Due to space constraints, Table 8 shows only the estimated coefficients on dummies for household income. We single out the income dummies because they are the only ones that systematically correlate with all of the MSE parameters in whatever way we estimate them, that is, when we combine data from both forms, when we use data only from one of the forms separately, or when we apply different interpolation methods for the age-range forms. High-income households (those whose annual income is above $105,000) tend to have lower values for MSE about ψ1 and ψ3, but higher values for ψ2.
Table 8.
Correlation between MSE and Household Income of PHD Study Participants
| Dummies for household income per year (y) | Both Forms | Subjective-Probability Form | Age-Range Form | ||||||
|---|---|---|---|---|---|---|---|---|---|
| μ i,ψ,1 | μ i,ψ,2 | μ i,ψ,3 | μ i,ψ,1 | μ i,ψ,2 | μ i,ψ,3 | μ i,ψ,1 | μ i,ψ,2 | μ i,ψ,3 | |
| 1($25,000 ≤ y< $55,0000) | 0.22** (0.10) | 0.35*** (0.09) | 0.19* (0.10) | −0.02 (0.10) | 0.32*** (0.10) | 0.02 (0.10) | q 29*** (0.10) | 0.28*** (0.09) | 0.24** (0.11) |
| 1($55,000 ≤ y< $105,0000) | −0.17 (0.13) | 0.37*** (0.12) | −0.25** (0.11) | −0.35*** (0.16) | 0.45*** (0.12) | −0.22* (0.13) | −0.09 (0.12) | 0.25** (0.12) | −0.14 (0.10) |
| 1(y ≥ $105,000) | −0.51*** (0.13) | 0.47*** (0.14) | −0.53*** (0.12) | −0.67*** (0.12) | 0.60*** (0.14) | −0.40*** (0.13) | −0.45*** (0.13) | 0.26* (0.14) | −0.37*** (0.11) |
| Observations | 822 | 822 | 822 | 822 | 822 | 822 | 822 | 822 | 822 |
| R 2 | 0.071 | 0.064 | 0.090 | 0.080 | 0.062 | 0.080 | 0.058 | 0.071 | 0.046 |
Notes: This table shows the association of MSE parameters with household income. We standardized MSE parameters so that they have mean = 0 and variance = 1. The higher the household income, the lower μi,ψ,1 and μi,ψ,3. In contrast, the higher the household income, the higher μi,ψ,2, thus indicating that higher-income families have higher expectations about the impact of investments in the human capital of children. In the regressions, we control for maternal birth cohort, race/ethnicity, educational attainment, marital status, and scores on the CESD scale. See Appendix Table C6 for the complete table of regression coefficients. Robust standard errors in parentheses.
p < 0.10,
p < 0.05,
p < 0.01.
The relationship between household income and μi,ψ,2 varies with the elicitation forms. When we disaggregate the data by form, the relationship with income is monotonic for the data produced by the subjective probability form but not so for the age-range form. The gradient in beliefs is consistent with findings from a vast literature that documents a positive income-gradient in investments across families (e.g., see summary in Kalil, 2014). The dominant economic theory attributes this relationship between family income and investments to the existence of credit constraints (e.g., Becker and Tomes, 1986). Our empirical results offer a different perspective: differences in investments across income groups may be due to differences in maternal beliefs. These explanations are not mutually exclusive. Thus, there may be low-income families with high expectations that face severe credit constraints and, thus, cannot invest optimally.
Notably, Caucutt and Lochner (2020) show that credit market imperfections may explain some of the cross-sectional heterogeneity in material investments. Some types of investments, however, require parental attention. For example, Hart and Risley (1995) show that the difference in the language environment across SES groups is due primarily to the way adults respond to conversations that children initiate. The work by Rowe (2008), in turn, demonstrates that parental knowledge predicts the types of parental responses. These findings confirm the research in developmental psychology that some low-income parents may invest “too little” in their children because they have low expectations about the returns on the investments. This research provides compelling evidence to justify the reason that public policy should aim to work directly with parents to improve children’s circumstances. The correlation between income and MSE is also significant because it allows for differences in investments across income groups even when there are no differences in parental patience or altruism toward children.
Table 9 presents the correlations between MSE variables and the factors that we predicted as part of the analysis in Section 2.7. To create Table 9, we residualized the “structural” factors to make sure that we purge any correlation with “measurement error” factors.14 We then standardized the residualized factors to aid in the interpretation of our findings. We analyze the relationship between “structural” factors and MSE as estimated from subjective probability and age-range forms separately.
Table 9.
Relationship between MSE Parameters and Structural Factors
| Variable | Subjective-Probability Form | ||
|---|---|---|---|
| μ i,ψ,1 | μ i,ψ,2 | μ i,ψ,3 | |
| Structural Factor 1 | −0.294*** (0.010) | 0.966*** (0.023) | −0.052 (0.033) |
| Structural Factor 6 | 0.892*** (0.017) | 0.031* (0.017) | 0.677*** (0.043) |
| Observations | 822 | 822 | 822 |
| R 2 | 0.935 | 0.871 | 0.468 |
| Variable | Age-Range Form | ||
| μ i,ψ,1 | μ i,ψ,2 | μ i,ψ,3 | |
| Structural Factor 5 | −0.038*** (0.014) | 0.855*** (0.022) | −0.015 (0.035) |
| Structural Factor 6 | 0.923*** (0.019) | 0.147*** (0.022) | 0.506*** (0.042) |
| Observations | 822 | 822 | 822 |
| R 2 | 0.849 | 0.727 | 0.255 |
Notes: This table shows the relationships between the Structural Factors we introduced in 2.7 with the MSE parameters in equation (2). As we show in Table 5, the Structural Factor 1 in the data from the subjective probability form loads in the equations that identify the MSE parameter μi,ψ,2. This table shows that, indeed, the RCM estimator for the MSE parameter μi,ψ,2 correlates with Structural Factor 1. In the analysis of the subjective probability data, Structural Factor 6 loaded in the moments to identify μi,ψ,1 and μi,ψ,2. We have a similar, but not as robust, relationship for the data from the age ranges elicitation form. We have standardized all Structural Factors and MSE parameters so that they have mean = 0 and variance = 1. Robust standard error in parenthesis.
p < 0.10,
p < 0.05,
p < 0.01.
The results from Table 9 reinforce some of our key findings. First, the data from the subjective probability form is consistent with the predictions of the model. The MSE latent variables μi,ψ,1 and μi,ψ,2 correlate strongly with the “structural” factors predicted by our model. For example, the correlation between μi,ψ,1 and Structural Factor 6 is around 90% for the subjective probability form. Similarly, the correlation between μi,ψ,2 and Structural Factor 1 is also high, above 97%. These results are in line with the predictions of the latent variable model we derived in Section 2.7.
The μi,ψ,3 correlation is more substantial with Structural Factor 6, again indicating that μi,ψ,1 and μi,ψ,3 explore the same source of identifying information. Qualitatively, we observe the same patterns when we use age-range forms. The RCM explores the moments predicted by the model for these two latent MSE variables.
4.5. MSE and Correlation with the HOME Score
Next, we investigate whether the heterogeneity in MSE predicts heterogeneity in investments in children. When the children of the PHD study were 9 to 12 months old, we visited their homes and interviewed mothers to assess the levels of investment in their children. Therefore, there is a one-year gap between reports of maternal beliefs and information about investments in the human capital of children.
We follow the HOME Inventory manual, and we estimate the total score by averaging maternal answers across all 45 items. Because the responses are dichotomous (recorded as “0” for “No” and “1” for “Yes”), the scores are between 0 and 45, and higher values denote higher levels of investments. However, in the regressions that follow, we standardized both the HOME score and the MSE parameters.
Table 10 shows that μi,ψ,2 consistently predicts higher levels of investments as measured by the scores on the HOME scale. One standard deviation in μi,ψ,2 is associated with 11% of a standard deviation in investments even after we control for the mother’s race, ethnicity, marital status, educational attainment, and household income.15 The association between investments and μi,ψ,2 is similar for the subjective probability and age range forms.
Table 10.
Correlation between MSE Latent Variables and HOME Score
| Variable | Both | Subjective Probability | Age Range | |||
|---|---|---|---|---|---|---|
| Standardized μi,ψ,1 | −0.024 (0.081) | −0.002 (0.074) | −0.095 (0.080) | −0.058 (0.074) | −0.014 (0.059) | 0.031 (0.053) |
| Standardized μi,ψ,2 | 0.167*** (0.045) | 0114*** (0.039) | 0.119*** (0.043) | 0.098** (0.040) | 0.170*** (0.045) | 0.083** (0.038) |
| Standardized μi,ψ,3 | −0.086 (0.067) | 0.010 (0.061) | −0.040 (0.066) | 0.034 (0.062) | −0.058 (0.048) | −0.014 (0.042) |
| Demographic variables included | No | Yes | No | Yes | No | Yes |
| Observations | 687 | 687 | 687 | 687 | 687 | 687 |
| R 2 | 0.037 | 0.270 | 0.034 | 0.271 | 0.031 | 0.265 |
Notes: This table shows the correlation between the measure of investment (the Home Observation for the Measurement of the Environment – HOME scores) and the MSE parameters. We find that the MSE parameter about the elasticity of child development with respect to investment - μi,ψ,2 – consistently predicts variation in the HOME score. In these regressions, we include the following control variables: a dummy variable takes the value of 1 if the mother’s year of birth is between 1978 and 1987 and 0 otherwise; a dummy variable takes the value of 1 if the mother’s year of birth is between 1988 and 1997 and 0 otherwise; a dummy variable takes the value of 1 if the mother is Hispanic and 0 otherwise; a dummy variable takes the value of 1 if the mother is non-Hispanic black and 0 otherwise; a dummy variable takes the value of 1 if the mother has at least a college degree and 0 otherwise; a dummy variable takes the value of 1 if the mother is married and 0 otherwise; a dummy variable takes the value of 1 if the maternal score on the CESD is greater than or equal to 16 and 0 otherwise; three dummy variables indicate the level of household income. Appendix Table C7 displays all of the estimated coefficients and their robust standard errors.
p < 0.10,
p < 0.05,
p < 0.01
Finally, we provide an additional test of the importance of maternal beliefs in the prediction of investment choices. We estimate LASSO regressions, in which the dependent variable is the standardized HOME score, and the prediction variables are all of the demographic characteristics as well as the MSE variables estimated by the RCM estimator. We do so for both forms jointly, and then for each elicitation form separately. In our LASSO regression, we use two selection criteria: cross-validation and adaptive method.16 Table 11 presents the results. We mark with an “x” the variables the LASSO regression included in the prediction model. Otherwise, we leave the table cell empty. The LASSO models include μi,ψ,2 in the models in Table 11, regardless of the elicitation form (subjective probability or age range) or selection method (cross-validation or adaptive).
Table 11.
LASSO Regression Dependent Variable: Standardized HOME Scores
| Variable | Both Forms | Subjective Probability | Age Range | |||
|---|---|---|---|---|---|---|
| CV | Adaptive | CV | Adaptive | CV | Adaptive | |
| μi,ψ,1 | x | x | ||||
| μi,ψ,2 | x | x | x | x | x | x |
| μi,ψ,3 | ||||||
Notes: This table shows the MSE parameters that are included in the final prediction model, as estimated by LASSO regressions. The dependent variable is the measure of investment (the Home Observation for the Measurement of the Environment – HOME scores). The explanatory variables are the MSE parameters; a dummy variable takes the value of 1 if the mother’s year of birth is between 1978 and 1987 and 0 otherwise; a dummy variable takes the value of 1 if the mother’s year of birth is between 1988 and 1997 and 0 otherwise; a dummy variable takes the value of 1 if the mother is Hispanic and 0 otherwise; a dummy variable takes the value of 1 if the mother is non-Hispanic black and 0 otherwise; a dummy variable takes the value of 1 if the mother has at least a college degree and 0 otherwise; a dummy variable takes the value of 1 if the mother is married and 0 otherwise; a dummy variable takes the value of 1 if the maternal score on the CESD is greater than or equal to 16 and 0 otherwise; three dummy variables indicate the level of household income. We find that the MSE parameter about the elasticity of child development with respect to investment - μi,ψ,2 – consistently predicts variation in the HOME score and is included in the LASSO models.
p < 0.10,
p < 0.05,
p < 0.01
We further investigate the correlation between HOME scores and MSE by breaking the analysis at the HOME subscale level. Appendix Table C7 displays the correlation between μi,ψ,2 and the HOME subscales. The only consistent result we find is that heterogeneity in μi,ψ,2 predicts differences in scores in the Learning Materials subscale. This subscale contains items such as the availability of toys (e.g., push/pull; cuddly, role-playing, complex eye-hand coordination), learning facilitators such as table and chair, and materials for literature and music. We note that the regressions in Appendix Table C7 control for dummies that describe the level of household income as well as variables that control for demographic characteristics, such as education, marital status, race, ethnicity, and age.17
4.6. Robustness
We investigate the robustness of our findings by making different assumptions about the distribution of in equation (6) and distinct values for the parameters Δ0 and Δ1. Assumptions about these variables affect the interpolation method that we introduced in Section 2.4.2. Appendix D contains the details of our analysis. Appendix Table D1 shows the estimates of mean MSE parameters. They vary little as we vary interpolation methods.
Appendix Table D2 shows that the sign and the magnitude of the correlation between μi,ψ,2 and household income is generally robust to different interpolation methods and similar to the values reported in Table 8. Similarly, Appendix Table D3 shows that the correlation between μi,ψ,2 and the HOME is mainly consistent with the values reported in Table 11. The one exception is the interpolation method in which we assume that the distribution of follows a “lower” triangular distribution. Note, however, that the “lower” triangular distribution generates the model with the worst fit. For example, the R2 for the “lower” triangular distribution is about half of the R2 for the normal distribution. Finally, Appendix Table D4 shows that the relationship between MSE and the Learning Materials subscale of the HOME is consistent across forms and assumptions for interpolation. We do not find such consistency for other subscales, even though we find that the relationship between MSE and HOME is consistent, as demonstrated by our analysis.
In our empirical results, we noted that both the factor analysis of the identifying moments and the estimates from the RCM estimator produced results consistent with the Cobb-Douglas production function. In Appendix E, we re-estimate the model, imposing the Cobb-Douglas functional form. Appendix Tables E1 through E5 confirm our findings when we adopt the more parsimonious model specification. Our empirical results are not sensitive to the approach we choose.
5. Conclusion
In this paper, we implement the framework developed in Cunha et al. (2013) in a longitudinal study to elicit MSE about the technology of skill formation. We elicit MSE by asking mothers to provide probabilities or age ranges that children will learn how to do specific developmental tasks according to scenarios of human capital at birth and investments.
We explore previous work by Swamy (1970) to estimate MSE. We show how the methodology is robust to measurement error processes and heaping. We go beyond past research and derive testable restrictions from assumptions about the technology of skill formation and the process for measurement error. We show that these restrictions predict the number of factors in a factor analysis approach. We map these factors to the MSE and to measurement error that is specific to each MSD item.
Empirically, we show that the data have predictable patterns that are consistent with assumptions about the technology of skill formation and the economics of human development. The higher the input, the higher the probability that children will learn specific tasks by a given age. We document that the data, from both forms, suffer from significant heaping and measurement error. We demonstrate, step by step, the way our methodological approach handles these two problems empirically.
Ideally, respondents would pay attention to two dimensions of the elicitation forms. In the first dimension, they would compare across scenarios within an MSD item. In the second dimension, they would compare across MSD items within scenarios. Our results indicate that parents can do the former, but not the latter. Based on this observation, we propose and empirically confirm the existence of predictable patterns in measurement error. This finding suggests an important avenue for future research: the development of elicitation instruments that reduce measurement error.
We show that the data satisfy the testable restrictions of the model. Parameterization (2) and the assumptions about measurement error predict that five to seven potentially correlated factors can summarize the informational content of the model. In our empirical analysis, we find six factors. The findings are similar to both forms. Two factors contain identifying information about MSE, and the remaining four factors describe dependence in measurement errors that is consistent with our modeling assumptions.
We find homogeneity in beliefs about the parameterization of the technology of skill formation. The vast majority of the parents in our study believe that child development follows a Cobb-Douglas specification. In contrast, we find substantial heterogeneity in both μi,ψ,1 and μi,ψ,2. These parameters capture MSE about the impact of human capital at birth and investments on human capital at age two, respectively. We find that the family income predicts heterogeneity: the higher the family income, the lower μi,ψ,1 and the higher μi,ψ,2. These patterns of correlation are consistent with the facts about inequality in investments across income groups.
Our analysis provides strong evidence that μi,ψ,2 predict investment choices. The correlation is robust to the inclusion of demographic characteristics that predict both MSE and maternal investments. When we estimate LASSO regression models, we find that LASSO selects μi,ψ,2. Moreover, it drops many of the SES variables.
We believe that an essential area of work is to continue to develop instruments to elicit maternal beliefs about the technology of skill formation. It is desirable to improve our instruments in several dimensions.
First, they are long. Second, as we have demonstrated, the elicitation suffers from measurement error. Third, while respondents can compare scenarios within an item, they cannot compare items within a scenario. Fourth, it is unclear how the definition of scenarios affect the quality of the answers. All of these questions represent a significant advancement in this literature.
Unfortunately, given our data, we cannot conclude that the correlation between MSE and early investments in the human capital of children is causal. Future work should build on our study by including the elicitation of MSE in randomized controlled trials in parenting programs and investigating whether parenting interventions change MSE and, if so, whether changes in MSE lead to changes in early investments. At a time when proven-effective social programs are needed to address human capital gaps that open early in life, this work would identify critical levers that produce lasting improvements in the lives of children.
Supplementary Material
Acknowledgments
We thank Dalton Banks, Michelle Gifford, Delitza Hernandez, Debbie Jaffe, Snejana Nihtienova, Ben Sapp, Shanae Smith, and Cheryl Tocci for excellent research assistance. We are grateful to Orazio Attanasio, Jere Behrman, Pietro Biroli, Adeline Delavande, Hanming Fang, Marsha Gerdes, Limor Golan, Katja Kaufmann, James Heckman, Pedro Mira, Robert Moffitt, Krishna Pendakur, Matt Wiswall, and Ken Wolpin for their comments in different stages of this research. We thank participants at the Early Childhood Development and Human Capital Accumulation conference at University College London; the Institute for Research on Poverty’s Summer Workshop at the University of Wisconsin-Madison; the Children’s Human Capital Development workshop at Aarhus University in Denmark; the CES-IFO conference on the Economics of Education; the Conference on the Economics of the Family at the University of Chicago; the Latin American Meetings of the Econometric Society in Sao Paulo; the Lumen Christi Institute Conference in Chicago; and seminar participants at Columbia University; the University of Pennsylvania; UCLA; Stanford University; UC Berkeley; Insper São Paulo; CHPPP at the Harris School; the International Food and Policy Research Institute; Duke University; University of Chicago; Toulouse School of Economics; Johns Hopkins University; CEMFI; McMaster University; Universidade Nova de Lisboa; Fundação Getúlio Vargas Rio de Janeiro; Universidade Católica do Rio de Janeiro; University of California, Irvine; and the Federal Reserve Bank in New York. We thank the editors and reviewers of this special issue of the Journal of Econometrics. This research was supported by Grant INO12-00013 from the Institute for New Economic Thinking and Grant 1R01HD073221-01A1 by the National Institute of Health. All remaining errors are ours.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
In this paper, we eliminate the constant term by standardizing the variables to have mean 0 and variance 1. This reduces significantly the number of individual-level parameters that we need to estimate.
We use the NHANES dataset to estimate the IRT model and to obtain consistent estimates for the parameters bj,0, bj,1, and bj,2. See Appendix A for details.
We present the subjective probability elicitation form instrument in Appendix Figure A1.
We present the age range elicitation form instrument in Appendix Figure A2.
In the single category, we include one participant who reported being separated and two participants who reported being divorced at the time of enrollment in the study. The remaining individuals in this category (496 out of 499) reported being single and never married at the time of enrollment into the study.
More precisely, according to the 2016 IPUMS-CPS data, the yearly amounts of $25,000, $55,000, and $105,000 were, respectively, percentiles 22.6, 49.1, and 75.9 in the 2016 distribution of household income in the United States. Therefore, we use the terms first (or bottom), second, third, and fourth (or top) quartiles of income to denote the four groups of household income displayed in Table 2.
Our choice of focusing on the MSD item “speak a partial sentence” is without loss of generality. The patterns of answers are similar across MSD items. See Appendix C Figures C1 to C8 for histograms of all of the MSD items for all scenarios and for both elicitation forms.
See Appendix Table C1 for the correlation across maternal reports of subjective probability across all scenarios and MSD items.
We give all measures the same weight. The RCM estimator, in contrast, weighs observations optimally according to the amount of measurement error.
We use the word structural to denote that these factors contain information that is used to identify structural elements of our model. The factors, per se, are not structural.
The thirteenth factor has small factor loadings which do not reproduce any pattern.
Table 7 shows point estimates and their standard errors, which are quite small. For this reason, we do not discuss our findings about standard errors. We do not include an intercept because all of the variables have been standardized.
We investigated how these beliefs vary as we change the values for the parameters Δ0 and Δ1 and different distribution functions for in equation (6). We summarize the results in Section 4.6 and provide details in D.
In practice, the correlations between structural and measurement error factors are small and the residualization does not change the results in any substantial way.
Appendix Table C6 displays all of the estimated coefficients and their robust standard errors.
We also estimated LASSO regressions with the plug-in selection method. This method selected only a very small set of demographic variables, and it did not select any of the belief variables. For this reason, we omit these results from Table 11.
Appendix Table C7 also shows that the HOME Organization subscale is positively correlated with μi,ψ,1 and negatively correlated with μi,ψ,3. The Organization subscale contains items that describe activities that the child does on a frequent basis. For example, it contains variables such as taking the child to the grocery store at least once a week, taking the child out of the house at least four times a week, and taking the child regularly to the doctor’s office or clinic as well as one variable that describes the child’s play environment as safe. Unlike μi,ψ,2 however, neither μi,ψ,1 nor μi,ψ,3 correlates with the total HOME score in a systematic fashion.
References
- Agostinelli F, Wiswall MJ, 2020. Estimating the Technology of Children’s Skill Formation, NBER Working Paper 22442. [Google Scholar]
- Aizer A, Stroud L, 2010. Education, Medical Knowledge and the Evolution of Disparities in Health, NBER Working Paper 15840. [Google Scholar]
- Attanasio O, Cattan S, Fitzsimons E, Meghir C, Rubio-Codina M, 2020, Estimating the Production Function for Human Capital: Results from a Randomized Control Trial in Colombia. American Economic Review 110, 48–85. [Google Scholar]
- Attanasio O, Cunha F, Jervis P, 2019. Subjective Parental Beliefs: Their Measurement and Role, NBER Working Paper 26516. [Google Scholar]
- Attanasio O, Kaufmann K, 2014, Education choices and returns to schooling: Mothers’ and youths’ subjective expectations and their role by gender. Journal of Development Economics 109, 203–216. [Google Scholar]
- Attanasio OP, Fernandes C, Fitzsimons EOA, Grantham-McGregor SM, Meghir C, Rubio-Codina M, 2014, Using the infrastructure of a conditional cash transfer program to deliver a scalable integrated early child development program in Colombia: cluster randomized controlled trial. British Medical Journal 349. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Becker G, Tomes N, 1986, Human Capital and the Rise and Fall of Families. Journal of Labor Economics 4, S1–S39. [DOI] [PubMed] [Google Scholar]
- Bhalotra S, Delavande A, Font Gilabert P, Maselko J, 2020. Maternal Investments in Children: The Role of Expected Effort and Returns, IZA Institute of Labor Economics Discussion Paper 13056. [Google Scholar]
- Biroli P, Boneva T, Raja A, Rauh C, 2018. Parental Beliefs about Returns to Child Health Investments., IZA Discussion Paper 11336. [Google Scholar]
- Boneva T, Rauh C, 2018, Parental beliefs about returns to educational investments—the later the better? Journal of the European Economic Association, 16, 1669–1711. [Google Scholar]
- Boneva T, Rauh C, 2019. Socio-economic gaps in university enrollment: The role of perceived pecuniary and non-pecuniary returns., CESifo Working Paper Series No. 6756. [Google Scholar]
- Bradley RH, Caldwell BM, 1980, The Relation of Home-Environment, Cognitive Competence, and Iq among Males and Females. Child Development 51, 1140–1148. [Google Scholar]
- Caucutt EM, Lochner L, 2020, Early and late human capital investments, borrowing constraints, and the family. Journal of Political Economy 128, 1065–1147. [Google Scholar]
- Cunha F, Elo I, Culhane J, 2013. Eliciting Maternal Expectations about the Technology of Cognitive Skill Formation, NBER Working Paper 19144. [Google Scholar]
- Cunha F, Heckman JJ, Schennach S, M., 2010, Estimating the Technology of Cognitive and Noncognitive Skill Formation. Econometrica 78, 883–931. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Delavande A, 2008, Pill, patch, or shot? Subjective expectations and birth control choice. International Economic Review 49, 999–1042. [Google Scholar]
- Delavande A, Gine X, McKenzie D, 2011a, Eliciting Probabilistic Expectations with Visual Aids in Developing Countries: How Sensitive Are Answers to Variations in Elicitation Design? Journal of Applied Econometrics 26, 479–497. [Google Scholar]
- Delavande A, Gine X, McKenzie D, 2011b, Measuring subjective expectations in developing countries: A critical review and new evidence. Journal of Development Economics 94, 151–163. [Google Scholar]
- Epstein AS, 1980. Assessing the Child Development Information Needed by Adolescent Parents with Very Young Children. High/Scope Educational Research Foundation, pp. 1–41. [Google Scholar]
- Gertler P, Heckman J, Pinto R, Zanolini A, Vermeersch C, Walker S, Chang SM, Grantham-McGregor S, 2014, Labor market returns to an early childhood stimulation intervention in Jamaica. Science 344, 998–1001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hamm RM, 1991, Selection of verbal probabilities: A solution for some problems of verbal probability expression. Organizational Behavior and Human Decision Processes 48, 193–223. [Google Scholar]
- Hart B, Risley TR, 1995, Meaningful Differences in the Everyday Experience of Young American Children. Paul H. Brookes Publishing Co., Baltimore, MD. [Google Scholar]
- Heckman JJ, Holland ML, Makino KK, Pinto R, Rosales-Rueda M, 2017. An Analysis of the Memphis Nurse-Family Partnership Program, NBER Working Paper 23610. [Google Scholar]
- Hunt JM, 1961, Intelligence and experience. Ronald Press, New York, NY. [Google Scholar]
- Judge GG, 1985, The Theory and practice of econometrics, 2nd ed. Wiley, New York. [Google Scholar]
- Kalil A, 2014, Inequality Begins at Home: The Role of Parenting in the Diverging Destinies of Rich and Poor Children, in: Amato PR, Booth A, McHale SM, Van Hook J (Eds.), Families in an Era of Increasing Inequality: Diverging Destinies. Springer, New York, pp. 63–82. [Google Scholar]
- Mansbach IK, Greenbaum CW, 1999, Developmental maturity expectations of Israeli fathers and mothers: Effects of education, ethnic origin, and religiosity. International Journal of Behavioral Development 23, 771–797. [Google Scholar]
- Manski CF, 2004, Measuring expectations. Econometrica 72, 1329–1376. [Google Scholar]
- Ninio A, 1988, The Effects of Cultural Background, Sex, and Parenthood on Beliefs About the Timetable of Cognitive-Development in Infancy. Merrill-Palmer Quarterly-Journal of Developmental Psychology 34, 369–388. [Google Scholar]
- Ninio A, Rinott N, 1988, Fathers Involvement in the Care of Their Infants and Their Attributions of Cognitive Competence to Infants. Child Development 59, 652–663. [DOI] [PubMed] [Google Scholar]
- Olds D, 2002, Prenatal and infancy home visiting by nurses: From randomized trials tocommunity replication. Prevention Science 3, 153–172. [DOI] [PubMed] [Google Scholar]
- Rowe ML, 2008, Child-directed speech: relation to socioeconomic status, knowledge of child development and child vocabulary skill. Journal of Child Language 35, 185–205. [DOI] [PubMed] [Google Scholar]
- Schennach SM, 2016, Recent Advances in the Measurement Error Literature. Annual Review of Economics 8, 341–377. [Google Scholar]
- Swamy PAVB, 1970, Efficient Inference in a Random Coefficient Regression Model. Econometrica 38, 311–323. [Google Scholar]
- Totskika V, Sylva K, 2004, The Home Observation for Measurement of the Environment Revisited. Child Adolescent and Mental Health 9, 25–35. [DOI] [PubMed] [Google Scholar]
- Vygostky LS, 1978, Mind in Society. MIT Press, Cambridge, MA. [Google Scholar]
- Wallsten TS, Budescu DV, Rapoport A, Zwick R, Forsyth B, 1986, Measuring the vague meanings of probability terms. Journal of Experimental Psychology: General 115, 348–365. [Google Scholar]
- Wiswall M, Zafar B, 2015, Determinants of College Major Choice: Identification using an Information Experiment. Review of Economic Studies 82, 791–824. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


