Quantitative landscapes reveal trajectories of cell-state transitions associated with drug resistance in melanoma

Summary

Drug resistance and tumor relapse in patients with melanoma is attributed to a combination of genetic and non-genetic mechanisms. Dedifferentiation, a common mechanism of non-genetic resistance in melanoma is characterized by the loss of melanocytic markers. While various molecular attributes of de-differentiation have been identified, the transition dynamics remain poorly understood. Here, we construct cell-state transition landscapes, to quantify the stochastic dynamics driving phenotypic switching in melanoma based on its underlying regulatory network. These landscapes reveal the existence of multiple alternative paths to resistance—de-differentiation and transition to a hyper-pigmented phenotype. Finally, by visualizing the changes in the landscape during in silico molecular perturbations, we identify combinatorial strategies that can lead to the most optimal outcome—a landscape with the minimum occupancy of the two drug-resistant states. Therefore, we present these landscapes as platforms to screen possible therapeutic interventions in terms of their ability to lead to the most favorable patient outcomes.

Graphical abstract

Highlights

• •Quantified energy landscapes underlying cell-state transitions in melanoma
• •Landscapes can resolve two distinct drug resistance trajectories in cells
• •Model provides a mechanistic basis for the low abundance of hyper-pigmented phenotype
• •Energy landscapes act as a platform to identify potential therapeutic interventions

Computational bioinformatics; Cancer systems biology; Cancer.

Introduction

Phenotypic heterogeneity in melanoma has been attributed to drug resistance, relapse, and recalcitrance in patients.^1,2,3,4 Clinically, phenotypic classification of tumor samples was introduced to distinguish between the metastatic potential of melanoma tumors. Cells were classified as proliferative or invasive, based on their ability to contribute to tumor growth (non-metastatic) and their ability to migrate to secondary tumor sites (metastatic), respectively.⁵ These two phenotypes were shown to be capable of switching between one another and giving rise to heterogeneous tumors independently.^6,7 Although the classification started as a binary system for metastatic and non-metastatic samples, intermediate phenotypes displaying features of both the extreme phenotypes have also been identified.^5,8,9,10,11 A recent study classified melanoma samples into four phenotypes: melanocytic, transitory, neural crest stem cell like (NCSC) and undifferentiated (in a decreasing order of proliferative behavior, or in an increasing order of invasive traits).¹² Treatment of melanocytic samples with BRAF inhibitors (BRAFi) or MEK inhibitors (MEKi) can cause cells to follow a distinct de-differentiation trajectory, where they first transition to being intermediate phenotypes on the proliferative-invasive axis (transitory and NCSC) and finally get undifferentiated.^13,14,15 De-differentiation has been dynamically characterized as a response to targeted therapy, a response driven by underlying gene regulatory network that determines the changes in gene expression (during drug treatment or other perturbations) and the consequent switching of phenotypes. Dynamical simulations of such networks suggest that the four abovementioned phenotypes exist as “microstates” within two larger “macro-states”, namely the proliferative and invasive phenotypes.¹⁶ However, the stochastic cell-state transition dynamics among these four phenotypes remain to be determined.

Besides de-differentiation, recent studies have identified alternate pathways to therapy resistance.^17,18,19 Single-cell profiling of patient-derived xenograft models revealed an alternate resistance pathway where cells increase expression of pigmentation genes and are referred to as hyper-pigmented.²⁰ The hyper-pigmented phenotype is characterized by high expression of melanocyte differentiation marker MITF and its downstream targets such as PMEL, TYR, and MLANA.²¹ While the existence of such an alternate pathway has been characterized, the underlying regulatory mechanism and the cell-state transition trajectory to this phenotype remains to be deciphered yet.

The (co-) existence of multiple cell-states is visualized as switching among diverse “attractors” in a given potential landscape, thus enabling the emergence of non-genetic heterogeneity. Waddington’s landscape is a classic example of such multi-stable potential landscapes being used to explain the dynamics of differentiation of cells, where each differentiated cell type is a stable state. In the context of cancer biology, such landscapes have been used to explain the progression from a normal to cancerous cell state, switching to a cancer stem-cell-like state, and epithelial-to-mesenchymal transition in carcinomas.^{22,23,24,25,26,27}

Here, we explain the existence of categorical multi-stability (Figure 1A) and dynamics governing resistant cell-fate decisions in melanoma, using quantitative landscapes. We infer cell-state transition probabilities and identify the de-differentiation trajectory followed by cells as the most likely transition path in the given landscape. Further, we reveal conditions under which cells can take an alternate trajectory for drug resistance: the acquisition of a hyper-pigmented state. Finally, we use these landscapes to identify combinatorial strategies to promote favorable outcomes. Our model not only provides a mechanistic understanding of phenotypic heterogeneity and underlying dynamics during phenotypic switching but also acts as a platform for the primary screening of target genes to identify potential therapeutic strategies that can drive desirable outcomes.

Figure 1.

Energy landscapes explain the existence of categorical multi-stability in melanoma tumors

(A) Schematic representation of categorical multi-stability.

(B) Gene regulatory network (GRN) governing phenotypic heterogeneity in melanoma.

(C) Energy landscape for the parameter set giving rise to 4 stable states/phenotypes.

(D) Heatmap for PCA loading coefficients categorizes genes as proliferative and invasive.

(E) Changes in transition probabilities from Melanocytic phenotype with simulation time.

(F) Heatmap for transition probability matrix derived from energy landscape (X axis: To; Y axis: From). Color bar denotes percentage probabilities.

Results

Quantitative landscapes capture categorical multi-stability in melanoma

We simulated the dynamics of a previously defined gene regulatory network (Figure 1B) that explains the existence of four phenotypes, namely, Melanocytic (M), Transitory (T), NCSC (N), and Undifferentiated (U),¹⁶ and generated corresponding landscape showcasing these four phenotypes observed in melanoma (Figure 1C). Previously, in order to estimate parameters and simulate the network-derived model, we had used RACIPE (RAndom CIrcuit PErturbation), which generates a large number of models by using an ensemble of parameter sets such that kinetic parameters are sampled randomly from a distribution corresponding to biologically feasible in vitro values.^28,29 For this study, we selected parameter sets corresponding to tetra-stable or penta-stable models (i.e., models that give rise to 4 or 5 stable states, respectively) (Table S3).

In our earlier work,¹⁶ we had proposed that the underlying regulatory network gives rise to multi-stability comprising of two broader categories or “macro-states” (Proliferative and Invasive) that can be subdivided into 4 phenotypes or “micro-states” (Proliferative comprises of Melanocytic, Transitory; while Invasive comprises of NCSC and Undifferentiated) (Figure 1A). However, this categorization was entirely based on clustering algorithms and Euclidean distance metrics applied to steady-state values obtained from RACIPE simulations. These methods do not provide any insight into the actual dynamics of the system. Thus, here, we focus on the relative stability of each state and its ability to transition to other states to quantify multi-stability transition dynamics in the system (characterized by the depth of the corresponding “attractor” on the landscape).

The methodology used to simulate the network in our previous study (RACIPE) generates an ensemble of kinetic models, each of which uses a set of kinetic parameters randomly generated within a specific biologically relevant range. Thus, each model is defined by a set of randomized parameters (also known as a parameter set). To analyze the dynamics of the system, we selected 3 such models or parameter sets, each of which gave rise to four stable state solutions i.e. tetra-stable parameter sets. In each of these models, the four stable states correspond to the four phenotypes, based on the classification defined in our previous work.

For the tetra-stable parameter sets, the landscape highlights the existence of these four phenotypes as four attractors lying within two larger “macro-states” (proliferative and invasive) (Figure 1C). The melanocytic and transitory phenotypes lie within the proliferative macro-state and the NCSC and undifferentiated phenotypes lie in the invasive macro-state, as expected. Here the landscape is acquired based on a dimension reduction of landscape (DRL) approach,²² by projecting the high-dimensional landscape to a two-dimensional space (PC1 and PC2). DRL identifies the contribution of each gene to the variability in the expression among the phenotypes. The loading coefficients corresponding to the first two principal components displayed clear segregation of proliferative genes (MITF, FOS, STAT5A, ETV5, SMAD4) and invasive genes (KLF4, NR3C1, SMAD3, JUN, NFIC, AHR, TBX3) (Figure 1D, Table 1). We also observe that the most likely transition path of cells recapitulates the de-differentiation trajectory (i.e., transition from M to T to N to U; highlighted using white arrows in Figure 1C). Transition probabilities for cells in the M state, display the maximum likelihood for transition to the T phenotype (Figures 1E and 1F, Table 2). These results are captured in three separate parameter sets/models that were selected (Figures S1A and S1B, Table S1), thus suggesting more generic features of the underlying tetra-stable landscapes corresponding to melanoma.

Table 1.

PCA coefficients for Figure 1

	PC1	PC2
AHR	0.010417856	−0.003509517
NFIC	0.169563069	−0.057414515
FOS	−0.010595336	0.00369566
KLF4	0.333410913	0.942556894
FOXF1	0.069210579	−0.023063742
JUN	0.233019618	−0.075501903
SMAD3	0.556252131	−0.185471997
MITF	−0.177958673	0.059335041
SMAD4	−0.091301187	0.030436385
MAFB	0.054437965	−0.018147989
NR3C1	0.657138108	−0.246967925
NR2F1	0.055335417	−0.017854324
STAT5A	−0.061691691	0.020573509
TBX3	0.002394554	0.006606184
TFE3	0.005726134	−0.001909402
ETV5	−0.051919583	0.017308019
TFAP2A	0.083419638	−0.027808951

Table 2.

Transition matrix for Figure 1

(%)	U	N	M	T
U	0	45.29	27.32	27.39
N	44.82	0	27.56	27.62
M	20.21	25.54	0	54.25
T	19.88	25.7	54.42	0

Penta-stability explains the existence of multiple trajectories for drug resistance

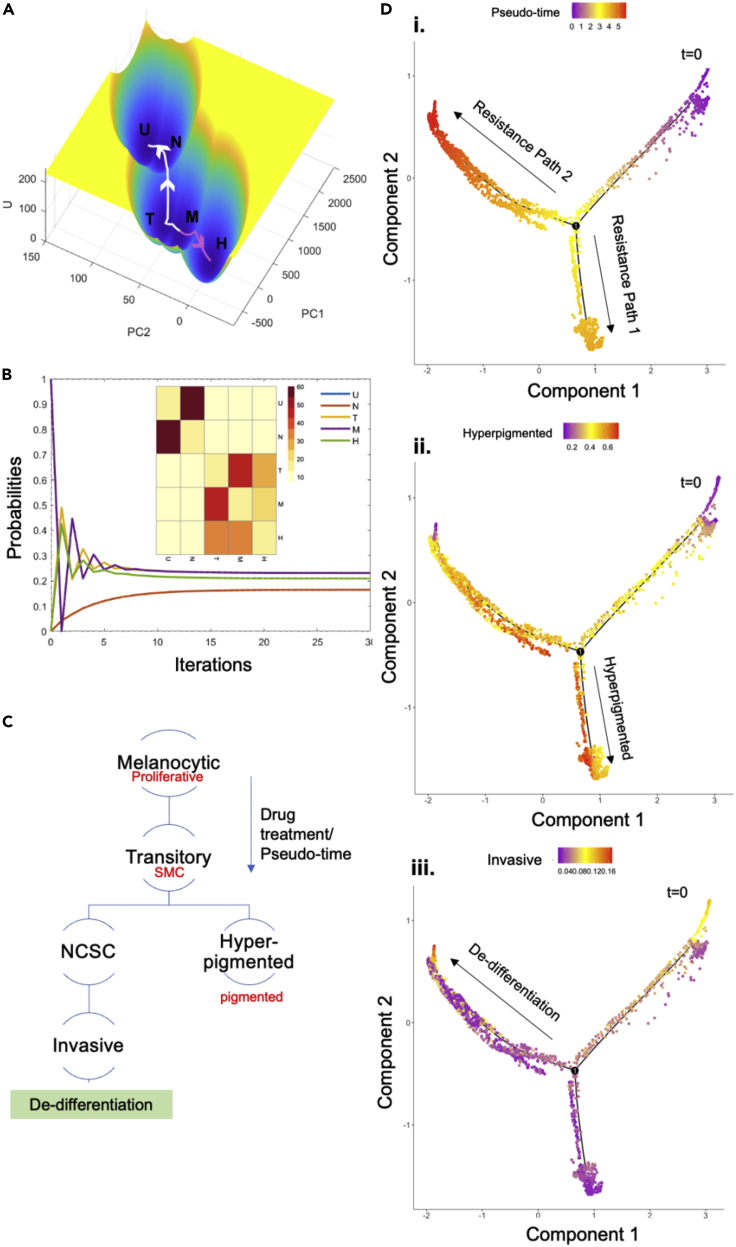
Besides de-differentiation, alternative trajectories to drug resistance in melanoma have been reported.^17,20 The hyper-pigmented phenotype is a resistant phenotype that does not arise out of de-differentiation per se. It is characterized by an increase in melanocytic markers such as MITF, PMEL, TYR, and MLANA which are commonly associated with pigmentation in melanocytes. We used our existing network to test whether it could explain the existence of this phenotype. To identify the fifth phenotype, we used k-means clustering (k = 5) on the RACIPE simulation dataset that was previously generated.¹⁶ Parameter sets that gave steady-state solutions for all five clusters were used to generate landscapes (Table S3B).

The landscapes revealed that the fifth state, which is characterized by very high levels of MITF (even higher than the melanocytic phenotype), fell outside the de-differentiation trajectory (highlighted using white arrows), suggesting that it represented the Hyperpigmented (H) phenotype (highlighted using pink arrows) as previously reported²⁰ (Figure 2A, Table 3). The melanocytic and transitory phenotypes showed the highest probability of switching to the hyper-pigmented phenotype (Figure 2B, Table 4). Similar results were witnessed for an alternate penta-stable parameter set too (Figures S2A and S2B, Table S2).

Figure 2.

Energy landscapes explain the existence of multiple paths to drug resistance

(A) Energy landscape for the parameter set giving rise to 5 stable states/phenotypes.

(B) Changes in transition probabilities from Melanocytic phenotype with simulation time. Inset represents heatmap for transition probability matrix derived from energy landscape (X axis: To; Y axis: From). Color bar denotes percentage probabilities.

(C) Schematic representation of multiple drug-resistant trajectories. Red labels indicate the classification system used by Rambow et al., 2018.

(D) Pseudo-time analysis reveals two trajectories to drug resistance in GSE115978 (single-cell patient tumor samples, treatment, and naive condition for immune checkpoint inhibitors). i. Pseudo-time analysis. ii. AUCell scores for hyper-pigmented gene set. iii. AUCell scores for the invasive gene set.

Table 3.

PCA coefficients for Figure 2

	PC1	PC2
AHR	0.001167897	0.008642988
NFIC	0.034337989	0.242185477
FOS	−0.001193013	−0.008820762
KLF4	0.624130725	−0.177068881
FOXF1	0.116256607	0.859853032
JUN	0.003198531	−0.000931729
SMAD3	0.67629151	−0.140333235
MITF	−0.0002368	−0.001758615
SMAD4	−0.001938843	−0.014034071
MAFB	0.030191703	0.071605455
NR3C1	0.368337014	0.222199211
NR2F1	0.002658593	0.018221392
STAT5A	−0.000236318	−0.001763789
TBX3	0.042007707	0.308887966
TFE3	0.004204146	0.004855628
ETV5	−0.002413455	−0.017914893
TFAP2A	0.000370301	0.002733477

Table 4.

Transition matrix for Figure 2

(%)	U	N	T	M	H
U	0	84.65	5.69	5.64	4.013
N	84.67	0	5.64	5.67	4.02
T	4.22	4.19	0	49.17	42.42
M	4.19	4.2	49.11	0	42.5
H	2.76	2.77	47.27	47.19	0

To validate this prediction made by landscape quantification, we performed a pseudo-time analysis of single-cell tumor samples (GSE115978, single-cell patient tumor samples, treatment, and naive condition for immune checkpoint inhibitors). Previous reports suggest that the treatment of tumors with immune checkpoints can lead to the progression of cells along the de-differentiation axis, suggesting that the two processes of immune checkpoint inhibitor resistance and de-differentiation are linked.³⁰ This analysis recapitulated similar trends, where melanoma cells transition, along the pseudo-time axis, from being in a proliferative phenotype to a transitory phenotype which further bifurcates to give rise to the de-differentiation and hyper-pigmentation trajectories for drug resistance (Figures 2C, 2D, S2C and S2D), thereby underlining two alternative or non-overlapping trajectories to resistance in melanoma. Scores for each phenotype were calculated using AUCell for gene sets reported earlier.^20,31 The genes regulating the hyper-pigmented phenotype (red labels) and the invasive phenotype (blue labels) form two mutually inhibiting “teams” of genes (Figure S2E), i.e., genes regulating a phenotype are positively correlated with each other and negatively correlated with genes regulating the other phenotype. Such “teams”-like interactions have been shown to play a role in regulating phenotype switching and multi-stability in biological systems.^32,33 Transition paths based on the energy landscapes for the two trajectories (de-differentiation and hyperpigmentation) reveal the changes in gene expression as cells transition from one state to another (Figure S3). The state transitions during de-differentiation (M to T to N to U) reveal a clear switch from high levels of expression of proliferative and melanocytic markers (MITF, FOS, SMAD4, ETV5) to lower levels and a concomitant increase in invasive markers (SMAD3, AHR, NFIC, KLF4, JUN) (Figures S3A and S3B). The state transitions for hyperpigmentation (M to H) not only reveal an increase in expression levels of MITF, a well-characterized regulator of pigmentation in melanocytes, but also an increase in expression of ETV5 and TFAP2A. Previous studies have reported regulation of MITF, ETV5, and TFAP2A by super-enhancer motifs during hyper-pigmentation.³⁴ While MITF and TFAP2A have been reported to display clear upregulation during hyperpigmentation. Overall, our model is able to recapitulate multiple paths to drug resistance and the associated transitions in cell states observed in melanoma tumors.

Quantifying intra-tumor and inter-tumor heterogeneity in melanoma samples

After analyzing above-mentioned experimental datasets, we investigated single-cell transcriptomic data gathered from multiple tumors. Interestingly, upon segregating these samples based on the tumor, we observed that most tumors comprised a heterogeneous population of cells, i.e., cells from a single tumor were proliferative, de-differentiated/invasive, and/or hyper-pigmented (Figure S2F), thus highlighting intra-tumor heterogeneity. The frequencies of these phenotypes also varied across tumors, thereby showcasing inter-tumor heterogeneity as well.

To quantify intra-tumor heterogeneity, we used the Shannon Diversity Index (SDI) (Figure 3A). Higher SDI indicates higher levels of diversity and thereby higher uncertainty in determining the phenotype of a random cell. For tumors comprising cells from a single phenotype, SDI is 0 (Mel121, Mel81, Mel84), and tumors with a high proportion of a single phenotype have SDI close to 0 (Mel106, Mel79, Mel80). Intriguingly, very few tumors had hyper-pigmented phenotype as the dominant phenotype, suggesting that this phenotype can be perhaps less abundant in tumors. This trend is also captured by the relative stability of the hyper-pigmented phenotype in simulated data (Figure 3B). Only a small fraction (<25%) of solutions corresponded to the hyper-pigmented phenotype in both cases. This low abundance might have possibly contributed to this phenotype being discovered more recently under the lens of single-cell profiling,²⁰ as opposed to previous bulk-level studies on heterogeneity in melanoma.¹²

Figure 3.

Patterns of intra-tumoral heterogeneity vary across patients

(A) Pie charts representing the proportion of cells belonging to each phenotype in a tumor. Titles include tumor name and Shannon’s Diversity Index (SDI) to quantify ITH.

(B) Pie charts representing the proportion of initial conditions giving rise to each of the 5 steady states/phenotypes in simulations for 2 penta-stable parameter sets.

In silico knockdowns predict optimal drug treatment strategy

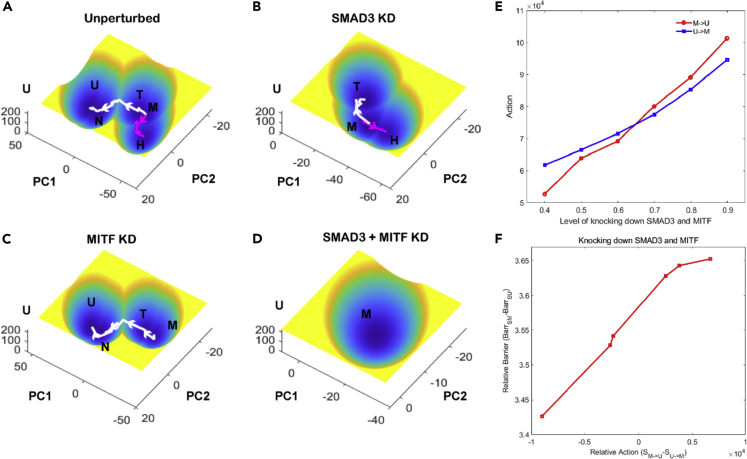
To check whether our landscape-based model could recapitulate the effects of targeted therapy as noted experimentally, we knocked down (KD) in silico some commonly targeted genes. We used MITF KD to mimic the effect of BRAF inhibition, since BRAF is a gene upstream of MITF.³⁵ Since MITF is required to identify the proliferative and hyperpigmented phenotype, we used the spatial localization of these states along the PC space as a proxy for identifying them. A recent study also highlighted the ability to overcome drug-resistant phenotypes by knocking down SMAD3 or its upstream regulator AHR, both of which are included in our network.³⁶ Knockdown of MITF alone, led to a loss of the hyper-pigmented phenotype from the landscape (as compared to the unperturbed landscape), leaving only the proliferative (melanocytic and transitory) and de-differentiated phenotypes (NCSC and Undifferentiated) (Figures 4A and 4C). SMAD3 KD led to the loss of invasive and de-differentiated phenotypes, leaving only the hyperpigmented and proliferative ones (Figure 4B). A recent study identified AHR and SMAD3 as regulators of resistant phenotypes that arise during BRAFi-induced de-differentiation. Knocking down AHR or SMAD3 prevented the emergence of resistant phenotypes during BRAFi treatment.³⁶ We recapitulated this experiment in silico by knocking down MITF and SMAD3 simultaneously. This led to the loss of both the de-differentiated (U) and the hyper-pigmented (H) resistant states (Figure 4D). Similar trends were also seen for the combined knockdown of AHR and MITF, further validating the ability of our model to make predictive outcomes for targeted therapy (Figure S4A).

Figure 4.

Energy landscapes recapitulate change in phenotypic distribution during targeted gene knockdown

(A) Energy landscape for the unperturbed system.

(B) Energy landscape for SMAD3 knockdown.

(C) Energy landscape for MITF knockdown.

(D) Energy landscape for MITF and SMAD3 dual knockdown.

(E) Variation in transition action between melanocytic and undifferentiated phenotype with increasing knockdown effect on MITF and SMAD3.

(F) The correlation between relative barrier height and relative transition action between melanocytic and undifferentiated phenotype with increasing knockdown effect on MITF and SMAD3. Barr_SM and Barr_SU represent the potential barrier between M state/U state and corresponding saddle point. S_M->U and S_U->M represent the transition action between M state and U state, respectively.

Moreover, with an increase in the extent of knockdown of MITF and SMAD3, we observed a lower rate of de-differentiation and a higher rate of differentiation toward the melanocytic phenotype (i.e., the transition rate of dedifferentiation from the melanocytic to undifferentiated phenotype became lesser than the reverse transition) (Figure 4E). Of note, the stability of states can be both measured from the potential and the transition actions, which should give consistent results. To verify this point, we compared the two approaches to see their consistency. We take the relative stability between M and U states as an example, when the landscape changes for knocking down SMAD3 and MITF. We found that the relative transition action and the relative potential barrier height between M and U states for knocking down SMD3 and MITF display a good correlation (Figure 4F), which supports the consistency between these two approaches. Given the potential of our model, we tried various combinations of gene targets to identify optimal combinations of target genes that can give rise to a landscape lacking the resistant phenotypes (similar to SMAD3+MITF KD or AHR + MITF KD) (Tables 5 and 6). For instance, AHR and NFIC KD displayed a loss of invasive and hyperpigmented resistant phenotypes, but still maintained the transitory phenotype (Figure S4B). AHR KD alone, also gave similar results (Figure S4C) while NFIC KD alone led to the loss of the invasive phenotypes alone (Figure S4D).

Table 5.

Steady-state solutions for single gene knockdown

KD gene	NFIC			SMAD4
Phenotypes	T′	M′	H′	U′	N′	T′	M′
AHR′	9.95 × 10−1	7.54 × 10−2	2.23 × 10−2	6.91E+00	6.91E+00	1.05E+00	1.05E+00
NFIC′	4.00 × 10−6	4.00 × 10−6	4.10 × 10−7	2.06 × 101	2.06 × 101	4.00 × 10−1	4.90 × 10−2
FOS′	5.57 × 10−1	3.65E+00	7.24E+00	1.76 × 10−4	1.77 × 10−4	6.55 × 10−3	8.27 × 10−2
KLF4′	1.11 × 10−4	1.78 × 10−5	2.88 × 10−7	5.64E+00	3.38 × 10−1	1.12 × 10−4	8.64 × 10−6
FOXF1′	2.38 × 101	2.38 × 101	2.38 × 101	1.34 × 102	2.40 × 101	2.38 × 101	2.38 × 101
JUN′	3.11 × 10−6	2.62 × 10−6	1.63 × 10−7	1.74 × 10−2	2.21 × 10−4	3.29 × 10−6	2.39 × 10−7
SMAD3′	8.95 × 10−1	5.50 × 10−2	1.30 × 10−3	1.19 × 102	1.19 × 102	9.72 × 10−1	9.63 × 10−1
MITF′	4.20 × 10−2	4.23 × 10−2	4.07E+00	2.40 × 10−5	6.83 × 10−4	3.76 × 10−2	3.62E+00
SMAD4′	6.52E+00	6.52E+00	6.52E+00	9.79 × 10−6	9.79 × 10−6	6.52 × 10−4	6.52 × 10−4
MAFB′	7.20 × 10−2	5.03 × 10−2	5.03 × 10−2	1.67 × 102	1.67 × 102	7.71 × 10−2	7.65 × 10−2
NR3C1′	1.35 × 10−2	1.50 × 10−5	5.87 × 10−6	4.37 × 101	4.37 × 101	1.68 × 10−2	1.64 × 10−2
NR2F1′	1.05 × 10−3	5.60 × 10−4	1.42 × 10−4	2.36 × 102	9.11 × 101	1.06 × 10−3	1.06 × 10−3
STAT5A′	4.91 × 10−2	4.91 × 10−2	1.33 × 102	4.91 × 10−2	4.91 × 10−2	4.91 × 10−2	1.21 × 102
TBX3′	2.11 × 10−6	1.66 × 10−6	1.66 × 10−6	1.28 × 101	1.75 × 10−3	2.23 × 10−6	2.21 × 10−6
TFE3′	4.12 × 10−1	4.83 × 10−3	2.35 × 10−4	2.56E+00	2.41E+00	4.43 × 10−1	2.94 × 10−2
ETV5′	7.64 × 10−2	7.64 × 10−2	1.76 × 101	2.43 × 10−3	2.43 × 10−3	7.63 × 10−2	1.76 × 101
TFAP2A′	2.28 × 10−2	2.29 × 10−2	3.36 × 10−1	3.62 × 10−1	3.85 × 10−1	2.09 × 10−2	3.28 × 10−1

KD gene	AHR		FOXF1
Phenotypes	M′	H′	U′	N′	T′	M′	H′
AHR′	1.17 × 10−5	2.24 × 10−6	6.91E+00	6.91E+00	1.00E+00	7.64 × 10−2	2.24 × 10−2
NFIC′	4.00 × 10−1	4.10 × 10−2	2.06 × 101	2.06 × 101	4.00 × 10−1	4.00 × 10−1	4.10 × 10−2
FOS′	3.04E+00	7.24E+00	1.76 × 10−4	1.77 × 10−4	5.46 × 10−1	3.64E+00	7.24E+00
KLF4′	4.63 × 10−6	2.25 × 10−7	5.64E+00	3.38 × 10−1	1.11 × 10−4	1.81 × 10−5	2.88 × 10−7
FOXF1′	2.38 × 101	2.38 × 101	1.34 × 10−3	2.40 × 10−4	2.38 × 10−4	2.38 × 10−4	2.38 × 10−4
JUN′	2.62 × 10−6	1.63 × 10−7	1.74 × 10−2	2.21 × 10−4	3.13 × 10−6	2.62 × 10−6	1.63 × 10−7
SMAD3′	4.78 × 10−3	1.29 × 10−3	1.19 × 102	1.19 × 102	9.05 × 10−1	5.88 × 10−2	1.30 × 10−3
MITF′	4.23 × 10−2	4.07E+00	2.40 × 10−5	6.83 × 10−4	4.20 × 10−2	4.23 × 10−2	4.07E+00
SMAD4′	6.52E+00	6.52E+00	9.79 × 10−2	9.79 × 10−2	6.52E+00	6.52E+00	6.52E+00
MAFB′	5.03 × 10−2	5.03 × 10−2	1.67 × 102	1.67 × 102	7.27 × 10−2	5.03 × 10−2	5.03 × 10−2
NR3C1′	2.78 × 10−5	5.87 × 10−6	4.37 × 101	4.37 × 101	1.40 × 10−2	1.52 × 10−5	5.87 × 10−6
NR2F1′	6.95 × 10−4	1.42 × 10−4	2.36 × 102	9.11 × 101	1.05 × 10−3	5.62 × 10−4	1.42 × 10−4
STAT5A′	4.91 × 10−2	1.33 × 102	4.91 × 10−2	4.91 × 10−2	4.91 × 10−2	4.91 × 10−2	1.33 × 102
TBX3′	1.66 × 10−6	1.66 × 10−6	1.28 × 101	1.75 × 10−3	2.12 × 10−6	1.66 × 10−6	1.66 × 10−6
TFE3′	4.97 × 10−3	2.35 × 10−4	2.56E+00	2.41E+00	4.15 × 10−1	4.83 × 10−3	2.35 × 10−4
ETV5′	7.64 × 10−2	1.76 × 101	2.43 × 10−3	2.43 × 10−3	7.64 × 10−2	7.64 × 10−2	1.76 × 101
TFAP2A′	2.29 × 10−2	3.36 × 10−1	3.62 × 10−1	3.85 × 10−1	2.27 × 10−2	2.29 × 10−2	3.36 × 10−1

KD gene	SMAD3			MITF
Phenotypes	T′	M′	H′	U′	N′	T′	M′
AHR′	1.42 × 101	1.05E+00	9.67 × 10−1	6.91E+00	6.91E+00	1.03E+00	8.74 × 10−2
NFIC′	2.28 × 102	4.00 × 10−1	4.10 × 10−2	2.06 × 101	2.06 × 101	4.00 × 10−1	4.00 × 10−1
FOS′	1.53 × 10−6	5.08 × 10−2	6.52 × 10−1	1.76 × 10−4	1.76 × 10−4	3.96 × 10−1	3.44E+00
KLF4′	1.04 × 10−1	1.10 × 10−4	5.27 × 10−6	5.64E+00	3.38 × 10−1	1.12 × 10−4	2.16 × 10−5
FOXF1′	2.28E+00	2.38 × 101	2.38 × 101	1.34 × 102	2.40 × 101	2.38 × 101	2.38 × 101
JUN′	5.62E+00	2.62 × 10−6	1.63 × 10−7	1.74 × 10−2	2.21 × 10−4	3.21 × 10−6	2.62 × 10−6
SMAD3′	7.10 × 10−3	9.72 × 10−6	8.72 × 10−6	1.19 × 102	1.19 × 102	9.36 × 10−1	1.08 × 10−1
MITF′	4.91 × 10−1	4.22 × 10−2	4.07E+00	2.40 × 10−9	6.83 × 10−8	4.18 × 10−6	4.23 × 10−6
SMAD4′	3.56E+00	6.52E+00	6.52E+00	9.79 × 10−2	9.79 × 10−2	6.52E+00	6.52E+00
MAFB′	7.36 × 101	5.12 × 10−2	5.11 × 10−2	1.67 × 102	1.67 × 102	7.49 × 10−2	5.03 × 10−2
NR3C1′	2.68 × 101	5.61 × 10−4	4.98 × 10−4	4.37 × 101	4.37 × 101	1.54 × 10−2	1.94 × 10−5
NR2F1′	1.35E+00	1.05 × 10−3	1.05 × 10−3	2.36 × 102	9.11 × 101	1.06 × 10−3	6.06 × 10−4
STAT5A′	6.78 × 10−2	4.91 × 10−2	1.33 × 102	4.91 × 10−2	4.91 × 10−2	4.91 × 10−2	4.91 × 10−2
TBX3′	6.02 × 10−5	1.66 × 10−6	1.66 × 10−6	1.28 × 101	1.75 × 10−3	2.17 × 10−6	1.66 × 10−6
TFE3′	6.33E+00	4.43 × 10−1	1.85 × 10−2	2.56E+00	2.41E+00	4.39 × 10−1	4.86 × 10−3
ETV5′	8.52 × 10−3	7.64 × 10−2	1.76 × 101	2.43 × 10−3	2.43 × 10−3	7.63 × 10−2	7.63 × 10−2
TFAP2A′	1.02 × 102	2.29 × 10−2	3.36 × 10−1	3.61 × 10−1	3.61 × 10−1	4.72 × 10−3	4.72 × 10−3

KD gene	FOS			MAFB
Phenotypes	U′	N′	T′	U′	N′	T′	M′
AHR′	6.91E+00	6.91E+00	1.05E+00	6.91E+00	6.91E+00	1.00E+00	7.64 × 10−2
NFIC′	2.06 × 101	2.06 × 101	4.00 × 10−1	2.06 × 101	2.06 × 101	4.00 × 10−1	4.00 × 10−1
FOS′	1.76 × 10−9	1.77 × 10−9	5.79 × 10−6	1.76 × 10−4	1.77 × 10−4	5.46 × 10−1	3.64E+00
KLF4′	5.64E+00	3.38 × 10−1	1.12 × 10−4	5.64E+00	3.38 × 10−1	1.11 × 10−4	1.81 × 10−5
FOXF1′	1.34 × 102	2.40 × 101	2.38 × 101	1.34 × 102	2.40 × 101	2.38 × 101	2.38 × 101
JUN′	1.74 × 10−2	2.21 × 10−4	3.30 × 10−6	1.74 × 10−2	2.21 × 10−4	3.13 × 10−6	2.62 × 10−6
SMAD3′	1.19 × 102	1.19 × 102	9.72 × 10−1	1.19 × 102	1.19 × 102	9.05 × 10−1	5.88 × 10−2
MITF′	2.40 × 10−5	6.83 × 10−4	4.16 × 10−2	2.40 × 10−5	6.83 × 10−4	4.20 × 10−2	4.23 × 10−2
SMAD4′	9.79 × 10−2	9.79 × 10−2	6.52E+00	9.79 × 10−2	9.79 × 10−2	6.52E+00	6.52E+00
MAFB′	1.67 × 102	1.67 × 102	7.71 × 10−2	3.75 × 10−4	3.75 × 10−4	7.27 × 10−6	5.03 × 10−6
NR3C1′	4.37 × 101	4.37 × 101	1.68 × 10−2	4.37 × 101	4.37 × 101	1.40 × 10−2	1.52 × 10−5
NR2F1′	2.36 × 102	9.11 × 101	1.06 × 10−3	2.36 × 102	9.11 × 101	1.05 × 10−3	5.62 × 10−4
STAT5A′	4.91 × 10−2	4.91 × 10−2	4.91 × 10−2	4.91 × 10−2	4.91 × 10−2	4.91 × 10−2	4.91 × 10−2
TBX3′	1.28 × 101	1.75 × 10−3	2.23 × 10−6	1.28 × 101	1.75 × 10−3	2.12 × 10−6	1.66 × 10−6
TFE3′	2.56E+00	2.41E+00	4.43 × 10−1	2.56E+00	2.41E+00	4.15 × 10−1	4.83 × 10−3
ETV5′	2.43 × 10−3	2.43 × 10−3	7.63 × 10−2	2.43 × 10−3	2.43 × 10−3	7.64 × 10−2	7.64 × 10−2
TFAP2A′	3.62 × 10−1	3.85 × 10−1	2.26 × 10−2	3.62 × 10−1	3.85 × 10−1	2.27 × 10−2	2.29 × 10−2

KD gene	KLF4			TBX3
Phenotypes	N′	T′	M′	N′	T′	M′	H′
AHR′	6.91E+00	1.00E+00	7.64 × 10−2	6.91E+00	1.00E+00	7.64 × 10−2	2.24 × 10−2
NFIC′	2.06 × 101	4.00 × 10−1	4.00 × 10−1	2.06 × 101	4.00 × 10−1	4.00 × 10−1	4.10 × 10−2
FOS′	1.78 × 10−4	5.46 × 10−1	3.64E+00	1.77 × 10−4	5.46 × 10−1	3.64E+00	7.24E+00
KLF4′	3.41 × 10−6	3.78 × 10−8	1.81E-10	3.38 × 10−1	1.11 × 10−4	1.81 × 10−5	2.88 × 10−7
FOXF1′	2.38 × 101	2.38 × 101	2.38 × 101	2.40 × 101	2.38 × 101	2.38 × 101	2.38 × 101
JUN′	2.19 × 10−4	3.13 × 10−6	2.62 × 10−6	2.21 × 10−4	3.13 × 10−6	2.62 × 10−6	1.63 × 10−7
SMAD3′	1.19 × 102	9.05 × 10−1	5.88 × 10−2	1.19 × 102	9.05 × 10−1	5.88 × 10−2	1.30 × 10−3
MITF′	6.91 × 10−4	4.20 × 10−2	4.23 × 10−2	6.83 × 10−4	4.20 × 10−2	4.23 × 10−2	4.07E+00
SMAD4′	9.79 × 10−2	6.52E+00	6.52E+00	9.79 × 10−2	6.52E+00	6.52E+00	6.52E+00
MAFB′	1.67 × 102	7.27 × 10−2	5.03 × 10−2	1.67 × 102	7.27 × 10−2	5.03 × 10−2	5.03 × 10−2
NR3C1′	4.37 × 101	1.40 × 10−2	1.52 × 10−5	4.37 × 101	1.40 × 10−2	1.52 × 10−5	5.87 × 10−6
NR2F1′	2.78E+00	1.05 × 10−3	5.62 × 10−4	9.11 × 101	1.05 × 10−3	5.62 × 10−4	1.42 × 10−4
STAT5A′	4.91 × 10−2	4.91 × 10−2	4.91 × 10−2	4.91 × 10−2	4.91 × 10−2	4.91 × 10−2	1.33 × 102
TBX3′	1.73 × 10−3	2.12 × 10−6	1.66 × 10−6	1.75 × 10−7	2.12E-10	1.66E-10	1.66E-10
TFE3′	2.41E+00	4.15 × 10−1	4.83 × 10−3	2.41E+00	4.15 × 10−1	4.83 × 10−3	2.35 × 10−4
ETV5′	2.43 × 10−3	7.64 × 10−2	7.64 × 10−2	2.43 × 10−3	7.64 × 10−2	7.64 × 10−2	1.76 × 101
TFAP2A′	3.25 × 10−1	2.27 × 10−2	2.29 × 10−2	3.85 × 10−1	2.27 × 10−2	2.29 × 10−2	3.36 × 10−1

KD gene	TFE3		STAT5A
Phenotypes	M′	H′	U′	N′	T′	M′	H′
AHR′	8.87 × 10−3	1.71 × 10−6	6.91E+00	6.91E+00	1.00E+00	7.64 × 10−2	2.24 × 10−2
NFIC′	1.33 × 102	6.06 × 10−2	2.06 × 101	2.06 × 101	4.00 × 10−1	4.00 × 10−1	4.10 × 10−2
FOS′	4.61 × 10−5	4.02E+00	1.76 × 10−4	1.77 × 10−4	5.46 × 10−1	3.64E+00	7.24E+00
KLF4′	7.88 × 101	1.34 × 10−6	5.64E+00	3.38 × 10−1	1.11 × 10−4	1.81 × 10−5	2.88 × 10−7
FOXF1′	2.26 × 102	3.96E+00	1.34 × 102	2.40 × 101	2.38 × 101	2.38 × 101	2.38 × 101
JUN′	3.02 × 101	2.11E+00	1.74 × 10−2	2.21 × 10−4	3.13 × 10−6	2.62 × 10−6	1.63 × 10−7
SMAD3′	3.37 × 101	3.16 × 10−4	1.19 × 102	1.19 × 102	9.05 × 10−1	5.88 × 10−2	1.30 × 10−3
MITF′	1.67 × 10−4	1.98 × 101	2.40 × 10−5	6.83 × 10−4	4.20 × 10−2	4.23 × 10−2	4.07E+00
SMAD4′	2.12E+00	9.76 × 101	9.79 × 10−2	9.79 × 10−2	6.52E+00	6.52E+00	6.52E+00
MAFB′	1.89 × 102	6.91 × 10−1	1.67 × 102	1.67 × 102	7.27 × 10−2	5.03 × 10−2	5.03 × 10−2
NR3C1′	2.38 × 102	5.50 × 10−4	4.37 × 101	4.37 × 101	1.40 × 10−2	1.52 × 10−5	5.87 × 10−6
NR2F1′	1.55 × 101	3.77 × 10−4	2.36 × 102	9.11 × 101	1.05 × 10−3	5.62 × 10−4	1.42 × 10−4
STAT5A′	3.69 × 101	1.82 × 102	4.91 × 10−6	4.91 × 10−6	4.91 × 10−6	4.91 × 10−6	1.61 × 10−4
TBX3′	2.68 × 101	1.96 × 10−6	1.28 × 101	1.75 × 10−3	2.12 × 10−6	1.66 × 10−6	1.66 × 10−6
TFE3′	3.85 × 10−1	1.94 × 10−6	2.56E+00	2.41E+00	4.15 × 10−1	4.83 × 10−3	2.35 × 10−4
ETV5′	3.46 × 10−3	4.15 × 102	2.43 × 10−3	2.43 × 10−3	7.64 × 10−2	7.64 × 10−2	1.76 × 101
TFAP2A′	1.16 × 10−1	1.04E+00	3.62 × 10−1	3.85 × 10−1	2.27 × 10−2	2.29 × 10−2	3.36 × 10−1

KD gene	ETV5		TFAP2A
Phenotypes	M′	H′	U′	N′	T′	M′	H′
AHR′	8.87 × 10−3	1.71 × 10−6	6.91E+00	6.91E+00	1.00E+00	7.64 × 10−2	2.24 × 10−2
NFIC′	1.33 × 102	6.06 × 10−2	2.06 × 101	2.06 × 101	4.00 × 10−1	4.00 × 10−1	4.10 × 10−2
FOS′	4.61 × 10−5	4.02E+00	1.76 × 10−4	1.77 × 10−4	5.46 × 10−1	3.64E+00	7.24E+00
KLF4′	7.88 × 101	1.34 × 10−6	5.64E+00	3.38 × 10−1	1.11 × 10−4	1.81 × 10−5	2.88 × 10−7
FOXF1′	2.26 × 102	3.96E+00	1.34 × 102	2.40 × 101	2.38 × 101	2.38 × 101	2.38 × 101
JUN′	3.02 × 101	2.11E+00	1.74 × 10−2	2.21 × 10−4	3.13 × 10−6	2.62 × 10−6	1.63 × 10−7
SMAD3′	3.37 × 101	3.16 × 10−4	1.19 × 102	1.19 × 102	9.05 × 10−1	5.88 × 10−2	1.30 × 10−3
MITF′	1.67 × 10−4	1.98 × 101	2.40 × 10−5	6.83 × 10−4	4.20 × 10−2	4.23 × 10−2	4.07E+00
SMAD4′	2.12E+00	9.76 × 101	9.79 × 10−2	9.79 × 10−2	6.52E+00	6.52E+00	6.52E+00
MAFB′	1.89 × 102	6.91 × 10−1	1.67 × 102	1.67 × 102	7.27 × 10−2	5.03 × 10−2	5.03 × 10−2
NR3C1′	2.38 × 102	5.50 × 10−4	4.37 × 101	4.37 × 101	1.40 × 10−2	1.52 × 10−5	5.87 × 10−6
NR2F1′	1.55 × 101	3.77 × 10−4	2.36 × 102	9.11 × 101	1.05 × 10−3	5.62 × 10−4	1.42 × 10−4
STAT5A′	3.69 × 101	1.82 × 102	4.91 × 10−2	4.91 × 10−2	4.91 × 10−2	4.91 × 10−2	1.33 × 102
TBX3′	2.68 × 101	1.96 × 10−6	1.28 × 101	1.75 × 10−3	2.12 × 10−6	1.66 × 10−6	1.66 × 10−6
TFE3′	7.94 × 101	1.94 × 10−2	2.56E+00	2.41E+00	4.15 × 10−1	4.83 × 10−3	2.35 × 10−4
ETV5′	3.26 × 10−7	1.00 × 10−3	2.43 × 10−3	2.43 × 10−3	7.64 × 10−2	7.64 × 10−2	1.76 × 101
TFAP2A′	1.16 × 10−1	1.04E+00	3.62 × 10−6	3.85 × 10−6	2.27 × 10−7	2.29 × 10−7	3.36 × 10−6

KD gene	NR2F1
Phenotypes	U′	N′	T′	M′	H′
AHR′	6.91E+00	6.91E+00	1.00E+00	7.64 × 10−2	2.24 × 10−2
NFIC′	2.06 × 101	2.06 × 101	4.00 × 10−1	4.00 × 10−1	4.10 × 10−2
FOS′	1.76 × 10−4	1.77 × 10−4	5.46 × 10−1	3.64E+00	7.24E+00
KLF4′	5.64E+00	3.38 × 10−1	1.11 × 10−4	1.81 × 10−5	2.88 × 10−7
FOXF1′	1.34 × 102	2.40 × 101	2.38 × 101	2.38 × 101	2.38 × 101
JUN′	1.74 × 10−2	2.21 × 10−4	3.13 × 10−6	2.62 × 10−6	1.63 × 10−7
SMAD3′	1.19 × 102	1.19 × 102	9.05 × 10−1	5.88 × 10−2	1.30 × 10−3
MITF′	2.40 × 10−5	6.83 × 10−4	4.20 × 10−2	4.23 × 10−2	4.07E+00
SMAD4′	9.79 × 10−2	9.79 × 10−2	6.52E+00	6.52E+00	6.52E+00
MAFB′	1.67 × 102	1.67 × 102	7.27 × 10−2	5.03 × 10−2	5.03 × 10−2
NR3C1′	4.37 × 101	4.37 × 101	1.40 × 10−2	1.52 × 10−5	5.87 × 10−6
NR2F1′	2.36 × 10−2	9.11 × 10−3	1.05 × 10−7	5.62 × 10−8	1.42 × 10−8
STAT5A′	4.91 × 10−2	4.91 × 10−2	4.91 × 10−2	4.91 × 10−2	1.33 × 102
TBX3′	1.28 × 101	1.75 × 10−3	2.12 × 10−6	1.66 × 10−6	1.66 × 10−6
TFE3′	2.56E+00	2.41E+00	4.15 × 10−1	4.83 × 10−3	2.35 × 10−4
ETV5′	2.43 × 10−3	2.43 × 10−3	7.64 × 10−2	7.64 × 10−2	1.76 × 101
TFAP2A′	4.73 × 10−3	5.03 × 10−3	2.27 × 10−2	2.29 × 10−2	3.36 × 10−1

KD gene	NR3C1			JUN
Phenotypes	T′	M′	H′	U′	N′	T′	M′	H′
AHR′	1.00E+00	7.64 × 10−2	2.24 × 10−2	6.91E+00	6.91E+00	1.00E+00	7.64 × 10−2	2.24 × 10−2
NFIC′	4.00 × 10−1	4.00 × 10−1	4.10 × 10−2	2.06 × 101	2.06 × 101	4.00 × 10−1	4.00 × 10−1	4.10 × 10−2
FOS′	5.41 × 10−1	3.64E+00	7.24E+00	1.76 × 10−4	1.77 × 10−4	5.46 × 10−1	3.64E+00	7.24E+00
KLF4′	1.11 × 10−4	1.81 × 10−5	2.88 × 10−7	5.53E+00	3.38 × 10−1	1.11 × 10−4	1.81 × 10−5	2.88 × 10−7
FOXF1′	2.38 × 101	2.38 × 101	2.38 × 101	1.34 × 102	2.40 × 101	2.38 × 101	2.38 × 101	2.38 × 101
JUN′	3.13 × 10−6	2.62 × 10−6	1.63 × 10−7	1.74 × 10−7	2.21 × 10−9	3.13 × 10−11	2.62 × 10−11	1.63 × 10−12
SMAD3′	9.06 × 10−1	5.88 × 10−2	1.30 × 10−3	1.19 × 102	1.19 × 102	9.05 × 10−1	5.88 × 10−2	1.30 × 10−3
MITF′	4.04 × 10−2	4.23 × 10−2	4.07E+00	2.46 × 10−5	6.83 × 10−4	4.20 × 10−2	4.23 × 10−2	4.07E+00
SMAD4′	6.52E+00	6.52E+00	6.52E+00	9.79 × 10−2	9.79 × 10−2	6.52E+00	6.52E+00	6.52E+00
MAFB′	5.03 × 10−2	5.03 × 10−2	5.03 × 10−2	1.67 × 102	1.67 × 102	7.27 × 10−2	5.03 × 10−2	5.03 × 10−2
NR3C1′	1.40 × 10−6	1.52 × 10−9	5.87E-10	4.37 × 101	4.37 × 101	1.40 × 10−2	1.52 × 10−5	5.87 × 10−6
NR2F1′	1.05 × 10−3	5.62 × 10−4	1.42 × 10−4	2.36 × 102	9.11 × 101	1.05 × 10−3	5.62 × 10−4	1.42 × 10−4
STAT5A′	4.91 × 10−2	4.91 × 10−2	1.33 × 102	4.91 × 10−2	4.91 × 10−2	4.91 × 10−2	4.91 × 10−2	1.33 × 102
TBX3′	2.12 × 10−6	1.66 × 10−6	1.66 × 10−6	1.28 × 101	1.75 × 10−3	2.12 × 10−6	1.66 × 10−6	1.66 × 10−6
TFE3′	4.17 × 10−1	4.83 × 10−3	2.35 × 10−4	2.41E+00	2.41E+00	4.15 × 10−1	4.83 × 10−3	2.35 × 10−4
ETV5′	7.63 × 10−2	7.64 × 10−2	1.76 × 101	2.43 × 10−3	2.43 × 10−3	7.64 × 10−2	7.64 × 10−2	1.76 × 101
TFAP2A′	2.21 × 10−2	2.29 × 10−2	3.36 × 10−1	3.62 × 10−1	3.85 × 10−1	2.27 × 10−2	2.29 × 10−2	3.36 × 10−1

KD = Knockdown.

Table 6.

Steady-state solutions for dual gene knockdown

Phenotypes	MITF and SMAD3	MITF and AHR	AHR and NFIC
	M′	M′	T′	M′
AHR′	1.0503817	7.70 × 10−7	4.87 × 10−7	9.66 × 10−8
NFIC′	0.400316825	0.400317	4.14 × 10−6	4.24 × 10−7
FOS′	0.035743824	2.56199	3.084827594	7.242724048
KLF4′	0.00011	4.63 × 10−6	4.63 × 10−6	2.25 × 10−7
FOXF1′	23.78235318	23.7824	23.78235318	23.78235318
JUN′	2.62 × 10−6	2.62 × 10−6	2.62 × 10−6	1.63 × 10−7
SMAD3′	1.32 × 10−7	0.00594595	0.004654585	0.001286979
MITF′	1.70 × 10−9	1.70543 × 10−9	0.042341203	4.073872874
SMAD4′	6.516547013	6.51655	6.516547013	6.516547013
MAFB′	0.051194033	0.050377	0.05033268	0.05029963
NR3C1′	0.000561	5.39 × 10−5	2.64 × 10−5	5.87 × 10−6
NR2F1′	0.00105124	0.000804865	0.0006858	0.00014206
STAT5A′	0.049106757	0.0491068	0.049106758	133.1022196
TBX3′	1.66 × 10−6	1.66 × 10−6	1.66 × 10−6	1.66 × 10−6
TFE3′	0.44330092	0.00533725	0.004950661	0.000234667
ETV5′	0.076287991	0.076288	0.076353649	17.64709871
TFAP2A′	0.004718464	0.0047184	0.022898683	0.335574884

Discussion

Phenotypic heterogeneity in melanoma has been identified as one of the major drivers of resistance to targeted therapy in melanoma. While previous studies have identified networks and mechanisms for how phenotypic heterogeneity is regulated,^10,16,37 here, we present a dynamical perspective of underlying energy landscapes that determine the resistant fate and trajectories of a cell that undergoes molecular perturbations. These landscapes confirmed the existence of multi-stability as previously suggested¹⁶ and capture the bifurcation of drug resistance trajectory into two distinct branches, as observed in time course experiments.²⁰ By integrating data coming from in silico simulations and in vitro experiments, we also offer possible reasons for the reduced abundance of hyper-differentiated phenotype in a tumor. Besides providing useful information on the dynamics of cell-state transitions, these (pseudo-)potential landscapes also recapitulate the effects of various targeted therapies (KD of individual genes). Thus, they provide a basis for running high-throughput screening of target gene combinations to identify therapeutic strategies to overcome drug resistance in cells.

Multi-stability was proposed to underlie the existence of multiple levels of classification of phenotypic heterogeneity in melanoma. We previously suggested that the initial system of classification of samples as proliferative and invasive could further be resolved into four phenotypes: melanocytic, transitory, NCSC, and undifferentiated. Previously, this analysis was restricted to using distance-based metrics that provided no insight into transition rates and cellular dynamics. Energy landscapes are able to reveal this property of phenotypic classification by using potential (U) as a metric that quantifies the ability of cells in one state to transition to another.^38,39 Although our model is only able to resolve up to five phenotypes, by increasing the resolution (by adding more genes or sub-networks for each phenotype to the existing 17-node network), possibly by adding sub-networks to the existing network, it might be possible to further resolve each of the 4 phenotypes into “micro-states.” The existence of such (often un-observable) “micro-states” within larger “macro-states” has been observed previously in the context of EMT as well.^40,41 The presence of a continuum of heterogeneity can potentially be attributed to the existence of such micro-states.^37,39

Potential (U) measures the stability of a cell at each point on the landscape. It provides information on the probability of a cell in a given state switching to another state. Higher potential barriers represent a lower likelihood of transitions between two states. These landscapes can be used to estimate the amount of “force” or perturbation needed to induce a switch from one attractor state to another. This can be used to identify molecular variables that can increase the transition probability toward a preferable state, therefore allowing us to push a population of cells toward a preferred state. This unleashes endless possibilities of tweaking the system to obtain desirable outcomes or predicting the effects of such perturbations on the outcome. Such (pseudo-) potential landscapes have been used extensively in developmental biology from modeling to understand cell-fate decision making and differentiation and can be useful tools to uncover cellular dynamics during cancer progression.^38,42,43

Our study delves into the effect of multiple drug-resistant phenotypes on intra-tumoral heterogeneity (ITH). We observe that the hyperpigmented phenotype forms a very small fraction of the total tumor population, at least in the 23 tumors investigated here in which only 2 tumors exhibited it as the dominant phenotype. Similar results (reduced abundance) were seen in our simulation results too, possibly explaining its rather recent identification/discovery, relative to that of four other melanoma phenotypes.²⁰ At a bulk level, it is likely that the transcriptomic signature of this phenotype is masked. To quantify ITH, we used Shannon’s diversity index, an entropy-based measure of uncertainty in predicting the phenotype of a random cell.⁴⁴ Interestingly, no consistent patterns were found among the multiple tumors, suggesting that variations at a genetic, microenvironmental or epigenetic level might influence the landscape and therefore the overall composition of the tumor.⁴⁵ Differences in treatment strategies can also lead to different outcomes in tumor heterogeneity. The dataset used here (GSE115978) comprises samples from treatment naive patients and patients that have been treated with immune checkpoint inhibitors, which might also contribute to additional variations in ITH.⁴⁶

Here, we highlight the ability of landscape models to be used as a basis for predictive modeling of targeted therapy strategies. Conventional drug screening for all possible combinations is time- and resource-intensive. Thus, by using such predictive models, we can identify rather quickly optimal combinations of target genes to achieve durable outcomes, making it a potential tool for primary screening of possible treatment strategies. Moreover, the model can be expanded to suggest sequential targeting too.

Limitations of the study

While our study provides a framework to run the initial screening of targeted gene therapy for melanoma, there are several limitations associated with our modeling framework. First, our model only accounts for transcriptional level interactions. It fails to account for the dynamics associated with translation, phosphorylation, and other post-translational modifications that play a role in regulating cellular signaling. Moreover, the model is unable to capture population-level variations (such as tumor growth dynamics⁴⁷) commonly associated with drug resistance. Secondly, the network used to map these landscapes is based on a previous transcriptomic data-derived model. Because the nodes in the network were derived using an unsupervised approach from the high-throughput data itself, several well-established key regulators identified in the literature, such as MAPK, BRAF, and MEK, have been inadvertently omitted from this network. To overcome this limitation and to mimic the effects of perturbing these genes absent in the network, we have used their downstream targets (for e.g., MITF for BRAF) as a proxy for their expression levels. Third, our model cannot capture the spatial flux of a cell population, as done in recent mesoscopic models for phenotypic heterogeneity in melanoma,⁴⁷ since it only considers structural fluxes. Future multi-scale modeling efforts can overcome these limitations by incorporating key elements from these diverse modeling strategies.

STAR★Methods

Key resources table

REAGENT or RESOURCE	SOURCE	IDENTIFIER
Deposited data
Analyzed dataset	Jerby-Arnon et al., 201846	GEO: GSE115978
Software and algorithms
RACIPE (Random Circuit Perturbation)	Huang et al., 201728	https://github.com/simonhb1990/RACIPE-1.0

Resource availability

Lead contact

Further information and requests for resources and reagents should be directed to and will be fulfilled by the lead contact Mohit Kumar jolly (mkjolly@iisc.ac.in).

Materials availability

This study did not generate new unique reagents.

Method details

RNAseq datasets used

scRNAseq dataset GSE115978 was used for pseudo-time analysis and measuring intra-tumoral heterogeneity.⁴⁶ The samples were filtered to remove non-tumor cells and only cells labeled as malignant melanoma cells were considered for the analysis. Since the dataset comprised of several single cell samples from multiple tumors, it was suitable for quantifying intra-tumor as well as inter-tumor heterogeneity.

Pseudo-time analysis

Pseudo-time analysis was done as previously reported.¹⁶ AUCell scores³¹ for the proliferative, hyper-pigmented, NCSC and invasive phenotype gene sets²⁰ were used to identify trajectory of cells along the pseudo-time axis.

Measuring heterogeneity

Intra-tumoral heterogeneity was measured using Shannon’s diversity Index (S) which is used to quantify the uncertainty or entropy of a system.⁴⁴ It is calculated as:

$$\text{S}=-\sum _{i=1}^n{p}_i\ln p_i$$

where, p_i is the proportion of the i^th phenotype in the population and n is the total number of phenotypes present.

Simulations for gene expression

RACIPE was used, as previously described,^16,28 to simulate gene expression in cells. RACIPE generates multiple models comprising of randomized kinetic parameters, within user-defined ranges, for the shifted Hill equation model of transcriptional regulation.

Each interaction where gene A influences the expression level of gene B is given as

$$\dot{B}=g_B·H\left(A,T_{AB},n_{AB},{\lambda }_{AB}\right)-k_{B}B$$

where, $g_B$ is basal production rate of B, $k_B$ is degradation rate of B and $H\left(A,T_{AB},n_B,{\lambda }_{AB}\right)$ is the shifted Hill function for the interaction, which is given as,

$$H\left(A,T_{AB},n_{AB},{\lambda }_{AB}\right)={\lambda }_{AB}+\left(1-{\lambda }_{AB}\right)\frac{1}{{\left(1+\left(\frac{A}{T_{AB}}\right)\right)}^{n_{AB}}}$$

where, $T_{AB}$ is the threshold level for A to influence B, $n_{AB}$ is the Hill’s coefficient for the reaction and ${\lambda }_{AB}$ is the maximum fold change in B caused by A. In this study, we have closely analyzed models (also referred to as parameter sets) that give rise to tetra-stability (four stable states/phenotypes) and penta-stability (five stable states/phenotypes) (Table S3).

Quantification of energy landscape

The time evolution of a dynamical system in the fluctuating environments can be described by the Langevin equation:

$$\stackrel{\cdot }{\overline{\mathbf{x}}}\left(t\right)=F\left[\overline{\mathbf{x}}\left(t\right)\right]+\zeta$$

Here, $\mathbf{x}=\left(x_1\left(t\right),x_2\left(t\right),\dots ,x_N\left(t\right)\right)$ represents the vector of the gene expression level. $\mathbf{F}\left[\mathbf{x}\left(t\right)\right]$ is the vector for the driving force for system, and $\text{ζ}$ is the Gaussian white noise, which satisfies $\text{E}\left[{\zeta }_i\left(t\right)\right]=0$ and $\text{E}\left[{\zeta }_i\left(t\right){\zeta }_j\left(0\right)\right]=2D{\delta }_{ij}\delta \left(t\right)$. By assuming that the noise is homogeneous and only considering external noise, we have the constant diffusion coefficient $D$ and

$$\{\begin{array}{l}{\delta }_{ij}=1,i=j\hfill \\ {\delta }_{ij}=0,i\ne j\hfill \end{array}$$

In above formula, ${\delta }_{ij}$ means that the noise is independent for different i and j, and $\delta \left(t\right)$ is Dirac Delta function, meaning that for one variable the noises are different at different time.

The Langevin equation is corresponding to a Fokker-Plank equation or probabilistic diffusion equation. To obtain the potential landscape, one way is to calculate the steady state probability distribution of the system. This requires us to solve an N-dimensional diffusion equation, which is hard to solve for a high-dimensional system. Here, we used a Gaussian approximation approach to obtain the probability distribution.^{38,48,49,50,51} The core idea of this approach is not directly solving probability diffusion equation, but working on the moment equations. By assuming a Gaussian density function, once we know the two moments, i.e., the mean and the variance, we can acquire the probability distribution. When the diffusion coefficient D (characterizing the noise level) is small, from the diffusion equation, the moment equations can be approximated to^38,52,53:

$$\dot{\overline{\mathbf{x}}}\left(\text{t}\right)=F\left[\overline{\mathbf{x}}\left(\mathbf{t}\right)\right]$$ (Equation 1)

$$\dot{\mathbf{\sigma }}\left(\text{t}\right)=\sigma \left(\text{t}\right){\mathbf{A}}^{\mathbf{T}}\left(\text{t}\right)+\mathbf{A}\left(\text{t}\right)\sigma \left(\text{t}\right)+2\mathbf{D}\left[\overline{\mathbf{x}}\left(\text{t}\right)\right]$$ (Equation 2)

Here, $\mathbf{x}$ is vector, $\mathbf{\sigma }\left(t\right)$ and $\mathbf{A}\left(t\right)$ are matrices, and ${\mathbf{A}}^{\mathbf{T}}\left(t\right)$ is the transpose of $\mathbf{A}\left(\text{t}\right)$. The elements of matrix $A$ are specified as: $A_{ij}=\frac{\partial F_i\left[X\left(t\right)\right]}{\partial x_j\left(t\right)}$.

We can solve $\overline{\mathbf{x}}\left(t\right)$ and $\mathbf{\sigma }\left(\text{t}\right)$ numerically. So, the probability density function $p\left(x,t\right)$ can be obtained from a multivariate Gaussian distribution function. Here, for simplicity, we only consider the diagonal elements (${\sigma }_i\left(t\right)$) of $\mathbf{\sigma }\left(t\right)$ based on the mean field approximation.^{38,48,49,50,51} The probability distribution for each variable can be obtained from the Gaussian approximation as:

$$P\left(x_i,t\right)=\frac{1}{\sqrt{2\pi {\sigma }_i\left(t\right)}}{e}^{-\frac{{\left[x_i-{\overline{x}}_i\left(t\right)\right]}^2}{2{\sigma }_i\left(t\right)}}$$ (Equation 3)

Here, ${\overline{x}}_i\left(t\right)$ and ${\sigma }_i\left(t\right)$ with $\mathit{\sigma }\left(t\right)=diag({\sigma }_1,{\sigma }_2,\dots ,{\sigma }_N)$ are the solutions of Equations 1 and 2. From the mean field approximation, we can extend this formula to the multidimensional case by assuming that the total probability is the product of individual probability for each variable: $P\left(x_1,x_2,\dots ,x_N,t\right)\sim \prod _i^{N}P\left(x_i,t\right)$. The probability distribution acquired above corresponds to the probability distribution of one attractor. If the system has multiple stable states, there are multiple probability distributions localized at each individual basin. The total probability of the system is the weighted sum of all these probability distributions. With the total probability, we can construct the potential landscape by,$U\left(x\right)=-ln{P}_{ss}\left(x\right)$^38,48with $P_{ss}$ representing steady state probability distribution.

Transition paths

Considering a stochastic dynamical system described by Langevin equation:

$$\stackrel{\cdot }{\overline{\mathbf{x}}}\left(t\right)=F\left[\overline{\mathbf{x}}\left(t\right)\right]+\zeta .$$

Following the approaches based on the Freidlin-Wentzell theory,⁵⁴ the most probable transition path from attractor i at time 0 to attractor j at time T, can be acquired by minimizing the action functional over all possible paths:

$$S_T\left[{\phi }_{ij}\right]=\frac{1}{2}{\underset{0}{\overset{T}{\int }}\left|{\dot{\phi }}_{ij}-F\left({\phi }_{ij}\right)\right|}^{2}dt$$

This path is called the minimum action path (MAP). We calculated MAPs numerically by applying minimum action methods used in previous study.⁵⁵ This type of approach has been used in many chemical and biological systems.^38,42,55,56

Calculation of transition matrix

The transition action characterizes the probability of transition from one attractor state to another, i.e., smaller transition action corresponds to larger transition probability. Based on the results of transition actions between attractors, we can estimate corresponding transition probability according to $P_{ij}\propto e^{-S_{ij}}$, where $S_{ij}$ represents the transition action from attractor $i$ to attractor $j$, while $P_{ij}$ represents the transition probability from attractor $i$ to attractor $j$. In this way, we can obtain an estimated transition probability matrix among five stable states. Considering the state transition process among attractors as a Markov process, we can calculate the probability evolution of each attractor state given any initial probability distribution of five stable states.

Quantification and statistical analysis

Statistical analysis was performed using R version 3.6.3, unless mentioned otherwise.

Published: December 22, 2022

Supplemental information

Table S3. Parameter sets for tetrastable and pentastable models

A. Parameter set for tetrastable models, related to Figures 1, S1A, and S1B.

B. Parameter set for pentastable models, related to Figures 2 and S2.

Prod = Production rate; Deg = Degradation rate; Trd = Threshold for interaction; Num = Hill coefficient for interaction; Act/Inh = Maximum fold change (lambda) for interaction.

Data and code availability

• •This paper analyses existing, publicly available data. The accession numbers for the datasets are listed in the key resources table.
• •All original code has been deposited at https://github.com/csbBSSE/Melanoma_Landscape, and https://github.com/chunhelilab/Melanoma_Landscape and is publicly available as of the date of publication. DOIs are listed in the key resources table.
• •Any additional information required to reanalyze the data reported in this paper is available from the lead contact upon request.