How global RNA-binding proteins coordinate the behaviour of RNA regulons: An information approach

Graphical abstract

Highlights

• •An information theory framework reveals salient features of RNA-protein networks.
• •Targets interacting with a common RNA-binding hub share information.
• •Competitive communication between targets drives noticeable biochemical effects.
• •Changes in target and hub abundances differentially affect crosstalk between them.
• •Information partially spreads to distal nodes in multi-hub networks.

Abstract

RNA-binding proteins are central players in post-transcriptional regulation. Some of them, such as the well-studied bacterial RNA chaperones Hfq and ProQ or the eukaryotic RNAi factor Argonaute, interact with hundreds-to-thousands of different RNAs and thereby globally affect gene expression. As a shared yet limited resource, these and other RNA-binding hubs drive strong competition between their multiple ligands. This creates a ground for significant cross-communication between RNA targets, which enables them to share information, “synchronise” their behaviour, and produce interesting biochemical effects, sometimes propagating across the highly connected RNA-protein network. This property is likely universally present in hub-centred networks and plays a key role in global gene expression programmes. It is also an important factor in biotechnology and synthetic biology applications of RNA/protein-based circuits. However, few studies so-far focused on describing and explaining this phenomenon from first principles. Here we introduce an information theory-based framework to comprehensively and exactly describe information flow in hub-centred networks. We show that information sharing can achieve significant levels in relatively small networks, provided the hub is present in limiting concentrations. The transmitted information is sufficient to noticeably affect the binding probabilities of competing targets but drops exponentially along the network. Target overexpression can disrupt communication between other targets, while hub sequestration boosts the crosstalk. We also find that overlaps between the interactomes of two different hubs create both entropic challenges and new forms of long-range communication between RNAs and proteins.

1. Introduction

Post-transcription regulation is an essential layer of gene expression control in all organisms. Among its key players, RNA-binding proteins (RBPs) hold a central stance. While some of them carry out specific regulation, directed at a single RNA target, many others associate with multiple transcripts and modulate their stability, localisation, translation, or interactions with other macromolecules [1], [2], [3]. Such global RNA-binding proteins appear as central nodes in RNA-protein interaction networks [4], and we will refer to them here as RNA-binding hubs (or simply hubs).

Over the last two decades, a number of such proteins have been identified and extensively studied, including such critical global regulators as Argonaute and Pumilio proteins in Eukarya and Hfq, ProQ and CsrA in Proteobacteria, each binding and functionally affecting hundreds-to-thousands of cellular RNAs [5], [6], [7]. Their regulatory centrality, which can be regarded as a special case of bottlenecked, bowtie-type, scale-free biological networks [4], [8], [9], creates a basis for concerted behaviour between targets: individual ligands, competing for a shared hub, are not fully independent anymore, they to some extent “sense” the status of each other and behave in a more-or-less coordinated fashion [10]. This kind of “information spread” between many transcripts has been well-studied on the examples of competing endogenous RNAs (ceRNA) and small RNA (sRNA)-mediated regulation [11], [12], [13], [14], [15]. In the case of RNA-binding hub-centred networks, it has been conceptualised in the notion of RNA regulons, or post-transcriptional operons [16], [17], [18].

Many properties of RNA-binding hub-centred networks have been learned empirically or assumed intuitively. For example, it is commonly agreed that hubs must be present in limiting concentrations to drive competition between targets (consider such well-established examples as sRNAs competing for RNAi machinery or various transcripts competing for the bacterial RNA chaperone Hfq [10], [19], [20], [21], [22], [23], [24]). It has also been observed that such networks are sensitive to hub sequestration [25], [26] and respond quickly and massively to changes in the transcriptome [27], [28]. However, few studies addressed the properties of RNA-binding hub-centred networks from first principles, to explain how the concerted behaviour of targets arises, how strong this coordination is, and on which parameters of the network it depends [10], [29]. These questions are important from both the fundamental and practical points of view since RBP/RNA-mediated regulatory modules, including those used for co-regulation of multiple targets, are getting ever more attractive in synthetic biology applications [30], [31], [32], [33], [34], [35], [36].

Here we propose an information theory-based framework to evaluate the impact of various parameters of hub-centred networks on their ability to drive information sharing and interdependent biochemical behaviour among multiple targets competitively interacting with the same RNA-binding hub.

2. Theory and calculation

2.1. General description of the model network

Consider a set of T distinct target RNAs (represented each by one molecule) interacting with a single RNA-binding hub (present in A copies), as shown in Fig. 1A. Each target molecule can be found in one of two mutually exclusive states: free or bound by the hub. For simplicity, all target RNAs are considered biochemically equivalent, i.e. they have the same probability to interact with the hub. Each hub molecule can interact with any target, but only one at a time (i.e. the binding is strictly competitive).

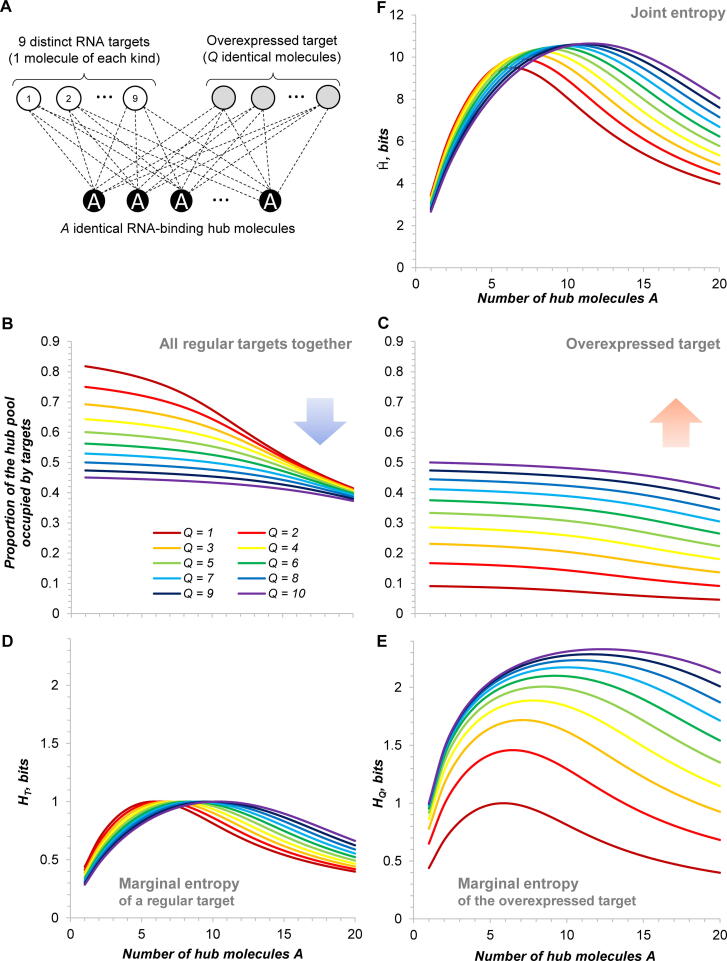
Fig. 1.

Information properties of a model hub-centred network. (A) Model of a network with T distinct single-copy RNA targets interacting with a shared RNA-binding hub present in A copies. (B) Joint entropy of targets as a function of the number of targets T and of the hub abundance A. (C) Peak position in joint and marginal entropy distributions shown in (B) and (D). (D, E) Marginal entropy and binding probability of a target as functions of T and A. Curves of different colours correspond to different T and are the same for all panels. See Table S5 for source data.

We will call a particular pattern of the targets, some being bound to the hub and some free, the configuration of the system (Figure S1). Due to the identity and interchangeability of the hub molecules, the same configuration can be realised in several equivalent and redundant ways, all of which are assumed to be equiprobable. Hence, the probability of each system configuration is defined by the number of such realisations (out of all combinatorially possible system states, either redundant or not). Such a system can be fully and exactly described in terms of Shannon information entropy [37]. Below we provide general expressions for all relevant quantities, and Table S1 gives an example of their calculation for T = 5 and 1 ≤ A ≤ 20.

2.1.1. Joint entropy of the targets

By combinatorially partitioning all system states to distinct, non-redundant configurations and counting their probabilities, one can calculate the joint entropy of the targets, which reflects the total amount of information contained in the system but also the degree of uncertainty about the actual system configuration [37]:

$$\widehat{H}=-\sum _{i=1}^N{p}_i{\log }_2{p}_i$$

where p_i is the probability of the i-th configuration, N is the total number of distinct configurations. Intuitively, the higher Ĥ the less one knows about the state in which the system currently is.

To calculate Ĥ, it is convenient to partition all states by the total number of bound targets 0 ≤ t ≤ T. Then there are $\left(\begin{array}{c}T\\ t\end{array}\right)$ non-redundant configurations, and each of them can be realised, by permuting the hub molecules, in $P_t^A$ redundant ways. Therefore, the joint entropy can be calculated as follows:

$$\hat{H}=-\frac{1}{N_{\mathit{total}}}\sum _{t=0}^T\left(\begin{array}{c}T\\ t\end{array}\right)P_t^A{\log }_2\frac{P_t^A}{N_{\mathit{total}}}$$ (1)

where $N_{\mathit{total}}={\sum }_{t=0}^T\left(\begin{array}{c}T\\ t\end{array}\right)P_t^A$ is the total number of states.

2.1.2. Marginal entropy of the targets and binding statistics

Similarly, we can define the marginal entropy of a target as follows:

$$H_T=-p_1{\log }_2{p}_1-p_0{\log }_2{p}_0$$

where p₁ and p₀ are the probabilities of one specific target to be in the bound or the free state, respectively. Therefore, the biochemical meaning of H_T is quite straightforward: it attains its maximum when it is virtually impossible to guess whether the target is rather in one state or the other (p₁ = p₀ = 0.5; H_T = 1 bit). By contrast, any biasing of the target status (e.g. by making it much more probable to be bound by the hub, or vice versa) will decrease H_T (down to 0, if the target is certain to be bound or free). In our fully symmetrical model, where all the targets are equally abundant and equally affine, H_T is identical for all targets.

To calculate H_T, one can use the same partition of the system states by t and hold one target out as bound. The number of ‘bound’ states at each t is given by $\left(\begin{array}{c}T-1\\ t-1\end{array}\right)P_t^A$, which is equivalent to weighting all system states by the probability of one specific target to be selected t/T. The binding probability is then calculated as follows:

$$p_1=\frac{1}{N_{\mathit{total}}}\sum _{t=1}^T\left(\begin{array}{c}T-1\\ t-1\end{array}\right)P_t^A=\frac{1}{{\mathit{TN}}_{\mathit{total}}}\sum _{t=1}^{T}t\left(\begin{array}{c}T\\ t\end{array}\right)P_t^A$$ (2)

and p₀ = 1 – p₁.

One can calculate, in a similar way, the expected hub occupancy, which is equivalent to the probability of a hub molecule to be in a bound state, no matter the ligand:

$$p_1^{Hub}=\frac{1}{A{N}_{total}}\sum _{t=1}^{T}t\left(\begin{array}{c}T\\ t\end{array}\right)P_t^A$$ (3)

And the probability of the hub to be free is p^Hub₀ = 1 – p^Hub₁.

2.1.3. Total correlation and redundancy

With data about the joint and marginal entropies of the targets, one can calculate the most straightforward and comprehensive kind of mutual information, the total correlation in the system [38]. Defined as the Kullback-Leibler divergence from the joint probability distribution to the independent distributions of variables, total correlation accounts for all kinds of information sharing between targets, however complex they are, and is calculated as follows:

$$C=\sum _{i=1}^T{H}_i-\widehat{H}$$

where H_i is the marginal entropy of the i-th target. In our model, where all H_i are identical (and denoted H_T), it simplifies to C = TH_T – Ĥ.

Total correlation can be normalised by its maximal possible value,$\max C=\sum _{i=0}^T{H}_i-\max H_i$. In this model, it simplifies to max C = (T – 1) H_T and only occurs when one variable fully defines all the others (i.e. knowing the status of one target automatically informs about the status of all the others targets). This provides an intuitive measure of redundancy:

$$R=\frac{C}{\max C}$$

2.1.4. Mutual information

While full partitioning of total correlation into components is complicated and is beyond the scope of this study, it is useful to calculate the most basic and widely used parameter, the pairwise, or bivariate, mutual information (or simply mutual information, MI) between two targets, which is defined as the Kullback-Leibler divergence from their joint probability distribution to the independent distributions [37], [39]. In our symmetrical model, where all targets are biochemically equivalent, it is calculated simply as:

$$I_{T-T}=p_{0,0}{\log }_2\frac{p_{0,0}}{p_0^2}+2p_{1,0}{\log }_2\frac{p_{1,0}}{p_1{p}_0}+p_{1,1}{\log }_2\frac{p_{1,1}}{p_1^2}$$

where I_T-T is the MI between any two targets, p_0,0 is the joint probability that both the targets are free, p_1,1 is the joint probability that both the targets are bound, p_1,0 is the joint probability that one target is bound while the other is not. I_T-T = 0 if and only if the behaviour of the two targets is fully independent. Similarly, C = 0 and R = 0 if and only if all targets behave independently.

For calculation, the system states are partitioned by t, as previously, and two targets are held out as their binding status is fixed. Then the number of states where two specific targets are simultaneously free, divided by the total number of system states, yields the joint ‘co-unbound’ probability, as follows:

$$p_{0,0}=\frac{1}{N_{\mathit{total}}}\sum _{t=0}^{T-2}\left(\begin{array}{c}T-2\\ t\end{array}\right)P_t^A$$

Analogously, the joint ‘anti-bound’ probability (where one selected target is bound and the other one not) is:

$$p_{1,0}=\frac{1}{N_{\mathit{total}}}\sum _{t=1}^{T-1}\left(\begin{array}{c}T-2\\ t-1\end{array}\right)P_t^A$$

Finally, the joint ‘co-bound’ probability (both the selected targets are bound) is:

$$p_{1,1}=\frac{1}{N_{\mathit{total}}}\sum _{t=2}^T\left(\begin{array}{c}T-2\\ t-2\end{array}\right)P_t^A$$

2.1.5. Normalised pointwise mutual information

MI captures all kinds of dependence between two targets (positive, negative, or non-monotonic). However, it is often desirable to have an easily interpretable correlation-like measure reflecting both the strength and the sign of the dependence. This is achieved by further decomposition of MI into pointwise mutual information (or ‘mutual information’ in Fano’s sense), eventually normalised by self-information to fit into the range [−1,1] (see references [40], [41]). The Normalised pointwise mutual information (npmi) equals 0 if and only if both the targets behave independently. It is negative if the targets are involved in an antagonistic (statistically repulsive) relationship. It is positive if the targets behave concertedly and in the same direction. The extreme values −1 and 1 correspond to perfect negative and perfect positive correlation, respectively. The npmi is defined for each combination of events, e.g. when both the targets are free:

$${\mathit{npmi}}_{0,0}^{T-T}=\frac{{\log }_2\frac{p_{0,0}}{p_0^2}}{-{\log }_2{p}_{0,0}}$$

Similarly, when both the targets co-occur in a bound state:

$${\mathit{npmi}}_{1,1}^{T-T}=\frac{{\log }_2\frac{p_{1,1}}{p_1^2}}{-{\log }_2{p}_{1,1}}$$

Finally, when they are in opposite states:

$${\mathit{npmi}}_{1,0}^{T-T}=\frac{{\log }_2\frac{p_{1,0}}{p_1{p}_0}}{-{\log }_2{p}_{1,0}}$$

2.2. Comparison with specific regulation of a single multi-copy target

It is useful to compare the above model with a simpler system containing only one RNA target, represented by Q identical copies and regulated by a specific RNA-binding protein (present in A identical copies; Fig. S2A). Such a target has (Q + 1) states, in which 0 ≤ q ≤ Q molecules are simultaneously bound and which can be realised in $\left(\begin{array}{c}Q\\ q\end{array}\right)P_q^A$ redundant ways (see Table S2 for an example of calculation at Q = 10, 1 ≤ A ≤ 20). Hence, the probability of each state is defined by:

$$p_{q/Q}=\frac{\left(\begin{array}{c}Q\\ q\end{array}\right)P_q^A}{N_{\mathit{total}}}$$

where $N_{\mathit{total}}=\sum _{q=0}^Q\left(\begin{array}{c}Q\\ q\end{array}\right)P_q^A$. Then the entropy of such a target is:

$$H_Q=-\frac{1}{N_{\mathit{total}}}\sum _{q=0}^Q\left(\begin{array}{c}Q\\ q\end{array}\right)P_q^A{\log }_2\frac{\left(\begin{array}{c}Q\\ q\end{array}\right)P_q^A}{N_{\mathit{total}}}$$

It is easy to see that this expression is similar to Equation (1), and both systems actually have an equal number of states at the same A and t = q (compare the expressions for their N_total). However, due to the interchangeability of the molecules of the Q-target, this specific regulation model contains many more redundant states than that described in section 2.1, and its entropy is correspondingly lower due to the $\left(\begin{array}{c}Q\\ q\end{array}\right)$ term under the logarithm. This feature will be useful for building the next, mixed model (section 2.3).

Despite the different state partitioning, the binding probability of the single RNA target in this specific regulation system is identical to that of any of the multiple RNA targets in the previous multi-target model at the same A and Q = T (see Equation (2)):

$$p_1=\frac{1}{{\mathit{QN}}_{\mathit{total}}}\sum _{q=0}^{Q}q\left(\begin{array}{c}Q\\ q\end{array}\right)P_q^A$$

Similarly, the expression for the expected hub occupancy, is formally identical to Equation (3) at the same A and Q = T:

$$p_1^{\mathit{Hub}}=\frac{1}{{\mathit{AN}}_{\mathit{total}}}\sum _{q=0}^{Q}q\left(\begin{array}{c}Q\\ q\end{array}\right)P_q^A$$

Therefore, except for target identity, the two systems are biochemically indistinguishable.

2.3. Model with an overexpressed target

To explicitly address the situation where one of the targets gets overexpressed, we will consider a system of T distinct targets, each present in one copy (henceforth regular targets), to which will be added another one, present in Q identical copies, as in section 2.2 (henceforth overexpressed target). All target molecules are biochemically equivalent and have the same chances to interact with a hub present in A identical copies. Below we will provide general expressions for all relevant quantities, while in this paper we will only consider an example case with T = 9, 1 ≤ Q ≤ 10, and 1 ≤ A ≤ 20 (Fig. 4A). At Q = 1 the system is obviously identical to the one described in section 2.1 (with T = 10). By contrast, at Q > 1, the redundant states introduced by the identical copies of the overexpressed target create a new, non-symmetrical, relationship between the targets, as detailed below.

Fig. 4.

Information properties of a model hub-centred network with an overexpressed target. (A) Model of a network with T = 9 distinct single-copy RNA targets and one overexpressed target (present in Q copies) interacting with a shared RNA-binding hub (present in A copies). (B, C) Proportion of the hub pool occupied by the regular and the overexpressed targets as a function of the overexpression level Q and the hub abundance A. (D, E) Marginal entropies of the regular and the overexpressed targets as functions of Q and A. (F) Joint entropy of the system as a function of Q and A. See Table S7 for source data.

2.3.1. Joint entropy

To calculate the joint entropy of such a complex system, it is practical to partition all its states by the total number of bound regular, non-overexpressed targets 0 ≤ t ≤ T and by the total number of bound molecules of the overexpressed target 0 ≤ q ≤ Q (see an explicit example of calculation for T = 9, Q = 5 in Table S3). Then there are $\left(\begin{array}{c}T\\ t\end{array}\right)$ non-redundant configurations for each (t, q), and each of them can be realised, by permuting the hub and the overexpressed target molecules, in $\left(\begin{array}{c}Q\\ q\end{array}\right)P_{t+q}^A$ redundant ways. Therefore, the joint entropy can be calculated as follows:

$$\hat{H}=-\frac{1}{N_{\mathit{total}}}\sum _{t=0}^T\sum _{q=0}^Q\left(\begin{array}{c}T\\ t\end{array}\right)\left(\begin{array}{c}Q\\ q\end{array}\right)P_{t+q}^A{\log }_2\frac{\left(\begin{array}{c}Q\\ q\end{array}\right)P_{t+q}^A}{N_{\mathit{total}}}$$

where $N_{\mathit{total}}={\sum }_{t=0}^T{\sum }_{q=0}^Q\left(\begin{array}{c}T\\ t\end{array}\right)\left(\begin{array}{c}Q\\ q\end{array}\right)P_{t+q}^A$.

2.3.2. Marginal entropies

The marginal entropy of the regular targets, which, being represented by one molecule each, only have two states, is calculated similarly as in section 2.1.2. Again, it is practical to partition all states by t and q and then hold one regular target out as bound. Then the number of ‘bound’ states at each (t, q) is given by $\frac{t}{T}\left(\begin{array}{c}T\\ t\end{array}\right)\left(\begin{array}{c}Q\\ q\end{array}\right)P_{t+q}^A$, and the binding probability can be calculated as follows:

$$p_1=\frac{1}{T{N}_{\mathit{total}}}\sum _{t=0}^T\sum _{q=0}^{Q}t\left(\begin{array}{c}T\\ t\end{array}\right)\left(\begin{array}{c}Q\\ q\end{array}\right)P_{t+q}^A$$

As described in section 2.2, the overexpressed target has (Q + 1) states, and its entropy is correspondingly more complex:

$$H_Q=-\sum _{q=0}^Q{p}_{q/Q}{\log }_2{p}_{q/Q}$$

where p_q/Q is the probability of exactly q molecules of the overexpressed target to be bound, which can be found from state partitioning:

$$p_{q/Q}=\frac{1}{N_{\mathit{total}}}\left(\begin{array}{c}Q\\ q\end{array}\right)\sum _{t=0}^T\left(\begin{array}{c}T\\ t\end{array}\right)P_{t+q}^A$$

The expected hub occupancy by one specific regular target is given analogously to Eq. 2 and 3:

$$p_T^{\mathit{Hub}}=\frac{1}{{\mathit{ATN}}_{\mathit{total}}}\sum _{t=0}^T\sum _{q=0}^{Q}t\left(\begin{array}{c}T\\ t\end{array}\right)\left(\begin{array}{c}Q\\ q\end{array}\right)P_{t+q}^A$$

The expected hub occupancy by the overexpressed target is calculated similarly:

$$p_Q^{\mathit{Hub}}=\frac{1}{{\mathit{AN}}_{\mathit{total}}}\sum _{t=0}^T\sum _{q=0}^{Q}q\left(\begin{array}{c}T\\ t\end{array}\right)\left(\begin{array}{c}Q\\ q\end{array}\right)P_{t+q}^A$$

2.3.3. Total correlation

In this case, the total correlation is calculated as C = TH_T + H_Q – Ĥ, and its maximal possible value is max C = TH_T, since H_Q is always the greatest marginal entropy in the system.

2.3.4. Mutual information and normalised pointwise mutual information

The MI and npmi between two regular targets is calculated as in sections 2.1.4 and 2.1.5, but joint probabilities need to take into account permutations of the overexpressed target:

$$p_{0,0}=\frac{1}{N_{\mathit{total}}}\sum _{t=0}^{T-2}\sum _{q=0}^Q\left(\begin{array}{c}T-2\\ t\end{array}\right)\left(\begin{array}{c}Q\\ q\end{array}\right)P_{t+q}^A$$

$$p_{1,0}=\frac{1}{N_{\mathit{total}}}\sum _{t=1}^{T-1}\sum _{q=0}^Q\left(\begin{array}{c}T-2\\ t-1\end{array}\right)\left(\begin{array}{c}Q\\ q\end{array}\right)P_{t+q}^A$$

$$p_{1,1}=\frac{1}{N_{\mathit{total}}}\sum _{t=2}^T\sum _{q=0}^Q\left(\begin{array}{c}T-2\\ t-2\end{array}\right)\left(\begin{array}{c}Q\\ q\end{array}\right)P_{t+q}^A$$

There arises additionally a new kind of MI – the one between a regular and the overexpressed target. Its calculation requires considering 2·(Q + 1) joint probabilities to account for all combinations of their states. All states are partitioned by t and q, and the joint probability for the states where the regular target is free while q molecules of the overexpressed target are bound is:

$$p_{0,q/Q}=\frac{1}{N_{\mathit{total}}}\left(\begin{array}{c}Q\\ q\end{array}\right)\sum _{t=0}^{T-1}\left(\begin{array}{c}T-1\\ t\end{array}\right)P_{t+q}^A$$

Analogously, for the states where the regular target is bound the joint probability is given by:

$$p_{1,q/Q}=\frac{1}{N_{\mathit{total}}}\left(\begin{array}{c}Q\\ q\end{array}\right)\sum _{t=1}^T\left(\begin{array}{c}T-1\\ t-1\end{array}\right)P_{t+q}^A$$

Hence the MI:

$$I_{T-Q}=\sum _{q=0}^Q{p}_{0,q/Q}{\log }_2\frac{p_{0,q/Q}}{p_0{p}_{q/Q}}+\sum _{q=0}^Q{p}_{1,q/Q}{\log }_2\frac{p_{1,q/Q}}{p_1{p}_{q/Q}}$$

The npmi is defined analogously, for example, for the states where the regular target is free:

$${\mathit{npmi}}_{0,q/Q}^{T-Q}=\frac{{\log }_2\frac{p_{0,q/Q}}{p_0{p}_{q/Q}}}{-{\log }_2{p}_{q/Q}}$$

2.4. Cross-regulation by two competing hubs

To study competitive cross-regulation by two different hubs which have shared targets, we will consider a system of (T_A + T_B + S) distinct RNA targets, each represented by 1 molecule, and of two distinct hubs (A and B), each present in A and B copies, respectively. The targets are classified in one of the three following categories: (i) T_A targets exclusively bound by the hub A, (ii) T_B targets exclusively bound by the hub B, and (iii) S shared targets, bound by either hub (but not by both at the same time). Below we will provide general expressions for all relevant quantities describing such a system, while in this paper we will specifically consider a network of T_A + T_B + S = 10 targets. For simplicity, we will only deal with symmetrical situations, where both the hubs are present in the same concentration (A = B) and have the same number of exclusive targets (T_A = T_B = T), and there are S shared targets, such that 2 T + S = 10 (Fig. 7A). Therefore, by varying T and S, i.e. by increasing or decreasing the overlap between the hubs, one can alter the wiring of the network without changing the number of its components (Fig. 7B).

Fig. 7.

Information properties of a model network with two overlapping hub interactomes. (A) Model of a network with T exclusive RNA targets interacting with the hub A, T exclusive targets interacting with the hub B, and S shared targets interacting with either hub. All the targets are single-copy. Each RNA-binding hub is present in A copies. (B) Graph representations of the symmetrical architectures considered in this study. (C, D) Expected hub occupancy by exclusive and shared targets as a function of the overlap between the interactomes S and the hub abundance A. (E, F) Marginal entropies of exclusive and shared targets as functions of S and A. (G) Joint entropy of the system as a function of S and A. See Table S8 for source data.

2.4.1. Joint entropy

Table S4 shows an example of joint entropy calculation for T = 3, S = 4, and 1 ≤ A ≤ 20. Here all system states are explicitly partitioned by the total number of bound exclusive targets of the hub A (t_A), the total number of bound exclusive targets of the hub B (t_B), and the total number of shared targets bound either by the hub A or B (s_A and s_B, respectively; s_A + s_B ≤ S). Then there are $\left(\begin{array}{c}{T}_A\\ t_A\end{array}\right)\left(\begin{array}{c}{T}_B\\ t_B\end{array}\right)\left(\begin{array}{c}S\\ s_A,s_B,S-s_A-s_B\end{array}\right)$ non-redundant configurations for each (t_A, t_B, s_A, s_B), and each configuration is realised, by permutation of the hub molecules, in $P_{t_A+s_A}^A{P}_{t_B+s_B}^B$ redundant ways. Therefore, the joint entropy can be calculated as follows:

$$\hat{H}=-\frac{1}{N_{\mathit{total}}}\sum _{t_A=0}^{T_A}\sum _{t_B=0}^{T_B}\sum _{s_A=0}^{S-s_B}\sum _{s_B=0}^{S-s_A}\left(\begin{array}{c}{T}_A\\ t_A\end{array}\right)\left(\begin{array}{c}{T}_B\\ t_B\end{array}\right)\left(\begin{array}{c}S\\ s_A,s_B,S-s_A-s_B\end{array}\right)P_{t_A+s_A}^A{P}_{t_B+s_B}^B{\log }_2\frac{P_{t_A+s_A}^A{P}_{t_B+s_B}^B}{N_{\mathit{total}}}$$

where $N_{\mathit{total}}={\sum }_{t_A=0}^{T_A}{\sum }_{t_B=0}^{T_B}{\sum }_{s_A=0}^{S-s_B}{\sum }_{s_B=0}^{S-s_A}\left(\begin{array}{c}{T}_A\\ t_A\end{array}\right)\left(\begin{array}{c}{T}_B\\ t_B\end{array}\right)\left(\begin{array}{c}S\\ s_A,s_B,S-s_A-s_B\end{array}\right)P_{t_A+s_A}^A{P}_{t_B+s_B}^B$.

2.4.2. Marginal entropies

The marginal entropy for exclusive targets is calculated similarly as in sections 2.1.2 and 2.3.2. Again it is practical to partition all states by t_A, t_B, s_A and s_B, and then hold one regular target out as bound (for example, we can “fix” an exclusive target bound by the hub A). Then the number of ‘bound’ states at each (t_A, t_B, s_A, s_B) is given by $\frac{t_A}{T_A}\left(\begin{array}{c}{T}_A\\ t_A\end{array}\right)\left(\begin{array}{c}{T}_B\\ t_B\end{array}\right)\left(\begin{array}{c}S\\ s_A,s_B,S-s_A-s_B\end{array}\right)P_{t_A+s_A}^A{P}_{t_B+s_B}^B$, and the binding probability can be calculated as follows:

$$p_1=\frac{1}{T_A{N}_{\mathit{total}}}\sum _{t_A=0}^{T_A}\sum _{t_B=0}^{T_B}\sum _{s_A}^{S-s_B}\sum _{s_B}^{S-s_A}{t}_A\left(\begin{array}{c}{T}_A\\ t_A\end{array}\right)\left(\begin{array}{c}{T}_B\\ t_B\end{array}\right)\left(\begin{array}{c}S\\ s_A,s_B,S-s_A-s_B\end{array}\right)P_{t_A+s_A}^A{P}_{t_B+s_B}^B$$

In our symmetrical system, where T_A = T_B and A = B, p₁ is obviously identical for both types of exclusive targets.

The shared targets have three states (free, bound by the hub A, bound by the hub B), and their marginal entropy is calculated as follows:

$$H_S=-p_0{\log }_2{p}_0-p_A{\log }_2{p}_A-p_B{\log }_2{p}_B$$

where p₀, p_A and p_B are the corresponding probabilities readily obtained from state partitioning by s_A and s_B:

$$p_A=-\frac{1}{{\mathit{SN}}_{\mathit{total}}}\sum _{t_A=0}^{T_A}\sum _{t_B=0}^{T_B}\sum _{s_A=0}^{S-s_B}\sum _{s_B=0}^{S-s_A}{s}_A\left(\begin{array}{c}{T}_A\\ t_A\end{array}\right)\left(\begin{array}{c}{T}_B\\ t_B\end{array}\right)\left(\begin{array}{c}S\\ s_A,s_B,S-s_A-s_B\end{array}\right)P_{t_A+s_A}^A{P}_{t_B+s_B}^B$$

$$p_B=-\frac{1}{{\mathit{SN}}_{\mathit{total}}}\sum _{t_A=0}^{T_A}\sum _{t_B=0}^{T_B}\sum _{s_A=0}^{S-s_B}\sum _{s_B=0}^{S-s_A}{s}_B\left(\begin{array}{c}{T}_A\\ t_A\end{array}\right)\left(\begin{array}{c}{T}_B\\ t_B\end{array}\right)\left(\begin{array}{c}S\\ s_A,s_B,S-s_A-s_B\end{array}\right)P_{t_A+s_A}^A{P}_{t_B+s_B}^B$$

p₀ = 1- p_A - p_B.

Because we only consider fully symmetrical cases, p_A = p_B.

The expected occupancy of a hub (e.g. the hub A) by one of its exclusive targets is given analogously to Eq. (2):

$$p_A^A=\frac{1}{A{T}_A{N}_{\mathit{total}}}\sum _{t_A=0}^{T_A}\sum _{t_B=0}^{T_B}\sum _{s_A}^{S-s_B}\sum _{s_B}^{S-s_A}{t}_A\left(\begin{array}{c}{T}_A\\ t_A\end{array}\right)\left(\begin{array}{c}{T}_B\\ t_B\end{array}\right)\left(\begin{array}{c}S\\ s_A,s_B,S-s_A-s_B\end{array}\right)P_{t_A+s_A}^A{P}_{t_B+s_B}^B$$

The expected occupancy of a hub (e.g. the hub A) by one of the shared targets is found similarly:

$$p_S^A=\frac{1}{\mathit{AS}{N}_{\mathit{total}}}\sum _{t_A=0}^{T_A}\sum _{t_B=0}^{T_B}\sum _{s_A}^{S-s_B}\sum _{s_B}^{S-s_A}{s}_A\left(\begin{array}{c}{T}_A\\ t_A\end{array}\right)\left(\begin{array}{c}{T}_B\\ t_B\end{array}\right)\left(\begin{array}{c}S\\ s_A,s_B,S-s_A-s_B\end{array}\right)P_{t_A+s_A}^A{P}_{t_B+s_B}^B$$

In our symmetrical cases, $p_A^A=p_B^B$ and $p_S^A=p_S^B$.

2.4.3. Total correlation

Generally, the total correlation is given by the following expression:

$$C=T_A{H}_{T_A}+T_B{H}_{T_B}+S{H}_S-\widehat{H}$$

where H_TA and H_TB are the marginal entropies of the two types of exclusive targets. In the symmetrical case considered in this paper, C = 2TH_T + SH_S – Ĥ, and its maximal possible value is max C = 2TH_T + (S – 1) H_S, since H_S is always the greatest marginal entropy in the system.

2.4.4. Mutual information and normalised pointwise mutual information

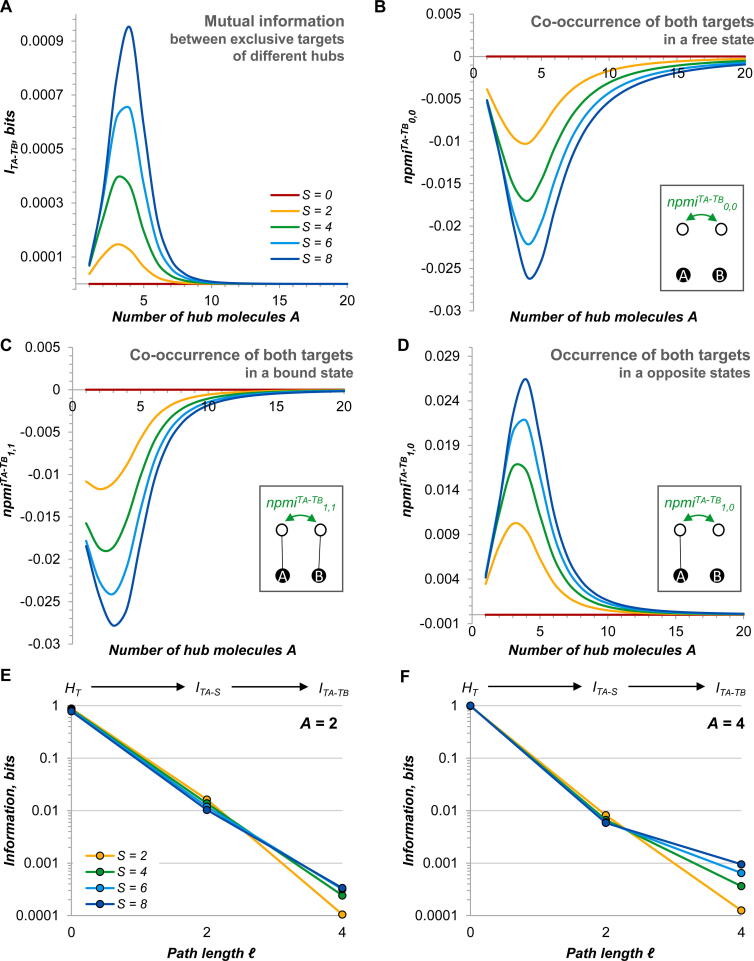
Three kinds of targets imply the existence of six kinds of pairwise MI in this system: five of them are proximal (path length $\ell$ = 2), connecting targets wired on the same hub, and one is distal ($\ell$ = 4), connecting exclusive targets interacting with different hubs (see Fig. 8C).

Fig. 8.

Structure of mutual information in a model network with two overlapping hub interactomes. (A, B) Total correlation and redundancy as functions of the overlap between the interactomes S and the hub abundance A. The black dotted lines show, for comparison, the total correlation and redundancy in the one-hub model system with T = 10 targets (A is divided by 2 to normalise for differences in the total amount of hub molecules between the systems). (C) Diagram showing the types of pairwise MI existing in this network. Six kinds of MI connect different targets (labelled on the top). Additional classes of MI, not considered here, involve one or both the hubs (shown on the bottom). (D-F) Proximal MI between two targets wired on the same hub (ℓ = 2) as a function of S and A. See Table S8 for source data.

The most basic proximal MI, analogous to I_T-T described in sections 2.1.4 and 2.3.4, measures the relationship between any two exclusive targets interacting with the same hub (I_TA-TA, I_TB-TB). The joint probabilities need to take into account the permutations of the hubs, with two targets interacting with the same hub (e.g. the hub A, as here) held out:

$$p_{0,0}^{T_A-T_A}=\frac{1}{N_{\mathit{total}}}\sum _{t_A=0}^{T_A-2}\sum _{t_B=0}^{T_B}\sum _{s_A=0}^{S-s_B}\sum _{s_B=0}^{S-s_A}\left(\begin{array}{c}{T}_A-2\\ t_A\end{array}\right)\left(\begin{array}{c}{T}_B\\ t_B\end{array}\right)\left(\begin{array}{c}S\\ s_A,s_B,S-s_A-s_B\end{array}\right)P_{t_A+s_A}^A{P}_{t_B+s_B}^B$$

$$p_{1,0}^{T_A-T_A}=\frac{1}{N_{\mathit{total}}}\sum _{t_A=1}^{T_A-1}\sum _{t_B=0}^{T_B}\sum _{s_A=0}^{S-s_B}\sum _{s_B=0}^{S-s_A}\left(\begin{array}{c}{T}_A-2\\ t_A-1\end{array}\right)\left(\begin{array}{c}{T}_B\\ t_B\end{array}\right)\left(\begin{array}{c}S\\ s_A,s_B,S-s_A-s_B\end{array}\right)P_{t_A+s_A}^A{P}_{t_B+s_B}^B$$

$$p_{1,1}^{T_A-T_A}=\frac{1}{N_{\mathit{total}}}\sum _{t_A=2}^{T_A}\sum _{t_B=0}^{T_B}\sum _{s_A=0}^{S-s_B}\sum _{s_B=0}^{S-s_A}\left(\begin{array}{c}{T}_A-2\\ t_A-2\end{array}\right)\left(\begin{array}{c}{T}_B\\ t_B\end{array}\right)\left(\begin{array}{c}S\\ s_A,s_B,S-s_A-s_B\end{array}\right)P_{t_A+s_A}^A{P}_{t_B+s_B}^B$$

Due to the symmetry of the system, I_TA-TA = I_TB-TB.

Two other kinds of proximal MI involve shared targets. The MI between any two shared targets (I_S-S) is defined by a more complex set of joint probabilities, including the ‘co-unbound’ ($p_{0,0}^{S-S}$), the ‘anti-bound’ (e.g., by the hub A, $p_{A,0}^{S-S}$), the ‘homo-co-bound’ (e.g., both the targets are bound by the hub A, $p_{A,A}^{S-S}$), and the ‘hetero-co-bound’ (i.e. one is bound by the hub A and the other by the hub B, $p_{A,B}^{S-S}$). They are calculated by holding out, in corresponding ways, two shared targets and by permuting the hubs:

$$p_{0,0}^{S-S}=\frac{1}{N_{\mathit{total}}}\sum _{t_A=0}^{T_A}\sum _{t_B=0}^{T_B}\sum _{s_A=0}^{S-2-s_B}\sum _{s_B=0}^{S-2-s_A}\left(\begin{array}{c}{T}_A\\ t_A\end{array}\right)\left(\begin{array}{c}{T}_B\\ t_B\end{array}\right)\left(\begin{array}{c}S\\ s_A,s_B,S-2-s_A-s_B\end{array}\right)P_{t_A+s_A}^A{P}_{t_B+s_B}^B$$

$$p_{A,0}^{S-S}=\frac{1}{N_{\mathit{total}}}\sum _{t_A=0}^{T_A}\sum _{t_B=0}^{T_B}\sum _{s_A=1}^{S-1-s_B}\sum _{s_B=0}^{S-2-s_A}\left(\begin{array}{c}{T}_A\\ t_A\end{array}\right)\left(\begin{array}{c}{T}_B\\ t_B\end{array}\right)\left(\begin{array}{c}S-2\\ s_A-1,s_B,S-1-s_A-s_B\end{array}\right)P_{t_A+s_A}^A{P}_{t_B+s_B}^B$$

$$p_{A,A}^{S-S}=\frac{1}{N_{\mathit{total}}}\sum _{t_A=0}^{T_A}\sum _{t_B=0}^{T_B}\sum _{s_A=2}^{S-s_B}\sum _{s_B=0}^{S-2-s_A}\left(\begin{array}{c}{T}_A\\ t_A\end{array}\right)\left(\begin{array}{c}{T}_B\\ t_B\end{array}\right)\left(\begin{array}{c}S-2\\ s_A-2,s_B,S-s_A-s_B\end{array}\right)P_{t_A+s_A}^A{P}_{t_B+s_B}^B$$

$$p_{A,B}^{S-S}=\frac{1}{N_{\mathit{total}}}\sum _{t_A=0}^{T_A}\sum _{t_B=0}^{T_B}\sum _{s_A=1}^{S-1-s_B}\sum _{s_B=1}^{S-1-s_A}\left(\begin{array}{c}{T}_A\\ t_A\end{array}\right)\left(\begin{array}{c}{T}_B\\ t_B\end{array}\right)\left(\begin{array}{c}S-2\\ s_A-1,s_B-1,S-s_A-s_B\end{array}\right)P_{t_A+s_A}^A{P}_{t_B+s_B}^B$$

The MI between two targets, one exclusive and the other shared (I_TA-S, I_TB-S), depends on a set of six joint probabilities. If we consider an exclusive target bound by the hub A, these will include the ‘co-unbound’ ($p_{0,0}^{T_A-S}$), the ‘exclusive target free / shared target bound by the hub A’ ($p_{0,A}^{T_A-S}$), the ‘exclusive target free / shared target bound by the hub B’ ($p_{0,B}^{T_A-S}$) states, and their counterparts where the exclusive target is bound ($p_{1,0}^{T_A-S}$, $p_{1,A}^{T_A-S}$, $p_{1,B}^{T_A-S}$). Their general expressions are given below:

$$p_{0,0}^{T_A-S}=\frac{1}{N_{\mathit{total}}}\sum _{t_A=0}^{T_A-1}\sum _{t_B=0}^{T_B}\sum _{s_A=0}^{S-1-s_B}\sum _{s_B=0}^{S-1-s_A}\left(\begin{array}{c}{T}_A-1\\ t_A\end{array}\right)\left(\begin{array}{c}{T}_B\\ t_B\end{array}\right)\left(\begin{array}{c}S-1\\ s_A,s_B,S-1-s_A-s_B\end{array}\right)P_{t_A+s_A}^A{P}_{t_B+s_B}^B$$

$$p_{0,A}^{T_A-S}=\frac{1}{N_{\mathit{total}}}\sum _{t_A=0}^{T_A-1}\sum _{t_B=0}^{T_B}\sum _{s_A=1}^{S-s_B}\sum _{s_B=0}^{S-1-s_A}\left(\begin{array}{c}{T}_A-1\\ t_A\end{array}\right)\left(\begin{array}{c}{T}_B\\ t_B\end{array}\right)\left(\begin{array}{c}S-1\\ s_A-1,s_B,S-s_A-s_B\end{array}\right)P_{t_A+s_A}^A{P}_{t_B+s_B}^B$$

$$p_{0,B}^{T_A-S}=\frac{1}{N_{\mathit{total}}}\sum _{t_A=0}^{T_A-1}\sum _{t_B=0}^{T_B}\sum _{s_A=0}^{S-1-s_B}\sum _{s_B=1}^{S-s_A}\left(\begin{array}{c}{T}_A-1\\ t_A\end{array}\right)\left(\begin{array}{c}{T}_B\\ t_B\end{array}\right)\left(\begin{array}{c}S-1\\ s_A,s_B-1,S-s_A-s_B\end{array}\right)P_{t_A+s_A}^A{P}_{t_B+s_B}^B$$

$$p_{1,0}^{T_A-S}=\frac{1}{N_{\mathit{total}}}\sum _{t_A=1}^{T_A}\sum _{t_B=0}^{T_B}\sum _{s_A=0}^{S-1-s_B}\sum _{s_B=0}^{S-1-s_A}\left(\begin{array}{c}{T}_A-1\\ t_A-1\end{array}\right)\left(\begin{array}{c}{T}_B\\ t_B\end{array}\right)\left(\begin{array}{c}S-1\\ s_A,s_B,S-1-s_A-s_B\end{array}\right)P_{t_A+s_A}^A{P}_{t_B+s_B}^B$$

$$p_{1,A}^{T_A-S}=\frac{1}{N_{\mathit{total}}}\sum _{t_A=1}^{T_A}\sum _{t_B=0}^{T_B}\sum _{s_A=1}^{S-s_B}\sum _{s_B=0}^{S-1-s_A}\left(\begin{array}{c}{T}_A-1\\ t_A-1\end{array}\right)\left(\begin{array}{c}{T}_B\\ t_B\end{array}\right)\left(\begin{array}{c}S-1\\ s_A-1,s_B,S-s_A-s_B\end{array}\right)P_{t_A+s_A}^A{P}_{t_B+s_B}^B$$

$$p_{1,B}^{T_A-S}=\frac{1}{N_{\mathit{total}}}\sum _{t_A=1}^{T_A}\sum _{t_B=0}^{T_B}\sum _{s_A=0}^{S-1-s_B}\sum _{s_B=1}^{S-s_A}\left(\begin{array}{c}{T}_A-1\\ t_A-1\end{array}\right)\left(\begin{array}{c}{T}_B\\ t_B\end{array}\right)\left(\begin{array}{c}S-1\\ s_A,s_B-1,S-s_A-s_B\end{array}\right)P_{t_A+s_A}^A{P}_{t_B+s_B}^B$$

Because of cross-wiring via the shared targets, a new kind of distal MI arises in this system, the one between two exclusive targets bound by different hubs (I_TA-TB). The joint probabilities for this case are calculated taking into account the permutations of the hubs, with one target held out on either side (i.e. one hub A- and one hub B-interacting target):

$$p_{0,0}^{T_A-T_B}=\frac{1}{N_{\mathit{total}}}\sum _{t_A=0}^{T_A-1}\sum _{t_B=0}^{T_B-1}\sum _{s_A=0}^{S-s_B}\sum _{s_B=0}^{S-s_A}\left(\begin{array}{c}{T}_A-1\\ t_A\end{array}\right)\left(\begin{array}{c}{T}_B-1\\ t_B\end{array}\right)\left(\begin{array}{c}S\\ s_A,s_B,S-s_A-s_B\end{array}\right)P_{t_A+s_A}^A{P}_{t_B+s_B}^B$$

$$p_{1,0}^{T_A-T_B}=\frac{1}{N_{\mathit{total}}}\sum _{t_A=1}^{T_A}\sum _{t_B=0}^{T_B-1}\sum _{s_A=0}^{S-s_B}\sum _{s_B=0}^{S-s_A}\left(\begin{array}{c}{T}_A-1\\ t_A-1\end{array}\right)\left(\begin{array}{c}{T}_B-1\\ t_B\end{array}\right)\left(\begin{array}{c}S\\ s_A,s_B,S-s_A-s_B\end{array}\right)P_{t_A+s_A}^A{P}_{t_B+s_B}^B$$

$$p_{1,1}^{T_A-T_B}=\frac{1}{N_{\mathit{total}}}\sum _{t_A=1}^{T_A}\sum _{t_B=1}^{T_B}\sum _{s_A=0}^{S-s_B}\sum _{s_B=0}^{S-s_A}\left(\begin{array}{c}{T}_A-1\\ t_A-1\end{array}\right)\left(\begin{array}{c}{T}_B-1\\ t_B-1\end{array}\right)\left(\begin{array}{c}S\\ s_A,s_B,S-s_A-s_B\end{array}\right)P_{t_A+s_A}^A{P}_{t_B+s_B}^B$$

3. Results and discussion

3.1. Minimal model of a hub-centred RNA network

To understand how in principle RNA-binding hubs can make their multiple targets act in a concerted way, we will consider a model network consisting of T distinct RNA targets, each present in one copy, connected to one hub, present in A copies (Fig. 1A). For simplicity, all the targets have the same probability to interact with the hub; their binding to the hub is mutually exclusive and competitive (i.e. each hub molecule can bind only one target molecule at a time). We will not consider here the regulatory consequences of their interactions and will simply focus on binding as an act by which RNA targets gain access to the molecular function provided by the hub. Although this model system is much simpler than natural RNA-protein interaction networks, it has the advantage of being amenable to full and exact Shannon information analysis (see section 2.1) and allows for capturing some salient features of such systems, which are likely to hold in other contexts.

3.1.1. Relationship between information and biochemical binding in hub-centred RNA networks

We varied the number of the hub molecules (1 ≤ A ≤ 20) and of targets (1 ≤ T ≤ 20) to test how the hub abundance and the size of its interactome affect information-related parameters of this model system. By combinatorially partitioning all possible states of the network (in a Shannon-Boltzmann-Gibbs sense), we can calculate the joint entropy of the targets, which measures the overall amount of information contained in the network and, at the same time, the degree of uncertainty about its actual state at any given moment [37], [42]. Therefore, joint entropy can be understood as a measure of dynamic complexity of the system (related to the number of ways it can be wired and rewired at every time point), which correlates with unpredictability of its outcomes. Fig. 1B, C shows that the joint entropy of this model network always has a unimodal distribution: its peak occurs at a specific amount of the hub A ≈ T/2. As expected, the height of the peak correlates with T, i.e. the more different targets the network has the more unpredictable and information-rich it gets.

Importantly, this characteristic unimodal behaviour can also be observed at the level of the underlying marginal entropies, which reflect the information content of each individual target (Fig. 1C, D). The marginal entropy of an RNA target is defined by its binding probability (section 2.1.2) and reaches its maximum value, max H_T = 1 bit, when the RNA is equally likely to be in a free state or bound by the hub (Fig. 1E). Therefore, the biochemical meaning of this measure is straightforward and echoes the notion of the dissociation constant. Indeed, the peak of marginal entropy also tends to occur at A ≈ T/2, i.e. a protein concentration at which statistically a half of RNA molecules are expected to be bound. At lower hub concentrations the target is more likely to be free, whereas at higher concentrations it is overall more bound, both cases meaning more certainty and a correspondingly lower marginal entropy (Fig. 1D and E).

This behaviour is similar to that of a single RNA target interacting with a specific RBP, when both are present in several identical copies (Figure S2), and they actually have identical binding probability distributions (Fig. 1E, Tables S5 and S6, section 2.2). Therefore, multiple RNA targets interacting with a shared hub show a biochemical behaviour normally found in specific RNA-protein interactions (one RNA – one protein), with the difference that the key active parameter in this case is the compounded concentration of all targets T, i.e. the ensemble of the hub targets act together, contributing to its binding thermodynamics. Similar behaviour has been modelled, from biochemical mass-action equations, in other scale-free networks, e.g. regulation of multiple mRNA targets by a shared sRNA [43], [44].

As we can see from the above, information in our RNA-protein network has clearly defined physical meaning: it is directly rooted in binding statistics of RNA-protein interactions and reflects the global biochemical state of the network.

3.1.2. Targets in hub-centred networks share information only when the hub is limiting

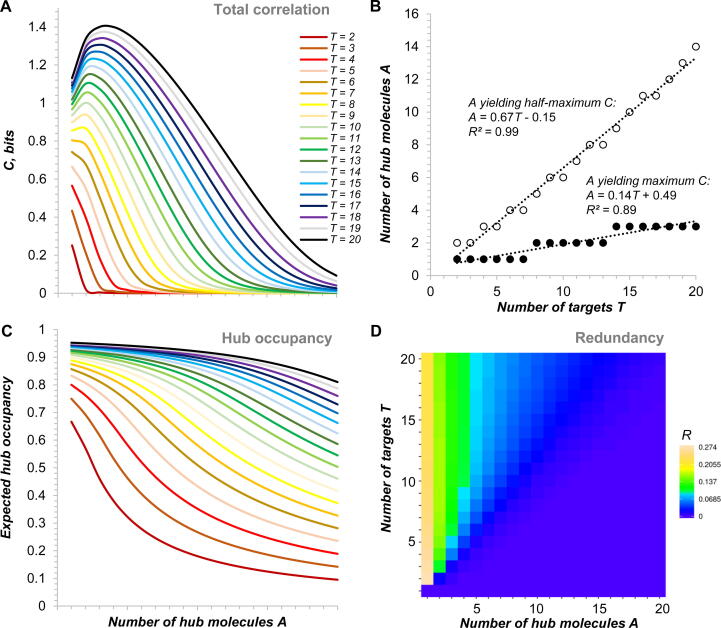
The RNA targets of the hub-centred network described above appear to behave in a concerted way. However, this does not yet mean that they actually share information with each other, since a correlated behaviour can be expected from a series of fully independent targets, provided they are biochemically similar [13]. The simplest, and most comprehensive, way to measure the strength of target “synchronisation” is calculating the total correlation in the network, which is a widely used multi-way generalisation of mutual information [38], [39]. Total correlation captures all information shared between targets, however complex it is, and, generally speaking, measures how far the studied system is from one in which all targets are statistically independent (i.e. when the status of one target does not affect the binding chances of another).

The distribution of total correlation in this hub-centred model network is shifted to the left with respect to that of joint entropy (Fig. 2A). This result is striking as it indicates that the targets of hub-centred networks do share information, but this happens nearly exclusively when the hub is maintained at a low level in comparison with the total concentration of the targets (the maximum of total correlation is attained at A ≈ 0.14 T and the half-maximum at A ≈ 0.67 T, Fig. 2B). At such stoichiometries, the hub is nearly fully occupied (Fig. 2C) whereas the targets are more likely to be unbound due to the limited availability of the hub (Fig. 1E), which exacerbates competition between them.

Fig. 2.

Total correlation and redundancy in the model hub-centred network. (A) Total correlation in the model network as a function of the number of targets T and of the hub abundance A. (B) Position of the maximum and the right half-maximum in the total correlation distribution shown in (A). (C) Expected hub occupancy as a function of T and A. (D) Redundancy in the network as a function of T and A (heat map generated in Heatmapper [94]). See Table S5 for source data.

The situation where the hub is limiting is quite common in natural RNA-protein networks: even though the overall abundance of hubs (e.g. ribosomes, Hfq, Argonaute) in the cell may be quite high, it is usually insufficient to accommodate all targets simultaneously [19], [20], [21], [22], [23]. This appears to be a desirable, selected-for property, given that special autoregulatory mechanisms are used by many hubs to restrain their own abundance [45], [46], [47]. Moreover, attempts to overexpress hubs (e.g. the bacterial RNA chaperones Hfq and ProQ) sometimes resulted in counter-productive regulatory consequences, such as disruption of hub-dependent functions and inability to complement deficient hub-mediated regulation in deletion strains [47], [48], [49]. On the other hand, at too low concentrations, the hub throughput can be insufficient to maintain its functions [23], [48], suggesting that there must be a trade-off between information sharing and the amount of regulation driven by the hub. Therefore, natural systems seem to impose a narrow bottleneck at the level of the hub pool, which may be an efficient way to enforce communication between its targets and at the same time sustain large-scale regulatory programmes [22], [24], [50]. Our finding seems to provide an information-based rationale for this important property of hub-centred RNA regulons.

Qualitatively very similar results were obtained in a rate equation-based simulation of small RNA competition over Ago [29]. The authors of that study observed that the competition (and the associated cross-regulation) gets considerably stronger at low Ago levels, especially when Ago recycling is allowed, like in our model, which agrees with experimental data [51]. This observation also parallels the findings of a ceRNA activity simulation, again based on mass-action equations: significant cross-talk between targets co-regulated by the same miRNA was only possible if the concentrations of the players were in the dynamic window allowing for significant shifts in target occupancies; essentially no cross-talk happened at saturating miRNA levels [13]. It appears that the hub bottlenecking may be a universal principle helping to drive efficient communication between targets in various types of networks.

3.1.3. Targets of small hub-centred networks share enough information to significantly influence each other’s behaviour

By comparing the scales in Fig. 2A and 1B one can immediately see that, even though total correlation increases proportionally to T, it is still much lesser than the joint entropy of targets. This means that the total amount of information shared between the targets is relatively small. This becomes particularly obvious if we consider a variant of total correlation normalised by its theoretical maximum, which provides a straightforward measure of redundancy within the system (section 2.1.3). Fig. 2D shows that redundancy reaches its maximal level (R ≈ 0.25) in the most strongly bottlenecked network (A = 1), i.e. at this architecture the targets share as much as a quarter of their information. As the hub concentration increases, redundancy monotonically decreases, and the targets progressively lose their ability to communicate via the hub. Interestingly, the more targets such a network has the overall higher and flatter its redundancy profile becomes. This indicates that by wiring even a relatively large number of targets on a well-bottlenecked hub one can achieve information sharing at a level of 5–10 % between all targets.

Although this value appears to be small, it translates into appreciable changes in target binding statistics. By analysing prior and posterior binding probabilities one can see how interaction of one target with the hub affects the binding chances of another target (Fig. 3A). In all cases, the posteriors are lesser than priors, indicating a significant deviation from independent binding statistics. This deviation is larger at lower hub concentrations and flattens at higher T (Fig. 3B), indicating progressive “dilution” of this effect as the number of competing targets increases. A similar “dilution” effect was observed in mRNA regulation by small RNAs in human cell lines [52]. Genome-wide studies of ceRNA cross-talk in human cells also found significant communication between targets only at low mRNA and miRNA levels, provided the binding is strong [53].

Fig. 3.

Communication between targets in the model hub-centred network is translated in significant shits in their binding probabilities. (A) Relationship between prior and posterior binding probabilities of targets showing how binding of one target changes the binding chances of another. The dotted black line shows the expectation for a fully independent binding. (B) Same as in (A) recast as a change in binding probability upon binding of one target molecule, as a function of the number of targets T and of the hub abundance A. (C, D) npmi for ‘co-bound’ and “anti-bound’ configurations of two targets as a function of T and A. (E) Proportion of the higher-order, multivariate MI (as opposed to pairwise, bivariate MI) in total correlation as a function of T and A (heat map generated in Heatmapper [94]). (F) Example of total correlation parsing for T = 10. See Table S5 for source data.

Thus, targets interacting with a shared hub antagonise each other, and the binding of one can decrease the binding probability of another by 0.05–0.1, at limiting hub concentrations and a relatively small number of targets. In information theory, this relationship is best formalised in the notion of pointwise mutual information (section 2.1.5), and especially its normalised variant (npmi) which ranges from −1 (perfect anti-correlation) to + 1 (perfect co-occurrence). npmi compares joint and marginal probabilities of an event (e.g. binding to the hub) and thereby assesses the strength and the sign of statistical dependency between two variables [40], [41]. In this model network, the npmi for two simultaneously bound targets (i.e. the strength of co-occurrence of binding events, ${\mathit{npmi}}_{\mathrm{1,1}}^{\mathit{T-T}}$) is always negative (Fig. 3C). So is the npmi for the two simultaneously unbound targets (${\mathit{npmi}}_{\mathrm{0,0}}^{\mathit{T-T}}$, Fig. S3A), meaning that two targets avoid to be in the same state. This statistical repulsion reflects competition between the targets for the limited resource (the hub) and is particularly strong at low hub concentrations or at higher numbers of competing targets. By contrast, the npmi for two targets occupying opposite states (one bound and the other free) is positive (${\mathit{npmi}}_{\mathrm{1,0}}^{\mathit{T-T}}$ Fig. 3D), i.e. targets interacting with a shared hub tend to occur in opposite states more often than expected under independent binding.

All in all, we conclude that the seemingly small amount of information shared between targets in hub-centred networks translates into noticeable shifts in their binding probabilities, especially when the hub is limiting and the number of targets is not too high.

3.1.4. Bottlenecked hub-centred networks have richer mutual information

We wondered whether the targets of this model network statistically interact only in a pairwise manner or engage in more complex relationships. As mentioned above, total correlation covers all kinds of information shared between targets (two-way, three-way etc), and by parsing it into components one can compare their relative contributions. Complete parsing of total correlation is complicated [38], [39] and beyond the scope of this study. However, one can easily compare total correlation with two-way (or bivariate) mutual information (MI), which measures the amount of information shared between any two targets and is directly calculated from the state probabilities (Fig. S3B, section 2.1.4). Fig. 3E, F shows that the part of total correlation contributed by higher-order, multivariate mutual information (i.e. more complex than the elementary-two-way MI) increases with the number of targets T and prevails at low hub levels, typically contributing more than a half of all shared information. As the hub abundance grows, this part decreases – the mutual information gets simpler. Therefore, at limiting hub concentrations, targets of hub-centred networks share more complex, higher-order information. Biochemically, this means that targets interact in more intertwined ways.

3.2. Effect of target overexpression

The many ligands of a hub are seldom present at the same concentration in the cell. Their expression levels are differentially sculpted by transcription and RNA stability. In especially striking cases, targets respond to external stimuli, leading to a spike in their concentration, as it happens, for instance, with some Hfq-dependent sRNAs [54], [55]. A similar scenario is produced artificially by forced overexpression of a target from a transgene or by transfection with RNA [19], [20], [22], [23], [27]. To understand how such a disproportional increase in the abundance of one target affects the information properties of hub-centred networks, we considered a system containing T = 9 distinct regular targets, each present in one copy, and 1 ≤ A ≤ 20 identical hub molecules, as above. But this time we introduced one more target, the level of which is varied in the range of 1 ≤ Q ≤ 10 identical copies (Fig. 4A; see section 2.3 for a generalised description and analysis of this set-up). With the exception of the higher abundance, this overexpressed target does not differ from the other, regular ones and has the same chances to interact with the hub (Fig. S4A).

3.2.1. Target overexpression changes the information structure of the network

As expected, with increasing Q, the regular targets get progressively evicted from the hub (Fig. 4B), whereas the binding of the overexpressed target augments (Fig. 4C) – the unusually abundant target titrates the hub out at the expense of the rest of the network, in agreement with experimental observations [20], [23], [27]. How does it affect the information properties of the system?

The marginal entropy of regular targets responds to the introduction of new RNA molecules similarly to the previous model (compare Fig. 4D and 1D): its distribution is again bell-shaped and peaks at a hub concentration roughly equal to a half of the compounded concentration of targets (Fig. S4B). By contrast, the marginal entropy of the overexpressed target evolves rather rapidly and expansively (Fig. 4E). As the number of the Q-target molecules spiked into the system grows, its marginal entropy increases and its distribution broadens dramatically, with the peak shifting to the right proportionally to A ≈ 0.74Q (i.e. faster than for regular targets, A ≈ 0.48Q, Fig. S4B). This behaviour foretells an ever-increasing contribution of the overexpressed target to the information structure and content of this hub-centred network. Indeed, as new copies of the overexpressed targets get added, the maximum of joint entropy shifts to the right slightly faster, in comparison to the previous model, proportionally to A ≈ 0.58·(T + Q) (Fig. 4F and S4C). However, its amplitude barely changes, since the added Q-target molecules are identical and do not contribute new variables, only introducing more “nuances” in an already existing one (compare Fig. 4F, 1B and S2). Correspondingly, total correlation C in this network shows a steady growth along with Q, confirming the intuition that the system is getting increasingly more redundant with every new added molecule of the overexpressed target (Fig. S4D and E). Importantly, the total correlation is again largely confined to the area where the hub is limiting (compare Fig. S4D and 2A). This indicates that the condition of the “bottlenecked” hub remains valid in hub-centred networks with an arbitrary number and identity of RNA targets: targets share information only when the hub is limiting.

3.2.2. Overexpression of one target disrupts information sharing between the other ones

The progressive increase of total correlation indicates more communication between targets, but it does not tell between which ones. To understand the effect of target overexpression on the information flow between targets, one needs to parse the total correlation into more elementary components. There are two kinds of pairwise MI in this network: between two regular targets (I_T-T) and between a regular and the overexpressed target (I_T-Q, Fig. 5A). Both MIs are expectedly maximised at low hub concentration but respond very differently to target overexpression (Fig. 5B and C). While I_T-Q rapidly increases, indicating the growing influence of the overexpressed target on the regular ones, I_T-T globally decreases and flattens. The latter phenomenon indicates that the regular targets lose communication between each other and progressively align with the dominant, overexpressed target. (This does not mean that binding of one molecule of the overexpressed target has a stronger effect on the binding probability of a regular target: these probability shifts remain identical between any kind of competing target molecules since all of them are considered biochemically equivalent – see Fig. S4A, F. However, the molecules of the overexpressed target interact with the hub more often due to their higher abundance, hence their stronger impact on the regular targets.) Globally, the proportion of pairwise MI between regular targets in total correlation shrinks, whereas that of MI with the overexpressed target increases (Fig. 5D and E). Higher-order mutual information remains confined to the low hub concentration range, as previously (Fig. 5F).

Fig. 5.

Mutual information in the model hub-centred network with an overexpressed target. (A) Diagram showing the two types of pairwise MI existing in this network. The grey node depicts the overexpressed target. (B, C) Mutual information between two regular targets (B) or between a regular and the overexpressed targets (C) as a function of the overexpression level Q and the hub abundance A. (D, E) Proportion of total correlation accounted for by bivariate MI of each type. (F) Proportion of higher-order, multivariate MI in total correlation as a function of Q and A. See Table S7 for source data.

We conclude that selective overexpression of one target disrupts information sharing between the remaining targets (at least, at the level of bivariate MI). This result echoes in vivo observations, e.g. the negative effect of sRNA overexpression on global Hfq-mediated regulation [22], [23], [27] or the deleterious impact of siRNA transfection or shRNA overexpression on endogenous RNAi circuitry [20], [56]. The already mentioned simulation study of small RNA competition for Ago made a strikingly similar observation. While the overexpressed miRNA exerted very consistent regulation on the ensemble of its target mRNAs, the remaining, “regular” miRNAs showed more disparate regulatory outcomes, suggesting a weaker coordination [29].

3.2.3. Hub titration and hub sequestration are two distinct scenarios

It is common in molecular biology literature to confuse titration mechanisms with true sequestration. Yet, from the biochemical point of view they are different. A hub is titrated out upon overexpression of one of its targets, which in terms of affinity is on the same foot with other targets, its unique advantage being an unusually high abundance (Fig. 4A). This is fair competition for the hub: exchanges with other targets are still possible, albeit they get increasingly less likely in steady state as the concentration of the overexpressed target grows (see above). As examples of such mechanisms one could mention the induction of the Hfq-dependent sRNA OxyS upon oxidative stress in E. coli [54] and the accumulation of the CsrA-titrating decoy mRNA fimAICDHF involved in the hierarchical control of fimbriae expression in Salmonella Typhimurium [57]. By contrast, true sequestration is operated by high-affinity ligands, which often show avidity for the hub due to several cooperatively acting binding sites. Such molecular sponges effectively remove hub molecules from circulation with little possibility of exchange (Fig. 6A), and in many cases the only efficient way to release the captured hub is to degrade the sponge altogether [58], [59], [60]. Examples of such regulators include bacterial CsrA/RsmA-sequestering sRNAs [26], [59], [61], the Pseudomonas Hfq-sponging sRNA CsrZ [25], [62], and the lncRNA NORAD sequestering human PUMILIO proteins [63], [64], [65].

Fig. 6.

Target overexpression and hub sequestration have different effects on the information properties of hub-centred networks. (A) Variant of the hub-centred network shown in Fig. 4A, where the overexpressed target is replaced by a true sponge, present in Q copies which stably bind and exclude from competition Q molecules of the hub. (B) Joint entropy distribution of the unperturbed system (Q = 0) showing three regions of interest: one where the target crosstalk is the strongest (low A), the entropy peak (average A), and the saturation zone (high A). (C) Evolution of joint entropy, npmi for co-bound states, and MI as a function of the abundance of the overexpressed target (blue lines) or the hub-sequestering sponge (red lines) at three hub regimes shown in (B). See Table S7 for source data. (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)

We compared how the information properties of our model network (T = 9) change in response to target overexpression (sections 3.2.1 and 3.2.2) and to genuine hub sequestration (i.e. when hub molecules are effectively removed from the system). To this end, we assessed the effect of introducing 0 ≤ Q ≤ 10 overexpressed target molecules (as in Fig. 4A) or sponge molecules (as in Fig. 6A) at three different hub levels: A = 3 (where communication between targets is most efficient), A = 6 (entropy peak), and A = 15 (where the targets are saturated and share little information, Fig. 6B).

As expected, the two scenarios perform similarly at A = 15, where targets practically do not communicate (Fig. 6C, right column). By contrast, at A = 3 and A = 6, where the targets enter their dynamic range of binding, hub sequestration produces neatly different effects (Fig. 6C, left and central columns). The joint entropy of the network changes little upon target overexpression (Fig. 4F). By contrast, hub sequestration results in a rapid Ĥ decrease, indicating less uncertainty about the system configuration and an overall lower information content (Fig. 6C, upper row). Analysis of coincident interactions of two regular targets by npmi indicates that overexpression has little effect on the co-occurrence of binding events (Fig. 6C, middle row). Hub sequestration, on the contrary, triggers potent statistical repulsion between targets, exacerbating competition between them. This is further reflected at the level of MI (Fig. 6C, lower row). As shown in section 3.2.2, overexpression progressively lowers I_T-T, indicating disruption of information sharing between targets. By contrast, sequestration boosts communication between targets: I_T-T increases sharply with every sequestered hub molecule.

We conclude that hub sequestration likely plays an important role in enforcing cross-communication between targets in hub-centred networks, which may explain the ubiquity of this mechanism in nature. By contrast, target overexpression is mildly deleterious to the information flow in the rest of the network and, in extreme cases, may completely “desynchronise” the other targets.

3.3. Competitive target regulation by two hubs

Situations where several RNA-binding hubs have overlapping regulons are widespread [1], [66]. Binding of shared targets by several RBPs can be competitive or involve various forms of cooperation [7], [18], [67], [68]. This permits to considerably extend post-transcriptional regulatory networks and combinatorially generate more complex regulatory outputs [69], [70], [71], [72]. We wondered what happens with information flow in such networks and how target sharing affects communication between RNAs in multi-hub systems.

To this end, we considered a network consisting of 10 targets, each present in one copy, and of two distinct hubs, each present in 1 ≤ A ≤ 20 copies (Fig. 7A). The targets are of three different kinds: two groups of exclusive targets, interacting with only one specific hub, and one group of shared targets, which can interact with either hub. For simplicity, we again consider that all targets have inherently the same chances to bind their cognate hubs. Only one hub molecule at a time can bind to a target, meaning that the interaction is strictly competitive. We will also restrict our analysis to symmetrical architectures, where each hub is present in A copies, has the same number of T exclusive targets, and shares S targets with the other hub, such that 2 T + S = 10. By varying 0 ≤ T ≤ 5 and 0 ≤ S ≤ 10 we can survey all topologies – from the complete separation of the interactomes (T = 5, S = 0) to their full merging into a perfect bifan (T = 0, S = 10, Fig. 7B). The resulting networks have an invariant number of components and solely differ by their wiring (see section 2.4 for a complete treatment of a generalised model of a two-hub network).

3.3.1. General information structure in two-hub RNA networks

As the regulons of the two hubs progressively merge, the hub occupancy by exclusive targets decreases and that by shared targets increases, as expected (Fig. 7C and D). However, the binding probabilities and the marginal entropies of targets suffer only subtle right shifts (Fig. 5, Fig. 7E, F). In previous models, such shifts were associated with an increase in the overall number of target molecules in the system (Fig. 1D, E, 4D, E, S2B, and S4A). Therefore, it appears that merging the interactomes of the two hubs is perceived by the latter as an effective increase in target concentration, which is biochemically meaningful. However, this effect remains modest.

The marginal entropies of the two kinds of targets are very different (Fig. 7E and F). Whereas exclusive targets keep the canonical bell shape with both sides low, the shared targets are overall higher in entropy (due to the possibility of binding to two different hubs) and the right side of the H_S distribution dwells at much higher a level. This means that, at high abundances of both hubs, the binding status of the shared targets is extremely uncertain: it can be bound by either protein. Obviously, if the hub A and the hub B have very different biological properties and functions, such an uncertainty presents a major liability in the network, meaning that the state of the shared target is not really under control.

Logically, as the size of the overlap between the two interactomes increases, the joint entropy of the targets grows and progressively shifts from a purely “exclusive” pattern to the purely “shared” one (Fig. 7G). Therefore, the extent to which the two hubs share their targets dramatically influences the information content of the network and presents significant regulatory challenges, especially at high hub levels. The definition of the status of individual targets becomes increasingly difficult, and the interpretation of the regulatory information flowing in the network subject to much uncertainty.

3.3.2. Target sharing creates new kinds of communication between targets and hubs

We wondered how exactly the information flows in these two-hub networks. Total correlation and redundancy in the system expectedly increase as the overlap between the regulons gets larger (Fig. 8A and B). Interestingly, comparing the C and R distributions with those in the first, one-hub model (section 3.1.2), one can see that wiring on two hubs enables overall more information sharing between the same number of targets. This cross-communication is again strictly confined to limiting hub levels.

But what does exactly communicate in this network? The three groups of targets imply-six kinds of MI (see section 2.4.4 for details). Five of them are proximal and involve targets wired directly on a shared hub (path length ℓ = 2); one is distal and connects exclusive targets of different hubs (ℓ = 4; Fig. 8C). Interestingly, the values of proximal MI, whatever the interacting targets, are roughly similar and decrease as the overlap between the two interactomes increases (Fig. 8D-F). This means that merging the two regulons somewhat weakens communication between proximal nodes (ℓ = 2).

These changes are not only quantitative but also qualitative. While analysis of the npmi distributions reveals canonical patterns in the case of two exclusive targets interacting with the same hub (Figure S6), new interesting features emerge when a shared target gets implicated (Fig. 9). Co-unbound states and those co-bound by the same hub show statistical repulsion due to competition, as expected (Fig. 9A, B, D, E). By contrast, co-bound states involving two different hubs have a substantial positive npmi, indicating a statistical attraction of such co-occurrences, certainly due to the associated relief of competition between the shared targets (Fig. 9C and F). This positive npmi betrays new kinds of competitive crosstalk arising between the two hubs (ℓ = 2) and between an exclusive target and a non-cognate hub (ℓ = 3, Fig. 8C). (Precisely addressing the MI types involving hubs – labelled as I_A-B, I_TA-B and I_TB-A in Fig. 8C – is mathematically straightforward but computationally difficult due to a very large number of state combinations. We will content ourselves by simply stating here that such relationships do exist and appear to be strongest when the overlap between two regulons is small, as follows from the npmi analysis.).

Fig. 9.

Positive interactions between proximal targets interacting with different hubs. (A-C) npmi for different combinations of binding statuses of two shared targets, as a function of the overlap between the interactomes S and the hub abundance A. When two shared targets are bound by different hubs, npmi becomes positive, indicating statistical attraction (C). (D-F) npmi for different combinations of binding statuses of one exclusive and one shared targets, as a function of S and A. When the two targets interact with different hubs, npmi is again positive (F). See Table S8 for source data.

3.3.3. Long-range information flow in two-hub RNA networks

An even more intriguing kind of distal communication emerges between two exclusive targets binding to different hubs (Fig. 10A, I_TA-TB in Fig. 8C). Although it is much weaker than proximal interactions, its strength increases as the two interactomes merge. Qualitatively, this interaction resembles that between two exclusive targets of the same hub: the npmi for analogous states is strictly negative, whereas that for opposite states is positive (Fig. 10B-D). Therefore, these targets behave as if they directly competed with each other, but in a considerably weaker manner. Analogous distant interactions have been described for miRNA-mRNA regulation and may in principle enable information propagation in other types of networks too [15], [73], [74].

Fig. 10.

Long-range interactions between targets in the model two-hub network. (A) Pairwise mutual information between two exclusive targets interacting with different hubs, as a function of the interactome overlap S and the abundance of the hubs A. (B-D) npmi for the corresponding configurations. (E, F) Information flow, at two different hub abundances (A = 2 or A = 4), in the two-hub network, where an exclusive target interacting with the hub A is the source and another exclusive target interacting with the hub B is the ultimate receiver (via both hubs and the shared targets). The information content of the source node is its marginal entropy H_T. The amount of transmitted information is measured by the corresponding MI (I_TA-S for ℓ = 2 and I_TA-TB for ℓ = 4). See Table S8 for source data.

Information transmission along the network, from one node to another, is typically described in terms of communication channel capacity, which is none else as the MI between the source and the receiver nodes [37], [75]. We wondered how much information actually makes it to ever more distant nodes along our model two-hub network. This question can now be explicitly answered (Fig. 10E, F). We will start with the marginal entropy of a selected source node (e.g. one of the exclusive targets of the hub A, H_T), which, at relevant hub concentrations, is usually close to 1 bit (Fig. 7E). The MI between this node and one of shared targets I_TA-S measures the maximal amount of information which can be transmitted over ℓ = 2 through the hub A (keeping in mind the potentially noisy channel). I_TA-S is fairly small, on the order of 0.01–0.015 bits (Fig. 8F). However, we have already shown that this must be sufficient to produce some mild but significant shifts in target binding probabilities in relatively small networks (Fig. 3B and S3B). Moving further, the MI between the exclusive targets interacting with different hubs I_TA-TB measures how much information from the source node can at best reach this most remote node in our network (ℓ = 4) over the two hubs and all of the shared targets. I_TA-TB is tiny, on the order of 0.0005–0.001 bits (Fig. 10A). It certainly cannot significantly affect the distal target. However, it steadily increases with S, indicating that the channel capacity between the two hubs critically contributes to the “conductivity” of the network, and if the overlap between their interactomes is large enough, distal communication between targets may attain noticeable levels. Indeed, information quenching along the network is roughly exponential, with barely 1–2 % of information reaching over ℓ = 2 from the source. However, at S = 8 and A = 4, as much as 1/6 of the ℓ = 2 level information is transmitted to the ℓ = 4 level, indicating a significant deviation from the exponential law under certain conditions (Fig. 10E and F). These results are qualitatively similar to mass-action simulations and experimental data describing the mRNA-miRNA crosstalk, which also revealed an exponential correlation propagation pattern and highlighted the importance of the ℓ = 3 level capacity in network “conductivity” [73].

Overall, our analysis of the two-hub system shows that regulons of competing hubs are subject to several opposed factors. Extensive merging of hub regulons permits efficient distant communication between targets (i.e. information flow through the network). But it is also associated with regulatory challenges, yielding a high-entropy, largely unpredictable system. On the other hand, small overlaps between regulons (e.g. S = 2 in our model) create ground for new unusual kinds of middle-to-distant communication between targets and hubs, with potentially interesting biochemical effects. It appears that, while combinatorial RNA regulation by multiple RBPs is widespread, natural systems tend to avoid large overlaps between regulons controlled by potentially competing hubs [1], [68], [69], [72], [76], [77].

4. Conclusions

We have introduced an information theory-based framework to comprehensively and exactly analyse competitive modes of communication in hub centred-networks with an arbitrary number of targets. It was possible, using relatively simple model systems, to uncover some recurrent themes and universal constraints such as the requirement of limiting hub levels and of a relatively low number of targets for an efficient cross-communication between them. This communication may have negative and, in the case of multi-hub networks, positive components and enable mild but significant changes in the binding probabilities of targets. Overexpression of individual targets usurps the information flow in the network and evicts the remaining targets from information exchange. By contrast, hub sequestration has a strong potential to stimulate communication between targets but at a cost of an overall lower functional throughput. Finally, we found that competitive regulatory overlaps between two hubs generate unique trade-offs between the system complexity, the control over the status of individual targets, and the ability to propagate information to distant nodes.

Placing our conclusions in a more general context of regulatory logic, we can see that only individual targets have entropies on the order of 1 bit, which is assumed to be the minimal amount of information required to operate simple ON/OFF switch circuits [75]. The amount of information that targets can transmit via hubs to neighbour nodes decreases exponentially and only permits subtle changes in their biochemical behaviour. On the other hand, the overall amount of shared information in our model networks (total correlation) is also on the order of bits, suggesting that a network as a whole has the potential to produce meaningful global logical responses to external cues. However, whether and how this information can be exploited by the cell remains unclear.

It is striking that our model, which is based exclusively on a stoichiometric relationship between RNA targets and their hubs, predicts many salient phenomena observed in complex mass-action-based models and experimental data. The high importance of stoichiometricity in target crosstalk has been often emphasised in previous works [10], [13], [73]. Although our model does not explicitly implement affinity, a nominal bulk dissociation constant can be calculated from target and hub binding probabilities and abundances, e.g. for the first model (section 2.1.2):

$$K_d=\frac{p_0{p}_0^{\mathit{Hub}}A}{p_1}=\frac{p_0{p}_0^{\mathit{Hub}}T}{p_1^{\mathit{Hub}}}$$

Table S5 indicates that in all cases K_d < 1, meaning that both the targets and the hubs operate at saturating concentrations and under a tight binding regime, as in natural systems [78], [79], but their free concentrations have the possibility to drop below K_d, which is a theoretical prerequisite for the observation of competitive communication between molecules [10]. In future, explicitly incorporating differential affinity (in a broad sense) in our model, e.g. by weighting states, may help to account for subtler competition effects and target hierarchy [23], [24], [80], [81].

The models introduced in this paper are relatively simple as they involve strictly competitive binding and mostly dichotomous outcomes (‘bound’ – ‘unbound’), which was necessary to demonstrate that our information approach is viable and produces biologically meaningful results. Real-life RNA-binding strategies, while based on the same fundamental principles, have many more facets and nuances, sometimes resulting in behaviour significantly deviating from the one described here [3]. For example, many RBPs, such as Hfq, possess multiple RNA-binding sites, which enable them to exploit semi-competitive, or even non-competitive, interactions with more than one transcript at a time, with different functional outcomes [50], [81], [82], [83]. Several RBPs can additively or cooperatively interact with one RNA, with a wide variety of consequences: from ‘silent’ binding, which only titrates an RBP out without affecting the target, to complex synergistic outputs, which cannot be achieved through isolated binding by individual RBPs [1], [18], [67], [84], [85], [86], [87], [88], [89], [90]. In a more complex, non-equilibrium in cellulo context, RBP binding may change the localisation or induce the rapid turnover of target RNAs, which would drastically affect their chances to interact – and share information – with other participants of the network [87], [88], [89], [91], [92], [93]. Modelling such ‘rich’ regulatory scenarios, albeit challenging, could provide unique insights into the post-transcriptional information flow in genetic systems.

CRediT authorship contribution statement

Alexandre Smirnov: Conceptualization, Data curation, Formal analysis, Funding acquisition, Investigation, Methodology, Project administration, Resources, Supervision, Validation, Visualization, Writing – original draft, Writing – review & editing.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Appendix A. Supplementary data

The following are the Supplementary data to this article: