Mathematical modeling of vaccination as a control measure of stress to fight COVID-19 infections

Abstract

The world experienced the life-threatening COVID-19 disease worldwide since its inversion. The whole world experienced difficult moments during the COVID-19 period, whereby most individual lives were affected by the disease socially and economically. The disease caused millions of illnesses and hundreds of thousands of deaths worldwide. To fight and control the COVID-19 disease intensity, mathematical modeling was an essential tool used to determine the potentiality and seriousness of the disease. Due to the effects of the COVID-19 disease, scientists observed that vaccination was the main option to fight against the disease for the betterment of human lives and the world economy. Unvaccinated individuals are more stressed with the disease, hence their body’s immune system are affected by the disease. In this study, the $SVEIHR$ deterministic model of COVID-19 with six compartments was proposed and analyzed. Analytically, the next-generation matrix method was used to determine the basic reproduction number ($R_0$). Detailed stability analysis of the no-disease equilibrium ($E_0$) of the proposed model to observe the dynamics of the system was carried out and the results showed that $E_0$ is stable if $R_0<1$ and unstable when $R_0>1$. The Bayesian Markov Chain Monte Carlo (MCMC) method for the parameter identifiability was discussed. Moreover, the sensitivity analysis of $R_0$ showed that vaccination was an essential method to control the disease. With the presence of a vaccine in our $SVEIHR$ model, the results showed that $R_0=0.208$, which means COVID-19 is fading out of the community and hence minimizes the transmission. Moreover, in the absence of a vaccine in our model, $R_0=1.7214$, which means the disease is in the community and spread very fast. The numerical simulations demonstrated the importance of the proposed model because the numerical results agree with the sensitivity results of the system. The numerical simulations also focused on preventing the disease to spread in the community.

1. Introduction

COVID-19 disease pandemic brought the world to its knees during its inversion. A coronavirus is a member of CORONAVIRIDAE which causes respiratory or gastrointestinal disease in a variety of vertebrates [1]. The world experienced hard times when the disease started to spread worldwide in early 2020 after its origin in Wuhan, China, in December 2019 [2]. The disease caused millions of illness and a hundred thousands of deaths within a short time worldwide which causes tension all over the world. The disease fighting strategies were introduced at the time by the World Health Organization (WHO) to fight against the pandemic to save human lives. The strategic measures are such as quarantine, social and physical distancing, mask-wearing, closing borders, and economic lock-downs. The measures taken affected the world socially and economically. To fight against COVID-19 disease, the best strategy is vaccination which helps the world to raise the lost economy [3], [4], [5]. Different types of vaccines were discovered by the scientists to fight the disease and authorized by the WHO [6]. The study carried out by [7] discussed vaccination in age group allocation strategies with their $SEIR$ model in India and came out with the results showing that the most group considered for vaccination was the older population aged $>60$ years, which was the most affected group by COVID-19 disease. Moreover, [8] discussed an age-structured model with time-varying contact rates.

Mathematical models are very essential tools used to determine the potential and seriousness of the disease and help in identifying the intervention measures to be taken to fight and control the disease intensity as presented in the study of [9], [10]. Alcohol consumption, which plays a fundamental role in depression, shows that mathematical models are very powerful tools to investigate an infectious disease more accurately [11]. From the beginning of the COVID-19 epidemic, a variety of mathematical models have been constructed.

Vaccination is the most significant component in disease prevention strategies globally [12], [13]. The $SIR$ epidemic model developed and discussed the effectiveness of the vaccine based on its ability to reduce transmission from infected individuals to the uninfected individuals and the community at large [14]. Vaccination restricts an infectious disease to spread by limiting the number of individuals to whom the infection can be transmitted [15].

There are various ways discussed in [6] which were used to fight the disease, and showed that vaccine was the most significant method used to fight COVID-19 disease although it took less than a year to be applicable and approved by WHO ready for human use. The impact of vaccine due to age groups and season was also discussed in [16], [17] in which they found that the impact depends on the timing of the doses by considering the type of the wave to boost the human body immune system. Vaccine is the most important measure to fight COVID-19 disease because it brings encouragement to people and adds the power to their immune systems as presented by [18] in their study of modeling vaccination strategy in which encouraged the WHO to prioritize vaccination in all countries. Vaccination brought a new hope among the population where fear minimized and human bodies started to build strong immunity and fought back the COVID-19 disease. In the study of COVID-19 vaccination and mental health to alleviate the psychological distress of individuals vaccinated against COVID-19 disease whereby before vaccination mental health problems were increased [19]. A mathematical model developed on timing the race of vaccination and observed that vaccination is essential as their results showed that it reduces 30% of deaths in German and 50% in Brazil [20].

This study aims to add a vaccination compartment to the epidemic model $SEQIHR$ [21], and obtain a new deterministic model with vaccination compartment, $SVEIHR$. The new model aims to investigate the effects of vaccination in reducing stress among the population, which will help them to build strong immune systems. The new formulated model consists of six compartmental classes (Susceptible, Vaccinated, Exposed, Infected, Hospitalized, and Recovered).

Section 1 contains the introduction to this work. Section 2 presents the model formulation, as well as its compartments and their descriptions. Model properties are discussed in Section 3. Stability analysis is discussed in Section 4. Numerical simulations are discussed in Section 5. Parameter identifiability using the MCMC method is discussed in Section 6. Section 7 is the conclusion of this work and potential extensions of this model are discussed.

2. Formulation of the model

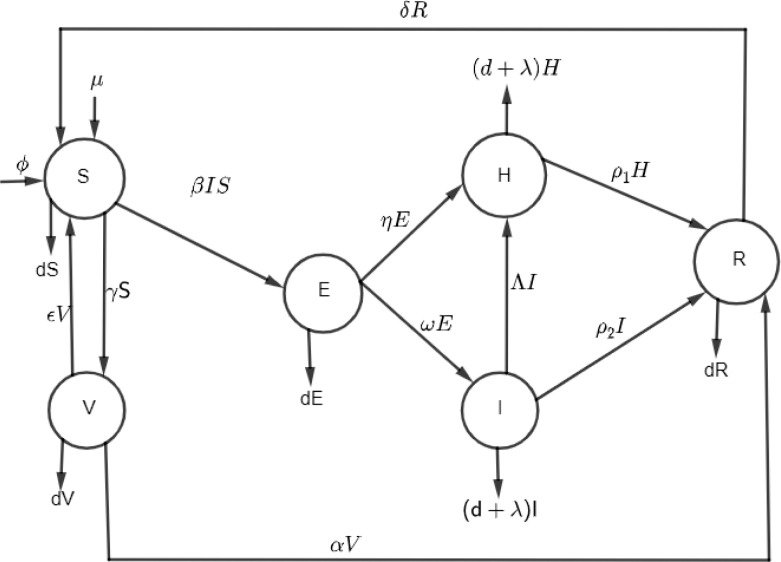
In this study, a deterministic model $SVEHIR$ was formulated to study the transmission dynamics of COVID-19 disease in a human population. The transmission of COVID-19 disease is direct or indirect contact with infected individual or infected place through touching. In this model, the human population is classified into six subpopulations; susceptible human (S), vaccinated human (V), exposed human (E), infected human (I), hospitalized human (H), and recovered human (R). Fig. 1 is considered that the susceptible population increases due to the recruitment rate $\mu$, individuals from infected countries, and the recovered individuals can lose their natural immunity and send back to the susceptible compartment at a rate $\delta$ and then the susceptible decreases due to the movement of individuals to the vaccinated compartment and natural death rate $d$. Where $\beta$ and $\gamma$ are the transmission rates from the susceptible class to the exposed and vaccination classes, respectively. The vaccinated population decreases due to the individual moving to the recovered class and natural death $d$ of individuals. If the vaccine is 100% effective, the vaccinated individuals may contact the disease but will not experience disease consequences. The exposed human population class decreases due to natural mortality rate $d$ and due to transfer of portions of exposed human into hospitalized and infected compartments at a rate of $\eta$ and $\omega$, respectively. The infected class increased due to the infected individuals, $\omega$ from exposed class and then decreases to hospitalized class ($\Lambda$), recovered class (${\rho }_2$), and diminished by the leaving rates (natural death $d$, and death due to disease $\lambda$). The hospitalized class is increased by the population from exposed, infected classes by $\eta$ and $\Lambda$, respectively, and then decreases by the recovered individuals ${\rho }_1$ and the leaving rates (natural death $d$, and death due to disease $\lambda$). The recovered class increases by individuals from hospitalized class ${\rho }_1$ and vaccinated class $\alpha$, and then decreases by the individuals going back to the susceptible class at the rate $\delta$ and then diminished at the rate of natural death $d$.

Fig. 1.

Compartmental model of COVID-19 dynamics.

Model assumptions

The formulated model has the following assumptions:

• (i)Immigrants from other countries are taken straight to the susceptible class.
• (ii)Equal natural death rate for all compartments.
• (iii)Only infected and hospitalized individuals are at risk of dying from COVID-19 disease.
• (iv)Recruitment rate is assumed to be susceptible.
• (v)Vaccinated individuals have an equal chance to be infected when coming into contact.
• (vi)Vaccinated individual will either recover or die regardless of treatment failure.
• (vii)Recruitment and leaving rates differ, then the population differs at a given time.
• (viii)Vaccination is assumed to be effective 100%.

Dynamics and model compartments

The model assumptions with variable and parameter descriptions are presented in Fig. 1.

The total population for the six subpopulations is presented by $N$ as shown in Table 1. when $t$ $>$ 0, the total population $N\left(t\right)$ as described in Table 1 is given by:

$$N\left(t\right)=S\left(t\right)+V\left(t\right)+E\left(t\right)+I\left(t\right)+H\left(t\right)+R\left(t\right)$$ (1)

Table 1.

Compartmental variables description.

Variable	Description
$S\left(t\right)$	The number of susceptible individuals at time $t$
$V\left(t\right)$	The number of vaccinated individuals at time $t$
$E\left(t\right)$	The number of exposed individuals at time $t$
$I\left(t\right)$	The number of infectious individuals at time $t$
$H\left(t\right)$	The number of hospitalized individuals at time $t$
$R\left(t\right)$	The number of recovered individuals at time $t$

Fig. 1, the parameter descriptions are presented in Table 2.

Table 2.

Description of the $SVEIHR$ model parameters.

Parameter	Description
$\beta$	Contact rate
$\mu$	Recruitment rate
$d$	Natural death rate
$\lambda$	Death rate due to the disease
$\varphi$	Susceptible individuals from infected nations
$\gamma$	Rate of Vaccinated individuals from susceptible class
$ϵ$	Rate of Vaccinated individuals to susceptible class
$\alpha$	Rate of recovered individuals from vaccinated class
$\eta$	Hospitalized individuals from exposed class
$\omega$	Rate of infected individuals from exposed class
${\rho }_1$	Recovered individuals from hospitalized class
${\rho }_2$	Recovered individuals rate from infected class
$\Lambda$	Hospitalized individuals from infected class
$\delta$	The recovered individuals rate moving back to susceptible

Model equations

The system of six ordinary differential equations was built by evaluating the model assumptions:

$$\frac{dS}{dt}=\mu +\varphi +\delta R+ϵV-(\beta I+\gamma +d)S,$$$$\frac{dV}{dt}=\gamma S-(ϵ+\alpha +d)V,$$$$\frac{dE}{dt}=\beta IS-(\eta +\omega +d)E,$$$$\frac{dI}{dt}=\omega E-(\Lambda +{\rho }_2+d+\lambda )I,$$$$\frac{dH}{dt}=\eta E+\Lambda I-({\rho }_1+d+\lambda )H,$$$$\frac{dR}{dt}={\rho }_{1}H+{\rho }_{2}I+\alpha V-(\delta +d)R.$$ (2)

3. The model properties

The two model properties positivity and bounded region are to be discussed under this section.

3.1. Positivity analysis for the proposed model

For the model (2) it is important to show that all state variables are non-negative so as to be epidemiologically meaningful $\forall t>0$. Consider Theorem 3.1.

Theorem 3.1

If the initial values of $(S,V,E,I,H,R)>0$ are positive, then the solutions $(S,V,E,I,H,R)\left(t\right)$ of the model (2) are positive $\forall t>0$ .

Proof

Let $(S,V,E,I,H,R)>0$. For the first equation in system (2)

$$\frac{dS}{dt}=\mu +\varphi +\delta R+ϵV-(\beta I+\gamma +d)S.$$ (3)

To consider the negative term and ignore the remaining

$$\frac{dS}{dt}\ge -(\beta I+\gamma +d)S.$$

The resultant equation is a first-order differential equation that can be solved by using a separable technique.

$$y^{\prime }=f\left(x\right)\times g\left(y\right)$$ (4)

where $S\ge 0$.

$${\int }_{S\left(0\right)}^{S\left(t\right)}\frac{dS}{S}\ge -{\int }_0^t(\beta I+\gamma +d)dt,$$

$$⟹S\left(t\right)\ge S\left(0\right)e^{-(\beta I+\gamma +d)t},$$

at no-disease,

$$S\left(t\right)\ge S\left(0\right)e^{-(\gamma +d)t},\text{where}S\left(0\right)\ge 0,\forall t>0.$$

The remaining equations solved by the same method: $V\left(0\right)\ge 0$, $E\left(0\right)\ge 0$, $I\left(0\right)\ge 0$, $H\left(0\right)\ge 0$, $R\left(0\right)\ge 0$. Then the solutions $S\left(t\right),V\left(t\right),E\left(t\right),I\left(t\right),H\left(t\right),R\left(t\right)$ of the model are positive $\forall t>0$. □

3.2. Bounded region for the proposed model

The region obtained by considering the following theorem.

Lemma 1

The region $\Psi$ $=$ (S,V,E,I,H,R) $ϵ{\mathbb{R}}_{+}^6$ for the model (2) is positively bounded and attracts all positive solutions of the model $\forall t>0$ .

Proof

For adding all equations of the model (2), where

$$N\left(t\right)=(S+V+E+I+H+R)\left(t\right).$$ (5)

Then, by differentiating Equation (5) with respect to time $t$ Eq. (6) obtained.

$$\frac{dN}{dt}=\frac{dS}{dt}+\frac{dV}{dt}+\frac{dE}{dt}+\frac{dI}{dt}+\frac{dH}{dt}+\frac{dR}{dt}.$$ (6)

Eq. (7) obtained by substituting model (2) equations.

$$\frac{dN}{dt}=\mu +\varphi +\delta R+ϵV-(\beta I+\gamma +d)S+\gamma S-(ϵ+\alpha +d)V+\beta IS-(\eta +\omega +d)E+\omega E-(\Lambda +{\rho }_2+d+\lambda )I+\eta E+\Lambda I-({\rho }_1+d+\lambda )H+{\rho }_{1}H+{\rho }_{2}I+\alpha V-(\delta +d)R.$$ (7)

For further simplification from Eq. (7) then, Eq. (8) obtained.

$$\frac{dN}{dt}=\mu +\varphi -(S+V+E+I+H+R)d-(\delta I+\delta H),$$ (8)

At no-disease $\delta I+\delta H=0$

$$\frac{dN}{dt}=\mu +\varphi -(S+V+E+I+H+R)d,$$ (9)

where, $S+V+E+I+H+R=N$

$$\frac{dN}{dt}\le \mu +\varphi -Nd$$ (10)

A separable method used to calculate Eq. (10) to obtain Eq. (11).

$${\int }_{N\left(0\right)}^{N\left(t\right)}\frac{dN}{(\mu +\varphi -dN)}\le {\int }_0^{t}dt,$$

$$N\left(t\right)\ge \frac{\varphi +\mu }{d}(1-e^{-dt})+N\left(0\right)e^{-dt}.$$ (11)

At t $=$ 0;

$$N\left(0\right)\ge 0,$$

at $t\to \infty$

$$N\left(\infty \right)\le \frac{\mu +\varphi }{d}.$$

At no-disease equilibrium, the bounded region is given in Eq. (12) whereby the $SVEIHR$ model has biological and epidemiological meaningful.

$$\Psi =(S,V,E,I,H,R)\in {\mathbb{R}}_{+}^6:0\le N\left(t\right)\le \frac{\mu +\varphi }{d}.\square$$ (12)

3.3. No-disease equilibrium point ($E_0$)

$E_0$ is attained when the infected components are zero, as in Eq. (13).

$$\frac{dS}{dt}=\frac{dV}{dt}=\frac{dE}{dt}=\frac{dI}{dt}=\frac{dH}{dt}=\frac{dR}{dt}=0.$$ (13)

Consider each of the model (2) equations:

$$\frac{dS}{dt}=\mu +\varphi +\delta R+ϵV-(\beta I+\gamma +d)S=0,$$ (14)

At no-disease it gives,

$$\mu +\varphi -(\gamma +d)S=0,$$

Then,

$$S=\frac{\mu +\varphi }{\gamma +d}.$$

Consider the second model equation:

$$\gamma S-(ϵ+\alpha +d)V=0,$$ (15)

gives,

$$V=\frac{\gamma S}{ϵ+\alpha +d}.$$

The third model equation is:

$$\beta IS-(\eta +\omega +d)E=0,$$ (16)

but,

$$E=\frac{\beta IS}{(\eta +\omega +d)}$$

then, at no-disease $I=0$. Therefore,

$$E=0.$$

From the fourth model equation:

$$\omega E-(\Lambda +{\rho }_2+d+\lambda )I=0,$$ (17)

$$I=\frac{\omega E}{\Lambda +{\rho }_2+d+\lambda },$$

but at no-disease $E=0$,

$$I=0$$

Then: $H=R=0$

Thus,

$$E_0=\left(S^0,V^0,E^0,I^0,H^0,R^0\right)={\left(\frac{\mu +\varphi }{\gamma +d},\frac{\gamma S}{ϵ+\alpha +d},0,0,0,0\right)}^T.$$ (18)

The state where there is no infection is the no-disease equilibrium point, which is given in Eq. (18).

3.4. Basic reproduction number ($R_0$)

$R_0$ is the mid-point number of infections which is caused by the infectious individual for the entire period of infectiousness [22]. When $R_0<1$ the infected individuals cause less than one secondary infection and die out. When $R_0>1$ the infected individual infects more than one secondary infections. The next-generation matrix method used to compute $R_0$ [23]. Obtaining the no-disease equilibrium point $E_0$ was crucial and the results were computed as: $F=\left(\frac{\partial F_i}{\partial x_j}\left(E_0\right)\right)$ and $U=\left(\frac{\partial U_i}{\partial x_j}\left(E_0\right)\right)$.

Then $j\le n$, $F$, and $1\le i$ are non-negative, and U is a non-singular n-matrix. $U^{-1}$ and $F{U}^{-1}$ are non-negative because F is non-negative and U is a non-singular matrix and the next-generation matrix $F{U}^{-1}$ was computed [24].

Note:$R_0$ is the spectral radius of the matrix $F{U}^{-1}$ [25].

$$R_0=\rho \left(F{U}^{-1}\right)$$ (19)

and

$$F{U}^{-1}=\left[\frac{\partial F_i}{\partial x_j}\left(E_0\right)\right]{\left[\frac{\partial U_i}{\partial x_j}\left(E_0\right)\right]}^{-1}.$$ (20)

Then:

$$\frac{dE}{dt}=\beta IS-(\eta +\omega +d)E,$$$$\frac{dI}{dt}=\omega E-(\Lambda +{\rho }_2+d+\lambda )I,$$$$\frac{dH}{dt}=\eta E+\Lambda I-({\rho }_1+d+\lambda )H.$$ (21)

Eq. (22) is obtained when I and S meet in Eq. (21).

$$F_i=\left(\begin{array}{c}\hfill f_1\hfill \\ \hfill f_2\hfill \\ \hfill f_3\hfill \end{array}\right)=\left(\begin{array}{c}\hfill \beta IS\hfill \\ \hfill 0\hfill \\ \hfill 0\hfill \end{array}\right),$$ (22)

Eq. (22) shows the Jacobian matrix of $E_0$ as presented in Eq. (23).

$$F_J=\left(\begin{array}{ccc}\hfill 0\hfill & \hfill \beta S\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \end{array}\right).$$ (23)

However,

$$S=\frac{\mu +\varphi }{\gamma +d}$$

Regarding V, E, I, and H, the partial derivative of Eq. (23) is:

$$U=\left(\begin{array}{ccc}\hfill d+\eta +\omega \hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill -\omega \hfill & \hfill d+\lambda +\Lambda +{\rho }_2\hfill & \hfill 0\hfill \\ \hfill -\eta \hfill & \hfill -\Lambda \hfill & \hfill d+\lambda +{\rho }_1\hfill \end{array}\right),$$ (24)

The inverse of $U$ is,

$$U^{-1}=\left(\begin{array}{ccc}\hfill \frac{1}{d+\eta +\omega }\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill \frac{\omega }{(d+\eta +\omega )\left(d+\lambda +\Lambda +{\rho }_2\right)}\hfill & \hfill \frac{1}{d+\lambda +\Lambda +{\rho }_2}\hfill & \hfill 0\hfill \\ \hfill \frac{d\eta +\eta \lambda +\eta \Lambda +\eta {\rho }_2+\Lambda \omega }{(d+\eta +\omega )\left(d+\lambda +{\rho }_1\right)\left(d+\lambda +\Lambda +{\rho }_2\right)}\frac{\Lambda }{\left(d+\lambda +{\rho }_1\right)\left(d+\lambda +\Lambda +{\rho }_2\right)}\hfill & \hfill \frac{1}{d+\lambda +{\rho }_1}\hfill \end{array}\right)$$ (25)

The product matrix $F{U}^{-1}$ after computation by using Mathematica Eq. (26) obtained.

$$F{U}^{-1}=\left(\begin{array}{ccc}\hfill \frac{\beta \omega (\mu +\varphi )}{(\gamma +d)(d+\eta +\omega )\left(d+\lambda +\Lambda +{\rho }_2\right)}\hfill & \hfill \frac{\beta (\mu +\varphi )}{(\gamma +d)\left(d+\lambda +\Lambda +{\rho }_2\right)}\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \end{array}\right).$$ (26)

$$\text{Eigenvalues}=\left\{0,0,\frac{\beta \omega (\mu +\varphi )}{(\gamma +d)(d+\eta +\omega )\left(d+\lambda +\Lambda +{\rho }_2\right)}\right\}.$$

where,

$${\lambda }_1=0$$

$${\lambda }_2=0$$

$${\lambda }_3=\frac{\beta \omega (\mu +\varphi )}{(\gamma +d)(d+\eta +\omega )\left(d+\lambda +\Lambda +{\rho }_2\right)}$$

The basic reproduction number, $R_0$ (dominant eigenvalue) is given by Eq. (27).

$$R_0=\frac{\beta \omega (\mu +\varphi )}{(\gamma +d)(d+\eta +\omega )\left(d+\lambda +\Lambda +{\rho }_2\right)}.$$ (27)

4. Stability analysis

Under this section, the local and global stability are discussed and presented.

4.1. Local stability of no-disease equilibrium ($E_0$)

The eigenvalues, which are obtained by calculating the partial derivatives of a vector-valued function, are used to study the local stability of $E_0$. The equilibrium point is asymptotically stable if the Jacobian matrix assessed at that point contains negative eigenvalues. In this paper, the Routh–Hurwitz criterion used to demonstrate local stability under Theorem 4.1 [26].

Theorem 4.1

For the system (2) , the no-disease equilibrium point $E_0$ is locally asymptotically stable if $R_0<1$ , and unstable when $R_0>1$ .

Proof

At $E_0$, the Jacobian matrix of the system (2) is presented in Eq. (28).

$$J_{E_0}=\left(\begin{array}{cccccc}\hfill -\gamma -d\hfill & \hfill \varepsilon \hfill & \hfill 0\hfill & \hfill -\beta S\hfill & \hfill 0\hfill & \hfill \delta \hfill \\ \hfill \gamma \hfill & \hfill -\alpha -d-\varepsilon \hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill -d-\eta -\omega \hfill & \hfill \beta S\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill \omega \hfill & \hfill -d-\lambda -\Lambda -{\rho }_2\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill \eta \hfill & \hfill \Lambda \hfill & \hfill -d-\lambda -{\rho }_1\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill \alpha \hfill & \hfill 0\hfill & \hfill {\rho }_2\hfill & \hfill {\rho }_1\hfill & \hfill -d-\delta \hfill \end{array}\right)$$ (28)

At no-disease: $E_0=\left(\frac{\mu +\varphi }{\gamma +d},\frac{\gamma S}{ϵ+\alpha +d},0,0,0,0\right)$

$$\left(\begin{array}{cccccc}\hfill -\gamma -d\hfill & \hfill \varepsilon \hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill \delta \hfill \\ \hfill \gamma \hfill & \hfill -\alpha -d-\varepsilon \hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill -d-\eta -\omega \hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill \omega \hfill & \hfill -d-\lambda -\Lambda -{\rho }_2\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill \eta \hfill & \hfill \Lambda \hfill & \hfill -d-\lambda -{\rho }_1\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill \alpha \hfill & \hfill 0\hfill & \hfill {\rho }_2\hfill & \hfill {\rho }_1\hfill & \hfill -d-\delta \hfill \end{array}\right)$$ (29)

By considering Eq. (30), the eigenvalues were determined.

$$\left|\begin{array}{cccccc}\hfill -\gamma -d\hfill & \hfill \varepsilon \hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill \delta \hfill \\ \hfill \gamma \hfill & \hfill -\alpha -d-\varepsilon \hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill -d-\eta -\omega \hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill \omega \hfill & \hfill -d-\lambda -\Lambda -{\rho }_2\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill \eta \hfill & \hfill \Lambda \hfill & \hfill -d-\lambda -{\rho }_1\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill \alpha \hfill & \hfill 0\hfill & \hfill {\rho }_2\hfill & \hfill {\rho }_1\hfill & \hfill -d-\delta \hfill \end{array}\right|=0$$ (30)

The eigenvalues of the matrix $J_{E_0}$ are:

$${\lambda }_1=-d,$$

$${\lambda }_2=\frac{1}{2}\left(-\sqrt{{\alpha }^2-2\alpha (\gamma +\delta -\varepsilon )+{(\gamma -\delta +\varepsilon )}^2}-\alpha -\gamma -2d-\delta -\varepsilon \right),$$

$${\lambda }_3=\frac{1}{2}\left(\sqrt{{\alpha }^2-2\alpha (\gamma +\delta -\varepsilon )+{(\gamma -\delta +\varepsilon )}^2}-\alpha -\gamma -2d-\delta -\varepsilon \right),$$

$${\lambda }_4=-d-\eta -\omega ,$$

$${\lambda }_5=-d-\lambda -{\rho }_1,$$

$${\lambda }_5=-d-\lambda -{\rho }_1,$$

$${\lambda }_6=-d-\lambda -\Lambda -{\rho }_2.$$

Since all eigenvalues of Eq. (30) are real and negative, therefore the model is Locally asymptomatically stable based on the idea of Routh-Hurwitz criterion [26], [27], [28]. □

4.2. Global stability of no-disease equilibrium ($E_0$)

Under this section, the two conditions $C_1$ and $C_2$ are considered to guarantee global asymptotically stable of the $E_0$. By adopting the approach developed by [25] to prove the global stability of the no-disease equilibrium point, we write system (2) in the form:

$$\frac{dy}{dt}=A(X_u-X_i)$$ (31)

$$\frac{dz}{dt}=B(X_u,X_i),B(X_u,0)=0$$ (32)

where $X_u=(S,V,R)$ denotes the vector of uninfected compartments and $X_i=(E,I,H)$ denotes the vector of infected compartments. The no-disease equilibrium point from Eq. (18) which can written as ($X_n^0,0$) with $X_n=(S^0,V^0,0)$ and $0ϵ{\mathbb{R}}^3$. Then, the $E_0$ is globally asymptotically stable if $R_0<1$, satisfied by the two conditions [25].

Condition, $C_1$: $\frac{dy}{dt}=A(X_u,0)$, $X_u^0$ is global asymptotically stable. Since $\frac{dy}{dt}=A(X_u,0)$ reads

$$\left\{\begin{array}{cc}\frac{dS}{dt}\hfill & =\mu +\varphi -(\gamma +d)S\hfill \\ \frac{dV}{dt}\hfill & =\gamma S-(ϵ+\alpha +d)V\hfill \\ \frac{dR}{dt}\hfill & =-(\delta +d)R\hfill \end{array}\right)$$ (33)

$$(S,V,R)\to \left(\frac{\mu +\varphi }{\gamma +d},\frac{\gamma S}{ϵ+\alpha +d},0\right),t\to +\infty$$

Condition, $C_2$: $B(X_u,X_i)=J_{x_i}-\tilde{B}(X_u,X_i)$,   $\tilde{B}(X_u,X_i)\ge 0$ for $(X_u,X_i)ϵD$, where

$$J=D_{x_i}(X_0^{\ast },0)$$

is a Metzler matrix (the off-diagonal elements are non-negative).

Theorem 4.2

The fixed point $V_0(X_n^{\ast },0)$ is globally asymptotically stable if $R_0\le 1$

Proof

Investigating the global stability of the $E_0$, we rewrite the system (2) in the form of Eq. (21). Then, $X_u=(S,V,R)$ and $X_i=(E,I,H)$, then, we have

$$A(X_u,0)=\left(\frac{\mu +\varphi }{\gamma +d},\frac{\gamma S}{ϵ+\alpha +d},0\right),$$

$$J=\left(\begin{array}{ccc}\hfill -(\eta +\omega +d)\hfill & \hfill \beta S\hfill & \hfill 0\hfill \\ \hfill \omega \hfill & \hfill -(\Lambda +{\rho }_2+d+\lambda )\hfill & \hfill 0\hfill \\ \hfill \eta \hfill & \hfill \Lambda \hfill & \hfill -({\rho }_1+d+\lambda )\hfill \end{array}\right),$$

and

$$\tilde{B}(X_u,X_i)=\left(\begin{array}{c}\hfill (N-S)\beta I\hfill \\ \hfill 0\hfill \end{array}\right).$$

Since $N\ge S\ge 0$, it is clear that $\tilde{B}(X_u,X_i)\ge 0$. Therefore, the no-disease equilibrium is globally stable. □

4.3. Global stability of endemic equilibrium point ($E_{\ast }$)

The global stability of endemic equilibrium point $E_{\ast }$ is determined by using the Lyapunov method [29], [30], [31], [32], [33], [34]. For the derivation of Lyapunov function $W$ consider Theorem 4.3 and its proof.

Theorem 4.3

If $R_0>1$ , the global endemic equilibrium point $E_{\ast }$ is asymptotically stable, while when $R_0<1$ the $E_{\ast }$ is unstable.

Proof

To determine the global stability of the system (2) for which $E_{\ast }$ exists and $R_0>1$, the Lyapunov function $W$ is defined and derived as follows:

$$W(x_i,\dots ,x_n)=\sum _{i=1}^n\frac{1}{2}{[x_i-x_i^{\ast }]}^2.$$ (34)

Where

$n$$=$ Number of compartments (in this study there are 6 compartments, then $n=6$),

$X_i$$=$ Disease-free compartment, and

$x_i^{\ast }$$=$ Endemic compartment.

$$W(S,V,E,I,H,R)=\frac{1}{2}[(S-S^{\ast })+(V-V^{\ast })+(E-E^{\ast })+(I-I^{\ast })+(H-H^{\ast })+(R-R^{\ast })]{}^2$$ (35)

Consider the derivative of function $W$ in Eq. (35) with respect to time corresponding to system (2), the following solution in Eq. (36) obtained.

$$\frac{dW}{dt}=[(S-S^{\ast })+(V-V^{\ast })+(E-E^{\ast })+(I-I^{\ast })+(H-H^{\ast })+(R-R^{\ast })]\frac{d}{dt}(S+V+E+I+H+R)$$ (36)

From Eq. (6) which is given as

$$\frac{dN}{dt}=\frac{d}{dt}(S+V+E+I+H+R)$$ (37)

Then, by using Eq. (10) therefore Eq. (37) gives

$$\frac{dN}{dt}=\mu +\varphi -Nd$$ (38)

But from Eq. (9) given that

$$[S^{\ast }+V^{\ast }+E^{\ast }+I^{\ast }+H^{\ast }+R^{\ast }]=\frac{\mu +\varphi }{d}$$ (39)

Consider the substitute of Eqs. (38), (39) into Eq. (36), gives Eq. (40).

$$\frac{dW}{dt}=\left[N-\frac{\mu +\varphi }{d}\right]\left[\mu +\varphi -Nd\right]$$ (40)

Then,

$$\frac{dW}{dt}=-\frac{1}{d}\left[{(\mu +\varphi )}^2-2N(\mu +\varphi )+N^2{d}^2\right]$$ (41)

The simplification of Eq. (41) is given in Eq. (42).

$$\frac{dW}{dt}=-\frac{1}{d}{\left[\mu +\varphi -Nd\right]}^2$$ (42)

$\frac{dW}{dt}<0$ is a strictly Lyapunov function as presented in Eq. (42), which shows that the endemic equilibrium point $E_{\ast }$ is globally asymtotically stable when $R_0>1$ in the region $△$.

From Eq. (42), $\frac{dW}{dt}=0$ if and only if we set $S=S^{\ast },V=V^{\ast },E=E^{\ast },I=I^{\ast },H=H^{\ast },R=R^{\ast }$ and then, $\frac{dW}{dt}$ converges in positive region $△$ as t$\to$ $\infty$. □

5. Numerical simulations

The first-order differential equations of the $SVEIHR$ model were solved numerically by the explicit Runge–Kutta fourth-order method. The sensitivity analysis for $R_0$ parameters were presented by using Partial Rank Correlation Coefficient (PRCC) method. The results were presented graphically and the parameter identifiability were presented by using Markov Chain Monte Carlo (MCMC) method.

5.1. Model sensitivity analysis

For the transmission of COVID-19 disease, the impact of each parameter on the endemic threshold was described in the sensitivity analysis. The sensitivity analysis is very essential method for the complex systems whereby the strength of the parameters of $SVEIHR$ model was determined [35]. Parameter values are presented in Table 3 which are from the literature and one parameter was assumed. The sensitivity index standard equation for $R_0$ is given in Eq. (43).

$${\Gamma }_{{\rm Y}}^{R_0}=\frac{\partial R_0}{\partial {\rm Y}}\times \frac{{\rm Y}}{R_0}.$$ (43)

From Eq. (43), the sensitivity indices were calculated and presented in Table 3.

Table 3.

Sensitivity indices and parameter values.

Parameter	Value	Source	Sensitivity index
$\beta$	0.45 day${}^{-1}$	[36]	0.4872
$\omega$	0.25 day${}^{-1}$	[37]	0.8799
$\mu$	50 day${}^{-1}$	[38]	−0.0205
$\varphi$	0.006 day${}^{-1}$	Assumed	0.0189
$\gamma$	0.85 day${}^{-1}$	[21]	−0.6549
$d$	0.0104 day${}^{-1}$	[39]	−0.0509
$\eta$	0.083 day${}^{-1}$	[21]	0.5780
$\lambda$	0.039 day${}^{-1}$	[40]	0.1399
$\Lambda$	0.94 day${}^{-1}$	[37]	0.1231
${\rho }_2$	0.07 day${}^{-1}$	[41]	0.1949

The most positive sensitive parameter is $\omega$ with the basic reproduction number by ${\Gamma }_L^{R_0}=0.8799$, which means non-vaccinated individuals are more infected by the COVID-19 disease as presented in Table 3. The most negative sensitive parameter is $\gamma$ with the basic reproduction number by ${\Gamma }_L^{R_0}=-0.6549$, which means 65% of vaccinated individuals were recovered from the disease even if they come into contact with the infected individual. The least sensitive parameter is $\varphi$ with the basic reproduction number of ${\Gamma }_L^{R_0}=0.0189$, which means the number of new comers from other infected countries is very small and in most cases are vaccinated. The sensitivity analysis for the 10 parameters are presented in Fig. 2, which shows all $R_0$ parameters from the most sensitive (positive and negative) parameters to the least (positive and negative) parameters.

Fig. 2.

PRCC results for $R_0$ and Global sensitivity analysis.

5.1.1. Simulation of $SVEIHR$ model dynamics

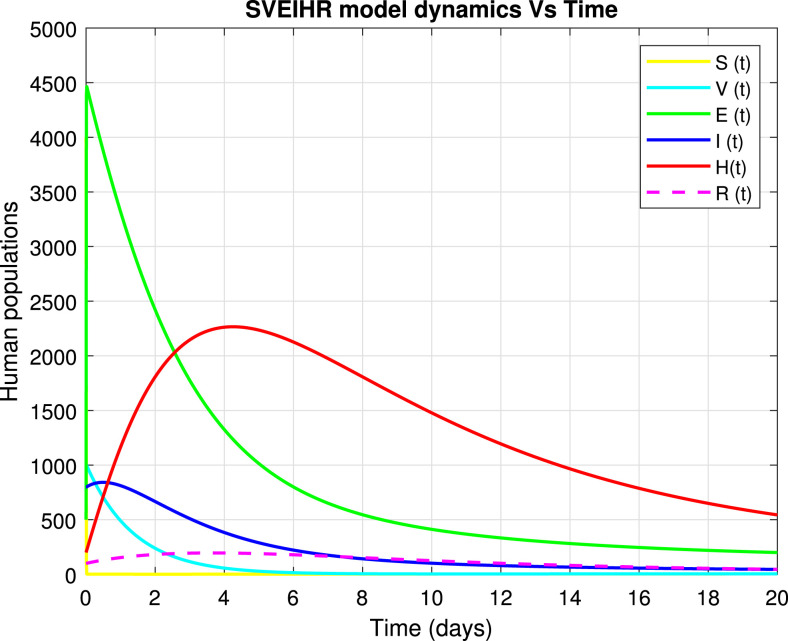
Numerical simulation of model variables as presented in Fig. 3, which shows that the susceptible class declines to obtain the endemic equilibrium point as individuals move to the exposed and vaccinated classes and other individuals die naturally. The vaccinated class increases as individuals move from susceptible class to be vaccinated and then, decreases due to the movement of individuals to the recovered class because vaccinated individuals may catch the disease but can not be affected. the exposed class increases due to individuals from the susceptible class and decreases as individuals move to the infected and hospitalized classes, and then diminished by the natural death of individuals. Hospitalized class grows as receive individuals from exposed and infected classes and at a time decreases due to the individuals moving to the recovered class to maintain equilibrium point. The recovered class receive individuals from hospitalized, infected and vaccinated classes and at a time decreases due to the population moving back to the susceptible class and others die naturally. The variables $S,V,E,I,H,R$ vary with time (t).

Fig. 3.

Simulation of dynamic population of a $SVEIHR$ model.

5.1.2. Stability analysis of $SVEIHR$ model

Based on $SVEIHR$ model analytical results, the numerical simulations investigated stability analysis of the model compartments. The trajectories of the state variables ($S,V,E,I,H,R$) originated from different origins which are colored differently and converge towards the equilibrium point as presented by a legend in each graph presented from Figs. 4(a) to 6(b) (see Fig. 5).

Fig. 4.

Endemic equilibrium of a vaccinated and exposed individuals. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)

Fig. 6.

Endemic equilibrium of a hospitalized and recovered individuals. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)

Fig. 5.

Endemic equilibrium of a vaccinated and infected individuals. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)

5.1.3. Control parameters

In the susceptible class, the decaying rate increases when the contact rate $\beta$ increases, whereby most individuals are sent to the exposed class, while other individuals are dying naturally, and then the decaying rate decreases when the contact rate decreases. The exposed class increases when the individuals contacted the disease and decreases by the individuals sent to the hospitalized class, infected class and the leaving rate due to natural death of individuals as presented in Fig. 7, Fig. 7. As presented in Fig. 8, Fig. 8, the hospitalized individuals from exposed class to be diagnosed for treatment and the recovered individuals increases as individuals move from hospitalized, infected and vaccinated classes. The number of vaccinated individuals $\gamma$ increases everyday, which makes the susceptible population to decrease as presented in Fig. 9(a), but in Fig. 9(b) the vaccinated population increases daily and then decreases due to the individuals going to the recovered class and whose die naturally. The infected population decreases by the individuals going to the hospital $\eta$ to get treatment as in Fig. 10(a) and later add the population in the hospitalized class as in Fig. 10(b) before released to a recovered class. The infected class decreases as individuals move to the hospitalized, recovered classes and natural death and death due the disease as presented in Fig. 11(a). The recovered population as presented in 11(b) increases. The exposed population moving to hospitalized class to be diagnosed and treated as presented in Fig. 12, Fig. 12.

Fig. 7.

Variation of $\beta$ in susceptible and exposed individuals.

Fig. 8.

Variation of $\beta$ in hospitalized and recovered individuals.

Fig. 9.

Variation of $\gamma$ in susceptible and vaccinated individuals.

Fig. 10.

Variation of $\Lambda$ in infected and hospitalized individuals.

Fig. 11.

Variation of ${\rho }_2$ in infected and recovered individuals.

Fig. 12.

Variation of $\eta$ in exposed and hospitalized individuals.

6. Parameter identifiability by MCMC method

The MCMC method is a statistical and Bayesian method for dealing with the parameters of complex ordinary differential equations that fit dynamical systems. For estimating effects in the epidemiological analysis, the MCMC methods are more popular because provide a manageable route to obtain estimations of parameters for large complicated models [42]. In this study, there are 14 parameters to be estimated and a sampling of $100,000\times 14$ parameters has been generated during the simulations, with the technique being adapted $50$ times. The initial values for the parameters are obtained from least squares estimates and the model parameters identifiability is mostly determined by the MCMC convergence. For the MCMC method, there are numerous graphical and statistical convergence tests [43], [44], [45]. The sum of squares was given by Eq. (44).

$$SS\left(y\right)=\sum _{i=1}^n{[y_i-g\left(f(x_i,y)\right)]}^2$$ (44)

Given that:

$y_i$$=$ a real data, and f($x_i$, $y$) $=$ model prediction solution. The Eq. (44) was used to measure the distance from the model to the observations. Parameter estimation, $SS\left(y\right)$ can be minimized with some iterative optimization method. By linearizing the model at the best fitting point $\tilde{y}$, statistics for parameter estimates obtained. For the estimated parameters the covariance matrix is given by Eq. (45).

$$Cov\left(y\right)={\sigma }^2{(J^T\times J)}^{-1},$$ (45)

where

$$J_{i_p}=\frac{\partial g\left(f(x_i,\tilde{y})\right)}{\partial y_p}$$

as a Jacobian matrix of the model. Nearly all parameters converge to their initial values as presented in Table 4, and the posterior means are within reasonable intervals with the posterior means and medians being practically equal. Furthermore, for determining the accurate estimates the MCerr and the standard deviation of the model parameters are both quite small, indicating that the method worked well. The auto-correlation time (tau) computed values are small, indicating the importance of sampling the subsequent posteriors independently as well as the method convergence. All Geweke values are close to $1$ and the Gaussian distribution of skewness and kurtosis values are approximately to be $0$ and $3$, respectively. As a result, the acquired samples skewness and kurtosis values demonstrate that all $14$ parameters incorporate the exact properties of the Gaussian distribution.

Table 4.

Parameter estimated least square and MCMC methods.

Parameter	Value	LSQE	MMean	MMed.	Std	MCerr	tau	Geweke	Kurtosis	Skewness
$\beta$	0.4500	0.5220	0.4483	0.4506	0.0023	0.00018	95.641	0.99796	3.2100	0.5191
$\omega$	0.2500	0.2483	0.2499	0.2500	0.0005	3.9954e−05	99.152	0.99975	3.4168	−0.0091
$\mu$	50.0000	49.2789	50.0034	50.0036	0.0077	0.0008	97.241	0.99999	3.4434	0.1638
$\varphi$	0.0060	0.0058	0.0068	0.0062	0.0042	0.0006	281.05	0.69359	3.4233	2.4568
$\gamma$	0.8500	0.9702	0.8523	0.8518	0.0039	0.0004	130.18	0.99818	2.6034	−0.1148
$d$	0.0104	0.0103	0.0104	0.0104	3.1803e−05	2.1891e−06	37.63	0.99992	3.2057	0.0377
$\eta$	0.0830	0.0853	0.0831	0.0830	0.0005	4.7383e−05	115.98	0.99878	3.2942	0.3464
$\lambda$	0.0390	0.0377	0.0390	0.0390	4.6686e−05	3.3099e−06	44.963	0.99997	3.4214	−0.0234
$\Lambda$	0.6500	0.6311	0.9398	0.9400	0.0018	0.0002	114.99	0.99957	3.4025	−0.3569
${\rho }_2$	0.0700	0.0793	0.0702	0.0702	0.0008	6.2611e−05	63.173	0.99713	3.0745	0.0072
$\alpha$	0.0800	0.0942	0.0801	0.0801	0.0006	4.8355e−05	62.716	0.99966	3.1453	−0.2076
${\rho }_1$	0.0500	0.0496	0.0500	0.0500	2.3293e−05	1.4948e−06	45.229	0.99988	2.5512	−0.1130
$\delta$	0.6500	0.6632	0.6502	0.6502	0.0008	5.6668e−05	49.862	0.99982	3.1163	−0.0645
$ϵ$	0.5400	0.5171	0.5402	0.5402	0.0006	5.2228e−05	60.207	0.9997	3.1163	0.4280

Where; LSQE$=$ Least Square Estimates, MMean$=$ MCMC Mean, MMed$=$ MCMC Median,   Std$=$ Standard deviation, MCerr$=$ MCMC error.

To assess the MCMC convergence we use Trace plots and posterior density as techniques among many techniques of MCMC to examine the mixing of generated sample of posteriors. The parameters which shows a good convergence are $\beta$, $\omega$, $\gamma$, $d$, $\eta$, $\lambda$, $\Lambda$, ${\rho }_2$, $\alpha$, ${\rho }_1$, $\delta$ and $ϵ$ as presented by the figures from Fig. 13, Fig. 14, Fig. 15, Fig. 16, Fig. 17, Fig. 18, Fig. 19, Fig. 20, Fig. 21, Fig. 22, Fig. 23, Fig. 24. The created chain of posteriors becomes stationary with no noticeable spikes for numerous beginning values, it indicates that the mixing is good, which is the sign of convergence. The convergence of MCMC is perfect for the parameters from Fig. 13, Fig. 14, Fig. 15, Fig. 16, Fig. 17, Fig. 18, Fig. 19, Fig. 20, Fig. 21, Fig. 22, Fig. 23, Fig. 24. The trace plots suggests that the samples are approximately independent, from the parameter distribution drawn randomly.

Fig. 13.

Trace plot and posterior density of $\beta$ parameter.

Fig. 14.

Trace plot and posterior density of $\omega$ parameter.

Fig. 15.

Trace plot and posterior density of $\gamma$ parameter.

Fig. 16.

Trace plot and posterior density of $d$ parameter.

Fig. 17.

Trace plot and posterior density of $\eta$ parameter.

Fig. 18.

Trace plot and posterior density of $\lambda$ parameter.

Fig. 19.

Trace plot and posterior density of $\Lambda$ parameter.

Fig. 20.

Trace plot and posterior density of ${\rho }_2$ parameter.

Fig. 21.

Trace plot and posterior density of $\alpha$ parameter.

Fig. 22.

Trace plot and posterior density of ${\rho }_1$ parameter.

Fig. 23.

Trace plot and posterior density of $\delta$ parameter.

Fig. 24.

Trace plot and posterior density of $ϵ$ parameter.

The sample mixing is excellent as presented with figures, therefore the chain converges, and the sample posterior values of parameters are sample means (centers). A low convergence of the MCMC approach results in a strong correlation between the estimated parameters. Practically, all parameter values are distributed normally which shows that for all $14$ parameters, the convergence of the MCMC is perfect.

7. Conclusion

The world faced hard times during COVID-19 pandemic before the scientists introduced vaccinations to reduce the fast spread of the COVID-19 disease from infected individuals or nations to uninfected ones. The world faced severe human and socio-economic burdens before vaccination because people stressed due to the fast spread of the disease which effects ones body immunity. The model was formulated to study vaccination as a control measure of stress to fight COVID-19 pandemic. The model formulated comprises of six compartments; $S$, $V$, $E$, $I$, $H$, and $R$. The no-disease equilibrium was theoretically examined, and the following results were obtained: invariant region, positivity, uniqueness of the solution, existence, and stability analysis was proven. When $R_0<1$ for both local and global stability of $E_0$ is stable and when $R_0>1$ is unstable. The basic reproduction number of this study indicates that the disease is endemic and distinct. In this study, when there is no vaccination (when $\gamma$ $=$ 0) the basic reproduction number is 1.7214, which shows that with no vaccination the disease spread very fast within the community. Furthermore, with vaccination $R_0$ is 0.208, which means the disease fade out and hence minimize the COVID-19 transmission in the community.

The numerical results showed that vaccination helps to reduce stress among the society which helps to boost the immune system. Graphical results showed that many individuals who are vaccinated recovered from the COVID-19 disease and minimize the spread of the disease in the community. Furthermore, the MCMC shows the statistical and convergence of parameters, whereby the convergence of all 14 parameters to their initial values observed and also, their posterior means are within reasonable intervals.

Vaccination is very important tool to fight COVID-19 disease as presented numerically in this study. Because of the good results obtained in this study, in the future we intend to implement optimal control strategies. The limitations of this study is the death due to COVID-19 disease can happen even before an individual is hospitalized, but the assumption of death due to disease in only two compartments limited this work.

CRediT authorship contribution statement

James Nicodemus Paul: Conceptualization, Model formulation, Model analysis, Preparation of the Manuscript. Isambi Sailon Mbalawata: Model formulation, Supervision. Silas Steven Mirau: Model formulation, Supervision. Lemjini Masandawa: Model formulation.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Data availability

No data was used for the research described in the article.