Topology and redescriptions detect multiple alternative biological pathways from clinical phenotypes

Abstract

Biological pathways play a crucial role in the properties of diseases and are important in drug discovery. Identifying the logical relationships among distinctive phenotypic clusters could reveal possible connections to the underlying pathways. However, this process is challenging since clinical phenotypes are often available through unstructured electronic health records. Moreover, in the absence of a standardized questionnaire, there could be bias among physicians toward selecting certain medical terms. In this article, we develop an efficient pipeline to address these challenges and help practitioners to reveal the pathways associated with the disease. We use topological data analysis and redescriptions and propose a pipeline of four phases: (1) pre-processing the clinical notes to extract the salient concepts, (2) constructing a feature space of the patients to characterize the extracted concepts, (3) leveraging the topological properties to distill the available knowledge and visualize the extracted features, and finally, (4) investigating the bias in the clinical notes of the selected features and identify possible pathways. Our experiments on a publicly available dataset of COVID-19 clinical notes testify that our pipeline can indeed extract meaningful pathways.

Impact Statement

The study of biological pathways is an active area of research and helps scientists develop drugs. We propose an efficient pipeline to infer the existence of alternative biological pathways from clinical phenotypes. Our source of data is unstructured clinical notes. First, we extract the phenotypes. Then use redescriptions to construct a topological space corresponding to the distinctive phenotypic clusters. Next, we utilize topological properties of the space to infer biological pathways. Samples highlighted by our extracted pathways are good candidates for analyzing their gene expression levels or other genetics or proteomics data that may mark these as distinctive pathways. This opens the window for further research on those samples, which helps better understand the mechanism of those biological pathways.

Introduction

The study of biological pathways helps scientists learn more about diseases and develop new drugs, hence tools that could assist scientists in identifying biological pathways associated with diseases are of great importance. The recent COVID-19 pandemic as well prompted the urgent need for efficient methods that could help researchers better understand the condition of the disease in a timely manner. In this article, we propose an efficient pipeline to infer the existence of multiple alternative biological pathways from clinical phenotypes. The shorter version of the article was presented by Karisani et al. ¹ As used here, “Pathway” refers to physiologically connected processes, ranging from a cascade such as the clotting cascade, to looser systems such as the renin–aldesterone–angiotensin system (RAAS) that angiotensin-converting enzyme 2 (ACE2) is a part of. Our approach is to identify distinctive phenotypic clusters satisfying logical relationships (implication) and to seek possible connections to the underlying pathways. For this aim, we utilize topological properties – homology cycles – among the phenotypic clusters. Given the possibility of multiple paths to severity that typically mark complex diseases, a goal would be to identify logical relationships among phenotypic clusters that may point to distinct pathways. Cycles in computational homology may identify candidates for multiple pathways. We use unstructured clinical notes as the source of information to automatically extract phenotypes to be used in our topological model. Phenotypes are the symptoms and signs that reflect the presence of disease – in the following, we refer to them as symptoms.

Advancement in technology has helped scientists to garner enormous amounts of biomedical data. This has provided the community with unprecedented opportunities to study and better understand the spread of diseases. However, this burst of information has posed significant challenges to the traditional data analysis and visualization techniques. Traditional infographics, such as Venn diagrams, which are still widely used to compare and contrast set of symptoms, fail to aid practitioners in analyzing large set of symptoms. Thus, tools that can effectively employ the techniques in other scientific communities to facilitate this process are of immense value.

Machine learning models and statistical methods are used to exploit biomedical data. Particularly, patient similarity and symptom clusters are the two concepts that have been widely explored in recent literature. Patient similarity aims to identify patients according to similarities of their health records, including phenotypes and genomic profiles. In this area, several models have been proposed for disease predictions and clustering patients based on selected similar biomarkers, ² to perform outcome prediction tasks, ³ and in general to improve precision medicine.^4,5 On the contrary, symptom clusters relate to sets of symptoms – usually more than two symptoms within each set – that occur together and might share the same etiology; moreover, relationships among symptoms within a cluster are stronger than the ones across the clusters. ⁶ For a thorough review of methods of identification of symptom clusters, see the study by Barsevick. ⁷ However, here we add to the body of literature by considering clusters of symptoms whose samples are not necessarily independent from each other but give rise to similar subsets of patients within a cohort – known as redescriptions. We construct a topological space based on the closeness of those clusters and investigate its topological properties to identify underlying pathways.

In our experiments, we use clinical notes as the source of data. Combining electronic health records from multiple sources provides a valuable pool of data for researchers to address crucial questions.^8,9 However, a well-designed epidemiological study would follow a standard questionnaire containing a response to all the symptoms and signs of interest. Hence, unstructured clinical notes may be biased by which physician filled out the forms; consequently, that could introduce a systematic bias in the study. ¹⁰ We apply statistical analysis on the symptoms associated with the extracted topological properties to investigate a possible bias.

We propose a pipeline to automatically extract candidate pathways associated with a disease from clinical notes. Our pipeline, which is based on the notion of redescriptions and the topological properties among them, consists of four phases: (1) pre-processing the notes and identifying the candidate symptoms, (2) mapping the symptoms to the space of the patients, (3) extracting the topological properties and their visualization, and finally, (4) perform statistical analysis to detect the possible bias in the extracted features. We have evaluated our pipeline in a publicly available dataset of COVID-19 clinical notes. The results show that our model can extract meaningful pathways. We demonstrate that there are potentially distinctive pathways between coughers and non-coughers among patients with abnormal sputum.

Background

In this section, we briefly introduce the notion of persistent homology, which is the main component of our proposed pipeline. Persistent homology is a tool from topological data analysis (TDA), which uses techniques from Algebraic Topology to analyze topological spaces, particularly point cloud data. TDA has been widely applied to solve biological problems. ¹¹ Here, we avoid the mathematical detail, which is beyond the scope of this article. For a thorough description, see the study by Dey and Wang. ¹²

Let $M$ be a continuous space equipped with a metric $\delta$ (used as a parameter), the topological invariants of $M$ are defined as the properties that do not change under continuous deformation (i.e. twisting but not tearing). The invariants of $M$ in lower dimensions are usually referred to as the connected components, the holes, and the void spaces, respectively, in dimension 0, 1, and 2; in the higher dimensions, they are understood as the $k$ -dimensional holes (also known as $k$ -dimensional homology cycles). The number of $k$ -dimensional holes in $M$ are called the kth betti numbers.

Given a set of data points $X$ and a distance function $\delta$ ( $X$ represents as the points sampled from $M$ ), the goal is to compute the topological invariants of the underlying space of $X$ (i.e. space $M$ ). A common approach to associate a structure to $X$ is by constructing $k$ -simplexes (or simplices) over $X$ . Intuitively, one could think of a $k$ -simplex as a convex hull of $k+1$ affinely independent points. A collection of simplexes over $X$ satisfying some conditions ¹² is called a simplicial complex. In particular, the simplexes are constructed in a sequence of steps (based on a parameter) to create a filtration of simplicial complexes over $X$ . First, the initial simplicial complex $S_0$ is set to be the collection of points in $X$ , each data point is considered as a 0-simplex; then the parameter is increased such that at each step $i$ only a finite set of simplexes that satisfy some conditions could be added to the current simplicial complex $S_{i-1}$ ; this procedure creates a filtration of simplicial complexes on $X$ (i.e. $S_0\subseteq S_1\subseteq \cdots$ ), which then is used to infer the topological invariants of the underlying space of $X$ . The conditions that are required to be satisfied for the simplexes in order to be added to $X$ give rise to a variety of simplicial complexes.

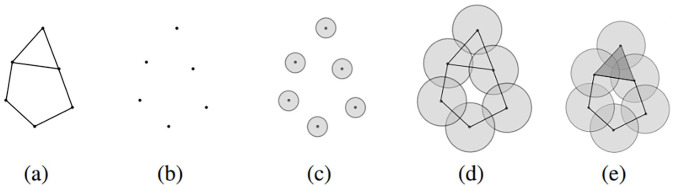
An example of a simplicial complex is Čech complex. Figure 1 shows a simple illustrative example. The goal is to recover the topological invariants of the space in Figure 1(a), in which the zeroth betti number is 1, since there is only one connected component; and the first betti number is 2, since there are two independent holes; the higher dimensional betti numbers are zero. The dataset $X$ is given by the six sampled points in Figure 1(b).

Figure 1.

Recovering topological properties using simplicial complexes.

To construct the Čech complex over $X$ , we begin with the points in $X$ as 0-simplexes, i.e. $S_0=X$ . To add to $S_0$ the higher dimensional simplexes, we start growing a ball at each point, as in Figure 1(c); at this state, the zeroth betti number is 6, and first betti number is 0. By increasing the radius, some of the balls start to overlap with each other; for each $k+1$ overlapped balls, we insert a $k$ -simplex. Figure 1(d) shows a collection of 1-simplexes, line segments joining the two points, created by the pairwise overlap of their corresponding balls; what can be clearly seen in this simplicial complex is that it recovers the topological properties of the underlying structure in Figure 1(a). If we increase the radius further, the three balls at the top begin to overlap with each other, hence we can add a 2-simplex – a filled in triangle – as in Figure 1(e). Therefore, the hole which was created at Figure 1(d) disappeared by increasing the radius at Figure 1(e), as a result that topological property is lost; this could eventually happen for the second hole as we continue to increase the radius and add more simplexes. It is important to notice that the topological properties that persist for a longer period, before they disappear, best represent the topological invariants of the underlying structure. This characteristic is the basic principle of the persistent homology method, which was first formalized in the study by Edelsbrunner et al. ¹³

A diagram known as barcode is commonly used to keep track of the lifetime of topological properties. In the barcode, each topological property is represented as a horizontal line segment. The line segments span the period that the corresponding topological properties exist, along the parameter axis (i.e. radius). In the above example, assuming the edges in Figure 1(a) have equal lengths, Figure 2 illustrates the barcode of 0-dimensional topological properties. Therefore, each line segment in the barcode is identified to a connected component. In the beginning of the filtration there are six data points corresponding to six connected components, hence there are six bars at radius zero. A 0-dimensional topological property disappears when its corresponding connected component gets merged with another connected component. In Figure 2, five bars last until the radius reaches $r_1$ , this identifies the time when the growing balls start to overlap with each other and create the 1-simplexes. Then, a single connected component is created that never disappears, which corresponds to the bar that lasts forever. This single long ball of 0-dimensional topological properties suggests that the data points in Figure 1(b) correspond to a single connected component.

Figure 2.

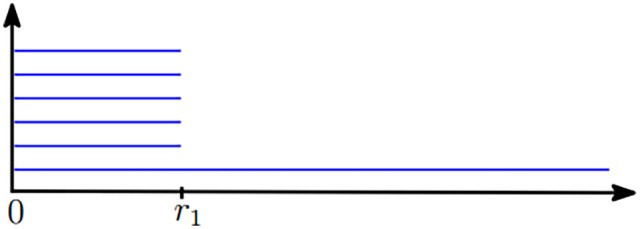
Barcode of 0-dimensional topological properties of the sampled points in Figure 1(b). (A color version of this figure is available in the online journal.)

Materials and methods

In this section, we first introduce our general pipeline and then discuss our experimental setup.

Proposed pipeline

We are seeking to identify evidence of multiple distinct biological pathways leading to disease; for this aim, we propose a pipeline of four phases. In the first phase, we process the unstructured clinical notes to extract the set of symptoms and their corresponding patients. In the next phase, we define the feature space, the sampling strategy, and the metric to measure the similarity between the data points that are based on the notion of redescription. Next, we extract the topological properties using persistent homology and then visualize them to identify important topological properties. Finally, we measure the bias among the symptoms of the selected topological properties to infer possible pathways.

Concept extraction

We carry out the first phase in three steps: (1) We parse the clinical notes and map the biological terms to the concepts in a medical ontology. This step uniforms physicians’ records and utilizes techniques in natural language processing (NLP), which are widely applied to analyze biomedical documents. (2) Since the clinical notes have informal language model, their parsing can be noisy. Thus, we ask a user (system user, e.g. practitioner) to cure the candidate relations and resolve the inconsistencies. Inconsistencies of the mappings could vary depending on the method used in the first step. Despite the significant advances in neural text processing over the last decade, the existing methods are not adequate to effectively parse the medical records.^14,15 An example of that is misspelling – the use of unknown words – which is a challenge in NLP. Manually curating the automated results is crucial to generate high-quality mappings. ¹⁶ Thus, to reduce the noise and ensure that the extracted terms are indeed valid medical concepts, we use manual supervision in step 2 (as mentioned above) to validate the automated associations between the extracted terms and the concepts in the medical ontology. (3) We use electronic health records to construct a binary association matrix between the patients and the extracted concepts.

Feature space construction

In our model, features correspond to the patients, and the data points correspond to the combination of concepts – we call them patterns. Given a feature vector – a data point – a feature is set to 1 if the corresponding patient shows all the symptoms associated with the data point. Thus, a data point is understood as a cluster of patients, who share the same set of symptoms, i.e. pattern.

Patterns are generated from the concepts that are extracted in the previous phase. We only select the patterns whose clusters are non-empty. However, the space of all $k$ -combinations of symptoms grows exponentially as $k$ increases. An efficient way to generate the patterns is to take advantage of the combinations of symptoms that are already recorded for the patients. Note that a set of $k$ symptoms associated with a patient suggests a pattern of size $k$ whose cluster is not empty – at least includes that single patient. Based on this idea, Figure 3 summarizes Algorithm 1 for generating the patterns.

Figure 3.

Algorithm 1 to construct patterns–i.e., data points–using the patients-symptoms association matrix.

Line 1 determines the variable $k$ , which is an upper bound for the number of symptoms in any pattern. Line 2 initializes the output with patterns of size $k$ . Lines 3–9 describe the construction of patterns of size $t$ , $t$ – the minimum of two symptoms and the maximum of $k-1$ symptoms. Note that a pattern of size $t$ either corresponded to patients with exactly $t$ symptoms (Line 4) or can be obtained from patterns of size $t+1$ (Lines 5–8). Finally, Line 10 describes the construction of patterns of size 1 associated to each extracted symptom.

The complexity of Algorithm 1 is exponential in terms of the total number of extracted symptoms. However, in real life, rarely the size of the search space will be exponential, since often not all possible $t$ -combinations of symptoms are recorded for the patients; moreover, $k$ is notably smaller than $m$ . Subsequently, in practice the running time improves significantly; our experiment in the next section demonstrates this fact.

To make an inference about the underlying pathways, it is important to analyze the patterns whose clusters are statistically significant. The challenge involving higher order correlations is that some moments may appear to be non-zero, even when there are subsets of participating variates that are statistically independent of each other. One solution to this problem is to compute joint cumulants (also called Ursell functions). Percus proved that cumulants involving products of independent subsets of variables are zero. ¹⁷ This provides a way to exclude patterns whose moments involve those subsets of independent variates.

Let $G_{•}$ represent the moments in moment-generating functions $\mathbb{E}[\exp ({\Sigma }_i{x}_i{J}_i)]$ , where the $J_i$ s are the conjugate variables, and let ${\Gamma }_{•}$ represent the higher dimensional cumulants, for example, for the symptoms $x_i,x_j,x_k$ , then $G_{ij}=\mathbb{E}(x_i{x}_j)$ and $G_{ijkk}=\mathbb{E}(x_i{x}_j{x}_k^2)$ , and ${\Gamma }_{ij}$ and ${\Gamma }_{ijkk}$ are the corresponding cummulants. The factorizations are as follows:

$$\begin{array}{c}\mathbb{E}\left[\exp \left(\sum _i{x}_i{J}_i\right)\right]=A+\sum _i{J}_i{G}_i+\frac{1}{2!}\sum _{ii\prime }{J}_i{J}_{i\prime }{G}_{ii\prime }+\frac{1}{3!}\sum _{ii\prime i″}{J}_i{J}_{i\prime }{J}_{i″}{G}_{ii\prime i″}+\frac{1}{4!}\sum _{ii\prime i″i″\prime }{J}_i{J}_{i\prime }{J}_{i″}{J}_{i″\prime }{G}_{ii\prime i″i″\prime }+\dots \\ =\exp \left(\sum _i{J}_i{\Gamma }_i+\frac{1}{2!}\sum _{ii\prime }{J}_i{J}_{i\prime }{\Gamma }_{ii\prime }+\frac{1}{3!}\sum _{ii\prime i″}{J}_i{J}_{i\prime }{J}_{i″}{\Gamma }_{ii\prime i″}+\frac{1}{4!}\sum _{ii\prime i″i″\prime }{J}_i{J}_{i\prime }{J}_{i″}{J}_{i″\prime }{\Gamma }_{ii\prime i″i″\prime }+\dots \right),\end{array}$$

where $A$ is nominally 1, seen by setting $J_i=0$ . The power series in the $J_i$ s then requires

$$\begin{array}{l}{G}_k={\Gamma }_k\\ G_{kk\prime }={\Gamma }_{kk\prime }+{\Gamma }_k{\Gamma }_{k\prime }\\ G_{kk\prime k″}={\Gamma }_{kk\prime k″}+{\Gamma }_k{\Gamma }_{k\prime k″}+{\Gamma }_{k\prime }{\Gamma }_{k″k}+{\Gamma }_{k″}{\Gamma }_{kk\prime }+{\Gamma }_k{\Gamma }_{k\prime }{\Gamma }_{k″}\\ G_{kk\prime k″k‴}={\Gamma }_{kk\prime k″k″\prime }+{\Gamma }_k{\Gamma }_{k\prime k″k″\prime }+{\Gamma }_{k\prime }{\Gamma }_{k″k″\prime k}+{\Gamma }_{k″}{\Gamma }_{k″\prime kk\prime }\\ +{\Gamma }_{k″\prime }{\Gamma }_{kk\prime k″}+{\Gamma }_{k″\prime k\prime }{\Gamma }_{k″k}+{\Gamma }_{k\prime k″}{\Gamma }_{k″\prime k}+{\Gamma }_{k″\prime k″}{\Gamma }_{kk\prime }\\ +2{\Gamma }_k{\Gamma }_{k\prime }{\Gamma }_{k″k″\prime }+2{\Gamma }_k{\Gamma }_{k″\prime }{\Gamma }_{k\prime k″}+2{\Gamma }_k{\Gamma }_{k″}{\Gamma }_{k\prime k″\prime }\\ +2{\Gamma }_{k\prime }{\Gamma }_{k″\prime }{\Gamma }_{kk″}+2{\Gamma }_{k\prime }{\Gamma }_{k″}{\Gamma }_{kk″\prime }+2{\Gamma }_{k″\prime }{\Gamma }_{k″}{\Gamma }_{kk\prime }\\ +{\Gamma }_k{\Gamma }_{k\prime }{\Gamma }_{k″}{\Gamma }_{k″\prime }\end{array}$$

We apply the above factorization to the clusters to obtain estimates of the cumulants. We constructed a null hypothesis representation by repeatedly computing the cumulants on randomly shuffled variates following Fisher-Yates (pp. 26–27) ¹⁸ to determine if the measured cumulants differed from variations expected for random uncorrelated samples.

After selecting the significant patterns, we associate to each selected pattern a vertex (i.e. data point). To define the distance function between all the patterns, we first introduce the notion of redescription.

Redescriptions are used to identify the phenomena that occur in separate ways.^19,20 Two different sets of symptoms, which correspond to the same group of patients are an example of redescriptions. They can highlight the underlying pathways and are used to derive rules in pathways. ²¹ Redescriptions are mathematically formalized using Boolean algebra. Suppose $s_1,s_2$ are two symptoms, and $P_1,P_2$ their respective sets of patients. If the presence of symptom $s_1$ implies the presence of symptom $s_2$ , then $P_1\subseteq P_2$ . If we consider the combination of the symptoms (i.e. $s_1\wedge s_2$ ), then the group of the patients who experience both symptoms is $P_1\cap P_2$ by assumption is equal to $P_1$ . Therefore $s_1$ and $s_1\wedge s_2$ are examples of redescriptions since both correspond to the same group of patients which is $P_1$ . To investigate redescriptions, we need to find patterns that give rise to an identical set of patients. However, in applications due to misclassifications of patients, for example, caused by wrong diagnosis, the set inclusion property does not hold in the data. Therefore, we should deal with approximate equalities. This estimation can be done by Jaccard distance, which measures the dissimilarity between sets. For the two sets A and B, Jaccard distance is defined by

$$d\left(A,B\right)=1-\frac{\left|A\cap B\right|}{\left|A\cup B\right|}$$

when $P_1\subseteq P_2$ , then the Jaccard distance $d(P_1\cap P_2,P_1)=0$ , otherwise, if $P_1⊈P_2$ then $0<d(P_1\cap P_2,P_1)\le 1$ , which can be interpreted as the probability that subjects picked from the two sets are not shared.

Thus, we consider Jaccard distance to measure the distances between the sampled data points.

Topological analysis and visualization

In this phase, we explore the underlying structure of the space of data points representing the patterns using TDA. We employ Vietoris-Rips (VR) complexes to construct the filtration. The VR complex is an abstract simplicial complex with 0-simplexes as the data points, and $k$ -simplexes are created for any $k+1$ points whose pairwise distances are at most r, while r is fixed and is selected experimentally based on the dataset.

First, the initial simplicial complex is set to be the collection of 0-simplexes corresponding to the sampled data points – that is, the clusters of patients selected in the previous phase – and the VR complexes are constructed considering Jaccard distance as the filtration parameter. Next, the barcodes corresponding to the topological properties of dimension one and higher are generated and visualized (Note that topological properties of dimension zero are the connected components. They show significant relationships between phenotypes, however, they do not reveal logical relationships – implications – among patterns). Finally, the important bars are identified, and their representative cycles are retrieved to identify the logical patterns and infer the hypotheses.

Bias in the clinical notes

Samples collected from unstructured clinical notes are prone to bias. In the absence of a standardized questionnaire, individual physicians could notice and record distinct sets of symptoms. To identify that there was a bias in whether a term might have been selected or not by certain physicians over others, we apply a standard ${\chi }^2$ test among the concepts in the selected cycles from the previous phase. For a specific concept, the variable of ${\chi }^2$ of degree $P-1$ for P populations would be

$$u=\sum _j^{\mathrm{P}}\frac{{(n_j-q{N}_j)}^2}{q{N}_j}$$

where, for a population j, $N_j$ is the total number of samples, $n_j$ is the number of observations of the concept in the population q, and q is the estimate of the proportion that the concept appears across all the populations, which is denoted by

$$q=\frac{\sum _j^P{n}_j}{\sum _j^P{N}_j}$$

Finally, we obtain a degree of certainty to infer hypotheses regarding the existence of alternative biological pathways.

Experimental setup

We begin this section by describing the dataset, then we discuss the experiments.

Dataset

We used the dataset introduced in the study by Xu et al. ²² The dataset is continually updated with the available records of confirmed COVID-19 patients. We used the version published on 8 June 2020. Among the available records in the data set, we retained all the records that their “symptom” field was non-empty, this amounted to 1513 patients. This field, which is a textual feature, is a clinical note describing the patient’s medical state. Of the 1513 subjects included in the study, 640 were women (42.3%) and 873 were men (57.7%).

Experimental details

In the first phase, to parse the clinical notes and extract the biomedical terms, we used Amazon Comprehend Medical (ACM), an online proprietary NLP programming interface to analyze the unstructured clinical notes. For technical details regarding ACM see the study by Jin et al. ²³ We also used the International Classification of Diseases (ICD-10-CM) to select the concepts. Extracted terms are mapped to the concepts by ACM, which brings more uniformity to the translated physician comments. ICD is a medical ontology, published by the World Health Organization to classify diseases, symptoms, and other medical conditions in a comprehensive, hierarchical manner.

ACM associates a list of ICD-10-CM codes to each extracted medical condition, ordered by their confidence scores. Hence, for each extracted term, we retained a code with the highest confidence score. If a medical condition was associated to more than one ICD-10-CM code with high confidence scores, to prevent loss of information we considered all those codes as a group and annotated them by their common prefix code. An example of that includes R53. = {R53.1: Weakness, R53.81: Malaise, R53.83: Other fatigue}. Table 1 provides the list of ICD-10-CM codes that are grouped together. We also incorporated manual supervision when ACM was not able to detect a term due to misspellings, such as “Mialgia” and “Milagia” for “Myalgia.”

Table 1.

Grouped ICD-10-CM concepts.

Class	ICD-10-CM groups
J18.	J18.9, J18.0
J96.	J96.00, J96.01, J96.90
R06.	R06.03, R06.00, R06.02, R06.89, R06.2
R07.	R07.89, R07.9, R07.81
R11.	R11.0, R11.10
R19.	R19.7, R19.8
R53.	R53.1, R53.83, R53.81

ICD-10-CM: International Classification of Diseases.

The first phase of the pipeline resulted in 86 ICD-10-CM codes. However, most clusters associated with the codes were sparse (two or three samples). We filtered sparse classes to enhance the validity of the analysis by obtaining stronger associations among redescriptions. Thus, we retained 31 ICD-10-CM codes. Table 2 presents the selected classes and their number of patients. Based on the data, fever, cough, and fatigue are the most common symptoms among the COVID-19 patients.

Table 2.

Thirty-one ICD-10-CM concepts with the number of patients in each class and their respective percentage of total.

Description	ICD-10-CM	#	%
Acute myocardial infarction	I21.9	5	0.3
Pulmonary heart disease	I27.	0.4	0.4
Cardiac arrhythmia	I49.9	5	0.3
Heart failure	I50.9	9	0.6
Acute pharyngitis	J02.9	136	8.8
Pneumonia	J18.	151	9.7
Nasal sinuses	J34.89	65	4.2
Respiratory failure	J96.	64	4.1
Pain in joint	M25.50	23	1.5
Muscle spasm	M62.838	24	1.6
Myalgia	M79.10	70	4.5
Disorders of bone	M89.8X9	10	0.6
Kidney failure	N17.9	9	0.6
Cough	R05	594	39.3
Abnormalities of breathing	R06.	138	9.1
Sneezing	R06.7	17	1.1
Chest pain	R07.	24	1.6
Abnormal sputum	R09.3	43	2.8
Nasal congestion	R09.81	11	0.7
Abdominal pain	R10.9	6	0.4
Nausea	R11.	29	1.9
Diarrhea	R19.	28	1.8
Dizziness	R42	6	0.4
Fever	R50.9	1073	71
Headache	R51	76	5
Unspecified pain	R52	24	1.6
Fatigue	R53.	177	11.7
Anorexia	R63.0	8	0.5
Sepsis	R65.21	17	1.1
Chills	R68.83	41	2.7
Dry mouth	R68.2	6	0.4

ICD-10-CM: International Classification of Diseases.

In the second phase, we used Algorithm 1 to generate the combinations of codes from the selected classes. Since the algorithm takes advantage of patterns obtained from each patient’s set of symptoms, we provided the number of patients who experienced $k$ symptoms in Table 3. This table suggests that clusters associated to combinations of more than seven symptoms are empty; moreover, there are at most two patterns of size 7 whose clusters are non-empty. Using Algorithm 1, we obtained 734 patterns of non-empty clusters. The runtime of our implementation was about 1 s on a regular personal computer, which is remarkable given that the total number of extracted symptoms is 31 and k = 7.

Table 3.

Number of patients with k symptoms.

$k$	#
1	663
2	462
3	277
4	84
5	23
6	2
7	2

In the third phase, we used Dionysus package for the construction of simplicial complexes and visualization. We also incorporated the Cyclonysus implementation to retrieve the representative cycles of the one-dimensional topological properties. To construct the VR filtration, we set the threshold of the filtration parameter to 0.5. Because Jaccard distance is interpreted as the fraction of subjects that are not shared between the two clusters, hence a distance exceeding 0.5 represents a situation where there is less than 50% chance for any subject to be in both clusters, which does not imply strong clinical relationship among the patterns.

Before we present the main results of the proposed pipeline as a motivating example, we report our experiments on analyzing the extracted data using one of the well-known algorithms.

Biclustering

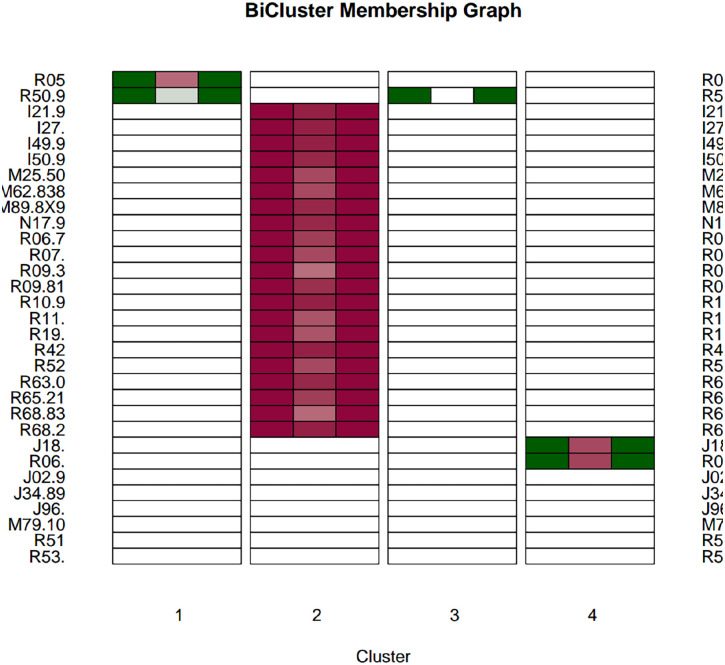
Biclustering algorithms ²⁴ have been widely applied to analyze the association matrix between the samples and the phenotype features and, in particular, are used to identify subgroups of patients who exhibit similar features.^24,25

We are interested in identifying evidence that highlights multiple distinctive biological pathways that lead to the disease. For redescription analysis, and TDA, we are seeking distinct and independent descriptions – patterns – that capture the same subjects, marking connections between phenotypes and underlying biological processes tying these phenotypes together. By Percus’ theorem, cumulants represent factored correlations, which cancel if the cumulant is comprised of independent subsets of features, so they provide a distinct and unique set of phenotype combinations that may be validated by significance tests. Since biclustering generally seeks relationships between subject subsets that share groups of features identified by some variant of low two-way analysis of variance (ANOVA)-like within-groups variations, we considered whether the information provided with these techniques would be informative.

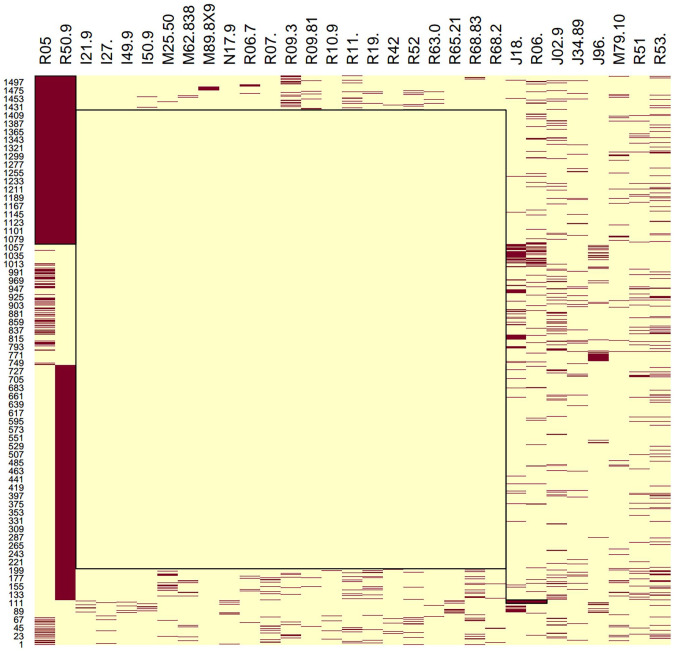
We applied several biclustering algorithms, implemented in the biclust package (version 2.0.3) using the R language (version 4.7.8), on the association matrix between the patients and the ICD-10-CM codes that we obtained from the first phase of the pipeline. The PLAID model offered the largest number of clusters. Figure 4 shows several clusters dominated by just one or two phenotypes, and one large cluster with a number of phenotypes. The heatmap is also shown in Figure 5. The largest cluster may indicate systematic reporting bias excluding some comorbid features among COVID patients. In this situation, approaches such as biclustering identify multivariate associations, but we require more information in order to (1) extract logical implications from the data as provided by redescriptions and (2) derive their topological connectivity elucidating the multiple etiological pathways typifying complex diseases.

Figure 4.

Bicluster membership graph. (A color version of this figure is available in the online journal.)

Figure 5.

Bicluster heatmap graph. (A color version of this figure is available in the online journal.)

Results

In this section, we report the main result and discuss its significance.

We obtained topological properties of dimension 1; there was no topological property of higher dimensions. Figure 6 shows the barcode of the one-dimensional topological properties whose lifetimes are within the interval (0, 0.5). The horizontal axis corresponds to the parameter of the filtration – Jaccard distance – and the vertical axis corresponds to the number of properties.

Figure 6.

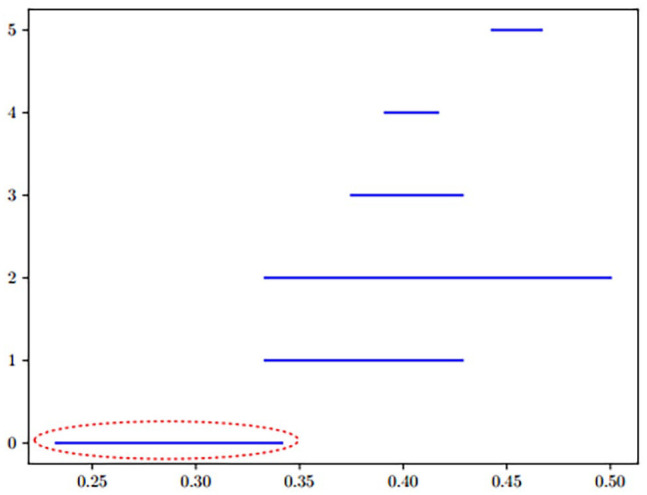
Barcode of one-dimensional topological properties. (A color version of this figure is available in the online journal.)

First, we retrieved a representative cycle for each bar in Figure 7. Next, we selected the cycles based on two factors: (1) Cycles that are dominated by sparse clusters are weak for inferring clinical hypothesis, hence it is important to note the number of subjects. (2) With respect to the size of the clusters, cycles with low Jaccard distances have higher preference. At any two data points, the lower the distance, the more similar are their sets of patients. Therefore, low Jaccard distances lead to better estimations of redescriptions. Considering these two factors, of the retrieved cycles, only one stood out; it corresponds to the first bar annotated by the circled line – spans between 0.23 and 0.34. The other bars not only belong to the higher Jaccard distances, but also correspond to small clusters. Hence, what follows is an account of the one-dimensional topological property, which is striking.

Figure 7.

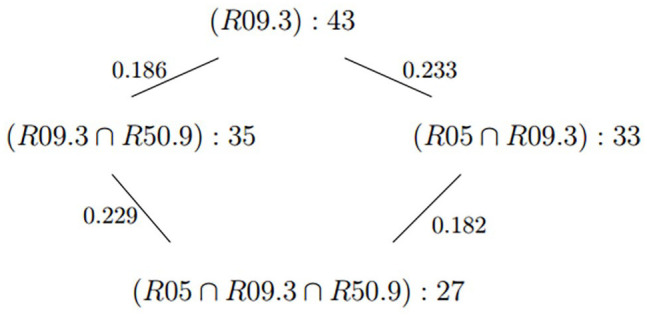
Representative cycle of the annotated bar.

This cycle suggests that among the subjects in R09.3 – abnormal sputum – there is not a particular interaction between subjects in R05 – Cough – with subjects in R50.9 – fever. This opens the question of whether there is a distinctive signature showing alternative pathways to disease among dry coughers compared to productive coughers.

Discussion

To interpret the relationships between the symptoms in Figure 7, we rely on Jaccard distance. Since the equivalence of sets of subjects matching different patterns produces logical constraints determined by biological processes, multiple pathways connecting phenotypes to disease may yield information about multigenic complex diseases marked by multiple pathways leading to disease. However, phenotype definitions are prone to misclassification for several reasons. Therefore, equivalence may be meaningfully characterized based on the chances that a subject in one or the other of two phenotype clusters is not in both, which is the Jaccard distance, described above.

In the case of Figure 7, which corresponds to a subset of patients of size 43 (Table 4), there are two paths leading from R09.3 (abnormal sputum) to $\mathrm{R}05\cap \mathrm{R}09.3\cap \mathrm{R}50.9$ , one passing through $\mathrm{R}09.3\cap \mathrm{R}50.9$ and the other through $\mathrm{R}05\cap \mathrm{R}09.3$ , where R05 is cough and R50.9 is fever. In both pathways, the distances between sputum and cough is larger than that between sputum and fever. So coughing is not as strong an association as fever for abnormal sputum production. In this case, the relationship between sputum and fever is independent of coughing since the cycle appears to be a parallelogram. So, a coughing symptom is independent of fever among sputum productive subjects. This suggests the paths are independent predictors of severe disease.

Table 4.

Age groups of the 43 subjects in R09.3.

Age	#	%
<30	4	9
30–39	4	9
40–49	11	26
50–59	7	16
60–69	6	14
70–79	5	12
80–89	6	14

The patient records were generally gleaned from hospital records, suggesting some level of severity among those we had any records for. Those items whose ICD-10-CM records we retained related to severity would include sepsis, pneumonia, kidney failure, and so on. Some cardiac features may refer to pre-existing comorbidities or were perhaps acutely induced in COVID-19; the records are not clear on the point. So, it may not be clear if associations with these features indicate susceptibility due to comorbidities, or whether they are caused by COVID-19 among more severe patients. In any case, any significant associations may be identified, even if the chronic/acute status has not been recorded.

One of the major limitations of the approach involves missing clinical outcomes and non-standardized physician records. Since there was no systematic design for study enrollment or questionnaire construction, correlations between recorded symptoms and outcomes could be induced by individual physician preferences at the facilities from which the records were gleaned. For example, it would not be clear whether cough productivity (sputum) would be due to a distinct set of severe cases, or whether a specific physician dealing with severe patients noted productivity. This would yield an apparently distinct group of severe patients with larger Jaccard distances from other groups.

COVID-19 refers to the disease that emerged from infection of severe acute respiratory syndrome coronavirus 2 (SARS-COV-2) virus. As such, disease presentation includes cytokine storms, vascular leaking, and other features that may be associated with physiological response to the virus. While cytokine storms are shared among some respiratory infections, COVID-19 shows some very distinctive features in response among severe patients. The nature of that response among patients with certain comorbidities is also a hallmark of COVID-19. Patients that are selected as relevant to specific clusters (redescriptions) are good candidates for identifying differences in gene expression levels or other genetics or proteomics that may mark these as distinctive pathways, offering a window to the process – if such associated data were available. As it stands, scope has been limited by what data have been available. We have no sequence (subject or virus), -omics, or other data associated with these records; so given available scope, we have not articulated this what-if.

Distinctive feature of COVID-19 is the rarity of productive coughs. Given that these symptom cycles reflect correlations among several features including phlegm, we sought to understand or identify bias in how this symptom was recorded. The first feature was that the choice of word was idiosyncratic. Some reports preferred “phlegm” others “sputum” or “expectoration” leading to the question of whether the words were specific to individual physicians more prone to reporting an observation of a productive cough. However, the records included in the database were scraped and translated from records in the languages of the source regions. The selection of terminology was an artifact of the translation software in the pre-processing step, and not necessarily reflective of individual physicians. Furthermore, in any one country, the reports spanned multiple provinces, indicating that the reports did not issue from any specific clinic, in general.

Another level of test was to check whether there were some regions more likely to pay attention to productivity in coughs due to variations in traditional medical practices and education. We applied the standard chi-square test, $n_j$ , as mentioned in the last phase of the pipeline, $N_j$ is the number of regional jurisdictions in the database, q is the number of records showing an ICD-10-CM of R09.3, q is the number of patient records scraped from the regional jurisdiction, and % is the estimate of the proportion of cases with ICD-10-CM of R09.3. Two outliers were identified in Heilongjiang, China, who had four patients, all with productive cough; and Ulsan, South Korea, which had two patients, all with productive cough. Excluding these, the representative q = 2.498 %, with a p-value of 0.996, indicating the variations in reported R09.3 across populations well within levels expected due to sampling variation. So, we do not accept the hypothesis that bias is present, except possibly in the two outliers.