PyNomo software dataset for sciences and engineering nomogram construction

Abstract

This article examines different python-based codes to be run under PyNomo nomographer software to represent alignment charts or nomograms for formulas commonly used in sciences and engineering studies. PyNomo nomographer supports nine basic types of nomograms based on the format of the mathematical equation. The examined PyNomo codes cover the construction of the following types of nomogram: type 1, type 2, type 7, type 8, type 9, and type 10. Each PyNomo script includes some background and the underlying mathematics for the nomogram construction and how to implement each code into PyNomo software. Potential users can use these PyNomo codes, as template scripts, to customize and construct their own nomograms for a variety of technical applications. That is especially true since a considerable number of science and engineering equations fall into one of these covered nomogram types depending on the equation form involved.

Specifications Table

Subject	Computer Science
Specific subject area	Computer Graphics and Computer-Aided Design. Computer nomograph construction aided by PyNomo nomographer software for science and engineering applications.
Type of data	Python-based code (for PyNomo nomographer software). Images
How the data were acquired	All source codes written in Python language and run through PyNomo software to produce nomograms or abacs in a PDF vector form.
Data format	Pynomo monographer software scripts (.py extension).
Description of data collection	Most PyNomo scripts are listed in a single file. These files were run under PyNomo software to generate each graph that solves the mathematical equation from which the nomogram is based on.
Data source location	Institution: Department of Mining and Civil Engineering, Universidad Politécnica de Cartagena City/Town/Region: Cartagena Country: Spain
Data accessibility	With the article and in Zenodo repository (please refer to References section for Zenedo repositoty URL addresses and data identification name (DOI))
Related research article	P. Martínez-Pagán, L. Roschier, Nomography: A renewed pedagogical tool to sciences and engineering high-education studies, Heliyon. (2022).10.1016/j.heliyon.2022.e09731 (Available online 15 June 2022, e09731).

Value of the Data

• •These PyNomo codes have significant value to potential PyNomo users in 2 ways: 1) they enable to realize of the actual capability of nomography to solve science and engineering equations, and 2) they will help to grasp the basic to produce useful nomograms for a wide range of mathematical expressions of common use in science and engineering.
• •Scientists, engineers and/or teachers could benefit from these datasets since they provide the basic skills to design and interpret nomograms as well as letting them include nomography as a valuable computational tool in an academic context, such as sciences and engineering studies.
• •With minimal editing effort, these PyNomo codes can be easily modified to produce nomograms for other types of equations where they could benefit of PyNomo software to produce in seconds outstanding and customized nomograms.

1. Data Description

In nomography, one of the most difficult or demanding stages is drawing reliable scales or grids. Presumably that has been one of the main reasons for the decline of nomogram use in an academic environment, in which the appearance of more capable and powerful personal computers and handheld calculators helped to intensify this tendency. However, the introduction of PyNomo software [1] solves the most cumbersome point of manually constructing precise nomograms. Thus, this software, which has been written by one of the authors (LR), is a significant step forward to promote users to introduce nomography successfully into an academic context. PyNomo can be found at http://lefakkomies.github.io/pynomo-doc/installation/installation.html. PyNomo is a Python library and thus requires the installation of several other Python-based software packages, such as numpy, scipy and pyx that requires LaTeX-installation. From more recent PyNomo versions (presently, from 0.3.0 to 0.3.2), the software is compatible with Python 2 and Python 3. For editing PyNomo scripts any text browser works but integrated development environment (IDE) for Python can speed up developments (e.g. PyCharm community edition and spyder). Also, comprehensive and detailed instructions for the successful installation of PyNomo on Windows, as well as OSX and Linux, platforms are found on the previously indicated website.

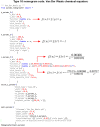
PyNomo scripts are written in text files saved with the suffix .py since they are interpreted by Python. Once the PyNomo script is run a PDF or EPS file is created, which is vector-based so it is totally scalable and suitable for additional artwork is desired. Moreover, PyNomo supports nine basic types of nomograms based simply on the format of the equation (Fig. 1).

Fig. 1.

Types of nomograms supported by PyNomo software.

2. Design, Materials and Methods

This section examines the methodology used for different python-based codes written to be run under PyNomo software to construct an appropriate representation of nomogram examples for equations commonly used in sciences and engineering studies. These examples enable potential users to grasp the importance and significant capabilities of PyNomo software in a science and engineering learning context. In line with that, the nomogram types covered with these examples will be type 1, type 2, type 7, type 8, type 9, and type 10. It is worth noting that these scripts are reusable since they can graphically represent a great number of common mathematical equations, by means of PyNomo software, with the appropriate code editing for the needs of each end-user.

The employ of these dataset to solve their associated nomograms by means of PyNomo software avoid the need of manually constructing the nomographic charts [2]. This point is relevant since the construction of nomographic charts is time demanding and require certain degree of skillfulness for obtaining them accurately [2]

2.1. Type 1 Nomogram Code

The code provided here below constructs Type 1, or 3 parallel scales nomogram. This type of script plots a considerable number of functions, commonly employed in engineering, of the form:

$$f_1\left(u_1\right)+f_2\left(u_2\right)+f_3\left(u_3\right)=0$$ (1)

Where u₁, u₂, and u₃ are the scale variables.

The code of this example enables to graph the slurry flow equation for pumped pipes, which is written as:

$$Q_{slurry}=0.28*\left(\frac{\%Water}{\%Solids}+\frac{1}{{\rho }_{solids}}\right)$$ (2)

Where Q_Slurry is the slurry flow per t/h of solids, in l/s; %Water indicates the percentage of water in the slurry; %Solids indicates the percentage of solids in the slurry; and ρ_solids is the specific density, in g/cm³. Now, by arranging the terms of this formula, the form that satisfies the expression (1) is:

$$\frac{Q_{slurry}}{0.28}-\frac{100-\%Solids}{\%Solids}-\frac{1}{{\rho }_{solids}}=0$$ (3)

Since:

$$f_1\left(Q_{slurry}\right)-f_2(\%Solids)-f_3\left({\rho }_{solids}\right)=0$$ (4)

Below is the PyNomo script that makes this 3 parallel scales nomogram. The script has a typical and simple structure composed of a different set of parameters. Commonly, this set of parameters comprises: scale parameters, which define the function, variable title, etc., block parameters that define the scale name, its type and size, and main parameters constituted by the block names, paper size, equation title and transformations to apply. Thus, the scale parameters of the Type 1 nomogram code of this example are defined by “S_params”, “P_params”, and “V_params”. The block parameters are defined by “block_1_params”, and the main parameters by “main_params”. In the script, the variable u represents the variables of the functions for the Eq. (4). Also, the script includes the construction of an isoplepth that helps interpret the nomogram. The code of this isopleth is written in “block_1_params” where the values of %Solids and ρ_solids, which are 40 and 2.65, respectively, will define the value of Q_slurry when the isopleth intersects the Q_slurry scale. The supplementary material provides this final nomogram under scalable format. Also, the script is available in the Zenodo repository [3]. It worth noting that this script could work as a guideline script to reproduce other equations of the form (1) with the appropriate modifications.

2.2. Type 2 Nomogram Code

This code constructs a Type 2, or N/Z nomogram, which graphically presents quite common functions in sciences and engineering studies that are under the form (included all their variations):

$$f_2\left(u_2\right)=\frac{f_1\left(u_1\right)}{f_3\left(u_3\right)}$$ (5)

Where u₁, u₂, and u₃, are the scale variables.

Below is the PyNomo script for the index of refraction nomogram, whose equation satisfies the form (7):

$$I_R=\frac{\sin I}{\sin R}$$ (6)

Knowing that I_R is the index of refraction, dimensionless (from 0 to 10); I is the angle of incidence, in degrees (from 0° to 90°); and R is the angle of refraction, in degrees (from 0° to 90°).

In the script the variables u₁, u₂, and u₃, represent I, I_R, and R. It has to be highlighted that PyNomo scripts require to formulate trigonometric functions in radians. The script has a typical and simple structure composed of a different set of parameters. Potential users can adjust this script to other similar formulations by making appropriate changes. The script is available in the Zenodo repository [4] to help accomplish this goal. Again, the supplementary material provides the scalable nomogram for this equation.

2.3. Type 7 Nomogram Code

This code constructs a Type 7 nomogram, which graphically displays functions related by their reciprocals. Thus, the nomogram constructed with the script of this example represents the equation:

$$\frac{1}{F_1}-\frac{1}{F_2}=\frac{1}{F_3}$$ (7)

Where F₁, F₂, and F₃, are variables.

Below is the PyNomo script that makes a three scales reciprocal type nomogram. In the script, the variable u represents the functions of the Eq. (9) that in this example are F₁, ranging from 10 to 100 (N_params_1), F₂ ranging from 10 to 300 (N_params_2), and F₃ ranging from 0 to 100 (N_params_3). Also, the script includes the construction of an isoplepth that helps interpret the nomogram. The code of this isopleth is written in “block_1_params” where the values of F₁ and F₃, which are 50 and 80, respectively, will define the value of F₂ when the isopleth intersects the F₂ scale. The supplementary material provides the created nomogram by PyNomo software. Also, the script ready to be run under PyNomo software is available in the Zenodo repository [5].

2.4. Type 1/Type 8 Combined Nomogram Code

This example examines the combination of two types of nomograms to represent the earthquake magnitude determination: type 1 and type 8 nomogram. This nomogram combination is especially useful when is required variable conversion taking place into a nomogram of any type. The variable conversion is obtained with the code provided for type 8 nomograms, which is named as single, simple function scale. It provides a means of aligning (or overlaying) a scale right on top of another scale using the parameter “tag”. Thus, scales with the same “tag” parameter will be aligned (overlaid) in the final nomogram. In this example the magnitude conversion between earthquake Richter magnitude and moment magnitude. The earthquake Richter magnitude function can be written as:

$$M_L-{\log }_{10}\left(A_{\max }\right)+0.000008\times D^2-0.01\times D-1.8783=0$$ (8)

Where M_L is the Richter magnitude, dimensionless; D is the distance between the point of earthquake occurrence and the seismic recording site, in km; A_max is the maximum amplitude, in mm.

Thus, the Eq. (9) fulfils a type 1 nomogram of the form:

$$f_1\left(M_L\right)+f_2\left(A_{\max }\right)+f_3\left(D\right)=0$$ (9)

On the other hand, the expression to convert Richter magnitude values to moment magnitude (M_w) values is given by Mereu [6]:

$$M_w=0.59\times M_L+1.32$$ (10)

Now the Eqs. (8) and (10) satisfy type 1 and type 8 nomogram expressions, respectively, so the code can be easily written. This finished code is provided below where “block_2_params” defines the code for creating type 8 nomograms, as it is described by Doerfler [7], and where the “tag” parameter is named ‘ML’. Also, the script is available in the Zenodo repository [8].

2.5. Type 8 Wheel Nomogram Code

This code consists of a set of circular scales based on Type 8 nomogram to convert pressure units in a very convenient way, which are of common use in the fields of hydraulics, geotechnics, physics, etc. Type 8 or single scale nomogram, which another example was described in Section 2.4, is the most basic nomogram type satisfying the basic form of:

$$y=f\left(u\right)$$ (11)

This Type 8-based circular nomogram was constructed following the comprehensive indications provided by Doerfler [7] to deal with this type of curved nomogram.

Below is provided the script block to construct the atmosphere unit curved scale from 0.1 to 9.99 atms, in which the function_x and function_y parameters allow the scale curvature to be defined by functions of u in terms of x and y. In this example, a linear scale from 0.1 to 9.99 atms to be laid out in a circle of radius 7.0 cm, should be written as:

$$\begin{array}{ccc}& & {}^{\prime }function\_x^{\prime }:lambdau:7.0*cos(2*pi*(log10\left(u\right)-log10\left(0.1\right))/(log10\left(9.99\right)-log10\left(0.1\right)\left)\right),\hfill \\ & & {}^{\prime }function\_y^{\prime }:lambdau:7.0*sin(2*pi*(log10\left(u\right)-log10\left(0.1\right))/(log10\left(9.99\right)-log10\left(0.1\right)\left)\right),\hfill \end{array}$$ (12)

By using the same radius but with the ticks on the opposite side, two scales can overlay. The other scales provide the conversion of PSI, mm Hg, kN/m², kPa, kg/cm², Bar, and m.c.a units. All the scales repeat the same basic set of parameters, making it easy to write the script. For sake of simplicity only the atmosphere unit script block is provided, however the complete script is available in the Zenodo repository [9] to help to obtain the circular nomogram.

2.6. Type 9 Nomogram Code

Type 9 nomogram code enables to construct of those mathematical expressions that can be put into determinant form as follows:

$$\left|\begin{array}{ccc}{f}_1\left(u_1,v_1\right)& g_1\left(u_1,v_1\right)& h_1\left(u_1,v_1\right)\\ f_2\left(u_2,v_2\right)& g_2\left(u_2,v_2\right)& h_2\left(u_2,v_2\right)\\ f_3\left(u_3,v_3\right)& g_3\left(u_3,v_3\right)& h_3\left(u_3,v_3\right)\end{array}\right|=0$$ (13)

Where u_i, and v_i, are variables.

Accordingly, the trajectory of a projectile could be determined through a type 9 nomogram, where its expression is given by [10]:

$$y=x·\tan \alpha -\frac{g·x^2}{2·V_0^2·{\cos }^2\alpha }$$ (14)

Knowing that Eq. (14) can be put under the determinant form that justifies the standard expression for Type 9 nomogram:

$$\left|\begin{array}{ccc}\frac{g}{2·V_0^2}& 0& 1\\ y& 1& 1\\ \frac{x·\tan \alpha ·{\cos }^2\alpha }{x^2+{\cos }^2\alpha }& \frac{{\cos }^2\alpha }{x^2+{\cos }^2\alpha }& 1\end{array}\right|=0$$ (15)

Next the complete script is provided, in which ‘f’ represents the function in u, given by the first column in the determinant row corresponding to the scale, ‘g’ represents the function in u, given by the second column in the determinant row corresponding to the scale, and ‘h’ represents the function in u, given by the third column in the determinant row corresponding to the scale. Consequently, following that criterion functions in the determinant (15) can be expressed as:

$$\begin{array}{ccc}& & f_1\left(u_1\right)=\frac{g}{2*V_0^2};g_1\left(u_1\right)=0;h_1\left(u_1\right)=1\hfill \\ & & f_2\left(u_2\right)=y;g_2\left(u_2\right)=1;h_2\left(u_2\right)=1\hfill \\ & & f_3\left(u_3,v_3\right)=\frac{x·\tan \alpha ·{\cos }^2\alpha }{x^2+{\cos }^2\alpha };g_3\left(u_3,v_3\right)=\frac{{\cos }^2\alpha }{x^2+{\cos }^2\alpha };h_3\left(u_3,v_3\right)=1\hfill \end{array}$$ (16)

Therefore, these functions are written accordingly in the script provided below, noting that angles are to be expressed in radians. Also, the complete script is available in the Zenodo repository [11] to help to obtain the type 9 based projectile trajectory nomogram using PyNomo software.

2.7. Type 10 Nomogram Code

A Type 10 nomogram consists of two straight scales and one curved scale. This type of nomogram represents equations of the form:

$$f_1\left(u_1\right)+f_2\left(u_2\right)*f_3\left(u_3\right)+f_4\left(u_4\right)=0$$ (17)

Where u_i are variables.

The Type 10 nomogram code is used in this example to graph the chemical equation of Van Der Waals, which is commonly written as:

$$\left(p+\frac{a}{v^2}\right)*\left(v-b\right)=R*\left(t+273.15\right)$$ (18)

Here p is the pressure, in Atm; v is the volume, in litres, L; R is a gas constant, in L-Atm/mol-°K; t is the absolute temperature, in centigrades degrees, °C; a and b are constants which depends on the type of gas. In this example, the carbon dioxide (CO₂) gas will be considered, whose R, a, and b constants are 0.00366, 0.00717, and 0.00191, respectively.

Thus, Eq. (18) can be put under a form that satisfies expression (17) as follows:

$$f_1\left(p\right)-f_2\left(t\right)*f_3\left(v\right)+f_4\left(v\right)=0$$ (19)

Therefore, the expression that is obtained once the different variables of Eq. (19) are properly arranged, in relation to the expression (17), will be:

$$p-t*\frac{0.00366}{v-0.00191}-\frac{273.15*0.00366}{v-0.00191}+\frac{0.00717}{v^2}=0$$ (20)

As shown below the complete script to construct the nomogram for the Van Der Waals chemical equation. Moreover, introducing the appropriate changes, that script can be reused to construct the nomogram for other formulas that could satisfy Eq. (17). Consequently, this reusable script is available in the Zenodo repository [12] to help to obtain any Type 10 nomogram through PyNomo software.

Ethics Statements

Authors state that the data supporting their paper meet the data requirements of the journal, ensuring that they have written a original work, not submitting this paper for consideration in another journal. Authors, also, declare not conflict of interest, or any financial of this work. Moreover, authors declares not potential ethical issues in the paper or during its writing.

CRediT authorship contribution statement

Pedro Martínez-Pagán: Conceptualization, Data curation, Methodology, Writing – original draft. Leif Roschier: Conceptualization, Methodology, Software, Validation, Writing – review & editing.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

The authors declare the following financial interests/personal relationships which may be considered as potential competing interests:

Please declare any financial interests/personal relationships which may be considered as potential competing interests here.

Data Availability

• Type 10 nomogram code for Pynomo software. Van Der Waals equation (Original data) (Zenodo).

• Type 9 nomogram code for Pynomo software. Projectile trajectory formula (Original data) (Zenodo).

• Type 8 nomogram code for Pynomo software. Pressure unit wheel conversion (Original data) (Zenodo).

• Type 1/Type 8 combined nomogram code for Pynomo software. Seismic magnitude of earthquakes (Original data) (Zenodo).

• Type 7 reciprocal nomogram code for Pynomo software (Original data) (Zenodo).

• Type 2 nomogram code for Pynomo software. Index of refraction formula (Original data) (Zenodo).

• Type 1 nomogram code for Pynomo software. Slurry flow formula (Original data) (Zenodo).