The Standardized S-X² Statistic for Assessing Item Fit

Abstract

The S-X² statistic (Orlando & Thissen, 2000) is popular among researchers and practitioners who are interested in the assessment of item fit. However, the statistic suffers from the Chernoff–Lehmann problem (Chernoff & Lehmann, 1954) and hence does not have a known asymptotic null distribution. This paper suggests a modified version of the S-X² statistic that is based on the modified Rao–Robson χ² statistic (Rao & Robson, 1974). A simulation study and a real data analyses demonstrate that the use of the modified statistic instead of the S-X² statistic would lead to fewer items being flagged for misfit.

Introduction

The Standard 4.10 of the Standards for Educational and Psychological Testing (American Educational Research Association, American Psychological Association, & National Council for Measurement in Education, 2014) recommends documenting evidence of model-data fit when an item response theory (IRT) model is employed in test development and score reporting. In practice, analysis of model-data fit for IRT models involves the use of item-fit residuals and χ²-type statistics (Hambleton & Han, 2005). Among the χ²-type statistics for IRT models, the S-X² statistic (Orlando & Thissen, 2000) is popular, presumably because of four reasons. First, to compute S-X², one has to divide the examinees into groups based on their observed total scores rather than the estimated abilities. Second, S-X² has been found to perform respectably in terms of Type I error rates and power in simulation studies (e.g., Glas & Suarez-Falcón, 2003; Sinharay, 2006; Sinharay & Lu, 2008; Stone & Zhang, 2003). Third, the simple and intuitive nature of S-X² has allowed it to be easily generalized to cases with polytomous items (Kang & Chen, 2008, 2010), multidimensional examinee abilities (Zhang & Stone, 2007), unfolding models (Roberts, 2008), and cognitive diagnostic models (e.g., Sorrel et al., 2017). Fourth, S-X² is implemented in multiple IRT software packages including irtplay (Lim, 2020), mirt (Chalmers, 2012), and IRTPRO (Cai et al., 2011)

Notwithstanding these appealing features, S-X² should not be used without considering its limitations. As noted by researchers such as Sinharay (2006), S-X², which is a special case of the Pearson’s χ² statistic (Pearson, 1900), does not have a known asymptotic null distribution in typical IRT applications where the traditional marginal maximum likelihood estimates (MMLEs) of item parameters are used to compute the statistic. Instead, the values of S-X² are stochastically larger than those from the theorized (χ²) distribution of the statistic. As a consequence, the Type I error rates of S-X² tend to be slightly larger than the nominal level even for large samples, which has been observed in multiple simulation studies (e.g., Glas & Suarez-Falcón, 2003; Sinharay, 2006; Sinharay & Lu, 2008). The aim of this paper is to introduce a modified S-X² statistic that has a known χ² asymptotic null distribution.

The next section includes a review of the Pearson’s χ² statistic used for assessing general model-data fit and the S-X² statistic (Orlando & Thissen, 2000) for assessing item fit, followed by a brief review of a potential problem associated with the use of the Pearson’s χ² statistic (Chernoff & Lehmann, 1954). The section also includes a description of the modified Pearson’s χ² statistic that Rao and Robson (1974) suggested to overcome the Chernoff–Lehmann problem. The method section presents the details of our modified S-X² statistic that is a special case of the modified Pearson’s χ² statistic. The section on simulation studies compares the modified S-X² statistic with the original S-X² statistic with respect to Type I error rates and power. The two statistics are compared using a real data set in the penultimate section. Conclusions and recommendations are provided in the last section. Although the S-X² statistic has been extended to tests with polytomously scored items (Kang & Chen, 2008, 2010), we will only consider tests with dichotomously scored items.

Background: Pearson’s χ², Orlando-Thissen’s S-X², Chernoff–Lehmann Problem, and Rao–Robson’s Modified χ²

Pearson’s χ² Statistic

Let us assume that a sample with N independent observations, y₁, y₂, …, y _N , is available from a population. Suppose that p(y _i ; η ), the probability distribution of y _i , involves a parameter vector η with L elements. Suppose that the observations are partitioned into K groups (or cells) and the proportion of observations belonging to group k is $p_k=\frac{Nk}{N}$ , where N _k represents the number of observations in group k, k = 1, 2, …, K. Let π _k ( η ) denote the expected value of p _k under the assumed probability distribution.

Pearson’s χ² statistic (Pearson, 1900) for assessing goodness of fit, denoted henceforth as P-X², is defined as

$$\mathrm{P}-X^2=N{\displaystyle \sum }_{k=1}^K\frac{{\left(p_k-{\pi }_k\left(\mathit{\eta }\right)\right)}^2}{{\pi }_k\left(\mathit{\eta }\right)}={\left[\mathit{u}\left(\mathit{\eta }\right)\right]}^{\top }\mathit{u}\left(\mathit{\eta }\right),$$ (1)

where

$$\mathit{u}\left(\mathit{\eta }\right)=\sqrt{N}{\left(\frac{p_1-{\pi }_1\left(\mathit{\eta }\right)}{\sqrt{{\pi }_1\left(\mathit{\eta }\right)}},\frac{p_2-{\pi }_2\left(\mathit{\eta }\right)}{\sqrt{{\pi }_2\left(\mathit{\eta }\right)}},\dots ,\frac{p_K-{\pi }_K\left(\mathit{\eta }\right)}{\sqrt{{\pi }_K\left(\mathit{\eta }\right)}}\right)}^{\top }.$$ (2)

In practice, the parameter vector η is unknown and P-X² is computed by replacing η by $\widehat{\mathit{\eta }}$ , which is the maximum likelihood estimate (MLE) of η , and is assumed to follow a χ² distribution with K − L − 1 degrees of freedom (df ), or, the ${\chi }_{K-L-1}^2$ distribution, for large samples under no item misfit.

Orlando and Thissen’s S-X² Statistic

Orlando and Thissen (2000) developed the S-X² statistic, which is a special case of the Pearson’s χ² statistic, to assess item fit in the context of IRT models for dichotomously scored items. Suppose that we are interested in assessing item fit for a J-item test. To compute S-X² for a given item of interest, the examinees are divided into (J + 1) groups, where group k includes all the examinees whose raw score is k. Let N _k denote the size of group k. One then computes, for each group k, O _k , which is the observed proportion of test-takers in the group who answered the item correctly. The statistic S-X² for the item is then computed as

$$\mathrm{S}-X^2={\displaystyle \sum }_{k=1}^K\frac{N_k{\left[O_k-E_k\left(\mathit{\eta }\right)\right]}^2}{E_k\left(\mathit{\eta }\right)\left[1-E_k\left(\mathit{\eta }\right)\right]}={\left[\mathit{v}\left(\mathit{\eta }\right)\right]}^{\top }\mathit{v}\left(\mathit{\eta }\right),$$ (3)

where K = J − 1, E _k ( η ) is the expected value, under the IRT model, of O _k

$$\mathit{v}\left(\mathit{\eta }\right)={\left(\frac{\sqrt{N_1}\left[O_1-E_1\left(\mathit{\eta }\right)\right]}{\sqrt{E_1\left(\mathit{\eta }\right)\left[1-E_1\left(\mathit{\eta }\right)\right]}},\frac{\sqrt{N_2}\left[O_2-E_2\left(\mathit{\eta }\right)\right]}{\sqrt{E_2\left(\mathit{\eta }\right)\left[1-E_2\left(\mathit{\eta }\right)\right]}},\dots ,\frac{\sqrt{N_K}\left[O_K-E_K\left(\mathit{\eta }\right)\right]}{\sqrt{E_K\left(\mathit{\eta }\right)\left[1-E_K\left(\mathit{\eta }\right)\right]}}\right)}^{\top },$$ (4)

and the L × 1 vector η includes the parameters of the item of interest, that is, $\mathit{\eta }={\left({\eta }_1,\dots ,{\eta }_L\right)}^{\top }$ , where L could vary over the items depending on the assumed IRT model, and, for example, would be equal to 2 if the two-parameter logistic (2PL) model is used. Let v _k ( η ) denote the k-th element of v ( η ).

In computing the S-X² statistic, the number of examinee groups (K) is typically equal to J − 1 because O₀ = E₀( η ) = 0 and O _J = E _J ( η ) = 1 for any data set. For small samples, to ensure that the expected number of examinees is not too small in any examinee group, some groups may be merged and K can be set equal to a number smaller than J − 1. In the simulations and empirical data examples for this paper, groups with fewer than 5 expected number of test-takers were merged, as was recommended by Orlando and Thissen (2000). However, for the sake of simplicity, merging is not considered in the theoretical derivations.

The expected proportion of examinees for group k, E _k ( η ), is computed as

$$E_k\left(\mathit{\eta }\right)=\frac{\int P\left(Y=1|\theta ,\mathit{\eta }\right)P\left(T_{-1}=k-1|\theta ,\mathit{\eta }\right)\psi \left(\theta \right)d\theta }{\int P\left(T=k|\theta ,\mathit{\eta }\right)\psi \left(\theta \right)d\theta },$$ (5)

where Y is the score of a randomly chosen examinee on the item of interest, P(Y = 1|θ, η ) is the probability that Y is equal to 1 given examinee ability θ and item parameters η , T is the total (raw) score on the test, T₋₁ is the rest score, or the total score on all items except the item of interest, $P\left(T=k|\theta ,\mathit{\eta }\right)$ is the probability that T is equal to k given ability θ and item parameters η , $P\left(T_{-1}=k-1|\theta ,\mathit{\eta }\right)$ is the probability that the rest score given ability θ is equal to k − 1, and ψ(θ) is the population distribution of the examinee ability and typically assumed to be the standard normal distribution. The integrals in equation (5) are approximated using numerical integration.

The expressions P(Y = 1|θ, η ), $P\left(T_{-1}=k-1|\theta ,\mathit{\eta }\right)$ , and $P\left(T=k|\theta ,\mathit{\eta }\right)$ depend on the IRT model fitted to the data. If, for example, the 2PL model is used, then

$$P\left(Y=1|\theta ,\mathit{\eta }\right)=\frac{\exp \left[a\left(\theta -b\right)\right]}{1+\exp \left[a\left(\theta -b\right)\right]},$$

where a and b, respectively, are the slope and difficulty parameters of the item of interest. Also, the terms $P\left(T_{-1}=k-1|\theta ,\mathit{\eta }\right)$ and $P\left(T=k|\theta ,\mathit{\eta }\right)$ are computed using the Lord–Wingersky recursion formula (Lord & Wingersky, 1984).

Orlando and Thissen (2000) assumed that the asymptotic null distribution of S-X² is the ${\chi }_{K-L}^2$ distribution.

The Chernoff–Lehmann Problem with the Pearson’s χ² Statistic

A critical step in defining P-X², the Pearson’s χ² Statistic, is the partitioning of the data into K groups. Under the setup of subsection 2.1, the grouped data comprise O _k = Np _k , k = 1, 2, …, K,. Because the O _k ’s follow the multinomial distribution (e.g., Agresti, 2013, p. 6), the log-likelihood of η based on the grouped data is given by

$$\log \prod _k{\left[{\pi }_k\left(\mathit{\eta }\right)\right]}^{N{p}_k}=N{\displaystyle \sum }_k{p}_k\log {\pi }_k\left(\mathit{\eta }\right).$$ (6)

Fisher (1924) proved that if P-X² is computed using the estimated parameter vectors $\stackrel{\sim }{\mathit{\eta }}$ that maximizes the log-likelihood provided in equation (6), then the asymptotic null distribution of P-X² is the ${\chi }_{K-L-1}^2$ distribution. That is, for large samples and under no model misfit

$$\mathrm{P}-X^2={\left[\mathit{u}\left(\stackrel{\sim }{\mathit{\eta }}\right)\right]}^{\top }\mathit{u}\left(\stackrel{\sim }{\mathit{\eta }}\right)\sim {\chi }_{K-L-1}^2.$$ (7)

The distribution reflects a loss of 1 df for each parameter that is estimated. The estimate $\stackrel{\sim }{\mathit{\eta }}$ is often referred to as the minimum χ² estimator (e.g., Harris & Kanji, 1983).

Let $\widehat{\mathit{\eta }}$ denote the MLE of η , which is computed by maximizing

$${\displaystyle \sum }_{i=1}^N\log f\left({\mathit{y}}_{\mathit{i}},\mathit{\eta }\right),$$

which is the log-likelihood for the original/ungrouped data.

Chernoff and Lehmann (1954) proved that if one uses $\widehat{\mathit{\eta }}$ to compute P-X², the corresponding statistic

$$\mathrm{P}-X^2={\left[\mathit{u}\left(\widehat{\mathit{\eta }}\right)\right]}^{\top }\mathit{u}\left(\widehat{\mathit{\eta }}\right)\sim {\chi }_{K-L-1}^2+{\displaystyle \sum }_{l=1}^L{\lambda }_l\left(\widehat{\mathit{\eta }}\right){\chi }_1^2,$$ (8)

where 0 < λ _l ( η ) < 1; that is, the statistic is somewhere between a ${\chi }_{K-L-1}^2$ variable and a ${\chi }_{K-1}^2$ variable on average. Equation (8) implies that if a statistic of the form ${\left[\mathit{u}\left(\widehat{\mathit{\eta }}\right)\right]}^{\top }\mathit{u}\left(\widehat{\mathit{\eta }}\right)$ is used to assess item fit and the ${\chi }_{K-L-1}^2$ distribution is used to approximate the limiting distribution of the statistic, the null hypothesis of adequate model fit will be rejected more often than is appropriate, which would result in an inflated Type I error rate of the fit-assessment approach.

Equations (1) and (4) imply that the S-X² statistic is a special case of the Pearson’s χ² statistic. In addition, S-X² is computed using the MMLE of the item parameters based on the original/ungrouped data and yet is assumed to have a ${\chi }_{J-L-1}^2$ asymptotic null distribution (Orlando & Thissen, 2000). Such a use of S-X² is exactly like the use of the Pearson’s χ² statistic along with the ${\chi }_{K-L-1}^2$ asymptotic null distribution. Therefore, S-X² is expected to suffer from the Chernoff-Lehmann Problem and is expected to follow not a χ² distribution, but a distribution like the one given by equation (8). Thus, S-X² is expected to be larger on average than a ${\chi }_{J-L-1}^2$ random variable for large samples under no model misfit. Existing simulation studies that examined the Type I error rates of S-X² corroborate this fact. Glas and Suarez-Falcón (2003), Sinharay (2006), and Sinharay and Lu (2008) found in simulation studies that the Type I error rates of S-X² are slightly inflated when it is computed using the MMLEs of item parameters from ungrouped data and is assumed to have the ${\chi }_{J-L-1}^2$ asymptotic null distribution. For example, Table 1 of Glas and Suarez-Falcón (2003) shows that the Type I error rates of S-X² at 5% significance level are 0.08, 0.08, and 0.07, respectively, for sample sizes 500, 1,000, and 4000 for 10-item tests. The resampling-based approaches developed by Sinharay (2006), Stone (2000), Stone and Zhang (2003), which involve the determination of the null distribution of S-X² using simulations, offer alternative solutions and successfully avoid the use of an inaccurate asymptotic null distribution, but these approaches are computation-intensive. The use of the minimum χ² estimator $\stackrel{\sim }{\mathit{\eta }}$ and the P-X² statistics defined in equation (7) is another possible approach to attain the target Type I error rate. However, $\widehat{\mathit{\eta }}$ is a more efficient estimator compared to $\stackrel{\sim }{\mathit{\eta }}$ because the former utilizes more information than the latter (e.g., Rao, 1962; Rao & Robson, 1974). Also, $\widehat{\mathit{\eta }}$ is more popular than $\stackrel{\sim }{\mathit{\eta }}$ . For example, the former is implemented in several publicly available IRT software packages such as BILOG (Mislevy & Bock, 1991), MULTILOG (Thissen, 1991), and PARSCALE (Muraki & Bock, 2003). Further, a χ²-type statistic that utilizes $\widehat{\mathit{\eta }}$ rather than $\stackrel{\sim }{\mathit{\eta }}$ is likely to be more useful and popular among researchers and practitioners.

Table 1.

The Type I Error Rates of S-X² and $S-X_{RR}^2$ for the 2PL model.

	Test	Sample size
Length	Statistic	500	1000	2000	4000
10	S-X2	0.092	0.087	0.074	0.068
	$S-X_{RR}^2$	0.035	0.042	0.043	0.044
20	S-X2	0.072	0.067	0.061	0.057
	$S-X_{RR}^2$	0.054	0.048	0.041	0.040
40	S-X2	0.062	0.057	0.053	0.051
	$S-X_{RR}^2$	0.054	0.053	0.049	0.047

The Modified χ² Statistic of Rao and Robson

One solution to the abovementioned Chernoff–Lehmann problem is to modify P-X² in a way such that the modified statistic has a known asymptotic null distribution.

One modification of the Pearson’s χ² statistic was suggested by Rao and Robson (1974) and is computed as

$$\mathrm{P}-X_{RR}^2={\left[\mathit{u}\left(\widehat{\mathit{\eta }}\right)\right]}^{\top }{\mathbf{\Sigma }}_{\mathit{u}\left(\widehat{\mathit{\eta }}\right)}^{-1}\mathit{u}\left(\widehat{\mathit{\eta }}\right),$$

where ${\mathbf{\Sigma }}_{\mathit{u}\left(\widehat{\mathit{\eta }}\right)}$ is the approximate covariance matrix of $\mathit{u}\left(\widehat{\mathit{\eta }}\right)$ for large samples. The modification is essentially a standardization of $\mathit{u}\left(\widehat{\mathit{\eta }}\right)$ such that ${\mathbf{\Sigma }}_{\mathit{u}\left(\widehat{\mathit{\eta }}\right)}^{-1/2}\mathit{u}\left(\widehat{\mathit{\eta }}\right)$ follows a multivariate normal distribution for large samples under no model misfit, and, consequently

$$\mathrm{P}-X_{RR}^2\sim {\chi }_{K-1}^2.$$

Note that there is no loss of df for parameter estimation in the null distribution of the $\mathrm{P}-X_{RR}^2$ statistic. Rao and Robson (1974) found that $\mathrm{P}-X_{RR}^2$ has larger power than the Pearson’s χ² statistic computed using the minimum χ² estimator defined in equation (7)—this result is presumably due to the larger degrees of freedom of the former statistic compared to the latter statistic.

In this paper, we borrow the idea underlying $\mathrm{P}-X_{RR}^2$ and derive the covariance matrix ${\mathbf{\Sigma }}_{\mathit{v}\left(\widehat{\mathit{\eta }}\right)}$ . The matrix ${\mathbf{\Sigma }}_{\mathit{v}\left(\widehat{\mathit{\eta }}\right)}$ allows us to compute the statistic $\mathrm{S}-X_{RR}^2$ , which is a special case of the $\mathrm{P}-X_{RR}^2$ statistic and is a modified version of the S-X² statistic, as

$$\mathrm{S}-X_{RR}^2={\left[\mathit{v}\left(\widehat{\mathit{\eta }}\right)\right]}^{\top }{\mathbf{\Sigma }}_{\mathit{v}\left(\widehat{\mathit{\eta }}\right)}^{-1}\mathit{v}\left(\widehat{\mathit{\eta }}\right).$$ (9)

Further

$$\mathrm{S}-X_{RR}^2\sim {\chi }_{J-1}^2$$

(Rao & Robson, 1974). The key of this modification is the computation of the covariance matrix ${\mathbf{\Sigma }}_{\mathit{v}\left(\widehat{\mathit{\eta }}\right)}$ . The detailed derivation of the matrix is provided below.

Method: Derivation of the Covariance Matrix Required in $\mathrm{S}-X_{RR}^2$

To obtain ${\mathbf{\Sigma }}_{\mathit{v}\left(\widehat{\mathit{\eta }}\right)}$ , we first approximate $\mathit{v}\left(\widehat{\mathit{\eta }}\right)$ using the first-order Taylor series expansion (e.g., Lehmann & Casella, 1998, p. 77) around η ₀ as

$$\mathit{v}\left(\widehat{\mathit{\eta }}\right)\approx \mathit{v}\left({\mathit{\eta }}_{\mathbf{0}}\right)+{\mathit{A}}_{\mathbf{0}}\left(\widehat{\mathit{\eta }}-{\mathit{\eta }}_{\mathbf{0}}\right),$$ (10)

where η ₀ is the unknown true item parameter vector

$$\mathit{v}\left({\mathit{\eta }}_{\mathbf{0}}\right)={\left(\frac{\sqrt{N_1}\left[O_1-E_1\left({\mathit{\eta }}_{\mathbf{0}}\right)\right]}{\sqrt{E_1\left({\mathit{\eta }}_{\mathbf{0}}\right)\left[1-E_1\left({\mathit{\eta }}_{\mathbf{0}}\right)\right]}},\frac{\sqrt{N_2}\left[O_2-E_2\left({\mathit{\eta }}_{\mathbf{0}}\right)\right]}{\sqrt{E_2\left({\mathit{\eta }}_{\mathbf{0}}\right)\left[1-E_2\left({\mathit{\eta }}_{\mathbf{0}}\right)\right]}},\dots ,\frac{\sqrt{N_K}\left[O_K-E_K\left({\mathit{\eta }}_{\mathbf{0}}\right)\right]}{\sqrt{E_K\left({\mathit{\eta }}_{\mathbf{0}}\right)\left[1-E_K\left({\mathit{\eta }}_{\mathbf{0}}\right)\right]}}\right)}^{\top },$$ (11)

and A ₀ is a K × L matrix whose (k, l)-th element is given by

$$\begin{array}{l}{\left({\mathit{A}}_{\mathbf{0}}\right)}_{k,l}={\frac{\partial v_k\left(\mathit{\eta }\right)}{\partial E_k\left(\mathit{\eta }\right)}\frac{\partial E_k\left(\mathit{\eta }\right)}{\partial {\eta }_l}|}_{\mathit{\eta }={\mathit{\eta }}_{\mathbf{0}}}\\ =N_k^{1/2}\left[-\frac{1}{E_k{\left({\mathit{\eta }}_{\mathbf{0}}\right)}^{1/2}{\left(1-E_k\left({\mathit{\eta }}_{\mathbf{0}}\right)\right)}^{1/2}}+\frac{\left(E_k\left({\mathit{\eta }}_{\mathbf{0}}\right)-0.5\right)\left(O_k-E_k\left({\mathit{\eta }}_{\mathbf{0}}\right)\right)}{E_k{\left({\mathit{\eta }}_{\mathbf{0}}\right)}^{3/2}{\left(1-E_k\left({\mathit{\eta }}_{\mathbf{0}}\right)\right)}^{3/2}}\right]{\frac{\partial E_k\left(\mathit{\eta }\right)}{\partial {\eta }_l}|}_{\mathit{\eta }={\mathit{\eta }}_{\mathbf{0}}}\end{array}.$$ (12)

Note that for large values of N _k , O _k is approximately equal to E _k ( η ₀ ), and, consequently, ${\left({\mathit{A}}_{\mathbf{0}}\right)}_{k,l}$ can be approximated as

$${\left({\mathit{A}}_{\mathbf{0}}\right)}_{k,l}\approx {-\sqrt{\frac{N_k}{E_k\left({\mathit{\eta }}_{\mathbf{0}}\right)\left(1-E_k\left({\mathit{\eta }}_{\mathbf{0}}\right)\right)}}\frac{\partial E_k\left(\mathit{\eta }\right)}{\partial {\eta }_l}|}_{\mathit{\eta }={\mathit{\eta }}_{\mathbf{0}}}.$$ (13)

Equation (10) implies that

$${\mathbf{\Sigma }}_{\mathit{v}\left(\widehat{\mathit{\eta }}\right)}\approx {\mathbf{\Sigma }}_{\mathit{v}\left({\mathit{\eta }}_{\mathbf{0}}\right)}+2\text{Cov}\left[{\mathit{A}}_{\mathbf{0}}\left(\widehat{\mathit{\eta }}-{\mathit{\eta }}_{\mathbf{0}}\right),\mathit{v}\left({\mathit{\eta }}_{\mathbf{0}}\right)\right]+{\mathit{A}}_{\mathbf{0}}{\mathbf{\Sigma }}_{\widehat{\mathit{\eta }}}{\mathbf{A}}_{\mathbf{0}}^{\top }.$$ (14)

Among the terms in equation (14), the elements of A ₀ can be approximated using equation (13) and ${\mathbf{\Sigma }}_{\widehat{\mathit{\eta }}}$ , which is the variance-covariance matrix among the estimates of the item parameters, can be obtained from the IRT software that was used to fit the IRT model to the data set. ¹ The computation of the other terms, ${\mathbf{\Sigma }}_{\mathit{v}\left({\mathit{\eta }}_{\mathbf{0}}\right)}$ and $\text{Cov}\left[{\mathit{A}}_{\mathbf{0}}\left(\widehat{\mathit{\eta }}-{\mathit{\eta }}_{\mathbf{0}}\right),\mathit{v}\left({\mathit{\eta }}_{\mathbf{0}}\right)\right]$ , are described below.

Computation of ${\mathbf{\Sigma }}_{\mathit{v}\left({\mathit{\eta }}_{\mathbf{0}}\right)}$

Because of equation (11), the diagonal elements of ${\mathbf{\Sigma }}_{\mathit{v}\left({\mathit{\eta }}_{\mathbf{0}}\right)}$ are terms such as Var(v _k ( η ₀ )), where

$$v_k\left({\mathit{\eta }}_{\mathbf{0}}\right)=\frac{\sqrt{N_k}\left[O_k-E_k\left({\mathit{\eta }}_{\mathbf{0}}\right)\right]}{\sqrt{E_k\left({\mathit{\eta }}_{\mathbf{0}}\right)\left[1-E_k\left({\mathit{\eta }}_{\mathbf{0}}\right)\right]}},k=\mathrm{1,2},\dots ,K,$$

computed at η = η ₀ and the off-diagonal elements of ${\mathbf{\Sigma }}_{\mathit{v}\left({\mathit{\eta }}_{\mathbf{0}}\right)}$ are terms such as $\text{Cov}\left(v_{k_1}\left({\mathit{\eta }}_{\mathbf{0}}\right),v_{k_2}\left({\mathit{\eta }}_{\mathbf{0}}\right)\right)$ for k₁ ≠ k₂ = 1, 2, …, K computed at η = η ₀ .

Because the variance of O _k computed at η = η ₀ is E _k ( η ₀ )[1 − E _k ( η ₀ )]/N _k , v _k ( η ₀ ) is standardized, that is, its variance is 1 for k = 1, 2, …, K. So, the diagonal elements of ${\mathbf{\Sigma }}_{\mathit{v}\left({\mathit{\eta }}_{\mathbf{0}}\right)}$ are all equal to 1. Because the quantities $E_{k_1}\left({\mathit{\eta }}_{\mathbf{0}}\right)$ are constants, $\text{Cov}\left(v_{k_1}\left({\mathit{\eta }}_{\mathbf{0}}\right),v_{k_2}\left({\mathit{\eta }}_{\mathbf{0}}\right)\right)$ is a multiple of $\text{Cov}\left(O_{k_1},O_{k_2}\right)$ , the covariance of $O_{k_1}$ and $O_{k_2}$ , computed at η = η ₀ . Appendix A includes a proof that $\text{Cov}\left(O_{k_1},O_{k_2}\right)$ , computed at η = η ₀ , is approximately equal to 0 for large samples. Therefore, the off-diagonal elements of ${\mathbf{\Sigma }}_{\mathit{v}\left({\mathit{\eta }}_{\mathbf{0}}\right)}$ are all approximately equal to 0 for large samples.

Consequently, for large samples

$${\mathbf{\Sigma }}_{\mathit{v}\left({\mathit{\eta }}_{\mathbf{0}}\right)}\approx {\mathit{I}}_{\mathit{K}},$$ (15)

where I _K denotes an identity matrix of dimension K × K.

Computation of $\text{Cov}\left[{\mathit{A}}_{\mathbf{0}}\left(\widehat{\mathit{\eta }}-{\mathit{\eta }}_{\mathbf{0}}\right),\mathit{v}\left({\mathit{\eta }}_{\mathbf{0}}\right)\right]$

The grouped data in the context of item-fit analysis comprise the quantities N _k O _k and N _k (1 − O _k ), which are the numbers of correct and incorrect answers on the item of interest for examinee group k. The log-likelihood of these grouped data is provided by $\stackrel{\sim }{\ell }\left(\widehat{\mathit{\eta }}\right)=\log \prod _k{E}_k{\left(\widehat{\mathit{\eta }}\right)}^{N_k{O}_k}{\left(1-E_k\left(\widehat{\mathit{\eta }}\right)\right)}^{N_k\left(1-O_k\right)}={\displaystyle \sum }_k\left[N_k{O}_k\log \left(E_k\left(\widehat{\mathit{\eta }}\right)\right)+N_k\left(1-O_k\right)\log \left(1-E_k\left(\widehat{\mathit{\eta }}\right)\right)\right]..$

As mentioned earlier, the minimum χ² estimator $\stackrel{\sim }{\mathit{\eta }}$ is obtained by solving

$$\frac{\partial \stackrel{\sim }{\ell }\left(\mathit{\eta }\right)}{\partial {\eta }_l}={\displaystyle \sum }_k\left[\frac{N_k{O}_k}{E_k\left(\mathit{\eta }\right)}-\frac{N_k\left(1-O_k\right)}{1-E_k\left(\mathit{\eta }\right)}\right]\frac{\partial E_k\left(\mathit{\eta }\right)}{\partial {\eta }_l}=0,l=\mathrm{1,2},\dots ,L,$$ (16)

or by solving

$${\displaystyle \sum }_k\frac{N_k\left[O_k-E_k\left(\mathit{\eta }\right)\right]}{E_k\left(\mathit{\eta }\right)\left[1-E_k\left(\mathit{\eta }\right)\right]}\frac{\partial E_k\left(\mathit{\eta }\right)}{\partial {\eta }_l}=0,l=\mathrm{1,2},\dots ,L.$$

Therefore, the solution $\stackrel{\sim }{\mathit{\eta }}$ to the above equations satisfies

$$\frac{\partial \stackrel{\sim }{\ell }\left(\mathit{\eta }\right)}{\partial \mathit{\eta }}{|}_{\mathit{\eta }=\stackrel{\sim }{\mathit{\eta }}}={\mathbf{0}}_{L\times 1},$$ (17)

where 0_L×1 is a vector of length L whose elements are zeroes. Also note that Equations (11), (13), and (16) imply that

$${\frac{\partial \stackrel{\sim }{\ell }\left(\mathit{\eta }\right)}{\partial \mathit{\eta }}|}_{\mathit{\eta }={\mathit{\eta }}_{\mathbf{0}}}=-{\mathit{A}}_{\mathbf{0}}^{\top }\mathit{v}\left({\mathit{\eta }}_{\mathbf{0}}\right).$$ (18)

By applying the Taylor series expansion around η = η ₀ to ${\frac{\partial \stackrel{\sim }{\ell }\left(\mathit{\eta }\right)}{\partial \mathit{\eta }}|}_{\mathit{\eta }=\stackrel{\sim }{\mathit{\eta }}}$ and using the result provided in Equations (17) and (18), we obtain

$${\frac{\partial \stackrel{\sim }{\ell }\left(\mathit{\eta }\right)}{\partial \mathit{\eta }}|}_{\mathit{\eta }=\stackrel{\sim }{\mathit{\eta }}}={\mathbf{0}}_{L\times 1}\approx -{\mathit{A}}_{\mathbf{0}}^{\top }\mathit{v}\left({\mathit{\eta }}_{\mathbf{0}}\right)+{\mathit{B}}_{\mathbf{0}}\left(\stackrel{\sim }{\mathit{\eta }}-{\mathit{\eta }}_{\mathbf{0}}\right),$$ (19)

where

$${\mathit{B}}_{\mathbf{0}}={\frac{{\partial }^2\stackrel{\sim }{\ell }\left(\mathit{\eta }\right)}{\partial \mathit{\eta }\partial {\mathit{\eta }}^{\prime }}|}_{\mathit{\eta }={\mathit{\eta }}_{\mathbf{0}}}.$$

Equation (19) implies that

$${\mathit{B}}_0^{-1}{\mathit{A}}_{\mathbf{0}}^{\top }\mathbf{v}\left({\mathit{\eta }}_{\mathbf{0}}\right)-\stackrel{\sim }{\mathit{\eta }}+{\mathit{\eta }}_{\mathbf{0}}\approx 0$$

or

$${\mathit{B}}_0^{-1}{\mathit{A}}_{\mathbf{0}}^{\top }\mathit{v}\left({\mathit{\eta }}_{\mathbf{0}}\right)+\widehat{\mathit{\eta }}-\stackrel{\sim }{\mathbf{\eta }}\approx \widehat{\mathit{\eta }}-{\mathit{\eta }}_{\mathbf{0}}.$$ (20)

Using equation (20), we can express the covariance $\text{Cov}\left[{\mathit{A}}_{\mathbf{0}}\left(\widehat{\mathit{\eta }}-{\mathit{\eta }}_{\mathbf{0}}\right),\mathit{v}\left({\mathit{\eta }}_{\mathbf{0}}\right)\right]$ in equation (14) as

$$\begin{array}{l}\text{Cov}\left[{\mathit{A}}_{\mathbf{0}}\left(\widehat{\mathit{\eta }}-{\mathit{\eta }}_{\mathbf{0}}\right),\mathit{v}\left({\mathit{\eta }}_{\mathbf{0}}\right)\right]\approx \text{Cov}\left[{\mathit{A}}_{\mathbf{0}}{\mathit{B}}_{\mathbf{0}}^{-1}{\mathit{A}}_{\mathbf{0}}^{\top }\mathit{v}\left({\mathit{\eta }}_{\mathbf{0}}\right)+{\mathit{A}}_{\mathbf{0}}\left(\widehat{\mathit{\eta }}-\stackrel{\sim }{\mathit{\eta }}\right),\mathit{v}\left({\mathit{\eta }}_{\mathbf{0}}\right)\right]\\ ={\mathit{A}}_{\mathbf{0}}{\mathit{B}}_{\mathbf{0}}^{-1}{\mathit{A}}_{\mathbf{0}}^{\top }{\mathbf{\Sigma }}_{\mathit{v}\left({\mathit{\eta }}_{\mathbf{0}}\right)}+\text{Cov}\left[{\mathit{A}}_{\mathbf{0}}\left(\widehat{\mathit{\eta }}-\stackrel{\sim }{\mathit{\eta }}\right),\mathit{v}\left({\mathit{\eta }}_{\mathbf{0}}\right)\right].\end{array}$$ (21)

However, note that $\text{Cov}\left[{\mathit{A}}_{\mathbf{0}}\left(\widehat{\mathit{\eta }}-\stackrel{\sim }{\mathit{\eta }}\right),\mathit{v}\left({\mathit{\eta }}_{\mathbf{0}}\right)\right]$ , the second term in the right side of equation (21), converges to a matrix of zeroes since A ₀ is a matrix of constants and $\widehat{\mathit{\eta }}-\stackrel{\sim }{\mathit{\eta }}$ , which is the difference between two sets of item parameter estimates, converges to a zero vector as sample size increases. Therefore, equation (21) yields the result that

$$\text{Cov}\left[{\mathit{A}}_{\mathbf{0}}\left(\widehat{\mathit{\eta }}-{\mathit{\eta }}_{\mathbf{0}}\right),\mathit{v}\left({\mathit{\eta }}_{\mathbf{0}}\right)\right]={\mathit{A}}_{\mathbf{0}}{\mathit{B}}_{\mathbf{0}}^{-1}{\mathit{A}}_{\mathbf{0}}^{\top }{\mathbf{\Sigma }}_{\mathit{v}\left({\mathit{\eta }}_{\mathbf{0}}\right)}$$ (22)

Equations (14), (15), and (22) imply that

$${\mathbf{\Sigma }}_{\mathit{v}\left(\widehat{\mathit{\eta }}\right)}\approx {\mathit{I}}_{\mathit{K}}+2{\mathit{A}}_{\mathbf{0}}{\mathit{B}}_0^{-1}{\mathit{A}}_{\mathbf{0}}^{\top }+{\mathit{A}}_{\mathbf{0}}{\mathbf{\Sigma }}_{\widehat{\mathit{\eta }}}{\mathit{A}}_{\mathbf{0}}^{\top }.$$ (23)

Although the minimum χ² estimator appears in the above derivation, one does not have to compute the estimator to compute ${\mathbf{\Sigma }}_{\mathit{v}\left(\widehat{\mathit{\eta }}\right)}$ . That is because A ₀ and B ₀ can be adequately approximated using the MLE $\widehat{\mathit{\eta }}$ that is an accurate estimator of η ₀ for common IRT models (e.g., Harwell et al., 1988).

After approximating ${\mathbf{\Sigma }}_{\mathit{v}\left(\widehat{\mathit{\eta }}\right)}$ using equation (23), one can compute our modified version of S-X² as

$$\mathrm{S}-X_{RR}^2={\left[\mathit{v}\left(\widehat{\mathit{\eta }}\right)\right]}^{\top }{\mathbf{\Sigma }}_{\mathit{v}\left(\widehat{\mathit{\eta }}\right)}^{-1}\mathit{v}\left(\widehat{\mathit{\eta }}\right),$$ (24)

where $\mathit{v}\left(\widehat{\mathit{\eta }}\right)$ is computed using equation (4) after replacing η by $\widehat{\mathit{\eta }}$ . The asymptotic null distribution of $\mathrm{S}-X_{RR}^2$ is a ${\chi }_{J-1}^2$ distribution (Rao & Robson, 1974). Thus, item misfit is indicated by values of $\mathrm{S}-X_{RR}^2$ that are larger than the appropriate percentiles (say 95th or 99th percentile) of the ${\chi }_{J-1}^2$ distribution.

Simulation Studies

We performed a simulation study to evaluate the Type I error rates and power of the new $\mathrm{S}-X_{RR}^2$ statistic defined in equation (24) and to compare its Type I error rates and power to those of the S-X² statistic (Orlando & Thissen, 2000) defined in equation (3). In the first part of the study, we compute and compare the Type I error rates of S-X² and $\mathrm{S}-X_{RR}^2$ for data simulated from the 2PL model. In the second part of the simulation study, we examine and compare the power of S-X² and $\mathrm{S}-X_{RR}^2$ for data simulated from the Rasch, the 2PL and the 3PL models. Both the statistics were computed using $\widehat{\mathbf{\eta }}$ , which is the vector of the MMLEs of the item parameters.

Simulation Design

In the simulations, item scores were simulated under the Rasch, 2PL, and 3PL models. The test length was set as equal to 10, 20, or 40. The sample size was set equal to 500, 1000, 2000, or 4000. The true slope parameters, difficulty parameters, and guessing parameters were randomly generated from uniform distributions U(1, 2), U( − 3, 3), and U(0.05, 0.3), respectively, where, for example, U(1, 2) denotes the uniform distribution between 1 and 2. Simulating the true parameter values from other distributions did not affect the comparative performance of the item-fit statistics. To investigate the Type I error rates of the two statistics, the data-generating model (the IRT model that was used to simulate the data) was fitted to the data. To investigate the power of the two statistics, the Rasch and 2PL models were fitted to data simulated from the 3PL model and the Rasch model was fitted to data simulated from the 2PL model. After the models were fitted to the data and the item fit statistics were computed, the Type I error rate of an item-fit statistic at the 5% significance level was computed as the proportion of values of the statistic that were larger than the 95th percentile of the χ² distribution with J − 1 (for $\mathrm{S}-X_{RR}^2$ ) or J − L − 1 (for S-X²) df for the simulation cases where the data-generating model and the fitted model were the same; the power of a statistic was computed as the proportion of values of the statistic that were larger than the 95th percentile of the χ² distribution with J − 1 or J − L − 1 df for the simulation cases where the data-generating model and the fitted model were different. Both Type I error rate and power for each combination of test length and sample size were computed from 100 replications. The true item parameters were resampled in each replication.

Results

Table 1 shows that the Type I error rates of the two statistics for the various simulation cases where the data-generating model and the fitted model were the same. The table shows that the Type I error rates of S-X² are larger than the nominal level in all simulation cases, a finding that is in agreement with findings on Type I error rates of S-X² in Glas and Suarez-Falcón (2003), Sinharay (2006), and Sinharay and Lu (2008). However, the Type I error rates of S-X² are not much larger than the nominal level for 40-item tests. The Type I error rates of the modified statistic $\mathrm{S}-X_{RR}^2$ are considerably smaller than those of S-X² in all cases. Thus, $\mathrm{S}-X_{RR}^2$ overcomes the Chernoff–Lehmann problem to a certain extent. However, the Type I error rates of $\mathrm{S}-X_{RR}^2$ is considerably smaller than the nominal level for 10-item tests—we plan to investigate this issue in future research.

Table 2 shows the values of power of the two item-fit statistics for the various simulation cases where the data-generating model and the fitted model were different. The two columns with heading, for example, “2PL/1PL,” show the power for the cases when the data were simulated from the 2PL model and analyzed using the Rasch model. Table 2 shows that the power of the modified statistic $\mathrm{S}-X_{RR}^2$ is smaller than that of S-X². However, the slightly better power of S-X² relative to $\mathrm{S}-X_{RR}^2$ is likely a consequence of the inflated Type I error rate of the former statistic. As the sample size increases, the power of both statistics approach 1.0 for the “2PL/1PL” and “3PL/1PL” cases. The small power of both item statistics for the “3PL/2PL” case is an outcome of the fact that the 2PL model can explain data simulated from the 3PL model except for the case that the difficulty and guessing parameters for the latter model are too high (Sinharay, 2006).

Table 2.

The Power of $\mathrm{S}-X_{RR}^2$ and S-X² for Various Combinations of Data-generating Model and Fitted Model.

Test Length	Sample Size	2PL/1PL		3PL/1PL		3PL/2PL
		S-X2	$S-X_{RR}^2$	S-X2	$S-X_{RR}^2$	S-X2	$S-X_{RR}^2$
10	500	0.26	0.19	0.34	0.26	0.06	0.05
	1000	0.48	0.40	0.49	0.37	0.07	0.06
	2000	0.65	0.57	0.67	0.55	0.08	0.06
	4000	0.80	0.69	0.82	0.68	0.11	0.05
20	500	0.17	0.17	0.30	0.27	0.07	0.04
	1000	0.39	0.35	0.47	0.40	0.09	0.05
	2000	0.64	0.61	0.67	0.59	0.10	0.08
	4000	0.80	0.75	0.82	0.76	0.13	0.10
40	500	0.18	0.17	0.27	0.25	0.08	0.05
	1000	0.25	0.24	0.42	0.38	0.11	0.08
	2000	0.54	0.48	0.66	0.64	0.11	0.09
	4000	0.77	0.66	0.79	0.75	0.15	0.13

Real Data Example

The two item-fit statistics, S-X² and $\mathrm{S}-X_{RR}^2$ , were computed for a real data set. The data set includes the item scores of 2000 examinees on a state test with 46 dichotomous and multiple-choice items (with 5 answer options for each item) designed to measure students’ achievement in mathematics and was previously analyzed in Sinharay (2017).

The Rasch, 2PL, and 3PL models were fitted to the data set and the values of $\mathrm{S}-X_{RR}^2$ and S-X² were computed for all items for each IRT model. Table 3 shows the number of items for which the item-fit statistics were statistically significant at the 5% level of significance for the three IRT models. The table shows that for each IRT model, the use of $\mathrm{S}-X_{RR}^2$ leads to fewer items being identified as misfitting compared to that of S-X², with the difference being more prominent for the 2PL model. This finding agrees with the finding of smaller Type I error rate and power of $\mathrm{S}-X_{RR}^2$ compared to S-X² in the simulation study. Although both statistics are significant for a considerable number of items for the Rasch and 2PL model, they are significant for only 6 and 3 items, respectively, for the 3PL model. Although the 3PL model seems to adequately fit the data set, more tests including tests for local independence (e.g., Chen & Thissen, 1997) and further investigations, should be conducted to finalize this conclusion.

Table 3.

The Number of Items with Statistically Significant Values of S-X² and $\mathrm{S}-X_{RR}^2$ for the Three IRT models for the real data set.

Statistic	Rasch	2PL	3PL
S-X2	33	18	6
$\mathrm{S}-X_{RR}^2$	31	12	3

Note. IRT = item response theory.

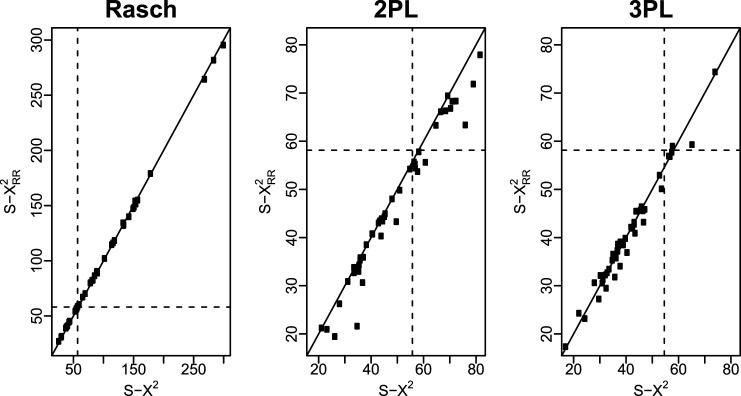
The three panels of Figure 1 show scatter plots of S-X² versus $\mathrm{S}-X_{RR}^2$ for the real data set under the three IRT models. The range of the X-axis is the same as that of the Y-axis in each panel. The range is much wider in the leftmost panel than in the other two panels. The panels include a diagonal line and also vertical and horizontal dashed lines indicating the critical values at 5% level of significance for the respective statistics. The last two panels show that for several items, S-X² is larger than its critical value, but $\mathrm{S}-X_{RR}^2$ is smaller than its critical value. Because item misfit often leads to an item being removed from the item pool (Sinharay & Haberman, 2014) and items are costly, these results indicate that the use of $\mathrm{S}-X_{RR}^2$ rather than S-X² may lead to considerable saving of resources in operational testing.

Figure 1.

Plot of S-X² versus $S-X_{RR}^2$ for three item response theory models for the real data.

Conclusions and Recommendations

The item-fit statistic S-X² (Orlando & Thissen, 2000), in spite of its simplicity and popularity, does not have a known asymptotic null distribution (Sinharay, 2006) and the Type I error rate of the statistic is larger than the nominal level, especially for shorter tests. The present study adopts the modification procedure suggested by Rao and Robson (1974) to provide a modified version of S-X² that has a known χ² asymptotic null distribution. The statistic S-X² can be written as ${\widehat{\mathit{v}}}^T\widehat{\mathit{v}}$ . The central idea of the modification of Rao and Robson (1974) is the computation of ${\widehat{\mathit{v}}}^T{\mathrm{\Sigma }}_{\widehat{\mathit{v}}}^{-1}\widehat{\mathit{v}}$ , where ${\mathrm{\Sigma }}_{\widehat{\mathit{v}}}$ is an approximate variance-covariance matrix of $\widehat{\mathit{v}}$ , so that ${\widehat{\mathit{v}}}^T{\mathrm{\Sigma }}_{\widehat{\mathit{v}}}^{-1}\widehat{\mathit{v}}$ has a known χ² asymptotic null distribution. A major contribution of this paper is the derivation of the appropriate ${\mathrm{\Sigma }}_{\widehat{\mathit{v}}}$ . Thus, this paper suggests a χ²-type statistic that (a) can be used to assess item fit for any IRT model for dichotomous items and (b) has a known asymptotic distribution under the null hypothesis. Item-fit statistics that have known asymptotic χ² distribution under the null hypothesis have been suggested for the Rasch model by, for example, Glas (1988), but there is a lack of such statistics for non-Rasch IRT models. Thus, this paper makes an important contribution given that experts such as Box (1979) called for statistics that have known null distribution in assessing the fit of statistical models. Note that researchers such as Haberman et al. (2013) have suggested residual-based item-fit statistics that follow the standard normal distributions for non-Rasch IRT models, but we do not consider such statistics.

Simulation studies were conducted to compare the performance of S-X² and $\mathrm{S}-X_{RR}^2$ with respect to Type I error rate and power. Results obtained from the simulation studies suggest that the Type I error rate of $\mathrm{S}-X_{RR}^2$ is closer to the nominal level than S-X² across different conditions. However, $\mathrm{S}-X_{RR}^2$ was found to be slightly conservative in comparison to S-X². Application of the two item-fit statistics to a real data set revealed that the number of misfitting items using $\mathrm{S}-X_{RR}^2$ was smaller than that for S-X². In practice, item fit statistics such as $\mathrm{S}-X_{RR}^2$ should be used along with other methods such as informative graphics and pair-wise item fit indexes in order to gain a thorough understanding of the type of misfit.

This paper has several limitations. First, it is possible to compare the two statistics for more simulated data and more real data. Second, the proposed statistic $\mathrm{S}-X_{RR}^2$ applies only to dichotomous IRT models—it is possible to extend the statistic to tests with polytomous items or a mix of dichotomous and polytomous items in future research. Third, the current manuscript only investigates three unidimensional IRT models assuming the latent variable follows a normal distribution. To obtain better understanding of the suggested statistic, one can look into its performance in other cases including for non-normal ability distributions, multidimensional latent variables, and discrete latent variables. Finally, this manuscript only considers statistical significance and does not discuss practical significance on IRT model misfit (Hambleton & Han, 2005; Sinharay & Haberman, 2014).

Appendix A. Proof that $\text{Cov}\left(O_{k_1},O_{k_2}\right)$ Computed at η = η ₀ is Approximately Equal to Zero for Large Samples

Let S _i denote the total score of examinee i, who is randomly chosen from the hypothetical population of all possible examinees. Let us define an indicator variable W _ik as

$$W_{ik}=\{\begin{array}{c}1, S_i=k\\ 0, S_i\ne k\end{array}$$

Then O _k for an item of interest can be expressed as

$$O_k=\frac{{\sum }_i{W}_{ik}{X}_i}{{\sum }_i{W}_{ik}}$$

where X _i is the score of examinee i on the item.

Let us consider two possible values k₁ and k₂ of S _i , where k₁ ≠ k₂, and define a vector U as

$$\mathit{U}={\left({\displaystyle \sum }_i{W}_{i{k}_1}{X}_i,{\displaystyle \sum }_i{W}_{i{k}_1},{\displaystyle \sum }_i{W}_{i{k}_2}{X}_i,{\displaystyle \sum }_i{W}_{i{k}_2}\right)}^{\top }$$

Then one can express $O_{k_1}$ and $O_{k_2}$ as

$$O_{k_1}=\frac{U_1}{U_2},\hspace{1em}{O}_{k_2}=\frac{U_3}{U_4}$$

where, for example, U₁ is the first component of U . The Jacobian for the transformation from $\mathit{O}={\left(O_{k_1},O_{k_2}\right)}^{\top }$ to U is given by a matrix of the first derivatives of the elements of O with respect to those of U , or, by

$$\mathit{J}=\left[\begin{array}{cccc}{J}_1& J_2& 0& 0\\ 0& 0& J_3& J_4\end{array}\right]$$ (A1)

where

$$J_1=\frac{1}{U_2},\hspace{0.17em}{J}_2=-\frac{U_1}{U_2^2},\hspace{0.17em}{J}_3=\frac{1}{U_4},\hspace{0.17em}{J}_4=-\frac{U_3}{U_4^2}$$ (A2)

Consequently, using the multivariate delta method (e.g., Lehmann & Casella, 1998, p. 61), the variance-covariance matrix of O for large samples can be approximated as

$$\text{Cov}\left(\mathit{O}\right)\approx \stackrel{\sim }{\mathit{J}}{\mathbf{\Sigma }}_{\mathit{U}}{\stackrel{\sim }{\mathit{J}}}^{\top }$$

where Σ _U is the variance-covariance matrix of the vector U , $\stackrel{\sim }{\mathit{J}}$ is the value of J provided in equation (A1) upon replacing the U _k ’s with their expected values computed at η = η ₀ , and the parameters η are fixed at η ₀. Using the result that the (i, j)-th element of the product of three matrices A, B and C is equal to the (matrix) product of the i-th row of A, the matrix B, and the j-th column of C (e.g., Banerjee & Roy, 2014, p. 12), the covariance between $O_{k_1}$ and $O_{k_2}$ can be approximated, for large samples, as

$$\text{Cov}\left(O_{k_1},O_{k_2}\right)\approx \left({\stackrel{\sim }{J}}_1,{\stackrel{\sim }{J}}_2,\mathrm{0,0}\right){\mathbf{\Sigma }}_{\mathit{U}}{\left(\mathrm{0,0},{\stackrel{\sim }{J}}_3,{\stackrel{\sim }{J}}_4\right)}^{\top }$$

where ${\stackrel{\sim }{J}}_i$ is the value of J _i upon replacing the U _k ’s with their expected values computed at η = η ₀ , or, as

$$\text{Cov}\left(O_{k_1},O_{k_2}\right)\approx {\stackrel{\sim }{J}}_1{\stackrel{\sim }{J}}_3{\sigma }_{13}+{\stackrel{\sim }{J}}_1{\stackrel{\sim }{J}}_4{\sigma }_{14}+{\stackrel{\sim }{J}}_2{\stackrel{\sim }{J}}_3{\sigma }_{23}+{\stackrel{\sim }{J}}_2{\stackrel{\sim }{J}}_4{\sigma }_{24}$$ (A3)

where σ _ij is the (i, j)-th element of Σ _U .

One can compute σ₂₄ as

$${\sigma }_{24}=\text{Cov}\left(U_2,U_4\right)=\text{Cov}\left({\displaystyle \sum }_i{W}_{i{k}_1},{\displaystyle \sum }_i{W}_{i{k}_2}\right)={\displaystyle \sum }_i\text{Cov}\left(W_{i{k}_1},W_{i{k}_2}\right)$$

where the last equality holds because the item scores are independent over two different examinees i₁ and i₂, which results in $\text{Cov}\left(W_{i_1{k}_1},W_{i_2{k}_2}\right)=0$ . Consequently

$${\sigma }_{24}={\displaystyle \sum }_i\left[E\left(W_{i{k}_1}{W}_{i{k}_2}\right)-E\left(W_{i{k}_1}\right)E\left(W_{i{k}_2}\right)\right]=-{\displaystyle \sum }_{i}E\left(W_{i{k}_1}\right)E\left(W_{i{k}_2}\right)$$ (A4)

because the raw score of examinee i cannot be equal to k₁ and also equal to k₂ so that $W_{i{k}_1}{W}_{i{k}_2}$ is equal to 0.

Now note that $E\left(W_{i{k}_1}\right)$ is the probability that the raw score on the test is k₁ for an examinee who is randomly chosen from the population of all examinees, is equal to $\int S\left(T=k_1|\theta ,\mathit{\eta }\right)\psi \left(\theta \right)d\theta$ , and hence is the same over all the examinees. Therefore

$$E\left(W_{i{k}_1}\right)=\frac{1}{N}{\displaystyle \sum }_{i}E\left(W_{i{k}_1}\right)=\frac{1}{N}E\left({\displaystyle \sum }_i{W}_{i{k}_1}\right)=\frac{1}{N}E\left(U_2\right)$$ (A5)

Similarly, one obtains

$$E\left(W_{i{k}_2}\right)=\frac{1}{N}E\left(U_4\right).$$ (A6)

Equations (A4) to (A6) imply that

$${\sigma }_{24}=-{\displaystyle \sum }_i\left[\frac{1}{N}E\left(U_2\right)\right]\left[\frac{1}{N}E\left(U_4\right)\right]=-\frac{1}{N}E\left(U_2\right)E\left(U_4\right)$$

Let ${\stackrel{\sim }{U}}_k$ denote E(U _k ), where the expectation is computed at η = η ₀ , k = 1, …, 4. Then

$${\sigma }_{24}=-\frac{1}{N}{\stackrel{\sim }{U}}_2{\stackrel{\sim }{U}}_4$$ (A7)

It is possible to prove in a similar manner that

$${\sigma }_{13}=-\frac{1}{N}{\stackrel{\sim }{U}}_1{\stackrel{\sim }{U}}_3,\hspace{1em}{\sigma }_{14}=-\frac{1}{N}{\stackrel{\sim }{U}}_1{\stackrel{\sim }{U}}_4,\hspace{1em}{\sigma }_{23}=-\frac{1}{N}{\stackrel{\sim }{U}}_2{\stackrel{\sim }{U}}_3$$ (A8)

Finally, equations (A2), (A3), (A7), and (A8) imply that

$$\begin{array}{l}\text{Cov}\left(O_{k_1},O_{k_2}\right)\approx -{\stackrel{\sim }{J}}_1{\stackrel{\sim }{J}}_3\frac{1}{N}{\stackrel{\sim }{U}}_1{\stackrel{\sim }{U}}_3-{\stackrel{\sim }{J}}_1{\stackrel{\sim }{J}}_4\frac{1}{N}{\stackrel{\sim }{U}}_1{\stackrel{\sim }{U}}_4-{\stackrel{\sim }{J}}_2{\stackrel{\sim }{J}}_3\frac{1}{N}{\stackrel{\sim }{U}}_2{\stackrel{\sim }{U}}_3-{\stackrel{\sim }{J}}_2{\stackrel{\sim }{J}}_4\frac{1}{N}{\stackrel{\sim }{U}}_2{\stackrel{\sim }{U}}_4\\ \approx -\frac{1}{N}\left[{\stackrel{\sim }{U}}_1{\stackrel{\sim }{U}}_3\frac{1}{{\stackrel{\sim }{U}}_2}\frac{1}{{\stackrel{\sim }{U}}_4}-{\stackrel{\sim }{U}}_1{\stackrel{\sim }{U}}_4\frac{1}{{\stackrel{\sim }{U}}_2}\frac{{\stackrel{\sim }{U}}_3}{{\stackrel{\sim }{U}}_4^2}-{\stackrel{\sim }{U}}_2{\stackrel{\sim }{U}}_3\frac{{\stackrel{\sim }{U}}_1}{{\stackrel{\sim }{U}}_2^2}\frac{1}{{\stackrel{\sim }{U}}_4}+{\stackrel{\sim }{U}}_2{\stackrel{\sim }{U}}_4\frac{{\stackrel{\sim }{U}}_1}{{\stackrel{\sim }{U}}_2^2}\frac{{\stackrel{\sim }{U}}_3}{{\stackrel{\sim }{U}}_4^2}\right]\\ =0\end{array}$$

ORCID iDs

Sandip Sinharay https://orcid.org/0000-0003-4491-8510

Matthew S. Johnson https://orcid.org/0000-0003-3157-4165