A multimodal IVA fusion approach to identify linked neuroimaging markers

Abstract

In this study, we introduce a method to perform independent vector analysis (IVA) fusion to estimate linked independent sources and apply to a large multimodal dataset of over 3000 subjects in the UK Biobank study, including structural (gray matter), diffusion (fractional anisotropy), and functional (amplitude of low frequency fluctuations) magnetic resonance imaging data from each subject. The approach reveals a number of linked sources showing significant and meaningful covariation with subject phenotypes. One such mode shows significant linear association with age across all three modalities. Robust age-associated reductions in gray matter density were observed in thalamus, caudate, and insular regions, as well as visual and cingulate regions, with covarying reductions of fractional anisotropy in the periventricular region, in addition to reductions in amplitude of low frequency fluctuations in visual and parietal regions. Another mode identified multimodal patterns that differentiated subjects in their time-to-recall during a prospective memory test. In sum, the proposed IVA-based approach provides a flexible, interpretable, and powerful approach for revealing links between multimodal neuroimaging data.

I. INTRODUCTION

Standard neuroimaging research practice involves collection of multimodal magnetic resonance imaging (MRI) data on every individual. Each modality provides rich, unique information about brain structure and/or function [1], [2]. Although separate analysis of each data modality can provide important insights into the structural or functional integrity of the brain, multimodal fusion analyses provide insights into cross-modal (joint) associations that can lend important missing links in brain development and disease [3].

While large scale neuroimaging datasets (1000+ subjects, with multimodal data acquired on the same subjects) increase our ability to recognize robust biomarkers for brain health and disorder, the relationship between modalities is often complex and unknown. Because of this, data-driven approaches play a key role in discovery of relationships between brain function and structure, which may not cooccur at the same spatial regions and may covary among subjects in complex ways [4]. Based on the marked success of independent component analysis (ICA) for exploratory analysis of brain imaging data, a number of approaches have attempted to capture these relationships leveraging independence. Rarely, however, they were able to directly estimate such covariation, typically resorting to an amalgamation of indirect methods [5]. Independent vector analysis (IVA) [6], a multidataset extension of independent component analysis (ICA), provides a natural and extendable way to directly link multivariate brain imaging data together. While separate unimodal ICAs can only identify modality-specific sources, IVA identifies sets of linked sources across modalities, which are called source component vectors (SCV).

Largely inspired by hybrid experiments in [7], this work demonstrates an application of IVA for multimodal fusion, combining unimodal features from structural MRI (sMRI), diffusion MRI (dMRI), and functional MRI (fMRI) data from a large UK Biobank sample. Specifically, we identify corresponding linked sources from gray matter (GM) probabilistic segmentation maps from sMRI data, fractional anisotropy (FA) maps from dMRI data, and amplitude of low frequency fluctuations (ALFF) maps from fMRI data. GM maps summarize variations in gray matter density. FA maps capture variation in the extent of directional diffusion within regional white matter. ALFF maps summarize the strength of local functional connectivity and the ability of brain regions to communicate with distant regions. Each SCV estimated with IVA represents a linked mode of shared variability across these modalities, providing a rich linked feature set for joint interpretation. Furthermore, we investigate potential associations between the extracted SCVs and non-imaging subject phenotypes. We show that the multimodal IVA fusion model can extract meaningful linked sources with statistically significant linear associations with the non-imaging phenotypes.

In the following, Section II describes the data, preprocessing, and methodology utilized in this work. Section III presents our results, which are further discussed in Section IV before presenting our final conclusions.

II. METHODS

A. Data

In this work, we use imaging data from a subset of 3497 subjects participating in the UK Biobank study, a prospective epidemiological study with a large imaging database. Specifically, we utilize multivariate features [8] from structural MRI (sMRI), diffusion MRI (dMRI) and resting functional MRI (rfMRI) data extracted from each subject. All data was collected in one of the three participating locations in the United Kingdom. All participants provided informed consent from their respective institutional review boards.

T1-weighted structural MRI images were acquired using a 3D MPRAGE sequence at 1mm³ isotropic sagittal slices with acquisition parameters: 208×256×256 matrix, R=2, TI/TR=880/2000 ms. Diffusion MRI images were acquired using a standard Stejskal-Tanner spin-echo sequence at 2mm³ isotropic resolution at two different b values (b = 1,000 and 2,000 s/mm²) and 50 distinct diffusion-encoding directions each acquired with a multi-band (MB) factor of 3. Resting functional MRI were acquired axially at 2.4mm³ resolution while the subjects fixated at a cross with the following acquisition parameters: 88×88×64 matrix, TE/TR=39/735ms, MB=8, R=1, flip angle 52°. A pair of spin echo scans of opposite phase encoding direction in the same imaging resolution as rFMRI scans were acquired to estimate and correct distortions in rFMRI echo-planar images, and a single band high resolution reference image was acquired at the start of the rFMRI scan to ensure good realignment and normalization.

B. Preprocessing

We processed each of the three imaging data modalities to obtain GM, FA, and ALFF feature maps, which were then used for multimodal fusion analysis. Besides summarizing information into features, the preprocessing also promotes dimensionality reduction and denoising, both of which facilitate latter analyses. Specifically, the sMRI images underwent segmentation and normalization to MNI space using the SPM12 toolbox, yielding gray matter (GM), white matter (WM), and cerebro-spinal fluid (CSF) tissue probability maps. The normalized GM segmentations were spatially smoothed using a 10mm FWHM Gaussian filter. The smoothed images were resampled to 3mm³. We defined a group mask to restrict the analysis to GM voxels as follows. First, an average GM segmentation map from all subjects was obtained from normalized segmentation images at 1mm³ resolution. This map was binarized at a 0.2 threshold and resampled to 3mm³ resolution, which resulted in 44318 in-brain voxels.

For dMRI data, we used the FA maps provided by the UK Biobank consortium. The preprocessing steps that raw dMRI images underwent are thoroughly described in [9]. The FA maps were then spatially smoothed using a 6mm FWHM Gaussian filter and resampled to 3mm³ voxels. For dMRI data, we computed a group mask similar to the approach described above for sMRI data. However, the group average WM segmentation was binarized at a threshold of 0.4, resulting in 18684 in-brain voxels in the group mask.

Lastly, we used distortion corrected, FIX-denoised [10], normalized rfMRI data provided by the UK Biobank data resource. We computed amplitude of low frequency fluctuation (ALFF) maps, defined as the area under the low frequency band [0.01–0.08 Hz] power spectrum of each voxel time course. We then obtained mean scaled ALFF maps (mALFF), ALFF maps divided by the global mean ALFF value, as this scaling has been shown to result in greater test-retest reliability of ALFF maps [11]. The mALFF maps were smoothed using a 6mm FWHM Gaussian filter and resampled to 3mm isotropic voxels. We used the same group mask learned from GM features for mALFF maps in the subsequent fusion analysis.

C. Multimodal IVA (MMIVA) fusion model

Here we present a general IVA approach for direct analysis of heterogeneous multimodal data. As mentioned earlier, IVA is a natural extension of ICA. While ICA operates on a single dataset to obtain statistically independent source signals via estimation of one linear unmixing matrix, IVA performs joint estimation of many unmixing matrices simultaneously across multiple datasets [12].

Briefly, ICA is a blind source separation model that assumes linear mixing of C statistically independent sources s, yielding the observed data x:

$$\mathbf{x}(n)=\mathbf{A}\mathbf{s}(n),1\le n\le N,\mathbf{x}(n),\mathbf{s}(n)\in {ℝ}^C,$$ (1)

where A is the mixing matrix, and N is the number of observations (here, the number of subjects). The ICA algorithm seeks to identify the sources $\widehat{\mathbf{s}}(n)=\mathbf{W}\mathbf{x}(n)$ by estimating an unmixing matrix W, according to certain properties of the sources such as higher-order statistics and non-Gaussianity. Typical ICA algorithms minimize the mutual information defined as:

$${ℐ}^{\text{ICA}}(\mathbf{W})=\sum _{i=1}^{C}H\left({\widehat{s}}_i\right)-\text{log}\left|\det \mathbf{W}\right|,$$ (2)

where $H\left({\widehat{s}}_i\right)$ is the differential entropy, given by $H\left({\widehat{s}}_i\right)=-\mathbb{E}\left\{\log p_{{\widehat{s}}_i}\left(w_i^{\top }x\right)\right\}$.

IVA extends the ICA model to multiple (K) datasets, assuming a linear mixture of C independent sources for each dataset:

$${\mathbf{x}}^{[k]}(n)={\mathbf{A}}^{[k]}{\mathbf{s}}^{[k]}(n),1\le k\le K,1\le n\le N,$$ (3)

additionally assuming statistical dependence (i.e., linkage) of corresponding sources. This collection of linked sources is defined as the source component vector (SCV) ${\mathbf{s}}_i(n)={[s_i^{[1]}(n),s_i^{[2]}(n),\dots ,s_i^{[k]}(n)]}^{\top }\in {ℝ}^K$. Here, K = 3, such that each SCV spans across modalities.

Solving the IVA problem comes from minimizing the following mutual information:

$${ℐ}^{\text{IVA}}(\mathbf{W})=\sum _{i=1}^C\left(\sum _{k=1}^{K}H\left({\widehat{s}}_i^{[k]}\right)-ℐ\left({\widehat{\mathbf{s}}}_i\right)\right)-\sum _{k=1}^K\text{log}\left|\det \left({\mathbf{W}}^{[\mathbf{k}]}\right)\right|$$ (4)

The second term $ℐ\left({\widehat{\mathbf{s}}}_i\right)$ in the equation above is mutual information accounting for dependence among sources in each SCV. Altogether, the terms in big parentheses correspond to the joint entropy of an $H\left({\widehat{\mathbf{s}}}_i\right)$, simply indicating that IVA identifies independence among SCVs while taking into account the dependence across datasets. See [12] for a general discussion on ICA and IVA algorithms and [13], [14] for their application to data fusion (particularly our choice of transposed IVA). See [7] for details on the multidataset independent subspace analysis (MISA) implementation we utilized to estimate the IVA model in this work.

We performed MMIVA fusion of the GM, mALFF, and FA features by treating each modality as one of the K datasets in the IVA model above. Each subject’s feature set was z-scored per modality and then reduced to 20 principal directions using multimodal group principal component analysis (MGPCA). Unlike standard PCA that finds orthogonal directions of maximal variation for each modality separately, MGPCA finds directions of maximal common variation, i.e., eigenvectors are computed based on the average of the scaled covariance matrices (Σ^[k]) of all three modalities. The scaling factor used is trace(Σ^[k])/N, which is the ratio of the variance in the modality to the number of observations (here, subjects). The MGPCA-reduced data then underwent an ICA estimation using the Infomax objective [15] to obtain 20 common independent sources.

We improved upon the Infomax estimation by configuring and running MISA as an ICA model [7], in which case it assumes source distributions to follow a univariate Kotz distribution. The final combined MGPCA+ICA estimates of W^[k] were then utilized as projection matrices for each modality. The resulting data were analyzed by the MMIVA model after reconfiguring and running MISA as an IVA model to obtain the final joint decomposition. As discussed earlier, MMIVA accounts for dependence within corresponding sources across modalities. For both MISA and MMIVA models, the source distributions are assumed to take a multivariate Kotz distribution, as this has been shown to generalize well across multivariate Gaussian, multivariate Laplace, and multivariate power exponential source distributions [16]. All methods have been implemented using the MISA toolbox [7].

D. Statistics

UK Biobank provides extensive phenotype information for each subject including age, sex, lifestyle measures, cognitive scores, etc. We used a subset of the subject measures (SM) reported in [17] to identify associations between the subject demographics and the MMIVA sources obtained from our decomposition. We computed a multivariate MANCOVA model $({\widehat{\mathbf{s}}}^{[k]}\sim \mathrm{S}\mathrm{M}+e)$ using the MANCOVAN toolbox, which implements multivariate stepwise regression, to identify associations between subject demographics and MMIVA sources for each modality separately.

Following the approach in [18], we dropped subject scores with more than 4% missing data. This resulted in 2907 subject scores out of 3497 for MANCOVAN analysis. Of 64 SMs, we dropped 10 columns which had extreme values. Extreme values are identified in 2 steps. First sum of square of absolute median deviations (ssqamdn) for each SM is computed. If there is any max(ssqamdn) >100*mean(ssqmdn), then the SM has subjects with extreme outliers which can influence statistical analysis and so were dropped. This resulted in 54 phenotypes that include age, sex, fluid intelligence, a set of phenotypes covering amount and duration of physical activity, frequency of alcohol intake, and cognitive test scores (see [17] for details).

For the measures that were retained, any missing values were imputed with K-Nearest Neighborhood (MATLAB’s knnimpute) method. Stepwise regression approach was used to retain only significant terms (SM_sig) at each step, using α < 0.01. Univariate tests $({\widehat{\mathbf{s}}}_i^{[k]}\sim \mathrm{S}{\mathrm{M}}_{sig}+e)$ were performed to identify significant SCVs and corrected for multiple comparisons at Bonferroni threshold (0.05/20 for 20 sources). In addition to the SMs, the following nuisance covariates were added to the design matrix:

1. sMRI: correlation of warped subject segmentation map to mean segmentation map (rSN_sMRI),

2. dMRI: correlation of warped subject FA map to mean FA map (rSN_sMRI),

3. ALFF: correlation of warped subject ALFF map to mean ALFF map (rSN_ALFF),

4. and mean framewise displacement (mFD) computed from rigid body movement estimates from resting fMRI scan realignment step.

Any variable with fewer than 8 levels were modeled as categorical variables and rest were modeled as continuous variables. Only age by sex interaction was considered.

III. RESULTS

The MANCOVA analysis revealed several SCVs showing significant effects of age, sex across the three modalities on several SCVs. Figure 1 shows the source (component 8) most significantly associated with age, along with the corresponding mixing weights (spatial maps).

Fig. 1.

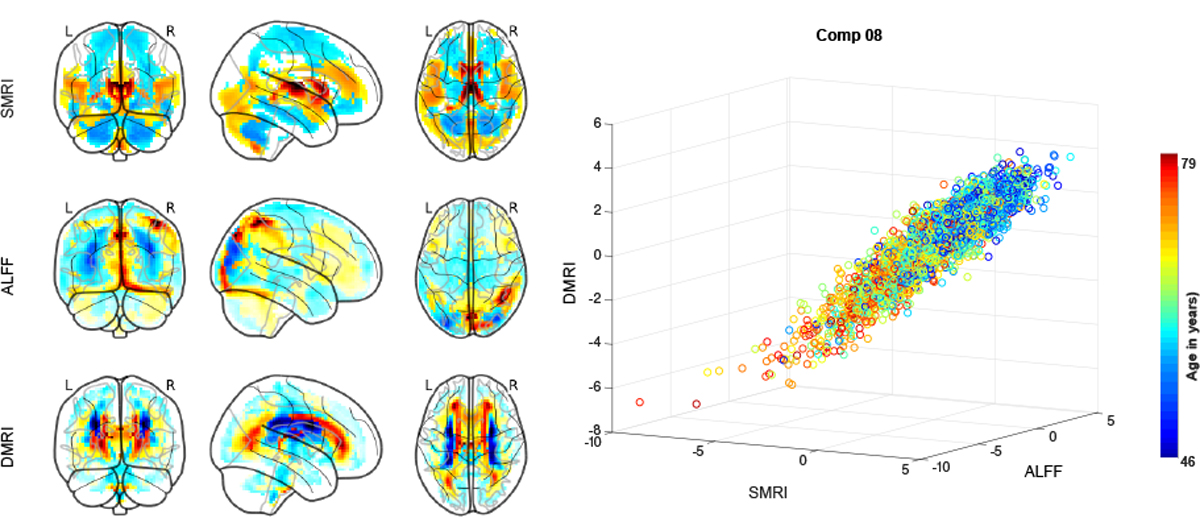
The sources corresponding to component 8 for each of the three modalities are plotted as scatter plot. Each point represents a subject color-coded by age. The component maps correspond to the mixing weights of the source for each modality.

Component 1 showed the most significant sex effects, as depicted in Figure 2. The interaction term age by sex was only weakly significant for a couple of components and did not survive multiple comparison correction for all of the three modalities for any component.

Fig. 2.

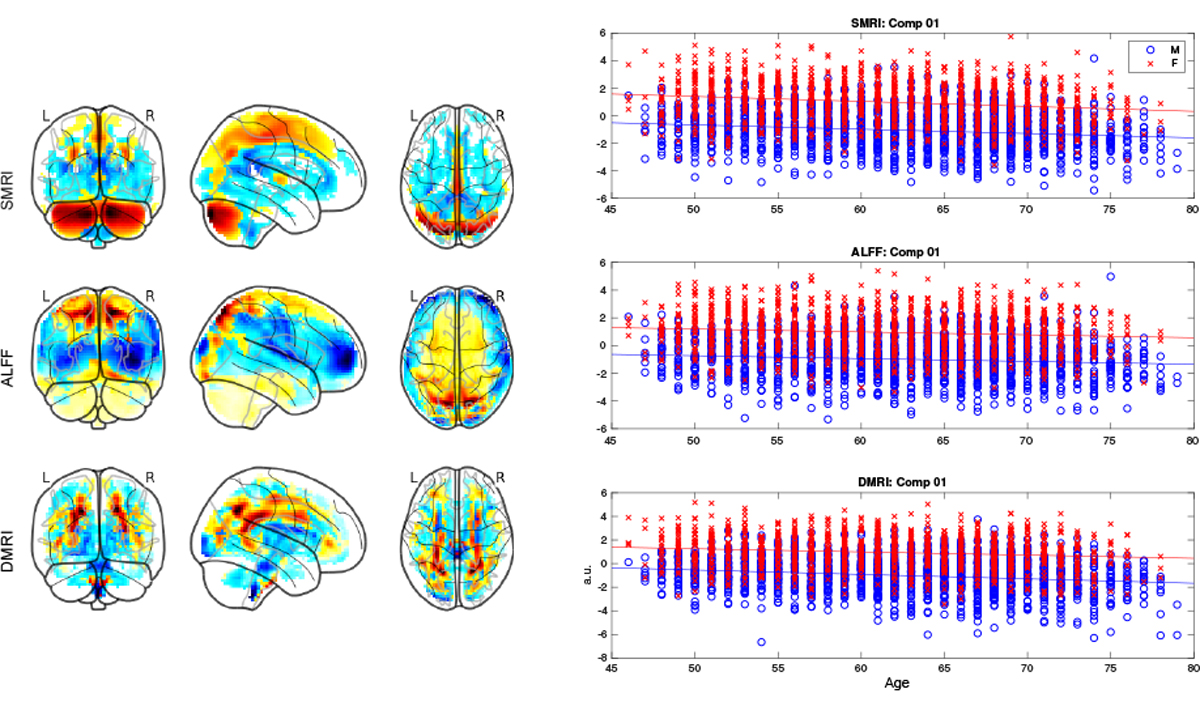
The sources corresponding to component 1 for each of the three modalities, by sex. The component maps shown, correspond to the mixing weights for each modality.

Among the remaining phenotypes, time-to-answer (TTA) in a prospective memory test showed linear association with each of the three modalities for component 3, as shown in Figure 3. As seen in the figure, subjects with faster responses have higher component values and vice versa.

Fig. 3.

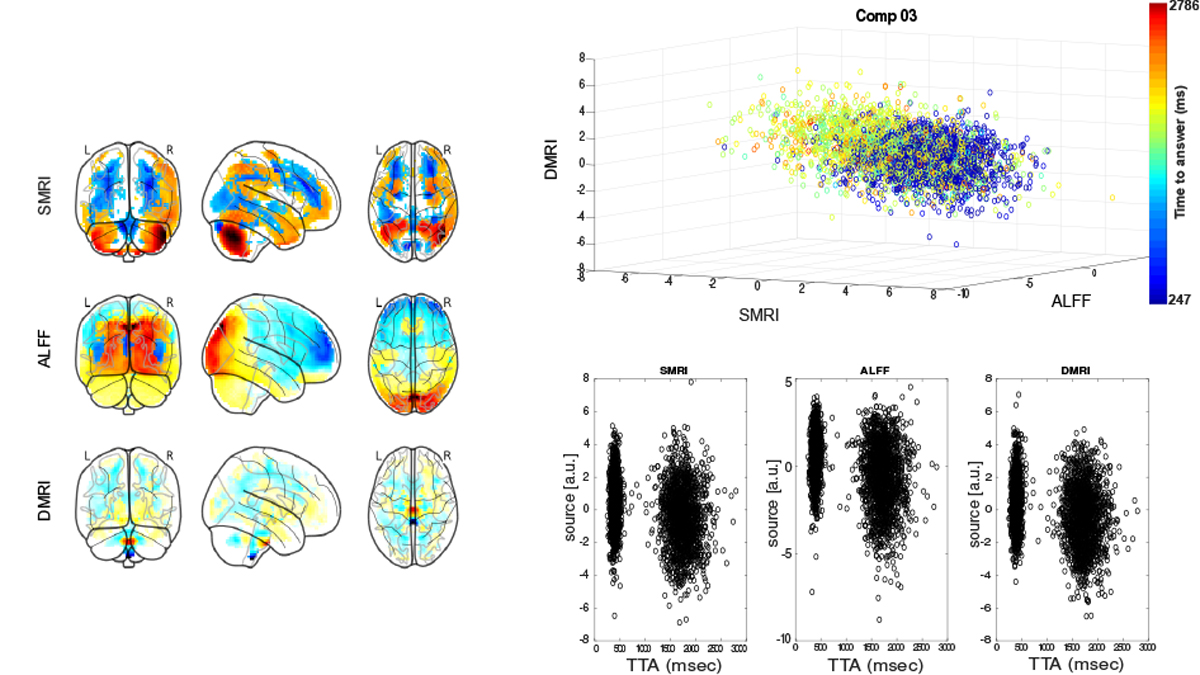
The sources corresponding to component 3 for each of the three modalities, plotted as scatter plot. Each point represents a subject color-coded by time-to-answer (TTA) in a prospective memory test. The component maps correspond to the mixing weights of the source for each modality. The source intensities are also plotted separately for each modality to show consistent shift in source distributions of fast and slow responders in prospective memory task.

Few components show significant variation with nuisance variables (subject movement and spatial normalization summaries), which are not shown here.

IV. DISCUSSION

In this work, we showed that multimodal IVA, initialized with multimodal group principal components estimated using data from all modalities, can help extract independent subspaces with strong multimodal linkage and that also show significant covariation with subject phenotypes.

Age associated decline (hot areas in the weight maps of sMRI component 8) in gray matter density was primarily seen in caudate, thalamus, insular regions, anterior and posterior cingulate cortex, and lingual gyrus, consistent with earlier findings [19]. Subject weights corresponding to dMRI modality suggest reductions in fractional anisotropy values with age in periventricular regions including superior and posterior thalamic radiation. ALFF maps corresponding to component 8 suggest reductions in parietal and visual regions of the brain that covary with structural changes.

MMIVA Component 1 showed the most significant sex differences for all 3 modalities. In both sexes, linear covariation with similar trajectory of decline with age in ALFF in parietal cortex, cerebellar regions in gray matter density, and fractional anisotropy in parietal cortico-pontine tracts was observed.

Variability in reaction times to prospective memory tests was captured in component 3 with subjects who exhibited faster reaction times showing greater gray matter densities in cerebellum (Crus 1), higher ALFF values in the areas corresponding to dorsal visual stream, and higher FA values in the cortico-spinal tract.

In summary, we demonstrate the ability of multimodal independent vector analysis to directly extract linked multimodal independent modes of subject variations that also capture different aspects of pheonotypical information. Further investigations are needed to verify if the observed covariation patterns across the different modalities are driven by common causes and replicate in patient populations.