Fibrin prestress due to platelet aggregation and contraction increases clot stiffness

Abstract

Efficient hemorrhagic control is attained through the formation of strong and stable blood clots at the site of injury. Although it is known that platelet-driven contraction can dramatically influence clot stiffness, the underlying mechanisms by which platelets assist fibrin in resisting external loads are not understood. In this study, we delineate the contribution of platelet-fibrin interactions to clot tensile mechanics using a combination of new mechanical measurements, image analysis, and structural mechanics simulation. Based on uniaxial tensile test data using custom-made microtensometer and fluorescence microscopy of platelet aggregation and platelet-fibrin interactions, we show that integrin-mediated platelet aggregation and actomyosin-driven platelet contraction synergistically increase the elastic modulus of the clots. We demonstrate that the mechanical and geometric response of an active contraction model of platelet aggregates compacting vicinal fibrin is consistent with the experimental data. The model suggests that platelet contraction induces prestress in fibrin fibers and increases the effective stiffness in both cross-linked and noncross-linked clots. Our results provide evidence for fibrin compaction at discrete nodes as a major determinant of mechanical response to applied loads.

Why it matters

Strength of blood clots is determined by the remodeling of fibrin by the contractile forces exercised by the platelets in the later stages of clotting. Therefore, determining how platelet-fibrin interactions increase clot stiffness is fundamental to the understanding of hemostasis and thrombosis. Here, we show from uniaxial tensile strain and quantitative microscopy data that the elastic moduli of blood clots correlate directly to the ability of platelets to aggregate and to apply prestress to fibrin fibers. A quasistatic contraction model based on the experimental data explains that the contractile fibrin-bound platelet aggregates act as prestressed nodes and increase the effective stiffness of the entire clot.

Introduction

Efficient hemostasis culminates in the formation of strong and stable plugs to dam blood flow in broken vessels or to stop leaks through injured vessel walls. The strength and stability of clots are important predictors of bleeding diathesis and thrombotic complications, and these properties are being adopted for new indications including trauma and anticoagulant monitoring (1,2). Clot components including platelets, fibrinogen, and red blood cells (RBCs) contribute to the mechanical properties of the clot (3, 4, 5, 6). The dynamics of interactions between these components on clot mechanics is an active area of investigation because of fundamental importance and translational benefits.

Fibrin is the key structural element of a clot. Platelets not only initiate and propagate fibrin formation but also modify the structure of the fibrin network extensively during the later stages of clotting through retraction. The hemostatic potential of the platelets, including their ability to activate, to aggregate, and–most importantly–to retract, determines the clot stiffness (7, 8, 9). It was recently shown that clot contraction and enhanced clot stiffness are the results of exquisitely organized, platelet-driven, and actomyosin- and integrin-mediated remodeling of fibrin (10). However, the mechanism by which platelet contraction enhances resistance of a clot against applied forces is unknown, and this question is of fundamental importance to the understanding of hemostasis.

To answer this question, first, we evaluate the stress-strain behavior of blood clots to uniaxial tensile strain using a custom-made microtensometer. To our knowledge, this is the first study to report the elastic properties of fresh human blood clots subjected to tensile strain. Uniaxial testing is a direct method to measure the tensile mechanical properties of several (vascular) biomaterials, including fibrin gels (11), collagen gels (12), stored porcine blood clots (13), cell-seeded scaffolds (14), and aortic tissue (15). Together with appropriate mathematical models, tensile tests have provided profound insights into the mechanobiology of cell-matrix interactions (16, 17, 18, 19). Second, using the experimental tensile and microstructural data in conjunction with a computational model for the response of fibrin to platelet compaction strain and externally applied strain, we elucidate the relationship between platelet-fibrin interactions and the mechanical response of clots to applied extension. We discover that platelet aggregates compacted with dense fibrin bundles act as prestressed nodes that dramatically increase the stiffness of the entire clot.

Materials and methods

Measurement of clot response to uniaxial strain

Blood was obtained from healthy adult human volunteers in 3.2% sodium citrate, and clotting was initiated within 15 min of blood draw after recalcification with final concentration of 20 mM CaCl₂ (Sigma-Aldrich, St. Louis, MO) (20). The clotting process was initiated by the addition of final concentration of 1 U/mL thrombin to 500 μL of recalcified blood, and the clot was incubated under humidified conditions for 1.5 h for full contraction (21). The clots were gently separated from the serum and loaded onto the clamps of a custom-made microtensometer. The microtensometer consists of a motorized nanopositioner (MP-285; Sutter Instrument, Novato, CA), a full-bridge thin cantilever load cell (113 g, LCL Series; OMEGA Engineering, Norwalk, CT), and a data acquisition signal conditioner DI-1000U (Loadstar Sensors, Fremont, CA). The load cell was zeroed without the bottom support to neglect the weight of the clot in the initial pull. The force recording from the data acquisition software (LoadVUE; Loadstar Sensors) and actuation of the nanopositioner were started simultaneously, and force measurements were recorded at 30 Hz. Two digital cameras were positioned at orthogonal angles to capture top-view and side-view images to extract the cross-sectional dimensions. Cross-section images were used to convert force-displacement curves to the respective true stress versus stretch ratio curves.

In designated cases, the following inhibitors were added to blood and incubated for 30 min at room temperature with gentle rocking (Vari-Mix Platform Rocker; Thermo Fisher Scientific, Waltham, MA) at ∼2 Hz before recalcification: 300 μM blebbistatin, 10 μM eptifibatide, or 10 μM T101. To investigate the effect of platelets in clotting, RBCs were separated by centrifugation for 15 min without brakes at 250 relative centrifugal force, 7 rad/s² acceleration, and after separating the RBCs from platelet-rich plasma, platelet-poor plasma (PPP) was obtained by further centrifugation of platelet-rich plasma for 20 min without brakes at 1500 relative centrifugal force, 7 rad/s² acceleration. The RBC was added back to PPP to restore the hematocrit to original levels in the whole blood. The hematocrit levels were estimated based on compacted RBC volume after centrifugation, and it typically ranged between 40 and 50%.

Microstructural characterization of clots

To visualize clot microstructure, platelets and fibrinogen were labeled with Alexa Fluor 488 (AF488) and Alexa Fluor 596 (AF596) fluorophores, and 100 μL of blood was used to form clots as described above. Platelets in whole blood were incubated with an AF488-conjugated CD42b antibody for 20 min before the start of clotting, and blood was doped with 5% AF596-conjugated fibrinogen, assuming a final concentration of 4 mg/mL. After 1.5 h, the clots were imaged at 63× magnification using an oil immersion lens (DMi8; Leica Microsystems, Wetzlar, Germany). Z-stack images were collected from at least five different locations for each clot. The fluorescence images were processed and analyze offline for quantification by two-dimensional (2-D) projection of the stack to estimate aggregate size and Pearson correlation coefficient (PCC) using Image-Pro 10 (Media Cybernetics, Rockville, MD) and ImageJ (National Institutes of Health).

Discrete prestressed fiber model simulations

Simulations were based on structural mechanics for a finite number of 2-D truss elements, with the platelet aggregate located within a prescribed initial radius R₀ at the center of a square region. Equal displacement and force equilibrium are maintained at the node, joining each “within aggregate” and “outside of aggregate” fiber. Given symmetry about two planes, only the upper right quadrant was necessary for simulations. Material properties were assigned distinctly to the line segments inside and outside of the prescribed radius. Poisson’s ratio was kept constant at a value of 0.49, assuming nearly ideal incompressibility. The elastic modulus of the interior line segments was based on relative modulus-β, defined as the ratio of elastic modulus of compacted fibrin to noncompacted fibrin. The effect of compaction was simulated by prescribing a compaction strain-α, defined as the extent of reduction from an initial radius R₀ to a compacted radius R_c (i.e., α = (R₀ − R_c)⁄R₀). The compaction strain provides a prestress that is analogous to the stress that would result from the strain associated with thermal shrinkage. Thus, the variable material inputs are fibrin Young’s modulus, relative modulus (for platelets), and compaction strain.

Simulations were performed using COMSOL Multiphysics (Stockholm, Sweden), using quasistatic 2-D truss elements with geometric nonlinearity enabled such that the direction of tension remained axial as each element changed orientation throughout the prescribed extension. Strain energy densities were simulated using parametric sweeps along values of compaction strain-α and applied uniaxial strain-ε, up to a strain of 50%. Compaction strain-α was mimicked using a thermal expansion coefficient. Convergence of the discrete fiber model was checked by varying the number of fibers and evaluating the average strain energy density. The range of solution values among five-fiber, six-fiber, and seven-fiber solutions was less than 0.6% of the mean (Fig. S3 A), and five fibers were used for all reported strain energy density simulations. For all clots involving platelets (i.e., untreated, blebbistatin, eptifibatide, and T101), geometric dimensions were set to match the compacted radius that was determined from image analysis. The relative size of the model quadrant was customized according to the spatial density of aggregates, which was determined by computing the average number of aggregates per unit area for each type of clot. The corresponding lengths of fibrin fibers were set to maintain the relative size of a single platelet aggregate to ensure correct proportion of aggregate area with respect to the bounding-box quadrant of the fiber model. The corresponding relative sizes (i.e., aggregate radius divided by quadrant box edge length) for untreated, blebbistatin-treated, eptifibatide-treated, and T101-treated clots were 0.087, 0.100, 0.103, and 0.118, respectively. Thus, the geometric model inputs are the number of fibers, bounding-box size, and initial aggregate radius.

Statistical analysis

The data were collected from clots prepared from five to seven different donors, and the experiments were performed on different days. For each donor and treatment, the microtensometry experiments were performed at least in triplicate, and the results from two or three replicates for each donor were averaged. To establish differences between untreated and treated clots, a paired, one-tailed Student’s t-test was performed to calculate p-values, for which a value of less than 0.05 was deemed statistically significant.

Results

Mechanical characterization of blood clots

Response of blood clots to uniaxial strain

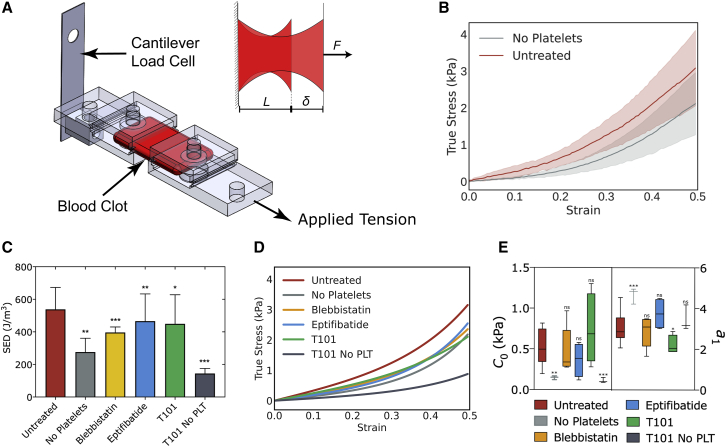
To measure the stress-strain response of blood clots in the ranges of micronewton force and submicron displacement, we designed a microtensometer that measures tension as the clots are stretched (Fig. 1 A). The design specifications, engineering details, and calibration of the instrument are presented elsewhere (22). Thrombin-initiated whole blood clots were loaded onto the microtensometer and secured using magnetic clamps (Fig. 1 A; Fig. S1). Clots having a 6-mm gauge length were extended by 3 mm (i.e., 50% strain) at 100 μm/s. Force measurements were recorded simultaneously at 30 Hz. The force-displacement curves were converted to true stress versus strain plots using cross-sectional area measured in two orthogonal directions (23). As expected for many biological tissues and fibrous-matrix materials, the stress-strain plot for untreated whole blood clots exhibits strain-stiffening behavior over the tested range of strains (Fig. 1 B). Next, we evaluated the contribution of platelets to the mechanical behavior of clots using blood reconstituted with PPP and obtained the stress-strain response as outlined above (Fig. 1 B). The clots from reconstituted blood without platelets were substantially more compliant than whole blood clots. The strain energy density, which is the potential energy stored in the clot due to the work done to deform the clot, is computed as the area under the stress-strain curve. At 50% strain, the strain energy density of whole blood clots was nearly twofold higher than that of clots formed without platelets, suggesting that the platelets contribute nearly twofold more work in deforming the clots (Fig. 1 C). The equivalent linear stiffness of the clot at 50% strain, which is the slope of an ideally linear stress-strain curve having the same strain energy density, was estimated to be 4.4 kPa, which is in the same range of Young’s modulus values reported recently for retracted clots using micropillars (9). The equivalent linear stiffness of clots without platelets was substantially lower at 2.5 kPa.

Figure 1.

Response of blood clots to uniaxial strain. (A) Oblique view and close-up top view of clot in between microtensometer grips. One grip is attached to a fixed load cell, and the opposite of the grip is moved by a nanopositioner.(B) Stress-strain response of clots formed by the addition of thrombin to whole blood or clots formed from platelet poor plasma reconstituted with RBCs. (C) Strain energy densities at 50% strain. (D) Stress-strain curves fitted to the nonlinear exponential model σ = 2C₀a₁exp(a₁ε²), where σ is stress, ε is strain, and C₀ and a₁ are model parameters. (E) C₀ and a₁ for untreated and treated clots. Mean ± standard deviation, ∗p < 0.05, ∗∗p < 0.01, ∗∗∗p < 0.001.

To parameterize the stress-strain response, we applied an empirical nonlinear fit using a uniaxial simplification of the Fung strain energy model that has been widely used for soft tissues composed of fibrous networks (24). For this model, the strain energy is given by u = C₀ exp(a₁ε²), where u is the strain energy density, ε is uniaxial strain, and C₀ and a₁ are fitted constants. Differentiating strain energy with respect to strain, we obtain an expression for tensile stress as σ = 2C₀ a₁ ε exp(a₁ ε²). The stress-strain experimental data were fitted to this equation (Fig. 1 D). The variables C₀ and a₁ parameterize stiffness at lower strains and strain-stiffening behavior, respectively. The estimates for C₀ and a₁ for whole blood clots are, as expected, significantly lower than those reported for aortic tissues (25,26) (Fig. 1 E). In the absence of platelets, the stress-strain curve fits yielded estimates of C₀ and a₁ that are threefold lower and twofold higher, respectively, than untreated clots. Because the stress-strain relationship is nonlinear, the elastic modulus of the clot increases with tensile strain and can be estimated from the equivalent area under the stress-strain curve. As can be seen from Fig. S2 A, platelets contribute to a nearly twofold increase in stiffness of the clots over the entire range of strain tested in this work.

Effect of platelet contraction and aggregation on clot response to uniaxial strain

Having established the role of platelets to the stress-strain response of blood clots, we sought to determine the role of two key processes, i.e., platelet compaction and aggregation, which are known to impact the overall contraction of a blood clot. To this end, we evaluated the stress-strain response of clots formed with platelets treated with blebbistatin, in which clot formation was initiated by the addition of thrombin. Blebbistatin inhibits the binding of myosin II to actin, which is critical to platelet contraction (27). As shown in Fig. 1 C, we observed that blebbistatin treatment significantly changed the response of clots to uniaxial strain compared with untreated clots. From these plots, we computed the total strain energy density, the nonlinear fit parameters, and the stiffness at 50% strain. The strain energy density was 25% lower in clots treated with blebbistatin compared with untreated clots (Fig. 1 C).

To evaluate the effect of platelet aggregation on the tensile response of the clots, we similarly tested clots prepared using platelets exposed to eptifibatide, an inhibitor of platelet GP IIb/IIIa, and hence aggregation (28). The uniaxial stress response shows that these clots are weaker than untreated clots, although only modestly so (Fig. 1 C). The strain energy density for eptifibatide-treated clots was 20% lower than for that of untreated clots (Fig. 1 C). The parameter C₀ was lower for blebbistatin- and eptifibatide-treated clots, indicative of overall lower stiffness. The parameter a₁ was only modestly different from that of whole blood clots, indicative of similar strain-stiffening behavior (Fig. 1 E; Fig. S2 A). To evaluate how much platelet aggregation and contraction contributes to the stiffness of whole blood clots over that only due to fibrin cross-linking, we normalized the increase in strain energy density of eptifibatide- and blebbistatin-treated clots over platelet-poor (i.e., “no-platelet”) clots by the increase in strain energy density of platelet-rich whole blood clots over platelet-poor clots. This calculation shows that eptifibatide and blebbistatin treatments reduce clot stiffness by 51 and 67%, respectively.

Of note, the tensile modulus of the no-platelet clots in the 1-kPa range is comparable with the previous measurements of tensile modulus of fibrin gels in the 2–10-kPa range (29). It is instructive to place the tensile elastic modulus E estimated in this work with other well-known measures of clot stiffness: shear modulus, G’, estimated by rheometry, and the maximal amplitude estimated by thromboelastography. It has been shown that maximal amplitude and G’ are significantly impacted by the inhibitors of GP IIb/IIIa or actin polymerization, similar to the microtensometry results. However, a direct comparison between these measurements and our results is limited not only because the of differences in types of strain (shear strain versus tensile strain) applied to the sample but also because in rheometry and thromboelastography, clots contain serum, whereas in tensometry, the contracted clots do not contain serum (20,30).

Contribution of fibrin cross-linking on clot response to uniaxial strain

To evaluate the effect of fibrin cross-linking, we evaluated the stress response of clots that were polymerized with thrombin but in the presence of T101. T101 inhibits transglutaminase activity of FXIII, thereby eliminating the lateral cross-linking of fibrin strands (20,31). The strain energy density of noncross-linked clots was ∼25% lower than that of cross-linked clots. We observed that noncross-linked clots show significantly lower stress at the same strain, i.e., weaker, compared with the clots formed by the direct addition of thrombin (Fig. 1 D). Correspondingly, the stiffness of 2.1 kPa at 50% strain was comparable with clots without platelets, indicating that the platelets are as influential as cross-linking in clots initiated with exogenous thrombin. The C₀-value was comparable with untreated whole blood clots, but a₁ was lower, revealing the relative importance of cross-links on stiffness at higher strains and that this is evident from weaker dependence of elastic modulus with applied strain (Fig. S2 B). The combined effect of cross-linking and platelets on clot stiffness can be seen from T101-treated blood without platelets. These clots were the weakest with strain energy density threefold lower than that of whole blood clots (Fig. 1 C).

Microstructural characterization of platelet-fibrin interactions in clots

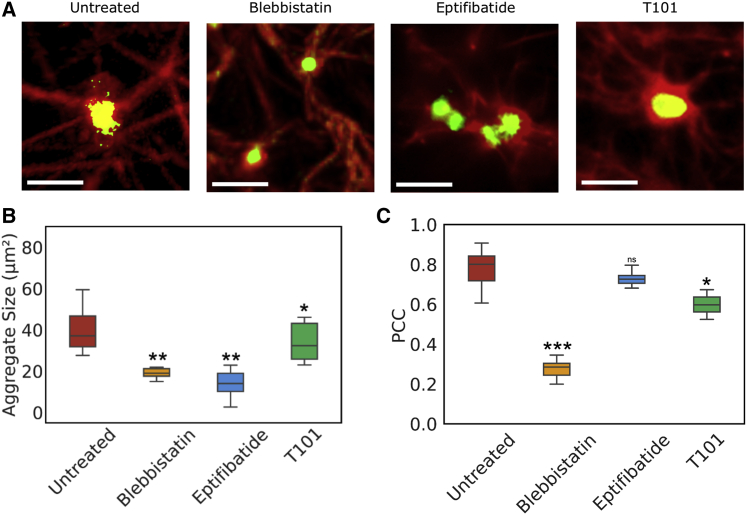
As seen from the mechanical data, platelets contribute to the stiffness of the clots through platelet contraction and aggregation. To understand the contribution of platelets, we analyzed clot microstructure through high-magnification fluorescence imaging, with emphasis on platelet-fibrin interactions in clots prepared from platelets that were untreated or treated with blebbistatin or eptifibatide (Fig. 2 A). As evidenced by the intensity of red and green fluorescence due to fibrin and platelets, respectively, interfering with platelet actomyosin or aggregation altered the size of the aggregates and the amount of fibrin present. Interestingly, T101 treatment did not seem to alter either platelet aggregates or the amount of fibrin present on the platelets.

Figure 2.

Microstructural characterization of platelet-fibrin aggregates. (A) Clots prepared from platelets that were either untreated or treated with blebbistatin, eptifibatide, or T101. Scale bars, 10 μm; Platelets are labeled with AF488-CD42b (green) and fibrinogen with AF594-fibrinogen (red). (B) Average size of platelet aggregates. (C) PCC for the colocalization of platelets and fibrin. Mean ± standard deviation, ∗p < 0.05; ∗∗p < 0.01; ∗∗∗p < 0.001.

To quantify platelet-fibrin interactions, we first estimated the size of platelet aggregates and the amount of fibrin in these aggregates. The average sizes computed based on these images revealed a mean aggregate size of 40 μm² in clots without any treatment, whereas blebbistatin and eptifibatide treatments reduced the average aggregate size by twofold and threefold, respectively (Fig. 2 B). In contrast, T101 treatment only had a modest effect on aggregate size. Next, we correlated the spatial distributions of the densities of platelets and fibrin based on the overlap in the fluorescence intensities between platelets (green, CD42b-AF488) and fibrin (red, fibrinogen-AF596) using the PCC (Fig. 2 C). A PCC closer to 1.0 signifies a higher incidence of localization between the green and red fluorophores (32). We observed that in untreated blood clots, 80% of the projected area of the platelet aggregates was also fibrin rich. In contrast, the spatial overlap between fibrin and platelet densities was low in clots formed from blebbistatin-treated platelets. PCC was only modestly affected by eptifibatide-treated clots, indicating that single platelets or microaggregates co-located strongly with fibrin. A similarly small difference in PCC compared with untreated clots was observed in clots treated with T101, suggesting that fibrin cross-linking may only modestly affect the colocalization of fibrin fibers on platelet aggregates.

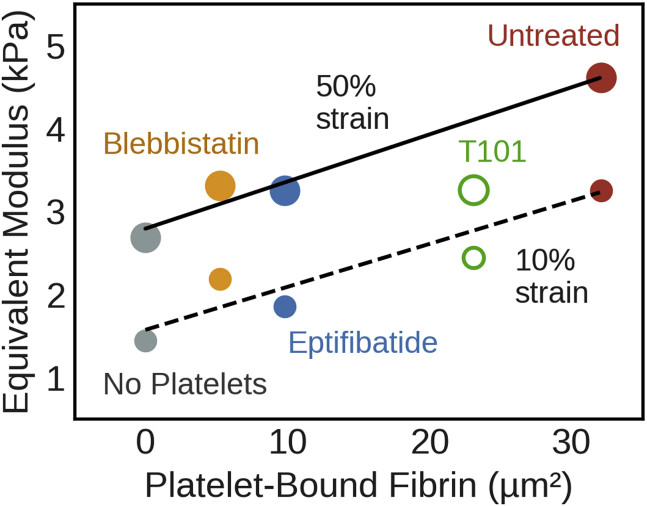
Both platelet aggregation and fibrin compaction determine clot stiffness

Upon observing the effect of platelet aggregation and platelet actomyosin on clot stiffness from microtensometry and also the effect on platelet-fibrin interactions from microstructure studies, we sought to establish a relationship between the two. We estimated the equivalent modulus based on strain energy density at 50% strain. We surmised that the size of the platelet aggregates and the amount of the fibrin bound to platelet aggregates, i.e., PCC, would be critical to clot stiffness. Although neither the size nor PCC individually show a meaningful correlation with equivalent modulus, we discovered that the product of these quantities, which estimates the density of the fibrin bound to platelet aggregates, is tightly correlated with the equivalent modulus of the clot (Fig. 3). The effect of the fibrin bound to the platelet aggregates on elastic modulus was independent of applied strain (i.e., slope of 52–57 kPa/μm² over 10–50% strain), indicating that the fibrin-platelet interactions determine the effective mechanical behavior of the clot. These data show that both platelet aggregation and actomyosin contraction result in comparable densities of fibrin-bound platelet aggregates, and they contribute similarly to increasing the stiffness beyond the baseline no-platelet clot, albeit by different mechanisms. Interestingly, disrupting fibrin cross-linking with T101 had two effects: it not only reduced the amount of fibrin bound to the platelet aggregates but also lowered the equivalent modulus from what may be expected of fully cross-linked clots.

Figure 3.

Platelet-fibrin interactions determine clot stiffness. Elastic modulus correlates linearly with the density of platelet-bound fibrin at various applied strains. The lines represent least-square best fits without T101 (with R² = 0.90 at 10% strain and R² = 0.97 at 50% strain, respectively).

A computational framework for understanding the contribution of fibrin-bound platelet aggregates on clot stiffness

The passive fiber adsorption model

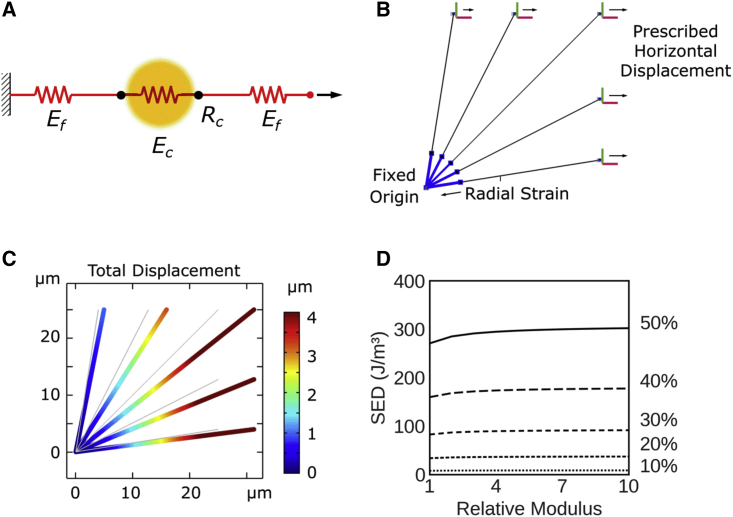
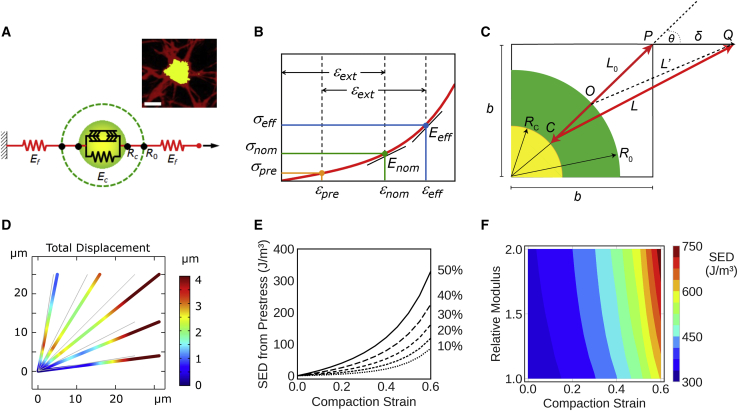
Having established a correlation between the density of fibrin-bound platelet aggregates and strain energy density, we sought to develop a computational model to interrogate the underlying physical basis of this relationship. We posited that the fibrin adsorbed on platelet aggregates will result in an increase in the elastic modulus of platelet-fibrin aggregates over that of the fibrin matrix in the bulk. The platelet-fibrin aggregate is represented by a contractile element with an elastic modulus E_c, which may be different from the modulus of elastic modulus E_f of distal fibers (Fig. 4 A). The ratio between moduli is defined as relative modulus, β = E_c/E_f. The fibers are bound to platelet GP IIb/IIIa receptor clusters at the focal adhesion sites located at a radial distance R_c.

Figure 4.

Passive fiber adsorption model. (A) Fibrin fibers (red) are connected to fibrin-bound platelets (yellow), and both fibers are modeled as springs with different stiffnesses. In this passive model, platelets do not exercise any active contractile stress. (B) Description of model elements and boundary conditions. (C) Representative deformation of a five-fiber model with a 5-μm aggregate radius and relative modulus of 10, pulled to 25% uniaxial strain. (D) Strain energy density as a function of relative modulus at various applied strains up to 50%.

Effect of fiber modulus on the strain energy density of the clots

Finite element simulations were performed using truss-element fibers at evenly spaced angles in a quadrant with two-plane symmetry (Fig. 4 B). The node (shared by all fibers) at the origin was fixed, and nodes on the right-side boundary were assigned prescribed uniaxial displacements, as indicated in Fig. 4 B. The two nodes along the top side are assigned correspondingly proportional strains according to their horizontal positions (i.e., mimicking a roller condition for a continuous body). The model showed convergence in strain energy density with as few as three fibers per quadrant, and simulations presented here used five fibers per quadrant (Fig. S3 A). Fig. 4 C shows the distribution of local deformation of the fibrin fibers under the combined effect of platelet contractile strain and externally applied strain. As expected, the fibers oriented in the direction of externally applied strain experienced the largest magnitudes of local displacement. However, we notice that merely passive spring elements failed to capture experimental observations. In the absence of compaction strain, even a 10-fold increase in elastic modulus of the fibrin bound to the platelet aggregates produced a barely perceptible increase in strain energy density (Fig. 4 D).

The discrete prestressed fiber model

Next, we modified the above model to replace passive platelet-fibrin spring elements with actively contracting platelet-fibrin aggregates. A discrete prestressed fiber model and its functional components that include a fibrin-bound platelet aggregate are shown in Fig. 5 A. Similar to the previous model, the platelet-fibrin aggregate is represented by a contractile element with an elastic modulus E_c, which may be different from the modulus of elastic modulus E_f of distal fibers, and the ratio between moduli is defined as relative modulus, β = E_c/E_f. To account for platelet contraction, the fibers are bound to platelet GP IIb/IIIa receptor clusters at the focal adhesion sites located at a radial distance R₀ from the center of the aggregate. Contractile forces during clotting due to actomyosin activity draw fibers inward, and these fibers are retracted to a tighter aggregate of radius R_c. This contraction induces a prestressed condition in the vicinity of the aggregate, and the prestress is retained by the clot even in the absence of an externally applied load. A quasistatic model of platelet contraction is a realistic approximation because the timescale of contraction-relaxation of nonmuscle myosin IIA is much smaller than the timescale of matrix contraction (33). This prestress is due to plasticity of the overall cell-matrix interaction, as has been observed for cells encapsulated in collagen and fibrin gels (34). Fig. 5 B, superimposed on the average stress-strain curve of the clots without platelets (i.e., fibrin network), illustrates how prestress can influence the effective modulus. In the absence of prestress, an externally applied strain ε_ext results in a nominal stress σ_nom. The local modulus at the corresponding nominal strain ε_nom is E_nom. However, when prestress σ_pre and prestrain ε_pre are present, the addition of the same externally applied strain results in a higher effective stress σ_eff, and the local effective modulus E_eff at the (total) effective strain ε_eff is steeper. The corresponding strain energy density, computed as the area under the curve up to the effective strain, is also substantially larger than nominal.

Figure 5.

Discrete prestressed fiber model for clot subjected to uniaxial strain. (A) The actomyosin contractile elements in platelets compact the fibrin fibers onto the aggregates. Given is the representative image of a single platelet aggregate with fibers emanating from the aggregate (scale bars, 5 μm) (inset). (B) Compaction strain is added to externally applied strain such that the effective modulus E_eff is higher than nominal; (C) Euclidean geometric representation of a fibrin fiber compacted by platelet contraction. (D) Representative finite element simulation of fiber deformation in the vicinity of a platelet aggregate, shown with a 5-μm aggregate radius, 0.5 compaction ratio, 2.0 relative modulus, and 25% applied strain. (E) Strain energy density due to prestress as a function of compaction strain for applied strain up to 50%. (F) Predicted strain energy density as a function of compaction strain and relative modulus.

The interaction between a representative fibrin fiber bundle and a platelet aggregate is depicted in Fig. 5 C. Platelet GP IIb/IIIa-fibrin(ogen) interactions anchor the fibrin fibers to the platelet surface. The fiber of an initial length L₀ is bound to the platelet aggregate at a focal adhesion at point O. A quarter circle that represents a single platelet aggregate with two orthogonal planes of symmetry is shown within a corresponding quadrant of a square having side length b. The fiber is oriented at an arbitrary angle θ with respect to the direction of applied external strain. The fiber OP experiences the combined effects of prestrain and applied external strain, resulting in a geometrically nonlinear response to strain. The individual fibers are modeled as linear elastic materials obeying Hooke’s law.

The global stiffness matrix for two fibers in series is written as shown in Eq. 1, where node 0 is at the center of a platelet aggregate, node 1 is at the focal adhesion, and node 2 is the free end subject to external strain. F represents nodal forces and d represents nodal displacements along the axial direction x. Spring constants k₁ and k₂ are associated with the platelet aggregate and (unbound) fibrin fiber, respectively.

$$\left\{\begin{array}{l}{F}_{0x}\hfill \\ F_{1x}\hfill \\ F_{2x}\hfill \end{array}\right\}=\left[\begin{array}{lll}{k}_1\hfill & -k_1\hfill & 0\hfill \\ -k_1\hfill & k_1+k_2\hfill & -k_2\hfill \\ 0\hfill & -k_2\hfill & k_2\hfill \end{array}\right]\left\{\begin{array}{l}{d}_{0x}\hfill \\ d_{1x}\hfill \\ d_{2x}\hfill \end{array}\right\}.$$ (1)

To represent prestress, we add a contractile force F = −αEA and the focal adhesion (i.e., node 1), where the elastic modulus E and cross-sectional area A pertain to the platelet aggregate. The parameter α is the compaction strain, defined as the extent of aggregate compaction from an initial radius R₀ to a compacted radius R_c (i.e., $\alpha =\left(R_0-R_C\right)/R_0$). At node 2 (i.e., the location where external strain is applied), the fiber is subjected to a horizontal displacement δ. Applying these assigned conditions, the equilibrium solution to axial force along the fiber assembly is as shown in Eq. 2, with details provided in the Supporting materials and methods.

$$F=\left(k_2-\frac{k_2^2}{k_1+k_2}\right)\delta +\frac{k_{2}EA}{k_1+k_2}\alpha .$$ (2)

In the presence of prestrain due to compaction (α > 0), the second term in the force solution above predicts a higher axial force along the fiber with increasing compaction strain. From this solution, the corresponding strain energy density can be calculated for any combination of relative modulus-β, compaction strain-α, and applied uniaxial strain ε = δ/b. The multidirectional orientation of fibers was accounted for by using coordinate transformations for fibers that are oriented off axis from the direction of externally applied strain, as explained in the Supporting materials and methods.

Effect of fibrin compaction and fiber modulus on the strain energy density of the clots

Fig. 5D shows the results of finite element simulations on the distribution of local deformation of the fibrin fibers under the combined effect of platelet contractile strain and externally applied strain. As expected, the fibers oriented in the direction of externally applied strain experienced the largest magnitudes of local displacement. For the same applied strain, the absence of platelets resulted in smaller local deformation of the fibers when compared with the deformation in the presence of platelet contraction (Fig. 5 D vs. Fig. S3 B). In the absence of platelets, the strain energy density of the fibrin fibers is purely due to externally applied strain and scales approximately as the square of strain (Fig. S3 C).

We computed strain energy densities using the five-element model for a range of compaction strains and externally applied strains. The compacted radius R_c and the bounding-box size b for each clot type were set accordingly to account for the average space occupied by a single platelet aggregate, based on the average density of aggregates measured from image analysis. Because strain energy density is additive, the effect of applied strain can be subtracted from the total strain energy density to obtain the effect of compaction strain. As shown in Fig. 5 E, we observed that the contribution to strain energy density from compaction increases exponentially with an increase in compaction strain and is more pronounced at higher externally applied strains because the fibers are effectively subjected to strains in a steeper region of the stress-strain curve.

The above simulations were performed assuming that the elastic modulus of the fibrin fibers is twice as much upon compaction on the platelet surface as when they are not bound to platelets. Because the actomyosin stress fibers are indeed rigidity sensors and respond to the increase in local stiffness by exerting larger traction forces, we also considered the effect of an increase in the elastic modulus of fibrin fibers that get compacted on the platelet surface due to contraction (35) (Fig. 5 F). We noticed that the total strain energy density was only modestly affected by the platelet-bound fibrin as being stiffer than unbound fibrin over a broad range of compaction strains. From these simulations, we demonstrated that our discrete fiber model accounts for the effects of both compaction strain due to platelets and strain due to externally applied tension, in agreement with the total strain energy density measured experimentally.

Fibrin compaction on platelet surface due to aggregation and actomyosin contraction increases the strain energy density of clots

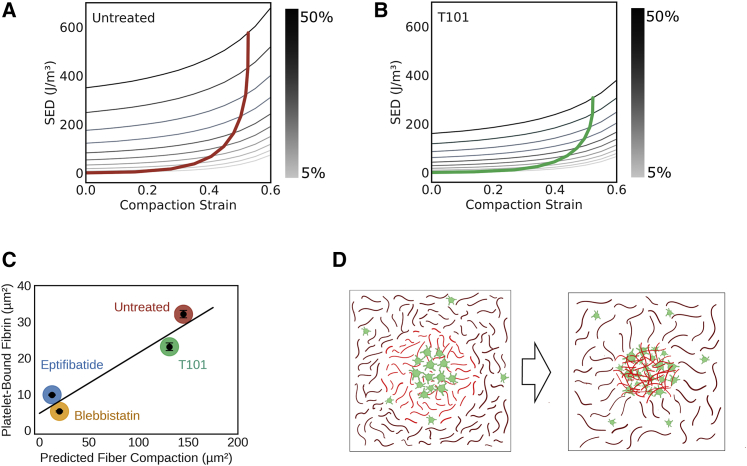
Next, we sought to obtain estimates of compaction strain by matching the total strain energy density from model predictions against experimentally measured values. Because the simulations show that the relative modulus has only a modest effect on strain energy density over the experimental range (i.e., 300–750 J/m³), without loss of generality, we considered a model wherein the modulus of the fiber increased by twofold upon compaction (Fig. 5 E). To compare the model predictions with experimental stress-strain data, we superimposed the experimentally determined strain energy densities at different applied strains (computed from Fig. 2 A) on to the model predictions (Fig. 6, A and B). To establish a baseline case without platelets (Fig. S2 B), the model with only fibrin fibers (i.e., R₀ = 0) was first calibrated to the average stress-strain curve of no-platelet clots to match the Young’s modulus that was consistent with strain energy density at each 10% increment of external uniaxial strain between 10 and 50%. The corresponding Young’s modulus values varied between 3.5 and 4.7 kPa over this range of strain. To establish a second baseline, a case with no fibrin cross-linking (and no platelets) was established based on average stress-strain data of clots treated with T101. The corresponding Young’s modulus values for the weaker fibers (i.e., without the benefit of cross-linking) varied between 1.8 and 2.1 kPa. Because the applied tensile strain increases beyond ∼20% and the resistance to deformation is due to fibrin fibers bound to platelets, the intersections between experimental and predicted strain energy densities converge at a characteristic compaction strain of ∼0.6.

Figure 6.

Discrete prestressed fiber model predicts the amount of fibrin fiber compacted by contracting platelets. (A and B) Mapping of experimentally determined strain energy density onto model predictions for cross-linked (A) and uncross-linked clots (B). The sets of grayscale lines plot simulated SED as a function of radial compaction strain (horizontal axis) for increasing values of externally applied tensile strain (grayscale bar). The single colored lines (red for untreated and green for T101) show the loci of intersections with experimentally measured SED at each level of applied strain. (C) Correlation between experimentally determined fibrin density on platelet surface and predicted fiber compaction based on area reduction (R² = 0.91). (D) Schematic representation of predicted fiber compaction by platelets. Platelet aggregates sequester fibrin fibers into dense nodes, thereby prestressing the fibers close to platelets.

Similarly, we estimated the compaction strain for clots formed from platelets treated with blebbistatin or eptifibatide (Fig. S4, A and B). Both blebbistatin and eptifibatide treatments significantly reduced the compaction strain to nearly threefold lower than for untreated platelets, indicating that both platelet aggregation and actomyosin contraction are critical in increasing the effective modulus of the clot. As shown in Fig. 6 B, for clots treated with T101, the predicted compaction strain was comparable with that of untreated clots, indicating that disrupting cross-linking of fibrin fibers does not alter the ability of the platelets to contract the fibrin fibers. For computing the compaction strain in T101-treated clots, we used the elastic modulus of fibrin fibers estimated from clots formed from blood depleted of platelets and also treated with T101. The elastic modulus of these clots formed from blood depleted of platelets but treated with T101 were much lower than the elastic modulus of clots treated with T101, indicating the significant impact of fibrin cross-linking on clot properties.

Fibrin compaction predicted from the model correlates with proportion of fibrin on platelet aggregates

As discussed above, the compaction strain predicted by the discrete fiber model provides a measure of fibrin densification on the platelet surface. In Fig. 6 C, we observe that this is indeed the case, as the total amount of fibrin sequestered onto the platelet surface due to compaction strain is linearly correlated to the fibrin bound to platelet aggregates, as estimated by the product of PCC and aggregate area. This observation suggests that the extent of colocalization on aggregates observed by microscopy may serve as an effective quantitative metric for estimating fibrin compaction that leads to prestress in the clots. We note that the amount of fibrin compacted by platelets decreases by fivefold if the actomyosin contraction or aggregation is inhibited, as evident from blebbistatin or eptifibatide treatments, respectively. Interestingly, the amount of fibrin compacted by platelets was not as strongly influenced by the ability of fibrin to cross-link, suggesting that the decrease in elastic modulus of T101-treated clots is caused mainly by lack of cross-linking in the matrix rather than by the inability of fibrin to interact with platelet aggregates.

Discussion

Both conventional rheometry and more recent micropost measurements have shown that the presence of platelets increases the stiffness of clots by, depending on the measurement techniques, twofold to fivefold in the 0.8–20-kPa range (9,20,36). The increase in clot stiffness is a result of clot retraction, volume shrinkage, and plasma exudation driven by platelet contraction. As platelets contract, they appear to tug along the fibrin fibers and actively remodel fibrin in their vicinity (10,37). However, the biophysical mechanisms by which these platelet-fibrin interactions increase clot stiffness is unknown. We show that the work done by contracting platelets in remodeling the fibrin fibers is stored as strain energy density even before an external load is applied and is a critical contribution to the mechanism by which the clots resist deformation (38). Analogous to macroscopically familiar structures such as a rope hammock or an anchor capstan, our experimental data and modeling support the hypothesis that the discrete prestressed nodes composed of fibrin-bound platelet aggregates are key to the structural stability of the clots (39) (Fig. 6 D).

The local contractile strain exerted by platelets on vicinal fibrin is somewhat similar to that from the contractile strain exercised on the extracellular matrix by contracting cells which remodels fibers in the immediate vicinity of the cells and increases the overall stiffness of fibrous-matrix gels (40,41). However, there are several important distinctions between the contractile strain exerted by platelets vis-à-vis fibroblasts: first, although cells rearrange the fibrous networks of the extracellular matrix in their immediate vicinity, platelet filopodia draw and spool the fibrin fibers inward so much that the platelets are wrapped in fibrin fibers, as evidenced by the colocalization indices. We have deliberately used the term “compaction strain” instead of “contractile strain” to underscore this distinction. Second, compared with cellular traction forces, the contractile forces generated by single platelets are more than an order of magnitude lower in the 2–20-nN range, suggesting that platelet aggregation may be key to compensating for the smaller size and force (42, 43, 44) compared with fibroblasts. Our experimental data suggest that this is indeed the case: 1) although disrupting platelet aggregation using eptifibatide did not alter platelet-fibrin interactions (i.e., PCC) at the single platelet level, it significantly weakened the clot; and 2) based on the increase in the stiffness of whole blood clots (4.4 kPa) compared with no-platelet clots (2.5 kPa), and using an average platelet aggregate diameter of 7 μm, we can estimate the mean contractile force exerted by a platelet aggregate to be in the few hundreds of nanonewtons, which is in a range comparable with cellular traction forces (45). Third, simultaneous and cooperative compaction of fibrin by platelet aggregates is likely to be important in increasing clot stiffness because neither activated, but poorly aggregating platelets nor a-priori-aggregated platelets retract efficiently (46,47). Our computational results confirm that this is indeed the case because only the model accounting for active platelet contraction but not passive stiffening of platelet-fibrin aggregates is capable of matching experimental strain energy density measurements.

A prominent result from this study is that fibrin that is taken in by the contraction of platelet aggregates from their immediate vicinity is sufficient to increase resistance to deformation substantially for the entire clot, even though most of the matrix may remain agnostic to platelet contraction. As a corollary, if the platelet-fibrin aggregates were not prestressed, to provide the strain energy density equivalent to that of a whole blood clot, the entire fibrin gel would have to be twice as stiff. This increase in stiffness would have to arise purely from higher levels of fibrin polymerization and cross-linking. In light of growing interest and relevance on the spatial heterogeneity in the composition of in vivo clots to their strength (48,49), our results, to our knowledge, present some of the first insights into the origins of clot response to external forces. We expect that these insights will lead to more detailed expositions of clot deformation through the use of appropriate image-based three-dimensional models of the network, accounting for nonlinear fiber properties, viscoelastic characteristics of the clot as well as the modification of these properties by red cell concentration, and deformability by platelet concentration and by platelet-fibrin interactions.

In summary, we have measured the elastic moduli of blood clots subjected to uniaxial tensile strain using microtensometry, and we have estimated the contribution of platelet contraction and aggregation to clot stiffness using specific inhibitors of nonmuscle myosin IIA, aggregation, and cross-linking. Our results show that the platelet contribution to clot stiffness is dominated by nodes in the fibrous matrix that are composed of platelet aggregates and compacted fibrin. The concept of nodal prestress introduced in this work provides insights into how fibrin sequestering during clot retraction serves as a key stabilizing factor in clot mechanics. The experimental and computational framework presented in this work, for the first time, to our knowledge, not only measures tensile properties of clots but also provides a simple yet powerful model to establish mechanobiological relationships between intracellular stress and tissue-scale external loads.

Author contributions

S.J.P. and W.E. performed experiments and analyzed the data. S.-J.L. performed the computational studies. S.-J.L. and A.K.R. conceived the research, designed the experiments, performed the data analysis, procured funding, and wrote the manuscript. All authors approved the manuscript.

Declaration of interests

The authors declare no competing interests.

Editor: Kandice Tanner.