Fano resonance line shapes in the Raman spectra of tubulin and microtubules reveal quantum effects

Abstract

Microtubules are self-assembling biological nanotubes made of the protein tubulin that are essential for cell motility, cell architecture, cell division, and intracellular trafficking. They demonstrate unique mechanical properties of high resilience and stiffness due to their quasi-crystalline helical structure. It has been theorized that this hollow molecular nanostructure may function like a quantum wire where optical transitions can take place, and photoinduced changes in microtubule architecture may be mediated via changes in disulfide or peptide bonds or stimulated by photoexcitation of tryptophan, tyrosine, or phenylalanine groups, resulting in subtle protein structural changes owing to alterations in aromatic flexibility. Here, we measured the Raman spectra of a microtubule and its constituent protein tubulin both in dry powdered form and in aqueous solution to determine if molecular bond vibrations show potential Fano resonances, which are indicative of quantum coupling between discrete phonon vibrational states and continuous excitonic many-body spectra. The key findings of this work are that we observed the Raman spectra of tubulin and microtubules and found line shapes characteristic of Fano resonances attributed to aromatic amino acids and disulfide bonds.

Introduction

Microtubules are self-assembling biological nanotubes made of the protein tubulin (Fig. 1) that are essential for cell motility, cell architecture, cell division, and intracellular trafficking and are specifically important in brain cell architecture and function (1). The unique mechanical properties of microtubules give rise to a high resilience and stiffness due to their quasi-crystalline helical structure. In nanotechnology, the closest equivalent to microtubule biology is the carbon nanotube (CNT), the ubiquitous molecular wire that pervades the fields of chemistry, physics, electronics, and the material sciences. Multiwalled CNTs can display a striking similarity in size and morphology to microtubules and can possess microtubule biomimetic properties, assisting and enhancing microtubule assembly and stabilization (2, 3, 4, 5, 6, 7). One long-term goal in bio-nanotechnology has been to mimic the properties of microtubules and microtubule bundles to produce new functional nanomaterials (8). Conversely, the resemblance of microtubules to CNTs suggests that tubulin and microtubules could possibly serve as units for optoelectronic and quantum information devices in cells, such as axons and dendrites in neurons (9).

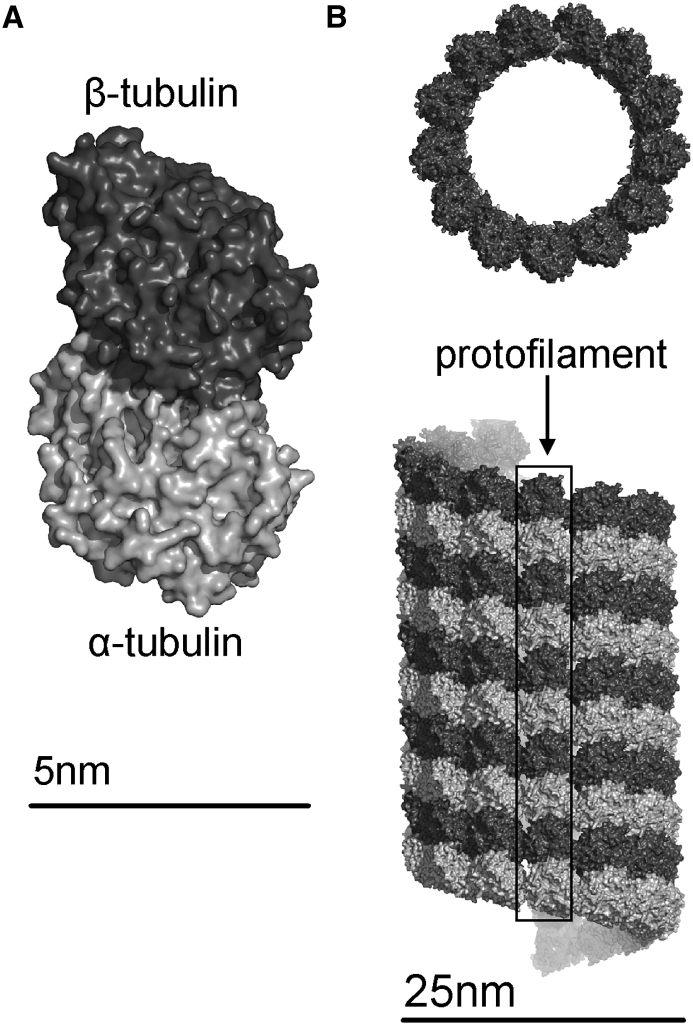
Figure 1.

(A) Tubulin heterodimer surface with α-tubulin monomer in light gray and β-tubulin monomer in dark grey (scale bar, ∼5 nm). (B) Section of microtubule B-lattice structure at two angles showing microtubule lumen (top) and left-handed helical symmetry and protofilament (bottom, outlined in black box) (scale bar, ∼25 nm). This image is reproduced from (11) under the Creative Commons Attribution 3.0 license.

Recent theoretical work has suggested that microtubules possess unique optical properties, including support of exciton transfer and superradiance, mediated by interactions between the aromatic amino acid tryptophan, indicating that they may behave as an optical metamaterial (10, 11, 12, 13). In the field of nanophotonics, current research is focused on all-dielectric metamaterials (14, 15, 16, 17, 18, 19) and two-dimensional successors of metamaterials, known as metasurfaces (20, 21, 22, 23, 24), as these provide less ohmic loss and heating, leading to better performing optical devices. Given that CNTs are one of these metasurfaces and given their aforementioned resemblance to microtubules, this further suggests that the aromatic amino acids of microtubules may be capable of supporting unique optical properties.

Raman microspectroscopy is one of the most actively pursued optical methods to unravel many of the fundamental processes resulting from excitations in condensed matter and biological media. It has been leveraged to use molecular vibrations for detection in cancer and optical phonons for imaging in biological media (25). Major advances in observing resonances in the visible region (532, 518, and 488 nm, in particular) have occurred for biological media stemming from the native absorption of chromophores like carotenoids and flavins (26) and aromatic amino acids (27) in tissues and cells. The focus of this technique in lipid and protein research has mainly been on the peaks of the Raman spectra resulting from vibrations, making them suitable to discriminate between different states of a given material. However, it is becoming evident that other salient features of the Raman spectra reveal more fundamental information on the interactions and processes than just the Raman line peak frequencies.

Several salient features of Raman spectra are leveraged to yield important information about the underlying physics beyond the location of the spectral peaks, including the full width half maximum and the overall signature line shape. Various processes affect the Raman line shape, shifting it away from a symmetrical Lorentzian, Gaussian, or Voigt function. Fano resonances cause the loss of symmetrical line shape, leading to a nonsymmetrical signature shape. Fano resonance is the result of a purely quantum process, with the coupling between external perturbation, discrete state, and continuum states determining the degree of asymmetry (Fig. 2). The line shape of the Raman spectra shows the degree of coupling of the electronic states to the vibrational states and is contained in the phenomenological Fano shape parameter, q. The sign of the q parameter is determined by the phase of the coupled state, which depends on the relative phase difference of the background continuum of states from the resonant discrete state (28). If the external perturbation does not couple to the continuum of states, the Raman line shape is symmetric, and q is big; the more the external perturbation couples to the continuum and the less it does to the discrete state, the more the Raman line will be distorted and become asymmetric, and q becomes small (29).

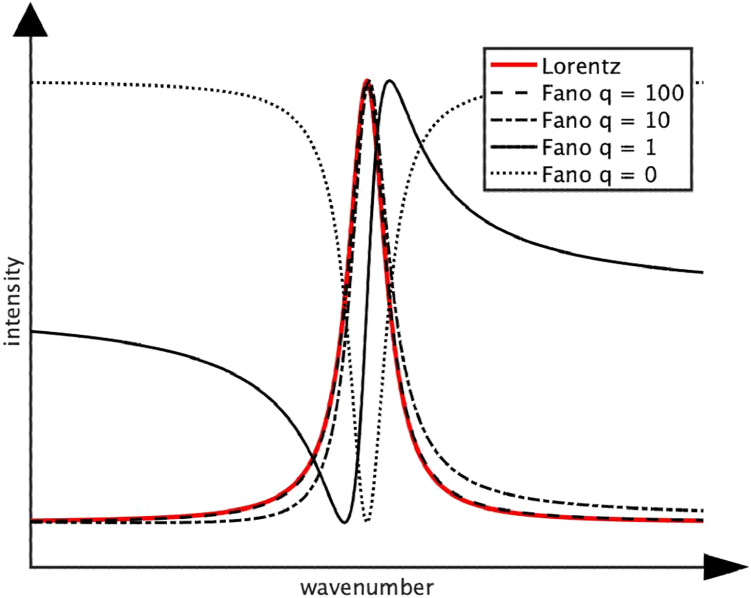
Figure 2.

Effect of Fano resonance and coupling strength on Raman peak intensity. When an external perturbation does not couple to the continuum of states, Fano parameter q → ±∞, and the Fano line shape becomes a symmetric Lorentzian. When an external perturbation does not couple to the discrete state, q = 0, and the Fano profile becomes a symmetric quasi-Lorentzian antiresonance in the continuum spectrum (q = 0), and it appears as a true zero in the spectrum (40). Coupling between these extremes gives rise to ever-increasing asymmetry as q → 0. Positive q giving right-handed asymmetry shown only. Negative q gives rise to left-handed asymmetry.

The Fano resonance line shape results from an interference effect between scattering within the continuum of background states and the excitation of a discrete state in the energy range of the continuum. This occurs because the scattering amplitude of the continuum typically varies slowly with energy while the scattering amplitude of the discrete state changes quickly both in magnitude and phase, resulting in the characteristic asymmetric profile. In Raman spectroscopy a sample is irradiated with light, resulting in the initial discrete vibrational ground state being coupled to a final discrete vibrational excited state through an intermediate state in the continuum of electronic excited states. In resonant Raman spectroscopy, the initial and final vibrational states are coupled via excitation to one of the discrete electronically excited states in the continuum. However, even if the incident radiation does not have enough energy to actually reach one of the electronically excited states, as in spontaneous Raman spectroscopy, Fano resonance can still occur (30). This is because the initial and final vibrational states are coupled through an intermediate “virtual” state that is part of the continuum of electronic states. This virtual state is not a discrete eigenstate of the system and has no defined energy but is rather a superposition state that includes the initial state, the continuum of electronic states that make up the virtual state, and the final state. This results in the coupling, which can give rise to Fano resonance in spontaneous Raman spectra.

Typically, Fano resonances in various spectra are characterized by asymmetric line broadening, expressed by the Breit-Wigner-Fano line shape (31,32). Fano resonances in material light scattering result from interferences between a discrete level of vibrational states coupled to a continuum spectrum of electronic excitations (31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43). Fano resonances have been found in a broad range of systems (29) including optomechanical resonators (44), semiconductor nanostructures (45,46), superconductors (47,48), photonic crystals (29,49, 50, 51, 52, 53, 54), dielectric nanoparticles (55), and plasmonic nanoantennas (56,57). More specifically, Fano resonances have been observed in the Raman spectra of single-layer graphene (58), metallic single-walled CNTs (59), semiconducting single-walled CNTs (60), graphite intercalation compounds (33, 34, 35, 36, 37,40,41), multiwalled CNTs (61), and bundles of nanotubes (62). This observed Fano resonance is interpreted as interferences between the discrete phonon and continuous excitonic many-body spectra (63).

Photoinduced changes in microtubule architecture may be mediated via changes in disulfide or peptide bonds or stimulated by photoexcitation of tryptophan, tyrosine, or phenylalanine groups, resulting in subtle protein structural changes owing to alterations in aromatic flexibility. Modeling of networks of aromatic amino acids in microtubules has previously shown the potential for electrical conduction ranging from semiconduction to superconduction (64, 65, 66, 67, 68), exciton transfer (10,13), and superradiance (12). However, experimental support of these results is lacking. Thus, the focus of this research is to obtain the Raman spectra of tubulin protein alone and in microtubule form, both in a dry powdered state and in aqueous solution, to analyze for the presence of Fano resonances similar to those observed in CNTs, determine the strength of the coupling parameters in these biological media, and assess the effects of both polymerization and solvation on these spectra.

Materials and methods

Spontaneous Raman spectroscopy

Raman spectra were obtained from microtubules as previously described (69). In brief, samples were placed on an upright confocal Raman microspectroscope (Xplora Plus, Horiba Scientific, Piscataway, NJ) equipped with a 532 nm diode laser source and 2,400 lines per mm grating at −60.1°C, giving a spectral resolution of ∼1.15 cm⁻¹. The excitation laser power was ∼10.5 mW onto the sample after passing through a ×50 air objective (MPlan N, 0.75 numerical aperture, Olympus, Waltham, MA), and acquisition times as designated (70 s) were used to collect Raman spectra of tubulin and microtubule powder, tubulin and microtubules in the water solution, and the water solution alone at a single point under identical conditions. Three replicates of each measurement were made. Averages of the three spectra were taken to find a nominal SD (i.e., not visible on graphs).

Sample preparation

Powdered tubulin and preformed powdered microtubules used in this study were purchased from Cytoskeleton (Denver, CO; catalog numbers [cat. nos.] TL238 and MT002-A, respectively). For acquisition of spectra in powder, the powder was directly put within the center region of an imaging spacer (0.12 mm thick; SecureSeal, Wellingborough, UK) and sandwiched between a coverslip (00.17 mm; Fisher, Waltham, MA) and a glass slide (1 mm thick; VWR, Radnor, PA). For the Raman measurement in aqueous solution, the powder was fully dissolved in water, and a small drop of 5 mg/mL solution was placed in the center of the spacer, which was sandwiched between the coverslip and glass slide. The operation was under room temperature.

Peak identification

We first corrected the raw Raman spectra baseline in the range of 300 to 1700 cm⁻¹ by applying the asymmetric least squares method with a smoothing parameter of 10⁷ and an asymmetry parameter of 10⁻³ (70) after subtracting the water signal from the signal collected for each sample condition. Peaks were then identified with the MATLAB function findpeaks. We preselected N peaks using their prominence and width. Those peaks were then sorted by prominence. We picked M peaks among all preselected peaks with prominence and width higher than the preset threshold for further analysis (see Model selection). For the microtubule powder and solution dataset, M is defined by findpeaks with MinPeakProminence as 200 a.u. and MinPeakDistance as 0 cm⁻¹. N is defined by findpeaks with MinPeakProminence as 20 a.u. and MinPeakDistance as 0 cm⁻¹. For the tubulin powder and solution dataset, M is defined by findpeaks with MinPeakProminence as 80 a.u. and MinPeakDistance as 10 cm⁻¹. For the tubulin powder dataset, N is defined by findpeaks with MinPeakProminence as 10 a.u. and MinPeakDistance as 10 cm⁻¹. For the tubulin solution dataset, N is defined by findpeaks with MinPeakProminence as 15 a.u. and MinPeakDistance as 10 cm⁻¹.

Spectral fitting

Fano function for individual peak intensity I_i (shown in Fig. 2) is described by:

$$I_i\left(\omega \right)=I_{i0}\frac{{\left(1+\omega -{\omega }_i/q_i{\Gamma }_i\right)}^2}{1+{\left(\omega -{\omega }_i/{\Gamma }_i\right)}^2},$$ (Equation 1)

where I_i0 is the intensity of the peak, the asymmetry factor q_i characterized the coupling strength, Γ_i is the broadening parameter, and ω_i is the centering peak frequency corresponding to the Raman shift value. The whole Raman spectra could be expressed as a sum of multiple Fano functions:

$$I\left(\omega \right)=\sum _{i=1}^k{I}_i\left(\omega \right)\text{,}$$ (Equation 2)

where k is the total number of peaks considered in our fitting model. Parameters I_i0, ω_i, −1/q_i, and Γ_i for i = 1 to k were optimized via a trust-region-reflective least squares algorithm using the MATLAB function lsqnonlin. Each model was fitted with 40,000 iterations. After the spectra were fit to a k peak model, peaks with small amplitude were removed. Among all sample datasets, this value was set as 1. For each model, I_i0 is estimated using the peak amplitude as the initial value with the lower and upper bounds repectively defined as 0 and the peak amplitude , and ω_i is estimated using the wavenumber of the peak as the initial value with ±10 cm⁻¹ as its lower and upper bounds. The coupling is estimated using −1/q_i = 0 as the initial value with −4 and 4 as the lower and upper bounds. The broadening parameter Γ_i is estimated using 20 as an initial value with 1 and 50 as the lower and upper bounds.

Model selection

Using the spectral fitting technique, Raman spectra were fit by multiple models I_M, I_M+1,…I_N between the minimum M and maximum N number of peaks identified, where I_n represents the model with the top n peaks as determined by prominence ranked in descending order. Each model was then assessed via the Akaike information criterion (AIC). This was performed for peaks in the range of 500 to 1,500 cm⁻¹ to account for potential edge effects in the fitting procedure. The AIC assesses the relative quality of the statistical model by estimating the prediction error. The AIC function is defined as:

$$AIC=2k+n\log \left(RSS/n\right),$$ (Equation 3)

where k is the number of parameters used in this model, RSS is the residual sum of squares between the experimental curve and fitting curve, and n is the number of sampled wavenumbers we set in the experiment. Lower AIC values indicate a better fit model. A new model is considered significantly better if its AIC value is more than 2 less than the model it is being compared with. The AIC values are high for underfit models as not enough peaks are considered as well as high for overfit models as these models are too complex. Thus, for the four different scenarios, the model with the optimal number of peaks in the range of M to N giving the minimum AIC score was selected as the model of best fit.

Results

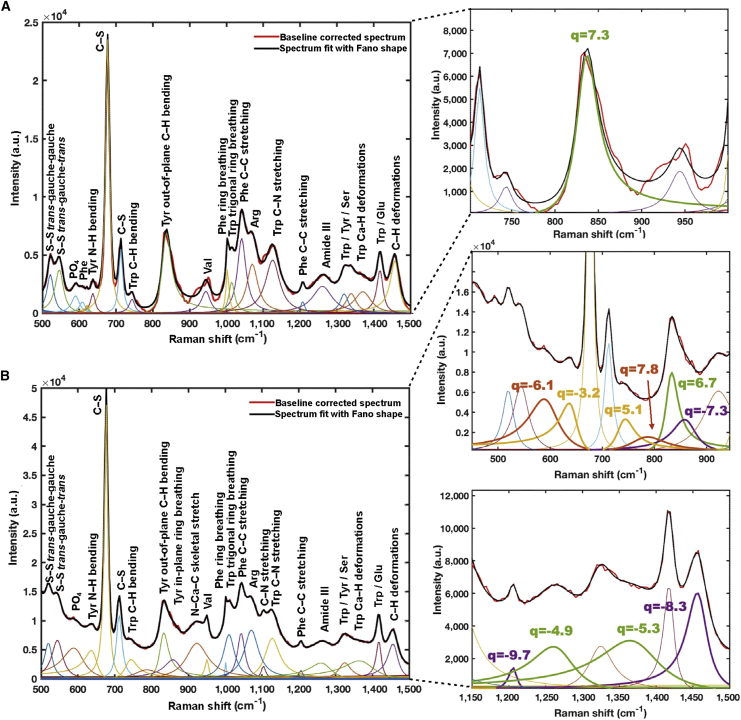
Peak identification and decomposition

Figure 3 shows the Raman spectra from an experiment with the baseline removed for dry powder and aqueous solution samples of tubulin protein and microtubules. For each of the four scenarios, the peak identification procedure identified a maximum of N and minimum of M possible peak positions, as described in the Materials and methods. For the powder form of tubulin, a minimum of M = 16 and a maximum of N = 27 peaks were determined by peak prominence and width. Following spectral fitting and model selection, it was found that the model of best fit contained 27 peaks (Fig. 4 A; Table S1). Similarly, for the tubulin in aqueous form, 46 peaks were identified (Fig. 4 B; Table S2), while for microtubules in dry and aqueous forms, 24 peaks each were identified (Fig. 5; Tables S3 and S4, respectively). The best overall models identified and their underlying decomposed spectral fittings for tubulin and microtubules in dry and aqueous forms are shown in Figs. 4 and 5, respectively, with parameters for the decomposition given in the Supporting information.

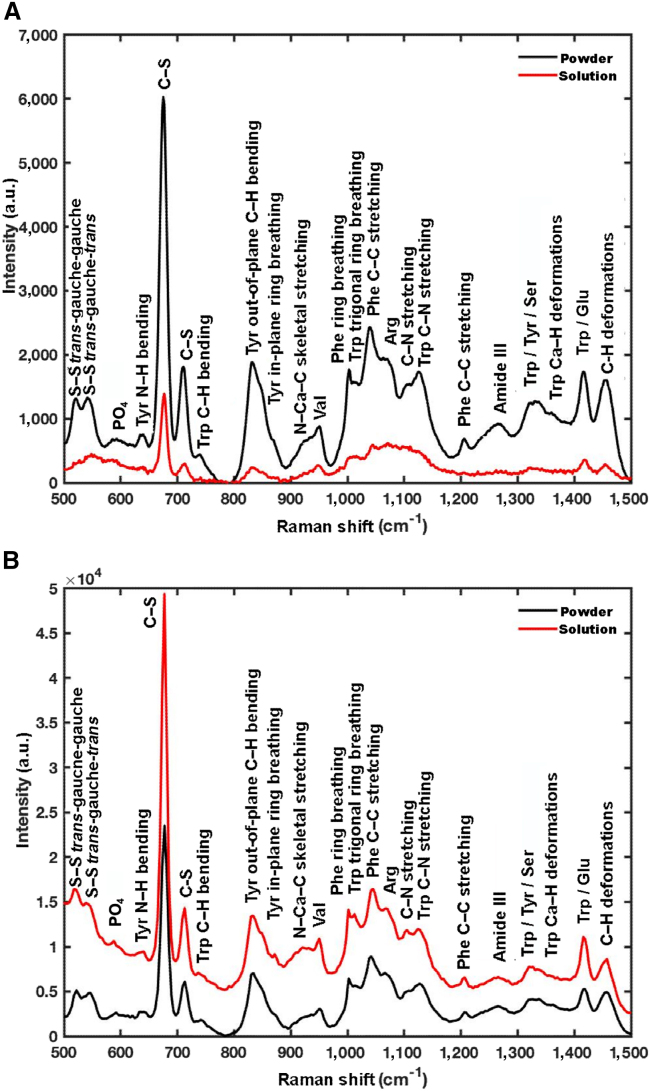
Figure 3.

Baseline corrected spontaneous Raman spectra of tubulin and microtubules. (A) Tubulin in powder and solution forms. (B) Microtubules in powder and solution forms.

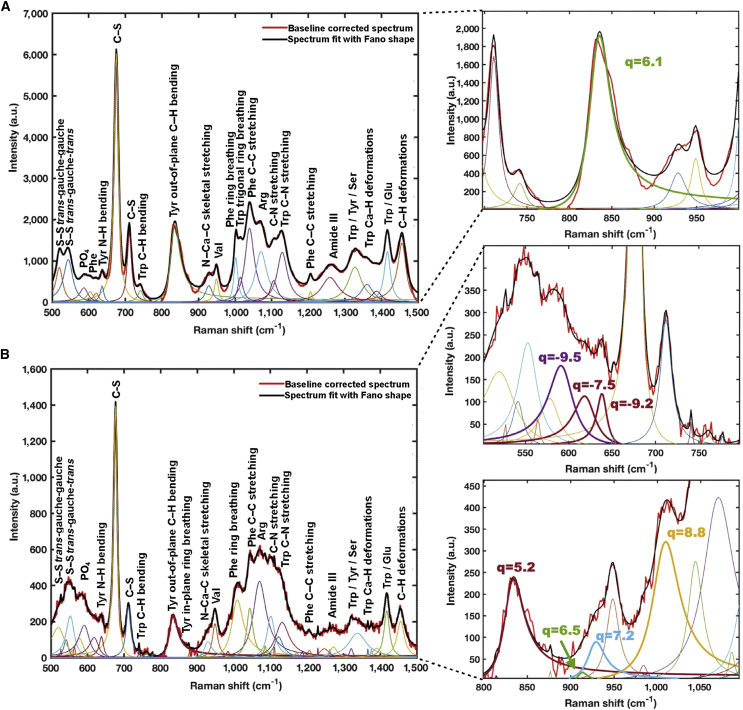
Figure 4.

Decomposition of tubulin Raman spectra. (A) Powder form showing 27 distinct peaks. (B) Solution form showing 46 distinct peaks.

Figure 5.

Decomposition of microtubule Raman spectra. (A) Powder form showing 24 distinct peaks. (B) Solution form showing 24 distinct peaks.

Peak assignment

In the dry form, the peaks in the Raman spectra represent the vibrational modes of the protein via internal and surface phonons since there are no routes to a solvent. In the solvated aqueous form, there are both internal/surface vibrations of the protein solutes as well as interactions between vibrations of the protein and solvent. To assess for the effect of both polymerization and solvation on these spectra, the spectrum of dry tubulin was taken as a baseline reference to which all other measures were compared. The peak assignment was determined from the 27 peaks identified in the corrected spontaneous Raman spectrum for tubulin in the powdered state (Fig. 3 A). The peaks identified for powdered tubulin are attributed as follows.

Amide bands

The peak at 1,258.6 cm⁻¹ is attributed to the amide III band, again stemming from C–N stretching and N–H bending (71,72). Amide III vibrations arise from very complex bands dependent on the details of the force field and the nature of side chains and hydrogen bonding and include tyrosine modes as discussed below.

Disulfide bridges

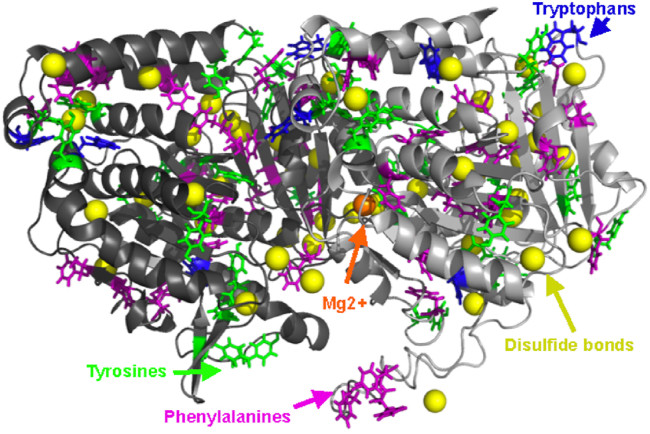
In general, the peaks between 500 and 600 cm⁻¹ are attributed to disulfide bridge stretching in tubulin and between tubulin in microtubules (see Fig. 6 for disulfide locations in tubulin). The peaks at 520.0 and 544.8 are assigned to two rotational vibrational modes (trans-gauche-gauche, trans-gauche-trans) (73), respectively. The peaks at 675.5 and 710.7 cm⁻¹ are attributed to C-S stretching modes (72).

Figure 6.

Cartoon representation of tubulin, the building block of microtubules, showing main contributors to Raman spectra. Gray cartoon: alpha tubulin; dark gray cartoon: beta tubulin; blue sticks: tryptophan; green sticks: tyrosine; purple sticks: phenylalanine; yellow spheres: sulfur in cysteine capable of forming disulfide bonds; and orange sphere: magnesium.

Aromatic amino acids

Three amino acids provide the main spectral features in protein spectra: the aromatics phenylalanine, tyrosine, and tryptophan. While tubulin, the microtubule constituent protein, does contain 22 histidine residues, these are expected to be relatively weak compared with its 39 phenylalanine, approximately 34 tyrosine (depending on the C-terminal tail composition), and 8 tryptophan (see Fig. 6 for aromatic amino acid locations in tubulin). Five peaks in the microtubule spectra are attributed to phenylalanine. The peaks at 1,001.7 cm⁻¹ are attributed to phenylalanine ring breathing (74), while the peaks at 1,038.7 and 1,205.8 cm⁻¹ are assigned to C–C aromatic stretching (71,75). The final two modes, 604.3 and 620.6 cm⁻¹, are attributed to weak and medium phenylalanine vibrational modes, respectively (76).

Vibrations in tyrosine are assigned to three peaks. The peak at 637.0 cm⁻¹ is attributed to tyrosine peptide N–H bending (77). The peak at 833.0 cm⁻¹ is attributed to out-of-plane C–H bending and C–C=O stretching (78) and is part of the tyrosine 830/850 doublet caused by Fermi resonance between the in-plane breathing mode of the phenol ring and an overtone of out-of-plane deformation mode. The band at 1,205.8 cm⁻¹, while attributed to phenylalanine C–C stretching, can also be attributed to the tyrosine benzene totally symmetric stretch (76).

Tryptophan is assigned to four bands. The peak at 742.1 cm⁻¹ is associated with tryptophan indole ring stretching and C–H out-of-plane bending (79), while 1,128.6 cm⁻¹ is defined as C–N stretching (77). The 1,014.0 cm⁻¹ peak is attributed to tryptophan trigonal ring breathing of the benzene ring (76). The 1,360.7 cm⁻¹ band is defined as C_a–H deformations in tryptophan (71,76).

Others

Several other peaks observed are assigned to general modes in amino acids. First, the peak at 587.4 cm⁻¹ could be assigned to the tubulin cofactors guanosine diphosphate (GDP) and GTP as this vibration is correlated to the stretching of PO₄ (80). The peaks at 906.2, 921.5, and 936.5 cm⁻¹ can be assigned to N–C_α–C skeletal stretching modes in general and, potentially, to valine and proline specifically (71,76). The peaks at 950.2 cm⁻¹ are attributable to a strong resonance peak in valine residues, while the peak at 1,070.1 cm⁻¹ coincides with a strong peak in arginine (76). Peaks near 1,105.3 cm⁻¹ have been attributed to general C–N stretching in other proteins (71), whereas the peaks at 1,327.6 cm⁻¹ are assigned to moderate to strong peaks in serine, tyrosine, or tryptophan (76) or to COO- stretching in lysine (79), while the peaks at 1,387.0 cm⁻¹ are assigned to a moderate proline peak (76). Finally, the peak at 1,416.5 cm⁻¹ is characteristic of strong peaks in tryptophan or glutamate (76). Finally, the peaks at 1,457.5 cm⁻¹ are attributable to general C–H deformations (71).

Polymerization effects on Raman spectra

To assess the effect of polymerization of tubulin into microtubules, the Raman spectra of microtubules and tubulin were compared. Twenty-four peaks were identified in dry microtubules. The majority of these align with the 27 peaks identified in dry tubulin with shifts of up to ±12 cm⁻¹. Four peaks were lost at 906.2, 936.5, 1,105.3, and 1,387.0 cm⁻¹, while one was gained at 1,339.4 cm⁻¹. The additional peak corresponds to a strong peak in the tryptophan spectra, likely due to C_a–H deformations (71,76).

Solvation effects on Raman spectra

To assess the effect of solvation in an aqueous solution, the Raman spectra of microtubules and tubulin in their dry and aqueous forms were compared. For tubulin, the aqueous solution greatly reduces the intensity of the observed peaks, and, as such, the signal-to-noise ratio is reduced overall. While the majority of the main peaks identified in tubulin remain, with some shifting of up to ±7 cm⁻¹, the reduced signal-to-noise ratio results in the detection of 46 distinct peaks rather than the 27 in the powder form. Beyond these shifts, three of the main peaks do not have corresponding peaks in the aqueous tubulin spectra 604.3, 936.5, and 1,014.0 cm⁻¹.

For microtubules, the aqueous solution increases the intensity of the observed peaks. In both the dry and aqueous microtubule samples, 24 peaks were identified. The majority of these peaks align with shifts of ±9 cm⁻¹. Three peaks were lost from in the solution at 609.0, 621.2, and 1,339.4 cm⁻¹, while three additional peaks were gained from the addition of the solution at 781.8, 861.6, and 1,103.7 cm⁻¹. The first of the additional peaks is associated with a moderate tryptophan peak (71,76), the second with a tyrosine or tryptophan peak (71,76), and the last with general C–N stretching in other proteins (71).

Fano resonance line shapes in Raman peaks of tubulin and microtubules

For each dataset, peaks with a coupling parameter q between −10 and +10 were taken as displaying a possible Fano resonance. For the dry samples, both tubulin and microtubules displayed only one possible peak near the tyrosine 833 cm⁻¹ peak, with a q of 6.1 for tubulin and 7.3 for microtubules.

Of the aqueous tubulin peaks that align with the dry tubulin peaks, 7 display possible Fano resonance behavior due to the presence of the solution. Among these is the tyrosine peak near 833 cm⁻¹ with a q of 5.2. The additional Fano resonance behaviors are observed at 592.6 cm⁻¹ (phosphate stretching), 620.1 cm⁻¹ (phenylalanine), 639.1 cm⁻¹ (tyrosine N–H bending), 912.7 cm⁻¹ (N–C_α–C skeletal stretching), 927.7 cm⁻¹ (N–C_α–C skeletal stretching), and 1,007.4 cm⁻¹ (phenylalanine ring breathing) with q values of −9.5, −7.5, −9.2, 6.9, 7.2, and 8.8, respectively.

For microtubules, the aqueous solution displays 10 possible Fano resonance behavior peaks including the one near 833 cm⁻¹ with a q of 6.7. The additional peaks occur at 593.9 cm⁻¹ (disulfide O=S=O stretching), 642.6 cm⁻¹ (tyrosine N–H bending), 740.1 cm⁻¹ (tryptophan indole ring stretching and C–H out-of-plane bending), 781.8 cm⁻¹ (tryptophan), 861.6 cm⁻¹ (tyrosine or tryptophan), 1,206.5 cm⁻¹ (phenylalanine C–C aromatic stretching), 1,267.9 cm⁻¹ (amide III C–N stretching and N–H bending), 1,373.9 cm⁻¹ (tryptophan C_a–H deformations), and 1,458.1 cm⁻¹ (C–H deformations) with q values of −6.1, −3.2, 5.1, 7.8, −7.3, −9.7, −4.9, −5.3, and −8.3, respectively.

Discussion

Measurement of the Raman spectra of tubulin and microtubules in both dry powdered form and in aqueous solution identified many molecular bond vibrations characteristic of protein profiles. These were dominated by vibrations of the amide III band, disulfide bonds, and aromatic amino acids.

When in microtubule form, compared with individual tubulin protein, the spectral profile remains consistent save for three notable changes. First, the intensity increase from tubulin to microtubules in the dry state is attributed to the regular structure of the microtubule enhancing the overall signal. Second, four peaks were lost. The losses at 906.2 and 936.5 cm⁻¹ indicate less flexibility in amino acid N–C_α–C skeletal stretching modes. This is attributed to the restricted motions of the tubulin proteins in polymerized form, which is bound within the microtubule lattice. This is similar to the loss of general C–N stretching at 1,105.3 cm⁻¹ and the potential proline modes at 1,387.0 cm⁻¹. Finally, the gain of a peak at 1,339.4 cm⁻¹, corresponding to tryptophan C_a–H deformations (71,76), is likely due to changes in tryptophan near the microtubule surface and at the tubulin dimer-dimer interfaces. It may also be attributed to changes in tubulin conformation within the microtubule lattice. Tubulin dimers may exist in either a straight or curved conformation, with the straight conformation occurring when bound to GTP and the curved one occurring when bound to GDP (81,82). However, since GDP-tubulins are buried in microtubules with the GTP-tubulin forming an end cap, the GDP-tubulins are constrained in a straight GTP-like conformation. This tension, caused by restraining the GDP-tubulin in an unstable GTP-like conformation, can allow for interior conformation changes leading to the increased mobility of buried residues like tryptophan. Further analysis can distinguish between these two possibilities, as discussed below.

The presence of aqueous solution was found to affect the spectral profiles. For tubulin, this resulted in an overall blunting of the signal. This may be attributed to the automatic self-assembly of tubulin proteins into microtubules in the presence of solution. The dynamic nature of this process is most likely the cause for the decreased signal and, unfortunately, is difficult to resolve. That being said, the main peaks observed in dry tubulin were still observable save for three. While the loss of peaks at 604.3, 936.5, and 1,014.0 cm⁻¹ may indicate changes in phenylalanine, N–C_α–C skeletal stretching modes, and tryptophan trigonal ring breathing, respectively, a closer inspection of the dry peak intensity suggests that these peaks may be lost due to the blunting of the signal.

Conversely to the solution effects on tubulin, the signal of microtubules in solution is enhanced in intensity. The loss of peaks at 609.0 and 621.2 cm⁻¹ are likely due to changes in surface phenylalanine vibrational modes, as phenylalanine is a hydrophobic residue and likely greatly affected by solvation. The observation of this effect in the sharp spectra of solvated microtubules lends evidence that the loss of the phenylalanine mode at 604.3 cm⁻¹ in solvated tubulin is an actual effect, and not an artifact, due to the noisy signal. The tryptophan peak gained at 1,339.4 cm⁻¹ in dry microtubules over dry tubulin is lost upon the addition of solvent. This indicates that the peak is due to a surface-level hydrophobic tryptophan, as it is affected by the solvent, and not due to a buried tryptophan in the protein interior. Similarly, the addition of peaks at 781.8, 861.6, and 1,103.7 cm⁻¹, all attributable to changes in hydrophobic aromatic amino acids, are likely due to surface-level tryptophan, tyrosine, and phenylalanine interacting with water.

Fitting of the experimental peaks identified several potential Fano resonances within tubulin and microtubules. In all four sample spectra, the peak around 830 cm⁻¹ showed an asymmetry best characterized by a Fano line shape. As mentioned above, this peak is attributable to part of the tyrosine 830/850 doublet. The lack of a clearly identified peak near 850 cm⁻¹ in wet and dry tubulin and in dry microtubules is interpreted to indicate that the average hydrogen bonding state of all tyrosine phenoxyls function as strong hydrogen bond donors, or as donors and acceptors, but not as strong acceptors (83). This suggests that the asymmetry may be due to the 850 cm⁻¹ part of this doublet, which is unidentified by the peak finding algorithm, and that this is not a true Fano resonance. However, in the aqueous microtubule sample, both the 830 and 850 cm⁻¹ peaks are identified at 831.0 and 861.6 cm⁻¹, respectively, and both are found to have a Fano line shape. Overall, this indicates that the hydrogen bonding capability of surface tyrosine resonates with the continuous excitonic many-body spectra.

The additional Fano resonance line shapes are only observed in the aqueous samples. In both aqueous tubulin and microtubules, Fano resonance line shapes are observed around 593 and 640 cm⁻¹. The first may be due to phosphate stretching in the tubulin GDP and GTP cofactors, while the latter is due to tyrosine peptide N–H bending. In the aqueous tubulin solution, additional Fano line shapes are observed for phenylalanine at 620.1 and 1,007.4 cm⁻¹ and for N–C_α–C skeletal stretching modes at 912.7 and 927.7 cm⁻¹. However, due to the noisy spectra of aqueous tubulin owing to tubulin self-polymerization, it is difficult to draw conclusions from these findings. Nevertheless, in the enhanced sharp spectra of aqueous microtubules, Fano resonance line shapes were observed in tryptophan at 740.1, 781.8, 861.6, and 1,373.9 cm⁻¹, with the latter being due to C_a–H stretching. Additionally, Fano shapes were observed for general C–H deformations at 1,458.1 cm⁻¹ and for C–N stretching and N–H bending at 1,267.9 cm⁻¹, and these may be a shared phenomenon with tryptophan. Finally, Fano shapes at 1,206.5 cm⁻¹ are attributed to tyrosine stretching as is the mode at 861.6 cm⁻¹. These findings in the aqueous microtubule sample show the presence of Fano resonances.

Further study is required to determine why these Fano-like resonances occur for the aqueous samples and why the Raman signal for tubulin is suppressed in water while it is enhanced for microtubules. One simple explanation for this latter effect is that there may be a larger number of tubulin molecules within the Raman interrogation volume owing to the effects of polymerization. Another explanation for this latter effect is stochastic resonance. With stochastic resonance, a normally weak signal is amplified to the level of detection due to resonance with the noise at an optimal intensity and frequency. The noise suggested in this case is the thermal vibration of the aqueous solution, which is expected to be a Gaussian white noise. This could allow for new peaks, unobserved in the dry state, to become detectable in the wet state due to the noise acquired by the aqueous environment. In the case of the microtubule, this would explain the enhanced response signal in the aqueous environment owing to the stability of the microtubule structure against thermal vibration, whereas free-floating tubulin would not be as robust to these perturbations, damping the overall signal. However, despite these explanations, neither increased concentrations in the interrogation volume nor stochastic resonance can explain the asymmetry in the observed peaks nor the select nature at where these asymmetries are found.

Overall, the Fano resonance line shapes found in tubulin and microtubules indicate that active Fano resonances are occurring for disulfide bonds and aromatic amino acids in general and tryptophan specifically, indicating the potential of quantum coupling between discrete phonon vibrational states and continuous excitonic many-body spectra. This would be consistent with past modeling efforts showing the potential for photoinduced excitonic transport behavior in microtubules mediated by aromatic amino acid networks (10,12,13). These unique optical properties in microtubules mediated by interactions between aromatic amino acids suggests that they may behave as an optical metamaterial and may serve as a template for bio-inspired technologies. Further experiments in this area are warranted to determine the extent of this phenomena and how it may be leveraged for new materials or biotechnologies.

Data availability statement

The parameter sets providing the fits analyzed for this study can be found in the Supporting information.

Author contributions

L.S., T.J.A.C., and R.R.A. conceived the idea. L.S., T.J.A.C., and R.R.A. designed the experiment. Y.L. and M.S. prepared the samples and performed the experiments. W.Z. coded the data-fitting algorithms and plotted the data. W.Z., T.J.A.C., Y.L., M.S., R.R.A., and L.S. analyzed the data and edited, revised, and finalized the manuscript. T.J.A.C., R.R.A., and L.S. provided funding. All authors contributed to the article and approved the submitted version.

Declaration of interests

The authors declare no competing interests.

Editor: Jörg Enderlein.