S K-edge XAS of Cu^II, Cu^I, and Zn^II Oxidized Dithiolene Complexes: Covalent Contributions to Structure and the Jahn-Teller Effect

Abstract

Reduced dithiolene ligands are bound to high valent Mo centers in the active site of the oxotransferase family of enzymes. Related model complexes have been studied with great insight by Prof. Holm and his colleagues. This study focuses on the other limit of dithiolene chemistry: an investigation of the 2-electron oxidized dithiolene bound to low-valent late transition metal (TM) ions (Zn^II, Cu^I, and Cu^II). The bonding descriptions of the oxidized dithiolene [N,N-dimethyl piperazine 2,3-dithione (Me₂Dt⁰)] complexes are probed using S K-edge X-ray absorption spectroscopy (XAS) and the results are correlated to density functional theory (DFT) calculations. These experimentally supported calculations are then extended to explain the different geometric structures of the three complexes. The Zn^II(Me₂Dt⁰)₂ complex has only ligand-ligand repulsion so it is stabilized at the D_2d symmetry limit. The Cu^I(Me₂Dt⁰)₂ complex has additional weak backbonding thus distorts somewhat from D_2d toward D_2h symmetry. The Cu^II(Me₂Dt⁰)₂ complex has a strong σ donor bond that leads to both a large Jahn-Teller stabilization to D_2h and an additional covalent contribution to the geometry. The combined strong stabilization results in the square planar, D_2h structure. This study quantifies the competition between the ligand-ligand repulsion and the change in electronic structures in determining the final geometric structures of the oxidized dithiolene complexes, and provides quantitative insights into the Jahn-Teller stabilization energy and its origin.

Graphical Abstract

Among the bis oxidized dithiolene compounds, the Zn^II complexe only has ligand-ligand repulsion thus a D_2d geometry. The Cu^I complex has additional weak backbonding thus distorts from D_2d toward D_2h. The Cu^II complex has a strong σ donor bonding that leads to both a large Jahn-Teller stabilization to D_2h and an additional covalent contribution to this distortion.

1. Introduction

Prof. Richard H. Holm was a pioneer in the field of Bioinorganic Chemistry.^1–4 His group successfully synthesized a wide range of model complexes, including Iron-sulfur and Molybdenum dithiolene compounds, characterized their structures, physical properties, and measured their reactivities.^5–14 Our groups collaborated with Prof. Holm and his group for decades, and applied both spectroscopic techniques and density functional theory (DFT) calculations to understand the electronic structures associated with the geometric structures, and how this enables the reactivities of these complexes as related to the metalloenzymes.^15–22

For the past decades, one component of our collaboration provided significant insights into the oxo transfer reactions of the Mo enzymes.^{16–17, 19–20} One of the interesting properties of the dithiolene ligands is their non-innocent behavior.^{18, 23–24} That is, in a redox reaction, the ligand orbital can be active while the metal orbital shows little change. The two limits are the fully reduced dithiolene and the 2-electron oxidized form. The former complexes have been studied extensively by the Holm group.^{8–9, 11–12, 15–20, 25}

The dithiolene ligands are strong π donors of up to two electrons when bound to high oxidation state transition metal (TM) ions (e.g. Mo^VI, W^VI). This π donor contribution is responsible for their non-innocent behavior. In this study, we investigate two 2-electron oxidized dithiolene ligands bound to low valent late TM ions (Zn^II, Cu^I, and Cu^II).²⁶ The oxidized dithiolene ligands, N,N-dimethyl piperazine 2,3-dithione (Me₂Dt⁰) and N,N-diisopropyl piperazine 2,3-dithione (iPr₂Dt⁰) were chosen for the stability of their oxidized forms.^27–30

The geometric and electronic structures of the fully reduced and 2 electron oxidized forms of the [Me₂Dt] free ligand are plotted on the left and right respectively in Figure 1. The three key valence orbitals that are involved in M-L bonds are the in plane σ−, out of plane π+, and out of plane π−, from low to high energies, respectively. The σ− and π+/− refer to the symmetric and anti-symmetric combinations of in and out of plane p orbitals on the S atoms. Upon oxidation, the filled out of plane π+ orbital of the reduced dithiolene is oxidized, as indicated by the dotted line in Figure 1. With respect to geometry, the C(S)=C(S) bond becomes longer and weaker, while the C-S and C-N bonds become shorter and stronger upon oxidation. In addition, the S-C-C-S dihedral angle increases dramatically from 8° to 40° in the DFT calculations. Similar distortions (increase in S-C-C-S dihedral angle) upon oxidation are generally observed in other dithiolene ligands including bdt (benzene-1,2-dithiolate) and mnt (maleonitriledithiolate) (Figure S1). This ligand distortion is responsible for some interesting properties and geometric distortions of their metal complexes^30–31, which will be analyzed in later sections.

Figure 1,

The top and side view of the fully reduced dithiolene Me₂Dt^2- (left) and the 2-electron oxidized dithiolene Me₂Dt⁰ (right). The change in C=C, C-N, C-S bond distances and S-C-C-S dihedral angle are indicated. Their molecular orbital (MO) diagrams are shown in the middle, with the highest occupied molecular orbital (HOMO) and lowest unoccupied molecular orbital (LUMO) separated by the horizontal dashed line. Three key MOs are listed. From bottom to top, they are the in plane σ−, out of plane π+, and out of plane π−, respectively. Note that the HOMO of the dithiolene becomes the LUMO upon oxidation, as indicated by the dotted line.

As indicated above, the reduced dithiolene ligand has been studied with early TM ions in high oxidations states (i.e. Mo^VI, W^VI) with respect to their non-innocent behavior and ligand π to TM dπ charge transfer (LMCT).^{17, 19–20} Certain oxidized dithiolene ligands, however, can be bound to the late TM ions in low oxidation states where the electronic structure can have contributions from the metal to ligand charge transfer (MLCT).²⁶ The role of this backbonding in the Cu^I complexes as well as a σ donor bonding in the Cu^II complexes will be evaluated in this study.

The S K-edge XAS method developed by our group has proven to be a powerful experimental tool to study the electronic structures of the M-S bonds. The S p character in the unoccupied orbitals can be probed directly from the intensity of the Sulfur 1s to the LUMOs pre-edge peak.^{19–20, 32–35} It is applied here to the study of oxidized dithiolene metal complexes for the first time. Multiple combinations of functionals and basis sets in DFT calculations as well as different data analysis methods are systematically tested in this study. DFT calculations that reasonably correlate with the S K-edge XAS data are employed to understand how the electronic structures impact the geometric structures of the Cu^II, Cu^I, and Zn^II oxidized dithiolene complexes.

2. Experimental

2.1. Sample preparation

The oxidized dithiolene metal complexes were synthesized as in the literature.²⁸

2.2. S K-edge XAS data collection and analysis

S K-edge XAS data were collected at beam line 4–3 at the Stanford Synchrotron Radiation Lightsource (SSRL). Samples from two independent preparations were measured at different beamtimes to confirm reproducibility. Samples were ground into fine powders and mounted on Kapton tape with a polypropylene front window. Data were processed and analyzed using EXAFSPAK³⁶ and PySpline³⁷. More details can be found in our previous literature.^{19–20, 33–35}

2.3. DFT calculations

DFT calculations were carried out using Gaussian 09³⁸. Combinations of different functionals (B3LYP, BP86, B3PW91, TPSSh) and basis sets (6-311G(d) and TZVP) were tested. Different guesses (initial geometry, charge and spin distributions) were also tested. DFT results were analyzed using QMForge³⁹. For orbital contributions, both C² population analysis⁴⁰ and fragment analysis were applied.

3. Results and Analysis

3.1. S K-edge XAS

Normalized S K-edge XAS spectra of the oxidized dithiolene complexes are shown in Figure 2A, and the baseline subtracted pre-edge regions are given in Figure 2B. Quantitative values of the sulfur contributions to the unoccupied orbitals derived from these experimental pre-edge areas are listed in Table 1, last column. From our previous studies, the S% character in the LUMO is proportional to the pre-edge intensity of the S K-edge XAS, and the details about the conversion is obtained are presented in reference^{23, 32} Note that the pre-edge features have multiple LUMOs and α and β spin contributions, thus the total %S value can exceed 100. Comparison of the experimental pre-edge energies and intensities (Figure 2 and Table 1) give the following observations: 1) The S K pre-edge of the Cu^II complex is more intense than its Cu^I counterpart; 2) the S K pre-edge of the Cu^I complex is more intense than its Zn^II counterpart; 3) with respect to varying the ligand, the pre-edges of the complexes with [Me₂Dt⁰] are slightly less intense than those of the same metal ion with the [ⁱPr₂Dt⁰] ligands, and 4) the pre-edge energies with [Me₂Dt⁰] ligands are also systematically lower by ~0.4 eV. These observations are analyzed with the assistance of DFT calculations in the next section.

Figure 2.

A) Normalized S K-edge XAS data of the oxidized dithiolene complexes; B) The baseline subtracted pre-edge region. The integrated intensities are converted to percentage S p characters based on ref²³ and are given in the last column of Table 1.

Table 1.

Comparison of the Experimental Data and the DFT Calculated Results

Compound		M-S (Å)	C-S (Å)	S-S (Å)	C=C (Å)	S-M-S angle	S-C-C-S Dihedral Angle	Dithiolene Angle (Θ)	%S
CuII(iPr2Dt0)2	Exp	2.27	1.69	3.19	1.50	89	23	0	142
	DFT	2.33	1.71	3.27	1.51	89	31	5	132
CuII(Me2Dt0)2	Exp	NA	NA	NA	NA	NA	NA	NA	NA
	DFT	2.33	1.70	3.28	1.51	89	22	0	138
CuI(iPr2Dt0)2	Exp	2.29	1.70	3.27	1.50	91	35	61	107
	DFT	2.34	1.69	3.31	1.51	90	33	74	114
CuI(Me2Dt0)2	Exp	2.27	1.67	3.26	1.51	91	14	78	115
	DFT	2.33	1.69	3.30	1.51	90	18	72	124
ZnII(iPr2Dt0)2	Exp	NA	NA	NA	NA	NA	NA	NA	100
	DFT	2.38	1.71	3.41	1.53	91	33	90	94
ZnII(iPr2Dt0)Cl2	Exp	2.36	1.68	3.36	1.53	91	31	87	104
	DFT	2.59	1.67	3.39	1.52	82	40	85	98
ZnII(Me2Dt0)Cl2	Exp	2.37	1.68	3.33	1.52	89	19	85	104
	DFT	2.59	1.67	3.38	1.52	81	27	85	91

There are some additional features at greater than 2eV above the pre-edge. They are assigned as overlapping contributions of S_1s to C-S σ*/ π* and M_4s-S_3p σ* transitions. Their total %S values could not be experimentally quantified because they overlap with the edge jump.

3.2. DFT calculations

DFT results with different functionals and basis sets are given in Table S1. Their results are reasonably consistent with respect to trends relative to experiments. For a given functional and basis set, the relative change in geometric structure and %S values are nicely reproduced. Here we present the results with B3LYP/6-311G(d) to be consistent with our previous studies.^{17–20, 33–34, 41} We also tested the effects of different initial guesses on geometry and fragment charge/spin distributions, and all converged to the same geometric and electronic structures.

The crystal structures of several of the oxidized dithiolene complexes were published in ref²⁸. For bis oxidized dithiolene complexes, the DFT optimized structures obtained here are in good agreement with the available crystal structures, including the key bond distances, bond angles, S-C-C-S dihedral angles in the dithiolene ligands, and the relative distortion angles between the two dithiolenes (defined by Θ). For Mixed-ligand compounds Zn^II(ⁱPr₂Dt⁰)Cl₂ and Zn^II(Me₂Dt⁰)Cl₂, calculated structures are less consistent with crystal structures. Thus we only present their experimental S K-edge XAS, while the analysis in the rest of this study is focused on the bis oxidized dithiolene complexes. Some of the crystal structures could not be obtained experimentally²⁸ (Cu^II(Me₂Dt⁰)₂ and Zn^II(ⁱPr₂Dt⁰)₂), thus only their geometry optimized structures are given. Geometric parameters from both the crystal structures and DFT optimizations are listed in Table 1, and the molecular structures are shown in Figure 3 and in the SI. Overall, the oxidized dithiolene S-C-C-S dihedral angles in the metal complexes are systematically smaller compared with those of the free oxidized dithiolene ligands. In comparing these complexes, the largest changes are in the Θ angles between the two dithiolene planes (or the angles between the dithiolene plane and the Cl-Zn-Cl plane in the Zn mixed-ligand compounds). In the Zn^II complexes, they are almost perpendicular to each other (Θ=90°, i.e. close to tetrahedral), while in the Cu^II complexes they are almost co-planar (Θ=0°, i.e. close to square planar), while in the Cu^I complexes the values are in between, with Θ=~75°.

Figure 3.

The geometry optimized molecular structures (coordinates in SI) and the MO diagrams of the Zn^II(Me₂Dt⁰)₂ (A), Cu^I(Me₂Dt⁰)₂ (B), and Cu^II(Me₂Dt⁰)₂ (C) complexes. Only the alpha orbitals were plotted for Zn^II and Cu^I, thus the total covalent mixing contributions need to be multiplied by 2.

Figure 3A shows the optimized structure and the MO diagram of the Zn^II(Me₂Dt⁰)₂ complex. The LUMO orbital (out of plane π+) of each ligand only weakly interacts with each other, leading to two almost degenerate MOs (the + and − combinations) each with ~25% S p character and ~0 Zn d character. Due to the high effective nuclear charge (Z_eff) of the Zn²⁺, the fully occupied Zn 3d orbitals are deep in energy. The highest MO with significant Zn 3d character is calculated at ~7 eV below the HOMO. Fragment analysis also shows no ligand LUMO character in the occupied orbitals (Table S4). There is a weak M_4s-S_3p σ interaction, but the M_4s σ* orbital is ~3eV above the LUMO (Figure S2), thus the pre-edge of the Zn^II(Me₂Dt⁰)₂ complex mainly reflects the ligand LUMO.

The geometry optimized structure and the MO diagram of the Cu^I(Me₂Dt⁰)₂ complex are shown in Figure 3B. The LUMOs are similar to those in the Zn^II(Me₂Dt⁰)₂ complex (the + and − combinations of the LUMOs of the free ligands). Their energy splitting is ~ 0.4 eV, which is higher than that in the Zn^II complex. This is consistent with the structure of the tilted oxidized dithiolene planes (Θ=78° experimentally, Θ=72° computationally) resulting in some S π p orbital overlap. There is also more S p character in the LUMOs, which is attributed to the decreased charge of the Cu^I center. In testing a series of closed shell metal ions that have different charges with the oxidized dithiolene ligands with the same geometry, increasing the positive charge on the metal center significantly decreases the S p character in the LUMOs (Table S2). The increasing positive charge attracts electron density thus resulting in more coordinated S character in the occupied orbitals and less S p character in the unoccupied levels. Alternatively, varying the M-S bond distances or the oxidized dithiolene plane angles has little impact (Table S3). Although both Cu^I and Zn^II have d¹⁰ configurations, the d manifold for Cu^I is higher in energy due to its lower Z_eff. This results in a small amount of filled Cu d character mixed into the unoccupied ligand based LUMOs, and a small amount of oxidized dithiolene LUMO mixed into the occupied valence orbitals due to backbonding. This backbonding contributes to the tilt of the dithiolene planes (Θ decreases from 90° in Figure 3A to 78° in Figure 3B), and is analyzed in the next section.

The Cu^II(Me₂Dt⁰)₂ complex has a d⁹ configuration, which requires a spin polarized electronic structure description with an additional unoccupied β LUMO having Cu d character that is σ antibonding with the in-plane σ− orbital from both oxidized dithiolene ligands (Figure 3C, β-LUMO). This additional β-LUMO contributes an additional covalent interaction between the Cu^II center and the ligands. However, the energy of the additional β-LUMO is close to the ligand out of plane π+ LUMO and thus cannot be separated experimentally. This results in a significant additional amount of S p character in the LUMO of the Cu^II complex, and is consistent with its broader, more intense S K-pre-edge peak observed experimentally (Figure 2B).²³

In all of these compounds, there are a few MOs ~3eV above the LUMO. They are assigned as C-S π* and σ*, as well as a weak M_4s-S_3p σ* orbitals, as shown in Figure S2. The calculated S p characters in these MOs are relatively small compared to the S p characters in the LUMO.

The [ⁱPr₂Dt⁰] complexes were also evaluated by DFT. In general, the experimental S K-edge XAS pre-edge intensities and their peak energies are consistent with the calculated S p character in their LUMOs and their energy splitting. Compared with the M(Me₂Dt⁰)₂ complexes with the same metal ion, the [ⁱPr₂Dt⁰] compounds have both slightly less S p character and higher orbital energies as observed experimentally (Figure 2 and Table 1). The isopropyl (ⁱPr) group is a better electron donor than the methyl (Me) group, leading to more charge density on the S. This results in the higher unoccupied orbital energies and their decreased S p characters.

3.3. Electronic structure contributions to geometric structures

When the geometric structures of the Zn^II(Me₂Dt⁰)₂, Cu^I(Me₂Dt⁰)₂, and Cu^II(Me₂Dt⁰)₂ complexes are compared, the most obvious difference is in the relative angles Θ between the two oxidized dithiolene planes in each molecule (Figure 3). The Zn^II(Me₂Dt⁰)₂ complex has almost D_2d (tetrahedral) symmetry with the two oxidized dithiolene planes perpendicular (Θ=90°) to each other. This minimizes their overall ligand-ligand repulsion, which has both steric and electrostatic contributions. The Cu^II(Me₂Dt⁰)₂ complex on the other hand, has almost D_2h symmetry (square planar) with the two oxidized dithiolenes in the same plane (Θ=0°), because of strong electronic structure contributions. Both the Jahn-Teller driving force and an increase in the covalency of the Cu-S bonds in D_2h favor the square planar geometry. The Cu^I(Me₂Dt⁰)₂ complex may be expected to have a similar geometric structure to that of the Zn complex due to its d¹⁰ configuration, but both the crystal structure and DFT optimized structure show a distortion away from D_2d (Θ=78° experimentally and Θ=72° computationally). This results from a competition between ligand-ligand repulsion and electronic stabilization.

Electronic structure contributions to the geometric structures were analyzed by a series of calculations on the M(Me₂Dt⁰)₂ complexes (M = Zn^II, Cu^I, Cu^II) with systematically varying the Θ angles from 90° (D_2d, tetrahedral) to 0° (D_2h, square planar), but with all other structural parameters fixed.

In Figure 4A, the total energy vs the Θ angle is plotted for both the Zn^II(Me₂Dt⁰)₂ (green) and the Cu^II(Me₂Dt⁰)₂ (red) complexes. Because the Zn^II complexes have only ligand-ligand repulsion that increases from D_2d to D_2h and no Θ angular dependence of the M_4s-S_3p σ bonding (Table S4), the difference of the two (magenta) reflects the angle dependent of the electronic contributions to the total energy, which gives 22 kcal/mol for the electronic energy stabilization in going from D_2d to D_2h. This large electronic stabilization energy for the Cu^II(Me₂Dt⁰)₂ complex overcomes the ligand-ligand repulsion (12kcal/mol at the D_2h limit) and results in its square planar geometry. This has both Jahn-Teller and covalency contributions (Figure 4A, orange line scale on the right gives the β-LUMO covalency) that are discussed below. In Figure 4B, the total energy vs Θ is plotted for the Zn^II (green) and Cu^I (black) complexes. Compared with the Cu^II(Me₂Dt⁰)₂ complex which has significant electronic contributions due to the Jahn-Teller effect and σ donor bonding, the electronic contribution for the Cu^I(Me₂Dt⁰)₂ complex is due to the backbonding. The energy difference of the Cu^I(Me₂Dt⁰)₂ relative to the Zn^II(Me₂Dt⁰)₂ complex (purple) shows that the maximum backbonding contribution (at Θ=30°, Figure 4B, cyan line scale on the right for amount of backbonding) is worth ~ 3kcal/mol, which leads to the distortion away from the D_2d steric limit as observed experimentally. In Figure 4B, the amount of M d backbonding is from the C² population analysis. A fragment analysis of the ligand LUMO mixed into the valence occupied orbitals gives similar results (Table S4). The backbonding dependence on Θ is discussed below.

Figure 4.

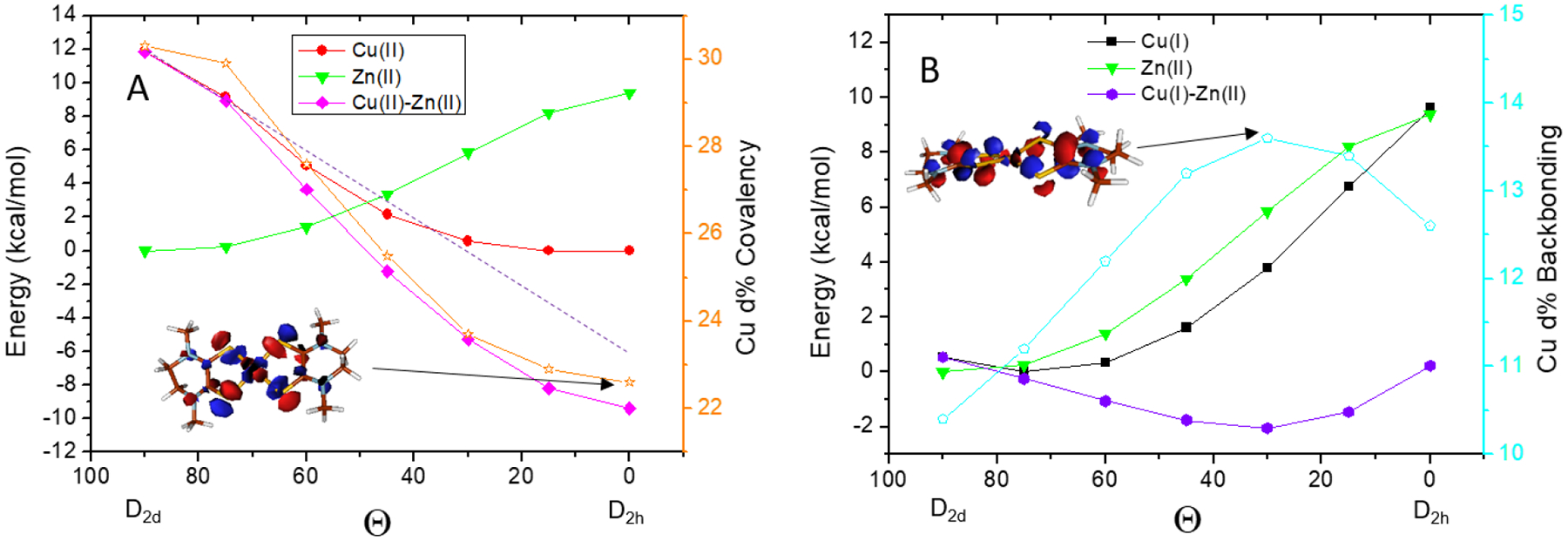
Dependence of total energy on the relative dithiolene angles Θ of (A) Zn^II(Me₂Dt⁰)₂, Cu^II(Me₂Dt⁰)₂ and (B) Zn^II(Me₂Dt⁰)₂, Cu^I(Me₂Dt⁰)₂. The magenta curve in (A) reflects the total electronic contribution in Cu^II(Me₂Dt⁰)₂ (from 12 to −10 kcal/mol), which can be further divided into the Jahn-Teller electron-nuclear coupling and the covalency contributions. The covalency (Cu d%) is plotted on the right axis in orange. The MO contour at 0° is given as inset. The purple curve in (B) reflects the contribution from the backbonding in Cu^I(Me₂Dt⁰)₂ (from 1 to −2 kcal/mol). The amount of backbonding is plotted on the right axis in cyan. The MO contour with maximum backbonding in Cu^I(Me₂Dt⁰)₂ (Θ=30°) is given as an inset.

4. Discussion

As presented above, varying the metal ions (Cu^I, Cu^II, Zn^II) in the bis-oxidized dithiolene complexes results in a change in the relative angle Θ between the two oxidized dithiolene planes. In the Zn^II(Me₂Dt⁰)₂ complex where there is little electronic stabilization and no angle dependence in Zn 4s mixing in the occupied orbitals, Θ=90° minimizes the ligand-ligand repulsion (Figure 5, green). In the Cu^II(Me₂Dt⁰)₂ complex, there are both a Jahn-Teller stabilization energy and a covalent contribution to the geometry (deriving from the increase in ligand character from ~70% at 0° to 78% at 90°), which gives 22 kcal/mol total electronic stabilization (Figure 4A). This significant stabilization energy overcomes the 12 kcal/mol ligand-ligand repulsion and results in the square planar geometry (Figure 5, red). In the Cu^I(Me₂Dt⁰)₂ complex, there is backbonding which makes a small contribution to the stabilization energy of 3 kcal/mol (Figure 4B). This competes with the ligand-ligand repulsion and distorts the geometry by Θ=15° from the D_2d limit (Figure 5, black).

Figure 5.

The final geometry (Θ angle) of the bis oxidized dithiolene complexes are determined by the competition between the ligand-ligand repulsion and electronic contributions. In Zn^II(Me₂Dt⁰)₂ complex (green), there is only ligand-ligand repulsion favoring the D_2d geometry. In the Cu^I(Me₂Dt⁰)₂ complex (black), relatively weak backbonding distorts the geometry away from D_2d. In the Cu^II(Me₂Dt⁰)₂ complex (red), significant electronic terms (Jahn-Teller + covalency) distorts to the D_2h limit.

The electronic stabilization can be divided into 2 parts. The Jahn-Teller stabilization energy and the change in M-S covalent bonding with changing geometry. In the Cu^I(Me₂Dt⁰)₂ complex, there is no Jahn-Teller contribution as it has a d¹⁰ configuration, but there is some backbonding due to the relatively low Z_eff of the Cu^I. Figure 4B shows that the stabilization maximizes (purple) along with the maximum backbonding (cyan); ~3% increase in the Cu d character in the π LUMO of the oxidized dithiolene corresponds to ~ 3kcal/mol in stabilization. Interestingly, the amount of backbonding maximizes at Θ=30°. This is because the oxidized dithiolene is not planar, thus the S-C-C-S dihedral angle of 18° requires the ~30° Θ angle to maximize the S p π orbital overlap (Figure 4B, insert MO contour, and Figure S3). There is also a weak M_4s-S_3p σ donor bonding interaction that minimizes at the D_2d limit which has the same trend as the metal backbonding (Table S4).

On the other hand, the Cu^II(Me₂Dt0)₂ complex has a d⁹ configuration and thus has both a Jahn-Teller stabilization energy and exhibits an increase in covalent M-S bonding toward D_2h that also contributes to its geometry. In Figure 4A, the Cu d character is plotted on the right axis. There is little change in Cu d% when Θ decreases from 90° to 75°, therefore an extrapolation along this region of the total stabilization energy (dashed line) gives an estimate of the Jahn-Teller electronic-nuclear coupling force enabling an evaluation of its energy contribution at the D_2h limit. This Jahn-Teller stabilization energy is ~17 kcal/mol. Thus, the remaining ~5kcal/mol energy derives from the covalency increase of ~8% in going to the square planar limit.

The Jahn-Teller distortion force derives from the electron-nuclear vibrational coupling. To understand the origin of this strong Jahn-Teller effect in the Cu^II(Me₂Dt⁰)₂ complex, a vibrational perturbation in the non-symmetric ε (in T_d symmetry) mode around the D_2d geometry was tested using the Cu^I(Me₂Dt⁰)₂ model as there is no spin polarization in d¹⁰. At the D_2d limit, the HOMO orbitals are doubly degenerate (Figure 6, left). Distortion along the ε vibrational mode by 15° toward the D_2h structure results in an energy splitting of these two orbitals by ~0.4 eV. One orbital is stabilized by this non-symmetric distortion having less M-S σ* and the other is destabilized having a larger M-S σ* interaction (Figure 6, right). Because of the strong σ* nature of the M-S bond for the oxidized dithiolenes, the Jahn-Teller distortion force dominates the stabilization energy.

Figure 6.

A) Jahn-Teller distortion near the D_2d limit estimated using the Cu^I(Me₂Dt⁰)₂ model. B) Scheme showing that the non-symmetric ε distortion decreases the σ* interaction thus stabilizing the d orbital on the left, and increases the σ* interaction thus destabilizing the orbital on the right.

5. Conclusion

S K-edge XAS combined with DFT calculations have been used to quantify the bonding in Zn^II(Me₂Dt⁰)₂, Cu^I(Me₂Dt⁰)₂, Cu^II(Me₂Dt⁰)₂ complexes. This has determined the structural distortions of the Cu^I(Me₂Dt⁰)₂ and Cu^II(Me₂Dt⁰)₂ complexes relative to the Zn^II(Me₂Dt⁰)₂ complex, which is D_2d due to ligand-ligand repulsion. For the Cu^I(Me₂Dt⁰)₂, because of its lower Z_eff relative to the Zn^II complex, a limited amount of backbonding is present that distorts the geometry by ~15° away from D_2d (Figure 5, Θ from 90° to 75°).For the Cu^II(Me₂Dt⁰)₂ square planar (D_2h) complex, there is additional σ donation that contributes to this structure. However, the Jahn-Teller distortion energy is dominant and derives from the change in sigma antibonding (σ*) interactions with the oxidized dithiolene ligands in the non-symmetric ε vibrational mode (in the T_d limit).

Highlights:

X-ray absorption spectroscopy (XAS) study of transition metal dithiolene compounds

Sulfur K-edge XAS and DFT are applied to oxidized dithiolene compounds for the first time

Electronic structures determine the corresponding geometric structures

Backbonding in the Cu^I complexes

The Jahn-Teller effect and change in covalent bonding in the Cu^II complexes