Development and validation of a prediction model for infant fat mass

Abstract

Objectives

To develop and validate a prediction model for fat mass in infants ≤ 12 kg using easily accessible measurements such as weight and length.

Study design

We used data from a pooled cohort of 359 infants aged 1–24 months and weighing 3–12kg from three studies across Southern California and New York City. The training data set (75% of the cohort) included 269 infants and the testing data set (25% of the cohort) included 90 infants aged 1–24 months. Quantitative magnetic resonance was used as the standard measure for fat mass. We used multivariable linear regression analysis, with backwards selection of predictor variables and fractional polynomials for non-linear relationships to predict infant fat mass (from which lean mass can be estimated by subtracting resulting estimates from total mass) in the training data set. We used 5-fold cross-validation to examine overfitting and generalizability of the model’s predictive performance. Finally, we tested the adjusted model on the testing data set.

Results

The final model included weight, length, sex, and age, and had high predictive ability for fat mass with good calibration of observed and predicted values in the training data set (optimism-adjusted R²: 92.1%). Performance on the test dataset showed promising generalizability (adjusted R²: 85.4%). The mean difference between observed and predicted values in the testing dataset was 0.015 kg (−0.043 to −0.072 kg; 0.7% of the mean).

Conclusions

Our model accurately predicted infant fat mass, and could be used to improve the accuracy of assessments of infant body composition for effective early identification, surveillance, prevention, and management of obesity and future chronic disease risk.

Childhood obesity represents an urgent public health issue, as almost 20% of children have obesity compared with ~10% in the year 2000¹. Childhood obesity can originate early in life, with 8% of infants and 20% of preschoolers already classified as overweight or obese². Identifying overweight and obesity in infancy could allow for early surveillance, prevention, and management of long-term obesity risk. Although simple-to-obtain measures such as growth z-scores and body mass index (BMI) can be useful for estimating obesity risk in later life^3,4, body composition is a more accurate indicator of metabolic health^5,6. This is because anthropometric-based measures do not provide insight on the proportion of fat versus lean mass⁶. However, there are many challenges with measuring body composition in infants, as outlined in a recent National Institutes of Health (NIH) workshop⁷. For example, skinfold measurements are relatively easy to obtain but are prone to measurement error⁸. More accurate and precise methods, such as dual energy X-ray absorptiometry (DEXA) require stillness for prolonged periods and expose infants to small amounts of radiation^9–12. Another highly accurate and precise method – quantitative magnetic resonance (QMR) – has benefits over DEXA in that it emits no radiation, does not require stillness, and takes just 3 minutes to complete¹¹. However, QMR is a relatively novel technology that is expensive and not widely available for use in infants. For this reason, simple methods for infant body composition assessment, based on routinely available measurements such as weight and length, would be of considerable value. Therefore, the aim of this study was to develop predictive models using easily obtained information (weight, length, sex, and age), for use by investigators and clinicians to estimate infant fat and lean mass without the need for more complex and burdensome assessment.

Methods

We pooled data from two on-going longitudinal cohort studies of Hispanic infants in the Los Angeles area (NIH R01DK110793 and NIH R01DK109161) and one multi-ethnic cohort from New York City (The Lifestyle Intervention for Two (LIFT) Study¹⁴). Inclusion criteria for the Los Angeles cohorts were maternal and paternal Hispanic self-identity; singleton pregnancy; and the ability to read/understand English or Spanish at a 5^th grade level. Exclusion criteria were pre-existing medical, mental, or cognitive issues preventing participation; medications that affect body weight or composition, insulin resistance, or lipid profiles; current smoking or use of other recreational drugs; gestational diabetes; pre-term/low birth weight infants or diagnosis of any fetal abnormalities; and maternal age less than 18 years at time of delivery. Infants in the Los Angeles cohorts were examined at 5 longitudinal timepoints in both studies: 1, 6, 12, 18, and 24 months. However, because both Los Angeles studies are on-going, no infants had more than three longitudinal QMR measurements in the current analysis. The New York City cohort contained two longitudinal timepoints at 3.5 and 12 months of age. Inclusion criteria for the New York City cohort were singleton viable pregnancy; body mass index ≥ 25; age ≥ 18 years; and ability to contact. Exclusion criteria were diagnosis of diabetes or hemoglobin A1c (HbA1c) ≥ 6.5%; ) known fetal anomaly; termination of pregnancy; history of 3 or more consecutive first trimester miscarriages; certain medications including metformin and mood stabilizers; smoking; and other medical, psychiatric, social, or behavioral factors that could interfere with study participation. Because both studies included data points from the same individual at multiple time points (up to a maximum of three time points per infant), we tested whether any correlation between measurements from the same infant affected results using generalized estimating equations (GEE). We only included infants ≤12kg because Infant QMR is calibrated for weights between 2 and 12 kg¹³. All infants were weighed without clothes and wearing a clean diaper. All studies included weight, length, sex, age, and fat and lean mass from Infant QMR (EchoMRI-Infant, Echo Medical Systems, Houston, TX). Precision and accuracy data for the Infant QMR instrument is provided as supplementary material (Appendix, Tables V and VI; available at www.jpeds.com).

Table 5.

Precision of measuring infant body composition (1 – 24 months old and ≤12 kg) using Goran Lab Infant QMR expressed in terms of SD in units of grams and CV (=(SD/mean) x 100) in units of % (n = 324) ¹

	Fat	Lean	Free Water	Total Water
Mean (SD) g	29.48	65.14	17.95	83.03
SD (SD) g	23.72	48.06	11.68	194.20
Mean CV %	1.71	1.90	10.54	2.36
SD CV %	1.19	1.31	7.20	4.62

¹Mean is the total mean of the mean standard deviation of three consecutive readings from the same infant. SD is the standard deviation of the standard deviations of three consecutive readings from the same infant. CV is calculated as (SD/Mean)*100 for each infant, and mean CV % is the mean CV%s, while SD CV% is the standard deviation of CV%s.

Table 6.

Accuracy of measuring body composition using Goran Lab Infant QMR with oil (3.584kg) and water (3.785kg) phantoms across 25 consecutive scans on one day¹

	Fat	Total Water
Mean difference (g)	92.24 (2.4%)	32.84 (0.9%)
SD of difference (g)	21.7	62.5

¹Mean is the mean difference between known phantom weight and Infant QMR output averaged across 25 consecutive scans. SD is the standard deviation of the difference between known phantom weight and Infant QMR output averaged across 25 consecutive scans.

During model development, we considered infant weight (kg), length (cm), sex, age (days), and ethnicity as candidate predictors. The full pooled data set of n = 574 observations from n = 359 individual infants was split into 75% training and 25% test datasets whereby repeated measures from the same infant were contained within the same split to reduce bias. The training dataset was restricted to those with complete data for each of these variables and fat mass, and had a sample size of n = 269 infants with n = 431 observations. This sample size satisfies both the minimum 10 people per candidate predictor rule of thumb and the minimum sample size requirements for prediction models proposed elsewhere^15,16.

RStudio version 1.2.5042 was used for all analyses¹⁷. We followed the TRIPOD (transparent reporting of a multivariable model for individual prognosis or diagnosis) guidance for development and reporting of multivariable prediction models¹⁸. We modelled our procedures after those of Hudda et al, who developed a similar predictive model in children aged 4–15 years¹⁹. Linear regression was used to develop a prediction model with fat mass as the outcome, and weight, length, age, ethnicity, and sex as candidate predictors. Using a stepwise approach through backwards elimination, candidate predictors were excluded based on their statistical significance (Wald test p > 0.05). Non-linear relationships between outcome and continuous predictors were considered by identifying, at each iterative step of the stepwise process, the best fitting fractional polynomial terms, using the mfp R package. This model development process led to final models for the prediction of fat and lean mass based on the selected predictors along with their corresponding estimated β coefficients and associated intercept terms.

Performance of the final model was assessed using several approaches:

• R² – proportion of the variance in fat and lean mass explained by the included predictors

• Calibration slope – based on regressing observed on predicted values of fat and lean mass (with a slope of 1 being ideal).

• Calibration intercept term – based on regressing observed on predicted values of fat and lean mass (with an intercept of 0 being ideal)

• Root mean square error (RMSE) – the standard deviation of the residuals

We also assessed calibration graphically by displaying fat and lean mass on calibration plots. We carried out an internal validation to estimate optimism (the level of model overfitting) and correct measures of predictive performance (R², calibration slope, and calibration intercept) for model overfitting by 5-fold cross validation of the test data using the rms R package. Each of these cross-validation sample models within the original dataset was applied to estimate optimism in the performance statistics (difference in test performance and apparent bootstrap performance) of R², calibration slope, and calibration intercept, referred to as optimism adjusted R², calibration slope, and calibration intercept, respectively. Estimates of a uniform shrinkage factor (the average calibration slope from each of the cross-validation samples) were multiplied by the original β coefficients to obtain optimism adjusted coefficients. Model intercepts were then re-estimated using the metamisc R package to maintain overall model calibration, producing a final model.

The final prediction model was applied to each participant in the test dataset, which contained n = 90 infants with n = 143 observations. Model performance was assessed using R², calibration slope, calibration intercept, and RMSE. Overall calibration of the model was assessed graphically by plotting agreement between predicted and observed values. Finally, the intercept term was re-estimated to maintain calibration of the model.

Results

The training dataset included 431 observations from 269 infants between 1–24 months of age and ≤12 kg with complete data on weight, length, sex, age, and triplicate Infant QMR measurements. Summary statistics are provided in Table I(available at www.jpeds.com).

Table 1.

Characteristics of participants in the training and testing datasets. Data shown are mean (standard deviation)

	Training n = 431	Testing n = 143
Weight (kg)	7.17 (±2.22)	7.03 (±2.16)
Length (cm)	64.91 (±8.51)	64.46 (±8.73)
Female, n (%)	216 (50.12%)	69 (48.25%)
Age (days)	183.30 (±143.70)	183.71 (±146.27)
Ethnicity
Asian	1 (0.23%)	0 (0.00%)
Black	35 (8.12%)	19 (13.29%)
Hispanic	269 (62.41%)	92 (64.34%)
Indian	2 (0.46%)	0 (0.00%)
Mixed race	22 (5.10%)	11 (7.69%)
Unknown	7 (1.62%)	0 (0.00%)
White	95 (22.04%)	21 (14.69%)
Fat mass (kg)	2.09 (±0.88)	2.04 (±0.91)
Lean mass (kg)	3.92 (±1.07)	3.93 (±1.13)
Free water (kg)	0.18 (±0.06)	0.18 (±0.06)
Total water (kg)	3.85 (±0.99)	3.84 (±1.02)

^{^}Encompassing 269 individual infants with data collected at up to 3 different timepoints between 1–24 months of age.

^†Encompassing 90 individual infants with data collected at up to 3 different timepoints between 1–24 months of age.

The final multivariable model included four out of the five candidate predictors (weight, length, age in days, and sex). Ethnicity was excluded by backwards stepwise selection, suggesting that ethnicity was not an important determinant of infant fat mass prediction in our model. Fractional polynomial terms for the continuous predictors were included in the final model to allow for non-linear relationships. The model showed high predictive performance for fat mass (R² = 92.6%) and was perfectly calibrated in the development data (apparent slope = 1, apparent intercept = 0). This was confirmed by the calibration plot, assessing agreement between observed and predicted fat and lean mass (Figure 1). The difference between mean observed and predicted values for fat and lean mass was zero. The RMSE value was 0.238 kg.

Figure 1.

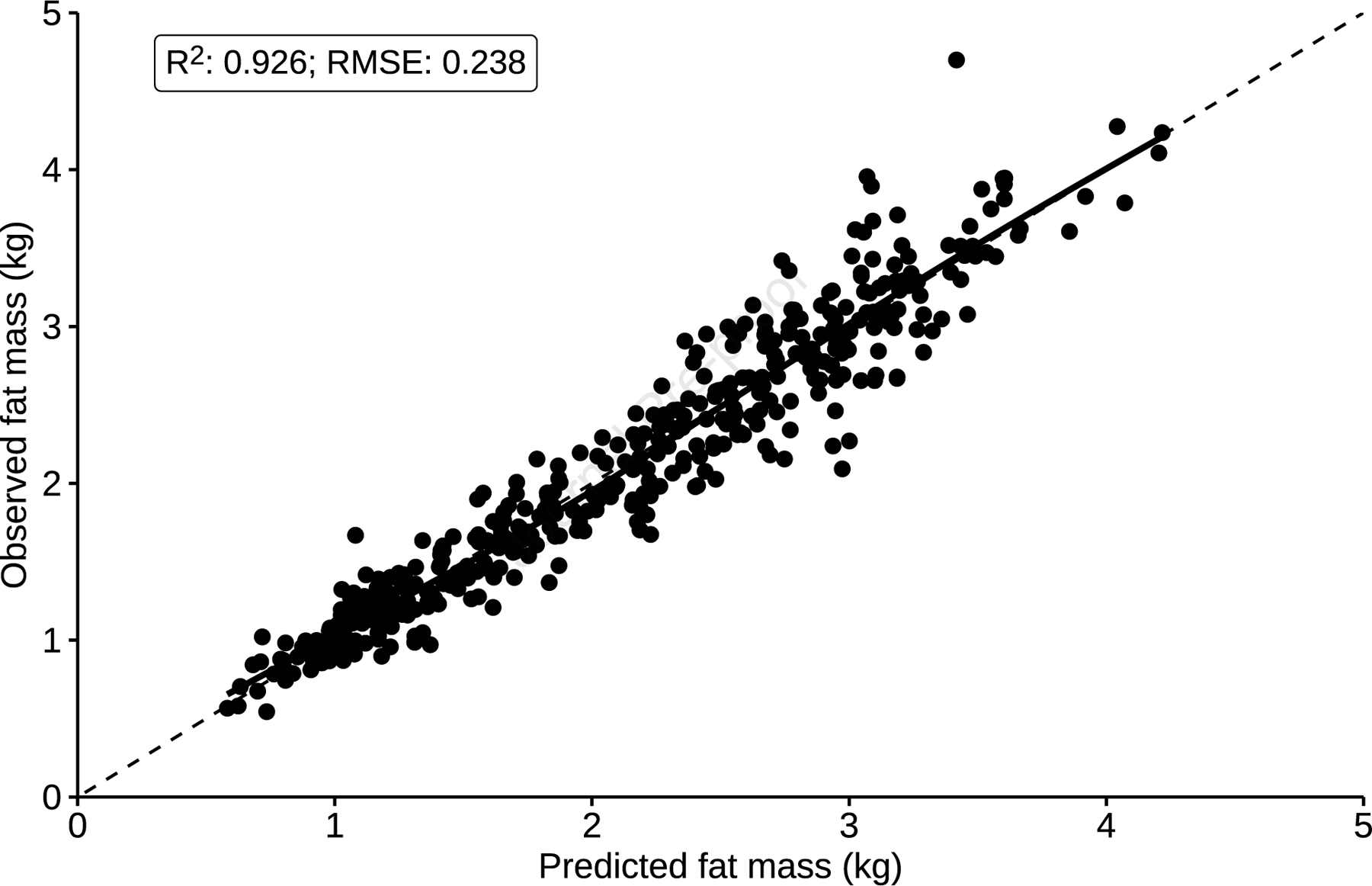
Assessment of model calibration for fat mass in the training dataset. The broken line depicts an ideal slope of one and intercept of zero, while the solid black line represents a loess smoother through the data points, showing a linear relationship between observed and predicted values of fat mass. Plot shows R² value prior to adjusting for optimism.

5-fold internal cross-validation on the training data set showed little model overfitting, which was reflected in the similar apparent and optimism-adjusted performance statistics (Table II). After adjustment for overfitting, the final prediction model maintained a high proportion of the variance in fat mass with an adjusted R² value of 92.1%. The uniform shrinkage factor was 0.996 – very close to an ideal slope of 1, meaning there was no important overfitting. This uniform shrinkage factor was multiplied by the original model β coefficients to obtain optimism-adjusted coefficients before re-estimation of the intercept term (Table III; available at www.jpeds.com). The final model is included in the Appendix.

Table 2.

Model performance statistics based on internal validation

Measure	Apparent performance	Average optimism	Optimism adjusted
R2 (%) (95% CI)	92.6 (91.3 to 94.0)	0.58	92.1
Calibration slope	1.00 (0.97 to 1.03)	0.004	0.996
Calibration intercept	0.00 (−0.06 to 0.06)	−0.007	0.007

Table 3.

Final multivariable analysis model in the development dataset and optimism adjusted β coefficients

	Developed model: coefficients (95% CI)	Final model coefficients after adjusting for overfitting*
Infant weight (kg)/103	4.11 (3.82 to 4.41)	4.10
Infant weight (kg)/103 x ln(Infant weight (kg)/10)	−6.90 (−7.85 to −5.96)	−6.88
Infant length (cm)/1003	−3.60 (−4.53 to −2.68)	−3.59
Infant length (cm)/1003 x ln(infant length (cm)/1003)	−14.76 (−20.94 to −8.58)	−14.70
Infant age/100 (days)3	−0.04 (−0.05 to −0.03)	−0.04
Infant age (days)/1003 x ln(age (days)/100)	0.02 (0.01 to 0.03)	0.02
Infant sex
Female	Reference
Male	−0.19 (−0.24 to −0.14)	−0.19
Constant	−0.62 (−1.15 to −0.09)	−0.62

^*Uniform shrinkage factor from cross-validation determined to be 0.996.

We applied our final prediction model to the test data set, which included 90 infants with 143 observations (Table I). The resulting R² was 85.4% with moderate RMSE values for fat and lean mass of 0.347 kg, respectively (Table IV; available at www.jpeds.com). The model showed great calibration, with an intercept of −0.076 and slope of 1.04. The mean difference between observed and predicted values was 0.015 kg (Figure 2).

Table 4.

External validation: model performance statistics in infants aged 1–12 months and ≤ 12 kg.

Measure	Overall performance
Adjusted R2 (95% CI) (%)	85.4% (81.1 to 89.8%)
Slope (95% CI)	1.044 (0.971 to 1.117)
Intercept (95% CI) kg	−0.076 (−0.234 to 0.083)

Figure 2.

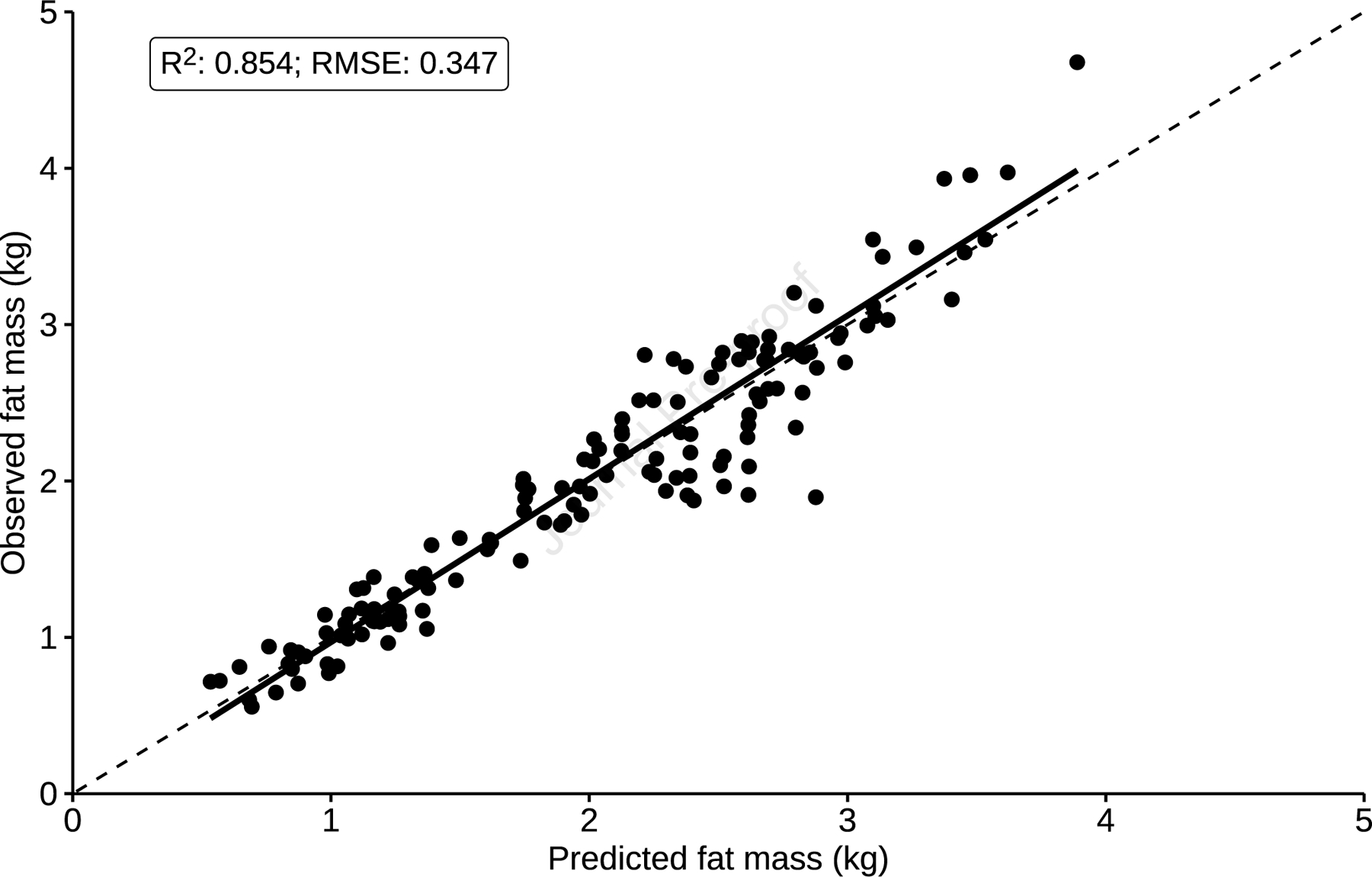
Calibration plot of mean observed fat mass against mean predicted fat mass values in the testing dataset.

To determine whether our predicted fat and lean mass measures are useful beyond standard World Health Organization (WHO) growth charts for infants, we tested how well infant fat mass correlated with WHO weight-for-length z scores – the recommended measure for infants aged 0–24 months²⁰. We also compared fat mass with infant BMI z-score, which uses the same input measures as our equation (weight, length, sex, and age). We found that infant fat mass correlated poorly with both weight-for-length and BMI z-scores (Pearson’s R = 0.39 and 0.36, respectively, both p < 0.0001). We also transformed predicted fat mass into z-scores and compared these against weight-for-length and BMI z-score. Again, there was a significant but weak relationship between predicted fat mass z-scores and both weight-for-length and BMI z-scores (Pearson’s R = 0.22, p = 0.008 and 0.36, p < 0.001, respectively), suggesting that our prediction equations are beneficial beyond the applications of standard growth measures.

Due to the longitudinal nature of the cohorts, we repeated our procedures using generalized estimating equations (GEE) rather than standard multivariable linear regression. GEE accounts for any correlation among repeated measures taken from an individual^21,22. However, the research for GEEs being applied to prediction modeling is not fully developed, which is why we did not use this as the primary method of model development. We found that GEE gave similar results to the previously described prediction model (Table VII; available at www.jpeds.com) suggesting that any correlation between repeated measures from the same individual did not affect the performance of the model.

Table 7.

Model performance statistics using generalized estimating equations rather than multivariable linear regression for model development.

Fat mass
Measure	Performance
Training dataset
R2 (%) (95% CI)	92.6 (91.3 to 94.0)
Slope (95% CI)	1.00 (0.97 to 1.03)
Intercept (95% CI)	0.00 (−0.06 to 0.06)
Testing dataset
R2 (%) (95% CI)	85.5% (81.1 to 89.8%)
Slope (95% CI)	1.04 (0.97 to 1.12)
Intercept (95% CI)	−0.08 (−0.23 to 0.08)

We also tested whether there were significant interactions between terms that could improve the model. We found two-way interactions between weight and age and length and age (and their respective fractional polynomial terms) to be statistically significant at the 5% level. However, inclusion of these interaction terms did not improve the apparent performance of the models (R² =91.5% and RMSE = 0.255 kg ) and therefore were not included in the final models.

Discussion

Although there are existing prediction models for infant fat mass, the majority were developed in neonates (i.e., within the first 72 hours after birth). Further, most require skinfold measurements in addition to weight, length, age, and/or sex, and there have been conflicting reports on their performance in validation studies. Josefson et al tested three prediction models of neonatal fat mass against air displacement plethysmography (ADP)²³. Catalano et al²⁴’s equation showed the best predictive power with a mean prediction error of −0.062kg and RMSE of 0.133kg, while the other tested equations^25,26) had “suboptimal predictive power”²³. Although these error values are lower than those reported in the current paper, the Catalano equation was developed and validated in neonates, whereas our cohort includes infants between 1–24 months of age. When expressed as a percentage of mean fat mass (0.483kg), the Catalano equation showed an error of 27.5% in the Josefson validation study - larger than the error of 17.0% that we found in our testing dataset. Cauble et al r performed a validation study of the same infant fat mass prediction equations (with the addition of Deierlein et al²⁷), and found poor agreement, precision, and accuracy of all tested equations against newborn ADP-measured fat mass²⁸. Of these existing equations, only a single equation developed by Lingwood et al²⁵ does not require skinfold measurements. The Lingwood equation uses similar predictors to our model (weight, length, sex) and provides an estimate of fat-free mass. Unfortunately, the authors did not include details of R² or RMSE in the development paper or in the validation paper, making it difficult to compare the performance of the two models. However, when we tested the Lingwood equation in our testing dataset, the resulting R² was 80.3% (vs 85.4% found by our model), mean prediction error was 0.508kg (vs −0.015kg) and RMSE was 0.661kg (vs 0.347kg). Taken together, these data suggest that our model performs better than previously developed models, has a much wider weight/age range, and has greater accessibility by not requiring skinfold measurements.

A limitation of this study is that, due to the recruitment criteria of two of the cohorts, Hispanic infants were overrepresented in our datasets (62–64%) vs ~18.5% in US population²⁹. To account for this, we included ethnicity as a feature in our model. However, ethnicity was dropped from the backwards stepwise selection suggesting it was not a factor that significantly influenced the prediction of infant fat mass All previously mentioned infant prediction models have similarly not included infant ethnicity in their models, and Josefson et al noted that the Aris and Catalano equations perform similarly despite being developed in Asian and multi-ethnic cohorts, respectively²³. Further, in a model for child and adolescent fat mass, ethnicity did not meaningfully affect results in sensitivity analyses, and the authors noted that “children of unknown ethnic origins can be treated as white with little effect on the predictive performance”¹⁹. Another limitation is that we had multiple observations from the same infant within both the development and validation datasets. However, when we performed GEE – which takes repeated measures into account – we obtained similar results, suggesting that this did not meaningfully affect model performance. Finally, we recognize that the inclusion of fractional polynomial terms makes the equation appear convoluted for practical use. We have therefore devised a Microsoft Excel calculator which we have included as an online-only Appendix and a web app (https://jasmineplows.shinyapps.io/FatLeanMassCalculator/) for straightforward calculation of predicted fat and lean mass. Finally, this model was developed in apparently healthy infants and so may not be suitable for infants with metabolic conditions without further evaluation.

This new predictive model could be used for early identification of increased body fat in infants – a trend that often tracks into childhood and adulthood – and early interventions could be designed accordingly. As we and others ^30–32 have demonstrated, true and predicted fat mass was not strongly correlated with WHO z-scores. This suggests that our model of estimated fat mass will be beneficial beyond the applications of WHO z-scores. This model could also be used for routine surveillance of adiposity in infants in national databases. This would allow for assessment of ethnic, geographical, and socioeconomic variations in fat mass rather than reliance on weight-based measures, which do not distinguish between fat and lean mass.

Box 1. Final predication equations for fat mass (lean mass can be predicted by subtracting predicted fat mass from total body weight).

Fat mass (predicted) = (4.09644221* ((weight/10)³)) - (6.87699828 *((weight/10)³ * ln((weight)/10)))) - (3.58838763* ((length/100)³)) - (14.70363829 * ((length/100)³ * ln((length/100)))) - (0.03962223 * ((age/100)³)) + (0.02136099* ((age/100)³ * ln((age/100)))) - (0.18975680* sex) - 0.61556255

Notes: Weight units are kg. Length units are cm. Age units are days. Sex units are female = 0 and male = 1. Predicted fat mass units are kg.

Abbreviations:

BMI

Body mass index

DEXA

dual energy X-ray absorptiometry

GEE

Generalized estimating equations

LIFT

Lifestyle Intervention for Two Study

NIH

National Institutes of Health

QMR

Quantitative magnetic resonance

RMSE

Root mean square error

WHO

World Health Organization