Computational modelling of multi-temporal ventricular–vascular interactions during the progression of pulmonary arterial hypertension

Abstract

A computational framework is developed to consider the concurrent growth and remodelling (G&R) processes occurring in the large pulmonary artery (PA) and right ventricle (RV), as well as ventricular–vascular interactions during the progression of pulmonary arterial hypertension (PAH). This computational framework couples the RV and the proximal PA in a closed-loop circulatory system that operates in a short timescale of a cardiac cycle, and evolves over a long timescale due to G&R processes in the PA and RV. The framework predicts changes in haemodynamics (e.g. 68.2% increase in mean PA pressure), RV geometry (e.g. 38% increase in RV end-diastolic volume) and PA tissue microstructure (e.g. 90% increase in collagen mass) that are consistent with clinical and experimental measurements of PAH. The framework also predicts that a reduction in RV contractility is associated with long-term RV chamber dilation, a common biomarker observed in the late-stage PAH. Sensitivity analyses on the G&R rate constants show that large PA stiffening (both short and long term) is affected by RV remodelling more than the reverse. This framework can serve as a foundation for the future development of a more predictive and comprehensive cardiovascular G&R model with realistic heart and vascular geometries.

1. Introduction

Pulmonary arterial hypertension (PAH) is a disease characterized by an increase in pulmonary vascular resistance (PVR) and an elevation in pulmonary arterial pressure. It is widely believed that the disease initiates with the remodelling of the distal pulmonary vasculature. During progression of PAH, the large proximal pulmonary arteries (PA) and the right ventricle (RV) are implicated and undergo significant remodelling. Without treatment, right heart failure develops ultimately in PAH [1].

Remodelling features found in individual compartments of the cardiopulmonary circulation are often used as biomarkers of PAH progression (e.g. elevated pulmonary vascular stiffness (PVS) [2], increased right ventricular end-diastolic volume (RVEDV) [3] and reduced right ventricular ejection fraction (RVEF) [4]). Interaction between the RV and pulmonary vasculature (i.e. ventricular–vascular coupling) is increasingly recognized as a key determinant of the progression of PAH [5]. This coupling is believed to play a critical role in the transition from compensated to decompensated phase of remodelling in PAH when pressure overload of the pulmonary vasculature exceeds the RV contractile forces that results in the RV failure [6]. We note that decompensated phase of cardiac growth and remodelling (G&R) is associated with ventricular dilation whereas the compensated phase of cardiac G&R is associated with ventricular wall thickening without significant dilation [7,8]. Despite its importance in PAH progression, studies on ventricular–vascular coupling are relatively limited [9]. Ventricular–vascular coupling is often indexed by the ratio between the end-systolic elastance and the arterial elastance (i.e. E_es/E_a ratio) [10]. While this ratio can characterize the state of coupling between the RV and the pulmonary vasculature during progression of PAH, it provides only limited insight into the interaction between the different G&R processes operating in the RV and pulmonary vasculature.

Computational models are also increasingly developed to improve our understanding of G&R found in different compartments of the cardiopulmonary circulation during the progression of PAH [11–13]. These models can bridge the gap associated with clinical measurements (e.g. limited spatial and temporal resolutions) and can also predict the disease progression [14]. Existing models are developed largely to simulate G&R in isolated components of the cardiopulmonary circulation such as the small pulmonary vascular tree [15], the large PAs [13–16] and the RV [12]. These models, however, do not consider ventricular–vascular interactions resulting from G&R occurring in the RV, the large PAs and small pulmonary vessels. Therefore, they are not able to comprehensively capture the evolution of cardiopulmonary haemodynamics and the transition from a compensated to a decompensated phase during the progression of PAH.

Motivated by the above-mentioned limitations, we seek here to develop and validate a computational modelling framework that describes the different G&R processes occurring concurrently in the RV and large PAs in the cardiopulmonary circulation, including ventricular–vascular interactions, in response to PAH. In this framework, the circulatory system operates over a short timescale of a cardiac cycle that evolves at a long timescale with progression of the disease. The framework is calibrated to match clinical haemodynamic data acquired from a paediatric idiopathic PAH patient and is used to simulate PAH progression initiated by an elevation in the flow resistance and stiffness of the distal pulmonary vessels. We show that the proposed computational framework with inputs commonly observed as PAH stimuli predicts the biomarkers commonly observed in the PAH progression. The model is applied to provide insights into how PAH enters its late-stage phase when the RV dilates in long term and how mechanical quantities such as stress and stretch influence G&R of the RV and PA in the presence of their coupled interaction.

2. Material and methods

2.1. Cardiopulmonary growth and remodelling computational framework

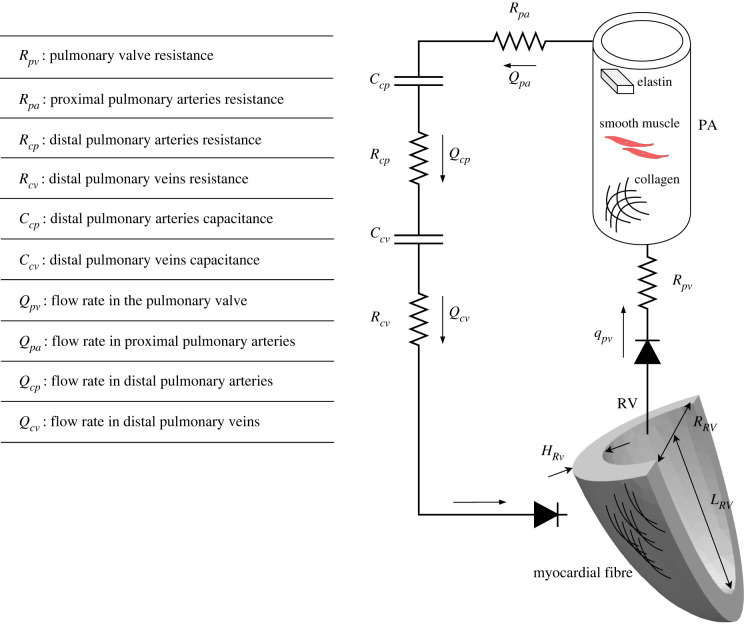
The computational framework consists of the RV and PA, which are coupled with the other lumped-parameter compartments to represent the cardiopulmonary circulation (figure 1). The RV is modelled as a thick-wall quarter prolate spheroid, and the PA is modelled as a thin-wall cylinder. Total blood volume (TBV) in the circulatory system is conserved at each cardiac cycle so that the sum of the rate of changes in the volume of each storage compartment is equal to the difference between the inflow and outflow rates of the connecting segments. Flow rate in each segment is determined by the pressure difference between its inlet and outlet (i.e. pressure gradient) and its prescribed flow resistance. Pressure in the storage compartments representing the distal vessels is defined by prescribed compliance. The pressure–volume (P–V) relationships of the PA and RV are described in the next sections. Details and equations related to the closed-loop circulatory system are given in appendix A.

Figure 1.

Schematic of the closed-loop circulatory system of the cardiopulmonary circulation. RV is modelled by a thick-wall quarter spheroid with myocardial fibre as its main constituent. PA is modelled as a thin-wall cylinder with load-bearing constituents i.e. collagen, elastin and SMC. The distal arteries and veins are modelled by resistance-capacitate sets. A list of definition for the individual parameters of the circulatory system is provided.

There are two timescales in the framework. The circulation model operates at a short timescale (t) that is defined by the duration of a heartbeat T. The model also evolves over a long timescale (s) that is defined by the duration of the remodelling processes S during disease progression. A characteristic value of each quantity $(\cdot )$ associated with the G&R processes is defined by its average value over the entire cardiac cycle, i.e.

$$\overline{(\cdot )}(s)={\displaystyle \frac{1}{T}{\int }_0^T(\cdot )(s,t)\mathrm{d}t.}$$ 2.1

2.2. Pulmonary artery

2.2.1. Constitutive relationships, constituents and pressure

The mechanical behaviour of PA and its G&R processes during disease progression are modelled using the theory of constrained mixture [17], which considers the contribution of each tissue constituent under the assumption that they have the same deformation in a mixture. The PA is composed of three major load-carrying constituents, namely, collagen (c), vascular smooth muscle cells (SMC) (m) and elastin (e) i.e. $\alpha \in \{c,m,e\}$. The mass of individual constituents is determined by a continual process of its production and removal over time s, i.e. constituent $\alpha$ has a certain lifespan over which it is produced at a mass production rate $m^{\alpha }$ per unit reference area and removed at the rate $k_q^{\alpha }$. The difference between mass production and removal determines the constituent's total mass $M^{\alpha }(s)$ in the PA.

The strain energy $w^{\alpha }(s,t)$ of constituent $\alpha$ per unit reference area is a function of ${\mathrm{C}}_n^{\alpha }(\tau ,s,t)$, which is the constituent's specific right Cauchy-Green stretch tensor produced at time $\tau$. Cauchy stress resultant and the corresponding stiffness of an individual constituent are calculated from its corresponding strain energy density. Specifically, mechanical behaviour of the collagen and passive mechanical behaviour of the SMC are both described by a fibre-based constitutive model. Active response of the SMC is prescribed in the circumferential direction that is described by an active constitutive model [18], whereas elastin is assumed to behave like an amorphous matrix described by a neo-Hookean strain energy. The deformed radius and circumferential Cauchy stress resultant of the PA are functions of its intramural pressure based on the Laplace equation of thin wall vessels. For more details on PA constituents' kinematic, constitutive and force balance equations, refer to appendix B.

2.2.2. Fibre stress and growth and remodelling mediation

We assume no turnover of elastin following the argument that functional elastin is produced during the perinatal period with half-life longer than the G&R period and tends to degrade very slowly [19]. As such, we only consider the turnover of collagen fibres and SMC, where it is assumed that their turnovers are driven by their corresponding stress. Fibre stress in the $\kappa$ direction is given by [17]

$${\sigma }_{\kappa }^{\alpha }(s,t)={\displaystyle \frac{\parallel {\mathbf{\text{T}}}^{\alpha }(s,t){\mathbf{\text{m}}}^{\kappa }\parallel }{h_{PA}(s,t)},}$$ 2.2

Where ${\mathbf{\text{T}}}^{\alpha }$ is the Cauchy stress resultant, ${\mathbf{\text{m}}}^{\kappa }$ is the fibre direction and $h_{PA}(s,t)$ is the arterial wall thickness, both in the current configuration. Following previous studies [17–20], the production rate of individual constituents is given as a function of fibre stress (namely, based on stress-mediated G&R) [20]

$$m^{\alpha }(s)=m_b^{\alpha }\left[1+K_g^{\alpha }\left({\displaystyle \frac{{\overline{\sigma }}^{\alpha }(s)}{{\sigma }_h^{\alpha }}-1}\right)\right],$$ 2.3

where $m_b^{\alpha }$ is the basal mass production rate and ${\sigma }_h^{\alpha }$ is reference stress for the constituent $\alpha$ both described at $s=0$, ${\overline{\sigma }}^{\alpha }(s)$ is the fibre stress averaged over the short timescale at the long timescale (equations (B 12) and (2.1)) and $K_g^{\alpha }$ is the rate constant for constituent α.

2.3. Right ventricle

2.3.1. Constitutive model

An active stress formulation in which the ventricular wall stress is separated into its passive and active component is used to describe the mechanical behaviour of RV, i.e. [21,22]

$${\sigma }_{\mathrm{RV}}(s,t)={\sigma }_{\mathrm{RV},p}(s,t)+{\sigma }_{\mathrm{RV},a}(s,t).$$ 2.4

In the above equation, ${\sigma }_{\mathrm{RV}}$ is the total Cauchy stress of the RV and ${\sigma }_{\mathrm{RV},p}$ and ${\sigma }_{\mathrm{RV},a}$ are, respectively, the passive and active components of the wall stress. The RV deformed radius, length, and thickness are used to calculate the RV deformed luminal volume $(V_{\mathrm{RV}}(s,t))$ and wall volume. Together with the RV stress given in equation (2.4), the luminal and wall volumes are used to calculate the RV pressure with the formula by Arts et al. [23]. For details of the RV constitutive relations and pressure calculation, see appendix C.

2.3.2. Growth and remodelling

Growth and remodelling of the RV are described based on the classical definitions of concentric and eccentric hypertrophy as well as passive stiffening. Concentric hypertrophy associated with wall thickening is driven by changes in the stress [24]

$${\displaystyle \frac{\mathrm{d}{H}_{\mathrm{RV}}(s)}{\mathrm{d}s}={\beta }_h\left[{\displaystyle \frac{{\overline{\sigma }}_{\mathrm{RV}}(s)}{{\sigma }_{\mathrm{RV},h}}-1}\right],}$$ 2.5

where ${\overline{\sigma }}_{\mathrm{RV}}$ is the RV wall stress averaged over a cardiac cycle, ${\sigma }_{\mathrm{RV},h}$ is the reference wall stress defined at $s=0$ and ${\beta }_h$ is the rate constant regulating the thickening of RV. The model of eccentric hypertrophy of the RV is derived by that of the left ventricle (LV) in which upregulation of luminal radius (volume in three-dimension) is associated with an increase in the ventricular stretch [24]

$${\displaystyle \frac{\mathrm{d}{R}_{\mathrm{RV}}(s)}{\mathrm{d}s}=\{\begin{array}{cc}{\beta }_{\mathrm{e}}\left[{\displaystyle \frac{{\overline{\lambda }}_f(s)}{{\lambda }_{\hspace{0.17em}f,h}}-1}\right]\hfill & {\overline{\lambda }}_f\ge {\lambda }_{\hspace{0.17em}f,h}\hfill \\ 0\hfill & {\overline{\lambda }}_f<{\lambda }_{\hspace{0.17em}f,h},\hfill \end{array}}$$ 2.6

where ${\overline{\lambda }}_f$ is the averaged myocardial fibre stretch over a cardiac cycle, ${\lambda }_{\hspace{0.17em}f,h}$ is the reference stretch defined at $s=0$ and ${\beta }_{\mathrm{e}}$ is the rate constant regulating the changes in RV luminal radius. In addition to geometrical remodelling, stiffening of the myocardium (by cardiac fibrosis and myocyte stiffening) during G&R is modelled by a change in the passive intrinsic stiffness of the RV wall in response to a change in the muscle fibre stress [25]

$${\displaystyle \frac{\mathrm{d}C(s)}{\mathrm{d}s}=\{\begin{array}{cc}{\beta }_f\left[{\displaystyle \frac{{\overline{\sigma }}_{\mathrm{RV}}(s)}{{\sigma }_{\mathrm{RV},h}}-1}\right]\hfill & C(s)>0\hfill \\ 0\hfill & C(s)\le 0,\hfill \end{array}}$$ 2.7

In the above equation, ${\beta }_f$ is the rate constant regulating RV stiffening.

2.4. Clinical and experimental data assimilation to the computational framework

Clinical data were acquired in a female 16-year-old paediatric patient who was diagnosed with idiopathic PAH. The study was approved by the University of Michigan Institutional Review Board (HUM00117706), and informed consent was obtained from the parents/guardians of the subject.

2.4.1. Vascular and right ventricle geometry

Phase-contrast magnetic resonance (MR) imaging was performed to obtain the dynamic changes of the PA luminal area and flow. Diameter of the main PA was measured from the MR images at the end of diastole, and was used to define the reference radius of the idealized cylindrical PA (R_PA) in the computational framework. Length of the PA (L_PA) was determined based on the measured diastolic volume of the main, left and right pulmonary arteries. Wall thickness of the PA (H_PA) was prescribed to be 9% of its radius based on a previous study [26].

Cine MR images were acquired in the patient and the RV endocardial surfaces were segmented from these images using MeVisLab (www.mevislab.de) to acquire the chamber cavity volume waveform. The average between the measured RV chamber end-diastolic and end-systolic volumes was used to prescribe the undeformed luminal radius of the idealized RV ($R_{\mathrm{RV}}$) in the computational framework. For simplicity, we assume that the length of the RV is equal to its diameter with $\gamma =1.0$ (i.e. RV is a quarter of a thick hollow sphere). RV wall thickness in the computational model ($H_{\mathrm{RV}}$) was prescribed to be constant throughout the RV and its value was determined based on measurements of the free wall thickness at the RV base in MR images.

These geometrical measurements of the PA and RV were used to prescribe their respective geometries before initiation of G&R simulation in the computational framework i.e. at $s=0$. Additionally, we also assume that the length of PA (L_PA) remains constant during G&R.

2.4.2. Vascular and right ventricle mechanical properties

Vascular mechanical properties of the PA, including the intrinsic stiffness and the deposition stretches, were prescribed based from the authors’ previous work on the same PAH patient [13]. Due to a lack of data, removal rate of the PA constituents ($k_q^{\alpha }$) and the PA mass density per unit volume ($\rho$) were set to those associated with the abdominal aortic tissue constituents in Zeinali-Davarani et al. [20] i.e. $k_q^{\kappa =1-4}=k_q^m=0.02$ day⁻¹ and $\rho =1.05\times {10}^{-6}$ kg mm⁻³. Knowing the PA initial thickness ($H_{\mathrm{PA}}(s=0)$) and $\rho$, we were able to calculate the initial mass density per unit area of the PA i.e. $M^{\alpha }(s=0)$ (equation (B 7)). With the prescribed removal rate and initial mass ($M^{\alpha }(s=0)$), the mass production rate at $s=0$ was determined by equation (B 9) ($m_b^{\kappa =1-2}=m^{\kappa =1-2}(s=0)=7.51\times {10}^{-10}$ kg mm⁻² day⁻¹, $m_b^{\kappa =3-4}=m^{\kappa =3-4}(s=0)=3.00\times {10}^{-9}$ kg mm⁻² day⁻¹ and $m_b^m=m^m(s=0)=5.37\times {10}^{-9}$ kg mm⁻² day⁻¹) to set up the mass equilibrium of the constituents before initiation of G&R. For the RV, passive and active tissue mechanical properties were set to those in Shavik et al. [9,27]. Parameters associated with the RV and PA geometries and properties are tabulated in (table 1).

Table 1.

The model parameters of the PA, the RV and the closed-loop system at s = 0.

PA	geometry		$R_{\mathrm{PA}}(s=0)$ (mm)a	11.3
			$L_{\mathrm{PA}}(s=0)$ (mm)a	64.0
			$H_{\mathrm{PA}}(s=0)$ (mm)a	1.02
	mass		$M(s=0)$ (kg mm−2)a,b	1.07 × 10−6
	collagen	mass fraction	${\varphi }^c(s=0)$c	0.35
		mass turnover	$k_q^{\kappa =1-4}$ (day−1)b	0.02
			$m_b^{\kappa =1-2}=m^{\kappa =1-2}(s=0)$ (kg mm−2 day−1)a,b	7.51 × 10−10
			$m_b^{\kappa =3-4}=m^{\kappa =3-4}(s=0)$ (kg mm−2 day−1)a,b	3.00 × 10−9
		deposition stretch	$G_h^{\kappa =1-4}$c	1.08
		mechanical properties	$k_1$ (N mm kg−1)c	2.29 × 105
			$k_2$	3.62
		reference stress	${\sigma }_h^{\kappa =1}={\sigma }^{\kappa =1}(s=0)$ (MPa)c	0.0183
			${\sigma }_h^{\kappa =2}={\sigma }^{\kappa =2}(s=0)$ (MPa)c	0.0318
			${\sigma }_h^{\kappa =3-4}={\sigma }^{\kappa =3-4}(s=0)$ (MPa)c	0.0269
	SMC	mass fraction	${\varphi }^m(s=0)$c	0.25
		mass turnover	$k_q^{\kappa =1-4}$ (1/day)b	0.02
			$m_b^m=m^m(s=0)$ (kg mm−2 day−1)a,b	5.37 × 10−9
		deposition stretch	$G_h^m$c	1.06
		mechanical properties	$m_1$ (N mm kg−1)c	5.47 × 104
			$m_2$c	3.63
		reference stress	${\sigma }_h^m$ (MPa)c	0.0203
	elastin	mass fraction	${\varphi }^e(s=0)$c	0.4
		deposition stretch	$G_{h,11}^e=G_{h,22}^e$c	1.15
		mechanical properties	$c$ (N mm kg−1)c	7.06 × 104
RV	geometry		$R_{\mathrm{RV}}(s=0)$ (mm)a	36.0
			$H_{\mathrm{RV}}(s=0)$ (mm)a	8.10
	passive properties		$C(s=0)$ (MPa)b	0.7 × 10−3
			$b_f$b	20.0
	active properties		$T_{\max }(s=0)$ (MPa)b	0.145
			$C{a}_0={(C{a}_0)}_{\max }$ (µM)b	4.35
			$l_r$ (µm)b	1.85
			$l_0$ (µm)b	1.58
			$B$ (µm−1)b	1.43
			$t_0$ (ms)b	270
			$t_{tr}$ (ms)b	405
			${\tau }_r$ (ms)b	25
circulatory system			$R_{\mathrm{pv}}=R_{\mathrm{pa}}$ (MPa ms−1 ml−1)d	0.002
			$R_{\mathrm{cp}}(s=0)$ (MPa ms−1 ml−1)d	0.05
			$R_{\mathrm{cv}}$ (MPa ms−1 ml−1)d	0.004
			$C_{\mathrm{cp}}(s=0)$ (ml MPa−1)d	6.5 × 103
			$C_{\mathrm{cv}}$ (ml MPa−1)d	3.5 × 103
			$V_{\mathrm{cp},r}$ (ml)d	2.0
			$V_{\mathrm{cv},r}$ (ml)d	10.0

^aPatient-specific acquired by the MR images.

^bGeneral estimation by the previous studies [9, 20, 27].

^cPatient-specific by optimization in the previous study [13].

^dCalibration to fit the patient-specific clinical P–V relationship of PA and RV.

2.4.3. Pressure waveforms

Invasive right heart catheterization was performed on the PAH patient under anaesthesia to measure pressure waveforms in the RV and PA. The patient had an elevated mean pulmonary arterial pressure (mPAP) of 44 mmHg, systolic pulmonary arterial pressure (sPAP) of 68 mmHg, pulmonary arterial pulse pressure (PAPP) of 38 mmHg, RV peak systolic pressure (RVPSP) of 73.8 mmHg, RV end-diastolic pressure (RVEDP) of 9.66 mmHg and PVR of 9.9 WU m². Heart rate was also measured, and the duration of a cardiac cycle is 740 ms.

2.5. Numerical implementation

2.5.1. Short timescale simulation

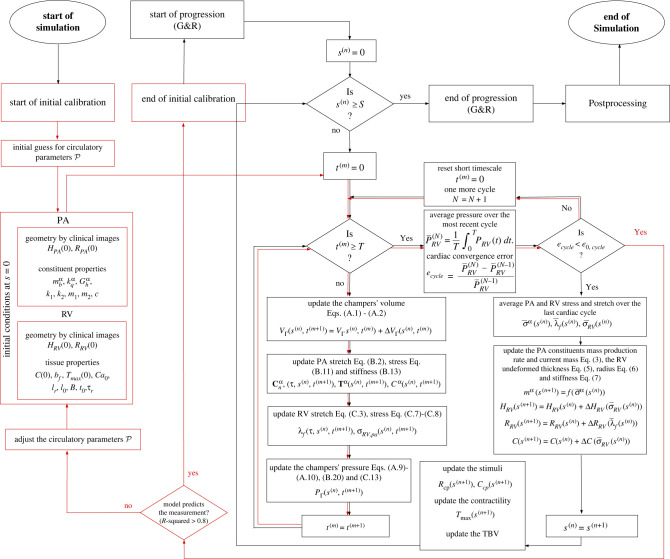
Forward Euler's method was used to solve the system of initial condition ordinary differential equations (ODE) related to the conservation of mass in equations (A 1)–(A 4) for the compartment volumes $V_{\mathrm{PA}}$, $V_{\mathrm{RV}}$, $V_{\mathrm{cp}}$, $V_{\mathrm{cv}}$ in $t\in [0\hspace{0.17em}T]$. A non-uniform time stepping scheme was adopted, where the time step $\mathrm{\Delta }t$ near peak systole is half of those in the other part of the cardiac cycle to prevent numerical instability. The rates of change in volumes at current time step in the time-discretized form of equations (A 1)–(A 4) are computed from the flow rates in the previous time step, which are defined by the pressure differences between compartments (equations (A 5)–(A 8)). On the other hand, compartmental pressures are defined by their respective volume: $P_{\mathrm{cp}}$ in equation (A 9), $P_{\mathrm{cv}}$ in equation (A 10), $P_{\mathrm{PA}}$ in equation (B 20) and $P_{\mathrm{RV}}$ in equation (C 13). Therefore, equations (A 5)–(A 10), (B 20) and (C 13) form the right-hand side of equations (A 1)–(A 4) in term of volumes at the current time step. Circulatory parameters as well as the RV and PA tissue properties and mass do not change during the short timescale simulation. Simulation was performed until a periodic steady-state (PSS) condition was obtained (figure 2). The PSS condition is defined by ($(({\overline{P}}_{RV}^{(N)}-{\overline{P}}_{RV}^{(N-1)})/{\overline{P}}_{RV}^{(N-1)})<e_{0,\mathrm{cycle}}$) where ${\overline{P}}_{RV}^{(N)}\hspace{0.17em}$ is the short-timescale-averaged RV pressure over cardiac cycle N. The clinically measured volume of the PA and RV were considered for the initial conditions $V_{\mathrm{PA},0}$, $V_{\mathrm{RV},0}$, respectively and $V_{\mathrm{cp},0}=2V_{\mathrm{PA},0}$, $V_{\mathrm{cv},0}=2V_{\mathrm{RV},0}$. Numerical parameters are tabulated in table 2.

Figure 2.

A flowchart of the numerical structure based on which the computational framework is built. The initial calibration (red flowline) in the short timescale was performed to obtain the circulatory parameters that reproduce the clinical P–V relationship of the RV and PA. After the initial calibration, the progression simulation over the short timescale starts (black flowline) and at each long timescale step the short timescale simulation is run that determine the stress and stretches that determine the G&R of the PA and RV.

Table 2.

Parameters of the numerical implementation in short and long timescale and sensitivity analysis.

short timescale	$T$ (ms)	740
	$\mathrm{\Delta }t$ (ms)	$\{\begin{array}{cc}0.5\hfill & 0\le t<50\hfill \\ 0.25\hfill & 50\le t\le 350\hfill \\ 0.5\hfill & 350<t\le 740\hfill \end{array}$
	$V_{PA,0}$ (ml)	27.2
	$V_{RV,0}$ (ml)	97.1
	$N_{\max }$	6
	$e_{0,\mathrm{cycle}}$	1.0 × 10−4
long timescale	$S$ (days)	1000
	$\mathrm{\Delta }s$ (day)	10
sensitivity analysis	${\beta }_h$ (mm day−1)	[0.1 2.0]
	${\beta }_e$ (mm day−1)	[0.3 2.2]
	${\beta }_f$ (MPa day−1)	[0.002 0.05]
	$K_g^{\alpha }$	[1.0 14.0]

2.5.2. Initial calibration

Short timescale simulation was performed to first calibrate the circulatory system parameters, $\mathcal{P}=[R_{\mathrm{pv}}\hspace{0.17em}{R}_{\mathrm{PA}}\hspace{0.17em}{R}_{\mathrm{cp}}(s=0)\hspace{0.17em}{R}_{\mathrm{cv}}\hspace{0.17em}$ $C_{\mathrm{cp}}(s=0)\hspace{0.17em}{C}_{\mathrm{cv}}\hspace{0.17em}{V}_{\mathrm{cp},r}\hspace{0.17em}{V}_{\mathrm{cv},r}]$ to simultaneously fit the RV pressure and volume waveforms as well as the PA pressure and diameter waveforms. For each short timescale simulation performed to calibrate the model, the PA and RV geometries, mass and material properties are fixed (table 1). Initial guesses for $\mathcal{P}$ were prescribed based on previous work [9–27]. The parameters $\mathcal{P}$ were manually adjusted until the model-predicted waveforms were in reasonable agreement with the corresponding clinically measured waveforms, i.e. coefficient of determination (R²) of the prediction for RV pressure, RV volume, PA pressure and PA diameter is greater than 0.8. The final adjusted parameters $\mathcal{P}$ were used to produce the waveforms of the system at $s=0$ and set the reference stresses and stretch of the PA and RV i.e. ${\sigma }_h^{\kappa =1-4}$, ${\sigma }_h^m$, ${\sigma }_{\mathrm{RV},h}$ and ${\lambda }_{\hspace{0.17em}f,h}$ in the G&R model.

2.5.3. Long timescale simulation

Based on the calibrated parameters from the short timescale simulation, long timescale simulations were performed by time-discretizing equations (2.5)–(2.7) using forward Euler's method with equally spaced step size $\mathrm{\Delta }s$ (days) for $s\in [0\hspace{0.17em}S]$. The initial conditions for the long timescale simulation are tabulated in table 1. At each step $\mathrm{\Delta }s\hspace{0.17em}$corresponding to the long timescale simulation, three major blocks of calculation are performed and updated as described below.

• A. Short timescale simulation. With given set of parameters $\mathcal{P}$ and geometry, mass and material properties of RV and PA at current day ($s$), the short timescale simulation ($t$) was performed until PSS is obtained. Deformation gradient tensor of the PA (equation (B 3)) and stretch of each constituent (equations (B 1) and (B 2)) were computed from $V_{\mathrm{PA}}$, which yields the stress of each constituent ${\sigma }^{\alpha }$ (equations (B 11) and (2.2)). Similarly, RV fibre stretch ${\lambda }_f$ (equation (C 3)) and therefore fibre passive stress ${\sigma }_{\mathrm{RV},p}$ (equation (C 7)) and active stress ${\sigma }_{\mathrm{RV},a}$ (equation (C 8)) were computed from the RV volume $V_{\mathrm{RV}}$. The quantities ${\sigma }^{\alpha }$, ${\lambda }_f$ and ${\sigma }_{\mathrm{RV}}={\sigma }_{\mathrm{RV},p}+{\sigma }_{\mathrm{RV},a}$ are time-averaged over a cardiac cycle using equation (2.1) (i.e.$\hspace{0.17em}{\overline{\sigma }}^{\alpha }$, ${\overline{\lambda }}_f$ and ${\overline{\sigma }}_{\mathrm{RV}}$) and imposed in the G&R simulation at each long timescale step as described next.

• B. Update PA and RV mass, geometries and properties. Mass production rates of the PA constituents were updated using ${\overline{\sigma }}^{\alpha }$ in equation (2.3) with the prescribed $K_g^{\alpha }$. RV thickness, radius and passive intrinsic stiffness were updated using ${\overline{\sigma }}_{\mathrm{RV}}$ and ${\overline{\lambda }}_f$ in equations (2.5)–(2.7) with the prescribed rate constants ${\beta }_h$, ${\beta }_e$ and ${\beta }_f$, respectively.

• C. Update the G&R stimuli. $R_{\mathrm{cp}}(s)$, $C_{cp}(s)$ (two elements in $\mathcal{P}$), $T_{\max }(s)$ and total blood volume (TBV) are then updated based on the prescribed time courses as described in §2.6.

With the prescribed change of $R_{\mathrm{cp}}(s)$, $C_{\mathrm{cp}}(s)$, $T_{\max }(s)$ and TBV(s) in a long timescale step $\mathrm{\Delta }s$ (Step C), haemodynamics quantities (e.g. pressure) in the circulatory model operating at the short timescale (Step A) are altered at the next long timescale step $s+\mathrm{\Delta }s$. The change in these quantities affects stress and stretch of the RV and PA, which in turn, affect the PA mass (therefore, PA thickness), RV thickness, radius and stiffness associated with the G&R processes. These processes are controlled by the prescribed rate constants, i.e. ${\beta }_h$, ${\beta }_e$, ${\beta }_f$ and $K_g^{\alpha }$ (Step B). This process is repeated for each long timescale step until the simulation terminates.

The computational framework was implemented using a code developed in Python 3.8 (https://docs.python.org/3.8/) and the numerical simulation was run on Michigan State University High Performance Computing Center clusters (https://docs.icer.msu.edu/). The computational framework run time is less than a minute in short timescale and 1 h and 48 min in long timescale.

2.6. Stimulations of progression

We prescribed the following time course of the parameters $R_{\mathrm{cp}}(s)$, $C_{\mathrm{cp}}(s)$, $T_{\max }(s)$ and TBV that drives the progression of PAH (figure 3).

• 1. Elevation of resistance $R_{\mathrm{cp}}$ by 100% and reduction of compliance $C_{\mathrm{cp}}$ by 50% from day 50 to 250, which remain until the end of simulation to mimic the elevation of PVR and progressive remodelling of the distal vessels in the pulmonary lower branches. Specifically, the narrowing and thickening of distal vessels can simultaneously contribute to an equal increase and decrease in flow resistance and vessel compliance, respectively, i.e. the product of resistance and compliance (RC-time) remains constant [28]. The prescribed changes in $R_{\mathrm{cp}}$ and$\hspace{0.17em}{C}_{\mathrm{cp}}$ reflect the hypothesis that PAH is initiated by remodelling of the distal vessels [2]. We also assume a twofold increase in PVR based on the values reported in the literature [10].
• 2. Reduction in RV contractility by 25% from day 250 to 400, which remains in the reduced value until the end of simulation to mimic RV failure during progression of PAH. Specifically, impaired RV contractility has been reported in PAH [29], especially in association with long-term RV dilation [30]. Therefore, in the simulation we prescribe a reduction in RV contractility reduction after the distal vessels completed the imposed remodelling.
• 3. Monotonic increase in the TBV from day 450 to the end of simulation to mimic fluid overload consequent of PAH-induced congestive heart failure [31]. TBV elevation is associated with end-stage heart failure. For this reason, we prescribed its initiation in the later part of the simulation.

Figure 3.

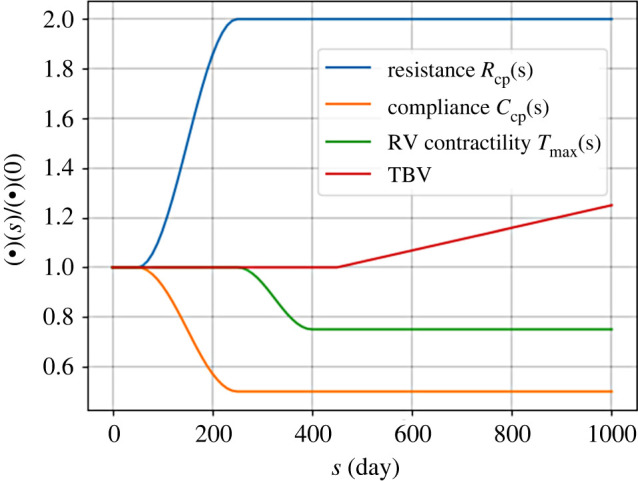
The time course of PVR elevation, contractility reduction and increase in TBV in the computational framework for PAH progression. The distal resistance $R_{cp}(s)$ is elevated by twofold and the distal capacitance $C_{cp}(s)$ is reduced by half to simulate the progressive remodelling of distal vessels as the initial cause of PAH. After the distal vessels are remodelled, RV contractility is reduced associated with the late-stage phase of PAH. And finally, TBV increases to mimic fluid overload consequent of PAH-induced heart failure.

2.7. Sensitivity analysis

The effects of four G&R rate constants (${\beta }_h$, ${\beta }_e$, ${\beta }_f$, $K_g^{\alpha }$) on quantities related to the geometry and haemodynamics of the PA and RV of the simulation at day 250 and 1000 was determined from a local sensitivity analysis (LSA). The rate parameters were selected because they control the G&R processes via equations (2.3) and (2.5)–(2.7), which, in return, affects the time course of disease progression in PAH. These 15 geometrical and haemodynamic quantities, which represent the main biomarkers of PAH in clinical applications, are given in a vector y = [mPAP PAPP $C_{\mathrm{PA}}$ $H_{\mathrm{PA}}$ $m^c$ $m^m$ $M^c$ $M^m$ RVPSP RVEDP RVEDV RVSV RVEF $H_{\mathrm{RV}}$ $C$]. Denoting the computational model as a map between these quantities and the parameters $\mathbf{\text{p}}=\left[\begin{array}{cccc}{\beta }_h\hfill & {\beta }_e\hfill & {\beta }_f\hfill & K_g^{\alpha }\hfill \end{array}\right]$, i.e. $\mathbf{\text{y}}=\mathrm{{\rm Y}}(\mathbf{\text{p}})$, the effect of each rate constant p_j on the geometrical and haemodynamic quantities $y_i$ is computed by [32]

$${\text{EE}}_{ij}={\frac{\partial y_i}{\partial p_j}|}_{p_{i,0}},$$ 2.8

where $p_{i,0}=\left[\begin{array}{cccc}{\beta }_{h,0}\hfill & {\beta }_{\hspace{0.17em}f,0}\hfill & {\beta }_{e,0}\hfill & K_{g,0}^{\alpha }\hfill \end{array}\right]$ is a set of baseline rate parameters that is able to reproduce the key G&R features found in PAH (see §3.2). The value of ${\mathrm{EE}}_{ij}$ was obtained by perturbing the corresponding rate constant from its baseline value and computing the changes in$\hspace{0.17em}{y}_i$. The baseline rate parameters and their span of perturbation are tabulated in table 2. To present a unique value for ${\mathrm{EE}}_{ij}$ for each pair of (y_i, p_j) we use its normalized average by integration over the span of the corresponding input,

$${\overline{\mathrm{EE}}}_{ij}={\displaystyle \frac{\hspace{0.17em}{p}_{i,0}}{y_{i,0}}{\displaystyle \frac{{\int }_{\hspace{0.17em}{p}_{i,0}}^{\hspace{0.17em}{p}_{i,e}}{\mathrm{EE}}_{ij}\mathrm{d}{p}_i}{{\int }_{\hspace{0.17em}{p}_{i,0}}^{\hspace{0.17em}{p}_{i,e}}\mathrm{d}{p}_i}.}}$$ 2.9

3. Results

3.1. Model calibration

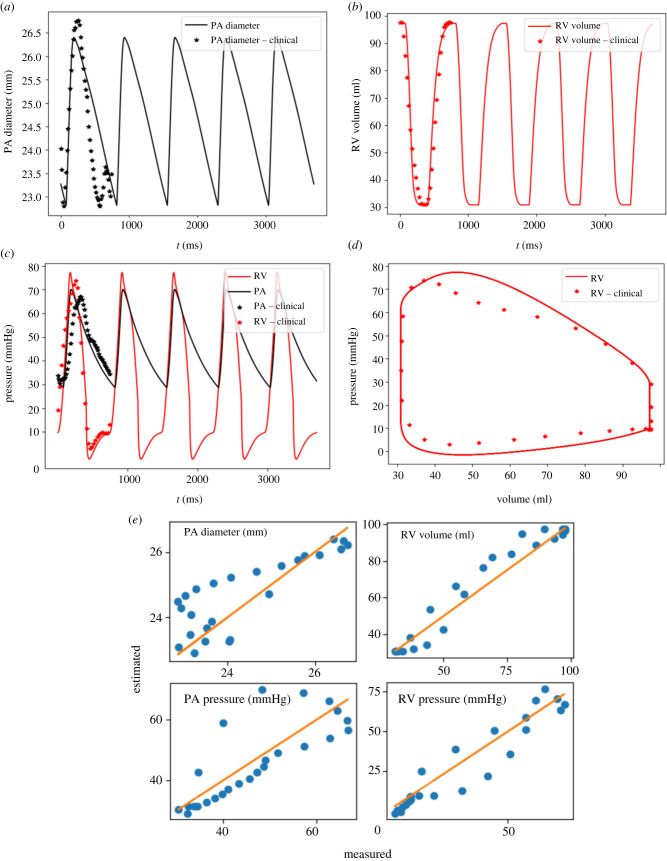
Model prediction of the PA diameter, RV volume, PA and RV pressure waveforms over the short timescale in the baseline case at day $s=0$ matched the clinical measurements well (figure 4). The calibrated parameters $\mathcal{P}$ are tabulated in (table 1). Coefficients of determination ($R$-squared) were 0.811 for the PA diameter, 0.978 for the RV volume, 0.873 for the PA pressure and 0.928 for the RV pressure (figure 4e). Model prediction of mPAP, sPAP, RVPSP and RVEDP were 42.5 mmHg, 70.2 mmHg, 73.8 mmHg and 10.2 mmHg, respectively. These values reflect the elevated pressure found in the pulmonary circulation caused by PAH. Right ventricular stroke volume (RVSV) and RVEF predicted by the model were 66.3 ml and 68.2%, respectively.

Figure 4.

Measurement and model predictions for the baseline case. (a) PA diameter waveform; (b) RV volume waveform; (c) RV and PA pressure waveform; (d) RV pressure–volume loop; (e) Scatter plot of the predicted values by the model at all cardiac time points of the baseline versus clinical measurements with a linear fit showing the zero-error reference.

3.2. Simulation of growth and remodelling in the baseline condition

With prescribed rate constants $K_g^{\alpha }=1.0$, ${\beta }_h=0.1\hspace{0.17em}\mathrm{mm}\hspace{0.17em}{\mathrm{day}}^{-1}$, ${\beta }_f=0.002\hspace{0.17em}\mathrm{MPa}\hspace{0.17em}{\mathrm{day}}^{-1}$ and ${\beta }_e=0.3\hspace{0.17em}\mathrm{mm}\hspace{0.17em}{\mathrm{day}}^{-1}$, the computational model predictions were largely consistent with the biomarkers found in PAH. Haemodynamics, geometrical and microstructural quantities during remodelling as simulated by the model are tabulated in table 2.

3.2.1. Remodelling phase up to day 250

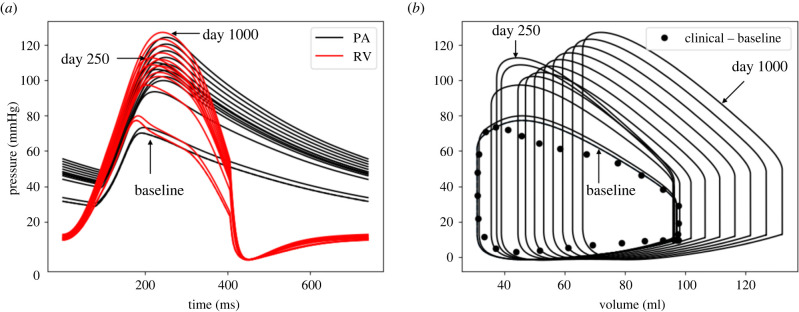
Specifically, pulmonary arterial pressures were increased in response to the prescribed elevation of distal pulmonary resistance and reduction in compliance starting at day 50. By day 250, mPAP, sPAP and PAPP were increased with respect to their original value at $s=0$ by 53.4%, 56.7% and 61.8%, respectively (figure 5a). There was no significant change in RVEDV, whereas RVSV was reduced by 11.2% during this period (figure 5b). As a result, RVEF was decreased by 10.4% at day 250. Right ventricular wall thickness was also increased by 36.6% during this period (figure 6a).

Figure 5.

The evolution of (a) pressure waveforms of RV and PA, and (b) RV pressure-volume loop over 1000-day period. From day 0 (baseline) to 250, the PA and RV pressures are elevated and RVEDV does not alter significantly. From day 250 to 1000 with drop in RV contractility and increase in TBV, RVPSP, RVEDP and RVEDV increases that mimic the decompensated phase of PAH.

Figure 6.

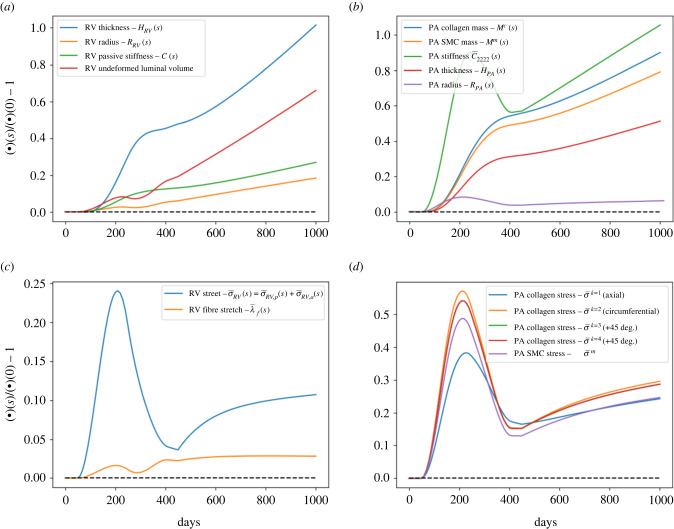
The PAH-induced changes in PA and RV for a period of 1000 days: (a) RV remodelling. Thickness increases to mimic concentric hypertrophy, undeformed radius and luminal volume increase after 250 days to mimic the eccentric hypertrophy of RV. (b) PA remodelling. Up to day 250, associated with increase in PVR and from day 450 due to increase in TBV, the PA mass thus thickness increases. PA stiffness, however, decreases due to drop in pressure associated with reduction in RV contractility after day 250. (c) RV fibre stress and (d) PA constituents stress. Stress and stretch for both RV and PA increase due to PVR elevation but significantly reduces due to adaptation to minimize the deviation from the reference stress and stretch.

In the PA, elevation of stress in the tissue constituents led to an increase in the collagen and SMC mass at day 250 by 34.6% and 31.8%, respectively (figure 6b–d). The increase in collagen and SMC mass produced a thicker PA wall (thickness increased by 20.1% at day 250). The elevation in PA pressure also caused a dilation in the chamber (7.9% larger radius in PA at day 250 compared with its value at day 0). Correspondingly, PA (circumferential) stiffness was increased by 89.7% at day 250, reducing the PA compliance by 46.7%.

3.2.2. Remodelling phase from day 250 to 1000

Superimposing the changes in distal pulmonary vascular resistance and compliance with a reduction in RV contractility starting at day 250 led to a reduction in PA pressure over a 150-day period (until day 400) (7% in mPAP, 9% in sPAP and 11% in PAPP) (figure 5a). The subsequent increase in TBV starting at day 450 led to a progressive increase in PA pressure. At day 1000 (termination of the simulation), mPAP, sPAP and PAPP were increased with respect to their original value by 76.2%, 79.2% and 83.8%, respectively. On the other hand, RVEDV was increased by 38.0% at day 1000 (figure 5b) accompanied by an RV overstretch (figure 6c). This led to a further decrease in RVEF from 68.2% (day 0) to 49.9% (day 1000). RVPSP and RVEDP both continued to increase and were, respectively, 66.4% and 31.4% larger than their original values (figure 5b). The RV wall also continued to thicken, and its intrinsic passive stiffness was elevated by 26.9% at day 1000 (figure 6a).

In the PA, collagen and SMC mass continued to increase, albeit at a slower rate immediately after a reduction in RV contractility. At day 1000, collagen and SMC mass were, respectively, 90.0% and 79.1% higher than their original value (figure 6b). Because of a reduction of mPAP accompanying the reduction in RV contractility immediately at day 250, PA stiffness (circumferential) was reduced initially at day 250 due to nonlinearity of its stress–strain relationship. The stiffness, however, progressively increased and was 105.6% larger than its original value at day 1000 (figure 6b).

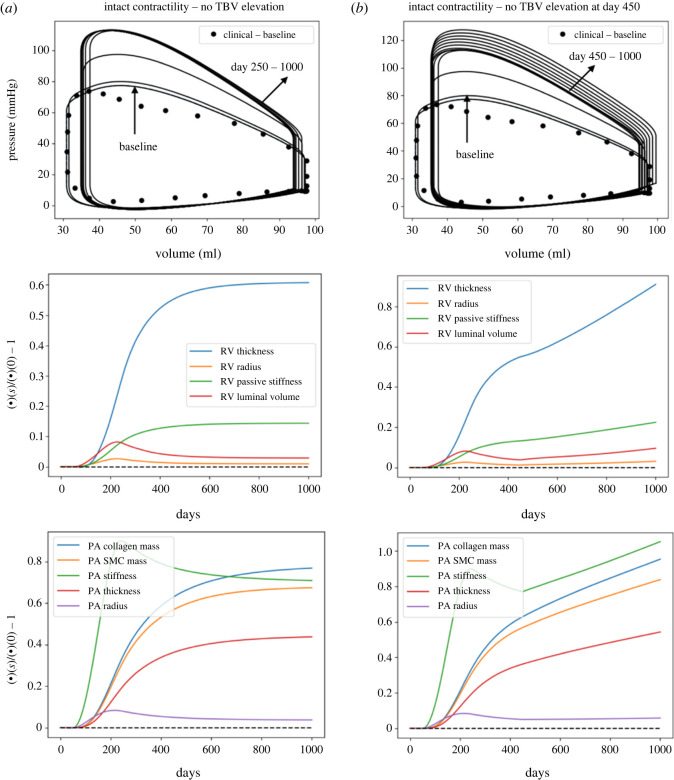
To show that the RV long-term dilation is associated with both a reduction in RV contractility from day 250 to 400 and an elevation of TBV elevation from day 450 to 1000, we also performed simulations where both RV contractility and/or TBV remained unchanged. Results from the simulations show that RV hypertrophy was largely concentric for the entire simulation duration with negligible change in the RVEDV and a large increase in RV undeformed thickness (approx. 62.2%) when both RV contractility and TBV remained unchanged (figure 7a). When only TBV was elevated with intact RV contractility, the dilation of RV was small (2.6% increase in RVEDV) and RV undeformed thickness was increased by 97.3% (figure 7b).

Figure 7.

The PAH progression predicted by the computational framework when the RV contractility remains unaltered during the process. RV remains in a concentric hypertrophy phase when RV contractility does not alter with (a) no TBV elevation and (b) TBV elevation at day 450.

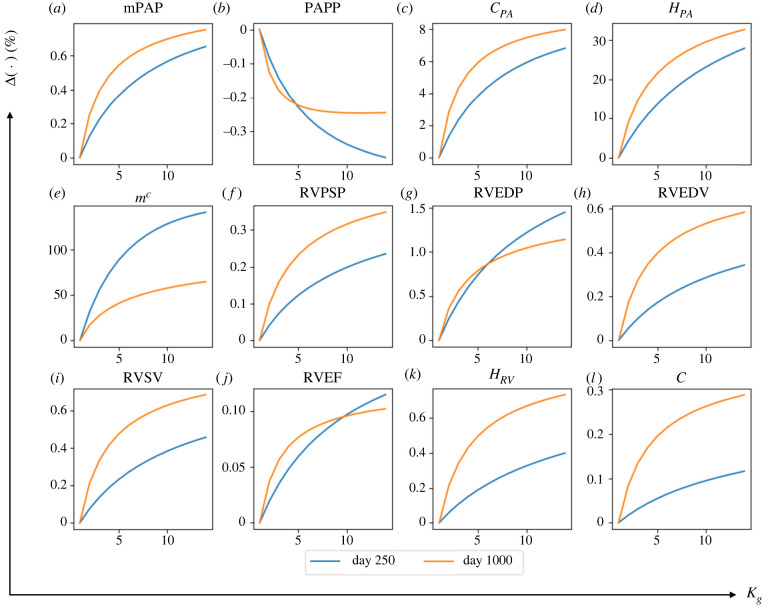
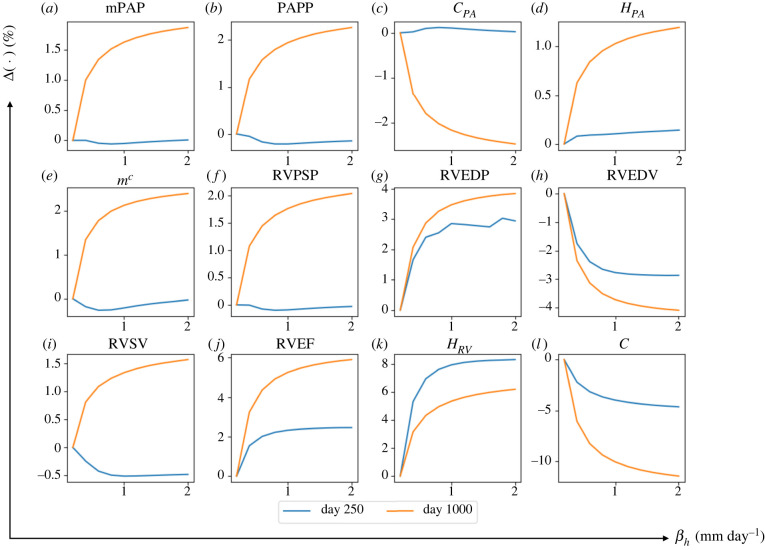
3.3. Sensitivity analysis

Local sensitivity analysis was performed on the rate constants ($p_i={\beta }_e$, ${\beta }_f$, ${\beta }_h$ and $K_g^{\alpha }$) regulating the G&R processes in the heart and vasculature. The sensitivity of quantities related to the geometry and haemodynamics of the PA and RV with respect to these rate constants are given in table 3. Here, we present results of two parameters (${\beta }_e$, ${\beta }_f$) that G&R is most sensitive to. Results of the other two parameters (${\beta }_h$, $K_g^{\alpha }$) are described in the appendices D and E.

Table 3.

Elementary effects of the rate constants on the outputs of the computational framework.

	day	$K_g^{\alpha }$	${\beta }_{\mathrm{h}}$	${\beta }_{\mathrm{e}}$	${\beta }_{\mathrm{f}}$
mPAP	250	5.19 × 10−4	1.22 × 10−5	0.00643	−0.00607
	1000	6.32 × 10−4	0.00237	−0.0118	−0.0122
PAPP	250	−3.01 × 10−4	−1.68 × 10−4	0.0134	−0.00992
	1000	−2.19 × 10−4	0.00286	0.00184	−0.0206
$C_{PA}$	250	5.40 × 10−4	2.88 × 10−5	−0.00894	0.0109
	1000	6.73 × 10−4	−0.00316	0.0197	0.0233
$H_{PA}$	250	0.0219	1.87 × 10−4	0.00239	−0.00213
	1000	0.0269	0.00152	−0.00453	−0.00909
$m^c$	250	0.113	−1.01 × 10−4	0.0160	−0.0137
	1000	0.0528	0.00309	−0.0216	−0.0168
$m^m$	250	0.0992	−1.26 × 10−4	0.0165	−0.0139
	1000	0.0429	0.00304	−0.020	−0.0167
$M^c$	250	0.0369	2.82 × 10−4	0.00359	−0.00322
	1000	0.0426	0.00208	−0.00653	−0.0125
$M^m$	250	0.0328	2.77 × 10−4	0.00356	−0.00315
	1000	0.0353	0.00201	−0.00562	−0.0122
RVPSP	250	1.85 × 10−4	−2.64 × 10−5	0.00917	−0.00772
	1000	2.87 × 10−4	0.00259	−0.00611	−0.0159
RVEDP	250	1.14 × 10−4	0.00373	−0.0287	0.00773
	1000	9.51 × 10−5	0.00490	−0.101	0.0177
RVEDV	250	2.69 × 10−4	−0.00374	0.0301	−0.00523
	1000	4.83 × 10−4	−0.00528	0.0992	−0.0140
RVSV	250	1.27 × 10−4	−6.00 × 10−4	0.0143	−0.00823
	1000	5.70 × 10−4	0.00199	0.00654	−0.0185
RVEF	250	9.06 × 10−5	0.00322	−0.0134	−0.00337
	1000	8.69 × 10−5	0.00755	−0.0639	−0.00619
$H_{\mathrm{RV}}$	250	3.12 × 10−4	0.0110	0.00763	−0.00362
	1000	6.06 × 10−4	0.00783	0.00893	−0.0123
$C$	250	9.07 × 10−5	−0.00579	0.00222	0.0539
	1000	2.38 × 10−4	−0.0146	0.00352	0.109

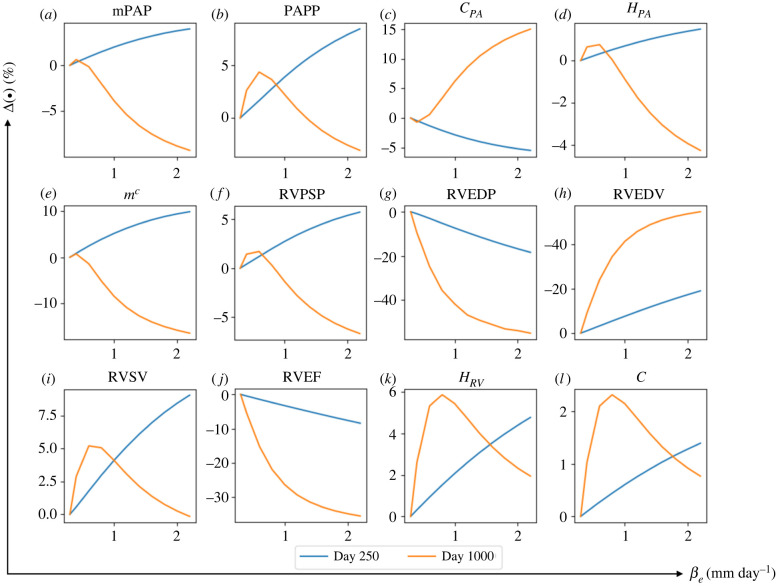
3.3.1. Effect of ${\beta }_{\mathrm{e}}$ that controls right ventricle long-term dilation

Increasing ${\beta }_{\mathrm{e}}$ from its baseline value of 0.3 to 2.2 mm day⁻¹ while fixing other rate constants at their baseline value produced a substantially larger increase in RVEDV (day 250: +17.7% and day 1000: +53.5%). This led to a substantial reduction in RVEF (day 250: −10.1% and day 1000: −36.7%) (figure 8). The effect of ${\beta }_{\mathrm{e}}$ on RVEDV was more substantial with a higher averaged elementary effect (${\overline{\mathrm{EE}}}_{{\beta }_{\mathrm{e}},\mathrm{RVEDV}}=0.0992$ at day 1000) compared with other geometrical quantities (table 3). Compared with RVEDV, RV wall thickness and intrinsic passive stiffness were not significantly affected by the increase in ${\beta }_e$, but nonetheless, exhibit a non-monotonic behaviour with respect to ${\beta }_{\mathrm{e}}$. For small values of ${\beta }_{\mathrm{e}}$ (0.3 < ${\beta }_{\mathrm{e}}$ < 0.8 mm day⁻¹), RV dilation was accompanied with more RV wall thickening and passive stiffening. With larger ${\beta }_{\mathrm{e}}$ (${\beta }_{\mathrm{e}}$ > 0.8 mm day⁻¹), however, this trend was reversed, where RV dilation was accompanied by a reduction in RV wall thickness and passive stiffness. In terms of RV pressure, increasing ${\beta }_{\mathrm{e}}$ to 2.2 mm day⁻¹ produced only a moderate change in RVPSP, but led to a substantial decrease in RVEDP (day 250: +19.5% and day 1000: +54.9%). The effect of ${\beta }_{\mathrm{e}}$ on RVEDP was also substantial (${\overline{EE}}_{{\beta }_{\mathrm{e}},\mathrm{RVEDV}}=-0.101$) compared with other haemodynamics quantities.

Figure 8.

The changes in major haemodynamics and structural factors of PA and RV in response to increasing rate constant controlling the RV long-term dilation, ${\beta }_{\mathrm{e}}$. By increasing ${\beta }_{\mathrm{e}}$ from its baseline value at ${\beta }_{\mathrm{e}}=0.3$ to β_e = 2 mm day⁻¹, RVEDP and RVEDV respectively decrease and increase up to 50%. RVEDP and RVEDV are more sensitive to ${\beta }_{\mathrm{e}}$ compared with other predicted output of the computational framework.

Concerning G&R in the PA, increasing ${\beta }_{\mathrm{e}}$ produced a substantial increase in the chamber compliance at day 1000 (+14.9%) which was moderately reduced at day 250. Mean pulmonary arterial pressure, mPAP and PA thickness were all moderately increased at day 250 and reduced at day 1000 (less than 10% change) with increasing ${\beta }_{\mathrm{e}}$.

3.3.2. Effect of ${\beta }_f$ that controls right ventricle passive stiffness

Increasing ${\beta }_f$ from its baseline value of 0.002 to 0.05 MPa day⁻¹ with other rate constants fixed at their baseline values produced a large increase in RV passive stiffness, which was elevated by 3.46-fold at day 1000 (${\overline{EE}}_{{\beta }_f,C}=0.109$) (figure 9). An increase in ${\beta }_f$ also produced substantial decrease in RVPSP and increase in RVEDP. At its largest value (${\beta }_f=0.05\hspace{0.17em}\mathrm{MPa}\hspace{0.17em}{\mathrm{day}}^{-1}$), RVPSP was 34.6% lower while RVEDP was 38.0% higher at day 1000 compared with their original value. Right ventricular end-diastolic volume, RVEF and RV wall thickness were also substantially reduced with increasing ${\beta }_f$ (RVEDV: −29.9%; RVEF: −15.5% and RV thickness: −26.9% at day 1000 with ${\beta }_f=0.05\hspace{0.17em}\mathrm{MPa}\hspace{0.17em}{\mathrm{day}}^{-1}$).

Figure 9.

The changes in major haemodynamics and structural factor in response to increasing rate constant controlling RV passive stiffening ${\beta }_{\mathrm{f}}$. The most sensitive output to stiffening ${\beta }_{\mathrm{f}}$ is RV passive stiffness that increases by two fold with increasing it from its baseline ${\beta }_{\mathrm{f}}=0.002$ to β_f = 0.05 MPa day⁻¹.

In the PA, increasing ${\beta }_f$ resulted in a substantial decrease in mPAP, PAPP and PA thickness, which were, respectively, reduced by 26.7%, 45.2% and 20.3% at day 1000 when ${\beta }_f$ was at its largest value of 0.05 MPa day⁻¹. As a result, PA compliance was substantially increased with increasing ${\beta }_f$ (+51.9% at day 1000).

4. Discussion

The key novelty of this computational framework is the consideration of ventricular–vascular G&R coupling/interaction occurring between both the pulmonary vasculature and the RV in a closed-loop circulation over a long timescale. Calibrated with clinical measurements from a paediatric patient with idiopathic PAH, the model was applied to predict disease progression associated with a sequential reduction of the lumen diameter and compliance of the small distal pulmonary vasculature [2], followed by a reduction in the RV myocardial contractile function [30] and a subsequent increase in TBV [31]. The calibrated model can reproduce primary features associated with the progression of PAH, such as upregulation of PA tissue constituents and stiffening [33], PA dilation [34], RV muscular hypertrophy [35], RV dilation [10], elevated RVEDP [25] and reduced RVEF [4]. The computational framework presented here serves as a foundation for future development of a more comprehensive and predictive G&R modelling framework with realistic heart and vascular geometries.

Based on the results of the computational framework, the key findings are as follows: (i) RV dilation is mainly associated with a reduction in contractility (figures 5b, 6a and 7) and is moderately associated with the increase in TBV (figure 7); (ii) RV concentric remodelling is largely driven by the remodelling of the distal pulmonary vessels (figures 6a and 7) while PA remodelling is sensitive to both remodelling of the distal pulmonary vessels as well as the RV (figures 6b and 7); (iii) increasing the rate constant ${\beta }_{\mathrm{e}}$, which controls eccentric hypertrophy and accelerates RV dilation (figure 8h), decreases RVEF (figure 8j) and RVEDP in PAH (figure 8g); (iv) increasing the rate constant ${\beta }_f$ controlling myocardial passive stiffening led to larger increase in RVEDP (figure 9g) and smaller increase in RVEDV (figure 9h); (v) increasing ${\beta }_{\mathrm{e}}$ and ${\beta }_f$ resulted in a smaller increase in PA pressure (figures 8a and 9a) that,in turn, produces a smaller upregulation of the PA mass (figures 8e and 9e).

4.1. Growth and remodelling in pulmonary arterial hypertension

Unlike existing models that describe the arterial G&R in isolation from the heart [20] or ventricular G&R in isolation from the arteries [36,37], the computational framework developed here considers concurrent ventricular–vascular G&R and their interactions. Specifically, G&R of the PA and RV were described simultaneously by a constrained mixture model and classical constitutive relations of concentric and eccentric hypertrophy, respectively. The choice of G&R constitutive model for PA and RV is based largely on precedent studies. Vascular G&R is frequently modelled using stress-mediated constrained mixture-based two-dimensional models [38] as described here. The focus of these models is largely on mass production and turnover of the tissue constituents (e.g. collagen, SMC and elastin). Conversely, ventricular G&R is frequently modelled using a volumetric growth framework [7–39] that focuses on the geometrical changes of cells/organs stemming from the historical classification of cardiac hypertrophy into concentric and eccentric phenotypes [7]. The probable reason for this focus is that adult cardiac myocytes, which accounts for the bulk of cardiac tissue, are terminally differentiated and non-regenerative (unlike most of the arterial tissue constituents) [40].

Initiated by an elevation and reduction of the distal pulmonary vascular resistance and compliance that are hallmarks of PAH [2–33], the model predicts an acceleration in vascular ECM and SMC mass production in the large PA, which resulted in the thickening of its wall. The upregulation of ECM and SMC production in the large PAs due to these changes in the distal arteries agrees with animal studies of PAH. Specifically, the modelling framework prediction that PA collagen mass is increased by 90% over a 1000-day period (table 4) agrees with the 98% increase in the collagen content found in the PAs of hypoxic mice [41], and the approximately 110% increase in the collagen content found in the PAs of monocrotaline (MCT)-induced PAH rats [42]. Moreover, the choice of four-fibre family constitutive model (with different mass fraction associated with each family) for modelling the collagen mechanical behaviour implies that the PA possesses an anisotropic mechanical behaviour that is described as follows. First, although the PA length was fixed, the axial stress (${\sigma }^{\kappa =1}$) is not zero (10%−30% lower than the circumferential stress ${\sigma }^{\kappa =2}$) (figure 6d). A contribution to the axial stress is the stressed oblique fibres oriented in the +45° and −45° direction (${\sigma }^{\kappa =3,4}$). Second, the collagen mass distribution was considered such that the oblique fibres had more mass compared with those in axial and circumferential directions. This mass allocation agrees with the observation in a previous study [43], where the vascular tissue is more fibrous in the oblique directions and retains the same fibre orientation under the inflation test. Additionally, each constituent is assumed to be synthesized under a pre-existing stretch ($G_h^{\alpha }$) that is defined by a mapping from a stress-free configuration to an in vivo configuration. Therefore, an unloaded artery (with removal of pressure) is not stress-free because of the prescribed deposition stretch. This is also observed when a radial cut on a cylindrical artery causes it to ‘open up’ and to produce an opening angle [44].

Table 4.

The haemodynamic evolution and remodelling of the PA and RV on day 250 and 1000.

		day 0 (time baseline)	day 250	day 1000
PA	mPAP (mmHg)	42.5	65.2	74.9
	sysPAP (mmHg)	73.3	110	126
	PAPP (mmHg)	46.2	67.0	76.2
	PA Compliance (ml mmHg−1)	0.213	0.114	0.098
	collagen mass (kg mm−2)	3.76 × 10−7	5.06 × 10−7	7.14 × 10−7
	SMC mass (kg mm−2)	2.68 × 10−7	3.54 × 10−7	4.80 × 10−7
	deformed thickness (mm)	1.02	1.23	1.55
	deformed radius (mm)	13.5	14.6	14.4
	stiffness ${\mathcal{C}}_{2222}$ (MPa mm)	0.362	0.689	0.746
RV	RVEDV (ml)	97.2	96.3	134
	RVSV (ml)	66.3	58.9	67.0
	RVEF (%)	68.2	61.1	49.9
	RVPSP (mmHg)	77.3	113	129
	RVEDP (mmHg)	10.2	10.8	13.4
	deformed thickness (mm)	8.1	11.1	17.5
	luminal volume (ml)	61.5	66.3	102
	intrinsic passive stiffness (MPa)	0.7 × 10−3	0.759 × 10−3	0.888 × 10−3

Together with the elevation of the pressure, the PA stiffens as a result of both tissue remodelling (ECM deposition or muscularization) and strain-induced stiffening [33]. The computational framework considers both stiffening mechanisms, which occur in the long (remodelling) and short (stretch during the cardiac cycle) timescales. In addition, the framework also predicts a dilation of the PA by 7.9% that is consistent with observations in the clinic [34], where PAH patients developed a 6% increase in PA diameter during a 942-days mean follow-up time and had significantly larger PA diameter compared with the control subjects. In the RV where wall thickness (concentric hypertrophy) is prescribed to depend on wall stress [45], the wall thickens as a result of the elevation in systolic pressure in both the PA and RV. Without any reduction in contractility, the wall thickens without a significant dilation of the chamber. Right ventricular EF was preserved also during this phase of remodelling. These changes are consistent with clinical observations showing that the RV initially adapts by increasing its active forces via muscular hypertrophy (similar to systemic hypertension) to preserve cardiac output and match the arterial load in PAH [30]. These features are similar to what is widely referred to as the ‘compensated’ phase of the remodelling process, when the heart is ‘coupled’ with its load [6–10]. Our model prediction of RV wall thickening by 36% with a relatively small increase in RVEDV is consistent with animal models of PAH at the early to intermediate stages, where RV wall thickens in MCT-induced PAH rats by 21%–29% after four weeks [46,47] and in Sugen/hypoxic rats by approximately 20% with just a slight increase in the RV end-diastolic diameter [48].

With a reduction in RV contractility prescribed in the model, however, overstretching of the muscle fibre occurs in the wall that in turn, causes long-term dilation of the chamber (eccentric hypertrophy) that persists indefinitely. This behaviour is similar to the ‘decompensated’ phase of the G&R process, where the RV chamber becomes dilated and is ‘uncoupled’ with its arterial load [6–10]. We note that without a reduction in RV contractility, RVEDV would remain relatively unchanged in the model (figure 7). While several factors are hypothesized to control the transition from the compensated to decompensated phase in cardiac remodelling (e.g. generic factors and neurohormonal activation [30]), our model prediction suggests that impaired myocardial contractile function, which may occur due to an imbalance of myocardial supply and demand, is a cause for this transition, as suggested in some studies [49–51].

The long-term dilation results in progressive increase of RVEDV with relatively preserved RVSV that led to a reduction in RVEF from 61.1% to 49.9%. This degree of reduction is consistent with the clinical studies of adult PAH patients [4] (RVEF: 63% in control subjects versus 42% in patients) and paediatric PAH patients [52] (RVEF: 58% in control subjects versus 46% in patients). Accompanying the RV dilation is a further increase in RV wall thickness, which together with the increase in myocardial passive stiffness (driven by stress in the model) led to a substantially higher RVEDP. The 31.4% increase in RVEDP predicted by the model (10.2 mmHg at day 0 and 13.4 mmHg at day 1000) is within the range of the reported RVEDP in PAH patients (6.8 mmHg in the control patients, 7.4 mmHg in mild patients and 10.7 in severe patients) [53]. Also, the 26.9% increase in the RV passive stiffness predicted by the model is comparable to the 21%–36% increase in the linearized stiffness calculated from the RV diastolic pressure-volume relationship measured in PAH patients [53].

A reduction in myocardial contractility also led to an immediate reduction in RV and PA systolic pressure, which progressively increases and becomes substantially elevated when compared to the compensated phase. As a result, PA stiffness is initially reduced over a period of approximately 200 days, but progressively increases with the accumulation of collagen and SMC mass in the PA. At day 1000, the constituent's mass and PA stiffness are all elevated compared with that prior to the initiation phase of remodelling (up to day 200).

4.2. Effects of growth and remodelling rate constants

Through a local sensitivity analysis, we found that increasing the rate constant ${\beta }_f$ that controls the rate of change in RV passive stiffening will lead to a reduction in RV thickening during remodelling. There are two possible explanations for this behaviour. First, because RV wall thickness and passive tissue stiffness are controlled by stress-mediation in the computational model, a higher rate of change in RV passive stiffness will reduce the deviation in stress from the reference value, which in turn, will lead to a lower rate of change in the RV wall thickness. Second, increasing ${\beta }_f$ leads to more RV passive stiffening that, as a result, caused less RV filling and reduces the RV systolic pressure and stresses. The reduction in pressure and stresses, in turn, produces less RV thickening. Such an inverse relationship between RV wall thickness and passive tissue stiffness has been observed in a clinical study by Gomez-Arroyo et al. [35], where patients with idiopathic PAH have significantly less RV thickening compared with patients with Eisenmenger's syndrome who exhibit less RV fibrosis (suggesting lower tissue passive stiffness) than idiopathic PAH patients.

Increasing ${\beta }_f$ also reduces RV dilation (as indexed by RVEDV) because the corresponding increase in RV passive stiffness prevents the tissue from overstretching when its contractility is reduced. Besides affecting RVEDV, increasing ${\beta }_f$ also results in a lower RVSV and RVEF, and a higher RVEDP. This is consistent with the inverse correlation between RVSV and RV passive stiffness, which are both associated with an elevated RVEDP in a clinical study by Rain et al. [25]. An inverse correlation between RVEF and RV passive stiffness was also observed in another clinical study on PAH patients [4].

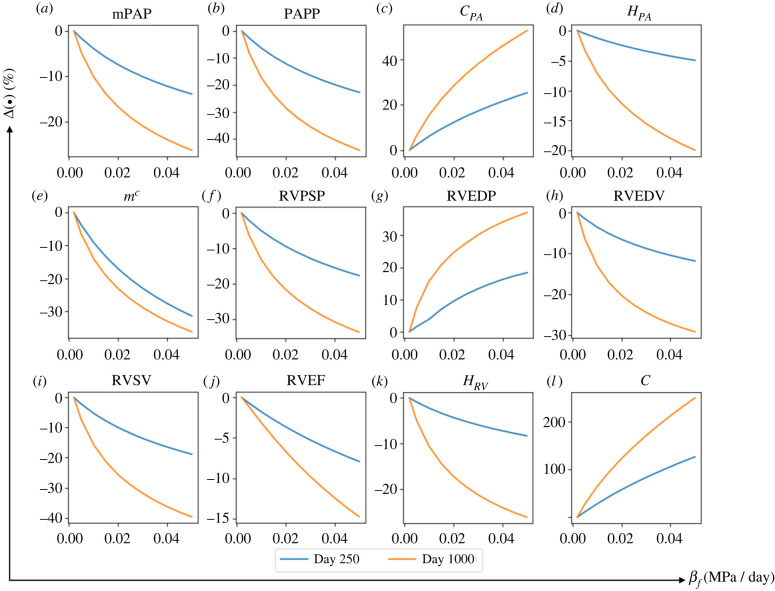
Other than the RV, ${\beta }_f$ also affects PA remodelling due to its effects on RV systolic and PA pressure. With increasing ${\beta }_f$, the increase in PA pressure is less and results in a lower upregulation of the constituents' mass and less stiffening. We note that the reduction in stiffening could be due to a lower PA pressure elevation and a lower mass upregulation.

By contrast to ${\beta }_f$, increasing the rate constant ${\beta }_e$ accelerates RV dilation during remodelling, which is associated with eccentric hypertrophy that typically occurs in the later stage of the progression of PAH [45]. An increase in RVEDV is a strong predictor of RV failure [3]. We found that ${\beta }_e$ is the only rate constant controlling RVEDV. Compared with RVEDV, RVSV was largely insensitive to an increase in ${\beta }_{\mathrm{e}}$, and as a result, the decrease in RVEF is larger with increasing ${\beta }_{\mathrm{e}}$. Furthermore, the rate constant ${\beta }_{\mathrm{e}}$ has a small effect on RVSP. An increase in ${\beta }_{\mathrm{e}}$ produces a slight reduction in RVSP and PA pressure that leads to a smaller upregulation of tissue constituents’ mass, which in turn, leads to a small increase in PA compliance.

Increasing the rate constant ${\beta }_{\mathrm{h}}$ only leads to a slightly larger increase in RV wall thickness and a lower increase in RV passive stiffness at day 1000, which have minimal effects on the PA. Conversely, the rate constants $K_g^{\alpha }$ affect the PA, in which an increase in its value accelerates collagen mass production (figure 10e) that resulted in higher PA mass and thickness as found in previous studies [54]. In a logic-based framework, Irons and Humphrey [55] modelled the changes in intramural cell phenotypes and extracellular matrix turnover in response to various inputs, including pressure elevation through several pathways. By contrast to their logic-based work, the computational study here directly connects the pressure-induced wall stress to the PA mass through $K_g^{\alpha }$ regardless of the pathways. The end result, however, shows the severity of PA remodelling due to PAH (figure 10e).

Figure 10.

The changes in major haemodynamics and structural factor in response to increasing rate constant controlling PA remodelling, $K_g^{\alpha }$. Increasing this rate constant from its baseline value $K_g^{\alpha }=1$ up to $K_g^{\alpha }=12$ results in an accelerated mass production of collagen which accelerates the thickening of PA.

4.3. Model limitations

There are some limitations associated with this study. First, the study is based on the geometry and haemodynamics data of only one patient (n = 1), and the rate constants were calibrated based on qualitative clinical observations. Longitudinal data from the same patient (that is not available here) can be used to better calibrate the rate constants. The application of this model to datasets from more patients (n > 1) will also enable us to investigate the variation of model parameters and how they may be related to the severity of PAH. Second, we have only compared our model's prediction of collagen with measurements from PAH animal model in the literature [56]. This is because studies reporting the collagen content in human PA during progression of PAH are limited. To the best of our knowledge, the available data are limited to the cadaveric studies reporting intimal and adventitial thickening of the PA due to primary pulmonary hypertension [57], and the degree of fibrosis in the large PAs of pulmonary hypertension patients with congenital heart diseases [58]. Third, mass density and mass removal rate in the PA G&R was estimated by those used for systemic arteries in the literature [20], due to the lack of such data in the PA. To the best of our knowledge, the values of the above parameters have not been reported for PA in the literature. Fourth, residual stress in the RV was not considered. While it is clear that residual stresses are present in the LV [59] (though it is smaller than that found in the arteries), it is not quite clear if residual stress is also present in the RV. As such, we have ignored this in the model. Fifth, the computational framework does not consider regional G&R in the RV (e.g. RV free wall versus septum) and the PA (e.g. main, left and right PA). This issue can be addressed in future studies coupling FE models of the PA and RV [27].

5. Conclusion

We developed and validated a multi-temporal scale computational framework to simulate PAH progression. The framework models G&R processes occurring concurrently in both RV and PA, which are bi-directionally coupled and interact with each other in the cardiopulmonary circulation. Incorporating G&R of RV and PA in the circulatory system enabled us to mimic the haemodynamics evolution associated with PAH as well as the effect of different compartments on each other that cannot be addressed in studies where G&R of cardiopulmonary compartments are modelled in isolation. A sensitivity analysis was also performed on rate constants in the computational framework governing the G&R processes. This analysis suggests that the rate constants governing RV G&R affect the PA remodelling more than the reverse. The computational framework presented here will serve as a basis for future development of a more realistic G&R computational framework using high-resolution finite-element models of the heart and pulmonary arteries chambers to predict regional changes associated with PAH.

Appendix A. Closed loop cardiopulmonary circulation model

The governing equations of the closed-loop system (volume conservation) at a certain day (s) are given as follows,

$${\displaystyle \frac{\mathrm{d}{V}_{\mathrm{RV}}(s,t)}{\mathrm{d}t}=q_{\mathrm{cv}}(s,t)-q_{\mathrm{pv}}(s,t),}$$ A 1

$${\displaystyle \frac{\mathrm{d}{V}_{\mathrm{PA}}(s,t)}{\mathrm{d}t}=q_{\mathrm{pv}}(s,t)-q_{\mathrm{PA}}(s,t),}$$ A 2

$${\displaystyle \frac{\mathrm{d}{V}_{\mathrm{cp}}(s,t)}{\mathrm{d}t}=q_{\mathrm{PA}}(s,t)-q_{\mathrm{cp}}(s,t)}$$ A 3

$$\mathrm{and}{\displaystyle \frac{\mathrm{d}{V}_{\mathrm{cv}}(s,t)}{\mathrm{d}t}=q_{\mathrm{cp}}(s,t)-q_{\mathrm{cv}}(s,t).}$$ A 4

In equations (A 1)–(A 4), $V_{\mathrm{\Gamma }}$, $\mathit{\Gamma }=\mathrm{PA},\mathrm{RV},\mathrm{cp},\mathrm{cv}$ are the instantaneous volumes of each compartment with the subscripts denoting the RV, PA, distal arterial and venous vessels, respectively. Accordingly, $q_{\mathrm{pv}}$, $q_{\mathrm{PA}}$, $q_{\mathrm{cp}}$ and $q_{\mathrm{cv}}$ are the flow rates connecting each cardiopulmonary segment (figure 1).

The flow rates depend on the difference between its inlet and outlet pressures (i.e. pressure gradient), as well as its prescribed flow resistance

$$q_{\mathrm{pv}}(s,t)=\{\begin{array}{c}{\displaystyle \frac{P_{\mathrm{RV}}(s,t)-P_{\mathrm{PA}}(s,t)}{R_{\mathrm{pv}}}\hspace{0.17em}\hspace{0.17em}\mathrm{when}\hspace{0.17em}{P}_{\mathrm{RV}}\ge P_{\mathrm{PA}}}\hfill \\ 0\hspace{0.17em}\mathrm{when}\hspace{0.17em}{P}_{\mathrm{RV}}<P_{\mathrm{PA}},\hfill \end{array}$$ A 5

$$q_{\mathrm{PA}}(s,t)={\displaystyle \frac{P_{\mathrm{PA}}(s,t)-P_{\mathrm{cp}}(s,t)}{R_{\mathrm{PA}}},}$$ A 6

$$q_{\mathrm{cp}}(s,t)={\displaystyle \frac{P_{\mathrm{cp}}(s,t)-P_{\mathrm{cv}}(s,t)}{R_{\mathrm{cp}}}}$$ A 7

$$\mathrm{and}{q}_{\mathrm{cv}}(s,t)=\{\begin{array}{c}{\displaystyle \frac{P_{\mathrm{cv}}(s,t)-P_{\mathrm{RV}}(s,t)}{R_{\mathrm{cv}}}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\mathrm{when}\hspace{0.17em}{P}_{\mathrm{cv}}\ge P_{\mathrm{RV}}}\hfill \\ 0\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\mathrm{when}\hspace{0.17em}{P}_{\mathrm{cv}}<P_{\mathrm{RV}}.\hfill \end{array}$$ A 8

In equations (A 5)–(A 8), $R_{\mathrm{pv}}$, $R_{\mathrm{PA}}$, $R_{\mathrm{cp}}$ and $R_{\mathrm{cv}}$ are the resistances corresponding to flow rates connecting the cardiopulmonary segments, $P_{\mathrm{RV}}$, $P_{\mathrm{PA}}$, $P_{\mathrm{cp}}$ and $P_{\mathrm{cv}}$ are the pressure of RV, PA, and distal arterial and venous vessels, respectively.

Pressure in distal vessels is related to its instantaneous volume by a prescribed compliance that is defined as

$$P_{\mathrm{cp}}(s,t)={\displaystyle \frac{V_{\mathrm{cp}}(s,t)-V_{\mathrm{cp},r}}{C_{\mathrm{cp}}}}$$ A 9

and

$$P_{cv}(s,t)={\displaystyle \frac{V_{cv}(s,t)-V_{cv,r}}{C_{cv}},}$$ A 10

where $V_{\mathrm{cp},r}$ and $V_{\mathrm{cv},r}$ are the prescribed constant resting volumes, and $C_{\mathrm{cp}}$ and $C_{\mathrm{cv}}$ are the prescribed total compliance of distal (arterial and venous) compartments.

Appendix B. Pulmonary artery constitutive formula and constituents

B.1. Kinematics

For a constituent $\alpha$ that is synthesized at time $\tau \in [0,s]$, the deformation gradient corresponding to the mapping from its natural stress-free configuration can be described as

$${\mathit{\text{F}}}_n^{\alpha }(\tau ,s,t)=\mathit{\text{F}}(s,t){\mathit{\text{F}}}^{-1}(\tau ,0){\mathit{\text{G}}}_h^{\alpha }(\tau ),$$ B 1

where ${\mathit{\text{G}}}_h^{\alpha }(\tau )$ is the deposition deformation gradient of the constituent $\alpha$, produced at time $\tau$ and $\mathit{\text{F}}(s,t)$ is the deformation gradient tensor of the mixture from the PA's unloaded cardiac configuration at time t of the cardiac cycle on day s. For further descriptions of the configurations and mapping associated with the theory of constrained mixture, refer to [20]. Based on the deformation gradient tensor in equation (B 1), the local stretch of constituent $\alpha$ oriented in direction $\kappa$ is obtained by

$${\lambda }_{n,\kappa }^{\alpha }(\tau ,s,t)={[C_{n,\kappa }^{\alpha }(\tau ,s,t)]}^{1/2}={[{\mathit{\text{M}}}^{(\kappa )}\cdot C_n^{\alpha }(\tau ,s,t){\mathit{\text{M}}}^{(\kappa )}]}^{1/2},$$ B 2

where ${\mathit{\text{C}}}_n^{\alpha }(\tau ,s,t)$ is the right Cauchy-Green stretch tensor corresponding to the deformation in equation (B 2) and ${\mathit{\text{M}}}^{(\kappa )}$ is the unit vector along the direction $\kappa$ in the reference configuration. This vector is described by ${\mathit{\text{m}}}^{(\kappa )}={\mathit{\text{F}}}_n^{\alpha }(\tau ,s,t){\mathit{\text{M}}}^{(\kappa )}/{\lambda }_{n,\kappa }^{\alpha }(\tau ,s,t)$ in the current configuration. In a cylindrical coordinates system, with incompressibility of the vascular tissue

$$\mathit{\text{F}}(s,t)=\mathrm{diag}\left({\displaystyle \frac{1}{{\gamma }_{\mathrm{PA}}(s)}{[V_{\mathrm{PA}}(s,t)]}^{-1/2},{\gamma }_{\mathrm{PA}}(s){[V_{\mathrm{PA}}(s,t)]}^{1/2},1}\right),$$ B 3

where ${\gamma }_{\mathrm{PA}}(s)={\displaystyle \frac{1}{R_{\mathrm{PA}}(s)\sqrt{L_{\mathrm{PA}}}}}$g is an undeformed length scale invariant in short timescale.

B.2. Constituents’ mass

The total mass of constituent $\alpha$ per unit area of the reference configuration is obtained by

$$M^{\alpha }(s)=M^{\alpha }(0)Q^{\alpha }(s)+{\int }_0^s{m}^{\alpha }(\tau )q^{\alpha }(s-\tau )\mathrm{d}\tau ,$$ B 4

where $M^{\alpha }(s)$ is the mass of constituent $\alpha$ per unit reference configuration, $m^{\alpha }(\tau )$ is the rate of mass production per unit reference area, $Q^{\alpha }(s)$ is the fraction of the initial mass that still exists at the current time $s,$ and $q^{\alpha }(\tilde{\tau })$ is the survival function of the deposited mass at time $\tau$. The survival function is defined as follows with $k_q^{\alpha }$ denoting the rate of removal of the constituent,

$$q^{\alpha }(\tilde{\tau })=\exp \left[-{\int }_{\tau }^s{k}_q^{\alpha }(\tilde{\tau })\mathrm{d}\tilde{\tau }\right].$$ B 5

Total mixture mass is the summation of the mass of each constituent given by

$$M(s)=\sum _{\alpha }{M}^{\alpha }(s).$$ B 6

Equivalently, $M^{\alpha }(s)={\varphi }^{\alpha }(s)M(s)$ with ${\varphi }^{\alpha }(s)$ denoting the mass fraction of the constituent $\hspace{0.17em}\alpha$. Assuming that the overall mass density of PA wall remains constant and homogeneous, we can relate the mass density per unit area of the PA to its thickness knowing the mass density of the PA per unit volume as follows [17]:

$$H_{\mathrm{PA}}(s)={\displaystyle \frac{M(s)}{\rho }}$$ B 7

and

$$h_{\mathrm{PA}}(s,t)={\displaystyle \frac{M(s)}{\rho J(s,t)}.}$$ B 8

In equations (B 7) and (B 8), $H_{\mathrm{PA}}(s)$ and $h_{\mathrm{PA}}(s,t)$ are the PA undeformed and deformed thickness, respectively. $\rho$ is the overall mass density and $J(s,t)$ is the Jacobian of the deformation gradient $\mathit{\text{F}}(s,t)$.

With removal rate of the PA constituents ($k_q^{\alpha }$), we can obtain the basal mass production rate of each constituent,

$$m_b^{\alpha }=m^{\alpha }(s=0))={\displaystyle \frac{M^{\alpha }(s)}{{\int }_0^{\mathrm{\infty }}{q}^{\alpha }(\tilde{\tau })\mathrm{d}\tilde{\tau }}.}$$ B 9

B.3. Energy, stress and stiffness

Due to the continual production and removal of the mass of each tissue constituent, the strain energy density per unit reference area of constituent $\alpha$ is defined as

$$w^{\alpha }(s,t)=M^{\alpha }(0)Q^{\alpha }(s){\mathrm{\Psi }}^{\alpha }(C_n^{\alpha }(0,s,t))+{\int }_0^s{m}^{\alpha }(\tau )q^{\alpha }(s-\tau ){\mathrm{\Psi }}^{\alpha }(C_n^{\alpha }(\tau ,s,t))\mathrm{d}\tau ,$$ B 10

where ${\mathrm{\Psi }}^{\alpha }({\mathit{\text{C}}}_n^{\alpha }(\tau ,s,t))$ is the strain energy of the constituent per unit mass. Accordingly, the Cauchy stress resultant of each constituent,

$${\mathit{\text{T}}}^{\alpha }(s,t)=M^{\alpha }(0)Q^{\alpha }(s){\widetilde{\mathit{\text{T}}}}^{\alpha }(C_n^{\alpha }(0,s,t))+{\int }_0^s{m}^{\alpha }(\tau )q^{\alpha }(s-\tau ){\widetilde{\mathit{\text{T}}}}^{\alpha }({\mathit{\text{C}}}_n^{\alpha }(\tau ,s,t))\mathrm{d}\tau ,$$ B 11

where

$${\widetilde{\mathit{\text{T}}}}^{\alpha }({\mathit{\text{C}}}_n^{\alpha }(\tau ,s,t))={\displaystyle \frac{2}{J(s,t)}\mathit{\text{F}}(s,t){\displaystyle \frac{\mathrm{\partial }{\mathrm{\Psi }}^{\alpha }}{\mathrm{\partial }{C}_n^{\alpha }(\tau ,s,t)}{\mathit{\text{F}}}^T(s,t).}}$$ B 12

The corresponding stiffness is defined (in indicial notation) by

$${\mathcal{C}}_{ijkl}^{\alpha }(s,t)=M^{\alpha }(0)Q^{\alpha }(s){\tilde{\mathcal{C}}}_{ijkl}^{\alpha }(C_n^{\alpha }(0,s,t))+{\int }_0^s{m}^{\alpha }(\tau )q^{\alpha }(s,\tau ){\tilde{\mathcal{C}}}_{ijkl}^{\alpha }(C_n^{\alpha }(\tau ,s,t))\mathrm{d}\tau ,$$ B 13

where

$${\mathcal{C}}_{ijkl}^{\alpha }(s,t)=-{\tilde{T}}_{ij}^{\alpha }{\delta }_{kl}+{\tilde{T}}_{il}^{\alpha }{\delta }_{kj}+{\tilde{T}}_{ik}^{\alpha }{\delta }_{lj}+{\displaystyle \frac{4}{J(s,t)}{F}_{iA}{F}_{\hspace{0.17em}jB}{F}_{kC}{F}_{lD}{K}_{ABCD}^{\alpha }.}$$ B 14

In the above equation, ${\tilde{T}}_{ij}^{\alpha }$ are components of the Cauchy stress resultant tensor described in equation (B 17), ${\delta }_{ij}$ is the Kronecker delta, $F_{iA}$ are components of the deformation gradient tensor in equation (B 1) and $K_{ABCD}^{\alpha }$ are components of a fourth-ranked tensor given as

$${\mathit{\text{K}}}^{\alpha }(C_n^{\alpha }(\tau ,s,t))={\displaystyle \frac{{\mathrm{\partial }}^2{\mathrm{\Psi }}^{\alpha }}{\mathrm{\partial }{\mathit{\text{C}}}_n^{\alpha }(\tau ,s,t)\mathrm{\partial }{\mathit{\text{C}}}_n^{\alpha }(\tau ,s,t)}.}$$ B 15

B.4. Vascular constituents

For collagen, the strain energy is given by a Holzapfel-type four-fibre family model,

$${\mathrm{\Psi }}^{\kappa }={\displaystyle \frac{k_1}{4k_2}[\exp [k_2{(C_{n,\kappa }^c(\tau ,s,t)-1)}^2]-1],}$$ B 16

where the four families of fibres are oriented along the arterial axis ($\kappa =1$) with 10% of total collagen mass, circumferential ($\kappa =2$) axis with 10% of total mass, as well as axes oriented at +45° and −45° with respect to the arterial axis ($\kappa =3,4$) with 80% of the total mass divided equally between them [18]. In equation (B 16), $k_1$ is a material parameter associated with the intrinsic stiffness of the collagen and $k_2$ is a material property.

For the vascular SMC, the strain energy includes both passive (${\mathrm{\Psi }}^{m,p}$) and an active component (${\mathrm{\Psi }}^{m,a}$) (i.e. ${\mathrm{\Psi }}^m={\mathrm{\Psi }}^{m,p}+{\mathrm{\Psi }}^{m,a}$). The passive component is similar to that of the collagen,

$${\mathrm{\Psi }}^{m,p}={\displaystyle \frac{m_1}{4m_2}[\exp [m_2{(C_{n,2}^m(\tau ,s,t)-1)}^2]-1],}$$ B 17

where it is assumed that the muscle fibres are aligned circumferentially ($\kappa =2$). In the above equation, $m_1$ is a material parameter associated with SMC intrinsic stiffness and $m_2$ is a material parameter. The active component of the strain energy of SMC is given by

$${\mathrm{\Psi }}^{m,a}={\displaystyle \frac{S_a}{{\rho }_m}\left[{\lambda }_2(s,t)+{\displaystyle \frac{1}{3}{\displaystyle \frac{{({\lambda }_M-{\lambda }_2(s,t))}^3}{{({\lambda }_M-{\lambda }_0)}^2}}}\right],}$$ B 18

where ${\lambda }_M$ and ${\lambda }_0$ are stretches at which the active force generation is maximum and zero, respectively. In the above equation, ${\lambda }_2$ is the circumferential stretch, $S_a$ is the stress at maximum contraction and ${\rho }_m$ is the overall mass density of the muscle.

For elastin, it is assumed that the constituent behaves like an amorphous matrix with a neo-Hookean strain energy given by

$${\mathrm{\Psi }}^e={\displaystyle \frac{c}{2}[{\mathit{\text{C}}}_n^e(\tau ,s,t):\mathit{\text{I}}-3],}$$ B 19

where c is a material parameter associated with the elastin intrinsic stiffness.

B.5. Pressure and force balance

Intramural pressure in the PA is evaluated by the balance of fibre forces in the circumferential direction. In the closed loop system, equation (A 2) is solved for the volume of the PA on day s and cardiac time t, the deformation gradient tensor in equation (B 1) can be obtained. The corresponding total Cauchy stress resultant $\mathit{\text{T}}(s,t)$ in the PA tissue can be obtained using the deformation gradient tensor as well as the constitutive relations of the constituents. Based on the assumption that the PA can be represented by a thin wall cylindrical structure, the PA pressure is given by a law that relates the circumferential stress to the intramural pressure.

$$P_{PA}(s,t)={\displaystyle \frac{1}{r(s,t)}{\mathit{\text{m}}}^{(2)}\cdot \left[\sum _{\alpha }{\mathit{\text{T}}}^{\alpha }(s,t)\right]{\mathit{\text{m}}}^{(2)},}$$ B 20

where $r(s,t)$ is the deformed radius of the PA evolving in the long timescale (s) and deforming in the short timescale in each cardiac cycle (t). In equation (B 20), the summation of stress in individual constituents will give the overall stress of the vessel in circumferential direction. In this equation, the PA intramural pressure is directly obtained by the tissue stress ${\mathit{\text{T}}}^{\mathit{\alpha }}(s,t)$ defined in equation (B 11). The tissue stress depends on the constituent deformation in equation (B 1), which is also prescribed by the instantaneous volume in equation (B 3). This chain of relationships can define the P–V relationship of the PA.

Also, with knowing the P–V relationship of PA, we define the PA capacitance,

$$C_{PA}(s)={\displaystyle \frac{V_{max}(s,t)-V_{min}(s,t)}{P_{max}(s,t)-P_{min}(s,t)},}$$ B 21

where min and max denote the maximum and minimum values in a cardiac cycle, $0\le t\le T$.

Appendix C. Right ventricle constitutive formula

C.1. Kinematics

The RV geometry is idealized as a quarter of a prolate spheroid with undeformed internal radius $R_{\mathrm{RV}}(s)$, long-axis radius $L_{\mathrm{RV}}(s)=\gamma R_{\mathrm{RV}}(s)$, and uniform thickness $H_{\mathrm{RV}}(s)$. Denoting these parameters in the deformed state as $r_{\mathrm{RV}}(s,t)$, $l_{\mathrm{RV}}(s,t)=\gamma r_{\mathrm{RV}}(s,t)$ and $h_{\mathrm{RV}}(s,t)$, the RV deformed luminal (cavity) volume $V_{\mathrm{RV}}(s,t)$ and tissue (wall) volume $v_{\mathrm{RV}}(s,t)$ are given as

$$V_{\mathrm{RV}}(s,t)={\displaystyle \frac{1}{3}\pi \gamma r_{\mathrm{RV}}^3(s,t)\hspace{0.17em}\hspace{0.17em}}$$ C 1

and

$$\begin{array}{rl}\hspace{0.17em}& v_{\mathrm{RV}}(s,t)={\displaystyle \frac{1}{3}\pi [(\gamma r_{\mathrm{RV}}(s,t)+h_{\mathrm{RV}}(s,t)){(r_{\mathrm{RV}}(s,t)+h_{\mathrm{RV}}(s,t))}^2}\hfill \\ \hspace{0.17em}& \hspace{0.17em}& -\gamma r_{\mathrm{RV}}^3(s,t)]\hfill \end{array}$$ C 2

Assuming the RV is stretch uniformly in two circumferential directions, the fibre stretch can be obtained by

$${\lambda }_f(s,t)={\displaystyle \frac{1}{R_{RV}(s)}{\left[{\displaystyle \frac{3V_{RV}(s,t)}{\pi \gamma }}\right]}^{1/3},}$$ C 3

and thus, fibre strain

$$E_f(s,t)={\displaystyle \frac{1}{2}({\lambda }_f^2(s,t)-1).}$$ C 4

C.2. Energy and stress

The RV passive energy is defined by a strain energy function

$$w_{\mathrm{RV},p}(s,t)={\displaystyle \frac{1}{2}C(s)(e^{Q(s,t)}-1),}$$ C 5

where

$$Q(s,t)=b_f{E}_f^2(s,t).$$ C 6

In equations (C 5) and (C 6), $C(s)$ and $b_f$ are parameters associated with the strain energy function. This passive energy formula yields the RV fibre passive stress,

$${\sigma }_{\mathrm{RV},p}(s,t)=\hspace{0.17em}2C(s)b_f{E}_f(s,t){\lambda }_f^2(s,t)e^{Q(s,t)}.$$ C 7

The active stress component is defined as

$${\sigma }_{\mathrm{RV},a}(s,t)=T_{max}(s){\displaystyle \frac{C{a}_0^2}{C{a}_0^2+EC{a}_{50}{(s,t)}^2}{C}_t(t).}$$ C 8

In the above equation, $T_{\max }$ is the isometric tension achieved at the longest sarcomere length and $C{a}_0$ denotes the peak intracellular calcium concentration. The length-dependent calcium sensitivity $EC{a}_{50}$ is given by

$$EC{a}_{50}(s,t)=\frac{{(C{a}_0)}_{\max }}{\sqrt{\exp [B({\lambda }_f(s,t)l_r-l_0)]-1}},$$ C 9

where B is a constant, ${(C{a}_0)}_{\max }$ is the maximum peak intracellular calcium concentration, $l_0$ is the sarcomere length at which no active tension develops, $l_r$ is the stress-free sarcomere length and $C_t$ is defined as

$$C_t(t)=\{\begin{array}{cc}{\displaystyle \frac{1}{2}\left(1-\cos \left(\pi {\displaystyle \frac{t}{t_0}}\right)\right)}\hfill & t\le t_{tr}\hfill \\ {\displaystyle \frac{1}{2}\left(1-\cos \left(\pi {\displaystyle \frac{t_{tr}}{t_0}}\right)\right)\exp \left({\displaystyle \frac{-t-t_{tr}}{{\tau }_r}}\right)}\hfill & t>t_{tr}\hfill \end{array}.$$ C 10

Here, $t_0$ is the time taken to reach peak tension, $t_{tr}$ is the time where the relaxation starts and ${\tau }_r$ is a prescribed relaxation time constant.

C.3. Pressure

The RV geometry is idealized as a quarter of a prolate spheroid with undeformed internal radius $R_{\mathrm{RV}}(s)$, long-axis radius $L_{\mathrm{RV}}(s)=\gamma R_{\mathrm{RV}}(s)$, and uniform thickness $H_{\mathrm{RV}}(s)$. Denoting these parameters in the deformed state as $r_{\mathrm{RV}}(s,t)$, $l_{\mathrm{RV}}(s,t)=\gamma r_{\mathrm{RV}}(s,t)$ and $h_{\mathrm{RV}}(s,t)$, the RV deformed luminal (cavity) volume $V_{\mathrm{RV}}(s,t)$ and tissue (wall) volume $v_{\mathrm{RV}}(s,t)$ are given as

$$V_{\mathrm{RV}}(s,t)={\displaystyle \frac{1}{3}\pi \gamma r_{\mathrm{RV}}^3(s,t);}$$ C 11

$$\begin{array}{rl}\hspace{0.17em}& v_{\mathrm{RV}}(s,t)={\displaystyle \frac{1}{3}\pi [(\gamma r_{\mathrm{RV}}(s,t)+h_{\mathrm{RV}}(s,t)){(r_{\mathrm{RV}}(s,t)+h_{\mathrm{RV}}(s,t))}^2}\hfill \\ \hspace{0.17em}& \hspace{0.17em}& -\gamma r_{\mathrm{RV}}^3(s,t)\hfill \end{array}$$ C 12

Unlike the PA, the RV cannot be treated as a thin-walled structure. To address this issue, intraluminal pressure of the RV is prescribed using the formula given by Arts et al. [23],

$$P_{\mathrm{RV}}(s,t)={\displaystyle \frac{1}{3}{\sigma }_{\mathrm{RV}}(s,t)\ln \left(1+{\displaystyle \frac{v_{\mathrm{RV}}(s,t)}{V_{\mathrm{RV}}(s,t)}}\right).}$$ C 13

Appendix D. Effect of ${\beta }_h$ that controls right ventricle thickening

Increasing ${\beta }_h$ from its baseline value of 0.1 to 2.0 mm day⁻¹ while fixing other rate constants at their baseline value produced a larger increase in RV thickness at day 250 (+8.2%) and day 1000 (+6.1%) and these increases approximately remain constant for larger ${\beta }_h$ (figure 10). This increase in RV thickening by larger ${\beta }_h$ was corresponding to lower RV passive stiffening (day 250: −4.95% and day 1000: −11.7%) and slightly higher RVEDP (day 1000: +3.8%). RVEDV slightly decreased by increasing ${\beta }_h$ which led to higher RVEF at day 250 (+2.3%) and at day 1000 (+5.8%). Effect of increasing ${\beta }_h$ on the mPAP, PAPP and thus PA mass upregulation, thickness and compliance was ±3% and lower.

Figure 11.

The changes in major haemodynamics and structural factor in response to increasing rate constant controlling RV thickening, ${\beta }_h$. Increasing ${\beta }_h$ from its baseline ${\beta }_h=0.1$ to β_h = 2 mm day⁻¹ affects RV thickness and RV passive stiffness more compared with other outcomes.

Appendix E. Effect of $K_g^{\alpha }$ that controls pulmonary artery remodelling

Increasing $K_g^{\alpha }$ from its baseline value of 1.0 to 14 while fixing other rate constants at their baseline values resulted in highest increase in PA mass upregulation thus PA thickness (+27.5% at day 250 and +32.3% at day 1000) (figure 10). Associated with this increase in $K_g^{\alpha }$, mPAP and PAPP elevation was not affected substantially, and PA compliance increased (+6.6% at day 250 and 7.8% at day 1000). Effect of increasing $K_g^{\alpha }$ on the RV remodelling and RV pressure and volume was not substantial.

Data accessibility

This article has no additional data.

Authors' contributions

R.P.: conceptualization, data curation, formal analysis, investigation, methodology, resources, software, validation, visualization, writing—original draft, writing—review and editing; Z.J.: conceptualization, formal analysis, validation; C.T.-B.: data curation, formal analysis, validation, writing—review and editing; A.L.D.: formal analysis, funding acquisition, project administration, resources, supervision; C.A.F.: formal analysis, funding acquisition, project administration, resources, supervision; S.B.: conceptualization, formal analysis, funding acquisition, investigation, project administration, resources, supervision, validation, writing—review and editing; L.C.-L.: conceptualization, formal analysis, funding acquisition, investigation, project administration, resources, supervision, validation, writing—review and editing.

All authors gave final approval for publication and agreed to be held accountable for the work performed therein.

Conflict of interest declaration

We declare we have no competing interests.

Funding

This work was supported by American Health Association (AHA) (no. 17SDG33370110) and National Institutes of Health (NIH) (no. U01HL135842). C.T.-B. acknowledges financial support from the National Science Foundation Graduate Research Fellowship Program (grant no. DGE1256260) and the University of Michigan Rackham Merit Fellowship.