Investigation of the Post-Synthetic Confinement of Fluorous Liquids Inside Mesoporous Silica Nanoparticles

Abstract

Perfluorocarbon (PFC) filled nanoparticles are increasingly being investigated for various biomedical applications. Common approaches for PFC liquid entrapment involve surfactant-based emulsification and Pickering emulsions. Alternatively, PFC liquids are capable of being entrapped inside hollow nanoparticles via a postsynthetic loading method (PSLM). While the methodology for the PSLM is straightforward, the effect each loading parameter has on the PFC entrapment has yet to be investigated. Previous work revealed incomplete filling of the hollow nanoparticles. Changing the loading parameters was expected to influence the ability of the PFC to fill the core of the nanoparticles. Hence, it would be possible to model the loading mechanism and determine the influence each factor has on PFC entrapment by tracking the change in loading yield and efficiency of PFC-filled nanoparticles. Herein, neat PFC liquid was loaded into silica nanoparticles and extracted into aqueous phases while varying the sonication time, concentration of nanoparticles, volume ratio between aqueous and fluorous phases, and pH of the extraction water. Loading yields and efficiency were determined via ¹⁹F nuclear magnetic resonance and N₂ physisorption isotherms. Sonication time was indicated to have the strongest correlation to loading yield and efficiency; however, method validation revealed that the current model does not fully explain the loading capabilities of the PSLM. Confounding variables and more finely controlled parameters need to be considered to better predict the behavior and loading capacity by the PSLM and warrants further study.

Graphical Abstract

INTRODUCTION

Perfluorocarbon (PFC) liquids are highly fluorinated (no C–H bonds) substances that have been investigated for their potential as biomedical sensors, contrast agents, cell trackers, and oxygen carriers.^1–10 These technological advances make use of the unique properties of PFC liquids: (1) they are biologically and chemically inert; (2) they can dissolve more gas per unit volume than any other liquids; and (3) they are less flammable than their hydrocarbon counterparts.¹¹ In nuclear magnetic resonance (NMR) applications, fluorine-19 (¹⁹F) atoms are naturally abundant, highly sensitive to their environment, and are absent of background signal from endogenous fluorine in biological studies.¹² These properties arise from the fluorine atoms, which have low polarizability and create an electronic sheath around the carbon backbone which limits intermolecular interactions. Thus, PFC liquids are highly hydrophobic, lipophobic, and behave similar to ideal gases due to the low van der Waal’s interactions between PFC molecules.¹³ In spite of their potential, PFC liquids are often difficult to use directly in aqueous environments due to their high interfacial tension and hydrophobicity/lipophobicity; as such, they often require some form of encapsulation or carrier agent.

Common methods to disperse PFC liquids into aqueous and biological environments include emulsification with engineered surfactants,^14–17 lipid micelles/liposomes,^18–21 solid particles,^22,23 or confinement inside nanoparticles.^3,24–26 Surfactant-based suspensions typically require amphiphilic and nonionic surfactants with high-pressure microfluidics or sonication to create micro- or nanoscale emulsions.¹⁵ Careful consideration of the properties of the surfactants is needed to maximize the formation and stability of the emulsions. Similarly, PFC-filled nanodroplets can be formed by creating a film on a solid surface and then trapping the PFC during vigorous homogenization.^21,27 Solid particles can also associate at the interface of the PFC and water phases to form a Pickering emulsion.^22,23 These emulsions rely on the solid particles having wettability in both phases with a higher preference for the continuous phase. In all of these cases, the formation of the emulsion is dependent on the properties of the emulsifying agents and the concentrations of the emulsifier and PFC in the continuous phase.

Emulsions are often destabilized by various mechanisms, such as flocculation, coalescence, Ostwald ripening, and surfactant degradation.^28,29 Additionally, the PFC molecular weight, interfacial tension, solubility, and diffusivity also affect the stability of the emulsions.^30,31 Despite these destabilization mechanisms, optimization of surfactant-based perfluorocarbon nanoemulsions has led to the successful translation of cell tracking technology to the clinic.^8,32–34

As an alternative to emulsions, recent advances have led to the use of metal-oxide or polymeric nanoparticles to act as stable carrier agents for fluorous material and PFC liquids.^3,35 Mesoporous silica nanoparticles are biocompatible and have tunable surfaces to incorporate colloidal stabilizers, targeting agents, fluorescent dyes, and therapeutic drugs.³⁶ These nanoparticles have been generated by forming a PFC emulsion where the silica precursors are templated onto the surface of the emulsion bubble.³⁷ Since the PFC liquids are trapped inside solid cages, they are resistant to coalescence and Ostwald ripening as the solid cages are unlikely to merge into one particle or to grow in size as a function of PFC volume.

While nanoparticle encapsulation can address the stability challenges of emulsions, the previously described process requires formation of an emulsion and in situ formation of the nanoparticle in the suspension. This process could slow down the redesign of PFC-loaded nanoparticles as well as the scalability of material for commercial application.

In 2017, Pochert et al. reported on the biodistribution of mesoporous silica nanoparticles postsynthetically loaded with perfluorocarbons.²⁶ They synthesized hollow mesoporous silica nanoparticles and then sonicated the nanoparticles in neat perfluoro-15-crown-5-ether (PFCE). Upon extraction into an aqueous medium, the PFC remained sequestered in the nanoparticles which allowed for tracking the particles in vivo via ¹⁹F magnetic resonance imaging (¹⁹F MRI). At the same time, we reported on ultraporous mesostructured silica nanoparticles (UMNs) loaded with various PFC liquids via a similar postsynthetic loading method (PSLM).³⁸ These perfluorocarbon-loaded UMNs (PERFUMNs) were able to encapsulate three different perfluorocarbons. Additionally, PERFUMNs were found to load five times more PFC than mesoporous silica nanoparticles with cylindrical pores, which would allow more signal in ¹⁹F MRI.

The primary advantages of the PSLM are the decreased time of encapsulating perfluorocarbon liquids and the ability to load various combinations of PFCs into presynthesized nanoparticles. As comparative examples, Kikuchi and collaborators reported on PFCE-loaded nanoparticles which required 6 h to encapsulate the PFCE liquid.³⁹ These particles were loaded with solid silica templated on preformed micelles. They later reported on mesoporous silica PFCE-filled nanoparticles by this same method; the process took 62 h for encapsulation.²⁴ Pochert et al. obtained suitable signal for ¹⁹F MRI measurements after an encapsulation time of 2 h.²⁶ In our work, the PFC liquids were encapsulated in 10–30 min. The decreased time allowed for the study of several PFC liquids to determine which sensor would be a better ¹⁹F NMR oxygen sensor within the nanoparticles.³⁸

Despite the expeditious and versatile loading with the PSLM, further analysis of our PERFUMNs revealed that there was a loading efficiency of less than 20%. Since the mechanism of the PSLM had yet to be studied, we sought to evaluate the PSLM to identify the relationship each loading factor had on the efficiency of loading. A better understanding of the factors influencing the PSLM will ultimately improve the versatile and high-throughput loading of various PFC liquids into nanoparticles for biomedical applications.

EXPERIMENTAL SECTION

Materials and Instruments.

The ultraporous mesostructured silica nanoparticles (UMNs) were synthesized using previously published methods.³⁸ Perfluorodecalin (PFD) was originally purchased from Fluoromed L.P (Round Rock, TX); PFD in this paper was recycled by filtering the fluorous liquid through 0.2 μm hydrophobic membrane, then distilling PFD by rotovap. PFCE was purchased from Neta Scientific, Inc. (Hainesport, NJ).

Particle porosity and surface area were measured with N₂ physisorption (Micromeritics ASAP 2020, GA). Samples were analyzed under the ASAP 2020 analysis port at cryogenic temperatures. The surface area and pore size of samples were determined by the BJH method. Nanoparticles and perfluorocarbons were sonicated (Branson 2510) to fill the void space of the nanoparticles with PFC molecules.

All NMR spectra were obtained at 470 MHz on a Bruker Avance III 500 MHz instrument equipped with a 5 mm Prodigy TCI Cryoprobe.

Electron micrographs of unloaded and loaded nanoparticles were obtained via transmission electron microscopy, that is, TEM (FEI Tecnai 12, Houston, TX), and cryogenic TEM, that is, cryo-TEM (Tecnai G2 Spirit Biotwin, Houston, TX), respectively. In TEM, 3 μL of UMNs were dried on Formvar-coated carbon grids overnight. For cryo-TEM, 3 μL of sample were placed on lacey carbon grids which were immediately dried with filter paper for 5 s at 100% humidity. The samples were vitrified by submerging the grids into liquid ethane. Electron micrographs were obtained at 120 kV with an emission current of 4 mA.

All pH measurements were collected on an Acumet AB150 digital pH meter.

Experimental Section.

Ultrapure water was obtained from an in-house Milli-Q water purifier. The pH was adjusted by adding drops of either 0.03 M HCl or 0.01 M NaOH solutions until the desired pH was stable.

UMNs were dried during their N₂ physisorption characterization. Dried nanoparticles were weighed on an analytical balance and were transferred to a Nalgene Teflon centrifuge tube. PFD was added to the tube at the volumes indicated below. The UMN-PFD suspension was sonicated for 10–60 min. For sonication up to 10 min, temperature increased slightly from 23 to 25 °C; the overall temperature change over 60 min was 12 °C. Nanoparticles were extracted with the previously prepared water (room temperature), thus generating perfluorocarbon-loaded UMNS (PERFUMNs).

NMR samples were prepared with 5% D₂O (v/v) and 52 μM trifluoroacetic acid (−76.5 ppm) as a reference and calibration standard to calculate loading values. Parameters for ¹⁹F NMR experiments included an 8.5 s delay time and a 2 s acquisition time, to allow for complete relaxation of magnetization following a full 90 deg pulse. For PFD, spectral width and offset were 80 and −110 ppm, respectively. The mass concentration of the PERFUMNs was determined by taking 3–4 mL aliquots of the PERFUMN suspension and drying the sample via rotary evaporation in a vial with known mass.

RESULTS AND DISCUSSION

Discrepancy in PSLM Efficiency.

The theory of loading liquid PFCs into the core of the UMNs is based on diffusion and the hydrophobic nature of perfluorinated compounds. The dried nanoparticles should be hollow cages of air ahead of suspension into the PFC liquid. As the nanoparticle-PFC suspension is sonicated, the PFC molecules will fill the void space of the nanoparticle core as the gaseous air is expelled. During the extraction process, the nanoparticles will partition into the aqueous phase, due to the hydrophilic silanol groups and polyethylene glycol surface modifications.^40,41 After mixing the aqueous and fluorous phases, the UMNs will be suspended in the water while the PFCs will be trapped in the core of the UMNs; this phenomenon is largely attributed to the low polarizability of the fluorine and the hydrophobicity of the PFC, causing the PFC to be repelled by the water molecules surrounding the nanoparticle pores.^11,42,43 Analogous to microemulsions and micelles, in an aqueous environment, it is more energetically favorable for the nanosized (≤200 nm diameter) PFC droplet to stay confined to the core of the UMNs, allowing water molecules to move freely, and reduce surface interactions.⁴⁴ It is also possible that the internal silanols from the SiO₂ cage act as an ionic barrier to the partially negative shield caused by the fluorine. As the SiO₂ cage is rigid, it prohibits the expansion of droplet size, thus, allowing the PFC droplets to be trapped inside the nanoparticle core.

Loading of PFCs was confirmed by cryogenic transmission electron microscopy (cryo-TEM) and ¹⁹F NMR. The ¹⁹F NMR quantitation of loaded fluorine was determined by comparing the ratio of PFD fluorines to an internal standard, trifluoroacetic acid. The maximum loaded volume of PFC liquid was theoretically calculated based on the porosity measurements from nitrogen physisorption, as described in later paragraphs. In our previously published loading procedure, we obtained a mean yield and efficiency of 36.5% and 16.0%, respectively, for PFD PERFUMNs (Supporting Information (SI) Figure S1), indicating that there was a loss of PFC during the loading and extraction process.

Furthermore, TEM and cryo-TEM images were obtained for the unloaded UMNs and loaded nanoparticles (i.e., PERFUMNs) showing that the large interior cavities of the UMNs were loaded with the densely packed, electron-rich, PFC molecules (Figure 1a,b). While there was evidence of some highly loaded nanoparticles, occasionally, we also observed nanosized bubbles and nanoparticles with incomplete loading (Figure 1c,d). These bubbles might be water trapped inside the PFC, as it is possible that some PFC was replaced by water during the mixing of aqueous and fluorous phases in the extraction process. The nanosized bubbles have diameters between 20 and 40 nm; the turbid flow of the vortex during the extraction could also have promoted nanosized emulsions while the PFC was agitated inside of the UMN cage.^45,46 Regardless, these results indicated that the original loading procedures were not optimal to maximize the amount of PFC loaded into UMNs.

Figure 1.

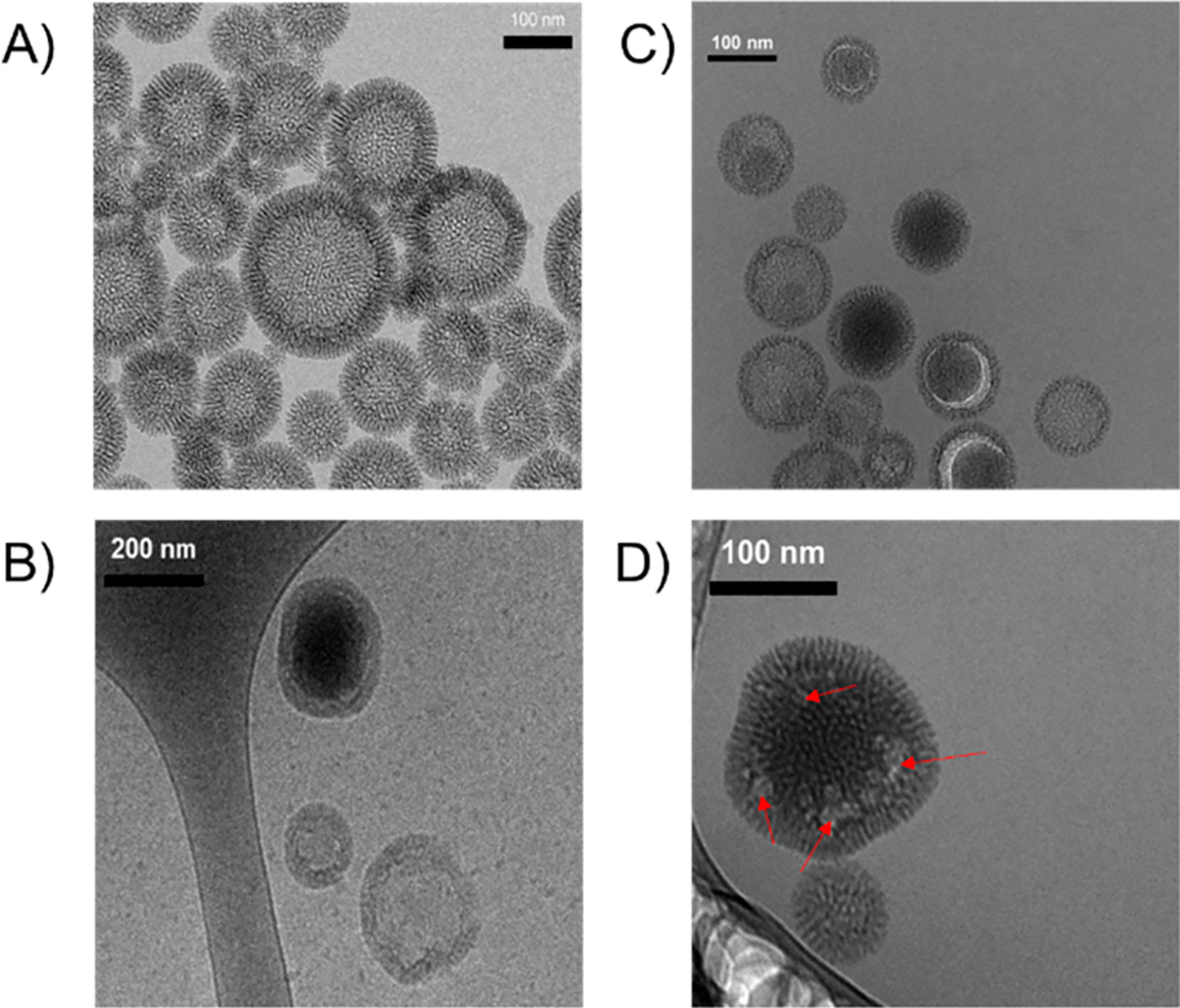
TEM images of PERFUMNs. (A) Image of unloaded UMNs. (B) Cryo-TEM images of a PERFUMN next to unloaded particles. (C) Image of partially loaded PERFUMNs with crescent shaped space in the internal cavity. (D) Presence of nanosized bubbles in PERFUMN.

Experimental Design and Theoretical Models of Loading PFC Liquids.

The overall UMN loading procedure is straightforward and quick (SI Scheme S1), allowing for parallel assessment of factors that may influence the variation in loading of PFC liquids (Table 1). The pH of the extraction water, the ratio of the volume of H₂O to the volume of PFC (V_R), and the UMN concentration were hypothesized to be the most variable and influential factors between loading attempts. The pH level of the extraction water was hypothesized to significantly impact the recovery of the particles as a basic environment would deprotonate silanols, creating more negatively charged nanoparticles and favoring partitioning into the aqueous phase. Conversely, with a decreased surface potential in the acidic environment, the more hydrophobic nanoparticles would be more susceptible to aggregation.⁴⁷

Table 1.

Experimental Factors for Optimization

	planned levels
factors	low	med	high
pH	5	7	8
sonication (min)	10	20	30
extraction VRa	0.8	1.0	1.2
[UMNs]o (mg mL−1)	1	3	4

^aV_R = volume H₂O/Volume PFC.

The V_R was expected to influence the extraction of PERFUMNs by changing the concentration gradient, which would change the population of particles that diffuse into the aqueous phase. In a similar fashion, increasing the UMN concentration would saturate the PFC phase and shift the equilibrium to promote the movement into the aqueous phase.

We were also interested in considering the impact of sonication time; we hypothesized that more time would increase the amount of space that is filled for each nanoparticle. In the report by Pochert et al., they sonicated the nanoparticles in PFC for 2 h, which led to sufficient levels of PFC-loaded nanoparticles for in vivo measurements at 11.7 T. Based on their theoretical calculations, ≥95% of the PFC was loaded and localized in the liver.²⁶ They calculated a loading capacity of ~66 wt % of PFC. The calculations for loading PFC in Pochert et al. were determined by theoretically calculating the density of the hollow nanoparticle, taking into account the hollow core and vacant space in the pores of the shell, based on their N₂ physisorption measurements and nanoparticle size distribution. This method of calculation requires assumptions about the density of the particles, as well as their size distribution within a given subset of the population. These calculations are also restricted to particles with spherical shape and hollow cavities, surrounded by a mesoporous shell.

Alternatively, we utilized specific batch concentrations and cumulative pore volumes of a full population of nanoparticles determined by the N₂ physisorption Barrett–Joyner–Halenda method.^48–50 The cumulative pore volume includes the void space from interparticle pores, leading to an overestimation of the amount of loadable space. Our method for determining loading capacity allowed us to utilize specific values for each nanoparticle batch to directly calculate the impact of each variable on loading yield and efficiency. Additionally, the method used herein is not restricted to particle shape, and it is assumed that the interparticle space does not change the overall relative difference in loading volume between batches or types of nanoparticles, as was compared in Lee et al.³⁸

The yield and efficiency differ from one another based on two types of scenarios (SI Figure S2). Briefly, the yield accounts for the loss of nanoparticle mass after extractions; thus the difference between the experimental and theoretical values should be due to the amount of PFC liquid that was not trapped. There are several mechanisms that could influence the loss of PFC liquids. During extraction, the PERFUMNs are vortexed; these turbulent forces could release PFC. Additionally, volatile PFCs could evaporate from the nanoparticle during temperature changes⁵¹ or potentially leak from the nanoparticle since there is no capping or amorphous layer blocking the pores. The theoretical PFC concentration determined by the efficiency model assumes that there is 100% recovery of the mass of UMNs added and that all of the loadable volume is occupied by PFC. In this case, aggregation of the physical nanoparticles could prevent a significant population from getting to the aqueous phase or cause sedimentation of particles in the extracted volume, affecting the efficiency determination. If the nanoparticles become hydrophobic, they might also be less likely to partition into the aqueous phase which will also reduce efficiency.

Mathematically, the yield and efficiency for a given batch of PERFUMNs is determined by the following equations.

$$C_{\text{PFC}}=\left(f_{\text{c}}\times f_{\text{d}}\right)\left(\frac{C_1\times V_{\text{avg}}^S\times {\rho }_{\text{PFC}}}{{\text{MM}}_{\text{PFC}}}\right)$$ (1)

$$\mathrm{{\rm Y}}=\frac{C_{\exp }}{C_{\text{PFC}}}\times 100$$ (2)

$${\mathrm{{\rm Y}}}^{*}=\frac{C_{\exp }}{C_{\text{PFC}}^{*}}\times 100$$ (3)

In eq 1, the C_PFC is the theoretical concentration of PFC ($C_{\text{PFC}}^{*}$ is the theoretical concentration for efficiency where C₁ = max concentration of UMNs possible); f_c is a conversion factor (10⁶), f_d is the dilution ratio (473 μL ÷ 500 μL) from stock volume to final NMR tube volume, C₁ is the concentration (mg Ml⁻¹) of the UMNs in the PERFUMN aqueous phase, $V_{\text{avg}}^S$ is the average loadable volume (cm³ mg⁻¹) determined by N₂ physisorption, ρ_PFC is the density of the neat PFC, and MM_PFC is the molar mass of the PFC. PFD has a density and molar mass of 1.92 g mL⁻¹ and 462 g mol⁻¹, respectively.

The loading yield and efficiency (ϒ and ϒ*, respectively) were determined by comparing the value of theoretical concentration with experimental concentration (C_exp). As noted previously, the efficiency C₁ is the maximum expected concentration based on the amount of extraction water added (in the original loading procedures, this was set to 1 mg mL⁻¹). In addition to sample-specific loading yield and efficiency, we wanted to compare each batch to other batches; thus we normalized the theoretical amount of fluorine by setting the loading capacity $(V_{\text{avg}}^S)$ to the upper limit of the 95% confidence interval (0.95 CI), 2.5 cm³ g⁻¹, from benchmark characterizations of UMN batches (SI Table S1).

The confidence interval gives a range of values where you would expect the mean $V_{\text{avg}}^S$ to appear. Thus, the upper limit should be the largest loading capacity a UMN batch could have, on average.

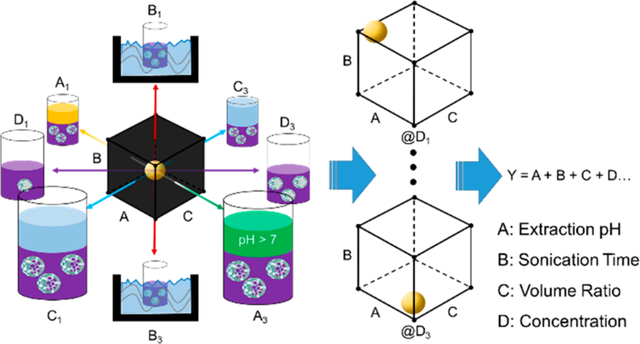
Overall, there were four factors with three levels of conditions, giving us a total of 81 combinations of trials. The trials were coded in a four-digit combination with positions WXYZ (pH, sonication time, V_R, [UMNs]_o respectively) and numbers 1, 2, or 3 standing for low, medium, or high condition, respectively. For statistical comparison, each trial (n = 81) was done in triplicate measurements.

pH Effects on Emulsion Formation.

An advantage of using neat PFC liquids as a fluorous phase is that, ideally, the PFC will fill the void space of the nanoparticles, and upon mixing with the aqueous phase, should quickly phase separate, as the liquid is hydrophobic and denser than water, allowing PERFUMNs to partition on the top in the aqueous phase for easy removal.³⁸ Since both liquid phases are generally clear, it is easy to track the opacity change as the PERFUMNs transfer from the fluorous phase to the aqueous phase. However, on occasion there was an observed formation of an emulsion layer between the two phases. Fluorescently labeled mesoporous silica nanoparticles (see SI for description of synthesis) were used to better visualize the location of the nanoparticles; the emulsion contained nanoparticles, which affects the extractions and decreases the amount of PERFUMNs that could be recovered (SI Figure S3).

Emulsions are typically stabilized by surfactants or other emulsifying agents. However, qualitative investigations showed that emulsion stability occurred solely between the PFC and ultrapure water. Moreover, it appeared that basic conditions stabilized the emulsion while acidic conditions allowed it to destabilize (SI Figure S4). When the pH of the water was varied, a pH ≥ 7 began stabilizing the emulsion. Varying the ionic strength of the water did not affect the emulsion stability compared to the pH of the water.

Furthermore, we showed that the lower pH does not have a significant effect on the PERFUMN recovery as it becomes more acidic (Table 2). In light of this discovery, we focused the remaining experiments within the acidic region (pH 5) to improve the extraction process and reduce variability.

Table 2.

Recovery of PERFUMNs at Different pH Levels

pH	percent recoverya
3	59.0 ± 6.5
5	43.0 ± 2.2
7	62.3 ± 13.0

^aPercent recovery from three batches. Mean ± SEM. No statistical significance was found.

Trends in PSLM Loading Factors via PFD PERFUMNs.

In our last report, we loaded various PFCs into the core of the UMNs. Out of the three PFCs we reported on, PFD had the lowest amount of PFC loaded per nanoparticle, but had the smallest variation among replicates.³⁸ Hypothesizing that the PFD variation would remain small with each trial experiment, we rationalized that PFD PERFUMNs would lead to more confidence in statistically significant improvements; best identify the weight each factor has on loading; and, potentially improve loading for other PFCs that performed with better loading.

Trials were tested in triplicate measurements, and data were collected for each parameter (Table 3 and SI Table S2). The data were compiled into a 4-factor heat map for easy identification of obvious correlations between factors and loading yield and efficiency improvements (Figure 2). Heat maps were based off of a 3-color percentile range, where the zeroth (blue), 95th (red) percentiles were end points with a 60th (yellow) percentile midpoint. Additionally, any trial with over 60% yield or efficiency is highlighted with bold yellow text; the 60% indicates trials with approximately 2-fold and 4-fold improvements in yield and efficiency, respectively, compared to the original PSLM conditions. Lastly, trials that had outliers were marked with red text and black backgrounds. Thus, trial conditions were easily screened and were considered good candidates for optimal conditions if both the batch-specific yield and efficiency were above the 60% threshold, without any outliers.

Table 3.

Experimental Data of Trial Factors and UMN Recovery

		sonication		[UMN]0	[UMN]max	[UMN]recovery
trial	pH	(min)	V R	mg mL−1	mg mL−1	mg mL−1
1322–1	5.0	30	1	3.1	0.8	0.6
1322–2	5.0	30	1	3.1	0.8	0.7
1322–3	5.0	30	1	3.1	0.8	0.6
1123–1	5.2	10	1	4.0	0.9	0.7
1123–2	5.2	10	1	3.8	0.8	0.5
1123–3	5.2	10	1	4.1	0.9	0.6
1112–1	5.2	10	0.8	2.9	0.9	0.6
1112–2	5.2	10	0.8	3.0	0.9	0.4
1112–3	5.2	10	0.8	3.0	0.9	0.5
1111–1	4.8	10	0.8	1.0	1.0	1.5b
1111–2	4.8	10	0.8	1.0	1.0	1.5b
1111–3	4.8	10	0.8	1.0	1.0	1.3b

^aExperimental trials with replicates (i.e., 1, 2, 3 after the hyphen in each trial name). Numbers are experimental values based on optimization design. The [UMN] recovery is the mass concentration of UMNs recovered after extraction of PERFUMNs. Trials are ordered from best to worst performance in both yield and efficiency; 1322 was the best performance, 1123 is the first trial above the average, 1112 was the first trial below average, 1111 had the worst performance.

^bindicates values that are above the expected maximum concentration.

Figure 2.

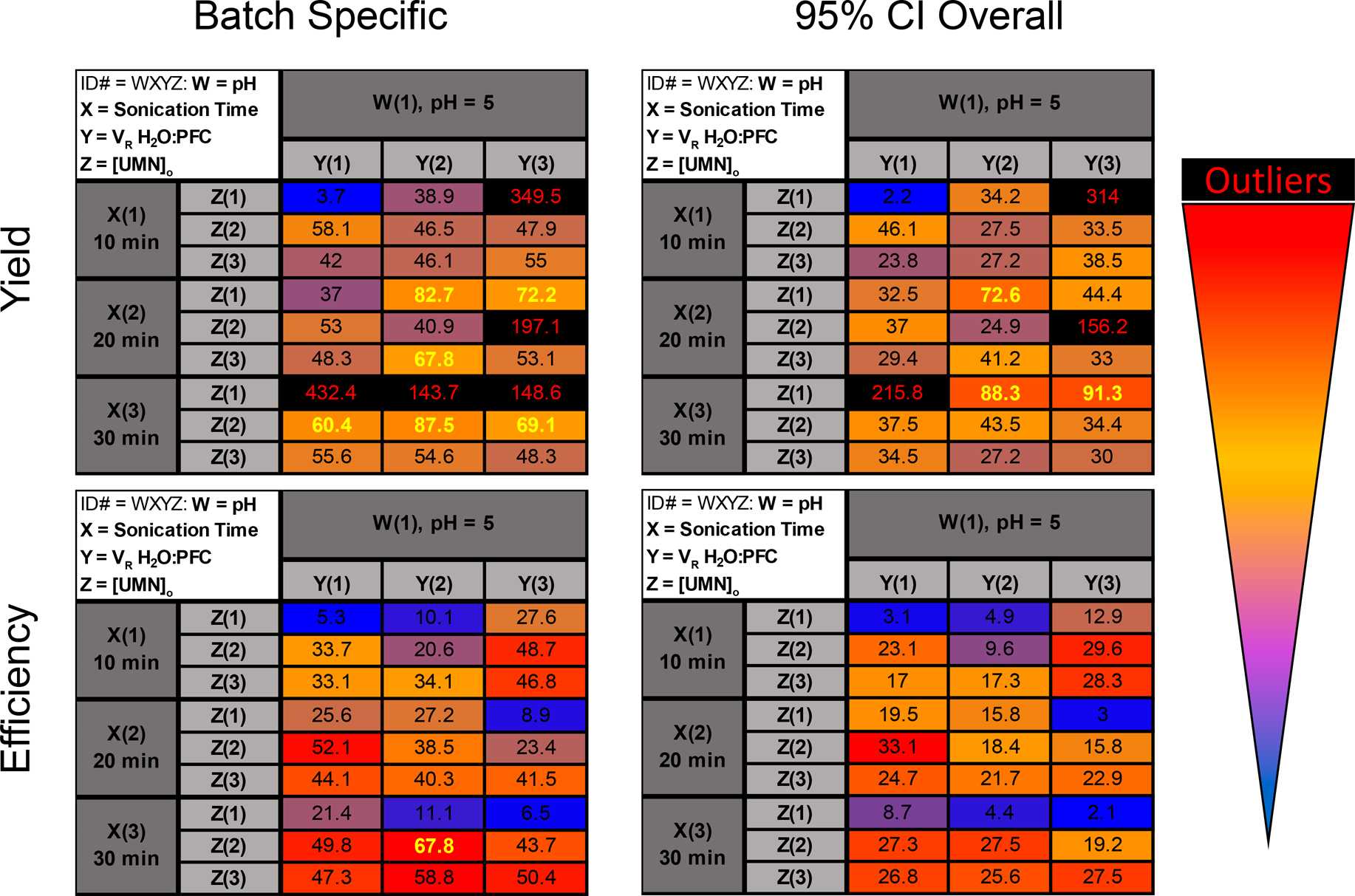
Heat maps of loading yields and efficiencies for PFD PERFUMN generation. Each spot is coded by a 4-digit number with positions “WXYZ” where W = pH, X = sonication time, Y = V_R, and Z = [UMN]_o. The positions are followed by a number (i.e., 1, 2, or 3), which corresponds to the level of the factor (i.e., low, medium, high conditions). Values are based on a 3-point percentile range from 0th (blue) to 95th (red) percentile end points and a 60th (yellow) percentile midpoint. Numbers that are highlighted in yellow bold text are above the 60% threshold, corresponding to 2-fold and 4-fold increase in yield and efficiency, respectively. The batch specific yield and efficiency are in the right column, and the comparison to the 95% CI upper limit is on the right. Yields are in the top row and efficiency heat maps are in the bottom row. Statistical outliers are marked with black background and red text. All trials were conducted in triplicate, and the reported values are the mean of the three replicates. No error is reported in this figure, please see the SI, Table S3, for raw values and error.

One trial met these criteria, trial 1322, which corresponds to pH 5, sonication = 30 min, V_R = 1, and [UMN]_o = 3 mg mL⁻¹. Trial 1322 has a loading yield of 87.5 ± 5.4% and efficiency of 67.8 ± 1.8% (mean ± SEM). When the loading capacity is set to the 0.95 CI limit of UMNs, trial 1322 has a yield of 43.5 ± 2.7% and an efficiency of 27.5 ± 0.7%. As noted earlier, the benchmark loading capacity is based off of the 95% confidence interval upper limit, which corresponds to the largest average loading capacity, $V_{\text{avg}}^S$, most UMN batches can have after synthesis. Using the same limit for the data set, the mean loading yield and efficiency are 38% and 18%, respectively, accounting for outliers. Overall, it is encouraging that trial 1322 is above the average for batch comparisons. Trial 1322 had a 2.4-fold and 4.2-fold increase in loading yield and efficiency, respectively, compared to the original loading procedure, by increasing the sonication time from 10 to 30 min and keeping the extraction under acidic conditions. The improvement appeared to be correlated with increasing sonication times which is likely from allowing the PFC molecules to further fill in the pores and cavities of the UMNs. However, while efficiency appeared to show a trend for sonication time, the yield had no obvious trends and contained several outliers. Furthermore, there was an effect with the concentration of UMN particles ([UMN]_o), since the lowest concentration always had low loading efficiency, regardless of sonication time. Based on these results, we sought to mathematically model and quantify the convoluted relationship between the different loading factors and the loading results.

Analysis of the Effects and Interactions of the Factors.

In addition to determining the main effects and confounding interactions between our loading factors, we were interested in identifying the weight each factor had on the yield and efficiency. Due to the challenges for extraction from emulsion stabilization at pH ≥ 7, statistical analyses were conducted on the trials with pH 5. Thus, we used a 3-factor analysis, in which case the sonication time, V_R, and [UMN]_o were analyzed and mathematically optimized.

The loading yield and efficiency of each trial was calculated based off of eqs 1–3 (SI Table S3). After outliers were removed from the analyses, the data were transformed by taking the square root of the yield and efficiency. The data were analyzed by multifactorial ANOVA, and the best model was chosen for yield and efficiency separately (see SI for details). All three of the loading parameters had confounding interactions with each other (SI Figures S5 and S6); in terms of the main effects, the yield and efficiency were affected the most by sonication time. The [UMN]_o influenced the yield more than V_R; however, V_R influenced the efficiency more than the [UMN]_o. Since the loading yield attempts to account for the loss of UMN mass, this could explain why the initial UMN concentration affects the yield more than the extraction volume ratio. Graphical analysis of the data suggested that increasing the sonication time would increase both the yield and efficiency (SI Figure S7).

Based on the fitted models, the data were theoretically optimized to get 100% loading yield and efficiency simultaneously (Figure 3a). The optimal conditions were found by changing the loading parameters within a given boundary until the most desirable set of conditions were found: sonication time = 37.4 min, V_R = 1.1, and [UMN]_o = 2.6 mg mL⁻¹. The model predicts that the highest yields can be found when sonication is maximized and both V_R and [UMN]_o are minimized (Figure 3b). On the other hand, the model predicts that efficiency will be at its highest when both sonication time and V_R are maximized; the [UMN]_o does not matter within 1–4 mg mL⁻¹ range considered herein. If the most optimal [UMN]₀ of 2.6 mg mL⁻¹ was used, then PERFUMNs with 60–100% yield and efficiency can be found between sonication times of 30–50 min, and V_R ratios between 0.9 and 1.2 (Figure 3c).

Figure 3.

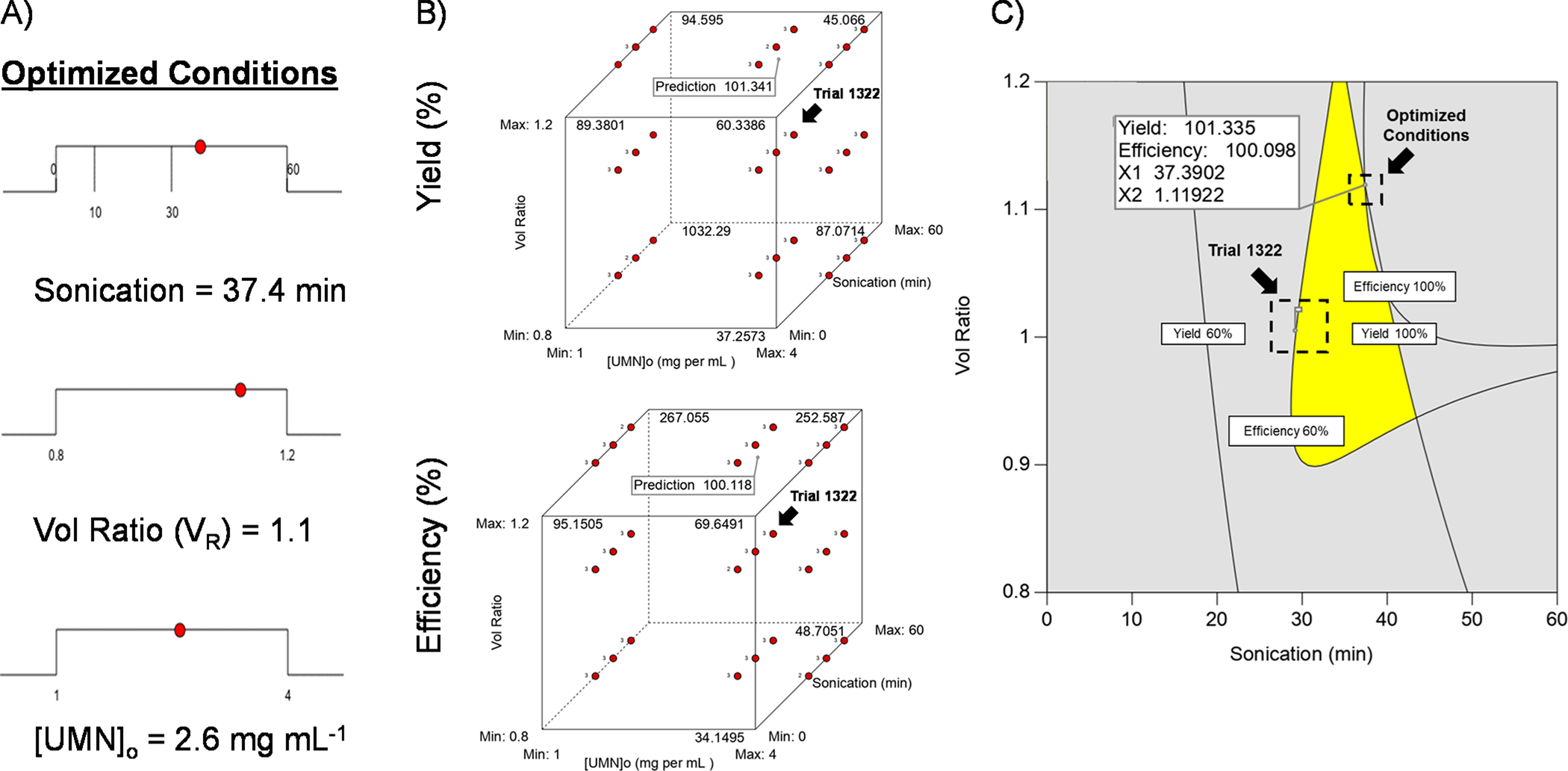
Optimized conditions for loading PFD PERFUMNs. (A) Ramp graphs showing optimization of factors: sonication (min), V_R, and [UMN]_o (mg mL⁻¹). (B) Cube plots showing the effect of all three factors on yield (top) and efficiency (bottom). The values at the vertices represent predicted values; the prediction flag is the position of the optimal conditions; trial 1322 was pointed out for comparison to predicted optimization. (C) Overlay plot of optimization. The gray shaded areas are outside of the desired yield and efficiency boundaries. The yellow region is the optimal zone to get 60–100% yield and efficiency. Both the optimal and experimental trial (1322) are identified on the graph. The optimal conditions flag was manually selected, and the coordinates are not the exact parameters from the optimized fit (i.e., x-axis, y-axis).

As noted previously, increasing sonication time appears to be a reasonable parameter to impact PFC loading since this should promote more space to be occupied by the PFC molecules. In terms of the benefits from keeping a higher volume ratio of water to PFC, one justification is that it facilitates the manual extraction of the aqueous phase as the top of the aqueous layer gets further away from the PFC-H₂O interface. Additionally, assuming maximum recovery of nanoparticles, a larger volume of aqueous phase should always be more “dilute” in terms of nanoparticle concentration. Thus, the nanoparticles would move from a high concentration phase to a lower concentration phase.

Validation of PSLM Model Accuracy and Applicability.

PFD PERFUMNs were experimentally loaded with the predicted optimized parameters to test the validity of the current model based on the analysis of the PSLM factors. All of the following validation data for PSLM model experiments are represented in SI Figure S8. Three separate trials, in triplicate loading, were conducted (n = 9); the averages of each trial (Trial A-C) reveal loading yields of 77.7 ± 21.7%, 31.3 ± 20.9%, and 45.3 ± 6.7%, respectively, with a grand mean of 51.4%. Trials A–C had loading efficiency of 28.7 ± 1.9%, 5.6 ± 1.1%, and 42.6 ± 2.1%, respectively, with a grand mean of 22.9%. Another trial was conducted by increasing the sonication time to 60 min (n = 3); the loading yield and efficiency were 32.4 ± 4.8% and 24.2 ± 2.5%, respectively. The optimized parameters remain similar to Trial 1322, and the main factor that was altered was the sonication time.

During sonication, the energy of the ultrasonic waves is absorbed, causing molecules to move and vibrate.^52,53 These molecular vibrations generate heat, effectively heating up the suspension of nanoparticles in PFC. The effects of temperature are not accounted for in our model. Changes in temperature can change the long-range ordering of PFC molecules, as analogous studies have shown cases where temperature induces PFC liquids to form ordered liquid crystals⁵⁴ or expands liquid droplet volumes during ultrasound applications.^55–57 A change in the average kinetic energy and intermolecular distances could also affect the PFC compressibility into the core of the UMNs. Furthermore, our model assumes that the packing of molecules into nanosized spaces of the UMNs has a linear correlation to sonication time (as well as other parameters). There may be an unknown behavior due to confinement that limits packing inside nanoparticles; for example, when water was confined inside nanoparticles, Knight et al. found it behaved drastically different than its bulk form.⁵⁸ Future experimentation with theoretical models might help elucidate these behaviors.⁵⁹ Either way, a more robust model design would be needed to consider the effects of these confounding variables in order to make better predictions about loading capability using the PSLM.

We know from our previous work that the PSLM allows for the versatile loading of different PFC liquids; however, we do not know if this optimization model applies to other PFCs or if it is applicable to only PFD. We cross-validated the applicability with perfluoro-15-crown-5-ether (PFCE), which has a density and molar mass of 1.78 g mL⁻¹ and 580 g mol⁻¹, respectively. In previous work, the PFCE PERFUMNs had a loading yield and efficiency of 33 ± 21% and 15 ± 9%, respectively. Using the optimized model parameters, PFCE PERFUMNs (n = 3) had a loading yield and efficiency of 33.6 ± 10.2% and 23.2 ± 5.5%, respectively, indicating a slight increase in efficiency but not loading yield (SI Figure S8). Interestingly, the mass recovery of nanoparticles after extraction shows a nearly 2-fold increase with PFCE PERFUMNs. The increase is likely due to the decrease in pH, as noted previously, which allows for better distinction and separation of the aqueous and fluorous phases after mixture. Further extrapolation from the data shows that the average concentrations of PFC in this study, assuming a 1 mg mL⁻¹ nanoparticle concentration, are 2.3 μmol PFD per mL and 0.64 μmol PFCE per mL. PFD PERFUMNs contain the same concentration as those prepared in Lee et al., while the previous PFCE PERFUMNs were 1.9 μmol PFCE per mL (n = 9).³⁸

Finally, we used cryo-TEM to analyze the PFD-loaded PERFUMNs prepared under the new conditions. TEM image analysis of the PFD PERFUMNs after 37 and 60 min sonication shows that the majority of nanoparticles are unloaded. However, those that are loaded appear to have more complete loading without the nanosized “bubbles” in the core. Crescent-shaped spaces near the boundary of the shell are still present, but reduced (SI Figure S9). In our previous work, the cryo-TEM images that showed more complete loading were from perfluoro(tert-butylcyclohexane) PERFUMNs.³⁸ In this manuscript and our previous work, cryo-TEM imaging shows a clear difference in contrast between PFC-loaded nanomaterial and the unloaded nanomaterials, which allowed us to observe the incomplete loading of PERFUMNs.³⁸ However, comparing our images to other published TEM analyses, we find there is a lack of contrast within the core of the nanoparticles.^24,26 Based on our observations (not shown), the PFC liquid is unstable in the TEM vacuum and could leak or evaporate. Assumptions must be made about the homogeneity of loading between individual nanoparticles in a population. Inaccurate measurements of loading could affect applications such as ¹⁹F MRI, where analyte concentrations would be critical, due to the low detection sensitivity of NMR-based techniques.

Overall, these data further suggest that there is a need to analyze the physicochemical properties of different fluorous liquids and how their molecular dynamics and interactions change from bulk to nanosized confined spaces. Following these future experiments, the predictive model can be improved upon allowing for more fine-tuning of sensors, to get maximal signal and reproducibility.

CONCLUSION

In this paper, we investigated the loading conditions that influence the efficiency of the PSLM for the confinement of perfluorocarbon liquids into the core of mesoporous silica nanoparticles.

Comparing methods (e.g., surfactant emulsion, Pickering emulsions, nanoencapsulation) has proven difficult for a lack of reporting or analysis on the conditions for loading or encapsulating PFC liquids into colloidal suspensions. Pochert et al. only reported a sonication time during entrapment. Furthermore, they quantified their fluorine loading in vivo by quantifying the MRI magnetization and comparing it to a signal of PFCE diluted in n-hexane. Of note, this approach requires assumptions about uniformity of the magnetic field and relaxation of the PFC while in different tissues. This process does not allow for the quick and accurate evaluation of PFC-loaded nanoparticles during the design of and optimization process for nanomaterials.

Diverging from Pochert et al., we investigated four factors hypothesized to influence the variability of the loading yield and efficiency. However, upon investigation we discovered that a pH ≥ 7, for the aqueous extraction phase, promotes stability of emulsions between the PFC liquid and aqueous phase in the absence of nanoparticles. In other loading methods, the pH is considered in terms of the surfactant or influence on colloidal stability; however, the effects of pH are lacking investigation at the interface between these perfluorocarbon liquids and aqueous phases. At this point in time, it is unclear what the exact mechanism is that drives this phenomenon. However, it warrants further investigation on how the pH of the continuous phase influences the size, formation, and stability of PFC-encapsulated nanoparticles.

Experimental design revealed that sonication time has the strongest influence on the loading yield and efficiency. Sonication time is a common step in PFC liquid encapsulation because it promotes emulsion formation or diffusion of unoccupied spaces.^30,60,61 The benefits of sonication time, for the PSLM, would likely be due to the increase in PFC molecules occupying the void space within the nanoparticle pores and cavities. While the sonication time influenced the yield and efficiency the most, the volume ratio and nanoparticle concentration inversely affected the yield and efficiency. However, validation experiments reveal the model does not fully explain the loading capability. The experiments suggest that there are confounding variables that need to be considered. With better sonication instruments, pulse time, temperature, energy, and other parameters can be controlled.

In addition to analyzing the mechanisms behind different loading methods, it should also be noted that characterization of material is also important to the conclusions of loading efficiency, as well as comparison of methodology. Differences in determining concentration of bulk material based on theoretical loading will vary between technique and calculation method. Therefore, the standardization of characterization and reporting is needed for future studies of the encapsulation of PFC liquids.

Regardless, the PSLM has potential as an alternative method to load and introduce large amounts of fluorous liquids into aqueous environments. The facile method of loading and extraction creates a versatility in nanoparticle design, where nanoparticles can be fine-tuned separately and utilized in situ when the fluorine-loaded nanoparticles are needed. Future applications are currently being pursued, and investigation in multi-PFC loaded nanoparticles are being developed, as dual PFC systems have potential to enhance biomedical diagnostics.^35,62,63