Rydberg polaritons in ReS₂ crystals

Abstract

Rhenium disulfide belongs to group VII transition metal dichalcogenides (TMDs) with attractive properties such as exceptionally high refractive index and remarkable oscillator strength, large in-plane birefringence, and good chemical stability. Unlike most other TMDs, the peculiar optical properties of rhenium disulfide persist from bulk to the monolayer, making this material potentially suitable for applications in optical devices. In this work, we demonstrate with unprecedented clarity the strong coupling between cavity modes and excited states, which results in a strong polariton interaction, showing the interest of these materials as a solid-state counterpart of Rydberg atomic systems. Moreover, we definitively clarify the nature of important spectral features, shedding light on some controversial aspects or incomplete interpretations and demonstrating that their origin is due to the interesting combination of the very high refractive index and the large oscillator strength expressed by these TMDs.

The strong coupling between light and Rydberg excitons in ReS2 crystals results in large polaritonic interactions.

INTRODUCTION

Transition metal dichalcogenides (TMDs) with chemical formula MX₂ (e.g., M = Mo, W, Re; X = S, Se) are van der Waals materials with outstanding structural and optical properties, such as chemical stability (1), mechanical flexibility (1), high binding energies (2, 3) and oscillator strengths, and narrow photoluminescence linewidths (4), which make them extremely attractive in a plethora of photonics and optoelectronics applications (5–7). Their optical and chemical properties vary according to which group the TMDs belong.

In particular, group VI TMDs—such as MoS₂, MoSe₂, WS₂, and WSe₂—are characterized by linear isotropic in-plane optical properties due to the high symmetry of their crystal structure. Moreover, they show a transition from indirect to direct bandgap when going from bulk to a monolayer. This is due to their strong interlayer coupling, which is broken when the out-of-plane confinement is achieved with single layers (8).

On the other hand, group VII TMDs, such as ReS₂ and ReSe₂, crystallize in a distorted single-layer trigonal (1T′) structure of triclinic symmetry (Fig. 1A) due to the Re-Re interaction aligned along the b axis. This results in reduced crystal symmetry, which leads to strong in-plane anisotropic optical properties (9, 10), inducing the formation of two almost orthogonally polarized in-plane excitons (9) and high optical birefringence (11, 12). These properties are exploited for different applications, such as field effect transistors (13, 14), polarized photodetectors (13, 15), and photocatalyst (16). Unlike other TMDs, ReS₂ and ReSe₂ are also characterized by a direct bandgap that persists from bulk to monolayer due to the distorted 1T structure (17) that hinders ordered stacking of neighboring layers and minimizes the interlayer overlap of wave functions, as shown by density functional theory calculations (18). Such a weak interlayer coupling makes it possible to achieve the same properties as two-dimensional (2D) systems, regardless of the number of layers, avoiding the challenging and time-consuming preparation of large-area monolayers. In addition, they have a very high refractive index in the visible/near-infrared spectral region, a quite unique feature compared to other materials (19). This makes ReS₂ extremely interesting for photonic applications and a unique platform for the exploration of novel topological properties when used as metamaterials.

Fig. 1. Origin of exciton splitting in reflection spectra.

(A) Sketch of ReS₂ monolayer atomic arrangement. The Re4 clustering chains, b axis, and the dipole direction of the main excitons are also indicated. The angle ϕ is defined as the polarization angle with respect to the b axis. (B) Reflection spectra of a 35-nm-thick (top) and an 80-nm-thick (bottom) ReS₂ crystal exfoliated on a glass substrate for parallel (black line) and perpendicular (red line) polarization respect to the b axis. a.u., arbitrary units. (C) Top panels show how different values of the real part background permittivity, ε_B, affect the reflectivity spectra close to the exciton resonance. Note that left and right panels reproduce the effect of a low and high permittivity on materials with a high oscillator strength, such as perovskites and ReS₂, respectively.

Materials with planar optical anisotropy that support matter-light quasiparticles (i.e., polaritons), resulting from the strong coupling between excitons and photons, are extremely interesting thanks to their potential for the realization of topological exciton-polariton systems. This is mainly due to the possibility of easily tuning the optoelectronic properties of the polariton device by actively changing different parameters, such as crystal thickness, polarization, external magnetic and electric field (20), and sample temperature. Moreover, it has been theoretically predicted that exciton-polariton condensates can exhibit longer-range algebraic correlations under nonequilibrium conditions only in strongly anisotropic systems (21). All these reasons make the highly anisotropic ReS₂ crystals, as active materials in exciton-polariton systems, very intriguing (22, 23).

In this work, we unambiguously demonstrate the polarization-dependent strong coupling in ReS₂ crystal and the hybridization between different higher-order exciton states resulting in Rydberg polaritons with enhanced interactions, making this material useful for the realization of polarization-controlled polaritonic devices. Taking advantage of the spectral features of strongly coupled ReS₂ polaritons, we demonstrate that ReS₂ crystals have only two orthogonally polarized excitons confuting previous studies, suggesting four excitonic resonances (24, 25).

RESULTS AND DISCUSSION

The ReS₂ crystal structure is shown in Fig. 1A: Each crystal layer of Re atoms is placed between two S sheets, with distorted trigonal antiprismatic coordination and strong covalent bonding between the Re and S atoms. Rhenium atoms (gray) form a chain due to the Re-Re bonds, which defines the b axis of the crystal. Because of the strong metal-metal bond, ReS₂ breaks preferentially along the b axis (26, 27), typically forming a longer crystal edge after mechanical exfoliation.

The distortion of the ReS₂ atomic structure induces the strong anisotropy of the exciton resonances, resulting in a different orientations and optical selection rules for linearly polarized light (25, 28, 29). The typical polarized reflection spectrum for a 35-nm-thick ReS₂ crystal exfoliated on glass substrate (top layer of Fig. 1B) are mainly characterized by one exciton resonance, E_x1, polarized parallel to the b axis (ϕ = 0°) (black line) and a second exciton resonance, E_x2, polarized almost perpendicular to the b axis (ϕ = 90°) (red line). Moving to thicker crystals, we observe some changes in the reflection spectra: 80-nm-thick ReS₂ exhibits an exciton resonance splitting for each polarization, and excited state transitions appear at higher energy (~1.65 eV) as shown in the bottom layer of Fig. 1B.

Additional resonances around the main exciton have already been observed in previous works (22, 23), and, as in our case, these features have been distinguishable for crystals exfoliated in thick flakes (≥50 nm) (9, 25), whereas for the thinner one, only the main exciton transition is distinctly observable (9, 29–31). However, their nature is still debated. In the work of Arora et al. (25), multiple close-lying bright excitons were associated to degenerate direct transitions twofold from the valence band maximum to the conduction band minimum, with each degenerate pair consisting of bands with opposite spins. Additional peaks appearing below the exciton in thick crystals have been attributed to donor bound excitons (9), whereas Dhara and colleagues (23, 24) hypothesized that these peaks are (i) due to the splitting of singlet and triplet states of excitons as a result of the electron-hole exchange interaction or (ii) induced from the broken rotational symmetry due to the structural anisotropy and spin-orbit coupling of ReS₂. Recently, Gogna et al. (22) hint at an apparent splitting of the exciton resonance due to the cavity effect caused by reflections within the flake. Here, we assess that the two resonances that appear for both polarized excitonic transitions are, in fact, the longitudinal and transverse excitons to which the polaritonic branches asymptotically tend and observable in ReS₂ crystals for flakes thicker than 50 nm. This is due to the unique combination of material optical parameters, mainly (i) the very high background refractive index and (ii) the large oscillator strength associated to the ReS₂ excitons.

To investigate the role of the high background refractive index on the reflectivity of the ReS₂, we consider the reflectance, at zero-order approximation, given by $R=\frac{(1-n{)}^2+k^2}{(1+n{)}^2+k^2}$, where n and n' are the real and imaginary part of the complex refractive index, respectively. Because of the very high real part of the refractive index, $n=\sqrt{\mathrm{Re}[\mathrm{ϵ}(\mathrm{\omega })]}>4$ (where ε(ω) is the complex permittivity), the crystal flakes, when lying on a low index material, behave as a dielectric slab resonator supporting Fabry-Perot modes. Because of the high oscillator strength, f ∼ 0.3 eV², of the excitonic transitions, there is a strong interaction between these modes and the exciton resonances, giving rise to new hybrid states called polaritons (32).

This can be easily described by modeling the two polarization-dependent exciton resonances, E_X1 and E_X2, with a Lorentz oscillator using a dielectric function given by

$${\mathrm{\epsilon }}_{1,2}(\mathrm{\omega })={\mathrm{\epsilon }}_{{\mathrm{B}}_{1,2}}+\frac{f_{1,2}}{{\mathrm{E}}_{{\mathrm{x}}_{1,2}}^2-E^2-\mathrm{i}E{\mathrm{\Gamma }}_{1,2}}$$ (1)

where E = ħω, ε_B is the background permittivity, E_X is the excitonic resonance, Γ is the exciton linewidth, and f is the oscillator strength. We found that in ReS₂, because of the peculiar combination of high refractive index and strong exciton oscillator strength, the real part of the permittivity crosses zero and becomes negative around the exciton resonance (Fig. 1C, top right). By considering the spatial evolution of the field in this negative epsilon region (negative permittivity), following Maxwell’s equations (33), we can obtain two class of solutions given by (i) ε (ω) = 0 and (ii) $\overrightarrow{k}\bullet \overrightarrow{E_{\mathrm{ElectricField}}}=0$. The first solution Ε_L = ħω_L corresponds to the appearing of a longitudinal mode, which is usually invisible in ordinary materials, while the second solution E_T = ħω_T corresponds to the standard transversal mode (34, 35). As a result of the appearance of both self-hybridized modes in the region with Re[ε] < 0, the electromagnetic wave cannot propagate into the material but rather exponentially decay, resulting in a strong effective reflectivity (36). Note that the energy position of the longitudinal mode and the gap between E_L and E_T strongly depend on the background permittivity of the material, ε_B. By decreasing ε_B, the longitudinal modes shift at higher energy, resulting in an increase in the longitudinal-transversal energy splitting ΔE_L/T = ħω_L − ħω_T. (Fig. 1C, top) but with a smoother transition between the region with Re[ε] < 0 and Re[ε] > 0. On the other hand, for fixed background permittivity, ε_B, ΔE_L/T increases for higher coupling strength between the exciton and photons (i.e., higher oscillator strength of the exciton resonance, fig.S1). It is therefore clear that both modes can be sharply seen only in those materials that have a high permittivity while keeping an equally high oscillator strength. ReS₂ has the chance to meet both criteria.

The polarized reflectance spectrum of ReS₂ crystals exfoliated on top of a glass substrate has therefore this characteristic. Simulations using the semianalytical rigorous coupled-wave analysis method (37) depict very well this behavior. Note that, looking at Fig. 1C, materials such as perovskites (parameters simulated in the bottom left panel) with a high background refractive index (n ∼ 2, i.e., ε_B ∼ 4) and a real part of the permittivity that also becomes negative do not show two sharp resonances due to the smooth variation of the permittivity if compared to the ReS₂, which is simulated in the righthand side of Fig. 1C.

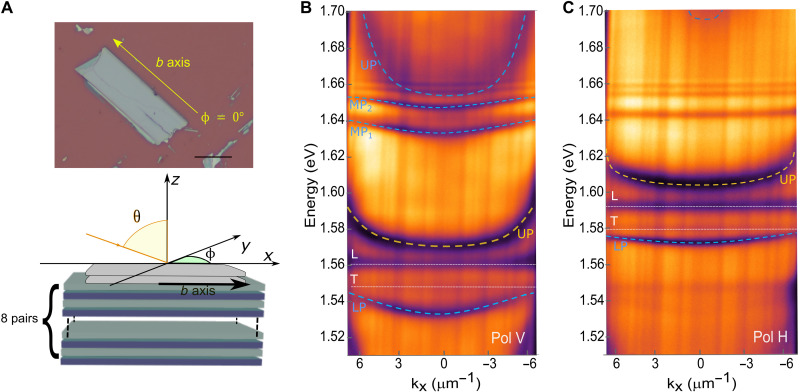
In the following, we exploit the high refractive index and the strong oscillator strength of the excitonic transitions in ReS₂ to investigate the full hybridized dispersion of the ground-state excitons and the first two excited states under strong coupling regime. To do so, we have exfoliated a 310-nm-thick ReS₂ crystal (Fig. 2A and fig. S3) on a distributed Bragg reflector (DBR) that increase the mode finesse without reducing the photoluminescence collection from the front side of the crystal. Figure 2 (B and C) shows the linearly polarized energy reflection as function of the in-plane momentum, k_x. The spectra unambiguously evidence the typical dispersions of a system in strong light-matter coupling regime, with the folding of the energy bands for the two excitons depending on the direction of polarization.

Fig. 2. Strong coupling with Rydberg excitons.

(A) Top: Optical microscope image of a 310-nm-thick ReS₂ flake exfoliated on a DBR. Scale bar, 20 μm. Bottom: Scheme of the structure composed of a bottom DBR made by eight SiO₂/TiO₂ pairs with a ReS₂ crystal (gray) on top. (B and C) Energy versus k_x in-plane momentum reflection spectra polarized parallel to the b axis (B) and perpendicular to the b axis (C). The blue dashed lines are the calculated polariton branches resulting from the strong coupling of the exciton with a cavity mode: LP is the lower polariton, whereas the MP_1,2 are the first and second middle polaritons; the yellow dashed line is the polariton upper polariton (UP) branch induced by the coupling of the exciton with the previous mode, whereas the white dashed lines are the energies of the transversal (T) and longitudinal (L) modes.

Because of the strong in-plane optical birefringence present in ReS₂ crystal, the real part of the refractive index along the Re-Re chain direction (b axis, ϕ = 0°, n = 4.1) is ∼20% higher than the ones along the perpendicular direction (ϕ = 90°, n = 3.2) (11, 38, 39). Consequently, the photonic modes of the structure shift at higher energy for the H polarization with respect to the V polarization. This results in a different detuning of the polariton states with a different fraction of photon and exciton for each polaritonic band in the two linear polarizations.

A detailed theoretical analysis of the reflectivity at {k_x, k_y}= 0 as a function of the crystal thickness has allowed to associate the various dispersion curves for the two polarizations. For the V polarization, both the exciton E_X1 and the excited states are strongly coupled to a Fabry-Perot photonic mode (fig. S4A), resulting in the formation of lower polariton (LP, at 1.533 eV), middle polaritons (MP₁, at 1.632 eV and MP₂ at 1.647 eV), and upper polariton (UP, at 1.653 eV) branches (dashed blue guidelines and label in Fig. 2B). The polariton state evidenced by the dashed yellow line instead represents the upper polariton branch, generated by the strong coupling of the exciton E_X1 with a previous Fabry-Perot photonic mode (energy of the bare mode ~ 1.4 eV). The corresponding lower polariton branch of this other Fabry-Perot mode is not experimentally observable because its energy is outside the stopband of the DBR. Last, the transitions evidenced by the pointed dashed white lines are the transversal and longitudinal modes as described in Fig. 1B and 1C.

The dispersion spectrum in the H-polarized direction (Fig. 3C) shows a similar behavior for the exciton E_x2 despite a different detuning of the mode and lower oscillator strength. However, the excited states remain uncoupled being the photonic modes highly detuned from these energies (see also fig. S3B). By changing the ReS₂ crystal thickness, we can also be able to tune the coupling of the exciton and the one of the excited states, varying the number and position of the photonic modes (figs. S5 and S6).

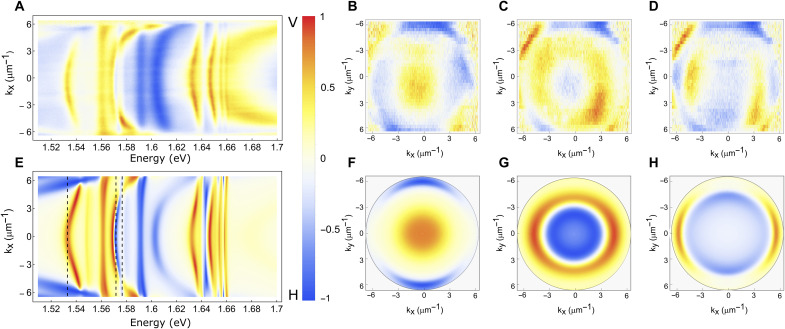
Fig. 3. Degree of polarization in k space.

(A to H) Experimental (A) and theoretical (E) degree of linear polarization (DOP) of the reflectance signal in the horizontal/vertical (H/V) basis. Experimental (B to D) and theoretical (F to H) DOP of the reflectance maps in the momentum space at isoenergetic cross sections corresponding to the lower polariton of the exciton E_X1 (B and F), the lower polariton of the exciton E_X2 (C and G), and at the energy where the lower polariton of exciton E_X2 that crosses at the higher k_x values the upper polariton of E_X1 (D and H).

By making a 1D raster scan, we can reconstruct the reflectance spectra in both directions of the Fourier plane. The k_x-k_y dispersion maps for the two polarizations are plotted in Fig. 3A in terms of the degree of linear polarization (DOP), defined as (I_V − I_H)/(I_V + I_H), where I_H and I_V are the reflected light intensities for horizontal and vertical polarizations, respectively. Figure 3 (A and E) demonstrates the good agreement between the experimental DOP (Fig. 3A) along the k_x direction at k_y = 0 with the theoretical calculations (Fig. 3E). In our structure, there are several contributions to the linear polarization of polariton states. One is the transverse electric (TE)/transverse magnetic (TM) splitting, which is due to the intrinsic difference between the in- and out-of-plane effective refractive indices. Note that this energy splitting is bigger at higher k vectors. The second contribution comes from the in-plane optical anisotropy (crystal birefringence), which splits the modes at any k vectors along the two preferential axis. Lastly, in this material, there is also a polarization-dependent strong coupling of the two orientation of the exciton dipoles. Unlike TE/TM splitting, the other two contributions do not induce any polarization rotation. Figure 3 (B, C, F, and G) shows the DOP of modes well separated in energy, having an isotropic polarization in k_x and k_y, due to the higher contribution of the birefringence compared to the TE/TM splitting. At the energy of about 1.574 eV, two different optical modes, respectively, coupled with one of the two excitons cross at high vector k, k_x ∼ ±6 μm⁻¹. At this energy, the TE/TM effect begins to be observable, showing preferential coupling along the two dipole directions (see Fig. 3, D and H).

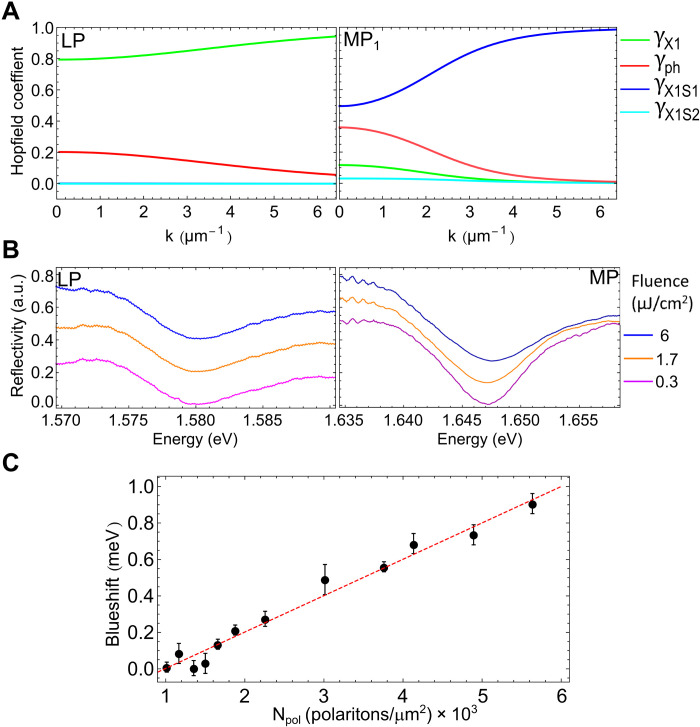
The excited states, visible in Fig. 2B above 1.64 eV, also show strong coupling with same slab cavity mode. The values of the Rabi and the coupling strength for each exciton state are extracted by fitting our dispersions with a four coupled oscillator models (one mode, the ground exciton state, and two excited states). The result of this fitting is shown in fig. S7A with an extracted Rabi splitting of 84, 20, and 12 meV for the lower and the middle polariton states, respectively. By focusing on the Hopfield coefficients, which give the contribution of the excitons and the photon mode to the different polariton states, we can estimate the character of the polariton modes and how the polariton-polariton interaction should change in each of the three polariton branches. In Fig. 4A, which shows the Hopfield coefficients calculated for the lower and the first middle polaritonic bands, it can be seen that the lowest exciton-polariton mode (Fig. 4A, left) is practically decoupled from the excited excitons, and the state is predominantly having a ground-state character (with 80% of the fundamental exciton and only a 20% of photon contribution). Unexpectedly, the first middle polariton branch (Fig. 4A, right) is composed of three excitonic components, the fundamental and the two excited excitons. We can speculate then that such a state should lead to stronger polariton nonlinearity described with an interaction coefficient, g_p−p, enhanced by the presence of higher-order excitons (40–42). For the excited states (called also Rydberg states), the radius of the different orbits scales as n². Because the exciton-exciton interaction g_{X − X}(n) depends linearly on the Bohr radius (a_B), its intensity should increase quadratically: g_{X − X}(n) = 6E_b(n)a_B²n², where E_b(n) is the binding energy of the nth state extracted by fitting the energy position of the different states in the absorption spectrum (fig. S8). Because the polariton-polariton interaction is given by the weighted sum of the different exciton contributions $g_{p-p}=\sum _n{{\mathrm{\gamma }}_{X_n}}^2{g}_{X-X}(n)$, where γ_Xn represents the normalized Hopfield coefficient for the nth state, it should be proportionally higher for the middle branch, which has higher content of the Rydberg excitons.

Fig. 4. Hopfield coefficients and polariton nonlinearity.

(A) Hopfield coefficients extracted for the lower (left) and first middle (right) polariton branch. (B) Reflection spectra obtained by resonantly exciting the lower and the middle polariton branches at k = 0 for different excitation pump powers. (C) Blueshift of the middle polariton by resonantly exciting the sample with a laser linearly polarized to the b axis; the dashed red line is the linear fit to the experimental data, resulting in a polariton-polariton interaction constant N_pol(X1_S1) = 0.2 μeV μm².

To experimentally observe this polariton-polariton interaction, we resonantly excite the ReS₂ crystal with a fast, broadband, pulsed laser (∼50 fs) polarized along the b axis. We observe that whereas the reflection spectrum of the lower polariton state does not change by increasing the excitation power (Fig. 4B, left), possibly due to the limited nonlinearity of the ground-state exciton, the spectrum of the first middle polariton branch shows a small shift toward higher energies (Fig. 4B, right) (43, 44). The energy blueshift of the reflection peak is plotted in Fig. 4C for the middle polariton state against the polariton density, resulting in a small but observable blueshift of about 1 meV. By fitting the experimental data (red shaded line in Fig. 4C), we are able to extract the polariton-polariton interaction constant g_pol (X1_S1) = 0.2 μeV μm². Although the second middle polariton should be characterized by a stronger polariton-polariton interaction, we do not observe any spectral shift with the pumping power. In general, we believe that because of the low quantum efficiency of this material (45), the real power density injected in resonant excitation is extremely low. This could be also the reason for such a small blueshift of the middle polariton branch and the lack of observable shift for the ground-state polariton.

In conclusion, we investigated the effect of the high refractive index and strong oscillator strength of the exciton transitions in ReS₂ crystals and elucidated it. By hybridizing the ground-state excitons and the two first excited states, we are able to measure the effect of exciton-exciton interaction on the Rydberg states, showing a much stronger polariton-polariton interaction compared to the lower-energy state. Moreover, we have definitively demonstrated that this material has only two orthogonally polarized excitons, and we attributed the additional line in the reflectivity spectra to the longitudinal exciton feature. This work, beyond shedding light on the presence of different transition lines previously observed in ReS₂ but mistakenly understood, provides new insights into this exciting material that could be successfully implemented in the realization of optical devices that exploit higher-order Rydberg states in solid-state materials.

MATERIALS AND METHODS

ReS₂ bulk crystals were grown by chemical vapor transport method using ICl₃ as the transport agent (9). Because of the weak vDW bonding between the layers, micrometer-sized ReS₂ flakes with desired thickness were obtained by mechanically exfoliating from bulk crystals and transferring them onto the final substrate by a dry transfer method (46) using commercial polydimethylsiloxane. The flakes were transferred on glass or DBR formed by eight pairs of SiO₂/TiO₂ with a stopband centered at λ_c = 785 nm and grown on glass substrate by electron-beam deposition (see the Supplementary Materials for details). By using a closed-cycle cryostat (attoDRY1000), the sample is cooled down to liquid helium temperature (T = 4 K) and excited by a white halogen lamp to measure the reflection spectra both in real and Fourier space. The polarized spectra along the b axis (V-polarized, ϕ = 0) and perpendicular to it (H-polarized, ϕ = 90) were obtained using a half wave plate and a polarizer placed in front of a spectrometer coupled to a charge-coupled device.

Supplementary Materials

This PDF file includes:

Supplementary Text

Figs. S1 to S8

Tables S1 and S2

References