Abstract
The Brier score has been a popular measure of prediction accuracy for binary outcomes. However, it is not straightforward to interpret the Brier score for a prediction model since its value depends on the outcome prevalence. We decompose the Brier score into two components, the mean squares between the estimated and true underlying binary probabilities, and the variance of the binary outcome that is not reflective of the model performance. We then propose to modify the Brier score by removing the variance of the binary outcome, estimated via a general sliding window approach. We show that the new proposed measure is more sensitive for comparing different models through simulation. A standardized performance improvement measure is also proposed based on the new criterion to quantify the improvement of prediction performance. We apply the new measures to the data from the Breast Cancer Surveillance Consortium and compare the performance of predicting breast cancer risk using the models with and without its most important predictor.
Keywords: Brier score, binary risk prediction, breast cancer risk
1. Introduction
Developing a risk prediction model for binary outcomes has been very popular in clinical research and practice. For example, the Framingham risk score was developed to predict the ten-year risk of developing coronary heart disease. Since its first development,1 the Framingham risk score has been validated in different population2 and become a useful risk stratification tool for cardiovascular disease in clinical practice. The Breast Cancer Surveillance Consortium (BCSC) risk calculator was developed to predict a woman’s five-year risk of developing invasive breast cancer,3 which is now commonly used for breast cancer screening in practice.
Guidelines on developing and validating risk prediction models have been discussed extensively in literature.4,5 A key exercise in developing a risk prediction model is to evaluate how well the model predicts the outcome. The performance of a prediction model is often evaluated in term of discrimination and calibration. For binary outcomes, discrimination refers to the model’s ability to separate those who developed the events from those who did not. Commonly used measures for model discrimination for binary outcomes include sensitivity, specificity, and C-statistic (i.e. the area under the receiver operating characteristic (ROC) curve).6–9 Calibration is a measure of how well the predicted probability of a binary outcome is in agreement with what was observed, which can be assessed by testing for lack-of-fit, such as the Hosmer-Lemeshow goodness-of-fit test.10 More recent developments in the literature suggest evaluating the relationship between the observed outcome and corresponding predicted probabilities through graphical tools,11 parametric models,12–14 and nonparametric smoothing methods.15 Van Calster et al.16 summarized different calibration measures using a hierarchy of four increasingly strict levels, referred to as mean, weak, moderate and strong calibration.
A prediction model that has good discrimination may not be well calibrated and vice versa. In addition to the discrimination and calibration evaluations, statistical measures for the overall prediction accuracy are also necessary. The Brier score has been a popular metric for evaluating the overall prediction accuracy of binary outcomes since it was introduced.17 It is defined as the mean squared difference between the observed value of a binary outcome and its predicted probability. Despite its popularity in clinical prediction research, there are a few issues for interpreting the value of Brier score. For example, the C-statistic is a measure for model discrimination with values between 0.5 and 1. A larger C-statistic indicates better model discrimination and prediction performance. A rule of thumb is that a model with C-statistic greater than 0.8 is considered a well performing prediction model. Unlike the C-statistic, the Brier score is not defined in a standardized scale. Consequently, there is no single standard on how small the Brier score should be for a model with good prediction performance. Part of the reason is that the Brier score depends on the variance of the binary outcome, which is a function of the binary outcome probability. In this manuscript, we propose a decomposition of the Brier score, separating the part that measures the model prediction performance from the binary data variability determined by the underlying data generation mechanism. Since the data generation mechanism is unknown, it is difficult to have an unbiased estimate of the outcome variance. Therefore, our goal focuses on developing a measure that is more sensitive in comparing prediction performance than having an unbiased estimation.
Our work is partially motivated by the decomposition of Brier score literature. Two popular methods were proposed that partitioned the Brier score into either two18 or three19 components. In the three-component setting, each component corresponds to measures of the so-called reliability, resolution and uncertainty respectively. The uncertainty component is defined as the variance of a Bernoulli experiment with the probability of an event calculated as the average proportion of events occurred over all samples. It is calculated as if all subjects in the sample have the same probability of the binary outcome. However, the uncertainty component is not truly reflective of the data variability since different subjects may have different probabilities due to different covariate values. Instead, we propose to estimate the variability of the Bernoulli experiment for each subject and subtract it from the Brier score. The modified criterion is a pure measure of model performance such that its lower limit is zero when the true model is used.
We also propose a scaled measure based on the modified Brier score for comparing the prediction performance between different models. Similar work for modifying the Brier score to compare different models was done by Kattan and Gerds.20In their work, the Brier score was scaled by comparing to a null model in which there is no predictor. The model improvement was defined as the reduction of the Brier score relative to the null model.
The rest of the article is organized as follows. We first describe the proposed modified criterion, followed by its estimation in two different settings. We then describe two extensions of the modified criterion. We demonstrate the performance of the modified criterion through simulation with an application to the BCSC risk prediction. We conclude the article with a discussion and brief summary.
2. A modified criterion
Let Y ∈ {0, 1} denote a binary outcome. Assume Y ~ Bernoulli(p), where p is the true probability of Y = 1. Let r denote a predicted probability of Y = 1. The prediction accuracy for r can be characterized by its squared difference from the observed binary outcome Y, that is, (r − Y)2. Its expectation can be decomposed as
| (1) |
The last step follows because p = E(Y). Note that r is considered a fixed quantity whose prediction accuracy is to be evaluated.
In the decomposition, the first component is the squared difference between the true and predicted probability of Y = 1. It measures how close the predicted probability r is to the true probability p and is a reflection of the prediction performance for r. The second component is the variance of Y, that is, Var(Y) = E{(p − Y)2}. It is determined by the underlying data generation mechanism for Y, and is not reflective of prediction performance. The decomposition is similar to what was proposed by Murphy18 where the two components are referred to as the reliability and resolution measures, respectively. Since the second component in equation (1) has nothing to do with the predicted probability r, we propose to use only the first component, that is, (r − p)2 to evaluate the prediction accuracy.
For a total of N subjects with observed outcome Yi, outcome probability pi and corresponding predicted probability ri, i = 1, . . . , N, the Brier score is defined as
| (2) |
Similar to equation (1), the Brier score can also be decomposed as following
| (3) |
Motivated by the decomposition in equation (1), we propose to use only the first term on the right side of equation (3) to evaluate prediction accuracy for all N subjects, and call it the mean square error for the probability of binary outcome (MSEP), that is,
| (4) |
Unlike the product term in equation (1) which is zero, the third component on the right side of equation (3) is in general not zero. However, as will be shown in the next section, we propose to estimate the true outcome probability pi such that the product term in equation (3) is either strictly zero or approximately zero. When the predicted probabilities ri are discrete, the product term is strictly zero within each stratum defined by the unique value of the predicted probability. When the predicted probabilities ri are continuous, the product term is asymptotically zero when the estimator for pi is consistent. Consequently, the MSEP can be seen as the Brier score subtracting the binary outcome variance.
Similar to the Brier score, a smaller value of MSEP indicates a better prediction performance. The smallest possible value of MSEP is zero, when the true and predicted probabilities are exactly the same for all subjects. Since the true outcome probability is not known, the MSEP cannot be calculated directly. Instead, we propose to estimate the MSEP by subtracting the variance of Y from the Brier score. The estimation of the outcome variance is given in the next section.
3. Estimation
We propose a nonparametric method for estimating the binary outcome variance. Assume the predicted probabilities ri have finite number of unique values, rk, k = 1, . . . , K. For example, this can happen if the predicted probabilities are estimated from a model that includes only categorical predictors. The data can be grouped into K strata, one corresponding to each unique rk. For each subject i, i = 1, . . . , N, who belongs to stratum k ∈ (1, . . . , K), Var(Yi) can be estimated as following
| (5) |
where is the average of Y within stratum k, that is, and Nk is the number of subjects in stratum k. Within each stratum k, the cross product component on the right side of equation (3) is
Consequently, the sum of cross product component across all K strata is also zero.
The MSEP can then be estimated as
| (6) |
where is estimated using equation (5).
When the number of unique predicted probabilities is large, the number of subjects within each stratum having the same predicted probabilities can be small so that in equation (5) may not be stable to estimate Var(Yi). Furthermore, if a prediction model includes continuous predictors, it is possible that all of the predicted probabilities are unique such that Nk = 1 for all strata. For these scenarios, we propose a general sliding window approach to estimate the variance of Y.
We first sort the outcome Yi, i = 1, . . . , N based on the corresponding predicted probability ri, i = 1, . . . , N, that is,
We then apply a moving average filter to estimate the variance for each subject i, i.e.,
| (7) |
where
and M is the width of the moving average filter. Since is a consistent estimator of pi within each sliding window, the cross product component on the right side of equation (3) is approximately zero. Consequently, the MSEP can be estimated using equation (6) where is estimated using equation (7). Note that the predictive probabilities are only used to order the subjects and not involved in the variance estimation.
In practice, it is very difficult to have an unbiased estimate of the variance and MSEP accordingly, since we do not know the true data generation mechanism. It is preferred to have an underestimated variance as otherwise the MSEP may be negative when the variance is overestimated. As we will show through simulation in the next section, the estimated outcome variance and MSEP are not very sensitive to the sliding window size. In general, a smaller window size is preferred given the negative consequence of overestimating the variance.
4. Extensions
The MSEP compares the difference between the true and predicted outcome probability. Sometimes, it may be useful to quantify the accuracy associated with the predicted probability relative to the true outcome probability. We can standardize the MSEP by taking its square root and then dividing by the outcome probability, referred to as the scaled root MSEP (SRMSEP), that is,
| (8) |
which can be estimated as
| (9) |
We can also use the MSEP to compare the prediction performance for different models and evaluate the performance improvement. Let us consider the comparison between an existing model and a revised model. Assume the MSEP for the existing and revised models are MSEP1 and MSEP2 respectively. The performance improvement (PI) of the revised model compared to the existing model can be defined as
| (10) |
If the model improvement is minimal, for example, MSEP1 − MSEP2 ≈ 0, then the performance improvement is close to zero, that is, PI ≈ 0. If the MSEP for the revised model is close to zero, that is, MSEP2 ≈ 0, meaning that the revised model predicts the true outcome probability almost perfectly, then the performance improvement is close to one, that is, PI ≈ 1. The PI is negative if the revised model is worse than the existing model, that is, MSEP2 > MSEP1.
The performance improvement measure can also be defined using the Brier score. Suppose we redefine the performance improvement in equation (10) by replacing the MSEP with the Brier score. Let BS1 and BS2 denote the Brier score for the existing and revised model, respectively. The performance improvement based on the Brier score is
| (11) |
Compared to equation (10), the numerators for the two definitions of PI are the same. They differ in the denominator where the denominator in equation (10) is the denominator in equation (11) subtracting the outcome variance. Consequently, the PI defined using the MSEP is less dependent on the outcome prevalence than the corresponding one using the Brier score. Consider again the scenario where the predicted probabilities from the revised model perfectly match the true outcome probabilities for all subjects, that is, MSEP2 = 0. The PI based on the MSEP is 1 and the PI based on the Brier score is less than 1 and its value depends on the outcome prevalence.
5. Simulation
We ran two simulation studies to evaluate the model prediction performance using the MSEP and compared it to the Brier score and index of prediction accuracy (IPA).20
We generated a binary outcome Y ~ Bernoulli(p), where
In the first simulation, X1, X2, and X3 were independent random variables following a Bernoulli(0.5) distribution and β0 = −1, β1 = 1, β2 = 1, β3 = 1. In the second simulation, X1, X2, and X3 followed a Uniform( − 1, 1) distribution with the same beta coefficients. The sample size for both simulations was 400, of which 200 random samples were used as the training data and the other 200 samples were used as the validation data.
We fit two logistic models in the training data. The first model included X1 and X2 in the model. The second model additionally included X3 in the model. The prediction performance of the two models were evaluated using the estimated BS, IPA, and MSEP in the validation data. We also compared them with the true MSEP. The MSEP was estimated using equation (6) in which the outcome variance was estimated using equations (5) and (7) in simulations I and II, respectively. We used the moving average window size of 10 in estimating the outcome variance in Simulation II. Both simulations were repeated 200 times.
Based on the second simulation, we additionally evaluated the sensitivity of the proposed variance estimator in equation (7) with respect to the moving average window size. We additionally increased the sample size of the validation data to 400 and 800. We also varied the β0 coefficient, that is, β0 = c( − 2, − 1, 0), which corresponds to the outcome prevalence of about 0.15, 0.3, and 0.5, respectively.
Figure 1 summarizes the results for the estimated BS, IPA, and MSEP for Simulation I. The distribution of the estimated BS and IPA for the two models overlapped, providing no clear evidence of model improvement by adding X3 in the model. In contrast, the estimated MSEPs for the two models had less overlap and provided stronger evidence of better performance comparing Model 2 to Model 1. In addition, the estimated MSEPs for both models were close to the true values despite underestimation, suggesting a good performance of variance estimation. Figure 2 shows the performance improvement defined in equation (10). As expected, the PI calculated using the estimated MSEP is underestimated comparing to the true value due to the variance underestimation. However, the PI based on the estimated MSEP showed much larger improvement in prediction accuracy than the corresponding one calculated using the Brier score.
Figure 1.
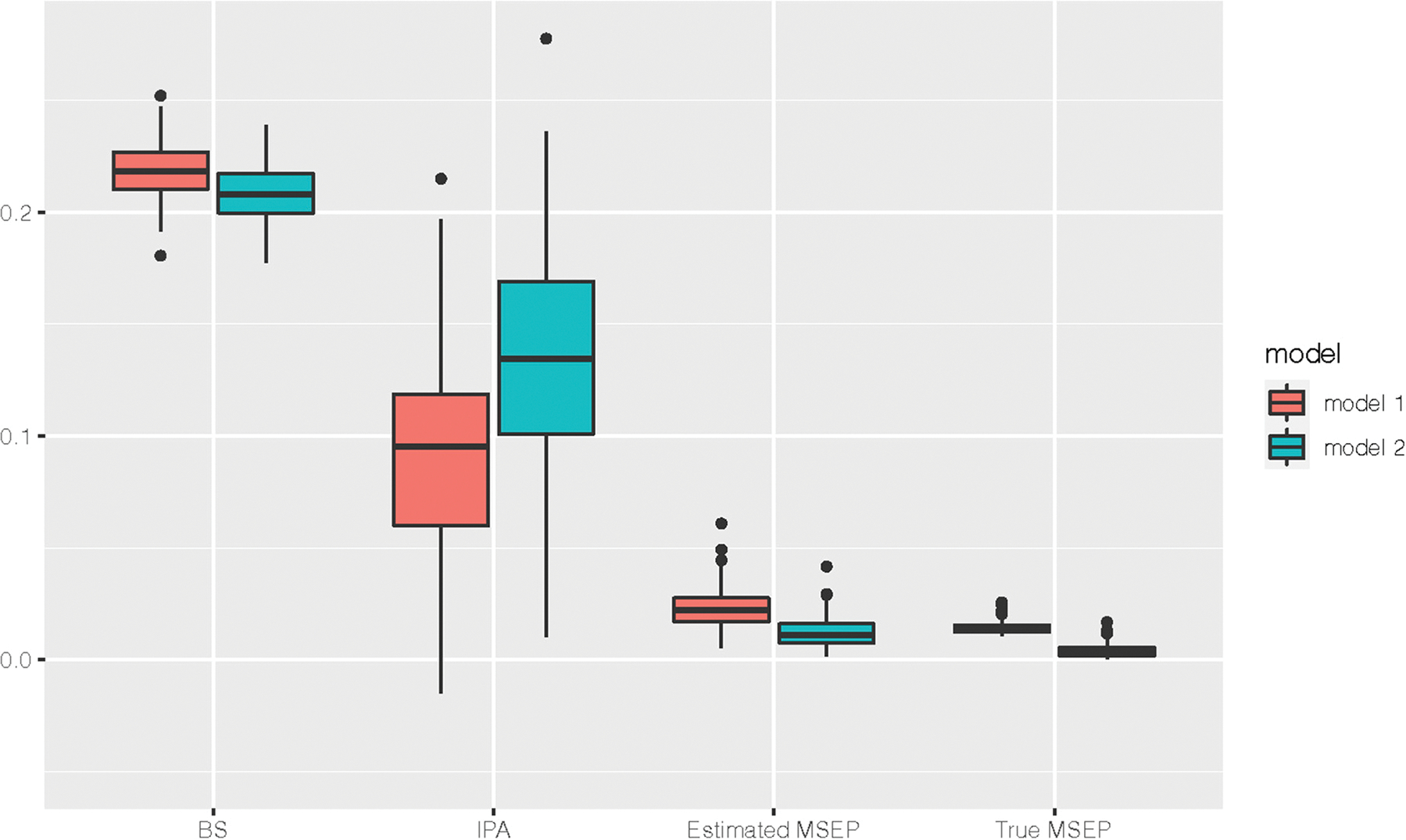
The comparison of BS, IPA, estimated and true MSEPs between the two models in Simulation I where all predictors are binary variables. MSEPs: mean square error for the probability of binary outcomes; BS: Brier score; IPA: index of prediction accuracy. Model 1 includes X1 and X2 as the predictor. Model 2 additionally includes X3 in the model.
Figure 2.
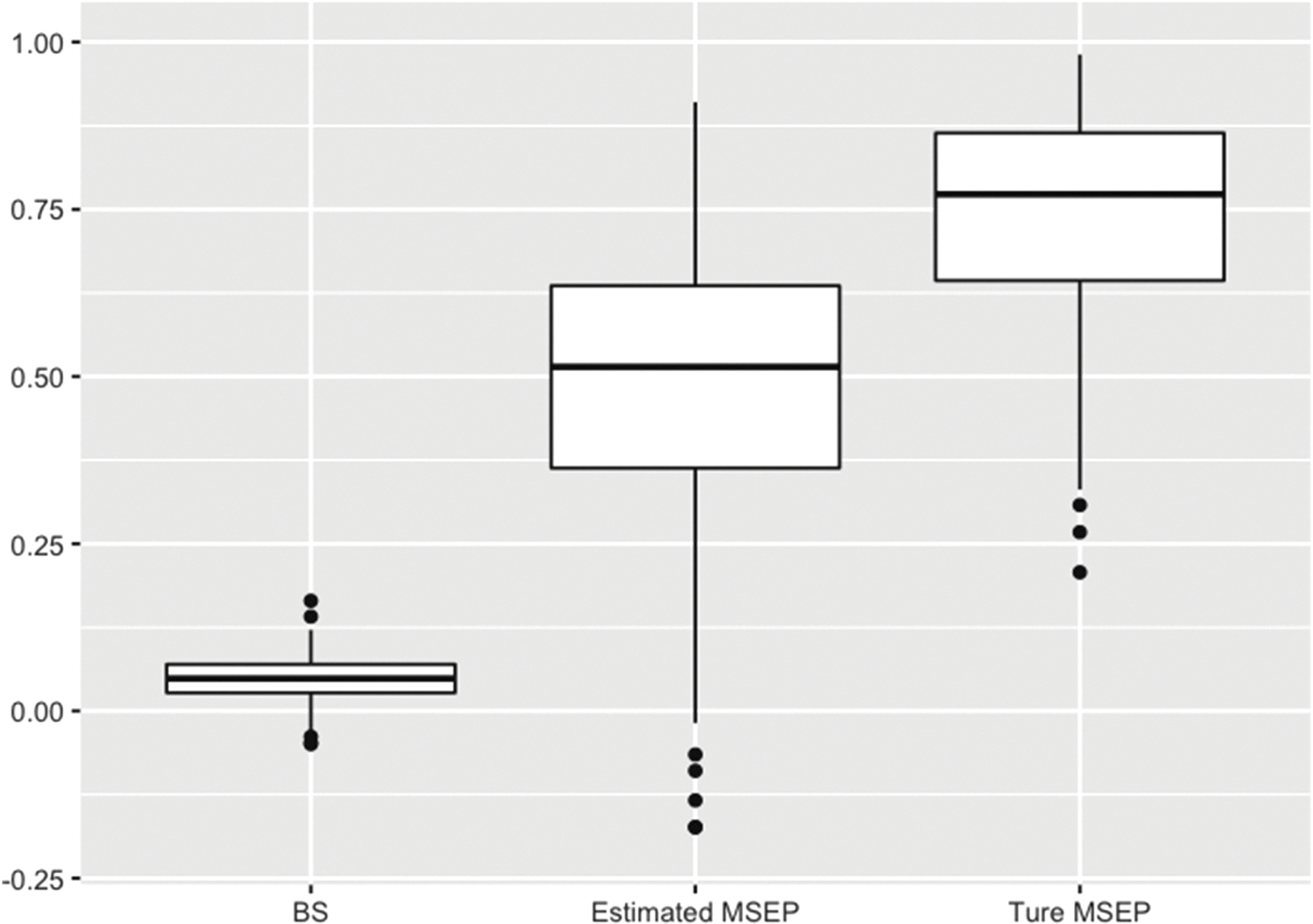
Performance improvement between the two models defined using the BS, estimated and true MSEPs in Simulation I. MSEPs: mean square error for the probability of binary outcomes; BS: Brier score.
Figure 3 summarizes the results for the BS, IPA, and MSEPs for Simulation II. To evaluate if the estimated MSEP is sensitive to how the subjects were ordered in the sliding window approach, the MSEPs were estimated in two ways, differed by how the outcome variable was sorted. The outcomes were sorted by the predicted probabilities from Models 1 and 2 when estimating MSEP1 and MSEP2, respectively. Both estimated MSEPs showed better separation between the two models compared to the BS and IPA. The estimated MSEPs were close to their true values. In addition, the estimated MSEPs using the two different subject ranking were close to each other, suggesting the results were not sensitive to how the outcomes were sorted when applying the moving average filter.
Figure 3.
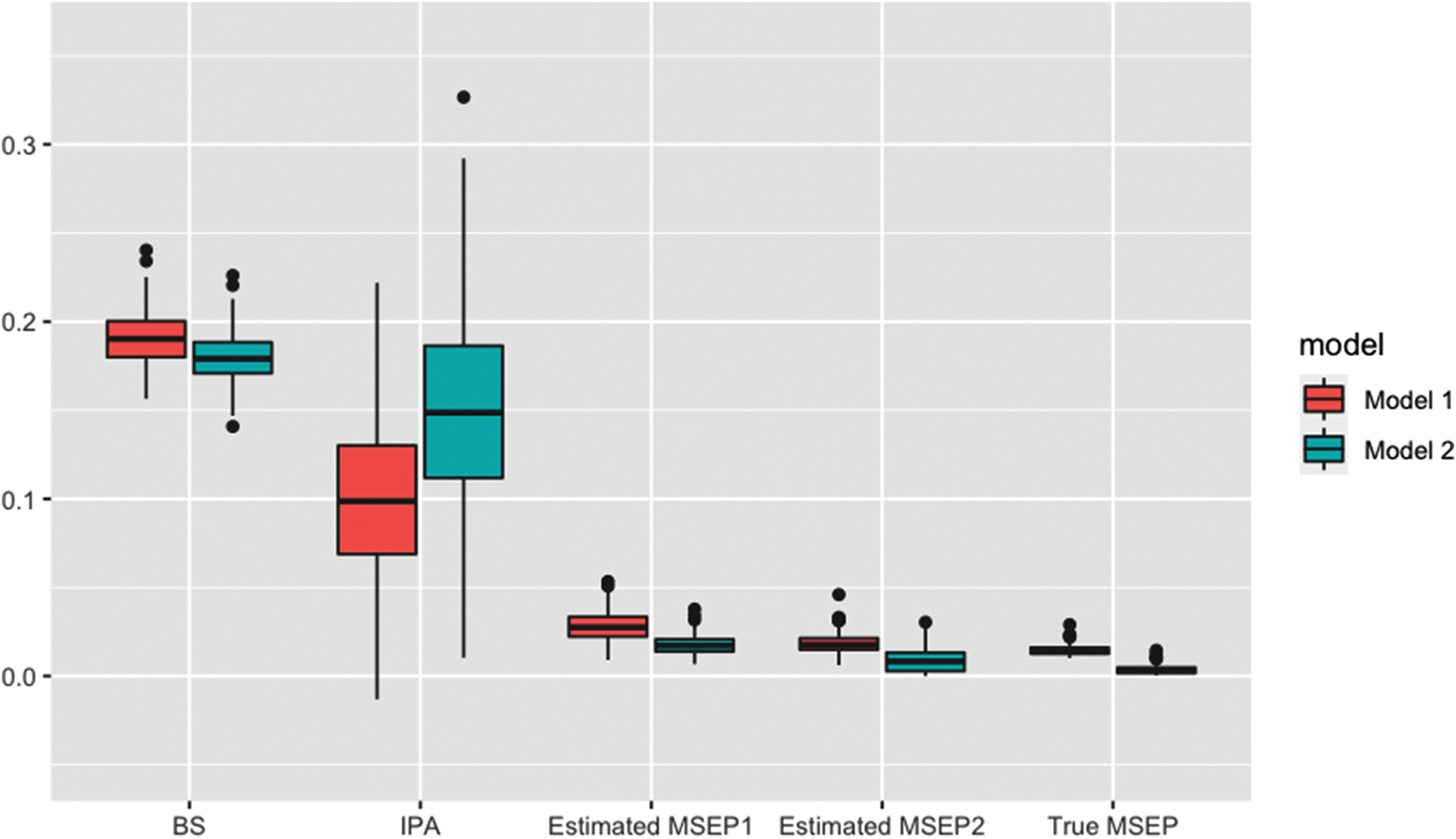
The comparison of BS, IPA, estimated and true MSEPs between the two models in Simulation II where all predictors are continuous variables. The MSEP1 and MSEP2 were estimated by ranking the subjects based on their predicted probabilities from Models 1 and 2, respectively. MSEPs: mean square error for the probability of binary outcome; BS: Brier score; IPA: index of prediction accuracy. Model 1 includes X1 and X2 as the predictor. Model 2 additionally includes X3 in the model.
Figure 4 shows the performance improvement comparing Models 1 and 2 in Simulation II, calculated using the BS, the two estimated MSEPs and true MSEP. The PI calculated using the two estimated MSEPs showed greater improvement compared to the one calculated using the Brier score, which is more consistent with the intuition that the prediction performance improves by adding an independent significant predictor.
Figure 4.
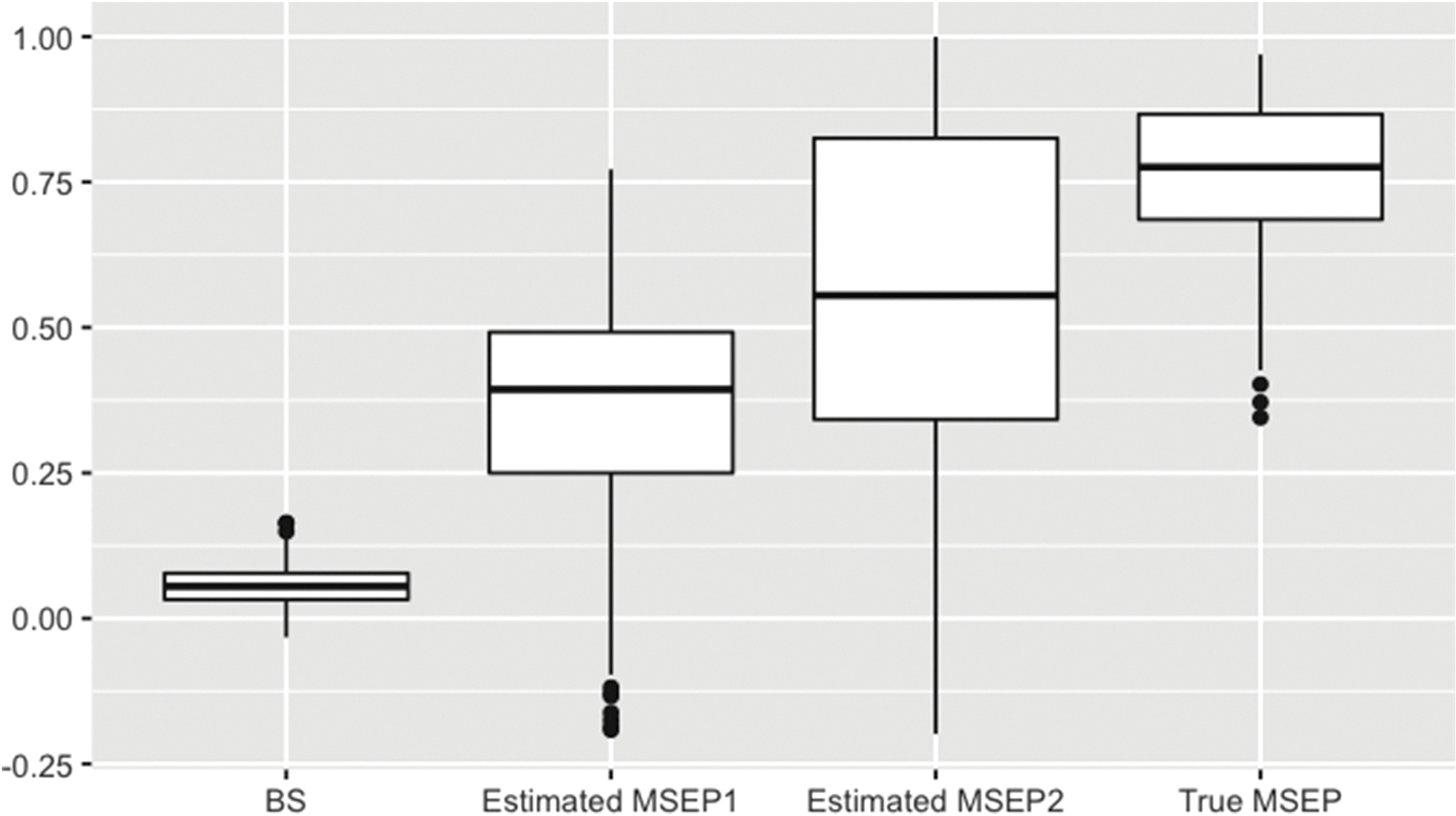
Performance improvement between the two models defined using the BS, estimated and true MSEPs in Simulation II. The MSEP1 and MSEP2 were estimated by ranking the subjects based on their predicted probabilities from Models 1 and 2, respectively. MSEPs: mean square error for the probability of binary outcome; BS: Brier score.
We evaluated the sensitivity of variance estimation with respect to the window size in Simulation II. Table 1 summarizes the bias and percent bias of the estimated outcome variance with varying window size under different sample sizes and outcome prevalences. In most scenarios, the bias reduces with increasing window size, although they are all relatively small. With fixed window size, the bias does not reduce with increasing total sample size. The largest bias is about 8% when the window size is 10. When the window size is relatively large compared to the total sample size (e.g. window size of 40 and total sample size of 200), the bias becomes negative, suggesting the variance is overestimated.
Table 1.
Mean (standard deviation) of the outcome variance, bias and percent bias of the estimated outcome variance across 200 simulations for different window size, total sample size and outcome prevalence. Bias is defined as the true minus estimated variance. Percent bias is defined as the true minus estimated variance divided by the true variance.
|
n = 200 |
n = 400 |
n = 800 |
|||||||
|---|---|---|---|---|---|---|---|---|---|
| Window size | p = 0.1 | p = 0.3 | p = 0.5 | p = 0.1 | p = 0.3 | p = 0.5 | p = 0.1 | p = 0.3 | p = 0.5 |
|
| |||||||||
| True value | |||||||||
|
| |||||||||
| 0.0850 (0.0155) | 0.1764 (0.0137) | 0.2052 (0.0119) | 0.0861 (0.0107) | 0.1767 (0.0103) | 0.2058 (0.0083) | 0.0851 (0.0074) | 0.1780 (0.0067) | 0.2055 (0.0059) | |
|
| |||||||||
| Bias | |||||||||
|
| |||||||||
| 10 | 0.0066 (0.0036) | 0.0141 (0.0050) | 0.0161 (0.0061) | 0.0068 (0.0024) | 0.0140 (0.0043) | 0.0166 (0.0046) | 0.0066 (0.0019) | 0.0143 (0.0029) | 0.0164 (0.0035) |
| 20 | 0.0029 (0.0032) | 0.0058 (0.0044) | 0.0065 (0.0052) | 0.0030 (0.0022) | 0.0059 (0.0038) | 0.0073 (0.0039) | 0.0029 (0.0018) | 0.0064 (0.0026) | 0.0073 (0.0034) |
| 30 | 0.0014 (0.0031) | 0.0021 (0.0044) | 0.0022 (0.0052) | 0.0017 (0.0021) | 0.0029 (0.0037) | 0.0037 (0.0036) | 0.0015 (0.0018) | 0.0035 (0.0025) | 0.0041 (0.0033) |
| 40 | 0.0006 (0.0031) | −0.0002 (0.0043) | −0.0006 (0.0051) | 0.0009 (0.0020) | 0.0012 (0.0036) | 0.0018 (0.0035) | 0.0008 (0.0018) | 0.0020 (0.0025) | 0.0024 (0.0032) |
|
| |||||||||
| Percent bias | |||||||||
|
| |||||||||
| 10 | 0.0792 (0.0442) | 0.0799 (0.0272) | 0.0785 (0.0296) | 0.0792 (0.0276) | 0.0789 (0.0237) | 0.0808 (0.0219) | 0.0774 (0.0217) | 0.0803 (0.0157) | 0.0798 (0.0166) |
| 20 | 0.0350 (0.0411) | 0.0325 (0.0249) | 0.0314 (0.0258) | 0.0351 (0.0256) | 0.0334 (0.0216) | 0.0353 (0.0188) | 0.0339 (0.0209) | 0.0358 (0.0144) | 0.0356 (0.0162) |
| 30 | 0.0182 (0.0417) | 0.0117 (0.0248) | 0.0109 (0.0256) | 0.0190 (0.0246) | 0.0163 (0.0209) | 0.0181 (0.0177) | 0.0182 (0.0208) | 0.0198 (0.0142) | 0.0198 (0.0161) |
| 40 | 0.0088 (0.0423) | −0.0016 (0.0247) | −0.0033 (0.0254) | 0.0102 (0.0238) | 0.0064 (0.0208) | 0.0085 (0.0172) | 0.0099 (0.0207) | 0.0112 (0.0143) | 0.0114 (0.0159) |
6. Data analysis
The Breast Cancer Surveillance Consortium (BCSC) was established in 1994 by the National Cancer Institute (NCI) to prospectively collect breast cancer risk factors at the time of each mammography screening, and ascertain outcomes for all women.21 Using the BCSC dataset, Barlow et al.22 developed a risk prediction model to estimate the probability of breast cancer diagnosis within one year after a screening mammogram. The model included race, ethnicity, breast density, BMI, use of hormone therapy, type of menopause, and previous mammographic result. The dataset included women aged between 35 and 84 years with mammograms screened from 1 January 1996 to 31 December 2002. There were 2,392,998 eligible screening mammograms from women who had not been previously diagnosed with breast cancer and had one prior mammogram in the preceding five years. Of those, 568,215 mammograms were from premenopausal women and 1726 were diagnosed with breast cancer within one year of the screening. The final model for premenopausal women included four predictors: age, breast density, number of first-degree relatives with breast cancer, and a prior breast procedure. Of the four predictors, breast density was the most significant predictor of breast cancer incidence.
Using four-fold cross validation method, we fit two logistic models: the model that included all predictors other than the breast density (Model 1) and the model with all four predictors (Model 2). Table 2 summarizes the comparison of the two models using different measures in the validation set. We first evaluated the performance of both models using the Brier score. The Brier scores are 3.0271e − 03 and 3.0266e − 03 for Models 1 and 2, respectively. The performance improvement comparing Model 1 versus 2 using the Brier score is . Since the Brier score for the null model in which there is no predictor is 3.0284e − 03, the IPAs for Models 1 and 2 are 0.042% and 0.060%, respectively. Next, we calculated the proposed MSEP measure. Since all the predictors in the model are categorical variables, we estimated the outcome variability based on Model 2 using equation (5) and calculated the MSEP using equation (6) accordingly. The estimated MSEPs for Models 1 and 2 are 6.0207e − 06 and 5.4617e − 06, respectively. The performance improvement comparing Model 1 versus 2 using the MSEP is , suggesting a large improvement when breast density was included in the risk prediction model. We also calculated the SRMSEP for Model 2. There were 568,215 records in the data with 1726 breast cancer events. Consequently, the breast cancer incidence is 1, 726/568, 215 = 0.00304. The SRMSEP for Model 2 is , indicating the error for the predicted probability of cancer incidence is on average 76.9% of the true outcome probability. Although there was a big improvement in predicting breast cancer incidence by including the breast density in Model 2, the error associated with the predicted probability is still quite large relative to the true outcome probability. Additional work may be required to improve the breast cancer risk prediction model.
Table 2.
Summary of prediction performance in the BCSC data. Model 1 included all predictors other than the breast density; model 2 included all four predictors. Since IPA is a relative measure with respect to the null model, the PI for the IPA is calculated as the difference of IPAs between the two models.
| BS | MSEP | IPA | |
|---|---|---|---|
|
| |||
| Model 1 | 3.0271E-03 | 6.0207E-06 | 0.042% |
| Model 2 | 3.0266E-03 | 5.4617E-06 | 0.060% |
| PI | 0.018% | 9.280% | 0.018% |
PI: performance improvement; BS: Brier score; IPA: index of prediction accuracy; MSEP: mean square error for the probability of binary outcome; BCSC: Breast Cancer Surveillance Consortium,
7. Summary
We proposed a modified criterion based on the Brier score to evaluate and compare model performance for predicting binary outcomes. We decomposed the Brier score into the mean square error for the estimated probabilities and the intrinsic variance in the data. Since the variance of the binary outcome is not reflective of the model performance, we subtracted it from the Brier score and used only the first component, referred to as the MSEP, as the criterion for evaluating model performance. We showed the MSEP is more sensitive than the Brier score for quantifying the improvement when comparing the prediction performance of different models using the same dataset.
A key step in estimating the MSEP is to estimate the variance of binary outcomes. If the prediction model includes all categorical predictors, as was the case in the BCSC example, it is natural to group the subjects based on their predicted probabilities, which have a finite number of unique values, and calculate the variance for all subjects who have the same predicted probability. To handle the scenario of small number of subjects within each group, which is especially the case when there are continuous predictors in the model, we proposed a sliding window approach to estimate the variance for each subject by borrowing information from neighboring subjects who have similar outcome probabilities. The average outcome within the sliding window is a consistent estimator of the true outcome probability, a necessary condition for the product term in the Brier score decomposition to be zero.
A key parameter that needs to be specified is the window size when estimating the outcome variance using the sliding window approach. Using the simulation, we showed the estimated outcome variance is relatively insensitive to the window size. In the scenarios with a range of sample size and outcome prevalence, the largest bias is about 8%. We observed the bias reduces as the window size increases in most scenarios. However, in the few scenarios where the windows size is relatively large compared to the sample size (e.g. window size is 40 and sample size is 200), the bias is negative suggesting the variance is overestimated. Since we do not know the true model for the outcome, it is very difficult to have an unbiased estimate of the outcome variance. It is possible to develop an asymptotic procedure to have consistent estimate of the variance and MSEP accordingly, in which the optimal window size may depend on the sample size, outcome prevalence and other factors. Future research is required for selecting the optimal window size, which is beyond the scope of this work. In practice, a smaller window size is preferred as otherwise the proposed MSEP measure can be negative when the variance is overestimated (i.e. the Brier score is smaller than the estimated outcome variance). Consequently, we used the window size of 10 in both simulations and the BCSC data analysis. The sliding window approach is similar to the smoothing methods that have been used to estimate the calibration curve in literature.15 Other methods may also be considered in estimating the outcome probability and associated variance, for example, kernel smoothing, repetitive sliding window. It will be interesting to see the comparison of performance using different methods in estimating the outcome variance, which can be another future direction of research.
A prediction model is meant to provide a tool for clinicians to improve decision-making in practice, which is not necessarily the true model for the relationship between predictors and outcome. To evaluate the performance of a new prediction model, it is important to compare it to a null model,20 or a currently established model. On the other hand, it is also important to know the gap between the current model performance with respect to the “true” model, that is, how well can we predict the outcome using the existing data. Our proposed MSEP measure falls in the latter category. Since the expected MSEP is zero for the true model, the MSEP reflects the model performance with respect to the true model. It is complimentary to evaluate a candidate model by comparing it to both the null and “true” models.
Acknowledgements
The authors thank the anonymous reviewers and the editor for their constructive comments, which greatly improved the the manuscript.
Funding
The author(s) disclosed receipt of the following financial support for the research, authorship, and/or publication of this article: WY was supported by NIH R01-HL141294, R01-DK118079 and R01-HL161303; JJ was supported by NIH R01-HL141294 and NSFC grant 12101054; ES, and SK were supported by NIH R01-HL141294; WG was supported by NIH R01-HL141294, R01-DK117208, R01-HL161303 and R01-DK130067.
Footnotes
Declaration of conflicting interests
The authors declared no potential conflicts of interest with respect to the research, authorship, and/or publication of this article.
References
- 1.Wilson PW, D’Agostino RB, Levy D et al. Prediction of coronary heart disease using risk factor categories. Circulation 1998; 97: 1837–1847. [DOI] [PubMed] [Google Scholar]
- 2.D’Agostino RB, Grundy S, Sullivan LM et al. Validation of the framingham coronary heart disease prediction scores: results of a multiple ethnic groups investigation. Jama 2001; 286: 180–187. [DOI] [PubMed] [Google Scholar]
- 3.Gail MH, Brinton LA, Byar DP et al. Projecting individualized probabilities of developing breast cancer for white females who are being examined annually. JNCI 1989; 81: 1879–1886. [DOI] [PubMed] [Google Scholar]
- 4.Steyerberg EW et al. Clinical prediction models. New York, NY: Springer, 2009. [Google Scholar]
- 5.Moons KG, Altman DG, Reitsma JB et al. Transparent reporting of a multivariable prediction model for individual prognosis or diagnosis (tripod): explanation and elaboration. Ann Intern Med 2015; 162: W1–W73. [DOI] [PubMed] [Google Scholar]
- 6.Hanley JA and McNeil BJ. The meaning and use of the area under a receiver operating characteristic (roc) curve. Radiology 1982; 143: 29–36. [DOI] [PubMed] [Google Scholar]
- 7.Austin PC and Steyerberg EW. Interpreting the concordance statistic of a logistic regression model: relation to the variance and odds ratio of a continuous explanatory variable. BMC Med Res Methodol 2012; 12: 82. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Pencina MJ and D’Agostino RB. Evaluating discrimination of risk prediction models: the C statistic. Jama 2015; 314: 1063–1064. [DOI] [PubMed] [Google Scholar]
- 9.Cook NR. Use and misuse of the receiver operating characteristic curve in risk prediction. Circulation 2007; 115: 928–935. [DOI] [PubMed] [Google Scholar]
- 10.Hosmer DW, Hosmer T, Le Cessie S et al. A comparison of goodness-of-fit tests for the logistic regression model. Stat Med 1997; 16: 965–980. [DOI] [PubMed] [Google Scholar]
- 11.Copas JB. Regression, prediction and shrinkage. J R Stat Soc: Ser B (Methodological) 1983; 45: 311–335. [Google Scholar]
- 12.Cox DR. Two further applications of a model for binary regression. Biometrika 1958; 45: 562–565. [Google Scholar]
- 13.Harrell F Regression modeling strategies: with applications to linear models, logistic regression, and survival analysis. New York: Springer, 2001. [Google Scholar]
- 14.Dalton JE. Flexible recalibration of binary clinical prediction models. Stat Med 2013; 32: 282–289. [DOI] [PubMed] [Google Scholar]
- 15.Austin PC and Steyerberg EW. Graphical assessment of internal and external calibration of logistic regression models by using loess smoothers. Stat Med 2014; 33: 517–535. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Van Calster B, Nieboer D, Vergouwe Y et al. A calibration hierarchy for risk models was defined: from utopia to empirical data. J Clin Epidemiol 2016; 74: 167–176. [DOI] [PubMed] [Google Scholar]
- 17.Brier GW. Verification of forecasts expressed in terms of probability. Mon Weather Rev 1950; 78: 1–3. [Google Scholar]
- 18.Murphy AH. Scalar and vector partitions of the probability score: Part ii. n-state situation. J Appl Meteorol 1972; 11: 1183–1192. [Google Scholar]
- 19.Murphy AH. A new vector partition of the probability score. J Appl Meteorol 1973; 12: 595–600. [Google Scholar]
- 20.Kattan MW and Gerds TA. The index of prediction accuracy: an intuitive measure useful for evaluating risk prediction models. Diagn Prognostic Res 2018; 2: 7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Ballard-Barbash R, Taplin SH, Yankaskas BC et al. Breast cancer surveillance consortium: a national mammography screening and outcomes database. AJR Am J Roentgenol 1997; 169: 1001–1008. [DOI] [PubMed] [Google Scholar]
- 22.Barlow WE, White E, Ballard-Barbash R et al. Prospective breast cancer risk prediction model for women undergoing screening mammography. J Natl Cancer Inst 2006; 98: 1204–1214. [DOI] [PubMed] [Google Scholar]


