Abstract
The growing interest in new classes of anti‐cancer agents, such as molecularly‐targeted therapies and immunotherapies with modes of action different from those of cytotoxic chemotherapies, has changed the dose‐finding paradigm. In this setting, the observation of late‐onset toxicity endpoints may be precluded by treatment and trial discontinuation due to disease progression, defining a competing event to toxicity. Trial designs where dose‐finding is modeled in the framework of a survival competing risks model appear particularly well‐suited. We aim to provide a phase I/II dose‐finding design that allows dose‐limiting toxicity (DLT) outcomes to be delayed or unobserved due to competing progression within the possibly long observation window. The proposed design named the Survival‐continual reassessment method‐12, uses survival models for right‐censored DLT and progression endpoints. In this competing risks framework, cause‐specific hazards for DLT and progression‐free of DLT were considered, with model parameters estimated using Bayesian inference. It aims to identify the optimal dose (OD), by minimizing the cumulative incidence of disease progression, given an acceptable toxicity threshold. In a simulation study, design operating characteristics were evaluated and compared to the TITE‐BOIN‐ET design and a nonparametric benchmark approach. The performance of the proposed method was consistent with the complexity of scenarios as assessed by the nonparametric benchmark. We found that the proposed design presents satisfying operating characteristics in selecting the OD and safety.
Keywords: competing risks, dose‐finding, oncology, phase I/II, survival data
Abbreviations
- CRM
continual reassessment method
- DLT
dose limiting toxicity
- MTD
maximum tolerated dose
- MTA
molecularly‐targeted therapies
- PCS
probability of correct selection
1. INTRODUCTION
Historically, phase I cancer dose‐finding clinical trial designs were developed for cytotoxic drugs and aimed at defining the maximal tolerated dose (MTD) of a new drug from a small and finite set of fixed dose levels; in this setting, the outcome is commonly measured by the occurrence of dose‐limiting toxicities (DLT) over a short period of time. This paradigm has been challenged with the arrival of new classes of anticancer agents, such as molecularly‐targeted therapies (MTAs) and immunotherapies. Their modes of action target the immune system or tumor specific pathways and differ from those of cytotoxic chemotherapies. In contrast to cytotoxic chemotherapies, which are administrated at discrete time points and may cause acute severe toxicities, new agents may be responsible for late‐onset toxicities, related to their pharmacological properties or prolonged and continuous administration. 1 , 2 , 3 To handle such prolonged observation windows of toxicities, 4 a number of model‐based designs have been proposed. Cheung and Chappell, 5 introduced the time‐to‐event continual reassessment method (TITE‐CRM), followed by Braun, 6 Yuan and Yin, 7 and Liu et al. 8 Model‐assisted designs have been also developed to provide solution for phase I trials with late‐onset toxicity. Yuan et al 9 proposed the Time‐to‐event Bayesian optimal interval design (TITE‐BOIN) based on the single mean imputation method, while Lin and Yuan 10 formulated a general methodology to allow model‐assisted trial designs to accommodate pending DLT data.
With prolonged observation windows, competing events observed during the trial, such as disease progressions or death, may also occur, resulting in early treatment or study discontinuation. Toxicity assessment may be precluded by such early terminations of the patient exposure to the drug. Usually, the occurrence of a progression followed by the trial discontinuation within the toxicity window results either in patient replacement leading to increased study duration and cost, or implementation of practical strategies to handle those partial observations. 11 However, considering progression as an independent censoring event ignores this information related to efficacy, and may impact the operating characteristics of the design, with decreased performances in selecting the correct dose. 11 Accounting for any discontinuation event as informative censoring, using the cumulative incidence of DLT in a survival CRM setting improved the design operating characteristics compared to the binomial TITE‐CRM. 12 The information provided by efficacy‐related outcomes, such as disease progression, could be also used in the process of selecting a dose, resulting in phase I/II trial designs. 13 , 14 , 15 , 16 , 17 , 18 , 19 , 20 However, most of these phase I/II designs treat toxicity and efficacy as binary outcomes observed within the timeframe of the trial. Some addressed the issue of late‐onset outcomes in phase I/II, assuming independent toxicity and efficacy outcomes. 16 , 21 , 22 Nevertheless, patients who experience toxicity generally have their dose reduced or discontinued and are inconsistently followed for efficacy or progression. Therefore, the occurrences of progression and DLT compete with each other.
In this particular setting of phase I/II with delayed outcomes, Takeda et al 22 proposed a Time‐to‐event Bayesian optimal interval design (TITE‐BOIN‐ET) to identify the optimal dose (OD), allowing staggered patient accrual by relaxing the need for complete follow‐up of previously included patients. They applied the likelihood approach with pending toxicity data proposed by Lin and Yuan for both efficacy and toxicity outcomes. 10 Allowing the continuous enrollment of new patients, when previous patients are still under observation, can shorten the duration of the trial, which is suitable for prolonged observation windows and late‐onset toxicities. However, although the TITE‐BOIN‐ET handles incomplete observations, it relies on binary endpoints for toxicity and efficacy, as stated above. Owing to the competing risks setting, a comprehensive method that formally includes the information of time‐to‐toxicity and time‐to‐progression using a survival working model for right‐censored endpoints, thus allowing the toxicity outcomes to be delayed or unobserved due to competing events within the observation window, appears fully appropriate for new anti‐cancer agents. In this setting, Biard et al recently developed the CR‐CRM, a seamless phase I/II design for novel anti‐cancer agents with competing disease progressions, 23 using a survival likelihood framework with three stages: first rule‐based initiation, second toxicity‐centered escalation, and third toxicity and efficacy optimization. The CR‐CRM relies on a cause‐specific approach targeting the marginal latent incidences of events (toxicity and progression) for dose finding, close to a hypothetical situation where the time‐to‐toxicity can be observed in the absence of failure due to progression, 24 which may be hard to estimate in practice.
In this article, we develop a novel Bayesian Survival‐continual reassessment method for phase I/II dose‐finding trials, named the Survival‐CRM‐12 (Surv‐CRM‐12), using survival models for right‐censored and competing DLT and progression endpoints: it allows the outcomes to be delayed or unobserved within the observation window. The proposed method aims to identify the OD, by minimizing the cumulative incidence of disease progression, given an acceptable toxicity threshold. With a single stage design, the Surv‐CRM‐12 design is easier to implement and allows for the use of both toxicity and efficacy information for the entire trial. The Surv‐CRM‐12 also targets the cumulative probability of events within the observation window, taking competing risks into account. It corresponds to an approach based on the observed patient outcomes, accounting for all competing events in dose finding and clinical decision making.
2. MOTIVATING EXAMPLE
The present work was retrospectively motivated by a phase I/II clinical trial setting in patients with low‐risk myelodysplastic syndrome (MDS) to evaluate the tolerance and efficacy of a new targeted therapy combined with erythropoietin (EPO). More specifically, the goal of the trial was to determine the OD level of this targeted therapy in terms of both toxicity and efficacy, with constant dose of EPO. Outcomes were assessed after the first treatment cycle, up to 42 days. The DLT was defined as any grade 3 drug‐related adverse event lasting more than 7 days, or any persisting cytopenias at day 42 without evidence of disease progression in bone marrow and/or peripheral blood. Treatment response was defined at day 21 by an increase in hemoglobin level of 1.5 g/dL or above. Progression free survival (PFS) was a secondary endpoint. The dose‐finding was scheduled to use the TITE‐BOIN‐ET design, 22 accounting for possible continuous recruitment during the 42‐days observation window for DLT. However, we wondered whether using a survival model to make full use of the DLT and PFS, defined as right‐censored competing risks outcomes, would be more informative in this setting.
3. METHODS
3.1. Problem formulation
We consider a dose‐finding clinical trial where patients are followed up for DLT within an observation window , with the additional issue of a non negligible risk of treatment discontinuation due to disease progression, that precludes the complete and reliable assessment of DLT. In this time‐to‐event framework in oncology, data are collected as dates and is defined in days, resulting in . During the trial, an aggravation of the patient status may occur, related to the progression of the malignancy, leading to treatment discontinuation in order to propose alternative therapies, if available. Similarly, patients who experience toxicity are generally dose reduced or discontinued and are inconsistently followed for efficacy or progression. In this setting, DLT and progression are competing events within , since both result in trial or treatment discontinuation. Consequently, by time , patient can experience one of these three outcomes within the trial: “DLT,” “disease progression,” and “neither DLT nor progression.” Death is considered as a DLT if related to the toxicity and as progression otherwise. Note that we assume no other cause of treatment discontinuation, and no censoring due to lost to follow‐up, since it is unlikely in a oncology dose‐finding trial, where patients are usually closely followed and in advanced stages of their disease.
Let , be the maximum sample size of the trial, the set of doses of the new drug investigated in the trial. The goal of our proposed design is to identify a dose that optimizes the efficacy outcome, among tolerable doses. First, we define the set of tolerable doses, , as those dose levels at or below the MTD, defined as the dose with toxicity probability, closest to the target .
| (1) |
Then, we incorporate information on time‐to‐progression to identify the “optimal” dose (OD), . We define the OD as the dose level(s) with minimum progression risk, among , the acceptable set of doses:
| (2) |
with , the probability of disease progression at time for dose level .
3.2. Survival model
Given the setting described above, we use a competing risks framework 25 , 26 to model the probabilities of DLT and disease progression. Let denote the time‐to‐failure and the cause of failure, with for DLT and for disease progression. We define , the cause‐specific instantaneous, and , the cumulative hazards of cause at dose level , with , the scaled dose obtained by substituting the initial guess of toxicity and progression probabilities.
We model both competing event processes with exponential hazard distributions. 27 , 28 Specifically, we assume the cause‐specific hazard for DLT is an increasing function of the dose:
| (3) |
and define the cause‐specific hazard for progression resulting in a decreasing function of the dose, as follows:
| (4) |
where and are model parameters of the dose‐toxicity and dose‐progression relationships, respectively.
, the cumulative incidence of event , at time for dose level , that is, the subdistribution function depending on both DLT and progression, expresses the probability of failing from cause at or before with dose level , as follows:
| (5) |
with , the event‐free survival, that is, the probability of not having experienced a failure, from any cause (DLT or disease progression), at time .
Given and included patients, the survival likelihood can be expressed as follows:
| (6) |
with the density function of , the time‐to‐event , the right‐censored failure time and the observed outcome defined as when DLT occurs first, when disease progression occurs first and when neither DLT nor progression occurs within the observation window.
Inference on cause‐specific hazards could be performed for DLT and disease progression separately, since the log‐likelihood factors into two pieces, one involving and the other involving . 27 , 28 Given the set of doses , the likelihood and normal prior distributions of , the posterior distributions for for event using Bayes inference is given by:
| (7) |
The posterior mean can be plugged in Equations (3) to (5) to compute , the mean estimated cumulative incidence of event at each dose level :
| (8) |
The toxicity and progression cumulative incidence estimates are then used to make decision regarding dose allocation as described in Section 3.3.
3.3. Dose‐finding algorithm
Based on the aforementioned probability model, we propose a one‐stage dose‐finding trial using both toxicity and efficacy information in the dose‐assignment process with the goal to identify a dose that optimizes the efficacy outcome, that is, the time‐to‐progression among a set of acceptable doses, , as defined below.
After the th patient being included, the set of acceptable doses (in terms of DLT), that excludes overly toxic doses, is estimated as follows:
| (9) |
with , the vector of estimates of choice for at each dose level, given available data.
The set of good doses, , is then defined as the dose levels among with an estimated incidence of progression at time t, , lying within a range from the minimum estimate:
| (10) |
where is a fixed known parameter that can be tuned based on clinical considerations related to the risk of progression under the standard of care.
To choose the dose allocated to the upcoming th patient (or cohort) among the set of good doses , we use an adaptive randomization algorithm, 17 unless only a single good dose level is identified. Otherwise, randomization across those good doses prevents the method from getting “stuck” on a single dose that has been tried early in the trial. Based on the estimated cumulative incidence of progression, , for doses , randomization probability is computed as follows:
| (11) |
and is used to allocate the next patient or cohort to dose with probability .
The trial ended either when the maximum sample size has been reached, or for safety decisions, that is, when the posterior probability of exceeding the target is at least 0.95. 29 In the latter, we consider all doses as over‐toxic and terminate the trial. If the maximum sample size has been reached and the follow‐up completed for every patient, the OD, , is then estimated as the dose with the minimum estimated cumulative incidence of progression among the acceptable set of doses, :
| (12) |
An optional preliminary stage centered on the dose‐toxicity relationship could also be conducted before the optimization presented above if clinical considerations justify increased caution related to patients safety at the beginning of the trial. More precisely, we propose to first use a continual reassessment method (CRM)‐like approach, in order to guide sequential dose‐assignments of the first subset of patients of the total sample size , with a design parameter to be pre‐specified when planning the trial. Relying on the monotonicity assumption of the dose‐toxicity relationship, the objective of this first stage is to identify the dose with a cumulative incidence of DLT at time t, , closest to a pre‐specified target . At this stage, an upcoming th cohort of patients is therefore allocated to dose in the following way:
| (13) |
After the patients have been included, we incorporate information on the dose‐progression relationship in the dose‐assignment process as presented above.
4. SIMULATION STUDY
We conducted a comprehensive simulation study to explore the properties of our proposed Surv‐CRM‐12 design across a variety of settings. The operating characteristics of the Surv‐CRM‐12 design were compared with that of the TITE‐BOIN‐ET 22 approach. Indeed, the objective of the TITE‐BOIN‐ET is also to determine the OD defined as the dose that maximizes the efficacy probability satisfying a tolerability constraint. Additionally, performances of the proposed design were assessed using a nonparametric benchmark approach. 30 , 31
4.1. Setting
In line with our motivating example, we set the observation window days. We considered candidate dose levels, and, within the time window , a target toxicity probability of DLT at and a threshold to define the good doses, . We simulated patient accrual using a Poisson process with an expected accrual rate of 4 patients in 42 days. The total sample size was set at using a single stage design for dose assignment (ie, ). Simulated trials were initiated with the first dose level, . The cohort size was 1, and no dose skipping was allowed.
To assess the robustness of our proposed method, sensitivity analyses were also conducted. We first conducted a simulation study to examine the sensitivity of our design to the specification of priors. We considered normal priors with different SDs for the unknown parameters and under each scenarios. We also varied the sample size from to , and the number of patients allocated to the first optional toxicity‐centered stage, and . Furthermore, we also evaluated our method in the case of correlated time‐to‐event data using the Clayton model following Yuan and Yin's approach. 16
4.2. Calibration of model parameters
To jointly calibrate the skeletons and the prior variance of the parameters and , we extended the calibration procedure using the concepts of the least informative prior variance and indifference intervals developed by Lee and Cheung. 32 Specifically, two design skeletons, for toxicity and progression respectively, were calibrated using the indifference interval approach, 33 , 34 using the working models of the proposed design (Equation 5).
Let be the target probability of toxicity and the expected probability of progression at the best guess or expected OD , at . Let be the parameter space for the working model of event (ie, with for toxicity and for progression). We define the indifference intervals for event , , for and , where solves
with the scaled doses.
By specifying a common half‐width indifference interval for all dose levels, that is , can be obtained recursively using the approach presented in Lee and Cheung, 33 as described below.
for ,
for .
Then, the least informative prior normal SD for , , can be obtained for a given using the toxicity working model with the least informative prior approach described in Lee and Cheung. 32 The least informative SD is the one such that the prior probability of selecting a dose corresponds to a uniform distribution among the candidate dose levels (ie, 1/J). We assume the prior normal SD for is equal to the SD of .
Based on this approach, we calibrated both skeletons (toxicity and progression) and the prior variance for the working models parameters, and , in our trial setting. We first evaluated the performances of the Surv‐CRM‐12 across values of based on a set of calibration scenarios where the true probabilities of DLT and progression followed plateau configurations as described by Lee and Cheung. 33 The algorithm was implemented with , a target toxicity probability and an expected progression probability at , dose levels and dose level 3 as the OD. We iterated from 0.01 to 0.6 in a discrete domain with a grid half‐width of 0.01 and calculate for each value. Based on 2000 simulations, on a set of calibration scenarios of the plateau configuration defined following, 33 we set the half‐width of the indifference interval at 0.07 and the prior SD at 0.379, as providing the highest average probability of correct selection (PCS) across the calibration scenarios, corresponding to the following skeletons for toxicity and progression respectively {0.055, 0.130, 0.250, 0.406, 0.571} and {0.666, 0.541, 0.400, 0.266, 0.158}. As a sensitivity analysis, we also considered fixing the SD at 35 and only calibrating the two skeletons using the indifference interval approach.
4.3. Simulated scenarios
Several non‐parametric scenarios of dose‐toxicity and dose‐progression relationships were examined (Figure 1). They differed in terms of the cumulative incidences of DLT and disease progression at time by dose level and encompassed different realistic shapes of dose‐DLT and dose‐progression relationships.
FIGURE 1.
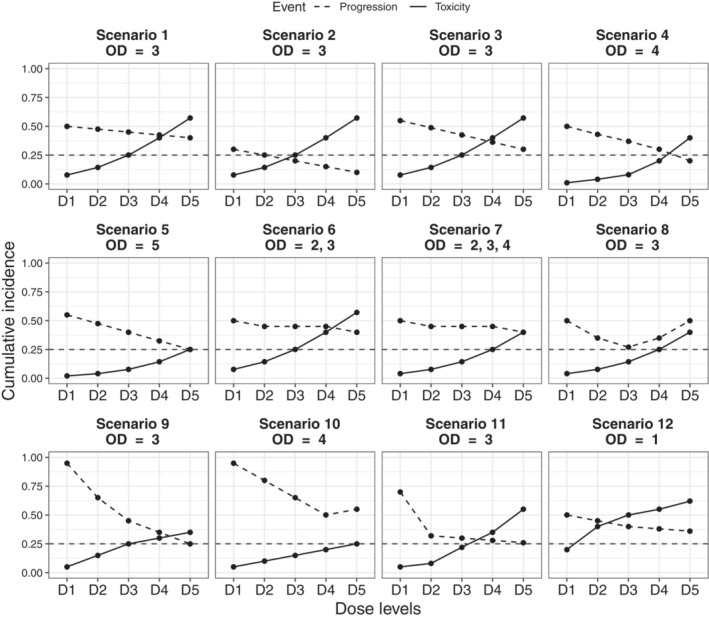
Simulation scenarios: True cumulative incidences of DLT (solid line) and progression (dashed line) at time for each dose level, D1 to D5. OD, optimal dose
The first seven scenarios (Sc) had varying optimal and acceptable doses in position over the range of the five candidate dose levels: for Sc1 to Sc3, Sc6, Sc9, and Sc11, acceptable doses were to ; for Sc4, Sc7, and Sc8, to , and for Sc5 and Sc10, to . Scenarios also differed regarding the shape of dose‐progression relationships including high (Sc9‐Sc11), low (Sc2) and moderate risk of disease progression, steeper slope (Sc1‐Sc5) and plateau (Sc6 and Sc7). We also examined operating characteristics of our proposed design in comparison with the benchmark approach and the TITE‐BOIN‐ET design on a U‐shape dose‐progression scenario (Sc8). To avoid cherry‐picked scenarios that favor the proposed design, we examined four additional scenarios previously used in the study by Takeda et al 22 (Sc9‐Sc12). For simplicity, we defined the true cumulative incidence of progression at time as the complementary of the true probability of efficacy.
Trial data were generated according to a tolerance profile procedure 30 , 31 drawn from a uniform distribution summarizing patient's toxicity and progression outcomes. Instantaneous cause‐specific hazards of both events, were back computed from cumulative incidence values of event assumed at time at each dose level, using exponentially distributed event times. Competing risks data were then simulated following Beyersmann et al's approach. 36 Observations were sampled from an exponential model for the time‐to‐first event (event‐free survival), with all‐cause hazard and the cause of failure determined by a random draw from a Bernoulli distribution with probability for toxicity (otherwise disease progression). Last, administrative censoring was applied at time to mimic the trial observation window. For trials generated under the Clayton model for time‐to‐event data, details are available in the Supporting Web Materials.
4.4. Comparative methods
To evaluate performances of our proposed design, we developed a nonparametric benchmark approach providing an upper bound estimate on selecting the OD under a given scenario, and at a fixed sample size. 12 , 30 , 31 We revised the benchmark approach proposed by Cheung 31 for complex designs with a bivariate dose‐finding objective, to account for right‐censored endpoints and competing risks events. These benchmark values for dose selection provide meaningful information on the complexity of scenario in terms of OD identification and provide a reference for the performance of a dose‐finding algorithm with complete potential information, that is, as if outcomes could be observed at all dose levels for all patients. In our setting of a bivariate dose‐finding objective relying on the cumulative incidence of DLT and progression, we computed a benchmark based on two endpoints (toxicity and progression). 31 In the presence of informative censoring, cumulative incidences were estimated as described by Gray. 37 Non parametric estimators for the benchmark were chosen, similarly to the original benchmark proposal for binary endpoints. 30 The OD was estimated from the complete dataset based on the trial objective defined in Equation (2). Details of the benchmark approach are provided in Supporting Web Material (Table S1).
For a comparison purpose in dose selection performances, we also applied the TITE‐BOIN‐ET design 22 to the simulation scenarios. With the TITE‐BOIN‐ET design, the method used to guide dose escalation is different from the method used for final estimation. Briefly, for OD estimation at the end of the trial, regression models for each of the toxicity and efficacy outcomes are fitted. For toxicity, an isotonic regression is performed and for efficacy, a model with fractional polynomials with two degrees of freedom is applied. The OD is then determined as the dose that maximizes the efficacy probability among a set satisfying tolerability, that is, dose levels equal or below the MTD (ie, dose with toxicity probability closest to the target toxicity probability ). In our setting, we assumed efficacy when a patient is alive without progression. Thus, the true cumulative incidence of progression at time are defined as the complementary of the true probability of efficacy. A set‐up for simulations as close as possible to our simulation setting was used for a fair comparison with respect to the maximum number of patients (), cohort size (=1), starting dose (), assessment windows for toxicity and efficacy (42 days) and accrual rate (one patient per 10 days). For dose assignment during the trial, the target toxicity probability and the target efficacy probability were and , respectively. To match the Surv‐CRM‐12 dose‐finding objective of minimizing time‐to‐progression, which corresponds to maximizing the efficacy probability in the TITE‐BOIN‐ET setting, we chose to set a target efficacy probability, , close to 100%. We set the highest acceptable toxicity probability (ie, 60% deviation from the target), the lowest DLT probability that is overly toxic , (ie, 40% deviation from the target), and the highest efficacy probability that is subtherapeutic (ie, 40% deviation from the target). As a result, the optimal values of the lower and upper cutoffs on toxicity and the cutoff on efficacy were estimated to be . We defined safety decisions as close as possible to our setting. Skipping dose(s) was not allowed. Early termination criteria were set as follows: when posterior probability of efficacy was less than 0.05 (ie, ) was above 0.95, or the posterior probability of toxicity was above 0.25 (ie, ) was above 0.95, the dose was removed. If all doses were removed, the dose‐finding trial was terminated. An early termination rule was applied based on at least 3 patients enrolled in a trial.
All the simulations were based on 10 000 replicates for the Surv‐CRM‐12 and TITE‐BOIN‐ET designs, and benchmark. For each scenario, we computed the percentage of times that each of the designs selected each dose level as the final OD, percentage of early trial stopping for safety decisions (P), the average overdose number (No. OV), defined as the average number of patients treated at a dose above the true OD during the trial, 38 the average number of patients that experienced DLT (No. DLT) and disease progression (No. Prog), and the average number of patients treated at the true OD (No. OD).
4.5. Results
Table 1 summarizes the simulation results with a total sample size of 45 patients. As expected, the performance of the methods depended on the scenario. The highest percents of correct selection (PCS) reached by the benchmark, 91% and 97%, were observed in scenarios with more than one OD due to a plateau shape of the dose‐progression relationship (Sc6 and Sc7, respectively). Performances of the proposed Surv‐CRM‐12 design were in line with these findings, as highest PCS, 91% and 93%, were reached for Sc6 and Sc7 respectively. On the other hand, the Surv‐CRM‐12 selected the relatively higher dose levels as the ODs even if the risks of toxicity were increased but acceptable among the dose levels when the risks of disease progression were the same. In scenarios with moderate risk of disease progression and monotone decreasing dose‐progression (Sc1 to Sc5), the Surv‐CRM‐12 correctly selected the OD in more than 60% of cases and outperformed the TITE‐BOIN‐ET method. The Surv‐CRM‐12 seemed robust to different dose‐progression relationships given a fixed risk of toxicity. Indeed, for Sc1 to Sc3, with the same dose‐toxicity relationship and different flat dose‐progression relationships, the Surv‐CRM‐12 provided a satisfactory PCS greater than or equal to 71% and outperformed the benchmark with PCS fluctuating between 52% and 70%. In scenarios with OD at extreme dose levels (Sc5 and Sc12), the Surv‐CRM‐12 picked the OD in 64% and 66% of cases respectively, contrary to 76% and 90% with the benchmark. As expected, the lowest PCS, 27%, was observed in the case of a U‐shape progression scenario (Sc8), while the PCS with the non‐parametric TITE‐BOIN‐ET was 51%, and 80% with the benchmark. Finally, with huge risks of progression, 95% for the first dose level (Sc9, Sc10), the Surv‐CRM‐12 and the TITE‐BOIN‐ET hesitated between the correct dose level and the one above: PCS were 55% and 48% with the Surv‐CRM‐12 for Sc9 and Sc10 respectively, slightly higher than the TITE‐BOIN‐ET (PCS of 43% and 34% respectively), while the PCS with the benchmark were 47% and 69% respectively. To conclude in terms of picking the correct dose, the Surv‐CRM‐12 outperformed the TITE‐BOIN‐ET method over all scenarios except in the case of a U‐shape dose‐progression relationship.
TABLE 1.
Simulation results for Sc1 to Sc6 of the Surv‐CRM‐12 design, TITE‐BOIN‐ET and benchmark; percent of stopped trials for safety (P); percent of selection; number of overdose (No. OV); number of observed DLT (No. DLT); number of observed progression (No. Prog) and number of patients treated with the true OD (No. OD) during the trial
| Percent of selection by dose level (%) | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Method | P (%) | 1 | 2 | 3 | 4 | 5 | No. OV | No. DLT | No. Prog | No. OD |
| Scenario 1 | ||||||||||
| True | 0.08 | 0.14 | 0.25 | 0.40 | 0.57 | |||||
| True | 0.50 | 0.48 | 0.45 | 0.43 | 0.40 | |||||
| Surv‐CRM‐12 | 0 | 0 | 18 | 73 | 9 | 0 | 7.0 | 11.0 | 20.4 | 25.5 |
| TITE‐BOIN‐ET | 1 | 15 | 30 | 41 | 9 | 4 | 13.1 | 10.4 | 21.5 | 15.3 |
| Benchmark | n/a | 12 | 34 | 52 | 1 | 0 | n/a | n/a | n/a | n/a |
| Scenario 2 | ||||||||||
| True | 0.08 | 0.14 | 0.25 | 0.40 | 0.57 | |||||
| True | 0.30 | 0.25 | 0.20 | 0.15 | 0.10 | |||||
| Surv‐CRM‐12 | 0 | 0 | 18 | 71 | 10 | 0 | 6.4 | 10.5 | 9.5 | 24.2 |
| TITE‐BOIN‐ET | 1 | 14 | 30 | 47 | 8 | 1 | 6.3 | 9.1 | 10 | 15.2 |
| Benchmark | n/a | 3 | 28 | 64 | 5 | 0 | n/a | n/a | n/a | n/a |
| Scenario 3 | ||||||||||
| True | 0.08 | 0.14 | 0.25 | 0.40 | 0.57 | |||||
| True | 0.55 | 0.49 | 0.43 | 0.36 | 0.30 | |||||
| Surv‐CRM‐12 | 0 | 0 | 17 | 73 | 10 | 0 | 7.5 | 11.0 | 19.5 | 25.3 |
| TITE‐BOIN‐ET | 1 | 12 | 25 | 47 | 12 | 3 | 13.1 | 10.7 | 20.3 | 15.8 |
| Benchmark | n/a | 2 | 25 | 70 | 3 | 0 | n/a | n/a | n/a | n/a |
| Scenario 4 | ||||||||||
| True | 0.01 | 0.04 | 0.08 | 0.20 | 0.40 | |||||
| True | 0.50 | 0.43 | 0.37 | 0.30 | 0.20 | |||||
| Surv‐CRM‐12 | 0 | 0 | 0 | 4 | 78 | 19 | 7.2 | 8.9 | 13.8 | 26.5 |
| TITE‐BOIN‐ET | 0 | 4 | 5 | 16 | 56 | 21 | 14 | 7.9 | 16.6 | 16 |
| Benchmark | n/a | 0 | 0 | 9 | 76 | 15 | n/a | n/a | n/a | n/a |
| Scenario 5 | ||||||||||
| True | 0.02 | 0.04 | 0.08 | 0.14 | 0.25 | |||||
| True | 0.55 | 0.48 | 0.40 | 0.32 | 0.25 | |||||
| Surv‐CRM‐12 | 0 | 0 | 0 | 1 | 35 | 64 | n/a | 7.5 | 14.3 | 17.1 |
| TITE‐BOIN‐ET | 5 | 2 | 3 | 11 | 25 | 54 | n/a | 6.2 | 19.4 | 26.9 |
| Benchmark | n/a | 0 | 0 | 1 | 23 | 76 | n/a | n/a | n/a | n/a |
| Scenario 6 | ||||||||||
| True | 0.08 | 0.14 | 0.25 | 0.40 | 0.57 | |||||
| True | 0.50 | 0.45 | 0.45 | 0.45 | 0.40 | |||||
| Surv‐CRM‐12 | 0 | 0 | 19 | 72 | 9 | 0 | 6.9 | 10.9 | 20.6 | 36.5 |
| TITE‐BOIN‐ET | 1 | 15 | 33 | 39 | 8 | 4 | 13 | 10.3 | 21.4 | 28 |
| Benchmark | n/a | 8 | 46 | 45 | 1 | 0 | n/a | n/a | n/a | n/a |
| Scenario 7 | ||||||||||
| True | 0.04 | 0.08 | 0.14 | 0.25 | 0.40 | |||||
| True | 0.50 | 0.45 | 0.45 | 0.45 | 0.40 | |||||
| Surv‐CRM‐12 | 0 | 0 | 0 | 26 | 67 | 6 | 3.7 | 9.4 | 20.1 | 40.1 |
| TITE‐BOIN‐ET | 0 | 8 | 15 | 30 | 30 | 17 | 14.1 | 7.5 | 24 | 28 |
| Benchmark | n/a | 2 | 27 | 36 | 34 | 1 | n/a | n/a | n/a | n/a |
| Scenario 8 | ||||||||||
| True | 0.04 | 0.08 | 0.14 | 0.25 | 0.40 | |||||
| True | 0.50 | 0.35 | 0.27 | 0.35 | 0.50 | |||||
| Surv‐CRM‐12 | 0 | 0 | 0 | 27 | 67 | 5 | 24.2 | 9.1 | 15.1 | 16.3 |
| TITE‐BOIN‐ET | 0 | 4 | 14 | 50 | 21 | 11 | 21.4 | 6.8 | 19.8 | 14.2 |
| Benchmark | n/a | 0 | 5 | 80 | 15 | 0 | n/a | n/a | n/a | n/a |
| Scenario 9 | ||||||||||
| True | 0.05 | 0.15 | 0.25 | 0.30 | 0.35 | |||||
| True | 0.95 | 0.65 | 0.45 | 0.35 | 0.25 | |||||
| Surv‐CRM‐12 | 0 | 0 | 14 | 55 | 26 | 5 | 14.1 | 11.0 | 21.0 | 20.8 |
| TITE‐BOIN‐ET | 1 | 1 | 18 | 43 | 25 | 13 | 18.1 | 9.5 | 23.6 | 13.9 |
| Benchmark | n/a | 0 | 10 | 47 | 31 | 11 | n/a | n/a | n/a | n/a |
| Scenario 10 | ||||||||||
| True | 0.05 | 0.10 | 0.15 | 0.20 | 0.25 | |||||
| True | 0.95 | 0.80 | 0.65 | 0.50 | 0.55 | |||||
| Surv‐CRM‐12 | 0 | 0 | 1 | 17 | 48 | 35 | 10.9 | 8.5 | 26.2 | 18.3 |
| TITE‐BOIN‐ET | 0 | 1 | 4 | 21 | 34 | 40 | 22.3 | 4.7 | 34 | 8.8 |
| Benchmark | n/a | 0 | 1 | 11 | 69 | 19 | n/a | n/a | n/a | n/a |
| Scenario 11 | ||||||||||
| True | 0.05 | 0.08 | 0.22 | 0.35 | 0.55 | |||||
| True | 0.70 | 0.32 | 0.30 | 0.28 | 0.26 | |||||
| Surv‐CRM‐12 | 0 | 0 | 4 | 71 | 25 | 0 | 12.3 | 10.6 | 13.8 | 25.8 |
| TITE‐BOIN‐ET | 0 | 1 | 23 | 55 | 18 | 3 | 14.2 | 9.6 | 15.1 | 16.9 |
| Benchmark | n/a | 0 | 29 | 61 | 10 | 0 | n/a | n/a | n/a | n/a |
| Scenario 12 | ||||||||||
| True | 0.20 | 0.40 | 0.50 | 0.55 | 0.62 | |||||
| True | 0.50 | 0.45 | 0.40 | 0.38 | 0.36 | |||||
| Surv‐CRM‐12 | 4 | 66 | 29 | 0 | 0 | 0 | 22.1 | 13.7 | 21.2 | 22.9 |
| TITE‐BOIN‐ET | 5 | 75 | 18 | 2 | 0 | 1 | 21.7 | 13.1 | 19.8 | 20.3 |
| Benchmark | n/a | 90 | 10 | 0 | 0 | 0 | n/a | n/a | n/a | n/a |
Note: 10 000 simulated trials (Surv‐CRM‐12 design and benchmark) with =45, and . 10 000 simulated trials (TITE‐BOIN‐ET) with , , , and . Correct selection results based on ODs are given in boldface.
Abbreviation: n/a, not applicable.
In terms of patient exposure during the trial over the 12 scenarios, the mean number of patients allocated to overdoses (OV) was 10.19 out of a total sample size of 45 patients with the Surv‐CRM‐12 design, below the 14.08 mean value observed with the TITE‐BOIN‐ET. However, fewer patients experienced DLT during the trial using the TITE‐BOIN‐ET: the average number of DLT over all scenarios was 8.73 vs 10.14 with Surv‐CRM‐12. Finally, for 11 out of the 12 scenarios, the average number of patients treated at the true OD was higher with the Surv‐CRM‐12 design and the average OD over all scenarios was 24.95 against 17.88 with the TITE‐BOIN‐ET.
As shown by Lee and Cheung, 32 having a larger prior variance changes the distribution of the prior probability of dose selection from uniform to U‐shaped, leading in higher chances of extreme doses selections. Indeed, with SD equal to , PCS was higher for Sc5 with OD at level 5, equal to 75%. For Sc12, with OD in dose level 1, PCS was lower with SD equal to , equal to 59% but the percent of stopped trial for safety decision was much higher (equal to 18% contrary to 4% with the least informative SD) (Table S2 in Supporting Web Materials).
Expectedly, the performances of all three compared designs improved with increasing sample sizes (Figure S2, Supporting Web Materials). Moreover, the impact of the sample size of the optional first stage was limited (Table S3, Supporting Web Materials), so that this could be left to clinicians' preference.
Finally, sensitivity simulations showed that the performance of the Surv‐CRM‐12 was mostly preserved in case of correlated events. The PCS was maintained under data generated with correlated times to toxicity and progression, but the POS increased; similar results were observed with the benchmark (Figure S3, Supporting Web Materials).
5. DISCUSSION
In this article, we proposed a novel one‐stage Bayesian adaptive phase I/II design, named the Survival‐CRM‐12, for novel anti‐cancer drugs such as immunotherapies and MTAs, with the purpose to identify the OD defined as the dose with acceptable risk of toxicity and a minimum risk of disease progression. Such a targeted dose, sometimes called the “best” dose 17 appeared suitable for such early phase I/II trials, with the aim of maximizing the likelihood of efficacy while only ensuring safety constrains. Our proposed design allows continuous enrollment of patients, and handles competing risks, including the information of time‐to‐event outcomes using survival working models for right‐censored endpoints. It allows the toxicity outcome to be delayed or unobserved due to competing progression within the observation window. Such an issue of late‐onset outcome is common and important in the field of novel anticancer agents. Indeed, it has been reported that 57% of the grades 3‐4 toxicities occur after the treatment cycle 1 in 36 clinical trials of molecularly targeted agents. 39 Moreover, disease progression is one of the main cause of premature discontinuation from a Phase I trial (approximately 70% of cases), 40 and should be managed other than by ad‐hoc strategies of replacing patients. As demonstrated in the simulation study across a variety of realistic scenarios, and assessed by the benchmark, our proposed method appears an interesting approach in this setting, exhibiting desirable operating characteristics. Indeed, our design performs well in selecting the OD, as well as treating patient at safe doses during the clinical trial.
Studies have examined the impact of model specification on the performance of the dose‐finding design and have shown the importance of selecting appropriate model parameters via simulation studies. 41 , 42 Instead of arbitrarily setting initial guesses of the probabilities of DLT and disease progression, and prior variance for model parameters, we proposed a systematic calibration process based on previous literature. 32 , 33 The calibration method which used jointly the half‐width of the indifference interval both for the toxicity and progression working models, and the least informative prior variance had satisfactory operating characteristics. Jointly calibrating the initial guesses of the probabilities of toxicity and progression at each dose and the prior variance, simplified the calibration process as it reduced the number of parameters to be specified. This approach makes the Bayesian Surv‐CRM‐12 model‐based design more accessible and easier to implement.
In this phase I/II setting, we chose to model disease progression instead of efficacy, highlighting its competition with the observation of toxicities. Indeed, unlike conventional chemotherapy that works by shrinking the tumor, immunotherapeutic agents often delay cancer progression and prolong survival without achieving rapid tumor shrinkage, and a certain percentage of patients who receive immunotherapy often achieve a long‐term durable response. 43 Therefore, for some early phase immunotherapeutic trials, it is preferable to use as efficacy criterion the disease progression, rather than the conventional treatment response. Recently, Zhang et al 44 developed a dose finding phase I/II design accounting for the late‐onset competing risk endpoint, relying on piecewise cause‐specific hazard to characterize the competing risk outcomes. However, it treats late‐onset outcomes as missing data while we incorporated them in our model, and requires the definition of a utility function for identifying the OD.
This study has some limitations. First, we modeled the cause‐specific hazard for progression as a decreasing function of dose. Although a model‐based approach allows the borrowing of information across dose levels, a potential limitation related to this choice of working model is that the Surv‐CRM‐12 tends to select higher doses among safe doses in cases of plateau scenarios for dose‐progression relationship and it does not perform well for U‐shaped dose‐progression relationships. Nonparametric approaches which do not rely on any assumption on the dose‐toxicity and dose‐efficacy curves, may be useful in those situations, 45 as the TITE‐BOIN‐ET approach proposed. This approach is part of the model‐assisted designs as its decision rule can be predetermined, but requires specification during the trial planning of several cutoffs by the clinician. A nonparametric approach was also considered with the benchmark method using the complete profiles of outcomes under all dose levels instead of the time‐to‐event outcome under the assigned dose in the Surv‐CRM‐12 or TITE‐BOIN‐ET designs. Nevertheless, the Surv‐CRM‐12 model‐based design outperformed the benchmark in some scenarios, which is not observed with the TITE‐BOIN‐ET model‐assisted design. In sparse settings such as phase I/II clinical, parametric working models may outperform the non‐parametric benchmark in capturing the dose‐response relationships since they allow sharing information across dose levels. 38 Second, the “optimal” dose level could have been defined as the dose with both the highest probability of efficacy and the lowest probability of toxicity. This could be the target in particularly frail populations, for example, in neonates and children. However, this assumes equal weighting of toxicity and efficacy, and at the time, the growing accelerated approvals of drugs, notably in oncology, suggests that the target of interest is mostly efficacy. 46 Nevertheless, we agree that some consensus regarding the target dose in such trials, should be reached in the future. This would allow a more relevant comparison of all the proposed designs.
Finally, with the emergence of anti‐cancer molecularly‐targeted agents and immunotherapy agents changing the landscape of dose‐finding in oncology, it is essential to incorporate both late‐onset toxicities and progression information which are often collected as mutually exclusive events into the identification of OD. The proposed phase I/II Surv‐CRM‐12 design achieved the best performance in selecting the OD and allocating patients to the OD when trial discontinuation after disease progression within the observation window is likely to preclude the observation of DLTs in a non‐negligible proportion of patients. It should be considered when designing dose‐finding trials of targeted therapies with prolonged observation windows in advanced cancer patients where treatment discontinuations due to disease progression are likely to occur.
CONFLICT OF INTEREST
The authors declare no potential conflict of interests.
Supporting information
Appendix S1 Supporting information
ACKNOWLEDGEMENTS
The authors thank the referees for their constructive comments and insightful suggestions on the manuscript. Shing M. Lee was supported by the National Center for Advancing Translational Sciences, National Institutes of Health, through Grant Number UL1TR001873.
Andrillon A, Chevret S, Lee SM, Biard L. Surv‐CRM‐12: A Bayesian phase I/II survival CRM for right‐censored toxicity endpoints with competing disease progression. Statistics in Medicine. 2022;41(29):5753‐5766. doi: 10.1002/sim.9591
Funding information National Center for Advancing Translational Sciences, UL1TR001873
DATA AVAILABILITY STATEMENT
Data sharing not applicable to this article as no datasets were generated or analyzed during the current study.
REFERENCES
- 1. Postel‐Vinay S, Gomez‐Roca C, Molife LR, et al. Phase I trials of molecularly targeted agents: should we pay more attention to late toxicities? J Clin Oncol. 2011;29(13):1728‐1735. [DOI] [PubMed] [Google Scholar]
- 2. Mathijssen RHJ, Sparreboom A, Verweij J. Determining the optimal dose in the development of anticancer agents. Nat Rev Clin Oncol. 2014;11(5):272‐281. [DOI] [PubMed] [Google Scholar]
- 3. Wages NA, Chiuzan C, Panageas KS. Design considerations for early‐phase clinical trials of immune‐oncology agents. J Immunother Cancer. 2018;6(1):81. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4. Postel‐Vinay S, Collette L, Paoletti X, et al. Towards new methods for the determination of dose limiting toxicities and the assessment of the recommended dose for further studies of molecularly targeted agents–Dose‐Limiting Toxicity and toxicity assessment recommendation group for early trials of targeted therapies, an European organisation for research and treatment of cancer‐led study. Eur J Cancer. 2014;50(12):2040‐2049. [DOI] [PubMed] [Google Scholar]
- 5. Cheung YK, Chappell R. Sequential designs for Phase I clinical trials with late–Onset toxicities. Biometrics. 2000;56(4):1177‐1182. [DOI] [PubMed] [Google Scholar]
- 6. Braun TM. Generalizing the TITE‐CRM to adapt for early and late‐onset toxicities. Stat Med. 2006;25(12):2071‐2083. [DOI] [PubMed] [Google Scholar]
- 7. Yuan Y, Yin G. Robust EM continual reassessment method in oncology dose finding. J Am Stat Assoc. 2011;106(495):818‐831. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8. Liu S, Yin G, Yuan Y. Bayesian data augmentation dose finding continual reassessment method and delayed toxicity. Ann Appl Stat. 2013;7(4):1837‐2457. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9. Yuan Y, Lin R, Li D, Nie L, Warren KE. Time‐to‐event Bayesian optimal interval design to accelerate Phase I trials. Clin Cancer Res. 2018;24(20):4921‐4930. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10. Lin R, Yuan Y. Time‐to‐event model‐assisted designs for dose‐finding trials with delayed toxicity. Biostatistics. 2020;21(4):807‐824. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11. Biard L, Cheng B, Manji GA, Lee SM. A simulation study of methods for handling disease progression in dose‐finding clinical trials. J Biopharm Stat. 2020;31(2):156‐167. [DOI] [PubMed] [Google Scholar]
- 12. Andrillon A, Chevret S, Lee SM, Biard L. Dose‐finding design and benchmark for a right censored endpoint. J Biopharm Stat. 2020;30(6):948‐963. [DOI] [PubMed] [Google Scholar]
- 13. Thall PF, Russell KE. A strategy for dose‐finding and safety monitoring based on efficacy and adverse outcomes in Phase I/II clinical trials. Biometrics. 1998;54(1):251‐264. [PubMed] [Google Scholar]
- 14. O'Quigley J, Hughes MD, Fenton T. Dose‐finding designs for HIV studies. Biometrics. 2001;57(4):1018‐1029. [DOI] [PubMed] [Google Scholar]
- 15. Braun TM. The bivariate continual reassessment method. Extending the CRM to Phase I trials of two competing outcomes. Control Clin Trials. 2002;23(3):240‐256. [DOI] [PubMed] [Google Scholar]
- 16. Yuan Y, Yin G. Bayesian dose finding by jointly modelling toxicity and efficacy as time‐to‐event outcomes. J R Stat Soc Ser C Appl Stat. 2009;58(5):719‐736. [Google Scholar]
- 17. Wages NA, Tait C. Seamless Phase I/II adaptive design for oncology trials of molecularly targeted agents. J Biopharm Stat. 2015;25(5):903‐920. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18. Lin R, Yin G. STEIN: a simple toxicity and efficacy interval design for seamless Phase I/II clinical trials. Stat Med. 2017;36(26):4106‐4120. [DOI] [PubMed] [Google Scholar]
- 19. Takeda K, Taguri M, Morita S. BOIN‐ET: Bayesian optimal interval design for dose finding based on both efficacy and toxicity outcomes. Pharm Stat. 2018;17(4):383‐395. [DOI] [PubMed] [Google Scholar]
- 20. Lin R, Zhou Y, Yan F, Li D, Yuan Y. BOIN12: Bayesian optimal interval Phase I/II trial design for utility‐based dose finding in immunotherapy and targeted therapies. JCO Precis Oncol. 2020;4:1393‐1402. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21. Jin I, Liu S, Thall P, Yuan Y. Using data augmentation to facilitate conduct of Phase I‐II clinical trials with delayed outcomes. J Am Stat Assoc. 2014;109(506):525‐536. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22. Takeda K, Morita S, Taguri M. TITE‐BOIN‐ET: time‐to‐event Bayesian optimal interval design to accelerate dose‐finding based on both efficacy and toxicity outcomes. Pharm Stat. 2020;19(3):335‐349. [DOI] [PubMed] [Google Scholar]
- 23. Biard L, Lee SM, Cheng B. Seamless Phase I/II design for novel anticancer agents with competing disease progression. Stat Med. 2021;40(21):4568‐4581. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24. Tsiatis A. A nonidentifiability aspect of the problem of competing risks. Proc Natl Acad Sci. 1975;72(1):20‐22. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25. Andersen PK, Abildstrom SZ, Rosthøj S. Competing risks as a multi‐state model. Stat Methods Med Res. 2002;11(2):203‐215. [DOI] [PubMed] [Google Scholar]
- 26. Putter H, Fiocco M, Geskus RB. Tutorial in biostatistics: competing risks and multi‐state models. Stat Med. 2006;26(11):2389‐2430. [DOI] [PubMed] [Google Scholar]
- 27. Jeong JH, Fine J. Direct parametric inference for the cumulative incidence function. J R Stat Soc Ser C Appl Stat. 2006;55(2):187‐200. [Google Scholar]
- 28. Benichou J, Gail MH. Estimates of absolute cause‐specific risk in cohort studies. Biometrics. 1990;46(3):813‐826. [PubMed] [Google Scholar]
- 29. Ivanova A, Wang Y, Foster MC. The rapid enrollment design for Phase I clinical trials. Stat Med. 2016;35(15):2516‐2124. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30. O'Quigley J, Paoletti X, Maccario J. Non‐parametric optimal design in dose finding studies. Biostatistics. 2002;3(1):51‐56. [DOI] [PubMed] [Google Scholar]
- 31. Cheung YK. Simple benchmark for complex dose finding studies. Biometrics. 2014;70(2):389‐397. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32. Lee SM, Cheung YK. Calibration of prior variance in the Bayesian continual reassessment method. Stat Med. 2011;30(17):2081‐2089. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33. Lee SM, Cheung YK. Model calibration in the continual reassessment method. Clin Trials. 2009;6(3):227‐238. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34. Wheeler GM, Mander AP, Bedding A, et al. How to design a dose‐finding study using the continual reassessment method. BMC Med Res Methodol. 2019;19(1):1‐15. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35. O'Quigley J, Shen LZ. Continual reassessment method: a likelihood approach. Biometrics. 1996;52(2):673‐684. [PubMed] [Google Scholar]
- 36. Beyersmann J, Latouche A, Buchholz A, Schumacher M. Simulating competing risks data in survival analysis. Stat Med. 2009;28(6):956‐971. [DOI] [PubMed] [Google Scholar]
- 37. Gray RJ. A class of K‐sample tests for comparing the cumulative incidence of a competing risk. Ann Stat. 1988;16(3):1141‐1154. [Google Scholar]
- 38. Cheung YK. Dose Finding by the Continual Reassessment Method. Biostatistics Series. New York: Chapman & Hall/CRC Press; 2011. [Google Scholar]
- 39. Colin P, Micallef S, Delattre M, Mancini P, Parent E. Towards using a full spectrum of early clinical trial data: a retrospective analysis to compare potential longitudinal categorical models for molecular targeted therapies in oncology. Stat Med. 2015;34(22):2999‐3016. [DOI] [PubMed] [Google Scholar]
- 40. Olmos D, A'hern R, Marsoni S, et al. Patient selection for oncology Phase I trials: a multi‐institutional study of prognostic factors. J Clin Oncol. 2012;30(9):996‐1004. [DOI] [PubMed] [Google Scholar]
- 41. Chevret S. The continual reassessment method in cancer Phase I clinical trials: a simulation study. Stat Med. 1993;12(12):1093‐1108. [DOI] [PubMed] [Google Scholar]
- 42. Paoletti X, Kramar A. A comparison of model choices for the continual reassessment method in Phase I cancer trials. Stat Med. 2009;28(24):3012‐3028. [DOI] [PubMed] [Google Scholar]
- 43. Topalian SL, Weiner GJ, Pardoll DM. Cancer immunotherapy comes of age. J Clin Oncol. 2011;29(36):4828‐4836. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44. Zhang Y, Cao S, Zhang C, Jin I, Zang Y. A Bayesian adaptive Phase I/II clinical trial design with late‐onset competing risk outcomes. Biometrics. 2020;77(3):796‐808. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45. Cheung YK. Sequential implementation of stepwise procedures for identifying the maximum tolerated dose. J Am Stat Assoc. 2007;102(480):1448‐1461. [Google Scholar]
- 46. Sachs RE, Donohue JM, Dusetzina SB. Accelerated approval ‐ taking the FDA's concerns seriously. N Engl J Med. 2022;387(3):199‐201. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Appendix S1 Supporting information
Data Availability Statement
Data sharing not applicable to this article as no datasets were generated or analyzed during the current study.


