Entangling free electrons and optical excitations

Abstract

The inelastic interaction between flying particles and optical nanocavities gives rise to entangled states in which some excitations of the latter are paired with momentum changes in the former. Specifically, free-electron entanglement with nanocavity modes opens appealing opportunities associated with the strong interaction capabilities of the electrons. However, the achievable degree of entanglement is currently limited by the lack of control over the resulting state mixtures. Here, we propose a scheme to generate pure entanglement between designated optical-cavity excitations and separable free-electron states. We shape the electron wave function profile to select the accessible cavity modes and simultaneously associate them with targeted electron scattering directions. This concept is exemplified through theoretical calculations of free-electron entanglement with degenerate and nondegenerate plasmon modes in silver nanoparticles and atomic vibrations in an inorganic molecule. The generated entanglement can be further propagated through its electron component to extend quantum interactions beyond existing protocols.

Quantum entanglement between free electrons and nanoscale optical excitations is achieved by shaping the electron wave function.

INTRODUCTION

Although entangled states in the context of quantum optics are generally relying on photons (1, 2), the exploration of entanglement with other types of information carriers could open a wealth of possibilities to find previously unexplored phenomena and materialize disruptive protocols for quantum metrology and microscopy (3–5). In particular, free electrons are advantageous candidates because they can undergo substantial inelastic scattering by nanostructures (6), which is an attribute enabling electron energy-loss spectroscopy (EELS) performed in electron microscopes to reveal the presence, strength, and spatial distribution of optical excitations down to the atomic scale (7–13). Actually, low-loss EELS has been extensively used to study atomic vibrations in low-dimensional materials (14, 15) and molecules (16–19), collective excitations such as plasmons (20–24) and phonon polaritons (11, 25–27), and photon confinement in optical cavities (28–30).

In momentum-resolved EELS, each excitation event produced by a traversing electron is individually identified through an electron measurement as a function of the deflection angle and energy loss (31–33), and therefore, this configuration already generates entanglement between electron states with different energy/momentum and excitations in the sampled structure. Consequently, the post-interaction electron-sample state has the form

$$\mid {\mathrm{\Psi }}_f\mathrm{\rangle }=\sum _n\int d^2{\mathbf{Q}}_f{\mathrm{\alpha }}_{{\mathbf{Q}}_f,n}^f\mid {\mathbf{Q}}_f\mathrm{\rangle }\otimes \mid n\mathrm{\rangle }$$ (1)

where n and Q_f run over final sample and electron-wave-vector states, respectively, and ${\mathrm{\alpha }}_{{\mathbf{Q}}_f,n}^f$ are complex scattering amplitudes (13). In some simple scenarios, such as the interaction with translationally invariant structures supporting surface polaritons, the excitation of these modes is associated with the transfer of definite amounts of energy and momentum, thus producing electron entanglement with a continuum of optical modes, which reveals their dispersion relation when measuring the electrons as a function of energy loss and deflection angle (31, 33–36). Entangled states produced by interaction with a polaritonic band in a translationally invariant specimen can even include the creation of multiple surfaces modes (32, 37, 38), as reported in the first experimental evidence of surface plasmons (37). However, for localized modes and, generally, in the interaction with photonic cavities, the resulting electron-specimen mixture of states is too complex to be of practical interest for quantum technologies.

Free-electron waves can be manipulated with great precision thanks to an impressive series of advances that occurred in electron microscopy over the past decades. Now, electron beams (e-beams) can be collimated and focused with sub-ångstrom spatial precision (39), as well as monochromatized and energy-filtered within a few millielectronvolt energy resolution (11, 25). In addition to traditional electron-optics elements such as lenses (40) and beam splitters (41–43), electron waves can be laterally shaped into on-demand profiles through static (44, 45) and programmable (46) plates, as well as through interaction with spatially modulated optical fields (47–51). The manipulation of the longitudinal electron wave function component is also possible in ultrafast electron microscopes (52), which enable temporal electron-pulse compression down to attosecond (53–55) time scales, and further endows free electrons with the ability to transfer quantum coherence among different systems (56, 57). The field is thus ripe for the exploitation of free electrons as additional elements in the quantum technology Lego, but as impressive as these advances may seem, they have not yet been leveraged to generate pure entanglement between light and free electrons in which only a few quantum states are involved in Eq. 1.

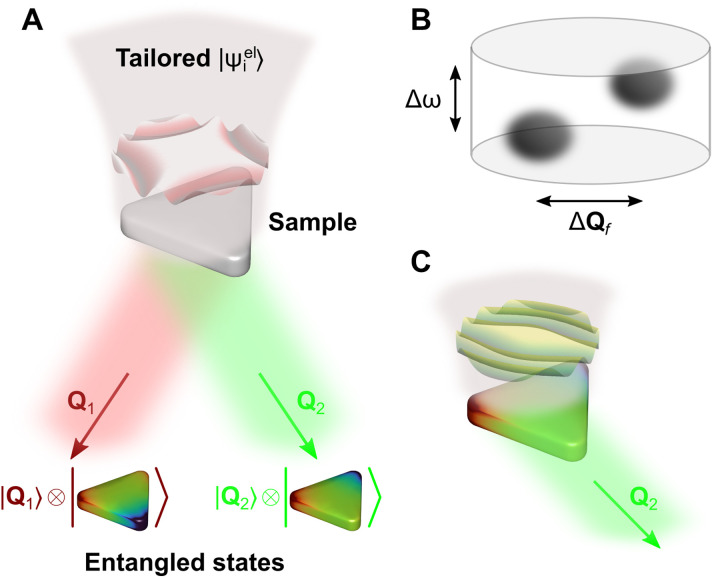
Here, we demonstrate through rigorous quantum theory that pure entanglement between electrons and confined optical modes can be generated by suitably patterning the transverse incident electron wave function. As schematically illustrated in Fig. 1A, the electron undergoes a change in the direction of propagation after being inelastically scattered by a specimen, and we prepare the incident electron wave profile (amplitude and phase) in such a way that only a few sample excitations are accessible (two in the figure), leading to separable transmission directions (transverse wave vectors Q₁ and Q₂). The two possible excitations created by the electron together with their different associated scattering directions form an entangled state. In essence, we specify a finite volume in the configuration space of transmitted electrons defined by an energy-loss window Δħω and a transverse momentum area ΔħQ_f in which the final state only populates two well-defined spots (Fig. 1B). As we demonstrate below, this approach can also be used to create heralded single sample excitations (Fig. 1C). In addition, manipulation of the electron component in electron–sample entangled states through, for example, electron interference could be used to process quantum information and imprint it on other (eventually macroscopic) objects via subsequent interactions.

Fig. 1. Proposed scheme for the generation of entangled electron–cavity states.

(A) A preshaped electron interacts with a nanostructure (a triangular plasmonic cavity) supporting well-defined optical or vibrational modes. The incident electron wave function $\mid {\mathrm{\psi }}_i^{\text{el}}\mathrm{\rangle }$ is tailored such that we obtain entangled states after interaction, correlating different specimen excitations (colored triangles) with separated electron scattering directions (final electron state having components of transverse wave vectors Q₁ and Q₂). A maximally entangled electron-specimen state is thus produced as the sample is in a superposition of excited states correlated with different electron scattering directions. (B) Electrons are emerging along separate spots within a finite region of size Δħω × ΔħQ_f in the configuration space of energy-loss and transverse-momentum transfers. (C) Momentum filtering at the electron detector allows us to project on the desired sample mode and eventually explore its dynamics through subsequent interrogation, for example, by exposure to a synchronized light pulse.

RESULTS

Free-electron interaction with confined optical modes

We intend to synthesize an electron–sample state, as described by Eq. 1, with the free-electron component piled up at separate regions in momentum–energy space (Fig. 1B) and a different sample excitation associated with each of those regions. The starting point is the initial combined state

$$\mid {\mathrm{\Psi }}_i\mathrm{\rangle }=\mid {\mathrm{\psi }}_i^{\text{el}}\mathrm{\rangle }\otimes \mid 0\mathrm{\rangle }$$

where the specimen is in its ground state ∣0〉 and the incident electron wave function, whose spatial dependence is given by

$${\mathrm{\psi }}_i^{\text{el}}(\mathbf{R})=\int d^2{\mathbf{Q}}_i {\mathrm{\alpha }}_{{\mathbf{Q}}_i}^i({\mathrm{e}}^{\mathrm{i}{\mathbf{Q}}_i·\mathbf{R}}/2\mathrm{\pi })$$ (2)

is prepared as a combination of momentum states with coefficients ${\mathrm{\alpha }}_{{\mathbf{Q}}_i}^i$ determined through the use of customized transmission masks (44, 45, 58) or phase imprinting based on electrostatic (46) and optical (47, 49) fields. We consider incident monochromatic electrons, such that the dependence of the electron wave function on two-dimensional (2D) transverse coordinates R and its decomposition in 2D wave vectors Q_i is everything we need to describe the electron in the interaction region without loss of generality.

The electron–specimen interaction operates a linear transformation relating the final coefficients ${\mathrm{\alpha }}_{{\mathbf{Q}}_f,n}^f$ in Eq. 1 to ${\mathrm{\alpha }}_{{\mathbf{Q}}_i}^i$ in Eq. 2. More precisely,

$${\mathrm{\alpha }}_{{\mathbf{Q}}_f,n}^f=\int d^2{\mathbf{Q}}_i M_{{\mathbf{Q}}_f-{\mathbf{Q}}_i,n} {\mathrm{\alpha }}_{{\mathbf{Q}}_i}^i$$ (3)

where M_{Qf −Qi,n} only depends on the momentum transfer ħ(Q_i − Q_f) for each excited state n (see Methods).

A connection can be readily established to EELS experiments, in which electron counts are recorded as a function of the energy loss ħω, thus yielding a frequency- and momentum-resolved loss probability ${\mathrm{\Gamma }}_{\text{EELS}}({\mathbf{Q}}_f,\mathrm{\omega })={\sum }_n{\mid {\mathrm{\alpha }}_{{\mathbf{Q}}_f,n}^f\mid }^2 \mathrm{\delta }(\mathrm{\omega }-{\mathrm{\omega }}_n)$, where ħω_n is the excitation energy of the sample mode n. Within first-order perturbation theory and further adopting the electrostatic and nonrecoil approximations, the angle-resolved EELS probability can be expressed in terms of mode-dependent dimensionless spectral functions g_n(ω) as

$$\begin{array}{cc}\hfill {\mathrm{\Gamma }}_{\text{EELS}}({\mathbf{Q}}_f,\mathrm{\omega })& =\frac{e^2}{4{\mathrm{\pi }}^3ħv^2}\sum _n{g}_n(\mathrm{\omega })\hfill \\ & \times {\mid \int d^2\mathbf{R} {\mathrm{\psi }}_i^{\text{el}}(\mathbf{R}){\mathrm{e}}^{-\mathrm{i}{\mathbf{Q}}_f·\mathbf{R}} w_n(\mathbf{R},\mathrm{\omega })\mid }^2\hfill \end{array}$$ (4)

where v is the electron velocity and

$$w_n(\mathbf{R},\mathrm{\omega })\propto \int d^2\mathbf{Q} {\mathrm{e}}^{\mathrm{i}\mathbf{Q}·\mathbf{R}} M_{\mathbf{Q},n}$$ (5)

describes the spatial profile of mode n [see details in Methods, including expressions for the quantities g_n(ω) and w_n(R, ω) associated with plasmons and atomic vibrations].

Here, we are interested in determining the incident electron wave function profile (i.e., the momentum-dependent coefficients ${\mathrm{\alpha }}_{{\mathbf{Q}}_i}^i$) such that different sample modes n are associated with final wave function coefficients ${\mathrm{\alpha }}_{{\mathbf{Q}}_{f,n}}^f$ within well-separated regions in momentum space (see Fig. 1B). To demonstrate the feasibility of this concept in the synthesis of electron–sample entanglement, we invert Eq. 3 with a predetermined choice of ${\mathrm{\alpha }}_{{\mathbf{Q}}_f,n}^f$, which we set to designated values for each sample excitation n within a targeted finite-size region in Q_f space (see details in Methods). This simple procedure is sufficient for the proof-of-principle demonstration that we pursue in this work. However, in one of the examples, we present further improvement of the results when using an iterative method. Other schemes for incident electron wave function optimization could rely on neural-network training (59).

Selected excitation of individual plamons

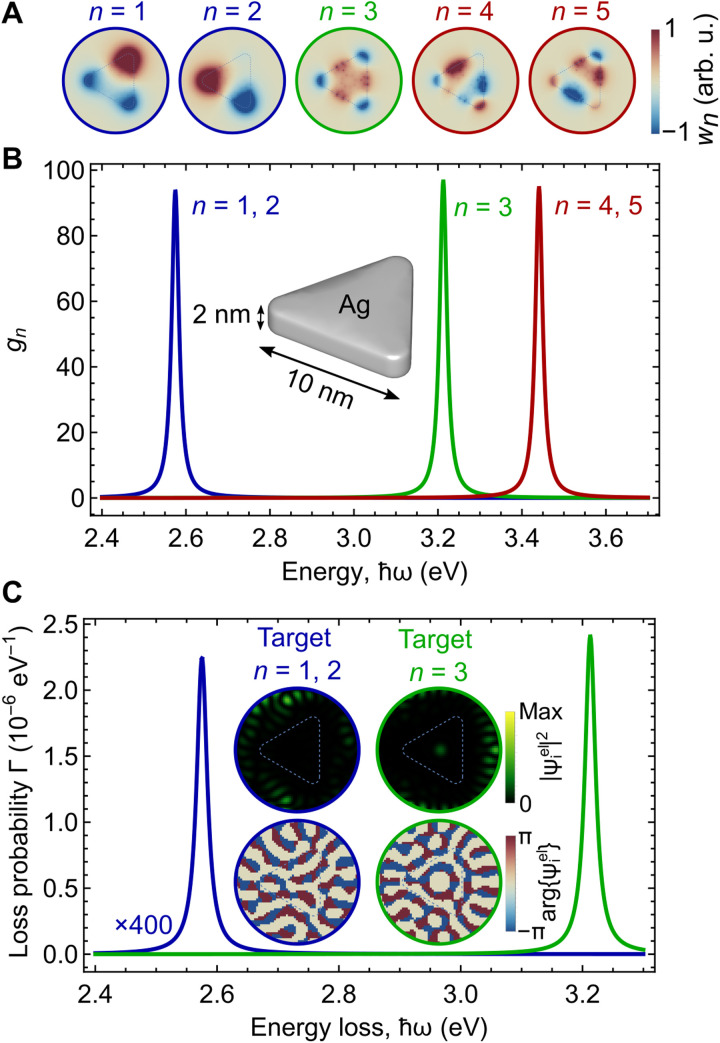
As a preliminary step before addressing electron–sample entanglement, we tackle the problem of selectively exciting a single plasmon in a metallic nanoparticle. Although this can be achieved through post-selection of a small range of scattered electron wave vectors (42), we formulate a solution in which the plasmon-exciting electrons emerge within a relatively large region in momentum space, and this solution is generalized below to create entanglement. We consider a silver triangle that sustains five plasmon modes in the spectral region between 2.4 and 3.7-eV spectral region (60): two sets of doubly degenerate dipolar (blue curve and circles, n = 1,2) and quadrupolar (red, n = 4,5) plasmons and one nondegenerate hexapolar mode (green, n = 3), as revealed by the spatial and spectral functions plotted in Fig. 2 (A and B) (see details of the calculation in Methods). We then optimize the incident electron wave function over a finite Q_i region discretized with 1257 pixels and defined by a convergence half-angle φ_i = 1.5 mrad, such that either n = 1,2 or n = 3 is the only mode excited when the scattered electrons are collected over a Q_f region spanning a half-angle φ_f = 0.75 mrad (discretized with 49 pixels) and energy-filtered between 2.4 and 3.3 eV. Incidentally, modes n = 1 and 2 are dipolar, so they can be effectively excited in the aloof configuration, while mode n = 3 is hexapolar and requires the electron to pass closer to the particle to be excited.

Fig. 2. Selective excitation of plasmon modes in a silver nanotriangle.

(A and B) Spatial profiles (A) and spectral functions (B) associated with plasmons in a silver nanotriangle with a thickness of 2 nm and a side length of 10 nm. We find two sets of degenerate modes (blue and red peaks) and one nondegenerate mode (green; see color labels matched with the index n). (C) Electron energy-loss spectra for two optimized incident electron wave function profiles ${\mathrm{\psi }}_i^{\text{el}}(\mathbf{R})$. The insets show maps of the probability density and phase of the incident wave functions in the space of transverse coordinates R, framed in color-matched circumferences. The optimization is carried out for 100 keV electrons, an electron detector consisting of 49 pixels, an incident convergence half-angle φ_i = 1.5 mrad, and a collection half-angle φ_f = 0.75 mrad. The nanotriangle contour is indicated by thin dashed lines in (A) and (C).

The resulting real-space profiles of ${\mathrm{\psi }}_i^{\text{el}}(\mathbf{R})$ are shown in the insets of Fig. 2C (circular color plots; see also fig. S6A for the incident electron wave functions in Q_i space), along with the color-matched EELS probability curves obtained from Eq. 4 by collecting only electrons that emerge within the indicated Q_f and energy region. In a typical experimental scenario with an unshaped electron beam, multiple modes are excited by the incident electron because they have overlapping spatial distributions (Fig. 2A), and the EELS probability integrated over all possible Q_f′s is rigorously given by the incoherent average over incident electron positions R, weighted by the electron probability ${\mid {\mathrm{\psi }}_i^{\text{el}}(\mathbf{R})\mid }^2$ (see Methods) (6, 61). However, our simple optimization procedure is capable of placing the weight of the excitation of either n = 1,2 or n = 3 mode preferably inside the Q_f region defined by a collection half-angle φ_f = 0.75 mrad. Such an optimization can be performed for smaller or larger convergence and collection angles as shown in fig. S1.

Generation of electron–plasmon entangled states

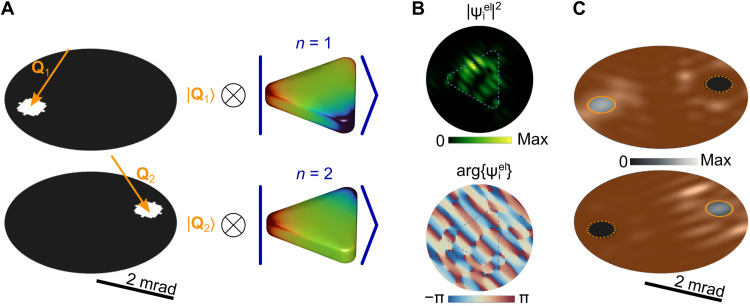
We now apply the principle of ${\mathrm{\psi }}_i^{\text{el}}$ shaping to demonstrate the generation of electron–sample entanglement for the same triangular particle as considered above. Specifically, we focus on the lowest-energy degenerate plasmons n = 1,2 (i.e., we consider post-selection of these final states by an energy filter) and aim at correlating these excitations with final electron momentum states along separate Q_f directions (Fig. 3A). By maximizing the fraction of the signal associated with the targeted excitation in each respective Q_f direction through the steepest-descent method, we find the optimized electron wave function shown in real space in Fig. 3B (and in momentum space in fig. S6B), from which we obtain the actual scattered electron distribution plotted in Fig. 3C in Q_f space for components corresponding to the excitation of n = 1 (top) and n = 2 (bottom) modes.

Fig. 3. Creation of electron–sample states with a high degree of entanglement.

(A) Pursued electron–sample entangled state, consisting of the superposition of selected (by means of two apertures) electron momentum states within the white pixels in Q_f space (left) and correlated degenerate dipolar plasmons in the silver nanotriangle sample considered in Fig. 2 (right). (B) Spatial profile of the optimized incident wave function ${\mathrm{\psi }}_i^{\text{el}}(\mathbf{R})$ required to produce the final state in (A). The contour of the triangular nanoparticle is indicated with dashed lines. (C) Resulting probability distributions ∣〈Q_f, n∣Ψ_f〉∣² with n = 1 (top) and n = 2 (bottom) in Q_f space, where each aperture (small circles) transmits nearly 100% of the targeted excitation n. The area outside the apertures (intended to be masked) is colored to emphasize the selected momentum regions of interest. The optimization is carried out for 100 keV electrons, 81 pixels in each of the detector apertures, φ_i = 4 mrad, and φ_f = 2 mrad.

When examining the resulting degree of entanglement, we express the final electron–sample state after energy filtering and momentum post-selection by two apertures defined by the orange circles in Fig. 3C as

$$\begin{array}{cc}\hfill \mid {\mathrm{\Psi }}_f\mathrm{\rangle }& =(p_{11}\mid {\mathbf{Q}}_1\mathrm{\rangle }+p_{12}\mid {\mathbf{Q}}_2\mathrm{\rangle })\otimes \mid 1\mathrm{\rangle }\hfill \\ & +(p_{22}\mid {\mathbf{Q}}_2\mathrm{\rangle }+p_{21}\mid {\mathbf{Q}}_1\mathrm{\rangle })\otimes \mid 2\mathrm{\rangle }\hfill \end{array}$$ (6)

where we assume that the apertures are small enough so that each of them captures coherently scattered electrons characterized by a well-defined state ∣Q_f〉 with f = 1,2 (in practice, each of them can be a coherent superposition of plane waves transmitted through the finite solid angle region spanned by each aperture). To achieve pure entanglement, we require p_nm → 0 for n ≠ m terms in Eq. 6, which happens after the noted numerical optimization: We obtain values $p_{11}^2/(p_{11}^2+p_{21}^2)=0.999991$ and $p_{22}^2/(p_{22}^2+p_{12}^2)=0.999779$, confirming a high degree of entanglement (62). Incidentally, a more direct inversion procedure without optimization still yields a level of entanglement exceeding 90% (fig. S2).

We note that the symmetry of the selected degenerate plasmons plays a similar role as photon polarization in light-based entanglement schemes (1). In the present instance, the electron wave function profiles are strongly affected by the threefold symmetry of the plasmonic nanoparticles and the choice of correlated electron output angles. Optimized profiles for more symmetric nanoparticles also become more symmetric, as shown for silver disks in fig. S3, where a high degree of entanglement (>99% mode separation) is achieved by direct inversion.

Electron entanglement with atomic vibrational states

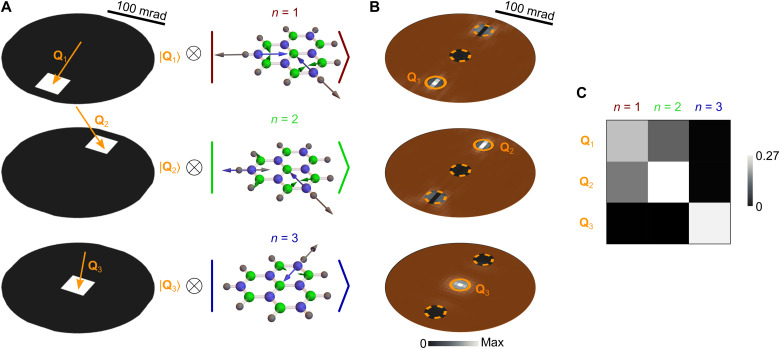
The electron–sample entanglement scheme under consideration can be applied to sample excitations of different nature. We illustrate this versatility by considering atomic vibrations in a hexagonal boron nitride (hBN) molecule (Fig. 4), which we simulate from first principles (see Methods) (63) assuming passivation of the edges with hydrogen atoms. This structure supports a number of vibrational excitations up to energies ∼450 meV, including a set of triply degenerate N─H bond-stretching modes at 440 meV (see EELS spectrum in fig. S4), on which we focus our analysis. We again optimize the incident electron wave function to achieve entanglement between final electron states and vibrational modes of the molecule [see the resulting ${\mathrm{\psi }}_i^{\text{el}}(\mathbf{R})$ and ${\mathrm{\psi }}_i^{\text{el}}({\mathbf{Q}}_i)$ profiles in figs. S5 and S6C]. Because of the strong spatial confinement of vibrational modes, the angular ranges that need to be used for the incident and scattered electron wave functions are now considerably larger than for plasmons (cf. angle scales in Figs. 3 and 4). The achieved electron–sample state, illustrated in Fig. 4B, exhibits a decent degree of entanglement when selecting electrons scattered along the colored circles in Q_f space, also revealed through the partial probabilities contributed by each of the three vibrational modes to each of the regions enclosed by those circles (see table in Fig. 4C).

Fig. 4. Entanglement of free electrons and atomic vibrations.

(A) Pursued electron–sample entangled state, consisting of the superposition of selected (by means of three apertures) electron-momentum states within the white pixels in Q_f space (left) and correlated triply degenerate 440-meV vibrational modes of an hBN molecule (right). (B) Resulting probability distributions ∣〈Q_f, n∣Ψ_f〉∣² with n = 1 (top), n = 2 (middle), and n = 3 (bottom) in Q_f space. The area outside the apertures (small circles) is colored to emphasize the selected momentum regions of interest. (C) Probability matrix showing the fractional contribution associated with the excitation of each of the three vibrational modes n = 1 to 3 to the energy-filtered electron signal contained within the three selected circular areas around final transverse wave vectors Q₁, Q₂, and Q₃ in (A). The sum of the nine matrix elements is normalized to one. We consider 60 keV electrons, 29 detector pixels, and φ_i = φ_f = 100 mrad.

DISCUSSION

By entangling the transverse momenta of free electrons with localized optical excitations in a nanostructure, we could selectively measure one of the corresponding outgoing electron directions, thus providing a way to herald the creation of single designated excitations in the studied specimen. This should allow us to follow the dynamics of the latter and gain insight into the state-dependent decay pathways, for example, by subsequently probing the evolution of the specimen through scattering of laser pulses that are synchronized with the electron in an electron-pump/photon-probe approach. An additional possibility is offered by correlating the angle-resolved electron signal with traces originating in the decay of excited states of the specimen (e.g., an electrical signal produced by coupling to electron-hole pairs in a proximal semiconductor or also the polarization- and angle-resolved cathodoluminescence emission associated with radiative decay). The present scheme could further be extended to incorporate gain processes similar to those in photon-induced near-field electron microscopy (PINEM) (54) upon illumination of the sample with symmetry-matched optical pulses that can simultaneously excite a subset of its supported excitations.

We remark that the proposed approach holds elements of novelty with respect to traditional quantum optics methods because one of the entangled particles (the free electron) can be highly energetic and, therefore, capable of undergoing subsequent strong collisions with other objects. These collisions could, for instance, trigger chemical reactions that would then be entangled with optical modes in the specimen with which the electron has previously interacted.

Although we have illustrated some possibilities based on heuristic electron wave function designs and a straightforward application of the steepest-descent maximization method, improved solutions to the problem of entanglement optimization could be obtained through neural-network training (59), possibly combined with iterative physical improvement of the wave function profile based on currently explored tunable electron phase plates (46–51). As an alternative to the use of aloof interaction with the optical modes of the sampled nanostructure to avoid strong electron collisions with atomic potentials, this type of adaptive improvement could potentially be used to compensate for the effect of these potentials and morphological imperfections. In addition to the investigated examples of plasmons in nanoparticles and atomic vibrations in molecules, we envision the entanglement of free electrons with optical modes in dielectric cavities (30) and photons guided along optical waveguides (64), which together configure a vast range of possibilities for leveraging the quantum nature of free electrons in the design of improved microscopy and metrology schemes.

METHODS

Transfer matrix for inelastic electron–sample scattering

The time-dependent electron–sample system can be generally described by a wave function of the form $\mid \mathrm{\psi }(t)\mathrm{\rangle }=\sum _n\int d^3\mathbf{q} {\mathrm{\alpha }}_{\mathbf{q},n}(t){\mathrm{e}}^{-\mathrm{i}({\mathrm{ϵ}}_{\mathbf{q}}+{\mathrm{\omega }}_n)t}\mid \mathbf{q}\mathrm{\rangle }\otimes \mid n\mathrm{\rangle }$, where ∣q〉 and ∣n〉 are electron and sample eigenstates of the noninteracting Hamiltonian with energies ħε_q and ħω_n, respectively. In particular, electron states are labeled by the 3D momentum ħq and satisfy the orthonormality relation 〈q∣q′〉 = δ(q − q′). The expansion coefficients α_q,n(t) are determined by solving the Schrödinger equation with an electron–sample interaction Hamiltonian $\widehat{{\mathscr{H}}_1}$, which is generally weak for the energetic electrons that are typically used in electron microscopes, so we can work within first-order perturbation theory. Then, taking the sample to be initially prepared in its ground state n = 0, the post-interaction wave function has coefficients ${\mathrm{\alpha }}_{\mathbf{q},n}(\infty )=(-2\mathrm{\pi }\mathrm{i}/ħ)\int d^3\mathbf{q}\prime \mathrm{\delta }({\mathrm{ϵ}}_{\mathbf{q}}-{\mathrm{ϵ}}_{\mathbf{q}\prime }+{\mathrm{\omega }}_n)\mathrm{\langle }n\mid \mathrm{\langle }\mathbf{q}\mid \widehat{{\mathcal{H}}_1}\mid \mathbf{q}\prime \mathrm{\rangle }\mid 0\mathrm{\rangle }{\mathrm{\alpha }}_{\mathbf{q}\prime ,0}(-\infty )$, where we set ω₀ = 0 without loss of generality. We further adopt the nonrecoil approximation (13) ϵ_q − ϵ_q′ ≈ (q − q′) · v under the assumption that the transverse electron energy is negligible compared with the longitudinal energy along the e-beam direction defined by the average electron velocity v. This condition is commonly satisfied in electron microscopes. In this approximation, the energy ħω_n transferred from the electron to the sample is fully absorbed by a change in the longitudinal electron wave vector given by −ω_n/v, so for monochromatic incident electrons, the initial and final longitudinal components of the electron wave function play a trivial role and can be disregarded in the description of the present problem. Consequently, we can expand the final wave function as shown in Eq. 1, with coefficients ${\mathrm{\alpha }}_{{\mathbf{Q}}_f,n}^f\equiv {\mathrm{\alpha }}_{\mathbf{q},n}(\infty )$ that only depend on the transverse electron wave vector Q_f for each sample excitation n and are determined from the incident electron wave function coefficients ${\mathrm{\alpha }}_{{\mathbf{Q}}_i}^i\equiv {\mathrm{\alpha }}_{\mathbf{q},0}(-\infty )$ through the linear relation ${\mathrm{\alpha }}_{{\mathbf{Q}}_f,n}^f=\int d^2{\mathbf{Q}}_i M_{{\mathbf{Q}}_f-{\mathbf{Q}}_i,n} {\mathrm{\alpha }}_{{\mathbf{Q}}_i}^i$ (Eq. 3) with

$$M_{{\mathbf{Q}}_f-{\mathbf{Q}}_i,n}=\frac{-2\mathrm{\pi }i}{ħv}\mathrm{\langle }n\mid \mathrm{\langle }{\mathbf{q}}_f\mid \widehat{{\mathcal{H}}_1}\mid {\mathbf{q}}_i\mathrm{\rangle }\mid 0\mathrm{\rangle }$$ (7)

We remark that the transfer matrix elements defined in Eq. 7 involve just the difference between incident and scattered transverse wave vectors. In what follows, we develop a formalism to relate M_{Qf −Qi,n} to the EELS probability and obtain specific expressions for plasmonic and atomic-vibration modes.

EELS with shaped electron beams

We consider the configuration of Fig. 1A and assume the electron velocity and sample dimensions to be small enough as to neglect retardation effects and work in the electrostatic regime. Further adopting the aforementioned nonrecoil approximation, we can disregard the longitudinal component of the electron wave function and only consider the dependence on transverse coordinates R = (x, y) (i.e., taking the electron velocity v along z). We can then write a general expression for the EELS probability Γ_EELS(ω) in terms of the energy loss ħω, the transverse wave vector ${\mathbf{Q}}_f\perp \widehat{\mathit{z}}$ of the final (f) electron state (corresponding to a wave function ∝ e^{iQ_f · R}), and the transverse component of the initial (i) electron wave function, ψ_i(R). More precisely, using equation 17 of (6), we have Γ_EELS(ω) = ∫ d²Q_f Γ_EELS(Q_f, ω), where

$$\begin{array}{cc}\hfill {\mathrm{\Gamma }}_{\text{EELS}}({\mathbf{Q}}_f,\mathrm{\omega })& =\frac{e^2}{4{\mathrm{\pi }}^3ħv^2}\int d^2\mathbf{R}\int d^2\mathbf{R}\prime {\mathrm{\psi }}_{\mathrm{i}}(\mathbf{R}){\mathrm{\psi }}_i^{*}(\mathbf{R}\prime )\hfill \\ & \times {\mathrm{e}}^{\mathrm{i}{\mathbf{Q}}_f·(\mathbf{R}\prime -\mathbf{R})}\mathcal{W}(\mathbf{R},\mathbf{R}\prime ,\mathrm{\omega })\hfill \end{array}$$ (8)

is the momentum-resolved probability and

$$\mathcal{W}(\mathbf{R},\mathbf{R}\prime ,\mathrm{\omega })={\int }_{-\infty }^{\infty }\mathit{dz}{\int }_{-\infty }^{\infty }dz\prime {\mathrm{e}}^{\mathrm{i}\mathrm{\omega }(z-z\prime )/v}\times \text{Im}\{-W(\mathbf{r},\mathbf{r}\prime ,\mathrm{\omega })\}$$ (9)

is a transverse screened interaction obtained from the full screened interaction W(r, r′, ω). The latter stands for the Coulomb potential created at r by a point charge of magnitude e^−iωt placed at r′, including the effect of screening by the environment. Now, as we show below for plasmonic and phononic structures, the transverse screened interaction in Eq. 9 is separable as

$$\mathcal{W}(\mathbf{R},\mathbf{R}\prime ,\mathrm{\omega })=\sum _n{g}_n(\mathrm{\omega })w_n(\mathbf{R},\mathrm{\omega })w_n^{*}(\mathbf{R}\prime ,\mathrm{\omega })$$ (10)

where n runs over excitation modes characterized by spatial profiles w_n(R, ω) and dimensionless spectral functions g_n(ω). Finally, inserting Eq. 10 into Eq. 8, we readily find Eq. 4 in the main text. Incidentally, the angle-integrated inelastic electron signal (i.e., the integral of Eq. 8 over Q_f) reduces to Γ_EELS(ω) = (e²/πħv²)∑_ng_n(ω) ∫ d²R ∣ψ_i(R)∣²∣w_n(R, ω)∣², which is an average over transverse positions R weighted by both the incident electron probability (6, 61) and the mode spatial profile, and consequently, because the e-beam can generally excite different modes n, the optimization scheme that we pursue here to produce entanglement essentially consists in rearranging the Q_f distribution of the scattered electron components associated with the excitation of each of those modes.

We note that the spectral functions in this formalism can be generally approximated by Lorentzians

$$g_n(\mathrm{\omega })\approx \text{Im}\left\{\frac{G_n/\mathrm{\pi }}{{\mathrm{\omega }}_n-\mathrm{\omega }-i{\mathrm{\gamma }}_n/2}\right\}$$

peaked at the mode energies ħω_n and having areas G_n and widths γ_n (see below) that determine the spectral positions and strengths of the EELS features.

Numerical determination of $\mathbf{\mid }{\mathbf{\psi }}_{\mathit{i}}^{\mathbf{\text{el}}}\mathbf{\rangle }$ for creating selected excitations and entangled electron–sample states

Given a desired final state defined through the coefficients ${\mathrm{\alpha }}_{{\mathbf{Q}}_f,n}^f$, we numerically obtain ${\mathrm{\alpha }}_{{\mathbf{Q}}_i}^i$ by inverting Eq. 3 upon discretization of Q_i using a finite number of points and pixels at the electron analyzer in the Fourier plane Q_f, as noted in the main text. More precisely, we follow a simple procedure consisting in specifying target values of ${\mathrm{\alpha }}_{{\mathbf{Q}}_f,n}^f$ within a region Q < Q_f,max (effectively setting it to zero outside it) and obtain ${\mathrm{\alpha }}_{{\mathbf{Q}}_i}^i$ for Q_i < Q_{i, max} through the aforementioned numerical inversion method. The wave vector ranges are related to the maximum incidence|collection half-angle φ_i∣f through Q_{i∣f, max} = (m_ev/ħ) sin φ_i∣f. In this scheme, to select a single sample excitation n = n₀ (Fig. 2), we set ${\mathrm{\alpha }}_{{\mathbf{Q}}_f,n}^f=C{\mathrm{\delta }}_{n{n}_0}\mathrm{\Theta }(Q_{f,\text{max}}-Q_f)$, where C is a constant and Θ is the step function. However, to produce electron–sample entanglement involving two (Fig. 3) or three (Fig. 4) sample states n_j correlated with final electron wave vectors Q_j (see Fig. 1B), we set ${\mathrm{\alpha }}_{{\mathbf{Q}}_f,n_j}^f$ to a constant at the Q_f space pixel that contains Q_j and zero elsewhere. We then construct $\mid {\mathrm{\psi }}_{\mathit{i}}^{\text{el}}\mathrm{\rangle }$ from the obtained coefficients ${\mathrm{\alpha }}_{{\mathbf{Q}}_i}^i$ (also setting them to zero for Q_i > Q_{i, max}) and insert this input wave function in Eq. 4 to generate the actual final probability distributions, plotted in the figures with a finer discretization in Q_f space.

Transfer matrix from the spectral and spatial mode functions

An expression for the EELS probability analogous to Eq. 4 can be readily obtained from Eq. 3 as

$${\mathrm{\Gamma }}_{\text{EELS}}({\mathbf{Q}}_f,\mathrm{\omega })=\sum _n{\mid \int d^2{\mathbf{Q}}_i M_{{\mathbf{Q}}_f-{\mathbf{Q}}_i,n} {\mathrm{\alpha }}_{{\mathbf{Q}}_i}^i\mid }^2 \mathrm{\delta }(\mathrm{\omega }-{\mathrm{\omega }}_n)$$ (11)

The connection between Eqs. 4 and 11 is established by adding finite mode widths γ_n to the latter and expanding the incident electron wave function in the former as an integral over momentum components, as indicated in Eq. 2. Comparing the two resulting expressions, we find

$$M_{\mathbf{Q},n}=\frac{e}{4{\mathrm{\pi }}^{2}v}\sqrt{\frac{G_n}{\pi \mathit{ħ}}}\int d^2\mathbf{R} {\mathrm{e}}^{\mathrm{-}\mathrm{i}\mathbf{Q}·\mathbf{R}}{w}_n(\mathbf{R},\mathrm{\omega })$$ (12)

which provides a prescription to obtain the transfer matrix coefficients defined in Eq. 7 directly from the screened interaction, thus bypassing the need for a detailed specification of the interaction Hamiltonian. Then, the spatial profiles in Eq. 5 are simply given by the inverse Fourier transform of Eq. 12.

Transfer matrix and transverse screened interaction for plasmonic nanoparticles

In the electrostatic limit under consideration, we can recast the response of an arbitrarily shaped homogeneous nanoparticle into an eigenvalue problem (65, 66). We then need to find the real eigenvalues λ_n and eigenvectors σ_n(s) of the integral equation 2πλ_nσ_n(s) = ∮ ds′F(s, s′)σ_n(s′), where s and s′ run over particle surface coordinates, F(s, s′) = − $\widehat{\mathrm{n}}$ · (s − s′)/∣s − s′∣³, and $\widehat{\mathrm{n}}$ is the outer surface normal. Here, we solve this eigensystem for triangular particles using the MNPBEM toolbox (67) based on a finite boundary element discretization of the particle surface. Then, the spectral functions in Eq. 10 reduce to (65, 66)

$$g_n(\mathrm{\omega })=\text{Im}\left\{\frac{-2}{\mathrm{ϵ}(1+{\mathrm{\lambda }}_n)+(1-{\mathrm{\lambda }}_n)}\right\}$$

whereas the spatial profiles become

$$w_n(\mathbf{R},\mathrm{\omega })=2\oint d\mathbf{s} {\mathrm{\sigma }}_n(\mathbf{s}){\mathrm{e}}^{-\mathrm{i\omega }{s}_z/v}{K}_0\left(\frac{\mathrm{\omega }\mid \mathbf{R}-\mathbf{S}\mid }{v}\right)$$

with $\mathbf{s}=\mathbf{S}+s_z\widehat{\mathbf{z}}$. This expression neglects the contribution of bulk modes, which should be a reasonable approximation at loss energies well below the bulk plasmon. Inserting it into Eq. 12, the transfer matrix elements reduce to

$$M_{\mathbf{Q},n}\approx \frac{e}{\mathrm{\pi }v}\sqrt{\frac{G_n}{\pi \mathit{ħ}}}\frac{1}{Q^2+{\mathrm{\omega }}_n^2/v^2}\oint d\mathbf{s}{\mathrm{\sigma }}_n(\mathbf{s}){\mathrm{e}}^{-\mathrm{i}(\mathbf{Q}+\hat{\mathbf{z}}{\mathrm{\omega }}_n/v)·\mathbf{s}}$$

where we have approximated ω ≈ ω_n. For silver, we model the dielectric function as (6) $\mathrm{ϵ}={\mathrm{ϵ}}_b-{\mathrm{\omega }}_p^2/\mathrm{\omega }(\mathrm{\omega }+\mathrm{i}\mathrm{\gamma })$ with ϵ_b = 4.0, ħω_p = 9.17 eV, and ħγ = 21 meV, yielding mode frequencies ${\mathrm{\omega }}_n={\mathrm{\omega }}_p/\sqrt{{\mathrm{ϵ}}_b+(1-{\mathrm{\lambda }}_n)/(1+{\mathrm{\lambda }}_n)}$, flat widths γ_n ≈ γ, and spectral weights $G_n=\mathrm{\pi }{\mathrm{\omega }}_n^3/[{\mathrm{\omega }}_p^2(1+{\mathrm{\lambda }}_n)]$.

Transfer matrix and transverse screened interaction for atomic vibrations

For molecules or nanoparticles whose mid-infrared response is dominated by atomic vibrations, we find the spectral and spatial dependence of the modes in Eq. 10 to be governed by (63, 68).

$$g_n(\mathrm{\omega })=\text{Im}\left\{\frac{{\mathrm{\omega }}_n^2}{{\mathrm{\omega }}_n^2-\mathrm{\omega }(\mathrm{\omega }+i\mathrm{\gamma })}\right\}$$ (13)

and

$$w_n(\mathbf{R},\mathrm{\omega })=\frac{2}{{\mathrm{\omega }}_n}\sum _l\frac{1}{\sqrt{M_l}}\int d^3\mathbf{r}\prime K_0(\mathrm{\omega }\mid \mathbf{R}-\mathbf{R}\prime \mid /v){\mathrm{e}}^{\mathrm{i\omega }z\prime /v}[{\mathit{e}}_{\mathrm{nl}}·{\overrightarrow{\mathrm{\rho }}}_l(\mathbf{r}\prime )]$$

where n now runs over vibrational modes, ω_n and e_nl are the corresponding real frequencies and normalized atomic displacement vectors (∑_l e_nl · e_n^′l = δ_nn^′), respectively, the l sum extends over the atoms in the structure, M_l is the mass of atom l, ${\overrightarrow{\mathrm{\rho }}}_l(\mathbf{r})$ denotes the gradient of the charge distribution associated with displacements of that atom, and we have incorporated a phenomenological damping rate γ (here set to ħγ = 1 meV). From Eq. 13, we have γ_n ≈ γ for all modes and G_n ≈ πω_n/2. Following (63), we use density functional theory (DFT) to calculate ${\overrightarrow{\mathrm{\rho }}}_l(\mathbf{r})$, ω_n, and e_nl (see below). The prescription $\mid \mathbf{R}-\mathbf{R}\prime \mid \to \sqrt{{\mid \mathbf{R}-\mathbf{R}\prime \mid }^2+{\mathrm{\Delta }}^2}$ is also adopted with $\mathrm{\Delta }=0.2 \stackrel{°}{\mathrm{A}}$ to approximately account for a cutoff ∼ħ/Δ in momentum transfer (6) and so avoid the unphysical divergence associated with close electron-atom encounters.

First-principles description of atomic vibrations

We use DFT and the projector augmented wave method (69) as implemented in the Vienna Ab initio Simulation Package (70–72) with the Perdew-Burke-Ernzerhof–generalized gradient approximation for electron exchange and correlation (73). This method is applied to describe hBN flakes with hydrogen-passivated edges using a plane wave cutoff energy of 500 eV and a sufficient amount of vacuum spacing in all directions around the structure to avoid interaction among the periodic images. Atomic equilibrium positions are found by minimizing the total energy using the conjugate gradient method with convergence criteria between consecutive iteration steps set to 10⁻⁵ eV for the total energy and 0.02 eV/Å for the atomic forces. Vibrational frequencies and eigenmodes are found by diagonalizing the dynamical matrix, which is calculated for 0.01-Å displacements. The corresponding gradients ${\overrightarrow{\mathrm{\rho }}}_l^{}(\mathbf{r})$ of the charge distribution are obtained by treating core electrons and nuclei as point particles, while the contribution coming from valence electrons is directly taken from DFT using a dense grid.

Supplementary Materials

This PDF file includes:

Figs. S1 to S6