Abstract
Background
Stress shielding (SS) is considered the main mechanical cause of femoral stem loosening after total hip arthroplasty (THA). This study introduces an auxetic lattice femoral stem structure with negative Poisson's ratio that can expand laterally, with the intent of transferring more load to surrounding bone and thereby reducing SS. This study aims to evaluate how the geometry profile of different femoral stems with auxetic structures affects the level of SS. Different re-entrant angles for the auxetic unit cells were also evaluated.
Methods
This study assessed three commercial femoral stem designs (Mayo, CLS and Fitmore) and three re-entrant angles for the auxetic structures (60°, 70° and 80°). Nine auxetic femoral stems (three M-type, three C-type and three F-type) and three solid femoral stems (control group) were designed. All femoral stems were implanted into a finite element model of the human femur to compare levels of SS between the auxetic stems and their traditional solid counterparts.
Results
The results showed that incorporating an auxetic structure into the stem design caused less SS of the surrounding bone than the control models. The M-type stems had the lowest level of SS, followed by the C-type and F-type stems. A re-entrant angle of 70° for the M-type stem, 80° for the C-type stem and 60° for the F-type stem were the designs most capable of reducing SS.
Conclusions
This study found that femoral stems with an auxetic lattice structure caused less SS after THA than comparable solid femoral stems. A femoral stem based on the M-type geometry profile is recommended when designing auxetic femoral stems to minimize SS of surrounding bone.
The translational potential of this article
The novel solution provided in this study may serve to increase the survival rate of femoral stems by reducing SS after THA.
Keywords: Auxetic structure, Femoral stem, Negative Poisson's ratio, Stress shielding, Total hip arthroplasty
1. Introduction
Total hip arthroplasty (THA) is considered the gold standard for treating severe hip disease when more conservative approaches offer little relief to the patient. However, as younger patients undergo hip replacement, it is becoming increasingly important to design implants that can withstand an active lifestyle and minimize complications after long-term implantation. Aseptic loosening of the femoral stem is one of the most common causes of implant failure [1], with stress shielding (SS) being the main mechanical factor leading to aseptic loosening [2].
In the intact femur, load transfers vertically from the femoral head through the femoral neck to the femur shaft, resulting in a tensile force in the lateral proximal femur and compressive force in the medial proximal femur. Replacing a section of the femur with a hip implant disrupts the natural load transmission down the bone shaft and introduces a new interface between the implant and bone through which the load must be transmitted [2]. Femoral stems with higher stiffness bear greater loads than the surrounding bone, leading to a reduction in stress transferred to the proximal femur, which is termed SS. SS can cause periprosthetic bone resorption due to insufficient mechanical stimulation at the stem-bone fixation interface, often leading to aseptic loosening of the implant.
Previous studies introduced a wide variety of femoral stem designs and features aimed at reducing the level of SS from the implant. Among them, short stems have been shown to increase the magnitude of load transferred to the proximal femur [3], while the use of a conical profile can convert shear forces at the bone-implant interface into normal forces to increase the stress on the femur [4]. Alternatively, incorporating a collar on the proximal part of the stem allows for direct loading of the calcar of the femur which increases the axial stress on the bone. For the stem structure, using a slotted or grooved design or hollow and porous structures can reduce the local stiffness of the stem by reducing the material volume, which can increase the load transmitted to the bone [5]. Although such designs have been shown to reduce SS [4,[6], [7], [8], [9], [10]], several studies found that the stress on the femur after implantation is still less than on the intact femur, especially around the proximal lateral side near the greater trochanter [6,7,11].
An auxetic structure is one with a negative Poisson's ratio, where the overall structure expands radially under axial tension (or retracts under compressive load). The auxetic property is due to the flexibility of the struts that constitute the structure. Alderson et al. proposed a design for a modular femoral stem with an auxetic structure which could improve the fit and fill of the femoral stem in the medullary cavity by rotating a screw structure inside the stem to expand the stem against the cavity walls [12]. Kolken et al. designed a femoral stem that combined both an auxetic structure and porous honeycomb structure. Kolken's stem could produce compressive stress on both the medial and lateral sides of the femoral cavity to reduce the risk of failure at the fixation interface [13]. Ghavidelnia et al. reported that femoral stems with an auxetic structure have a more smooth and even stress distribution within the implant and produce less micromotion at the bone-implant interface [14]. Eldesouky designed a femoral stem with auxetic structures to promote bone ingrowth and reduce implant stiffness [15]. Although some previous studies developed femoral stems with auxetic structures, they did not investigate the ideal location for the structure. This study proposes placing the auxetic structure on the tension side of the femoral stem and using the tensile stress to expand the auxetic structure laterally to reduce SS. The geometric profile of the femoral stem, such as the stem length, fixation method and the stem's offset, can also have a considerable impact on the mechanical transmission between the femoral stem and femur [3,6]. To the author's knowledge, there is a lack of corresponding research on what geometric shape of the femoral stem with an auxetic structure best facilitates load transmission. In addition, the re-entrant angle has a prominent influence on the mechanical properties of the auxetic structure. The impact of different re-entrant angles on SS with different stem types was investigated in this study.
The aim of this study was to develop a finite element model of a femur and implant it with various femoral stems to determine how the shape of the stem and location of the auxetic structure affect SS of the surrounding bone. There are three hypotheses to this study. (1) Placing the auxetic structure on the tensile region of the femoral stem can reduce SS in comparison to its solid counterpart; (2) The Mayo femoral stem design (Zimmer Biomet, Indiana, USA), termed M-type in this study, causes less SS than other femoral stem designs; (3) A re-entrant angle of 60° is suitable to reduce SS compared with the other two angles. The results of this study may be used to improve the design of femoral stems with auxetic structures to reduce SS after THA.
2. Method
2.1. Development and validation of implanted femoral model
The 3D geometry of an intact femur was reconstructed from CT images of a healthy male (40 years, 80 kg) using Mimics 17 (Materialise N.V., Leuven, Belgium). Computer-aided design (CAD) models of three common commercial femoral stems with different design features were constructed in NX 12.0 (Siemens, Germany): Fitmore (Zimmer Biomet, Indiana, USA), CLS (Zimmer Biomet, Indiana, USA) and Mayo (Zimmer Biomet, Indiana, USA). The stem size chosen for each was determined from the size of the femoral model. These stems were chosen because of reports of SS from using these products [7,16,17]. The Mayo and Fitmore prostheses are classified as short stems which rely on a proximal press-fit to achieve stability [18]. The CLS prosthesis is a cementless stem of standard length that uses a press fit insertion at metaphyseal-diaphyseal junction to achieve stability. The loading axis of the CLS and the Fitmore stems coincides with the femoral axis, whereas the tip of the Mayo stem contacts the lateral cortex, thus increasing the stem's offset (malalignment with the femoral axis). Each of the three stem models was virtually implanted into the femur using Mimics 17 under the guidance of an experienced orthopedist.
The femur and femoral stems were assumed to have isotropic, linear and elastic material properties [19]. All stems were modelled as a titanium alloy with an elastic modulus of 110 GPa and Poisson's ratio of 0.3 [6]. The Poisson's ratio of the whole femur was set as 0.3 [6] and the local Young's modulus of the femoral bone was mapped in Mimics 17 using equations (1), (2) [20]:
| (1) |
| (2) |
where ρ (g/cm3) is the density of the bone, HU is the Hounsfield value from the CT images, and E (Pa) is the elastic modulus of the bone.
A sliding surface-to-surface contact was applied between the stem and medullary cavity with a friction coefficient of 0.1 [21]. Using HyperMesh 12.0 (Altair Engineering, Tokyo, Japan), the femur was meshed with C3D4 elements (4-node tetrahedron linear solid elements) and the three dense stem models were meshed with C3D8 elements (8-node hexahedral linear solid elements). Mesh sensitivity analyses were conducted until there was a negligible change (relative error less than 5%) in the maximum von Mises stress. The final model had an element size of 2 mm for the femur and 1 mm for the femoral stems.
Bieger et al. investigated SS after in vitro implantation with Fitmore, CLS and Mayo femoral stems placed under a physiological load [7]. The boundary and loading conditions of the finite element model in this study were adopted from Bieger's study, as follows. The anatomical axis of the femoral shaft (a line connecting the center of the marrow cavity and the center of the femoral condyle) was abducted 6° from the sagittal plane and had a flexion angle of 8° from the coronal plane. The distal end of the femur was fixed, and a static load of 1600 N (approximately 2 times body weight of an 80 kg man) was applied to the center of the femoral head (Fig. 1a). After loading, the average major strain (strain with the largest absolute value) was recorded at six pre-defined points and the values were compared with those reported by Bieger et al. to verify the accuracy of the FEA model.
Figure 1.
(a) Loading and boundary conditions of finite element models, (b) design parameters of the auxetic unit cell, (c) illustration of femoral stem design features, (d) tensile region and neutral axis on the stem, (e) illustration of the region that need to be designed as solid titanium, (f) illustration of the tensile region after incorporating auxetic structure based on the previous step, (h) location of boundary lines between the auxetic and solid sections of the femoral stem. Original neutral axis (black dotted line); upper border (green line); lower border (yellow line); lateral boundary (red line); medial border (blue line). (For interpretation of the references to colour in this figure legend, the reader is referred to the Web version of this article.)
2.2. Auxetic femoral stem design
Femoral stems with an auxetic structure were modelled from the profiles of the same commercial prostheses as the solid models, namely the Mayo, CLS and Fitmore femoral prostheses. The auxetic stems were then modelled with three different re-entrant angles for the unit cell, resulting in nine unique auxetic femoral stems (three M-type, three C-type and three F-type) and three solid femoral stems, which acted as a control group (Table 1). All models were constructed in NX 12.0 (Siemens, Germany).
Table 1.
Femoral stems evaluated in this study.
| Inner micro-structure & stem body | Mayo | CLS | Fitmore |
|---|---|---|---|
| Dense | Ms | Cs | Fs |
| Auxetic with 60° re-entrant angle | M1 | C1 | F1 |
| Auxetic with 70° re-entrant angle | M2 | C2 | F2 |
| Auxetic with 80° re-entrant angle | M3 | C3 | F3 |
2.2.1. Unit cell selection
The most common auxetic structures used in the design of hip replacements are re-entrant structures, rotating polygonal structures and chiral structures [22]. A re-entrant honeycomb is a typical re-entrant auxetic structure. Due to its simple configuration, a pattern can be easily expanded from a 2D to 3D profile and it is relatively easy to fabricate with additive manufacturing. Therefore, the re-entrant honeycomb structure was selected for this study. There are four primary design parameters for this auxetic unit cell, as shown in Fig. 1b; length of the vertical struts (H), length of the re-entrant struts (L), re-entrant angle (θ) and strut thickness (t). Considering that the fabrication accuracy of most metal additive manufacturing equipment is about 400 μm, the strut thickness (t) in this study was set as 0.4 mm [23]. Also, since the pore size of the unit cell needs to be within the range suitable for bone ingrowth (300 μm–800 μm) [24], H and L were set as 1.6 mm and 0.5 mm, respectively. The re-entrant angle (θ) is defined as the angle between the vertical strut and the inclined strut and changes in this angle have a greater influence on the mechanical properties than the other parameters (H, L, t) [25]. When modeling the 3D model of auxetic structure through NX 12.0 software, we found that if the re-entrant angle is less than 54°, the auxetic structure would not be able to expand. If the re-entrant angle is greater than or equal to 90° the structure would no longer have a negative Poisson's ratio. Therefore, the value should be within 54°–90°. As such, the femoral stems in this study were modeled with auxetic structures with re-entrant angles of 60°, 70° and 80°.
2.2.2. Location of the auxetic structures in the stem
-
(1)
Given that auxetic structures expand in response to a tensile load, the auxetic unit cells were only located on the tension side of the femoral stem. The neutral axis of the three solid femoral stems (Ms, Fs and Cs) was determined from the stress distribution on the finite element models simulated per section 2.1 of this manuscript. The auxetic structure would be placed in the region under tensile stress (gray region in Fig. 1d), with the region being further refine as follows.
-
(2)
Since the femoral neck does not contact bone, no auxetic unit cells were placed around the neck of the stem, as shown by the shaded area 1 in Fig. 1e.
-
(3)
The shoulder of the stem was designed as solid titanium to facilitate the fixation of auxetic structures. In addition, since the auxetic unit cells are cubic, any region intended to incorporate an auxetic structure should be regular without sharp changes in curvature to facilitate the arrangement and stacking of unit cells. Fig. 1d and e show a sudden change in the path of the neutral axis at the proximal end of the Ms stem, similar turning points also occur on the other two femoral stems. The region above a horizontal line passing through this turning point was modeled as solid titanium (shaded area 2 in Fig. 1e).
-
(4)
The three femoral stems assessed in this study were designed to rely on metaphyseal or metaphyseal-diaphyseal load transmission for stability, and the distal end of the stems was not designed for implant fixation [26,27]. Therefore, no auxetic unit cells were placed around the distal end of the femoral stems. In addition to the proximal turning point identified previously, the distal end of the Ms stem also showed a sudden change in the path of the neutral axis, as shown in Fig. 1e. As such, the region below this turning point was modeled as solid titanium (shaded area 3 in Fig. 1e). As there were no evident sharp changes in the neutral axis around the distal end of the Cs and Fs stems, to unify the number of auxetic unit cells in the longitudinal direction, the distance between the upper and lower boundaries of the auxetic region on the Cs and Fs stems was set to be consistent with the Ms stem.
-
(5)
Incorporating an auxetic structure on the tensile side of the femoral stem would reduce the stiffness of this region, causing the neutral axis to shift towards the medial side (Fig. 1f). Therefore, the medial boundary of the auxetic region was expanded to the medial side. We found that the new neutral axis reaches near the central line between the original neutral axis (black dotted line in Fig. 1e) and the medial curve of the stem (Fig. 1f). To facilitate the arrangement of unit cells and to maximize the area under tension, the region on the lateral side of this central line was defined as auxetic structures and the medial side was defined as solid titanium (shaded area 4 in Fig. 1f).
Fig. 1h shows the final design of the femoral stem including the auxetic lattice structure. The upper border of the auxetic region is designated by the green line, which was set to pass through the proximal turning point of the neutral axis. The blue line shows the medial border of the auxetic region, being a central line between the original neutral axis and the medial curve of the femoral stem. The lateral boundary is marked by the red line which follows the lateral curve of the femoral stem, and the yellow line defines the lower border and was set to pass through the distal turning point of the neutral axis. The method described above applies to all three stems.
2.3. Biomechanical function of the femoral stems
Finite element models of the auxetic stem and femur system were developed with the auxetic unit cells being composed of 0.4 mm C3D8 elements. Other parameters, including the surgical implantation, mechanical properties of the implant and femur, contact conditions, and loading and boundary conditions were set up as described in section 2.1.
The average von Mises stress within each Gruen zone [28] on the femur was compared among the 12 femoral stems. The level of SS from each femoral stem was calculated using equation (3), with a positive SS value indicating greater SS.
| (3) |
Sint is the average von Mises stress on the intact femur, Sstem is the average von Mises stress on the implanted femur.
The difference in SS value between the auxetic stem and its solid counterpart showed how the auxetic structure influenced the level of SS.
As the flexibility of the stem body influences the load transferred from the femoral stem to the bone [5], finite element analysis was used to calculate the bending stiffness of the three solid stems and three auxetic femoral stems with a 70° re-entrant angle for the unit cells. Due to its porous nature, in theory, an auxetic stem should have a lower stiffness than its solid counterpart. The finite element models were constructed with the material properties, element type and element size being adopted from similar studies measuring the stiffness of femoral stems [29,30]. As shown in Fig. 2a, the stem was aligned at 10° in adduction and 9° in flexion, and the distal end of the femoral stem (80 mm below the center of the femoral head) was fixed. A uniform vertical displacement load of 1 mm was applied downward at the center of the femoral head.
Figure 2.
(a) Illustration of bending stiffness test setup, (b) load-displacement curve for auxetic stems and their solid counterparts.
3. Results
3.1. Validation of the finite element model
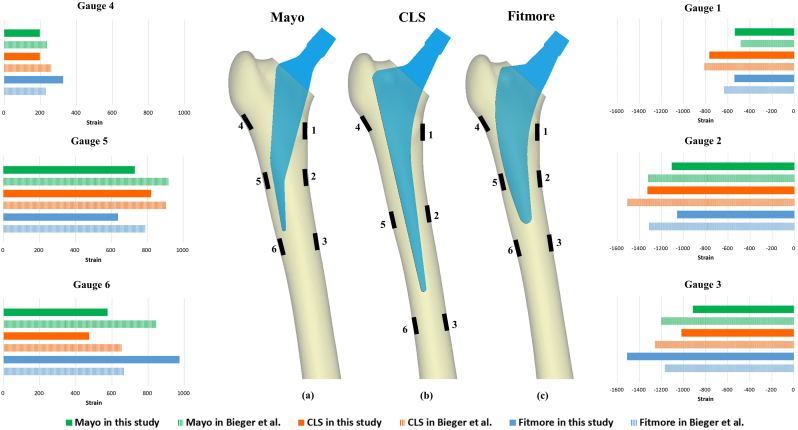
Fig. 3 shows the six measuring points on each femur, which were set according to the location of strain gauges in Bieger's study [7]. Gauge 1 and Gauge 4 were located at the level of lesser trochanter and below the greater trochanter, respectively. Gauge 2 and Gauge 5 were located medially and laterally at a distance 40 mm proximal to the tip of the stem. Gauge 3 and Gauge 6 were located medially and laterally 20 mm below the tip of the stem. The bone strain was measured after loading the implanted femoral stems, and the results were comparable to experimental measurements reported by Bieger et al. [7]. Specifically, tensile strains were observed on the lateral side of the femur and compressive strains on the medial side, while strain on the proximal femur at measuring points 1 and 4 was lower than at the other regions. The magnitude of strains in this study was also similar to those report by Bieger.
Figure 3.
Location of six measuring points on the medial and lateral sides of the femur after implanting (a) Mayo, (b) CLS and (c) Fitmore femoral stems. Histogram showing a comparison of strain measurements between this study and Bieger et al. [7] at the same measuring point.
3.2. Biomechanical evaluation of auxetic femoral stems
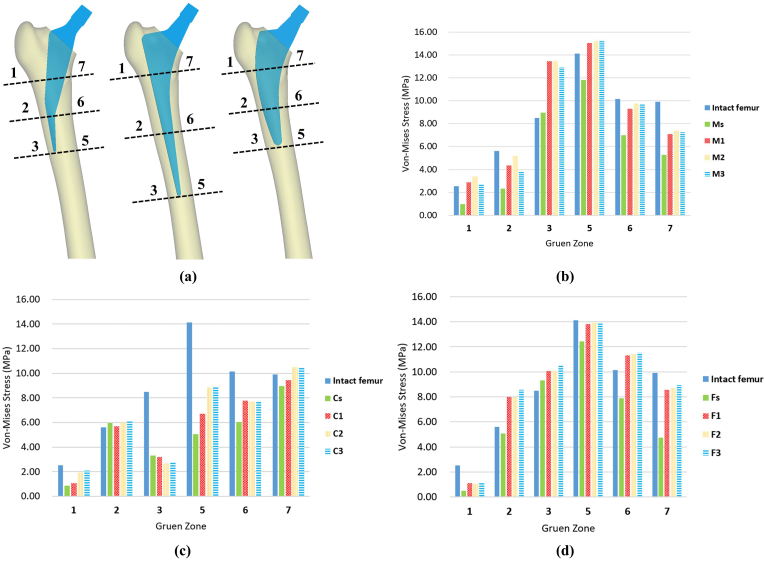
Fig. 4 shows the von Mises stress distribution on the intact femur and on the femur after implanting different femoral stems. High stress was mainly observed around the medial zone of the femur after implantation. Fig. 5b–d quantitatively compares the average von Mises stress on the femur in each Gruen zone for the intact femur and implanted femurs. Figure 4, Figure 5 show obvious SS at the lateral side (Gruen zone 1) and medial side (Gruen zone 7) of the proximal femur in all models implanted with a dense femoral stem. For the Mayo femoral stem, incorporating auxetic structures on the lateral side of the stem (M1, M2, M3) was found to increase the stress on the bone at all Gruen zones, and the stress values were higher than the threshold of bone resorption (2 MPa) [31]. Similarly, with the CLS stem, the stress on surrounding bone increased at all Gruen zones (except zone 3) when using an auxetic stem (C1, C2, C3) rather than a solid stem (Cs). Also, the stress values at all Gruen zones were higher than the threshold of bone resorption (2 MPa), except for C1 and C2 at Gruen zone 1. Compared with the solid Fitmore stem (Fs), the stress at all Gruen zones increased after implantation with auxetic stems (F1, F2, F3). However, the stress values at Gruen zone 1 with all three F-type stems were below the threshold of bone resorption.
Figure 4.
Distribution of von Mises stress on the (a) intact femur, (b) femur after implanting a solid Mayo stem and M1, M2, M3, (c) femur after implanting a solid CLS stem and C1, C2, C3, and (d) femur after implanting a solid Fitmore stem and F1, F2, F3.
Figure 5.
Comparison of the average von Mises stress on the femur in each Gruen zone. (a) Illustration of Gruen zones for each stem type, (b) von Mises stress recorded with M-type stems, (c) von Mises stress recorded with C-type stems, and (d) von Mises stress recorded with F-type stems.
3.2.1. Influence of stem geometry on SS
To evaluate the effect of stem geometry on SS, the difference in SS values between the auxetic stems and their solid counterparts was calculated (Table 2). In the lateral zones (zones 1, 2 and 3), the M-type stems (M1, M2 and M3) demonstrated the greatest reduction in SS in Gruen zone 1 (76%, 96% and 71% lower than Ms) and Gruen zone 3 (53%, 53% and 47% lower than Ms). The F-type stem showed the greatest reduction in Gruen zone 2 (52%, 52% and 63% lower than Fs), while around the medial zones (zone 5, 6 and 7), the greatest reduction in SS was found at zone 6 (33%, 35% and 36% lower than Fs) and zone 7 (39%, 40% and 42% lower than Fs). The C2 and C3 stems showed the second-largest reduction in SS in zones 1 and 2, but overall, the C-type stems were the least effective at reducing SS in the other zones (except for zone 5). Of note, the SS values at zones 2 and 3 were found to be 5% and 2% higher than their solid counterpart.
Table 2.
Difference in SS values (%) between auxetic stems (with 60°, 70° and 80° angle) and their solid counterparts.
| Implant | Zone 1 | Zone 2 | Zone 3 | Zone 5 | Zone 6 | Zone 7 |
|---|---|---|---|---|---|---|
| M1 | −76 | −36 | −53 | −23 | −23 | −18 |
| C1 | −7 | 5 | 2 | −12 | −17 | −5 |
| F1 | −24 | −52 | −9 | −10 | −33 | −39 |
| M2 | −96 | −51 | −53 | −24 | −27 | −22 |
| C2 | −41 | 0 | 7 | −27 | −16 | −15 |
| F2 | −22 | −52 | −9 | −11 | −35 | −40 |
| M3 | −71 | −27 | −47 | −24 | −26 | −20 |
| C3 | −47 | −2 | 7 | −27 | −16 | −15 |
| F3 | −25 | −63 | −14 | −10 | −36 | −42 |
3.2.2. Influence of re-entrant angle on SS
Table 3 shows the average von Mises stress on the femur implanted with different femoral stems and the ratio of these values as a percentage of the values recorded for the intact femur. For the M-type femoral stems, M2 demonstrated the greatest reduction in SS at all Gruen zones, especially at zones 1 and 2, with the load transmitted to these regions reaching 134% and 92% of the intact femur, respectively. Among the C-type femoral stems, C2 and C3 offered a similar reduction in SS, while the load transmitted to Gruen zone 1 by C1 was only 42% of the intact femur. For the F-type stems, F3 was best able to reduce SS of the bone. At zone 2, the von Mises stress recorded was 153% of the intact femur.
Table 3.
Average von Mises stress on the femur implanted with different femoral stems, and the ratio of these values (%) with respect to the intact femur.
| Model | Gruen zone 1 |
Gruen zone 2 |
Gruen zone 3 |
Gruen zone 5 |
Gruen zone 6 |
Gruen zone 7 |
||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Average Stress |
% of |
Average Stress |
% of |
Average Stress |
% of |
Average Stress |
% of |
Average Stress |
% of |
Average Stress |
% of |
|
| (MPa) | Intact | (MPa) | Intact | (MPa) | Intact | (MPa) | Intact | (MPa) | Intact | (MPa) | Intact | |
| Intact Femur | 2.53 | 100 | 5.61 | 100 | 8.49 | 100 | 14.13 | 100 | 10.15 | 100 | 9.91 | 100 |
| Ms | 0.96 | 38 | 2.33 | 42 | 8.95 | 105 | 11.82 | 84 | 7.01 | 69 | 5.27 | 53 |
| M1 | 2.89 | 114 | 4.35 | 77 | 13.46 | 159 | 15.06 | 107 | 9.30 | 92 | 7.10 | 72 |
| M2 | 3.40 | 134 | 5.19 | 92 | 13.49 | 159 | 15.22 | 108 | 9.77 | 96 | 7.41 | 75 |
| M3 | 2.76 | 109 | 3.87 | 69 | 12.94 | 152 | 15.25 | 108 | 9.68 | 95 | 7.24 | 73 |
| Cs | 0.87 | 35 | 5.96 | 106 | 3.32 | 39 | 5.06 | 36 | 6.05 | 60 | 8.96 | 90 |
| C1 | 1.05 | 42 | 5.68 | 101 | 3.18 | 37 | 6.70 | 47 | 7.77 | 77 | 9.43 | 95 |
| C2 | 1.92 | 76 | 5.98 | 107 | 2.69 | 32 | 8.82 | 62 | 7.71 | 76 | 10.49 | 106 |
| C3 | 2.08 | 82 | 6.06 | 108 | 2.74 | 32 | 8.85 | 63 | 7.70 | 76 | 10.44 | 105 |
| Fs | 0.49 | 19 | 5.06 | 90 | 9.31 | 110 | 12.43 | 88 | 7.89 | 78 | 4.75 | 48 |
| F1 | 1.09 | 43 | 8.00 | 143 | 10.05 | 118 | 13.82 | 98 | 11.29 | 111 | 8.57 | 87 |
| F2 | 1.05 | 41 | 7.97 | 142 | 10.07 | 119 | 13.93 | 99 | 11.41 | 112 | 8.70 | 88 |
| F3 | 1.13 | 45 | 8.57 | 153 | 10.48 | 123 | 13.87 | 98 | 11.54 | 114 | 8.92 | 90 |
3.2.3. Stiffness of femoral stems
Fig. 2b shows the load-displacement curves for the auxetic stems and solid stems. The bending stiffness of the solid stems (Ms, Cs and Fs) was recorded as 4639 N/mm, 5667 N/mm and 7490 N/mm. For the auxetic stems, the bending stiffness of M1, C2 and F2 was calculated as 514 N/mm, 1224 N/mm and 1918 N/mm, which is 89%, 78% and 74% lower than their solid counterparts.
4. Discussion
This study assessed the ability of femoral stems designed with a partial auxetic structure to reduce SS in comparison to similar commercial femoral prostheses. The results showed that auxetic stems cause less SS than their solid counterparts. The auxetic femoral stems based on the Mayo stem (M-type) caused less SS, in general, than the stems modeled from the CLS (C-type) and Fitmore (F-type) prostheses. There is no regularity in the effect of the re-entrant angle of the auxetic unit cell on the SS for all prostheses.
The strain distribution and magnitude observed on the FEA models in this study were similar to the strains reported in an in-vitro study by Bieger at al [7]. However, individual differences such as the femoral stem size, medullary cavity shape, bone mass, anteversion angle, and neck-shaft angle of the femur did lead to some differences between the results.
The results showed that SS occurred around the proximal region of the femur (zone 1 and 7). This is in agreement with clinical data [26,32]. As expected, the bone surrounding the auxetic stems experienced greater stress than the femurs implanted with solid stems, indicating less SS. The increased stress around the lateral region of the femur may be attributed to the auxetic structure moving outward under tensile load. The increased stress on the medial side of the femur might be due to a reduction in the stem's bending stiffness due to the presence of the auxetic structure (Fig. 2b).
Various femoral stems with auxetic structures have been proposed in literature for different purposes, but with the overall aim of improving implant survivorship. An auxetic modular stem introduced by Alderson et al. [12] aimed to strengthen fixation at the distal end of the stem, but did not consider SS at the proximal femur. Such modular designs may also lead to mechanical complications such as component interface corrosion, wear and cracking [33]. Kolken et al. [13] designed an auxetic femoral stem to reduce the risk of stem-bone interface failure by producing compressive stress on both the medial and lateral sides of the cavity walls. Because more stress was transferred to the bone, this design may reduce SS, although this was not specifically assessed. In addition, Kolken simulated surgical implantation by inserting the stem into a rectangular section of artificial bone secured on a rigid metal platform. These boundary conditions differ from those used in this study.
This study selected the Mayo, CLS and Fitmore femoral stems for evaluation because they represent three different stem geometry profiles and have been reported with high levels of SS [7,16,17]. Studies have shown other commercial stems with relatively low SS, such as PROXIMA stem, Corail stem, and Taperloc stem [6,34,35], but the results are divisive and since the purpose of this study was to investigate SS, these stems were not considered [[36], [37], [38]].
This study found that the M-type stems were best able to reduce SS of the proximal lateral femur. In Gruen zone 1, the M1, M2 and M3 stems reduced SS by 76%, 96% and 71%, respectively, in comparison to their solid counterparts. The M-type stems showed the greatest reduction among the three designs. In addition, all zones exhibited stress in excess of 2 MPa when using the M-type stems. In contrast, the stresses in Gruen zone 1 were below the 2 MPa threshold after implanting C1, C2, F1, F2 and F3, which indicated that bone resorption might occur. A femoral stem can be simplified as a cantilever beam under a hip contact force. The Mayo stem has a relatively longer force arm because the stem tip has a larger offset from the lateral cortex, and its stem body is angled away from the axis of the femoral medullary cavity (Fig. 1c). In addition, the Mayo stem has a relatively thin stem body, which may cause greater deformation when placed under load (Fig. 2b). The larger the bending deformation, the larger the tensile load and outward expansion of the auxetic structure. The F-type stem demonstrated the greatest reduction in SS around the medial zone of the proximal femur, in comparison to the solid Fs stem. The Fitmore prosthesis has a high bending stiffness (7490 N/mm) because of its thick stem body, and its bending deformation is relatively small (Fig. 2b). Incorporating an auxetic lattice structure acted to reduce the stiffness (74% lower than its solid counterpart), which increased the bending deformation medially and transferred more load to this zone. However, due to the lower tensile stress on the lateral zone of the femur, the F-type stem was generally less capable of transferring load to the lateral zones than the M-type (Fig. 4d).
The results of this study showed that a re-entrant angle of 70° for the M-type stem, 80° for the C-type and 60° for the F-type were the designs most capable of transferring load to the surrounding bone. Theoretically, the re-entrant angle of the unit cell may affect the mechanical properties of the re-entrant honeycomb structure. The greater the expansion (Δw) of the auxetic structure, the greater the corresponding stress transmitted to the bone. According to the definition of Youngs's modulus (eq. (4)) and Poisson's ratio (eq. (5)), it can be deduced from equation (6) that Δw may be calculated from a material's Poisson's ratio (v), Young's modulus (E), the force acting on it (F), and the width of the auxetic unit cell (w). Yang et al. reported that the Poisson's ratio and Young's modulus of a re-entrant honeycomb increase as the re-entrant angle increases [25,39]. Therefore, no correlation is anticipated between the re-entrant angle of the auxetic unit cell and resulting SS, which was confirmed by the results of this study (Table 3).
| (4) |
| (5) |
| (6) |
where σ is the stress, εx is the transverse strain, εz is the axial strain, F is the force acting on the auxetic unit cell, A is the cross-sectional area of the unit cell, L and ΔL are the length and change in length of the auxetic unit cell, and w and Δw are the initial width and change in width of the auxetic unit cell.
There are some limitations to this study. (1) The models did not include soft tissues such as muscles, ligaments and cartilage, or consider forces exerted on the limbs from surrounding soft tissues. (2) A static force was applied to the hip joint, which does not represent physiological loading during human gait. This study also did not simulate other common loading conditions, such as climbing stairs, running and squatting. (3) This study developed FEA models based on an adult male without considering the effect of medullary cavity morphology on the femoral stem's biomechanical function.
Bone ingrowth into the surface of a femoral stem is helpful for improving long-term stability [40]. Although the interconnected pores of auxetic structures are theoretically suitable for bone ingrowth, this needs to be further validated through in vivo experiments.
5. Conclusion
This study introduced femoral stem designs incorporating auxetic lattice structures as a potential solution for reducing SS following THA. The results showed that the use of auxetic structures caused less SS of bone around the femoral stem in comparison to their solid (non-auxetic) counterparts. The auxetic femoral stems based on the Mayo stem (M-type) were generally better able to reduce SS than the CLS (C-type) and Fitmore (F-type) femoral stems. There was no predictable effect of the re-entrant angle on SS, with the most effective re-entrant angles being different for each stem type. The findings from this study may serve as a basis for designing auxetic femoral stems with better survivorship than traditional solid femoral stems due to their ability to transfer greater load to the surrounding bone.
Author contributions
BLL and CKC contributed in the conception and design of the study. BLL, JWL, NZZ contributed in acquisition and analysis of data. BLL contributed in original draft preparation. All authors contributed towards revising the manuscript. All authors have read and approved the final submitted manuscript.
Ethics Statement
Written informed consent was obtained from the individual(s) for the publication of any potentially identifiable images or data included in this article.
Declaration of competing interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Acknowledgments
This work was supported by the National Key Research and Development Program, China (Grant number: 2016YFC1101904) and Medical Health Science and Technology Project of Zhejiang Provincial Health Commission (Grant number: 2022RC248). We would like to thank Colin McClean for his assistance with editing this manuscript.
References
- 1.Ulrich Slif D., Seyler T.M., Bennett Derek, Delanois Ronald E., Saleh Khaled J., Thongtrangan Issada, et al. Total hip arthroplasties: what are the reasons for revision? Int Orthop. 2008;32(5):597–604. doi: 10.1007/s00264-007-0364-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Huiskes R., Weinans H., Van R.B. The relationship between stress shielding and bone resorption around total hip stems and the effects of flexible materials. Clin Orthop Relat Res. 1992;274(274):124–134. [PubMed] [Google Scholar]
- 3.Sousa A., Vale J., Diniz S., Neves P., Ramos J., Coelho R. Comparison of short-stem versus conventional stem for hip arthroplasty in patients younger than 60 years: 7–14 years follow-up. Eur J Orthop Surg Traumatol. 2022;32(4):693–700. doi: 10.1007/s00590-021-03017-w. [DOI] [PubMed] [Google Scholar]
- 4.Maji P.K., Roychowdhury A., Datta D. Minimizing stress shielding effect of femoral stem—a review. J Med Imag Health Inform. 2013;3:171–178. [Google Scholar]
- 5.Liu B., Wang H., Zhang N., Zhang M., Cheng C.-K. Femoral stems with porous lattice structures: a review. Front Bioeng Biotechnol. 2021;9:772539. doi: 10.3389/fbioe.2021.772539. 39. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Levadnyi I., Awrejcewicz J., Gubaua J.E., Pereira J.T. Numerical evaluation of bone remodelling and adaptation considering different hip prosthesis designs. Clin BioMech. 2017;50:122–129. doi: 10.1016/j.clinbiomech.2017.10.015. [DOI] [PubMed] [Google Scholar]
- 7.Bieger R., Ignatius A., Decking R., Claes L., Reichel H., Dürselen L. Primary stability and strain distribution of cementless hip stems as a function of implant design. Clin BioMech. 2012;27(2):158–164. doi: 10.1016/j.clinbiomech.2011.08.004. [DOI] [PubMed] [Google Scholar]
- 8.Heyland M., Checa S., Kendoff D., Duda G.N. Anatomic grooved stem mitigates strain shielding compared to established total hip arthroplasty stem designs in finite-element models. Sci Rep. 2019;9(1):482–493. doi: 10.1038/s41598-018-36503-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Mehboob H., Ahmad F., Tarlochan F., Mehboob A., Chang S.H. A comprehensive analysis of bio-inspired design of femoral stem on primary and secondary stabilities using mechanoregulatory algorithm. Biomech Model Mechanobiol. 2020;19:2213–2226. doi: 10.1007/s10237-020-01334-3. [DOI] [PubMed] [Google Scholar]
- 10.Al Zoubi N.F., Tarlochan F., Mehboob H., Jarrar F. Design of titanium alloy femoral stem cellular structure for stress shielding and stem stability: computational analysis. Appl Sci. 2022;12(3):1548. [Google Scholar]
- 11.Jette B., Brailovski V., Simoneau C., Dumas M., Terriault P. Development and in vitro validation of a simplified numerical model for the design of a biomimetic femoral stem. J Mech Behav Biomed Mater. 2018;77:539–550. doi: 10.1016/j.jmbbm.2017.10.019. [DOI] [PubMed] [Google Scholar]
- 12.Alderson A., Alderson K.L., Sanami M. Bone Implant Comprising Auxetic Material. No. 1116625.3. GB2495272A. Br. Patent Application. 2013.
- 13.Kolken H.M.A., Janbaz S., Leeflang S., Lietaert K., Weinans H., Zadpoor A.A. Rationally designed meta-implants: a combination of auxetic and conventional meta-biomaterials. Mater Horiz. 2018;5:28–35. [Google Scholar]
- 14.Ghavidelnia N., Bodaghi M., Hedayati R. Femur auxetic meta-implants with tuned micromotion distribution. Materials. 2020;14(1):1–29. doi: 10.3390/ma14010114. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Eldesouky I., El-Hofy H. Design and prototyping of a novel low stiffness cementless hip stem. Int J Biomed Eng Technol. 2020;32:228–244. [Google Scholar]
- 16.Martins L.G., Garcia F.L., Picado C.H. Aseptic loosening rate of the Mayo femoral stem with medium-term follow up. J Arthroplasty. 2014;29(11):2122–2126. doi: 10.1016/j.arth.2014.06.023. [DOI] [PubMed] [Google Scholar]
- 17.Nam D., Salih R., Barrack R.L., Nunley R.M. An evaluation of proximal femur bone density in young, active patients undergoing total hip arthroplasty at one year postoperatively. Hip Int : the journal of clinical and experimental research on hip pathology and therapy. 2019;29(1):51–57. doi: 10.1177/1120700018761152. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Feyen H., Shimmin A. Is the length of the femoral component important in primary total hip replacement? The Bone & Joint Journal. 2014;96-B:442–448. doi: 10.1302/0301-620X.96B4.33036. [DOI] [PubMed] [Google Scholar]
- 19.Wang S., Zhou X., Liu L., Shi Z., Hao Y. On the design and properties of porous femoral stems with adjustable stiffness gradient. Med Eng Phys. 2020;81:30–38. doi: 10.1016/j.medengphy.2020.05.003. [DOI] [PubMed] [Google Scholar]
- 20.Sun C., Wang L., Kang J., Li D., Jin Z. Biomechanical optimization of elastic modulus distribution in porous femoral stem for artificial hip joints. JBE. 2018;15(4):693–702. [Google Scholar]
- 21.Matsuyama K., Ishidou Y., Guo Y.M., Kakoi H., Setoguchi T., Nagano S., et al. Finite element analysis of cementless femoral stems based on mid- and long-term radiological evaluation. BMC Muscoskel Disord. 2016;17(1):397. doi: 10.1186/s12891-016-1260-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Ren X., Das R., Tran P., Ngo T.D., Xie Y.M. Auxetic metamaterials and structures: a review. Smart Mater Struct. 2018;27 [Google Scholar]
- 23.Arabnejad S., Johnston R.B., Pura J.A., Singh B., Tanzer M., Pasini D. High-strength porous biomaterials for bone replacement: a strategy to assess the interplay between cell morphology, mechanical properties, bone ingrowth and manufacturing constraints. Acta Biomater. 2016;30:345–356. doi: 10.1016/j.actbio.2015.10.048. [DOI] [PubMed] [Google Scholar]
- 24.Tarlochan F., Mehboob H., Mehboob A., Chang S.H. Influence of functionally graded pores on bone ingrowth in cementless hip prosthesis: a finite element study using mechano-regulatory algorithm. Biomech Model Mechanobiol. 2018;17(3):701–716. doi: 10.1007/s10237-017-0987-2. [DOI] [PubMed] [Google Scholar]
- 25.Yang L., Harrysson O., West H., Cormier D. Mechanical properties of 3D re-entrant honeycomb auxetic structures realized via additive manufacturing. Int J Solid Struct. 2015;69-70:475–490. [Google Scholar]
- 26.Brodt S., Matziolis G., Buckwitz B., Zippelius T., Strube P., Roth A. Long-term follow-up of bone remodelling after cementless hip arthroplasty using different stems. Sci Rep. 2020;10(1) doi: 10.1038/s41598-020-67189-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Pepke W., Nadorf J., Ewerbeck V., Streit M.R., Kinkel S., Gotterbarm T., et al. Primary stability of the Fitmore stem: biomechanical comparison. Int Orthop. 2014;38(3):483–488. doi: 10.1007/s00264-013-2138-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Gruen T.A., McNeice G.M., Amstutz H.C. Modes of failure" of cemented stem-type femoral components: a radiographic analysis of loosening. Clin Orthop Relat Res. 1979;(141):17–27. [PubMed] [Google Scholar]
- 29.Jetté B., Brailovski V., Dumas M., Simoneau C., Terriault P. Femoral stem incorporating a diamond cubic lattice structure: design, manufacture and testing. J Mech Behav Biomed Mater. 2018;77:58–72. doi: 10.1016/j.jmbbm.2017.08.034. [DOI] [PubMed] [Google Scholar]
- 30.Simoneau C., Terriault P., Jetté B., Dumas M., Brailovski V. Development of a porous metallic femoral stem: design, manufacturing, simulation and mechanical testing. Mater Des. 2017;114:546–556. [Google Scholar]
- 31.Frost H.M.A. Update of bone physiology and Wolff's Law for clinicians. Angle Orthod. 2003;74(1):3–15. doi: 10.1043/0003-3219(2004)074<0003:AUOBPA>2.0.CO;2. 2004. [DOI] [PubMed] [Google Scholar]
- 32.Kutzner K.P., Pfeil D., Kovacevic M.P., Rehbein P., Mai S., Siebert W., et al. Radiographic alterations in short-stem total hip arthroplasty: a 2-year follow-up study of 216 cases. Hip Int : the journal of clinical and experimental research on hip pathology and therapy. 2016;26(3):278–283. doi: 10.5301/hipint.5000339. [DOI] [PubMed] [Google Scholar]
- 33.Canham C.D., Muradov P.I., Simpson J.B., Incavo S.J. Corrosion and adverse local tissue reaction after total hip arthroplasty with a modular titanium alloy femoral neck. Arthroplast Today. 2017;3(4):211–214. doi: 10.1016/j.artd.2017.03.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Rivière C., Grappiolo G., Engh C.A., Jr., Vidalain J.P., Chen A.F., Boehler N., et al. Long-term bone remodelling around 'legendary' cementless femoral stems. EFORT open reviews. 2018;3(2):45–57. doi: 10.1302/2058-5241.3.170024. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Saragaglia D., Orfeuvre B. Mid-term results of 119 Taperloc Microplasty™ femoral stems after a mean 61 months (50–82) of follow-up. J Orthop Traumatol: Surgery & Research. 2020;106(8):1501–1506. doi: 10.1016/j.otsr.2020.06.019. [DOI] [PubMed] [Google Scholar]
- 36.Melišík M., Hrubina M., Heřt J., Cibula Z., Čabala J., Nečas L. Mid-term results of proxima ultra-short anatomical stem: analysis of 130 cases. Acta Chir Orthop Traumatol Cech. 2021;88(1):50–57. [PubMed] [Google Scholar]
- 37.Guo J., Tan J., Peng L., Song Q., Kong H.R., Wang P., et al. Comparison of tri-lock bone preservation stem and the conventional standard Corail stem in primary total hip arthroplasty. Orthop Surg. 2021;13(3):749–757. doi: 10.1111/os.12946. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.McLaughlin J.R., Lee K.R. Long-term results of uncemented total hip arthroplasty with the Taperloc femoral component in patients with Dorr type C proximal femoral morphology. The Bone & Joint Journal. 2016;98-b(5):595–600. doi: 10.1302/0301-620X.98B5.35816. [DOI] [PubMed] [Google Scholar]
- 39.Yang L., Harrysson O., West H., Cormier D. Modeling of uniaxial compression in a 3D periodic re-entrant lattice structure. J Mater Sci. 2013;25:1413–1422. [Google Scholar]
- 40.Fujibayashi S., Takemoto M., Sasaki K., Otsuki B., Nakamura T., Matsushita T., et al. Effect of pore size on bone ingrowth into porous titanium implants fabricated by additive manufacturing: an in vivo experiment. Mater Sci Eng C. 2016;59:690–701. doi: 10.1016/j.msec.2015.10.069. [DOI] [PubMed] [Google Scholar]