Measuring Local Electrostatic Potentials Around Nucleic Acids by Paramagnetic NMR Spectroscopy

Abstract

Electrostatic potentials around macromolecules in the presence of mobile charges are difficult to assess especially for highly charged systems. Here, we report measurements of local electrostatic potentials around DNA by paramagnetic NMR. Through quantitative analysis of NMR paramagnetic relaxation enhancement arising from positively charged or neutral paramagnetic cosolutes, we were able to determine local electrostatic potentials around ¹H nuclei at >100 sites in major and minor grooves of ¹³C,¹⁵N-labeled 15-bp DNA at 100 mM NaCl. Our experimental electrostatic potential data directly confirmed the Coulombic end effects of DNA. The effective near-surface electrostatic potentials from the NMR data were in good agreement with the theoretical predictions with the Poisson-Boltzmann equation. This NMR method allows for unprecedented experimental investigations into the electrostatic properties of nucleic acids.

Graphical Abstract

Electrostatic potentials around a biological macromolecule depend not only on the macromolecular charges, but also on mobile ions that are attracted to or repelled by the macromolecules.¹ Due to the strong negative charge on their molecular surface, DNA and RNA attract many cations as counterions. The spatial distribution of these counterions around the nucleic acids has been studied for five decades. According to Manning’s theory on counterion condensation,² counterions around B-form DNA are condensed to a concentration of 1.2 M in the space within the Bjerrum length (7.1 Å in water) from DNA phosphates.³ The Poisson-Boltzmann theory predicts a broader and smoother distribution of counterions around DNA.^4-5 Molecular dynamics simulations, as well as reference interaction site model (RISM) integral equation theory, suggest a more rugged distribution of counterions.^6-12 In the 21^st century, ion-counting and diffusion methods have provided quantitative experimental data at a macroscopic level about counterions around DNA and RNA.^13-15 However, these experimental methods do not provide electrostatic potentials. The validity of theoretical electrostatic potentials around nucleic acids remains to be examined through experiments.

In this paper, we demonstrate that paramagnetic NMR allows for determination of local electrostatic potentials around nucleic acids. We recently developed an NMR method to determine local electrostatic potentials around proteins without any use of structural information.¹⁶ This method utilizes paramagnetic relaxation enhancement (PRE) arising from two analogous cosolute molecules with opposite charges. We modified this paramagnet NMR method so that it can be applied to highly negatively charged systems. The method allows us to examine theoretical electrostatic models for nucleic acids.

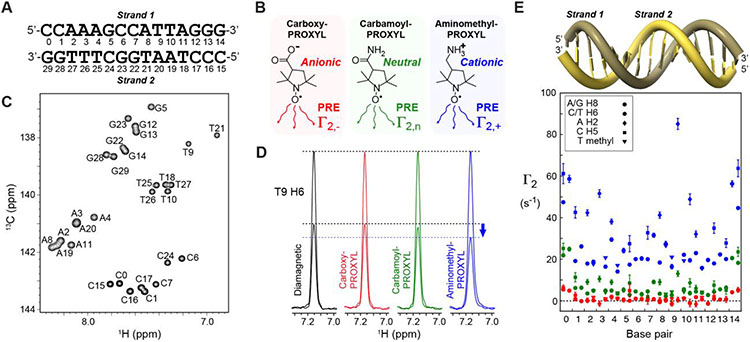
We investigated local electrostatic potentials around the 15-bp DNA duplex shown in Figure 1A. This DNA was ¹³C/¹⁵N-labeled and prepared as previously described.¹⁷ Using the PROXYL-derivatives shown in Figure 1B as a paramagnetic cosolute at 20 mM, we measured the ¹H transverse PRE rates Γ₂ for ¹H nuclei of CH/CH₂/CH₃ groups of DNA. ¹³C heteronuclear single-quantum coherence(HSQC)-based pulse sequences with homonuclear ¹³C decoupling to eliminate ¹J_CC splitting were used to measure PRE for many carbon-attached ¹H nuclei (Fig. S1 in the Supporting Information [SI]). Figure 1C shows an example of the recorded ¹H-¹³C correlation spectra (see also Fig. S2 in SI). Although some of our earlier studies on proteins utilized ¹H PRE data for NH groups,^16,19 we decided to use PRE data for CH/CH₂/CH₃ groups in the current study on DNA because rapid hydrogen exchange of DNA NH/NH₂ groups may adversely impact measurements of PRE rates. Cosolutes may catalyze hydrogen exchange,²⁰ which can introduce significant errors in Γ₂ rates due to different hydrogen exchange rates for the paramagnetic and diamagnetic samples. This concern is irrelevant to PRE for nonlabile ¹H nuclei of CH/CH₂/CH₃ groups.

Figure 1.

Paramagnetic NMR data to analyze local electrostatic potentials around DNA. (A) 15-bp DNA duplex used in the current study. The residue numbering is according to Wang et al.¹⁷ (B) Paramagnetic cosolute molecules used in the current study. (C) C6/C8 region of 2D ¹H-¹³C HSQC spectrum recorded for the diamagnetic sample of the DNA duplex. Spectra for other moieties are shown in Fig. S2 in the SI. (D) Examples of signal intensity modulation used to measure ¹H PRE rates Γ₂ using two time-point approach¹⁸. The ¹H slices of the signals from T9 H6 in the two 2-D sub-spectra for each sample are overlaid and normalized to the intensity at the shorter time point. Due to larger PRE, the intensity at the second time point for the paramagnetic sample with aminomethyl-PROXYL is clearly smaller than those of the other samples. (E) PRE rates Γ_2,+ (blue), Γ_2,n (green), and Γ_2,− (red) measured for DNA base ¹H nuclei. For each base pair position, the data for strands 1 (left) and 2 (right) are plotted. The concentration of each PROXYL derivative was 20 mM.

PRE Γ₂ data for DNA base ¹H nuclei are shown in Figure 1D-E. Corresponding PRE data for DNA sugar ¹H nuclei are shown in Fig. S3 in the SI. As proposed in our previous studies on proteins,^16,19,21 we initially used positively charged aminomethyl-PROXYL and negatively charged carboxy-PROXYL as paramagnetic cosolutes. Interestingly, the PRE rates were virtually zero for most ¹H nuclei of DNA when carboxy-PROXYL was used. This suggests that the negatively charged cosolutes are excluded from the space proximal to DNA, presumably due to strong electrostatic repulsion. By contrast, when positively charged aminomethyl-PROXYL was used, the PRE rates for all ¹H nuclei were remarkably larger than 10 s⁻¹, reflecting electrostatic attraction of the positively charged cosolute to the negatively charged DNA surface.

Since the magnitude of PRE arising from carboxy-PROXYL was too small for quantitative analysis of electrostatic potentials, we also measured PRE arising from a neutral analogue, carbamoyl-PROXYL (see Figure 1B). The observed PRE arising from carbamoyl-PROXYL was larger than those for carboxyl-PROXYL, but smaller than those for aminomethyl-PROXYL (Figure 1E). This relative magnitude likely reflects the absence of electrostatic repulsion or attraction for the neutral cosolute. Using these data sets we determined effective near-surface electrostatic potentials ϕ_ENS for individual ¹H nuclei of the 15-bp DNA. The following equation was used to determine ϕ_ENS potential:¹⁶

$${\varphi }_{ENS}=\frac{k_{B}T}{(z_b-z_a)e}\text{ln}(\frac{{\Gamma }_{2,a}}{{\Gamma }_{2,b}}),$$ (1)

where, e is the elementary electric charge; z is a charge valence of a PROXYL derivative; k_B is the Boltzmann constant; T is temperature; and annotations a and b are for two different PROXYL derivatives. At neutral pH, z = +1 for aminomethyl-PROXYL; z = 0 for carbamoyl-PROXYL; and z = −1 for carboxy-PROXYL. In our current case, a and b are aminomethyl-PROXYL and carbamoyl-PROXYL, respectively.

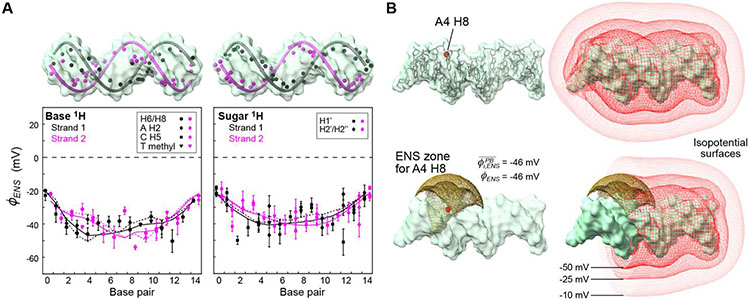
Using the data of PRE arising from aminomethyl-PROXYL and carbamoyl-PROXYL, we determined the effective near-surface electrostatic potentials ϕ_ENS for ¹H nuclei at 112 sites of the 15-bp DNA duplex (Figure 2A). The ϕ_ENS potentials were determined only for ¹H nuclei that exhibited statistically significant PRE rates and Γ_2,+ /Γ_2,− ratios, using the criteria described in the SI. The electrostatic potentials ranged from −54 mV to −18 mV. Compared with the previous data for proteins,^16,19,21 our current data for DNA reveal a relatively smooth landscape of near-surface electrostatic potentials. This seems reasonable because proteins contain both positive and negative charges, whereas DNA contains virtually no positive charges. Only protonated bases in a very minor state are positively charged in DNA.^{22-23 1}H nuclei near the two ends of DNA exhibited smaller magnitudes of ϕ_ENS potentials. This corresponds to the so-called “Coulombic end effects”.^24-25 Our experimental data confirm that the local electrostatic potentials near the DNA ends are weaker.

Figure 2.

Effective near-surface electrostatic potentials ϕ_ENS determined from the ¹H PRE Γ₂ rates measured with aminomethyl-PROXYL or carbamoyl-PROXYL as a paramagnetic cosolute. (A) ϕ_ENS potentials measured for base and deoxyribose ¹H atoms. Solid and dashed lines represent Poisson-Boltzmann equation-based predictions from the B-form structure and a structural model based on PDB 9ANT, respectively, for H6/H8 (left) and H1’ (right) atoms only. (B) ENS zone for the A4 H8 atom as an example. A ϕ_ENS potential approximates the average of the electrostatic potentials within an ENS zone, which is defined as a zone that makes a 68% contribution to $\sum r_i^{-6}$, where r_i is the distance between the observed ¹H nucleus and a grid point.¹⁶ The panel also shows isopotential surfaces for the electrostatic potentials calculated with the APBS software²⁶ In the lower right panel, the isopotential surfaces are clipped at the 2-D plane that contains the A4 H8 atom and is perpendicular to the DNA axis.

The effective near-surface electrostatic potential ϕ_ENS can be predicted from structure. As previously explained,¹⁶ a physical meaning of ϕ_ENS is that it approximates the average of the electrostatic potentials in a near-surface zone proximal to the observed ¹H nucleus. Due to the strong distance dependence imposed by r⁻⁶, each PRE Γ₂ rate is dominated by the paramagnetic cosolute molecules diffusing in this zone. When electrostatic potentials in 3-D lattice grid space around a macromolecule are used, the ϕ_ENS potential agrees well with the average of electrostatic potentials in a zone within a distance that makes a 68% contribution to $\sum r_i^{-6}$, where r_i is a distance between an accessible grid point i and the observed ¹H nucleus.¹⁶ We refer to this zone as the effective near-surface (ENS) zone. Using the Adaptive Poisson-Boltzmann Solver (APBS) software²⁶ along with structural models of DNA, we computed electrostatic potentials $\overline{{\varphi }_{ı,ENS}^{PB}}$, from which the average potential ${\varphi }_i^{PB}$ within the ENS zone was calculated for each ¹H nucleus. Each ENS zone covers a large volume of accessible space with a radius of ~8-20 Å. Figure 2B shows the effective near-surface (ENS) zone for the A4 H8 atoms as an example together with isopotential surfaces of the electrostatic potentials computed with the Poisson-Boltzmann equation.

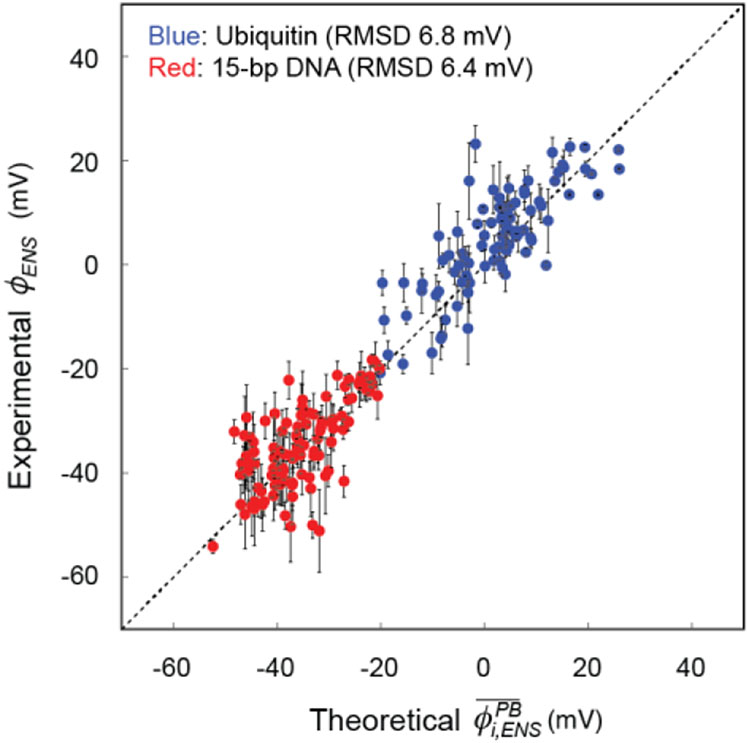
The experimental ϕ_ENS data were generally in good agreement with the Poisson-Boltzmann theory-based predictions $\overline{{\varphi }_{ı,ENS}^{PB}}$. The overall root-mean squared difference (RMSD) between the experimental and predicted values was 6.4 mV for an ideal B-form DNA structure (6.7 mV for a structure model based on PDB 9ANT). Some ¹H nuclei (e.g., A2 H1’ and G12 H1’/H8) exhibited relatively large discrepancy between the experimental and predicted values, which may reflect limitations of ϕ_ENS prediction using a spherical model for the PROXYL derivatives.¹⁹ Figure 3 shows a correlation plot for the experimental data and the theoretical predictions. For the sake of comparison, this figure also shows the corresponding data for the ϕ_ENS potentials for ¹³C-attached ¹H nuclei of ubiquitin reported in our previous study²¹. We should point out that because of different z_b − z_a in Eq. 1, uncertainties in experimental ϕ_ENS potentials increase two-fold when carbamoyl-PROXYL (z = 0) is used instead of carboxy-PROXYL (z = −1). Nonetheless, in terms of RMSD, the agreement between the experimental and theoretical data for the 15-bp DNA was as good as that for ubiquitin. These data validate predictions by the Poisson-Boltzmann theory, even for such a highly charged system as DNA, which attracts many counterions.

Figure 3.

Correlation between the experimental ϕ_ENS and predicted potentials for ¹³C-attached ¹H atoms. The data for ubiquitin was taken from Yu et al.²¹ The potentials for the 15-bp DNA were predicted using a B-form structure. Corresponding data with the predictions using a model based on PDB 9ANT are shown in Fig. S4 in the SI.

Prior to the current work, experimental assessment of electrostatic potentials for nucleic acids has been difficult. An electron-electron double-resonance (ELDOR) study using 9-tempaminoacridine spin label intercalated into DNA suggested that the magnitude of electrostatic potential around DNA was significantly smaller than the prediction from the Poisson-Boltzmann theory.²⁷ However, the intercalation of the paramagnetic probe used in the ELDOR method can distort DNA. The ELDOR data are also limited to the probe whose location is not well defined. These weaknesses make it difficult to judge whether the discrepancy reflects the limitations of the ELDOR experiment or those of the theoretical model. The paramagnetic NMR method is clearly more powerful for examination of electrostatic models because it can provide electrostatic potentials around native DNA for numerous ¹H nuclei without any chemical modification.

It should be noted that the paramagnetic NMR method is directly applicable to investigate electrostatic potentials around RNA. Structural dynamics are often important for RNA functions.^28-29 Due to the requirement of precise measurements of PRE rates for multiple paramagnetic cosolutes, applications of this method to large (e.g., >40 kDa) nucleic acid molecules may be challenging. Nonetheless, the paramagnetic NMR method can in principle provide local electrostatic potentials even for highly flexible macromolecules such as single-stranded RNA and intrinsically disordered proteins. This aspect is important because the electrostatic properties of structurally disordered macromolecules are difficult to computationally assess with the Poisson-Boltzmann theory.

In conclusion, we have developed a paramagnetic NMR-based method to measure local electrostatic potentials around nucleic acids without any use of structural information. This method allows for unprecedented experimental investigations into the electrostatic properties of nucleic acids. Experimental data of near-surface electrostatic potentials will be useful not only for validation of theoretical electrostatic models, but also for a better understanding of the role of electrostatic interactions in the function of nucleic acids.

Experimental Methods

The NMR samples of the ¹³C/¹⁵N-labeled DNA duplex was prepared as previously described. All NMR experiments were conducted at 25°C using a Bruker Avance III NMR spectrometer operated at the ¹H frequency of 600 MHz. A cryogenic ¹H/¹³C/¹⁵N/³¹P QCI probe was used for NMR detection. Experimental and computational details are described in the SI.