Clinical Validation of the Covariates Pharmacokinetic Model for Propofol in an Adult Population

Abstract

Background and Objective

Pharmacokinetic or pharmacokinetic-pharmacodynamic models have been instrumental in facilitating the clinical use of propofol in target-controlled infusion systems in anaesthetic practice. There has been debate over which model should be recommended for practice. The covariates model is an updated pharmacokinetic model for propofol. The aim of this study was to prospectively validate this model in an adult population.

Methods

Twenty-nine patients were included, with a range of ages to assess model performance in younger and older individuals. Subjects received propofol through a target-controlled infusion device programmed with the covariates model. Subjects were randomised to one of two increasing/decreasing regimes of propofol plasma target concentrations between 2 and 5 μg.mL⁻¹. After the start of the infusion, arterial and venous blood samples were drawn at pre-specified timepoints between 1.5 and 20 min and between 1.5 and 45 min, respectively. Predictive performance was assessed using established methodology.

Results

The model achieved a bias of 9 (− 45 to 82) and precision of 24 (9–82) for arterial samples and bias of − 8 (− 64 to 70) and precision of 23 (9–70) for venous samples. Predicted concentrations tended to be higher than the measured concentrations in female individuals but lower in male individuals. There was no clear systematic difference in the bias between younger and older patients.

Conclusions

The covariates propofol pharmacokinetic model achieved an acceptable level of predictive performance, as assessed by both arterial and venous sampling, for use in target-controlled infusion in clinical practice.

Clinical Trial Registration

NCT01492712 (15 December, 2011)

Supplementary Information

The online version contains supplementary material available at 10.1007/s40268-022-00404-4.

Plain Language Summary

Pharmacokinetic models can estimate the changes in the concentration of a drug in the body over time. These have been instrumental in facilitating the clinical use of anaesthetic agents such as propofol in target-controlled infusions, which aim to achieve a set concentration in either plasma or the brain to achieve anaesthesia. The covariates model is a previously described pharmacokinetic model for propofol. The aim of the described study was to validate the performance of the model in an independent adult population. Participants received anaesthesia with propofol through a target-controlled infusion device programmed with the covariates model. The concentration of propofol in the blood was measured at various timepoints and compared to the target concentration specified by the target-controlled infusion device. The analysis showed that overall, the covariates model performed to a level acceptable for use in clinical practice and compared favourably to other pharmacokinetic models.

Supplementary Information

The online version contains supplementary material available at 10.1007/s40268-022-00404-4.

Key Points

The covariates propofol pharmacokinetic model showed an acceptable level of performance for use in target-controlled infusions of propofol in adult clinical practice.

The covariates model performed non-inferiorly when compared to other published pharmacokinetic models for propofol target-controlled infusions.

Introduction

Target-controlled infusion (TCI) of propofol represents a significant component of anaesthetic practice in the UK [1] and has contributed to an increased uptake of intravenous anaesthetic techniques in general worldwide [2]. While the physicochemical properties and clinical effects of propofol make it particularly suitable for intravenous infusions, it is the development of pharmacokinetic (PK) and PK-pharmacodynamic models that has been instrumental in facilitating its clinical use in TCI. There has been debate over which PK model should be recommended for practice and, in particular, whether the Marsh et al. [3] or Schnider et al. [4, 5] PK model for propofol is clinically advantageous [6]. More recently, the model developed by Eleveld at al. has generated significant interest for use in populations with a wide range of ages and body weights [7].

The covariates model represents a potential alternative to the above models. It has the theoretical advantage over the Marsh et al. model of adjusting for the additional patient variables of age and sex [8], whilst is simpler than the Eleveld et al. model. Prior to being used in clinical practice, a PK model should be validated in an independent population. The study described below is the first to use the covariates model to deliver anaesthesia to patients and had the primary objective to validate the predictive performance of the covariates PK model for propofol. The secondary objective was to compare its PK performance to that of the Marsh et al., Schnider et al. and Eleveld et al. models.

Methods

Ethical Approval

Ethical approval was granted for the study by the West of Scotland Research Ethics Committee on 9 April, 2010 (reference number: 10/S0709/8) and registered with ClinicalTrials.gov (NCT01492712). The study was conducted in accordance with the ethical standards as laid down in the Declaration of Helsinki [9]. Patients were approached during their pre-operative clinic attendance and provided with a participant information sheet and a verbal description of the study procedure. They either consented at this stage or were allowed further time to consider their involvement prior to attendance on the day of surgery.

Patient Population

Study participants were prospectively recruited from patients attending the Golden Jubilee National Hospital, Clydebank for elective surgery between 26 January, 2011 and 10 June, 2014. Ultimately 41 patients were enrolled in the study.

Inclusion/Exclusion

Included patients were over 18 years of age and undergoing non-cardiac surgery requiring general anaesthesia and expected to last more than 30 min. Patients were excluded from the study if they refused consent or were unable to consent on the basis of a lack of capacity. If a patient was due to receive pre-medication or had received sedative or anaesthetic agents the preceding 12 h, they were excluded because of the potential impact on the depth of anaesthesia monitoring on a parallel pharmacodynamic study. For similar reasons, patients with a history of excessive alcohol intake or illicit drug use were excluded. Patients were excluded if they had a body mass index of greater than 35, predictors of a difficult airway or a history of allergy to any of the constituents of propofol.

Sample Size

There is no consensus agreement on the required sample size for this type of PK validation study. Similar published studies have recruited around 30 patients [10] and the same number was determined to be appropriate in this study.

Conduct of Study

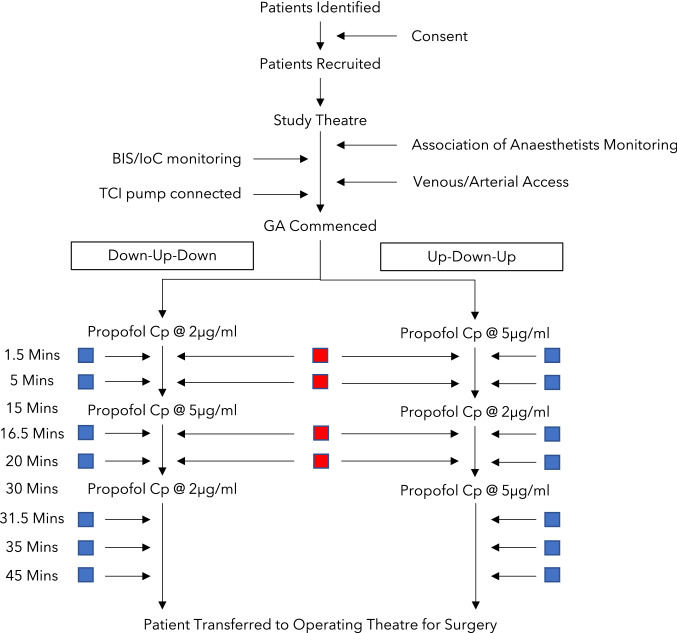
The study was a single-centre, randomised, non-comparative validation study of the covariates model. The study protocol is summarised in Fig. 1.

Fig. 1.

Study algorithm. Red box represents an arterial sample taken, blue box represents a venous sample taken. BIS bispectral index, Cp target plasma concentration, GA general anaesthesia, loC level of consciousness, TCI target-controlled infusion

During conduct of the study protocol, patients were cared for in an anaesthetic room or operating theatre by a minimum of two anaesthetists or one anaesthetist and one trained physician’s assistant for anaesthesia. A skilled anaesthetic assistant was present at all times. Standards of monitoring developed by the Association of Anaesthetists were followed [11]. Monitoring of vital parameters was performed using the Draeger Primus anaesthetic machine (Draeger Medical UK Ltd., Hemel Hempstead, UK) and the Carescape B850 patient monitoring system (GE Healthcare, Chalfont Saint Giles, Buckinghamshire, UK).

Following confirmation of stable vital signs, all patients had an 18G or 20G intravenous cannula inserted into a large forearm vein to allow the infusion of propofol. In the contra-lateral arm, a second 18G intravenous cannula was inserted to allow sampling of venous blood. A further cannula was then inserted into the radial artery on this side to allow sampling of arterial blood and continuous measurement of arterial blood pressure.

Prior to initiation of the study protocol, the collection of continuous physiological data was confirmed. All routinely collected standard monitoring data, invasive arterial blood pressure and details of all medications administered were recorded using the Recall digital anaesthetic record (Informatics, Glasgow, UK).

Propofol (Propofol Lipuro 2%; B. Braun Medical Ltd., Sheffield, UK) was infused using an Injectomat TIVA Agilia syringe pump (Fresenius Kabi, Louviers, France) programmed with the covariates model. Patency of the intravenous cannula was confirmed by a concomitant slow and constant infusion of compound sodium lactate solution (Hartmann’s solution). As described in the study protocol (Fig. 1), patients were alternately randomised to either a 2-5-2 infusion or a 5-2-5 infusion. In the 2-5-2 group, an initial propofol plasma target concentration of 2 μg.mL^-1 was maintained for 15 min prior to an increase to 5 μg.mL^–1 for 15 min and finally a reduction to 2 μg.mL^–1 for 15 min. The reverse was performed in the 5-2-5 group.

The study procedure lasted 45 min in total and was performed prior to the initiation of surgery. During this time, the patient remained spontaneously breathing via a face mask and the concentration of oxygen was titrated to maintain arterial oxygen saturations of at least 95%. Intravenous boluses of metaraminol 0.1 mg and glycopyrrolate 200 mcg were used to treat hypotension and bradycardia as clinically indicated. No medications that could interfere with the pharmacodynamics of propofol, such as volatile anaesthetic agents, benzodiazepines or opioids, were administered during the study procedure.

Throughout the study procedure, arterial and venous blood samples were drawn at pre-specified timepoints as indicated in Fig. 1. The sampling schedule was designed to allow a comparison of arterial and venous propofol concentrations as well as to allow the examination of the model performance close to plasma target changes and during stable anaesthesia.

Following collection of the final blood sample, the patient was prepared for their surgical procedure. Anaesthetic management from this stage onwards followed local procedures. Participation in the study did not influence the patient’s ongoing clinical care.

Arterial and venous blood samples were heparinised by collection into a blood gas syringe. The sample was then transferred into a fluoride oxalate sample bottle to provide stability prior to storage at 4 °C. Samples were stored for a maximum of 8 weeks prior to analysis. Quality control was performed to ensure that the samples did not deteriorate over time. Propofol concentrations in whole blood samples were analysed by C3P Analysis (Plymouth, UK) using a validated, whole-blood, high-performance liquid chromatography technique [12].

Data Handling

Infusion profiles from the Injectomat TIVA Agilia syringe pump were downloaded into Microsoft Excel (2007) using the software provided (Partner Agilia; Fresenius Kabi). Similarly, all arterial and venous blood results and individual patient demographic details were stored in Microsoft Excel.

Statistics

The majority of data processing and analysis was performed using RStudio Version 1.2.5033 running R Version 4.0.3 [13]. The approach to PK model validation published by Varvel et al. was adapted for use in this study [14], with performance errors for each arterial and venous blood samples calculated using the equation:

$${\text{PE}}_{\mathit{ij}}=\frac{C{b}_{\mathit{ij}}-C{p}_{\mathit{ij}}}{C{p}_{\mathit{ij}}}\times 100,$$ 1

where PE_ij is the percentage performance error j in the ith patient, Cb is the concentration measured in blood, and Cp is the concentration predicted by the TCI device. These performance errors were summarised for each individual as MDPE_i and MDAPE_i using the below equations:

$${\text{MDPE}}_i=\text{median}\left\{P{E}_{\mathit{ij}},j=1,\dots ,N_i\right\}$$ 2

$${\text{MADAPE}}_i=\text{median}\left\{\left|{\text{PE}}_{\mathit{ij}}\right|,j=1,\dots ,N_i\right\},$$ 3

where N_i is the number of performance errors in the ith individual. The median performance error (MDPE) quantifies bias, the tendency of the TCI device to over-predict or under-predict the actual drug concentration. The median absolute performance error (MDAPE) quantifies precision, a summary of the overall size of the performance errors. For population estimates, the medians with interquartile ranges are reported.

Wilcoxon signed rank tests were performed to compare performance errors measured using arterial and venous sampling. A p-value of < 0.05 was regarded as significant. Comparisons were made between male and female patients and patients over and under 65 years of age to confirm that adjusting the model by the covariates of age and sex resulted in a consistent bias.

Model Comparisons

A TCI device infusion profile for each participant was used to simulate the propofol plasma concentrations predicted by the covariates, Marsh et al., Schnider et al. and Eleveld et al. models using the deSolve package in R [15]. MDPE_i and MDAPE_i were calculated as previously described, with the variability within an individual calculated using WOBBLE_i (Equation 4). Statistical comparison between models was performed on the basis of inaccuracy (MDAPEs) and variability (WOBBLE) across the population.

$${\text{WOBBLE}}_i=\text{median}\left\{\left|{\text{PE}}_{\mathit{ij}}-{\text{MDPE}}_i\right|,j=1,\dots ,N_i\right\}.$$ 4

The Friedman rank sum test was used to compare the models for a statistically significant difference in inaccuracy. The Nemenyi multiple comparison test was then used to determine which, if any, models were statistically different.

For each model, similar comparisons as for the validation study were performed by sex and age to explore any systematic differences in bias. The effect of time since changes in plasma concentration was similarly explored.

Results

Forty patients contributed data to the study. Because of an initial misspecification of the TCI device, datasets from ten female patients were unsuitable for the validation analysis. One further dataset from a female patient was excluded from the validation analysis because of a pump programming error. Ultimately, there were 29 patients with datasets suitable for a validation analysis and 40 for simulation studies. The characteristics of the populations are shown in Table 1.

Table 1.

Characteristics of subjects studied. Data presented as median (range) or counts

Characteristic	Validation cohort	Simulation cohort
Male/female	15/14	15/25
Age (years)	47 (28–75)	47 (28–75)
< 65	20	29
≥ 65	9	11
Weight (kg)	76 (49–120)	72 (49–120)
Height (cm)	173 (151–192)	171 (151–192)
BMI (kg/m2)	26 (20–34)	25 (19–34)
Infusion protocol
2-5-2	14	21
5-2-5	15	19

BMI body mass index

Overall PK Validation

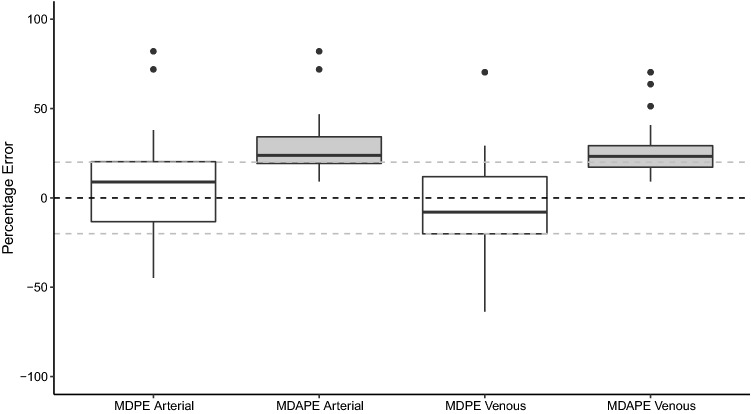
The model performed with a reasonable degree of bias and inaccuracy with a MDPE of 9 (− 45 to 82) and an MDAPE of 24 (9–82) for arterial samples and an MDPE of −8 (− 64 to 70) and an MDAPE of 23 (9–70) for venous samples (Table 2 and Fig. 2). There was a statistically significant difference between performance errors for each arterial and venous blood sample (p < 0.0001) and between the arterial and venous MDPEs for each patient (p < 0.001).

Table 2.

MDPE and MDAPE for arterial and venous sample for the covariates model. Data are presented as median (range)

Measure	Overall	Female	Male	Younger	Older
MDPE A	9 (– 45 to 82)	− 14 (− 45 to 28)*	19 (– 11 to 82)*	1 (– 43 to 72)	20 (– 45 to 82)
MDAPE A	24 (9–82)	23 (9–45)	24 (13–82)	22 (9–72)	27 (13–82)
MDPE V	8 (– 64 to 70)	– 20 (– 64 to – 8) ♦	12 (– 9 to 70) ♦	− 6 (− 64 to 29)	− 9 (− 51 to 70)
MDAPE V	23 (9–70)	21 (11–64)	23 (9–70)	22 (9–64)	24 (10–70)

A arterial, MDAPE median absolute performance error, MDPE median performance error, V venous.* denotes a statistically significant difference of p < 0.001 between MDPEs, ^♦ denotes a statistically significant difference of p < 0.0001 between MDPEs

Fig. 2.

Validation study results showing the median performance error (MDPE) and median absolute performance error (MDAPE) for arterial and venous samples. The horizontal black dashed line signifies an MDPE of 0, while the horizontal grey dashed lines signify MDPEs of + 20 and − 20, which represents clinically acceptable performance [16]

Comparison by Sex

Measured concentrations tended to be lower than the predicted concentrations in female patients but higher than predicted concentrations in male patients (Table 2). This was confirmed by significant differences when comparing MDPEs for female and male patients on arterial (p < 0.001) and venous (p < 0.0001) samples. The result of these opposing biases (over-prediction in female patients and under-prediction in male patients) was that the overall population bias was reduced to nearer to zero.

Younger and Older Patient Comparison

There was no clear systematic difference in the bias of model predictions between younger (aged < 65 years) and older (aged > 65 years) patients (Table 2), confirmed by non-significant comparisons between MDPEs for younger and older patients on arterial (p = 0.36) and venous (p = 0.80) samples. There was a tendency for an older age to emphasise existing differences in bias between female and male patients as supported by arterial MDPEs of − 12 (− 43 to 18) and −23 (− 45 to 28) in younger and older female patients and 16 (− 11 to 72) and 27 (13–82) in younger and older male patients.

Model Comparison

The summary results for overall performances of each model in the simulation study are displayed in Tables 3 and 4 and Figs. 3 and 4. Study data comparing measured blood propofol concentrations (arterial and venous) versus predicted blood propofol concentrations for each of the simulated models are contained in the Electronic Supplementary Material.

Table 3.

Summary of results for prediction errors in simulation studies for each of the covariates, Marsh et al., Schnider et al. and Eleveld et al. models. Data are presented as median (range)

Measure	Covariates	Marsh et al.	Schnider et al.	Eleveld et al.
MDPE A	3 (− 45 to 73)	18 (− 44 to 112)	9 (− 40 to 68)	15 (− 35 to 87)
MDAPE A	25 (3–73)*	34 (9–112*♦	22 (7–68)•	26 (4–87)♦
MDPE V	−11 (− 64 to 56)	5 (− 56 to 84)	− 6 (− 59 to 40)	8 (− 56 to 81)
MDAPE V	20 (9–64)	25 (9–84)	26 (9–59)	26 (5–81)

A arterial, MDAPE median absolute performance error, MDPE median performance error, V venous

*Denotes a statistically significant difference of p = 0.0021 between MDAPEs

^♦Denotes a statistically significant difference of p = 0.0055 between MDAPEs

^•Denotes a statistically significant difference of p = 0.0001 between MDAPEs

Table 4.

Summary of results for prediction errors in simulation studies for each of the covariates, Marsh et al., Schnider et al. and Eleveld et al. models. Data are presented as median (range)

WOBBLE	Covariates	Marsh et al.	Schnider et al.	Eleveld et al.
WOBBLE A	14 (1–48)*	17 (4–61)*♦	13 (3–51)♦	13 (1–39)♦
WOBBLE V	14 (4–29) •	19 (3–44)	22 (3–58) •	15 (4–43)

A arterial, V venous

*Denotes a statistically significant difference of p = 0.0055 between WOBBLEs calculated for each model

^♦Denotes a statistically significant difference of p = 0.0041 between WOBBLEs

^•Denotes a statistically significant difference of p = 0.0365 between WOBBLEs

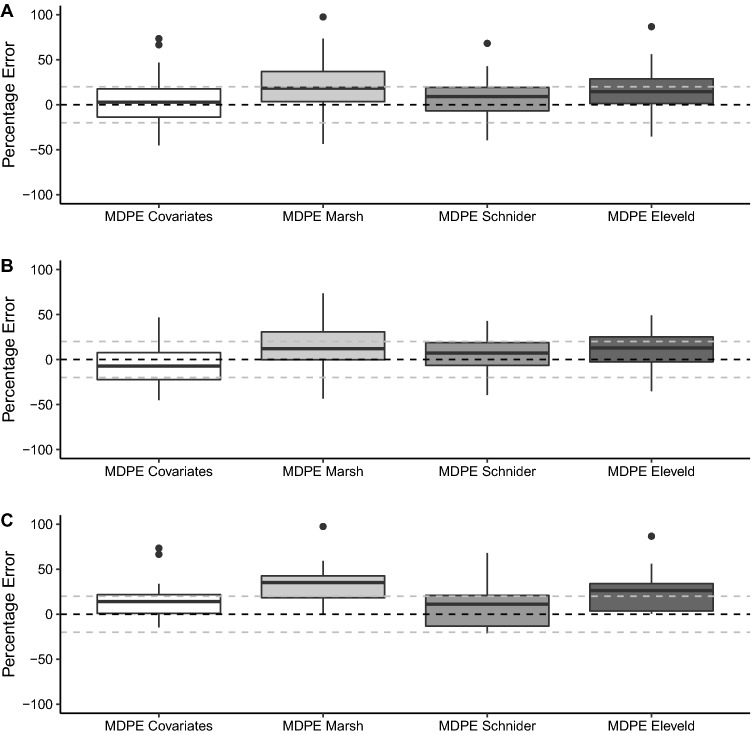
Fig. 3.

Summary of results for prediction errors based on arterial blood sampling in simulation studies for each of the covariates, Marsh et al., Schnider et al. and Eleveld et al. models in all patients (A), female patients (B) and male patients (C). The horizontal black dashed line signifies a median performance error (MDPE) of 0, while the horizontal grey dashed lines signify MDPEs of + 20 and − 20, which represents clinically acceptable performance [16]

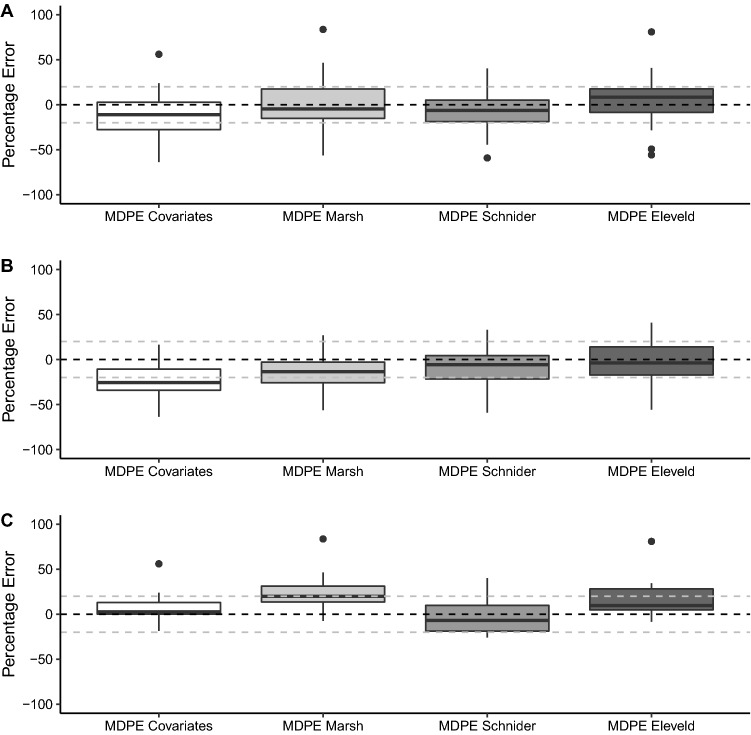
Fig. 4.

Summary of results for prediction errors based on venous blood sampling in simulation studies for each of the covariates, Marsh et al., Schnider et al. and Eleveld et al. models in all patients (A), female patients (B) and male patients (C). The horizontal black dashed line signifies a median performance error (MDPE) of 0, while the horizontal grey dashed lines signify MDPEs of + 20 and − 20, which represents clinically acceptable performance [16]

On the basis of arterial sampling, the overall bias of the covariates model was closest to zero but with no statistically significant difference between models. Accuracy of the covariates model was similar to that of the Schnider et al. and Eleveld et al. models. The Marsh et al. model demonstrated statistically significant lower accuracy than the other models (p < 0.01 for all comparisons). On the basis of venous sampling, there was no significant difference in the bias or accuracies of the models (p = 0.20).

Intra-individual variability (WOBBLE) was significantly different between the models on both arterial and venous sampling (p < 0.001 and p = 0.025, respectively). Post-hoc testing confirmed the similarity of the covariates, Schnider et al. and Eleveld et al. models on arterial sampling and a significantly greater WOBBLE in the Marsh et al. model. Conversely, on venous samples, the Schnider et al. model had the greatest WOBBLE, which reached a significant difference with the covariates model only.

Model Comparison by Sex

The performance of the models in female and male patients is summarised in Table 5 and Figs. 3 and 4. In line with the validation study results, the simulation studies using the covariates model confirmed the tendency to over-predict in female patients and under-predict in male patients. This was confirmed by significant comparisons between MDPEs for female and male patients on arterial (p < 0.0001) and venous (p < 0.0001) samples. The tendency for the Marsh et al. and Eleveld et al. models to under-predict was consistent across both female and male patients on arterial but not venous samples. There was a statistically significant difference in bias between female and male patients in both arterial (p < 0.001) and venous samples (p < 0.0001). In contrast, there was no significant difference in bias between female and male patients in the predictions made by the Schnider et al. model in either arterial (p = 0.55) or venous samples (p = 0.12).

Table 5.

Results for prediction errors in simulation studies for each of the covariates, Marsh et al., Schnider et al. and Eleveld et al. models for female and male patients. Data are presented as median (range)

Model	Covariates		Marsh et al.		Schnider et al.		Eleveld et al.
Sex	Male	Female	Male	Female	Male	Female	Male	Female
MDPE A	14 (– 15 to 73)*	7 (– 45 to 47)*	36 (0–112)*	12 (– 44 to 74)*	11 (– 21 to 68)	7 (– 40 to 43)	26 (0–87)♦	13 (– 35 to 49)♦
MDAPE A	25 (8 to 73)	24 (3–47)	36 (9–112)	32 (10–74)	20 (9–68)	24 (7–48)	27 (4–87)	25 (8–49)
MDPE V	3 (– 18 to 56)*	– 26 (– 64 to 16)*	20 (– 7 to 84)*	– 13 (– 56 to 27)*	– 7 (– 26 to 40)	– 6 (– 59 to 33)	10 (– 8 to 81)*	– 4 (– 56 to 41)*
MDAPE V	18 (9–56)	26 (12–64)	24 (17–84)	25 (9–56)	24 (10–59)	27 (9–59)	31 (5–81)	23 (8–56)

A arterial, MDAPE median absolute performance error, MDPE median performance error, V venous

*Denotes a statistically significant difference of p < 0.0001 between MDPEs in female and male patients

^♦Denotes a statistically significant difference of p < 0.001 between MDPEs in female and male patients

Model Comparison by Age

The results of the predictive performance of the models between older and younger patients are summarised in Table 6. With the exception of the Schnider et al. and Eleveld et al. models as assessed on venous blood sampling (p = 0.01), there was no statistical difference between the model biases in younger and older patients. There was a non-significant trend for increased under-prediction in older patients for the Marsh et al. model.

Table 6.

Results for prediction errors in simulation studies for each of the covariates, Marsh et al., Schnider et al. and Eleveld et al. models for younger and older patients. Data are presented as median (range)

Model	Covariates		Marsh et al.		Schnider et al.		Eleveld et al.
Sex	Younger	Older	Younger	Older	Younger	Older	Younger	Older
MDPE A	4 (– 45 to 67)	1 (– 45 to 73)	15 (– 44 to 97)	31 (– 23 to 112)	11 (– 34 to 43)	– 4 (– 40 to 68)	15 (– 35 to 56)	8 (– 35 to 87)
MDAPE A	25 (3–67)	24 (8–73)	34 (9–97)	36 (10–112)	19 (8–46)	29 (7–68)	26 (4–56)	29 (11–87)
MDPE V	– 8 (– 64 to 24)	– 15 (– 51 to 56)	– 6 (– 56 to 47)	5 (– 43 to 84)	– 7 (– 59 to 27)*	3 (– 31 to 40)*	8 (– 56 to 35)*	12 (– 28 to 81)*
MDAPE V	20 (11–64)	21 (9–56)	25 (9–56)	22 (10–84)	24 (9–59)	33 (13–58)	23 (5–56)	28 (17–81)

A arterial, MDAPE median absolute performance error, MDPE median performance error, V venous

*Denotes a statistically significant difference of p = 0.01 between MDPEs in younger and older patients

Model Comparison by Timing

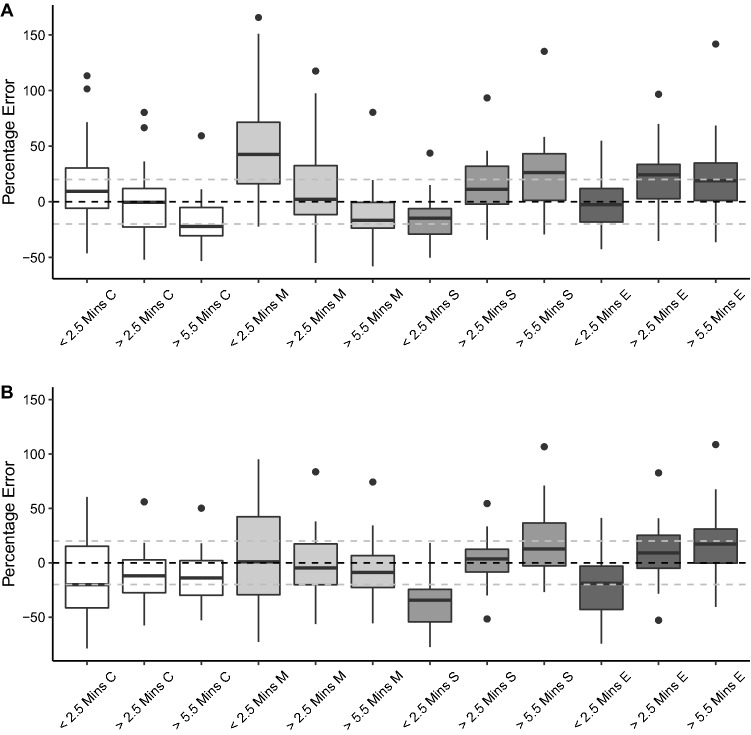
The performances of the models following an increase in plasma target concentration are summarised in Table 7 and Fig. 5. For both the covariates and the Marsh et al. models, there was a trend from the early to the late time window from model under-prediction to over-prediction on the basis of arterial sampling. The reverse was true for the Schnider et al. and Eleveld et al. models.

Table 7.

Results for prediction errors at specified time intervals in simulation studies for each of the covariates, Marsh et al., Schnider et al. and Eleveld et al. models. Data are presented as median (range)

Time since change (minutes)	Measure	Covariates	Marsh et al.	Schnider et al.	Eleveld et al.
< 2.5	MDPE A	9 (– 46 to 113)	43 (– 22 to 166)	– 15 (– 50 to 44)	– 3 (– 43 to 55)
	MDAPE A	31 (0–113)*	47 (2–166)*♦	27 (1–50)♦	29 (3–55)*
	MDPE V	– 20 (– 79 to 61)	1 (– 73 to 95)	– 34 (– 77 to 18)	– 19 (– 74 to 41)
	MDAPE V	53 (7–79)•	56 (9–95)•	47 (7–77)•	50 (8–83)•
> 2.5	MDPE A	0 (– 52 to 80)	2 (– 55 to 118)	11 (– 34 to 93)	24 (– 35 to 97)
	MDAPE A	25 (8–80)	30 (5 to 118)•	25 (4–93)•	28 (3–97)
	MDPE V	– 12 (– 58 to 56)	– 4.5 (– 56 to 84)	3.5 (– 52 to 54)	9 (– 53 to 83)
	MDAPE V	18 (2–58)	21 (6–84)	22 (6–59)	22 (5–83)
> 5.5	MDPE A	– 22 (– 53 to 59)	– 17 (– 58 to 80)	26 (– 29 to 135)	19 (– 36 to 142)
	MDAPE A	26 (6–59)	22 (3–80)	29 (6–135)	25 (2–142)
	MDPE V	– 14 (– 53 to 50)	– 8.5 (– 56 to 74)	13 (– 27 to 107)	17 (– 41 to 109)
	MDAPE V	18 (2–53)	21 (6–74)	25 (3–107)	20 (2–109)

A arterial, MDAPE median absolute performance error, MDPE median performance error, V venous

^*Denotes a statistically significant difference of p < 0.001 between MDAPEs calculated for each model at a given time interval

^♦Denotes a statistically significant difference of p < 0.01 between MDAPEs calculated for each model at a given time interval

^•Denotes a statistically significant difference of p < 0.05 between MDAPEs calculated for each model at a given time interval

Fig. 5.

Summary of results for prediction errors based on arterial (A) and venous (B) blood sampling in simulation studies for each of the covariates (“C”), Marsh et al. (“M”), Schnider et al. (“S) and Eleveld et al. (“E”) models at set timepoints following an increase in target plasma concentrations. The horizontal black dashed line signifies a median performance error of 0, while the horizontal grey dashed lines signify MDPEs of + 20 and − 20, which represents clinically acceptable performance [16]. mins minutes

At the early time window, there was a significant difference between the accuracy of the models on arterial and venous sampling (p < 0.0001 and p = 0.0087, respectively). Pairwise comparisons confirmed the similarity of the covariates, Schnider et al. and Eleveld et al. models, but significant differences between these and the Marsh et al. model for both arterial and venous sampling.

At the intermediate time window, there was a persisting statistically significant difference in the accuracies of the models on the basis of arterial (p = 0.01) but not venous sampling (p = 0.86). On pairwise comparison, the statistical difference on the basis of arterial sampling was only present between the Marsh et al. and Schnider et al. models (p = 0.01). At the later time window, there was no significant difference between accuracies of the models on arterial (p = 0.17) or venous sampling (p = 0.79).

Discussion

Our study aimed to prospectively validate the PK component of the covariates model and compare its performance to that of the Marsh et al., Schnider et al. and Eleveld et al. models. Schüttler et al. suggested that a mean variation in measured drug plasma concentrations of 20–30%, with a total bias of 10–20% from TCI device predictions, represented acceptable performance [16]. Therefore, this study has demonstrated that the Injectomat TIVA Agilia syringe pump implementation of the covariates model achieved an acceptable level of predictive performance, as assessed by both arterial and venous sampling, for use in clinical practice.

The overall minimal bias of the covariates model (MDPE of 9 for arterial samples and − 8 for venous samples) was not consistent across patient subgroups. On both sampling methods, there was a tendency to under-predict plasma concentrations in female patients and over-predict in male patients. The covariates model was more successful in adjusting for the covariate of age and there was no significant difference in bias between younger and older patients.

The importance of the choice of blood sampling site (arterial or venous) has undergone detailed discussion elsewhere [17]. In their comparative study of PK models for propofol, Coetzee et al. noted marked differences in calculated model performance based on arterial or venous sampling [18]. Similar results were noted in the VaSCoM Study. Indeed, the Eleveld et al. model specifically addresses this by adjusting the model predictions based on whether arterial or venous sampling is used.

In our population, there were no significant differences between the PK performance of the simulations of all studied models on venous sampling; however, on arterial sampling, the Marsh et al. model performed significantly worse than the other models. The model biases were different depending on whether venous or arterial sampling was used. On arterial sampling, the covariates model had the bias closest to zero, suggesting the least tendency to over-predict or under-predict plasma concentrations.

In patient sub-populations, the covariates, Marsh et al. and Eleveld et al. models, on the basis of both arterial and venous sampling, showed a significant tendency towards a more positive bias in male patients. The Schnider et al. model did not demonstrate any significant difference in bias between female and male patients and therefore may effectively account for the covariate of sex better than the other models.

In contrast, only the Schnider et al. and Eleveld et al. model, on the basis of venous sampling, showed a significant tendency towards an increased positive bias in older patients. The Marsh et al. model had a non-significant tendency towards a more positive bias in older patients on the basis of arterial sampling. The difference in bias was negligible in the covariates model and supports the rationale for adjustment of the central compartment volume and clearance for age.

During the early sampling period, on the basis of both arterial and venous samples, the Marsh et al. model was associated with increased inaccuracy compared with the other models. By the late sampling period, this difference was no longer significant and instead the Schnider et al. model was trending towards increased inaccuracy. The above results need consideration when using the above models in clinical practice. The anaesthetist must be aware of how the bias of the selected model will change with time and be prepared to adjust target plasma or effect-site concentrations based on this knowledge.

Two prior studies have directly compared the performance of the covariates model to that of the Marsh et al. and Schnider et al. models [19, 20]. The first of these studies used data from nine patients who had received a propofol infusion [19] and the second used data from 42 patients undergoing surgery with TCI of propofol via the Diprifusor™ [20]. One study compared the covariates model to the Eleveld et al. model [7]. This study by Eleveld et al., in which they compared the PK performance of their PK-pharmacodynamic model with other published models, also included data on the performance of the Marsh et al. and Schnider et al. models and used a large diverse population using data from 1033 individuals from a variety of previous studies.

For assessing the performance of the covariates model, our study has several advantages over the previous studies. It is the first to provide a new PK dataset and validate the covariates model by directly testing it with a demanding schedule of increasing and decreasing target plasma concentrations. Patients recruited received no pre-medication and during the study period, anaesthesia was provided only by TCI of propofol. In the other studies, patients were routinely pre-medicated and received other drugs that could affect the PK profile of propofol.

Despite the technical differences between the studies, there are important similarities in the results. In common with the above studies, our study highlighted the favourable overall performance of the covariates model as compared with the Marsh et al. model. As was demonstrated in the previous TCI study [20], the tendency of the Marsh et al. model to under-predict in male patients relative to female patients remained present (albeit to a lesser degree) in the covariates model despite the adjustments made to the model on the basis of sex.

Our study confirmed the observation of earlier studies that the Schnider et al. model tends to over-predict in the induction phases and under-predict in the later phases of anaesthesia [19, 20]. Our study agreed with the finding of the previous TCI study that the bias of the covariates, Schnider et al. and Marsh et al. models did not remain constant across changing target plasma concentrations [20]. This finding was similar for the Eleveld et al. model in our study.

Similar to the previous study by Eleveld et al. [7], we found both the covariates and Eleveld et al. models performed to a level deemed to be appropriate for clinical practice. The Eleveld et al. model showed some bias in older patients in our study. This finding has been replicated in a separate prospective validation study [21]. This validation study also found that the Eleveld et al. model had lower intra-individual variability than the Marsh et al. or Schnider et al. model on arterial samples, similarly to this study, however, it did not compare to the covariates model [21]. In our study, the covariates and Eleveld et al. model performed very similarly, with slightly less variability in arterial samples with the Eleveld et al. model but greater in venous samples. The clinical relevance of these modest differences is unlikely to be significant. The absolute values for WOBBLE for the Eleveld et al., Marsh et al. and Schnider et al. models were greater in our study than in the validation study, likely reflecting our study protocol of changing infusion rates and earlier blood sampling following a change.

As noted by Hüppe et al., it may be unrealistic to develop a PK model to propofol with an MDAPE <20 using currently available covariates [22]. Further advances may come from physiology-based models, from data-driven or “machine-learning” approaches or techniques utilising “feedback control” [23, 24]. For the time being, the safest approach is likely to be each anaesthetist using the model that they know best, in the mode (plasma vs effect) that they always use and with an appreciation of model performances in different patient populations.

Conclusions

Our study performed the first clinical PK validation of the covariates model for propofol, showing a clinically acceptable performance with an MDAPE <30 for both arterial and venous samples. Compared to other published models, the covariates model performed non-inferiorly.

Supplementary Information

Below is the link to the electronic supplementary material.

Declarations

Funding

This study was funded by the Perioperative Research Fund at the Golden Jubilee National Hospital. Fresinius Kabi provided the infusion pumps required for the study.

Conflicts of interest/Competing interests

Injectomat TIVA Agilia with covariates model was provided by Fresenius Kabi (Brezins, France). SS received consultant honoraria from Fresenius Kabi and lecture honoraria from Aspen Pharmaceuticals. CH received consultant honoraria from Integra LifeSciences and lecture honoraria from AstraZeneca. MS, RC, NS and SM have no conflicts of interest that are directly relevant to the content of this article.

Ethics approval

Ethical approval was granted for the study by the West of Scotland Research Ethics Committee on 9 April, 2010 (reference number: 10/S0709/8) and registered with ClinicalTrials.gov (NCT01492712). The study was conducted in accordance with the ethical standards as laid down in the Declaration of Helsinki.

Consent to participate

Informed consent was obtained from all individual participants included in the study.

Consent for publication

Not applicable.

Availability of data and material

The datasets generated during and/or analysed during the current study are available from the corresponding author on reasonable request.

Code availability

Not applicable.

Authors’ contributions

SS, NS and CH contributed to study conception and design. SS, NS, CH and SM contributed to the study conduct and data collection. CH, MS and RC contributed to the data analyses. The first draft of the manuscript was written by CH and RC and all authors commented on previous versions of the manuscript. All authors read and approved the final manuscript.

Previous presentations/publications

Presented in part at the World Congress of Anaesthesiologists, Hong Kong, September 2016 [25]. Presented in part at the Anaesthetic Research Society Meeting, Aberdeen, June 2012 [26]. Submitted in part as part of a doctoral thesis for Dr. C. Hawthorne [27].