Phenotyping polarization dynamics of immune cells using a lipid droplet-cell pairing microfluidic platform

Summary

The immune synapse is the tight contact zone between a lymphocyte and a cell presenting its cognate antigen. This structure serves as a signaling platform and entails a polarization of intracellular components necessary to the immunological function of the cell. While the surface properties of the presenting cell are known to control the formation of the synapse, their impact on polarization has not yet been studied. Using functional lipid droplets as tunable artificial presenting cells combined with a microfluidic pairing device, we simultaneously observe synchronized synapses and dynamically quantify polarization patterns of individual B cells. By assessing how ligand concentration, surface fluidity, and substrate rigidity impact lysosome polarization, we show that its onset and kinetics depend on the local antigen concentration at the synapse and on substrate rigidity. Our experimental system enables a fine phenotyping of monoclonal cell populations based on their synaptic readout.

Graphical abstract

Highlights

• •Microfluidic pairing chip allows simultaneous study of multiple immune synapses
• •Lipid droplets can be formulated with different rigidity and surface fluidity
• •Lipid droplets are presented to B cells in the chip to study cell polarity
• •Ligand concentration, surface fluidity, and rigidity impact cell polarity

Motivation

Visualizing and phenotyping the polarization of an immune cell upon interaction with a stimulating cell (in the context of antigen presentation) can be challenging. It requires a good control of the physicochemical properties of the antigen-presenting surface and a method to synchronize and observe multiple interactions. We combined a microfluidic pairing chip with functionalized lipid droplets with different physicochemical properties to study the polarization of B cells upon interaction with an antigen.

Pinon et al. develop functionalized lipid droplets with different mechanical and chemical properties and use them in a microfluidic pairing chip to activate B cells and to investigate the kinetic of cell polarization.

Introduction

Direct contact is an important channel of communication for cells in multicellular organisms. This is true for cells in tissues as well as for cells that mostly live as independent entities like immune cells.¹ Their activation, their immune function, and ultimately their fate depend on signal exchanges with other cells through an organized structure called the immune synapse. In both B and T lymphocytes, the formation of the immune synapse is associated with a global rearrangement of the cytoskeleton and the establishment of a polarity axis.^2,3,4 B lymphocytes, the cells responsible for antibody production, encounter antigens in the subcapsular sinus of the lymph node, in soluble form or grafted on other cell surface, such as macrophages or follicular dendritic cells. They recognize the antigen through their specific B cell receptor (BCR), internalize, process, and further present it to a cognate T cell. Antigen recognition entails membrane and intracellular reorganizations leading to the formation of the immune synapse.⁵ Engagement of the BCR leads to the clusterization of signaling complexes in a mechanosensitive way: signaling and size of the complexes depend on the rigidity and topography of the substrate.^6,7,8 The synapse, in its final form, displays a stereotypical concentric shape with antigens/BCRs accumulated in a central cluster, surrounded by adhesion molecules and an actin ring at the periphery.^9,10,11 A similar geometry is mirrored by cytoplasmic molecules close to the membrane.¹² At the same time, the microtubule network re-orients the traffic toward the synapse (polarization of the centrosome) to secrete lysosomal proteases and degrade the antigen in the synaptic cleft, in a process named enzymatic extraction.¹³ It has been shown that, depending on the deformability of the substrate, the antigen can be internalized also by mechanical pulling.^14,15,16,17 When mechanical extraction fails, such as on non-deformable substrates, cells trigger the enzymatic extraction pathways described above.¹⁶ Interestingly, the mutual exclusivity of mechanical and enzymatic extractions suggests that the polarization mechanism is also sensitive to the mechanical properties of the substrate. Ultimately, the B cell immune synapse results in signal transduction, cell differentiation, and production of high-affinity antibodies.⁴ It has been also proposed that, by polarizing, B cells can divide asymmetrically to give rise to B cells that present more efficiently the antigen to T cells. Polarity, therefore, has consequences on B cell fate.^18,19

All these experimental results point to a crucial role of physicochemical properties of the antigen-presenting surface in B cell activation. Different systems have been used to address this mechanism. For instance, cluster formation has been revealed on fluid interfaces allowing antigen mobility (lipid bilayers⁹); mechanosensitivity has been shown using deformable substrates, such as soft gels^7,8; antigen mechanical extraction has been uncovered on plasma membrane sheets,¹⁵ and quantified by calibrated DNA force sensors.^16,20 Despite the amount of information gathered in these systems, the variety of assays hinders the comparison between experiments performed on different materials and makes it impossible to evaluate the impact of independent properties on synapse formation. This prompts us to introduce an alternative model to stimulate B cells while independently controlling physical (rigidity, fluidity, size) and chemical (functionalization) properties: lipid droplets.

Emulsions are colloidal liquid-liquid metastable suspensions stabilized by a surfactant monolayer, that have already shown their biocompatibility and their interest as probes when functionalized with proteins of interest in biophysical,²¹ developmental,²² and immunological contexts, such as phagocytosis^23,24,25 or T cell synapse studies.²⁶ By varying the bulk and surface composition, it is possible to tune the surface tension, hence the mechanical rigidity, independently from the ligand surface concentration, thus making lipid droplets a relevant antigen-presenting cell (APC) surrogate to stimulate B cells with the highest control on the physicochemical properties of the cognate surface.

In this work, we introduce several droplet formulations and functionalizations to access different physical and chemical properties that we finely characterize. Finally, we validate our methods by addressing how cells polarize depending on the properties of those antigen-presenting substrates. This question has been neglected in the past, partially because of the heterogeneity of experimental models, partially because of the lack of reproducible way to study the global cell rearrangement following immune synapse formation over time. Therefore, for a proper quantitative study, we engineered antigen-functionalized lipid droplets with a pertinent set of physicochemical properties and presented them to B cells in a controlled microfluidic pairing device that minimizes the stress to mimic the flow conditions of the lymph node. This allowed us to simultaneously observe multiple synchronized synapses with a high spatiotemporal resolution and finally provide a phenotyping map of variability of B cell polarity both in terms of polarization onset and kinetics.

Results

Microfluidic cell-cell pairing platform for the study of B cell synapses

To characterize the influence of rigidity and antigen concentration on B cell polarity, we observe by epifluorescence microscopy the polarization of murine B cells activated by antigen-coated fluid microparticles having different mechanical and interfacial properties.

Because B cells are non-adherent cells, to control the B cell synapse in space and time, we used a microfluidic chip that forces the encounter between a single B cell and an activating APC surrogate (Figure 1A). The microfluidic chip (Figure 1B), inspired by Skelley et al.,²⁷ consists of staggered arrays of double-layered U-shaped traps where the two objects (ideally of the same size) are sequentially immobilized (see STAR Methods) and imaged. The double-layer structures result in fluid streamlines not being deviated from the weir structures when a first object is trapped, thus allowing the easy capture of a second object.^27,28 The trapping array was engineered to apply the least perturbative shear stress as possible on the cells, mimicking the in vivo-like shear stress estimated in the subcapsular sinus lumen of lymphoid tissues.²⁹ Finite element simulations (see STAR Methods; Figure S1) indicate that, at the inlet speed used in our experiments, the maximal wall shear stresses on wall (Figure 1C) and trapped cell (Figure 1D) are below 1 Pa (value compatible with the shear stress estimated in the lymph nodes²⁹). Overall, the microfluidic chip we designed minimizes the stress to mimic conditions that a cell experiences in lymph nodes.

Figure 1.

Microfluidic cell-cell pairing platform for the study of B cell synapses

(A) Schematic view of the experimental setup. The microfluidic trap-based chip is imaged with an epifluorescence video-microscope, and is connected to a pressure controller inducing a low flow for droplets—then cells—circulation.

(B) SEM images of the microfluidic chamber containing 288 two-layered traps. Scale bar, 30 μm.

(C) 2D FEM simulation of fluid shear rate (left) and shear stress (right) passing through the pillars along the whole chip, for an inlet pressure of 1,000 Pa corresponding to a maximal fluid velocity of 1.6 mm/s. The shear rate is constant along the chamber. The maximal wall shear rate is 514 s⁻¹ that corresponds to a maximal wall shear stress of 0.514 Pa.

(D) 3D simulation of the shear stress that a trapped cell experiences in the microfluidic device when it is immobilized with a droplet (wireframe representation). For a maximal inlet pressure of 1,000 Pa—maximal fluid velocity of 1.6 mm/s in the chamber—the maximal shear stress is about 1.0 Pa.

Droplets mimic APCs both in antigen concentrations and mechanical properties

Our study has been conducted with B lymphoma murine cell line IIA1.6, which is described to be a homogeneous population of non-activated mature B cells. These cells constitute an ideal model for functional studies of antigen presentation, since they lack FcγRIIB1 receptors on their surface^30,31 and hence can be conveniently activated through specific antibodies against the BCR (F(ab’)₂). We stimulated these cells with lipid droplets functionalized with such antibodies (which will be referred to as antigens, Ag), linked to droplet surface with biotinylated phospholipids (DPSE-PEG₂₀₀₀-biotin)/streptavidin complex Figure 2A. As negative control, droplets were coated with biotinylated hemmila, which do not engage the BCR, in lieu of F(ab’)₂.¹⁴ In both cases, fluorescent streptavidin linker allows us to observe the functionalization (Figure 2B).

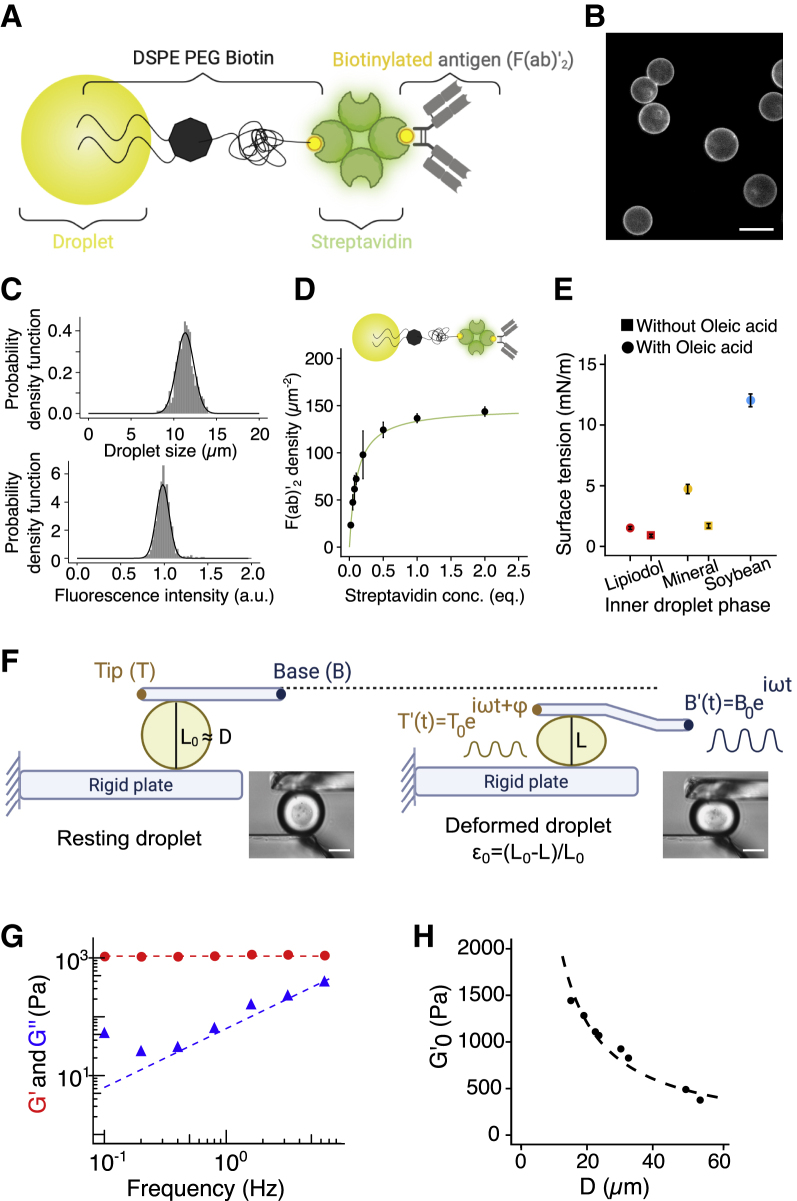
Figure 2.

Droplets mimic APCs both in antigen concentrations and mechanical properties

(A) Schematic of the droplet coating complex with DSPE-PEG₂₀₀₀-biotin/streptavidin/F(ab’)₂.

(B) Representative epifluorescence image of coated droplet. Scale bar, 7 μm.

(C) Size (mean ± SD = 11.0 ± 0.7 μm) and fluorescence (mean ± SD = 1 ± 0.075) histograms of N = 700 droplets.

(D) Titration curve of F(ab’)₂ fragments depending on the streptavidin concentration on droplets. The fit follows to the Langmuir’s isotherm with a plateau at 147 F(ab’)₂/µm². These data are obtained from previous fluorescence intensity assessments of both streptavidin and F(ab’)₂ on 11-μm droplets, initially functionalized with 100 equiv of DSPE-PEG₂₀₀₀-biotin.

(E) Pendant drop measurements of surface tension for three different oil mixtures—Lipiodol (red), mineral (yellow), and soybean (blue) oils, enriched (dots) or not (squares) with oleic acid.

(F) Schematic of the microplate experiment. A cell or a droplet is trapped between two glass microplates, one being immobile (bottom) the other flexible (top) with a base position oscillating as B $\left(t\right)=B_0{e}^{i\omega t}$. We measure the oscillating displacement of the tip of the flexible plate as T(t) = T₀$e^{\left(i\omega t+\phi \right)}$ that relates to the immobilized cell or droplet visco-elastic properties. T is determined for a frequency range between 0.1 and 6.4 Hz (droplet) or 1.6 Hz (cells). Representative bright-field images of a resting (left) and a deformed (right) droplet. Scale bars, 30 μm.

(G) Elastic G′ and viscous G″ moduli of a single droplet (diameter: 19.1 μm) as a function of the probing frequency. In this frequency range, G′ is constant, whereas G″ linearly depends on frequency.

(H) Elastic modulus of droplets plotted as a function of the resting droplet diameter, for a constant initial deformation ${\mathrm{ϵ}}_0$ = 0.2. The fitting equation is written as G' = 4γ/ $\mathrm{ϵ}$ L₀ and leads to a surface tension $\mathrm{\gamma }=1.21\pm 0.04$ mN m⁻¹.

Lipid droplets were fabricated by shearing an oil phase in an aqueous buffer containing surface-active agents (surfactants) to improve suspension stability over time.³² To avoid a possible bias in the analysis of the synapse formation and cell polarization, that could exist if cells were put into contact with particles of different diameters (hence curvature), we decided to work with monodisperse size distributions with an average diameter of 11 μm, comparable with the one of a B cell (Figures 2B and 2C).

After droplet emulsification, we coated the droplet surface by adsorbing phospholipids onto the surface with the help of a polar co-solvent, as done in Pinon et al.³³ Then, fluorescent streptavidins, used as linker, was added to attach on the one side to the biotinylated phospholids, and bind to the other side to biotinylated F(ab’)₂, added in the last step. This protocol ensures a finely controlled and homogeneous lipid coating. Ultimately, protein functionalization of the droplets surface (streptavidin) is performed, as shown in Figures 2B and 2C. To quantify the surface concentration in F(ab’)₂, we used specific and fluorescent secondary antibodies at saturating concentrations and correlated streptavidin fluorescence intensity to assess the absolute F(ab’)₂ concentration over droplet surface (see STAR Methods; Figure S2). Figure 2D shows that the F(ab’)₂ adsorption is well described by a Langmuir isotherm, making straightforward the quantification of their surface density (see STAR Methods). F(ab’)₂ surface density, expressed as a number of proteins per unit of surface area, has a maximal value of 150 antigens/μm² at saturating conditions. This value has been previously shown to be sufficient to trigger B cell activation.¹⁰

Antigen-presenting cell stiffness has been reported to be a relevant mechanical property for immune cell activation^34,35 and in particular for B cell functions.^8,16 The stiffness of a material is related to its ability to resist reversible deformations when submitted to stress, i.e., to its apparent elastic properties. For oil droplets, the origin of elastic-like resistance to deformation is expected to be the excess pressure inside the droplet, i.e., the Laplace pressure $\Delta$ P written as $\Delta$ P = 2γ/R, where R is the droplet radius. The stiffness of a droplet can, therefore, be modulated by changing the surface tension γ between the oil and the surrounding liquid medium. We measured the surface tension of diverse droplet formulations by the pendant drop technique and micropipette^36,37 (Figures S3A and S3B). We found that the interfacial tension of the oil/water interface ranges from about 1 to 12 mN/m between the softest and stiffest formulations, thus varying by about one order of magnitude (Figure 2E). In addition, micropipette aspiration³⁸ measurements on single functionalized or non-functionalized droplets show that the effect of phospholipid adsorption at the oil/water interfacial is negligible (see STAR Methods and tables therein).

The mechanical properties of complex materials are characterized by both elastic and viscous behaviors,³⁹ which depend on the timescale of the solicitation. We used a microplate rheometer to measure the complex dynamic modulus G∗(f) = G' + iG″ of single droplets over a frequency range of biological relevance,⁴⁰ and to correlate the droplet interfacial tension γ to their storage modulus G'^34,41 (Figure 2F).

The experiment consists in trapping a spherical deformable object between two glass microplates, a rigid one and a flexible one of calibrated stiffness. The flexible plate is oscillated, applying a sinusoidal stress on the studied sample, compressing it against the rigid plate. From the applied oscillatory normal stress and the sinusoidal strain (deformation) of the object, one can infer its complex dynamic modulus G∗(f) = G' + iG″, with the real part G′ representing the storage modulus (elastic-like response), and the imaginary part G″ accounting for energy dissipation (viscous-like response).

Sinking droplets (Lipiodol, oil denser than water, used here as reference) exhibited a Kelvin-Voigt behavior, with a constant elastic modulus G′, and a viscous modulus G″ proportional to the frequency (Figure 2G), where elastic-like response is dominant (G′ >> G″) (see STAR Methods).

We found that, for a mean strain (${\mathrm{ϵ}}_0$ = 0.2), the droplet storage modulus decreases as the inverse of the diameter of the resting droplet (Figure 2H), in agreement with the assumption that the only restoring force resisting compression originates from Laplace pressure $\Delta$P = 4γ/L₀ (see STAR Methods), with $L_0$ being the resting droplet diameter. Thus, by fitting the storage modulus G′ as function of the droplet diameter, one gets a calibration curve for which we extract an estimation of the droplet surface tension, compatible with the pendant drop measurements ($\gamma =1.21\pm 0.04$ mN/m) (Figure 2E). Therefore, according to this quantification, we conclude that the droplets used in our experiments, i.e., diameter of 11 μm and tension ranging from 1 to 12 mN/m, exhibit an apparent rigidity (storage modulus G′) ranging from 4 to 30 kPa. As comparison, we used the same method to measure B cell stiffness and found G∗ = 165 Pa (see STAR Methods; Figures S3C–S3F). Antigen-presenting cells range from 1 kPa (macrophages³⁴) to 5–10 kPa (follicular dendritic cells,¹⁶ which are essentially fibroblasts). This indicates that the droplets are, as APCs, several times stiffer than B cells and definitely in the range of the substrate rigidity capable of eliciting a strong B cell signal according to Wan et al.⁸

B cells actively gather antigens at the synapse

We assessed the impact of antigen enrichment during synapse formation by using two droplet types, one favoring and the other one hindering such enrichment. We thus used two alternative methods to graft the lipids on the droplets: via the surface where lipids are inserted after the emulsification processes,³³ or in bulk where lipids are inserted prior to emulsification.^23,26 Using the microfluidics traps described above to immobilize the droplet-B cell contact, we notice that cells interacting with bulk-functionalized droplets gather the antigen to a sustainable central cluster (Figure 3A; Video S1) in less than 20 min, similarly to that described on planar lipid bilayers¹⁰ or for other cell types.²³ By contrast, surface-functionalized droplets do not allow antigen accumulation (Figure 3B), similar to the negative BSA control (Figure 3C). We further quantified the kinetics of antigen accumulation by an index I_antigen (Figure 3D), which increases for bulk-functionalized antigen-coated droplets as a monotonic exponential saturation curve over 40 min, with a characteristic time of 5 min (Figure 3E, bulk-functionalized antigen-coated droplets). The plateau is directly related to the accumulated antigen concentration: the cluster is 1.5-fold brighter than the initial time point (Figure 3E). We took advantage of the fine calibration of antigen concentration shown above (Figure 2E; STAR Methods) to conclude that B cells are able to gather up to 75 antigens/μm² on droplets in 15 min (plateau, Figure 3E) functionalized with initially 50 antigens/μm² (Antigen^low) (time zero, Figure 3E). We thus named the two types of functionalization—favoring and hindering antigen gathering—cluster⁺ and cluster⁻_, respectively. We will further inquire whether antigen accumulation is an important feature impacting the polarization of B cells.

Figure 3.

B cells actively gather antigens at the synapse

(A) Time-lapse images of the antigen aggregation in a bulk-functionalized droplet-cell contact. All droplets are functionalized with 50 F(ab’)₂ fragments/μm² on average. Scale bar, 10 μm.

(B) Time-lapse images of the antigen aggregation (not occurring) in a surface-functionalized droplet-cell contact. Droplets are functionalized with 100 F(ab’)₂ fragments/μm². Scale bar, 10 μm.

(C) Time-lapse images of the antigen aggregation in a BSA bulk-functionalized droplet-cell contact. Droplets are functionalized with 100 BSA/μm². Scale bar, 10 μm.

(D) Scheme of antigen accumulation analysis. The antigen recruitment index (I_antigen) is defined as the ratio of the intensity at the time zero (I_min) and the intensity over time (I_max), both at the synapse area.

(E) I_antigen time evolution for three different conditions. Only bulk-functionalized antigen-coated droplets show antigen recruitment (left, N = 18 cells), while neither bulk-functionalized BSA-coated (right, N = 27 cells) nor surface-functionalized antigen-coated droplets (center, N = 34 cells) show antigen accumulation. For the bulk-functionalized antigen-coated droplets, the kinetic of antigen accumulation follows $y=\left(p-1\right)\left(1-\exp \left(-t/\tau \right)\right)+1$, where $\tau$ = 5.07 ± 0.14 s. The related plateau p = 1.50 ± 0.06 allows to calculate the number of antigens aggregated at the synapse by the cell: droplets are initially coated with 50 antigens/μm² and cells cluster up to 1.5 $\times$ 50 = 75 antigens/μm². Green solid curves represent average values of all cells at each time point, and shaded surrounded curves the related 95% confidence interval.

Video S1. Active recruitment of antigen at the B cell (IIA1.6) synapse in contact with an F(ab’)²-coated bulk-functionalized stiff droplet, related to Figure 3

40× objective, epifluorescence microscope, LysoTracker DND staining. Time interval, 50 s.

B cells exhibit different polarization responses after being activated

As a proxy for cell polarization, we followed lysosomes distribution in time—as it has been already intensively studied as a polarization readout^12,13,16,42—by imaging them using an acidic compartment dye (Lysotracker) over 40 min. This method is fast, reliable, and does not interfere with organelles and cytoskeleton dynamics.¹³ We observe three distinct behaviors for B cells even in contact with the same droplet type (Figure 4A): within 40 min from the contact, lysosomes either stay uniformly distributed in the cytoplasm (no polarization), move toward the synapse area (polarization, Video S2), or accumulate in the side opposite to the synapse (anti-polarization, Video S3). We quantified the asymmetry in lysosomes distribution (polarity) by defining a polarization index I_pol as the ratio between the fluorescence signals in the half cell close and opposite to the droplet, as sketched in Figure 4B.

Figure 4.

B cells exhibit different polarization responses after being activated, and the onset of polarity is determined by stiffness and local concentration at the synapse

(A) Representative time-lapse imaging of the three cell behaviors: non-polarizing (top, droplet: 4 kPa—cluster⁻—100 antigens/μm², I_pol = 0.92), polarizing (center, droplet: 29.8 kPa—cluster⁺—50 antigens/μm², I_pol = 1.21), and anti-polarizing (bottom, droplet: 29.8 kPa—cluster⁻—100 antigens/μm²—I_pol = 0.34) cells. Scale bar, 10 μm.

(B) Schematic representation of the polarization analysis and quantification: the polarization index (I_pol) is the ratio between the fluorescence intensity integrated over the front part, in contact with the droplet, and the fluorescence intensity integrated over the back of the cell. The ratio is normalized by its value at time zero.

(C) Distribution of the I_pol, p values are computed by pairwise Kolmogorov-Smirnov test—when not written, the pair is not significantly different. I_pol is the value for which the polarization behavior is sustained, i.e., at 40 min. Dotted lines represent the mean ± 2σ (standard deviation).

(D) Percentages of the three cell behaviors depending on the droplet types, error bars are computed as half SD of the percentage obtained by random subsampling 1,000 groups of 15 values (typical size of the experimental pool in one day). Stiffness^low, Stiffness^medium, and Stiffness^high in the text, denotes quantitative stiffness of, respectively, 4.0, 11.7, and 29.8 kPa. Antigen concentration relative to 100 and 50 antigens/μm² denotes, respectively, Antigen^high and Antigen^low. Respective number of analyzed cells from left (pink plot) to right (gray plot): N = 50, N = 39, N = 53, N = 85, N = 56, N = 34, from at least three independent experiments. #p < 0.0001, ∗∗∗p < 0.001, ∗∗p < 0.01, ∗p < 0.05.

Video S2. Polarized B cell IIA1.6 in contact with an F(ab’)²-coated surface-functionalized stiff droplet, related to Figures 4 and 5

40x objective, epifluorescence microscope, LysoTracker DND staining. Time frame, 50 s.

Video S3. Anti-polarized B cell IIA1.6 in contact with an F(ab’)²-coated surface-functionalized stiff droplet, related to Figures 4 and 5

40× objective, epifluorescence microscope, LysoTracker DND staining. Time frame, 50 s.

We investigated the impact of antigen enrichment, antigen concentration, and droplet stiffness on lysosome polarization. We compared the cellular responses upon interaction with five different droplets: Stiffness^low (γ = 1.7 mN/m), Stiffness^medium (γ = 4.7 mN/m) or Stiffness^high (γ = 12 mN/m), covered with 50 (Antigen^low) or 100 (Antigen^high) antigens/μm², with bulk-functionalized (cluster⁺) or surface-functionalized (cluster⁻) droplets (Figures 4C and 4D). The panel of activating droplets allows us to investigate the effect on polarization of different stiffness (at constant antigen concentration) and different antigen coating conditions (at constant stiffness).

To establish the value of I_pol for which we consider a cell to be polarized or not, we observe the I_pol distribution for cells in contact with the non-activating droplet (BSA-coated, gray plot, Figure 4C). As spontaneous polarization has been reported,⁴³ we considered 2σ of the I_pol distribution for BSA-coated droplets as a threshold. This results in classifying the cells with I_pol ≥ 1 + 2σ = 1.18 as polarized. Symmetrically, we defined cells with I_pol < 1−2σ = 0.82 as anti-polarized and, consequently, 0.82 ≤ I_pol < 1.18 for non-polarized cells (Figure 4C). Furthermore, to check that the polarization occurs specifically upon BCR engagement, we performed two major controls: (1) we excluded an impact of the flow by checking that no cell polarized in absence of interaction at maximal flow of 1.6 mm/s (control no. 1, Figure S3G); (2) we excluded an activation from potential soluble antigens coming from the droplet functionalization by observing no polarized cells among the non-interacting ones in the presence of antigen-coated droplets in nearby traps (control no. 2, Figure S3H). Altogether, these results show that B cells polarize only when they form a specific contact with antigen-coated droplets, suggesting that polarization is triggered by specific BCR engagement in our system, and that flow conditions do not alter polarization in our experiments.

Figure 4C shows the polarity index distributions of the global cell populations for each droplet condition. For more accurate analysis in each cell population, we classified the cells into the three categories of phenotypes described above (Figure 4D).

B cell polarization onset depends on antigen concentration and droplet stiffness

We first studied the mechanosensitivity of the polarization process by changing the surface tension of the droplets, hence their effective stiffness. For soft droplets, cells behave essentially as the negative control, although anti-polarized cell number increases. However, increasing stiffness from 4 to 11.7 kPa induces a greater number of polarized cells and with much higher indexes, corresponding to an increased lysosome concentration in the synaptic area. Polarity index distributions do not significantly change between Stiffness^medium (4 kPa) and Stiffness^high ($\approx$ 12 kPa). These results show that polarization is a mechanosensitive process and that the threshold of effective stiffness triggering the polarization is between 4 and 12 kPa. Of note, antigen concentration does not depend on droplet stiffness (Figure S4).

The major difference between bulk and surface functionalized droplets, antigen gathering, is related to the different fluidity of the surfaces, as we showed by FRAP experiments (see STAR Methods; Figure S4). Of note, surface tension does not depend on functionalization method (Figure S4). We characterized, therefore, the effects of both antigen concentration and gathering on B cell polarization, by using droplets of similar stiffness (high). Surprisingly, despite not showing antigen accumulation (Figure 3B), cluster⁻ droplets stimulate rather well B cell polarization regardless of antigen concentration. Remarkably, cluster⁺/Antigen^low droplets, inducing antigen enrichment, are able to generate the same amount of polarized cells (52%) as cluster⁻/Antigen^high (55%) conditions, which initially bear twice as many antigens (respectively, 50 and 100 antigens/μm²). However, even in polarized cells, polarity indexes are lower in cluster⁺ cells, suggesting that a higher local concentration of antigen stimulates stronger lysosome polarization. In addition, on cluster⁻ droplets, when antigen concentration is halved, the percentage of polarized cells decreases from 55% to 35% (Figure 4D). These results show that, by increasing local concentration at the synapse, antigen accumulation overcomes the lack of initial presented antigens and lowers the threshold to established polarity when the density of presented antigens is below 75 antigens/μm².

A recapitulation of all conditions and outcome of polarization is shown in Table 1. Figure 4D shows that the population of anti-polarized cells does not change with stiffness for cluster⁻ droplets coated with a high concentration of ligands, suggesting that, for such interfacial conditions, anti-polarization does not depend on the mechanics of the lipid droplet. Considering the set of stiff droplets with contrasting interfacial properties, our results show that cluster⁺ droplets with a low ligand level share a similar anti-polarization value than cluster⁺ droplets with a high ligand level. On the contrary to the polarization measurement, anti-polarization fully disappears for cluster⁻ droplets coated with a low amount of antigens. Although origin of such a discrepancy remains elusive, these results suggest that polarization and anti-polarization behaviors come from two distinct mechanisms.

Table 1.

Recapitulation of droplet conditions, properties, and outcomes

Droplet condition	Oil phase	Surf tension (mN/m) [pendant drop]	Stiffness (kPa)	Functionalization type	Observed antigen enrichment	Antigen concentration	Droplet size (mean $\pm$ SD) (μm)	Polarization	No polarization		Anti-polarization
(i)	mineral oil oleic acid 5% v/v	1.7	4.0	surface	no	100	11.06 $\pm$ 0.88	+		+++	+
(ii)	mineral oil	4.7	11.7	surface	no	100	10.04 $\pm$ 1.92	+++		+	++
(iii)	soybean oil	12	29.8	surface	no	100	11.0 $\pm$ 0.7	+++		+	++
(iv)	soybean oil	12	29.8	surface	no	50	11.0 $\pm$ 0.7	+		++	+
(v)	soybean oil	12	29.8	bulk	yes	50	11.30 $\pm$ 2.88	++		+	++
Control, BSA	soybean oil	12	29.8	bulk	no	–	11.30 $\pm$ 2.88	–		+++	–

The polarization kinetic is affected by droplet mechanical properties

We then assessed the impact of droplet properties on the B cell polarization dynamics by measuring the evolution of the polarization index I_pol over time (Figures 5A–5C and S5). The kinetics of polarization (anti-polarization) events shows increasing (decreasing) curves that reach a steady state about 15 min after the droplet-cell encounter. Lysosome polarity depends on microtubule network orientation and organelle motility on this network. One single parameter cannot capture this complex kinetics. We chose the model that appears to us by visual inspection of the kinetic curves: an exponential relaxation of the form $1-\exp (-t/\tau )$ (or for anti-polarizing cells $\exp (-t/\tau )$. By contrast, curves related to no polarization show no evolution over 40 min and are centered around I_pol = 1.

Figure 5.

B cell polarization kinetics depends on the mechanical properties of the droplets

(A–C) Kinetics of polarization in the three types of behavior for the (A) non-polarized Stiffness^low/cluster⁻/Antigen^high condition (N = 28 cells), polarized Stiffness^medium/cluster⁻/Antigen^high condition (N = 16), and anti-polarized Stiffness^high/cluster⁻/Antigen^high condition (N = 13) cells (from at least three independent experiments). Fitting curves of I_pol (black solid curves) for polarized cells and anti-polarized cells, respectively, follow $y_{pol}=\left(p-1\right)(1-\exp \left(-t/\tau \right))+1$ and $y_{antipol}=(1-p)(1-\exp (-t/\tau ))+1$ (with $\tau$ characteristic times of polarization/anti-polarization kinetics; p, parameter that controls the plateau). Red shaded curves represent the average values of dynamics at each time point and their 95% confidence interval.

(D and E) (D) Characteristic times of polarization and (E) anti-polarization kinetics (column: median ± interquartile range, whiskers represent 5th–95th percentile; statistical test: Mann-Whitney test). Stiffness^low, Stiffness^medium, and Stiffness^high denotes quantitative stiffness of, respectively, 4.0, 11.7, and 29.8 kPa. Antigen concentration relative to 100 and 50 antigens/μm² denotes, respectively, Antigen^high and Antigen^low. ∗p < 0.05; n.s., not significant.

From the plateauing exponential curves of polarization and anti-polarization events (Figures 5B and 5C), one can extract the characteristic times $\tau$ of the respective kinetics (Figures 5D and 5E). This time is inversely related to the rate of polarization, i.e., larger values of $\tau$ indicate slower kinetics. Figure 5D shows similar characteristic times for cluster⁻/Antigen^low and cluster⁻/Antigen^high droplets, meaning that, independently of the antigen concentration, once the polarization is triggered, it reaches a plateau within 15 min (mean value). This suggests that polarization kinetics do not depend on the initial antigen concentration, as long as these conditions are sufficient to initiate polarization. By contrast, characteristic times are significantly different for stiffer versus softer droplets, suggesting that stiffness affects the polarization dynamics: B cells polarize faster in the case for a stiffness of about 12 than 30 kPa. Noteworthy, polarization is faster when droplets allow accumulation of antigens at the synapse (at equal conditions, see Stiffness^high/cluster⁺/Antigen^low versus Stiffness^high/cluster⁻/Antigen^high). Although the differences in some cases are not significant (most likely due to low statistics of anti-polarization cell subpopulations), a similar tendency is found in anti-polarizing behavior.

Altogether, these results reveal that B cells are dynamically mechanosensitive, as they are able to discriminate stiffness changes, and significantly adjust the polarization rate according to the apparent stiffness of the substrates they face. Also, accumulating antigens at the synapse allow cells to polarize as fast as on softer (Stiffness^medium) substrates. Therefore, the local antigen concentration is an important feature to induce an efficient polarization, suggesting a synergistic role of low stiffness and antigen mobility in accelerating lysosome polarization.

Discussion

In this work we introduced lipid-coated droplets as a material to activate B cell. We characterized the physical and chemical properties of functionalized droplets and studied their effect on lysosome polarization in B cells. We could prove that these objects are able to activate B cells and that the onset of polarization is sensitive to ligand concentration and apparent droplet stiffness. This is consistent with previous observations showing that lysosome polarization, necessary for protease secretion, antigen degradation, and extraction,¹³ occurs predominantly on non-deformable/stiff substrates, where mechanical internalization is not possible.¹⁶ We could not access whether there is antigen internalization from the droplets. However, in a recent study we showed that there is, at least on stiff droplets, exocyst enrichment at the synapse, a signature of proteases release.⁴⁴ Future efforts will be directed to make droplets where mechanical extraction is possible.

We showed that B cells polarize only when they interact with substrates presenting a surface tension greater than 4.7 mN/m (corresponding to an apparent stiffness of 11.7 kPa). This is consistent with observations on macrophages and follicular dendritic cells.¹⁶ Of note, the stiffest (11.7 and 29.8 kPa) and softest (4.0 kPa) droplets induce responses similar to, respectively, follicular dendritic cells and dendritic cells.¹⁶ We propose that this is linked to the BCR mechanosensitivity. Indeed, the BCR signal is known to depend on the substrate stiffness⁸ and the signal downstream of the BCR to induce the accumulation of polarity cues.^2,12,17 These polarity cues establish the pole by anchoring the centrosome,⁴⁵ reorienting the microtubule-based traffic toward the synapse: the stronger the signal, the stronger the establishment of polarity cues, the higher the probability of polarizing. Unexpectedly, we also found that the kinetic of polarization is sensitive to the model APC stiffness. Mechanosensitivity of dynamical properties has been shown in adhesive cells: actin flows increase with the rigidity of the substrate,⁴⁶ cells adjust their contractility in real time to the stiffness change of the substrate,⁴⁷ and T cells adapt their pulling force at the synapse to the stiffness of the interacting object.^48,49 One explanation for the dependency of polarization kinetics on the mechanics of the substrate could be that the increase in stiffness downstream of the BCR activation (see, e.g., Merino-Cortés et al.⁵⁰) hinders the displacement of the centrosome and hence the polarization of lysosomes, effectively lowering the polarization rate on the stiffest substrates. Although we have no direct readout of the signal, it is interesting to compare these results with recently published data on cytotoxic granules release in CD8⁺ T cells³: in this case the stronger the signal, the higher the frequency of polarizing cells. However, the kinetics of polarization does not seem to be influenced by the strength of the signal. Future investigations on the relation between signal, rheological changes, and polarization following BCR activation will better highlight differences and analogies between the two lymphocytes.

We quantified the statistics of cell polarization when they were able to accumulate antigens at the contact zone or not, and to interact with 50–100 antigens/μm². Our results showed that the maximal amount of polarized cells is reached for $\sim$ 75 antigens/μm², suggesting that above this density, antigen concentration has no effect on the polarization process. This value is compatible with the maximal density of BCRs available in an activated synapse. (This number comes from an estimation that considers: 20,000 receptors [IgM in primary cells]⁵¹ squeezed in a synaptic region of radius $\sim$ 7 μm: 20,000/ $\mathrm{\pi }{7}^2\approx 130$ mol/μm² interacting with bivalent ligands.) In addition, previous work reported that antigen concentrations from 15 to 150 antigens/μm² modulate the B cell activation with a threshold that depends on the affinity.¹⁰ Although we cannot quantitatively compare these results to ours (different antigens and presentation assays), this suggests that the concentration threshold for polarization might also depend on the antigen affinity. Further experiments will better elucidate the link between early signaling, lysosome polarization, and antigen affinity. Other works have shown that B cells interacting with mobile ligands displayed significantly greater signaling because of the formation, the accumulation, and the merging of BCR microclusters.^11,42,52 We herein show that lysosomes polarize independently of the ability to form a central antigen cluster. We showed, however, that “mobility,” allowing the local increase of antigen concentration at the synapse, helps B cells overcome the low initial antigen concentration (below 75 antigens/μm²), increases the chance for a cell to polarize and its polarization rate. This suggests that local antigen concentration at the synapse is a crucial feature for inducing polarization and make it quicker.

One interesting aspect of our system is to allow stimulation of B cells using the same presentation assay, which combines a fluid (such as bilayers) and soft material (such as gels) to investigate new synergies. In addition, the droplets are a highly reproducible and well-calibrated tool in terms of chemical and mechanical properties (compared, e.g., with beads or gels), which makes them adapted to study cell-to-cell variability. This has allowed us to show that, in clonal B cell lines, not all cells polarize their lysosome toward the synapse, but some even displace them in the opposite side of the synapse (anti-polarize). In T lymphocytes, a transient anti-polarization of actin and myosin has been observed in the early stage of the T cell/APC contact, and does not depend on antigen recognition.⁵³ By contrast, B cell anti-polarization is stable (over 40 min), BCR specific, and is only triggered above 75 antigens/μm². Interestingly, the stiffness does not influence the onset of anti-polarization. Like the polarization process, antigen mobility and concentration does not affect the anti-polarization kinetics, but stiffness does. Of note, we observed that anti-polarized cells are more elongated and considerably less round than the polarizing or non-responsive ones. Similar events have been described in frustrated T cell-APC conjugates,⁵⁴ where the centrosome is blocked behind the nucleus while membranes accumulate at the synapse, which ultimately deforms the cell. Alternatively, the anti-synapse might represent a signaling complex in its own right as already described in T cells.⁵³ Further comparison of the proteins implicated in the proximal and distal poles, both during the polarization and the anti-polarization formation, would elucidate this latter suggestion.

Compared with existent antigen-presenting surfaces, our method allows us to modify fluidity, concentration, and stiffness on the same material. While we achieved similar results as on bilayers (for concentration/fluidity) and rigidity threshold for activation, we will investigate more thoroughly (e.g., looking at signal magnitude) the interplay between the different properties in future work. Our method allowed us to precisely phenotype lysosome polarization dynamics. This may be combined with classic (genetic or pharmacological) perturbations to dissect single-cell polarization mechanisms in real time and further understand the biological significance and functions of the phenotypes we described. We anticipate that this approach will be of interest in many other contexts, where cell-cell variability is important for the immune function, such as T cell immune synapses,⁵⁵ cytotoxic cell encounter,^56,57 and phagocytosis.^23,58

Limitations of the study

Despite the flexibility offered by the system, there are some limitations. First, the microfluidic chip requires to be adapted to the cell size (e.g., primary cells would need smaller traps and more shallow channels, see Pineau et al.⁴⁴) and this might require some setting at the moment of injection. Second, some combination of rigidity and fluidity cannot be achieved, for practical reasons: for example, with the oil we used it was not possible to obtain surface functionalized ultrasoft (<4 kPa) droplets of a radius comparable with the cellular one, as they become unstable. Finally, imaging with high temporal and spatial resolution is limited by the field of view and the acquisition time of the microscope: if one wants to capture dynamic events with a resolution of few tens of seconds and a spatial resolution of less than a micron, even with an efficient filling of traps, it is difficult to capture more than ten different positions, hence to increase of an order of magnitude the number of cell simultaneously acquired. However, this aspect could be improved in the future using large-field confocal microscopes and multi-layer chips.

STAR★Methods

Key resources table

REAGENT or RESOURCE	SOURCE	IDENTIFIER
Antibodies
Alexa Fluor® 647 Donkey anti-Goat IgG (H + L) Cross-Adsorbed Secondary Antibody	Invitrogen	Cat# A-21447, RRID: AB_2535864
Alexa Fluor® 647 Mouse IgG1, κ Iso-type Ctrl (ICFC) Antibody	Biolegend	Cat# 400135, RRID: AB_2832978
AffiniPure F(ab’)2 Fragment Goat Anti-Mouse IgG, F(ab’)2 fragment specific (min X Hu, Bov, Hrs Sr Prot)	Jackson ImmunoResearch	Cat# 115-066-072, RRID: AB_2338583
Chemicals, peptides, and recombinant proteins
Pluronic F-68 (Poloxamer 188)	Sigma Aldrich	Cat# 9003-11-6
Sodium alginate	Sigma Aldrich	Cat# 9005-38-3
Tween 20 (polyethylene glycol sorbitan monolaurate)	Sigma Aldrich	Cat# 9005-64-5
Oleic acid	Sigma Aldrich	Cat# 112-80-1, ref. O1008
Silicone oil (viscosity 350 cSt at 25°C)	Sigma Aldrich	Cat# 63148-62-9
Mineral oil	Sigma Aldrich	Cat# 8042-47-5
DSPE-PEG(2000)-Biotin	Avanti Polar Lipids	Cat# 880129
FluoProbes 488 streptavidin	Interchim	Cat# FP-BA2221
Lipiodol ®	Guerbet LLC (kindly provided)	Cat# 8002-46-8
RPMI 1640 Medium GlutaMAX™ Supplement	Life Technologies - Gibco	Cat# 61870036
Fetal calf serum	Life Technologies - Gibco	Cat# 16140063
Penicillin-Streptomycin,	Life Technologies - Gibco	Cat# 15070063
Sodium pyruvate	Life Technologies - Gibco	Cat# 11360070
2-Mercaptoethanol	Life Technologies - Gibco	Cat# 31350010
HEPES (4- (2-hydroxyethyl) - 1- piperazineethanesulfonic acid)	Life Technologies - Gibco	Cat# 15630080
LysoTracker™ Red DND-99	Life Technologies | Thermo Fisher Scientific (Invitrogen)	Cat# L7528
Trichloro (1,1,2H,2H-perfluorooctyl) silane	Merck-Sigma-Aldrich	Cat# 102488-49-3
PDMS (polydimethil-syloxane) RTV 615	Momentive Performance	Cat# 3227415
Polyvinylpyrrolidone (PVP, K90)	Merck-Sigma Aldrich	Cat# 81440
Deposited data
Raw data	Zenodo	https://doi.org/10.5281/zenodo.7182828
Experimental models: Cell lines
B cell lines IIA.1.6 (ATCC ♯: TIB-208], listed in Cellosaurus as A20.IIA CVCL_0J27)	Provided by Lennon’s Team	D. Lankar et al.30
Software and algorithms
ImageJ/Fiji ver. 1.52i	Schindelin et al.59	https://imagej.nih.gov/ij/
R (RStudio) ver. 1.0.153		https://www.r-project.org/
COMSOL Multiphysics 5.3	COMSOL
Prism GraphPad 8	GraphPad Software
ImageJ macros, R codes	Zenodo	https://doi.org/10.5281/zenodo.7194171
Other
Microfluidic mask layout designs (DXF)	Zenodo	https://doi.org/10.5281/zenodo.7194171

Resource availability

Lead contact

Further information and requests for resources and reagents should be directed to and will be fulfilled by the lead contact, jacques.fattaccioli@ens.psl.eu.

Materials availability

The oil droplets generated in these paper cannot be easily shared, but can be reproduced following the described protocol. Further practical suggestions can be asked to the Lead Contact.

Experimental model and subject details

Cell culture

Mouse IgG+ B-lymphoma cell lines IIA1.6,³⁰ derived from A20 cell lines (ATTC# TIB-208), were cultured at 37°C in a 5% CO2 atmosphere in CLICK medium (RPMI 1640 Medium GlutaMAX Supplement; supplemented with 10%v/v decomplemented fetal calf serum; 1%v/v antibiotic Penicillin-Streptomycin; 2%v/v sodium pyruvate at 100 mM; and 0.1%v/v 2-Mercaptoethanol at 50 mM) as previously described.¹³ The cell line was confirmed to be free of mycoplasma contamination. Experiments were performed with cell densities close to 10⁶ cells/mL, which were diluted to ca. 200,000 cells/mL and split in 10 samples of 1 mL, inserted in a 12-well plate (Falcon, ref. 353,043). For each experiment, a 1 mL cell sample and 25 $\mu$ L of HEPES (4- (2-hydroxyethyl) - 1- piperazineethanesulfonic acid) were put in a 1.8 mL tube compatible with the pressure controller (Fluigent, France). In the meantime, other samples remained incubated at 37°C, 5% of CO2 for a maximum of 4h.

Method details

Cell staining

Lysosomes were stained by loading the cells with LysoTracker Red DND-99 (1 mM) at a final concentration of 50 nM, into CLICK Medium, 37°C, 5% CO₂ for 30 min. The cell concentration is about 0.5 M cells/mL.

Bulk droplet functionalization protocol with phospholipids

The lipid-containing oil was obtained by dilution of DSPE-PEG₂₀₀₀-Biotin phospholipids in soybean oil at 0.03 mg/mL, followed by 30 min of sonication and evaporation of the chloroform from the oil at room temperature. This oil was dispersed and emulsified by hand in an aqueous continuous phase containing 15% w/w of Pluronic F68 block polymer surfactant and 1% w/w sodium alginate at a final oil fraction equal to 75% w/w. The rough emulsion was then sheared in a Couette cell apparatus at a controlled shear rate following the method developed by Mason et al.⁶⁰ to narrow the droplet size distribution to 12.4 $\mu$ m $\pm$ 2.3 $\mu$ m (Table 1). For storage, emulsions are diluted to an oil fraction of 60 wt % with 1 wt % Pluronic F68 in the continuous phase and stored at 12°C in a Peltier storage cupboard for several weeks.

Surface Droplet functionalization protocol with phospholipids

Droplets were formulated using a Shirasu Porous Glass apparatus (SPG Technology Co., Japan) by extruding the oil phase (with or without 5%v/v of oleic acid) through a ceramic membrane (with pores of 3.1 $\mu$ m, SPG Technology Co., Ltd) within an aqueous solution containing 15%v/v of Pluronic F68, continuously and vigorously stirred. We obtained droplets measuring 10.98 $\pm$ 0.68 $\mu$ m in diameter. Once stabilized, droplets were washed out 3 times with an aqueous solution of Tween 20 at CMC (0.0007% w/v). The supernatant was removed and replenished after each centrifugation step (30 s at 2000 RPM). The suspension is centrifuged and rinsed four times with phosphate buffer (PB)/Tween 20 to decrease the amount of Pluronic F68 in the continuous phase. After the last rinsing step, most of the continuous phase is removed from the microtube to decrease the total volume of emulsion to 10 $\mu$ L. We then add 10%v/v of the DMSO stock solvent solution containing the phospholipids. We then add a phosphate buffer supplemented with Tween 20 at the CMC (PB - Tween 20) to reach a total volume of 200 $\mu$ L of suspension. Droplets are incubated for 30 min at room temperature in the presence of lipids in the bulk phase and finally rinsed several times with a PB - Tween 20 buffer to remove the phospholipids in excess. The quantity of phospholipids available in the bulk phase at the initial stage is adjusted by diluting the stock solutions in DMSO so that the volume fraction of co-solvent remains constant for all experimental conditions. For a given working volume (200 $\mu$ L), the lipid concentration in the bulk phase is expressed as a droplet surface area equivalent. One equivalent (eq.) corresponds to the number of molecules required to cover the total area of a droplet sample with a compact monolayer.³³

Coating of biotinylated droplets with streptavidin and F(ab’)₂ fragments

After the first step of emulsification and insertion of biotinylated lipids at the interface, 1 equiv of streptavidin solution at 1 mg/mL was added, followed by an incubation time of 30 min and a washing step to remove all excess streptavidin. Finally, 1 equiv of F(ab’)₂ fragments (1 mg/mL) or BSA (1 mg/mL) was added to the droplet solution, followed by an incubation time of 30 min and a washing step to remove all excess F(ab’)₂ or hemmi. One equivalent (1 equiv) of a given macromolecule (lipid or protein) corresponds to the theoretical number of molecules needed to cover the entire surface with a monolayer of molecules or proteins, considering the available surface of droplet and molecule dimensions as previously reported in.³³

Titration of antigen concentration on droplet surface

We first titrate streptavidin attachment by measuring the adsorption isotherm onto the phospholipid-coated droplet surface. The bulk concentration of streptavidin is expressed in molar equivalents, i.e., the theoretical amount of proteins necessary to cover the droplet sample with a close-packed monolayer as described in.³³ For instance, 1 equiv of streptavidin for 10 million of 11 $\mu$ m-large droplets corresponds to 4 × 10⁻¹⁰ mol of proteins (see table of equivalents below).

Table depicting the equivalent and the volume required to coat 2 millions of 12 $\mu$ m-large droplets, via surface functionalization method.

Functionalization	Equivalent	Conc.(mg/mL)	Volume ($\mu$ L)
DSPE-PEG(2000)-Biotin	100	10	3.60
Streptavidin	1	1	5.43
Biotinylated F(ab’)2	1	1.4	0.98
Secondary Antibody	1	0.8	2.35

The fluorescence of the droplets is characterized by epifluorescence microscopy, following the method detailed in Pinon et al.³³ The streptavidin adsorption isotherm fits with a Langmuir isotherm with a K_Strep, the streptavidin concentration producing half occupation, equal to 9.7 $\pm$ 4.7 equiv⁻¹ compatible with our previous analyses (Figure 1D).³³

For a bulk concentration of streptavidin corresponding to a maximal surface coverage (1 equiv), we measured the adsorption isotherm of antigens (F(ab’)₂) using fluorescent secondary antibodies and epifluorescence microscopy for the quantitative fluorescence measurements of the total amount of proteins attached to droplets. Figure 1E shows that the antigen adsorption isotherm fits with a Langmuir isotherm with a K_Ag = 1.74 $\pm$ 0.74 equiv⁻¹. We finally converted the streptavidin fluorescence intensity value in a molecular equivalent of proteins using fluorescence calibration beads, and knowing the average number of dyes attached per streptavidin (and therefore per F(ab’)₂).).

The fitting curves of titrations used in Figure 2 follow Langmuir isotherms, hence the fluorescence intensity varies in time as

$$I\left(C\right)=I_{Max}\frac{KC}{1+KC}$$ (Equation 1)

where $C$ is the bulk concentration of the molecule of interest, $K$ the affinity constant and $I_{Max}$ the fluorescence intensity at large $C$.

Molecules of equivalent soluble fluorophore (MESF) is converted to antigen surface concentration as follows:

$${\rho }_{Ag}={\text{N}}_{Ag}/{\text{S}}_{droplet}=\frac{\text{MESF}}{{\text{N}}_f\frac{{\text{S}}_{Strep}}{{\text{S}}_{Ag}}·{\text{S}}_{droplet}}$$ (Equation 2)

where S_Strep and S_Ag, are the respective geometric area of a streptavidin molecule⁶¹ and of an F(ab’)₂ fragment,⁶² S_droplet is the droplet surface, and N_f is the number of fluorophores per streptavidin (as streptavidin is tetravalent, and one bond is occupied by the lipid biotin, we considered N_f = 3).

Measurement of the adsorption isotherms of the surface-functionalized droplets

To quantify the amount of antigens presented by droplets, we first titrated the antigens (from 0.05 to 5 equiv) bound to streptavidin molecules (1 equiv) and biotinylated DSPE-PEG₂₀₀₀ lipids (100 equiv). We revealed the antigens coating with a Donkey anti-Goat IgG (H + L) Cross-Adsorbed Secondary Antibody (Alexa Fluor 647, Invitrogen, ref. A-21447) and analyzed the fluorescence intensity. In our case, the droplets are saturated for 4 equiv of F(ab’)₂ fragments. We then converted this relative concentration into absolute value by comparing fluorescence intensity of droplets and commercial tagged beads (Quantum MESF, Bang Laboratories, Inc.). We assessed the related fluorescence intensities of droplets coated with a concentration of streptavidin ranging from 0 to 2 equiv and saturated in biotinylated DSPE-PEG₂₀₀₀ lipids (100 equiv). These values are added on a calibration curve correlating the molecular equivalent surface fluorescence (MESF) of beads (Quantum MESF, Bang Laboratories, Inc.) with their fluorescence intensities (Figure S2). Finally, we converted the droplet MESF into absolute values of F(ab’)₂ fragments in antigens per $\mu$ m² (Figure 2D) depending on different droplet and protein features. We obtained that droplets present from 0 to 150 antigens/ $\mu$ m² when they are functionalized with DSPE-PEG₂₀₀₀-Biotin (100 equiv), streptavidin from 0 to 2 equiv and F(ab’)₂ fragments (4 equiv). For the rest of the experiment, we use droplets coated with 50 and 100 antigens/ $\mu$ m². Fluorescence measurements in Figure S4 have been performed using Alexa Fluor 647 Mouse IgG1, $\kappa$ Iso-type Ctrl (ICFC) Antibody, Biolegend 400,135, at a concentration of 0.5 equiv.

Measurement of oil/water interfacial tension by the pendant drop technique

The pendant drop technique consists in inferring the interfacial tension from the shape profile of a pendant drop of one liquid in another at mechanical equilibrium (see Figures S3A and S3B). We used a pending drop apparatus (drop shape analyzer, Krüss, PSA30) to measure the interfacial tension of the various oils considered in this study - mineral oil, mineral oil supplemented with 5%v/v of oleic acid, soybean oil, lipiodol and lipiodol supplemented with 5%v/v of oleic acid - versus an aqueous solution composed of 15%w/w Pluronic 68. The interfacial tensions reported below correspond to the equilibrium value reached when the drop surface has been entirely covered by surfactants coming from the continuous phase.

Interfacial tension of oil/aqueous phases via pendant drop technique.

Oil phase	Water Phase	Surface tension (mN/m)
Mineral oil + Oleic acid 5%v/v	F68 15%	1.69 $\pm$ 0.19
Mineral oil	F68 15%	4.73 $\pm$ 0.38
Soybean oil	F68 15%	12.03 $\pm$ 0.52
Lipiodol oil	F68 15%	1.52 $\pm$ 0.12
Lipiodol oil + Oleic acid 5%v/v	F68 15%	0.88 $\pm$ 0.12

Measurement of droplets interfacial tension by the micropipette technique

The micropipette-aspiration method that has been described in detail in a previous article.³⁸ Micropipettes were made from 1 mm borosilicate glass-tube capillaries (Harvard Apparatus, USA) that were pulled in a pipette heater and puller (P-2000, Sutter instrument Co., USA) to tip diameters in the range of 3–5 $\mu$ m. A 3 axis-micromanipulator (Narishige) allowed for pipette positioning and manipulation. The pipette was connected to a pressure controller (Fluigent) to apply precise negative pressures. A solution of sinking droplets, made with lipiodol oil coated or not with phospholipids, was inserted into a glass/coverslip chamber. The pipette aspired the droplet until reaching an equilibrium where the elongation part is equal to the pipette inner dimension. The interfacial tension $\mathrm{\gamma }$ is $\mathrm{\gamma }=\Delta \text{P}·\left({\text{R}}_p/2\right)$ where $\Delta$ P is the negative pressure and R_p the micropipette radius. Upon aspiration by the very thin glass pipette, the droplet deforms and a spherical cap of radius R_c forms at the tip of the pipette. At equilibrium, the value of R_c depends on the interfacial tension $\mathrm{\gamma }$ of the droplets, the radius of the droplet R_D, the aspiration pressure $\Delta$ P and can be expressed as:

$$\frac{1}{{\text{R}}_C}=\frac{\Delta \text{P}}{2\mathrm{\gamma }}+\frac{1}{{\text{R}}_D}$$ (Equation 3)

The aspiration $\Delta$ P corresponds to the pressure difference between the inside of the pipette and the external pressure. $\mathrm{\gamma }$ and $R_p$ are constant throughout the experiment. Hence, varying $\Delta$ P induces changes in R_c: the larger $\Delta$ P, the smaller $R_c$. During measurements, $\Delta$ P is slowly increased and R_c decreases until reaching the radius of the pipette R_p. Up to that critical aspiration $\Delta$ P_c, little change is observed in the geometry of the system. As soon as $\Delta$ P becomes greater than $\Delta$ P_c, R_c becomes smaller than R_p, which results in the sudden entry of the oil droplet in the pipette. This provides a direct measurement of the surface tension of the droplet:

$$\mathrm{\gamma }=\frac{\Delta {\text{P}}_c}{2\left(\frac{1}{{\text{R}}_D}-\frac{1}{{\text{R}}_p}\right)}$$ (Equation 4)

The interfacial tensions reported below have been measured via micropipette on phospholipid-fonctionalized and non-functionalized droplets. Droplets are stabilized by F68 and bath into an aqueous phase made of phosphate buffer/Tween 20 at CMC.

Interfacial tension of oil/aqueous phases via micropipette technique. Measurements have been performed on droplets stabilized by Pluronic F68 and surrounded by an aqueous phase (Phosphaste buffer/Tween 20 at CMC). From⁶³

Oil phase	Functionalization	Surface tension $\pm$ SD (mN/m)
Lipiodol oil + Oleic acid 5%v/v	None	2.36 $\pm$ 0.31
Lipiodol oil + Oleic acid 5%v/v	DSPE-PEG-Biotin	2.50 $\pm$ 0.24
Soybean oil	DSPE-PEG-Biotin	10 $\pm$ 2∗

Measurement of droplet mechanical properties by the microplate rheology

The microplate micro-rehology experiment consists in applying a sinusoidal displacement to the base of a flexible microplate B∗(t) = B₀ $e^{i\omega t}$ and measuring the resulting amplitude T₀ and the phase shift $\phi$ of the displacement of the flexible microplate tip in contact with the droplet (see Figure 2F). The flexible plate acts as a spring of calibrated stiffness $\left(k\right)$ and the rigid plate, about 1000 times stiffer, acts as a support: the stress applied to the sample is deduced from the normal force exerted by the flexible plate: $F^{\ast }=k(B^{\ast }\left(t\right)-T^{\ast }\left(t\right))$ where $(B^{\ast }\left(t\right)-T^{\ast }\left(t\right))$ is the deflection of the flexible plate. The resulting sinusoidal deformation of the sample ${\mathrm{ϵ}}_s^{\ast }\left(t\right)$ is related to $T^{\ast }\left(t\right)$: ${\mathrm{ϵ}}_s^{\ast }\left(t\right)$ = $T^{\ast }\left(t\right)/L$ where $L$ is the mean length of the compressed sample. Indeed, when trapped between the microplates, droplets are initially compressed to a strain ${\mathrm{ϵ}}_0=(L_0-L)/L_0$ where $L_0$ is the resting droplet diameter. Then, the sample is sinusoidally deformed around this mean position to measure the complex modulus. Thus the overall strain applied to the droplet writes ${\mathrm{ϵ}}^{\ast }\left(t\right)={\mathrm{ϵ}}_0+{\mathrm{ϵ}}_s^{\ast }\left(t\right)={\mathrm{ϵ}}_0+{\mathrm{ϵ}}_s{e}^{i(\omega t+\phi )}$. We worked at ${\mathrm{ϵ}}_0=0.2$, and ${\mathrm{ϵ}}_s$ was kept below 0.05.

The droplet complex dynamic modulus G∗ is obtained from the applied oscillatory normal stress ${\sigma }^{\ast }=F^{\ast }/S$, where $S$ is the contact area, and from the sinusoidal resulting deformation ${\mathrm{ϵ}}_{s^{\ast }\left(t\right)}$: $G^{\ast }={\sigma }^{\ast }/{\mathrm{ϵ}}_{s^{\ast }\left(t\right)}$. Microplates were made from glass lamellae of 100 × 2mm with 0.1–0.3 mm thickness. The rigid plate can be either pulled out of 0.2 or 0.3 mm original thickness, but must be kept short to ensure a high stiffness. Lamellae were heated and pulled (Narishige PB-7, Japan) until breaking in two similar parts. Microplates were calibrated using a microplate of known bending stiffness as a reference. The bending stiffness of the reference microplate has been initially determined by weighing copper micro-wires at the extremity of the plate, following the protocol reported in.⁶⁴

The flexible plate was oscillated from 0.1 to 6.4Hz for droplets and until 1.6 Hz for cells. Micrometric displacements of plates are controlled via highly-resolutive piezoelectric micromanipulators (PI Gmbh). For droplet experiments, Lipiodol (Guerbet) oil (that sediment being denser than water) was used to fabricate droplets and glass microplates were coated with PLL at 0.1%v/v. For cells, only the chamber was coated with Sigmacote (Sigma-Aldrich).

Elastic and viscous moduli of oil droplets

Elastic-like behavior is characterized by proportionality between the stress $\sigma$ and strain $\mathrm{ϵ}$, typically ${\sigma }_e=E\mathrm{ϵ}$, with E the elastic modulus characteristic of the material. Viscous response is characterized by proportionality between the stress $\sigma$ and strain rate $\frac{d\mathrm{ϵ}}{dt}$, typically ${\sigma }_v=\eta .\frac{d\mathrm{ϵ}}{dt}$, with $\eta$ the viscosity of the material. When elastic and viscous stresses add up, and using complex notation to describe dynamic rheology (oscillating stress and strain at $\omega =2\pi$ f, where f is the frequency), one gets:

$${\sigma }^{\ast }=(E+\text{i}\eta \omega ){\mathrm{ϵ}}^{\ast }$$ (Equation 5)

The complex viscoelastic modulus $G^{\ast }$ is defined as:

$$G^{\ast }={\sigma }^{\ast }/{\mathrm{ϵ}}^{\ast }={\text{G}}^{\prime }+i{\text{G}}^{″}$$ (Equation 6)

Thus, one finds, for the so called Kelvin-Voigt viscoelastic model:

$${\text{G}}^{\prime }=E$$ (Equation 7)

and

$${\text{G}}^{″}=\eta \omega$$ (Equation 8)

Let us now consider an oil droplet of resting diameter $L_0$, characterized by a surface tension $\mathrm{\gamma }$ and a shear viscosity $\eta$. When uniaxially compressed between parallel microplates, it develops a restoring (elastic-like) force due to Laplace pressure $\Delta$ p = 4 γ/L₀ and a viscous dissipative drag proportional to the elongational viscosity, ${\eta }_e=3\eta$ for a newtonian liquid.

When the droplet is compressed from its resting diameter $L_0$ to a slightly smaller size $L$, using a Hertz-like model for a small indentation (L₀−L)/2, one finds that the static force resisting compression is simply F_e = $\Delta$ PπL₀(L₀−L)/4, where πL₀(L₀−L)/4 is the droplet-microplate contact area and $\Delta$P the Laplace excess pressure. Thus, the elastic-like stress is simply $\Delta$P, and the storage modulus G' = $\Delta$P/, ${\mathrm{ϵ}}_0$ ⁶⁵ where ${\mathrm{ϵ}}_0=(L_0-L)/L_0$ is the droplet strain. Expressing the modulus as function of the surface tension, one finds G' = $4\mathrm{\gamma }/\mathrm{ϵ}{L}_0$, hence the fitting curve used in Figure 2D to estimate the surface tension of the droplets. Indeed, setting the strain to ${\mathrm{ϵ}}_0$ = 0.2 as in our experiments, with typically $L_0$ = 20 $\mu$ m and $\mathrm{\gamma }$ = 1 mN/m, one finds G’ = 1000 Pa as typically measured with the microplates setup.

The viscous contribution to the complex modulus can be estimated from the drag force F_v $\sim 3\mathrm{\pi }\eta V{L}_0$. Using the Hertz-like estimation of the droplet-microplate contact area, the stress is expressed as:

$$\sigma =\frac{F_v}{\mathrm{\pi }{L}_0(L_0-L)/4}\sim \frac{12\eta V}{(L_0-L)}$$ (Equation 9)

Expressing the typical speed V as function of the rate of strain V = $L_0(d\mathrm{ϵ}/dt)$, one gets:

$$\sigma \sim \frac{12\eta }{{\mathrm{ϵ}}_0}.\frac{d{\mathrm{ϵ}}_s}{dt}$$ (Equation 10)

Using the Equation 6, one finds:

$${\text{G}}^{″}\sim \frac{12\eta \omega }{{\mathrm{ϵ}}_0}=\frac{24\pi \eta f}{{\mathrm{ϵ}}_0}$$ (Equation 11)

For $f$ = 1 Hz, ${\mathrm{ϵ}}_0$ = 0.2 and the lipiodol viscosity at 37°C $\eta$ = 0.025 Pa s, one finds G'' (1 Hz) = 10 Pa which is the right order of magnitude (Figure 2G).

As a consequence, comparing G' = 1000 Pa and G'' = 10 Pa, we consider that the viscous contribution can be neglected for processes taking place over time scales longer than a second, and we only take into account the storage modulus over the loss one: $G^{\ast }\left(f\right)\sim$ G'. Since G′ is constant over the explored frequency range (Figure 2G), G∗ $\left(f\right)\sim$ G′ is thus considered as an apparent Young modulus.

Characterization of B cell mechanics

B cell viscoelastic properties was assessed by microplate microrheology. Experiment on single cells show that B cell mechanical properties follow a damping model (Figure 2F). G′ and G″ mainly behave as weak power laws of the frequency^66,67 (Figure 2F) with a power law exponent similar to those already reported for immune cells $(\alpha \approx 0.16)$, and exhibit an apparent visco-elastic modulus of about 165 Pa (Figure 2G).

Measurement of diffusion coefficient - FRAP experiments

Droplets have been coated with DSPE-PEG-Biotin/streptavidin and F(ab)’₂ and then image with a spinning-disk confocal microscope Nikon Eclipse 2 equipped with a Yokogawa CSU head, objective Apochromat 63× NA1.3. Droplets were photobleached with circular ROIs of D = 2.5, 5.1 and 8.8 $\mu$ m at the top of their surface following.⁶⁸ Movies of the recovery were taken with a frame rate of 30 s before and after a photobleaching pulse of 150 ms. Experiments were performed at 37°C. The recovery time was inferred from exponential fit of the measured intensity. The diffusion coefficient was extracted from a linear fit of the mean of the measured times at different radius.⁶⁸

Characterization of antigen mobility on droplets

An interesting difference between two types of functionalization (bulk vs. surface) is that the B cell is able to gather the antigen only in the first case, despite polarizing correctly in both cases. One possible cause could be a difference in the antigen mobility. We quantified the mobility of the antigen in the two types of droplet by measuring the diffusion coefficient by Fluorescence Recovery After Photo bleaching (FRAP) following the protocol described in.⁶⁸ Diffusion coefficients of bulk- and surface-functionalized droplets are respectively equal to 0.13 $\pm$ 0.09 $\mu$ m²/s (N = 12) and 0.05 $\pm$ 0.03 $\mu$ m²/s (N = 12): the two values are significantly different (Figure S4).

Of note, cells known to exert stronger forces, such as macrophages,⁶⁹ are able to form a cluster of antigens on both types of droplets²⁵ meaning independently of functionalization process, confirming that the antigen cluster is driven by cell forces. Further molecular dynamic simulations or FRAP experiments out of equilibrium are required to elucidate the physical mechanisms linking pulling forces and active antigen accumulation.

Design and microfabrication of the microfluidic trapping array

Microfluidic chips were designed on CleWin (WieWeb Software). The double layer technique required the creation of two masks: traps and pillars. Chrome masks were fabricated with the $\mu$ PG 101 maskless aligner (Heidelberg Instruments Mikrotechnik GmbH), and the final silicon mold with the MJB4 aligner system (Karl Süss). Two SU8 photoresists (Microchem) have been used, 2005 and 2010 to respectively obtain 5 $\mu$ m-thick pillars and 10 $\mu$ m-thick traps. To avoid any PDMS sticking to the small SU8 structures and long-term mold damage, we coated the wafer with a fluorinated silane by vapor deposition (trichloro (1,1,2H,2H-perfluorooctyl) silane. Liquid PDMS (RTV 615) at a base:crosslinker 1:10 ratio was poured on the silicon-SU8 mold and cured for more than 2h at 70°C to complete the crosslinking. After cutting PDMS pieces and punching out inlets and outlets with a biopsy puncher (OD = 0.75 mm, Electron Microscopy Sciences, Hatfield, UK), the top PDMS part was bonded to a glass-bottom Petri dish (FluoroDish FD35-100, WPI) together after a O₂ plasma treatment of both surfaces (50 W for 30 s, 20 sccm O₂ flow, 0.15 torr pressure, Cute Plasma oven, Femto Science, Korea), and left for 30 s at 90°C to improve the bonding. For a long-term hydrophilic coating⁷⁰ of the inner PDMS channels, a 0.25 wt % polyvinylpyrrolidone (PVP, K90) solution was injected in the chip. Finally, the chip channels were rinsed with culture media before inserting droplets and cells.

Experimental setup for the cell-droplet encounters

By connecting the microfluidic devices to a pressure controller, a fixed pressure drop $\Delta$ P between the inlet and the outlet of the chamber is set (maximum 1000 Pa, corresponding to a fluid velocity of 1.6 mm/s). Traps are initially rinsed with CLICK medium during at least 5 min. Then, 200 $\mu$ L of the droplets suspension (10⁶ droplets/mL in CLICK medium) are inserted in the microchip using the pressure regulator. Once a desired number of droplets is trapped, the first tubing is carefully removed and replaced by the tubing connected to the B cell-containing tube. Different positions and focus are marked and cells are progressively inserted at a maximum speed of 1.6 mm/s while the acquisition is launched. To avoid a saturation of traps in cells while ensuring culture medium replenishment, the flow is lessened at 0.4 mm/s. Particle displacements and trapping are observed by video-microscopy.

Microscopy-imaging of B cell polarization dynamics

Brightfield and fluorescent images of the synapses are acquired on a Leica DMI8 microscope (Germany) connected to an Orca Flash4.0 sCMOS camera (Hamamatsu Photonics, Japan). Epi-illumination is done with a LED light (PE-4000, CoolLED) and a GFP filter set (Excitation/Emission: 470/525 nm) for the fluorescent coated droplets, and a Texas Red filter set (Excitation/Emission: 561/594 nm) for the fluorescent cells. Time zero of the experiment is defined manually when a cell encounters a droplet. All pictures of cell-droplet pairs were imaged with a 40× objective (Leica, dry, N.A. = 0.8, Framerate: 50 s).

Microfluidic chip computational fluid dynamics characterization

We sought to determine the inlet pressure to impose into the chamber to mimic a shear stress in the same order of magnitude of 0.6 Pa, representing the wall shear stress close to the afferent vessel.²⁹ We first developed a two-dimensional depth-averaged computational fluid dynamics - finite element model of the microfluidic chamber with exactly the same approach that the one proposed in.⁷¹ The numerical simulations are performed with COMSOL Multiphysics (version 5.3). We consider a planar and incompressible flow, at steady state, and a Newtonian fluid with a dynamic viscosity of $\mu ={10}^{-3}$ Pa.s. Hence, the equation set verified inside the fluid domain is written as $-\nabla$ P+ $\mu \Delta v+f_v=0$ and $\nabla ·v=0$, where P is the pressure field, $v$ the velocity field and $f_v$ the volume force. In addition, the non-slip condition on the out-of-plane walls is considered with a Darcy’s law (also called ”shallow channel approximation”) thus follows $f_v=-12\mu /d^{2}v$. On physical walls, a non-slip boundary condition is added. The pressure is set as uniform both at the inlet and outlet. This pressure is equal to the pressure drop in the chamber or equal to 0 Pa, respectively at the inlet and outlet. Finally, we deduced the pressure drop through a single trap $\Delta$ P_trap from the isobar lines plot.

A 3D model focused on the geometry of one trap. We used the same hypotheses and set of equations than the previously detailed 2D model except that we do not consider Darcy’s law, thus we consider a non-slip condition on the upper and lower faces of the chamber as $f_v=0$. On the inlet, the pressure is set as uniform and equal to $\Delta$ P_trap while on the outlet, it is considered as uniform and equal to 0 Pa. Finally, we considered the flow as symmetric on the boundary linking with the rest of the microfluidic chamber.

The 15 $\mu$ m-thick U-traps can immobilize 12 $\mu$ m-large droplets and B lymphocytes (IIA1.6 cell lines) of comparable size. The traps are 10 $\mu$ m-thick traps and are raised by 5 $\mu$ m-thick pillars to ensure a continuous flow into the chip (Figure 3C). Thanks to the pillars, the fluid streamlines are not deviated when a first object is trapped in the weir structures, hence they allow the easy capture of a second object such as a B lymphocyte.

We first modeled the fluid flow into the entire designed microfluidic chamber with a 2D depth averaged Computational Fluid Dynamic (CFD) model according to inlet pressures from 0 to 1000 Pa. We deduced the corresponding pressure gap occurring around each trap thanks to isobar lines (Figures 1D and 1E). From these pressure gap values we built a 3D CFD model of the flow inside and around a U-trap occupied by a droplet and a B-cell that we considered as rigid bodies. This approach is very similar to the one proposed in.⁷² From the fluid velocity field, we calculated the fluid shear rate and deduced the fluid shear stress norm applied on the B cell (considering the fluid as Newtonian). Particular attention was paid to ensure mesh convergence of the results using boundary layer elements and mesh refinement on the B-cell boundaries. We obtained a maximal shear stress on B cell between 0.07 and 0.75 Pa (lower blue dashed and pointed curve in Figure S1C and S1D) for the least loaded trap and between 0 and 1.0 Pa for the most loaded trap (above red dashed curve Figures S1C and S1D). These values suggest that shear stress occurring on the B cell in our device is totally comparable to the in vivo shear stress experienced by B cells in lymph nodes.

Quantification and statistical analysis

Image analysis

Image analyses were performed with ImageJ/Fiji⁵⁹ (version 1.52i), and data analyses were performed with R (RStudio) software (version 2). For all processes, 16-bit images were analyzed. Codes are available on request.

Quantification of antigen recruitment

The recruitment index is defined as the ratio between the fluorescence intensity over time I(t) divided by the fluorescence intensity at the initial time I(0), both at the synapse area. The synapse area is countered by hand for each time point. The maximum and mean fluorescence intensities were measured at each time point (from time zero to 40 min).

Quantification of lysosome polarization and cell classification

Each cell shape was contoured by hand for each time point (from time zero to 40 min) and using a ImageJ macro, automatically divided in two parts according to the main orientation of the cell-droplet pair. It extracted the fluorescence intensity at the middle front side of the cell (in contact with droplet) I_front(t) and at the back of the cell I_back(t) at each time point, and computed the polarization index defined as $[{\text{I}}_{front}\left(t\right)/{\text{I}}_{back}\left(t\right)]\times [{\text{I}}_{back}\left(0\right)/{\text{I}}_{front}\left(0\right)]$ (Figure 4D). To classify the cells we noticed that most of I_pol curves reach a plateau, hence focused on the final I_pol defined as averaged over last 5 min (in the rare case where this was not possible as the polarization kinetics followed a non-plateauing growth we considered only the last time point.). Transient polarizing cells were not classed as polarized.

Statistical analysis

All statistical analysis have been performed using Prism GraphPad (version 8) and R programming language. Codes are available on request. Tests and p values are specified in the figures.

Published: November 9, 2022

Data and code availability

• •Microfluidic trap DXF files (necessary to reproduce by lithography the mold to cast the PDMS chip) have been deposited in Zenodo: https://doi.org/10.5281/zenodo.7194171 and are publicly available at the time of publication. The DOI is also listed in the key resources table.
• •ImageJ macros, R codes are all deposited in Zenodo: https://doi.org/10.5281/zenodo.7194171 and are publicly available at the time of publication. The DOI is also listed in the key resources table.
• •Raw data ara available in Zenodo: https://doi.org/10.5281/zenodo.7182828. Any additional information required to reanalyze the data reported in this paper is available from the lead contact upon request.