Normalization benchmark of ATAC-seq datasets shows the importance of accounting for GC-content effects

Summary

The assay for transposase-accessible chromatin using sequencing (ATAC-seq) allows the study of epigenetic regulation of gene expression by assessing chromatin configuration for an entire genome. Despite its popularity, there have been limited studies investigating the analytical challenges related to ATAC-seq data, with most studies leveraging tools developed for bulk transcriptome sequencing. Here, we show that GC-content effects are omnipresent in ATAC-seq datasets. Since the GC-content effects are sample specific, they can bias downstream analyses such as clustering and differential accessibility analysis. We introduce a normalization method based on smooth-quantile normalization within GC-content bins and evaluate it together with 11 different normalization procedures on 8 public ATAC-seq datasets. Accounting for GC-content effects in the normalization is crucial for common downstream ATAC-seq data analyses, improving accuracy and interpretability. Through case studies, we show that exploratory data analysis is essential to guide the choice of an appropriate normalization method for a given dataset.

Graphical abstract

Highlights

• •Sample-specific GC-content effects are omnipresent in ATAC-seq data
• •Suitable normalization can account for such technical variation
• •Sample-specific GC-content effects can bias downstream analyses (e.g., clustering)

Motivation

Normalization procedures developed for bulk transcriptome sequencing are commonly applied to ATAC-seq datasets. Furthermore, there are well-known GC-content effects on peak counts. Here, we explore major sources of technical variation for ATAC-seq data, investigate the suitability of commonly used normalization methods, and propose normalization methods that account for GC-content effects.

Datasets from high-throughput sequencing are infested with technical variation, which needs to be accounted for in order to unmask the underlying biological signal. Here, Van den Berge et al. propose and evaluate procedures to account for a major source of technical variation in ATAC-seq datasets, namely sample-specific GC-content effects.

Introduction

Genomic DNA is packaged into chromatin in the eukaryotic nucleus via a highly deliberate and dynamic process. The study of chromatin configuration aids in unraveling the complex epigenetic regulation of gene expression. Chromatin accessibility, which reflects the relatively open or closed chromatin conformation, affects the ability of nuclear proteins to physically interact with chromatin DNA and hence regulate gene expression (Klemm et al., 2019). Genome-wide mapping of chromatin accessibility delineates the functional chromatin landscape corresponding to transcription start sites, transcription factor binding sites, and all classes of cis-regulatory elements (e.g., promoters and enhancers) (Boyle et al., 2008; Thurman et al., 2012). ATAC-seq, a robust assay for transposase-accessible chromatin using sequencing, has been used to provide insight into chromatin accessibility with a relatively simple and time-saving protocol (Buenrostro et al., 2013; Klemm et al., 2019).

ATAC-seq relies on a hyperactive Tn5 transposase that can simultaneously cut accessible DNA fragments and ligate sequencing adapters to both strands (Buenrostro et al., 2013). The tagged DNA fragments are amplified, sequenced, and mapped back to the genome, upon which accessible regions are identified by the enrichment of mapped read ends, traditionally using peak-calling algorithms (Zhang et al., 2008; Kharchenko et al., 2008). The data used for downstream analysis thus typically consist of a count matrix, where each row corresponds to a genomic region (or “peak”) and each column corresponds to a sample. The count in each cell of the matrix represents the number of read ends mapped to a particular peak for a given sample, and is a proxy for the accessibility of the genomic region. Note that not all regions (i.e., peaks) identified by the protocol will be functionally relevant, while other truly functionally relevant regions are likely to be missed.

High-throughput sequencing studies are typically influenced by a range of factors of (unwanted) technical variation, e.g., sample preparation, library preparation, and sequencing batch (Li et al., 2014; Su et al., 2014). Notably, GC-content, the fraction of guanine and cytosine nucleotides in a particular genomic region or gene, has previously been identified as a sample-specific technical bias factor, e.g., in peak-calling for chromatin immunoprecipitation sequencing (ChIP-seq) data (Teng and Irizarry, 2017) or normalization and differential expression for RNA sequencing (RNA-seq) data (Risso et al., 2011; Love et al., 2016). Similarly, ATAC-seq data have been shown to be affected by technical variation due to, for example, enzymatic cleavage effects, PCR bias, and duplicate reads (Meyer and Liu, 2014). Importantly, the sample-specific effect of GC-content in ATAC-seq data has been noted and accounted for in previous studies (Corces et al., 2016; de la Torre-Ubieta et al., 2018), typically using conditional quantile normalization (cqn) (Hansen et al., 2012). While the ATAC-seq protocol is experimentally simpler as compared with, e.g., the RNA-seq protocol, there are several common steps that have been shown to contribute to technical GC-content effects. Aird et al. (2011) “identified library amplification by PCR as by far the most discriminatory step” in terms of base-composition bias in fragment libraries, and Ross et al. (2013) clearly document library-specific GC-content bias in Illumina sequencing data. Furthermore, it has been shown that stretches of high GC-content within a fragment can influence whether the fragment will be amplified, and thus sequenced (Hron et al., 2015).

In general, since a large fraction of accessible regions are around gene promoters, which often have a high GC-content and are enriched in CpG islands (Fenouil et al., 2012), we naturally expect an association between accessibility and GC-content. However, we confirm that these associations are sample specific, also, in many ATAC-seq datasets. These sample-specific effects, which could reflect both biological as well as technical factors, may then, in turn, result in systematic differences between biological groups, such as a treatment and a control group, although not necessarily. Notwithstanding these observations, the impact of sample-specific GC-content effects in ATAC-seq data on downstream analyses has not been studied in depth. Surprisingly few studies investigate the analytical challenges of ATAC-seq data, e.g., normalization and differential accessibility (DA) analysis. Indeed, most data analysis workflows rely on statistical methods originally developed for ChIP-seq or bulk RNA-seq data to analyze bulk ATAC-seq datasets (Rizzardi et al., 2019; Philip et al., 2017; Reske et al., 2020). Recently, Reske et al. (2020) compared pipelines for DA analysis and showed that normalization has a large influence on the results. While the authors advised comparing multiple normalization methods for a particular dataset at hand, they did not elaborate on GC-content effects or normalization methods that take this into account. In particular, while most research papers analyzing bulk ATAC-seq data adopt standard bulk RNA-seq global-scaling normalization procedures (e.g., Philip et al., 2017; Rizzardi et al. 2019), such as total-count normalization, edgeR’s trimmed mean of M values (TMM) (Robinson and Oshlack, 2010), or DESeq2’s median of ratios (Love et al., 2014), some account for GC-content effects (de la Torre-Ubieta et al., 2018), typically through cqn (Hansen et al., 2012). Given this dichotomy in normalization choices, we investigate the influence of accounting for possible GC-content effects on downstream analyses for ATAC-seq data.

In this article, we show that GC-content effects in ATAC-seq data can be sample specific, which indicates that they can bias downstream analyses, such as clustering and DA analysis. We introduce a normalization method, smooth GC-full-quantile (FQ), based on smooth-quantile normalization (Hicks et al., 2015) within GC-content bins, and evaluate it together with several GC-aware as well as GC-unaware normalization methods using a principled framework. We further study the impact of GC-content effects on the accuracy and interpretation of DA analysis results. While no normalization method uniformly performs best across all datasets, smooth GC-FQ performs best on average, and GC-aware normalization methods typically perform better than GC-unaware methods, emphasizing the need to correct for GC-content effects. We recommend that researchers use exploratory data analysis methods to guide the choice of normalization method.

Results

GC-content effects are sample specific and confound downstream analyses

In ATAC-seq, accessibility counts are often positively associated with GC-content. We explore this using data from Calderon et al. (2019), who generated an ATAC-seq atlas of human immune cell types. Here, we focus on six replicate samples of memory natural killer (MNK) cells in a control condition.

Figure 1A shows that the accessibility count of a particular genomic region is associated with its GC-content. However, the slope and shape of the curves may differ between samples, in a manner that is not fully explained by sequencing depth differences, which indicates that GC-content effects are sample specific and can therefore bias between-sample comparisons (e.g., compare sample 1 with samples 3 and 4). This can be similarly observed for other cell types in this dataset (Figure S1). Note that, while the width of each peak is also associated with its accessibility, this effect tends to be more uniform across different samples and therefore have lower impact on between-sample comparisons (Figure S2). This could be considered analogous to the effect of gene length on read counts in RNA-seq data.

Figure 1.

GC-content effects are sample specific and confound differential accessibility analysis

(A) Fitted lowess curves of log-count as a function of GC-content for the six MNK cell control samples in Calderon et al. (2019). The shape and slope of the curves can be different for different samples, especially sample 1 in comparison with other samples. This is also reflected in the data for other cell types (Figure S1).

(B) Differential accessibility log fold changes for a 3 versus 3 mock null comparison, based on normalization and differential accessibility analysis using edgeR, show a bias for peaks with low and high GC-content (in a null setting, LFC should be centered around zero). The blue curve represents a generalized additive model (GAM) fit.

(C) Similar to (B), but using DESeq2 for normalization and differential accessibility analysis.

(D) Similar to (B), but using full-quantile normalization and edgeR differential accessibility analysis.

(E) Lowess-smoothed log2-fold-change effects as a function of GC-content. Each line represents a within- or between-tissue comparison for the data from Liu et al. (2019). The GC-content effects on the log fold changes can be of a similar magnitude for comparisons within a tissue as compared with between tissues.

(F) Lowess-smoothed log2-fold-change effects as a function of GC-content for within- and between-brain region comparisons for the data from de la Torre-Ubieta et al. (2018). The GC-content effects on the log fold changes are typically of lower magnitude for comparisons within a brain region as compared with between brain regions.

One might initially think that, because DA analyses involve comparing read counts between samples for a given genomic region with a fixed GC-content, GC-content effects would cancel out. However, because of their sample specificity, GC-content effects also impact log fold changes (LFCs) comparing accessibility between samples for a given region. A 3 versus 3 mock null comparison of the MNK cells (i.e., a comparison of the same type of cells which should not exhibit DA), using both edgeR (Robinson et al., 2010) and DESeq2 (Love et al., 2014), reveals a bias in the LFCs with respect to GC-content (Figures 1B and 1C). That is, the LFCs are not centered around zero, as expected for a null comparison of normalized data, and also vary with GC-content. Furthermore, both TMM and DESeq2 normalizations, which are frequently used for DA analysis in ATAC-seq data, fail to remove GC-content effects. FQ normalization (Bullard et al., 2010), another popular normalization method, also fails at removing GC-content effects (Figure 1D). Similar effects can be observed for other cell types for which six replicates are available in the same condition (Figure S3).

The sample-specific GC-content effects may be of biological or technical origin, as well as a combination of both (Figures 1E and 1F). For example, primed stem cells may have many accessible promotors, which are typically GC-rich regions, as compared with resting stem cells, and therefore the association of accessibility with GC-content can be different between cell types, thus leading to biological GC-content effects. Below, we demonstrate two comparisons from two different datasets where the GC-content effects are mostly either technical or biological. In the dataset from de la Torre-Ubieta et al. (2018), four technical replicates (i.e., aliquots from the same DNA library) were sequenced from a single donor for the GZ brain region (the neuronal progenitor-enriched region of the developing human fetal cortex). Since all replicates were derived from the same biological sample, there cannot be any biological effects and any GC-content effect must be technical. Performing a 2 versus 2 comparison between these technical replicates using edgeR, demonstrates a small, but consistent, GC-content effect on the LFCs, indicative of sample-specific GC-content technical artifacts (Figure S4). Extending this analysis, we can observe that the GC-content effects for technical comparisons within a brain region are typically of smaller magnitude as compared with comparisons between brain regions (Figure 1F), suggesting that, for this dataset, the GC-content effects may thus be mostly of biological nature. We can perform a similar analysis for the mouse tissue atlas from Liu et al. (2019). The observational units in this study correspond to lab mice, all of which are from the same C57BL/6J strain. Here, one can consider the mice as genetically identical clones and treat them as technical replicates; thus, when performing within-tissue comparisons, interpret the observed GC-content effects as technical effects. Upon doing so, we observe that the GC-content effects for technical comparisons within a tissue are typically of similar magnitude as compared with comparisons between tissues (Figure 1E), suggesting that, for this dataset, the GC-content effects may thus be mostly of technical rather than biological nature.

If not accounted for, GC-content effects can have a significant impact on a downstream DA analysis, masking biological signal and also leading to false positives, as was similarly observed previously in RNA-seq data (Risso et al., 2011; Hansen et al., 2012; Love et al., 2016).

GC-aware normalization

GC-content effects have been observed and accounted for in other work on ATAC-seq data (Liang et al., 2020; de la Torre-Ubieta et al., 2018), typically using cqn (Hansen et al., 2012) (see STAR Methods). While this method removes GC-content effects in many datasets, Risso et al. (2011) observed that, in the context of RNA-seq, cqn’s regression approach may be “too weak” for some datasets and “more aggressive normalization procedures” may be required. They proposed a method, implemented in the Bioconductor R package EDASeq, based on two rounds of FQ normalization: First, FQ normalization within a sample across bins of features (e.g., peaks or genes) with similar GC-content and, subsequently, FQ normalization between samples. We will denote this method as FQ-FQ normalization.

However, read count distributions may in some datasets be more comparable across samples within a GC-content bin than across GC-content bins within a sample (see Figure 2A). This motivates a variant of FQ-FQ normalization, which we call GC-FQ, that applies FQ normalization across samples for each GC-content bin separately. Note that this attempts to equalize the GC-content effect across samples and therefore performs both within- and between-sample normalization simultaneously.

Figure 2.

GC-aware normalization methods cqn, FQ-FQ, and GC-FQ are successful in eliminating GC-content effects on the differential accessibility log-fold-change estimates

(A) Accessibility distributions for three replicates from the dataset of Philip et al. (2017). The peaks are grouped into 10 equally sized bins according to their GC-content (rows) and the accessibility distribution (kernel density estimate) is plotted for each bin. The distributional shapes are more comparable across samples for a particular GC-content bin, than they are across GC-content bins for a particular replicate.

(B–D) There is no visible GC-content effect on log fold changes estimated using edgeR following normalization with GC-aware methods cqn, FQ-FQ, and GC-FQ, in the mock comparisons for the dataset from Calderon et al. (2019). The blue curve represents a GAM fit.

For the ATAC-seq dataset of Calderon et al. (2019), all three GC-aware methods (cqn, GC-FQ, and FQ-FQ) indeed effectively remove GC-content effects (Figures 2B–2D) on the fold changes. Note that a similar mock analysis on other datasets, shows that cqn may not always succeed in eliminating sample-specific GC-content effects, as shown in Figures S5 and S6 for the data from Rizzardi et al. (2019).

All three of these GC-aware normalization methods rely on FQ between-sample normalization, which is an aggressive normalization method that does not come without assumptions. Since FQ normalization forces read count distributions to be equal across all samples, the underlying assumption is that global differences between distributions are the result of technical effects. In other words, if there were neither technical nor sampling variability in the data, the distributions of all samples should be identical, hence comparable; this is what FQ normalization is trying to achieve. This assumption is restrictive and is not guaranteed to hold for all datasets. Hicks et al. (2018) recently developed a generalization of FQ normalization, smooth-quantile normalization, or qsmooth, that can account for global differences between distributions due to biological effects of interest. The method is based on the assumption that the read count distribution of each sample should be equal within biological groups or conditions, but could vary between groups. Essentially, the method is a weighted combination of FQ normalization between samples for each biological group separately and FQ normalization across all samples and all biological groups.

We therefore also implement a variant of GC-FQ, which we call smooth GC-FQ, that applies smooth-quantile normalization across samples within each GC-content bin separately and is therefore capable of dealing with biological groups that have global distributional differences between them. This procedure is incorporated in the R/Bioconductor package qsmooth.

Benchmarking ATAC-seq normalization

We evaluate normalization methods using eight public bulk ATAC-seq datasets (Bryois et al., 2018; Calderon et al., 2019; Fullard et al., 2018; Liu et al., 2019; Murphy et al., 2019; Philip et al., 2017; Rizzardi et al., 2017; de la Torre-Ubieta et al., 2018), including ATAC-seq atlases of mouse tissues (Liu et al., 2019), human blood cells (Calderon et al., 2019), and human brain cells (Fullard et al., 2018), thus spanning a multitude of biological systems. For each dataset, we use the publicly available raw (i.e., unnormalized) accessibility count matrix; the different datasets hence also span a realistic range of preprocessing and peak-calling pipelines. We compare GC-aware normalization methods (smooth) GC-FQ, cqn, and FQ-FQ, with GC-unaware normalization methods qsmooth, TMM, DESeq2, FQ, total-count, upper-quartile, and no normalization; see STAR methods for a description of each normalization procedure.

Our benchmarking framework evaluates different aspects of each normalization method, which can broadly be categorized as follows: (1) between-sample comparison of normalized expression measures, (2) performance in DA analysis, and (3) removal of GC-content effects, each of which are described in more detail below. A schematic of the framework is provided in Figure 3A. The specific measures used and their definitions for each of these components are described in STAR methods.

Figure 3.

Benchmark of 12 normalization methods across 8 public ATAC-seq datasets

(A) A schematic of the benchmarking framework. The benchmark assesses normalization, differential accessibility performance, and GC-content effect removal, the results of which are each represented as a heatmap.

(B) Results of the benchmark. The pseudo-color images display matrices of average ranks (see STAR Methods), with rows corresponding to normalization procedures and columns to datasets and where the darker the color the better the performance. Methods are ordered according to their average rank across all evaluation criteria and the three evaluation categories and datasets, and their names colored based on whether they explicitly account for GC-content (blue) or not (black).

Between-sample comparison of normalized expression measures

We evaluate and rank normalization methods based on a range of performance measures implemented in scone (Cole et al., 2019). While scone provides a valuable framework for benchmarking normalization procedures, we find that some default measures may favor certain normalization methods over others. We therefore use simulated mock datasets as well as real datasets to select relevant measures for our context, as described in supplemental methods S1. Based on this evaluation, we benchmark normalization methods using five summary measures. The first three are the average silhouette width for (1) a clustering of samples according to biological covariate(s) of interest (Bio Sil); (2) a clustering of samples according to (unwanted) batch covariates (Batch Sil); (3) an empirical clustering of samples using partitioning around medoids (PAM Sil). We also evaluate normalized data based on the correlation of their log-count principal components with (4) principal components of QC variables (see STAR methods section for which QC variables are used in each dataset), and (5) principal components of factors of unwanted variation, derived from negative control features. Here, we use peaks that overlap with housekeeping genes as negative control features.

Performance in DA analysis

The DA analysis performance evaluation relies on two scenarios, based on synthetic null and synthetic signal datasets.

First, a mock null analysis is performed for each real dataset where, for each stratum of the biological covariate of interest, samples are split randomly into two groups to create a mock variable. Since the two mock groups therefore contain a similar number of samples from each stratum, we expect no systematic differences between the groups. A DA analysis is then performed using each of the normalization procedures (see STAR methods). The following two evaluation measures are computed: the fraction of DA peaks returned at a nominal marginal significance level of $5\text{\%}$ (FPR) and the Hellinger distance of the marginal p value distribution with a uniform distribution on the interval $\left[\mathrm{0,1}\right]$ (P-val unif). Both measures aim to assess control of false positives in a DA analysis.

Second, we use each real dataset to construct synthetic signal datasets of 12 samples each, based on the simulation framework described in STAR methods. We use the simulated datasets to assess DA analysis performance based on the area under the receiver operating characteristic curve (auroc).

GC-content effect removal

Finally, we use the evaluations in both components above in combination with three measures that assess the removal of GC-content effects. In the scone normalization performance evaluation, we use a measure based on relative log-expression (RLE) values (Gandolfo and Speed, 2018) to investigate whether the normalization works across the range of GC-content values (RLE GC) (see STAR methods for details). In the mock comparison, we assess deviation of p value uniformity as a function of GC-content by calculating the variability in Hellinger distance between the p value distributions in each of 20 equally sized GC-content bins and a uniform distribution. Good normalization methods should have a similar p value distribution across GC-content bins (p-val GC), and therefore a low value for this measure. Finally, we use the DA analysis on the simulated datasets to calculate the distance in empirical cumulative distribution functions between the observed GC-content distribution of called DA peaks and the GC-content distribution of truly DA peaks (GC-dist DA; see STAR methods for implementation details). Good normalization methods should return a GC-content distribution of called DA peaks that is similar to the GC-content distribution of truly DA peaks, and therefore a low value for this measure. We do not expect a systematic relationship between peak width and GC-content bias (Figure S7). Plots of scores versus median peak width likewise did not suggest any systematic relationship between peak width and GC-content effect (data not shown).

The benchmark results for each dataset are shown in Figure 4, and summarized across datasets in Figure 3B, the results of which are used below as a basis to evaluate and rank normalization procedures. While no method uniformly outcompetes all others, smooth GC-FQ performs best in four out of eight datasets, and is among the top methods for the other datasets. Other GC-aware normalization methods, such as FQ-FQ and GC-FQ, also often perform well, while the performance of cqn is variable across datasets. GC-unaware normalization methods typically perform worse than GC-aware methods. Out of the latter, qsmooth and FQ consistently perform reasonably well. The good performance of both smooth GC-FQ and qsmooth suggests that, in bulk ATAC-seq data, there are often large numbers of differentially abundant features between biological conditions, possibly more so than what is typically observed in bulk RNA-seq data. Indeed, this is also what we observe in the two case studies discussed below, where, for both datasets, many methods flag over $35\text{\%}$ of all features as differentially accessible between biological conditions.

Figure 4.

Benchmarking results for each of eight public ATAC-seq datasets

Each panel corresponds to the benchmarking results for one of the datasets, as indicated by the first author and publishing year in the top-left corner. Within each panel, normalization methods are ordered from best (top) to worst (bottom) overall performance; method names are colored based on whether they explicitly account for GC-content (blue) or not (black). The benchmark focuses on three main aspects: normalization performance assessment using scone, differential accessibility analysis performance, and the removal of GC-content effects, each represented by a heatmap. The pseudocolors in the heatmaps represent the rank of each normalization method as compared with the other methods for that particular measure; a darker color corresponds to a better rank. All measures and normalization procedures are described in STAR Methods. Note that not all normalization performance measures could be assessed in all datasets, since we did not have batch or QC information for some datasets.

To check the robustness of these results, we also rank normalization methods for each of the three benchmarking components separately (Figure S8). In terms of scone normalization performance, each GC-aware method performs better than each GC-unaware method. The same holds for GC-content effects removal, with the exception of FQ normalization performing better than cqn. In terms of differential analysis performance, smooth GC-FQ is still the top-performing method, followed by qsmooth and FQ-FQ normalization. GC-FQ and FQ also show fairly consistent good performances. While cqn performs well in terms of between-sample normalization, it performs mediocre in terms of differential analysis and GC-content bias removal. We further use these results to determine the top-performing method for each dataset and benchmarking component. In terms of normalization performance, cqn and smooth GC-FQ each perform best for three out of eight datasets. The top methods for the remaining two datasets are FQ-FQ and FQ. For DA analysis, FQ-FQ, qsmooth, and GC-FQ each perform best in two datasets. Smooth GC-FQ and UQ each perform best in one of the two remaining datasets. Finally, in terms of removal of GC-content effects, smooth GC-FQ and FQ-FQ each perform best in three datasets. DESeq2 and TMM are best performers in one other dataset. These results confirm that, even for benchmarking methods not explicitly using GC-content bias removal for evaluation, accounting for GC-content bias is beneficial for the normalization of ATAC-seq datasets.

We also check the concordance of common downstream analyses often being performed in ATAC-seq data, such as DA analysis or clustering, across different normalization procedures (Figure S9). In terms of DA analysis we find, on average, a higher concordance in discovered peaks between procedures accounting for GC-content effects, as compared with GC-unaware methods. In addition, GC-aware methods perform better in clustering samples according to their known biological grouping, as compared with GC-unaware methods.

Taken together, our evaluation findings show that accounting for GC-content effect is critical for normalization of ATAC-seq datasets and, in particular, smooth GC-FQ provides good results across several datasets.

Case studies

In what follows, we consider the normalization of ATAC-seq datasets in greater depth using two case studies. These serve as demonstrations of how one can evaluate normalization procedures in practice using exploratory data analysis techniques. We assess each of the normalization methods that were benchmarked above, except for the basic total-count and upper-quartile normalization methods.

Mouse tissue atlas

Liu et al. (2019) presented an ATAC-seq atlas of 20 tissues in adult mice, consisting of $\mathrm{296,416}$ peaks across 66 samples. Hierarchical clustering based on the Euclidean distance of the log-transformed normalized counts shows that normalization is essential to derive a biologically sensible clustering of the samples (Figure S10). Without normalization, several tissues do not cluster together. The clustering is improved by using FQ normalization or global-scaling normalization methods TMM and DESeq2, but these still fail to cluster the ovary and adrenal gland tissue samples properly. By contrast, GC-aware methods cqn, FQ-FQ, and smooth GC-FQ, successfully group the samples of each tissue type together, while GC-FQ misclusters one adrenal gland sample.

Next, we perform a DA analysis using the normalized counts from each normalization method as input (see STAR methods for how normalized counts were obtained). We model the accessibility counts using a negative binomial distribution as implemented in edgeR (or DESeq2 for DESeq2 normalization) and assess DA between heart and liver tissues. Assuming that either a small fraction of peaks are DA, or that there is symmetry in the direction of DA between the groups under comparison, LFCs should be centered at zero and similarly distributed across different GC-content bins. However, LFCs are biased for peaks with both low GC-content and high GC-content values for all GC-unaware normalization methods (Figure S11). While this technical artefact is successfully removed by FQ-FQ and GC-FQ normalizations, cqn and smooth GC-FQ still suffer from substantial bias (Figure S11). Since a high GC-content is also associated with a high accessibility count, which is in turn associated with high statistical power, we naturally expect the top DA peaks to be skewed in terms of GC-content, i.e., we expect a dominance of high GC-content values for the DA peaks. This is indeed the case for all normalization methods (Figure S12), except TMM normalization for which the top peaks are remarkably balanced across GC-content bins. If we focus on the significant peaks at a nominal false discovery rate (FDR) threshold of $5\text{\%}$ (Benjamini and Hochberg, 1995), most methods discover a comparable number of around $130\times {10}^3$ peaks. However, cqn flags a substantially higher number of peaks, $\sim 153\times {10}^3$, and therefore seems likely to return more false positives. The peaks discovered by cqn are also more balanced with respect to GC-content compared with other methods (Figure S13).

To determine whether accounting for GC-content effects improves the biological relevance of the results, we group normalization methods into GC-aware and GC-unaware methods, as indicated by the text color in Figure 3B. Since cqn is a clear outlier in terms of the number of DA peaks it returns, we do not consider it further. For each normalization method, we check the overlap of the set of DA peaks with functional genomic elements, such as promotors (see STAR methods). GC-aware normalization methods have a higher enrichment in functionally relevant elements, such as promotors and 5ʹ untranslated regions (UTRs), as compared with GC-unaware methods (Figure S14).

Brain Open Chromatin Atlas

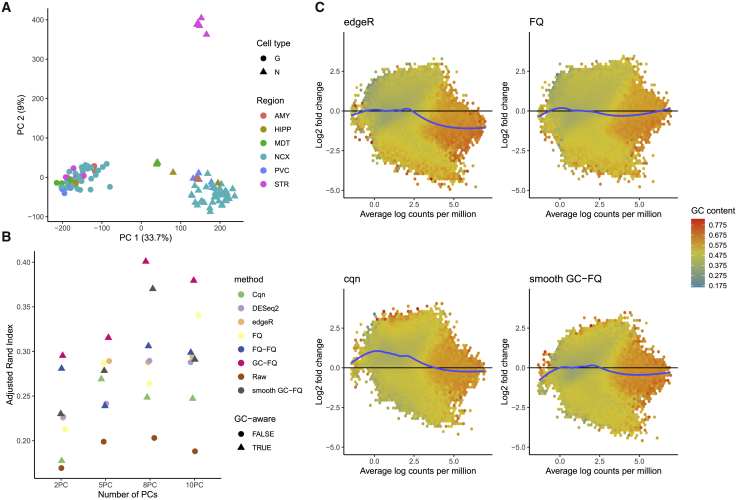
Fullard et al. (2018) published the Brain Open Chromatin Atlas, where chromatin accessibility is measured in five human postmortem brain samples. The dataset consists of a total of 14 brain regions and two cell types (neuronal and glial/non-neuronal). These 14 brain regions can be classified into six broader regions, namely, the neocortex, primary visual cortex, amygdala, hippocampus, mediodorsal thalamus (MDT), and striatum (STR). After normalizing the counts using each normalization method (see STAR methods), we first assess how well each normalization method is able to recover the cell types and the major brain regions within each of these cell types by clustering the datasets using partitioning around medoids (PAM) based on the first 2 to 10 principal components. We consider PAM clustering at two resolution levels: First, we search for two clusters and check how well these correspond to the known cell types (i.e., glial and neuronal); next, we search for 12 clusters and check how well these correspond to the 6 known broad regions within each cell type. We evaluate the clusterings using the adjusted Rand index (Rand, 1971; Hubert and Arabie, 1985), comparing the derived partitions with the ground truth. Interestingly, all methods typically cluster the majority of samples correctly according to cell type, except for cqn and no normalization (Figure S15). However, when checking how well the different brain regions within each cell type are recovered by clustering the normalized datasets into 12 clusters (Figure 5B), for each selected number of PCs, GC-FQ, smooth GC-FQ, and FQ-FQ perform best, while cqn and no normalization perform worst. The good performance of (smooth) GC-FQ and FQ-FQ was already noticeable in the PCA plots in Figure S16, since these are the only methods where the STR and MDT regions are clearly separated from other brain regions for the neuronal cells in two dimensions.

Figure 5.

Analysis of the Brain Open Chromatin Atlas dataset

(A) PCA plot of the dataset after smooth GC-FQ normalization. The plotting symbols denote cell type, neuronal (N) and glial (G); the colors represent the six broad brain regions.

(B) The samples were clustered using PAM based on a variable number of PCs (x axis), after normalization with each of nine methods. The y axis corresponds to the adjusted Rand index comparing the PAM clusters with the true partitioning according to brain region and cell type (12 clusters in total). Different normalizations are represented by different colors and GC-aware normalization methods are represented with triangles. GC-aware methods generally perform better, on average.

(C) Mean-difference plots (MD-plots) for differential accessibility analysis comparing neuronal versus non-neuronal cells. The peaks are grouped into hexagons, where the color of each hexagon denotes the average GC-content of its corresponding peaks. There is substantial GC-content bias for GC-unaware normalization methods edgeR and FQ, and similarly for all other GC-unaware methods (Figure S18), where low GC-content is associated with high log fold changes and vice versa. The log-fold-change distribution for cqn is skewed toward positive values, also see Figure S19. These issues are alleviated for GC-aware normalization smooth GC-FQ.

Aside from clustering, researchers often focus on discovering peaks that are differentially accessible between biological groups. Here, we use edgeR (or DESeq2 for DESeq2 normalization) to fit a negative binomial generalized linear model for each peak in each normalized dataset. For each peak, we test for differences in average accessibility between neuronal and non-neuronal cells, across all brain regions. Mean-difference plots (Dudoit et al., 2002) show a prominent GC-content effect on the fold changes for all GC-unaware normalization methods (Figures 5C and S17). Likewise, stratified violin plots of the foldchanges by GC-content show substantial GC-content effects on the fold changes (Figure S18). FQ-FQ and GC-FQ successfully remove GC-content effects on the fold changes, while smooth GC-FQ removes the effect partially. Interestingly, the LFCs following cqn tend to be biased (Figure S19). The peculiar results for cqn are also reflected in the number of DA peaks, which is at least $\sim 20\text{\%}$ higher as compared with all other methods (Figure S20). These results emphasize the need for exploratory data analysis to choose an appropriate normalization method.

To assess the relevance of the discovered DA peaks, we examine the genomic features and enriched gene sets associated with them, where we assign a gene to a peak if its promoter is within a $\mathrm{5,000}$ bp distance of the peak. The intersection of $\mathrm{134,601}$ DA peaks discovered across all methods is enriched in genomic features such as exons, promoters, and 5ʹ UTRs, while depleted in intergenic regions, as compared with the background of all peaks (Figure S21). The enriched biological process gene sets are highly relevant, including neurogenesis and nervous system development, among others (Table S1). When investigating the overlap with genomic features for each normalization procedure, we observe that DA peaks according to cqn are depleted in promotors and 5ʹ UTRs, while enriched in intergenic regions, therefore possibly returning the least relevant DA peaks (Figure S22). This is further reinforced by the fact that, even though cqn returns significantly more peaks in intergenic regions, it still has a lower overlap with enhancers identified in Andersson et al. (2014), as compared with any other normalization method.

The DA results also allow us to assess whether accounting for GC-content effects can aid biological interpretation. We examine the set of $\mathrm{9,866}$ peaks discovered by each of FQ-FQ, smooth GC-FQ, and GC-FQ, while not by their GC-unaware counterpart, FQ normalization. These peaks are enriched in genomic features such as promoters, 5ʹ UTRs, and exons (Figure S21). While no biological process gene sets are significantly enriched at a $5\text{\%}$ nominal FDR level, the top gene sets are still relevant, including regulation of synapse structure or activity and synapse organization (Table S2). We also further investigate the peaks uniquely discovered by cqn. These peaks are enriched in intergenic regions (Figure S21), which supports our intuition that these are likely false-positive peaks. While again no enriched gene sets are found at a $5\text{\%}$ nominal FDR level, in this case the top gene sets are not relevant to the experiment, mostly involving gene sets on the kidney and eye (Table S3), reinforcing the hypothesis that these could be false positives.

Taken together, these results again suggest that GC-content normalization is crucial for the analysis of ATAC-seq data, improving downstream analyses and biological interpretation. Exploratory data analysis is essential for evaluating and guiding the choice of effective normalization and removal of technical GC-content effects.

Discussion

The evaluations in this manuscript highlight the importance of accounting for GC-content effects in ATAC-seq datasets. Because of the sample specificity of GC-content effects, failing to adjust for GC-content using an appropriate normalization method can bias downstream analyses, such as clustering and DA analysis. We have proposed GC-aware normalization procedures and benchmarked these against state-of-the-art procedures using eight public ATAC-seq datasets. While GC-aware procedures perform better than GC-unaware procedures, none uniformly outperforms all others, although smooth GC-FQ generally performs well on average. The choice of an appropriate normalization procedure is dataset specific, and exploratory data analysis is essential to guide this choice.

Similar GC-content effects have also been noted in DNA-seq (Benjamini and Speed, 2012), RNA-seq (Hansen et al., 2012; Love et al., 2016), and ChIP-seq (Teng and Irizarry, 2017), among others. For ChIP-seq datasets, Teng and Irizarry (2017) recently developed a negative binomial mixture model to correct for GC-content effects in both background and binding signal regions at the peak-calling stage, by accounting for GC-content in the abundance estimation for a particular genomic region. While their method has been evaluated using ChIP-seq data, it may also be useful for ATAC-seq data. We therefore examined sample-specific GC-content effects following GC-aware peak-calling for the six samples from Calderon et al. (2019) used in Figures 1 and 2, and similarly observed sample-specific effects that affect the DA analysis (Figures 6 and S23). Thus, while GC-aware peak-calling may, in some cases, alleviate sample-specific GC-content bias, it does not eliminate it.

Figure 6.

GC-content effects are sample specific and confound differential accessibility analysis, also after GC-aware peak calling

Peaks were called using gcapc, the GC-aware peak caller from Teng and Irizarry (2017).

(A) Fitted lowess curves of log-count as a function of GC-content for the six MNK cell control samples in Calderon et al. (2019). The shape and slope of the curves can be different for different samples, especially sample 1 in comparison with other samples, as was also observed in Figure 1.

(B) Differential accessibility log fold changes for the same 3 versus 3 mock null comparison as in Figure 1, based on normalization and differential accessibility analysis using edgeR, show a bias for peaks with moderate GC-content (in a null setting, log fold changes should be centered around zero). The blue curve represents a generalized additive model (GAM) fit.

(C) Similar to (B), but using DESeq2 for normalization and differential accessibility analysis.

(D) Similar to (B), but using full-quantile normalization and edgeR differential accessibility analysis.

While in this manuscript we have focused on adjusting for GC-content effects at the level of called peaks, other approaches are possible. For example, Benjamini and Speed (2012) argue that it is the GC-content of the full DNA fragment (versus only the sequenced read) that most influences read counts. A comparison of the peak-level normalization approaches discussed here with fragment-level approaches would be an interesting avenue for further research on how to best correct for GC-content effects.

Other sources of technical variation, such as sample-specific peak width effects, may simultaneously be present together with GC-content effects, although these two sources of technical variation are likely independent. The only method in our evaluation that is capable of accounting for both effects is cqn, whose performance is, however, quite low in general. This could be explained by the fact that cqn does not always successfully eliminate sample-specific GC-content effects (for example, see Figure S6).

Our work has focused on normalization of bulk ATAC-seq datasets. While FQ-based normalization procedures were found to perform favorably in this setting, it remains to be seen whether they perform equally well on single-cell ATAC-seq (scATAC-seq) datasets. The sparsity associated with scATAC-seq data suggests that their application could be limited and alternative normalization procedures may be needed.

Limitations of the study

In this study, we identified GC-content effects as a major source of technical variation in ATAC-seq datasets, and proposed and evaluated normalization procedures to account for this. However, not all sample-specific GC-content variation is technical. Indeed, there is most likely a combination of technical and biological variation. While our analyses show that some variation must be technical, it is typically very hard to distinguish technical from biological GC-content variation, and one may therefore risk eliminating part of the (wanted) biological signal while attempting to remove unwanted technical variation.

In our evaluation, we discuss and recommend normalization methods that perform well on average; however, none of these consistently perform best across all datasets. The benchmarking framework relies on our chosen benchmarking measures; however, others may similarly be appropriate. While our benchmarking allowed us to sketch out broad recommendations, the eventual choice of normalization method is dataset specific. We therefore advise researchers to perform exploratory data analysis before adopting one of our suggested methods.

Sample-specific GC-content effects have been brought forward as a prominent source of technical variation, although other sources are surely present at some magnitude, e.g., peak width effects. However, we do not expect a strong systematic association between the width of a peak and its GC-content, and it may therefore be treated as a distinct issue, although accounting for both peak width and GC-content simultaneously is possible, as demonstrated by cqn.

Finally, our manuscript has focused on bulk ATAC-seq, but similar evaluations may be of interest for scATAC-seq and other high-throughput assays, such as bulk or single-cell transcriptome sequencing.

STAR★Methods

Key resources table

REAGENT or RESOURCE	SOURCE	IDENTIFIER
Deposited data
Simulated datasets	This paper	https://zenodo.org/record/6109369
Real datasets	This paper	https://zenodo.org/record/6646500
Analysis results of benchmark and case studies	This paper	https://zenodo.org/badge/latest doi:269151763
Software and algorithms
qsmooth, including the ‘smooth GC-QN’ implementation	Bioconductor	https://www.bioconductor.org/packages/release/bioc/html/qsmooth.html
Analysis code	This paper	https://zenodo.org/badge/latest doi:269151763

Resource availability

Lead contact

Resource-related questions may be directed to the lead contact at koen.vdberge@gmail.com.

Materials availability

This study did not generate new unique reagents.

Method details

Datasets

Philip et al. (2017) study CD8 T-cell dysfunction in acutely infected and chronic tumoral tissue, over several time points. We only focus on the mouse samples and consider time and treatment as the biological variables of interest. We did not find metadata on quality control (QC) or batch variables, so we do not use any in the scone evaluation. The count matrix corresponds to $\mathrm{75,689}$ peaks for 41 samples and was downloaded from the Gene Expression Omnibus (GEO) with accession number GSE89308.

Bryois et al. (2018) study the adult human prefrontal cortex brain. We remove samples that are not schizophrenic or control samples, leaving a total of 272 samples, consisting of 135 individuals with schizophrenia and 137 controls. We consider the disease status as the biological variable of interest. In the evaluation, we use the 32 QC variables that were available in the metadata, along with the top 10 principal components derived from the patients’ genotypes. The sequencing index in the metadata is used as batch variable. The count matrix corresponds to $\mathrm{118,152}$ peaks and was obtained through personal communication with the authors. It was not relevant to correct for the width of the peaks using cqn in this dataset, since all peaks have a length of 301bp.

de la Torre-Ubieta et al. (2018) study human cortical neurogenesis in the germinal zone and cortical plate of the developing cerebral cortex. Samples were derived from three individual donors and each donor was handled and processed separately, so we treat each donor as a batch and the brain region as the biological variable of interest. The count matrix corresponds of $\mathrm{62,005}$ peaks across 19 samples and was downloaded from the GEO with accession number GSE95023. Note that the replication in this dataset is technical, i.e., consists of samples from the same human donor.

Calderon et al. (2019) study a repertoire of 32 immune cell types under resting and activated conditions in humans. The metadata include three QC variables (number of peaks called, number of sequenced reads, and transcription start site enrichment for each sample), which we use in the scone evaluation. Most donors are processed and sequenced separately, and therefore each donor represents a different batch. However, for several donors, some samples underwent a second round of sequencing and this set of resequenced samples constitutes another batch. In the published dataset, the accessibility counts from the two sequencing rounds were summed for each donor. The biological variables of interest are cell type and treatment. The count matrix corresponds to $\mathrm{829,942}$ peaks across 175 samples and was downloaded from the GEO with accession number GSE118189. This dataset was filtered to retain peaks with at least 2 counts per million in at least 10 samples, reducing the dataset to $\mathrm{203,448}$ peaks.

Murphy et al. (2019) study photoreceptors and bipolar cells in the mouse retina. The dataset combines two experiments and we define each experiment as a batch. We consider the cell type as the biological variable of interest. The count matrix corresponds to $\mathrm{110,715}$ peaks across 12 samples and was downloaded from the GEO with accession number GSE131625. It was not relevant to correct for the width of the peaks using cqn in this dataset, since all peaks have a length of 201bp.

Rizzardi et al. (2019) study neuronal and non-neuronal cell populations in the prefrontal cortex and nucleus accumbens in humans. We consider the combination of brain region and cell type as the biological variable of interest. We define a batch variable as the combination of the donor, flow cytometry run, and sequencing date variables. The count matrix corresponds to $\mathrm{961,916}$ peaks across 22 samples and was downloaded from the GEO with accession number GSE96614.

Brain Open Chromatin Atlas (case study)

Fullard et al. (2018) developed a human brain atlas of neuronal and non-neuronal cells across 14 distinct brain regions from 5 human donors. We define a batch variable as the flow cytometry date. Note that while the sequencing date is nested within the flow cytometry date, there are other variables in the metadata that might also be considered to define batches, e.g., PCR date. A total of 49 variables corresponding to potential technical effects were included as QC measures. The biological variable of interest is defined as the combination of cell type and brain region. The count matrix corresponds to $\mathrm{300,444}$ peaks across 115 samples and was downloaded from the Brain Open Chromatin Atlas (BOCA) website, at https://bendlj01.u.hpc.mssm.edu/multireg/.

Mouse tissue atlas (case study)

Liu et al. (2019) created an ATAC-seq atlas of mouse tissues, spanning a total of 20 tissues for both male and female mice. We use the “Slide lane of sequencer” variable recorded in the metadata as batch variable. Four variables (mitochondrial reads, usable reads, transcription start site (TSS) enrichment, and number of reproducible peaks, as identified using the irreproducible discovery rate (IDR) (Li et al., 2011)) are used as QC measures. The combination of gender and tissue type is used as the biological variable of interest. The count matrix corresponds to $\mathrm{296,574}$ peaks across 79 samples and was downloaded from Figshare at https://doi.org/10.6084/m9.figshare.c.4436264.v1.

GC-content retrieval

For each dataset, we use the Bioconductor R package Biostrings to retrieve the GC-content of every peak region, using the reference genome of the relevant organism. The table below provides the genome version used for each dataset.

Dataset	Organism	Genome
Philip et al. (2017)	Mouse	GRCm38
Bryois et al. (2018)	Human	GRCh37.75
Calderon et al. (2019)	Human	GRCh37.75
de la Torre-Ubieta et al. (2018)	Human	GRCh37.75
Murphy et al. (2019)	Mouse	GRCm38
Rizzardi et al. (2019)	Human	GRCh37.75
Fullard et al. (2018)	Human	GRCh37.75
Liu et al. (2019)	Mouse	GRCm37.67

Benchmarking

Defining scone evaluation measures

By default, scone uses a range of evaluation measures to assess normalization. The relevant measures for this work can be divided into three categories, where we use the definitions from the scone paper (Cole et al., 2019).

Clustering properties

• •BIO_SIL: Group the samples according to the value of a categorical covariate of interest (e.g., known cell type, genotype) and compute the average silhouette width for the resulting clustering.
• •BATCH_SIL: Group the samples according to the value of a categorical nuisance covariate (e.g., batch) and compute the average silhouette width for the resulting clustering.
• •PAM_SIL: Cluster the samples using partitioning around medoids (PAM) for a range of user-supplied numbers of clusters and compute the maximum average silhouette width for these clusterings.

Association of accessibility measures with factors of unwanted variation

• •EXP_QC_COR: The weighted coefficient of determination (see Cole et al. (2019) for details) for the regression of log-count principal components on all principal components of user-supplied QC measures.
• •EXP_UV_COR: The weighted coefficient of determination for the regression of log-count principal components on factors of unwanted variation (default 3) derived from negative control genes.

Global distributional properties

• •RLE_MED: Mean squared median relative log-expression (RLE).
• •RLE_IQR: Variance of inter-quartile range (IQR) of RLE.

Differential accessibility analysis performance measures

In addition to evaluating normalization performance using scone, we also examine differential accessibility (DA) performance. The performance evaluation relies on DA analysis results for mock null datasets based on a real dataset, as well as signal datasets simulated based on each real dataset. We define the following set of measures.

Mock null datasets

• •False positive rate: The false positive rate at a nominal $5\text{\%}$ significance level for each peak. In this null setting, a good-performing method is expected to have $5\text{\%}$ of its p-values less than or equal to 0.05.
• •p-value uniformity: The Hellinger distance between the observed p-value distribution and a uniform $\left(\mathrm{0,1}\right)$p-value distribution. A good-performing method is expected to have a small distance.

Simulated datasets with signal

• •Area under receiver operating characteristic curve (AUROC): The area under the receiver operating characteristic (TPR-FPR) curve. A good method is expected to have a high value of AUROC, i.e., is capable of identifying the truly DA peaks without simultaneously calling too many false positives.

GC-content bias evaluation measures

To assess GC-content bias after normalization, we define two measures based on relative log-expression values (Gandolfo and Speed, 2018) across GC-content bins, which are inspired by the RLE_MED and RLE_IQR measures already implemented in scone. We additionally use two measures in the DA analysis assessment.

Let $Y_{ji}$ denote the accessibility measure for peak j in sample i and $L_{ji}=\text{log}\left(Y_{ji}+1\right)$. Then, the RLE is defined as

$$r_{ji}={\mathrm{Ł}}_{ji}-{\overline{L}}_{j.}$$

where ${\overline{L}}_{j.}$ denotes the median of $L_{ji}$ across all samples i. For a set of peaks within a GC-content bin b, we can define a measure of GC-content bias as the mean squared median RLE (Cole et al., 2019), i.e., as the average squared deviation of the median RLE from zero,

$$d_b=\frac{1}{n}\sum _{i=1}^n{\overline{r}}_{.ib}^2$$

where ${\overline{r}}_{.ib}$ is the median RLE value for peaks in bin b for sample i. A small value of $d_b$ generally corresponds to a good normalization of the data, since the median RLE is close to zero. However, if sample-specific GC-content effects exist, then the normalization may only be working for certain ranges of GC-content. We therefore assess whether the mean squared median RLE varies with GC-content by computing its variance across GC-content bins,

$$RLE\_ME{D}_{GC}=\frac{1}{B-1}\sum _{b=1}^B{\left(d_b-\overline{d}\right)}^2$$ (Equation 1)

where $\overline{d}={\sum }_b{d}_b/B$ is the average of $d_b$ across GC-content bins. In the evaluation, we let the number of bins B depend on the total number of peaks in a given dataset by constructing bins containing around $\mathrm{4,000}$ peaks each.

A similar measure is calculated based on the variance of the interquartile range of the RLE measures for each bin,

$$v_b=\frac{1}{n-1}\sum _{i=1}^n{\left(q_{ib}-{\overline{q}}_b\right)}^2$$

where $q_{ib}$ is the interquartile range of the RLE values for peaks in bin b for sample i and ${\overline{q}}_b$ its average across all samples. Using a similar reasoning as above, we then evaluate the variance of $v_b$ across different GC-content bins

$$RLE\_IQ{R}_{GC}=\frac{1}{B-1}\sum _{b=1}^B{\left(v_b-\overline{v}\right)}^2$$ (Equation 2)

where $\overline{v}$ is the average of $v_b$ across all bins.

In addition to RLE measures, we also use two metrics that are evaluated along with the mock and simulated datasets in the DA analysis performance assessment.

Mock null datasets

• •p-value uniformity as function of GC-content: The variance in Hellinger distance between the observed p-value distribution and a uniform $\left(\mathrm{0,1}\right)$p-value distribution across GC-content bins. A good-performing method is expected to have no GC-content bias in terms of p-value uniformity.

Simulated datasets with signal

• •GC-content distribution of DA peaks: Distance between the empirical cumulative distribution functions (ECDF) of the GC-content of called DA peaks and of truly DA peaks. This distance is calculated over a grid of 100 points as the sum of the absolute differences between the two ECDFs. A good-performing method should have a small distance.

Normalization performance: Scone benchmark

We use the Bioconductor R package scone (Cole et al., 2019) to implement and evaluate different normalization procedures. The first step in the scone workflow is to normalize the data using all normalization methods of interest. A range of evaluation measures are then computed for each of the normalized datasets, as described in the previous paragraph. Since some measures tend to be biased towards particular normalization methods, we rely on a subset, selected based on our evaluation as described in supplemental methods S1. As part of the evaluation, the principal components of the log-normalized counts are correlated to factors of unwanted variation as well as quality control variables (if available). The factors of unwanted variation are inferred using RUVSeq (Risso et al., 2014), based on negative control features, here chosen to be the peaks within known housekeeping genes.

Differential accessibility analysis performance in synthetic null and signal scenarios

Our approach to evaluate the impact of normalization on DA analysis is two-fold: First, we perform synthetic null comparisons for each real dataset; second, we generate synthetic signal datasets by simulating DA peaks from each real dataset (see STAR methods, Datasets for a descriptions of each dataset).

Synthetic null scenario

In the null scenario, for each dataset, we create a two-group mock variable so that we expect no systematic differences between the groups. Specifically, for each dataset, we perform stratified random sampling, where the samples for each biological condition are randomly split into two approximately equally-sized groups (e.g., for a biological condition with 4 samples, there are 2 samples per group, and for a biological condition with 3 samples, one group comprises 1 sample and the other 2 samples). For each dataset, following the assignment of samples to groups, we evaluate the performance of normalization methods based on a differential accessibility analysis using this mock variable. Under the synthetic null scenario, all peaks identified as DA are false positives.

Synthetic signal scenario

Additionally, we also evaluate the performance of normalization and DA analysis methods on synthetic signal datasets created from each of the real dataset. Each synthetic dataset comprises 12 samples, which is the minimum number of samples across the eight datasets used in this manuscript (based on 6 randomly selected samples from each group in the mock variable) and has $10\text{\%}$ of all peaks DA. For each selected sample i, we calculate its accessibility fraction for each peak j as

$$F_{ji}=\frac{Y_{ji}}{{\sum }_{j=1}^J{Y}_{ji}}.$$ (Equation 3)

A random subset comprising $10\text{\%}$ of all peaks is simulated to be differentially accessible, with equal up-/down-regulation between groups, via independent binary random variables $S_j$, equal to either $-1$ or 1, each with $1/2$ probability. The $S_j$’s define the group $g\in \left\{\mathrm{1,2}\right\}$ of samples for which the accessibility fractions will be altered as follows

$${\gamma }_{ji}=\{\begin{array}{ll}{F}_{ji}{\exp }^{I(S_j=-1)Z_j},\hfill & \text{if }g\left(i\right)=1\hfill \\ F_{ji}{\exp }^{I(S_j=1)Z_j},\hfill & \text{if }g\left(i\right)=2\hfill \end{array}.$$ (Equation 4)

where $g\left(i\right)\in \left\{\mathrm{1,2}\right\}$ denotes the group to which sample i belongs and $Z_j$ are independent Gaussian random variables with mean 0.8 and standard deviation 0.1. That is, the log-fold-change in accessibility between groups 2 and 1 is $S_j{Z}_j$. The choice of the mean and standard deviation for the log-fold-changes corresponds to fold-changes being on average 2.25, with a minimum of $\sim 1.5$ and a max of $\sim 3.5$, a reasonable scenario. Sequencing depths $N_i^{\text{∗}}$ are simulated from a uniform distribution

$$N_i^{\text{∗}}\sim U\left(N_{min},N_{max}\right).$$

where $N_{min}={\text{min}}_i{\sum }_j{Y}_{ji}$ and $N_{max}={\text{max}}_i{\sum }_j{Y}_{ji}$ denote, respectively, the minimum and maximum library sizes across all samples in the dataset. Given ${\gamma }_{ji}$ and $N_i^{\text{∗}}$, accessibility counts $Y_{ji}^{\text{∗}}$ are then simulated using a Multinomial distribution

$$Y_{ji}^{\text{∗}}|{\gamma }_{ji},N_i^{\text{∗}}\sim Mult\left({\gamma }_{ji},N_i^{\text{∗}}\right).$$ (Equation 5)

For each combination of sample size and DA signal strength, we evaluate 14 simulated datasets (a greater number of simulations was not feasible due to local memory limitations). Differential accessibility analysis is performed using edgeR for all normalization methods, except for DESeq2 normalization where we rely on the native DESeq2 pipeline.

For each simulated dataset, we calculate the true positive rate (TPR) and false discovery rate (FDR), defined as

$$\begin{array}{l}TPR=\frac{TP}{TP+FN}\\ FDR=\frac{FP}{TP+FP}\end{array}.$$ (Equation 6)

where $FN$, $FP$, and $TP$ denote, respectively, the numbers of false negatives, false positives, and true positives. Method performance is visualized using FDR-TPR curves, constructed by calculating, for each of the 14 simulated datasets, FDR and TPR ratios by sequentially moving from the most to the least significant DA peak and then averaging the FDR and TPR over the 14 simulations.

Method ranking

Each normalization procedure is assigned a score for each evaluation criterion (7 normalization performance criteria, 3 GC-content effect removal criteria, and 3 DA performance criteria), constructed such that a high score corresponds to a good performance of the normalization procedure with respect to that evaluation criterion. Since scores are not directly comparable between criteria, we first rank the normalization methods for each evaluation criterion separately, where a high rank reflects good normalization. As a summary for each normalization procedure, we average the ranks across evaluation criteria.

Case studies

Mouse tissue atlas

The raw count matrix from Liu et al. (2019) is obtained as described in the datasets section and is normalized using each of the twelve evaluated normalization procedures, with no peaks filtered out. Euclidean distances between samples are calculated on the log-normalized counts, adding an offset of 1 to avoid taking the log of zero. Hierarchical clustering trees are derived using complete linkage. Differential accessibility analysis is performed using edgeR for all normalization methods, except for DESeq2 normalization where we rely on the native DESeq2 pipeline. Normalized counts are used directly as input for FQ, FQ-FQ, and (smooth) GC-FQ normalization, while normalization offsets are used for TMM and cqn. Overlap of peaks with functional genomic regions is assessed by assigning a peak to known genomic features using ChIPpeakAnno (Zhu et al., 2010) with default settings.

Brain Open Chromatin Atlas

The raw count matrix from Fullard et al. (2018) is obtained as described in the datasets section. We do not filter out any peaks. PCA and hierarchical trees are based on the log-normalized counts, adding an offset of 1 to avoid taking the log of zero. Hierarchical trees use the Euclidean distance between samples and are constructed using complete linkage. DA analysis is performed as described in the mouse tissue atlas (case study). The contrast matrix is defined for comparing the average expression of neuronal vs. non-neuronal samples.

Quantification and statistical analysis

Normalization procedures

Let $Y_{ji}$ denote the accessibility count for peak $j=1,\dots ,J$ in sample $i=1,\dots ,n$. The evaluated normalization procedures can be summarized as follows.

No normalization

The raw counts are used for analysis.

Total-count (TC) / sum normalization

Each count is divided by the total library size, $N_i={\sum }_j{Y}_{ji}$, for its corresponding sample.

Upper-quartile (UQ) normalization

Each count is divided by the upper-quartile (i.e., 75th percentile) of the counts for its corresponding sample. UQ can be beneficial over TC normalization, as the latter can be affected by a few very high counts that dominate the total library size $N_i$.

Trimmed mean of M-values (TMM) normalization

TMM is a global-scaling normalization procedure that was originally proposed by Robinson and Oshlack (2010). As the name suggests, it is based on a trimmed mean of fold-changes (M-values) as the scaling factor. A trimmed mean is an average after removing a set of “extreme” values. Specifically, TMM calculates a normalization factor $F_i^{\left(r\right)}$ for each sample i as compared to a reference sample r,

$${\text{log}}_2\left(F_i^{\left(r\right)}\right)=\frac{{\sum }_{j\in {\mathcal{J}}^{\text{∗}}}{w}_{ji}^r{M}_{ji}^r}{{\sum }_{j\in {\mathcal{J}}^{\text{∗}}}{w}_{ji}^r},$$ (Equation 7)

where $M_{ji}^r$ represents the ${\text{log}}_2$-fold-change of the accessibility fraction as compared to a reference sample r, i.e.,

$$M_{ji}^r={\text{log}}_2\left(\frac{Y_{ji}/N_i}{Y_{jr}/N_r}\right).$$

$w_{ji}^r$ represents a weight calculated as

$$w_{ji}^r=\frac{N_i-Y_{ji}}{N_i{Y}_{ji}}+\frac{N_r-Y_{jr}}{N_r{Y}_{jr}}.$$ (Equation 8)

and ${\mathcal{J}}^{\text{∗}}$ represents the set of peaks after trimming those with the most extreme values.

The procedure only takes peaks into account where both $Y_{ji}>0$ and $Y_{jr}>0$. By default, TMM trims peaks with the $30\text{\%}$ most extreme (i.e., 15% high and 15% low) M-values and $5\text{\%}$ most extreme average accessibility, and chooses as reference r the sample whose upper-quartile is closest to the across-sample average upper-quartile. The normalized counts are then given by ${\tilde{Y}}_{ji}=Y_{ji}/N_i^s$, where

$$N_i^s=\frac{N_i{F}_i^{\left(r\right)}}{{\sum }_i{N}_i{F}_i^{\left(r\right)}/n}.$$

DESeq2 normalization

The median-of-ratios method is used in DESeq2 (Love et al., 2014). It assumes that the expected value ${\mu }_{ji}=E\left(Y_{ji}\right)$ is proportional to the true accessibility of the peak, $q_{ji}$, scaled by a normalization factor $s_i$ for each sample,

$${\mu }_{ji}=s_i{q}_{ji}.$$

The normalization factor $s_i$ is then estimated using the median-of-ratios method compared to a synthetic reference sample r defined based on geometric means of counts across samples

$$s_i={\text{median}}_{\left\{j:Y_{jr}^{\text{∗}}\ne 0\right\}}\frac{Y_{ji}}{Y_{jr}^{\text{∗}}}.$$ (Equation 9)

with

$$Y_{jr}^{\text{∗}}={\left(\prod _{i=1}^n{Y}_{ji}\right)}^{1/n}.$$

From this, we calculate the normalized count as ${\tilde{Y}}_{ji}=Y_{ji}/s_i$.

Full-quantile (FQ) normalization

In full-quantile normalization (Bolstad et al., 2003), the samples are forced to each have a distribution identical to the distribution of the median/average of the quantiles across samples. In practice, we implement full-quantile normalization using the following procedure.

• 1.given a data matrix $Y_{J\times n}$ for J peaks (rows) and n samples (columns),
• 2.sort each column to get $Y^S$,
• 3.replace all elements of each row by the median (or average) for that row,
• 4.obtain the normalized counts $\tilde{Y}$ by re-arranging (i.e., unsorting) each column.

Smooth-quantile (SQ) normalization (qsmooth)

Full-quantile normalization assumes that the read count distribution is similar for each sample and that observed differences in distributions correspond to technical effects. However, this may not always be the case in practice. To tackle this, Hicks et al. (2018) developed smooth-quantile normalization, a variant of full-quantile normalization that is able to deal with datasets where there are large global differences between biological conditions of interest. It provides a balance between (a) full-quantile normalization between samples of each condition separately, and (b) full-quantile normalization on the full dataset. This balance is struck by calculating data-driven weights for each quantile, that specify which of the two normalization options is more appropriate. The weights are estimated in a smooth way across the quantiles, by contrasting the within-condition with the between-condition variability for each quantile. If the within-condition variability is smaller than the between-condition variability, then the weights will favor normalization for each condition separately.

Within-and-between-sample full-quantile (FQ-FQ) normalization

The FQ-FQ method, implemented in the EDASeq package (Risso et al., 2011), accounts for GC-content effects by performing two rounds of full-quantile normalization. First, the features of each sample are grouped into (by default, 10) GC-content bins and full-quantile normalization is performed across bins within each sample (referred to as ‘within-lane normalization’). Next, the data are normalized using full-quantile normalization across all samples.

Conditional-quantile normalization (cqn)

The cqn method (Hansen et al., 2012) uses median regression to model, for each sample, the log-transformed accessibility count $\text{log}{Y}_{ij}$ as a smooth function of GC-content as well as peak width, focusing on peaks with high average count (above 50 by default). Note that for the datasets from Bryois et al. (2018), Murphy et al. (2019), and Rizzardi et al. (2019), all peaks have the same width and hence there is no peak width normalization. Next, subset quantile normalization (Wu and Aryee, 2010) is performed on the residuals of that model (i.e., on the counts adjusted for GC-content) for between-sample normalization. The method could intuitively be thought of as full-quantile normalization after removing a smoothed sample-specific GC-content effect. Normalized counts are calculated as recommended in the cqn vignette, i.e.,

$${\tilde{Y}}_{ji}=\left(\frac{\left(Y_{ji}+1\right){10}^6}{{\sum }_j{Y}_{ji}}\right)2^{O_{ji}}.$$ (Equation 10)

with $O_{ji}$ the normalization offset estimated by cqn, which is on the ${\text{log}}_2$ scale.

GC-full-quantile (GC-FQ) normalization

GC-FQ is similar to FQ-FQ, but relies on the observation that, in ATAC-seq, read count distributions are often more comparable between samples within a GC-content bin, than between GC-content bins within a sample (Figure 2). It therefore applies between-sample FQ normalization for each GC-content bin separately, with 50 bins by default.

Smooth GC-FQ normalization

Smooth GC-FQ is a variant of GC-FQ that applies smooth-quantile normalization across samples within each GC-content bin. Like GC-FQ, it uses 50 bins by default.

Published: October 27, 2022

Data and code availability

• •This paper analyzes existing, publicly available data. The accession numbers for the datasets are listed in the key resources table, or shared on our Zenodo repository at https://doi.org/10.5281/zenodo.6646500. The simulated datasets are also available through the Zenodo repository.
• •All original code is available on GitHub and is publicly available at https://github.com/koenvandenberge/bulkATACGC. DOIs are listed in the key resources table. The normalization method is implemented as part of the qsmooth Bioconductor package.
• •Any additional information required to reanalyze the data reported in this paper is available from the lead contact upon request.