Abstract
Recently, chaotic maps have been considered to design pseudorandom number generator (PRNG). However, some chaotic maps present security disadvantages, such as low uniformity and low randomness properties. Nowadays, chaos-based PRNGs are used as the main source for the development of cryptographic algorithms. In this work, to overcome such weaknesses, a novel 2D hyperchaotic map is proposed based on discrete-time feedback by using Hénon map and Sine map. In addition, the dynamics of the hyperchaotic map are enhanced by using the remainder after division function (rem), where better random statistical properties are obtained. A comparison is made between the enhanced Hénon-Sine hyperchaotic map (EHSHM) and the Hénon-Sine hyperchaotic map through Lyapunov exponent analysis, attractor trajectory, histograms and sensitivity at initialization. Then, 8-bit pseudorandom number generator based on the proposed hyperchaotic map (PRNG–EHSHM) is designed and the initial seed of the PRNG is calculated by a secret key of 60 hexadecimal characters. It is implemented in both MATLAB and Arduino Mega microcontroller for experimental results. A complete security analysis is presented from a cryptographic point of view, such as key space, floating frequency, histograms and entropy of the information. Moreover, the randomness is verified with the tests of the National Institute of Standards and Technology (NIST 800-22). Based on the security results obtained, the proposed PRNG–EHSHM can be implemented in embedded cryptographic applications based on chaos.
Keywords: Chaos, Pseudorandom number generator, 2D Hénon-Sine hyperchaotic map, Microcontroller implementation, Security analysis
Introduction
In the last 2 years, the use of digital communication, especially the Internet and mobile applications have been increased due to user demand and more recently to COVID-19, where various types of personal information are transmitted and stored in the cloud by using different types of networks in telemedicine [1]. There is a growing demand to develop encryption techniques using chaos as main core to design a PRNG to provide confidentiality and protect digital information from unauthorized users. Chaos is nonlinear, very sensitive to initial conditions, control parameters and unpredictability, which make them highly attractive in security applications [2]. Encryption algorithms based on chaos offer many benefits such high speed in stream ciphers, high-security level, increased modularity, flexibility and easier to be performed. In last years, encryption algorithms based on chaotic maps have been used to encrypt information such as images [3, 4], text [5], clinical signals [6] and biometric features [7].
The PRNG is an algorithm for producing deterministic sequences of pseudorandom numbers with mathematical formulas and the chaotic maps are the main core to generate such numbers to be applied in cryptography [8]. Basically, the purpose of cryptography is to allow the transmission and/or storage of private information, so that any intruder who accesses the information does not understand its meaning.
In addition, the security issues can be solved with the intrinsic properties of chaos that are highly similar with cryptographic properties, where encryption algorithms can be developed with the PRNG as the main source for the generation of random data. These properties are: the encryption rounds of a cryptographic algorithm lead to the desired diffusion and confusion properties of the algorithm and the iterations of a chaotic map extend the initial region over the entire phase space, the key of the encryption algorithm can represent the parameters of the chaotic map, whereas the secret key space is larger, more choice of values can be obtained for the control parameters and initial conditions and with more choice of values, the more sensitive the chaotic system and the diffusion process for the algorithm (Table 1) [9]. Although many new chaotic systems were proposed in the literature to serve for the applications of encryption, these systems have complex structures that may limit their implementation due to low randomness, low data and low-speed time [10].
Table 1.
Similarities and differences between chaotic systems and cryptographic algorithms
| Chaotic systems | Cryptographic algorithms |
|---|---|
| Phase space: (sub)set of real numbers | Phase space: finite set of integers |
| Iterations | Rounds |
| Parameters | Key |
| Sensitivity to initial conditions and parameters | Diffusion |
| Ergodicity | Confusion |
Related works
The first part of related works includes the design of PRNGs. Then, we comment about works of chaos-based cryptographic schemes for data encryption. Recently, the development of pseudorandom number generators based on chaotic maps has been proposed with implementation in MATLAB [11, 12] and microcontrollers [13–15], where in some papers, the initial conditions and control parameters are considered the seed of the pseudorandom number generator. In 2022 [16], the authors present a PRNG using the Piecewise Linear Chaotic Map, is a simple chaotic system that is popularly used to generate numbers and proposed a hardware architecture. In 2021 [17], the authors proposed a PRNG using the logistic map where the turbulence is padded into the existing map to improve its chaotic behavior and increase the periodicity, the authors present a comprehensive security analysis. Nevertheless, they mention that it is for lightweight cryptographic applications. In the same year in [18], the authors used two different feedback controllers based on four-dimensional (4D) hyperchaotic systems to design a PRNG and is implemented in microcontroller to encrypt images and present a comprehensive security analysis. In [19], Wang and Cheng also presented a PRNG based on the chaotic logistic map, where they select the seed of the PRNG manually using the initial conditions and control parameters, but the initial seed could be reused to produce the same pseudorandom sequence.
In [20], the authors proposed a deep-zoom analysis of the composition of the logistic map and the tent map, deep-zoom technique transforms each point of a given chaotic orbit by removing the first k-digits after decimal separator and use this to improve the pseudorandom qualities of the composition map as a pseudorandom number generator. In [21], the authors proposed a new 4D chaotic system with rich dynamic characteristics, such as hidden attractors and coexisting attractors, they proposed a RNG using the new 4D chaotic system, the initial conditions and control parameters are introduced manually and the algorithm is validated with the NIST 800-22.
Li-Hua et al. proposed a new 4D chaotic system and a RNG for image encryption, presents the dynamic properties of the new 4D chaotic system and the RNG design was validated with the NIST 800-22; also, a security analysis of the image encryption was made [22]. In 2021, a new quantum multi-image compression and encryption algorithm for image, combining quantum discrete cosine transform with 4D hyperchaotic Hénon map is proposed and presents a statistical analysis attack, such as histogram, correlation and compression performance [23]. In [24], the authors proposed a method to improved chaotic maps to encrypt digital images in a wireless communication scheme, shows that function mod 255 improves the randomness of the pseudorandom number generators and verified performing with statistical tests.
Contribution
Basic chaotic systems such as the Logistic map and Tent map usually perform poorly in terms of chaotic ranges and resisting cracks [25]. In some of chaos-based PRNG’s schemes in literature, the chaotic data are not uniform or analyses are limited to randomness tests without check the statistical properties for cryptographic applications, discrete time chaotic maps are preferred rather than continuous systems because of the convenience for digital realizations. However, most chaotic maps suffer from limited key space, and their low dimensions provide weak security. Therefore, improve pseudorandom properties of chaotic maps with PRNG applications are desirable to improve security in chaos-based cryptographic systems.
In this work, motivated by the above discussion, to overcome low uniformity and low randomness, a novel auto-feedback two-dimensional Hénon-Sine hyperchaotic map (2D-HSHM) is proposed from the feedback of the 1D-Hénon map and 1D-Sine map. Furthermore, we enhanced the pseudorandom properties of the proposed chaotic map applying the arithmetic remainder after division function (rem) and generating the 2D-EHSHM, a comparison of the two hyperchaotic maps is presented with a Lyapunov analysis, attractor trajectory, bifurcation diagram, histograms and sensitivity at initialization to show the advantages obtained, where the enhanced map presents better statistical properties, high complexity and sensitivity to initial condition and control parameters. The 2D-EHSHM is used for a design in a pseudorandom number generator, where the initial seed is calculated by a secret key of 60 hexadecimal characters. The proposed algorithm is implemented in both MATLAB and Arduino Mega microcontroller. A comprehensive security analysis is presented from a cryptographic point of view to validate the algorithm in cryptographic applications, where both software and hardware implementations passed the NIST 800-22 test, a comparison with recent schemes in the literature is presented. The mains contributions of this work are:
The novel 2D Hénon-Sine hyperchaotic map by using discrete-time feedback is proposed.
The remainder after division function to improve randomness of chaos is used for first time in literature.
A PRNG algorithm is designed and implemented in microcontroller with the most complete statistical and security analysis in the literature.
This work is arranged in the following: In Sect. 2, the novel 2D Hénon-Sine hyperchaotic map and the proposed chaotic enhanced process are described, a comparison is made between the original and enhanced hyperchaotic map with different analyses. In Sect. 3, the details of the proposed algorithm and the implementation in MATLAB are presented. In Sect. 4, the PRNG–EHSHM is implemented in Arduino Mega microcontroller. A comprehensive security analysis is presented in Sect. 5. Finally, some conclusions are given in Sect. 6.
Proposed enhanced hyperchaotic map
In this Section, we present the 2D hyperchaotic map model from the 1D Hénon map (1) and the 1D Sine map (2) and the proposed enhanced process. The structure diagram of the proposed model is shown in Fig. 1.
Fig. 1.
Structural diagram of proposed 2D hyperchaotic map
In Fig. 1, the symbol represents a multiplier, represents one delay in discrete time, H and S are the Hénon map and Sine map, respectively.
The Hénon map can be represented as a one-dimensional chaotic map to produces nonlinear chaotic sequences, it used as one-dimensional based on the classic Hénon map [26]. The Hénon map can be mathematically described as one-dimensional map as follows
| 1 |
where is the state of the map, is the initial condition, and are the control parameters and is the number of iterations. The Hénon map presents chaotic dynamics with and .
The Sine map is a one-dimensional chaotic map [27]. The Sine map can be mathematically described as follows
| 2 |
where is the state of the map, is the initial condition, is the control parameter and is the number of iterations.
Based on the Hénon map and Sine map with the proposed structural diagram in Fig. 1, the proposed 2D Hénon-Sine hyperchaotic map is described as follows
| 3a |
| 3b |
where and are the states of the map, , and are the control parameters.
We propose a method to improve the chaotic dynamics of the proposed hyperchaotic map to produce better pseudorandom sequences, increase the range of the control parameters and the sensitivity to initial conditions applying the mathematical function remainder after division (rem).
The enhanced Hénon-Sine hyperchaotic map has the following expression
| 4a |
| 4b |
where and are the states of the hyperchaotic map, and are the initial conditions and , and are the control parameters, the function rem is the operation of remainder after division considering 32-bits floating-point arithmetic.
| 5 |
where a is the dividend, b is the divisor and round a number to the nearest integer, basically calculate the remainder after integer division is performed on the dividend expression by the divisor expression.
By applying the rem function and multiplying the chaotic dynamics by 101 in (5), we obtain a much more uniform distribution of the chaotic dynamics, since we transform all the original data to data with values between 0 and 1. These results are shown by comparing the HSHM and EHSHM through the Lyapunov exponent, attractor trajectory, bifurcation diagram, histograms and sensitivity at initialization in the following subsections.
Lyapunov exponent
We verified the chaotic dynamics numerically with the Lyapunov exponent (LE). The Lyapunov exponent measures the average rate of divergence or convergence of two nearby trajectories in phase space. A positive Lyapunov exponent indicates chaos [28], a 1D map has only one Lyapunov exponent and a 2D map has two Lyapunov exponents, the higher the value of the Lyapunov exponent, the chaotic map is more sensitive to initial conditions and control parameters. We calculate the Lyapunov exponent with (6) of the Hénon map, Sine map, HSHM and EHSHM with two trajectories using the same control parameters but very close initial conditions.
| 6 |
where is the Lyapunov exponent, is the initial condition, is another very close initial condition and I is the number of iterations. The values used for initial conditions are and , for control parameters are , and , a disturbance of and iteration . In Table 2, we present the results obtained from , where we can see that EHSHM has larger Lyapunov exponents (6.2466 and 6.0612), which indicates that it is more sensitive to initial conditions and control parameters compared to HSHM which has low values of LE. In addition, it has two positive LE, which indicates hyperchaos, hyperchaotic system is mathematically defined as a chaotic system, implying that its dynamics are expended in many different directions simultaneously, improving the chaotic features of the map. The hyperchaotic attractor has more complex dynamic behaviors as compared with chaotic system [29, 30].
Table 2.
Lyapunov exponents of Hénon map, Sine map, HSHM and EHSHM
| Hénon map | Sine map | HSHM | EHSHM | |
|---|---|---|---|---|
| x | 0.1718367 | 0.4152323 | 0.6570296 | 6.2466736 |
| y | – | – | 0.5953513 | 6.0612888 |
Attractor trajectory
The chaotic attractor trajectory is a direct observation method, it is distributed in a limited phase space of the chaotic system. For the chaotic system, if the movement of the attractor trajectory is distributed in a uniform and wide range, it indicates that the output values of the system have better randomness. We iterate 20,000 times and we have shown the trajectory of the Hénon map (Fig. 2a), Sine map (Fig. 2b), HSHM (Fig. 2c) and EHSHM (Fig. 2d). The results in Fig. 2d show that the trajectory of the EHSHM attractor is more evenly distributed throughout the phase space. Therefore, the output values have better randomness, because the data is distributed throughout all the phase space.
Fig. 2.
Attractor trajectory: a Hénon map, b Sine map, c HSHM and d EHSHM
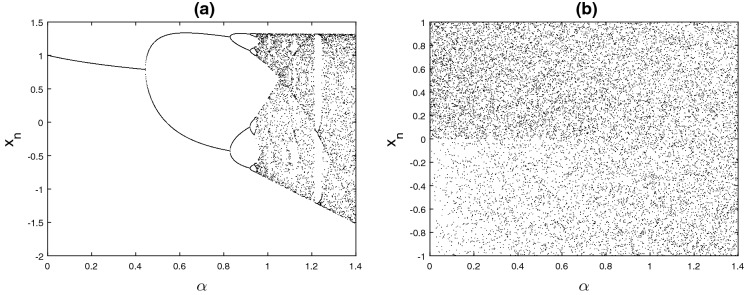
Bifurcation diagram
When the system parameter is changed, the motion state of the system is also changed. The bifurcation diagram can visually see the process of the system state change with the control parameters. The bifurcation diagram of the HSHM and EHSHM of state x with fixed is shown in Fig. 3a, b respectively. The results in Fig. 3b, demonstrate that the EHSHM does not have any periodic state, it is a chaotic state between the range . Therefore, the chaotic state has a wide range of parameters, indicating that can increase the key space for cryptographic applications.
Fig. 3.
Bifurcation diagram: a HSHM and b EHSHM
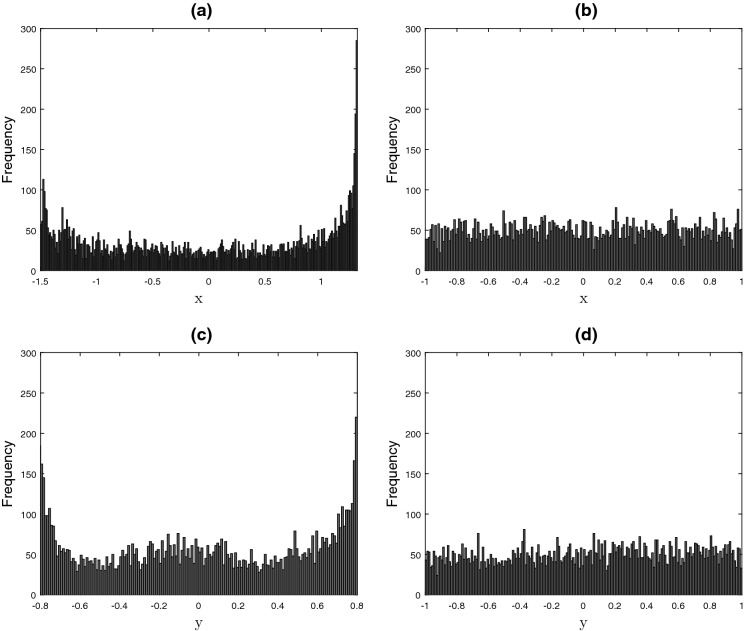
Histogram
A histogram shows the frequency of each element in a graphical form that is, how many times each symbol appears in a sequence. In Fig. 4a, b, the histogram of 10,000 values of state x from HSHM and EHSHM is shown; it is clear that state x of HSHM does not present good distribution of chaotic data, where high frequencies are close to 1.5 and 1.4. However, in EHSHM after applying the rem function, the results show better distribution of chaotic data with values between 0 and 1. In Fig. 4c, d, it is the same case with state y.
Fig. 4.
Histogram of state x: a HSHM and b EHSHM, histogram of state y: c HSHM and d EHSHM
Sensitivity at initialization
We present the divergence in time of two trajectories with similar initial conditions and . In Fig. 5a, b, the state x and state y for HSHM, Fig. 5c, d, state x and y for EHSHM. In Fig. 5c, d, we can observe that the EHSHM is more sensitive to initial conditions, the trajectories start to diverge around iteration 30 for HSHM and 3 for EHSHM.
Fig. 5.

Graphical sensitivity to the initial conditions: a state x, b state y of HSHM, c state x and d state y of EHSHM
As a result, the enhanced Hénon-Sine hyperchaotic map presents better uniform statistical properties and higher sensitivity at initial conditions and control parameters, according to the analysis presented, are used in the proposal of a PRNG to produce pseudorandom numbers with high randomness that is described in the next section.
Pseudorandom number generator based on enhanced 2D Hénon-Sine hyperchaotic map
A pseudorandom number generator is an algorithm that produces sequences of numbers that is a very good approximation to a random set of numbers [14]. For the proposed PRNG–EHSHM algorithm, we use the chaotic sequences of Eqs. (4a) and (4b), to increase randomness. We implement an indirect way of calculating the initial conditions and control parameters by using 60 hexadecimal characters based on work in [31].
The steps of the proposed PRNH-EHSHM algorithm are described as follows
Defined the secret key The initial conditions and control parameters of the EHSHM are determined from 60 hexadecimal characters selected manually or randomly. The 230-bits key is divided into 10 sections , as shown in Table 3.
Iterate the EHSHM The hyperchaotic map is iterated N times using the Eq.(4a) and Eq.(4b), to produce pseudorandom sequence with decimal numbers between (0, 1) considering 32-bits floating-point arithmetic, achieving decimal precision.
- The sequences from step 2 are converted from decimal to 8-bit integer Each value of the chaotic sequence is transformed into an 8-bit integer with the following expressions.
7a
where is the number of iterations, is the round to the nearest operation and , are the pseudorandom sequences.7b
Table 3.
Secret key definition
| Secret key | PRNG–EHSHM | ||
|---|---|---|---|
| 60 Hex characters | where | ||
| Values | |||
| Control parameters | |||
| Initial conditions | |||
Analyses of PRNG–EHSHM in MATLAB
We first implement the PRNG–EHSHM at software level in MATLAB to observe the temporal graphs, histograms, verify the entropy of the information and randomness with the set of NIST 800-22 statistical tests, since it is necessary to determine the security, efficiency and pseudorandomness for applications in cryptography. In Fig. 6, we observe the temporal graphs of the PRNG–EHSHM, the first 100 iterations where the evolution with time of the trajectories of the state x and y is shown, we obtained values between 0 and 1. In Fig. 7, the histogram of 10,000 data from values of 0-255 are obtained from the x and y states sequences, where we can observe a uniform distribution of the data obtained.
Fig. 6.

Temporal graphs of the PRNG–EHSHM: a state x and b state y
Fig. 7.

Histogram of the PRNG–EHSHM: a state x and b state y
The information entropy measures the randomness of the sequence in integer values and high entropy values signify a robust PRNG. When the more chaotic a sequence is, the greater the information entropy. The entropy H(m) of a sequence m is defined as follows
| 8 |
where N is the number of bits of each element of the sequence m, is all possible symbols in the sequence, represents a probability of the element in the sequence and the entropy is expressed in bits. In the proposed PRNG–EHSHM, the maximum entropy is 8. Figure 8 shows the result of entropy calculated from 50 pseudorandom sequences by using 50 keys selected randomly. The average entropy of 50 test is 7.9934. Therefore, the proposed PRNG–EHSHM has high pseudorandom properties.
Fig. 8.

Information entropy analysis for MATLAB implementation
NIST 800-22 randomness test
The NIST 800-22 is a statistical test suite to determine the level of randomness in pseudorandom number generators for cryptographic applications. Table 4 presents the name of the 15 tests of the NIST 800-22 [32].
Table 4.
NIST 800-22 tests definition
| Number | NIST 800-22 test |
|---|---|
| 1 | Frequency test (FT) |
| 2 | Frequency test within a block (FBT) |
| 3 | Cumulative sum test (CST) |
| 4 | Runs test (RT) |
| 5 | Test for the longest run of ones in a block (LROBT) |
| 6 | Binary matrix rank test (BMRT) |
| 7 | Discrete Fourier transform test (DFTT) |
| 8 | Non-overlapping template matching test (NTMT) |
| 8 | Overlapping template matching test (OTMT) |
| 10 | Maurer’s universal statistical test (MUST) |
| 11 | Approximate entropy test (AET) |
| 12 | Random excursions test (RET) |
| 13 | Random excursions variant test (REVT) |
| 14 | Serial test (ST) |
| 15 | Linear complexity test (LCT) |
The 15 tests are applied to 1000 PRNG–EHSHM sequences generated by 1000 different randomly selected keys. Based on [33], we calculate the probability P-value. The P-value must be greater than a predefined threshold to pass the test. If all tests pass, then the sequence is considered random with a confidence of ; otherwise, the sequence is not considered random. Table 5 shows the result of the 15 tests carried out, where all the tests are over the acceptable interval according with [33], the acceptable proportion range is [0.9833245, 0.9966745], we obtain that most of the sequences pass all randomness tests and the average value is 99%.
Table 5.
The NIST 800-22 test results based in MATLAB implementation
| No. | Statistical test | Count of sequences with P-value | Count of sequences with P-value | Proportion successful |
|---|---|---|---|---|
| 1 | FT | 993 | 7 | 0.993 |
| 2 | FTB | 999 | 1 | 0.999 |
| 3 | CST | 999 | 1 | 0.999 |
| 4 | RT | 989 | 11 | 0.989 |
| 5 | LROBT | 983 | 17 | 0.983 |
| 6 | BMRT | 984 | 16 | 0.984 |
| 7 | DFTT | 984 | 16 | 0.984 |
| 8 | NTMT | 984 | 16 | 0.984 |
| 9 | OTMT | 999 | 1 | 0.999 |
| 10 | MUST | 990 | 10 | 0.990 |
| 11 | AET | 993 | 7 | 0.993 |
| 12 | RET | 984 | 16 | 0.984 |
| 13 | REVT | 993 | 7 | 0.993 |
| 14 | ST | 983 | 17 | 0.983 |
| 15 | LCT | 988 | 12 | 0.988 |
Microcontroller implementation of PRNG–EHSHM
The proposed PRNG–EHSHM is implemented at hardware level in Arduino Mega microcontroller (Fig. 9) [34]. Arduino Mega uses the ATmega2560 microcontroller, the high performance, low power microcontroller, RISC-based AVR 8-bit microchip and 32 general purpose work registers. The device reaches a performance of 16 MIPS at 16 MHz and operates between 4.55.5 volts, among other important features for almost any application. The open-source Arduino Software (IDE) makes it easy to write the code and upload it to the board.
Fig. 9.

Arduino Mega board
The PRNG–EHSHM is implemented in Arduino Mega with 32-bit floating-point arithmetic and the output is defined as 8-bit unsigned integer. Figure 10 shows the histogram of 20,000 8-bit data (values between 0 and 255), which are stored in a *.tex file to be analyzed in MATLAB.
Fig. 10.
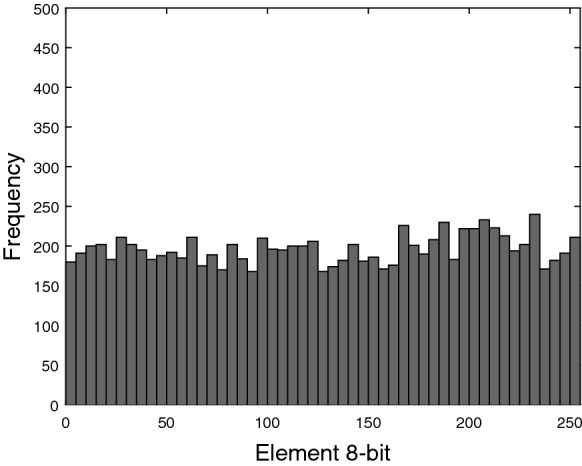
Histogram of 8-bit data extracted from Arduino Mega
We calculated the Lyapunov exponent of the PRNG–EHSHM from three sequences obtained from Arduino Mega with three randomly keys. In Table 6, we present the results, which indicate that the sequences in Arduino Mega are chaotic and highly sensitive to initial conditions and control parameters.
Table 6.
Lyapunov exponent for PRNG–EHSHM in microcontroller
| Sequence | x | y |
|---|---|---|
| 1 | 6.2245 | 6.0351 |
| 2 | 6.2512 | 6.0187 |
| 3 | 6.2685 | 6.0415 |
Security analyses based on microcontroller implementation
In this section, several security analyses are made from a cryptographic point of view by cryptograms extracted from the microcontroller and using MATLAB for the different security analysis. The PRNG must resist all the known attacks, such as key space, key sensitivity, floating frequency, histograms, correlation, autocorrelation and information entropy. In addition, the NIST 800-22 test to verify the randomness of the proposed PRNG–EHSHM for applications in cryptography.
Key space
The seed or the secret key of a PRNG must have more than possible secret keys as mentioned in [35], to resist an exhaustive attack. In the proposed PRNG, the key is given by 60 hexadecimal characters and according to the IEEE standard floating-point [36], specifically binary 32, the computational precision of the 32-bits single-precision number is about . If we assume the precision of and 32-bits floating-point arithmetic, where only 23-bits are considered for the key, the proposed PRNG–EHSHM has possible keys, where all of them are considered strong.
Key sensitivity
A basic property of chaotic maps and PRNGs are to be sensitive to small changes in the initial conditions. Secret key sensitivity means that just a small change in the key causes large changes in the output, generating a totally different pseudo-random sequence. The following key sensitivity tests of the PRNG–EHSHM algorithm were performed using four similar keys, which differ by only one bit (Table 7). In Fig. 11, we present the pseudorandom trajectory (the first 20) generated by the proposed PRNG by using the four keys. After three iterations, the dynamics are totally different from each other.
Table 7.
Secret keys used for key sensitivity analysis
| Key number | Secret key |
|---|---|
| KEY 1 | 11223344556677889900AABBCCDDEEFF1122334455667788112233445566 |
| KEY 2 | 21223344556677889900AABBCCDDEEFF1122334455667788112233445566 |
| KEY 3 | 31223344556677889900AABBCCDDEEFF1122334455667788112233445566 |
| KEY 4 | 41223344556677889900AABBCCDDEEFF1122334455667788112233445566 |
Fig. 11.
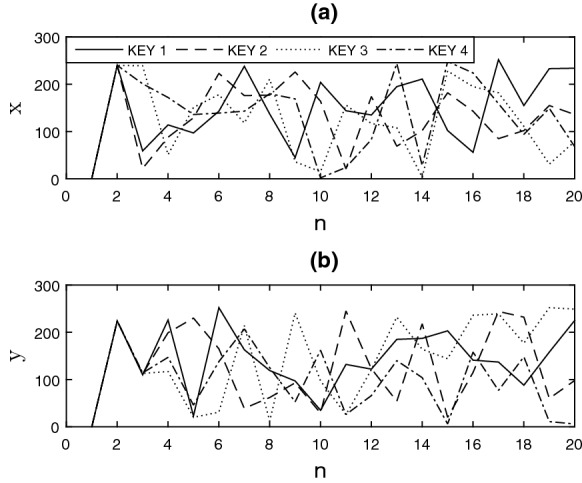
Key sensitivity of first 20 iterations for PRNG–EHSHM in Arduino Mega: a state x and b state y
Another analysis that is used to measure the difference between two sequences is NPCR (Net Pixel Change Rate), which is determined according to (9). Determines how many elements are different between the sequences in percentage.
| 9 |
where
| 10 |
The UACI (Unified Average Changing Intensity) which is determined in (11), measures how much one sequence differs from another in magnitude on average.
| 11 |
In this analysis, we determined a sequence of PNRG-EHSHM using the KEY 1 of Table 7 to produce . Twenty sequences are generated for with 20 keys with one bit different with the KEY 1. The results of NPCR and UACI are shown in Table 8, where the proposed algorithm is highly sensitive at bit-level in the secret key since tested sequences are more than 99.60% different with a magnitude of 33.29% in average.
Table 8.
Key sensitivity results
| Analysis | Results (%) |
|---|---|
| NPCR | 99.6077 |
| UACI | 33.2951 |
Floating frequency
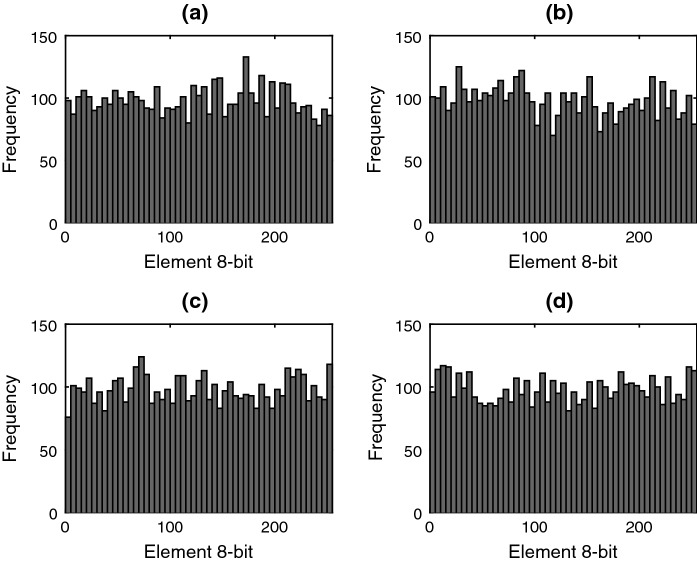
Floating frequency (FF) analysis is used to determine whether pseudorandom sequences exhibit weak or strong sections. In the proposed PRNG–EHSHM, windows of 256 symbols are evaluated, expecting to have the most different elements. First, a window of the 256 symbols is selected and it is checked how many elements are different, then the window is shifted one item to the right and the floating frequency is obtained again. Figure 12 shows the result of the floating frequency for four sequences of 2500 elements (8-bit) using the four keys of Table 7.
Fig. 12.

Floating frequency analysis: a FF results for KEY 1, b FF results for KEY 2, c FF results for KEY 3 and d FF results for KEY 4
The results show uniformity in Fig. 12a: 161.69, Fig. 12b: 161.96, Fig. 12c: 161.84 and Fig. 12d: 162.66, have different elements in average. Therefore, the PRNG produces uniform pseudorandom properties.
Histogram
A good PRNG should present a uniform histogram with any secret key. In Fig. 13, four histograms with 5000 8-bit numbers are obtained from the PRNG–EHSHM with four different secret keys of Table 7. Based on the histograms, the proposed PRNG generates uniform outputs.
Fig. 13.
Histograms of PRNG–EHSHM: a Histogram for KEY 1, b Histogram for KEY 2, c Histogram for KEY 3 and d Histogram for KEY 4
Correlation
The correlation determines if there is a relationship between two sequences of the same length, it is calculated with (12). The value of correlation is , where 0 means null correlation and 1 high correlation.
| 12 |
where x and y are values of two sequences and N is the number of elements in one sequence.
The correlation average is from 10 pseudorandom sequences generated by 10 keys selected randomly. The result is close to 0 indicating that the sequences are independent with no relation to each other.
Autocorrelation
Autocorrelation (AC) is calculated with (13) and determines if the PRNG–EHSHM generates repetitive sequences or patterns.
| 13 |
where AC, the autocorrelation of the PRNG shifted k positions, A is the number of matches between the original and the shifted sequence, D is the number of mismatches and N is the length of the sequence. Values close to 1 means that many bits are identical, values close to -1 means that many bits are opposed and values of 0 means there are the same number of identical and opposed bits.
In this analysis, the bit-level autocorrelation is calculated, the autocorrelation is achieved up to k = 500 to the right using circular shift. In Fig. 14, the AC results are shown of three sequences of 2500 8-bit data, generated from the first three keys of Table 7. The results present AC close to zero for all the tests. Therefore, the PRNG–EHSHM produces uniform pseudorandom numbers with no repeating patterns and no periodicity.
Fig. 14.

Autocorrelation analysis: a AC for KEY 1, b AC for KEY 2 and c AC for KEY 3
Information entropy
The information entropy it measures how much disorder the PRNG has in the output, since the PRNG must produce unpredictable numbers. High values of entropy mean a robust pseudorandom generator, whereas low values of entropy mean a weak pseudorandom generator with certain degree of predictability. The average result of 10 sequences with 10 keys selected randomly of the PRNG–EHSHM implemented in Arduino Mega is 7.9965. Therefore, the sequences are unpredictable.
NIST 800-22 test
In cryptosystems based on chaos, it is important to verify the PRNG. The sequences generated by the PRNG–EHSHM implemented in Arduino Mega are subjected to NIST 800-22 (see Sect. 3.2) to verify the randomness. We extracted 20 sequences from Arduino Mega and the average results are shown in Table 9, where the PRNG–EHSHM implemented in Arduino Mega can generate pseudorandom sequences passing the NIST 800-22 test suite.
Table 9.
The NIST 800-22 tests results based on microcontroller implementation
| No. | Statistical test | P-value | Result | |
|---|---|---|---|---|
| 1 | FT | 0.1768 | Passed | |
| 2 | FTB | 0.8736 | Passed | |
| 3 | CST | 0.5016 | Passed | |
| 4 | RT | 0.2407 | Passed | |
| 5 | LROBT | 0.4275 | Passed | |
| 6 | BMRT | 0.8794 | Passed | |
| 7 | DFTT | 0.8203 | Passed | |
| 8 | NTMT | 0.9040 | Passed | |
| 9 | OTMT | 0.8103 | Passed | |
| 10 | MUST | 0.9967 | Passed | |
| 11 | AET | 0.6105 | Passed | |
| 12 | RET | 0.2562 | Passed | |
| 13 | LCT | 0.3621 | Passed | |
| 14 | ST | 0.1768 | Passed | |
| − 3 | 0.6030 | |||
| − 2 | 0.8239 | |||
| − 1 | 0.9614 | |||
| 15 | REVT | 1 | 0.7371 | Passed |
| 2 | 0.5880 | |||
| 3 | 0.9562 |
Throughput
We calculate the time that the PRNG takes to generate 1000 chaotic data in MATLAB and Arduino Mega, we generate 10 chaotic sequences with 10 different secret keys and we obtain the average. In Table 10, the results obtained are shown with a satisfactory speed.
Table 10.
Time obtained to generate 1000 chaotic data
| Implementation | Time (Mbit/s) | |||
|---|---|---|---|---|
| MATLAB | 237.38 | |||
| Arduino Mega | 20.76 |
Discussion and comparisons with the literature
The properties of chaos such as random behavior, ergodic behavior and extreme sensitivity to initial conditions, make chaotic systems very attractive for PRNG design and cryptographic applications. Chaotic maps with uniform data and high processing speed are important for the development of a PRNG, since they generate more random data and reduce repeatability. Also, the speed of generating this data is necessary when it is used in security applications. The PRNG is an important module in the development of cryptosystems to be robust against different types of security attacks. Thus, development of a PRNG with good random qualities and high processing speed is necessary.
The EHSHM present better results than the original map (HSHM) according to the analyses above, the enhancement of the chaotic map is satisfactory since better dynamics are obtained that benefit the development of the proposed PRNG. The results obtained in the proposed scheme are summarized in Table 11.
Table 11.
General results of the proposed chaotic map EHSHM
| Characteristic | Description |
|---|---|
| High Lyapunov exponent | Increased sensitive to initial conditions and control parameters |
| Hyperchaotic attractor | More complex dynamic behaviors (high randomness) |
| Good bifurcation diagram | Wide range of parameters |
| Better histogram | Excellent uniformity of chaotic data |
| Secret key | 60 hexadecimal characters |
The advantages of the PRNG are: a high value of the Lyapunov exponent, which makes it even more sensitive to initial conditions and control parameters, more complex dynamics, more randomness, a large key space of , in [37] is and in [38], better distribution and fast generation of chaotic data, 20.76 Mbit/s in microcontroller Arduino Mega, in [39] is 14.48 Mbit/s. In addition, the level of security against various attacks and the simplicity of implementation. The disadvantages of the proposed scheme: the hyperchaotic map with a trigonometric function could not be implemented on some microcontrollers and the feedback process reduces slightly the processing speed. The comparisons of the PRNG–EHSHM with similar schemes in the literature are presented in Table 12.
Table 12.
Comparisons with similar schemes in the literature
| PRNG–EHSHM | Ref. 2022 [16] | Ref. 2021 [17] | Ref. 2021 [18] | |
|---|---|---|---|---|
| Chaos properties | ||||
| Chaotic map | Hénon-Sine | Piece-wise linear | Duffing and | 4D-Hyperchaotic |
| map | Chaotic map | 2D-Logistic map | map | |
| Lyapunov exponent | ||||
| Attractor trajectory | − | − | ||
| Bifurcation diagram | ||||
| Histogram | − | − | − | |
| Sensitivity at initialization | − | − | − | |
| Security analysis | ||||
| Key space | − | |||
| Key sensitivity | − | |||
| NPCR and/or UACI | − | − | ||
| Floating frequency | − | − | − | |
| Histogram | − | − | ||
| Correlation | ||||
| Autocorrelation | − | |||
| Information entropy | ||||
| Statistical analysis | ||||
| NIST 800-22 | ||||
| Other | − | − | − | − |
| Implementation | ||||
| MATLAB | ||||
| Microcontroller | − |
Conclusions
In this work, we presented a two-dimensional hyperchaotic map based on the 1D Hénon map and 1D Sine map, the randomness and uniformity was improved with the remainder after division function, we obtained the two-dimensional enhanced hyperchaotic Hénon-Sine map (2D-EHSHM) that produces better pseudorandom properties than the original map according to the Lyapunov exponent, attractor trajectory, bifurcation diagram, histograms and sensitivity at initialization. In addition, we proposed a new pseudorandom number generator algorithm that produces 8-bit pseudorandom numbers generated with high randomness according to the analysis presented, where the seed of the PRNG is calculated indirectly by a secret key of 60 hexadecimal characters to obtain the initial conditions and control parameters. It was implemented in both MATLAB and Arduino Mega microcontroller. The PRNG–EHSHM was validated with the most complex set of randomness tests, the NIST 800-22, different security analyses were carried out from a cryptographic point of view, where the results obtained are satisfactory to apply it in cryptography, particularly in embedded security using low-cost microcontrollers.
Acknowledgements
This work was supported by the CONACYT, Mexico, under Research Grant 166654 (A1-S-31628).
Data availability
The datasets generated during and/or analyzed during the current study are available from the corresponding author on reasonable request.
Declarations
Conflict of interest
The authors declare that there are no conflicts of interest regarding the publication of this paper.
Footnotes
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Contributor Information
Daniel Murillo-Escobar, Email: dmurillo38@uabc.edu.mx.
Miguel Ángel Murillo-Escobar, Email: murillo.miguel@uabc.edu.mx.
César Cruz-Hernández, Email: ccruz@cicese.mx.
Adrian Arellano-Delgado, Email: adrian.arellano@uabc.edu.mx.
Rosa Martha López-Gutiérrez, Email: roslopez@uabc.edu.mx.
References
- 1.Payán D, Frehn L, Garcia L, Tierney A, Rodriguez P. Telemedicine implementation and use in community health centers during COVID-19: clinic personnel and patient perspectives. SSM: Qual. Res. Health. 2022;2:100054. doi: 10.1016/j.ssmqr.2022.100054. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Arboleda E, Balaba J, Espineli J. Chaotic Rivest–Shamir–Adlerman algorithm with data encryption standard scheduling. Bull. Electr. Eng. Inform. 2017;6:219–227. doi: 10.11591/eei.v6i3.627. [DOI] [Google Scholar]
- 3.Huang ZW, Zhou NR. Image encryption scheme based on discrete cosine Stockwell transform and DNA-level modulus diffusion. Opt. Laser Technol. 2022;149:107879. doi: 10.1016/j.optlastec.2022.107879. [DOI] [Google Scholar]
- 4.Gao X. Image encryption algorithm based on 2D hyperchaotic map. Opt. Laser Technol. 2021;142:107252. doi: 10.1016/j.optlastec.2021.107252. [DOI] [Google Scholar]
- 5.Song W, Wang B, Wang Q, Peng Z, Lou W, Cui Y. A privacy-preserved full-text retrieval algorithm over encrypted data for cloud storage applications. J. Parallel Distrib. Computing. 2017;99:14–27. doi: 10.1016/j.jpdc.2016.05.017. [DOI] [Google Scholar]
- 6.Michel-Macarty JA, Murillo-Escobar MA, López-Gutiérrez RM, Cruz-Hernández C, Cardoza-Avendaño L. Multiuser communication scheme based on binary phase-shift keying and chaos for telemedicine. Comput. Methods Progr. Biomed. 2018;162:165–175. doi: 10.1016/j.cmpb.2018.05.021. [DOI] [PubMed] [Google Scholar]
- 7.Nagakrishnan R, Revathi A. A robust cryptosystem to enhance the security in speech based person authentication. Multimed. Tools Appl. 2020;79:20795–20819. doi: 10.1007/s11042-020-08846-1. [DOI] [Google Scholar]
- 8.Pushpalatha, G.S., Ramesh, S.: Chaotic based encryption algorithms for speech signal and cryptographic requirements: a brief survey. Mater. Today: Proc. (2021)
- 9.Kocarev L. Chaos-based cryptography: a brief overview. IEEE Circuits Syst. Mag. 2001;1:6–21. doi: 10.1109/7384.963463. [DOI] [Google Scholar]
- 10.Hamsa A, Abdullah-Hikmat N, Abdullah-Waleed A, Mahmoud AJ. A hybrid chaotic map for communication security applications. Int. J. Commun. Syst. 2019;33:1–20. [Google Scholar]
- 11.Lambić D. Security analysis and improvement of the pseudo-random number generator based on quantum chaotic map. Nonlinear Dyn. 2018;94:1117–1126. doi: 10.1007/s11071-018-4412-x. [DOI] [Google Scholar]
- 12.Lambić D, Nikolić M. Pseudo-random number generator based on discrete-space chaotic map. Nonlinear Dyn. 2017;90:223–232. doi: 10.1007/s11071-017-3656-1. [DOI] [Google Scholar]
- 13.Meranza-Castillón MO, Murillo-Escobar MA, López-Gutiérrez RM, Cruz-Hernández C. Pseudorandom number generator based on enhanced Hénon map and its implementation. AEU: Int. J. Electr. Commun. 2019;107:239–251. [Google Scholar]
- 14.Elmanfaloty RA, Abou-Bakr E. Random property enhancement of a 1D chaotic PRNG with finite precision implementation. Chaos Solitons Fractals. 2019;118:134–144. doi: 10.1016/j.chaos.2018.11.019. [DOI] [Google Scholar]
- 15.Rezk AA, Madian AH, Radwan AG, Soliman AM. Reconfigurable chaotic pseudo random number generator based on FPGA. AEU: Int. J. Electr. Commun. 2019;98:174–180. [Google Scholar]
- 16.Kopparthi VR, Kali A, Sabat SL, Anumandla KK, Peesapati R, Eyebe-Fouda JS. Hardware architecture of a digital piecewise linear chaotic map with perturbation for pseudorandom number generation. AEU: Int. J. Electr. Commun. 2022;147:154138. [Google Scholar]
- 17.Krishnamoorthi S, Jayapaul P, Dhanaraj RK, Rajasekar V, Balusamy B, Islam H. Design of pseudo-random number generator from turbulence padded chaotic map. Nonlinear Dyn. 2021;104:1627–1643. doi: 10.1007/s11071-021-06346-x. [DOI] [Google Scholar]
- 18.Deep-Gupta M, Chauhan RK. Secure image encryption scheme using 4D-hyperchaotic systems based reconfigurable pseudo-random number generator and S-Box. Integration. 2021;81:137–159. doi: 10.1016/j.vlsi.2021.07.002. [DOI] [Google Scholar]
- 19.Wang L, Cheng H. Pseudo-random number generator based on logistic chaotic system. Entropy. 2019;21:960. doi: 10.3390/e21100960. [DOI] [Google Scholar]
- 20.Valle J, Machicao J, Odemir M. Chaotical PRNG based on composition of logistic and tent maps using deep-zoom. Chaos Solitons Fractals. 2022;161:112296. doi: 10.1016/j.chaos.2022.112296. [DOI] [Google Scholar]
- 21.Li-Hua G, Rouqing W, Nanrun Z. A new 4D chaotic system with coexisting hidden chaotic attractors. Int. J. Bifurc. Chaos. 2020;30:2050142. doi: 10.1142/S0218127420501424. [DOI] [Google Scholar]
- 22.Li-Hua G, Hui-Xin L, Rou-Qing W, Nan-Run Z. New 4D chaotic system with hidden attractors and self-excited attractors and its application in image encryption based on RNG. Phys. A. 2022;591:126793. doi: 10.1016/j.physa.2021.126793. [DOI] [Google Scholar]
- 23.Jing-Yi D, Yan M, Nan-Run Z. Quantum multi-image compression-encryption scheme based on quantum discrete cosine transform and 4D hyper-chaotic Henon map. Quantum Inf. Process. 2021;20:246. doi: 10.1007/s11128-021-03187-w. [DOI] [Google Scholar]
- 24.García-Guerrero EE, Inzunza-González E, López-Bonilla OR, Cárdenas-Valdez JR, Tlelo-Cuautle E. Randomness improvement of chaotic maps for image encryption in a wireless communication scheme using PIC-microcontroller via Zigbee channels. Chaos Solitons Fractals. 2020;113:109646. doi: 10.1016/j.chaos.2020.109646. [DOI] [Google Scholar]
- 25.Lan R, He J, Wang S, Liu Y, Luo X. A parameter-selection-based chaotic system. IEEE Trans. Circuits Syst. 2019;66:492–496. doi: 10.1109/TCSII.2018.2865255. [DOI] [Google Scholar]
- 26.Hénon M. A two-dimensional mapping with a strange attractor. Commun. Math. Phys. 1976;50:69–77. doi: 10.1007/BF01608556. [DOI] [Google Scholar]
- 27.Mahaboob-Basha S, Mathivanan P, Balaji-Ganesh A. Bit level color image encryption using Logistic–Sine–Tent–Chebyshev (LSTC) map. Optik. 2022;259:168956. doi: 10.1016/j.ijleo.2022.168956. [DOI] [Google Scholar]
- 28.Wolf, A.: Quantifying Chaos with Lyapunov Exponents. Princeton University Press. 13, 273–289 (1986)
- 29.Lai Q, Lai C, Zhang Z, Li C. Hidden coexisting hyperchaos of new memristive neuron model and its application in image encryption. Chaos Solitons Fractals. 2022;158:112017. doi: 10.1016/j.chaos.2022.112017. [DOI] [Google Scholar]
- 30.Bonny T. Chaotic or hyper-chaotic oscillator? Numerical solution, circuit design, MATLAB HDL-coder implementation, VHDL code, security analysis, and FPGA realization. Circ. Syst. Signal Process. 2020;40:1061–1088. doi: 10.1007/s00034-020-01521-8. [DOI] [Google Scholar]
- 31.Murillo-Escobar MA, Cruz-Hernández C, Abundiz-Pérez F, López-Gutiérrez RM, Del Acosta Campo OR. A RGB image encryption algorithm based on total plain image characteristics and chaos. Signal Process. 2015;109:119–131. doi: 10.1016/j.sigpro.2014.10.033. [DOI] [Google Scholar]
- 32.Liu X, Tong X, Wang Z, Zhan M. A new n-dimensional conservative chaos based on generalized Hamiltonian system and it’s applications in image encryption. Chaos Solitons Fractals. 2022;154:111693. doi: 10.1016/j.chaos.2021.111693. [DOI] [Google Scholar]
- 33.Wang Y, Liu Z, Ma J, He H. A pseudorandom number generator based on piecewise logistic map. Nonlinear Dyn. 2016;83:2373–2391. doi: 10.1007/s11071-015-2488-0. [DOI] [Google Scholar]
- 34.Atmel Corporation., 8-bit Microcontroller with 256K Bytes In-System Programmable Flash. Atmel. 2549A-AVR-03/05
- 35.Alvarez G, Li S. Some basic cryptographic requirements for chaos-based cryptosystems. Int. J. Bifurc. Chaos. 2006;16:2129–2151. doi: 10.1142/S0218127406015970. [DOI] [Google Scholar]
- 36.IEEE Computer Society., IEEE standard for binary floating-point arithmetic. ANSI/IEEE Std. 754
- 37.Tutueva AV, Nepomuceno EG, Karimov AI, Andreev AS, Butusov DN. Adaptive chaotic maps and their application to pseudo-random numbers generation. Chaos Solitons Fractals. 2020;133:109615. doi: 10.1016/j.chaos.2020.109615. [DOI] [Google Scholar]
- 38.Nesa N, Ghosh T, Banerjee I. Design of a chaos-based encryption scheme for sensor data using a novel logarithmic chaotic map. J. Inf. Secur. Appl. 2019;47:320–328. [Google Scholar]
- 39.Alhadawi HS, Zolkipli MF, Ismail SM, Lambi D. Designing a pseudorandom bit generator based on LFSRs and a discrete chaotic map. Cryptologia. 2019;42:1–22. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
The datasets generated during and/or analyzed during the current study are available from the corresponding author on reasonable request.