Collective organization from cellular disorder

In biology, form follows function. Spatial organization of cells within tissues is a critical aspect of this form. Injuries, drugs, and genetic mutations that perturb cellular organization disrupt tissue and organ functions. Indeed, the high degree of order and organization in tissues like heart muscle and bone is one impressive aspect of histological images.

Biologists have long investigated how cellular organization within tissues is achieved and how the genetic program encodes this information. Bioengineers seek to design conditions that force cells in vitro to attain in-vivo-like organization, as this causes cells to respond to drugs and other stimuli more similarly to the manner in which they would have responded in vivo (1,2). Computational approaches, ranging from agent-based models that account for cellular signaling (3) to simplistic models that treat cells like particles undergoing Brownian motion (4), have provided tremendous insight into how tissues are organized through collective migration events that guide tissue morphogenesis (5,6). In the context of such models, transcriptional networks that control tissue organization (7) could do so both by initiating changes within individual cells but also by tuning feedback that individual cells receive from surrounding cells.

Cellular alignment is a crucial component of tissue organization, and many experimentalists apply mechanical and geometric boundary conditions to in vitro culture systems to achieve such organization (8,9,10,11). In two-dimensional model systems, experimentalists have observed a strong dependence of overall cellular alignment on density: as density decreases, individual cells’ ability to polarize and extend improves. However, paradoxically, at higher cell density, although individual cells’ polarization is diminished, the overall population-level alignment increases (10).

Here, elegant modeling work by Ippolito and Desphande (12) explains and reconciles these apparently contradictory observations. The authors improved upon their established computational model (13), which assumes that cells can explore a wide range of morphological states while maintaining constant volume. The mechanical energy barrier that must be overcome to achieve a given state depends on 1) resistance of the cytoskeleton to extreme changes in overall cell spreading and 2) dissipation of mechanical energy via deformation of the substrate. As the authors demonstrate, these assumptions predict that as substrates become less rigid, they increasingly dissipate mechanical energy via deformation—as a result, and in qualitative agreement with historical experimental observations (14), the model predicts less cell spreading and fewer overall morphological states when cells adhere to compliant substrates.

Strikingly, while still images of cell monolayers suggest a low level of organizational disorder within organized, aligned tissues, the authors’ modeling suggests that, in fact, overall disorder of the system is maximized when cells are aligned parallel to one another. This prediction is similar to the predicted behavior of the nematic phase of liquid crystals (15)—in this state, loss of orientational entropy via local orientational ordering is offset by gains in translational entropy. While the original models of liquid crystals assume rigid molecules driven to move by thermal energy from the environment, the “thermal energy” available for cell movements is even greater because cells actively convert nutrients into ATP—allowing high levels of motion. The idea that entropy might actually contribute to tissue organization is intriguing and does not require a priori knowledge of biological signaling downstream of cell-cell contact. The notion of cells in constant motion may be challenging to appreciate from static snapshots but is easily understood from video microscopy studies (5,16).

Ippolito and Deshpande’s models bring up important questions for future experimental studies. First, it will be interesting to determine whether there is an upper limit above which increasing cell density does not enhance population-level organization. This might occur if density confines cell spreading to the extent that cells are unable to achieve any polarity and may explain why cells plated at extremely high densities have not been reported to exhibit spontaneous, population-level organization in culture. For example, stem-cell-derived cardiomyocytes are typically plated into monolayers at densities exceeding 200,000 cells/cm², which corresponds to a volumetric density of ∼10⁸ cells/cm³ in the heart; without appropriate geometric constraints (e.g., micro-patterned extracellular matrix proteins (9)), these monolayers have not been reported to exhibit a polarized orientation.

A second interesting outcome of Ippolito and Desphande’s current model is the prediction that sudden changes in substrate elasticity would lead to shifts in the organization of cell monolayers; this prediction is readily testable with substrates that are programmed to dynamically shift in elastic modulus through external stimuli like light (17) or magnetic fields (18).

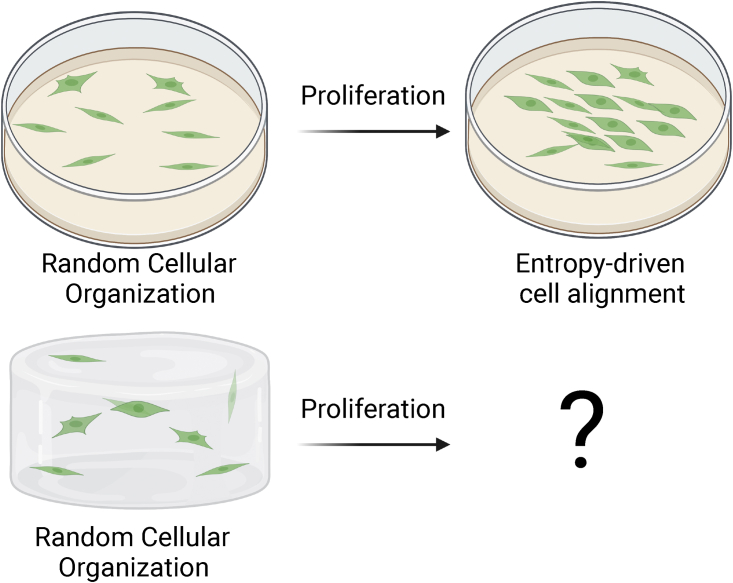
Finally, and most importantly, it will be interesting to determine in future experimental studies whether cell density impacts organization in three-dimensional environments (Fig. 1) where the surrounding matrix is soft and cellular consumption of nutrients and growth factor alter the energy available depending on cells’ position with the tissue. Within the soft, mechanically continuous environment tissues, traction forces can be transmitted efficiently from one cell to another (19), and the mechanical properties of the environment can influence both cells’ polarization (20) and their rigidity (21).

Figure 1.

Predicting the effects of cell density on cellular alignment in two-dimensional (2D) culture versus in 3D tissues. The model by Ippolito and Deshpande accurately predicts experimentally observed alignment of cells within high-density monolayers in 2D culture. It will be interesting in future experimental studies to see whether their models also predict potential entropically driven organization in dense 3D tissues. To see this figure in color, go online.

Considering the robustness of organization in natural tissues, it is highly likely that the mechanisms that dictate cells’ alignment and spatial patterning are inherently resistant to small perturbations (for example, microtrauma) under typical conditions. The models suggested here by Ippolito and Deshpande provide a generalizable explanation for cellular alignment within tissues that can guide new experiments related to how individual cells sense and respond to the spatial organization of tissues they reside within.

Editor: Guy Genin.