Penetration of hydroxyl radicals in the aqueous phase surrounding a cavitation bubble

Highlights

• •Strong radical production diminishes radical delievery efficiency in the bulk solution.
• •The shortest radical penetration depth appears in the main bubble collapse.
• •The penetration depth peaks at certain acoustic driving pressure.
• •The excessively intense recombination reactions cause the shortening of penetration depth.

Abstract

In the sonochemical degradation of nonvolatile compounds, the free radicals must be delivered into the aqueous solution from the cavitation bubble to initiate reduction–oxidation reactions. The penetration depth in the liquid becomes an important parameter that influences the radical delivery efficiency and eventual treatment performance. However, the transport of radicals in the liquid phase is not well understood yet. In this paper, we focus on the most reactive OH radical and numerically simulate its penetration behavior. This is realized by solving the coupled equations of bubble dynamics, intracavity chemistry, and radical dispersion in the aqueous phase. The results present both the local and global penetration patterns for the OH radicals. By performing simulations over a wide range of acoustic parameters, we find an undesirable phenomenon that the penetration can be adversely suppressed when strengthening the radical production. A mechanistic analysis attributes this to the excessively vigorous recombination reactions associated with high radical concentrations near the bubble interface. In this circumstance, the radicals are massively consumed and converted into molecular species before they can appreciably diffuse away. Our study sheds light on the interplay between radical production inside the bubble and dispersion in the outside liquid. The derived conclusions provide guides for sonochemical applications from a new perspective.

1. Introduction

Sonochemistry refers to the chemical effects arising from ultrasonic irradiance into aqueous solutions. It is capable of initiating or accelerating various reduction–oxidation reactions with an otherwise unattainable efficiency. In some cases, the enhancement in reactivity under sonication is up to a millionfold [1]. The superior performance of sonochemistry largely originates from the free radicals produced from acoustic cavitation. The quasi-adiabatic collapse of microbubbles creates extreme conditions in the interior, where water vapor and other gases are dissociated into free radicals. Among the various products, the hydroxyl radical (OH^•) constitutes the bulk of the generated reactive species and plays a central role in the sonochemical reactions [2], [3], [4], [5]. Owing to the high oxidation potential and nonselective nature, hydroxyl radicals can attack and degrade most organic pollutants, including those recalcitrant ones, such as hydrocarbons [6], pesticides [7], and pharmaceutical compounds [8]. Therefore, it is traditionally perceived that the production of hydroxyl radicals should be maximized in sonochemistry applications [9], [10], [11].

However, the pursuit of high radical production is not necessarily justified when treating hydrophilic and nonvolatile compounds. To decompose these substrates present in the solutions, the radicals produced within the collapsing cavitation bubble must first diffuse to the outside aqueous media as illustrated in Fig. 1. Previous studies [3], [12] have established that due to the slow diffusivity (on the order of 10^-5 cm²/s), the free radicals that escape from the bubble accumulate to high concentrations within a boundary layer near the gas–liquid interface. There, strong recombination reactions among the reactive species ensue and rapidly deplete the radicals. For OH radicals, the most consequential reaction is OH^•_(aq) + OH^•_(aq) → H₂O_2(aq). The molecular product H₂O₂ formed from the recombination reactions is inert when treating recalcitrant pollutants. As a result, the oxidation potential of the produced radicals is largely lost.

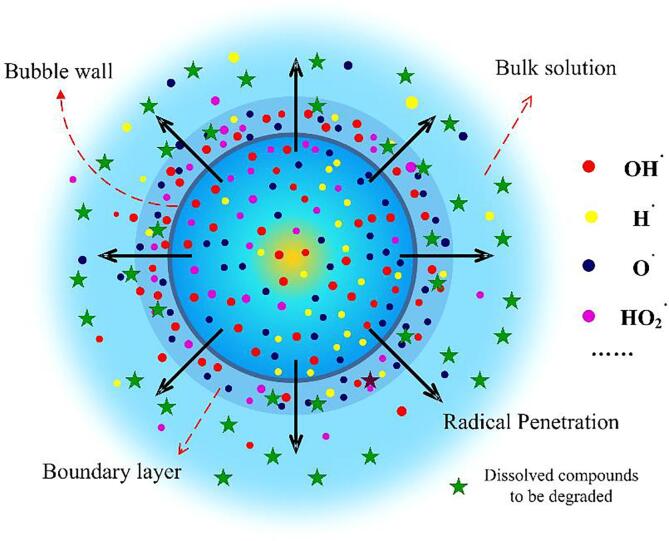
Fig. 1.

Schematic of dispersion of free radicals from the cavitation bubble to the surrounding liquid.

It is therefore conceivable that the sonolytic degradation of nonvolatile compounds depends on both the radical production inside the bubble and the penetration in the outside liquid. Regarding the latter process, the penetration depth is an important metric for gauging the delivery efficiency of the radicals into the aqueous phase. Evidently, a larger penetration depth means a higher contact probability between the radicals and dissolved compounds. In contrast, the suppression of radical penetration risks weakening the overall sonolysis performance, even in cases where the OH radicals are massively produced within the bubble.

However, previous studies are mainly concerned with the radical production process within the bubble [10], [13], [14], [15]. The penetration behavior of the radicals on the liquid side is not well understood yet. In this paper, we examine closely the penetration of the OH radicals over a wide range of acoustic parameters. The numerical model we used to simulate the radical production-dispersion is first introduced in Section 2 and validated in Section 3. Next, the simulation results of radical penetration are discussed in two aspects. Section 4.1 details the dispersion pattern in the liquid within a single acoustic cycle. Then the complete spatial–temporal distribution of the radicals is investigated in Section 4.2 to reveal the global characteristics of the penetration behavior. Based on parametric simulations, the variation of the key parameter, i.e., the penetration depth, is obtained and discussed in association with bubble collapse and intracavity radical production. From the analysis, we identify an adverse effect brought about by increased radical production with respect to penetration capability. To explain this phenomenon, a qualitative explanation is proposed in Section 5 together with some implications for the sonolytic degradation of nonvolatile pollutants. Finally, the main findings are summarized in Section 6. We want to emphasize that the radical behavior in the liquid phase surrounding the cavitation bubble is critical for sonochemistry but remains elusive. There are no systematic studies devoted to examining the complex physicochemical details in this area. Previous literatures [12], [16], [17], [18] tend to use speculative and descriptive language when introducing this topic. The study reported here serves as a testament to our belief that mechanistic and deterministic studies are required to grasp the factors that govern the dynamics of radicals and the ultimate efficacy of sonochemistry.

2. Methods

In this study, we consider an acoustically levitated bubble in water. It is initially filled with oxygen and water vapor, and their amounts are determined by the thermal and mechanical equilibrium between the bubble and the ambient liquid as will be introduced later. The choice of oxygen bubble is based on several previous sonochemical studies [19], [20], [21], [22] that showed an improved removal efficiency of organic pollutants in wastewater treatment when oxygen is used as the sparging gas. Also, there are several theoretical investigations to analyze the radicals produced inside the oxygen bubble [3], [15], [23]. Our research follows these efforts and extends the focus to the penetration of radicals in the liquid phase. Moreover, two salient features of the oxygen bubble make it an ideal prototype for studying sonochemical effects. First, compared with inert gases such as argon, the presence of oxygen can trigger more complex chemical reactions both inside and outside of the bubble [3], [20]. On the other hand, however, OH radicals constitute the main bulk of radical yields [3], [15], just as in the case of an inert gas bubble. Considering that the recombination reactions are the main pathway for consuming radicals in the liquid phase, the reported penetration behavior based on oxygen bubbles can be translated to other inert gas bubbles.

Driven by high-intensity ultrasounds, the bubble undergoes cyclical growth and collapse. The compressional heating in the collapse stage creates hotspots within the bubble, triggers intense intracavity chemical reactions, and generates OH radicals among other reactive species. The radicals diffuse from the highly compressed bubble to the surrounding liquid under concentration gradient. Assuming spherical symmetry, the dispersion of OH radicals in the liquid phase is governed by the following advection-reaction equation:

$$\frac{\partial c_i}{\partial \mathit{\text{t}}}+\dot{R}{\left(\frac{R}{r}\right)}^2\frac{\partial {\mathit{\text{c}}}_i}{\partial r}=\frac{D_i}{r^2}\frac{\partial }{\partial r}\left(r^2\frac{\partial c_i}{\partial r}\right)+\sum _{\mathit{\text{j}}}{\alpha }_{i,j}{\gamma }_j,r>R.$$ (1)

The equation describes the spatial–temporal evolution of mass concentration c_i for the species i, where r is the radial position, D_i the diffusion coefficients, and R and $\dot{R}$ the bubble radius and velocity, respectively. The superposed dots denote derivatives with respect to time. The last term in the equation represents the chemical reactions, in which α_{i, j} is the stoichiometric weight of species i in the reaction γ_j. For the oxygen bubble considered herein, the main radicals with their diffusivities in water and the relevant chemical reactions in the aqueous phase are listed in Table 1, Table 2, respectively.

Table 1.

The main radicals and diffusion coefficients in water [60], 10^-5 cm²/s.

OH•	H2O2	O	H•	HO•2	H2	O2	O3	HO•3
2.3	1.0	2.0	4.5	1.0	4.5	1.97	1.7	1.0

Table 2.

The chemical reactions with the rate coefficients in the liquid [60], [61].

No.	Reactions	Rate coefficients (M−1s−1, 1 M = 1 × 103 mol/m3)
R.1	OH•(aq) + OH•(aq) → H2O2(aq)	3.6 × 109
R.2	O•(aq) + O•(aq) → O2(aq)	2.8 × 1010
R.3	H•(aq) + H•(aq) → H2(aq)	7.8 × 109
R.4	H•(aq) + OH•(aq) → H2O(aq)	7.0 × 109
R.5	H•(aq) + H2O2(aq) → OH•(aq) + H2O(aq)	9.0 × 107
R.6	H•(aq) + O2(aq) → HO•2(aq)	2.1 × 1010
R.7	H•(aq) + HO•2(aq) → H2O2(aq)	1.8 × 1010
R.8	OH•(aq) + HO•2(aq) → H2O(aq) + O2(aq)	6.0 × 109
R.9	OH•(aq) + H2(aq) → H2O(aq) + H•(aq)	4.3 × 107
R.10	H2O2(aq) + OH•(aq) → HO•2(aq) + H2O(aq)	2.7 × 107
R.11	HO•2(aq) + HO•2(aq) → H2O2(aq) + O2(aq)	7.0 × 105
R.12	H2O2(aq) + O•(aq) → HO•2(aq) + OH(aq)	1.6 × 105
R.13	O•(aq) + H2O(aq) → OH(aq) + OH•(aq)	1.3 × 104
R.14	H•(aq) + H2O(aq) → H2(aq) + OH•(aq)	1.0 × 101
R.15	H2(aq) + H2O2(aq) → H•(aq) + OH•(aq) + H2O(aq)	6.0 × 106
R.16	O2(aq) + O•(aq) → O3(aq)	4.0 × 109
R.17	H(aq) + O3(aq) → HO•3(aq)	3.8 × 1010
R.18	OH(aq) + O3(aq) → HO2• (aq) + O2(aq)	1.1 × 108
R.19	HO•2(aq) + O3(aq) → HO•3(aq) + O2(aq)	5.0 × 108
R.20	HO•3(aq) → OH•(aq) + O2(aq)	1.1 × 105
R.21	H2O2(aq) + O3(aq) → OH•(aq) + HO•2(aq) + O2(aq)	3.0 × 109

The simulated domain for radical dispersion is semi-infinite extending radially from the bubble surface. The problem is closed by specifying the boundary conditions as follows. At the infinite (r→∞), the concentration of radicals is assumed to have reached the asymptotic value. At the bubble wall (r = R), a radical flux Γ_i is imposed by considering the interfacial transport of the radicals. Therefore,

$$\frac{\partial c_i}{\partial r}=\frac{{\mathrm{\Gamma }}_i}{4\pi R^2{D}_i},r=R.$$ (2)

$$\frac{\partial c_i}{\partial r}=0,r\to \infty .$$ (3)

The exact value of Γ_i will be introduced later. The simulation of radical dispersion must be coupled with that of bubble dynamics and intracavity chemistry as the radicals are supplied from the collapsing bubble. This is manifest by the parameters R and $\dot{R}$ appearing in the advection-reaction (Eq.1) and Γ_i in the boundary condition (Eq.2). In our simulation of bubble dynamics, the Gilmore equation is used to model the radial oscillation of the bubble [24]:

$$\left(1\text{-}\frac{\dot{R}}{C}\right)R\ddot{R}+\frac{3}{2}\left(1-\frac{\dot{R}}{3C}\right){\dot{R}}^2=\left(1+\frac{\dot{R}}{C}\right)H+\left(1-\frac{\dot{R}}{C}\right)\frac{R}{C}\dot{H},$$ (4)

where C is the speed of sound in water and H the enthalpy evaluated at the bubble wall. Within the bubble, the pressure p_g and temperature T are assumed as homogenous and follow the van der Waals equation of state [25].

$${\mathit{\text{p}}}_g=\frac{\mathcal{B}T}{\upsilon -b}-\frac{a}{{\upsilon }^2},$$ (5)

in which ℛ is the universal gas constant, a and b are van der Waals constants, and υ is the molar volume, $\upsilon =V/\sum n_i$ with V being the bubble volume and n_i the moles of the species i. As the bubble contains multiple species, the van der Waals constants a and b are calculated with a quadratic mixing rule considering the molar fraction of each species [25].

The heat transfer between the bubble and surrounding liquid is estimated as heat conduction through a thermal boundary layer of thickness δ_g.

$$\dot{Q}=4\pi R^2{\kappa }_{\mathit{mix}}{\left(T_{\infty }-T\right)/\delta }_{\text{g}},$$ (6)

where T_∞ is the ambient temperature, T_∞=300 K, and κ_mix is the averaged thermal conductivity of the gas mixture. The value of κ_mix can be determined using a similar approach with van der Waals constants. The thickness of the thermal layer δ_g is estimated as a diffusion-induced thermal penetration depth with an upper limit R/π [26].

$${\delta }_g\text{=}\min \left({\left({\kappa }_{\mathit{mix}}/\left({\rho }_{\mathit{mix}}{c}_{p,mix}\right)R\sqrt{{\rho }_l/p_b}\right)}^{0.5},R/\pi \right),$$ (7)

in which ρ_l is the density of liquid water and c_p,mix the heat capacity at constant pressure for the mixture.

The evaporation and condensation of water at the bubble surface are modeled by the Hertz–Knudsen–Langmuir formula [27], [28], [29]:

$${\dot{n}}_{{\mathrm{H}}_2\mathrm{O}}=4\pi R^2\frac{{\alpha }_M\left(p_{\mathit{sat}}-p_v\right)}{\sqrt{2\pi M_{{\mathrm{H}}_2\mathrm{O}}R{T}_i}},$$ (8)

where p_sat is the saturation vapor pressure at the bubble wall, p_v is the partial pressure of vapor inside the bubble, M_H2O is the molecular weight of water molecules, ${\mathit{\text{M}}}_{{\text{H}}_2\text{O}}=18$ g/mol, and α_M is the accommodation coefficient, α_M = 0.4 [30].

For the moderately soluble species such as H₂ and O₂, their mass transfers across the bubble interface are neglected since the time duration involved in the simulated bubble oscillation is too short. For the highly soluble species i, such as the free radicals discussed in the present study, two approximation methods have been proposed to estimate the interfacial flux Γ_i. The first approach treats the transport of radicals across the bubble surface as a diffusion process driven by the concentration gradient across an assumed boundary layer [31], [32]:

$${\mathrm{\Gamma }}_i=4\pi R^2{D}_i\frac{c_{i,1}-c_{i,0}}{l_{i,d}},$$ (9)

with the diffusive boundary layer thickness

$$l_{i,d}=\min \left(\sqrt{\frac{R{D}_i}{\left|\dot{R}\right|}},\frac{R}{\pi }\right),$$ (10)

where c_i,1 refers to the radical concentration inside the bubble, and c_i,0 the equilibrium concentration at the bubble wall. Since the free radicals are highly soluble in the water, c_i,0 is set as zero.

In the second approach, the radical transport is considered as an absorption process onto the liquid surface and Γ_i is calculated as [13], [30].

$${\mathrm{\Gamma }}_i=4\pi R^2\mathrm{\Theta }{c}_{i,1}\sqrt{\frac{k_{B}T}{2\pi M_i}},$$ (11)

where k_B is the Boltzmann constant and Θ the uptake coefficient, Θ = 0.001 [13], [30].

It has been shown [3] that the specific choice of the two abovementioned estimation methods for radical flux doesn’t affect the simulated radical distribution significantly. In this study, the second approach is employed and Γ_i is determined by Eq. (11).

For the oxygen bubble discussed in this paper, the chemical reactions inside the collapsing bubble are modeled with an H₂/O₂/H₂O reaction mechanism [15]. This mechanism contains all the radical species of interest, including OH^•, H^•, O^•, HO^•₂, H₂O₂, O_3, and HO^•₃. The rate parameters of the reactions have been updated continuously and represent the latest development in high-temperature gas reactions. For brevity, the reaction data is not listed here but can be accessed through the reference [15]. The simulation of intracavity chemistry is integrated into the calculation of bubble dynamics by the open-source platform Cantera [33], [34].

To solve the advection-reaction equation (Eq.1), an Eulerian-to-Lagrangian transformation technique is used to transform the infinite domain into a finite one [3], [35]. This is realized by introducing a new variable ζ, ζ = R/r, and reformulating the advection-reaction equation in the spatial domain [0, 1]. Then, the equation is spatially discretized by a second-order central difference scheme on the Gauss-Lobatto points. For the time marching, the fully implicit method coupled with an adaptive time step scheme is used to maintain numerical stability. For the simulation of bubble dynamics, the Gilmore equation (Eq.4) is solved by a fourth-order Runge-Kutta method with adaptive time steps [36], [37]. Generally, the time step required in the radical dispersion simulation is much smaller than that in the dynamic simulation, especially when the collapse point is approached. As a result, multiple iterations of the dispersion simulation are performed within a single step for the dynamic simulation. The coupling between radical production-dispersion is enforced at each time step and the distribution of the radicals in the liquid is updated continuously.

The equilibrium radius of the bubble is assumed as R_e = 4 μm. At the initial state, the bubble contains water vapor and oxygen. Their quantities are determined by applying the equilibrium condition [36], [38], [39]:

$$n_{{\mathrm{H}}_2\mathrm{O},0}\text{=}\frac{p_{\mathit{sat}}V}{\mathcal{R}{T}_{\infty }},n_{{\mathrm{O}}_2,0}\text{=}\frac{\left(p_0-p_{\mathit{sat}}\right)V}{\mathcal{R}{T}_{\infty }},$$ (12)

where $n_{{\mathrm{H}}_2\mathrm{O},0}$ and $n_{g,0}$ are the initial amounts of water vapor and oxygen, and p₀ the total bubble pressure. Based on the pressure balance across the bubble wall, p₀ is calculated by.

$$p_0\text{=}{p}_{\infty }+\frac{2\sigma }{R_e},$$ (13)

in which p_∞ is the ambient pressure and σ the surface tension. In the outside liquid, the water is assumed to be saturated with oxygen as we considered the bubble is nucleated by bubbling oxygen gas into the water. For other reactive species, their initial concentrations are zero.

It should be pointed out that our model neglects the thermal effect in the aqueous phase. When using the approximation method like the one in the present study to simulate bubble dynamics, Stricker et al.[40] has validated this simplification. They demonstrated that even in cases where the bubble collapses violently with interior temperature increasing to thousands of Kelvins, the rise of temperature in the liquid boundary layer is about a dozen Kelvins. Therefore, the diffusion and chemical reaction of the radicals in the outside liquid are calculated based on the ambient temperature.

3. Validation

As will be illustrated below, the penetration process of OH radicals in the liquid is transient. For each release of radicals from the collapsing bubble, the penetration lasts for about 10^-9 ∼ 10^-7 s with the maximum penetration depth smaller than 1 μm. To our best knowledge, there is no reported test that captures such nuanced behavior of radicals and can therefore be used for a direct comparison with our simulation results. To circumvent this difficulty, we employed an indirect approach for validation.

First, note that the numerical model in our study consists of two parts: one for the radical production inside the bubble (Eq. 4–11), and the other for radical penetration in the liquid phase (Eq.1). The calculated radical flux from the first part serves as the boundary condition for the radical penetration simulation (See Eq. (2), (11)). For the second submodel, there are no adjustable variables. In the calculation, we have used densely distributed Gauss-Lobatto points (>100) for the spatial discretization, and a fully implicit method for time marching to ensure accuracy. Consequently, the reliability of the whole simulation is determined by the first submodel, i.e., the one for radical production inside the bubble.

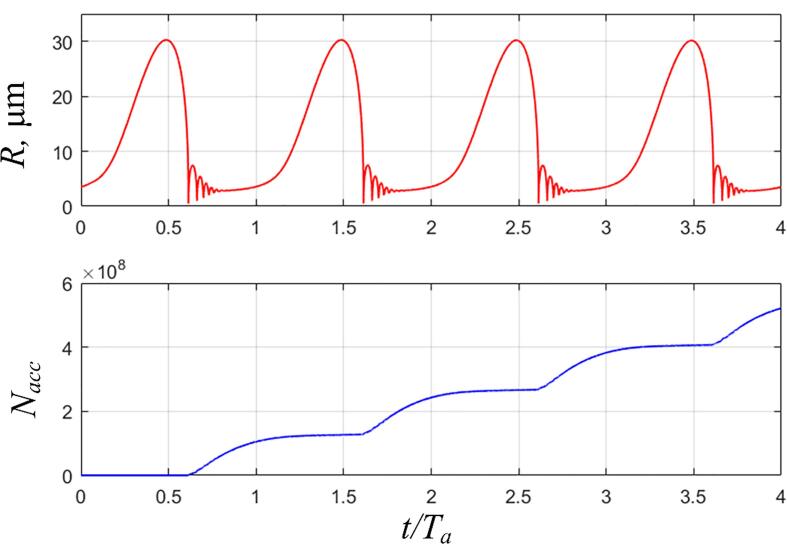
To validate the simulated radical production, we refer to the single bubble sonoluminescence (SBSL) test of Didenko & Suslick [41]. They measured the number of OH radicals produced per acoustic cycle, N, from the SBSL bubble with terephthalic acid (TA) dosimetry. At acoustic pressure amplitude p_a = 1.5 bar, frequency f = 52 kHz, and ambient water temperature T_∞ = 3 ℃, they reported N = 8.2 × 10⁵ for a pulsating bubble with a maximum radius of 30.5 μm. However, it is well known that TA dosimetry underestimates the number of OH radicals due to the limited trapping efficiency [16], [42]. A significant source for the deviation comes from the recombination reaction between the radicals themselves. As a result, a difference with a factor up to 30 has been observed between TA dosimetry and the more reliable Weissler dosimetry [16]. To account for this deviation, we calibrate the measured N by multiplying it by the factor 30. The crude estimate, 2.46 × 10⁷, will be used as benchmark data for the simulation validation. For a more detailed discussion on the accuracy issue with TA dosimetry, the readers are referred to the study by Rajamma et al.[16].

In the test, the water is degassed and equilibrated with an air pressure of 150 Torr. Correspondingly, an air bubble is assumed in the simulation and the chemical reactions are modeled with the GRI-Mech 3.0 mechanism [43]. With the initial radius of 3.6 μm, the simulated maximum bubble size matches well with the test data as shown in Fig. 2(a). Fig. 2(b) displays the accumulative number of OH radicals escaping from the bubble (calculated by Eq. (11)). The average number of OH radicals per cycle is 1.30 × 10⁸, which is about 5 times larger than the calibrated test data. However, considering the simplifications we made in estimating the benchmark data and neglect of other pathways through which the OH radicals are consumed, a satisfactory agreement is considered to have been reached.

Fig. 2.

Validation of the simulation results based on the SBSL test by Didenko & Suslick [41]. (a) The simulated temporal variation of bubble radius; (b) The accumulative number of OH radicals escaping from the bubble. The simulation parameters are: p_a = 1.5 bar, f = 52 kHz, R_e = 3.6 μm, and T_∞=3 ℃. The time t on the horizontal axis is normalized by the period of the ultrasound T_a, T_a = 1/f.

4. Results

4.1. Radical penetration within a single acoustic cycle

We first check the details of OH radical penetration in the liquid phase surrounding an oxygen bubble within a single acoustic cycle as displayed in Fig. 3. For this case, the acoustic driving frequency f = 100 kHz and pressure amplitude p_a = 1.8 bar. The data shown in the figure is extracted from the simulation after 30 acoustic cycles to exclude any initial transient effects.

Fig. 3.

The radical production and dispersion within a single acoustic cycle. (a) The bubble radius and temperature; (b) The concentration of OH radicals inside the bubble; (c) The concentration of OH radicals at the gas–liquid phase (r = R); (d) The distribution of OH radicals in the bulk liquid. To better display the overall dispersion pattern, all regions with concentrations higher than 0.5 mol/m³ are colored red in (d). The maximum concentration at each collapse can be referenced from (c). The parameters for the calculated case are: p_a = 1.8 bar, f = 100 kHz, R_e = 4 μm, and T_∞=300 K. The results are extracted from the simulation of 30 acoustic cycles.

The evolution of bubble radius shown in Fig. 3(a) conforms to the typical dynamics of inertial cavitation bubbles. The bubble expands substantially in the rarefication phase of acoustic driving before collapsing violently. In the main collapse, compressional heating generates extreme conditions inside the bubble with a peak temperature of 4880 K. The chemical reactions among the gases in this hotspot produce free radicals such as OH^•, O^•, and HO^•₂. Among the radicals, the OH radical is the most abundant one, and its concentration peaks at 4887 mol/m³ in the highly compressed bubble as shown in Fig. 3(b). On the liquid side, Fig. 3(c) displays that the rapid dissolution of the OH radicals in the liquid leads to a high radical concentration at the gas–liquid interface. As mentioned above, the accumulation is strengthened by the small diffusivity of the radicals. As a result, a peak concentration of about 400 mol/m³ is formed.

The subsequent bubble rebounds and collapses following the main collapse are much milder, leading to substantially lower collapsing temperatures and radical productions. The peak temperature in the second and third collapses is only 1232 K and 683 K, respectively. The decrease in the generated radicals is more significant. The maximum concentration of OH radicals inside the bubble decreases to 8.6 mol/m³ in the second collapse and further to 3.4 mol/m³ in the third collapse. At the bubble interface, the peak concentration of the dissolved OH radicals decreases to only 5.3 and 1.2 mol/m³ in the second and third collapses, respectively.

The most interesting result revealed from Fig. 3 is the radical dispersion as displayed in (d). The simulation shows that each compression of the bubble discharges radicals from the interior, which is followed by significant dispersion in the bulk liquid. Nevertheless, the region of significant radical concentrations in the aqueous phase lasts briefly and is confined narrowly near the interface. That forms a boundary layer with a small thickness and steep concentration gradient. The largest radial extent of this boundary layer is less than 0.8 μm for the investigated case.

Fig. 3(d) demonstrates that there is a good correspondence between the bubble collapse and the emergence of the radical layer with varying thicknesses. Surprisingly, the radical layer with the shortest thickness appears in the most violent main collapse, while that with the largest thickness is formed in the second collapse. From the second to fourth collapse, the thickness decreases consecutively. As the thickness of the radical layer represents the largest depth that the OH radicals can penetrate in the liquid, the variation of layer thickness demonstrates that both excessively strong and weak bubble collapses lead to weakened radical penetration. This is in stark contrast to the change of radical production level under different bubble collapse intensities, where a positive correlation is observed as noted in the above analysis.

4.2. Global penetration pattern

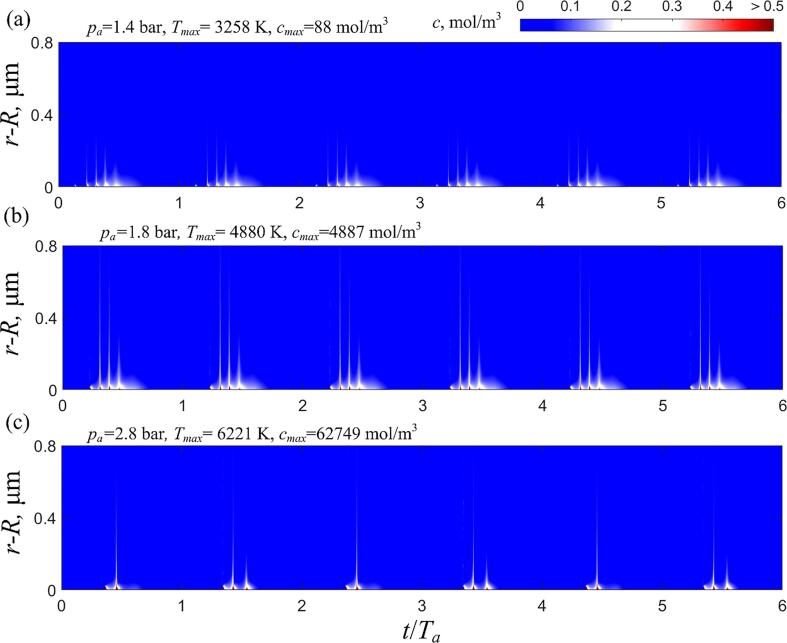
Next, we turn our attention to the global radical penetration pattern spanning multiple acoustic cycles. Fig. 4 displays the complete distribution of OH radicals in the liquid within 6 acoustic cycles. The results shown in (a) to (c) correspond to the ultrasonic driving with the frequency f = 100 kHz and pressure amplitudes p_a = 1.4 bar, 1.8 bar, and 2.8 bar, respectively. In order to interpret the results of radical penetration against bubble collapse and radical production, the maximum temperature and radical concentration inside the collapsing bubble are also indicated in each figure. Again, all the results are derived from the simulation after 30 acoustic cycles to eliminate the initial transient effects.

Fig. 4.

The dispersion of OH radicals into the bulk water at acoustic pressure amplitudes of 1.4 bar (a), 1.8 bar (b), and 2.8 bar (c). The maximum collapsing temperature, T_max, and peak hydroxyl radical concentration inside the bubble, c_max, for each case are indicated in the figure. The acoustic frequency f = 100 kHz and the ambient radius R_e = 4 μm.

The figure shows that as the driving pressure increases, the intensity of bubble collapse is strengthened, leading to higher collapsing temperature and stronger radical production. The maximum collapsing temperature increases from 3258 K at 1.4 bar to 6221 K at 2.8 bar, while the peak concentration of OH radicals within the bubble rises from 88 mol/m³ to an astonishing 62749 mol/m³. However, the penetration capability of the radicals doesn’t follow this trend. Defining the penetration depth, d_p, as the furthest radial position measured from the bubble surface where the radical concentration is 0.1 mol/m³, d_p is 0.18 μm at 1.4 bar, 0.70 μm at 1.8 bar, and 0.55 μm at 2.8 bar. Consistent with results in a single acoustic cycle, the global penetration pattern shows that both excessively weak and strong bubble collapses are associated with weak penetration for the OH radicals.

To elucidate the complete variation trend of penetration depth, parametric simulations are performed by scanning the acoustic pressure amplitude p_a at frequencies of 50, 100, and 200 kHz. The result is displayed in Fig. 5 together with the maximum concentration of OH radicals, c_max, reached inside the bubble for each acoustic driving. It shows that c_max increases with the driving pressure p_a, indicating increased radical production under larger acoustic driving. However, such a monotonic relationship is not observed between d_p and p_a. Fig. 5 (b) reveals that the penetration depth increases first with the driving pressure. After peaking at a certain value, it begins to decrease. Refer to the driving pressure corresponding to the peak d_p at a certain frequency as $p_a^{\ast }$, then$p_a^{\ast }$ = 1.50 bar for f = 50 kHz, 1.82 bar for f = 100 kHz, and 2.43 bar for f = 200 kHz. That means the penetration depth peaks at higher driving pressures for larger acoustic frequencies. In addition, it is interesting to note that for different acoustic frequencies, when the peak penetration depth is reached, the maximum temperature in the collapsing bubble at the corresponding acoustic driving nears 5000 K as shown in Fig. 5(b). A similar phenomenon is not observed in c_max due to its sensitive response to any subtle changes in the compression of the bubble.

Fig. 5.

The maximum concentration of OH radicals inside the bubble (a) and the penetration depth (b) as a function of acoustic driving pressure. The calculation is based on the oxygen bubble with R_e = 4 μm driven by the ultrasound at f = 50, 100, and 200 kHz, respectively. The maximum collapsing temperatures under the acoustic driving corresponding to the peak penetration depth are indicated in (b).

5. Discussion

The results presented in the above section show that the radical penetration exhibits a non-monotonic relationship with the intensity of bubble collapse. On the other hand, a more violent bubble collapse always leads to increased radical production, at least in the acoustic range discussed in this study. Therefore, there exists a complex relationship between the radical production inside the bubble and penetration in the outside liquid. When the production is relatively weak, the radical penetration depth is positively associated with the production intensity. This is reflected in Fig. 3(d), where the penetration depth decreases from the second to fourth collapse. Following the same principle, the penetration depth in Fig. 5(b) increases with the driving pressure before the peak value is reached.

Nevertheless, when the production of radicals is enhanced to relatively high levels, radical production and penetration show diverging trends. The appearance of the shortest penetration depth at the main bubble collapse depicted in Fig. 3(d) clearly demonstrates this phenomenon. Similarly, the decrease in penetration depth observed in Fig. 5(b) when the driving pressure surpasses the optimum value also illustrates this tendency.

To explain the variation of radical penetration with respect to production inside the bubble, we examine the two main underlying activities of radicals, i.e., diffusion and chemical reactions, behind the dispersion in the liquid. Diffusion under concentration gradient drives the radicals outwards, while the chemical reactions in the aqueous phase consume them along the dispersion process. They jointly determine the furthest distance that the radicals can reach. When the radical production within the bubble is weak, the overall concentration of radicals in the boundary layer is low and the associated recombination reactions are relatively mild. In this situation, diffusion dominates the radical penetration. A larger concentration gradient as a result of more supplies of radicals from the increased production promotes diffusion and furthers the penetration distances. Therefore, radical penetration is observed to increase with the production level, and vice versa.

However, when the production is intense and the radical concentration within the boundary layer is high, the recombination reactions are strengthened. In this circumstance, the chemical reactions replace diffusion and become the controlling factor influencing radical penetration. Enhanced production leads to high radical concentrations and stronger reactions, which in turn deplete the radicals more efficiently and shortens the penetration depth. In consequence, an inverse relationship between radical production and penetration emerges.

We stress that in our simulation, the water is assumed as neat and doesn’t contain other radical scavengers. The reported results should be viewed as the upper limit for the penetration depth in the simulated cases. Adding reactive species to the water would strengthen the reactions and lead to an earlier transition to the fall-off of penetration depth as the production is strengthened.

The results from the present study can help explain some sonochemical phenomena from a new perspective. For example, it has long been observed [44], [45], [46] that increasing ultrasonic frequency leads to a higher rate of degradation of phenol and p-nitrophenol (PNP). However, theoretical studies demonstrated [4], [47] that higher frequency causes a lower production of OH radicals per collapse inside the cavitation bubble by weakening the collapse intensity and decreasing the pressure and temperature. Several researchers [48], [49] speculated that the improved degradation performance is attributed to the more efficient ejection of OH radicals from the bubble to the bulk solution before they recombine into H₂O₂. This vague picture becomes clear immediately when extrapolating the main findings from our study to the discussed case. We have clearly shown that a mismatch may appear between radical production inside the bubble and penetration in the outside liquid. Note that for phenol and PNP, OH radical attack in the bulk solution is the predominant degradation pathway. Applying our results to this case of varying frequency, the disagreement between the theoretical prediction [4], [47] and experimental observations [44], [45], [46] is well reconciled.

As another example, we consider the effects of saturation level (dissolved air content) on the sonolysis of p-nitrophenol (PNP), nitrobenzene (NB), and 2,4-dichlorophenol (2,4-DCP). Owing to rectified diffusion, the bubble contains more gases and grows to a larger equilibrium size in solutions with higher saturation levels. This would result in milder bubble collapse and weaker radical production as the air cushions the inwards motion of the bubble wall. Given this context, however, the experimental test [21] showed that the degradation of PNP increases with the saturation level, while it decreases for NB and 2,4-DCP as expected. Due to the nonvolatility, all three pollutants are considered to be degraded mainly by hydroxylation in the bulk solution. The diverging trends for the three substances can be understood according to the results reported here and by taking their differences in solubility and hydrophilicity into account. Compared with PNP, NB and 2,4-DCP have a larger hydrophobicity and lower solubility in water, which promote their accumulations near the bubble interface. In this case, the radicals are not required to travel a long distance to get in contact with these compounds. As a result, the degradation efficiency mainly depends on the amount of produced radicals, which varies inversely with the saturation level. In contrast, for the highly soluble and hydrophilic PNP, its concentration near the bubble interface is rather low. The radicals must travel deep into the liquid to reach and decompose the compounds. Therefore, the penetration distance is a rate-determining factor for the degradation efficiency. Any decrease in the radical penetration depth caused by excessive radical supplies from the bubble imposes a more constraining effect. Conversely, a milder radical production may benefit the penetration, which explains the improved degradation efficiency of PNP when the saturation level is increased.

In our simulation, the bubble is assumed to be acoustically trapped and maintain sphericity while performing radial oscillations. Also, the outside fluid is considered irrotational. In an actual ultrasonic field, however, cavitation microstreaming can arise when instability on the bubble surface is developed or the bubble makes translational moves [50], [51]. The streaming originates from vortices generated within an oscillatory viscous layer surrounding the bubble and can extend much further into the outer fluid [52]. However, the influence of microstreaming on radical penetration is expected to be small. As a boundary layer, the flow activities within the viscous layer are usually weak [53]. On the contrary, radical recombination reaction is a violent and intense process as revealed from the above discussion. To consider the effect of the streaming in the outer flow field, we first estimate the thickness of the inner viscous layer as $\delta =\sqrt{2\mu /\rho \omega }$ [54], where the viscosity of water $\mu$ = 1 × 10^-3 kg m^-1s⁻¹, density$\rho$ = 1 × 10³ kg m^-3, and the angular frequency of the acoustic driving $\omega =2\pi f$. For the case discussed in Fig. 3 (f = 100 kHz), $\delta$ is about 1.8 μm, which is much larger than the maximum radical penetration depth at around 0.7 μm as shown in Fig. 3, Fig. 4. In other words, the conversion of the radicals into molecular products have largely completed within the viscous layer. The impacts from the various flow structures in the outer flow field can be safely disregarded.

When the asphericity develops to the extent that a jet is formed and pierces the bubble in the collapse, the above analysis still holds and the influences of the vortex structures in the outer flow can be neglected as well. However, the variation of radical productions inside the bubble should be considered. Due to the lower energy focusing in the nonspherical bubble collapse, the compressional heating would be diminished [55], [56], which in turn would decrease the radical production. On the other hand, the deformed and elongated bubble provides a larger surface area for the dissolution of radicals into the outside solution. Also, the breakup of the bubble as a result of the jet piercing may release radicals directly into the surrounding solution. Both processes favor the transport of radicals from the bubble interior to the outside solution. However, they are difficult to be modeled and quantified. We leave these issues to future studies.

In the last, we highlight that the numerical model in the present study is portable, i.e., the submodel for radical penetration can be modified readily to account for different radical production mechanisms. For example, Nikitenko and Pflieger [57] have argued that the inertial collapse gives rise to a nonthermal plasma inside the bubble as evidenced by spectroscopic analysis of sonoluminescence [58], [59]. In that case, the model for radical production should be replaced with others that describe plasma chemistry. With the flux of radicals derived from the new model, they can be incorporated into the penetration simulation as a boundary condition (Eq. (2), (11)) in the same way as in the calculation reported here. In addition, as ions and electrons are generated in the plasma and diffuse to the outside liquid, the reaction term in the penetration equation (Eq.1) should be changed to reflect their contributions. Such a reaction scheme in the liquid has been proposed before [60], [61].

6. Conclusion

In this paper, we numerically investigated the behavior of OH radicals in the liquid phase around a cavitation bubble. The variation of penetration depth with respect to the radical production intensity was obtained. Especially, the phenomenon of suppression of radical penetration was identified in both a single acoustic cycle and the global dispersion process. The mechanistic analysis identified mass diffusion and chemical reactions in the bulk solution as the main driving forces for radical penetration. Their competing influences jointly determine the penetration depth. Under strong radical productions, the rapid depletion of radicals by chemical reactions causes the shortening of penetration depth. The revealed suppression effect has important implications for the sonolytic degradation of nonvolatile compounds.

CRediT authorship contribution statement

Kewen Peng: Conceptualization, Methodology, Investigation, Formal analysis, Funding acquisition, Writing – original draft. Shouceng Tian: Formal analysis, Investigation, Funding acquisition. Yiqun Zhang: Investigation. Qing He: Investigation. Qianxi Wang: Formal analysis, Investigation.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.