Organizations of melittin peptides after spontaneous penetration into cell membranes

Abstract

The antimicrobial peptide, melittin, is a potential next-generation antibiotic because melittin can spontaneously form pores in bacterial cell membranes and cause cytoplasm leakage. However, the organizations of melittin peptides in cell membranes remain elusive, which impedes the understanding of the poration mechanism. In this work, we use coarse-grained and all-atom molecular dynamics (MD) simulations to investigate the organizations of melittin peptides during and after spontaneous penetration into DPPC/POPG lipid bilayers. We find that the peptides in lipid bilayers adopt either a transmembrane conformation or a U-shaped conformation, which are referred to as T- and U-peptides, respectively. Several U-peptides and/or T-peptides aggregate to form stable pores. We analyze a T-pore consisting of four T-peptides and a U-pore consisting of three U-peptides and one T-peptide. In both pores, peptides are organized in a manner such that polar residues face inward and hydrophobic residues face outward, which stabilizes the pores and produces water channels. Compared with the U-pore, the T-pore has lower energy, larger pore diameter, and higher permeability. However, the T-pore occurs less frequently than the U-pore in our simulations, probably because the formation of the T-pore is kinetically slower than the U-pore. The stability and permeability of both pores are confirmed by 300 ns all-atom MD simulations. The peptide organizations obtained in this work should deepen the understanding of the stability, poration mechanism, and permeability of melittin, and facilitate the optimization of melittin to enhance the antibacterial ability.

Significance

The antimicrobial peptide, melittin, is a potential antibacterial drug to address the drug-resistance issue because melittin kills bacteria through pore formation in bacterial membranes. Membrane lipids are very conservative and unlikely to be modified by genetic mutations of bacteria. Accordingly, the antibacterial ability of melittin is often not affected by genetic mutations of bacteria. The antibacterial activity of melittin strongly depends on the water permeability and stability of the pores produced by melittin, while the pore permeability and stability rely on the melittin organization within the pores, which has remained unclear until now. In this work, we use multiscale molecular dynamics simulations to investigate the melittin organizations in the pores after spontaneous penetration. Intriguingly, we observe different types of pores with distinct peptide organizations. Furthermore, we find that different types of pores have distinct stability and permeability. These results should provide new insights into the poration mechanism of melittin and facilitate the optimization of antimicrobial peptides to enhance the antibacterial activity.

Introduction

Melittin, one of the antimicrobial peptides (AMPs), is a potential drug to address the drug-resistance issue, which poses a big threat to human health. Melittin can spontaneously form pores in bacterial cell membranes and causes cytoplasm leakage. Because membrane lipids are very conservative and unlikely to be modified by genetic mutations of bacteria, the antibacterial ability of melittin is often not affected by genetic mutations of bacteria.

While many experiments have confirmed melittin-induced cytoplasm leakage in bacterial cell membranes (1,2,3,4) and model lipid bilayers (5,6,7,8), the poration mechanism remains elusive. Poration can be induced by not only melittin, but also some other AMPs (9,10,11,12). It is widely accepted that multiple peptides aggregate to produce pores, but the organizations of melittin peptides in lipid bilayers remain unclear, which impedes the understanding of the poration mechanism. Note that the organizations of melittin peptides in lipid bilayers are generally difficult to be measured by experiments because the pores are at the length scale of nanometers and undergo dynamic fluctuations.

Molecular dynamics (MD) simulations are effective tools to study the interactions of AMPs and lipid bilayers, which has been demonstrated in previous studies (13,14,15). However, there is an obstacle when applying MD simulations to study the interactions of AMPs and lipid bilayers. Spontaneous penetration of AMPs into lipid bilayers usually takes a long time, typically beyond 1 μs, which makes it computationally expensive to perform all-atom MD simulations. To address this issue, two approaches have been adopted. First, melittin or other AMPs are initially placed inside lipid bilayers or are pulled into lipid bilayers by external forces (10,16,17,18). This approach has some limitations: 1) the simulations are unable to capture the process of spontaneous penetration; 2) the peptide organizations may be different with the case of spontaneous penetration. Second, coarse-grained (CG) MD simulations can be used to accelerate simulation speed. Many CG force fields have been developed for peptides and lipid bilayers in recent years (19,20,21,22,23,24). Among them, the Martini force field is a popular one with many successful applications. Rzepiela et al. used the Martini CG force field to capture the spontaneous poration by magainin-H2 peptides in lipid bilayers, and found that the spontaneous pore formed in the CG simulations is also stable in the atomistic simulations (25). Later, Santo and co-workers performed a series of Martini CG MD simulations to study the penetration of two AMPs, magainin-2 and melittin, into the phosphatidylcholine bilayers (26,27,28). Sun et al. used the Martini force field to simulate melittin interacting with the lipid bilayer and found that a precursor defect on the bilayer plays an important role in pore formation and a cooperative mechanism of melittin is indispensable for poration (29,30). Yang and co-workers combined experiments and Martini CG MD simulations to reveal intermediate states during melittin-induced poration on a cell membrane (31). The Martini force field was applied not only to linear AMPs but also cyclic AMPs (32,33). One limitation of CG simulations is the omission of atomistic structures. To solve this problem, one can backmap the CG structures obtained from CG MD simulations to all-atom structures and then perform all-atom MD simulations.

In this work, we employ the CG MD simulations with the Martini 2.2 force field to investigate the spontaneous penetration of melittin peptides into lipid bilayers and the peptide organizations during and after spontaneous penetration. Through a large number of simulations, we successfully observe many instances of spontaneous penetration, which allows us to obtain a comprehensive understanding of peptide organizations. Furthermore, we also analyze the effect of peptide organization on pore stability and permeability and carry out all-atom simulations to confirm the stability of the pores obtained from CG simulations.

Methods

CG MD simulation

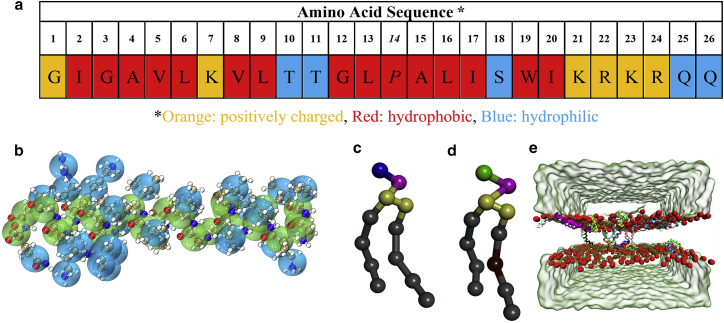
We carry out CG MD simulations using the GROMACS package (34) with the Martini force field (version 2.2) (23). The initial lipid bilayer structure is generated by a CHARMM-GUI online server (35). The lipid bilayer consists of 216 DPPC lipids and 88 POPG lipids on each leaflet. These lipids are randomly distributed in the bilayer. The crystal structure of melittin is downloaded from the PDB database (PDB: 2MLT) and is converted to a CG melittin model. Implementation of a Martini force field needs to assign the secondary structure for each residue, which is determined using the Dictionary of Secondary Structure of Proteins (DSSP) algorithm (36). The DSSP shows that the secondary structures of GLY-1 and GLN-26 are coil, THR-11 is turn, and all other amino acids are helices. Although the secondary structures are assigned in CG simulations, the melittin chain still has great structural flexibility (see Fig. S1). In the beginning of each simulation, a number of melittin peptides, ranging from 1 to 28, are placed on the surface of one leaflet of the lipid bilayer. For the melittin number in the range of $1\le N_{\text{melittin}}\le 27$, we conduct a single simulation to quickly obtain a rough value of the minimum $N_{\text{melittin}}$ for spontaneous melittin penetration (see Table S1). For, we perform 16 simulations with different random seeds to increase the sampling of penetration and pore formation events and obtain statistically significant results (see Table S1). Here, the net charge of melittin is +5 (see Fig. 1 a and its caption). Each POPG carries a negative charge and DPPC is neutral. Counterions, Na⁺, are added to neutralize the system (see Table 1). No extra ions are added.

Figure 1.

(a) Amino acid sequence of melittin. Proline (14th residue) tends to cause a bend, which can facilitate U-shape formation of melittin in lipid bilayers. Here, one melittin contains six positively charged residues: G (1st), K (7th), K (21th), R (22th), K (23rd), and R (24th), and one negatively charged residue Q (26th). Hence, the net charge of melittin is +5. (b) The coarse-grained mapping scheme of melittin. The backbone atoms and the side-chain atoms are mapped to lime and cyan beads, respectively. (c and d) CG models of DPPC and POPG. (e) A simulation snapshot after a 5 μs run. The water molecules are rendered to surface representation. Different melittin chains are rendered with different colors. For lipid bilayers, only the headgroups are shown for clarity. To see this figure in color, go online.

Table 1.

Parameters of some simulations in this work

Systems	Melittin	DPPC	POPG	Counterions	Force field	Replicas	Simulation time
CG	28	432	176	36 Na+	Martini 2.2	16	5 μs
AA (T-pore)	4	432	176	156 Na+	CHARMM36M	3	300 ns
AA (U-pore)	4	432	176	156 Na+	CHARMM36M	3	300 ns

See Table S1 for a complete list of CG simulation parameters.

Each simulation starts with energy minimization by steepest descent method (37), which is followed by a series of equilibration NPT simulations. During the NPT equilibration, we impose harmonic position restraints on melittin backbones, and then gradually reduce the restrain force in five NPT simulations with a total simulation time of 4.75 ns. The pressure is kept at 1 bar using Berendsen with a coupling constant of 5 ps. A semi-isotropic coupling scheme is employed to control the pressure in the x–y direction and z-direction independently. The temperature coupling algorithm is V-rescale thermostat with a reference temperature of 325 K, and the time constant is set to 1.0 ps. We set the temperature as 325 K to accelerate spontaneous penetration. The temperature of 325 K has also been used previous studies (28). Lenard-Jones (LJ) interactions are truncated at 1.1 nm and electrostatic interactions are calculated using the reaction-field method, which are default Martini settings. In the final production, the pressure coupling method is switched to a Parrinello-Rahman barostat (38). The time step is set as 20 fs, and each simulation runs for 5 μs. All simulation snapshots are rendered by visual MD simulations (39).

All-atom MD simulations

We also perform all-atom MD simulations to confirm the stability of peptide aggregates obtained from the CG simulations. We first backmap the final structures from some CG simulations to atomistic structures, which serve as initial structures for all-atom simulations. The all-atom MD simulations are carried out with the GROMACS package using a CHARMM36M force field (40,41). The particle mesh Ewald method (42) is used for electrostatic interactions. The cutoff of nonbonded LJ interactions is set as 1.2 nm. The temperature is maintained at 325 K using a Nose-Hoover coupling scheme, and the pressure is kept at 1.0 bar with isotropic coupling type using a Parrinello-Rahman barostat (38). All bonds containing hydrogen atoms are constrained by a LINCS algorithm (43). We set the time step as 2 fs and run each simulation for 300 ns.

Calculation of interaction energies

We choose six simulations to calculate the energies of LJ and electrostatic interactions. These six simulations include: one melittin in a water box (referred as 1PW), one melittin binding on the surface of the lipid bilayer (referred as 1PS), one melittin inserted in the lipid bilayer (referred as 1PT), one aggregate (pore) consisting of four transmembrane melittin peptides (referred as T-pore), one aggregate (pore) consisting of one transmembrane melittin peptide, three U-shaped melittin peptides (referred as U-pore), and four melittin peptides randomly binding on the surface of lipid bilayer (referred as 4PS).

Free energy calculations of a single water molecule across the pores

To compare the water permeability of different pores, we employ umbrella sampling (44) to estimate the free energy barrier experienced by a water molecule when passing across a pore at atomistic scale. In umbrella sampling, we use a collective variable (CV), which corresponds to the distance between the center of mass (COM) of one selected water molecule and the COM of the lipid membrane. The ranges of CV for T-pore (from −3.99 to 4.61 nm) and U-pore (from −4.74 to 3.84 nm) are slightly different, because the COM of the lipid bilayer in the two simulations is slightly different. A series of simulations are used to sample over different values of the CV with a spacing of 0.2 nm, which correspond to 42 umbrella windows. The simulation time for each window is 20 ns, and the last 10 ns are used for potential of mean force (PMF) calculation. The umbrella potential is applied to the selected water molecule and the force constant is set to 1000 kJ/mol⁻¹ nm⁻². Our simulations obtain abundant sampling over the whole range of CV (see Fig. S13). We analyze the PMF as well as its statistical errors using the GROMACS wham tool, which is based on the weighted histogram analysis method (45) (see Fig. S13).

PMF calculation for the formation of U-shaped melittin on a membrane surface

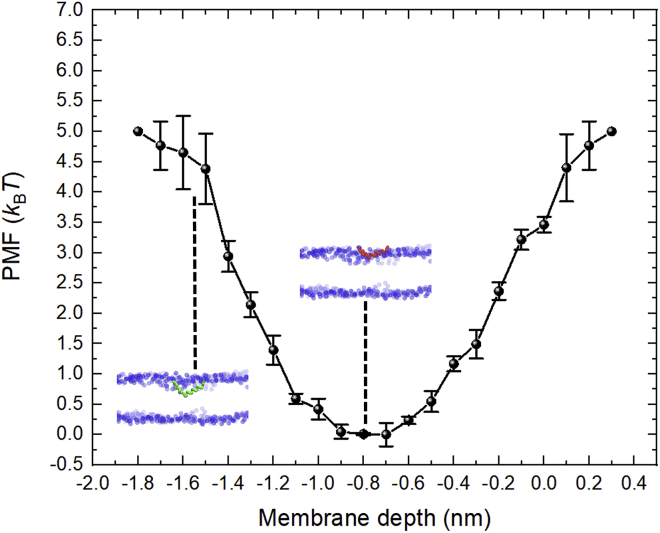
For a melittin on a membrane surface, the central residue can spontaneously insert the membrane with a certain depth, which results in a U-shaped melittin. We calculate the PMF as a function of the depth. The depth, z, is defined as the distance of the central residue (proline-14) to the membrane surface. The calculation is based on a one-peptide CG simulation. In this simulation, the peptide is free to move without any pulling force. From each frame in the simulation trajectory from 3.5 to 5 μs, we calculate the distance along the z-direction between the COM of the proline-14 residue of melittin and COM of PO₄ beads on membrane surface. Then, we calculate the probability distribution $P\left(z\right)$ of these z distances, and then convert to the PMF using $F\left(z\right)/\left(k_{B}T\right)=-\ln \left[P\left(z\right)\right]$. Note that in one-peptide CG simulations, one melittin moves from water to membrane surface within typically hundreds of nanoseconds, and stays at the membrane surface for a long time (see Fig. S2). Hence, we obtain abundant sampling of U-shaped melittin, which lead to quite accurate $F\left(z\right)$ values. To estimate the statistical errors of $F\left(z\right)$, we divide the simulation sampling into three portions and calculate the standard deviations of three PMFs from the three portions.

Results and discussion

Spontaneous penetration of melittin peptides

In the CG MD simulations, we fix the number of lipids (432 DPPCs and 176 POPGs) and systematically increase the number of melittin peptides from 1 to 28. A complete list of simulations is presented in Table S1. Each CG simulation runs for 5 μs, which is large enough to allow melittin to diffuse and explore the entire simulation box in the x and y directions (see Figs. S4 and S5). Note that the peptide always refers to melittin in this work. As shown in Fig. 2 a, when the number of peptides is less than 14, all peptides bind to the membrane surface. In such binding state, the hydrophobic residues of peptides are partially or fully buried in the lipid bilayers to promote the hydrophobic attractions between the residues and hydrophobic tails of lipids, while the polar residues of peptides are left in water. Accordingly, peptides binding on the membrane surface are more stable than the peptides fully immersed in water.

Figure 2.

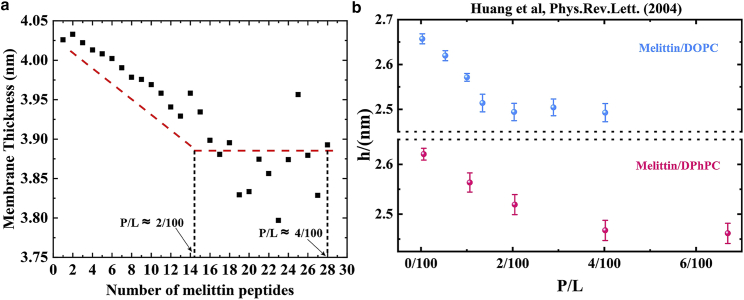
(a) Equilibrium membrane thickness as a function of the number of peptides in our 5 μs CG MD simulations. (b) Experimental results of the hydrocarbon thickness as a function of the peptide-to-lipid (P/L) ratio. Adapted from Huang et al. (6) with permission. To see this figure in color, go online.

Spontaneous penetration of peptides is observed when the number of peptides exceeds 13, or the peptide-to-lipid ratio (P/L) ratio exceeds 13/(432 + 176) ≈ 2/100. Simulation animations of the spontaneous penetration can be found in the supporting material. As reported by previous studies (6), the spontaneous penetration is associated with the change in membrane thickness. The membrane thickness decreases with the P/L ratio and reaches a plateau when the P/L ratio exceeds a threshold value (Fig. 2 b). The spontaneous penetration starts to occur around the threshold of the P/L ratio (Fig. 2 a). A similar trend is observed in our simulations: the spontaneous penetration starts to occur when the membrane thickness reaches a plateau (Fig. 2 a). The threshold of the P/L ratio, ∼2/100 in our simulations, is close to the threshold values in previous experiments (Fig. 2). See Figs. S6 and S7 for more analysis of simulations with the increase of melittin number.

Organizations of peptides in membranes

After spontaneous penetration, the peptides do not randomly distribute in membranes but aggregate with several distinct structures (Fig. 3). The aggregates can maintain their peptide organizations for a long time during 5 μs simulations, which suggests that they are stable or metastable. Their stabilities will be analyzed in the next subsection. To obtain good statistics of these aggregates, we need to acquire a large number of such aggregates. Accordingly, we perform 16 replicas of simulations for the 28 peptide system. These 16 replica simulations use the same parameters except different random seeds. Each replica simulation runs for 5 μs. In each replica, we can observe spontaneous penetration of melittin. The numbers of penetration events and pore formation in each replica simulation are summarized in Table S2. We set the number of peptides as 28, corresponding to a P/L ratio of 4.6/100, which is larger than the threshold value such that the spontaneous penetration can occur more quickly in our simulations.

Figure 3.

Various types of peptide organizations in membranes after spontaneous penetrations in 16 replicas of CG MD simulations. Each simulation contains 432 DPPC, 176 POPG, and 28 melittin peptides and runs for 5 μs. For each type of aggregate, there is a bracket showing the numbers and percentages of occurrences of this aggregate. The percentage corresponds to the fraction of a given organization in the pentamers, tetramers, or trimer. To see this figure in color, go online.

In these aggregates, the peptides adopt either transmembrane conformations or U-shaped conformations, which are referred to as T- and U-peptides, respectively. In the T-peptide, the two ends locate at two different leaflets of a membrane; while in the U-peptide, the two ends locate at the same leaflet of a membrane. We can conveniently distinguish T- and U-peptides using the peptide end positions (see Fig. S3). Recall that both C-terminal and N-terminal residues of melittin, ILE, and positively charged GLY are polar and prefer to stay in the polar environment of the membrane surface consisting of lipid heads. Such boundary conditions enforce the peptides in membranes to adopt either transmembrane or U-shaped conformations.

A number of T-peptides and/or U-peptides can aggregate in various forms, as shown in Fig. 3. The statistics of these aggregates are presented in the brackets followed the name of each aggregate. The compositions of T- and U-peptides vary significantly among the aggregates. Some aggregates consist of purely T- or U-peptides, such as 3T, 4T, 3U, and 4U in Fig. 3. Note that we do not observe any stable aggregate with purely U-peptides that locate at the same leaflet, probably because the penetration depth of U-peptides cannot reach the membrane thickness. Most aggregates consist of a mixture of T- and U-peptides. Trimers, tetramers, and pentamers occur 23, 28, and 8 times, respectively, in our simulations.

While different forms of aggregates spontaneously occur in our simulations, it is of importance to explore the reason for the distribution of these aggregates. If the simulation time is long enough to reach equilibrium, the distribution should follow the Boltzmann distribution: the aggregate with a lower free energy occurs more frequently. It is worth mentioning that spontaneous penetration of peptides and the kinetics of aggregate formation usually need to overcome high free energy barriers. Accordingly, in our 5 μs simulations, the distribution of the aggregates may be biased toward the aggregates that require lower free energy barriers. Note that, even in experiments, the pore formation of AMPs usually takes a long time up to a few minutes (5).

To investigate the effects of the peptide organizations on the aggregate stability and pore formation kinetics, we focus on two examples of aggregates. In one aggregate, there are four T-peptides (Fig. 4); while, in the other aggregate, there are one T-peptide and three U-shaped peptides (Fig. 5). These two aggregates are referred to as T- and U-pores, respectively. The two aggregates are called pores because of their water permeability, which will be elaborated latter. Comparison of the stability and formation kinetics of the T- and U-pores should provide insights into the effects of T- and U-peptides on the stability and formation kinetics of the pore, which will be elaborated in the following subsections.

Figure 4.

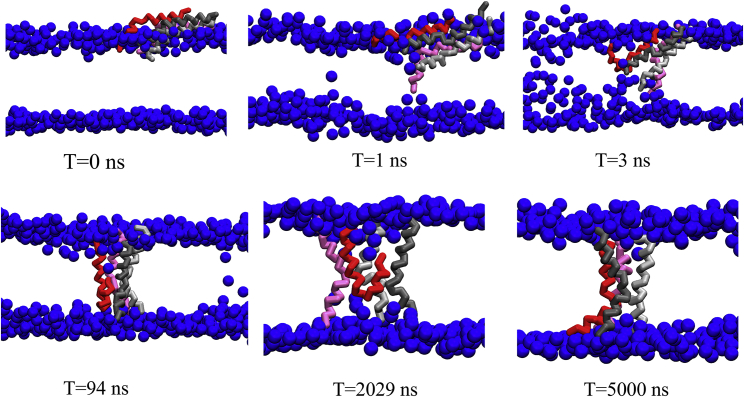
Simulation snapshots during the formation of a T-pore. This simulation contains 432 DPPC, 176 POPG, and 25 melittin peptides. The lipid head groups are rendered to blue balls, and the tails groups are not shown for clarity. The four melittin peptides are colored pink, red, silver, and gray. The animation of T-pore formation can be found in Videos S1. To see this figure in color, go online.

Figure 5.

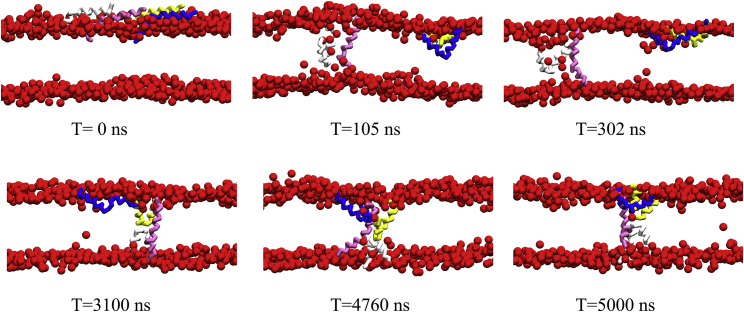
Simulation snapshots during the formation of a U-pore. This simulation contains 432 DPPC, 176 POPG, and 28 melittin peptides. The lipid head groups are rendered to red balls, and the tails groups are not shown for clarity. The four melittin peptides are colored pink, blue, silver, and yellow. The animation of U-pore formation can be found in Video S2. To see this figure in color, go online.

Energetic analysis of the T- and U-pores

To compare the stability of the T- and U-pores formed after spontaneous penetration (Figs. 4 and 5), we calculate the interaction energies in the T- and U-pores. Before moving to the energies of the two pores, it is useful to compare the energies of a single melittin peptide in three states: a peptide immersed in water (1PW), a transmembrane peptide (1PT), and a peptide binding to the membrane surface (1PS). As shown in Table 2, the energies of the 1PT and 1PS states are 191.6 and 275.3 kJ/mol, respectively, lower than that of 1PW state. Here, the energy refers to the interaction energy of one peptide with the environment, including water, ions, and lipids (except for 1PW). In CG simulations, the energies are dominated by LJ interactions, while electrostatic interactions only play a minor role. These results suggest that a single peptide prefers to bind on the membrane surface, which is consistent with the PMF calculation by Miyazaki et al. (46). The reason why 1PS is the most stable state for a single melittin peptide is that melittin is amphiphilic and the membrane surface locates at the boundary between polar and hydrophobic environments. In the 1PS state, the hydrophobic residues can insert into the hydrophobic region of the lipid bilayers, while the polar residues can stay in water. In the 1PT state, some polar residues in the middle of melittin are inevitable to stay in the hydrophobic environment. Accordingly, the penetration of a single peptide, i.e., the transition from 1PS to 1PT, is disfavored and occurs rarely. The energy contributions of each residue in the three single-melittin states are plotted in Fig. S8.

Table 2.

Interaction energies of single melittin peptides in three states

System	1PW		1PT		1PS
Schematic
Energies	LJ	electrostatic	LJ	electrostatic	LJ	electrostatic
	−2331.4 ± 5.0 (0)	−1.1 ± 0.1 (0)	−2512.1 ± 2.7 (−180.8)	−12.0 ± 0.1 (−10.9)	−2597.2 ± 6.3 (−265.9)	−10.5 ± 0.1 (−9.4)
Total	−2332.5 ± 5.1 (0)		−2524.1 ± 2.8 (−191.6)		−2607.8 ± 6.4 (−275.3)

The energies are in kJ/mol. The numbers in parentheses are the energy differences with respect to the case of 1PW.

While single melittin is unstable in the membrane, the aggregates of four peptides in the T- and U-pores are stable in the membrane. Table 3 shows that the interaction energies of four peptides in the T- and U-pores are much lower than the four peptides on the membrane surface (4PS). The lower energies in the T- and U-pores should be attributed to the LJ interaction, as shown in Table 3. To find out the reason why the peptide organizations in the T- and U-pores can lower the LJ interaction energies, we plot the distributions of hydrophobic and polar residues in the T- and U-pores (Fig. 6). It is obvious to see the segregation of hydrophobic and polar residues in the T- and U-pores. Such segregation strongly favors the attraction among hydrophobic residues and/or polar residues, hence lowering the LJ interaction energies. It is worth pointing out that such segregation can only be realized by multiple peptides that form a closed (roughly circular) polar environment at the interior of the T- or U-pores. Such segregation cannot be achieved by a single peptide. Accordingly, for a single peptide inserted in a membrane, the polar residues are inevitable to contact the hydrophobic tails, which are energetically disfavored.

Table 3.

Interaction energies for four peptides in different organizations

System	4PS		T-pore		U-pore
Schematic
	LJ	electrostatic	LJ	electrostatic	LJ	electrostatic
Total	−10,400.6 ± 28.0 (0)	−42.4 ± 0.4 (0)	−10,811.8 ± 124.4 (−411.2)	−43.2 ± 1.6 (−0.8)	−10,707.0 ± 64.4 (−306.4)	−42.8 ± 1.2 (−0.4)
	−10,443.0 ± 28.4 (0)		−10,855.0 ± 126.0 (−412.0)		−10,749.8 ± 65.6 (−306.8)

The energies are in kJ/mol. The numbers in parentheses are the energy differences with respect to the case of 4PS.

Figure 6.

The distributions of hydrophobic (red points) and polar (blue points) residues in the T- and U-pores. Each dot represents a residue. The figure is generated by 500 simulation snapshots after alignment using translation and rotation. Yellow bonds represent peptide backbones. A cylinder-like pore is added for better viewing of the pore structure and residue segregation. To see this figure in color, go online.

While both the T- and U-pores can lower their interaction energies through the segregation of hydrophobic and polar residues, there is an energy difference between the T- and U-pores, as shown in Table 3. Such difference should be attributed to the arrangement of hydrophobic and polar residues in the T- and U-pores. Note that the peptide backbone conformations (transmembrane or U-shaped) impose some boundary conditions for the arrangements of hydrophobic and polar residues in the T- and U-pores, although the residues in peptides have a certain freedom to rotate.

To analyze how the difference in the residue arrangements leads to the energy difference between the T- and U-pores, we calculate the residue-residue distance map as shown in Fig. 7 (see residue-residue interaction energy map in Figs. S10–S12). For a given pair of residues, we calculate the smallest distance between them at each simulation snapshot and then record the average of these smallest distances, as shown in the contact maps. If the average distance is less than 1.1 nm (the cutoff distance of LJ interactions in CG simulations), we consider these two residues are in contact. The contact maps exhibit several clusters. To illustrate the residue arrangements in the clusters, four conformational structures are shown in Fig. 7. The T-pore appears to organize the four peptides in a neater manner than the U-pore and hence the T-pore contains more pairs of residue-residue contacts. The numbers of residue-residue contacts are 216 and 178, in the T- and U-pores, respectively. The more residue-residues contacts in the T-pore than in the U-pore is probably responsible for the lower energy of the T-pore. The energy contributions of each residue in the T- and U-pores are plotted in Fig. S9.

Figure 7.

Residue-residue distance maps for the T- and U-pores. In the contact maps, each color indicates a certain residue-residue distance, while the distance is calculated as the mean value of the smallest distances between a pair of residues during simulations. The residues in the four peptides correspond to the index ranges: 1–26, 27–52, 53–78, and 79–104. Four conformational images are included to visualize four large clusters in the contact maps. The residues involved in the clusters are shown in color. To see this figure in color, go online.

Formation kinetics of the T- and U-pores

Next, we analyze the formation kinetics of the T- and U-pores. Fig. 4 shows the trajectory of the peptides and lipid bilayers during the formation of a T-pore. Initially, 25 peptides are placed on the upper surface of the membrane. In this simulation, four peptides start to penetrate into the membrane synergically in the first few nanoseconds. During this penetration, the four peptides probably protect their polar residues from contacting the hydrophobic region by forming the cluster of polar residues. At 94 ns, three peptides (gray, silver, and pink) reach the lower leaflet and achieve the transmembrane conformation, while one peptide (red) assumes a U-shape-like conformation. This peptide (red) stays in this U-shape-like state for a couple of μs, indicating a metastable state before achieving the transmembrane conformation finally.

Fig. 5 shows the trajectory of the formation of a U-pore. Twenty-eight peptides are initially placed on the upper surface of the membrane. At 105 ns, the pink peptide penetrates the membrane accompanied by the silver peptide and reaches a transmembrane state. Simultaneously, the silver peptide completely crosses the membrane. It appears that there is a synergy between the pink and silver peptides. Such synergy is also possible through the protections of their polar residues from the hydrophobic region. In the subsequent thousands of nanoseconds, the other two peptides (blue and yellow) join the pink and silver peptides to form a stable aggregate.

We have visually inspected the formation kinetics of other T- and U-pores. A notable difference between them is as follows: T-pore formation appears to strongly rely on synergy, i.e., a few peptides come close simultaneously and form a T-pore in one step. U-pore formation can occur via multiple steps, i.e., peptides come to the aggregate sequentially. This means that the U-pore does not rely on synergy as strongly as T-pore formation.

Another key factor facilitating the U-pore formation is that U-peptides are much easier to form than the T-peptides. Note that there are always abundant surface-binding peptides. The transition from an isolated surface-binding peptide (1PS) to a U-peptide just requires the movement of the middle residues toward the membrane center. Such transition does not need the cooperation of other peptides and can be driven easily by thermal fluctuations. To quantify the free energy cost from a surface peptide to a U-peptide, we calculate the PMF as a function of the depth of a U-peptide (Fig. 8). The transition typically costs several k_BT depending on the depth of the U-peptide. Note that the transition from a surface peptide to a U-peptide is gradual and there is no clear boundary between the two states. Overall, the more occurrences of U-pores than T-pores, as shown in Fig. 3, are probably caused by the requirement of strong synergy in T-pore formation and the easy formation of U-peptides.

Figure 8.

PMF as a function of the depth of the central residue (proline-14) of melittin. Two simulation snapshots are added to illustrate the conformations of two depths. Error bars correspond to the standard deviations of the results from three simulation portions. To see this figure in color, go online.

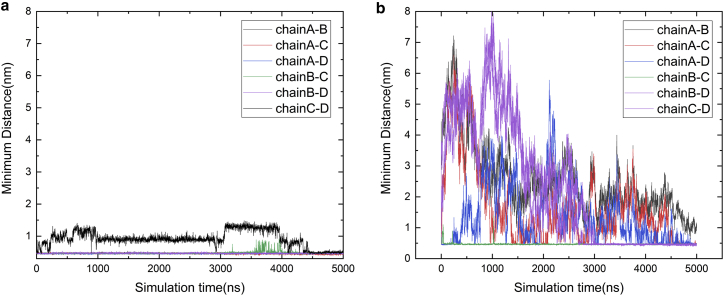
Next, we analyze the conformational fluctuations of the T- and U-pores to infer their conformation entropy. As shown in Fig. 9, the fluctuations of the interpeptide distances in the U-pore are substantially larger than those in the T-pore, which indicates that the peptide organization in the U-pore has larger structural flexibility than the T-pore. It means the U-pore has a much larger conformational entropy than the T-pore. In the previous subsection, we show that the U-pore has a higher interaction energy. Considering that the U-pore has a larger entropy and a higher interaction energy, we are unable to conclude whether the U- or T-pore has a lower free energy.

Figure 9.

Time evolutions of the minimum distances among four melittin chains in the T-pore (a) and U-pore (b). To see this figure in color, go online.

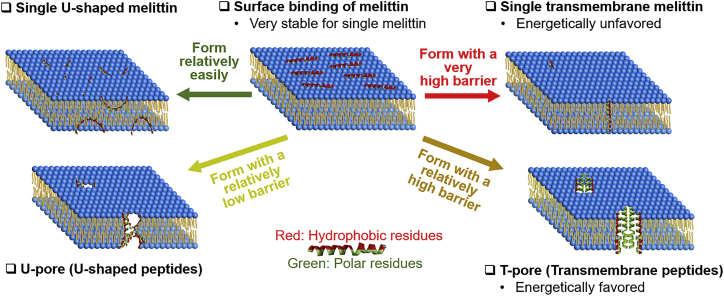
The above results provide valuable insights into various peptide organizations in membranes and their properties. We draw an illustration to compare several peptide organizations in Fig. 10. A single U-peptide can easily form because the formation kinetics is relatively simple, and the energy cost is relatively small. Recall that a single U-peptide is not as stable as a surface peptide. The formation of U- and T-pores is generally not easy and requires cooperation among several peptides. Compared with the T-pore, the U-pore can form with a relatively low free energy barrier. However, the energy of the U-pore is not as low as the T-pore. The formation of a single T-peptide needs to overcome a high barrier and is quite unlikely to occur.

Figure 10.

Various peptide organizations in membranes and their properties. To see this figure in color, go online.

Confirmation of the stability of the T- and U-pores in atomistic simulations

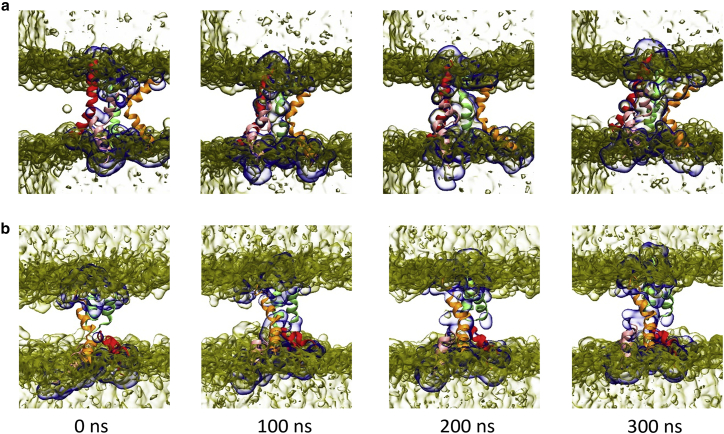
The CG modeling of membranes and peptides in the above simulations is crucially important for capturing the spontaneous penetration because atomistic simulations are usually unable to capture long dynamics (∼μs) in large systems. Here, our simulation box size is approximately 14 × 14 × 16 nm. The force field of our CG simulations is Martini version 2.2, which is a standardized force field for lipids. The good performance of Martini 2.2 force field in lipid bilayers has been demonstrated in many previous studies. To further confirm the validity of our CG simulation results, especially the stability of the T- and U-pores, we also perform atomistic simulations. We pick the last structures of the T- and U-pores from CG simulations and backmap the CG structures to atomistic structures using the back-mapping program CHARMM-GUI (35). Then, atomistic simulations with explicit water molecules are carried out using the CHARMM36M force field. Both the T- and U-pores maintain their structures through the whole 300 ns simulations, which confirms the stability of the T- and U-pores (Fig. 11). The animations of all-atom simulations can be found in the supporting material.

Figure 11.

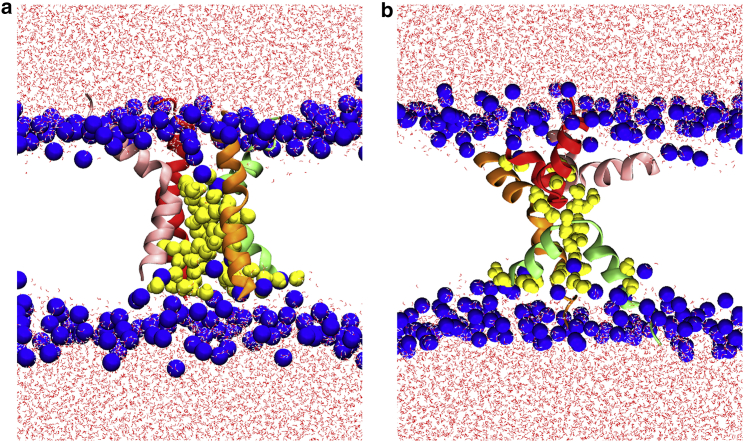
Snapshots of atomistic MD simulations of the T-pore (a) and U-pore (b). Four melittin peptide chains are rendered in red, green, pink, and orange. The water channels are highlighted by blue surface representation. The initial conformations of the atomistic simulations are replicated from the last conformations of the CG models by the back-mapping program CHARMM-GUI. The animation of T-pore and U-pore in atomistic MD simulations can be found in Videos S3 and S4, respectively. To see this figure in color, go online.

Atomistic simulations can be used to analyze the helicity of peptides during simulations. It is worth mentioning that the helicity of melittin plays an important role in its poration ability (47). We find the average helicity is 84.6% for the transmembrane peptides and 60.6% for U-shaped peptides, respectively. These results support that melittin conformations are mostly helical in lipid bilayers. The helicity of U-shape melittin is lower than that of transmembrane melittin, probably because a U-shaped peptide contains a U-turn point.

Note that atomistic simulations can capture electrostatic interactions more precisely than CG simulations. It is intriguing that, although CG simulations cannot capture electrostatic interactions precisely, spontaneous penetration and pore formation occur in CG simulations. Furthermore, these pores remain stable in atomistic simulations. Note that, if we manually assemble a pore of four melittin, the pore usually disintegrates in atomistic simulations. Overall, observation of pore formation in our CG simulations and validation of the pore stability in our atomistic simulation can provide insights into the role of electrostatic interactions in poration.

Water permeability and pore diameter of the T- and U-pores in atomistic simulations

The antibacterial activity of melittin strongly relies on the water permeability of the pores produced in lipid bilayers. The water permeability can be analyzed in atomistic simulations. We observe quite a large number of water molecules in both the T- and U-pores of atomistic simulations, which clearly demonstrates the water permeability (Fig. 12, Video S5. One water molecule spontaneously penetrates T-pore, Video S6. One water molecule spontaneously penetrates U-pore). The time-averaged numbers of water molecules, $N_w$, in the T- and U-pores are 81 and 42, respectively, which indicates a higher water permeability of the T-pore than the U-pore. The water permeability can be quantified by the pore diameter. The inner diameter of a pore, $d_{\text{pore}}$, is estimated using an equation developed by Sun et al. (29):

$$d_{\text{pore}}=2\sqrt{\frac{18N_w}{602\pi H}},$$

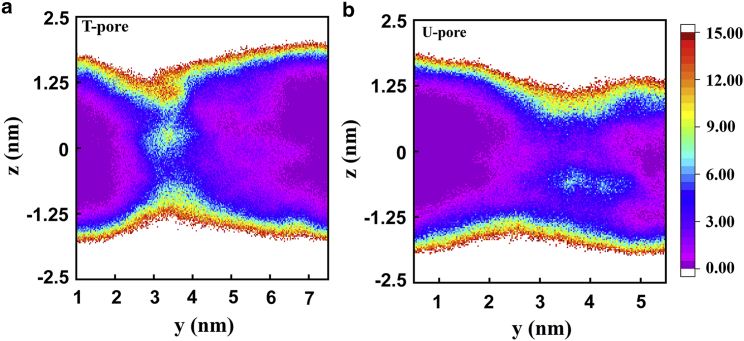
where H is the height of the pore. This equation is based on an approximation that the pore assumes a cylindrical shape. Using $H\approx$ 2 nm and substituting $N_w\approx 81$ and 42 into the equation, we obtain $d_{\text{pore}}^T\approx 1.24$ nm and $d_{\text{pore}}^U\approx 0.89$ nm for the T- and U-pores, respectively. The water channel widths are not uniform along the z-direction. To view the shapes of water channels of T- and U-pores, we plot the water density in the yz plane, as shown in Fig. 13.

Figure 12.

The water molecules in the T-pore (a) and U-pore (b) of atomistic simulations. The lipid head groups are rendered by bule beads, the water molecules in the pores are highlighted by yellow beads and. Lipid tails are not shown for clarity. To see this figure in color, go online.

Figure 13.

The two-dimensional number density of water (nm⁻³) in the y–z plane for T-pore (a) and U-pore (b). The energies are in kJ/mol. The numbers in parentheses are the energy differences with respect to the case of 1 PW. To see this figure in color, go online.

To further understand the water permeability, we estimate the free energy barrier of a water molecule crossing the pores through the calculation of the PMF, which has been used by Sun et al. (29). See the free energy barriers in Fig. S13. The barrier is approximately 12.5 kJ/mol for the T-pore and 15 kJ/mol for the U-pore. The lower energy barrier of the T-pore is consistent with the larger pore diameter of the T-pore.

In our 300 ns atomistic simulations, we observe six events of water molecules crossing the T-pore, and four events of water molecules crossing the U-pore (see Figs. S14 and S15). See the animations of water crossing the U- and T-pores in the supporting material. Based on these data, we very roughly estimate the water permeability as $2\times {10}^7{s}^{-1}$ and $1.3\times {10}^7{s}^{-1}$ for the T- and U-pores, respectively.

The stable pores and the water permeability of the pores observed in our simulations agree with previous experiments (5). Huang et al. observed stable pores produced by melittin in giant unilamellar vesicle experiments. They also observed the fluorescence dyes leaking out the vesicle.

Validation of pore formation in CG simulation using the latest Martini force field (version 3)

Martini force field is under continuous development. After we finished the CG simulations using Martini force field version 2.2, a newer version (version 3) was released. As suggested by referees during the review process, we also carried out one CG simulation using Martini force field version 3. The major observations are as follows. First, spontaneous penetration and pore formation can also be observed (Fig. S16). Second, the T-pore formed in Martini 3 is larger than that in Martini 2.2 (Fig. S17). Third, CG water molecules can be found in the T-pore formed by Martini 3 (Fig. S18), which is consistent with our atomistic simulations.

Comparison with previous simulation studies

Previous studies have also employed CG simulations with Martini force fields to investigate spontaneous poration of melittin in lipid bilayers and obtained many valuable insights (26,28,48). Our work is different from previous simulation studies in many aspects. First, in the simulation study by Santo and Berkowitz (26), melittin peptides were initially placed on both leaflets of lipid bilayers and the spontaneous pores consist of purely U-shaped melittin. In our work, melittin peptides are initially placed on a single leaflet, which should be closer to experimental conditions. Second, Santo et al. used the Martini force field version 2.1, which was the latest version then, and observed transient pores (28). Our work used the Martini force field version 2.2 and observed stable pores. The difference in the pore stability may be caused by the different Martini force field versions. Note that Martini 2.1 underestimates the binding affinity of polar residues in an apolar environment (49). Third, a more recent simulation study by Deng et al. observed spontaneous poration for DLPC lipid bilayers (18), which are thinner than the DPPC lipid bilayers in our work. The thickness of the lipid bilayers in our work should be relatively closer to the ones in experiments. In addition to the above differences with respect to previous simulation studies, our work focuses on analyzing the effects of peptide organizations on the pore stability and permeability. Here, we only compare three simulation studies whose systems are similar to ours, while there are many other simulation studies of AMPs in lipid bilayers (10,50,51,52). Last but not least, we devote a large portion of this work to analyzing the residue-residue contact map, peptide organizations in pores, and the effect of peptide organizations on water permeability, which are often missing in previous studies. We believe such analysis is useful, because the practical applications of melittin need rational selection of point mutations to enhance its antimicrobial ability, while the rational selection of point mutations strongly relies on the knowledge of residue-residue contact map and peptide organizations; for example, in the case of searching mutations to enlarge the pores and enhance water permeability. See more comparison of our work with previous studies in Fig. S19.

Conclusions

In conclusion, our CG MD simulations reveal the organizations of melittin peptides in lipid bilayers during and after spontaneous penetration. We find that the peptides in lipid bilayer adopt either a transmembrane conformation or a U-shaped conformation, which are referred to as T- and U-peptides, respectively. Several U-peptides and/or T-peptides aggregate to form stable pores. Two pores, a U-pore and a T-pore, are selected for careful inspection and analysis. In both pores, peptides are organized in a manner such that most polar residues face inward and most hydrophobic residues face outward (Fig. 6). Such organizations are stable because they dramatically reduce the contacts between polar and hydrophobic residues. In addition, such organizations produce a polar environment in the interior of pores, which favors the water permeability and the antibacterial ability.

While both pores appear to be stable, they differ in many aspects. First, the T-pore has a lower interaction energy but also a smaller conformational entropy with respect to the U-pore. Hence, we are unable to conclude whether the T-pore or U-pore has a lower free energy. Second, in the term of formation kinetics, the U-pore can occur easier due to the less requirement of the synergy among multiple peptides and the abundance of U-peptides. Note that the penetration and poration rely on the synergy among multiple peptides. Peptides are stable in membranes only when multiple peptides aggregate in the forms that segregate polar and hydrophobic residues. Single T-peptides are very unstable in membranes, while single U-peptides appear to be metastable. The metastability of U-peptides weakens the requirement of the synergy of multiple peptides during penetration and hence lowers the penetration barrier of U-pore formation. Third, the T-pore is more water permeable because of a larger pore diameter.

The stabilities of the U- and T-pores are confirmed by 300 ns all-atom MD simulations. In both pores, all peptides maintain high helicity in atomistic simulations. Atomistic simulations also demonstrate the water permeability of both pores.

The peptide organizations obtained in this work should deepen the understanding of the stability, poration mechanism, and permeability of melittin. Unveiling the peptide organizations should facilitate the optimization of melittin to enhance the antibacterial ability, such as rationally selecting mutations to further stabilize the T-pore for a better antibacterial activity. In addition, the melittin organizations in lipid bilayers may also be relevant to other AMPs.

Author contributions

L.D. and L.S. designed the research. L.S. and L.D. performed the research. L.D., L.S., S.W., F.T., and H.Z. analyzed the data. L.D. and L.S. wrote the paper.

Editor: Alemayehu Gorfe.