Modelling the impact of timelines of testing and isolation on disease control

Abstract

Testing and isolation remain a key component of public health responses to both persistent and emerging infectious diseases. Although the value of these measures have been demonstrated in combating recent outbreaks including the COVID-19 pandemic and monkeypox, their impact depends critically on the timelines of testing and start of isolation during the course of disease. To investigate this impact, we developed a delay differential model and incorporated age-since-symptom-onset as a parameter for delay in testing. We then used the model to compare the outcomes of reverse-transcription polymerase chain reaction (RT-PCR) and rapid antigen (RA) testing methods when isolation starts either at the time of testing or at the time of test result. Parameterizing the model with estimates of SARS-CoV-2 infection and diagnostic sensitivity of the tests, we found that the reduction of disease transmission using the RA test can be comparable to that achieved by applying the RT-PCR test. Given constraints and inevitable delays associated with sample collection and laboratory assays in RT-PCR testing post symptom onset, self-administered RA tests with short turnaround times present a viable alternative for timely isolation of infectious cases.

Highlights

• •Testing and isolation can substantially reduce disease transmission.
• •Isolation at the time of RT-PCR testing can alleviate the effect of turnaround times.
• •RA tests can outperform RT-PCR tests with delay longer than 1 day post symptom onset.

1. Introduction

Emerging infectious diseases often pose significant and unique challenges for their controllability. Pandemic diseases are particularly concerning due to their scale and speed of spread globally (Morens et al., 2020). The COVID-19 pandemic has demonstrated these challenges, especially at the early stages of SARS-CoV-2 emergence in the absence of vaccination.

One of the key measures that have been widely used during COVID-19 is testing to identify infected cases and isolate them to reduce onward transmission (CDC, 2022b; Grassly et al., 2020; MacIntyre, 2020; Mercer & Salit, 2021; Wells et al., 2021). Prior to the widespread availability of RA tests, RT-PCR was the predominant approach to identifying SARS-CoV-2 infections (Rosenberg & Holtgrave, 2021; Wells et al., 2021, 2022b,a). However, RT-PCR requires laboratory assay, a process that often delays the test results after sample collection, which could lead to a late start of isolation (Rosenberg & Holtgrave, 2021). Even without considering resources required for, and costs associated with RT-PCR method, the scale of testing could overwhelm the system with limited capacity, further lengthening the turnaround times (Kucharski et al., 2020). While awaiting test results, the possibility of disease transmission from positive cases can be reduced by initiating isolation at the time of sample collection.

The availability of RA tests has provided an alternative means of scaling up testing capacity and shortening turnaround times from days to minutes (Wells, Pandey, Moghadas, et al., 2022). The low-cost, self-administered RA tests can mitigate the impact of disease through the immediate start of isolation for positive cases. However, diagnostic sensitivity of RA tests may be lower than RT-PCR, which could lead to higher rates of false-negatives (Wells, Pandey, Moghadas, et al., 2022).

Understanding the effect of timelines of testing and isolation on disease dynamics can help to improve testing strategies. In this study, we aimed to formulate a delay-differential model to investigate the dynamics of disease transmission encapsulating three important factors: (i) time of testing after the onset of disease symptoms; (ii) delay in turnaround times of the test results and start of isolation; and (iii) diagnostic sensitivity of the test which varies with time. We formulated our model with the natural history of COVID-19, and simulated it to illustrate the findings using parameters estimated for SARS-CoV-2 infection, while presenting relevant theoretical analyses.

2. Model formulation

To develop our model from the classical susceptible-infected-recovered (SIR) framework, we made the following assumptions:

• (A1)Disease transmission occurs through contacts between susceptible and infectious individuals in a mass action form.
• (A2)Immunity generated from natural infection is long-lasting, hence omitting the possibility of reinfection following recovery.
• (A3)The epidemic timelines are short compared to the lifespan of individuals, thus excluding the effect of demographics such as births and natural deaths.

Denoting the class of susceptible individuals by S, we have

$$\begin{array}{l}S\text{'}\left(t\right)=-\beta S\left(t\right)\mathrm{\Lambda }\left(t\right),\\ E\text{'}\left(t\right)=\beta S\left(t\right)\mathrm{\Lambda }\left(t\right)-\sigma E\left(t\right),\end{array}$$

where ‘′’ represents the derivative of the variables with respect to time t and Λ(t) is the force of infection which will be formulated later. Upon infection, individuals will be placed in the E class for a duration of time (referred to as latent period) before becoming infectious. During latency, the disease is not transmissible. We assumed that a proportion p of latent individuals develop symptoms, and the remaining will be asymptomatic without presenting any clinical symptoms of the disease during the course of infection. Denoting asymptomatic individuals by A, we have

$$A^{\prime }(t)=(1-p)\sigma E(t)-{\gamma }_{A}A(t),$$

where 1/σ represents the average latent period and 1/γ_A is the average duration of asymptomatic infectiousness.

Infected individuals who become symptomatic will be infectious in a stage of disease prior to the onset of symptoms, referred to as pre-symptomatic. Letting P denote this stage with an average duration of 1/γ_P, we have

$$P^{\prime }(t)=p\sigma E(t)-{\gamma }_{P}P(t).$$ (1)

For identification of infected individuals, we assume that only symptomatic cases will be tested, and isolated once the results are confirmed as positive. Let a represent the time elapsed since the onset of symptoms. We define i(t, a), v(t, a), k(t, a), and w(t, a) to be the densities of populations, with respect to age a at time t, who are not tested, tested and waiting for the results, isolated with positive results, and not isolated due to false-negative results. At any age a post symptom onset, the testing rate is defined by μ(a) with the diagnostic sensitivity q(a). The dynamics of population densities are thus governed by the following first-order partial differential equations

$$\begin{array}{l}\frac{\partial i(t,a)}{\partial t}+\frac{\partial i(t,a)}{\partial a}=-\mu \left(a\right)i(t,a)-\gamma i(t,a),\\ \frac{\partial v(t,a)}{\partial t}+\frac{\partial v(t,a)}{\partial a}=\mu \left(a\right)i(t,a)-\mu (a-\tau )e^{-\gamma \tau }i(t-\tau ,a-\tau )-\gamma v(t,a),\\ \frac{\partial k(t,a)}{\partial t}+\frac{\partial k(t,a)}{\partial a}=q(a-\tau )\mu (a-\tau )e^{-\gamma \tau }i(t-\tau ,a-\tau )-\gamma k(t,a),\\ \frac{\partial w(t,a)}{\partial t}+\frac{\partial w(t,a)}{\partial a}=(1-q(a-\tau ))\mu (a-\tau )e^{-\gamma \tau }i(t-\tau ,a-\tau )-\gamma w(t,a),\end{array}$$ (2)

where 1/γ is the average infectious period after the onset of symptoms, and τ is the time delay in receiving the test results. Let a₀ > 0 denote the minimum amount of time elapsed post symptom onset before performing a test. We define μ(a) by

$$\mu (a)=\left\{\begin{array}{cc}\left(C{e}^{-1/a}\right)/a& a_0\le a\le \frac{1}{\gamma }\\ 0& \text{otherwise}\end{array}\right)$$

In this formulation, [a₀, 1/γ] represents the window of opportunity for testing after the onset of symptoms. In general, testing and isolation of individuals beyond the average duration of infectiousness for symptomatic disease will not be effective in reducing transmission. The testing rate increases with a to a maximum at one (a = 1) day after the onset of symptoms and then declines. We considered this rate to reasonably reflect the reality of RT-PCR testing which may involve traveling time of an individual to a testing centre and possible waiting time for sample collection. However, for self-administered RA tests, the rate of testing can be at the maximum without any significant delay after the onset of symptoms. Thus, for RA testing, we considered:

$${\mu }^{\ast }(a)=\left\{\begin{array}{cc}C{e}^{-1}& a_0\le a\le 1\\ \mu (a)& \text{otherwise}\end{array}\right)$$

where Ce⁻¹ = max{μ(a)}. Using (2), the force of infection is expressed by

$$\begin{array}{l}\mathrm{\Lambda }\left(t\right)={\delta }_{A}A\left(t\right)+P\left(t\right)+{\delta }_I{\int }_0^{\infty }\left(i\right(t,a)+v(t,a)+w(t,a\left)\right)da+{\delta }_k{\int }_0^{\infty }k(t,a)da.\end{array}$$ (3)

where δ_A, δ_I, and δ_k are the transmissibilities of asymptomatic, non-isolated symptomatic, and isolated symptomatic individuals relative to pre-symptomatic cases, respectively. Fig. 1 illustrates a schematic diagram of the model with testing and isolation.

Fig. 1.

Schematic representation of the model dynamics.

To derive the equations for transmission dynamics of the model, it is biologically reasonable to assume that

$$i(t,\infty )=v(t,\infty )=k(t,\infty )=w(t,\infty )=0.$$ (4)

Solving (2) subject to the following boundary and initial conditions, respectively,

$$\begin{array}{l}i(t,0)={\gamma }_{p}P\left(t\right)\\ i(0,a)=i_0\left(a\right)\\ v(t,0)=0\\ v(0,a)=v_0\left(a\right)\end{array}\begin{array}{l}k(t,0)=0\\ k(0,a)=k_0\left(a\right)\\ w(t,0)=0\\ w(0,a)=w_0\left(a\right)\end{array}$$ (5)

we obtained

$$\begin{array}{l}i(t,a)={\gamma }_P{b}_1(a)P(t-a),\\ v(t,a)={\gamma }_P{e}^{-\gamma a}P(t-a){\int }_0^a{e}^{\gamma u}\mu (u)b_1(u)du-e^{-\gamma \tau }{\int }_0^a{e}^{\gamma u}\mu (u-\tau )b_1(u-\tau )du,\\ k(t,a)={\gamma }_P{e}^{-\gamma (a+\tau )}P(t-a){\int }_0^a{e}^{\gamma u}q(u-\tau )\mu (u-\tau )b_1(u-\tau )du,\\ w(t,a)={\gamma }_P{e}^{-\gamma (a+\tau )}P(t-a){\int }_0^a{e}^{\gamma u}(1-q(u-\tau ))\mu (u-\tau )b_1(u-\tau )du,\end{array}$$

where

$$b_1(a)=e^{-{\int }_0^a(\mu (u)+\gamma )du}$$

Let

$$\begin{array}{l}I\left(t\right)={\int }_0^{\infty }i(t,a)da\\ V\left(t\right)={\int }_0^{\infty }v(t,a)da\\ K\left(t\right)={\int }_0^{\infty }k(t,a)da\\ W\left(t\right)={\int }_0^{\infty }w(t,a)da\end{array}$$ (6)

be the number of individuals at time t who are not tested, tested, and waiting for the results, isolated with positive results, and non-isolated due to false-negative results, respectively. Therefore, we have the following differential equations:

$$\begin{array}{l}I\text{'}(t)=p\sigma {\gamma }_P{\int }_0^{\infty }{b}_1(a)E(t-a)da-{\gamma }_{P}I(t),\\ V\text{'}(t)=p\sigma {\gamma }_P{\int }_0^{\infty }{e}^{-\gamma a}E(t-a)({\int }_0^a{e}^{\gamma u}\mu (u)b_1(u)du-e^{-\gamma \tau }{\int }_0^a{e}^{\gamma u}\mu (u-\tau )b_1(u-\tau )du)da-{\gamma }_{P}V(t),\\ K\text{'}(t)=p\sigma {\gamma }_P{\int }_0^{\infty }(e^{-\gamma (a+\tau )}E(t-a){\int }_0^a{e}^{\gamma u}q(u-\tau )\mu (u-\tau )b_1(u-\tau )du)da-{\gamma }_{P}K(t),\\ W\text{'}(t)=p\sigma {\gamma }_P{\int }_0^{\infty }(e^{-\gamma (a+\tau )}E(t-a){\int }_0^a{e}^{\gamma u}(1-q(u-\tau ))\mu (u-\tau )b_1(u-\tau )du)da-{\gamma }_{P}W(t).\end{array}$$

The force of infection Λ(t) can be expressed by

$$\Lambda (t)={\delta }_{A}A(t)+P(t)+{\delta }_I(I(t)+V(t)+W(t))+{\delta }_{k}K(t),t\ge a.$$

Summarizing the above details, we arrived at the following model equations with both discrete and distributed delays:

$$\begin{array}{l}S\text{'}\left(t\right)=-\beta S\left(t\right)\Lambda \left(t\right),\\ E\text{'}\left(t\right)=\beta S\left(t\right)\Lambda \left(t\right)-\sigma E\left(t\right),\\ A\text{'}\left(t\right)=(1-p)\sigma E\left(t\right)-{\gamma }_{A}A\left(t\right),\\ P\text{'}\left(t\right)=p\sigma E\left(t\right)-{\gamma }_{P}P\left(t\right),\\ I\text{'}(t)=p\sigma {\gamma }_P{\int }_0^{\infty }{b}_1(a)E(t-a)da-{\gamma }_{P}I(t),\\ V\text{'}(t)=p\sigma {\gamma }_P{\int }_0^{\infty }{e}^{-\gamma a}E(t-a)({\int }_0^a{e}^{\gamma u}\mu (u)b_1(u)du-e^{-\gamma \tau }{\int }_0^a{e}^{\gamma u}\mu (u-\tau )b_1(u-\tau )du)da-{\gamma }_{P}V(t),\\ K\text{'}(t)=p\sigma {\gamma }_P{\int }_0^{\infty }(e^{-\gamma (a+\tau )}E(t-a){\int }_0^a{e}^{\gamma u}q(u-\tau )\mu (u-\tau )b_1(u-\tau )du)da-{\gamma }_{P}K(t),\\ W\text{'}(t)=p\sigma {\gamma }_P{\int }_0^{\infty }(e^{-\gamma (a+\tau )}E(t-a){\int }_0^a{e}^{\gamma u}(1-q(u-\tau ))\mu (u-\tau )b_1(u-\tau )du)da-{\gamma }_{P}W(t).\end{array}$$ (7)

3. Reproduction number

The basic reproduction number $({\mathcal{R}}_0)$ is a fundamental quantity defined as the expected number of secondary infections generated by a single infectious individual in an entirely susceptible population (Diekmann & Heesterbeek, 2000). According to the theory of epidemics, we would expect the disease to die out if ${\mathcal{R}}_0<1$, while it will cause a short-term outbreak or persist in the population if ${\mathcal{R}}_0>1$. A related quantity, the control reproduction number $({\mathcal{R}}_c)$, can be defined when certain control measures (such as testing and isolation, treatment, or vaccination) are implemented, which is often used to determine whether the disease can be controlled.

To derive these quantities, we note that S(t), E(t), A(t), P(t), I(t), V(t), K(t) and W(t) are non-negative for all t > 0. The model has a family of disease equilibria: ${\mathcal{E}}_0=(S(0),0,\dots ,0)$ with any initial value of S(0) for the susceptible population. From (7), we see that S(t) is strictly decreasing in the presence of infection. Hence, the model has no endemic equilibrium point. Considering the duration and transmissibility of asymptomatic, non-isolated symptomatic, isolated symptomatic, and non-isolated false-negative cases, the total number of secondary cases generated in the presence of testing and isolation can be calculated using a previous method (Alexander et al., 2008), and is given by

$$\begin{array}{l}{\mathcal{R}}_c=\beta S(0)[\frac{(1-p){\delta }_A}{{\gamma }_A}+\frac{p}{{\gamma }_P}+\frac{p{\delta }_I}{\gamma }+p({\delta }_k-{\delta }_I){\int }_0^{\infty }(e^{-\gamma (a+\tau )}{\int }_0^a{e}^{\gamma u}q(u-\tau )\mu (u-\tau )b_1(u-\tau )du\left)da\right]\end{array}$$

In the absence of testing and isolation (μ(a) ≡ 0), ${\mathcal{R}}_c$ reduces to the basic reproduction number

$${\mathcal{R}}_0=\beta S(0)\left(\frac{(1-p){\delta }_A}{{\gamma }_A}+\frac{p}{{\gamma }_P}+\frac{p{\delta }_I}{\gamma }\right).$$ (8)

4. Modified model

Unlike RT-PCR test results that are associated with some delay from the time of sample collection, there are several rapid antigen tests that provide results within minutes (Wells, Pandey, Moghadas, et al., 2022), allowing infected individuals with positive results to initiate isolation immediately. One possible way that may help reduce disease transmission is to initiate isolation at the time of RT-PCR testing while awaiting the test result. If the result is positive, then the individuals will continue their isolation until recovery. If the test result is negative (which may be false-negative based on the diagnostic sensitivity of the test), individuals can end their isolation and return to normal activities. In the context of our model, individuals who end their isolation due to a false-negative result can transmit the disease similar to infectious, non-isolated cases without restrictions. Similar to the model (7), we let i(t, a), v(t, a), k(t, a) and w(t, a) represent the population densities with respect to age a at time t that are not tested, tested and waiting for the results but isolated, isolated with positive result, and non-isolated due to a false negative result, respectively. Defining

$$\begin{array}{l}I\left(t\right)={\int }_0^{\infty }i(t,a)da,\\ V\left(t\right)={\int }_0^{\infty }v(t,a)da,\\ K\left(t\right)={\int }_0^{\infty }k(t,a)da,\\ W\left(t\right)={\int }_0^{\infty }w(t,a)da\end{array}$$

and solving for densities i(t, a), v(t, a), k(t, a), and w(t, a), we obtained the same equations as (7) with the modified force of infection:

$$\begin{array}{l}\hat{\Lambda }\left(t\right)={\delta }_{A}A\left(t\right)+P\left(t\right)+{\delta }_I\left(I\right(t)+W(t\left)\right)+{\delta }_k\left(V\right(t)+K(t\left)\right).\end{array}$$ (9)

The control reproduction number for the modified model can then be expressed by

$$\begin{array}{l}\widehat{{\mathcal{R}}_c}=\beta S(0)[\frac{(1-p){\delta }_A}{{\gamma }_A}+\frac{p}{{\gamma }_P}+\frac{p{\delta }_I}{\gamma }+p({\delta }_k-{\delta }_I){\int }_0^{\infty }{e}^{-\gamma a}{\int }_0^a{e}^{\gamma u}\mu (u)b_1(u)duda\\ -p({\delta }_k-{\delta }_I){\int }_0^{\infty }(e^{-\gamma (a+\tau )}{\int }_0^a{e}^{\gamma u}(1-q(u-\tau ))\mu (u-\tau )b_1(u-\tau )du)da]\end{array}$$ (10)

5. Parameterization and results

To illustrate the effect of timelines of testing and isolation with a delay in the test result, we simulated the model with estimates of parameters specific to SARS-CoV-2 infection. We used early estimates related to the original Wuhan-I strain, summarized in Table 1. Assuming ${\mathcal{R}}_0=1.5$ and S(0) = 10, 000, the transmission rate β = 3.9501 × 10⁻⁵ was computed from equation (8).

Table 1.

Model parameters and their associated values.

Parameter	Description	Value	Source
${\mathcal{R}}_0$	Basic reproduction number	1.5	Assumed
β	Transmission rate	3.9501 × 10−5	Computed from (8)
δA	Relative transmissibility of asymptomatic infection	0.26	(Sayampanathan et al., 2021; Moghadas et al., 2020; Sayampanathan et al., 2021; Moghadas et al., 2020)
δI	Relative transmissibility of non-isolated symptomatic infection	0.89	(Ferretti et al., 2020; Moghadas et al., 2020; Ferretti et al., 2020; Moghadas et al., 2020)
δk	Reduction in transmissibility of isolated symptomatic infection	0.2	Assumed
1/σ	Average latent period	2.2 days	(Li et al., 2020; Moghadas et al., 2021; Li et al., 2020; Moghadas et al., 2021)
1/γA	Average duration of asymptomatic stage	5 days	(Gatto et al., 2020; Moghadas et al., 2020; Gatto et al., 2020; Moghadas et al., 2020)
1/γP	Average duration of pre-symptomatic stage	2.3 days	(Li et al., 2020; Moghadas et al., 2020; Li et al., 2020; Moghadas et al., 2020)
1/γ	Average infectious period following the onset of symptoms	3.2 days	(Li et al., 2020; Moghadas et al., 2020; Li et al., 2020; Moghadas et al., 2020)
p	Proportion of infected individuals who develop symptoms	0.649	(Sah et al., 2021; Sah et al., 2021)

We set the minimum delay (a₀) in testing after the onset of symptoms to 0.1 day (i.e., 2.4 h). We then varied a₀ to a maximum of 2 days. We also varied the delay in obtaining the results of testing (τ) between 0.1667 days (i.e., 4 h) and 2 days when simulating the model for the RT-PCR test. For RA testing, given the short turnaround times, τ was set to 0.0104 (i.e., 15 min).

To determine the constant parameter C in the testing rate μ(a), we used the conversion formulae for probability of an event occurring given its rate. Assuming an 80% probability that a symptomatic individual is tested 1 day after the onset of symptoms, we calculated C by using the formulae $0.8=1-e^{-C{e}^{-1}}$ at a = 1, corresponding to the maximum value μ(1), giving C = 4.375.

To incorporate the test sensitivity, we fitted the function

$$q(t)=c_1{t}^{c_2}{e}^{[-c_3{t}^{c_4}+c_5]}$$ (11)

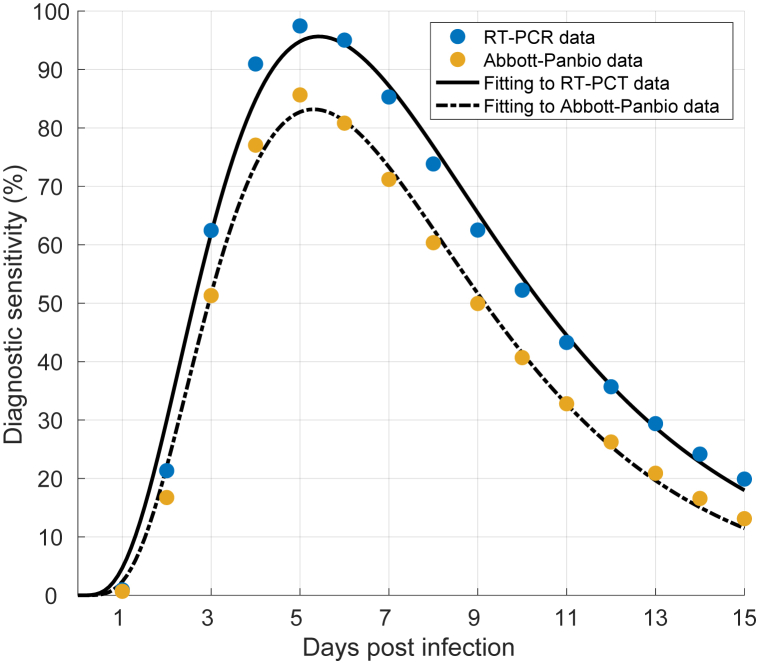
to discretized temporal diagnostic sensitivity of the RT-PCR derived from a previous study (Wells, Pandey, Moghadas, et al., 2022), giving the values c₁ = 1.722, c₂ = 5.625, c₃ = 5.127, c₄ = 0.484, and c₅ = 1.523. For the RA test, we considered the diagnostic sensitivity of Abbott-Panbio, which was expressed as the product of the diagnostic sensitivity of the RT-PCR and the temporal percent positive agreement between Abbott-Panbio and RT-PCR tests in serial testing data (Wells, Pandey, Moghadas, et al., 2022). Fitting (11) to Abbott-Panbio sensitivity estimates, we obtained c₁ = 3.393, c₂ = 7.869, c₃ = 9.963, c₄ = 0.4031, c₅ = 4.985 (Fig. 2). The sensitivity curves were used to determine the probability of an infected individual being identified as positive at the time of testing.

Fig. 2.

Fitting equation (11) to estimates of temporal diagnostic sensitivity of RT-PCT and Abbott-Panbio rapid antigen tests.

5.1. Effect of delay in testing and test result on ${\mathcal{R}}_c$

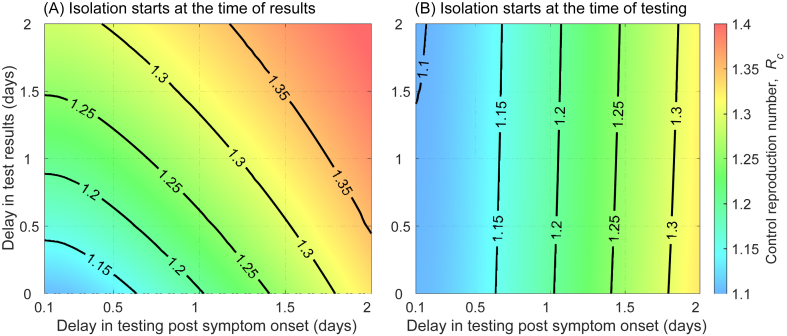
We evaluated the reduction in ${\mathcal{R}}_c$ achieved by testing and isolating infected individuals. For the RT-PCR test with isolation of positive cases starting at the time of test result, we found that ${\mathcal{R}}_0$ can be reduced by at least 23% (from 1.5 to below 1.15) if testing started within 16 h of symptom onset, and results are available within 10 h of sample collection (Fig. 3A). As the delay in testing increases, a shorter turnaround time is required to achieve the same reduction in the reproduction number. In contrast, when isolation started at the time of sample collection and continued for those whose results are positive, turnaround time has little effect on changing the outcomes. For example, for testing within 16 h of symptom onset, ${\mathcal{R}}_0$ reduces to below 1.15 even if the test turnaround time is 2 days (Fig. 3B).

Fig. 3.

Control reproduction number as a function of delay in RT-PCR testing and delay in test results when isolation starts at: (A) the time of results for positive cases; (B) the time of testing.

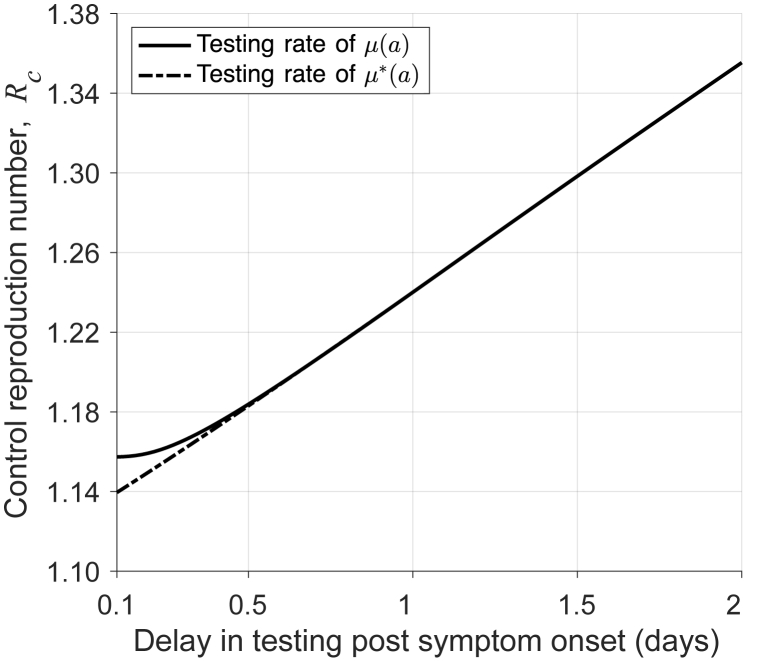
For the RA test, the delay in start of isolation is negligible due to the short (15-min) turnaround time. We found that the reduction in ${\mathcal{R}}_0$ can exceed 20% (from 1.5 to below 1.2) when symptomatic individuals performed a test within 16 h of symptom onset (Fig. 4). These results suggest that, despite higher sensitivity of the RT-PCR test, RA testing can be a viable alternative to costly and resource consuming RT-PCR testing.

Fig. 4.

Control reproduction number as a function of delay in RA testing with 15 min turnaround time.

5.2. Effect of testing and isolation on incidence

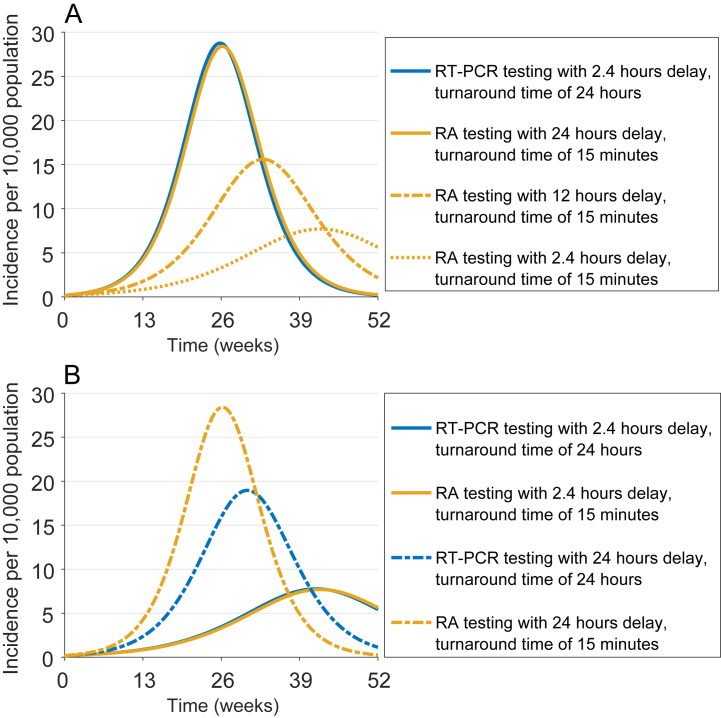
We simulated the model for a 1-year time horizon to compare the incidence of infection under scenarios of RT-PCR and RA testing, when isolation starts at the time of test result. Fig. 5A shows that the performance of RT-PCR testing with delay of 2.4 h after the onset of symptoms and turnaround time of 24 h is virtually equivalent to RA testing with delay of 24 h. Since self-administered RA tests do not involve logistical and practical constraints of the RT-PCR test, their early application could outperform RT-PCR testing with prolonged turnaround times in reducing the overall incidence (Fig. 5A).

Fig. 5.

Incidence of infection under different scenarios of delay in RT-PCR and RA testing with the start of isolation (A) at the time of results, and (B) at the time of testing.

When isolation starts at the time of sample collection, the turnaround time of RT-PCR has a counterintuitive effect compared with RA testing (Fig. 5B). For example, RT-PCR testing with a 24-h delay and turnaround time of 24 h outperforms RA testing with a 24-h delay after the onset of symptoms. This arises from a higher rate of false negatives for the RA test, which allows infectious individuals to continue with their normal activities shortly (i.e., 15 min) after the test without isolation. In contrast, isolation of infectious individuals for a duration of 24 h before the RT-PCR test results are available would reduce the transmission (Fig. 5B). Furthermore, higher diagnostic sensitivity of the RT-PCR test compared with the RA test leads to fewer cases of false negatives. However, this comparative advantage diminishes with shorter delay in testing post symptom onset, and/or faster turnaround times for the RT-PCR test. For instance, reduction of incidence in RT-PCR testing with 2.4 h delay and turnaround time of 24 h is equivalent to that in RA testing with 2.4 h delay.

5.3. Effect of testing and isolation on the attack rate

The patterns observed in the control reproduction number, ${\mathcal{R}}_c$, were also reflected in the attack rate (i.e., the proportion of the population infected throughout the epidemic). We computed the reduction in the attack rate achieved when isolation started at the time of testing as opposed to at the time of test result. This relative reduction (RR) was calculated by

$$\text{RR}=\frac{\text{Total infections }{\left(\text{RT-PCR}\right)}_{TR}-\text{Total infections }{\left(\text{RT-PCR}\right)}_{TT}}{\text{Total infections }{\left(\text{RT-PCR}\right)}_{TR}},$$

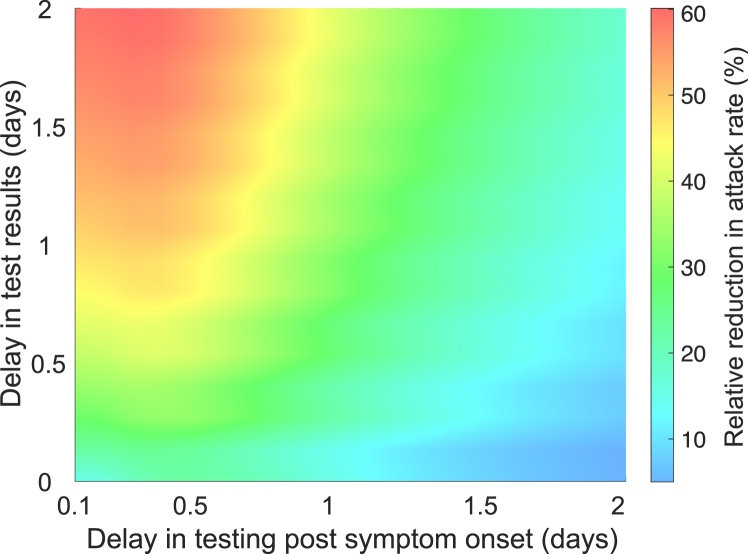
where subscripts TR and TT represent the start of isolation at the time of result and testing, respectively. Fig. 6 shows that the RR reduces as delay in testing increases, but also increases as the turnaround time increases. The lowest RR (10%) occurs when tests are performed with a delay of at least 2 days post symptom onset and a short turnaround time of 4 h. The greatest RR (60%) is achieved when delay in testing is short (i.e., 2.4 h after the onset of symptoms), but the turnaround time is 2 days. This is expected as longer turnaround times extend the duration of isolation, which further reduces transmission in the scenario when isolation starts at the time of testing.

Fig. 6.

Relative reduction in the attack rate achieved with RT-PCR testing when isolation starts at the time of test result compared to at the time of testing.

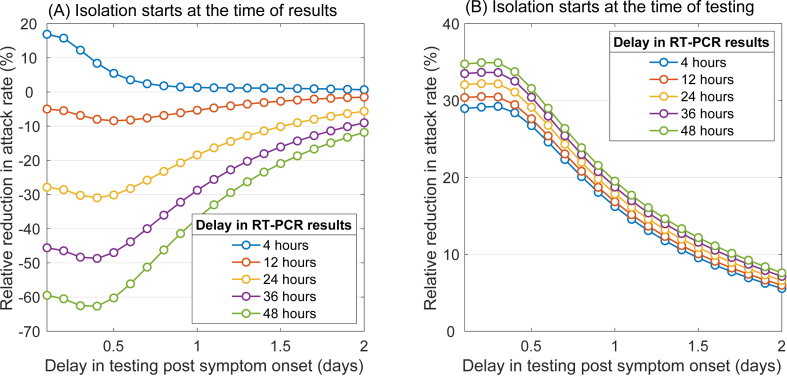
We then calculated the RR, comparing RT-PCR and RA testing. The RR was calculated by

$$\text{RR}=\frac{\text{Total infections }\left(\text{RA}\right)-\text{Total infections }{\left(\text{RT-PCR}\right)}_i}{\text{Total infections }\left(\text{RA}\right)},$$

where either i = TR or i = TT, with a fixed delay of 15 min for the RA test result. When isolation starts at the time of test result (Fig. 7A), we found that the RT-PCR test outperforms the RA test (i.e., RR > 0) only if the test was performed within 20 h of symptom onset, and turnaround times were relatively short (i.e., within 4 h of testing). However, if isolation starts at the time of testing (Fig. 7B), the RT-PCR test (with a higher diagnostic sensitivity) outperforms the RA test regardless of delay in testing or turnaround times, but the RR reduces to under 10% as delay in testing increases to 2 days. Considering the practical timelines of RT-PCR testing post symptom onset and limited laboratory capacity that may lead to longer turnaround times during the peak of an epidemic, RA testing may lead to a similar or an even larger reduction in the attack rate.

Fig. 7.

Relative reduction in the attack rate achieved with RT-PCR testing compared with RA testing, as a function of delay in testing and turnaround time of the RT-PCR test result.

6. Discussion

Testing and isolation of positive cases have been used as a key strategy to quell the spread of some infectious diseases, with COVID-19 and monkeypox presenting two recent examples of such diseases (MacIntyre, 2020; Titanji et al., 2022). There are several methods to test for the identification of infected individuals (CDC, 2022a). In the context of COVID-19 pandemic, the two commonly used methods are RT-PCR and rapid antigen tests, which have different temporal diagnostic sensitivities (Wells, Pandey, Moghadas, et al., 2022). The former has been shown to have a higher diagnostic sensitivity, but involves sample collection by trained individuals and laboratory assays, which would impose logistical considerations with implications for timely isolation of positive cases. The latter, on the other hand, can be self-administered with turnaround times within minutes, facilitating rapid case isolation despite having a comparatively lower diagnostic sensitivity. We considered these factors and developed a delay-differential model to investigate the trade-offs between higher sensitivity and rapid results of these tests with case isolation for mitigating disease spread.

Parameterizing the model with estimates associated with SARS-CoV-2 infection, and sensitivity of RT-PCR and Abbott-Panbio rapid antigen tests (Wells, Pandey, Moghadas, et al., 2022), we found that the reduction of disease transmission, reflected in ${\mathcal{R}}_c$, using the RA test could be comparable to that achieved by the RT-PCR test. In practice, sample collection and laboratory results of the RT-PCR test are, in large measures, unlikely to occur within 1 day of symptom onset in the general population. If infected individuals are not isolated prior to the RT-PCR test result, our model indicates that using the RA test would lead to a significantly higher reduction in the attack rate. However, when isolation starts immediately after the test, then application of the RT-PCR test would confer a higher reduction in the attack rate, although this effect diminishes with delay in testing, thus arguing in favor of inexpensive, self-administered RA tests.

Our model provides a theoretical framework for evaluating the effect of testing and isolation. However, it is subject to several limitations. For example, we parameterized the model with a testing rate with some underlying assumptions that are plausible, but not based on specific quantifications in real-world settings. Furthermore, during an epidemic, it is likely that different methods of testing are used concomitantly with varying turnaround times. Our study considered testing of only symptomatic individuals, and after the onset of symptoms, while testing before the start of symptoms is also common during the epidemic, especially for close contacts and asymptomatic individuals (Day, 2020). We also assumed that those who are tested adhere to guidelines for isolation, for example in the scenario that isolation starts immediately after testing. However, with the perception that their symptoms may not indicate infection with the particular disease, they may defer isolation until confirmation of positive results. Under these assumptions, we highlight the qualitative aspects of our findings on the value of testing and timely isolation of infected cases.

Funding

SMM acknowledges the support from Natural Sciences and Engineering Research Council of Canada (NSERC) through Individual Discovery Grant, and EIDM Mathematics for Public Health (MfPH) grant.

Authors’ contributions

SMM conceived the study; AL and ZW developed the model, analyzed the results theoretically, and simulated the model; SMM analyzed simulation results and wrote the draft of the paper; AL and ZW contributed to providing contextual information, writing of the paper, and interpretation of the results.

Declaration of competing interest

None declared.

Handling Editor: Dr HE DAIHAI

Appendix A.

Here, we show that if ${\mathcal{R}}_c<1$, then the disease can be controlled. From (7), we see that S(t) ≤ S(0) for all t ≥ 0. Thus, we have

$$E^{\prime }(t)\le \beta S(0)\mathrm{\Lambda }(t)-\sigma E(t).$$ (A.1)

The standard comparison argument implies that the solutions of (E, A, P, I, V, K, W) in the model are bounded by the solutions of the corresponding compartments of the following system:

$$\begin{array}{l}{E}^{\text{'}}\left(t\right)=\beta S\left(0\right)\mathrm{\Lambda }\left(t\right)-\sigma E\left(t\right),\\ A^{\text{'}}\left(t\right)=(1-p)\sigma E\left(t\right)-{\gamma }_{A}A\left(t\right),\\ P^{\text{'}}\left(t\right)=p\sigma E\left(t\right)-{\gamma }_{P}P\left(t\right),\\ I^{\text{'}}\left(t\right)=p\sigma {\gamma }_P{\int }_0^{\infty }{b}_1\left(a\right)E(t-a)da-{\gamma }_{P}I\left(t\right),\\ V^{\text{'}}\left(t\right)=p\sigma {\gamma }_P{\int }_0^{\infty }{e}^{-\gamma a}E(t-a)\left({\int }_0^a{e}^{\gamma u}\mu \left(u\right)b_1\left(u\right)du-e^{-\gamma \tau }{\int }_0^a{e}^{\gamma u}\mu (u-\tau )b_1(u-\tau )du\right)da-{\gamma }_{P}V\left(t\right),\\ K^{\text{'}}\left(t\right)=p\sigma {\gamma }_P{\int }_0^{\infty }{e}^{-\gamma (a+\tau )}E(t-a)\left({\int }_0^a{e}^{\gamma u}q(u-\tau )\mu (u-\tau )b_1(u-\tau )du\right)da-{\gamma }_{P}K\left(t\right),\\ W^{\text{'}}\left(t\right)=p\sigma {\gamma }_P{\int }_0^{\infty }{e}^{-\gamma (a+\tau )}E(t-a)\left({\int }_0^a{e}^{\gamma u}(1-q(u-\tau ))\mu (u-\tau )b_1(u-\tau )du\right)da-{\gamma }_{P}W\left(t\right).\end{array}$$ (A.2)

We now substitute the ansatz ωe^λt, where ω = (E⁰, A⁰, P⁰, I⁰, V⁰, K⁰, W⁰) into the above equation. Without loss of generality, let us assume E⁰ = 1 and eliminate e^λt. It then follows that

$$\begin{array}{l}\lambda =\beta S\left(0\right)\left({\delta }_A{A}^0+P^0+{\delta }_I{I}^0+{\delta }_I{V}^0+{\delta }_k{K}^0+{\delta }_I{W}^0\right)-\sigma ,\\ A^0\lambda =(1-p)\sigma -{\gamma }_A{A}^0,\\ P^0\lambda =p\sigma -{\gamma }_P{P}^0,\\ I^0\lambda =p\sigma {\gamma }_P{\int }_0^{\infty }{b}_1\left(a\right)e^{-\lambda a}da-{\gamma }_P{I}^0,\\ V^0\lambda =p\sigma {\gamma }_P{\int }_0^{\infty }{e}^{-\gamma a}\left({\int }_0^a{e}^{\gamma u}\mu \left(u\right)b_1\left(u\right)du-e^{-\gamma \tau }{\int }_0^a{e}^{\gamma u}\mu (u-\tau )b_1(u-\tau )du\right)e^{-\lambda a}da-{\gamma }_P{V}^0,\\ K^0\lambda =p\sigma {\gamma }_P{\int }_0^{\infty }{e}^{-\gamma (a+\tau )}\left({\int }_0^a{e}^{\gamma u}q(u-\tau )\mu (u-\tau )b_1(u-\tau )du\right)e^{-\lambda a}da-{\gamma }_P{K}^0,\\ W^0\lambda =p\sigma {\gamma }_P{\int }_0^{\infty }{e}^{-\gamma (a+\tau )}\left({\int }_0^a{e}^{\gamma u}(1-q(u-\tau ))\mu (u-\tau )b_1(u-\tau )du\right)e^{-\lambda a}da-{\gamma }_P{W}^0.\end{array}$$ (A.3)

Solving the equations for A⁰, P⁰, I⁰, V⁰, K⁰ and W⁰ gives

$$\begin{array}{l}{A}^0=\frac{(1-p)\sigma }{\lambda +{\gamma }_A},P^0=\frac{p\sigma }{\lambda +{\gamma }_P},I^0=\frac{p\sigma {\gamma }_P{\int }_0^{\infty }{b}_1\left(a\right)e^{-\lambda a}da}{\lambda +{\gamma }_P},\\ V^0=\frac{p\sigma {\gamma }_P{\int }_0^{\infty }{e}^{-\gamma a}\left({\int }_0^a{e}^{\gamma u}\mu \left(u\right)b_1\left(u\right)du-e^{-\gamma \tau }{\int }_0^a{e}^{\gamma u}\mu (u-\tau )b_1(u-\tau )du\right)e^{-\lambda a}da}{\lambda +{\gamma }_P},\\ K^0=\frac{p\sigma {\gamma }_P{\int }_0^{\infty }{e}^{-\gamma (a+\tau )}\left({\int }_0^a{e}^{\gamma u}q(u-\tau )\mu (u-\tau )b_1(u-\tau )du\right)e^{-\lambda a}da}{\lambda +{\gamma }_P},\\ W^0=\frac{p\sigma {\gamma }_P{\int }_0^{\infty }{e}^{-\gamma (a+\tau )}\left({\int }_0^a{e}^{\gamma u}(1-q(u-\tau ))\mu (u-\tau )b_1(u-\tau )du\right)e^{-\lambda a}da}{\lambda +{\gamma }_P}\end{array}$$

The characteristic equation can then be expressed by:

$$\begin{array}{l}h(\lambda )=\beta S(0)\sigma [\frac{{\delta }_A(1-p)}{\lambda +{\gamma }_A}+\frac{p}{\lambda +{\gamma }_P}+{\delta }_{I}p{\gamma }_P(\frac{{\int }_0^{\infty }{b}_1(a)e^{-\lambda a}da}{\lambda +{\gamma }_P}\\ +\frac{{\int }_0^{\infty }{e}^{-\gamma a}({\int }_0^a{e}^{\gamma u}\mu (u)b_1(u)du-e^{-\gamma \tau }{\int }_0^a{e}^{\gamma u}\mu (u-\tau )b_1(u-\tau )du)e^{-\lambda a}da}{\lambda +{\gamma }_P}\\ +\frac{{\int }_0^{\infty }{e}^{-\gamma (a+\tau )}({\int }_0^a{e}^{\gamma u}(1-q(u-\tau ))\mu (u-\tau )b_1(u-\tau )du)e^{-\lambda a}da}{\lambda +{\gamma }_P})\\ +{\delta }_k{\gamma }_P\frac{{\int }_0^{\infty }{e}^{-\gamma (a+\tau )}({\int }_0^a{e}^{\gamma u}q(u-\tau )\mu (u-\tau )b_1(u-\tau )du)e^{-\lambda a}da}{\lambda +{\gamma }_P}]-(\lambda +\sigma )\end{array}$$ (A.4)

Let λ = x + iy be a complex root with x ≥ 0. Thus, |e^−λa| ≤ 1 for all a ≥ 0. A simple calculation yields that

$$\begin{array}{l}1=\left|\frac{\beta S\left(0\right)\sigma }{(\lambda +\sigma )}\right[\frac{{\delta }_A(1-p)}{\lambda +{\gamma }_A}+\frac{p}{\lambda +{\gamma }_P}+{\delta }_{I}p{\gamma }_P(\frac{{\int }_0^{\infty }{b}_1(a)e^{-\lambda a}da}{\lambda +{\gamma }_P}\\ +\frac{{\int }_0^{\infty }{e}^{-\gamma a}({\int }_0^a{e}^{\gamma u}\mu (u)b_1(u)du-e^{-\gamma \tau }{\int }_0^a{e}^{\gamma u}\mu (u-\tau )b_1(u-\tau )du)e^{-\lambda a}da}{\lambda +{\gamma }_P}\\ +\frac{{\int }_0^{\infty }{e}^{-\gamma (a+\tau )}({\int }_0^a{e}^{\gamma u}(1-q(u-\tau ))\mu (u-\tau )b_1(u-\tau )du)e^{-\lambda a}da}{\lambda +{\gamma }_P})\\ +{\delta }_{k}p{\gamma }_P\frac{{\int }_0^{\infty }{e}^{-\gamma (a+\tau )}({\int }_0^a{e}^{\gamma u}q(u-\tau )\mu (u-\tau )b_1(u-\tau )du)e^{-\lambda a}da}{\lambda +{\gamma }_P}\left]\right|\\ \le \frac{\beta S\left(0\right)\sigma }{|\lambda +\sigma |}[\frac{{\delta }_A(1-p)}{|\lambda +{\gamma }_A|}+\frac{p}{|\lambda +{\gamma }_P|}+\frac{{\delta }_{I}p{\gamma }_P}{|\lambda +{\gamma }_P|}({\int }_0^{\infty }{b}_1(a)da\\ +{\int }_0^{\infty }{e}^{-\gamma a}({\int }_0^a{e}^{\gamma u}\mu (u)b_1(u)du-e^{-\gamma \tau }{\int }_0^a{e}^{\gamma u}\mu (u-\tau )b_1(u-\tau )du)da\\ +{\int }_0^{\infty }{e}^{-\gamma (a+\tau )}({\int }_0^a{e}^{\gamma u}(1-q(u-\tau ))\mu (u-\tau )b_1(u-\tau )du)da)\\ +\frac{{\delta }_{k}p{\gamma }_P}{|\lambda +{\gamma }_P|}{\int }_0^{\infty }{e}^{-\gamma (a+\tau )}({\int }_0^a{e}^{\gamma u}q(u-\tau )\mu (u-\tau )b_1(u-\tau )du)da]\\ <\beta S(0)[\frac{{\delta }_A(1-p)}{{\gamma }_A}+\frac{p}{{\gamma }_P}+{\delta }_{I}p({\int }_0^{\infty }{b}_1(a)da\\ +{\int }_0^{\infty }{e}^{-\gamma a}({\int }_0^a{e}^{\gamma u}\mu (u)b_1(u)du-e^{-\gamma \tau }{\int }_0^a{e}^{\gamma u}\mu (u-\tau )b_1(u-\tau )du)da\\ +{\int }_0^{\infty }{e}^{-\gamma (a+\tau )}({\int }_0^a{e}^{\gamma u}(1-q(u-\tau ))\mu (u-\tau )b_1(u-\tau )du)da)\\ +{\delta }_{k}p{\int }_0^{\infty }{e}^{-\gamma (a+\tau )}({\int }_0^a{e}^{\gamma u}q(u-\tau )\mu (u-\tau )b_1(u-\tau )du)da]={\mathcal{R}}_c\end{array}$$

Thus, if ${\mathcal{R}}_c<1$, all complex roots of h(λ) have negative real parts. We now consider the real roots of h(λ). Let $M=\max \left\{-{\gamma }_P,-{\gamma }_A\right\}$. It is easy to see that h′(λ) < 0 for all λ > M, indicating that h(λ) is monotonically decreasing on (M, ∞). Note that h(M) = ∞, h(∞) = −∞, and $h(0)=\sigma ({\mathcal{R}}_c-1)$. This implies that h(λ) has a unique negative real root if and only if ${\mathcal{R}}_c<1$.

By considering the complex and real roots, we arrive at the conclusion that if ${\mathcal{R}}_c<1$, all roots of the characteristic equation h(λ) have negative real parts. Hence, the zero solution of the model is asymptomatically stable.

Finally, we note that our system is a cooperative and irreducible, and thus a standard comparison argument shows that when ${\mathcal{R}}_c<1$, the infection compartments are bounded by exponential functions with negative exponents for t ≥ a. Hence, the occurrence of an outbreak is prevented if ${\mathcal{R}}_c<1$.