Abstract
Untreated ventricular septal defects (VSDs) can lead to pulmonary arterial hypertension (PAH) characterized by elevated pulmonary artery (PA) pressure and vascular remodeling, known as PAH associated with congenital heart disease (PAH-CHD). Though previous studies have investigated hemodynamic effects on vascular mechanobiology in late-stage PAH, hemodynamics leading to PAH-CHD initiation have not been fully quantified. We hypothesize that abnormal hemodynamics from left-to-right shunting in early stage VSDs affects PA biomechanical properties leading to PAH initiation. To model PA hemodynamics in healthy, small, moderate, and large VSD conditions prior to the onset of vascular remodeling, computational fluid dynamics simulations were performed using a 3D finite element model of a healthy 1-year-old’s proximal PAs and a body-surface-area-scaled 0D distal PA tree. VSD conditions were modeled with increased pulmonary blood flow to represent degrees of left-to-right shunting. In the proximal PAs, pressure, flow, strain, and wall shear stress (WSS) increased with increasing VSD size; oscillatory shear index decreased with increasing VSD size in the larger PA vessels. WSS was higher in smaller diameter vessels and increased with VSD size, with the large VSD condition exhibiting WSS >100 dyn/cm2, well above values typically used to study dysfunctional mechanotransduction pathways in PAH. This study is the first to estimate hemodynamic and biomechanical metrics in the entire pediatric PA tree with VSD severity at the stage leading to PAH initiation and has implications for future studies assessing effects of abnormal mechanical stimuli on endothelial cells and vascular wall mechanics that occur during PAH-CHD initiation and progression.
Keywords: Pulmonary arterial hypertension, Computational cardiovascular biomechanics, Congenital heart defect, Ventricular septal defect, Pulmonary arterial tree
1. Introduction
Pulmonary arterial hypertension (PAH) is characterized by elevated mean pulmonary artery (PA) pressure >20 mmHg and a pulmonary vascular resistance >3 Wood units (WU) (Simonneau et al. 2019), enlargement and stiffening of the proximal PA vessels, distal PA remodeling leading to occlusion or pruning of the PA vasculature, and eventually right heart failure. PAH associated with congenital heart disease (CHD) is clinically diagnosed under WHO Group I pulmonary hypertension (PH), known specifically as PAH associated with congenital heart disease, or PAH-CHD (Simonneau et al. 2019). For CHDs with systemic-to-pulmonary shunts, or left-to-right shunting, irreversible pulmonary vascular disease is likely to develop if the defect is not repaired or if the patient undergoes a late-stage repair, especially for large shunts where the pulmonary to systemic flow ratio (Qp:Qs) is greater than two (Kulik 2012). A ventricular septal defect (VSD), or a hole located in the interventricular septum between the two ventricles, constitutes the most common type of CHD, accounting for >20% of all diagnosed CHDs (Koh et al. 2020). Under the pressure differential between the left and right heart caused by an unrestricted VSD, left-to-right shunting yields increased blood flow to the right ventricle and PAs. The severity of the VSD is often diagnosed by the shunt size, which is measured by the Qp:Qs ratio with small, moderate, and large VSDs having a <1.5:1, 1.5:1-2.2:1, and a >2.25:1 Qp:Qs ratio, respectively (Muralidaran and Shen 2018; Uebing and Kaemmerer 2011). Given this underlying hemodynamic abnormality, the disease progression of PAH-CHD has been categorized into reversible PAH for which vascular remodeling can be reversed with hemodynamic unloading (Egito et al. 2003; Sakao et al. 2010; Van Der Feen et al. 2017, 2020) and irreversible PAH.
Previous studies have shown that mechanotransduction pathways triggered by hemodynamic forces significantly affect endothelial cell response and overall vascular health (Chiu and Chien 2011; Davies 2009; Lipowsky 1995; White et al. 2011) and furthermore induce PAH and the vascular remodeling process (Dickinson et al. 2011; Ghorishi et al. 2007; Kameny et al. 2019; Sharma et al. 2013; Tanaka et al. 1996). In in utero twin lamb studies, Kameny et al. surgically created a left PA ligation to mimic increased pulmonary blood flow and pressures and showed that abnormal hemodynamics alone could induce vascular remodeling with dysfunctional endothelial cell phenotypes displaying hyperproliferation, uncoupling of atheroprotective vasodilative pathways, and angiogenesis (2019). Since hemodynamic forces have been shown to play a large role in the development of PAH, many studies have investigated PAH disease progression through the vascular endothelial cell response to healthy and disturbed levels of wall shear stress (WSS), defined as 10-20 dyn/cm2 and 0-5 dyn/cm2, respectively (Dickinson et al. 2013; Mahmoud et al. 2017; Song et al. 2014; Szulcek et al. 2016; Van Der Feen et al. 2020; Wang et al. 2019). A small number of studies have explored the endothelial cell response to higher WSS levels and have found either functional or dysfunctional phenotypes at WSS levels >40 dyn/cm2 depending on the endothelial cell type used (Dolan et al. 2012; Garcia-Polite et al. 2017; Levesque and Nerem 1985; Li et al. 2009; Ostrowski et al. 2014; Sho et al. 2002). However, the healthy laminar WSS values cited in these studies were originally derived from estimates of systemic WSS in the context of atherosclerosis in the carotid and coronary arteries (Giddens et al. 1993; Malek et al. 1999; Schmid-Schonbein 1981; Zarins et al. 1983) or computational estimates for the large PAs (Tang et al. 2012; Hunter et al. 2006). There is currently no method of measuring in vivo WSS in the small, distal PAs, where much of the vascular remodeling process occurs; this study aims to address this gap with computational modeling.
Computational fluid dynamics (CFD) and imaging studies have investigated the hemodynamics of PAH with disease progression focusing mainly on the large PAs. Using 4D magnetic resonance imaging (4DMRI) and CFD analysis, these studies have revealed significant changes in WSS, pressure, vorticity, pulsatility, and rarefaction associated with PAH in adult patients (Barker et al. 2015; Kheyfets et al. 2015, 2016; Odagiri et al. 2016; Schäfer et al. 2016; Tang et al. 2012; Terada et al. 2016). In pediatric patients, similar significant biomarkers in WSS, pulsatility, energy loss, and stiffness were also associated with PAH severity against healthy controls in the large PAs (main, left, and right PA) (Schäfer et al. 2017, 2019; Truong et al. 2013; Wang et al. 2020; Yang et al. 2019). Estimates of hemodynamics in small, distal PAs have been made using computational models; however, these studies only investigated later stages of WHO Group 1-3 pulmonary hypertension or idiopathic PAH in rats and human patients with a simplified distal PA model or a generalized pediatric distal PA geometry (Acosta et al. 2017; Qureshi et al. 2014, 2019; Yang et al. 2019). Though these studies reported many hemodynamic findings in PAH, they examined PAH severity and late-stage progression with little focus on the PA hemodynamics leading to PAH initiation, not to mention the hemodynamics in pediatric patients with PAH-CHD.
We hypothesize that unrestricted left-to-right shunts, which commonly occur in VSDs, alter PA hemodynamics and mechanical stimuli on vessel walls, thereby initiating vascular remodeling in the distal PAs and subsequently PAH. Changes in the distal PA vasculature due to a shunt have been characterized first by muscularization of the intra-acinar PAs (<50 μm in diameter) followed by medial hypertrophy and total obstruction of the vessels occurring on a timescale of weeks to months (Dickinson et al. 2011; Fineman and Black 2019; Rabinovitch et al. 1978, 1981; Van Der Feen et al. 2020; Zhang et al. 2018). However, the exact mechanism triggering this response is still unknown. While the literature has predominantly focused on disease progression of late-stage PAH, understanding the hemodynamics in the distal PAs prior to the initiation of PAH and remodeling can better inform biological studies and further characterize the mechanisms triggering vascular remodeling, potentially enabling preventative treatment of asymptomatic patients before late-stage complex pathways are activated (Rafikova et al. 2019). For PAH-CHD patients, such as in an unrestricted VSD, a purely abnormal hemodynamic trigger can lead to vascular remodeling and biological responses found in other PAH groups (Dickinson et al. 2013; Fineman and Black 2019).
In this study, we computationally study the hemodynamics of the entire PA tree in different sized VSDs to quantify the mechanical forces experienced by the vasculature prior to the initiation of PAH. We use a 3D healthy 1-year-old patient-specific model to simulate large proximal PA hemodynamics (>1 mm diameter vessels) and a pediatric PA morphometry tree to estimate hemodynamics in the distal PAs (<1 mm diameter) in which the initiation of vascular remodeling and PAH occur. To our knowledge, this is the first study investigating hemodynamics in the entire PA tree in an early-stage VSD to elucidate the abnormal mechanical environment giving way to vascular remodeling and the initiation of VSD-induced PAH.
2. Methods
2.1. Proximal PA model
2.1.1. Proximal PA geometry
To model the PAs of a patient at the age in which they could develop PAH due to a VSD, we constructed a patient-specific anatomic PA model directly from the CT angiogram of a healthy 1-year-old male (body surface area, BSA = 0.49 m2) using the open-source software package, SimVascular (simvascular.org) (Updegrove et al. 2017). From the CT images, we manually created three-dimensional centerline paths following the PAs from the left and right PA branches down 1-2 generations in the upper, middle, and lower lobes of both lungs. We created segmentations of the PA lumens along the defined paths using a machine-learning automated segmentation algorithm (Maher et al. 2020). These segmentations were manually verified by an experienced SimVascular user and lofted into a 3D anatomical representation of the PA anatomy which included 35 outlets and a minimum outlet diameter of 0.15 cm.
2.1.2. 3D simulation setup
We simulated hemodynamics in the 1-year-old proximal PA model by solving the three-dimensional Navier-Stokes equations on a linear tetrahedral mesh using SimVascular’s stabilized finite-element solver (Taylor et al. 1998) with coupled Windkessel (RCR circuit) boundary conditions (Vignon-Clementel et al. 2006, 2010) and backflow stabilization (Esmaily Moghadam et al. 2011) (details of the finite element solver in “Appendix A.1.”). To capture the deformability of the PA walls, we used the coupled momentum method (Figueroa et al. 2006) for fluid-solid interaction, modeling the PA wall as a deformable linear elastic membrane with variable wall thickness. The linear elastic wall model was coupled to the Navier-Stokes equations via a Neumann boundary condition replacing the conventional noslip boundary condition at the walls (Figueroa et al. 2006). To improve numerical stability and reduce non-physiologic oscillations in the wall displacement, an external tissue support model using a spring-dashpot analogy was applied at the walls with a damping constant of 104 dyn· s/cm3 and a stiffness constant of 103 dyn/cm3 - values found opposite to the spine in Moireau et al’s study (2012). We prescribed a pulsatile flow waveform at the main PA (MPA) inlet and 3-element Windkessel boundary conditions at the outlets to represent the downstream, distal vascular PAs, capillaries, and veins (Fig. 1).
Fig. 1.
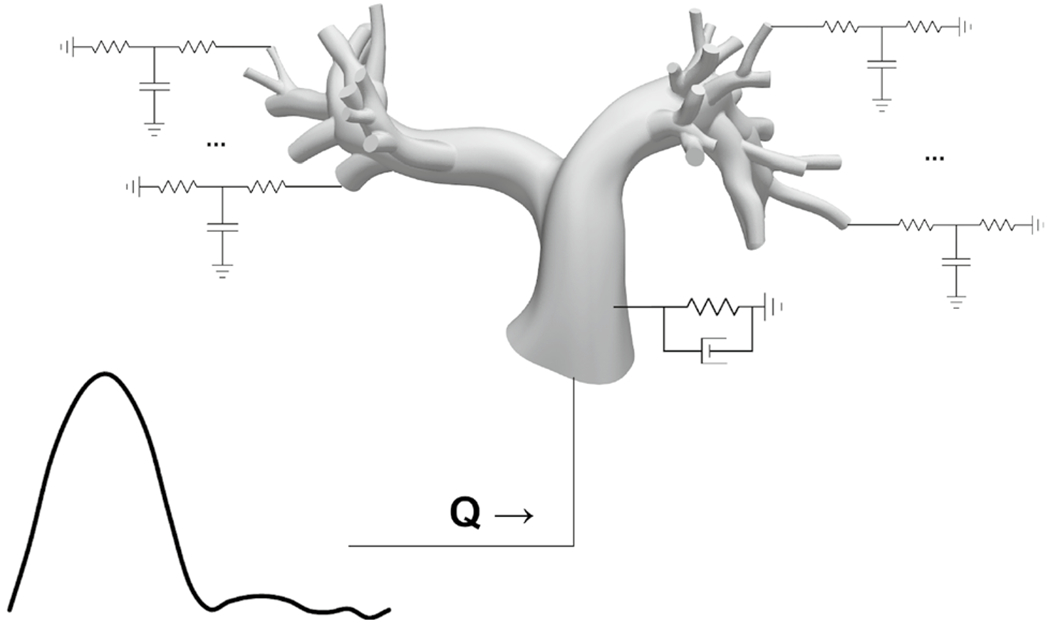
Simulation set up for the 3D PA model with a flow waveform prescribed at the MPA inlet and 3-element Windkessel models prescribed at every outlet to represent the downstream vascular dynamics. Fluid-structure interaction of PA wall deformability was modeled using the coupled momentum method, and external tissue support was prescribed on the walls via Robin boundary conditions representing springs and dashpots
To simulate VSD hemodynamics in the proximal PA model, we prescribed boundary conditions and model parameters that best represented a healthy control, small, moderate, and large VSD conditions (listed in “Appendix” Table 2). The pulsatile inlet flow waveform was based on a phase-contrast-MRI derived flow waveform of a pediatric patient without any abnormalities in the pulmonary circulation (Yang et al. 2019). The baseline cardiac output was computed via BSA-scaling with literature data for healthy 1-year-old patients based on their cardiac index and heart rate (Cattermole et al. 2017). To simulate increasing VSD severities, the mean pulmonary flow in the healthy waveform was scaled according to the Qp:Qs ratios found in VSD patients - 1:1 (healthy control), 1.5:1 (small VSD), 2:1 (moderate VSD), and 3:1 (large VSD) (Kosecik et al. 2007; Muralidaran and Shen 2018; Uebing and Kaemmerer 2011). To scale the flow waveform, the flow at each time point in the cardiac cycle was scaled to ensure that both the systolic and diastolic flows would be representative of the increasing systolic amplitude of the waveform found in VSD patients.
Table 2.
Model Parameters for the 3D and 0D Models
| Normal | Small VSD | Moderate VSD | Large VSD | |
|---|---|---|---|---|
| 3D Elastic modulus (dyn/cm2) ×106 | 1.26 | 1.26 | 1.63 | 2.91 |
| External tissue support stiffness constant, k (dyn/cm3) | 103 | |||
| External tissue support damping constant, c (dyn · s/cm3) | 104 | |||
| 3D total outlet Rp (dyn · s/cm5) | 5 | |||
| 3D total outlet Rd (dyn · s/cm5) | 265 | |||
| 3D total outlet capacitance, C (cm5/dyn) | 5 × 10−4 | |||
| Left atrial pressure (mmHg) | 5 | |||
| Heart rate (bpm) | 105 | |||
| Optimized PA resistance (dyn · s/cm5) | 128.4 | |||
| 0D radius scaling constant limits | 0.8 – 1.2× | |||
| 0D length scaling constant limits | 0.4 – 1.6× |
Because this study focuses on the initiation of PAH before any downstream vascular remodeling occurs, all VSD conditions were prescribed the same 3-element Windkessel models at the vessel outlets to represent the resistance and compliance of the downstream pulmonary arterioles, capillaries, and veins in a healthy patient. The total proximal resistance, distal resistance, and capacitance values were tuned to achieve a target healthy mean MPA pressure of 15 mmHg in the 3D PA geometry with a normal flow and a left atrial pressure of 5 mmHg (Levitsky 2018). The total resistance and capacitance values were then distributed to the outlets assuming a 45%-to-55% left PA (LPA)-to-right PA (RPA) flow split (Cheng et al. 2005) and an outlet area-based rule (Eqs. 1 and 2), where C is the capacitance, R is the resistance, RLPA/RPA is the resistance distribution for outlets in the left or right lung, Ai is the cross-sectional area of the outlet, Atotal,LPA/RPA is the sum of the cross-sectional areas of all outlets in the entire tree in Eq. 1 or in either the left or right tree in Eq. 2, and i denotes an individual outlet in either the left or right tree. For each VSD condition, at least 6 cardiac cycles were simulated to ensure convergence of results.
| (1) |
| (2) |
To approximate the nonlinear PA vessel wall dynamics with a VSD under higher flow and pressure, we modified the elastic modulus assigned to the PA walls for the moderate and large VSD conditions. Previous animal studies have shown nonlinear stress-strain curves of the MPA, with nonlinear regions occurring at pressures >30 mmHg (Hunter et al. 2010; Jia et al. 2015; Kobs et al. 2005; Ramachandra and Humphrey 2019; Wang et al. 2013) suggesting that the large PAs exhibit a stiffer passive material at higher pressures. In the context of initiation of PAH in which the PAs have not yet undergone abnormal vascular remodeling, parallels to exercise studies can be drawn to determine the PA wall elastic moduli in the VSD conditions exhibiting similarly high flows and pressures in healthy subjects.
Using the MPA pressure and radius from initial simulations of a moderate and large VSD and a relative area change (RAC) of 0.24 reported from the exercise conditions with cardiac outputs similar to a small VSD in Forouzan et al’s study (2015), a target overall elastic modulus of 467 kPa and 830 kPa was estimated for the moderate and large VSD, respectively, using Eq. 3 (Long et al. 2012):
| (3) |
where E is the overall elastic modulus, ΔP is the difference in pressure between diastole and systole, R is the diastolic MPA radius, Δr is the difference in MPA radius between diastole and systole, and ζ is the MPA wall thickness assumed to be 10% of the diastolic MPA radius (Long et al. 2012). Since the overall elastic modulus encompasses the effects from the vascular wall stiffness and the external tissue support, a PA wall elastic modulus of 163 kPa and 291 kPa with the same external tissue support constants was prescribed for the moderate and large VSD conditions, respectively. We verified that the overall elastic moduli (Eq. 3) computed with the MPA pressure and radius from these final simulations were within 5% of the target values. For the control and small VSD conditions, we prescribed the healthy pediatric PA wall elastic modulus of 126 kPa based on healthy vessel stiffness of the main pulmonary artery (MPA) in pediatric patients (Long et al. 2012; Yang et al. 2019) since the small VSD simulation already produced an overall elastic modulus within 2% of the target value. For all simulations, we obtained smooth variable thickness distribution (Olufsen 1999; Hislop and Reid 1973) over the model by solving a Laplace equation with a prescribed thickness of 10% of the inlet and outlet radii (Long et al. 2012).
2.1.3. Mesh independence
To conserve computational costs, a mesh independence study was performed for a rigid wall simulation of the large VSD condition to ensure convergence of time-averaged pressure and velocity, and temporally and spatially averaged WSS. Based on convergence of pressures and flow within 1% at all outlets and WSS within 10% at six randomly selected vessel segments in the model, as well as computational cost, we chose a ~3.2 million linear tetrahedral element mesh with three boundary layers generated using MeshSim (Simmetrix Inc, Clifton Park, NY, USA). The edge size was 0.06 cm globally and 0.03 cm at the boundary layer farthest from the walls, with a boundary layer decreasing ratio of 0.5.
2.1.4. Analysis of 3D PA hemodynamics
Only the hemodynamic quantities of interest extracted from the final cardiac cycle were used for analysis. These quantities were extracted from every vessel segment in the PA model, which were identified using the centerline extraction methods from the Vascular Modeling Toolkit (VMTK, vmtk. org) (Antiga et al. 2008). Branching regions were identified from the centerlines in the 3D model as the region between the intersection of the daughter centerline with the parent vessel and a maximum inscribed radial distance proximal to that intersection (Online Resource 1). Vessel segments were defined as the region between consecutive branching regions. Each vessel segment’s length was calculated as the length of the centerline through the segment, and each segment’s diameter was defined as twice the average maximum inscribed sphere radius down the segment. Pressure, flow, and cross-sectional area waveforms in time were measured from a cross-sectional slice in the middle of every vessel segment in the 3D model. Cross-sectional strain was calculated as , where rsys and rdia are the systolic and diastolic radius calculated from the cross-sectional vessel area with an assumption of circularity. To provide consistency with previous mechanobiological studies utilizing WSS, the temporally averaged WSS magnitude, which arises from the stress component parallel to the vascular wall due to fluid flow near the boundary, and the OSI, which represents the change in direction of the WSS, were extracted as spatially averaged values for each vessel segment (details of calculation in “Appendix” A.2). To describe changes in hemodynamics with PA morphometry, diameter-defined Strahler orders were assigned to every vessel segment in the 3D model based on proximity of diameters to the vessel orders’ diameters defined by BSA-scaling laws (Dong et al. 2020) and setting the MPA vessel segment’s order to 16 in congruence with conventions in Dong et al. (2020) and Huang et al. (1996). This resulted in five vessel orders (12-16), where order 16 corresponds to the MPA, order 15 corresponds to the LPA and RPA, and order 12 corresponds to the smallest 3D model’s outlet vessels.
2.2. Distal PA model
Given the resolution constraints of the CT angiogram, the 3D proximal PA model fails to capture <1 mm vessel diameters. We therefore approximated distal PA hemodynamics using a zero-dimensional (0D) model consisting of resistances in parallel and series based on existing PA morphometry data of vessel segment diameters, lengths, and branching patterns. Huang et al.’s study (1996) reported the branching pattern, diameter, and lengths for all PAs in a resin-casted ex-vivo healthy adult left lung and used a diameter-defined Strahler ordering system to categorize the entire PA tree into 15 orders based on branching points and diameters, starting with pre-capillary order 1 vessels to the largest LPA segment of order 15. To account for hemodynamics in a 1-year-old PA anatomy with a small BSA, we generated and optimized a distal 0D PA tree per 3D outlet using BSA-scaled morphometric data, such that (1) the total PA resistance from both the proximal 3D PAs and the distal 0D PAs was within a generally accepted range of 33.2 ± 2% of the total pulmonary vascular resistance(Raj and Chen 1986), and (2) the optimized diameters and lengths of vessel segments in the distal PA trees represented physiologic dimensions. This optimization of the distal PA morphometry, which will be described in detail in the following sub-sections, was performed using hemodynamics from the normal control simulation only. The same optimized distal PA morphometry was subsequently applied to all VSD conditions to study the hemodynamics at the initial timepoint prior to remodeling and the onset of PAH.
2.2.1. Calculation of 3D proximal PA resistance
The total PA resistance encompasses the resistance from the 3D proximal PA model (starting from the MPA down to ~1-mm-diameter vessels) as well as the distal PA trees (representing vessels from the outlets of the 3D PA model down to pre-capillary arterioles). The resistance in the 3D model was computed according to Fig. 2a where the resistance of each vessel segment was added in parallel and in series in an upstream manner, from the outlets to the MPA, based on the 3D model’s connectivity. The PA connectivity was determined using VMTK’s centerline extraction algorithm and geometric analysis (Antiga et al. 2008) where vessel segments were connected by a shared junction region (Online resource 1). Each vessel segment’s resistance was calculated from the simulated pressures and flows of the normal control using a Poiseuille assumption (Eq. 4)
| (4) |
Fig. 2.
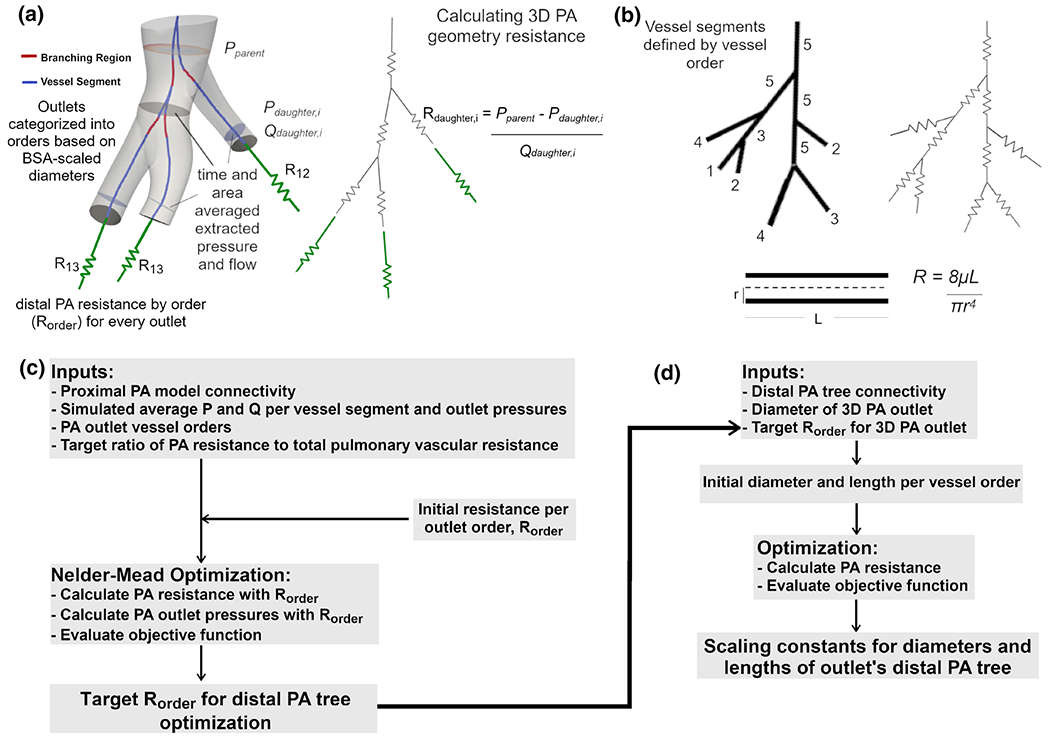
Optimization of distal PA morphometric tree incorporating a resistance of 3D PA model, b resistance calculation of distal PA tree with Poiseuille assumptions, c Nelder-Mead optimization of target distal PA tree resistances per order, and d optimization of the scaling constants for the diameter and lengths of the PA tree defining the geometry and informed by BSA scaling laws, 3D outlet diameters, and morphometric PA data
where Pparent represents the pressure at a cross-sectional slice in the parent vessel segment, Pdaughter,i and Qdaughter,i represent the pressure and flow at a slice in a daughter vessel segment, and Rdaughter,i represents the resistance of that daughter segment. Pressures and flows were temporally and spatially averaged over a cross-sectional slice located 80% down the length of the segment in order to obtain values closer to junction regions and incorporate pressure losses down the length of the segment.
2.2.2. Calculation of 0D distal PA resistance
The resistance of the distal PA tree was calculated using Poiseuille assumptions (Fig. 2b) and the distal PA tree geometry. For each 3D outlet, an initial distal PA geometry was generated according to the 3D outlet’s diameter-defined Strahler order using a BSA-based morphometric scaling of the pre-acinar tree to the dimensions of the 1-year-old subject (Dong et al. 2020) in combination with the morphometric data in Huang et al.’s study of an adult PA tree (1996). Based on evidence that the maximum intra-acinar vessel diameter increases from 50μm at age 1 to 120 μm at age 14 (Haworth and Hislop 1983; Hislop and Reid 1973), a corresponding vessel order of 5 was used as the cutoff between intra-acinar and pre-acinar vessels. Because the growth of intra-acinar PAs in infants has not been studied in detail, we used a power fit from the smallest pre-capillary vessels in Huang et al.’s adult morphometry study (1996) to the smallest pre-acinar vessel in Dong et al.’s diameter-based BSA scaling law (2020) to obtain diameters for the intra-acinar portion of the PA tree. This ensured that intra-acinar diameters were not greater than any of the BSA-scaled pre-acinar diameters. The lengths of vessel segments were defined based on the BSA-scaling law of length with order (Dong et al. 2020). Because pre-acinar vessels remain constant in number and branching pattern after birth (Hislop and Reid 1972), the connectivity of the scaled morphometric tree was generated using the adult connectivity matrix in Huang et al.’s study (1996) and methods outlined in Spilker et al. (2007), which assume bifurcations only. The resistance of each vessel segment was calculated with a Poiseuille assumption (Eq. 5),
| (5) |
where μapp is the apparent viscosity accounting for the Fahraeus-Lindqvist effect, L is the length, and r is the radius. The Fahraeus-Lindqvist effect was modeled with the in vivo viscosity-diameter exponential function from Secomb et al. (2017) (Eqs. 6–8)
| (6) |
where
| (7) |
| (8) |
and D represents the vessel diameter in units of μm, HD is the discharge hematocrit of 0.45, and μplasma is the apparent viscosity of plasma of 0.0124 Poise. The total resistance contained within each distal morphometric tree was then computed by summing all segment resistances in series and parallel in accordance with the bifurcation pattern proceeding from distal to proximal (Fig. 2b).
To estimate the total PA resistance, the downstream resistance from each 3D PA outlet’s unique distal PA tree was connected in series to the 3D PA outlet resistance before continuing the upstream resistance calculation in the 3D model.
2.2.3. Optimization of distal PA geometry
Although the BSA-scaled morphometric tree (Dong et al. 2020) provided an initial distal PA geometry, additional optimization of this distal tree geometry was needed to obtain a total PA resistance, RPA, within a physiologic range. We assumed RPA (representing resistance from the MPA to pre-capillary arterioles) comprised 33.2 ± 2% of the total pulmonary vascular resistance (i.e., PAs, capillaries, and pulmonary veins) based on pressure distributions and standard deviations from lamb studies (Online Resource 2) (Raj and Chen 1986). This assumption yielded a target RPA of 106.6 dyn·s/cm5 corresponding to a healthy pulmonary vascular resistance index (PVRI) of 2 WU·m2 (<3 WU·m2 considered healthy). Given the unknown resistance and morphometry of the distal PA tree downstream of each 3D outlet, optimization of the distal PA morphometry was needed and occurred in two steps: (1) determination of target resistances for the distal PA trees, and (2) tuning of scaling factors for diameters and lengths of vessel segments in the distal PA trees to achieve the target distal PA resistance.
We used the Nelder-Mead optimization algorithm to identify optimal distal PA tree resistances downstream of each 3D outlet (Fig. 2c), that best achieves the target RPA and the simulated 3D outlet pressures, Poutlet,i, according to the objective function in Eq. 9 where bolded variables represent the target values.
| (9) |
To limit the degrees of freedom in the optimization, the distal morphometric tree resistance was assumed to be a function of the 3D outlet’s BSA-scaled vessel order only, such that only three resistances corresponding to the three unique outlet vessel orders (12-14), Rorder, were optimized. An initial estimate of each Rorder was computed based on the resistance from an un-optimized distal PA tree created using BSA-scaled diameters and lengths (Dong et al. 2020; Huang et al. 1996). For each function evaluation in the optimization algorithm, the total PA resistance including the Rorder and the 3D model was calculated using the methods described previously. 3D outlet pressures, , were calculated with a Poiseuille assumption (Eq. 10) using the corresponding outlet’s Rorder , mean outlet flow (Qoutlet) from the control simulation, and an assumed capillary pressure (Pcapillary), which was determined from the target 33.2% PA resistance proportion so that
| (10) |
By using the Nelder-Mead optimization algorithm, we were able to simultaneously minimize the deviation of the total PA resistance and all 3D outlet pressures with equal weight and with quick convergence that has been effective in a previous optimization study (Tran et al. 2017). With this optimization, we identified target distal PA tree resistances of 5095, 2163, and 992 dyn·s/cm5 for 3D vessel outlet orders 12, 13, and 14, respectively, resulting in a total PA resistance of 107.6 dyn·s/cm5. These optimized Rorder’s were 35% of the resistances in the tuned outlet boundary conditions for the 3D PA model, which is expected since the target PA resistance is 33% of the total PVRI with a majority of the resistance originating from the distal PAs (Levy et al. 2001; Pries et al. 1995).
For each 3D outlet, we generated an optimal distal PA morphometric tree to achieve the identified resistance Rorder by optimizing scaling factors for all vessel orders’ diameter and length using MATLAB’s interior-point minimizing function algorithm (Fig. 2d). We note the following constraints in our tuning process: (1) each morphometric tree’s root diameter is equivalent to its corresponding 3D outlet diameter, (2) diameters increase with increasing vessel order, and (3) diameters and lengths do not change by a large scaling factor (Reneman and Hoeks 2008) and can only be scaled within the coefficient of variation for diameters and lengths reported in Huang’s adult PA morphometry study (1996). These constraints yielded scaling bounds of 0.8-1.2x for diameter and 0.4-1.6x for length. While some morphometric trees from order 12 and 13 outlets failed to achieve the target distal PA resistances under these constraints, the total PA resistance accounting for the 3D model resistance and all of the tuned morphometric tree resistances was 128.4 dyn·s/cm5 (corresponding to a PVRI of 2.4 WU·m2) which constitutes a 20.5% deviation from the corresponding physiological value.
Although it was not possible to validate the actual structure and geometry of the distal morphometric PA trees, we validated the tree structure and geometry of Huang’s study and the BSA diameter scaling laws by comparing the resistance of the entire PA tree to expected values found in literature. Specifically, we created a full PA tree from the MPA to the pre-acinar arteries for an adult using BSA-scaling laws (Dong et al. 2020) and measured MPA diameters; the corresponding PA resistance differed by only 0.06 WU from the reported PVRs (Lange et al. 2013).
2.2.4. Distal PA hemodynamics
To quantify the hemodynamics in the distal PA trees, time-averaged flows from the 3D simulation for each VSD condition were propagated down to the 0D distal PA trees (Fig. 3). For each 3D vessel outlet, the mean flow was distributed down the morphometric tree according to the downstream resistances of the daughter vessels. Pressure in the morphometric tree was assumed to be constant at bifurcations with pressure losses neglected (Eq. 11):
| (11) |
Fig. 3.
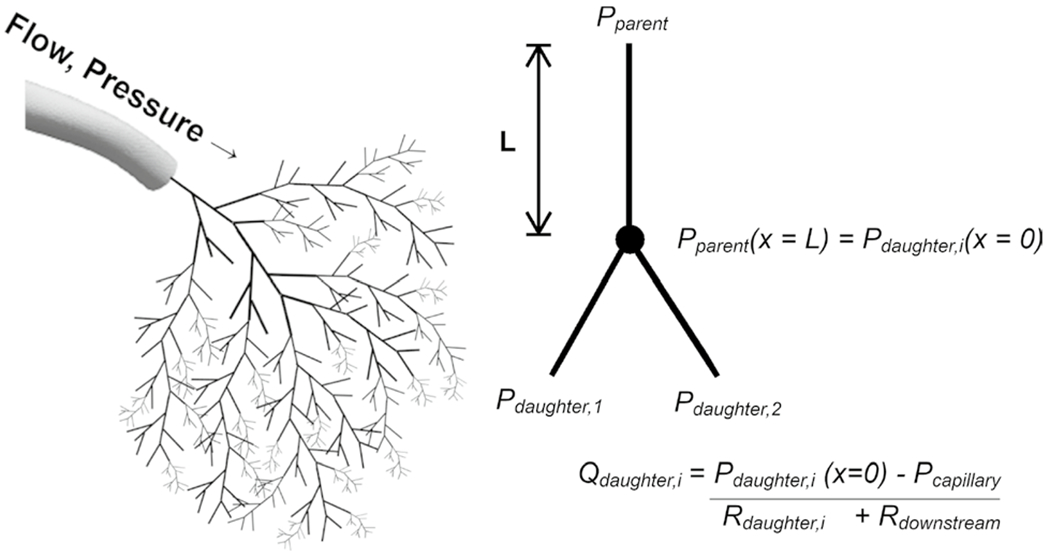
Hemodynamics of the distal 0D PA tree were calculated from extrapolated flows from the 3D PA simulation and optimized geometry (illustrated) using Poiseuille assumptions
where x is the direction down the length (L) of a vessel segmen, Pdaughter1, and Pdaughter2 are the pressures in the daughter vessels, and Pparent is the pressure in the parent vessel. Because the Reynolds number at the transition between the 3D and the 0D model is <500, and the entrance lengths needed for fully developed flows are larger than the vessel lengths, the effects of non-fully developed flow should be considered. To account for this in the vessel orders transitioning from the 3D model to the 0D model , we used the WSS formulation from Al-Nassri and Unny (1981) (Eqs. 12–14) for distal vessel orders >10 for the small, moderate, and large VSD conditions and in distal vessel orders >11 for the normal control.
| (12) |
where
| (13) |
| (14) |
and τ is the WSS magnitude, Q is the flow, A is the area, l is the length of the vessel, v is the kinematic viscosity, and μapp is the is the diameter-dependent apparent viscosity computed from Eqs. 6–8. The vessel orders represented by this WSS formulation were chosen based on a percent difference of >200% between the entrance lengths and the vessel lengths, which accounts for changes in more developed incoming velocity profiles in downstream vessels, as well as the dominance of a parabolic velocity profile resulting in similar WSS values between the Poiseuille solution and the power velocity profile. For all other orders in the distal PA tree, the WSS magnitude was calculated at each vessel segment in the morphometric tree with a Poiseuille assumption (Eq. 15).
| (15) |
Because detailed information about infant intra-acinar arterial growth and connectivity are unknown, hemodynamic estimates in the distal PA tree were limited to pre-acinar PAs corresponding to vessel orders ≥ 5 and diameters >60 μm.
2.3. Statistics
Welch’s t-test was used to determine significant differences in hemodynamic quantities across VSD conditions. A power-law regression model was fit to changes in vessel flows with diameters. A linear regression model was fit to the systolic upstroke in MPA flow and pressure waveforms. Pearson’s coefficient of determination was used to quantify the statistical correlation between variables.
3. Results
3.1. 3D proximal PA results
With increasing VSD size, the pressures and flow waveforms increased in all vessel segments with noticeable differences in the MPA, where the slope of the systolic upstroke in the flow and pressure waveforms increased linearly with VSD severity (Fig. 4a). The pressure waveforms exhibited a slight phase shift in the smaller 3D distal PA vessels compared to more proximal PA vessels, as is expected from the healthy compliance of the vessel walls prior to any vascular remodeling. The temporally and spatially averaged pressures in the 3D PA vessel segments increased with VSD severity and very slightly with diameter (Fig. 4b). The average flows in the 3D PA vessel segments also increased with VSD severity and increased with diameter in a power law (Q = adb), where d is diameter (cm), and a and b are the power-law coefficients. The constant coefficient, a, was 29.3, 43.9, 58.5, and 87.8, and the power coefficient, b, was 2.415, 2.418, 2.420, and 2.427 for the normal, small, moderate, and large VSD conditions, respectively (coefficients of determination, R2 > 0.94) (Fig. 4c). A summary of the global pressure and flows found in the normal and VSD cases are shown in Table 1.
Fig. 4.
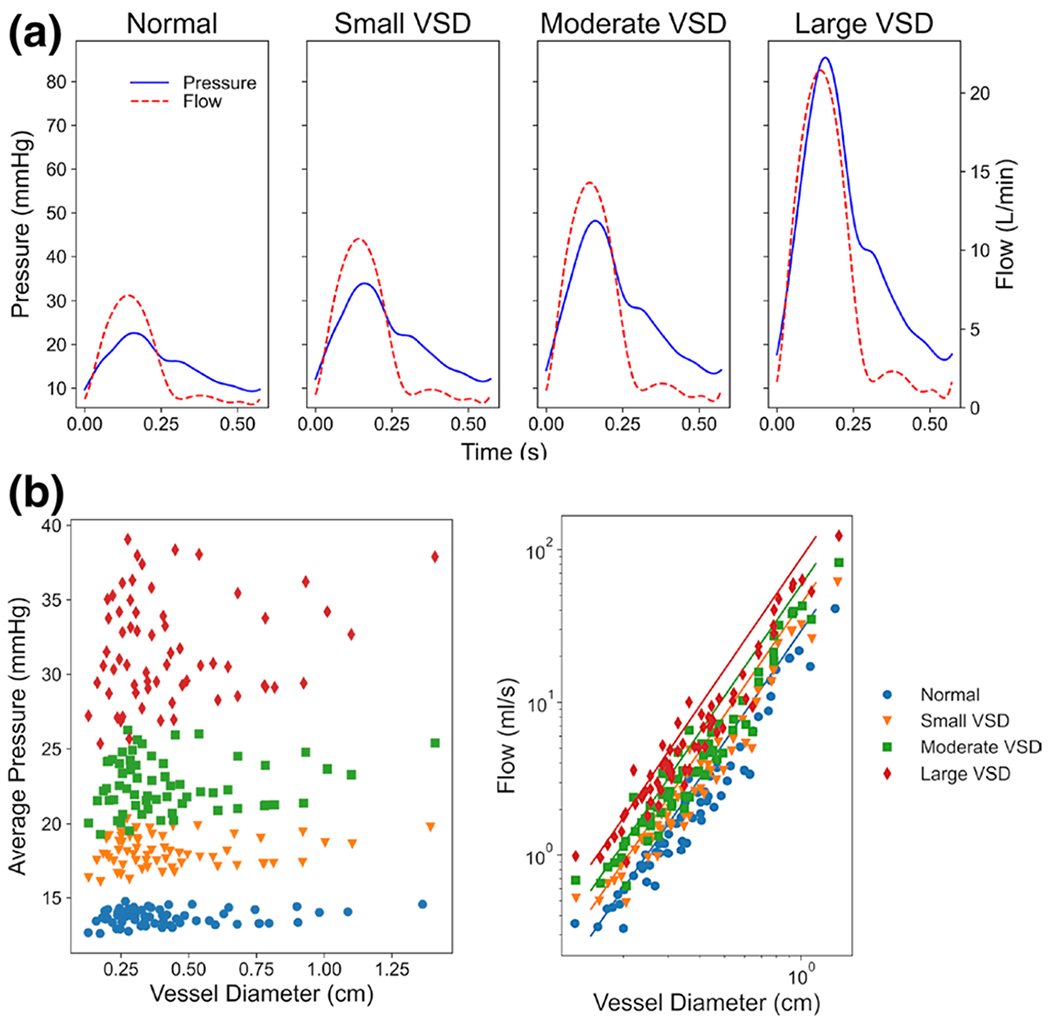
The 3D hemodynamic simulations show a the pressure (blue) and flow (red) in the MPA increasing with increased VSD severity, b the spatially and temporally averaged pressure in all segments increasing with VSD severity, and c the average flow in all segments increased with a power law of diameter (represented by solid lines) for all VSD conditions
Table 1.
Global hemodynamics for control and VSD simulated conditions in 3D PA model
| CO | MPA | MPA Psys | MPA Pdia | |||
|---|---|---|---|---|---|---|
| (L/min) | (ml/s) | (mmHg) | (mmHg) | (mmHg) | (mmHg) | |
| Normal | 2.5 | 1.18 | 15.0 | 22.6 | 9.3 | 13.4 |
| Small VSD | 3.7 | 1.77 | 20.8 | 33.8 | 11.6 | 17.7 |
| Moderate VSD | 4.9 | 2.35 | 27.1 | 47.9 | 13.4 | 21.9 |
| Large VSD | 7.4 | 3.53 | 41.7 | 84.5 | 16.5 | 30.3 |
CO = Cardiac Output, = mean flow, averaged across all 3D vessel outlets, = temporally and spatially averaged pulmonary pressure at main PA, = temporally and spatially averaged pressure, averaged across all 3D vessel outlets
We prescribed increasing PA stiffness with VSD size to reflect the nonlinearity of the passive PA mechanical properties under the higher pressures found in VSD conditions. As a result of increased pressure in the large VSD case, there was an increase in strain of the MPA with VSD size (Fig. 5a). This increase in strain was nonlinear with VSD size due to the increased stiffness estimated for the large VSD to account for nonlinear material wall properties in the upper pressure ranges. On average, the global average strain for the entire PAs increased with VSD severity from 0.21 ± 0.07 in the normal control to 0.31 ± 0.11, 0.35 ± 0.13, and 0.34 ± 0.14 in the small, moderate, and large VSD conditions, respectively. Figure 5b shows the increase in strain with VSD severity for each vessel order in the 3D PA model. Only the normal condition was significantly different from all VSD conditions in all vessel orders. Regions where strain was higher in the moderate VSD than the large VSD can be attributed to dynamics in the middle lobe where many branching points are located that modify the deformations of the arterial segments in addition to the higher elastic modulus prescribed for the large VSD.
Fig. 5.
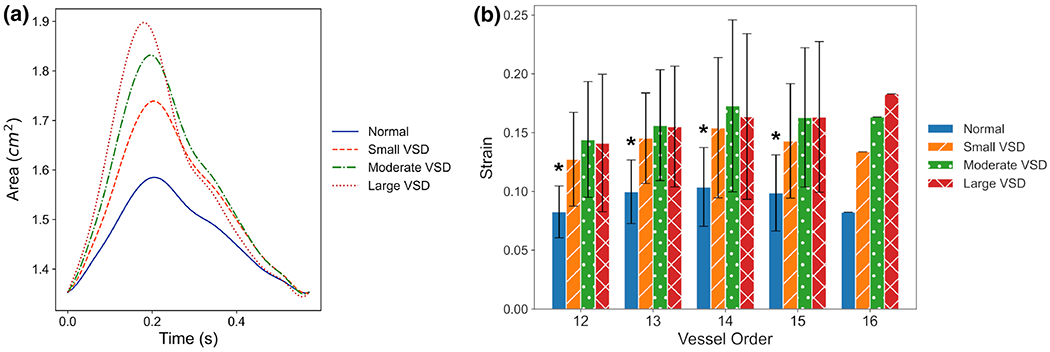
The 3D proximal PA simulations show a increasing amplitudes in the time-dependent area waveform of the main PA (MPA) with VSD severity and b increases in the strain with VSD severity for each diameter-defined Strahler order identified in the 3D PA model. Order 12 corresponds to the most distal and smallest vessels in the PA model, and order 16 represents the MPA. (*) denotes significant differences with p-values < 0.05 between normal and all VSD conditions for orders 12-15
The global OSI did not significantly change with VSD severity, as the spatially averaged OSI from all vessel segments were 0.054 ± 0.034, 0.051 ± 0.031, 0.049 ± 0.027, and 0.050 ± 0.026 for the normal control, small, moderate, and large VSD conditions, respectively. The OSI generally decreased with VSD severity for vessel segments of orders 14-16, in which order 16 corresponds to the MPA (Fig. 6). There were significantly lower OSI values in the smallest order 12 and order 13 vessels compared to order 14 vessels in all control and VSD conditions (p < 0.01). Normal OSI values in order 12 and order 13 were significantly different from order 15 OSI values (p < 0.05). The large VSD condition had significant differences between order 12 and order 15 OSI values (p < 0.05). No other differences in OSI between orders or VSD conditions were significant. The decrease in OSI with VSD severity is expected, as increased flow through the PAs allows less time for blood to stagnate in areas of high OSI, such as bifurcations and immediately following tortuous branching regions.
Fig. 6.
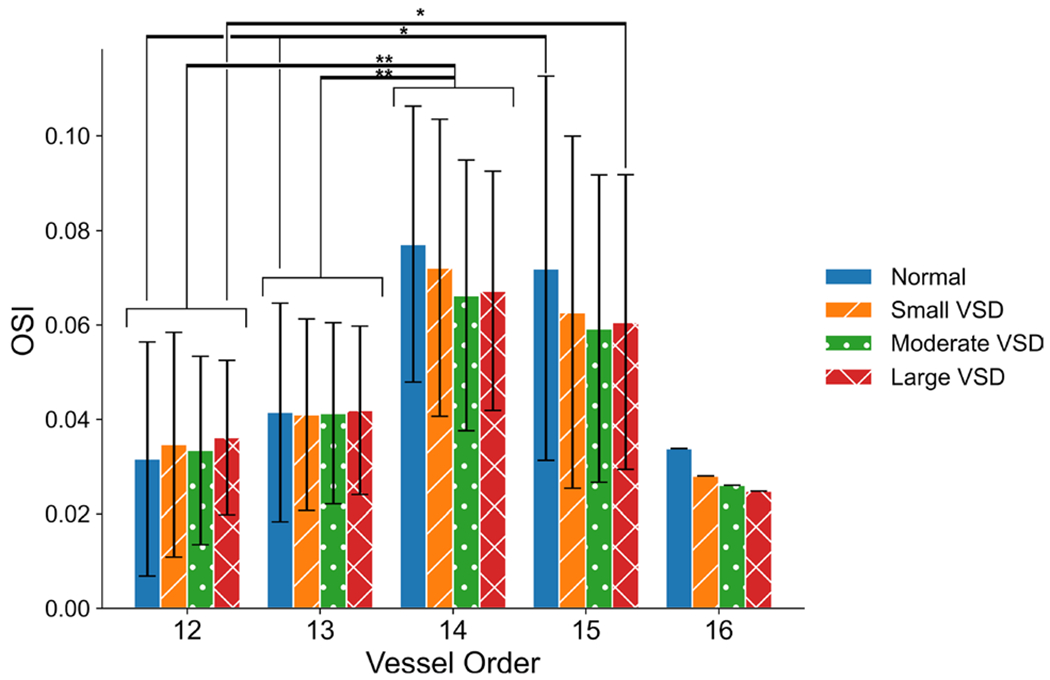
Oscillatory shear index (OSI) in the 3D proximal PA simulations generally decrease with VSD severity in the larger vessel orders representing segmental, interlobar, and the main PAs. (*) denotes significance with p-value < 0.05, (**) denotes significance with p-value < 0.01
The temporally and spatially averaged WSS magnitude averaged over all vessel segments increased significantly with VSD severity (Fig. 7a), with 42.3 ± 12.2, 76.9 ± 22.9, 117.8 ± 35.6, and 214.0 ± 66.2 dyn/cm2 in the normal, small, moderate, and large VSD conditions, respectively. The WSS magnitude in the MPA was 29.1 dyn/cm2 in the normal condition, 52.5 dyn/cm2 for the small VSD, 79.4 dyn/cm2 for the moderate VSD, and 140.3 dyn/cm2 for the large VSD. These WSS values increased dramatically in the LPA and RPA from 48.4 and 45.2 dyn/cm2, respectively, in the normal case to 242.3 and 217.0 dyn/cm2 in the large VSD condition (Fig. 7b). Higher average WSS magnitudes were observed in order 12-15 vessels in the 3D proximal PA model as compared to the MPA. Figure 7c demonstrates dynamic changes in WSS within each vessel segment due to the tortuosity and branching of the PAs in the smaller 3D PAs. We note that the WSS magnitudes are higher in the smaller order segments than in the MPA. Furthermore, these WSS magnitudes in the smaller order vessels significantly increase with VSD condition and, in the normal condition, are already much higher than the <20 dyn/cm2 laminar WSS that has been commonly used as a healthy WSS magnitude for large and small PA mechanotransduction studies (Giddens et al. 1993; Malek et al. 1999; Schmid-Schönbein 1981; Zarins et al. 1983).
Fig. 7.
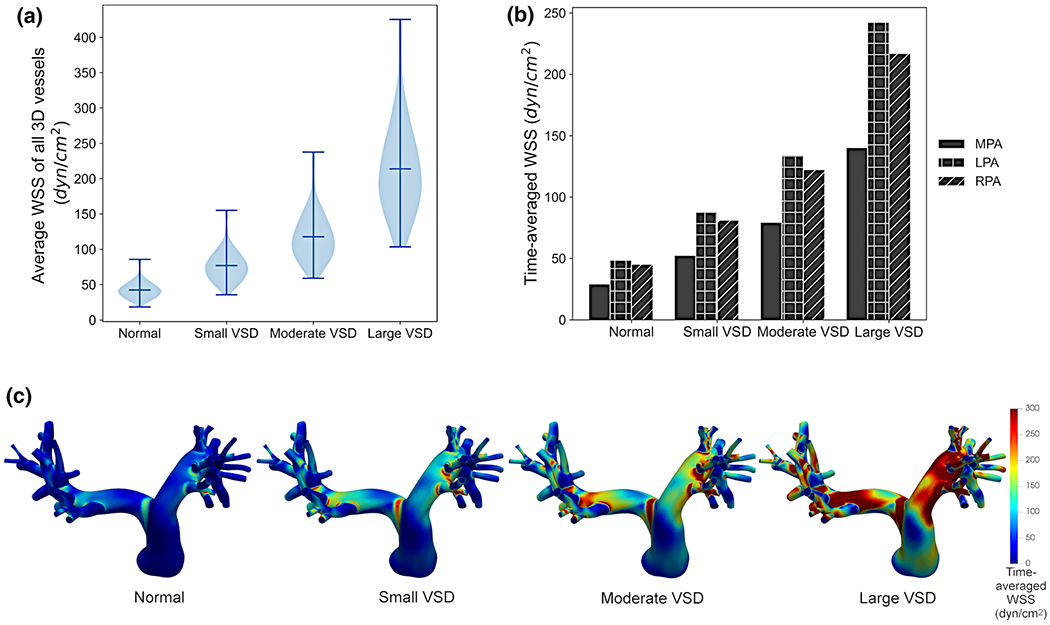
Hemodynamic simulations of the 3D proximal PA model show that a the temporally and spatially averaged wall shear stress (WSS) in all 3D PA vessels increased with VSD severity with significant differences across all VSD conditions. b For the main PA (MPA), left PA (LPA), and right PA (RPA), the WSS increased with VSD severity and had a marked increase in value from MPA to the LPA and RPA lobar branches. c The time-averaged WSS magnitude in the 3D proximal PA models shows dynamic changes throughout the PA tree with higher WSS in the smaller vessels and in the larger VSD conditions
3.2. 0D distal PA tree results
In the 0D model simulations of the small distal PAs, the WSS magnitude increases down the PA tree to the pre-capillary arterioles (>10 μm) (Fig. 8). In agreement with the 3D proximal PA simulations, the WSS magnitude also increases with VSD severity in the distal PA tree. There was approximately a 3x increase in the WSS magnitude in the smallest pre-acinar vessels (67 ± 8 μm diameter) with 43.9 ± 11.2, 65.9 ± 17.1, 87.6 ± 23.0, and 131.2 ± 35.5 dyn/cm2 in the normal, small, moderate, and large VSD conditions, respectively. For distal PA vessels with diameters within 100–200 μm, the average WSS magnitude was 22.4 ± 12.9, 33.5 ± 19.5, 44.7 ± 26.0, and 67.0 ± 39.5 dyn/cm2 in the normal, small, moderate, and large VSD conditions, respectively. For the more proximal vessels with diameters within 200–500 μm, the average WSS magnitude was smaller at 18.0 ± 19.8, 26.9 ± 14.9, 35.9 ± 19.9, and 53.8 ± 30.1 dyn/cm2 in the normal, small, moderate, and large VSD conditions.
Fig. 8.
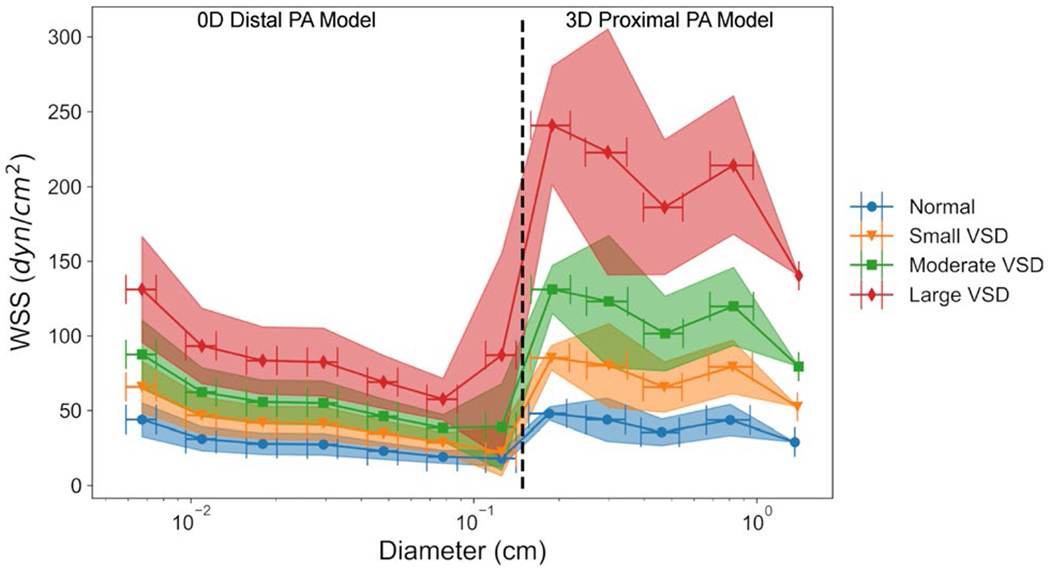
Simulations in the distal PA morphometric tree using a 0D model and the proximal 3D PA model show increases in WSS magnitude with VSD severity grouped by vessel orders against vessel diameter. The WSS in the 0D distal PA model increased down the PA tree as vessel diameters decreased
Noticeable differences in the WSS magnitudes exist between the 3D proximal PA model and the 0D distal PA model, especially for vessels in the transitional ~1–2-mm-diameter range between the two models. These can be attributed to the underlying assumption of steady laminar Poiseuille flow in the 0D distal PA model. While this assumption is valid for small distal arteries in which the blood velocity is sufficiently slow for fully developed flow (Secomb 2016), it is less valid in the larger more proximal PAs where the Reynolds number in vessel segments range in magnitude from 102 in the ~1-cm-diameter vessels to 103 in the MPA showing deviation from a fully developed parabolic profile. In the 0D distal PA model, the Reynolds number was much higher in the order 12 vessels at the transition between the 0D and 3D PA models with an average value of 566 for the 0D model and 88 for the 3D model in the normal condition. This marked difference between the 3D proximal and 0D distal PA model can also be explained by short curved vessel segments and branching regions in the 3D model where flow is less likely to be fully developed with non-zero velocity components in the radial and tangential directions which are not accounted for in the 0D model.
Overall, our 0D simulations indicated that WSS magnitude increases with VSD size and further increased down the tree. In small PA vessel segments, the WSS magnitude exceeded 20 dyn/cm2 in the normal control and exceeded 100 dyn/cm2 in the large VSD condition. Given the large heterogeneity in the branching structure of the distal PA morphometric trees, vessel segments of the same order receive disparate amounts of flow, causing large standard deviations of the WSS estimates. This mimics physiological conditions, as previous reports suggest that portions of the pulmonary tree, specifically the upper lobe, receive less total flow than the lower lobe in a resting position (Cheng et al. 2006).
Given the high sensitivity of WSS to the vessel segment radius, the tuning of the morphometric tree was a highly sensitive process with potentially large consequences in WSS estimates. A sensitivity analysis showed that a 20% increase in the radius, corresponding to the limits of the optimization of the radii, resulted in a 42% decrease in the WSS; increases in flow resulted in a linear increase in WSS as expected. Additional information on the sensitivity analysis can be found in “Appendix” A.3. We conducted simulations with multiple distal PA geometries and found that despite large variability, the WSS consistently increased with VSD size and down the PA tree. Despite a lack of studies on the structure of the distal PA trees in a 1-year-old, we have made rigorously informed estimates of WSS using physiological PA resistances and morphometric PA scaling laws.
4. Discussion
Our computational study of hemodynamics in the PAs with VSD conditions is the first to establish estimates for in vivo hemodynamic markers in the entire PA tree with different unrestricted VSD sizes before any vascular remodeling occurs leading to PAH. Using a 1-year-old patient-specific normal PA geometry with increased pulmonary blood flow to represent larger shunt sizes present in severe VSD cases, we found that pressures, flows, strain, and WSS globally increased with larger VSDs in the proximal 3D PA model. We also found that OSI decreased slightly with VSD severity in the larger, proximal PA vessels. In the distal PA tree, we found that WSS increased with smaller PA vessels and increased with larger VSD conditions, exceeding 100 dyn/cm2 in the smallest pre-acinar PAs. Because in vivo measurements of hemodynamics in the small PAs are unattainable, we leveraged computational models to simulate the abnormal PA hemodynamics during VSD conditions, which is critical for understanding the abnormal physiology contributing to the initiation of vascular remodeling and PAH in future studies.
A majority of studies have focused on disease progression of late-stage PAH, but it is necessary to study the conditions prior to the onset of PAH to understand the conditions leading to vascular remodeling and disease progression as well as to characterize complex pathways that can be used to identify and treat asymptomatic patients before late-stage disease occurs (Rafikova et al. 2019). Biological studies have found marked differences in the phenotypes of vascular endothelial and smooth muscle cells at different stages of PAH (Dereddy et al. 2012; Sakao et al. 2010) indicating that hemodynamics may also change between initiation and at severe end-stages of PAH over a period of weeks to months. It is commonly understood that abnormal hemodynamics due to the presence of left-to-right shunting in unrepaired CHDs are a significant contributing factor in PAH. By leveraging the simplicity of PAH-CHD initiation due to abnormal hemodynamics, future biological studies can use the hemodynamic values estimated in this study to understand the effects of mechanical loads experienced by the vascular wall on complex mechanotransduction pathways of endothelial and smooth muscle cell dysfunction. Morphometrically, vascular remodeling starts with muscularization of the intra-acinar PAs leading to medial hypertrophy and loss of small PAs (Rabinovitch 1981) which can be modeled with decreases in vessel diameter and increased wall stiffness similar to previous studies (Qureshi 2014, Yang 2019) and developed upon further with experimental studies. To inform the mechanisms leading to these changes, our study estimates hemodynamics at an initial timepoint before vascular remodeling occurs; future growth and remodeling studies (Humphrey 2021) including autoregulatory response and long-term effects of VSD induced abnormal hemodynamics are needed to further elucidate the disease initiation process.
PAH-CHD progression and prognosis has been distinguished in high pressure and high flow conditions, such as in an unrestricted VSD, from low pressure and high flow conditions, such as an atrial septal defect. We focused on an unrestricted VSD which has a high probability of causing PAH-CHD if unrepaired (Kulik 2012) and found higher pressures and flows throughout the PA tree. The MPA pressures, PVRI, and Qp : Qs ratio in the simulated VSD conditions were similar to hemodynamics reported in previous studies (Online Resource 3) of catheterized VSD patients without a PH diagnosis (Beekman et al. 1982; Hedvall 1978; Hoffman and Rudolph 1965; Silverman et al. 1980). The higher pressures associated with larger VSDs also resulted in greater strain. Although higher elastic moduli significantly changed the strain and systolic pressures, a sensitivity analysis of the effects of elastic moduli in the large VSD showed that the OSI, WSS, and flow remained unaffected (additional details in “Appendix” A.3). Additionally, studies of late-stage PAH where MPA dilation occurs have found slightly smaller strains than in healthy patients (Schäfer et al. 2016; Yang et al. 2019). However, VSD conditions in normal MPA diameters, without dilation, may result in larger strains in vivo similar to our simulation estimates. Similar dichotomous findings for OSI in the MPA were found; late-stage PAH studies showed increases in OSI with severity of disease (Yang et al. 2019) while our simulations showed decreases in OSI with VSD conditions before initiation of PAH. These differences could again be explained by the dilation of the MPA in late-stage PAH increasing flow separation as compared to the non-dilated MPA and faster velocity blood flow resulting from the VSD. The complex progression of PAH from initiation to late-stage disease could be due in part to these large differences in hemodynamic conditions and highlights the need for further study of pre-PAH initiation in VSD patients. Additional MR and 4DMR imaging of the PAs in patients with a VSD and without PAH are needed to verify our in silico estimates.
Our results showed increases in WSS values with more distal PAs and with larger VSDs. Similarly, previous computational studies also found similar increases in WSS in the distal PAs (Ghorishi et al. 2007; Kheyfets et al. 2015; Postles et al. 2014; Yang et al. 2019). One study investigating the effects of increased flow from CHD in a fetal lamb and its effects on the pulmonary branching and shear stress in an 8-week-old lamb predicted, with Poiseuille assumptions, that WSS increases into the 102 dyn/cm2 order of magnitude range for vessel segments between 1 to 0.1 mm in diameter (Ghorishi et al. 2007), which is a similar range to our simulations (~14-100 dyn/cm2). However, they used a simplified PA geometry that did not account for the size of the human subject nor the complexity of the branching pattern. Our use of a BSA-scaled morphometric PA tree that has been tuned to match expected PA resistance is novel in its incorporation of physiologic and subject-specific parameters that further inform the geometry and hemodynamic estimates in an infant.
Many studies on the effects of shear stress on PA endothelial cells cite a normal laminar WSS of 15 dyn/cm2 corresponding to findings in the large PAs (Tang et al. 2012; Truong et al. 2013; Yang et al. 2019; Zambrano et al. 2018), but this value was originally derived from estimates of systemic arteriole WSS (Davies 2009). Studies have shown that WSS varies widely in the body and within an organ (Cheng et al. 2006; Yang et al. 2019), but WSS values have not been definitively confirmed in the small distal PAs, much less in the distal PAs with a VSD in previous studies. Our study shows that normal conditions can have a wide range of WSS values greater than the 15 dyn/cm2 standard in many parts of the proximal and distal PA tree, with values ranging from ~15-50 dyn/cm2. A previous study found upregulated markers associated with vasoconstriction and weakened vascular endothelial cadherin junction in bovine PA endothelial cells in response to higher WSS levels similar to the abnormal WSS values found in our moderate and large VSD conditions (Li et al. 2009). Other studies using endothelial cells derived from different animal models and vessels found contrasting results for similarly elevated WSS values with atheroprotective endothelial cell phenotypes and excellent alignment in some studies (Dolan et al. 2012; Levesque and Nerem 1985) and dysfunctional phenotypes and poor alignment in others (Garcia-Polite et al. 2017; Ostrowski et al. 2014; Sho et al. 2002). However, PAH has yet to be explored in depth with PA endothelial cells derived from the small, distal PAs under informed shear stress conditions. Emerging studies and hypotheses support the notion that endothelial cells, which play a major role in vascular health, are phenotypically and genotypically different between tissues of the same body and between vessel segments of the same organ (Aird 2012; Cleuren et al. 2019; Krüger-Genge et al. 2019; Thorin et al. 1997). This would suggest that homeostatic hemodynamics may differ between vessels and studying the mechanotransduction pathways as well as the growth, and remodeling of PAH must be conducted using the correct hemodynamics for the vessel segment that is most affected - in this case, the smaller distal PAs where vascular remodeling is most predominant.
5. Limitations
Our simulation-based estimates are not without limitations. Our simulations in the 3D proximal PAs were generalized to a single patient-specific model of a 1-year-old, and the scaled flow waveform used to model large VSDs may not accurately represent the true pulmonary blood flow volume. Additional analysis using a VSD patient-specific flow waveform on multiple models of different ages in the early course of a VSD could improve the accuracy of our hemodynamic estimates. Furthermore, the elastic moduli prescribed for the VSD conditions were based on exercise studies which may not reflect the true PA wall mechanics in a pediatric VSD patient; additional mechanical tissue testing is needed in the pediatric population. The vessel wall deformation was modeled by a linear elastic wall model even though larger pulmonary flows and pressures may need to be modeled with nonlinear, anisotropic material properties.
In the 0D distal PA model, limitations are present in both the assumptions and geometry of the distal PAs. As the 3D proximal and 0D distal PA models are not numerically coupled and have different model assumptions, the transition is not perfectly continuous; in the region where the 3D PA model transitions to the 0D PA tree, the distal PA WSS may be underestimated due to inherent differences in the 0D model’s assumptions. Though we mediated this transition by using a velocity profile representing developing flows at the transition, future studies should investigate the flow transition from the large PAs to the small PAs with extensive 3D PA trees and experimental validation to develop improved 0D models. Additional studies of the PAs could use a coupled system modeling the arteries, capillaries, and veins separately to capture the changing dynamics and physiologic resistance in each component of the pulmonary vasculature. Finally, the distal morphometric tree does not represent the full pulmonary arteriole dynamics. As the precise intra-acinar and small PA hemodynamics during infancy are unknown, we had to make a series of assumptions for the anatomic branching patterns and the longitudinal distribution of the arterial, capillary, and venous resistance to recreate physiological PA conditions. Vasodilation in response to increased flow, which is particularly significant in the distal arterioles and capillaries, was not considered in this in silico study since the goal of this study was to identify an initial timepoint before any vascular remodeling. However, a sensitivity analysis (“Appendix” A.3) of changes in vessel diameter, which occurs during vasodilation, showed a 42% decrease in WSS with a 20% increase in radii. Short-term and long-term effects of the prolonged hemodynamics shown in this study could significantly affect WSS due to its high sensitivity on diameter. Additional studies of the vasodilative morphometry and physiology of the small PAs, specifically in infants, are needed for further development and investigation into its effects before employing models accounting for autoregulatory stimuli driving hemodynamics.
6. Conclusion
This study is the first to use in silico methods to capture in vivo hemodynamics of the entire PA tree under VSD conditions in the context of PAH initiation. We estimate several hemodynamic markers, including pressure, flow, strain, OSI, and WSS, under conditions of increasing VSD severity to understand the mechanical loads present at the timepoint before the initiation of PA vascular remodeling leading to PAH-CHD. Specifically, WSS magnitudes in the small distal PAs, where the most prevalent remodeling occurs, are reported in our study and can be used to inform biological studies of PA vascular remodeling and the triggers leading to widespread remodeling and severe PAH.
Acknowledgements
We acknowledge Dr. Irene Vignon-Clementel for insight into distal pulmonary vascular modeling. This work was supported in part by the Vera Moulton Wall Center at Stanford University. Melody L. Dong was supported by a National Science Foundation Graduate Research Fellowship and the Vera Moulton Wall Center Benchmark Capital Fellowship. Ingrid S. Lan was supported by a National Science Foundation Graduate Research Fellowship and the Stanford Graduate Fellowship in Science and Engineering. This work used the computational resources from the Sherlock cluster through the Stanford Research Computing Center and Expanse through the Extreme Science and Engineering Discovery Environment (XSEDE), which is supported by National Science Foundation grant number ACI-1548562.
Appendix
A.1. 3D CFD blood flow finite element solver
Blood flow was simulated by solving the 3D Navier-Stokes equations with the finite element method. The following is the weak form of the governing equations:
Find v, p ∈ S for any w, q ∈ W such that
| (16) |
where ρ is the density, v is the velocity, p is the pressure, S is the trial solution space, w and q are weighting functions for momentum and continuity, W is the weighting function space, f is the body force, τ is the viscous stress tensor, Ω is the fluid domain, and Γh and ΓS are the Neumann boundaries corresponding to the traction forces h prescribed on the outlet faces and Tf on the vessel walls, respectively.
To model the deformable vessel walls, the coupled momentum method with a thin wall assumption was used, where the body force, fs, and the surface traction acting on the vessel wall, Ts, are related in the following form:
| (17) |
where ζ is the wall thickness. This results in the following equation coupling the linear elastodynamic equation to the fluid momentum equation:
| (18) |
where σS is the vessel wall stress tensor is defined by Eq. 19:
| (19) |
where C is the fourth-order tensor of material constants and the strain tensor, ϵ:
| (20) |
where u is the wall displacement. External tissue support was implemented as Robin boundary conditions on the vessel walls imparting a viscoelastic response:
| (21) |
where ns is the outward unit normal on the wall, ks and cs are the spring and damping constants, respectively, p0 is the intrathoracic pressure assumed to be 0, and vs is the velocity of the solid domain at a material point.
A.2. Hemodynamic quantities of interest
The following are details for how hemodynamic quantities of interest from 3D PA simulations are calculated. The temporally averaged magnitude of wall shear stress () is computed from the wall shear stress vector (), representing the tangential traction force of fluid along the solid vessel walls, over the duration of one cardiac cycle, tc computed as:
| (22) |
The oscillatory shear index (OSI) is a measure of the change in direction of the WSS vector and represents the oscillatory component of blood flow computed as:
| (23) |
A.3. Sensitivity analysis
To analyze the sensitivity of the simulated hemodynamics to model parameters, a range of parameter values for the radius, length, flow, and target resistance in the distal PA model were analyzed. We scaled all radii, length, and flow in the distal PA tree by a constant. With changes in the radius scaling constant within the constraints of the distal tree optimization (0.8–1.2), the WSS decreased by 42% with a 20% increase in radii; all WSS fluctuations with the constrained scaling constant were <150 in the large VSD simulation. With changes in the length scaling constant within the constraints of the distal tree optimization (0.4-1.6), the WSS and flow remained unchanged, but the pressure increased linearly with a 200% increase from a 0.4 to 1.6× length scaling constant. With changes in the flow, there was a linear increase in the WSS as expected. With increases in the target resistance for the distal PA tree, the optimized diameter scaling constants used to generate an optimized distal PA geometry decreased from the maximum value (maximum scaling constant of 1.2) to 1.1 at a resistance approximately twice the initial target resistance. The length scaling constant increased from 0.4, the minimum length scaling constant, to 0.75 with increases in the target resistance to approximately twice the initial target resistance. Though the changes in length due to sensitivity from the target resistance do not affect the WSS, changes in the diameter scaling constant from 1.2 to 1.1 due to the target resistance would reduce the WSS by 30%. In the 3D proximal PA model, we tested the sensitivity of the large VSD simulated hemodynamics to changes in the elastic modulus. Variation in the elastic modulus from 126 kPa to 750 kPa significantly reduced the strain by 75% for the MPA and systolic PA pressures from 77 mmHg to 90 mmHg. However, WSS, OSI, and flow did not significantly change.
Footnotes
Supplementary Information The online version contains supplementary material available at https://doi.org/10.1007/s10237-021-01519-4.
References
- Acosta S, Puelz C, Rivière B, Penny DJ, Brady KM, Rusin CG (2017) Cardiovascular mechanics in the early stages of pulmonary hypertension: a computational study. Biomech Model Mechanobiol 16(6):2093–2112. 10.1007/s10237-017-0940-4 [DOI] [PubMed] [Google Scholar]
- Aird WC (2012) Endothelial cell heterogeneity. Cold Spring Harb Perspect Med. 10.1101/cshperspect.a006429 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Al-Nassri S, Unny T (1981) Developing laminar flow in the inlet length of a smooth pipe. Appl Sci Res 36:313–332. 10.1007/BF00411891 [DOI] [Google Scholar]
- Antiga L, Piccinelli M, Botti L, Ene-Iordache B, Remuzzi A, Steinman DA (2008) An image-based modeling framework for patient-specific computational hemodynamics. Med Biol Eng Comput 46(11): 1097–1112. 10.1007/s11517-008-0420-1 [DOI] [PubMed] [Google Scholar]
- Barker AJ, Roldán-Alzate A, Entezari P, Shah SJ, Chesler NC, Wieben O, Markl M, François CJ (2015) Four-dimensional flow assessment of pulmonary artery flow and wall shear stress in adult pulmonary arterial hypertension: results from two institutions. Magn Reson Med 73(5):1904–1913. 10.1002/mrm.25326 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Beekman RH, Rocchini AP, Rosenthal A (1982) Hemodynamic effects of hydralazine in infants with a large ventricular septal defect. Circulation 65(3):523–528. 10.1161/01.CIR.65.3.523 [DOI] [PubMed] [Google Scholar]
- Cattermole GN, Leung PYM, Ho GYL, Lau PWS, Chan CPY, Chan SSW, Smith BE, Graham CA, Rainer TH (2017) The normal ranges of cardiovascular parameters measured using the ultrasonic cardiac output monitor. Physiol Rep 5(6): 10.14814/phy2.13195 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cheng CP, Herfkens RJ, Taylor CA, Feinstein JA (2005) Proximal pulmonary artery blood flow characteristics in healthy subjects measured in an upright posture using mri: the effects of exercise and age. J Magn Reson Imag 21(6):752–758. 10.1002/jmri.20333 [DOI] [PubMed] [Google Scholar]
- Cheng CP, Taur AS, Lee GS, Goris ML, Feinstein JA (2006) Relative lung perfusion distribution in normal lung scans: observations and clinical implications. Congenit Heart Dis 1(5):210–216. 10.1111/j.1747-0803.2006.00037.x [DOI] [PubMed] [Google Scholar]
- Chiu J-J, Chien S (2011) Effects of disturbed flow on vascular endothelium: pathophysiological basis and clinical perspectives. Physiol Rev 91:327–387. 10.1152/physrev.00047.2009 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cleuren AC, van der Ent MA, Jiang H, Hunker KL, Yee A, Siemieniak DR, Molema G, Aird WC, Ganesh SK, Ginsburg D (2019) The in vivo endothelial cell translatome is highly heterogeneous across vascular beds. PNAS 116(47):23618–23624. 10.1073/pnas.1912409116 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Davies PF (2009) Hemodynamic shear stress and the endothelium in cardiovascular pathophysiology. Nat Clin Pract Cardiovasc Med 6(1):16–26. 10.1038/ncpcardio1397 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dereddy N, Huang J, Erb M, Guzel S, Wolk JH, Sett SS, Gewitz MH, Mathew R (2012) Associated inflammation or increased flow-mediated shear stress, but not pressure alone, disrupts endothelial caveolin-1 in infants with pulmonary hypertension. Pulm Circ 2(4):492–500. 10.4103/2045-8932.105038 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dickinson MG, Bartelds B, Borgdorff MAJ, Berger RMF (2013) The role of disturbed blood flow in the development of pulmonary arterial hypertension: lessons from preclinical animal models. Am J Physiol Lung Cell Mol Physiol 305(1):L1–L14. 10.1152/ajplung.00031.2013 [DOI] [PubMed] [Google Scholar]
- Dickinson MG, Bartelds B, Molema G, Borgdorff MA, Boersma B, Takens J, Weij M, Wichers P, Sietsma H, Berger RM (2011) Egr-1 expression during neointimal development in flow-associated pulmonary hypertension. Am J Pathol 179(5):2199–2209. 10.1016/j.ajpath.2011.07.030 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dolan JM, Sim FJ, Meng H, Kolega J (2012) Endothelial cells express a unique transcriptional profile under very high wall shear stress known to induce expansive arterial remodeling. Am J Physiol Cell Physiol 302(8):C1109–C1118. 10.1152/ajpcell.00369.2011 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dong M, Yang W, Tamaresis JS, Chan FP, Zucker EJ, Kumar S, Rabinovitch M, Marsden AL, Feinstein JA (2020) Image-based scaling laws for somatic growth and pulmonary artery morphometry from infancy to adulthood. Am J Physiol Heart Circ Physiol 319(2):H432–H442. 10.1152/ajpheart.00123.2020 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Egito ES, Aiello VD, Bosisio IB, Lichtenfels AJ, Horta AL, Saldiva PH, Capelozzi VL (2003) Vascular remodeling process in reversibility of pulmonary arterial hypertension secondary to congenital heart disease. Pathol Res Pract 199(8):521–532. 10.1078/0344-0338-00457 [DOI] [PubMed] [Google Scholar]
- Esmaily Moghadam M, Bazilevs Y, Hsia TY, Vignon-Clementel IE, Marsden AL (2011) A comparison of outlet boundary treatments for prevention of backflow divergence with relevance to blood flow simulations. Comput Mech 48(3):277–291. 10.1007/s00466-011-0599-0 [DOI] [Google Scholar]
- Figueroa CA, Vignon-Clementel IE, Jansen KE, Hughes TJ, Taylor CA (2006) A coupled momentum method for modeling blood flow in three-dimensional deformable arteries. Comput Methods Appl Mech Eng 195(41–43):5685–5706. 10.1016/j.cma.2005.11.011 [DOI] [Google Scholar]
- Fineman JR, Black SM (2019) Pressure vs flow-induced pulmonary hypertension. Adv Pulm Hypertens 18(1), 19–24: 10.21693/1933-088x-18.1.19 [DOI] [Google Scholar]
- Forouzan O, Warczytowa J, Wieben O, François CJ, Chesler NC (2015) Non-invasive measurement using cardiovascular magnetic resonance of changes in pulmonary artery stiffness with exercise. J Cardiovasc Magn Reson. 10.1186/s12968-015-0213-2 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Garcia-Polite F, Martorell J, Del Rey-Puech P, Melgar-Lesmes P, O’Brien CC, Roquer J, Ois A, Principe A, Edelman ER, Balcells M (2017) Pulsatility and high shear stress deteriorate barrier phenotype in brain microvascular endothelium. J Cereb Blood Flow Metab 37(7):2614–2625. 10.1177/0271678X16672482 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ghorishi Z, Milstein JM, Poulain FR, Moon-Grady A, Tacy T, Bennett SH, Fineman JR, Eldridge MW (2007) Shear stress paradigm for perinatal fractal arterial network remodeling in lambs with pulmonary hypertension and increased pulmonary blood flow. Am J Physiol Heart Circ Physiol 292(6):H3006–H3018. 10.1152/ajpheart.01012.2006 [DOI] [PubMed] [Google Scholar]
- Giddens DP, Zarins CK, Glagov S (1993) The role of fluid mechanics in the localization and detection of atherosclerosis. J Biomech Eng 115(4):588–594. 10.1115/1.2895545 [DOI] [PubMed] [Google Scholar]
- Haworth SG, Hislop AA (1983) Pulmonary vascular development: normal values of peripheral vascular structure. Am J Cardiol 52(5):578–583. 10.1016/0002-9149(83)90030-9 [DOI] [PubMed] [Google Scholar]
- Hedvall G (1978) The applicability of the thermodilution method for determination of pulmonary blood flow and pulmonary vascular resistance in infants and children with ventricular septal defects. Scan J Clin Lab Invest 38(6):581–585. 10.1080/00365517809108823 [DOI] [PubMed] [Google Scholar]
- Hislop A, Reid L (1972) Intra-pulmonary arterial development during fetal life-branching pattern and structure. J Anat 113(Pt 1):35–48 [PMC free article] [PubMed] [Google Scholar]
- Hislop A, Reid L (1973) Pulmonary arterial development during childhood: branching pattern and structure. Thorax 28(2):129–35. 10.1136/THX.28.2.129 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hoffman JI, Rudolph AM (1965) The natural history of ventricular septal defects in infancy. Am J Cardiol 16(5):634–653. 10.1016/0002-9149(65)90047-0 [DOI] [PubMed] [Google Scholar]
- Huang W, Yen RT, McLaurine M, Bledsoe G (1996) Morphometry of the human pulmonary vasculature. J Appl Physiol 81(5):2123— 2133. 10.1152/jappl.1996.81.5.2123 [DOI] [PubMed] [Google Scholar]
- Hunter KS, Albietz JA, Lee P-F, Lanning CJ, Lammers SR, Hofmeister SH, Kao PH, Qi HJ, Stenmark KR, Shandas R (2010) In vivo measurement of proximal pulmonary artery elastic modulus in the neonatal calf model of pulmonary hypertension: development and ex vivo validation. J Appl Physiol 108(4):968–975. 10.1152/japplphysiol.01173.2009 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hunter KS, Lanning CJ, Chen S-YJ, Zhang Y, Garg R, Ivy DD, Shandas R (2006) Simulations of congenital septal defect closure and reactivity testing in patient-specific models of the pediatric pulmonary vasculature: A 3d numerical study with fluid-structure interaction. J Biomech Eng 128(4):564–572. 10.1152/japplphysiol.01173.2009 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jia Y, Argueta-Morales IR, Liu M, Bai Y, Divo E, Kassab AJ, Decampli WM (2015) Experimental study of anisotropic stress/strain relationships of the piglet great vessels and relevance to pediatric congenital heart disease. Ann Thorac Surg 99(4):1399–1407. 10.1016/j.athoracsur.2014.11.032 [DOI] [PubMed] [Google Scholar]
- Kameny RJ, Datar SA, Boehme JB, Morris C, Zhu T, Goudy BD, Johnson EG, Galambos C, Raff GW, Sun X, Wang T, Chiacchia SR, Lu Q, Black SM, Maltepe E, Fineman JR (2019) Ovine models of congenital heart disease and the consequences of hemodynamic alterations for pulmonary artery remodeling. Am J Respir Cell Mol Biol 60(5):503–514. 10.1165/rcmb.2018-0305MA [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kheyfets VO, Rios L, Smith T, Schroeder T, Mueller J, Murali S, Lasorda D, Zikos A, Spotti J, Reilly JJ, Finol EA (2015) Patient-specific computational modeling of blood flow in the pulmonary arterial circulation. Comput Methods Programs Biomed 120:88–101. 10.1016/j.cmpb.2015.04.005 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kheyfets VO, Schafer M, Podgorski CA, Schroeder JD, Browning J, Hertzberg J, Buckner JK, Hunter KS, Shandas R, Fenster BE (2016) 4d magnetic resonance flow imaging for estimating pulmonary vascular resistance in pulmonary hypertension. J Magn Reson 44(4):914–922. 10.1002/jmri.25251 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kobs RW, Muvarak NE, Eickhoff JC, Chesler NC (2005) Linked mechanical and biological aspects of remodeling in mouse pulmonary arteries with hypoxia-induced hypertension. Am J Physiol Heart Circ Physiol 288(3):H1209–H1217. 10.1152/ajpheart.01129.2003 [DOI] [PubMed] [Google Scholar]
- Koh W, Morell E, Viegas M, Moguillansky D, Kazmerski TM, Munoz RA (2020) Ventricular septal defects. In: Munoz RA, Morell VO, da Cruz EM, Vetterly CG, da Silva JP (eds) Critical Care of Children with Heart Disease. Springer, Cham, pp 165–171. 10.1007/978-3-030-21870-6_15 [DOI] [Google Scholar]
- Kosecik M, Sagin-Saylam G, Unal N, Kir M, Paytoncu S (2007) Non-invasive assessment of left-to-right shunting in ventricular septal defects by the proximal isovelocity surface area method on doppler colour flow mapping. Can J Cardiol 23(13):1049–1053. 10.1016/S0828-282X(07)70872-3 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Krüger-Genge A, Blocki A, Franke RP, Jung F (2019) Vascular endothelial cell biology an update. Int J Mol Sci. 10.3390/ijms20184411 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kulik TJ (2012) Pulmonary blood flow and pulmonary hypertension: is the pulmonary circulation flowophobic or flowophilic? Pulm Circ 2(3):327–339. 10.4103/2045-8932.101644 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lange TJ, Dornia C, Stiefel J, Stroszczynski C, Arzt M, Pfeifer M, Hamer OW (2013) Increased pulmonary artery diameter on chest computed tomography can predict borderline pulmonary hypertension. Pulm Circ 3(2):363–368. 10.4103/2045-8932.113175 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Levesque MJ, Nerem RM (1985) The elongation and orientation of cultured endothelial cells in response to shear stress. J Biomech Eng 107(4):341–347. 10.1115/1.3138567 [DOI] [PubMed] [Google Scholar]
- Levitsky MG (2018) Blood flow to the lung. In Levitsky MG, editor, Pulmonary Physiology, chapter 4. McGraw-Hill, 9e edition [Google Scholar]
- Levy B, Ambrosio G, Pries A, Struijker-Boudier H (2001) Microcirculation in hypertension: a new target for treatment? Circulation 104(6):735–740. 10.1161/HC3101.091158 [DOI] [PubMed] [Google Scholar]
- Li M, Stenmark KR, Shandas R, Tan W (2009) Effects of pathological flow on pulmonary artery endothelial production of vasoactive mediators and growth factors. J Vasc Res 46(6):561–71. 10.1159/000226224 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lipowsky HH (1995) Shear stress in the circulation. In: Bevan JA, Kaley G, Rubanyi GM (eds) Flow-Dependent Regulation of Vascular Function. Springer, New York, pp 28–45. 10.1007/978-1-4614-7527-9_2 [DOI] [Google Scholar]
- Long CC, Hsu M-C, Bazilevs Y, Feinstein JA, Marsden AL (2012) Fluid-structure interaction simulations of the fontan procedure using variable wall properties. Int J Numer Meth Biomed Eng 28(5):513–527. 10.1002/cnm.1485 [DOI] [PubMed] [Google Scholar]
- Maher G, Parker D, Wilson N, Marsden A (2020) Neural network vessel lumen regression for automated lumen cross-section segmentation in cardiovascular image-based modeling. Cardiovasc Eng Technol 11:621–635. 10.1007/s13239-020-00497-5 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mahmoud MM, Serbanovic-Canic J, Feng S, Souilhol C, Xing R, Hsiao S, Mammoto A, Chen J, Ariaans M, Francis SE, Van Der Heiden K, Ridger V, Evans PC (2017) Shear stress induces endothelial-to-mesenchymal transition via the transcription factor snail. Sci Rep 7(1):1–12. 10.1038/s41598-017-03532-z [DOI] [PMC free article] [PubMed] [Google Scholar]
- Malek AM, Alper SL, Izumo S (1999) Hemodynamic shear stress and its role in atherosclerosis. JAMA 282(21):2035–2042. 10.1001/jama.282.21.2035 [DOI] [PubMed] [Google Scholar]
- Moireau P, Xiao N, Astorino M, Figueroa CA, Chapelle D, Taylor CA, Gerbeau J-F (2012) External tissue support and fluid-structure simulation in blood flows. Biomech Model Mechanobiol 11:1–18. 10.1007/s10237-011-0289-z [DOI] [PubMed] [Google Scholar]
- Muralidaran A, Shen I (2018) Ventricular septal defects. In: Ungerleider RM, Meliones JN, McMillan KN, Cooper DS, Jacobs JP (eds) Critical Heart Disease in Infants and Children, chapter 49, pp 597–605.e2. Elsevier, 3e edition. 10.1016/B978-1-4557-0760-7.00049-8 [DOI] [Google Scholar]
- Odagiri K, Inui N, Hakamata A, Inoue Y, Suda T, Takehara Y, Sakahara H, Sugiyama M, Alley MT, Wakayama T, Watanabe H (2016) Non-invasive evaluation of pulmonary arterial blood flow and wall shear stress in pulmonary arterial hypertension with 3d phase contrast magnetic resonance imaging. SpringerPlus 5(1):1071. 10.1186/s40064-016-2755-7 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Olufsen MS (1999) Structured tree outflow condition for blood flow in larger systemic arteries. Am J Physiol Heart Circ Physiol 276:H257–H268. 10.1152/ajpheart.1999.276.1.h257 [DOI] [PubMed] [Google Scholar]
- Ostrowski MA, Huang NF, Walker TW, Verwijlen T, Poplawski C, Khoo AS, Cooke JP, Fuller GG, Dunn AR (2014) Microvascular endothelial cells migrate upstream and align against the shear stress field created by impinging flow. Biophys J 106(2):366–374. 10.1016/j.bpj.2013.11.4502 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Postles A, Clark AR, Tawhai MH (2014) Dynamic blood flow and wall shear stress in pulmonary hypertensive disease. Annu Int Conf IEEE Eng Med Biol Soc. Chicago. IEEE, pp 5671–5674. 10.1109/EMBC.2014.6944914 [DOI] [PubMed] [Google Scholar]
- Pries AR, Secomb TW, Gaehtgens P (1995) Design principles of vascular beds. Circ Res 77(5):1017–1023. 10.1161/01.RES.77.5.1017 [DOI] [PubMed] [Google Scholar]
- Qureshi MU, Colebank MJ, Paun LM, Ellwein Fix L, Chesler N, Haider MA, Hill NA, Husmeier D, Olufsen MS (2019) Hemodynamic assessment of pulmonary hypertension in mice: a model-based analysis of the disease mechanism. Biomech Model Mechanobiol 18(1):219–243. 10.1007/s10237-018-1078-8 [DOI] [PubMed] [Google Scholar]
- Qureshi MU, Vaughan GD, Sainsbury C, Johnson M, Peskin CS, Olufsen MS, Hill NA (2014) Numerical simulation of blood flow and pressure drop in the pulmonary arterial and venous circulation. Biomech Model Mechanobiol 13(5):1137–1154. 10.1007/s10237-014-0563-y [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rabinovitch M, Haworth SG, Castaneda AR, Nadas AS, Reid LM (1978) Lung biopsy in congenital heart disease: a morphometric approach to pulmonary vascular disease. Circulation 58(6):1107–1122. 10.1161/01.CIR.58.6.1107 [DOI] [PubMed] [Google Scholar]
- Rabinovitch M, Herrera-deLeon V, Castaneda AR, Reid L (1981) Growth and development of the pulmonary vascular bed in patients with tetralogy of fallot with or without pulmonary atresia. Circulation 64(6):1234–1249. 10.1161/01.CIR.64.6.1234 [DOI] [PubMed] [Google Scholar]
- Rafikova O, Al Ghouleh I, Rafikov R (2019) Focus on early events: pathogenesis of pulmonary arterial hypertension development. Antioxid Redox Signal 31(13):933–953. 10.1089/ars.2018.7673 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Raj JU, Chen P (1986) Micropuncture measurement of microvascular pressures in isolated lamb lungs during hypoxia. Circ Res 59(4):398–404. 10.1161/01.RES.59.4.398 [DOI] [PubMed] [Google Scholar]
- Ramachandra AB, Humphrey JD (2019) Biomechanical characterization of murine pulmonary arteries. J Biomech 84:18–26. 10.1016/j.jbiomech.2018.12.012 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Reneman RS, Hoeks AP (2008) Wall shear stress as measured in vivo: consequences for the design of the arterial system. Med Biol Eng Comput 46(5):499–507. 10.1007/s11517-008-0330-2 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sakao S, Tatsumi K, Voelkel NF (2010) Reversible or irreversible remodeling in pulmonary arterial hypertension. Am J Respir Cell Mol Biol 43(6):629–634. 10.1165/rcmb.2009-0389TR [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schäfer M, Ivy DD, Abman SH, Stenmark K, Browne LP, Barker AJ, Mitchell MB, Morgan GJ, Wilson N, Shah A, Kollengode M, Naresh N, Fonseca B, DiMaria M, Buckner JK, Hunter KS, Kheyfets V, Fenster BE, Truong U (2019) Differences in pulmonary arterial flow hemodynamics between children and adults with pulmonary arterial hypertension as assessed by 4d-flow cmr studies. Am J Physiol Heart Circ Physiol 316(5):H1091–H1104. 10.1152/ajpheart.00802.2018 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schäfer M, Ivy DD, Barker AJ, Kheyfets V, Shandas R, Abman SH, Hunter KS, Truong U (2017) Characterization of cmr-derived haemodynamic data in children with pulmonary arterial hypertension. Eur Heart J Cardiovasc Imag 18(4):424–431. 10.1093/ehjci/jew152 [DOI] [PubMed] [Google Scholar]
- Schäfer M, Kheyfets VO, Schroeder JD, Dunning J, Shandas R, Buckner JK, Browning J, Hertzberg J, Hunter KS, Fenster BE (2016) Main pulmonary arterial wall shear stress correlates with invasive hemodynamics and stiffness in pulmonary hypertension. Pulm Circ 6(1):37–45. 10.1086/685024 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schmid-Schönbein H (1981) Interaction of vasomotion and blood rheology in haemodynamics. In: Lowe G, Barbenel J, Forbes C (eds) Clinical Aspects of Blood Viscosity and Cell Deformability, chapter 6. Springer, London, pp 49–66. 10.1007/978-1-4471-3105-2_6 [DOI] [Google Scholar]
- Secomb TW (2016) Hemodynamics. Compr Physiol 6(2):975–1003. 10.1002/cphy.c150038 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Secomb TW (2017) Blood flow in the microcirculation. Annu Rev Fluid Mech 49:443–61. 10.1146/annurev-fluid-010816-060302 [DOI] [Google Scholar]
- Sharma S, Aramburo A, Rafikov R, Sun X, Kumar S, Oishi PE, Datar SA, Raff G, Xoinis K, Kalkan G, Fratz S, Fineman JR, Black SM (2013) L-carnitine preserves endothelial function in a lamb model of increased pulmonary blood flow. Pediatr Res 74(1):39–47. 10.1038/pr.2013.71 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sho E, Sho M, Singh TM, Nanjo H, Komatsu M, Xu C, Masuda H, Zarins CK (2002) Arterial enlargement in response to high flow requires early expression of matrix metalloproteinases to degrade extracellular matrix. Exp Mol Pathol 73(2):142–153. 10.1006/exmp.2002.2457 [DOI] [PubMed] [Google Scholar]
- Silverman NH, Snider AR, Rudolph AM (1980) Evaluation of pulmonary hypertension by m-mode echocardiography in children with ventricular septal defect. Circulation 61(6):1125–1132 [DOI] [PubMed] [Google Scholar]
- Simonneau G, Montani D, Celermajer DS, Denton CP, Gatzoulis MA, Krowka M, Williams PG, Souza R (2019) Haemodynamic definitions and updated clinical classification of pulmonary hypertension. Eur Respir J 53(1):1801913. 10.1183/13993003.01913-2018 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Song S, Yamamura A, Yamamura H, Ayon RJ, Smith KA, Tang H, Makino A, Yuan JX-J (2014) Flow shear stress enhances intracellular Ca2+ signaling in pulmonary artery smooth muscle cells from patients with pulmonary arterial hypertension. Am J Physiol Cell Physiol 307(4):C373–C383. 10.1152/ajpcell.00115.2014 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Spilker RL, Feinstein JA, Parker DW, Reddy VM, Taylor CA (2007) Morphometry-based impedance boundary conditions for patient-specific modeling of blood flow in pulmonary arteries. Ann Biomed Eng 35(4):546–559. 10.1007/s10439-006-9240-3 [DOI] [PubMed] [Google Scholar]
- Szulcek R, Happe CM, Rol N, Fontijn RD, Dickhoff C, Hartemink KJ, Grunberg K, Tu L, Timens W, Nossent GD, Paul MA, Leyen TA, Horrevoets AJ, De Man FS, Guignabert C, Yu PB, Vonk-Noordegraaf A, Amerongen GPN, Bogaard HJ (2016) Delayed microvascular shear adaptation in pulmonary arterial hypertension: role of platelet endothelial cell adhesion molecule-1 cleavage. Am J Respir Crit Care Med 193(12):1410–1420. 10.1164/rccm.201506-1231OC [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tanaka Y, Schuster DP, Davis EC, Patterson GA, Botney MD (1996) The role of vascular injury and hemodynamics in rat pulmonary artery remodeling. J Clin Invest 98(2):434–442. 10.1172/JCI118809 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tang BT, Pickard SS, Chan FP, Tsao PS, Taylor CA, Feinstein JA (2012) Wall shear stress is decreased in the pulmonary arteries of patients with pulmonary arterial hypertension: an image-based, computational fluid dynamics study. Pulm Circ 2(4):470–6. 10.4103/2045-8932.105035 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Taylor CA, Hughes TJ, Zarins CK (1998) Finite element modeling of blood flow in arteries. Comput Methods Appl Mech Eng 158(1–2):155–196. 10.1016/S0045-7825(98)80008-X [DOI] [Google Scholar]
- Terada M, Takehara Y, Isoda H, Matsunaga T, Alley M (2016) Low wss and high osi measured by 3d cine pc mri reflect high pulmonary artery pressures in suspected secondary pulmonary arterial hypertension. Magn Reson Med Sci 15(2):193–202. 10.2463/mrms.mp.2015-0038 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Thorin E, Shatos MA, Shreeve SM, Walters CL, Bevan JA (1997) Human vascular endothelium heterogeneity. Stroke 28(2):375–381. 10.1161/01.STR.28.2.375 [DOI] [PubMed] [Google Scholar]
- Tran JS, Schiavazzi DE, Ramachandra AB, Kahn AM, Marsden AL (2017) Automated tuning for parameter identification and uncertainty quantification in multi-scale coronary simulations. Comput Fluids 142:128–138. 10.1016/J.COMPFLUID.2016.05.015 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Truong U, Fonseca B, Dunning J, Burgett S, Lanning C, Ivy DD, Shandas R, Hunter K, Barker AJ (2013) Wall shear stress measured by phase contrast cardiovascular magnetic resonance in children and adolescents with pulmonary arterial hypertension. J Cardiovasc Magn Reson 15(1):81. 10.1186/1532-429X-15-81 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Uebing A, Kaemmerer H (2011) Ventricular septal defect. In: Gatzoulis MA, Webb GD, Daubeney PE (eds) Diagnosis and management of adult congenital heart disease. Churchill Livingstone, London, pp 188–195 [Google Scholar]
- Updegrove A, Wilson NM, Merkow J, Lan H, Marsden AL, Shadden SC (2017) Simvascular: an open source pipeline for cardiovascular simulation. Ann Biomed Eng 45(3):525–541. 10.1007/s10439-016-1762-8 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Van Der Feen DE, Bartelds B, De Boer RA, Berger RM (2017) Pulmonary arterial hypertension in congenital heart disease: translational opportunities to study the reversibility of pulmonary vascular disease. Eur Heart J 38(26):2034–2040. 10.1093/eurheartj/ehx034 [DOI] [PubMed] [Google Scholar]
- Van Der Feen DE, Bossers GP, Hagdorn QA, Moonen JR, Kurakula K, Szulcek R, Chappell J, Vallania F, Donato M, Kok K, Kohli JS, Petersen AH, Van Leusden T, Demaria M, Goumans MJT, De Boer RA, Khatri P, Rabinovitch M, Berger RM, Bartelds B (2020) Cellular senescence impairs the reversibility of pulmonary arterial hypertension. Sci Transl Med. 10.1126/SCITRANSLMED.AAW4974 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vignon-Clementel I, Figueroa C, Jansen K, Taylor C (2010) Outflow boundary conditions for 3d simulations of non-periodic blood flow and pressure fields in deformable arteries. Comput Methods Biomech Biomed Engin 13(5):625–640. 10.1080/10255840903413565 [DOI] [PubMed] [Google Scholar]
- Vignon-Clementel IE, Alberto Figueroa C, Jansen KE, Taylor CA (2006) Outflow boundary conditions for three-dimensional finite element modeling of blood flow and pressure in arteries. Comput Methods Appl Mech Eng 195(29–32):3776–3796. 10.1016/j.cma.2005.04.014 [DOI] [Google Scholar]
- Wang L, Liu J, Zhong Y, Zhang M, Xiong J, Shen J, Tong Z, Xu Z (2020) Medical image-based hemodynamic analyses in a study of the pulmonary artery in children with pulmonary hypertension related to congenital heart disease. Front Pediatr. 10.3389/fped.2020.521936 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang Y, Sun HY, Kumar S, Puerta M (2019) Zbtb46 is a shear-sensitive transcription factor inhibiting endothelial cell proliferation via gene expression regulation of cell cycle proteins. Lab Invest 99(3):305–318. 10.1038/s41374-018-0060-5 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang Z, Lakes RS, Golob M, Eickhoff JC, Chesler NC (2013) Changes in large pulmonary arterial viscoelasticity in chronic pulmonary hypertension. PLoS ONE 8(11):e78569. 10.1371/journal.pone.0078569 [DOI] [PMC free article] [PubMed] [Google Scholar]
- White SJ, Hayes EM, Lehoux S, Jeremy JY, Horrevoets AJ, Newby AC (2011) Characterization of the differential response of endothelial cells exposed to normal and elevated laminar shear stress. J Cell Physiol 226(11):2841–2848. 10.1002/jcp.22629 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yang W, Dong M, Rabinovitch M, Chan FP, Marsden AL, Feinstein JA (2019) Evolution of hemodynamic forces in the pulmonary tree with progressively worsening pulmonary arterial hypertension in pediatric patients. Biomech Model Mechanobiol 18:779–796. 10.1007/s10237-018-01114-0 [DOI] [PubMed] [Google Scholar]
- Zambrano BA, McLean NA, Zhao X, Tan JL, Zhong L, Figueroa CA, Lee LC, Baek S (2018) Image-based computational assessment of vascular wall mechanics and hemodynamics in pulmonary arterial hypertension patients. J Biomech 68:84–92. 10.1016/j.jbiomech.2017.12.022 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zarins CK, Giddens DP, Bharadvaj BK, Sottiurai VS, Mabon RF, Glagov S (1983) Carotid bifurcation atherosclerosis. quantitative correlation of plaque localization with flow velocity profiles and wall shear stress. Circ Res 53(4):502–514. 10.1161/01.RES.53.4.502 [DOI] [PubMed] [Google Scholar]
- Zhang M, Feng Z, Huang R, Sun C, Xu Z (2018) Characteristics of pulmonary vascular remodeling in a novel model of shunt-associated pulmonary arterial hypertension. Med Sci Monit 24:1624–1632. 10.12659/MSM.905654 [DOI] [PMC free article] [PubMed] [Google Scholar]


