Internal variability and forcing influence model–satellite differences in the rate of tropical tropospheric warming

Significance

Comparisons between climate models and satellite observations consistently find that simulated warming of the tropical troposphere outpaces observations after 1979. There are a number of factors that may contribute to this discrepancy. Using machine learning and large ensembles of climate-model simulations, we find that internal variations in Earth’s climate have, by chance, reduced real-world tropospheric warming over the satellite era. A spurious discontinuity in prescribed biomass-burning aerosol emissions has also artificially enhanced simulated warming. These two effects largely explain the difference between simulated and observed tropical tropospheric warming. This offsetting effect of internal climate variability on greenhouse warming cannot, however, be relied on to reduce future warming and may, instead, lead to periods of accelerated change.

Abstract

Climate-model simulations exhibit approximately two times more tropical tropospheric warming than satellite observations since 1979. The causes of this difference are not fully understood and are poorly quantified. Here, we apply machine learning to relate the patterns of surface-temperature change to the forced and unforced components of tropical tropospheric warming. This approach allows us to disentangle the forced and unforced change in the model-simulated temperature of the midtroposphere (TMT). In applying the climate-model-trained machine-learning framework to observations, we estimate that external forcing has produced a tropical TMT trend of 0.25 ± 0.08 K⋅decade⁻¹ between 1979 and 2014, but internal variability has offset this warming by 0.07 ± 0.07 K⋅decade⁻¹. Using the Community Earth System Model version 2 (CESM2) large ensemble, we also find that a discontinuity in the variability of prescribed biomass-burning aerosol emissions artificially enhances simulated tropical TMT change by 0.04 K⋅decade⁻¹. The magnitude of this aerosol-forcing bias will vary across climate models, but since the latest generation of climate models all use the same emissions dataset, the bias may systematically enhance climate-model trends over the satellite era. Our results indicate that internal variability and forcing uncertainties largely explain differences in satellite-versus-model warming and are important considerations when evaluating climate models.

It has long been understood that the accumulation of atmospheric greenhouse gases (GHGs) produces global surface warming (1, 2). In addition to global-mean surface warming, early general circulation model (GCM) simulations of the response to GHG increases exhibited stratospheric cooling and enhanced warming in both the tropical upper troposphere and the Arctic lower troposphere (3, 4). These features are evident in modern, state-of-the-art GCM simulations (5) and are broadly consistent with long-term satellite-based microwave sounding unit observations of atmospheric temperature change (5–7).

Despite model–satellite agreement on the overall pattern of atmospheric temperature change, there is still considerable debate regarding the significance of model-versus-observed differences in the rate of tropical tropospheric warming and whether these differences can be attributed to deficiencies in GCMs. The average simulated temperature change in phases 3, 5, and 6 of the Coupled Model Intercomparison Project (CMIP) exhibits greater tropospheric warming than observations over the satellite era (1979 to present), particularly in the tropics (8–13).

In the latest generation of CMIP6 GCMs, the multimodel mean trend in the temperature of the midtroposphere (TMT) in the tropics over 1979 to 2014 is approximately two times larger than the average observed trend across several satellite datasets. A small fraction (12%) of individual model simulations are within the range of observed trends (10, 11, 14). Possible explanations for this difference include a bias in model sensitivity to atmospheric carbon dioxide increases (climate sensitivity) (9, 10), systematic errors in prescribed emissions of aerosols and aerosol precursors (15–17), model biases in the rate and distribution of ocean heat content changes (18, 19), and residual biases in satellite observations of tropospheric warming (20).

Internal climate variability, which can substantially enhance or damp externally forced temperature trends, is an additional factor that affects comparisons of simulated and observed warming (21–23). While GCMs simulate natural oscillations in atmospheric temperature, such variations are stochastic and are not expected to match the timing of real-world climate variability. Recent evidence suggests that the observed tropical TMT change over the satellite era has been reduced by internal variability, particularly in the early 21st century (11, 21, 22, 24). One implication of this finding is that GCMs are expected to show more warming than observations (assuming that GCMs accurately represent the forced climate response).

The increasing availability of large initial condition ensembles of climate simulations from individual models has enhanced the ability of researchers to quantify both internal climate variations and the forced climate response to external factors (25, 26). In contrast, neither the forced nor the unforced component of tropospheric warming is precisely known in observations.

Here, we apply machine learning (ML) to large GCM ensembles in order to relate patterns of surface-temperature change to the magnitude of forced and unforced tropical (30°S to 30°N) TMT change. After demonstrating skill in separating the individual components of satellite-era TMT change in GCMs, we apply our ML framework to observations to estimate the magnitude of tropical tropospheric warming attributable to external forcing and internal variability. We then place the impact of internal multidecadal climate variability in the context of existing observational uncertainty and climate sensitivity. We also consider recent work indicating that an artifact in the biomass-burning (BB) aerosol emissions prescribed in CMIP6 historical simulations may systematically inflate satellite-era warming (17).

Disentangling Internally and Externally Generated Warming

To disentangle the effects of external forcing and internal variability on tropical TMT change, we assemble an ML training dataset consisting of surface-warming maps and corresponding values of the forced and unforced tropical TMT trends. This training dataset makes use of output from the 14 CMIP6 GCMs that provide at least 10 historical ensemble members (SI Appendix, Fig. S1 and Table S1). For each individual model ensemble, we compute the ensemble average tropical TMT time series using all model-ensemble members (n ≥ 10), which approximately represents the forced climate response to anthropogenic (e.g., GHG changes and anthropogenic aerosol emissions) and natural external forcing (changes in volcanic and solar activity). We assume that the difference between each ensemble member’s tropical TMT time series and the forced climate response represents the TMT fluctuations that arise from internal variability.

The standard TMT satellite product measures the temperature of a broad vertical layer from the surface to the lower stratosphere (27). Since we are primarily interested in tropospheric temperature changes, we remove stratospheric influence on TMT for both the observations and the GCM synthetic satellite brightness temperatures (Materials and Methods).

We focus on the 36-y period spanning 1979 to 2014 because it represents the period of overlap between the satellite observations (1979 to present) and the CMIP6 historical experiment (1850 to 2014). As noted above, this period is also of interest because it is a time interval during which simulated warming tends to exceed the warming inferred from satellites (8, 10, 11). We construct ML training data from model historical simulations by sampling overlapping 36-y periods, with the start of each period spaced 5 y apart. This results in 25 samples within each model historical simulation (i.e., 1854 to 1889, 1859 to 1894, …, 1974 to 2009; Materials and Methods and SI Appendix). For each period, we consider the spatial pattern of surface warming (the predictor), as well as the forced and unforced tropical TMT trends (the predictands).

Partial least squares (PLS) regression is the primary ML technique used in this study. This method is useful because it is physically interpretable and has been employed, for example, to relate circulation patterns and sea-surface temperature (SST) anomalies to variability in western US snowpack (28, 29). Our application differs slightly in that we have two predictands (see above). To avoid overfitting our PLS model, we use a leave-one-out validation approach: We fit our PLS regression model to simulation output from 13 GCMs and subsequently use the PLS model to estimate the forced and unforced tropical TMT trend over 1979 to 2014 for each ensemble member of the 14th GCM (Materials and Methods and SI Appendix).

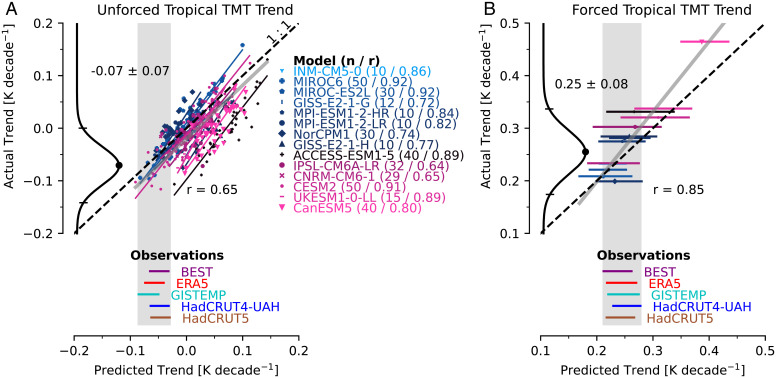
Fig. 1 shows the predicted unforced and forced tropical TMT trends compared to the actual values computed from each model ensemble. In the case of the unforced tropical TMT trend, the predicted-versus-actual trend values are well correlated for each ensemble: The correlation coefficient r ranges from 0.64 to 0.92 (Fig. 1A). We are unable to compute the intraensemble correlation for the forced-trend predictions since each model ensemble only has one value for the estimated forced trend (Fig. 1B), but across all models, the predicted-versus-actual forced trends are highly correlated (r = 0.85).

Fig. 1.

(A) The PLS predicted-versus-actual unforced tropical (30°S to 30°N) TMT trend for 14 climate-model ensembles for the time period 1979 to 2014. Colored lines represent the best-fit line for each model, and the light gray line is the best-fit line across all models. The dashed black line is the one-to-one line (y = x). The horizontal lines show the PLS prediction of the unforced TMT trend using the five different surface-temperature datasets (Materials and Methods). Note that the y value of these observation-based predictions is arbitrary. The gray vertical bar represents the full range of all the observational predictions. The observation-based predictions are convolved with the scatter plot to produce a bias-corrected estimate of the unforced tropical TMT trend (normalized probability density function along the y axis; Materials and Methods and SI Appendix). The dot and lines along this distribution represent the central value and 95% CIs, respectively. These values are noted in the panel. (B) As in A, but for the forced component of tropical TMT change. In this case, each model is represented by a horizontal line (spanning the range of PLS predictions) because the forced component of the TMT change is the same for all ensemble members. The legend in the center shows the color code for each model and also lists the number of ensemble members (n) and the correlation coefficient (r) for the regression in A. The ordering of models in the list corresponds to increasing climate sensitivity. The best-fit lines utilize orthogonal regression, and each model receives equal weight for the calculation of multimodel regressions (see the SI Appendix for more information).

Over all models, the predicted values of the unforced trends are close to the actual unforced trend values with a bias of 0.02 K⋅decade⁻¹ (compare the gray line to the dashed one-to-one line in Fig. 1A). Forced trend predictions have a bias that is close to zero for predictions near 0.2 K⋅decade⁻¹, but the bias grows for climate models with larger predicted forced tropical TMT trends (and for the Canadian Earth System Model version 5, CanESM5, in particular). Such biases are not surprising, given our approach: Recall that we are training our ML algorithm across a diverse set of physical climate models and time periods spanning a wide range of patterns of forcing and model response. We note that other linear (ridge regression) and nonlinear (artificial neural networks) methods exhibit similar skill (SI Appendix, Fig. S2). In general, our results indicate that the spatial pattern of surface warming can be used to reliably separate and quantify the forced and unforced components of simulated tropical TMT trends.

Having demonstrated appreciable skill in disentangling the effects of external forcing and internal variability in GCMs, we apply our trained ML models to estimate the forced and unforced components of the real-world tropical TMT trend. Input to the trained ML models consists of five different observational estimates of the pattern of surface-temperature change over 1979 to 2014 (SI Appendix, Fig. S3). These inputs are provided for each of the 14 leave-one-out PLS regression models, yielding observed estimates of the forced and unforced tropical TMT trend (see horizontal lines along the x axis of Fig. 1). For each of the five observational datasets, ∼60% of the uncertainty is a result of uncertainty in the observed pattern of warming (derived from the Met Office Hadley Centre/Climatic Research Unit global surface temperature dataset version 5 [HadCRUT5] observational ensemble; SI Appendix), and the remainder of the uncertainty results from differences across the 14 leave-one-out PLS regression models. We incorporate the uncertainty information from our leave-one-out GCM predictions by convolving the error in the regression in Fig. 1 with the observation-based predictions (Materials and Methods and SI Appendix) to produce an estimate of the overall uncertainties in the unforced and forced components of the observed tropical TMT trend (see probability distribution functions along the y axes of Fig. 1).

We estimate that the unforced and forced tropical TMT trends are −0.07 ± 0.07 and 0.25 ± 0.08 K⋅decade⁻¹, respectively (95% CI). ML predictions relying on ridge regression or a neural network yield similar results (SI Appendix, Fig. S2). When we use SST trends (instead of combined land- and ocean-surface trends) as a predictor of the forced and unforced components of tropical TMT change, we obtain a similar decomposition of tropical tropospheric temperature trends (−0.09 and 0.25 K⋅decade⁻¹ for the unforced and forced components of the trend, respectively; SI Appendix, Fig. S4 and Extended Methods). The internal variability component of the tropical TMT trend remains negative, even when we extend our analysis through 2021 (SI Appendix, Fig. S5; −0.04 ± 0.06 K⋅decade⁻¹ versus a forced trend of 0.29 ± 0.10 K⋅decade⁻¹). If we focus instead on trends in global-mean TMT, we find a smaller, but still substantial, unforced TMT trend over 1979 to 2014 (SI Appendix, Fig. S6; −0.05 ± 0.06 K⋅decade⁻¹ versus a forced trend of 0.24 ± 0.07 K⋅decade⁻¹).

These results indicate that the observed forced component of tropical tropospheric warming is large, but is partly offset (by ∼25%) by internal variability over 1979 to 2014. The effect of internal variability on TMT trends decreases when we consider trends through 2021, consistent with other studies that demonstrate that the magnitude of internal variability decreases when longer periods of time are considered (8, 30).

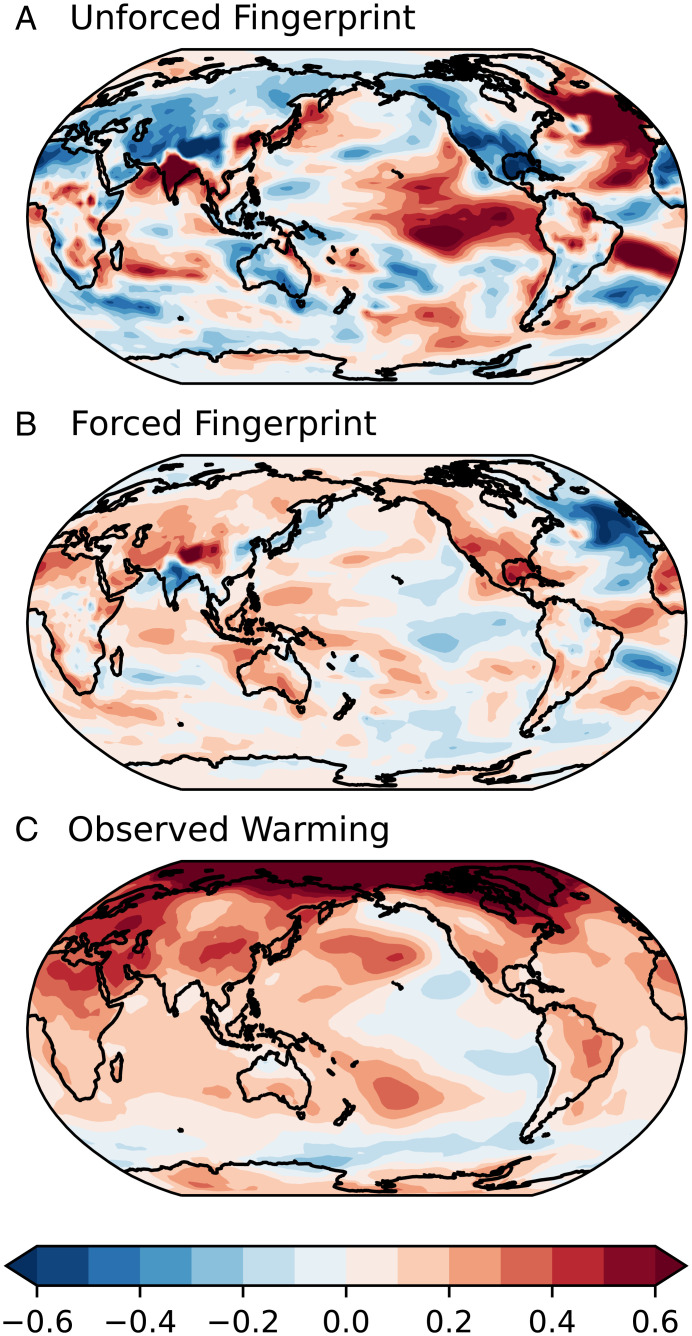
The fitted PLS regression model includes coefficient maps, which we refer to as “fingerprint patterns” (SI Appendix, Extended Methods, Text 1, and Fig. S7) (6, 31, 32). These maps represent the patterns associated with internal variability (Fig. 2A) and the externally forced climate signal (Fig. 2B). The dot product of the normalized surface-temperature trend map (Fig. 2C) and the coefficient maps (Fig. 2 A and B) provides an estimate of the normalized forced or unforced component of the tropical TMT trend (SI Appendix). The unforced fingerprint has large positive coefficient values in the tropical eastern Pacific and north Atlantic. These regions have large internal variability relative to the magnitude of forced surface warming (SI Appendix, Fig. S8). The unforced fingerprint resembles a pattern similar to the El Niño Southern Oscillation and appears to be imprinted on the observed pattern of warming (Fig. 2C and SI Appendix, Fig. S3) (21, 33, 34). The observed cooling in the eastern tropical Pacific strongly projects onto the positive values of the unforced fingerprint in this region and, thus, contributes to a negative value for the unforced component of the tropical TMT trend.

Fig. 2.

Maps of the coefficients that result from PLS regression for the unforced (A) and forced (B) component of tropical tropospheric temperature change. (C) The average (across five different datasets) observed surface-temperature trend map over 1979 to 2014. The coefficient maps displayed in A and B are the averages across each of the 14 leave-one-out predictions. Individual maps are highly correlated (r ≥ 0.96) with the average maps shown in A and B. The units for C are K⋅decade⁻¹; the coefficient maps are unitless, but are multiplied by 250 to conform to the color bar used for C.

The forced coefficient map (Fig. 2B) tends to have the reverse pattern. Positive coefficient values over land areas and the western tropical Pacific are associated with a greater forced component of tropical TMT change and have substantial surface warming relative to the magnitude of internal variability (SI Appendix, Fig. S8). Although the forced fingerprint places the most weight in areas that have a large forced component of warming relative to internal variability, warming in these areas is not isolated from the influence of internal variability. Internal variability is removed from the estimated forced response via negative coefficient values in areas of large internal variability relative to the magnitude of surface warming. This forced fingerprint pattern is qualitatively similar to fingerprints estimated in recent research that quantified the forced component of the global surface-temperature trend, while explicitly considering and accounting for the confounding effects of decadal internal variability (32). We note that our results are robust across different ML methods and a wide range of plausible parameter selections in the ML models (SI Appendix, Text 1 and Figs. S2 and S9–S12).

Implications for Model–Satellite Trend Differences

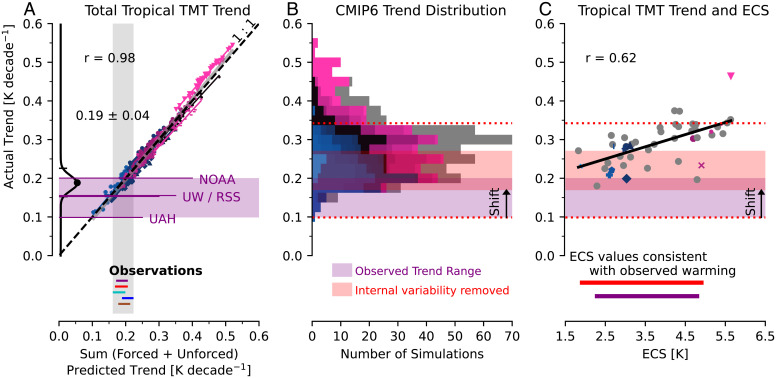
The sum of the predicted forced and unforced TMT trends is an accurate estimate of the total simulated TMT trend (Fig. 3A). This result is unsurprising, given that predictions are based on surface warming. Analyses spanning several generations of GCMs have shown that the total tropical tropospheric warming scales closely with tropical average surface warming across models and timescales (20, 35). Tropical TMT trends are roughly 1.6 times larger than surface-temperature trends as a result of moist thermodynamics (20, 36, 37). In applying our ML model to the observed surface warming, we estimate a total tropical TMT warming rate of 0.19 ± 0.04 K⋅decade⁻¹, which is consistent with the satellite-derived range of warming (0.10 to 0.20 K⋅decade⁻¹).

Fig. 3.

(A) As in Fig. 1, but for the sum of the predicted unforced and the predicted forced tropical TMT trend versus the actual total tropical TMT trend. The satellite-observed range of warming is shaded in purple, and individual observed trends (Materials and Methods) are indicated with four labeled horizontal purple lines (the line length is arbitrary). (B) The distribution of tropical TMT trends (11) with the range of satellite-observed trends shaded in purple. The partially overlapping red shading represents the same observed range of trends, but with the estimated effects of internal climate variability (−0.07 K⋅decade⁻¹) removed via subtraction (the magnitude of this shift is represented with a black arrow). The red dashed lines represent the 95% CIs of the observed trends (after removing internal variability). (C) Model tropical TMT trend versus ECS. For models with more than one simulation, the ensemble average is plotted. The purple and red shading are as described in B. The purple and red horizontal lines represent the range of ECS values from all models that fall within the observed range of trends before and after internal variability is removed, respectively. In each panel, the GCM color codes and markers are the same as in Fig. 1. Gray bars in B and dots in C represent values from 45 different CMIP6 models that did not have at least 10 ensemble members. Note that the y axis is the same across the three panels. In each panel, the tropical averaging is across 30°S to 30°N, and the trend period is 1979 to 2014.

Using SST trend maps as a predictor (rather than maps with combined land-ocean surface temperature changes) yields consistent results, though the uncertainty in the observational prediction is nearly two times larger (0.17 ± 0.07 K⋅decade⁻¹; SI Appendix, Fig. S4). This is consistent with several analyses that have demonstrated that the rate of tropical tropospheric warming in climate-model simulations with prescribed SST changes depends on the pattern of surface warming (11, 36, 37). The pattern and amplitude of tropical SST change varies substantially across observational datasets, leading to a wide range of plausible tropical TMT trends (11, 37). This underscores the importance of further scrutiny of datasets of sea-surface warming to understand and reduce structural uncertainty.

Recent work has shown that tropical sea-surface warming, atmospheric moistening, and tropospheric temperature change are closely interrelated in GCMs (20). Observations of surface warming and atmospheric moistening were most consistent with larger observed tropical TMT trends. Our surface-based prediction of tropical TMT trends is consistent with those findings: Observational datasets with larger tropical TMT trends are in closer agreement with ML results. This conclusion is dependent upon: 1) the accuracy of observations of surface warming and atmospheric moistening; and 2) realistic representation of the coupled relationships between these complementary geophysical fields in GCMs. Further analysis of tropical warming and moistening may help to impose tighter constraints on observational TMT trend estimates.

As noted earlier, relatively few model simulations reproduce the satellite-observed rate of tropical tropospheric warming (Fig. 3B) (11). When we subtract the effect of internal variability (−0.07 ± 0.07 K⋅decade⁻¹) from the observed tropical TMT trend range, the satellite observations are in better agreement with model simulations (compare purple and red shading to GCM histogram in Fig. 3B). The effects of climate variability appear to explain the bulk of the model-versus-satellite tropospheric warming discrepancy.

An alternate explanation for greater-than-observed tropical tropospheric warming is that GCMs are overly sensitive to GHG forcing (10). Consistent with this hypothesis, we find that GCMs with greater surface warming in response to atmospheric CO₂ doubling [referred to as effective climate sensitivity (ECS) (38)] tend to have larger tropical TMT trends (Fig. 3C). We note, however, that models with tropical TMT trends within the envelope of satellite trends have ECS values spanning 2.3 to 4.8 (purple horizontal line in Fig. 3C), a range that is consistent with current best estimates of climate sensitivity (39, 40). Furthermore, when we remove the effects of internal variability, observed tropical TMT trends are compatible with climate-sensitivity values from most models (red horizontal line in Fig. 3C). Given these results, it is difficult to conclude that GCMs have systematic biases in ECS; while such biases may be a factor in model-versus-observed tropospheric warming differences, the effects of internal variability are nonnegligible and must also be considered when attempting to constrain model ECS with historical observations (11, 23).

A Role for Forcing Biases

In CMIP experiments, the external forcing inputs are intended to be uniform for all GCMs. This design is useful for interpreting intermodel simulation differences, which then can be primarily attributed to differences in model formulation. If biases exist in the prescribed inputs, however, there will be systematic errors in model simulations of historical climate change. Biases in the CMIP5 solar, volcanic, and anthropogenic aerosol forcing fields had a significant effect on the simulated evolution of surface and tropospheric warming (15, 41, 42).

Recent research has demonstrated that forcing biases may also influence CMIP6 historical simulations. Specifically, the prescribed aerosol emissions from BB have a spurious increase in interannual variability beginning in 1997, which is accompanied by a substantial increase in downwelling shortwave radiation arising from aerosol–cloud interactions (17). To determine the sensitivity to this BB discontinuity, BB aerosol emissions were temporally smoothed in a targeted Community Earth System Model version 2 (CESM2) experiment. The smoothed BB (SBB) simulation exhibits reduced surface warming relative to the standard unsmoothed simulations, particularly over the northern extratropics. This behavior is in better agreement with surface-temperature observations after 1997 (17, 43). Other models also have substantial increases in downwelling solar radiation during this period, which suggests that this BB aerosol inhomogeneity may systematically enhance the simulated surface warming in CMIP6 GCMs.

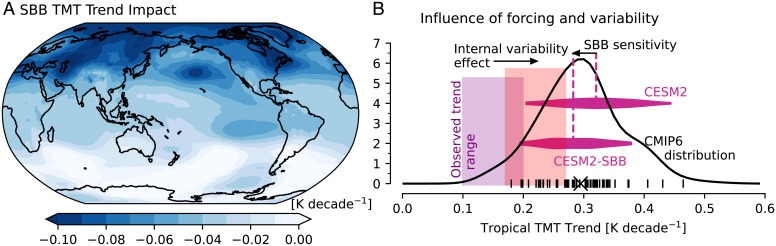
The CMIP6 BB aerosol discontinuity has a nonnegligible effect on TMT trends. Tropospheric warming is reduced in simulations with SBB forcing, particularly over the northern extratropics (Fig. 4A). In the tropics, the TMT trend is reduced by 0.04 K⋅decade⁻¹ in the CESM2-SBB experiment compared to the standard CESM2 simulations (Fig. 4B).

Fig. 4.

(A) TMT trend (1979 to 2014) for the CESM2-SBB ensemble average minus the CESM2 ensemble average. (B) Probability distribution function of tropical (30°S to 30°N) TMT trends for CMIP6 models (black line with units of [K⋅decade⁻¹]⁻¹ corresponding to the y axis). Individual model ensemble averages are denoted by the short vertical lines along the x axis; the “X” denotes the multimodel average). The distributions of CESM2 and CESM2-SBB trends are shown with purple “violin” probability distributions (their vertical position on the y axis is arbitrary). The difference between the CESM2 and CESM2-SBB ensemble average trends represents the effect of BB aerosol forcing artifacts, and the magnitude of this difference is denoted with an arrow labeled “SBB sensitivity.” As in Fig. 3, we subtract the estimated impact of internal variability (−0.07 ± 0.07 K⋅decade⁻¹) from the observed range of trends (purple shading), which has the effect of shifting the observations to the right (red shading). The magnitude of this shift is denoted with an arrow labeled “Internal variability effect.”

The joint effect of this forcing bias (0.04 K⋅decade⁻¹) and the observed manifestation of internal variability (−0.07 ± 0.07 K⋅decade⁻¹) on tropical TMT trends explains a substantial portion of the gap in warming between CMIP6 models and satellite observations. If these joint effects are not accounted for, 12% of all CMIP6 historical simulations considered here have tropical TMT trends within the range of satellite observations (Fig. 4B). Removing the effect of internal variability by subtracting our central estimate of the unforced tropical TMT trend (−0.07 K⋅decade⁻¹) from the satellite observed trends yields a markedly different result: 44% of model simulations have tropical TMT trends below the upper bound of satellite-derived warming. Although the effect of the BB aerosol discontinuity has thus far been assessed in CESM2 only, removing this bias would likely further reduce differences between GCMs and satellite observations. Our results suggest that, in addition to internal variability, uncertainty in prescribed model forcing is an important consideration when evaluating GCMs with satellite observations of tropospheric warming (42, 44).

Summary and Discussion

Estimating the partitioning of forced and unforced changes in climate is challenging, but important for interpreting trends in climate observations and assessing model performance (8, 11, 32, 45). Our study builds on recent research that applies climate-model-based learning and pattern-recognition techniques to the observational record in order to improve understanding of forced and unforced climate change (32, 46–48). Our results indicate that over 1979 to 2014, internal variability offset the forced component of tropical TMT change (0.25 ± 0.08 K⋅decade⁻¹) by 0.07 ± 0.07 K⋅decade⁻¹, which helps to explain why model simulations exhibit larger tropical TMT trends compared to satellite observations. This finding is robust across several different ML models.

Based on CESM2 simulations, it appears that a discontinuity in aerosol forcing from BB also contributes to the apparent model–satellite tropospheric warming discrepancy. This discontinuity spuriously inflates CESM2 tropical TMT trends by 0.04 K⋅decade⁻¹, though the magnitude of this effect remains to be quantified in other GCMs. In addition to model forcing biases and internal variability, GCM response errors and residual satellite biases are also likely to contribute to model-versus-satellite differences in tropospheric warming (9, 49–51).

Our estimate of the effect of internal variability on the observed tropical TMT trend is large. In control simulations with no external forcing, only 4.4% of sampled 36-y time periods (n = 2,205) produce simulated tropical TMT trends with greater cooling than in our estimate of the observed unforced trend (SI Appendix, Fig. S13). This suggests that the observed manifestation of internal variability is relatively extreme compared to estimates of internal variability obtained from climate models. Some studies suggest that internal variability is enhanced by anthropogenic forcing (52–54), though this is not evident in our analysis of 36-y temperature trends (SI Appendix, Fig. S13). Consistent with the control-run results mentioned above, the historical climate simulations on which our ML training dataset is based have relatively few time periods in which internal variability is as large as our central estimate (4.0% of 9,568 sampled time periods; SI Appendix, Fig. S13).

Since our estimate of the forced and unforced components of tropical TMT trends are based on learning from climate models, the paucity of simulated periods with large manifestations of internal variability could limit a precise and accurate prediction of the internal variability component of the TMT trend. The substantial uncertainty (±0.07 K⋅decade⁻¹) in our prediction of the unforced component of TMT is consistent with the possibility that the estimated observed manifestation of internal variability is less (or more) extreme than our central estimate. An alternative explanation for the small percentage of model internal variability estimates rivaling or exceeding the predicted observed component obtained here is that climate models may underestimate observed multidecadal variability (55, 56). While this remains a possibility, some studies show little evidence for a systematic bias in the amplitude of simulated low-frequency variability (57, 58).

The reliability of our partitioning of forced and unforced components of TMT trends ultimately depends on realistic simulation of patterns of climate variability and change. If the true forced pattern of warming more closely resembles the observed trend pattern (e.g., with muted tropical east Pacific warming), then our estimate of internal variability would be exaggerated (59–63). It is therefore important to continue to investigate and improve estimates of the forced pattern of surface temperature change—a challenge, given the uncertainty in historical forcing, structural uncertainty in observations of satellite-era warming (20, 37), and the confounding effects of multidecadal climate variability (11).

Materials and Methods

Model Simulations.

We analyzed output from CMIP6 historical simulations for the time period 1979 to 2014 (64). We augmented CMIP6 data with simulation output from CESM2, which included standard CMIP6 historical simulations and simulations in which the BB aerosol emissions were temporally smoothed (43). Each of these CESM2 experiments included 50 ensemble members; the difference between the ensemble averages was used to determine the sensitivity to treatment of BB aerosols (17). All CMIP6 three-dimensional model temperature fields were converted to synthetic TMT time series by using temperature-weighting functions (SI Appendix). The influence of stratospheric temperature change was removed from the GCM simulations by using a standard regression-based approach (27).

Observations.

Observations of TMT change are based on records from more than a dozen satellites. Distinct efforts to merge these records into a single homogenized dataset have resulted in four independent and up-to-date TMT datasets. These data are from the University of Alabama at Huntsville (UAH), the University of Washington (UW), Remote Sensing Systems (RSS), and the National Oceanic and Atmospheric Administration (NOAA) Center for Satellite Applications and Research (STAR) (65–68). As with the model simulations, the influence of stratospheric temperature change was removed.

Surface-temperature datasets (encompassing land and ocean observations) include the Berkeley Earth Surface Temperature dataset (BEST) (69), the Goddard Institute for Space Sciences Temperature Analysis (GISTEMP) version 4 (70), HadCRUT5 (71), an infilled version of the HadCRUT4 dataset (HadCRUT4-UAH) (72), and version 5 of the ​​European Centre for Medium-Range Weather Forecasts reanalysis (ERA5) (73).

ML Approach.

Our basic approach is to use maps of surface-temperature change (predictors) to predict the 1) internal variability and 2) forced components of tropical TMT change (predictands) using ML. Our primary ML method is PLS regression, which linearly relates predictor maps to predictand trends with coefficient maps (referred to as fingerprint patterns). Each surface-temperature trend map is regridded to a standard 2.5° × 2.5° grid. We first train our ML models using simulation data from all but 1 of the 14 GCMs with at least 10 ensemble members and then attempt to predict the components of tropical TMT change over 1979 to 2014 using surface-temperature trend maps for this period obtained from the GCM not used in training. Training datasets consist of data from 13 (of 14) GCMs, with 10 realizations per GCM and 25 different 36-y time periods per historical realization. Using this leave-one-out approach, we iteratively train and test our ML-based predictions for each of the 14 GCMs. Note that while our training dataset uses 10 ensemble members from each climate model, we apply our ML model to all ensemble members (n ≥ 10) when predicting the forced and unforced component of the tropical TMT trend. For each iteration, we also apply our ML model to observations of surface warming to predict the real-world forced and unforced components of tropical TMT change over 1979 to 2014. These ML-based observational predictions are convolved with model test data to produce an estimate of the central values and uncertainties of observed forced and unforced tropical TMT trends (SI Appendix).

Data, Materials, and Software Availability

All datasets used here are publicly available (see references for further information about individual datasets). The processed data (https://doi.org/10.5281/zenodo.7199961) and software (https://github.com/LLNL/MDAS) are also freely available via public archives (74, 75).