Selective sweeps in SARS-CoV-2 variant competition

Significance

The main contribution of this paper is to show that the transition from one SARS-CoV-2 variant to the next is mathematically equivalent to a selective sweep, which follows the logistic equation. Data show that this prediction is accurate. The increase in fitness from one variant to the next has two components: the increase in transmissibility and the contribution of breakthrough infections. This predicts that future dominant strains will be the ones that best evade immunity.

Abstract

The main mathematical result in this paper is that change of variables in the ordinary differential equation (ODE) for the competition of two infections in a Susceptible–Infected–Removed (SIR) model shows that the fraction of cases due to the new variant satisfies the logistic differential equation, which models selective sweeps. Fitting the logistic to data from the Global Initiative on Sharing All Influenza Data (GISAID) shows that this correctly predicts the rapid turnover from one dominant variant to another. In addition, our fitting gives sensible estimates of the increase in infectivity. These arguments are applicable to any epidemic modeled by SIR equations.

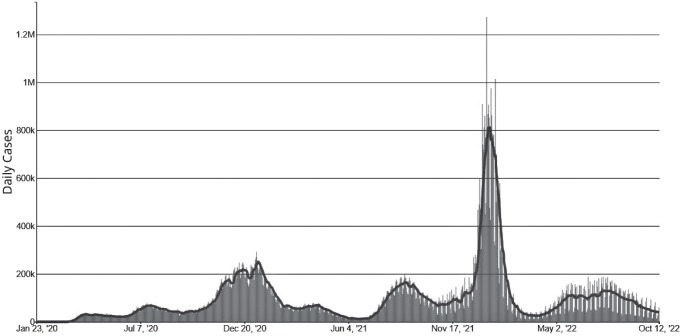
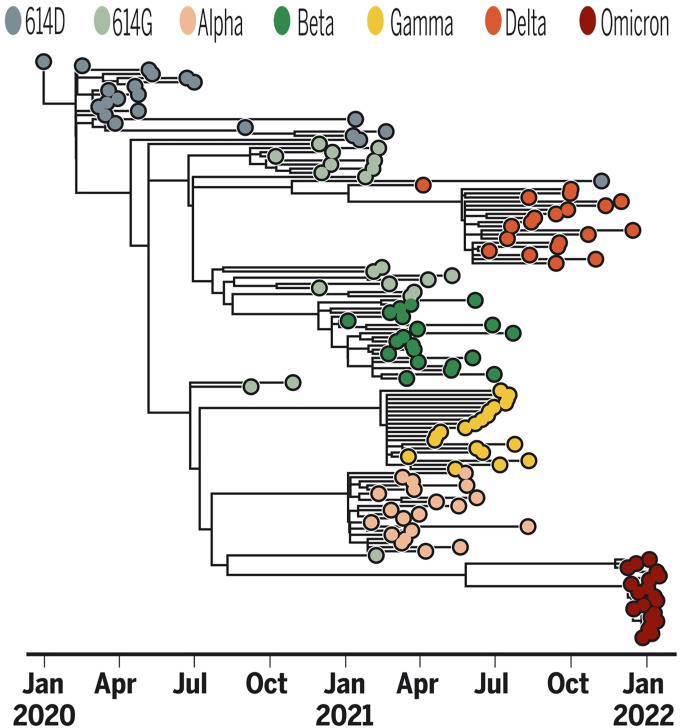
As most readers know, the COVID-19 pandemic began in China in December 2019, then slowly spread around the world. By early 2022, there had been more than 400 million infections worldwide and almost 6 million deaths. The first confirmed case of COVID-19 in the United States was diagnosed in Washington state on January 21, 2020. On February 11, 2020, the disease was officially named “severe acute respiratory syndrome coronavirus 2” (SARS-CoV-2) because the virus is genetically related to the coronavirus responsible for the SARS outbreak of 2003. The early spread of the virus is an interesting topic. Work done by Alessandro Vespignani’s group (1) suggested that on March 1, 2020, when New York recorded its first case and there were only 23 confirmed cases in the United States, there could have actually been about 28,000 infections nationwide and 10,700 in New York. Many papers have been written on the effects of interventions such as masking, lockdowns, and social distancing to control the spread of the disease. Here, we will concentrate on the evolution of the virus, primarily focusing on the changes in the spike protein, which the virus uses to gain entry into cells through binding to the ACE2 surface protein. (For a detailed description of this process, see refs. 2 and 3.) Figure 1 shows the rise and fall of variants over time. Figure 2 indicates their phylogenetic relationship.

Fig. 1.

Epidemic waves in the SARS-CoV-2 pandemic. From left to right: Beta, Delta, early Omicron variants, and Omicron BA.4/BA.5. Graphic is from The New York Times, July 18, 2002.

Fig. 2.

SARS-CoV-2 variant phylogeny from ref. 4.

Early Evolution

The article by Koelle et al. (4) gives a nice account of the evolution of the virus up to the end of February 2022. An early mutation in the spike protein was a glycine residue, G, replacing an aspartic acid residue, D, at position 614, or G614D for short. (There are 20 amino acids, each abbreviated to a single letter, but the exact coding is not important for our purposes.) This dramatically increased the ability of the original Wuhan strain to infect cells.

The Alpha variant (named B.1.1.7 for its position in the phylogenetic tree of samples) was identified in the United Kingdom in September 2020. It had enhanced binding to ACE2 and spread 50% faster than circulating lineages. Around the same time, Beta (B.1.351) was found in South Africa, and a highly transmissible variant, Gamma, arose in the Amazonas state in Brazil.

The Delta variant was identified in India’s Maharashtra state in Spring 2021. It had additional mutations that increased the ability of the spike protein to infect cells, resulting in increased transmissibility, disease severity, and breakthrough infections in vaccinated individuals (5, 6). A notable example is the P681R mutation, located at a furin cleavage site that separates the spike protein into S1 and S2 subunits (7). A second is the L452R mutation in the receptor binding domain of the spike protein (8), which is involved in evasion from neutralizing antibodies. Once Delta arrived in the United Kingdom, it spread quickly, and epidemiologists determined that it was about 60% more transmissible than Alpha. In vitro, it is 6 times less sensitive to serum-neutralizing antibodies from recovered individuals compared to the wild-type Wuhan-1 bearing D614G. It swept through India and Great Britain before reaching the United States, where it surged from being 1.3% of variants on May 2, 2021, to 94.4% on July 31.

Omicron Subvariants

Two articles by Ewen Callaway (9, 10) give an excellent account of this phase of the epidemic. Omicron (B.1.1.529) was first reported in South Africa in November 2021. It has 37 mutations in the spike protein relative to the original Wuhan strain. Among these mutations, 15 were in the receptor binding domain, increasing its binding efficiency to ACE2 (11). An early article (12) suggested that the most recent common ancestor of Delta and Omicron went back to the beginning of the pandemic, but the picture changed when Omicron was realized to be a close relative of Gamma.

After a period of using Greek letters to mark significant changes in the virus, the system broke down when a large number of Omicron variants started appearing. See ref. 13 for the story behind the names. The initial variant, now referred to as BA.1, has continued to evolve, creating two sublineages: BA.1.1 = BA.1 with an R346K mutation and BA.2. The BA.2 subvariant spreads more quickly than BA.1. Two laboratory studies have shown that antibodies against BA.1 can protect against BA.2 infection, but they have similar abilities to resist neutralizing antibodies in the blood of individuals that have been vaccinated or infected (10, 14). For the reader who is interested in the mutations found in the early Omicron variants, see ref. 15 for an analysis of 6.4 million sequenced genomes.

Studies by virologists Michael Chan at the University of Hong Kong and Wendy Barclay at Imperial College London have shown that BA.1 and BA.2 create a higher concentration of viral particles in the nose. In earlier variants, after SARS-CoV-2 binds to ACE2, it relies on a cellular enzyme, TMPRSS2, to cleave the spike protein, granting the virus entry into the cell, but Omicron has largely abandoned this route. This could give Omicron an edge, since many cells in the nose do not make this enzyme, which is more widely expressed in the lung and other organs (16).

Omicron Subvariants.

BA.4 and BA.5.

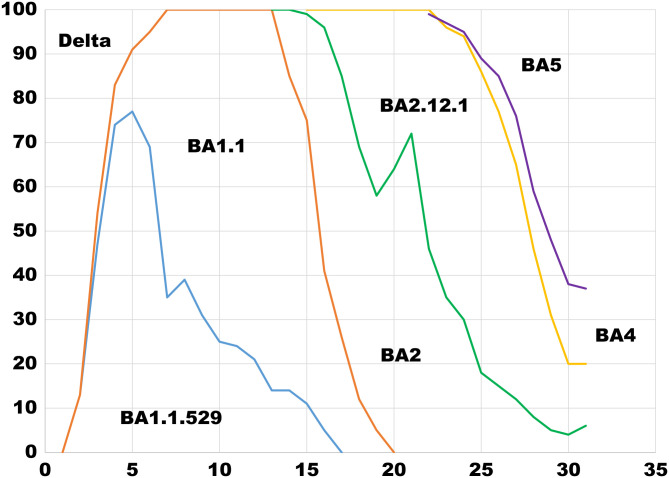
The earliest samples of variants BA.4 and BA.5 were collected in January 2022 in South Africa. Generally, they cause mild disease, but spread in large numbers potentially because, unlike the Wuhan strain, which settles in the lungs, these new variants seem to attach to the more benign upper nasal passage. The incubation time of these new variants is significantly shorter (2 to 3 d), and they seem to undergo mutational sprints, mutating as much as 4 times faster than normal Omicron. Like earlier Omicron variants, they have a remarkable ability to evade immunity from vaccines, previous infection, or both (17–19). Figure 3 shows the rise and fall of Omicron variants over time.

Fig. 3.

Weekly Omicron variant frequencies in North Carolina during June 26 through July 9, 2022. Data are from the North Carolina COVID-19 Dashboard.

Results

We use a traditional Susceptible–Infected–Removed (SIR) epidemic model in a homogeneously mixing population. In many models, 1) an Exposed phase is included, in which individuals have the disease, but are not yet infectious; and 2) the population is divided into a half-dozen groups according to age (20–22). However, we choose the simplicity of the SIR model in order to easily make clear mathematical statements that reveal the dependence of the observed phenomena on underlying parameters.

To get rid of the population size from the SIR equations, we rewrite them in terms of the scaled variables $s=S/N,\hspace{0.17em}{i}_j=I_j/N$, and $r=R/N$. Generalizing the basic model to the competition of two infections, we can write the differential equations as

$$\begin{array}{l}\frac{ds}{dt}=-{\beta }_{1}s{i}_1-{\beta }_{2}s{i}_2\\ \frac{d{i}_1}{dt}={\beta }_{1}s{i}_1-\gamma i_1\\ \frac{d{i}_2}{dt}={\beta }_2(s+\theta r_1)i_2-\gamma i_2\\ \frac{d{r}_1}{dt}=\gamma i_1-\theta r_1{i}_2\\ \frac{d{r}_2}{dt}=\gamma i_2.\end{array}$$ [1]

Here, infecteds of type i at rate β_i attempt to infect a randomly chosen individual from the population. Individuals recovered from infection by strain i are immune to further infection by that strain. θ is the reduction in the infection rate by strain 2 of an individual immune to strain 1.

In Materials and Methods, we will show that the fraction of individuals infected with strain 2, $x(t)=i_2(t)/(i_1(t)+i_2(t))$, satisfies a logistic differential equation,

$$\begin{array}{l}x\prime (t)=\hspace{0.17em}\lambda (t)x(t)(1-x(t))\\ \lambda =\hspace{0.17em}({\beta }_2-{\beta }_1)s(t)+\theta {\beta }_2{r}_1(t).\end{array}$$ [2]

When $\lambda (t)$ is constant, this models a selective sweep, in which an advantageous mutation increases in frequency and eventually takes over the population (23). To simplify the formulas, we assume that the recovery rates are equal for the two strains. If they are different, then ${\gamma }_1-{\gamma }_2$ is added to the formula for $\lambda (t)$.

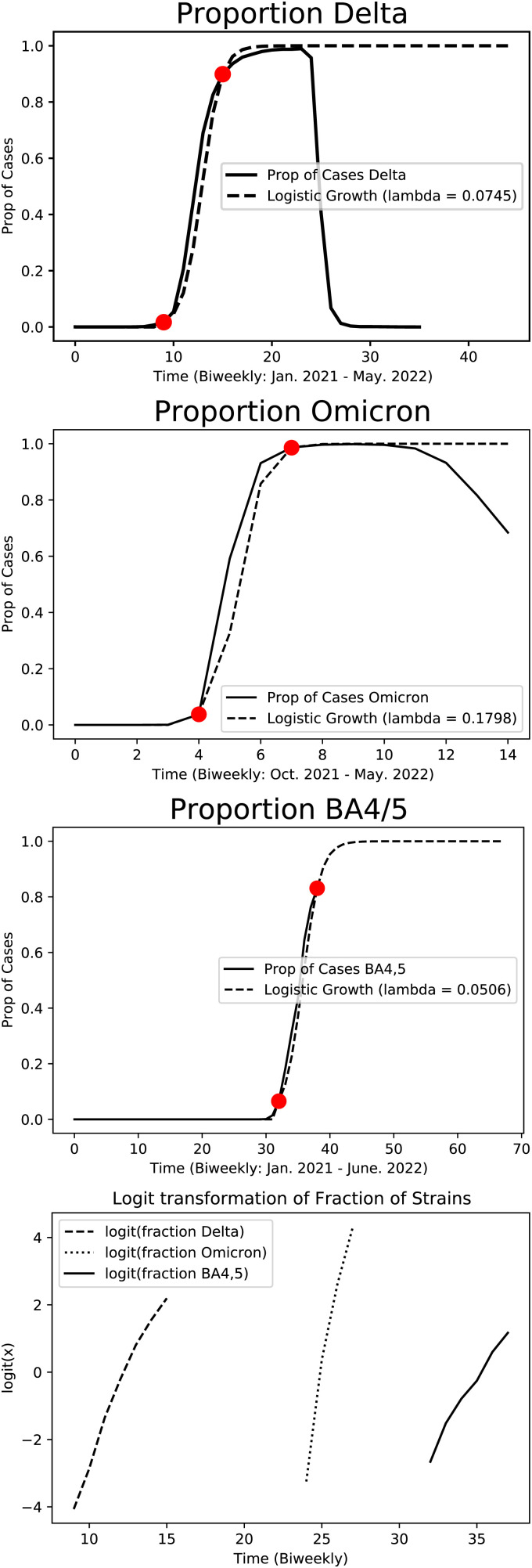
To test this prediction, we used SARS-CoV-2 variant data from the Global Initiative on Sharing All Influenza Data (GISAID) to fit our model (24). These data consisted of biweekly SARS-CoV-2 variant cases in the United States from the period between December 12, 2021, and June 13, 2022. For each transition—Beta to Delta, Delta to Omicron, and Omicron to BA.4/BA.5—we fit the logistic differential equation to data points at the beginning and end of each selective sweep curve (Table 1).

Table 1.

Estimates of λ

Transition	λ
Beta to Delta	0.0745
Delta to Omicron	0.1798
Omicron to BA.4/BA.5	0.0506

The increase in infectivity in the Delta to Omicron transition is much larger than Beta to Delta due to breakthrough infections. The increase from Omicron to BA.4/BA.5 is the smallest, since the Omicron subvariants are more similar than Beta and Delta. Another contributing factor is that the size of the susceptible population was decreased by the first Omicron wave.

In fitting the data, we have assumed that $\lambda (t)$ is constant. The selective sweeps pictured in the top three panels of Fig. 4 took from 6 to 10 wk, so the values of $s(t)/s(0)$ and $r_1(t)/r_1(0)$ should not have changed by much over the course of the sweep, but perhaps this is the source of the departure from linearity seen in the bottom panel.

Fig. 4.

The top three panels show logistic fits to COVID variant transitions. If the fraction of cases due to the new variant, x(t), was the solution of a logistic equation, then $\log (x(t)/(1-x(t))$ would be linear. In the bottom panel, we plot this transformation of the three curves. The resulting plots are approximately linear with R² values 0.98, 0.97, and 0.98, respectively.

Discussion

Our results in Fig. 4 show that the rapid turnover from one variant to another follows the solution to the logistic differential equation. The formula for the fitness advantage λ given in Eq. 2 has two terms:

• •$({\beta }_2-{\beta }_1)s(t)$ is the increased infection rate of strain 2;
• •$\theta {\beta }_2{r}_1(t)$ is the contribution of breakthrough infections.

There have been a number of mutations that have significantly improved the ability of SARS-CoV-2 to infect humans. It is natural to expect that, as time goes on, such gains will become even smaller, since the spike protein has explored the space of possibilities. Thus, given our formula for $\lambda (t)$, strains that become dominant will need to evade existing immunity. Experts agree with this conclusion (9). Sarah Cobey, an evolutionary biologist at the University of Chicago, stated: “As gains in infectivity start to slow, the virus will have to maintain its fitness by overcoming immunity.” Kristian Andersen of Scripps Research stated: “Variants such as Omicron that gain much of their transmission advantage from evading immune response may become the norm, as is the case for seasonal influenza.”

Given the similarities (and differences) with the flu, it is an important problem to understand the mechanisms of immune evasion in SARS-CoV-2 in order to predict its future evolution. Readers who want to tackle this problem should look at the excellent work of Dushoff, Levin, and Plotkin (25, 26) on influenza.

Materials and Methods

Here, we derive the result given in Eq. 2. Let $x(t)=i_2(t)/(i_1(t)+i_2(t))$. To prepare for the change of variables, we note that

$$\left(\frac{i_2}{i_1+i_2}\right)\prime =\frac{i_2\prime (i_1+i_2)-i_2(i_1\prime +i_2\prime )}{{(i_1+i_2)}^2}=\frac{i_2\prime i_1-i_2{i}_1\prime }{{(i_1+i_2)}^2}.$$

Using this in Eq. 1, we get

$$\begin{array}{l}x\prime (t)=\frac{i_2}{i_1+i_2}·\frac{i_1}{i_1+i_2}·\left(\frac{i_2\prime }{i_2}-\frac{i_1\prime }{i_1}\right)\\ =\frac{i_2}{i_1+i_2}·\frac{i_1}{i_1+i_2}·[({\beta }_2-{\beta }_1)s+\theta r_1(t)],\end{array}$$

writing $\lambda (t)=({\beta }_2-{\beta }_1)s(t)+\theta {\beta }_2{r}_1(t)$. This is a logistic differential equation, with carrying capacity K = 1 and a temporally varying growth rate:

$$x\prime (t)=\lambda (t)x(t)(1-x(t)).$$

Data Availability

Previously published data were used for this work (GISAID database) (https://gisaid.org/).