Calculation of centralities in protein kinase A

Significance

Protein structures can be viewed as networks of residues. Analysis of these networks can reveal roles of single amino acids. We introduce a new method to generate such networks and compare it to several traditional approaches. We tested these methods to see if they can detect residues in protein kinase A that are known to play functional and regulatory roles. We show that our method can reliably separate a large group of such residues from the rest of the molecule. In comparison, the traditional methods were much less efficient. As our method uses a new definition of links in residue networks, our results can be important for network analysis of proteins in general.

Abstract

Topological analysis of protein residue networks (PRNs) is a common method that can help to understand the roles of individual residues. Here, we used protein kinase A as a study object and asked what already known functionally important residues can be detected by network analysis. Along several traditional approaches to weight edges in PRNs we used local spatial pattern (LSP) alignment that assigns high weights to edges only if CαCβ vectors for the corresponding residues retain their mutual positions and orientation. Our results show that even short molecular dynamic simulations of 10 to 20 ns can give convergent values for betweenness and degree centralities calculated from the LSP-based PRNs. Using these centralities, we were able to clearly distinguish a group of residues that are highly conserved in protein kinases and play important functional and regulatory roles. In comparison, traditional methods based on cross-correlation and linear mutual information were much less efficient for this particular task. These results call for reevaluation of the current methods to generate PRNs.

Complex networks are ubiquitous and are studied by diverse fields of science, from physics and biology to sociology and cosmology. Complex networks, unlike random networks or regular lattices, have a modular distribution of their elements (1). Such structural heterogeneity implies that different elements of complex networks have different “importance”. That brings up a graph theoretical problem of network centrality, that is, metrics that can quantify this importance. Obviously, the definition of “important” elements depends on the context. It can be super spreaders in a pandemic (2), vulnerability points of transportation networks (3), or essential proteins in a metabolic pathway map (4). First attempts to analyze connectivity in social networks were made as early as the 1950s and 1960s (5, 6), but the concept of centrality was clarified and formalized in a set of influential papers by Freeman and coworkers in the 1980s (7–9). Since then, multiple centrality measures have been introduced and analyzed in different networks; however, there is no consensus on what centralities should be used for different networks (10). For example, it was shown that centrality measures can be correlated or not correlated depending on the nature of the network (10, 11). It is, therefore, important to study networks on a case-by-case basis with proper benchmark data that can serve as a guide for the selection of efficient centrality metrics.

Protein structures can be represented as graphs in many different ways (12). Nodes are usually associated with residues, and links between them are created if the residues are within a predefined distance. Such protein residue networks (PRNs) can be created from a single structure (SS) or from multiple structures generated by molecular dynamics (MD) simulation. Links in the networks can be weighted using different approaches, such as estimated energy of interaction (13), average number of contacts (14), their frequency (15), or the absolute value of cross-correlation (CC) between α carbon coordinates (16–18). Treating anticorrelation as correlation is usually justified by the argument that the sign of interaction between residues is not important if information is transmitted between them. A similar argument was made when mutual information was introduced as a measure for interaction between residues in proteins (19). Mutual information is currently widely used in protein network studies (20–22).

Different centralities have been reported to be useful for the analysis of different protein properties. It was shown that closeness centrality (CL) can detect residues that are critical for folding of chymotrypsin inhibitor 2 and the SH3 domain of C-Src kinase (23). A study of 178 protein structures, including ERK2 MAP protein kinase, showed that active-site residues have higher CL but not degree centrality (DC) (24). Another work, confirming a high level of CL of active-site residues was done using structures of 46 different families of proteins (25). A study of voltage-gated sodium channel NaV1.7 showed that residues related to gain-of-function mutations are associated with significant changes of their betweenness centrality (BC) but not their CL, DC, or eccentricity (26). A computational study of the Hsp90 chaperone found that residues with high BC are implicated in allosteric communication within the molecule (27). Similar results were reported for G protein–coupled receptor A2AAR (28). The authors found that BC was significantly more effective in detecting functionally important residues than degree or CLs. Several other works concluded that BC was a good metric to study allosteric signaling (16, 29–31). A study of allostery in imidazole glycerol phosphate synthase showed that eigenvector centrality (EG) can detect regions responsible for allosteric communication (22).

In this paper, we studied PRNs of protein kinase A (PKA) generated by several popular methods and evaluated the ability of different centrality measures to detect residues that are known to be important for protein kinase function and its regulation. The selection of PKA as an object for this study was dictated by three reasons. First, protein kinases represent one of the largest and crucially important protein families (32) that makes kinases attractive therapeutic targets (33). Understanding the mechanism of their function and regulation is essential for the rational design of protein kinase inhibitors. Second, protein kinases are dynamic molecules that switch between active and inactive conformations in response to extracellular signals (34). Often, their function can be modified by distant effects when a small inhibitor or another protein binds far from the active site (35–37). Such long-distance signaling, known as allostery, is a universal feature in molecular biology (38, 39). Understanding regulatory mechanisms in protein kinases can also be beneficial for studies of other allosteric enzymes. Third, PKA is, arguably, the most studied protein kinase with a large volume of experimental data accumulated in the past 30 years (40, 41). Therefore, it is easy to create a benchmark for this study, as a large set of key residues that play important functional and regulatory roles are well known.

We compared nonweighted PRNs created from a single protein structure (SS) and PRNs generated from MD simulations (NW). Three different weighting methods were also used for MD simulation–based PRNs: the absolute value of CC, linear mutual information (LMI), and local spatial patterns (LSP) alignment. The latter is a method we developed earlier to discover nonsequential structural motifs conserved in all eukaryotic protein kinases (42, 43). These motifs known as “hydrophobic spines” have been shown to serve as major connectors in protein kinases that are important for their function and regulation (35, 41, 44, 45). Our results indicate that BC was the most efficient metric to detect critical connections in PKA. Unexpectedly, CC- and LMI-based PRNs were less effective than binary (NW) PRNs or even PRNs based on a SS. At the same time, LSP-based PRNs proved to be significantly more informative. Possible explanations and further recommendations for the network analysis of protein kinases and proteins in general are discussed.

Results

Selection of Key Residues.

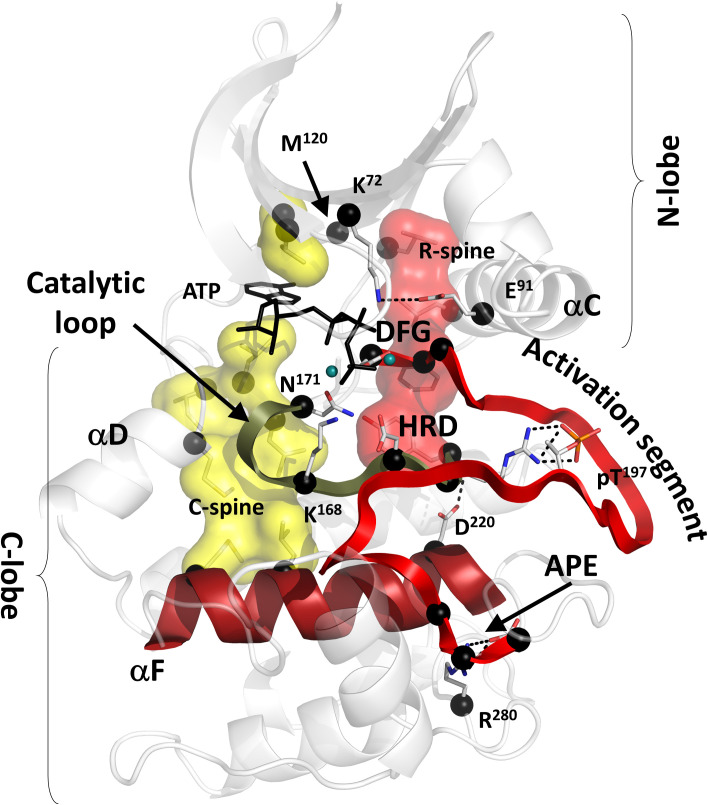
To estimate the efficiency of different metrics in detecting the essential residues of PKA, we selected 26 key residues that are highly conserved in the protein kinase family and are known to be involved in different catalytic and regulatory functions (Fig. 1 and Table 1). Twelve out of 26 residues are known as hydrophobic spine residues (shown on Fig. 1 as transparent surfaces). These nonsequential motifs connect two lobes of the protein kinase molecule, spanning it from the αF-helix in the center of the C-lobe to the rigid sheet in its N-lobe. It is well known that their assembly and stability are vital for protein kinase dynamics, function, and allosteric communication (46–53). As the spines are important connectors, we expected them to be detected by topological analysis of PRNs. Two other residues, K72 and E91, are known to be critical connectors between the sheet of the N-lobe and mobile αC-helix. Universal conservation of these residues was discovered very early (54), and the salt bridge formed by them is considered to be a signature of an active protein kinase conformation (41). Other, highly conserved residues were included in the set to test if they can be detected by the topological analysis. These residues include the Asp-Phe-Gly (DFG) motif in the activation segment and the His-Arg-Asp (HRD) motif, K168, and N171 in the catalytic loop (Fig. 1). These residues are known to be indispensable for catalysis, and their mutations impair protein kinase function (55–57). Another universally conserved motif, Ala-Pro-Glu (APE), is positioned at the end of the activation segment (54). A206 and P207 bind to the αF-helix and serve as an anchor for the substrate binding loop (58). E208 is bound to another universally conserved arginine R280 in the αH-αI loop. The E208–R280 salt bridge was shown to be an important part of the C-lobe that determines its stability (59) and can alter protein–protein interactions (60). R280 was also included in the key residues set.

Fig. 1.

Conserved core of the eukaryotic protein kinases with the 26 preselected key residues (black spheres). The core consists of two lobes: N-lobe and C-lobe. ATP (shown as black sticks) is sandwiched between the lobes bound to two magnesium ions (teal spheres). Two hydrophobic ensembles C-spine (yellow surface) and R-spine (red surface) span the core, providing global connectivity within the molecule. The DFG motif and APE motif are flanking the activation segment (red ribbon). The HRD motif is a part of the catalytic loop (olive ribbon). Both spines are anchored to the αF-helix (dark red) that spans the C-lobe and serves as a foundation for the catalytic machinery of the kinase. Additional description of the selected key residues is provided in the Table 1.

Table 1.

Description of the 26 key residues selected for centrality scoring presented in Fig. 1

Residue	Motif	Function
V57	Catalytic spine	Serves as a terminal residue in the catalytic spine (42). Binding ATP to this residue leads to global allosteric effects (96).
A70	Catalytic spine	Serves as a terminal residue in the catalytic spine (42). Binding ATP to this residue leads to global allosteric effects (96).
K72	Lys-Glu bridge	Positions α- and β-phosphates of ATP, binds to the conserved E91 providing critical connectivity in the kinase (97).
E91	Lys-Glu bridge	Binds to the conserved K72 providing critical connectivity in the kinase (97).
L95	Regulatory spine	Serves as an intermediate residue in the regulatory spine, a hallmark of active kinases (41, 42).
L106	Regulatory spine	Serves as a terminal residue in the regulatory spine, a hallmark of active kinases (41, 42).
M120	The gatekeeper	A part of ATP-binding pocket. Its mutation can lead to a major change in connectivity in kinases and causes their constitutive activity (45).
M128	Catalytic spine	Provides connectivity between two lobes of the kinase (42).
Y164	H/YRD motif, regulatory spine	Serves as a terminal residue in the regulatory spine, a hallmark of active kinases (41, 42).
R165	H/YRD motif	Binds to the primary phosphate in kinase activation loop stabilizing active conformation (98). Harbors multiple disease-related mutations (99).
D166	H/YRD motif	The catalytic residue plays a critical role in phosphotransfer (100). Harbors multiple disease-related mutations (99).
K168	Catalytic loop	The catalytic residue plays a critical role in phosphotransfer (100). Binds to the γ-phosphate of ATP and performs multiple function (101).
N171	Catalytic loop	Coordinates catalytically important atom of magnesium. Harbors multiple disease-related mutations (99).
L172	Catalytic spine	Serves as an intermediate residue in the catalytic spine (42, 99).
L173	Catalytic spine	Serves as an intermediate residue in the catalytic spine (42). Binding ATP to this residue leads to global allosteric effects (96).
L174	Catalytic spine	Serves as an intermediate residue in the catalytic spine (42).
D184	DFG motif	Coordinates catalytically important atom of magnesium.
F185	DFG motif, regulatory spine	Serves as an intermediate residue in the regulatory spine, a hallmark of active kinases (41, 42).
G186	DFG motif	Provides flexibility of the DFG motif during the transition between active and inactive states (41).
A206	APE motif	Serves as a connector in the C-terminal lobe of the kinase molecule.
P207	APE motif	Serves as a connector in the C-terminal lobe of the kinase molecule.
E208	APE motif	Serves as a connector in the C-terminal lobe of the kinase molecule. Its mutation leads to a decrease in PKA catalytic efficiency (58).
D220	αF-helix/regulatory spine	Anchors the regulatory spine to the αF-helix that serves as a scaffold for the kinase molecule (42).
L227	Catalytic spine	Serves as a terminal residue in the catalytic spine (42).
M231	Catalytic spine	Serves as a terminal residue in the catalytic spine (42).
R280	APE motif binding partner	Conserved binding partner for E208 from the APE motif. Its mutation causes long distance destabilization of the kinase (58).

Scoring of Key Residues.

We used four popular centrality measures: DC, BC, CL, and EG to analyze a set of PRNs created from a SS of PKA and multiple structures generated by MD simulations of different lengths. Key scores were a sum of the corresponding centrality values for the 26 key residues as a percentage of the centrality values sum for the molecule. We did not expect all 26 residues to be detected by the protein topology analysis, as their strict conservation in kinases can be dictated by different reasons related to the kinase topology or not. However, we anticipated that this approach can be helpful for comparative purposes between different topological metrics. If a metric would score residues randomly, the accumulated score for 26 residues should be ∼8% of the total score for the kinase molecule with 336 residues. We, thus, suggested that metrics that can detect important residues should score the selected key residues higher than 8%.

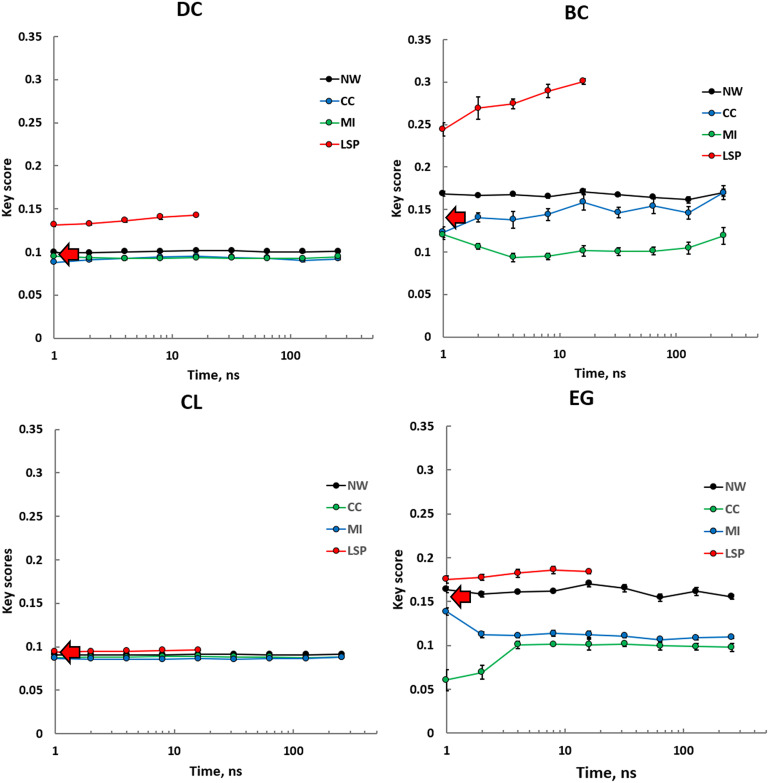
Our first goal was to test how key scores calculated from MD-based PRNs are different from key scores from an SS PRN and if there is a computationally feasible time scale when key scores for different centralities converge to stable values. It should be noted that due to the high computational cost of the LSP-based method, the corresponding trajectories were limited to 16 ns. Almost all PRNs and metrics appear to give stable and convergent key scores in a wide range of trajectory lengths, from 1 ns to 256 ns. In several cases, however, trajectories shorter than 10 ns showed certain drift and increased noise of the key scores. We, thus, concluded that MD trajectories of about 10 ns in length can give reliable values of the key scores, and longer simulations do not provide any significant advantages for our purpose. Surprisingly, PRNs with edges weighted by traditional CC and LMI methods performed, almost universally, worse than NW PRNs or even SS-based PRNs (Fig. 2). Interestingly, the latter was nearly as efficient as NW PRNs in all studied time scales. LSP-based PRNs proved to be significantly more efficient especially for BC and DC metrics.

Fig. 2.

Key scores calculated using four different centrality metrics, DC, BC, CL, and EG, for different types of PRNs, binary PRNs with no weights assigned to the edges (NW), and three different weighting methods, CC, LMI, and LSP alignment. Calculations were repeated five times using consecutive intervals of MD trajectory of varying length (x axis). SE values are shown. Key scores calculated from an SS are shown as red arrows.

Comparison of different metrics showed that CL was the least effective in separating 26 key residues from the rest of the molecule. All PRNs and all MD simulation durations, including SS-based PRN, gave CL key scores between 8 and 9%, suggesting that random selection of 26 residues from PKA would be equally efficient. As the LSP-based PRNs were constructed using a larger ΔCαα cutoff level (12 Å; Materials and Methods and SI Appendix, Fig. S1) than the rest of the PRNs (8 Å), we questioned if the other PRNs could benefit from the increased ΔCαα. Our results, however, showed that the increase of the key score levels for ΔCαα = 12 Å was either incremental or had a negative effect (SI Appendix, Fig. S2).

Analyzing Centralities for the Whole Protein.

So far, our evaluation of the different centralities and methods to generate PRNs was based on a hypothesis that efficient metrics should distinguish at least some of the 26 key residues from the rest of the molecule. Obviously, not all of them are conserved or known for their functional roles due to their central positions in graph-theoretical sense. Equally, there may be residues that play important topological roles but are still unknown. To evaluate the efficiency of our approach, we analyzed different centralities for the whole PKA molecule.

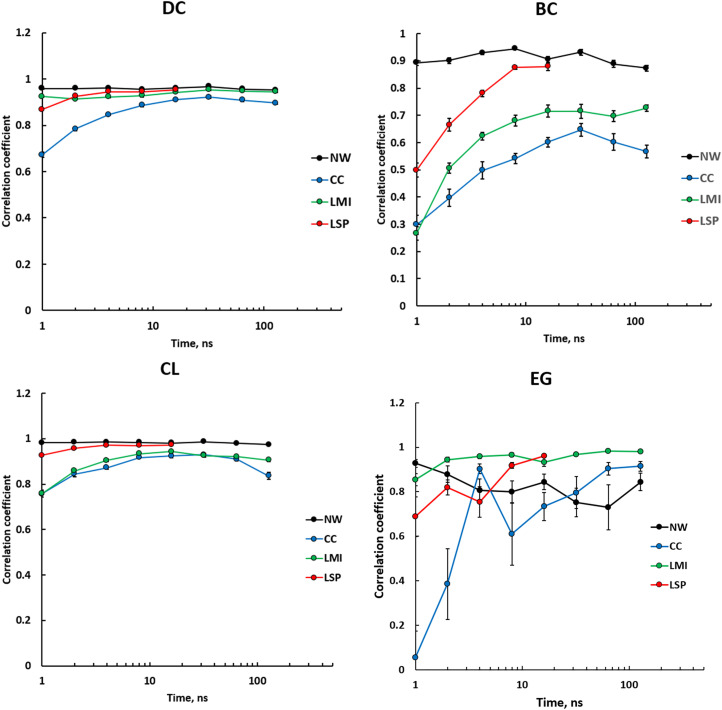
First, we wanted to know how convergent the centrality values generated by different metrics are. Fig. 3 shows average correlation coefficients between centralities calculated from five consecutive intervals of varying length. DCs and CLs had a rather high level of convergence for all types of PRNs, particularly with trajectory length of around 10 ns and longer. BC for NW PRNs had very high convergence for all time scales. Weighted PRNs showed low consistency at short intervals that increased rapidly and plateaued after 10 ns. LSP-based PRNs showed a significantly higher level of consistency and reached the level for NW-based PRNs at the 16-ns point. CC and LMI-based PRNs gave lower convergent values of BC. EG provided the least consistent values with an exception for LMI-based PRNs.

Fig. 3.

Average correlation coefficients between centralities calculated for 336 residues of PKA from five consecutive intervals of varying length. DC, BC, CL, and EG are based on the first eigenvector for different types of PRNs, NW weighted by CC, LMI, and LSP alignment. SE values are shown.

Second, we questioned how similar are the centrality values calculated from different PRNs for the whole molecule? We calculated correlation coefficients between four different centralities in an SS PRN and four MD-based PRNs taken at 16 ns. Earlier, we observed that key scores for a single PKA structure and for NW PRNs were very close (Fig. 2). Consistently, correlations for these PRNs that included all 366 residues were very high for all four centralities (Table 2). Similarly, whole-molecule CLs for all PRNs were roughly identical. DC correlations were rather high for all PRNs, with the LSP-based PRN being the most distinctive. A similar trend was observed for the BC; the LSP-based PRN had the most distinctive values of DC. EG values for SS, NW, and LSP-based PRNs were rather similar to the CC and LMI-based PRNs and were mostly uncorrelated, with a surprisingly high correlation between CC and LMI-based PRNs.

Table 2.

Correlation coefficients between four different centralities for 336 residues of PKA calculated in PRNs based on an SS, NW PRN (NW), and PRNs weighted using CC, LMI, and LSP alignment (LSP)

	SS	NW	CC	LMI
DC
NW	0.91
CC	0.72	0.85
LMI	0.80	0.93	0.97
LSP	0.67	0.75	0.66	0.65
BC
NW	0.84
CC	0.58	0.71
LMI	0.43	0.50	0.68
LSP	0.38	0.47	0.48	0.18
CL
NW	0.97
CC	0.88	0.91
LMI	0.82	0.84	0.94
LSP	0.84	0.89	0.87	0.73
EG
NW	0.75
CC	−0.25	0.27
LMI	−0.25	0.29	0.98
LSP	0.78	0.55	−0.21	−0.21

Sixteen-ns trajectories were used for the MD simulation–based PRNs.

Third, to evaluate the validity of the key score–based method for different PRNs, we visualized the data on scatter plots showing BC versus DC. This choice was dictated by several reasons. First, these centralities are the most fundamental metrics that reflect qualitatively different features of a network; DC is a local characteristic, and nodes with high DC values are local “hubs”, while BC is a global network parameter, and high BC characterizes global “bottlenecks”. This approach is similar to the so-called “functional cartography” approach proposed by Guimerà and Amaral for classification of nodes in complex networks (61). This method was successfully used for protein molecules to identify residues important for allosteric signaling (62–64). The cartography method also characterizes network nodes with respect to their hub and bottleneck characteristics. However, instead of using DC and BC values directly, it separates the network into modules and evaluates the nodes with respect to their role in the correspondent modules: module component (partition coefficient) or a connector between modules (intercluster connectivity). Our preliminary analysis showed that in our case, almost all residues fell into categories of “nonconnectors” and “nonhubs”, although several key residues scored relatively high with respect to the rest of the molecule (SI Appendix, Fig. S3). Similar concepts were used in protein interaction networks in yeast where concepts of “date-hubs” and “party-hubs” were introduced (65). The former are nodes with high BC and high DC levels, while the latter are nodes with low BC but high DC values. Such distinction proved to be useful in the characterization of protein essentiality and expression dynamics (4, 66).

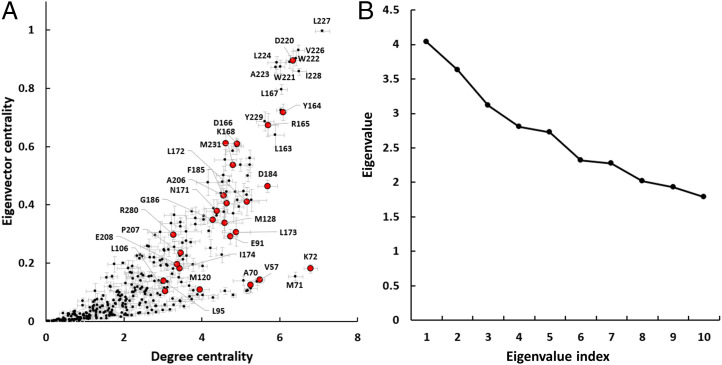
Recently, EG was proposed as an alternative that can combine local and global characteristics and serve as an efficient predictor of residues that are involved in allosteric signaling (22). In our case, EG key scores for the LSP-based PRNs were higher than the DC scores (Fig. 2). However, overall convergence of EG values for the whole molecule was erratic, especially at shorter time intervals (Fig. 3). We compared EG and DC values for the LSP-based PRN and found that for the highly scored residues, these values are almost linearly correlated with the notable exception of a few residues from the N-lobe (V57, A70, K72, and M120) (Fig. 4A). These residues had high DC but low EG values. This can be explained by the basic feature of EG that is bound to the largest eigenvalue of the adjacency matrix that, in its turn, is associated with the largest clique of the network (67). In our case, the first and the second largest eigenvalues were very close (Fig. 4B), which corresponds to the bilobal structure of protein kinases (Fig. 1). Our analysis showed that the largest eigenvalue was mostly associated with the larger C-lobe; however, in certain cases, the first and second eigenvalues would swap, leading to underestimation of the C-lobe residues and elevated EG values for N-lobe residues (SI Appendix, Fig. S4). Due to these limitations, we continued our analysis using BC and DC as the main PRN characteristics.

Fig. 4.

EG and eigenvalues in the LSP-based PRNs. (A) Scatter plot of EG versus DC with 26 key residues shown as red dots. Calculations were made on five 16-ns consecutive intervals. SE bars are shown. (B) The top ten eigenvalues of a typical adjacency matrix taken from LSP-based PRN.

As the LSP-based PRNs were so much more efficient in detecting the key residues, especially by the BC-based scores (Fig. 2), we wanted to understand if this advantage was associated with this particular set of 26 residues (Table 1). In other words, are there other residues that are important in a topological sense but were not included in the set of the key residues? If this is the case and other PRNs were capable of detecting them while the LSP-based PRNs failed to do so, then the advantage of the LSP-based PRNs should be reevaluated.

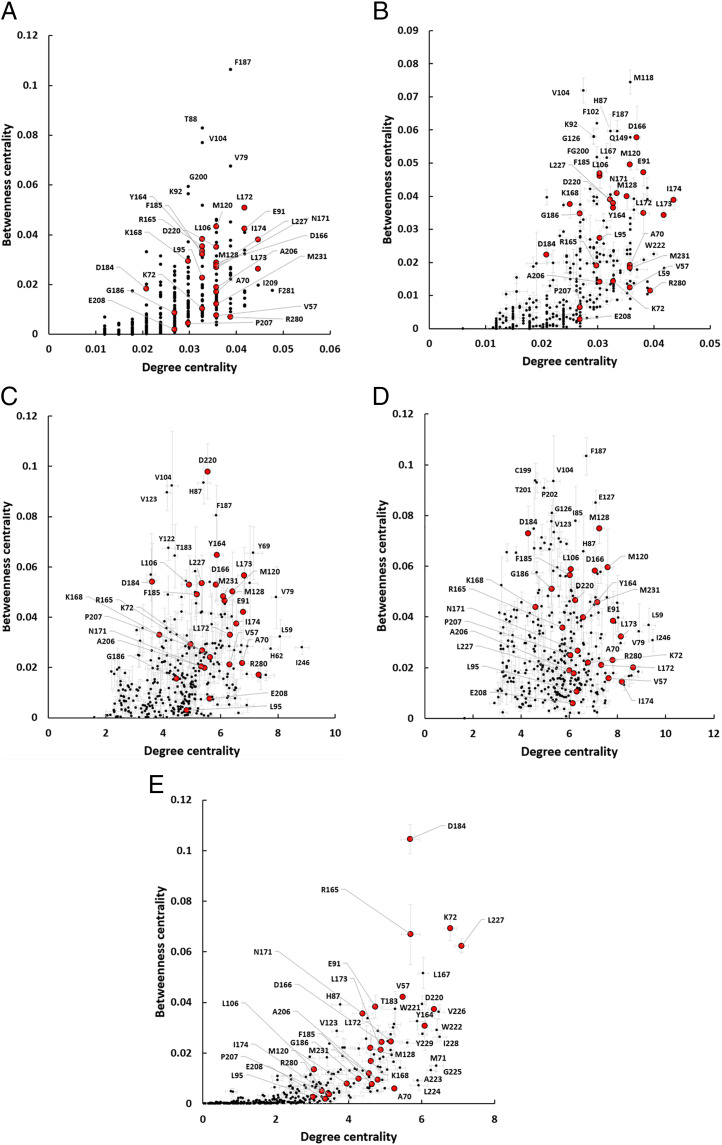
SS PRN provided a densely packed set of points with the key residues at the core of it (Fig. 5A). Out of the six residues with the highest BC values, only F187 and V104 were reported to play certain roles in protein kinases. F187 is positioned right after the DFG motif and defines substrate specificity (68). V104 occupies an important position contacting the regulatory spine; residues in this position are predominantly hydrophobic, and its mutations can lead to inactivation of the kinase (69). Residues that had distinctively high BC values in NW PRN included F187 and V104 and also three other residues that are known for their functions, H87, M118, and L167. H87 was shown to be important for PKA substrate recognition and stabilization of the catalytically competent conformation (70), M118 is an important part of hydrophobic core of the N-lobe (69), and L167 is a critical anchor for the catalytic loop that binds it to the αF-helix (43) (Fig. 5B).

Fig. 5.

BC and DC distribution of 336 PKA residues in five different PRNs based on an SS (A) and NW (B) weighted by CC (C), LMI (D), and LSP alignment (E). For the MD simulation–based PRNs, 6-ns long trajectories were used; 26 key residues are shown in red. SEs for five replications values are shown.

Distributions of points on both CC and LMI-based PRNs (Fig. 5 C and D) were rather dense, similar to the SS PRN, with a few residues having high BC values. CC-based PRN again detected H87, V104, and F187. LMI-based PRN also scored these three residues relatively high. Three other residues from the activation segment (C199, T201, and P202) had high BC values. C199 was shown to be important for preserving the PKA active state (71). T201 and P202 are known to be important for proper substrate binding (72).

LSP-based PRN had a distinctively different distribution of points, with a group of five residues clearly separated from the rest of the molecule by their high BC values (Fig. 5E). Four of them were a part of the key set, and the fifth was L167 and was also detected by the NW PRN and, notably, was the only “connector” identified by the Guimerà-Amaral cartography (SI Appendix, Fig. S3). Almost every residue in the αF-helix (residues 219 to 231) had very high DC values with relatively low BC values. This characterizes them as important hubs, which is consistent with the well-accepted view of this helix as a major scaffold for the protein kinase core (43). H87, which had high BC values in NW, CC, and LMI-based PRNs, also had high BC and DC in the LSP PRN. V104 and F187 that had high BC levels in all other PRNs had very low BC and DC levels in the LSP-based PRN. There is a chance that these two residues represent a “false-negative” result of the LSP-based PRN, V104 in particular; but in general, we concluded that the key residue score approach that we used to evaluate efficiency of different PRNs was well justified.

Discussion

In this work, we performed systematic analysis of several methods to create PRNs for the well-studied PKA to understand what methods can reliably identify residues that have important functional and regulatory roles. As proteins are dynamic objects, it is logical to suggest that using MD simulation and averaging multiple protein conformations should be beneficial in comparison to PRN based on an SS. Another reasonable suggestion is that favoring consistent, stable contacts over transient contacts should provide more relevant results. This explains the popular use of MD simulation and several weighting methods to create PRNs, although it was shown that binary PRNs based on an SS can be very informative (12). Using MD simulations for PRN creation poses a question—how long should the simulation be? Again, it is reasonable to suggest that the longer the MD simulation is, the more precise and biologically relevant results can be deduced from the PRNs. We decided to test these suggestions for the PKA case and obtained several surprising results.

First, our results show that to get convergent numbers for different centralities, 10-ns MD simulations can be sufficient (Figs. 2 and 4). This does not suggest that centralities calculated from the 10-ns simulations provide a complete picture of residues connectivity. In fact, a distinctive decrease of convergence level for some centralities at 100- to 200-ns timescales (Fig. 3) can be interpreted as a reflection of slower dynamics that slightly changes the PKA molecular topology. Highly convergent numbers for the LSP-based PRNs, however, indicate that it is possible to obtain reliable graph theoretical parameters for PRNs at a short time scale. Analysis of these values using longer trajectories can provide important information about the dynamic behavior of the protein molecule and to analyze its slow motions in a reliable way.

Second, a very surprising result was that traditional methods to weight PRN edges; CC and LMI performed very poorly. Although they are widely accepted and proven to be efficient methods to study collective motions in proteins (16, 17, 20–22), they could not differentiate functionally important residues from the rest of the molecule. In fact, in our key score test, they showed significantly worse numbers that NW binary PRNs or even PRNs based on an SS (Fig. 2). Different centrality values from these PRNs were also much less convergent in the tested timescales (Fig. 3). General distributions of BC and DC for these PRNs were very dense with no clear distinction between functionally important residues and the rest of the molecule (Fig. 5 C and D). By contrast, the LSP-based PRNs provided highly reproducible centrality values and were capable of separating a group of 20 to 30 residues, with most of them already being known as important elements of PKA structure or function (Figs. 4 and 5E).

LSP alignment was clearly the most efficient way to weight edges in our PRNs. Analysis of the BC versus DC scatter plot allowed us to make several conclusions (Fig. 5E). First, our key residues score method was based on a suggestion that the hydrophobic spines residues should be detected as important connectors, that is, having high levels of BC. It was true only partially. Only one residue from the C-spine (L227) had a very high BC value. The rest of the spine residues had, however, medium levels of BC and were clearly separated from the bulk of the molecule. Two universally conserved motifs, DFG and HRD, had high BC and DC values, with the catalytically important D184 having the highest BC value in the molecule. R165 from the HRD motif is known to be a major link between the activation loop and DFG motif (42), and it had the third highest BC. Both residues from the universally conserved salt bridge E91–K72 were also well separated from the rest of the molecule. Although the APE motif is conserved in all eukaryotic kinases and was included in our 26–key residue set, these residues had low values of both BC and DC. However, W222, another highly conserved residue that binds to the A206 and P207 (43), had a very high DC value. In general, the results provided by the LSP-based PRNs were very consistent with our current knowledge of PKA structure and function.

The reason for the bad performance of CC and LMI-based PRNs in comparison to LSP PRNs is not obvious, and it is not clear at this point if this is a universal feature or if it is only a peculiar characteristic of PKA and the timescales used in this work. A possible explanation can be inferred from the “violin” model of allostery that we proposed earlier (35). This model is based on a collective behavior of residues and can be viewed as a self-organization phenomenon (73). According to the model, residues act as oscillators that undergo synchronization and form cohesive clusters/communities with decreased entropy. The size of these clusters, their number, and their distribution throughout the network is defined by intrinsic oscillator properties and coupling properties of the network. Binding of an allosteric modulator causes a global change in the dynamic pattern of the protein similar to changes of “Chladni figures” observed on vibrating plates. Such redistribution of dynamic properties in the protein molecule can lead to changes in the active site and, hence, its function. This model does not require the existence of contiguous “allosteric pathways” and relies on a single suggestion that residues can be represented by oscillators, similar to Coarse Grain models (74). Synchronization of coupled oscillators is a well-known phenomenon observed in a wide variety of processes (75–77). This model predicts the existence of semirigid clusters of residues similar to the communities detected by community analysis, widely used in protein allostery studies (16–18, 21). The violin model approach, thus, calls for detection of cohesive regions in proteins where residues are moving in synch. From the violin model point of view using absolute value of CC to weight edges in PRN is counterproductive as it mixes up residues that move in synch and in counterphase. The traditional model of allosteric signaling is usually seen as a series of sequential interactions that start at the allosteric site and propagate in a domino-like fashion to the active site along a well-defined allosteric pathway (78–80). From this point of view combining correlation and anticorrelation for the PRN weighting procedure is perfectly justified, as strong interactions remain strong irrespective of their sign. The LMI approach goes even further and includes not only colinear anticorrelations but all orientations of residue fluctuations (19). However, if the violin model is correct, then considering the sign of interactions in a network is critical. In social sciences, this problem is well recognized, as in certain cases, social networks have to distinguish “friends” and “foes”, that is, networks have to include negative links (81, 82). LSP analysis from this point of view eliminates these problems as it has the opposite characteristic; instead of being overinclusive like CC or LMI, it is overrestrictive as it preserves connections only if both CαCα distances and the orientation of CαCβ vectors remain the same.

We, thus, suggest that two different types of PRNs should be differentiated, based on correlated dynamics of residues and on their spatial stability. The former are successfully used in methods like elastic network models (ENMs) where connections are viewed as Hookean springs (83). Obviously, a spring connecting two nodes does not suggest conservation of the distance between the residues but implies interactions between them. ENMs are very successful in predicting slow motions in proteins and are widely used. The latter, on the contrary, does not suggest any interactions between residues but creates a PRN link if and only if they preserve their mutual positions in time. A similar approach is used for analysis of rigid elements in proteins and their role in protein function and allostery (84–86). This difference between the “interaction”-based PRNs and “stability”-based PRNs requires reconsideration of the CαCα distance cutoff that is imposed to reduce computational cost. In the interaction-based PRNs, it is usually 4 to 8 Å (12) and can be extended up to 12 Å to include long-distance electrostatic interactions (87). As the stability-based PRNs disregard residue interactions per se and reflect the presence of stable clusters in the molecule, it is logical to use larger cutoff values comparable with the size of the clusters. Indeed, our results show that larger cutoff levels improve sensitivity of the method (SI Appendix, Fig. S1). Our results indicate that while the interaction-based PRNs can be very effective in predicting global motions of proteins, the “structure”-based PRNs can efficiently predict individual residues that play important functional and regulatory roles. To validate these assumptions and to understand the underlying causes of our observations, more studies are necessary. The LSP alignment method, although being very efficient in detecting functionally important residues, at this point is relatively slow in comparison to traditional methods. However, parallelization of the current algorithm is a straightforward task. Improving its computational efficiency will facilitate analysis of longer trajectories and bigger protein complexes.

Materials and Methods

MD Simulations.

The catalytic subunit of PKA was prepared for all atom MD simulations using the crystal structure of wild-type PKA in a ternary complex with Mn²⁺ ATP and inhibitor peptide PKI 6-25 (Protein Data Bank ID: 3FJQ). Mn ions were replaced with Mg, and models were processed in Maestro (Schrodinger). Protein Preparation Wizard was used to build missing sidechains and model charge states of ionizable residues at neutral pH. Hydrogens and counter ions were added, and the model was solvated in a cubic box of TIP4P-EW (88) and 150 mM KCl with a 10-Å buffer in AMBER tools (89). Parameters from the Bryce AMBER Parameter Database were used for ATP (90), phosphothreonine (91), and phosphoserine (91). AMBER16 was used for energy minimization, heating, and equilibration steps. Systems were minimized by 1,000 steps of hydrogen-only minimization, 2,000 steps of solvent minimization, 2,000 steps of ligand minimization, 2,000 steps of side chain minimization, and 5,000 steps of all-atom minimization. Systems were heated from 0 °K to 300 °K linearly over 250 ps with 2-fs time-steps and 10.0 kcal·mol·Å position restraints on protein. Temperature was maintained by the Langevin thermostat. Constant pressure equilibration with a 10-Å nonbonded cutoff with particle mesh Ewald was performed with 300 ps of protein and ligand restraints followed by 300 ps of unrestrained equilibration. Hydrogen mass repartition was implemented to achieve a 4-fs time-step for production runs (92). Production simulations were performed on Graphic Processing Unit-enabled AMBER16 (93, 94) as above in triplicate for an aggregate of 1.2 ms.

Network Creation.

LSP-based networks.

LSP alignment was performed using previously created software (42, 43) adapted for MD simulation. Graphs were generated, as described earlier (42), using coordinates of Cα and C atoms for all residues with the exception of glycine (Cα and N) and ATP molecule (N1,C8). In brief, protein structure is represented by a graph with residues as nodes. Links are formed if the distance between Cα atoms of the corresponding residues are within a predefined cutoff level ΔCαα. Each link carries information about mutual orientation of the corresponding CαCβ vectors, three distances (Cα1-Cα2, Cα1-Cβ2, and Cβ1-Cα2) and the dihedral angle θ (Cβ1-Cα1-Cα2-Cβ2). Comparison of two protein structures is presented as a graph with residues as nodes and links created only if all the three distances and the dihedral angles are similar, that is, within predefined cutoff levels: ΔCα1α2 < 0.2 Å, ΔCα1β2 < 0.45 Å, Δθ < 10°. Weights for the links are calculated using the following formula:

$$W=\frac{1}{4}*\left(\left(1-\frac{{\delta }_{\mathrm{\text{α1α2}}}}{\mathrm{\Delta }{C}_{\mathrm{\text{α1α2}}}}\right)+\left(1-\frac{{\delta }_{\mathrm{\text{α1β2}}}}{\mathrm{\Delta }{C}_{\mathrm{\text{α1β2}}}}\right)+\left(1-\frac{{\delta }_{\mathrm{\text{β1α2}}}}{\mathrm{\Delta }{C}_{\mathrm{\text{α1β2}}}}\right)+\left(1-\frac{\delta \theta }{\mathrm{\Delta }\theta }\right)\right),$$

where δ_α1α2, δ_α1β2, δ_β1α2, and δθ are the corresponding differences between two CαCβ vectors. Weights for the not-matching links are assigned zero values.

In our preliminary experiments, we showed that increasing ΔCαα cutoff levels can be beneficial for the key scores of the LSP-based PRNs (SI Appendix, Fig. S1). We thus used ΔCαα = 12 Å, which we found to be an acceptable compromise between increased sensitivity and lower computational costs that were increasing significantly for ΔCαα levels higher than 12 Å. For LSP alignment of multiple structures, comparisons were made in all-to-all way. The resulting adjacency matrices were averaged and used for the subsequent analysis.

NW, CC, and LMI-based networks.

CC and LMI matrices were calculated using the Bio3D R package (version 2.4) (95). Three production trajectories, 400 ns each, were aligned by their Cα atoms and merged. Binary contact maps were calculated with the requirement that the residues were in contact for at least 75% of the trajectory run and used as NW matrices. These matrices were subsequently weighted by absolute values of CC and LMI.

SS PRN was built using the first structure of PKA in the trajectory and function ‘cmap’ from the Bio3D R package.

Calculation of centralities.

Normalized centralities were calculated using igraph R library (version 1.2.5) (96). To calculate BC and CL weights were converted to distances using the following formula: $D=-\text{log} W$. The “strength” function was used to calculate weighted DC.

Guimerà-Amaral cartography map was built using “rnetcarto” R library (version 0.2.5) (97).

Data, Materials, and Software Availability

All study data are included in the main text and/or the SI Appendix.