Ultrasonographic fetal thigh measurement in the estimation of fetal weight based on Isobe’s formula in women with an engaged fetal head in the pelvis: a comparative study

Abstract

Purpose

Because of the inaccuracy of the biparietal diameter in cases with an engaged fetal head in the pelvis, measuring the estimated fetal weigh (EFW) using Hadlock’s formula could be compromised in these cases. The aim of this prospective study is to determine the accuracy of using only two thigh parameters, the femur length (FL) and the cross-sectional area of the thigh (CSAT) (Isobe’s formula), in detecting the fetal weight of both engaged pelvis fetuses and non-engaged head fetuses and to compare this method with Hadlock’s formula in both groups using the actual birth weight as a gold standard.

Methods

The study included 51 cases with an engaged fetal head and 51 cases with a non-engaged fetal head that came in active labour. 2D ultrasonography examination was performed to determine the EFW using both Hadlock’s formula and Isobe’s formula. The EFW was then compared with the actual birth weight after delivery.

Results

There was a strong positive correlation between Isobe’s formula and the actual birth weight in the engaged fetal head group (r = 0.993, p < 0.01), but there was a strong positive correlation between Hadlock’s formula and the actual birth weight in the non-engaged fetal head group (r = 0.994, p < 0.01).

Conclusion

We concluded that Isobe’s formula is convenient in predicting the fetal weight, especially when head measurements are difficult to assess (in the engaged fetal head group). It can be used with 2D ultrasonography as an alternative to Hadlock’s formula in cases with an engaged fetal head in the pelvis.

Background

In the process of antenatal care, ultrasonographic assessment of fetal weight is mandatory for detecting fetuses that are appropriately grown, small and large for gestational age (AGA, SGA, and LGA, respectively). The estimation of fetal weight is important for the management of labour and for the determination of a suitable mode of delivery. The estimated fetal weight (EFW) is measured by four parameters: the fetal head circumference (HC), biparietal diameter (BPD), femur length (FL), and abdominal circumference (AC) [1].

Hadlock’s formula is one of the commonly used formulas for estimating fetal weight, including measurements of the HC, AC, FL, and BPD alone and in combination [2].

The accuracy of the fetal biparital diameter is uncertain in conditions such as an engaged fetal head and breech presentation and for fetuses in direct occipito-anterior or occipito-posterior position. The estimation of fetal weight using only two fetal thigh dimensions, as in Isobe’s formula, could be used to avoid these situations [2, 3].

In this comparative study, we aimed to determine the accuracy of using only two thigh parameters, the femur length and the cross-sectional area of the thigh (CSAT) (Isobe’s formula), in detecting the fetal weight of both engaged pelvis fetuses and non-engaged head fetuses and to compare this method with Hadlock's formula in both groups using the actual birth weight as a gold standard.

Methods

The current study has been approved by the Research and Ethical Committee of Kasr El-Aini Hospital.

The study population included 102 mothers with singleton term pregnancy in cephalic presentation at term (37–40 weeks of gestation) and who came in active labour to the labour room between February 2020 and May 2021 and delivered within the next 24 h.

In total, 82 patients had a vaginal delivery, and only 20 patients underwent a caesarean section due to an obstetric cause.

Two groups of patients were included in this study:

1. The first group included 51 cases with an engaged fetal head in the pelvis.

   The fetal head is considered “engaged” when the largest part of the head (BPD) has entered the pelvis (at the level of the ischial spines – station zero). If the presenting part lies above the ischial spines, the station is reported as a negative number (not considered to be engaged).

2. The second group included 51 cases with a non-engaged fetal head in the pelvis.

All the patients were examined by an expert obstetrician to determine the engagement of the head and to decide the mode of delivery.

The patients were then subjected to two-dimensional ultrasonography examinations to estimate the fetal weight using the well-established Hadlock and Isobe formulas.

After delivery, the actual birth weight was then measured to compare it with the EFW detected by the two formulas.

The cases included in this study were only those with an average fetal weight for gestational age (2.5–4 kg).

Patients with fetal malpresentation, multiple pregnancies, and oligohydramnios were excluded from the study because the exact fetal thigh circumference is difficult to obtain in these patients owing to the blurring of the echographs and the deformation of the fetal thigh circumference under compression. Preterm babies and fetuses with growth abnormalities were also excluded from the study.

Technique of the examination

The patients were examined using a LOGIQ P6, GE (General Electric) ultrasound machine equipped with a 5-MHz transducer. Examinations were performed by two consultant radiologists experienced in fetal ultrasound (more than 10 years’ experience).

Each fetus was examined on a single occasion. Gestational age was determined from the last menstrual period and confirmed by ultrasound; it was given in exact number of weeks (37–40 weeks). The patient lied in a flat position, and after good exposure a conducting gel was applied. First, a rapid overview was performed to confirm positive fetal life and longitudinal lie. Cephalic presentation head parameters, such as bi parital diameter and HC, were measured, as well as abdominal circumference, femur length and cross sectional area of the thigh. Amniotic fluid was assessed using the amniotic fluid index method by dividing the abdomen into four quadrants and then measuring amniotic fluid pockets in each quadrant.

BPD is measured from the outer edge of the proximal parietal bone to the inner edge of the distal parietal bone (outer to inner) at the level of the widest part of the fetal skull [4].

FL measurement includes the ossified portion of the diaphysis and metaphysis. Although the proximal and distal epiphyseal cartilages should not be measured, they should be visualized to ensure that the entire osseous femur is measured without shortening or elongation [4].

AC is measured at the level of the stomach bubble and a short segment of the umbilical vein at the level of the portal sinus using the ellipse facility of the ultrasound imaging [4].

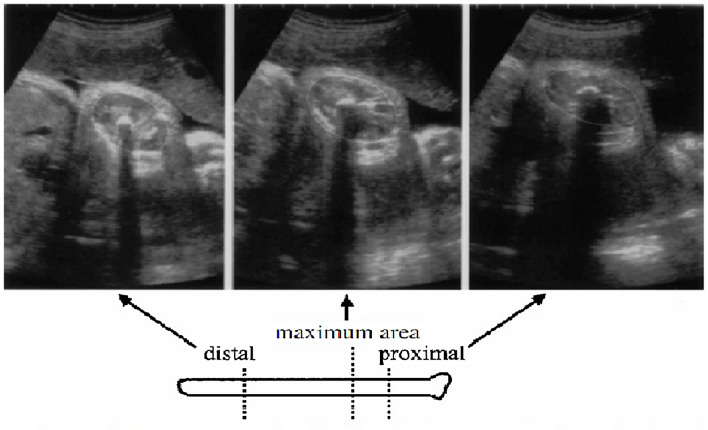
The CSAT is defined as the cross-sectional area of the muscles and bones of the thigh on the plane at a right angle to the long axis of the femur, where the area is the largest. The CSAT was measured as follows. The fetal thigh circumference was recorded at a transverse plane at the junction of the upper and middle thirds of the thigh, at the level of the proximal nutrient foramen of the femur (Fig. 1) [5]. Measurements made within 1–2 cm of the transition plane were quite similar, demonstrating that exact positioning of the plane is not necessary. At the point where the cross-sectional area of the thigh reached its maximum, the probe motion was stopped. The area was then measured using the HC and AC ellipse function.

Fig. 1.

Sonographic views of the cross sectional area of the thigh at right angles to the long axis in the proximal, maximum and distal portions. Isobe [5]

Then the estimated fetal body weight was calculated as follows:

1. Using Hadlock's formula: calculated by the machine software using the BPD, HC, AC, and FL parameters.

2. Using Isobe's formula: calculated using FL and CSAT:

$$\text{EFBW}=13\times \left(\text{FL}\times \surd \text{CSAT}\right)+39\left(\text{gm}\right).$$

where FL is in millimeters and CSAT is in centimetres. The actual birth weight (ABW) of the infant was measured immediately after delivery and after clamping the umbilical cord at an equal distance (7 cm) in every baby.

Statistical methods

Data were coded and entered using the Statistical Package for the Social Sciences (SPSS) version 26 (IBM Corp., Armonk, NY, USA). The data were summarized using the mean, standard deviation, median, minimum, and maximum for quantitative variables and frequencies (number of cases) and relative frequencies (percentages) for categorical variables. Comparisons between groups were made using an unpaired t-test. Comparisons with the actual weight in each group were carried out using a paired t-test. For comparing categorical data, a chi-square test was performed. An exact test was used instead when the expected frequency was less than 5. Correlations between quantitative variables were calculated using Pearson’s correlation coefficient; p values less than 0.05 were considered statistically significant.

We used the following terms:

1. Error: the difference between the EFW (by either formula) and the actual birth weight.

2. Absolute error: the absolute value of the error.

3. Absolute error percentage: the absolute error divided by the actual birth weight as percentage. The accepted range was 10% of the actual birth weight.

The actual birth weight was considered the gold standard in our study.

Results

This study was carried out on 102 patients referred to us from the emergency department between February 2020 and May 2021; their age ranged from 22 to 42 years (mean age 31). The gestational age of the women was from 37 to 40 weeks (mean gestational age 38.5).

All patients were subjected to relevant history taking, ultrasonographic examination, and estimation of the actual birth weight after delivery.

Correlation in each group

The correlation between the actual birth weight and the EFW (using both Hadlock’s formula and Isobe’s formula) was calculated in each group.

Engaged group

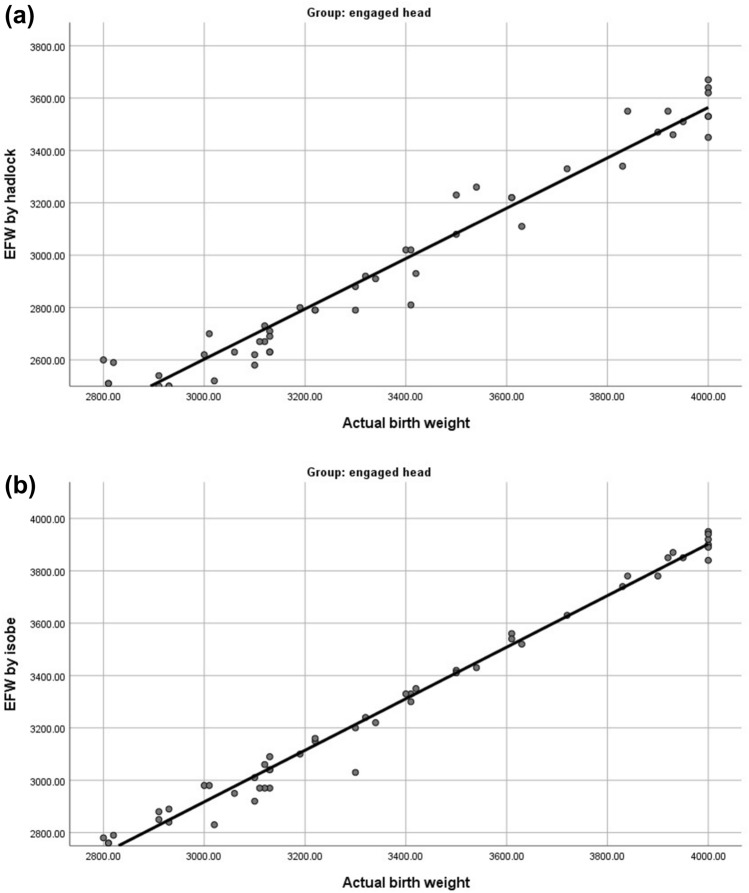
There was a strong positive correlation between the EFW (obtained by either Hadlock’s formula or Isobe’s formula) and the actual birth weight in the engaged fetal head group, with a higher correlation coefficient with Isobe’s formula (r = 0.993, p < 0.01) (Table 1, Figs. 2 and 3).

Table 1.

Correlation between EFW by both formulae and actual birth weight

	EFW by Hadlock	EFW by Isobe
Engaged head
Actual birth weight
r	0.978	0.993
P value	< 0.001	< 0.001
N	51	51
Non engaged head
Actual birth weight
r	0.994	0.975
P value	< 0.001	< 0.001
N	51	51

Significant P values are given in bold (P < 0.005)

Fig. 2.

Scatter-Plots showing. a Correlation between Actual Birth Weight and EFW using Hadlock’s Formula in engaged head group. b Correlation between Actual Birth Weight and EFW using Isobe’s Formula in engaged head group

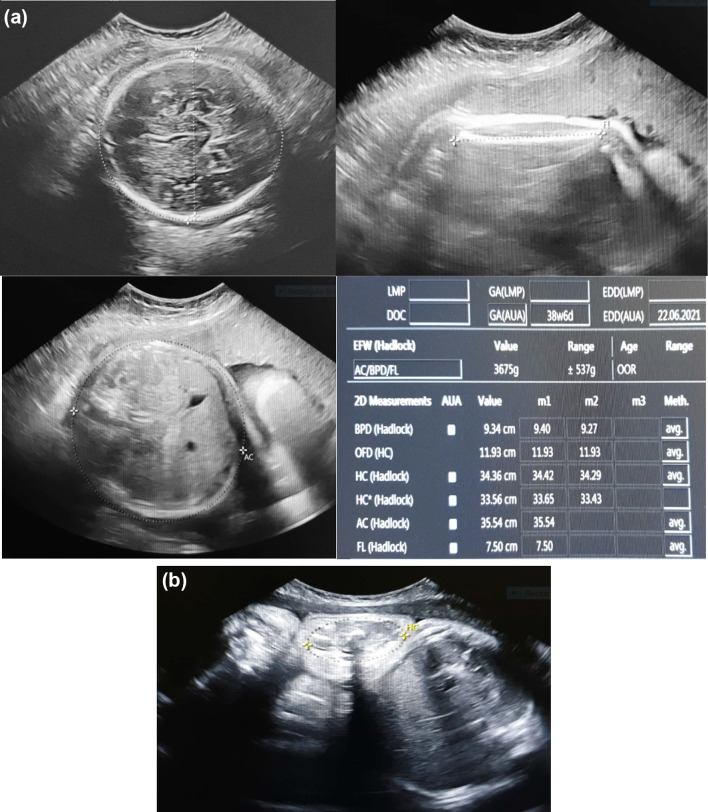
Fig. 3.

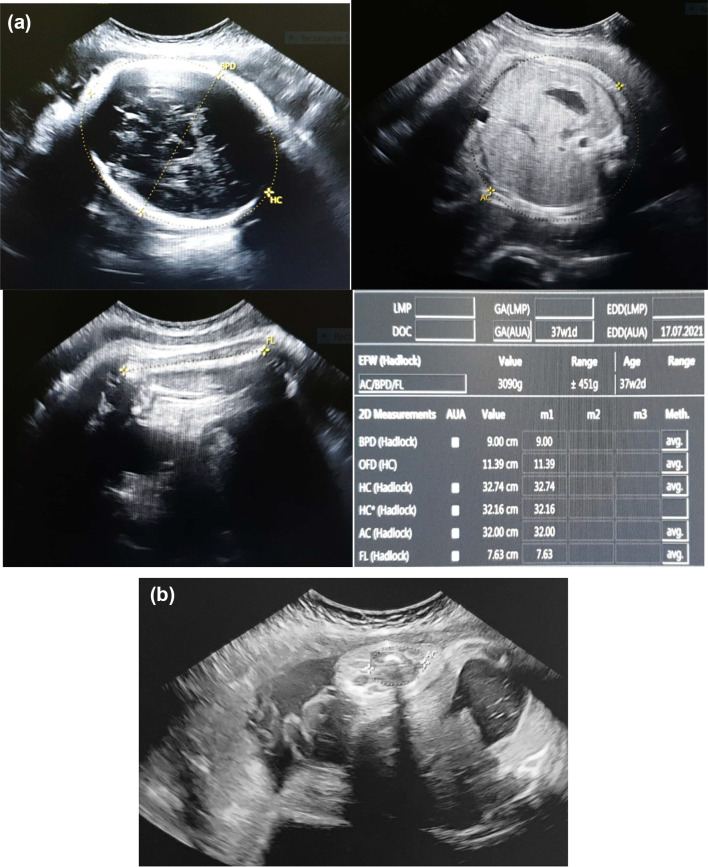
38 weeks and 6 days pregnant primigravida with engaged fetal head (at + 1 station). a Estimation of fetal weight using Hadlock’s formula. b Measurement of CSAT in the same patient

Non-engaged group

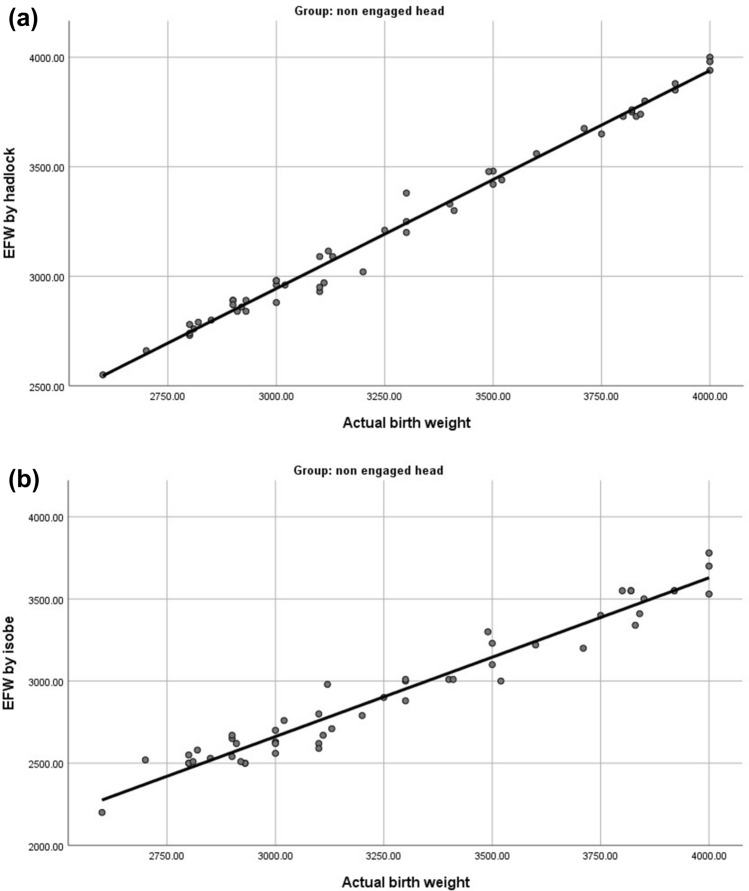
There was a strong positive correlation between the EFW (obtained by either Hadlock’s formula or Isobe’s formula) and the actual birth weight in the non-engaged fetal head group, with a higher correlation coefficient with Hadlock’s formula (r = 0.994, p < 0.01) (Table 1, Figs. 4 and 5).

Fig. 4.

Scatter-Plots showing. a Correlation between Actual Birth Weight and EFW using Hadlock’s Formula in non-engaged head group. b Correlation between Actual Birth Weight and EFW using Isobe’s Formula in non-engaged head group

Fig. 5.

37 weeks and 1 day pregnant primigravida with non-engaged fetal head. a Estimation of fetal weight using Hadlock’s formula. b Measurement of CSAT in the same patient

The paired difference between each method and the actual birth weight was measured in each group.

Engaged group

The paired difference between the EFW obtained by Hadlock’s formula and the actual birth weight was 411.96078 ± 81.09302, but the paired difference between the EFW obtained by Isobe’s formula and the actual birth weight was 88.23529 ± 46.93425.

The narrow 95% CI for Isobe’s formula compared to Hadlock’s formula shows that in the engaged head group, the EFW can be determined more accurately by Isobe’s formula (Table 2).

Table 2.

The paired difference between each method and actual birth weight in engaged and non-engaged fetal head groups

	Paired Differences					P value
	Mean	Std. Deviation	Std. Error Mean	95% confidence interval of the difference
				Lower	Upper
Engaged head
EFW by Hadlock - Actual birth weight	411.96078	81.09302	11.35529	434.76856	389.15300	<0.001
EFW by Isobe - Actual birth weight	88.23529	46.93425	6.57211	101.43576	75.03482	<0.001
Non engaged head
EFW by Hadlock - Actual birth weight	57.49020	45.87652	6.42400	70.39317	44.58722	<0.001
EFW by Isobe - Actual birth weight	347.05882	91.65793	12.83468	372.83803	321.27961	<0.001

Significant P values are given in bold (P < 0.005)

Non-engaged group

The paired difference between the EFW obtained by Hadlock’s formula and the actual birth weight was 57.49020 ± 45.87652, but the paired difference between the EFW obtained by Isobe’s and the actual birth weight was 347.05882 ± 91.65793.

The narrow 95% CI for Hadlock’s formula compared to Isobe’s formula shows that in the non-engaged head group, the EFW can be determined more accurately by Hadlock’s formula (Table 2).

Comparison between the two groups

In the engaged fetal head group, the mean EFW predicted by Hadlock’s formula was 2962.35 kg, and the mean EFW predicted by Isobe’s formula was 3286.08 kg. The mean actual birth weight was 3374.31 kg. This shows that the EFW obtained by Isobe’s formula is significantly higher in the engaged head group (Table 3).

Table 3.

Comparison between EFW and mean absolute error percentages by Hadlock’s and Isobe’s formula in both groups

	Engaged head					Non engaged head					P value
	Mean	SD	Median	Minimum	Maximum	Mean	SD	Median	Minimum	Maximum
EFW by Hadlock	2962.35	384.00	2810.00	2500.00	3670.00	3222.51	413.50	3090.00	2550.00	4000.00	0.001
EFW by Isobe	3286.08	387.52	3200.00	2760.00	3950.00	2932.94	409.21	2800.00	2200.00	3780.00	< 0.001
Actual birth weight	3374.31	390.65	3300.00	2800.00	4000.00	3280.00	412.87	3130.00	2600.00	4000.00	0.239
Absolute error of Hadlock	411.96	81.09	420.00	200.00	600.00	60.63	41.55	50.00	0.00	180.00	< 0.001
Absolute error of Isobe	88.24	46.93	80.00	20.00	270.00	347.06	91.66	350.00	140.00	520.00	< 0.001
Absolute error % of Hadlock	12.31	2.57	12.50	7.14	17.60	1.86	1.30	1.75	0.00	5.63	< 0.001
Absolute error % of Isobe	2.62	1.45	2.35	0.67	8.18	10.68	2.90	10.71	4.49	16.45	< 0.001

Significant P values are given in bold (P < 0.005)

In the non-engaged fetal head group, the mean EFW predicted by Hadlock’s formula was 3222.51 kg, and the mean EFW predicted by Isobe’s formula was 2932.94 kg. The mean actual birth weight was 3280.00 kg. This shows that the EFW obtained by Hadlock’s formula is significantly higher in the non-engaged head group (Table 3).

In the engaged fetal head group, the mean absolute error percentage of the actual birth weight was 12.31% using Hadlock’s formula and 2.62% using Isobe’s formula. This indicates that the absolute error percentage of Hadlock’s formula is higher in the engaged group (Table 3).

In the non-engaged fetal head group, the mean absolute error percentage of the actual birth weight was 1.86% using Hadlock’s formula and 10.68% using Isobe’s formula. This indicates that the absolute error percentage of Isobe’s formula is higher in the non-engaged group (Table 3).

In the engaged fetal head group, of the included 51 cases, 9 (17.6%) had their absolute error in the EFW predicted by Hadlock’s formula within 10% of the actual birth weight, while 42 (82.4%) had their absolute error above 10% of the actual birth weight. However, all 51 cases (100%) had their absolute error in the EFW predicted by Isobe’s formula within 10% of the actual birth weight, with no cases with an error percentage above 10% of the actual birth weight (Table 4).

Table 4.

The absolute error of both formulae in the two studied groups

	Engaged head		Non engaged head		P value
	Count	%	Count	%
Absolute error of hadlock
Within 10% of actual birth weight	9	17.6%	51	100.0%	< 0.001
> 10% of actual birth weight	42	82.4%	0	0.0%
Absolute error of isobe
Within 10% of actual birth weight	51	100.0%	23	45.1%	< 0.001
> 10% of actual birth weight	0	0.0%	28	54.9%

Significant P values are given in bold (P < 0.005)

In the non-engaged fetal head group, of the included 51 cases, 23 (45.1%) had their absolute error in the EFW predicted by Isobe’s formula within 10% of the actual birth weight, while 28 (54.9%) had their absolute error above 10% of the actual birth weight. However, all 51 cases (100%) cases had their absolute error in the EFW predicted by Hadlock’s formula within 10% of the actual birth weight, with no cases with an error percentage above 10% of the actual birth weight (Table 4).

This shows that Hadlock’s formula is better in the non-engaged group, as 100% of the error is within 10% of the actual birth weight, but that Isobe’s formula is better in the engaged group, as 100% of the error is within 10% of the actual birth weight.

Discussion

Estimated fetal weight has been used in the routine antepartum evaluation of high-risk pregnancies and deliveries. The management of diabetic pregnancy, vaginal birth after a previous caesarean section, and breech presentations will be affected by estimated fetal weight. Hence, accurate estimation of fetal weight is important in the management of labour and delivery [6].

The two main methods for predicting birth weight are the clinical and the sonographic method. Although some investigators consider ultrasonography to be more accurate than clinical assessment, others found that both have the same level of accuracy [7].

The estimation of fetal weight commonly includes head circumference, abdomen circumference, and femur length, either separately or, more often, all together. Adding thigh measurements to these measurements have been studied to detect their role. Head measurements are inconvenient in certain conditions, such as when the fetal head is engaged deeply in the pelvis. In this situation, other methods for fetal weight estimation are needed to avoid head measurement [8].

This study showed that there was a strong positive correlation between the EFW (obtained by either Hadlock’s formula or Isobe’s formula) and the actual birth weight in the engaged fetal head group, with a higher correlation coefficient with Isobe’s formula (r = 0.993, p < 0.01). This agreed with a study by Rizwan et al., which found a high correlation coefficient of 0.910 with Isobe’s formula.

This present study found that there was a strong positive correlation between the EFW (obtained by either Hadlock’s formula or Isobe’s formula) and the actual birth weight in the non-engaged fetal head group, with a higher correlation coefficient with Hadlock’s formula (r = 0.994, p < 0.01).

In agreement with our results, Sonica et al. conducted a study that showed that the EFW obtained by Hadlock’s formula was not significantly different from the actual birth weight (p = 0.00001) [9].

When comparing the EFW in both groups with the actual birth weight, we found that the EFW obtained by Hadlock’s formula is significantly lower in the engaged head group and that the absolute error percentage of Hadlock’s formula is higher in the engaged head group, indicating that Hadlock’s formula is less accurate in measuring the EFW in the engaged fetal head group than in the non-engaged fetal head group. This agrees with a study by Joanna et al., which concluded that when head measurements are difficult to estimate by ultrasonography, Hadlock’s formula can be used without head measurements, indicating that Hadlock’s formula with head measurements is inaccurate in certain situations [10].

Our study is the first to indicate that the EFW obtained by Isobe’s formula is significantly higher in the engaged fetal head group and that the absolute error percentage of Isobe’s formula is lower in the engaged fetal head group, indicating that Isobe’s formula is more accurate in measuring the EFW in the engaged fetal head group than in the non-engaged fetal head group. Ayman et al. conducted a study that showed that using new algorithms, such as measuring fetal thigh soft tissue, is more important than using Hadlock’s formula in the estimation of fetal weight [11].

Conclusion

We concluded that the ultrasonographic estimation of fetal weight was statistically significant with both formulas, although Isobe’s formula was more accurate in detecting the fetal weight in cases with an engaged fetal head in the pelvis.

Hadlock’s formula was superior to Isobe’s formula in the non-engaged fetal head group, but Isobe’s formula was superior in the engaged fetal head group.

Isobe’s formula can be used as an accurate method for the estimation of fetal weight when head measurements are difficult to obtain because of an engaged fetal head in the pelvis.

Abbreviations

AC

Abdominal circumference

BPD

Bi- parietal diameter

CI

Confidence interval

Cm

Centimeter

CS

Cesarean section

CSAT

Cross sectional area of the thigh

EFBW

Estimated fetal body weight

EFW

Estimated fetal weight

FL

Femur length

gm

Gram

HC

Head circumference

Kg

Kilogram

MHz

Mega Hertz

SD

Standard deviation

SPSS

Statistical Package for the Social Science

USA

United States of America

2D

Two dimensional

Author contributions

NK and AH analyzed and interpreted the patient data regarding the ultrasonographic results of both Hadlock’s and Isobe’s formula. AE examined the patients, analyzed and interpreted the data regarding the status of the fetal head during labour and the actual birth weight after delivery. MF revised all the data interpreted by other authors. All authors read and approved the final manuscript.

Funding

The authors declare that no funds, grants, or other support were received during the preparation of this manuscript.

Availability of data and material

The datasets used and/or analyzed during the current study are available from the corresponding author on reasonable request.

Declarations

Conflict of interest

The authors have no relevant financial or non-financial interests to disclose.

Ethics approval and consent to participate

The current study had been approved by Kasr El-Aini Hospital, Research and Ethical committee. Informed consent was obtained from all individual participants included in the study.

Consent for publication

The authors affirm that human research participants provided informed consent for publication of the images in the figures.