Abstract
A longstanding goal in polymer rheology is to develop a physical picture that relates the growth of mechanical moduli during polymer crystallization to that of a structure. Here, we utilize simultaneous mechanical rheology and optical microscopy, with augmentation by deterministic reconstruction and stochastic simulations, to study isothermal crystallization in isotactic polypropylene. We observe the nucleation and growth of the surface and bulk spherulites, which are initially isolated and then impinge to form clusters and superstructures that eventually span the gap. We find that spherulitic superstructures play a critical role in the rheology, especially in the characteristic sharp upturn in moduli. Both the rheology and the spherulitic superstructures show pronounced gap dependencies, which we explain via finite-size effects in percolation phenomena and via surface-induced nucleation. The modulus-crystallinity relationship can be described through a general effective medium theory. It indicates that for thicker gaps, the viscoelastic liquid to solid transition can be described via percolation, whereas for our thinnest gap, it is best described by the linear mixing rule. We describe our results in terms of dimensionless nucleation rates and spherulite size, which enable the estimation of when gap-dependent superstructure effects can be anticipated.
I. INTRODUCTION
The kinetics of polymer crystallization has fascinated researchers for decades due to its industrial relevance and the complexities of its associated multiple length and time scales. At the structural level, polymer crystallization is well known to occur via cascading length scales. Starting at the nanoscale, crystal domains nucleate and grow in a lamellar fashion of alternating crystalline and amorphous layers. These lamellae organize into microscale semicrystalline spherulites that impinge with each other to form clusters [1]. At the mechanical level, the transformation is equally dramatic. As the polymer transforms from a viscoelastic melt to a semicrystalline solid, there are three distinct rheological regimes as viewed through small amplitude oscillatory shear (SAOS): induction, upturn, and plateau. These regimes, and the times of the transitions between them, are observed across a broad range of mechanical frequencies [2–18].
Industrially, the design strategies for the processing of semicrystalline polymers must consider the evolving modulus-structure relationships throughout any given process route [9,10,19–25]. For example, in film blowing [22], the crystallization commences near the frost line in the bubble and increases as the polymer traverses upward toward the pulling pinch rollers; at some point, the polymer must be able to maintain a stress along the length of the film in the machine direction. In the newer process of materials extrusion additive manufacturing with semicrystalline polymers (a 3D printing technique), the relationship between processing and crystallization must be understood to design parts that maximize both mechanical strength and dimensional accuracy [24,26].
However, the relationship between rheology and structure during the crystallization process is unresolved, despite much work [10,27]. In a pioneering research by Winter and co-workers it was found that tan(δ), the ratio of the loss to storage modulus (G″/G′), becomes independent of oscillation frequency (ω) at a certain time in the process, termed the physical gelation point [6,8]. This occurs during the upturn regime. The concept of percolation of spherulites during crystallization has been explored by Boutahar et al. and used to compare rheological results between two polyolefins with very different nucleation densities [4].
A primary difficulty in relating rheology to the structure in these systems has been the lack of in situ knowledge regarding the spherulitic structure and the degree of crystallinity during rheological measurements. Particular interest has focused on the crystallinity at the gelation point. The experimental difficulty stems from the nonsimultaneous nature of the early measurements. In one approach, Pogodina et al. used isothermal differential scanning calorimetry (extrapolated from lower temperature) to estimate that the crystallinity in isotactic polypropylene (iPP) at the gelation point is about 2% mass fraction [6]. However, crystallization rates can be highly dependent on gap thickness, substrate composition [11,28–33], and thermal history, meaning the differential scanning calorimetry (DSC) results may provide poor guidance in determining the crystallinity at a given time in a rheometer. Another approach is to invoke a mathematical model relating transient modulus to transient crystallinity. Coppola et al. used a linear mixing rule to relate the two and found a value of 1.3% at the point that corresponds to physical gelation [13]. However, depending on what model is used, one could arrive at significantly larger values of crystallinity for a given modulus [14]. It is important to point out that the spherulitic superstructures in these experimental works are not reported.
If such a low value of crystallinity at the rheological gel point were true, it would imply that the easily observed spherulites could not be responsible for the gelation, because a spherical object at a few percent volume fraction cannot cause a percolation or gelation. Instead, highly elongated objects, perhaps at the nanoscale would be needed to explain such a mechanical response at low fraction of crystallinity; or it would indicate that spherulites in the induction and upturn regimes are mainly amorphous [34]; however, micro-Raman measurements during crystallization are not consistent with this idea [35].
But some recent works differ from the early reports. The simultaneous measurements of the structure and rheology during crystallization require hyphenated techniques and there has recently been much development and application of such methods [11,15,36–41]. When applied to isothermal crystallization of polymers, larger values of crystallinity in the upturn regime at the gelation point have been reported as compared to the original works. Pantani et al. used depth-resolved optical microscopy to measure spherulitic volume fraction during the induction and upturn regimes of iPP [11]. They then created 3D reconstructions of the spherulite distributions during the process. Their data show spherulitic volume fractions in the range of approximately (5–25)% in what we here call the upturn regime. (One must be careful not to confuse spherulitic volume fraction with percent crystallinity.) Wilhelm and co-workers used simultaneous optical microscopy and rheology to estimate a volume fraction of approximately 15% at the point of tan(δ) = 1 in iPP, which they associated with gelation. From this number, they suggested that a spherulitic superstructure is responsible for the rheological upturn [15].
Simultaneous measurements of modulus and crystallinity over the full crystallization process enable critical tests of various models relating transient moduli to crystallinity. Kotula and Migler used rheo-Raman and found that proposed models (linear, log, inverse, suspension, and composite sphere) do not fit the data well over the full range [14]. Instead, the general effective medium (GEM) model, originally developed and previously applied for two-phase conductive systems [42,43], was adapted to the present problem of crystallizing polymers. It is a phenomenological suspension-based model at low crystallinity, which incorporates a percolation transition and then a rollover at high crystallinity into a semicrystalline state. It was found to provide a good fit over the full range using only two fitting parameters [14].
The success in fitting the modulus-crystallinity data to a percolation-based model spurs interest the fundamental nature of this percolation itself. Can we obtain direct evidence of the percolation, and if so, what is the fundamental structural unit causing it? How do we relate percolation behavior to well-known fundamentals of polymer crystallization such as nucleation followed by spherulitic growth and impingement? Here, we focus on the spherulite and its superstructures as the structural unit to be measured in conjunction with rheology during isothermal crystallization measurements. We note that for isothermal crystallization in iPP that is conducted at temperatures T > 80 °C, one anticipates heterogeneous nucleation [44].
One potential independent variable for such a study is the gap height. To our knowledge, there are no systematic measurements of the gap dependence of rheological response of crystallizing polymers, though an effect has been postulated [11]. It is known from the analytical work, simulation, and DSC that spherulitic structures and the overall rates of crystalline growth can be highly modified by changing the gap height [11,28–31]. For example, in the absence of surface nucleation, if the gap height is less than the spacing between nucleated spherulites, the overall crystallization rate decreases compared to large gap because for large radius, the crystallinity induced by a given spherulite increases as the square of its radius, rather than the cube.
If the percolation of spherulites plays an important role in the rheology of crystallizing polymers [4], then one may ask what happens when the superstructure underlying the percolating entities is varied by changing the gap height. In the case of electrical percolation, it has been shown theoretically and experimentally that finite-size effects can dramatically modify the percolation threshold [45,46]. Gap-dependent effects could thus be a useful variable to explore the relationship between the structure and rheology because they provide a means to vary the spherulite superstructure, while leaving the molecular structure, nucleation rates, front growth velocity, and temperature unchanged.
In this work, we utilize the simultaneous rheology-microscopy approach of Pantani et al., along with their use of iPP, as it allows for the measurement of spherulites and their superstructure [11]. We extend their approach in several critical ways to enable exploration of the percolation behavior. First, we conduct deterministic experimental reconstructions (to be described later), which allows us to work over the full range of spherulite volume fractions, whereas Pantani et al. were limited to about 30% by volume due to turbidity issues [11]. Second, we augment these experimental reconstructions with those obtained by stochastic numerical simulations, enabling the exploration of the role of surface nucleation and of gap dependence. These methods allow us to construct modulus-crystallinity plots and through comparison with our reconstructions, to determine the nature of the percolation transition. Third, we conduct measurements over a range of gap sizes, for reasons indicated above.
We first present results at a single gap height in Sec. III A to show how the rheology integrates with the optical images, the experimental deterministic reconstructions and the extracted information about the spherulitic superstructure. In Sec. III B, we then show the gap-dependent results along with numerical simulations. We use GEM fits to show how typical gap heights of ≈1 mm exhibit a percolation transition, whereas narrower ones exhibit more of a linear one (Sec. III C). Finally, we show numerical simulations that are designed to highlight the relative roles of the surface and bulk nucleation, as these are confounding effects in these experiments (Sec. III D).
II. METHODS
The experimental setup integrates a microscope and rotational rheometer, coupled through an optically transparent base and is described elsewhere (though we do not use the Raman capability in these experiments) [36]. It is functionally equivalent to the HAAKE MARS rheometer with the RheoScope attachment. The bottom surface is composed of glass and the top is steel. We use the instrument to measure isothermal crystallization kinetics by simultaneous measurement of dynamic modulus and depth-resolved optical microscopy. We use a plate-plate geometry with 8 mm upper plate diameter and utilize four different gap heights, h = (0.1, 0.2, 0.5, and 1 mm). The temperature protocol is identical for all experiments; the sample is heated to 220 °C and maintained there for at least 10 min to erase thermal history, then cooled at a rate of 10° C/min to T = 141 °C, then cooled at a slower rate of 2 °C/min until it reaches the selected value of Tc = 131 °C, where it is maintained for the duration of the experiment. This temperature profile is chosen to match the thermal response time of the rheometer. We define t = 0 s as the time when the temperature reaches Tc. The optical images showed no evidence of spherulite nucleation before Tc is reached. The modulus was measured at Tc via SAOS at a frequency ω = 2 rad/s using a fixed strain amplitude of γ = 6 × 10(−3).
Optical microscopy was conducted in the nonpolarized reflection mode with a 10× objective lens. The focus of the objective lens was scanned repeatedly from the bottom surface to top [11]. The objective lens can also translate in the rheometric radial direction. The radial position (r) of the objective was set to approximately r = 3 mm. Images were acquired when the focal plane coincided with spherulites, as ascertained by image sharpness. The height (z) of a given spherulite was thus obtained from the knowledge of the focal position and its (x,y) position and its diameter were determined by subsequent image analysis. Since the depth resolution of the optical microscope is approximately 0.075 mm, we do not attempt depth-resolved measurement for the h = 0.1 mm experiment. While radial flow is anticipated due to the change in density during crystallization, we did not explicitly measure it.
Measurement of the spherulite growth rate, vs, is made from the slope of diameter versus time for six spherulites. We found vs = (0.09 ± 0.1) μm/s, with no observed systematic variation as a function of the gap height, of the position within the sample, or between the surface versus bulk-nucleated spherulites. Given the strong variation of spherulitic growth rate versus temperature [47,48], this also indicates minimal temperature variation in our observation volume. Measurement of bulk spherulitic nucleation density was made by the measurement of the number of spherulites produced in a given time over a given 3D volume. Measurements were made before the spherulitic volume fraction exceeded 10%. We measured the bulk nucleation rate as . The surface nucleation rate was made in an analogous fashion. We found run to run variability in , as documented later. Once the work was completed, we traced this variability to minor differences in the plate cleaning process, as opposed to an inherent gap-dependent difference. This is discussed further in the supplementary material [52]. The time and spatial coordinates for every nucleation event were recorded for use in reconstructions.
3D renderings of the spherulite structure were performed in two modes via computation using Python. The first mode is a deterministic experimental reconstruction and is based on the coordinates of all the observed nucleation events, along with vs; the second is a stochastic numerical simulation, based on the inputted nucleation rates.
At every timestep, existing spherulites undergo growth. Specifically, each spherulites is represented by a radially growing sphere centered at the location of the nucleation with the theoretical unobstructed radius of spherulite i, ri, growing with rate . This equation is then discretized such that vs with timestep Δt. The resulting list of ri is stored at every timestep. However, as multiple spherulites can impinge on each other, a 3D grid with grid spacing ΔV is superimposed over the entire simulation to keep track of which voxels are occupied by a spherulite and if occupied, from which spherulite. At every time step after ri, every unoccupied grid point is checked to see if it is now occupied by a spherulite. Thus, a voxel becomes occupied by spherulite i if the distance between the center of the spherulite i and the center of the voxel is less than ri. To make the above procedure more concrete, imagine two spherulites nucleated on the surface growing toward each other. Their (theoretical) ri will continue to grow such that it extends beyond the surface and overlaps with each other, but in the grid representation no voxel will be occupied by two spherulites and the grid does not extend beyond the confines of surfaces. The grid representation allows for ease of calculating the volume fraction (number of voxels occupied by a spherulite divided by the total number of voxels), surface area (number of surface voxels occupied by a spherulite divided by the number of surface voxels), and cluster quantities (using image processing libraries in Python).
Second, nucleation events occur. If the code is in experimental reconstruction mode, it is provided a list of the locations and times at which nucleation events were observed in an experiment. If a nucleation event occurred between the previous timestep and the current timestep, a new sphere is created with a radius that accounts for any growth between when the spherulite nucleated and the current time. If the code is in numerical simulation mode, the nucleation events are determined using the definitions and . From a numerical implementation perspective, at every time step, an open bulk voxel is allowed to nucleate with probability , while an open surface voxel is allowed to nucleate with probability .
In numerical simulation mode, was set to the experimentally determined value, and was set match individual experiments, or as indicated. For the reconstructions, the simulation box was set to be 1.05 mm by 0.78 mm, while for the simulations it was set to be 5 × 5 mm2 with the height in all cases specified by experiments or as indicated. The grid size was chosen to be 10 μm, and the timestep was chosen so that for our measured value of vs, a radial growth of 5 μm occurs per timestep; this leads to a timestep of 55.5 s. All of these parameters were chosen to ensure the convergence of the volume fraction and surface area profiles, and in the case of the numerical simulations, the inputted nucleation rates match the simulated nucleation rates. The Python code, as well as a text files for reproducing results, can be found as part of the supplementary material [52].
Note that our method is for homogeneous nucleation, while the experimental nucleation is expected to be heterogeneous. However, by comparing with the heterogeneous method of Haudin and co-workers [28], we find that the two methods are mathematically equivalent in the limit that our grid sizes, our time steps, and their grid sizes are sufficiently small, while their maximum number of nucleation sites is large. More specifically, their activation frequency, q, is equal to our times their grid size cubed [see their Eq. (25)]. This means that as long as the nucleation density is high enough, both homogeneous and heterogeneous nucleation will produce the same results. Given the agreement between the volume fraction for our numerical simulations and reconstructions, we are in this limit. However, there is a subtle difference between the experimental reconstructions and the simulations in terms of late time nucleation events, which we discuss later.
The iPP utilized in these experiments was kindly supplied by the Colby group and has been used in several publications on flow induced crystallization [49–51]. They characterize the iPP as having Mw = 448 kg mol−1, a molar distribution of Mw/MN = 7.2 and a tacticity of 95.7% [49].
III. RESULTS
A. Single gap: Rheology and reconstructions
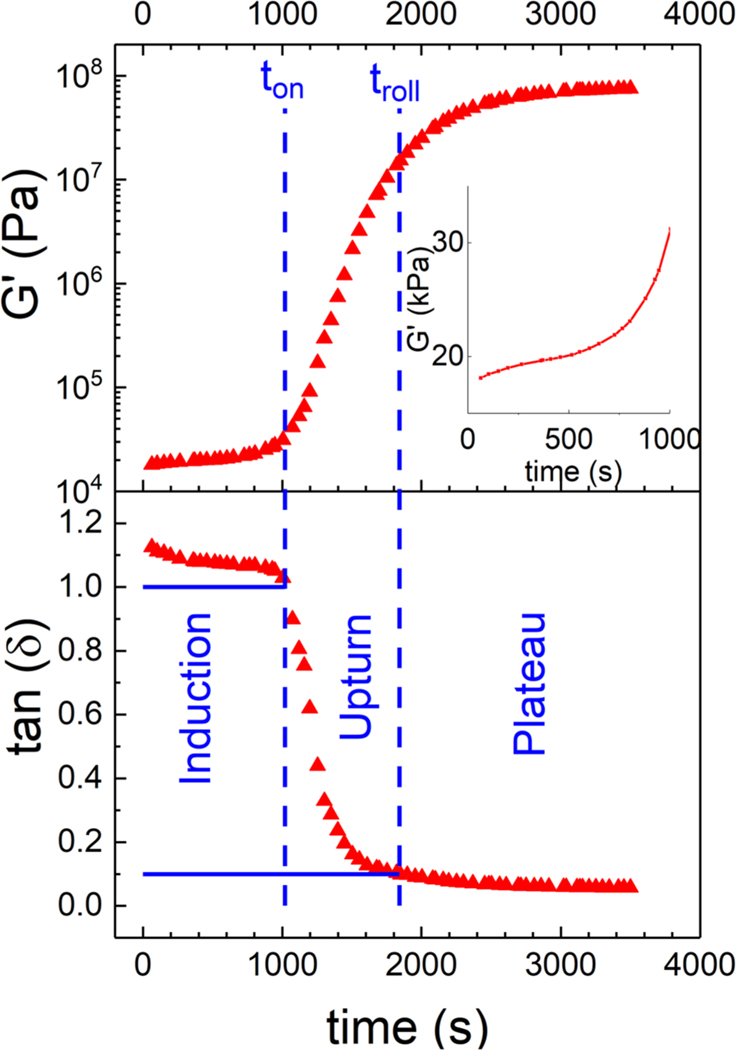
Figure 1 shows typical growth of the transient elastic modulus, along with the concomitant decrease of tan(δ), for the gap height h = 0.5 mm following the protocol described in the Methods section. The estimated relative uncertainty is 5%. It exhibits three regimes: induction, upturn, and plateau. We draw vertical lines indicating transitions between them labeled as the onset time (ton), which is defined as the time when tan(δ) = 1.0, and the rollover time (troll), defined as the time when tan(δ) = 0.1. These two chosen values of tan(δ) that define ton and troll were selected because they correspond to the points of large change in the slope of tan(δ) versus time. This works well at our chosen frequency (ω) but due to the frequency dependence of tan(δ) in the melt state, it may not be appropriate at other frequencies.
FIG. 1.
Transient elastic modulus (G′) and corresponding tan(δ) during isothermal crystallization for a gap height of h = 0.5 mm. The onset time (ton) and rollover time (troll) are defined as the times at which tan(δ) = 1.0 and at 0.1. The inset shows the growth of the elastic modulus on a linear scale during the induction regime.
The induction regime is characterized by relatively modest growth of G′ when plotted full scale, but the inset shows it increases by a factor of two during this regime. The upturn regime is characterized by a rapid growth in moduli; G′(t) and G″(t) increase by several orders of magnitude. The gel point that has been reported occurs in this regime. Finally, plateau refers to the regime where the growth rate of ln(G′) diminishes. We note, however, that at the rollover point, G′ is still only about 15% of the value that it reaches at late time.
Having examined the rheology at a particular gap, we turn to the structure. Figure 2 shows selected optical images collected at four points during the crystallization process: one during the induction regime; one at ton; one during the upturn regime; and one at troll. For each point, an image is shown from the bottom surface (z = 0) and one from a plane in the bulk. The spherulites that appear in sharp focus are those centered at the focusing image plane. The particular height of z = 410 μm in the bulk was selected in Fig. 2 primarily for esthetic reasons as multiple spherulites happen to be centered in this image plane and also aligned with each other; this is not generally the case. (Also, note that the image times between the surface and bulk images for a given time point are close but not identical; this is due to the manual mode in which images were collected.) Uncertainty in the image focus in the z direction is 75 μm. The orientation of the images with respect to the cylindrical coordinate system of the rheometer is shown in the lower left image. The z direction is out of the plane of these images. The dashed vertical line corresponds to a radial direction of the rheometer (note the θ vector has a slight curvature).
FIG. 2.
Microscopic images during isothermal crystallization for h = 0.5 mm. Images are displayed during four points of the process. The lower row of images shows the bottom surface at z = 0 mm, while the upper row shows a selected plane in the bulk at z = 410 μm. The images are offest from the center of the plates, as described in the text. The orientation of the images with respect to the (r, θ) directions in the rheometer are shown in the lower left image.
While the images show the growth and impingement of spherulites during crystallization; however, they do not provide an effective means to visualize the 3D structure. We thus carry out 3D deterministic reconstructions of the crystallization process, as described in the Methods section. In Fig. 3, we show deterministic reconstructions at similar time points as the images in Fig. 2. In the induction regime, one predominately observes isolated spherulites and clusters consisting of two impinged spherulites. As the spherulites grow, the clustering increases; both in terms of the number of spherulites in a cluster and the total size of a cluster. Eventually, a cluster spans the gap from the bottom surface to top in what we term a spherulitic superstructure. This occurs during the upturn regime. Those spherulites part of such a superstructure are then colored red, as seen in Fig. 3(c); we call this first gap span and denote its time of occurrence as ts. Also note the existence of both bulk and surface nucleated spherulites. Eventually, all spherulites become part of one superstructure and are colored red. The orientation of the images with respect to the cylindrical coordinate system of the rheometer is shown in the lower left image. Video of this process can be seen in the supplemental material [52].
FIG. 3.
Experimental reconstruction of a developing spherulitic superstructure during polymer crystallization. Blue is used to represent isolated spherulites and their clusters, while red represents a cluster (superstructure) that spans the gap from upper to lower surfaces. (a) Isolated spherulites and dimers, (b) larger spherulitic structures, (c) first gap-spanning structure, and (d) rollover. The orientation of the images with respect to the rheometer is shown in the lower left image. Video of this process can be seen in the supplementary material [52].
From the above efforts, we can compare simple measurands from the deterministic reconstructions with rheological data. In Fig. 4, we plot the spherulitic volume fraction , the surface areal fraction , and the number of independent gap-spanning superstructures S(t). Due to the stochastic nature of the process, and variations in the structure from one microscopic image to the one taken in a different location, we estimate the relative uncertainty to be 10%. The transition from S = 0 to S = 1 indicates the first gap-spanning superstructure (at ts), and it occurs during the upturn regime. The later transition from S = 2 to S = 1 occurs near troll, and it indicates that two independent superstructures have merged to become a single larger one. The induction regime covers values of that range from 0 to 0.16 and at ts, we find . Note that the diameters of the larger spherulites in Fig. 3(c) are nearly one-half of the gap height. This indicates that if the spherulites play an important role in the rheology, then there may be significant gap height effects.
FIG. 4.
(a) Spherulitic volume fraction () and surface area fraction () as a function of time for crystallization at h = 0.5 mm. The G′ data from Fig. 1 are included for comparison. (Note the linear scale on left and logarithmic on right.) (b) The number of independent gap-spanning superstructures (S) during crystallization.
B. Gap dependence
Figure 5 shows transient rheology for four gap heights ranging from h = (0.1–1.0) mm. Each plot still has the three distinct regimes, but their transition times are clearly a function of the gap height. One can ascertain by visual inspection that the slope of G′(t) in the upturn regime decreases as h increases. For h = 0.5 mm, we previously showed a correlation between the structure and the rheological regimes. If that concept holds, there should be gap-dependent changes in the spherulitic structure. Due to difficulties in setting and maintaining the gap at h = 0.1 mm, the estimated relative uncertainty there is 20%.
FIG. 5.
Gap-dependent kinetics of isothermal crystallization. The dashed vertical lines indicate the time of the formation of the gap-spanning superstructures for the larger three experimental gap heights. (a) Transient elastic modulus and (b) the tan(δ) during isothermal crystallization for the four indicated gap heights. (c) Corresponding spherulitic volume fraction for the larger three experimental gaps heights.
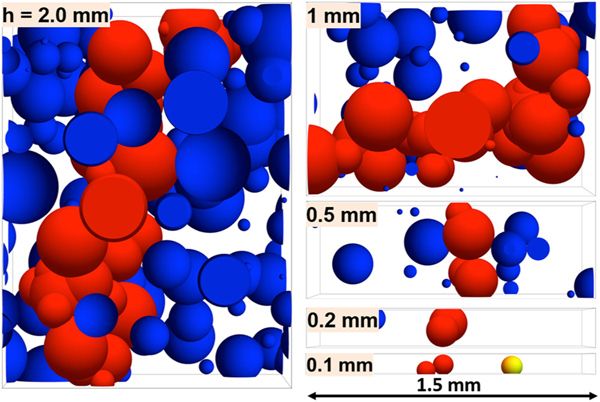
Figure 6 shows deterministic experimental reconstructions for h = (0.2, 0.5, and 1.0) mm at ts. The reconstructions of the right column are rotated 90° with respect to those on the left. When there are two independent gap-spanning structures (as seen for h = 0.2 mm), the second one is colored yellow until they merge. There are several trends that can be seen by visual inspection. First, the time of first gap span (ts) decreases with h. Second, the largest spherulite in a given image, rm, increases with h. Third, fewer spherulites are required to span the gap at small h than at large; i.e., (rm/h) decreases with h. Finally, the number of spherulites that are part of the first gap-spanning superstructure increases with h. Also, one can note differences in the coverage of the upper and lower surfaces by surface nucleated spherulites. As noted in the supplementary material [52], this variation is due to minor variations in surface cleanliness, rather than in the intrinsic gap-dependent effect.
FIG. 6.
Experimental reconstruction of spherulitic superstructures at the time of first gap span. The images in the right column are rotated about the z (vertical) axis by 90° from those in the left. Blue indicates an isolated spherulite/cluster, red indicates a gap-spanning cluster, and yellow indicates a second independent gap-spanning cluster. (a) h = 1.0 mm, (b) h = 0.5 mm, and (c) h = 0.2 mm. The orientation of the images with respect to the (r, θ) directions in the rheometer are shown in the upper two images.
Since we cannot perform an experimental deterministic reconstruction for the h = 0.1 mm experiment, we instead employ a numerical simulation as described in the Methods section. To gain confidence in the method, we employ numerical simulations for the h = (0.2, 0.5, and 1.0) mm gaps to compare with experiment. We also perform a simulation at h = 2.0 mm to gain information about gap dependencies as bulk behavior is approached.
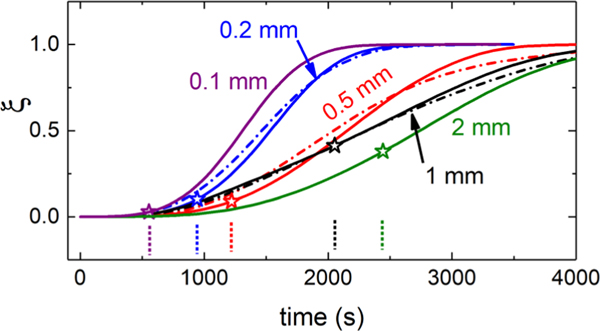
The volume fraction as a function of time for various gaps is shown in Fig. 7 for both experiment and simulation. For the experimental reconstructions (dashed-dotted lines), we can only construct data for h ranging from 0.2 to 1.0 mm for reasons described previously. For the numerical simulation method (solid lines), we show data over for a wider h range, from 0.1 to 2.0 mm. For the experimental reconstruction, the data at h = 0.5 mm are the same as that shown in Fig. 4. Good correspondence between the two is observed. The stars indicate the point of first gap span for the five simulations. The correspondence gives confidence in allowing us to use data from the simulations in situations where it is not accessible experimentally.
FIG. 7.
Volume fraction of spherulites as determined by stochastic numerical simulation (solid lines) and by experimental reconstruction (dashed-dotted lines, where achievable). The star symbols mark the point of the first gap-spanning superstructure for the simulations (the vertical dashed lines are pointers to their locations).
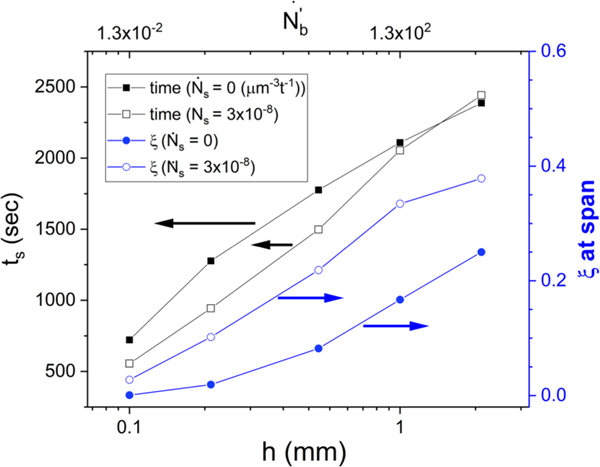
We can now compare the gap dependence of the time of the rheological transitions with that of the spherulitic superstructure formation. In Fig. 8(a), we show the rheological times (ton and troll) which are measured via the data in Fig. 5, while the structural gap span time (ts) is measured from the simulations in Fig. 7. The estimated relative uncertainty is 20% for the thinnest gap and 10% for the others. All exhibit an increase with h, demonstrating strong gap-dependent effects and correlations between spherulitic superstructure and rheology. It also shows that the system has not necessarily reached gap-independent bulk behavior by h = 1 mm; this is notable because this is a default gap height for many rheological measurements of crystallization. Figure 8 shows that when h is small, ton and ts are nearly coincident, but for larger gaps ts occurs roughly midway between the two rheological transition times. This hints that there may be differences in the superstructure at small gaps as compared to large gaps during these rheological transformations.
FIG. 8.
(a) Gap dependence of the rheological transition times (ton) and (troll) and the time of first gap span time ts. (b) The same data replotted in terms of dimensionless size and nucleation rate.
We can gain further insight into the above gap dependencies by replotting this data in terms of dimensionless quantities. We define a characteristic time for a spherulite that is nucleated on one surface to grow and impinge on the far surface a distance h away as
| (1) |
The dimensionless radial size of a spherulite that has grown for a time t is then defined as
| (2) |
Thus, r′ = 1 corresponds to a spherulite whose radius equals the gap height. We can also define a dimensionless volumetric bulk nucleation rate
| (3) |
where is again the bulk nucleation rate per volume. This can be considered as the number of nuclei to form in a time th in a volume h3, ignoring excluded volume constraints. For the current work, ranges from 0.013 for h = 0.1 mm and up to 130 for h = 1 mm. These are listed in Table I.
TABLE I.
For a given height (h), the table shows , the measured surface nucleation rate; , the computed dimensionless bulk nucleation rate [from Eq. (3)]; and the dimensionless surface to bulk nucleation rate . The final two columns pertain to the dimensionless fitting parameters from the GEM model (Sec. III C): the exponent is q and the critical volume fraction is ξc.
| h (mm) | q | ||||
|---|---|---|---|---|---|
| 0.10 | 2.9 × 10−8 | 0.013 | 25 | 0.89 | 0.06 |
| 0.20 | 2.9 × 10−8 | 0.21 | 12 | 1.5 | 0.22 |
| 0.50 | 1.9 × 10−8 | 8.1 | 3.2 | 1.5 | 0.19 |
| 1.00 | 1.6 × 10−7 | 130 | 14 | 2.0 | 0.37 |
The corresponding dimensionless parameter for surface nucleation is then
| (4) |
and the ratio of the surface to the bulk is then , which is also shown in Table I.
In Fig. 8(b), we replot the data from Fig. 8(a) in terms of the dimensionless quantities r′ and . Note that the curves now slope in the negative direction; this is because, as noted before, the size of the largest spherulites relative to h decreases as a function of h. One can equate r′ at gap span with the structure that forms at that point. For example, for , we find at first gap span. This indicates that the first gap-spanning superstructure is composed of a relatively simple structure such as two spherulites nucleated from opposite surfaces that impinge on each other in the center, or one bulk spherulite nucleated halfway between the two surfaces. In principle, the largest value of r′ is 1; however, this limit is not reached in the current experiments. In contrast, for , we find indicating that the simplest gap-spanning superstructure must be composed of multiple spherulites. We expect that bulk behavior corresponds to , which has not been reached at the largest gap of h = 1 mm. These data suggest that is a controlling parameter for bulk versus confined behavior, and we note that it is a function of , vs, and h.
C. Modulus-crystallinity relationship
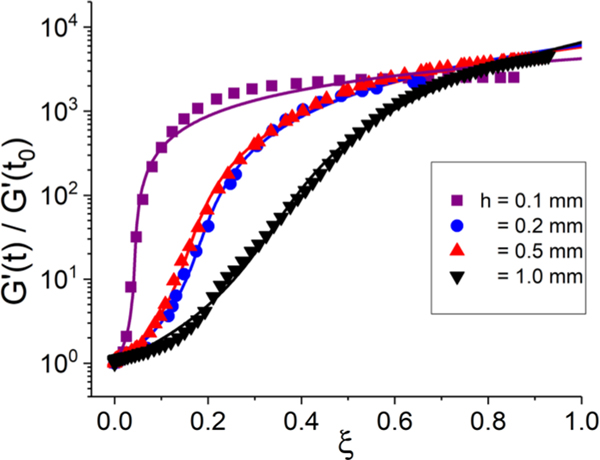
We can further explore the modulus-structure relationships by focusing on the functional relationship between G′ and . As seen in Fig. 9, the modulus-volume curves show significant gap-dependent behavior. Estimated relative uncertainty is as indicated previously. For the lowest gap of 0.1 mm, the upturn in G′ happens at low values of , whereas for 1.0 mm, we observe drastically different behavior with a more gradual upturn. The two intermediate thicknesses lie in between these extrema.
FIG. 9.
Normalized modulus versus spherulitic volume fraction for four gaps. The solid lines are fits to a GEM model.
In Fig. 9, the solid lines are fits of the data to the GEM model [43]
| (5) |
where
| (6) |
Here, denotes the value of G′ in the melt state when , and refers to that when spherulites have filled all available volume (). The exponents s and t describe the slope of the curves in the induction and plateau regimes; similar to recent work, we assume that s = t = q. (Nomenclature note: this q is distinct from, and not related to, the activation frequency referred to earlier in the text.) The fitted value ξc refers to the critical volume fraction associated with the percolation. In the present case of setting s = t, refers to the spherulite volume fraction at the point of maximum slope in the curve of G′ versus . Thus, the two important fitting parameters are and q [14]. We also treat as a fitting parameter because the quality of the measurements is limited due to the high modulus and volume change associated with late stage crystallinity.
The fitted GEM parameters show an interesting trend with respect to the gap height and are shown in Table I. For h = 1.0 mm, our values for and q are close to those found in polycaprolactone ( and q ≈ 1.8) where the typical spherulite size is much less than the gap height and so one anticipates gap-independent bulk behavior [14]. Thus, while previous plots indicated that there are still finite-size effects at this thickness, these GEM results nevertheless indicate that it is near bulk behavior. As the gap height decreases, both fitted parameters decrease. For the case of h = 0.1 mm, we find that and q ≈ 0.87. These values are close to what is anticipated in the case of a simple linear mixing rule relationship between G′ and
| (7) |
In this case, the GEM equation reduces to and q = 1. Our fitted values are thus close to those expected in a linear mixing rule case. Thus, at h = 0.1 mm, the system does not exhibit percolating behavior but something closer to a linear mixing rule.
D. Surface versus bulk effects
An important question is the origin of the gap-dependent effects; do they stem from surface crystallinity, or are we observing effects due to finite-size in percolation phenomena? Because showed run to run variation (Table I), it was difficult to tease out the differences between the two effects experimentally. Therefore, we turn to numerical simulations. Our approach is to compare two sets of simulations; the first set contains suppresses surface nucleation (bulk-only) by setting . The second set allows for bulk and surface nucleation; this has already been described (Fig. 7).
The bulk-only simulations () are shown in Fig. 10 for five thicknesses at the point of first gap span. The spherulites are larger and the nucleation density is higher with increasing gap height because the time at which the gap spanning occurs is greater for larger h. As expected, one clear difference between the earlier bulk plus surface nucleation (Fig. 6) as compared to bulk-only (Fig. 10) is that no surface nucleated spherulites are observed in the latter. But by visual inspection, we find many of the same trends with respect to h. In particular, the time at first span ts, as well as the number of spherulites that are part of the first gap-spanning structure increase with h. On the other hand, the relative size (rm/h) decreases with h. This indicates that major gap-dependent effects have an origin in the finite-size effects in bulk nucleation.
FIG. 10.
Numerical simulation of the spherulitic superstructure at first gap span in the absence of surface nucleation (). Simulations for five gaps ranging from h = (0.1–2) mm. The times at which these first spans occur increase with h and are plotted in Fig. 12. The same color scheme as Fig. 6.
We can quantify trends in the bulk-only simulations by measuring several kinetic features, as done before in the bulk with surface case. In Fig. 11(a), we find pronounced gap dependence for S as a function of time. Further, the time of first span (ts), seen as the point when the curves first deviate from 0, is an increasing function of h. This point is seen more clearly in Fig. 11(c), which shows the time of gap span versus the gap height. One can clearly observe that the saturation of ts with h occurs at about 2 mm. It indicates that 2 mm is approximately the height at which gap-independent behavior is expected. Further, these results show that bulk-nucleated spherulites lead to gap-dependent effects. In Fig. 11(b), there is a pronounced effect of the gap height on volume fraction as a function of time, but the effect is opposite to the case of both bulk and surface nucleation, as seen in by comparing Fig. 7 with Fig. 11(b). This demonstrates the intuitive result that at low gap, surfaces can profoundly increase the overall volume fraction of spherulites. It also shows the counterintuitive result that for the bulk-only case, (), the growth rate of the crystallinity is suppressed as gap decreases, as described previously [28,33]. This plot predicts that if one could experimentally work in the regime of , then one might observe an effect where at small gap, the rheological onset time occurs earlier, but the slope of modulus with time is decreased compared to large h. Figures 10 and 11 taken together show that the character of the gap-spanning transition is entirely different as a function of (or equivalently, h). For , e.g. (h = 0.1 mm), we see that there are a large number of independent gap-spanning pathways and that each path is composed of a small number (one or two) of spherulites. In contrast, for , e.g. (h = 2 mm), we observe only one or two independent pathways, but a large number of spherulites per pathway.
FIG. 11.
Numerical simulation results for . (a) The number of independent spanning superstructures (S) during crystallization. Note that S starts at 0 and ends at 1 for each gap. (b) Spherulitic volume fraction, ξ. (c) The time of the first gap-spanning superstructure (ts) versus the gap height (h).
One way to compare the two sets of simulations is to examine the time and volume fraction at first gap span. According to the dimensionless quantity , one anticipates the effects of surface nucleated spherulites to increase in importance as h decreases. In Fig. 12, where we compare numerical simulation conducted with against those with , note that ts (black squares), increases with h in both cases. For a given value of h, we see that the bulk with surface nucleation causes an overall decrease in ts as compared to bulk-only. This effect is greatest at low h and disappears by the point of h = 2.0 mm. This indicates that while there is a bulk dependent effect to ts, it is accelerated by the presence of surface nucleation, especially at lower gaps. An analogous effect can be seen with the spherulitic volume fraction where both values of show an increase with h. But for , we find increases because the surface nucleation adds additional spherulites at all gap heights, though the relative effect diminishes again at larger h. We thus find that gap-dependent effects originate from both surface and bulk nucleation effects.
FIG. 12.
Numerical simulation showing the difference between zero surface nucleation (filled points) and an experimentally typical value (open points) on the time and spherulitic volume fraction at first gap span.
IV. DISCUSSION
We now discuss the primary themes of this work and its implications, and a few subtler issues. First, emerges as a controlling parameter for the determination of the rheological character of crystallization transition. Since , the gap-dependent effects are embedded in this parameter. For , a percolation-based transition with bulklike behavior will occur. For , there should be a direct transition where a single spherulite could bridge the gap from one surface to the other and the modulus during this process would obey the linear mixing rule. A second important parameter, especially at the lower values of , is . These parameters directly affect how the spherulitic superstructures span the gap. In this work, we find that gap-independent behavior is reached at h ≈ 2 mm, which corresponds approximately to and r′ ≈ 0.1.
The existence of a gap dependence in the rheological measurements rules out certain explanations that have been postulated to explain the rheological behavior. As discussed above, the explanation for the gap dependence lies in the superstructure of the spherulites. Explanations that are based around the idea that changes in the amorphous region are responsible for the kinetics, such as physical gelation [8] or bridging molecules between spherulites [13], are not consistent with the observations presented here. It would be extremely useful to know the values of and in those experiments. We note that the current experiments do not rule out the existence of a possible exotic state developing in the melt region, such as a liquid crystalline phase, but it is not responsible for the rheological behavior reported here. The rheological kinetics are caused by the growth and impingement of spherulites. Once there is impingement, the impinged sites act as crosslinks (at the low stresses typical of SAOS) that stitch the spherulites together.
These experiments, like most conducted with torsional rheometers, are conducted at slower crystallization rates than one often encounters in polymer processing. However, if one can deduce fundamental physics from these longer timescale experiments, it will still apply at shorter time scales. For example, for crystallizing systems that form spherulites, the concept of percolation, and the dimensionless parameters deduced here, should still hold.
These experiments have been conducted at a single frequency (ω). Though more work is needed to understand the full frequency response, we can anticipate some results by examining Fig. 8, which summarizes much of the gap-dependent kinetics. The points representing the gap-spanning superstructure formation will of course be unaffected since this structural formation is not related to mechanical frequency. The rollover points should also be unaffected because visual inspection of the prior literature indicates that at later times, there is little frequency dependence to this point [34]. However, there should be some frequency dependence to the onset time, as lower frequencies start turning up before higher frequencies. The range of time over which the upturn occurs is rather limited [34], so the qualitative picture described here is expected to hold over the full range of mechanical frequencies.
One the difference between the experiments and the simulations is that the former pertains to heterogeneous nucleation, while the latter to homogeneous, as noted earlier. The method by which the nucleation rates in the homogeneous case were designed ensures good agreement between the overall crystallinity as a function of time between the two methods. However, one can perceive a subtle effect of the difference between the methods by comparing the longer time images from the experiments [Figs. 3(d), 6(a), and 6(b)], with those from the simulation (Fig. 10). In the experiments (heterogeneous), there are no spherulites that are nucleated at late, whereas in the simulations, one can observe small spherulites that nucleated at late times. These small spherulites do little to affect the spherulitic superstructure and their gap spanning, and so this difference between experiment and simulation is not expected to have a practical significance in the current work.
While the experiments conducted here employed a plate-plate geometry, the results contain clear cautions for experiments that utilize a cone and plate geometry. In the cone and plate geometry, there is of course a linear variation of h with the radial position in the sample. Since is a controlling parameter in the rheological response, and since it is proportional to h4, then it means that varies with radial position to the 4th power. One can imagine a scenario where at a given moment in time the inner radial region is in the rollover regime, the midradial is in the upturn regime, and the outer edge is in the induction regime. Thus, one must use caution in quantitative interpretation of such results.
We make a final comment on the term induction. This term has been used in the rheological literature to refer to this early time behavior where there is little growth in modulus when plotted on a log-linear fashion. However, as noted in the inset of Fig. 1, there is in fact growth in modulus by roughly a factor of 2 in this regime. Further, as shown by the optical images, there is significant nucleation and growth in it. Indeed, standard crystallization kinetics theory, for example, from the Avrami model, does not recognize the existence of an induction phase. Thus, in some sense, the word induction is a misnomer, this early time response is better described as the regime where there is little impingement or gap-spanning superstructures.
V. CONCLUSION
These results illuminate the critical role of the spherulitic superstructure on the rheology of a crystallizing polymer. The superstructures are rather complex, consisting of surface nucleated spherulites connected to bulk-nucleated ones. Depending on the values of the bulk and surface nucleation rates, these superstructures can be quite different and cause different behavior in the GEM plot. The gap-dependent effects are expected to be significant under conditions of low nucleation density, defined loosely here to mean that a small number of spherulites are required to span the gap in the crystallized polymer. For any polymer, one can anticipate whether gap-dependent effects are expected through the dimensionless quantities r′ or . Our results show gap-dependent effects for r′ > 0.1 and .
The results here raise questions and offer opportunities for more understanding. At the molecular level, it would be important to determine how these results translate to other polymeric systems. If one can experimentally control and , then one can expect to generate a range of rheological responses. In our approach, we have treated the spherulites as structureless spheres that have a fixed modulus as a function of time. But what is the effect of considering the actual complexity of a spherulite? How do these results change if we consider shear-induced structures, which are frequently nonspherical? What are effects of precrystalline or mesomorphic transitions that have been postulated? Most importantly, can one now use these insights into models of real-world polymer processing, such as film blowing or additive manufacturing?
Supplementary Material
ACKNOWLEDGMENTS
The authors thank Anthony Kotula and Jack Douglas for important conversations and Ralph Colby for kindly supplying the material. Certain commercial equipment, instruments, or materials are identified in this paper in order to adequately specify the experimental procedure. Such identification does not imply recommendation or endorsement by the National Institute of Standards and Technology, nor does it imply that the materials or equipment identified are necessarily the best available for the purpose.
REFERENCES
- [1].Piorkowska E, and Rutledge GC, Handbook of Polymer Crystallization (Wiley, Hoboken, NJ, 2013). [Google Scholar]
- [2].Carrot C, Guillet J, and Boutahar K, “Rheological behavior of a semicrystalline polymer during isothermal crystallization,” Rheol. Acta 32, 566–574 (1993). [Google Scholar]
- [3].Boutahar K, Carrot C, and Guillet J, “Polypropylene during crystallization from the melt as a model for the rheology of molten-filled polymers,” J. Appl. Polym. Sci 60, 103–114 (1996). [Google Scholar]
- [4].Boutahar K, Carrot C, and Guillet J, “Crystallization of polyolefins from rheological measurements—Relation between the transformed fraction and the dynamic moduli,” Macromolecules 31, 1921–1929 (1998). [Google Scholar]
- [5].Schwittay C, Mours M, and Winter HH, “Rheological expression of physical gelation in polymers,” Faraday Discuss. 101, 93–104 (1995). [Google Scholar]
- [6].Pogodina NV, and Winter HH, “Polypropylene crystallization as a physical gelation process,” Macromolecules 31, 8164–8172 (1998). [Google Scholar]
- [7].Pogodina NV, Winter HH, and Srinivas S, “Early stages of polypropylene crystallization as physical gelation,” in Abstracts of Papers of the American Chemical Society (ACS, 1999), Vol. 218, pp. U637–U637. [Google Scholar]
- [8].Pogodina NV, Lavrenko VP, Srinivas S, and Winter HH, “Rheology and structure of isotactic polypropylene near the gel point: Quiescent and shear-induced crystallization,” Polymer 42, 9031–9043 (2001). [Google Scholar]
- [9].Gelfer M, Horst RH, Winter HH, Heintz AM, and Hsu SL, “Physical gelation of crystallizing metallocene and Ziegler-Natta ethylene-hexene copolymers,” Polymer 44, 2363–2371 (2003). [Google Scholar]
- [10].Lamberti G, Peters GWM, and Titomanlio G, “Crystallinity and linear rheological properties of polymers,” Int. Polym. Proc 22, 303–310 (2007). [Google Scholar]
- [11].Pantani R, Speranza V, and Titomanlio G, “Simultaneous morphological and rheological measurements on polypropylene: Effect of crystallinity on viscoelastic parameters,” J. Rheol 59, 377–390 (2015). [Google Scholar]
- [12].Acierno S, and Grizzuti N, “Measurements of the rheological behavior of a crystallizing polymer by an “inverse quenching” technique,” J. Rheol 47, 563–576 (2003). [Google Scholar]
- [13].Coppola S, Acierno S, Grizzuti N, and Vlassopoulos D, “Viscoelastic behavior of semicrystalline thermoplastic polymers during the early stages of crystallization,” Macromolecules 39, 1507–1514 (2006). [Google Scholar]
- [14].Kotula AP, and Migler KB, “Evaluating models for polycaprolactone crystallization via simultaneous rheology and Raman spectroscopy,” J. Rheol 62, 343–356 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [15].Räntzsch V, Begüm M, Ratzsch KF, Stellamanns E, Sprung M, Guthausen G, and Wilhelm M, “Polymer crystallization studied by hyphenated rheology techniques: Rheo-NMR, Rheo-SAXS, and Rheo-microscopy,” Macromol. Mater. Eng 304, 1800586 (2018). [Google Scholar]
- [16].Aris-Brosou M, Vincent M, Agassant JF, and Billon N, “Viscoelastic rheology in the melting and crystallization domain: Application to polypropylene copolymers,” J. Appl. Polym. Sci 134, 44690 (2017). [Google Scholar]
- [17].Hadinata C, Gabriel C, Ruellmann M, Kao N, and Laun HM, “Correlation between the gel time and quiescent/quasi-quiescent crystallization onset time of poly(butene-1) as determined from rheological methods,” Rheol. Acta 45, 631–639 (2006). [Google Scholar]
- [18].Van Ruth NJL, Vega JF, Rastogi S, and Martinez-Salazar J, “Viscoelastic behaviour during the crystallisation of isotactic polypropylene,” J. Mater. Sci 41, 3899–3905 (2006). [Google Scholar]
- [19].Custodio F, Steenbakkers RJA, Anderson PD, Peters GWM, and Meijer HEH, “Model development and validation of crystallization behavior in injection molding prototype flows,” Macromol. Theor. Simul 18, 469–494 (2009). [Google Scholar]
- [20].van Erp TB, Govaert LE, and Peters GWM, “Mechanical performance of injection-molded poly(propylene): Characterization and modeling,” Macromol. Mater. Eng 298, 348–358 (2013). [Google Scholar]
- [21].Titomanlio G, and Lamberti G, “Modeling flow induced crystallization in film casting of polypropylene,” Rheol. Acta 43, 146–158 (2004). [Google Scholar]
- [22].Zhang QL, Li LF, Su FM, Ji YX, Ali S, Zhao HY, Meng LP, and Li LB, “From molecular entanglement network to crystal-cross-linked network and crystal scaffold during film blowing of polyethylene: An in situ synchrotron radiation small- and wide-angle x-ray scattering study,” Macromolecules 51, 4350–4362 (2018). [Google Scholar]
- [23].McIlroy C, and Graham RS, “Modelling flow-enhanced crystallisation during fused filament fabrication of semi-crystalline polymer melts,” Addit. Manuf 24, 323–340 (2018). [Google Scholar]
- [24].Northcut LA, Orski SV, Migler KB, and Kotula AP, “Effect of processing conditions on crystallization kinetics during materials extrusion additive manufacturing,” Polymer 154, 182–187 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [25].Zhao M, Wudy K, and Drummer D, “Crystallization kinetics of polyamide 12 during selective laser sintering,” Polymers 10, 168 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [26].McIlroy C, and Graham RS, “Modelling flow-enhanced crystallisation during fused filament fabrication of semi-crystalline polymer melts,” Addit. Manuf 24, 323–340 (2018). [Google Scholar]
- [27].He P, Yu W, and Zhou CX, “Agglomeration of crystals during crystallization of semicrystalline polymers: A suspension-based rheological study,” Macromolecules 52, 1042–1054 (2019). [Google Scholar]
- [28].Billon N, Escleine JM, and Haudin JM, “Isothermal crystallization kinetics in a limited volume—A geometrical approach based on Evans theory,” Colloid Polym. Sci 267, 668–680 (1989). [Google Scholar]
- [29].Billon N, and Haudin JM, “Overall crystallization kinetics of thin polymer-films—General theoretical approach. 1. Volume nucleation,” Colloid Polym. Sci 267, 1064–1076 (1989). [Google Scholar]
- [30].Durin A, Chenot JL, Haudin JM, Boyard N, and Bailleul JL, “Simulating polymer crystallization in thin films: Numerical and analytical methods,” Eur. Polym. J 73, 1–16 (2015). [Google Scholar]
- [31].Yuryev Y, and Wood-Adams P, “Effect of surface nucleation on isothermal crystallization kinetics: Theory, simulation and experiment,” Polymer 52, 708–717 (2011). [Google Scholar]
- [32].Lin Y, and Fan YR, “Substrate effect on the crystallization of isotactic polypropylene,” J. Appl. Polym. Sci 125, 233–245 (2012). [Google Scholar]
- [33].Piorkowska E, Galeski A, and Haudin JM, “Critical assessment of overall crystallization kinetics theories and predictions,” Prog. Polym. Sci 31, 549–575 (2006). [Google Scholar]
- [34].Arora D, and Winter HH, “Network formation in a crystallizing polymer,” in Abstracts of Papers of the American Chemical Society (ACS, 2010), Vol. 240. [Google Scholar]
- [35].Gatos KG, Minogianni C, and Galiotis C, “Quantifying crystalline fraction within polymer spherulites,” Macromolecules 40, 786–789 (2007). [Google Scholar]
- [36].Kotula AP, Meyer MW, De Vito F, Plog J, Walker ARH, and Migler KB, “The rheo-Raman microscope: Simultaneous chemical, conformational, mechanical, and microstructural measures of soft materials,” Rev. Sci. Instrum 87, 105105 (2016). [DOI] [PubMed] [Google Scholar]
- [37].Tiang JS, and Dealy JM, “Shear-induced crystallization of isotactic polypropylene studied by simultaneous light intensity and rheological measurements,” Polym. Eng. Sci 52, 835–848 (2012). [Google Scholar]
- [38].Ratzsch KF, Friedrich C, and Wilhelm M, “Low-field rheo-NMR: A novel combination of NMR relaxometry with high end shear rheology,” J. Rheol 61, 905–917 (2017). [Google Scholar]
- [39].Janssens V, Block C, Van Assche G, Van Mele B, and Van Puyvelde P, “RheoDSC analysis of hardening of semi-crystalline polymers during quiescent isothermal crystallization,” Int. Polym. Proc 25, 304–310 (2010). [Google Scholar]
- [40].Rantzsch V, Wilhelm M, and Guthausen G, “Hyphenated low-field NMR techniques: Combining NMR with NIR, GPC/SEC and rheometry,” Magn. Reson. Chem 54, 494–501 (2016). [DOI] [PubMed] [Google Scholar]
- [41].Derakhshandeh M, Doufas AK, and Hatzikiriakos SG, “Quiescent and shear-induced crystallization of polyprophylenes,” Rheol. Acta 53, 519–535 (2014). [Google Scholar]
- [42].Obrzut J, Douglas JF, Kharchenko SB, and Migler KB, “Shear-induced conductor-insulator transition in melt-mixed polypropylene-carbon nanotube dispersions,” Phys. Rev. B 76, 195420 (2007). [Google Scholar]
- [43].McLachlan DS, “An equation for the conductivity of binary-mixtures with anisotropic grain structures,” J. Phys. C Solid State Phys 20, 865–877 (1987). [Google Scholar]
- [44].Silvestre C, Cimmino S, Duraccio D, and Schick C, “Isothermal crystallization of isotactic poly(propylene) studied by superfast calorimetry,” Macromol. Rapid Commun 28, 875–881 (2007). [Google Scholar]
- [45].Tremblay AMS, and Machta J, “Finite-size effects in continuum percolation,” Phys. Rev. B 40, 5131–5139 (1989). [DOI] [PubMed] [Google Scholar]
- [46].Schmelzer J, Brown SA, Wurl A, Hyslop M, and Blaikie RJ, “Finite-size effects in the conductivity of cluster assembled nanostructures,” Phys. Rev. Lett 88, 226802 (2002). [DOI] [PubMed] [Google Scholar]
- [47].Sajkiewicz P, “Transient and athermal effects in the crystallization of polymers. I. Isothermal crystallization,” J. Polym. Sci. B Polym. Phys 40, 1835–1849 (2002). [Google Scholar]
- [48].Derakhshandeh M, Mozaffari G, Doufas AK, and Hatzikiriakos SG, “Quiescent crystallization of polypropylene: Experiments and modeling,” J. Polym. Sci. B Polym. Phys 52, 1259–1275 (2014). [Google Scholar]
- [49].Hamad FG, Colby RH, and Milner ST, “Onset of flow-induced crystallization kinetics of highly isotactic polypropylene,” Macromolecules 48, 3725–3738 (2015). [Google Scholar]
- [50].Hamad FG, Colby RH, and Milner ST, “Lifetime of flow-induced precursors in isotactic polypropylene,” Macromolecules 48, 7286–7299 (2015). [Google Scholar]
- [51].Hamad FG, Colby RH, and Milner ST, “Transition in crystal morphology for flow-induced crystallization of isotactic polypropylene,” Macromolecules 49, 5561–5575 (2016). [Google Scholar]
- [52].See supplementary material at 10.1122/1.5109893 for information about cleaning, for an animated movie of a reconstruction of the growth of the spherulitic superstructure, and for the code and input data used in the simulations and reconstructions. [DOI]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.