Human Representation Learning

Abstract

The central theme of this review is the dynamic interaction between information selection and learning. We pose a fundamental question about this interaction: How do we learn what features of our experiences are worth learning about? In humans, this process depends on attention and memory, two cognitive functions that together constrain representations of the world to features that are relevant for goal attainment. Recent evidence suggests that the representations shaped by attention and memory are themselves inferred from experience with each task. We review this evidence and place it in the context of work that has explicitly characterized representation learning as statistical inference. We discuss how inference can be scaled to real-world decisions by approximating beliefs based on a small number of experiences. Finally, we highlight some implications of this inference process for human decision-making in social environments.

1. INTRODUCTION

Millennial decision-making can be complicated. We have a myriad of gamified apps that provide us with ever more goals to strive toward. Our attention is in high demand by different facets of social media. Our working memory is taxed by constant multitasking. To go about our daily lives, we must somehow discount the distal sense of catastrophe surrounding climate change (and the not-so-distal one brought on by a global pandemic). Yet, even in these conditions, we strive to make sense of the world and make good decisions. At the core of this flexibility is the ability to select relevant sources of information and use them for appropriate action selection.

Humans learn more from their experiences than just how to behave in different situations; they also learn to organize experiences into internal representations that facilitate future behavior. This organization depends on two core cognitive functions: selective attention and memory. In this review, we discuss evidence that attention and memory can be thought of as interacting components of representation learning. We show how humans rely on different forms of statistical inference to organize past experiences and how this inference process gives rise to compact representations of tasks that guide action in complex environments. We illustrate the generality of this framework by showing that people spontaneously rely on such inference in social environments.

Representation learning: the process of learning a useful and compact mapping between observations and states in a specific task. Usefulness can be measured by how efficiently one can solve a task given the current representation.

1.1. Partially-Observable Markov Decision Processes

We first lay out a framework for defining information selection from the point of view of a goal-directed agent that is trying to make optimal decisions in a multidimensional world.

A Partially-Observable Markov decision process (POMDP) formalizes an agent’s internal model of the way the world unfolds throughout a task (Kaelbling, Littman, & Cassandra, 1998; Russell & Norvig, 2002; Sutton & Barto, 2018; note that while POMDPs are often considered a formalization of the actual generative structure of the environment, here we focus on POMDPs as formalizing the agent’s internal representation of a task). POMDPs consist of tuples {S, A, T, R, O}. We can define the state space S as a set of features (known as dimensions or attributes in the psychology literature) relevant to the agent’s goal. For instance, when making tea, the state may include the location of the cup, the existence or absence of different ingredients already in the cup, and the temperature of the water in the kettle. Given a set of possible actions A (e.g., pour water into the cup), the transition function T = p(s_t+1|s_t, a_t) describes how the agent believes the state will change after an action, that is, the probability that each state will unfold given the current state and action. The reward function R = p(r_t|s_t, a_t) takes in the current state and action and returns r, a scalar representing the immediate utility of performing that action in that state (when making tea, reward is obtained only when drinking the prepared tea). Transition and reward functions can be either deterministic or probabilistic.

Importantly, in a POMDP, the state of the world is not directly observable. Instead, agents have access to noisy observations emitted by the state as per the observation function O = p (s_t|o_1:t, a_1:t), which they can use to infer the underlying state. However, observations do not uniquely identify states. For instance, the cup of tea will look identical before and after sugar was added to the hot water. As a result of this aliasing, observations are not a sufficient statistic for determining the probability that different events will unfold in the future (e.g., will the tea be sweet, and therefore highly rewarding). POMDPs, in this sense, are a formal representation of many real-world situations in which we must infer, using current and past observations and actions, the current state of the world. Observation, transition and reward functions together comprise a “world model” – a model of how the world would unfold henceforward, as per the current knowledge of the agent (Hamrick 2019). Based on this model, the agent can simulate different decisions in order to plan future action.

One might think of this process of inferring states from observations in two different ways. In the machine-learning POMDP literature, the observation function encodes a probability distribution over true states of the environment. Alternatively, we do not have to assume that a true Markov state that encompasses all that is necessary to determine T and R actually exists (R. Sutton, personal communication) and can instead interpret S_t as a state representation internal to an agent that balances accurately capturing the causal relationships between events in the world and the computational and representational constraints of the agent. Under this view, representation learning is the process of developing a mapping from raw observations to state representations that are appropriate for the current task. The usefulness of this mapping, and the inferred underlying states, can be determined by experience (McCallum 1997).

1.2. The curse of dimensionality

To make correct actions, many reinforcement-learning algorithms postulate that agents estimate, either through planning or through trial and error, the future value (i.e., the expected sum of future rewards) contingent on taking different actions at each state of the world. For instance, the value of adding sugar to an otherwise sugar-less cup of tea may be high, but the value of adding sugar once sugar had already been added is very low. There is much evidence that humans and animals learn such values from trial and error, and the neural substrates of this learning process are well mapped (Barto 1995, Collins & Frank 2014, Daw et al. 2005, Joel et al. 2002, Montague et al. 1996, Niv 2009, Schultz et al. 1997, Sutton 1988). But the same algorithms that explain behavior and neural activity on simple learning tasks learn much more slowly as the dimensionality of the environment grows (Bellman 1957, Sutton 1988)—too slow to accurately account for real-world learning (Lake et al. 2017). This is because representing all features of the environment quickly leads to a combinatorial explosion, yielding too many different states for which values and policies need to be learned (Figure 1).

Figure 1.

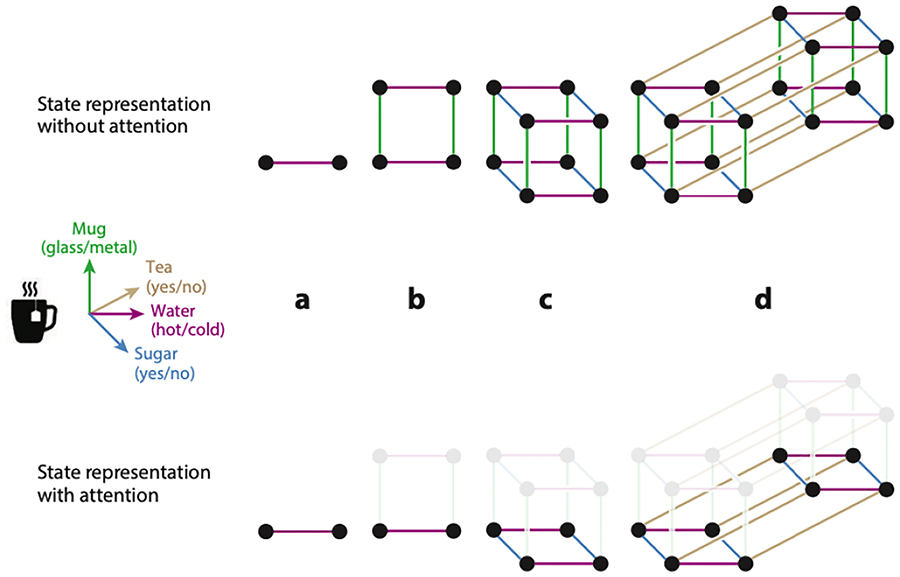
Selective attention for state representation. Consider a representational space for the task of making tea, defined along four dimensions: Water temperature (hot/cold), Mug material (glass/metal), Sugar (yes/no), and Tea (yes/no), each involving, for simplicity, a binary feature. The top row depicts how the number of states grows as we add dimensions. Considering only one dimension (Water) results in two possible states (a). Two dimensions would mean four states (b), three dimensions eight states (c), and four dimensions would mean 16 unique states (d). This exponential increase in the number of states as the number of dimensions grows is known as the curse of dimensionality. The bottom row shows how selective attention can solve this problem: ignoring even one dimension (Mug) reduces the size of the state space by a factor of two.

Nevertheless, given multidimensional observations, an agent could compress the state space by representing only some features and not others. This would improve learning through generalization – what is learned in one situation (adding sugar to a red mug of tea) can be used to estimate values and choose actions in other situations (making tea in a glass, or in a blue mug, or at the office rather than at home), as long as those differences (cup material, color and location) are not represented as part of the state. In the rest of this review, we discuss work on human representation learning: how humans learn a useful and compact mapping between observations and states that affords efficient learning.

2. ATTENTION AND MEMORY CONSTRAINTS IN REPRESENTATION LEARNING

At the core of representation learning is a need for efficient compression of experiences into a small number of states that summarize the task-relevant information in a way that supports efficient learning of action policies. The optimal level of compression depends on the task, and is also influenced by the capacity of the agent’s attention and memory systems (Luck & Vogel 1997, Ungerleider & Kastner 2000). Recent work suggests that both selective attention (Leong, Radulescu et al. 2017, Mack et al. 2016, Marković et al. 2015, Niv et al. 2015) and memory (Bornstein et al. 2017, Collins & Frank 2012) independently influence learning and action selection. However, a fundamental feature of both systems is their limited capacity: We cannot attend equally to all the features of an observation, and we cannot remember every observation we experience. This gives rise to a credit-assignment problem for meta-decisions (Griffiths, Lieder, & Goodman, 2015; Sutton, 1984): Which features of the observation space are important for inferring latent state and predicting future reward, and should thus survive attentional selection? And which past events (observations and actions) are necessary for correctly predicting state and reward dynamics and should therefore be remembered for later recall?

Credit-assignment problem: The problem of correctly allocating credit (or blame) for an outcome to antecedent actions or states.

2.1. Learning to Attend

Within psychology and neuroscience, attention has classically been defined as the selective processing of a subset of features at any stage between sensation and action (Gottlieb 2012, Lindsay 2020). We suggest that a useful way to think about the need for selective attention is as a solution to the curse of dimensionality (Section 1.2)—attending to irrelevant features of the environment will cause a proliferation of states that will slow down learning (Niv 2019). We next review literature that has formalized attention learning as a policy solution for the curse of dimensionality, allowing agents’ decision about what is relevant to inferring latent states change with experience (Figure 1). By selectively attending to only some aspects of the environment, an agent can easily generalize behavior across multiple different observations o, as long as they are similar along attended dimensions.

Recent theories of dimensional attention learning are rooted in the study of human category learning (Jones & Cañas 2010, Kruschke 1992): the process of grouping experiences into meaningful mental representations. In a classic categorization study, Shepard et al. (1961) showed that the ease with which we learn categories depends on the structure of the categorization problem. Human participants had to learn six types of category structures, each constructed from three binary stimulus dimensions (similar to Figure 1). Type I was based on a unidimensional rule, so attending to a single dimension was sufficient for perfect classification; type II instantiated an exclusive– or (XOR) logical rule in which membership depends upon whether one (not both) of two specific dimension values is present. In this case, correct classification depended on attending to two dimensions. Types III, IV, and V had some regularity, but an exception to the rule was always present. To perform well, attention to all three dimensions was necessary. Finally, type VI could only be learned by memorizing the mapping between individual items and category labels; that is, no generalization across the eight stimuli was possible. Human categorization performance reflected the underlying structure: People were fastest at learning type I problems and slowest at learning type VI problems.

To explain this pattern of results, the influential attention learning–covering map (ALCOVE) model formalized two key cognitive principles (Kruschke 1992): (a) The basis of classification is similarity to all exemplars in a category, and (b) classification requires dynamic selective attention to different stimulus dimensions. To accomplish the second principle, ALCOVE uses error-driven learning to learn attention weights that dictate how much each dimension should factor into the similarity computation. Notably, for the benchmark data set (Shepard et al. 1961), dynamic selective attention is critical for reproducing the patterns of human behavior, outperforming approaches based on rule learning (Nosofsky et al. 1994). The ALCOVE model is one example in a class of models that formalize dimensional attention in a connectionist framework, and show how attention could be learned via an error-correcting mechanism (Cohen et al. 1990, Jones & Cañas 2010, Roelfsema & Ooyen 2005). The model has also led to the insight that learners restrict their attention to dimensions that are needed to succeed at the task at hand (McCallum 1997, Rehder & Hoffman 2005).

In a striking example of such representation learning, Schuck et al. (2015) instructed participants to press a button to indicate the location of a patch of colored squares within a reference frame: regardless of the color of the squares, if the patch was closer to the bottom left or top right, one key was to be pressed, whereas if the patch was closer to the bottom right or top left, a different key was to be pressed. Initially, the task was perceptually difficult albeit conceptually straightforward. At some point during the task, unbeknownst to the participants, a deterministic mapping between the color of the patch and the correct response was introduced—all patches that were near the bottom left or top right were red, whereas the other patches were blue. Despite extended practice with the location-based policy, some participants spontaneously adapted their state representation to the new structure of the task, using color to respond faster. The strategy shift was preceded by an increase in color information content in the medial prefrontal cortex (Schuck et al. 2015). These results directly show that humans can quickly and flexibly change strategies from one feature to another in the absence of explicit instructions, as had been hinted at by the category learning work.

Notably, categorization tasks, and other commonly used dimensional attention learning tasks such as the Wisconsin Card Sorting Task in humans (Berg, 1948; Milner, 1963; Steinke, Lange, Seer, & Kopp, 2018), and the intradimensional/extradimensional shift task in animals (Birrell & Brown, 2000), commonly test attention learning with deterministic feedback (Radulescu et al. 2019a). To address attention learning in POMDPs, we focus on studies that use probabilistic reinforcement, as such an impoverished feedback signal places stringent requirements on the representation learning algorithm.

Several recent studies directly address the interaction between attention and reinforcement learning in probabilistic settings. Tasks in this literature bear a strong resemblance to category learning tasks, in that learning a response policy can be construed as categorizing multidimensional stimuli according to the response that maximizes reward for each. An important methodological development for studying representation learning in these tasks has been the adoption of trial-by-trial model fitting (Bishara et al., 2010; Daw, 2011; Marković, Gläscher, Bossaerts, O’Doherty, & Kiebel, 2015; Wilson & Collins, 2019). This method allows for inferring the dynamics of internal states (such as attention), predicting individual participants’ future behavior given those states (e.g., what they will choose, or how quickly) and searching for brain correlates of computational components underlying ongoing behavior.

Using this approach, Niv et al. (2015) have demonstrated that representation learning recruits the same brain areas known to engage in goal-directed attentional selection (Corbetta & Shulman 2002). A subsequent study that directly measured dimensional attention using a combination of functional MRI and eye tracking showed that humans choose and learn based on an attentionally filtered state representation that dynamically changes as a function of experience (Leong, Radulescu et al. 2017). Indeed, the same attentional-control network that is engaged during instructed attentional set shifting is sensitive to learned attention, broadening the role of cortical networks classically thought of as supporting visual attention to include representation learning (Scolari et al. 2015).

We note here that the question of attentional selection has also been longstanding in associative learning, albeit with a focus on attention as enhancing learning about features of a stimulus, or making decisions based on some features and not others, rather than subselecting features for processing and representing. Two prominent theories emphasize opposing factors that might determine how attention is allocated between competing stimuli: the consistency with which a feature predicts reward (Mackintosh, 1975), and its inverse, uncertainty about the prediction (Pearce & Hall, 1980). The balance between these two factors might depend on the purpose of selective attention, with attention to predictive features affecting action selection, and attention to uncertain features enhancing allocation of learning from feedback (Dayan, Kakade, & Montague, 2000; Gottlieb, 2012; Grossberg, 1987). These theories emphasize how quickly one should update reward expectations, whereas attention-learning theories in the categorization literature focus more on how we choose what to attend to.

Finally, current models of human attention learning are limited to selecting among a finite set of possible features, rather than modifying representational spaces to accommodate new ones. But a more general form of representation learning would require flexibly changing representational spaces, a problem we turn to in section 2.2.1.

2.2. Learning to Remember

Reducing the size of the representation space using attention is one half of representation learning. The other half requires the opposite operation: augmenting the current observation, for example using information stored in memory (Barron et al. 2013, Biderman et al. 2020, Bornstein & Norman 2017, Shadlen & Shohamy 2016). For instance, remembering our recent actions when making tea will helpfully resolve whether the state of the world already includes sugar in the cup, and whether water has been boiled or not. This gives rise to two additional representation learning problems: 1) learning what to store in working memory to augment the current observation (e.g., recent sugar-related actions), and 2) organizing past experience in long-term memory in a way that facilitates retrieval of their summary statistics in the relevant circumstances (Figure 2). In particular, for the latter, rather than encoding each observation into memory, say, by order of appearance, it is useful to infer which future situations current information might be relevant to—that is, to categorize observations by the states to which they pertain—and update the summary statistics of that state in long-term memory with the current observation. When the state (and thus the prior observation) becomes relevant again, it can be retrieved and used, and potentially updated with new, pertinent information (Gershman et al. 2017). This ability to actively select different aspects of our memories in the service of decision-making depends on the interaction between multiple memory systems that may operate on different timescales (Brunec et al., 2018; Hoskin, Bornstein, Norman, & Cohen, 2019).

Figure 2:

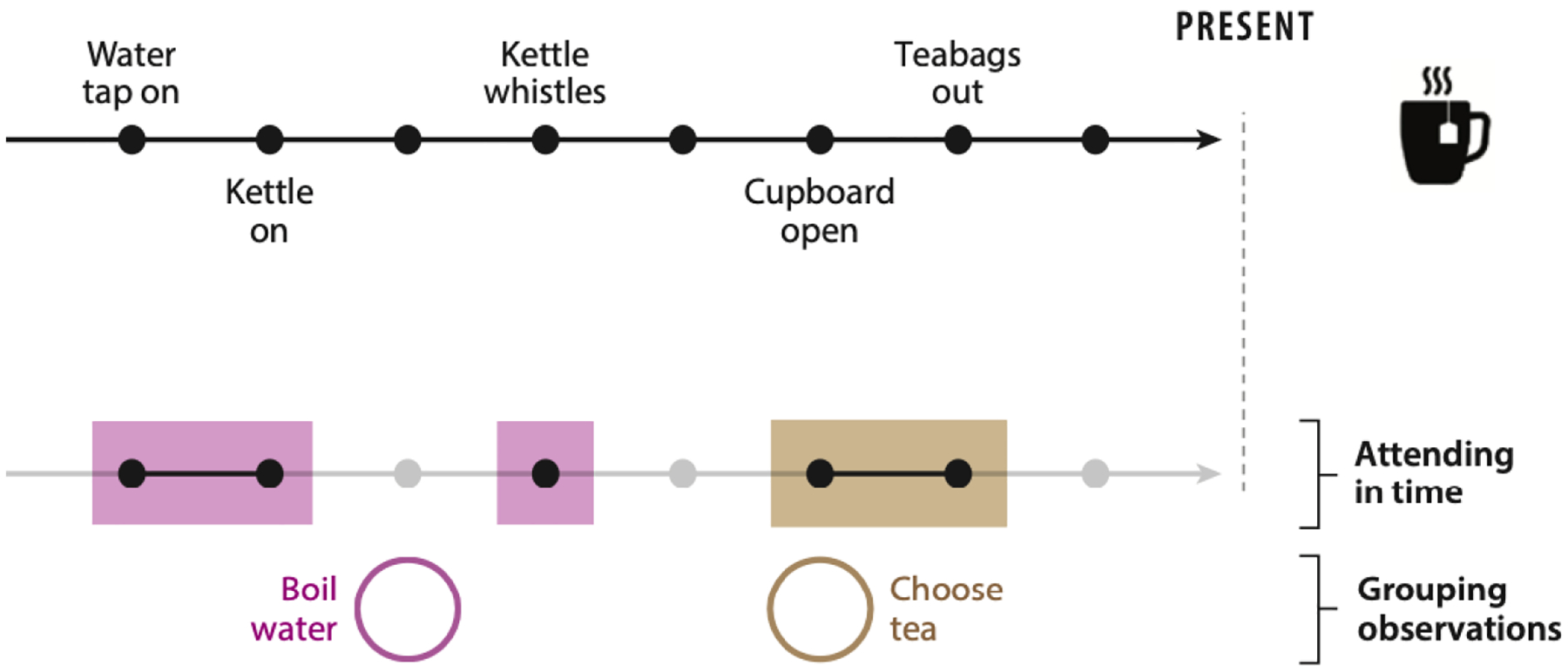
Selectively remembering and organizing past observations. For any given task, time can be viewed as an axis of the representational space (Figure 1). Consider a chain of observations one could make during the task of making tea. Only some of those past observations have relevance for the task. The question of which observations to remember can thus be reframed as attention learning in time. The agent has to selectively attend not only to different aspects of present sensory data but also to different past observations that should be included in the state. Once stored in memory, observations can be grouped in such a way as to facilitate retrieval when they become relevant for the task.

2.2.1. Organizing memory around latent causes

As is the case with attention, adaptive accounts of memory cast memory formation as a problem of generalization, but in time, rather than in perceptual space (Anderson & Milson 1989). From a reinforcement learning perspective, remembering can be viewed as a meta-decision that affects an agent’s construal of state. The broader question of representation learning can therefore be phrased as follows: Which past and present sensory data should the agent use to define the state?

Latent-cause inference provides a statistical framework for answering this question by grouping related experiences into latent (i.e., hidden) causes (Courville et al. 2006, Gershman et al. 2015). Latent-cause inference treats memory formation as a clustering problem, grouping experiences into memory traces based on similarity. Experiences that belong to the same latent cause can then be summarized, stored and recalled as part of the same memory trace (Gershman et al. 2017). One important insight of latent-cause inference theory is that creating new latent causes in memory depends on the extent to which new experiences are different enough from old ones to trigger the formation of a new latent cause. This organizational principle has helped unify a broad range of phenomena in psychology and neuroscience, most notably fear conditioning, categorization, and event segmentation (Anderson 1991; Gershman et al. 2010; 2017; Sanborn et al. 2010; Shin & DuBrow 2020; Franklin et al., 2020).

To illustrate how latent-cause inference can organize the way we use past memories to direct prediction and action in a new situation, consider compound generalization, the process by which animals and humans combine past learning about individual stimuli to form new predictions when encountering a combination of these stimuli. Experimentally, in compound generalization the agent first learns the predictive value of two simple stimuli. The agent is then tested on a novel compound that shares features with both of the simple stimuli. The degree to which the agent generalizes experience from simple to compound stimuli is measured through the resulting behavior.

The study of compound generalization has long been driven by a debate between elemental and configural theories. In elemental processing, a compound stimulus is treated as the sum of its parts, each with its own predictive value; in configural processing, the parts are integrated into a unique perceptual whole for which predictions are learned separately, with behavior depending both on the compound and on each of its elements/subcompounds, weighted by their similarity to the current configuration. Elemental and configural theories fundamentally differ in the degree of generalization they assume (Soto et al. 2014): Because individual cues are expressed independently in elemental theories, elemental generalization is stronger than configural generalization.

Soto et al. (2014) integrated elemental and configural theories into an account of compound generalization based on latent-cause inference. Their model grouped simple stimuli into latent causes based on their statistical association with reward (Courville et al. 2006, Navarro 2006, Shepard 1987, Soto et al. 2014). When the agent encountered a novel compound stimulus, it used the features of the compound stimulus to infer whether one or several latent causes are present. Critically, recognizing that even repeated presentations of the same stimulus (in training) may lead to somewhat different perceptions trial by trial, latent causes in this model were associated with whole regions in perceptual space. These are called consequential regions, as they describe a region in perceptual space that leads to the same reward consequences. According to the model, experiences in the same consequential region are stored together at learning and recalled together at decision time. Indeed, the model does not remember every experience – it summarizes them in sufficient statistics (the extent of the consequential region, and the probability of reward) that are associated with the latent cause. From this organization follows generalization: the extent to which a particular experience will generalize to related ones depends on the structure and size of the consequential regions. This principle explains, for instance, the effect of sensory modality on elemental versus configural processing (Melchers et al. 2008). When two stimuli are from different modalities, they are more likely to be clustered into two separate consequential regions (leading to summation of predictions when the compound is presented); whereas when two stimuli are from the same modality, they are most often clustered into a single consequential region (leading to averaging of predictions for the compound) (Soto et al. 2014).

Viewing memory organization through the lens of latent-cause inference suggests that signals that disambiguate latent causes will be useful in organizing memory encoding and retrieval. One such signal is the context (i.e., the set of features that remain relatively constant over time). Indeed, observations encoded in a similar context are putatively bound in memory by the context in which they were encoded and tend to jointly influence decisions (Bornstein & Norman 2017). In fact, one can argue, based on latent-cause inference theory, that context can be defined as the currently active latent cause. And, as predicted by latent-cause theory, recent work suggests that events that deviate from our expectations—and therefore signal a new latent cause—help organize memories into distinct memory traces (Rouhani et al. 2018, 2020).

2.2.2. Using memory to augment state representations.

Memory also influences state inference and representation by augmenting immediately available sensory observations with previous ones that are germane to inferring the current state or latent cause. Todd et al. (2009) articulated this problem in the form of a POMDP that defines its internal state as the current observation augmented with a working memory component. Their model learned what recent observations are important to store in working memory through trial and error: The action space included not only external actions (i.e., pressing a button) but also memory actions (i.e., replacing current working memory content with a new observation). Learning the optimal memory policy for this POMDP was similar to learning external actions through trial and error and updating state values and action policies based on prediction errors. The algorithm learned to behave optimally in a benchmark human sequence-learning task and exhibited computational constraints similar to those seen in human working memory.

Collins et al. (2014) used a different implementation of working memory to model a deterministic instrumental learning task with a varying number of states (stimuli) and three possible actions. Their agent had two independent components: a standard action value-learning module and a working-memory module that retained the most recent observations and decayed over time. On each trial, the agent’s policy was a mixture of the two components, where the mixing proportion was determined by the stimulus set-size (how many states humans had to learn about) and a fixed working-memory capacity. Collins et al. (2014) found that incorporating a limited-capacity working memory into the model captured human behavior better than did simple reinforcement learning. However, this model did not learn what to store in working memory.

Neither of the above models incorporated the idea of latent causes into the structure of memories used to augment reinforcement learning. Future work on representation learning stands to benefit from modifying these theories of working memory to account for the latent structure of memories, which can itself change with experience.

2.2.3. Memory for relational structure.

Models of memory that we have discussed so far address the question of which memories should be included in which state. But another aspect of memory that may be critical for generalization is its relational structure. Within the same state, humans group memories and concepts in relation to one other, and use this structure to make predictions about the future (Behrens et al., 2018; Schapiro, Rogers, Cordova, Turk-Browne, & Botvinick, 2013). One recent proposal by Whittington et al. (2020) combines one-shot Hebbian memory with a mechanism for learning the relational structure between individual memories. This mechanism enables the model to address a memory based on its position in a graph. Since the graph structure is abstracted away from sensory input, the model can efficiently generalize to new, unseen environments. Evidence suggests that humans can indeed learn to represent the temporal structure of memories as graphs, and use this knowledge to infer relationships that they do not directly experience (Garvert, Dolan, & Behrens, 2017; Mark, Moran, Parr, Kennerley, & Behrens, 2020).

3. APPROXIMATE INFERENCE IN REPRESENTATION LEARNING

In the above discussion, we eschewed implementational constraints on latent-cause inference. However, these are nontrivial. In particular, in this framework, the agent’s interpretation of the world relies on inferring a probability distribution over possible states given current and past observations. Exact Bayesian inference of this distribution is typically intractable in most cases (Niv et al. 2015, Roy et al. 2005). For this reason, sampling algorithms have recently gained popularity as neurally-plausible mechanistic accounts of how Bayesian inference may be realized in the brain online as new information comes in (Fiser & Lengyel, 2019; Haefner & Berkes, 2016; Sanborn & Chater, 2016; Sanborn, Griffiths, & Navarro, 2010; Schneegans, Taylor, & Bays, 2020; Speekenbrink, 2016).

Sequential sampling algorithms: algorithms that approximate a probability distribution using a finite set of samples and update the samples after each experience

Taking a sequential sampling view of learning explains the puzzling finding that even though learning behavior is often consistent with Bayesian inference at the group level, individuals are much more variable in their actions during a single learning episode, and learning can be an all-or-nothing process (Bower & Trabasso 1963, Daw & Courville 2008, Gallistel et al. 2004). This type of insight learning has been observed not only in simple associative learning studies, but also in experiments in which humans inferred hidden task structure (Schuck et al. 2015). Insight learning through sampling is also consistent with eye-tracking studies of multidimensional learning, in which humans appear to abruptly switch between different task representations (Leong, Radulescu et al. 2017, Rehder & Hoffman 2005). These findings suggest a mechanism by which humans sample different hypotheses about task structure and use them as a stand-in for the true structure of the task.

One recent study has explicitly modeled selective attention measured with eye-tracking as a sequential sampling algorithm that performs approximate statistical inference about task structure (Radulescu et al. 2019b). Under this view, humans build task representations by testing one hypothesis at a time about which features of the world are relevant for representing states. The hypothesis is updated by sampling new hypotheses in proportion to how consistently they predict recent observations stored in memory. The current hypothesis, in turn, directs attention to particular aspects of multidimensional stimuli (Radulescu et al. 2019a). Sequential sampling can thus provide a coherent mechanistic account for how attention and memory processes support representation learning, grounding it in principles of statistical inference (Daw & Courville 2008, Radulescu et al. 2019b). This view is consistent with empirical work showing that the focus of attention depends on what aspects of past experience are remembered (Goldfarb et al. 2016, Günseli & Aly 2020, Hutchinson & Turk-Browne 2012, Myers et al. 2017).

It is possible that sequential sampling algorithms could accommodate problems of increasing complexity, as those proposed by Shepard et al. (1961), by gradually adding more than one hypothesis or by considering alternative ways to parametrize the proposal distribution for new particles (Ballard et al. 2018, Goodman et al. 2008, Radulescu et al. 2019a, Song et al. 2020, Wilson & Niv 2012). Hypotheses themselves could take the form of task rules or causal links between observations and latent causes (Radulescu et al. 2019a). While additional work is needed to disambiguate between these different implementations, sequential sampling algorithms are a useful general way to think about how people test hypotheses about which features are most relevant for the task at hand (Ballard et al. 2018, Radulescu et al. 2019b, Sanborn et al. 2010, Song et al. 2020, Wilson & Niv 2012).

But how do humans know how long to sample in order to approximate the utility of a task representation well enough to make good decisions? Resource-rational theory provides a principled answer to this question by framing the problem in terms of the computational cost of sampling additional hypotheses (Hay et al. 2014, Russell & Wefald 1992). To be resource rational, an agent should only sample for as long as the cost of sampling is smaller than the additional value gained by expending computational resources. This idea has successfully been applied to modeling how humans make decisions in consumer choice. Analyzing gaze data in a ternary choice experiment, Callaway & Griffiths (2019) have shown that people’s fixation sequences are consistent with an agent that optimally solves the trade-off between performance and cost of computation. This approach has also been leveraged to model more complex computations, including planning and task decomposition (Callaway et al. 2018, Correa et al. 2020). In conjunction with sampling-based approaches to representation learning, resource rationality may therefore provide a set of mechanistic principles by which good-enough representations can flexibly be learned for a variety of tasks.

4. FATHOMING THE UNFATHOMABLE MINDS OF OTHERS

Arguably the most complex part of our environment consists of other people, whose key features such as current beliefs (Baker et al. 2017), mental states, and traits (Tamir & Thornton 2018) are rarely observable. As a result, we often infer these latent states from observable actions, physical characteristics of the target person (e.g., formal attire), and situational factors (e.g., job interview) with the overall goal of making accurate predictions about behaviors of others (Vélez & Gweon 2020).

The interactive-POMDP framework by Gmytrasiewicz & Doshi (2005) extended POMDPs to situations where multiple agents interact, each representing the other agents in their own POMDP. A later Bayesian theory of mind (BToM) model (Baker et al. 2017) further assumed that an observer uses POMDPs to represent the relationship between the inherently hidden minds of others (e.g., beliefs and desires) and observable variables such as actions and environments. In this study, human observers watched an animated agent (henceforth, a target) attempting to navigate to different goals (food trucks) with its view partially blocked by obstacles. The BToM model correctly predicted observers’ answers to questions regarding beliefs (e.g., does the target believe a Korean food truck is on the other side of the parking lot?) and desires (e.g., does the target like Korean food better than Lebanese food?) given the observation (e.g., the target goes past the Lebanese food truck to where they can look beyond an obstacle), appropriately capturing an observer’s inference about the target’s beliefs and desires given the observation.

Beyond predicting other people’s actions, inferring other people’s hidden cognitive states (e.g., knowledge and intention) is useful when we need to learn from feedback given by other people. For instance, we can make inferences about someone’s knowledge from observed actions and adjust how much we learn from them (for a review, see Shafto et al. 2012). Similarly, if we receive evaluative feedback (reward) from someone who we believe intends to communicate a rule to us, we can use their feedback to figure out the rule rather than trying to maximize the reward (Ho et al. 2019). On top of knowledgeability and intention to teach, people consider whether the teacher is trustworthy or has bad intentions (Landrum et al. 2015). Children and adults take into account niceness and honesty (Mascaro & Sperber 2009) as much as the smartness of a teacher when deciding whom to ask for information, suggesting that we draw inferences from traits, a deeper layer of hidden states.

Trait inference is beneficial in that it provides a stable basis for generalizing behaviors across different situations. People spontaneously form mental representations of other people’s traits (Winter & Uleman 1984), even when the immediate task does not require trait inference and could be performed better when ignoring such information. For instance, Hackel et al. (2015) had participants make a series of decisions about a partner in a game where the other player divided a pool of points between the two players. Importantly, immediate rewards (the number of points the target shared with the participant on a trial) and generosity (the proportion shared from the pool) were orthogonalized, and participants could maximize their share by just focusing on the immediate rewards, ignoring the trait generosity. Supporting the idea that spontaneous trait inference guides decisions, participants used both the reward magnitude and learned generosity information in making their decisions, with the ventral striatum responding to both reward and trait prediction errors. These results suggest the importance of including a mental model of other people in the state space, as a basis for guiding decisions. In addition to traits such as generosity, people seem to spontaneously represent how powerful are people around them, relative to themselves (Kumaran et al. 2016), with the hippocampus representing information regarding other people’s power and affiliation, creating a social map that can help humans navigate the social world (Tavares et al. 2015).

We also often build models of entire social groups—namely, stereotypes (Hilton & von Hippel 1996). For example, people associate gender with different professions, and even after learning counter-stereotypic information (e.g., “Elizabeth is a doctor, and Jonathan is a nurse.”), the stereotypic association lingers and slows down responses that are counter-stereotypic (Cao & Banaji 2016). Such associations emerge early in development and bias inferences, for instance about racial group membership when information about characteristics such as wealth is provided (Olson et al. 2012). It is worth noting that, as in nonsocial decision-making, features that are relevant to social decision-making can vary depending on the problem at hand. Therefore, the same questions about representation learning, and the involvement of attention and memory processes, are likely to be relevant—and even exacerbated—in the social setting. For instance, when people are evaluating a group of people based on interactions with group members, experiences with outlying group members weigh more heavily in the overall evaluation of the group, as predicted by models that assume representation learning and latent-cause inference. In particular, these models infer that outlier experiences come from a separate latent cause or group, and as a result overweigh their contribution to overall assessment (Shin & Niv, in press). Considering the hierarchical nature of groups composed of individuals therefore suggests another open question: How do the inferred characteristics of social groups inform the state inference of stable traits of an individual group member and, in turn, the transient mental state of the individual?

In the real world, we often generate spontaneous thoughts by representing the mental models of others (Mildner & Tamir 2018). And we effortlessly copy others’ strategies to solve complex tasks (Rendell et al. 2010). Studying how we build models of the highly rich and partially observable social world is therefore valuable not only because it will help understand social decision-making, but also because it will provide deeper insights into how we represent the world as a whole (Kampis & Southgate 2020). The field of social psychology has generated a wealth of research on topics that parallel questions in representation learning, for instance, how social groups organize memories about group members (Sherman et al 2002), how memory about a person and group-level representations interact with one another to guide predictions about individual behavior (Brewer et al. 1995), and how attention is allocated to information that fits our stereotypes (Plaks et al. 2001; Bastian & Haslam 2007). It would be useful to draw upon this existing body of research to further our understanding of inference processes and representation learning, especially given that our partially observable world so often involves making decisions about other people.

5. ISSUES AND FUTURE DIRECTIONS

We have reviewed work on how attention and memory processes contribute to representation learning, describing how these processes can be formalized within the framework of approximate Bayesian statistical inference within partially observable Markov decision processes, and arguing that people often organize experiences around their inferences about the social world. We now outline some open questions and possible future directions.

5.1. Determining the Balance Between Elements and Configurations

Echoing the debate between elemental and configural theories discussed in Section 2.2.1, several studies on representation learning have employed trial-by-trial model fitting to ask under which conditions humans adopt feature- versus object-based representations (Ballard et al. 2018; Farashahi et al. 2017, 2020; Mack et al. 2016; Marković et al. 2015). An open question concerns the dynamics of the balance between the two and their neural implementation.

Humans and animals are able to encode unique conjunctions on the fly (Melchers et al. 2008), with the hippocampus arbitrating the degree to which individual memories generalize into a coherent whole (Ballard et al. 2019, Duncan et al. 2018, Kumaran & McClelland 2012). Some recent evidence suggests the possibility that feature- and object-based representations may be reinforced in parallel (Ballard et al. 2019) and could be subserved by different specialized neural systems, all of which project to parts of the striatum. For instance, while the hippocampus may support object-based representations via projections to the ventral striatum (Haber & Knutson 2010), visual areas could convey feature-based representations via projections to the caudate tail (Seger 2013). This specialized organization in corticostriatal synapses appears to be maintained downstream in nigrostriatal dopaminergic synapses, potentially allowing updates of both elemental and configural state features in parallel (Engelhard et al. 2019, Hebart et al. 2018, Lee et al. 2020).

5.2. Hypothesis Spaces for State Representation

All algorithms for representation learning discussed in this review assume a low-dimensional hypothesis space over which inference can occur. In most experiments, this space is assumed to consist of separable dimensions such as color or shape. A pressing question remains regarding what are the building-block dimensions that define the axes of hypotheses in the real world (Boroditsky & Ramscar 2001, Medin et al. 1993, Navarro 2006). One possibility is that these dimensions are themselves learned via an unsupervised statistical inference process that extracts natural variation in the environment (e.g., covariance and hierarchical structure) (Kemp et al. 2007, Sanborn et al. 2009). For instance, Sanborn et al. (2009) showed that human-like dimensional biases emerge when training latent-cause inference algorithms (see section 2.2.1) on perceptual inputs that match those encountered by children.

But there remains a gap between the computational-level description of such models and their algorithmic implementation and neural substrates. Future work on Bayesian approaches to representation learning stands to benefit from understanding whether the assumptions such models make about representational primitives (e.g., simple features, conjunctions/compositions, cluster assignments, and motor programs) are borne out in neural data (Mack et al. 2016, Park et al. 2020, Tomov et al. 2018).

Another way to bridge this gap is to ask whether the kinds of structure that Bayesian models capture can be learned and represented in biologically plausible artificial neural networks (ANNs). Research at the intersection of human and artificial intelligence is focused on endowing ANNs with the kinds of dimensional biases humans display, for example, by tailoring the training regime to data constraints present in human development (Feinman & Lake 2018, Orhan et al. 2020, Smith et al. 2011) or by teaching agents to implicitly represent structure (e.g., objects and scenes) in an unsupervised manner (van den Oord et al. 2018, Sitzmann et al. 2019).

Various data-driven approaches have also led to the insight that conceptual representations are much richer than previously thought (Battleday, Peterson, & Griffiths, 2020; Hebart, Zheng, Pereira, & Baker, 2020; Hornsby, Evans, Riefer, Prior, & Love, 2020). For example, Hornsby et al. (2020) applied a Bayesian nonparametric model to consumer rating data to challenge a long-standing assumption of laboratory studies. They found that rather than organizing concepts only by their intrinsic dimensions and features (e.g., bananas are long and yellow), people organize concepts around what they can do with them (e.g., bananas go well in smoothies). Such work demonstrates the special status of actions in conceptual organization and points to a possible role for affordances as a key element of hypothesis spaces that guide representation learning (Khetarpal et al. 2020).

5.3. Toward Domain Generality in Representation Learning

Several recent studies suggests that human task representations differ across domains. For instance, Wu et al. (2020) found significant differences in exploration behavior depending on whether the task was defined in a spatial or conceptual domain, and the extent to which humans adopt elemental or configural representations depends on whether task stimuli are abstract or naturalistic (Farashahi et al. 2020). These results point to the possibility that the so-called psychological space (Shepard 1987) may be meaningfully decomposed into domains that have vastly different, yet relevant, underlying structures (e.g., perceptual features, physical properties, abstract conceptual properties, social graphs, and time).

Whether there exist learning mechanisms that can capture structure across different domains remains an open question. One approach that may move us closer to an answer is to complement typical laboratory experiments with naturalistic data from task environments that more closely match those that humans are likely to encounter in real life (Nastase et al. 2020, Smith et al. 2011). Allowing humans to be embodied and interact with naturalistic environments would allow us to study the full gamut of inductive biases that they use to solve in the real world even those tasks that have long been considered canonical lab experiments, such as visual search (Radulescu et al. 2020).

In the social realm, it is plausible, for example, that people reason by learning the structure of discrete graphs (Lau et al. 2020, Parkinson & Du 2020, Parkinson et al. 2017, Wu et al. 2020) and build a cognitive map from piecemeal learning (Park et al. 2020). Integrating this knowledge with models of other agents (Baker et al. 2017) may support a range of functions, from cooperation to imitation learning (Kleiman-Weiner et al. 2016, Rendell et al. 2010), and facilitate the transmission of knowledge about task structure.

In short, systematically testing, in naturalistic domains, the theories of representation learning reviewed here is a critical step forward in building a richer picture of how humans learn to represent a wide range of tasks.

SUMMARY POINTS

1. Humans learn compact representations of tasks that help them learn faster in the future.

2. Such representation learning relies on selective attention and memory to extract the most relevant features of both past and present experiences.

3. Approximate Bayesian inference provides an integrative framework for modeling how experiences are converted into task representations.

4. The ubiquity of this framework becomes clear when we consider how people use abstract world models to interpret social cues and predict others’ behavior.

FUTURE ISSUES

1. How do attention and memory interact to give rise to task representations?

2. Are elemental features and configural objects represented and reinforced in parallel?

3. What are the so-called primitives that constrain inference of task representations, and are they also learned from experience?

4. Do inference algorithms for representation learning extend to naturalistic settings?