Assessing the methodology used to study the ascending aorta haemodynamics in bicuspid aortic valve

Abstract

Aims 

Modern imaging techniques provide evermore-detailed anatomical and physiological information for use in computational fluid dynamics to predict the behaviour of physiological phenomena. Computer modelling can help plan suitable interventions. Our group used magnetic resonance imaging and computational fluid dynamics to study the haemodynamic variables in the ascending aorta in patients with bicuspid aortic valve before and after isolated tissue aortic valve replacement. Computer modelling requires turning a physiological model into a mathematical one, solvable by equations that undergo multiple iterations in four dimensions. Creating these models involves several steps with manual inputs, making the process prone to errors and limiting its inter- and intra-operator reproducibility. Despite these challenges, we created computational models for each patient to study ascending aorta blood flow before and after surgery.

Methods and results 

Magnetic resonance imaging provided the anatomical and velocity data required for the blood flow simulation. Patient-specific in- and outflow boundary conditions were used for the computational fluid dynamics analysis. Haemodynamic variables pertaining to blood flow pattern and derived from the magnetic resonance imaging data were calculated. However, we encountered problems in our multi-step methodology, most notably processing the flow data. This meant that other variables requiring computation with computational fluid dynamics could not be calculated.

Conclusion 

Creating a model for computational fluid dynamics analysis is as complex as the physiology under scrutiny. We discuss some of the difficulties associated with creating such models, along with suggestions for improvements in order to yield reliable and beneficial results.

Introduction

The aetiology of bicuspid aortic valve (BAV) aortopathy is still contested as reflected in the discrepant international treatment guidelines.^1–3 Much attention has therefore been paid to understanding the likely contributing factors—cardiovascular risk factors, genetics, and altered haemodynamic forces resulting from both a healthy and diseased BAV. Computational fluid dynamics (CFD), used in a multitude of engineering applications for decades, is now applied as a means of studying the blood flow and resulting forces exerted on the ascending aorta in patients with BAV.

Imaging and flow data, from either magnetic resonance imaging (MRI) or computer tomography (CT), applied to CFD has revealed that BAV is associated with altered blood flow patterns and wall shear stress (WSS) in the ascending aorta^4–8 even in the absence of stenosis. The resulting altered mechanical forces that are exerted on the aortic wall lead to dysregulation of the extracellular matrix and medial elastin fibre degeneration, partially mediated by matrix metaloprotein-dependent pathways.⁹ The application of simulated streamlines to flow MRI data has enabled visualization of blood flow in the thoracic aorta. This mathematical way of visualizing blood flow is prone to errors, which can impact measurement of both velocity magnitude and direction.¹⁰ Nonetheless, its application has revealed helical blood flow in BAV patients, with eccentric outflow jet patterns disrupting laminar flow and flow impingement zones along the greater curvature of the ascending aorta.¹¹ By contrast, non-diseased tricuspid aortic valve (TAV) subjects exhibit a laminar flow pattern in the ascending aorta.¹² Flow displacement or asymmetry and WSS influence blood flow pattern.

Parameters used to quantify the degree of helical and eccentric flow have been studied in an attempt to describe the changes associated with BAV aortopathy. Flow eccentricity is the deviation of ejected blood in systole compared to healthy TAV subjects. Parameters that quantify flow eccentricity include flow displacement and flow angle. Flow displacement is defined as ‘the distance between the vessel centreline node and the forward velocity-weighted centre of mass position’.⁶ Normalized flow displacement has been shown to be a more reliable quantification of flow eccentricity than systolic flow angle.¹³ It is also larger in BAV patients compared to TAV subjects matched to aortic diameter and valvular function^7,11 and correlates with distal ascending aorta diameter in BAV patients with fusion of the right and non-coronary cusps.⁷ Flow displacement has also been identified as a potential marker for BAV aortopathy phenotype.^11,14,15

Compared to TAV, BAV has been shown to generate higher and asymmetrically distributed WSS along the greater curvature of the ascending aorta,^16–19 where dilatation and thinning is typically found.²⁰ This corresponds to patterns of flow displacement¹¹ and may explain the dilatation pattern seen in the ascending aorta of BAV patients.²¹ Moreover, peak systolic WSS has been found to travel in a right-handed helix in both non-stenotic and stenotic BAV patients with fusion of the right and left coronary cusps.^22,23 Several studies show an elevated and asymmetrical distribution of WSS in stenotic BAV compared to TAV controls that varies with the degree of valve stenosis and BAV cusp fusion pattern.^{16,18,19,24,25} Wall shear stress has been shown to affect both vessel remodelling on a cellular level and have an impact on atherosclerosis.^9,26

Our research group has previously employed CFD and MRI to study WSS and other blood flow parameters in the ascending aorta in patients with diseased and healthy BAV and TAV.²⁷ In our latest endeavour, we sought to investigate the haemodynamic behaviour of blood flow in the ascending aorta before and after isolated tissue aortic valve replacement in patients with stenosed BAV and TAV.

Computational fluid dynamics

Computational fluid dynamics can analyse haemodynamic processes at ever-increasing spatial and temporal resolution. The CFD simulations of blood flow can be used to study aortic wall biomechanics and blood flow characteristics believed to be involved in the aortic disease process.

Fluid dynamics uses mathematical equations to describe the flow of fluids. For incompressible fluids that behave in a Newtonian manner, the momentum equations are known as the Navier–Stokes equations. These are used in a finite element analysis (FEA) model to calculate the blood flow and pressure gradients throughout the aorta and along its wall. Although blood has a complex rheological behaviour, it is modelled as a Newtonian fluid with a constant density (ρ = 1.06 kg/m³) and viscosity (µ = 0.004 Pa.s). For these equations to be applied successfully, pulsatile flow is modelled assuming a rigid aorta, i.e. without systolic expansion and diastolic elastic recoil. In order for the equations to be solved an anatomical model is constructed using a mesh that FEA can be applied to. As it is too complex to directly represent the heart and entire vascular system beyond the thoracic aorta, boundary conditions on the surface of the model are used to represent the system outside of the anatomical mesh.

The inflow boundary condition in our model is the patient-specific velocity profile recorded at the sinotubular junction (STJ) from phase-contrast MRI (PC-MRI). The outflow boundary condition is made up of a lumped parameter model for the distal vessels (innominate, left common carotid, and left subclavian arteries and the descending aorta at the level of the diaphragm) linked using a coupled multi-domain formulation (Figure 1). The patient’s recorded diastolic blood pressure (DBP) is used as the initial pressure in the simulation and is applied at the inlet boundary to create the initial stress load and start the simulation. The simulation continues in a pulsatile manner according to the inflow boundary conditions until periodicity in the flow and pressure is achieved.

Figure 1.

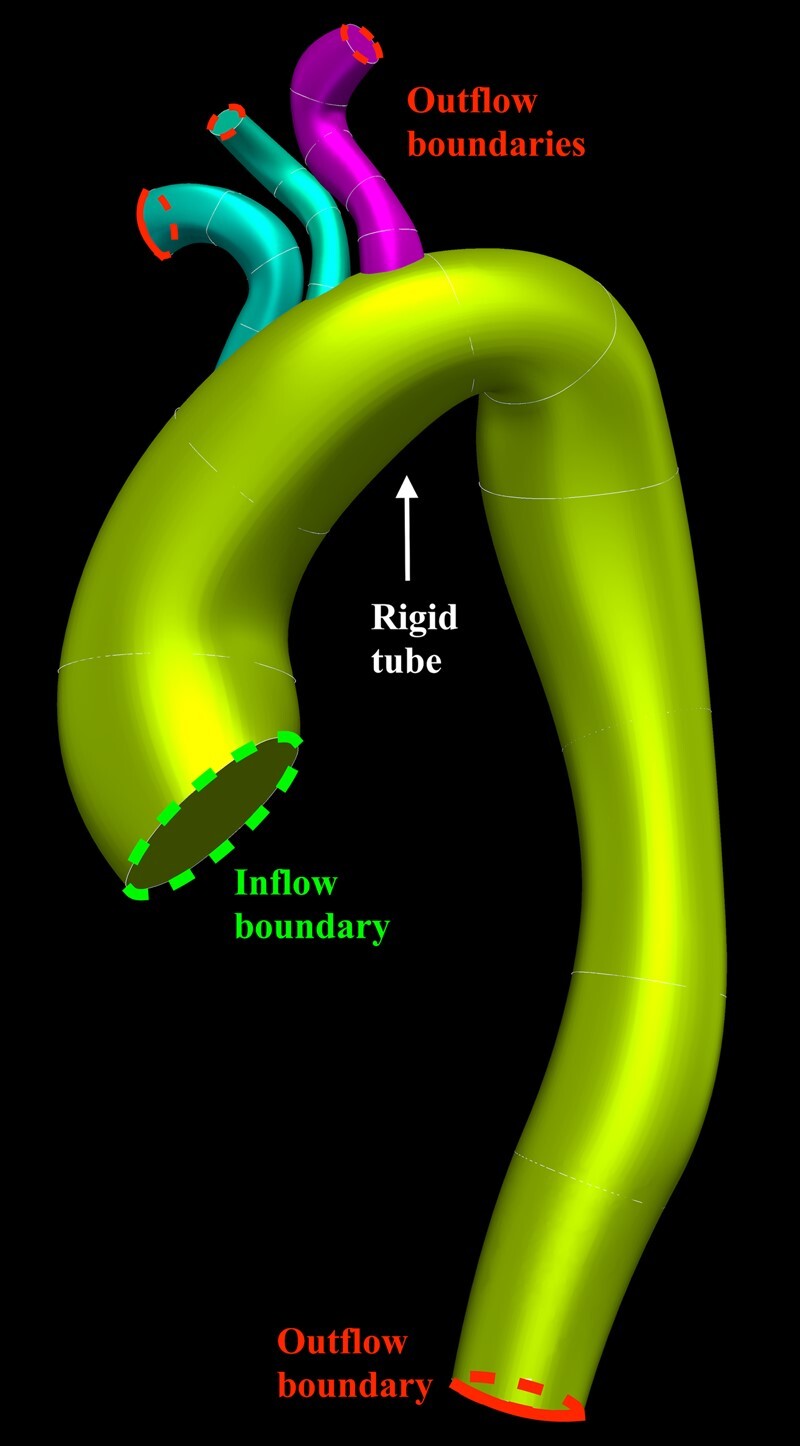
Lofted model of the thoracic aorta modelled as a rigid tube, including the head and neck vessels. Demarcation of the inflow and outflow boundaries of the defined domain.

Patient-specific outflow boundary conditions are assigned to each of the four outlets based on the patient’s supine upper limb blood pressure (BP). Superimposed on each outlet is a three-element Windkessel model, which represents the vessel tree beyond the boundaries of the model domain.^28,29 The three elements are proximal resistance (Rp), compliance (C), and distal resistance (Rd). Our group is the first to create a patient-specific model in this way with both patient-specific inflow and outflow boundary conditions.²⁷

Blood flow pattern was studied, using streamlines, as well as the associated variables flow asymmetry, velocity profile, and flow displacement. Computational fluid dynamics was employed to calculate WSS.

Due to problems with our method, software, and coding issues, we were unable to analyse all of these variables. Presented here are the results we were able to achieve, along with thoughts for improvement.

Methods

Patient group

Two patient groups were investigated before and after isolated tissue aortic valve replacement surgery; six patients with BAV and six patients with TAV. All underwent MRI before and after surgery. The two groups consisted of 6 females and 6 males, with ages ranging from 45 to 71 years and 68 to 82 years in the BAV and TAV groups, respectively. All patients in the study received the Carpentier-Edwards Magna Ease Pericardial aortic bioprosthesis, with valve sizes ranging from 21 to 25 mm.

Imaging

Gadolinium (0.3 mL/kg; galodiamide, Omniscan^®, GE Healthcare, Waukesha, WI, USA) was infused with a breath-held 3D fast gradient echo sequence using a Philips Achieva 3T scanner (Philips Medical Systems, Eindhoven, Netherlands) for all MRIs.

The entire thoracic aorta, including the head and neck vessels, were imaged using standard of care cardiac MRI imaging and magnetic resonance angiography (MRA).

Flow imaging was achieved with time-resolved 2D through-plane flow-MRI, or PC-MRI, acquired orthogonally in the ascending aorta above the aortic valve at the level of the sinotubular junction (STJ).

Software and hardware

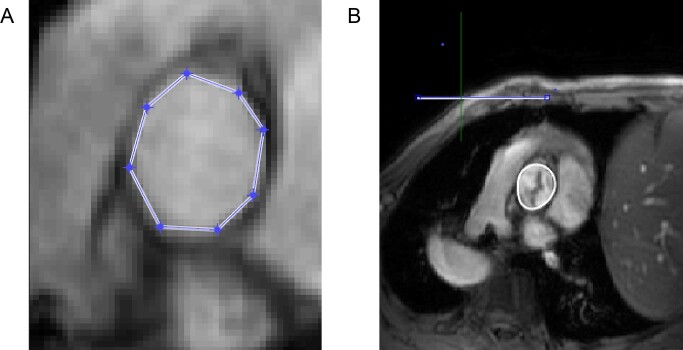
Anatomical models and their meshes required for FEA were generated in the software CRIMSON,³⁰ which was created by our biomedical engineering collaborators. It was also used to set the outflow boundary conditions of the model. They also wrote the code for Matlab (The Mathworks Inc., MA, USA) to create the flow rate waveform and the velocity profile from the PC-MRI data that is applied to the model at the inlet boundary condition. The Matlab code processes the velocity data by multiplying the velocity encoding constant (V_enc) by the image pixel intensity. This data are then ready for segmentation, which involves manually segmenting an axial cross-section of the aorta (tracing the vessel wall), at the level of the STJ, at regular time intervals for one cardiac cycle.

A high performance supercomputer (HPC) with a 640 core SGI Altix-UV with Nehalem-EX architecture was then used to perform the FEA, which solves the equations throughout the model to determine the pressures and velocities at all points in the aorta for the entire cardiac cycle.

Hypotheses

We hypothesized the following:

• Flow asymmetry is expected to normalize after tissue aortic valve replacement surgery, which allows a wider and symmetric opening of the prosthetic aortic valve (AV) cusps.

• A stenosed AV with restricted cusp motion is expected to give a peaked and narrow velocity profile at the level of the STJ. Due to unrestricted cusp motion, surgery is expected to soften, or broaden this velocity profile.

• Flow dispersion quantifies the appearance of the velocity profile and should mirror these results.

• We expect to see a helical or turbulent blood flow pattern in BAV patients pre-operatively, with a larger laminar component post-operatively.

• We expect to see a higher and asymmetrically distributed WSS in the ascending aorta in the BAV compared to the TAV group, which reduces and becomes more evenly distributed post-operatively.

Defining the domain

Based on the MRA data for each subject, 3D geometric computer aided design (CAD) models of the thoracic aorta were created. This involved creating centreline paths along the thoracic aorta, innominate artery (IA), left common carotid artery (LCCA), and left subclavian artery (LSA). Subsequent vessel segmentation involved identifying the vessel boundary by identifying differences in pixel intensity, related to contrast content. This was performed manually, where the user traced and placed a polygon around the vessel boundary. Three-dimensional models of the arteries were then created through an automated lofting process that interpolated all segmented boundaries (Figure 1). In order to ensure accuracy, a careful visual comparison was made by superimposing this model onto the maximum intensity projections (MIPs) of the MRAs.

The STJ was the first plane to be segmented. This would ultimately become the inlet boundary of the aorta model where inflow boundary conditions would be applied. The descending aorta, at the level of the diaphragm, was the last plane of the aorta to be segmented. This would become one of the model outlets. The final segmented planes of the head and neck vessels would become the other three outlets and form the outflow boundary conditions of the IA, LCCA, and LSA.

Finite element analysis requires a 3D model to be defined by a mesh consisting of data points. For each mesh point, equations are run to solve the haemodynamic parameters sought for the system or model. Our aortic model was discretized to generate a tetrahedral mesh. A pulsatile flow simulation was run, followed by a field-based anisotropic mesh refinement.³¹ This yielded a final mesh consisting of 4 million tetrahedral elements amongst the different subjects (Figure 2).

Figure 2.

Tetrahedral elements of the mesh. Global mesh size 1.0 mm with maximum curvature size 0.02 mm. A boundary layer size of 0.5 mm was applied with 5 layers of incremental expansion. This meant that at the boundary layer, i.e. at the vessel walls, the mesh was much finer in order to appreciate differences in wall mechanics, such as WSS to a much higher degree of detail and resolution.

Boundary conditions

Similar to the segmentation required for the anatomical model, the velocity data for one cardiac cycle was segmented manually from the PC-MRI images (Figure 3). This permits accurate data extraction despite movements of the aorta during the cardiac cycle. B-splines are used to smooth the segmented boundaries in order to reduce inaccuracies from the manual delineation of the lumen boundary. This generates a segmentation mask, which is applied to the flow MRI data, creating the velocity profile. Peak velocity, flow rate, and corresponding cardiac output (CO) generated by the Matlab code for the profile are compared to the corresponding physiological values, ascertained from the MRI data, validating the process. Additionally, the orientation of the velocity profile is manually mapped by the researcher in the Matlab software to copy that in the MRI images. This is corroborated using a third piece of visualization software called ParaView.³²

Figure 3.

Vessel segmentation in Matlab.

The patient’s DBP was used as the initial pressure of the simulation, which continued in a pulsatile manner according to the inflow boundary condition until periodicity in the flow and pressure were reached, usually 3–9 cardiac cycles. Once there was no intercycle variation in BP or flow splits, periodicity was attained. The limb BP recording of the patient before the MRI scan was compared to the BP in the LSA as generated by the CFD simulation. The aim was for these to be the same, indicating that the CFD simulation had accurately replicated the patient’s in vivo haemodynamics. The last cardiac cycle was used for the CFD analysis. If there were differences between the simulated and recorded BP, the Windkessel parameters were adjusted and the simulation re-run until the simulated BP equalled the measured BP.

Haemodynamic variables

The focus of our study was the ascending aorta, as the majority of BAV aneurysms involve this section. In order to look for asymmetry and differences in wall indices on different sides of the aorta it was divided into four parts; anterior greater (AG), as in the greater curvature, anterior lesser (AL), as in the lesser curvature, and posterior greater (PG) and posterior lesser (PL) sectors.

Flow asymmetry (Flow_asymmetry) at the level of the STJ was calculated to assess whether flow was central or eccentric.¹¹ It was obtained by calculating the centroid of the top 15% of peak systolic velocities (V_max^15%) $\left(po\mathrm{int}{\overrightarrow{x}}_b=\left(x_b,y_b,z_b\right)\right)$ and measuring its distance to the geometric centroid of the aortic plane $\left(po\mathrm{int}{\overrightarrow{x}}_a=\left(x_a,y_a,z_a\right)\right)$. The distance between centroids $\left(\Vert \overrightarrow{x_b}-\overrightarrow{x_a}\Vert \right)$ is then divided by the equivalent radius of the plane (R_eq). Flow asymmetry (Equation 1):

$${\mathit{FLOW}}_{\mathit{asymmetry}}=100\times \frac{\sqrt{{\left(x_b-x_a\right)}^2+{\left(y_b-y_a\right)}^2+{\left(z_b-z_a\right)}^2}}{R_{eq}}.$$ (1)

Flow_asymmetry is measured as a percentage, 0% indicating that flow is central to the axis of the vessel and 100% that flow is completely eccentric and biased towards the periphery of the lumen.

The metric Flow_dispersion represents whether the flow at each plane is peaked or broad. Flow_dispersion was calculated by dividing the area of the top 15% of peak systolic velocities (V_max^15%) by the total area of the plane. Flow dispersion (Equation 2):

$${\mathrm{FLOW}}_{\mathrm{dispersion}}=100 \text{Area} \text{of} {\mathrm{V}}_{\text{max}}{15}^{\%}/\text{Area} \text{of} \text{plane}.$$ (2)

A high percentage value of Flow_dispersion suggests that the flow profile is broad and wide, whereas a low value indicates a pointed, sharp velocity profile.

Wall shear stress refers to the force (N) per unit area (m2) exerted by a moving fluid in the direction of the local tangent of the tubular surface. It was measured throughout the cardiac cycle in the ascending aorta and the four sectors of the ascending aorta. WSS (τ_w) (Equation 3):

$${\tau }_w=\mu {\left(\frac{\partial \upsilon }{\partial r}\right)|}_{r=r_w}$$ (3)

where µ is viscosity, υ is velocity and r is the radius.

Results

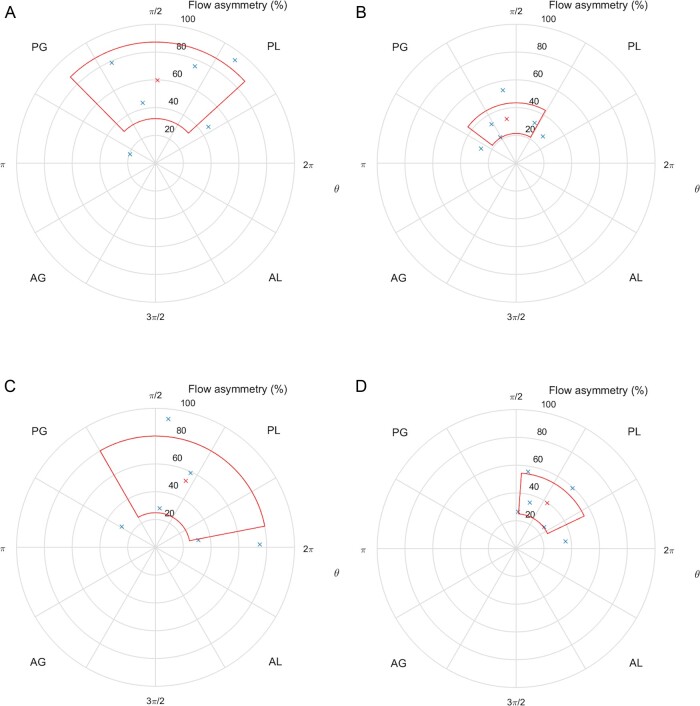
There was marked mean flow asymmetry in both the BAV and TAV patients pre-operatively. After surgery, the flow asymmetry reduced significantly in both groups (Table 1) as blood was ejected through freely mobile and fully opening cusps of a bioprosthetic valve. The flow ejected through the diseased AV, defined as the peak velocity centroid, was directed posteriorly in the ascending aorta in both groups. This centralized post-operatively, but still remained in the posterior half of the ascending aorta in both groups (Figure 4). The velocity profile in both groups was narrow pre-operatively, as blood passed through a narrowed AV. Post-operatively, the valve was wider, so blood was seen to move with less hindrance through the new valve. Flow dispersion echoed this behaviour (Table 1). No group pattern or in-between group difference in blood flow pattern was observed before or after surgery.

Table 1.

Summary of mean flow asymmetry and mean flow dispersion

	Patient group
	BAV		TAV
	Pre-operatively	Post-operatively	Pre-operatively	Post-operatively
Flow asymmetry	59.3 ± 27.5% (19.5–93.6%)	32.4 ± 11.0% (21.8–53.4%)	52.5 ± 27.6% (28.2–92.8%)	39.7 ± 14.6% (25.5–59.5%)
Flow dispersion	12.4 ± 6.3	53.6 ± 12.7	27.1 ± 16.7	56.7 ± 11.1

BAV, bicuspid aortic valve; TAV, tricuspid aortic valve

Figure 4.

(A) Position of peak velocity centroids (blue crosses), expressed as flow asymmetry (%), mean (red cross), and standard deviation (red area) in a cross-section of the STJ in the pre-operative BAV group. Coordinates are polar, with θ = 0° at the junction of the AL and PL quadrants. AG, anterior-greater curvature; AL, anterior-lesser curvature; PG, posterior-greater curvature; PL, posterior-lesser curvature. (B) Position of peak velocity centroids (blue crosses), expressed as flow asymmetry (%), mean (red cross), and standard deviation (red area) in a cross-section of the STJ in the post-operative BAV group. (C) Position of peak velocity centroids (blue crosses), expressed as flow asymmetry (%), mean (red cross), and standard deviation (red area) in a cross-section of the STJ in the pre-operative TAV group. (D) Position of peak velocity centroids (blue crosses), expressed as flow asymmetry (%), mean (red cross), and standard deviation (red area) in a cross-section of the STJ in the post-operative TAV group.

We were unable to achieve a satisfactory correlation (within 10% difference) between our outflow boundary condition and the physiological values in many of the cases. This applied to BP and cardiac output (CO). In turn, this meant that we were unable to calculate mean WSS for all cases. Pre-operatively, we found that mean WSS was greatest along the greater curvature of the ascending aorta—3 Pa compared to 1 Pa in the lesser curvature. We were unable to make a comparison with post-operative data. The reasons for this are described below.

Discussion

Our results, although limited, reflect what would be expected from replacing a diseased AV with one where the valve cusps open widely and freely. There was a marked reduction in mean flow asymmetry post-operatively, although it did not normalize. Healthy volunteers have been found to have a flow asymmetry of 4.7 ± 2.1%.²⁷ These results suggest that replacing the AV may reduce any haemodynamic forces that contribute to aneurysm formation. However, the sample size is too small to draw this conclusion. The small sample size likely contributed to the inconclusive findings of blood flow pattern too.

Even though we were unable to compare pre- and post-operative values of mean WSS, we found that it was larger and asymmetrically distributed along the greater curvature of the ascending aorta pre-operatively. This is echoed in other studies¹⁷ and corresponds to areas of wall thinning and aneurysm formation.²⁰

In all experimental methods, results must be checked against what is expected or actual physiological values. When manually segmenting the velocity data, we found that the resulting velocity magnitude and flow rate often corresponded to the real physiological values, but there was often a discrepancy in the CO. Despite repeating the segmentation, the generated CO often varied from the previous attempt and from the measured CO. This has two likely explanations. We used the validated MRI reporting software cvi42 to calculate the CO from our PC-MRI data and found that it often gave us a CO that better corresponded to that measured from calculating the left ventricular volumes in end-diastole and systole. This lead us to conclude that there was a problem with the code written for Matlab, related to its ability to interpret vessel boundaries in both the magnitude and velocity images. The CO discrepancy may also be attributed to the level of the aorta, the STJ, at which we chose to record the flow data. In some cases, it was likely too close to the native and prosthetic valve, which may have given rise to an underestimation of the velocities here and therefore the CO.³³ As we were unable to generate a reliable CO for our subjects, we were unable to calculate reliable values of WSS.

Although CFD is being applied more widely to help solve clinical problems, our experience has shown difficulties with the modelling. These need to be solved before a method involving CFD can find a wider clinical application.

We have identified some of the problems with our method. The first pertains to the level of the aorta chosen to record the flow data. It is recognized that high velocities, as generated by stenosed valves, lead to velocity displacement and to an underestimation of CO.³³ If the valve cusps are caught in the recording (as seen in Figure 3B) this also gives rise to inaccurate flow acquisition and CO measurement. Recording flow at the STJ may therefore lead to an underestimation of CO. This could be overcome by recording flow higher up the aorta, but not too high to lose flow information in the ascending aorta, the area of particular interest in BAV disease. The same caveat applies to patients with a prosthetic aortic valve as artefact and signal drop-out will also impact flow measurements and therefore CO calculations, as well as anatomic data.

Secondly, there was a problem with the Matlab code written to process the velocity data from the PC-MRI sequence. The manual segmenting of the velocity data at regular intervals of the cardiac cycle showed a large variation in output (peak velocity, flow rate, and CO) in between attempts for the same patient. This is either attributed to the programme’s ability to read pixel intensity or distinguish velocity magnitude and vectors.³⁴ Commercial software, such as cvi42,³⁵ exists that can perform this function. Future versions of CRIMSON look to have this function built into the software.

The third problem is that the method involves multiple manual steps, which will differ based on the user, introducing errors and ultimately, lead to a cumulative error impacting the results.

The creation of the anatomical model, or defined domain, required several steps. Firstly, the user places the position of the centreline, it is not an automated process based on pixel density to map the surface area and calculate its centre position. The subsequent vessel segmentation involves identifying the vessel boundary visually, where differences in pixel density, related to contrast content, are used to detect vessel boundaries. During this process, the user can see both a contrast and non-contrast cross-section of the vessel. Accordingly, the user can choose to draw the segment just inside the vessel wall, on the vessel wall, just outside the vessel wall, or anywhere in between. For example, creating two models where the descending aorta outlet radius differs by 6 × 10⁻⁴ m, generates a difference in SBP of 1333 Pa (10 mmHg). The spacing in between the generated segments also dictates the smoothness and angulation of the vessel. Feedback from our bioengineering collaborators suggests that surgeons generate more accurate vessel models than others. Although the generated anatomical model is checked for accuracy against the MIPs, there is scope for error. The segmentation step could be automated through thresholding and should be the method used in future work in this field, enabling repeatability and consistency.

Image segmentation involves object recognition and delineation. Manual image segmentation is influenced by time and reproducibility. The more accurate the segmentation, the more detailed images are required and this takes time to segment as ever more data is acquired with ever more sophisticated imaging techniques. Reproducibility is affected by inter- and intra-operator variability, influenced by the differences in interpreting the image and performing the segmentation task.³⁶ The solution is automating the segmentation process and many examples of this process exist.³⁷ Yet in many instances automated segmentation techniques are still inaccurate or lack sufficient anatomical detail and are therefore substituted by a degree of manual input.³⁸

The code written for the FEA assumed a textbook aortic arch with three head and neck vessels—the IA, LCCA, and LSA. However, natural variations in arch anatomy exist. For two patients in our cohort, we made approximations in the anatomical model to fit the code. An example of this is a patient with a so-called bovine aortic arch, where the IA and LCCA share an origin on the aortic arch. We separated the two vessels in our model, as our FEA code was written for three vessels originating in the arch. This will have impacted the results and how well they describe the real physiology. In order that patient anatomy and physiology is accurately reflected in the FEA, the number of outflow boundary conditions would need to be adjusted for each case deviating from a standard model.

Artefacts from prosthetic valves cause signal interference and drop-out, which impacts the origin of the anatomical model as well as flow measurements. This problem is easily overcome, as discussed above, but needs to be taken into consideration and accounted for.

Our method involved flow measurement from 2D PC-MRI to measure blood flow and velocity at a given plane along the aorta. This plane was at the level of the STJ. Incorrect placement of the MRI acquisition plane can result in underestimation of peak velocities, which could also introduce error. Some units use 4D flow MRI, or 3D cine PC-MRI, to measure flow velocities in all dimensions. Although this method allows calculation of WSS without the need for CFD, the accuracy of it and other haemodynamic variables is influenced by the MRI scan protocol. Wall shear stress could be underestimated due to spatial resolution and noise.³⁹ Irrespective of the imaging used, it is vital that any variables calculated are checked against and correlate with in vivo physiology to ensure reliable values.

We assumed a system with a Newtonian fluid. Blood, however, is a non-Newtonian fluid. Shear-thinning generalized Newtonian models, also known as non-Newtonian models, have been suggested to model the non-Newtonian behaviour of blood. When the shear rate is greater than 50 s⁻¹, these models approach the behaviour of a Newtonian fluid and justify the Newtonian assumption in larger vessels.⁴⁰

Conclusion

We undertook research with the aim of studying the behaviour of blood flow in the ascending aorta in patients with stenosed BAV and TAV before and after isolated tissue aortic valve replacement surgery. Even though we were able to show a normalization of flow asymmetry and dispersion along with widening of the velocity profile post-operatively in both the BAV and TAV groups, we were unable to calculate and simulate other variables of interest. Despite this, we have chosen to share our experience in order that developments in this area may continue.

The multistep process described has associated errors at each step. In order to vastly reduce the process requires automation. Once accurate anatomical and velocity models can be created in a reliable and reproducible manner, interrogation of haemodynamic behaviour of a system can be undertaken with confidence.

Our study results are modest, but our experience is nonetheless relevant to develop the methodology for computer simulation of physiological systems. We will continue to develop this work and hope that our experience can encourage others to do the same.

Conflict of interest: none declared.

Data availability

The data underlying this article will be shared on reasonable request to the corresponding author.