Real-time imputation of missing predictor values in clinical practice

Abstract

Aims

Use of prediction models is widely recommended by clinical guidelines, but usually requires complete information on all predictors, which is not always available in daily practice. We aim to describe two methods for real-time handling of missing predictor values when using prediction models in practice.

Methods and results

We compare the widely used method of mean imputation (M-imp) to a method that personalizes the imputations by taking advantage of the observed patient characteristics. These characteristics may include both prediction model variables and other characteristics (auxiliary variables). The method was implemented using imputation from a joint multivariate normal model of the patient characteristics (joint modelling imputation; JMI). Data from two different cardiovascular cohorts with cardiovascular predictors and outcome were used to evaluate the real-time imputation methods. We quantified the prediction model’s overall performance [mean squared error (MSE) of linear predictor], discrimination (c-index), calibration (intercept and slope), and net benefit (decision curve analysis). When compared with mean imputation, JMI substantially improved the MSE (0.10 vs. 0.13), c-index (0.70 vs. 0.68), and calibration (calibration-in-the-large: 0.04 vs. 0.06; calibration slope: 1.01 vs. 0.92), especially when incorporating auxiliary variables. When the imputation method was based on an external cohort, calibration deteriorated, but discrimination remained similar.

Conclusions

We recommend JMI with auxiliary variables for real-time imputation of missing values, and to update imputation models when implementing them in new settings or (sub)populations.

Introduction

The identification and treatment of patients at increased risk for disease is a cornerstone of personalized and stratified medicine.^1–3 Often, identification of high-risk patients involves the use of multivariable risk prediction models. These models combine patient and disease characteristics to provide estimates of absolute risk of a disease in an individual.^4–8 For example, prediction models for cardiovascular disease such as Framingham heart score (FHS),⁹ HEART score,¹ ADVANCE,¹⁰ Elderly,¹¹ and SMART¹² are well-known examples.¹³ Additionally, cardiovascular guidelines recommend use of prediction models integrated in computerized decision support systems (CDSS), to support guideline adherent, risk-informed decision making.^1,13

When applying a risk prediction model in real time, which constitutes its application to individual patients in routine clinical practice, one needs to have the individual’s information (values) on all predictors in the model Otherwise no absolute risk prediction by the model can be generated, restricting its use in situations when a physician is unable to acquire certain patient measurements. For example, for cardiovascular risk assessment, prediction models require complete information typically on age, sex, smoking, co-morbidities, blood pressure, and lipid levels.¹⁴ With the increased availability of large databases with information from electronic healthcare records (EHRs), automated implementation, and use of risk prediction models within CDSS using routine care (EHR) data has gained much interest.^15–19 However, the use of EHR databases faces many challenges, notably the incompleteness of data in the records.^19–22 The usability of a prediction model may thus still be limited in clinical practice if its implementation cannot standardly handle missing predictor values in real time. A detailed example is given in Box 1.

Box 1 An example of real-time imputation in an individual patient

Example: A patient visits their physician for a regular check-up. The patient and physician have access to a clinical decision support system that provides information on previously ordered test results (automatically retrieved from a registry). The physician would like to know the 10-year risk for the patient to suffer from a cardiovascular event, in order to determine whether any lifestyle changes or preventative therapies are needed. A calculator to determine this risk (e.g. the pooled cohort equations) is incorporated in the clinical decision support system, but requires complete information on several patient characteristics, including their BMI, cholesterol levels, and blood pressure. Many of these predictors are directly available (e.g. age, gender) at the visit. However, for some patients, important lab results (e.g. LDL cholesterol) are yet unknown or outdated (e.g. when retrieved from the registry). It is then not possible to determine the absolute risk of CVD for these patients. Our algorithm provides a substitute value for the missing LDL-cholesterol in real-time, enabling the calculation of a risk estimate ‘on the spot’.

A variety of strategies have been developed for daily practice to handle missing predictor values in real time.^23,24 Imputation strategies are of interest since they allow for direct use of well-known prediction models in their original form. In short, imputation substitutes a missing predictor value with one or more plausible values (imputations). In its simplest form, these imputations solely rely on the estimated averages of the missing variables in the targeted population. Therefore, they reflect what is known about the average patient. These simple methods can be applied directly in real-time clinical practice, provided that summary information (e.g. mean predictor values) about the targeted population is directly available. Additionally, imputations can account for the individual patient’s observed predictor values by making use of the estimated associations between the patient characteristics in other patients. In that case, the imputations reflect all what is known about the specific individual at hand. Usually, the implementation of more complex imputation strategies requires direct access to the raw data from multiple individuals, which is typically problematic in clinical practice (e.g. due to operational or privacy constraints). As such, alternative strategies are required to make the imputation model applicable in real-time clinical practice.

Although real-time imputation of missing predictor values in clinical practice offers an elegant solution to generate predictions in the presence of incomplete data, the accuracy of these predictions may be severely limited if imputed values are a poor representation of the unobserved predictor values. In particular, problems may arise when (i) the imputation procedure does not adequately leverage information from the observed patient data, and (ii) if the estimated population characteristics used to generate the imputation(s) poorly represent the population to which the individual patient belongs. It is currently unclear how these novel real-time imputation methods influence the accuracy of available prediction models.

In this article, we explicitly focus on the relatively new area of real-time imputation, which has not been studied often before in similar literature. Most similar studies that address missing data consider and attempt to halt the onset of missing data in a particular dataset with missing values in study individuals, rather than a missing predictor in a single individual that is encountered in real-time clinical practice. Briefly, we investigate the performance of these two real-time imputation methods to handle missing predictor values when using a prediction model in daily practice. We evaluated both the accuracy of imputation and the impact of imputation on the prediction model’s performance. Furthermore, transportability of the imputation procedures across different populations was empirically examined in two cardiovascular cohorts.

Methods

Short description

We conducted a simulation study to evaluate the impact of real-time imputation of missing predictor values on the absolute risk predictions in routine care. Hereto, we considered two large datasets and two real-time imputation methods. The datasets considered were the ongoing Utrecht Cardiovascular cohort–Cardiovascular risk management (UCC-CVRM) and the Utrecht Cardiovascular cohort–Secondary Manifestation of ARTerial disease (UCC-SMART) study.^25,26 Both studies focused on cardiovascular disease prevention and included newly referred patients visiting the University Medical Center (UMC) Utrecht for evaluation of cardiovascular disease.^25,26 Baseline examinations (i.e. predictors) for the UCC-CVRM included only the minimum set as suggested by the Dutch Cardiovascular Risk Management Guidelines.²⁷

Imputation methods

We considered mean imputation (M-Imp) and joint modelling imputation (JMI).^28,29 Mean imputation was chosen as a comparison due to its straightforward implementation and extensive use during prediction model development and validation.^30–33 A major advantage of mean imputation is that it does not require information on individual patient characteristics and can be implemented without much difficulty in daily clinical practice. Using mean imputation, missing predictor values are simply imputed by their respective mean, usually from a representative sample (e.g. observational study). JMI was chosen because it allows to personalize imputations by adjusting for observed characteristics. To this purpose, JMI implements multivariate methods that have extensively been studied in the literature.^28,29,34,35 Some modifications are required to implement JMI for real-time imputation, these have been discussed previously.²³ In JMI, missing predictor values are imputed by taking the expected value from a multivariate distribution that is conditioned on the observed patient data. Implementations of JMI commonly assume that all variables are normally distributed, as this greatly simplifies the necessary calculations. This method then minimally requires mean and covariance estimates for all variables that are included as predictors in the prediction model from a representative sample (e.g. observational study). As an extension to JMI, we also consider that additional patient data (auxiliary variables) are available and can be used to inform the imputation of missing values (denoted as JMI^aux).³⁶

All imputation methods can be directly applied to individuals and only require access to estimated population characteristics (i.e. mean and covariance estimates of the predictors) to account for missing predictor values. For both imputation methods, the required population characteristics are easily stored and accessible in ‘live’ clinical practice within any accompanying CDSS. The outcome is excluded from the imputation procedure as this information is not available when imputing the missing predictor values, and is the target of the prediction model. The corresponding source code is available from the Supplementary material online, Appendix E.

Study population

The UCC-CVRM sample consisted of 3880 patients with 23 variables and the UCC-SMART study consisted of 12 616 patients with 155 variables. Some patient values were missing in UCC-CVRM (for 1057/3880 patients) and in UCC-SMART (for 2028/12 616 patients). For the purpose of our methodological study, we had to have complete control over the patterns of missing predictor data and the true underlying predictor values, and needed to start with a fully observed data set that could be considered as the reference situation. To that end, for each dataset separately, we imputed all missing data once using Multiple Imputation by Chained Equations (for UCC-SMART) and nearest neighbour imputation (for UCC-CVRM).³⁴ These then completed data sets formed the reference situation after which missing predictor values were generated according to various patterns (see below). Table 1 provides an overview of the completed variables in both cohorts, and how they were subsequently used in our simulation study. To assess the relatedness between UCC-CVRM and UCC-SMART, we calculated the membership c-statistic,³⁷ which ranges between 0.5 (both samples have a similar case-mix) and 1 (the case-mix between both samples does not have any overlap). We found a membership c-statistic of 0.86, which indicates that the population characteristics of UCC-CVRM and UCC-SMART differ greatly.

Table 1.

General characteristics of the study populations

	UCC-SMART Mean (SD) or n/total (%)a	Role	UCC-CVRM Mean (SD) or n/total (%)b	Role
Age (years)	56.28 (12.45)	Predictor	61.7 (18.18)	Predictor
Gender (1 = male)	8258 (65.50)	Predictor	1987 (51.21)	Predictor
Smoking (1 = yes)	3560 (28.24)	Predictor	363 (9.36)	Predictor
SBP (mmHg)	144.67 (21.58)	Predictor	142.75 (24.24)	Predictor
TC (mmol/L)	5.11 (1.37)	Predictor	5.07 (1.24)	Predictor
HDL-c (mmol/L)	1.27 (0.38)	Predictor	1.36 (0.36)	Predictor
DM (1 = yes)	2299 (18.23)	Predictor	755 (19.46)	Predictor
AD (1 = yes)	8332 (66.09)	Predictor	705 (18.17)	Predictor
LDL-c (mmol/L)	3.15 (1.22)	Auxiliary	3.08 (1.27)	Auxiliary
HbA1c (mmol/mol)	3.69 (0.20)	Auxiliary	3.66 (0.22)	Auxiliary
MDRD (mL/min/1.73 m2)	79.90 (19.54)	Auxiliary	81.79 (24.56)	Auxiliary
History of CVD (1 = yes)	8134 (64.51)	Auxiliary	1971 (50.80)	Auxiliary
Time since 1st CVD event (years)	2.37 (5.93)	Auxiliary	4.642 (8.06)	Auxiliary
MPKR (mg/mmol)	4.10 (13.71)	Auxiliary	NA	None
CRP (mg/L)	0.71 (1.13)	Auxiliary	NA	None
AF (1 = yes)	164 (1.30)	Auxiliary	NA	None
LLD (1 = yes)	6836 (54.22%)	Auxiliary	NA	None
PAI (1 = yes)	6805 (53.97%)	Auxiliary	NA	None

AD, antihypertensive drugs; AF, atrial fibrillation, lipid-lowering drugs; DM, diabetes mellitus; HbA1c, glycated haemoglobin; HDL-c, high-density lipoprotein cholesterol; LDL-c, low-density lipoprotein cholesterol; MDRD, modification of diet in renal diseases; MPKR, micro-protein/creatinine ratio; PAI, platelet aggregation inhibitors; SBP, systolic blood pressure; TC, total cholesterol.

^aAfter multiple imputation by chained equations.b After k-nearest neighbor imputation.

Simulation study

We performed four simulation studies to investigate the impact of real-time predictor imputation on absolute risk predictions (Figure 1). In the first simulation, we considered the ideal situation where a (new) patient stems from the same population (i.e. UCC-SMART) as the one that is used to develop the prediction model, to derive the population characteristics, and to test the accuracy of individual risk predictions after the real-time imputations. In the second simulation, we considered a less ideal situation where imputations are based on the characteristics from a different, but related, population (i.e. UCC-CVRM). This simulation mimics the situation where development data are unavailable (or otherwise insufficient) to inform the imputation procedure, and thus assesses the transportability of the imputation model. In the third simulation, we investigated the situation where the estimated population characteristics underlying the imputations are derived from an external cohort (UCC-CVRM) and subsequently updated using local data (from UCC-SMART). This resembles a situation in which a small amount of local data is available, though insufficient to entirely inform the real-time imputation procedure. In the final simulation, we considered the most extreme scenario where three different populations are used to derive a prediction model (Framingham Risk Score⁹) the imputation model (UCC-CVRM), and to test the accuracy of the real-time imputations on the individuals’ absolute risk predictions (UCC-SMART). This simulation mimics a more common predicament in which local data is insufficient to inform the imputation procedure and there is no access to the data from which the prediction model had been developed.

Figure 1.

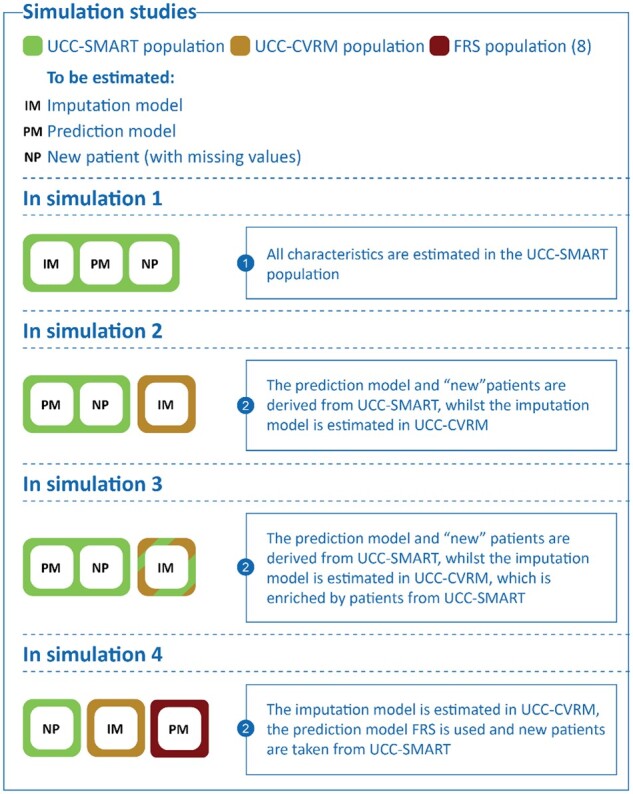
The simulation studies illustrated.

In all simulation studies, we considered UCC-SMART as the target population. For Simulations 1–3, we adopted a leave-one-out-cross-validation (LOOCV) approach to develop the prediction model, to derive the population characteristics, and to evaluate the accuracy of risk predictions. This procedure ensures that independent data are used for the evaluation of risk predictions. In the LOOCV approach, both the prediction model imputation model were derived from all but one patient (leave-one-out) of UCC-SMART. In the remaining hold-out patient, one or more predictor variables were then set to missing (see Figure 2 for an overview of which sets of predictor values were set to missing). The leave-one-out procedure was repeated until all patients had been removed from UCC-SMART exactly once (Figure 3).

Figure 2.

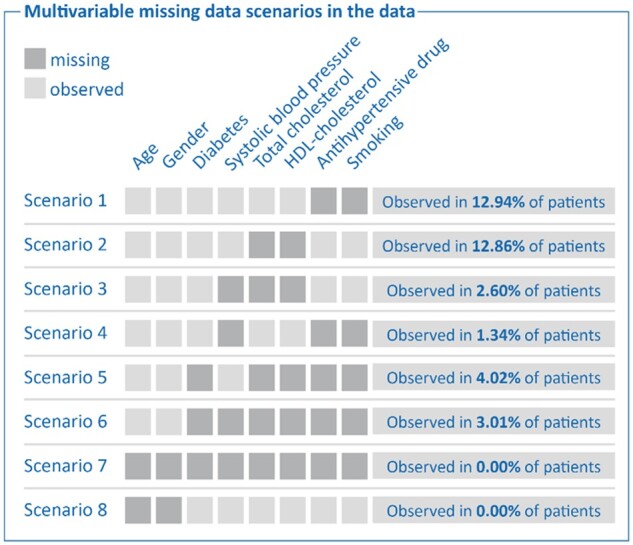
Multivariate scenarios of missing predictor values observed in UCC-CVRM.

Figure 3.

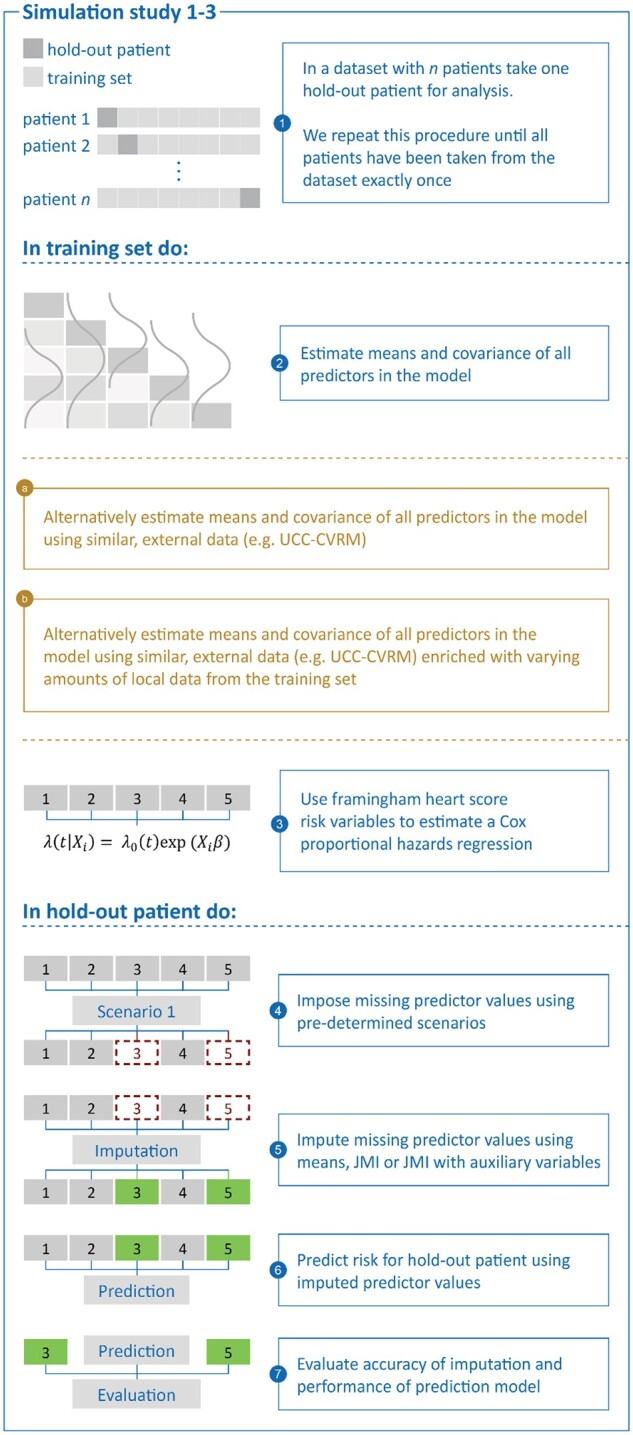
Simulation study 1–3 in detail.

LOOCV was not needed for the 4th simulation as each task (prediction model development, derivation of population characteristics, and evaluation of risk predictions) involved a different dataset (Figure 4).

Figure 4.

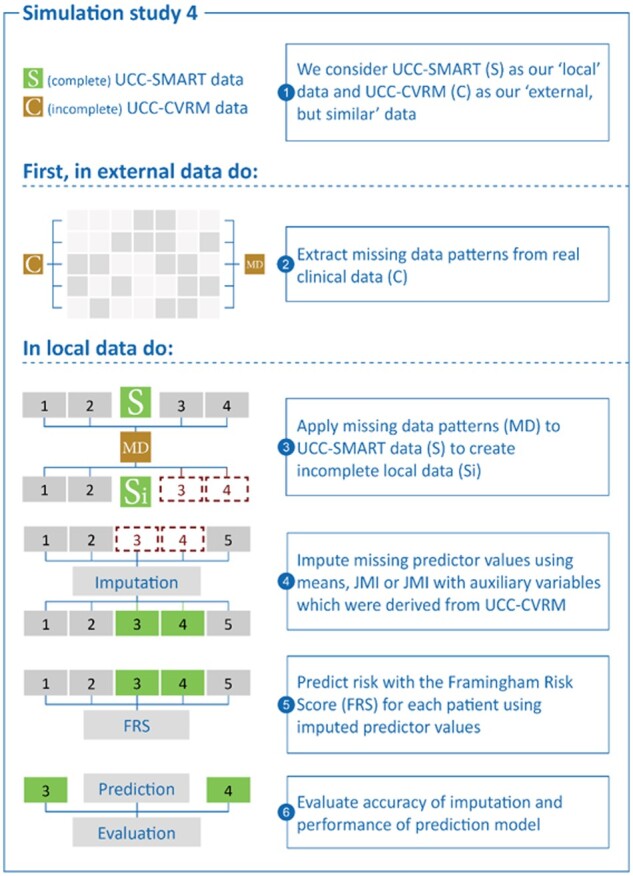
Simulation study 4 in detail.

Step 1: Estimation of the prediction model

For all simulation studies, the prediction model of interest was a Cox proportional hazards model predicting the onset of cardiovascular disease or coronary death. This model was derived in the LOO (leave-one-out) subset of UCC-SMART using predictors from the original FRS (Simulations 1–3), or retrieved from the literature (Simulation 4). A detailed description of how the prediction models were fit and the R code is listed in Supplementary material online, Appendix E. As a sensitivity analysis, we fitted a Cox regression model with only age and gender as predictors and included a scenario where, though unrealistic, age and gender were missing.

Step 2: Estimation of the population characteristics

We estimated the population characteristics necessary for the real-time missing data methods (i.e. the imputation models) in the following data (Figure 1):

• in the entire LOO subset of UCC-SMART (Simulation 1),

• in the entire dataset of UCC-CVRM (Simulations 2 and 4), and

• in the entire dataset of UCC-CVRM, plus a random sample of the LOO subset of UCC-SMART, which were simply stacked. (Simulation 3).

Step 3: Introduction and imputation of missing values

For Simulations 1–3, we set one or more predictor variables to missing in each hold-out patient of UCC-SMART (scenarios illustrated in Figure 2). To match the introduction of missing values with real-life occurrences of missingness, we included scenarios based on observed patterns of missingness in UCC-CVRM. For Simulation 4, missing values were generated for the entire UCC-SMART dataset, rather than for individual patients. We subsequently impute the missing values once using the following strategies:

1. Mean imputation. Any missing predictor value was imputed with their respective mean as estimated in Step 2.

2. JMI with observed predictors only. Each missing predictor value is replaced by its expected value conditional on the individual’s observed predictors. The expected value is derived using the estimated population means and covariances from Step 2.

3. JMI with observed predictors and auxiliary variables. Each missing predictor value is replaced by its expected values conditional on all the observed patient data. Note that this includes additional patient data that are not included as predictors in the prediction model (Table 1).

Step 4: Risk prediction and validation of model performance

The imputed missing predictor values were then used together with the observed predictor values to calculate the linear predictor η_i (where η_i = β₁x_i1 + β₂x_i2 + …) and the 10-year predicted absolute risk. The predictions from all UCC-SMART patients were then used to assess the following performance measures: (i) mean squared error (MSE) of the prediction model’s linear predictor, (ii) concordance (C-)statistic, (iii) calibration-in-the-large, (iv) the calibration slope, and (v) the decision curve.^4,16,38,39

1. The MSE of the linear predictor of the prediction model can be described as the average squared difference between the linear predictor after imputation and the true, original linear predictor (i.e. before introducing missing values).⁴⁰ The linear predictor can be described as the weighted sum of the predictors of a given patient, where the weights consist of the model coefficients.³⁸ Lower values for the MSE are preferred.

2. The C-statistic can be described as the ability of the model to discern those who have experienced an event and those who haven’t.^7,40,41 It is represented by the probability of correctly discerning who, between two random subjects, has the higher predicted probability of survival. The C-statistic is ideally close to 1.

3. Calibration-in-the-large (CITL) can be described as the overall calibration of the model (i.e. agreement between average predicted risk and average observed risk).^4,7,41,42 It is interpreted as an indication of the extent to which the predictions systematically over- or underestimate the risk; the ideal value is 0.

4. The calibration slope can be described as a quantification of the extent that predicted risks vary too much (slope < 1) or too little (slope > 1) and is often used as an indication of overfitting or lack of transportability.^7,16,40–42 The ideal value is 1.

5. The decision curve can be described as a way of identifying the potential impact of leveraging individual risk predictions for decision-making.^4,39,43 It considers a range of thresholds (e.g. 10%) to classify patients into high risk (indication of treatment) or low risk (no treatment required) and calculates the net benefit (NB) for each cut-off value. A decision curve is then constructed for three different treatment strategies: treat all, treat none, or treat according to risk predictions. Ideally, the decision curve of the latter strategy depicts consistently better NB over the complete range of thresholds.

Results

Prediction model performance in the absence of missing values

Based on internal validation by means of LOOCV, the optimism corrected c-statistic for our newly derived prediction model in UCC-SMART was 0.705. As expected, the CITL and calibration slope were near 0 (−0.0005) and 1 (0.9999), respectively. Therefore, there were no signs of miscalibrations and/or over/underfitting of the developed cardiovascular disease risk prediction model. The prediction model that was based on age and gender yielded an optimism corrected c-statistic of 0.679, with a slope of 0.9999 and an intercept of −0.00005. Finally, the refitted FRS model (as derived from the literature) yielded a c-statistic of 0.6280 and a slope of 0.8205 in UCC-SMART.

Prediction model performance in presence of missing data

Mean squared error

The MSE of the linear predictor was consistently lower when adopting JMI, as compared to M-Imp. The implementation of JMI was particularly advantageous when adjusting for auxiliary variables that were not part of the prediction model (see Table 2 for the results of Scenarios 1 and 5). For instance, when total cholesterol (TC), HDL-cholesterol (HDL-c), use of antihypertensive drugs (ADs), smoking, and diabetes mellitus (DM) were missing (i.e. Scenario 5), M-Imp yielded an MSE of 0.130, whereas the MSE for JMI was 0.126 or even 0.101 when utilizing auxiliary variables. As expected, differences in MSE were lower, when imputing other predictors that did not have a strong contribution in the prediction model, or much more pronounced when imputing important predictors (see Table 3 for the results of the sensitivity analysis with age and gender missing). This expected discrepancy results from the fact that the linear predictor is a weighted average of the predictors and the important variables simply have larger weights. When imputation was based on the characteristics of a different, but related, cohort to UCC-SMART, all imputation strategies yielded a substantially larger MSE. For instance, when TC, HDL-c, AD, smoking, and DM were missing (i.e. Scenario 5), the MSE increased from 0.130 to 0.193 for M-Imp, and from 0.1014 to 0.159 for JMI^aux. Again, JMI^aux was superior to M-Imp and JMI based on predictor variables only. As expected, the MSE for all imputation methods improved when the imputation model was based on a mixture of patients from both the UCC-CVRM (different but related) and the UCC-SMART (the target cohort for predictions). However, the lowest MSE’s were obtained when imputations were based on UCC-SMART data only.

Table 2.

Results of simulating scenarios with small and large amounts of missing data

Scenario 1 (small amount of missing data): (1) SBP, (2) smoking	Imputation methods	MSE of the LP (% difference to M-Imp)	C-index	CITL	Calibration slope
Apparent performance (reference)			0.7051	−0.0001	0.9999
Simulation 1 Local data (for informing imputation)	M-Imp	0.0702	0.6908	0.0228	0.9415
	JMI	0.0685 (−2.35%)	0.6913	0.0242	0.9552
	JMIaux	0.0649 (−7.50%)	0.6975	0.0221	0.9928
Simulation 2 External data (for informing imputation)	M-Imp	0.0802	0.6908	0.1227	0.9415
	JMI	0.0782 (−2.56%)	0.6911	0.1018	0.9269
	JMIaux	0.0801 (0.001%)	0.6902	0.1123	0.9251
Simulation 3 External data with 1.500 local patients	M-Imp	0.0746	0.6909	0.0845	0.9393
	JMI	0.0718 (−3.90%)	0.6913	0.0510	0.9278
	JMIaux	0.0708 (−5.37%)	0.6911	0.0485	0.9315
Scenario 5 (large amount of missing data): (1) TC, (2) HDL-c, (3) AD (4) smoking, (5) DM missing	Imputation methods	MSE of the LP	(% difference to M-Imp)	C-index	CITL	Calibration slope
Apparent performance (reference)			0.7051	−0.0001	0.9999
Simulation 1 Local data (for informing imputation)	M-Imp	0.1300	0.6797	0.0581	0.9199
	JMI	0.1262 (−2.98%)	0.6803	0.0549	0.9211
	JMIaux	0.1014 (−21.98%)	0.6960	0.0369	1.0052
Simulation 2 External data (for informing imputation)	M-Imp	0.1930	0.6797	0.3090	0.9199
	JMI	0.1806 (−6.42%)	0.6803	0.2797	0.9067
	JMIaux	0.1591 (−17.57%)	0.6844	0.2595	0.9475
Simulation 3 External data with 1.500 local patients	M-Imp	0.1683	0.6790	0.2418	0.9387
	JMI	0.1603 (−4.78%)	0.6792	0.2078	0.9095
	JMIaux	0.1334 (−20.72%)	0.6851	0.1677	0.9573

AD, antihypertensive drug; CITL, calibration in the large; DM, diabetes mellitus; HDL-c, HDL-cholesterol; JMI, joint modelling imputation; JMI^aux, joint modelling imputation with auxiliary variables; LP, linear predictor; M-Imp, mean imputation; MSE, mean squared error; SBP, systolic blood pressure; SBP, systolic blood pressure; TC, total cholesterol.

Table 3.

Results sensitivity analysis

Scenario 8: (1) Age, (2) gender missing	Imputation methods	MSE of the LP (% difference to M-Imp)	C-index	CITL	Calibration slope
Apparent performance (reference)			0.7051	−0.0001	0.9999
Simulation 1 Local data (for informing imputation)	M-Imp	0.7438	0.6063	0.1958	0.8225
	JMI	0.6373 (−14.32%)	0.6223	0.1616	0.8052
	JMIaux	0.4517 (−39.26%)	0.6931	0.0794	1.0828
Simulation 2 External data (for informing imputation)	M-Imp	0.8334	0.6064	−0.1037	0.8230
	JMI	0.7963 (−4.45%)	0.6116	−0.2221	0.5769
	JMIaux	0.7018 (−15.79%)	0.6721	−0.3649	0.8453
Simulation 3 External data with 1.500 local patients	M-Imp	0.792383	0.6107	−0.0205	0.8429
	JMI	0.7252996 (−9.25%)	0.6131	−0.0659	0.6480
	JMIaux	0.5739753 (−38.05%	0.6856	−0.1451	0.9654

CITL, calibration in the large; JMI, joint modelling imputation; JMI+, joint modelling imputation with auxiliary variables; LP, linear predictor; M-Imp, mean imputation; MSE, mean squared error.

C-statistic

The c-statistic was higher for both implementations of JMI, when compared with M-Imp (Table 2). Using JMI^aux further increased the c-statistic substantially, especially when important predictors (i.e. age and gender) were missing (Table 3). In this scenario, M-Imp yielded a c-statistic of 0.61, whereas JMI yielded a c-statistic of 0.62 or even 0.67 if auxiliary variables were used. Discrimination performance did not much deteriorate when imputation was based on the characteristics from a different but related population. Again, JMI^aux was superior to M-Imp and JMI based on predictor variables only. The c-statistic, for all imputation methods, improved when the population characteristics from UCC-CVRM were augmented with data from UCC-SMART. However, when an external prediction model was used in combination with external population characteristics (Simulation 4), the utilization of auxiliary variables did not seem to improve on the discriminatory ability of risk predictions (Table 4). The highest c-statistics were obtained when imputations were based on UCC-SMART data only and a locally derived prediction model was used.

Table 4.

Multivariable missing data imputation (Simulation 4): the use of an external prediction and imputation model

Combination of all missing data scenarios	Imputation methods	MSE of the LP (% difference to M-Imp)	C-index	CITL	Calibration slope
Reference when no variables are missing			0.6280	−0.0888	0.8205
Simulation 4 External prediction and imputation model	M-Imp	0.1689	0.6095	−0.1674	0.7424
	JMI	0.1585 (−6.56%)	0.6145	−0.2030	0.7549
	JMIaux	0.1334 (−26.61%)	0.6135	−0.2257	0.7495

CITL, calibration in the large; JMI, joint modelling imputation; JMI^aux, joint modelling imputation with auxiliary variables; M-Imp: mean imputation.

Calibration-in-the-large

The CITL was consistently closer to the ideal value (i.e. 0) for all scenarios when using both implementations of JMI, when compared with M-Imp. Using JMI^aux improved the CITLs further towards their ideal value (Table 2). When imputation used estimated population characteristics from UCC-CVRM, all imputation strategies had a substantially worse CITL. The performance drop was most notable as more predictors in the model were missing. Again, JMI^aux was superior to M-Imp and JMI based on predictor variables only. The CITL, for all imputation methods, improved when the population characteristics from UCC-CVRM were augmented with data from UCC-SMART. When an external prediction model was used, M-Imp yielded the ‘best’ CITL (−0.167 as opposed to −0.2030 for JMI and −0.2256 for JMI^aux; Table 4). The CITLs were closest to 0 when imputations were based on UCC-SMART data only.

Calibration slope

The use of JMI^aux improved the calibration slope as compared to M-Imp or JMI using predictor variables only (Table 2). When imputation used population characteristics from UCC-CVRM, the variability of predicted risks generally became too large (slope < 1 for all imputation methods). The performance drop was most notable as more predictors were missing. When an external prediction model was used, both JMI and JMI^aux yielded better calibration as compared to M-Imp (Table 4), although JMI^aux performed worse than JMI. The best calibration slopes were found for imputations based on UCC-SMART data only.

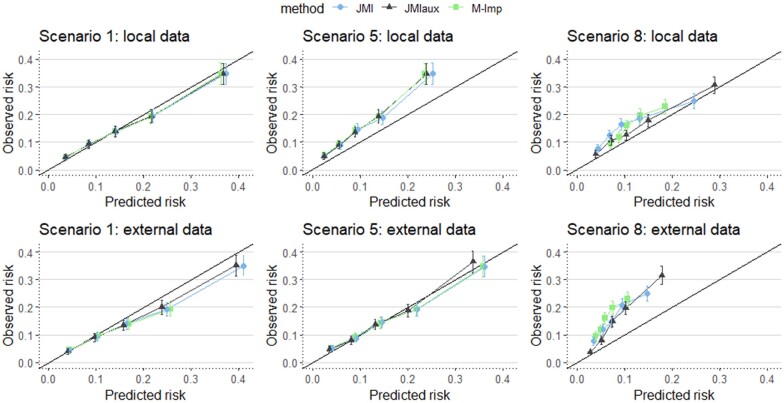
Figure 5 visualizes calibration plots for Scenarios 1, 5, and 8. It shows that when important predictors (i.e. age and gender in Scenario 8) are missing there is a notable impact on the calibration of 10-year risk predictions, especially when using external data for generating imputations. When less important predictors are missing (Scenarios 1 and 5) the differences between the imputation methods are much less pronounced in the calibration plots.

Figure 5.

Calibration plots for Scenarios 1, 5, and 8.

Decision curve

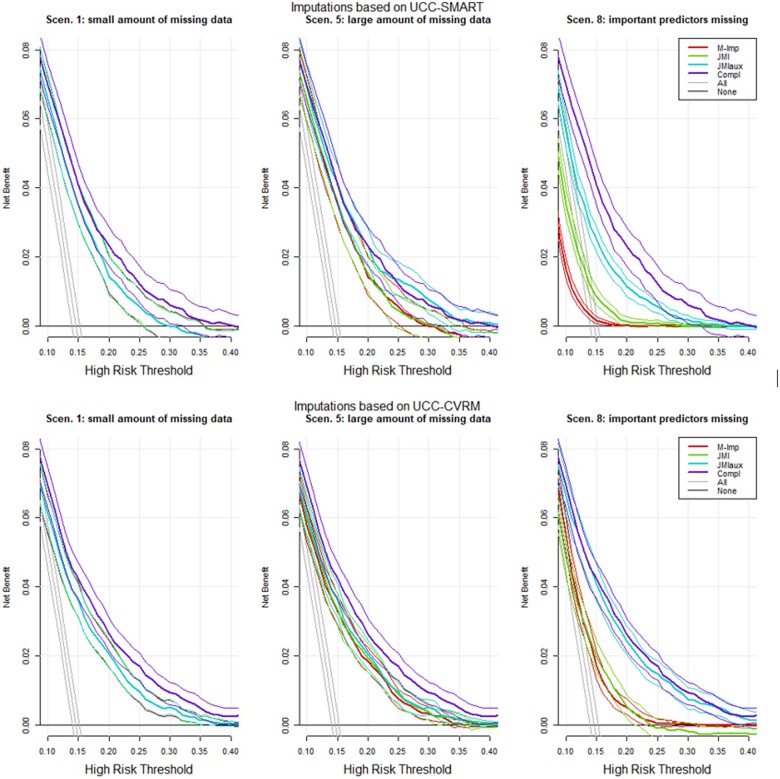
When important variables were missing, imputation through JMI with auxiliary variables yielded an improved NB over the whole range of thresholds when compared with M-Imp and JMI (Figure 6) and was substantially better than treat-all or treat-none strategies. The observed NB did not much deteriorate when imputation was based on a different, but related, dataset.

Figure 6.

Decision curve analysis Simulation 1.

A complete detailed overview of all results (e.g. all scenarios) can be found in the Supplementary material online.

Discussion

Our aim was to evaluate the impact of using real-time imputation of missing predictor values on the performance of cardiovascular risk prediction models in individual patients. We considered mean imputation and JMI to provide automated real-time imputations. Our results demonstrate that in all scenarios and for all parameters studied (c-index, calibration, and decision curve analysis) JMI leads to more accurate risk predictions than M-Imp, especially when used to impute a higher number of missing predictors (e.g. Scenario 5 for prediction of cardiovascular events). The performance of JMI greatly improved when imputations were based on all observed patient data, and not restricted to only the predictors that were in the prediction model. Finally, we found that real-time missing predictor imputations were most accurate when the imputation method relied on characteristics that were directly estimated a sample from the target population (i.e. the population for which predictions are required), rather than from an external though related dataset. In the latter case, while discriminative performance was stable, calibration clearly deteriorated (in terms of both CITL and calibration slope). This implies that the need for local updating, as is well known in clinical prediction modelling, may extend to imputation models. In practice, a prediction model is ideally developed together with an appropriate missing data method for real-time imputation. When high-quality local data are available, performance gains can be expected for that setting by local updating of both the prediction model and the imputation model.

Our findings suggest that JMI should be preferred over M-Imp for real-time imputation of missing predictor values in routine care, ideally making use of additional patient data (variables) that are not part of the prediction model. The underlying rationale, is that some variables that are highly correlated are unlikely to both end up in a prediction model (due to little added value), but are quite valuable for imputation purposes when one or the other is missing. The implementation of JMI is very straightforward, and only requires estimating the mean and covariance of all relevant patient variables in a representative sample. Imputations are then generated using a set of mathematical equations that are well established in the statistical literature.²³ As JMI does not rely on disease-specific patient characteristic and lends itself excellently for local tailoring,⁴⁴ it is considered highly scalable to a multitude of clinical settings and populations. Routine reporting of population characteristics (i.e. means and covariance) would greatly facilitate the implementation of risk prediction models in the presence of missing predictor data in daily practice and has previously been recommended to improve the interpretation of validation study results.³⁷

A limitation we observed in the data was that most of the explained variability in risk of cardiovascular disease, as defined in our study, could be inferred based on age and gender. Although additional predictors (e.g. blood pressure, cholesterol levels) somewhat improved the model’s discrimination and calibration performance, their individual added value appears small. A further limitation of the data was the lack of strong correlations between predictors other than age and gender (Supplementary material online, Appendix D). Consequently, the information available for JMI to leverage observed patient characteristics was limited. These findings are in line with earlier research, suggesting that M-Imp performs similarly to more advanced imputation methods when considering commonly encountered missing data patterns in cardiovascular routine care.⁴⁵ However, our study reveals that JMI had the advantage even under these typical but difficult settings. Gains are expected to be larger when the interrelation of predictors is stronger and especially when key auxiliary variables can be identified. Moreover, for many disease areas, risk prediction relies more strongly on a multitude patient characteristic that are more likely to be missing (e.g. certain imaging characteristics, biomarkers or genetic profiles), and JMI offers a larger advantage.

Various other aspects need to be addressed to fully appreciate these results. First, we restricted our comparison to M-Imp and JMI. Considering M-Imp was picked as a comparator, we choose JMI as it was well established in the statistical literature and permitted relatively straightforward adjustments to be applied in clinical practice via the EHR.^29,34 Other, more flexible, imputation strategies exist, and have been discussed at length.²³ These strategies generally require more complex descriptions of the population characteristics and adopt more advanced procedures to generate imputations. For this reason, their implementation appears less straightforward in routine care. A more detailed overview of the impact of using other strategies for handling real-time missing predictor value imputation is warranted. Also, the use of multiple imputation may be preferable with respect to prediction accuracy in case of models with a non-linear link function such as the Cox or logistic model, the reason is multiple imputation can correctly convey the influence of imputation uncertainty on the expected prediction. The available R code already provides in this, though in this study we explicitly choose to use single imputation. We choose single imputation due to its convenience in real-time clinical practice. The imputation process is quick, in contrast to the usually computationally expensive multiple imputation, and it presents an individual’s imputed predictor value which may be informative to the clinician. Additionally, rather than imputing a random draw, we impute the most likely value in order to be able to easily reproduce model predictions from the imputed data. Ideally, the predictions would be based on multiple imputation from the conditional distribution of the missing predictors rather than representing their conditional means. Further extensions, for example multilevel multiple imputation, may also be recommended in specific situations where the prediction model and accompanying imputation models are derived from large datasets with clustering.⁴⁶ Lastly, whilst there are many clinical settings and populations the study only considered cardiovascular risk prediction. The performance of JMI, when compared with M-Imp, might have been further emphasized had other clinical settings been considered.

In summary, this study evaluates the use of two imputation methods for handling missing predictor values when applying risk prediction models in daily practice. We recommend JMI over mean imputation, preferably based on estimated from local data and with the use of available auxiliary variables. The added value of JMI is most evident when missing predictors are associated with either observed predictor values or auxiliary variables.

Supplementary material

Supplementary material is available at European Heart Journal – Digital Health online.